Violation and Conservation of Symmetries in Atomic Systems

In the next part of this thesis, we focus on the use of the Sturm basis set for relativistic calculations. The use of the proposed method and its importance are illustrated on a series of calculations.

The Standard Model and Beyond

Parity Violation

Note that ϑ is the only parameter in EW theory (as opposed to e.g. the many parameters in the once famous string theory). Therefore, it is clear that a low-energy input, completely independent of the high-energy experiments, could help solve this problem.

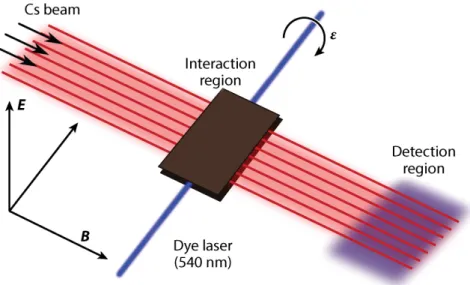
Measurement of PNC

From this expression, we can see that the biggest experimental challenge is to eliminate the magnetic transition that mimics the true PNC contribution. Finally, the PNC signal is observed as a modulation of the received signal (that is, the ratio of the second term to the first term on the right-hand side of Eq.

Calculation of PNC

They are defined by the combined spin and orbital angular momentum of the electrons, ˆJ=Sˆ+Lˆ (hence the quantum number J), the spin of the nucleus, ˆI (hence I), and the. For the electric part AelFI of the amplitude (1.4) we consider the expansion to the first order, Eq.

Recent Theoretical Works and their Shortcomings

This methodology uses the single-reference CC method for the calculation of the ground state of closed-shell systems and the equation of motion CC (EOM-CC) for the calculation of the excited states and simple open shells, see Chapter 5. Note that all these relations are completely general and hold irrespective of the specific forms of the one- and two-body operators ˆz and ˆv and spin orbitals a.

Sturmian Basis Set

Hartree-Fock Method

In this way, we ignore a significant part of the electron correlation (usually around 95% of the exact energy is obtained), but unlike, for example, the DFT method, the missing correlation contribution can be replaced by one of the post-HF methods and systematically improve the accuracy of the result. In the strictest case, we assume that the radial part is the same for all possible angular and spin parts.

Properties of HF Solutions

Given the practical importance of knowing whether a SA or an SB solution is the energy minimum for a given system, whether an HF solution exists at all, and how to obtain an HF solution, we decided to systematically analyze all closed-shell atomic systems of Mendeleev's periodic table.

Theory

Restricted Hartree-Fock Model

Here |a⟩and|b⟩ are the radial orbitals in the abstract notation; their projections on the coordinate basis are the radial functions ⟨r|a⟩= φna,la(r), cf. hˆl0 is the radial part of the hydrogenic Hamiltonian, see Eq. and the radial operators of Coulomb and exchange interaction read ˆvc=r>−1, ˆve. The non-relativistic spin and orbital RHF equations are then read off, see Eq. 3.3) The one-electron energies εa are related to the total energy via the relation.

Stability Matrix

To investigate the stability of the RHF solution, we need to solve the eigenvalue problem (we suppress here the superscript S). According to the sign of the lowest eigenvalue λ, the RHF solution is stable (if λ >0) or unstable (if λ <0).

Critical Nuclear Charge

Each mono-excitation is determined by the occupied and virtual orbitals labeled oa and oa, respectively. These orbitals are eigenstates of the Fock operator and are uniquely defined by the triples of quantum numbers (na, la, ma) and (na, la, ma), respectively.

Our Systematic Approach

Symmetry-Adapted Stability Matrix

Monoexcitations generally preserve Sz and Lz, but not S(S+ 1), L(L+ 1), and Π. Thus, the stability matrix can be factorized in terms of the total spin, the total orbital moment, and the total parity of the monoexcitations. Further factorization with respect to the total angular momentum L and the parity Π of the monoexcitations is achieved by the CG coefficients; the spin and orbital stability matrix SA reads as follows. When using SA monoexcitations, one block of the stability matrix preserves all the symmetries of the Hamiltonian.

Perturbative Series for the Eigenvalues of the Stability Matrix 26

Finally, we use this perturbative expansion of the stability matrix (or more precisely of its each block) to find the perturbative series (3.8) for the lowest eigenvalue. Note that our implementation of the perturbative approach to the stability matrix requires the introduction of so-called projectors. The total energy is then obtained by substitution of Eq. 3.11) Perturbative solution of the RHF equations.

Results and Discussion

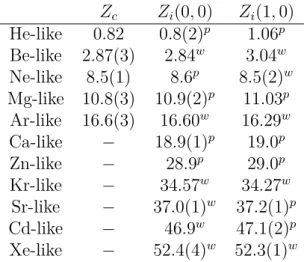
Zc is the radius of convergence of the perturbative series for the total energy of the given atom. We have analyzed all closed shell systems in Mendeleev's periodic table up to xenon-like systems. You are then only left with the radial degree of freedom; however, evaluation of the radial integrals is usually the biggest problem.

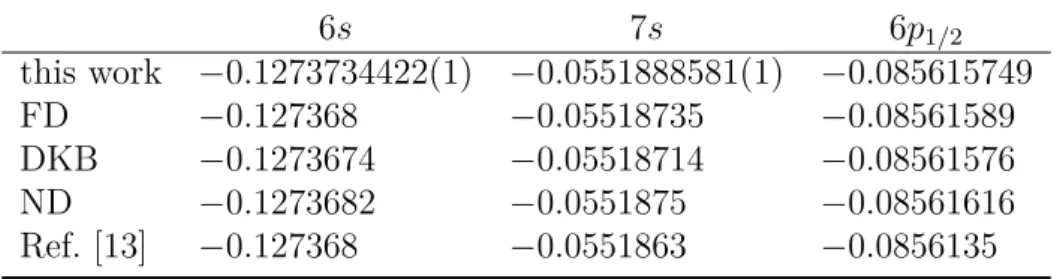
Matrix Elements in the Sturmian Basis

One-Electron Matrix Elements

The method for a numerically stable evaluation of these integrals is described in the attached article [4], see also [50]. Here we will focus on the evaluation of the integrals of two electrons, see below, as they are clearly more complicated.

Two-Electron Matrix Elements

So we reduce the double integral over four functions, Eq. 4.10) Recall that ˜Rk,l(ξ, r) are non-normalized functions, defined in Eq. First we replace the non-normalized functions (4.4) in Eq. 4.12) First, by means of fundamental commutation relations, we exchange the positions of r−l2 and the bracketed term on the lhs of (4.12). As in the case of K2, we first move rl+11 on the lhs to the left, then replace Eq. 4.11) in the lhs of the "analytical" equation modified above, and finally we find, see Eq.

Illustration on the DHF Model

• Dirac-Hartree-Fock Model
• Integrals of Motion
• Form of the Spin-Orbitals
• Roothaan Form of the DHF Equations
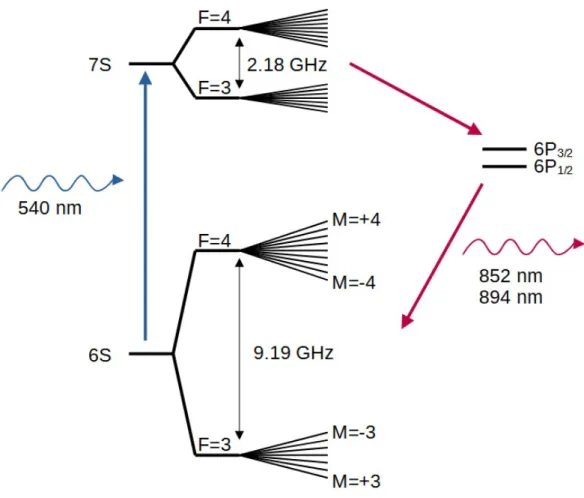
• PNC Amplitude in Cesium

The screening constant ξA is set to ξA= 1/nA, nA being the nonrelativistic principal quantum number of the corresponding shell. If we now substitute the expansions and (4.33) into the DHF equation (4.18) and project this equation onto the considered basis vectors, we obtain the Roothaan form of the DHF equations. The Hamiltonian of the one-particle valence electron is taken in the form of the Fock operator, Eq. 4.18) with (4.19) and (4.20) where we use the Z-1 core electron field obtained by solving the constrained DHF equations for the corresponding closed-shell cation, e.g.

Results and Discussion

To obtain the energy of the closed-shell cation, we perform the DHF calculation followed by the CC method to add the missing electron correlation. To calculate the energy of a one-electron open shell, we first perform a DHF calculation of the relevant closed-shell cation and then use the CI-CC method to include the extra electron and the electron correlation. In this chapter we show how to take advantage of the spherical symmetry of atoms and simplify the CC and CI methods.

Introduction

Therefore, considerable attention has been devoted to the adaptation of the CC method to spin symmetry [108, 109]. Adapting the CC method to this symmetry has, to the best of our knowledge, not been done so far and is therefore the subject of this part of this thesis. The non-trivial aspect of the symmetry fitting is that one wants the wavefunction to be fitted to the spherical symmetry and at the same time to be antisymmetric with respect to the exchange of two electrons.

Atomic Hamiltonian in the Second Quantization Formalism

However, unlike Racah, who first considers states conforming to the spherical symmetry and only then attends to permutation symmetry using coefficients of fractional parentage, we found that for computer implementation it is somewhat easier to first conform to the permutation symmetry and only then attend to of spherical symmetry. The atomic N-electron-no-pair Hamiltonian in the second quantization formalism takes the form (using Einstein's summation convention and dimensionless atomic entities with electronic coordinates scaled r(i) →r(i)/Z). 5.4) These matrix elements are antisymmetric with respect to the exchange of any index pair, i.e.

Coupled Cluster Method For Closed Shells

CCD Method in the Standard Spin-Orbital Form

Thus, based on Eq. 5.3) and (5.9), is the correlation energy in terms of the cluster amplitudes. 5.15). Using the expressions (5.1) and (5.11) for the Hamiltonian and cluster operators, respectively, the anticommutation relations (5.3) and the definition of the Fermi vacuum state, Eq. 5.9), we obtain the spin-orbital form of the coupled CC equations for the cluster amplitudes (eabrs denotes the equation for the (ab)→(rs) bi-excitation). 25tuvcdtxyefQab,uv,xyrs,cd,ef. However, for further manipulation and then for the actual programming of the CC methods, it is advantageous to keep this form.

Adaptation to the Permutation Symmetry

Adaptation to the Spherical Symmetry

If this is the case, the result is independent of the total magnetic quantum number m. But if, for example, orbitals A and B are the same, then the order requirement first enforces the constraint ma < mb. In this way, the orthogonality is preserved, and you only have to take care of the normalization.

Configuration Interaction Method for Open Shells

Adaptation to the Permutation Symmetry

Following the same reasoning as in the case of CC in chapter 5.3.2, we can change the disordered amplitudes into ordered ones.

Adaptation to the Spherical Symmetry

The equation (5.35) requires some explanation. In general, we have to distinguish three cases about three virtual radial orbitals, denoted by Q, R, S: 1) all of them are different, 2) the two are the same and the third is different, 3) all of them are the same. The second case can always be arranged so that the same orbitals are marked by R and S. In the third case, the value of Jr is irrelevant, since all the possible symmetry-adjusted states with different values ​​of Jrs are linearly dependent.

A Combined CI-CC Method for Open Shells

Adaptation to the Permutation and Spherical Symmetry . 60

Again we change firstly to the ordered and secondly to the SA amplitudes and CI coefficients; so we have

Implementation of Symmetry Adaptation

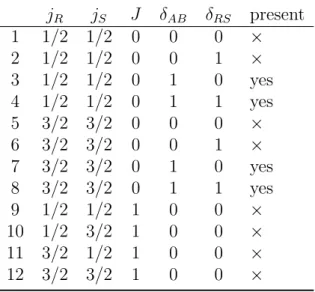
In the CCD calculation, the occupied SA orbitals are A = B = 1s1/2 and the virtual SA orbitals R, S are all the remaining ones from the above list, cf. However, the 15 possible biexcitations (AB) → (RS) only lead to for 4 types of spinor angle factors, see Tab. Note that for He-like systems jA=jB = 1/2 and therefore not listed in the table.

Computational Details

The most time-consuming part is the sum over orbital coefficients in the evaluation of two-electron integral vklij. In terms of memory, the most problematic are the final matrices to be diagonalized in the CI or CI-CC methods. The reason is simply that there are many three-particle states and even many more five-particle states that must be included in the calculation to obtain satisfactory results.

Results and Discussion

Measurement of the 6S-7S Transition Polarisability in Atomic Cesium and an Improved Test of the Standard Model. High Accuracy Calculation of the 6S-7S Parity-Preserving Transition in Atomic Cesium and Implications for the Standard Model. High-precision calculation of parity non-conservation in cesium and test of the standard model.

Stability conditions for solutions of the Hartree-Fock equations for atomic and molecular systems. Stability Conditions for Solutions of the Hartree-Fock Equations for Atomic and Molecular Systems.

Symmetry-Adapted Form of CI Method

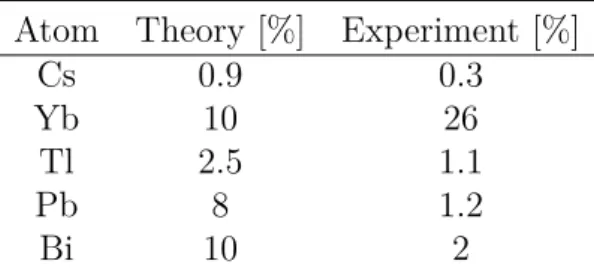
• Uncertainty in the determination of PNC
• Critical nuclear charges and spin instabilities
• Excited one-particle energies of Cs
• Hyperfine integrals for Cs
• Reduced dipole matrix elements for Cs
• PNC amplitude for Cs
• Spinor-angular configurations in He
• Number of configurations for CCD
• Number of configurations for CI

Stability of closed-shell atomic configurations with respect to variations in nuclear charge.