Modelos dinâmicos de hedging: um estudo sobre a volatilidade

FUNDAÇÃO GETÚLIO VARGAS ESCOLA DE ECONOMIA DE SÃO PAULO

GUILHERME K. P. DE AGUIRRE

MODELOS DINÂMICOS DE HEDGING: UM ESTUDO SOBRE A VOLATILIDADE

GUILHERME K. P. DE AGUIRRE

MODELOS DINÂMICOS DE HEDGING: UM ESTUDO SOBRE A VOLATILIDADE

Dissertação apresentada ao Programa de Mestrado Profissional em Economia e Finanças da Fundação Getúlio Vargas/EESP, como parte dos requisitos para a obtenção do título de Mestre em Finanças e Economia Empresarial.

Orientador:

Prof. Dr. André Cury Maiali

GUILHERME KUPPER PACHECO DE AGUIRRE

MODELOS DINÂMICOS DE HEDGING: UM ESTUDO SOBRE A VOLATILIDADE

Dissertação apresentada ao Programa de

Mestrado Profissional em Economia e Finanças da Fundação Getúlio Vargas/EESP, como parte dos requisitos para a obtenção do título de Mestre em Finanças e Economia Empresarial.

Data da Aprovação: ____/____/________ Banca Examinadora:

________________________________________ Prof. Dr. André Cury Maiali

(Orientador) FGV - EESP

________________________________________ Prof. Dr. Afonso de Campos Pinto

FGV - EAESP

________________________________________ Prof. Dr. Oswaldo Luiz do Valle Costa

Agradecimentos

Aos meus pais, pela minha educação.

Resumo

Nesta dissertação estudamos diferentes modelos de hedging para uma opção plain

vanilla comprada do tipo europeu.

Este estudo nos leva a uma análise onde a volatilidade é uma variável de extrema importância em todos os modelos abordados. De natureza incerta e muitas vezes incompreensível, a volatilidade é uma peça fundamental pelo sucesso ou fracasso de muitos agentes financeiros.

Os modelos em que trabalhamos o hedging da opção comprada são: o modelo

Black& Scholes (1976) e o moldelo de Hoggard-Whaley-Wilmott (1994).

A opção analisada é referente ao ativo base Itaú PN. Trabalhamos com uma série histórica do retorno dos preços de fechamento deste ativo de 02/01/1998 até 30/05/2011 de onde extraímos os parâmetros de volatilidade utilizados para as simulações do ativo base, gerando diferentes regimes de mercado.

Por fim, realizamos o hedging com diferentes freqüências de ajustes e diferentes

volatilidades de hedging com os modelos mencionados acima.

Abstract

In this thesis we studied diferente dinamic hedging moldels for a long position on a plain vanilla european option.

This work lead us to an analise where the volatility is a very important variable on all the models demonstrated here. From an uncertain nature and many times incomprehensive, the volatility is a fundamental key for the success or failure of many financial players.

The models the we worked our hedge was: the Black&Scholes (1976) and the Hoggard Whaley Wilmott (1994).

The following option refers to Itaú PN underlying. We worked with a time series of the return of the closing prices from this underlying from 02/01/1998 until 30/05/2011, were we extract volatility parameters used to simulate different paths with different market regimes for the underlying.

Sumário

1 Introdução………..11

1.1 Motivação para a Dissertação ...11

1.2 Objetivo da Dissertação ...12

1.3 Estrutura da Dissertaçao ...12

2 Revisão Bibliográfica...13

2.1 Conceitos Básicos ...13

2.2 Estratégias de Hedging ...17

3 Modelos Teóricos...20

3.1 Modelos de Hedging ...20

3.1.1 O Modelo de Black and Scholes………..20

3.1.2 O Modelo UVM – Uncertain Volatility Model………...21

3.1.2 O Modelo de Leland……….………...……...24

3.1.3 O Modelo de Hoggard-Whalley-Wilmott…………...………...27

3.2 Modelos para o processo do ativo base...28

3.2.1 O Modelo de volatilidade estocástica...28

3.2.1.1 O Modelo de Vasicek……….…30

3.2.1.2 O Modelo de Fitting Parameters...31

4 Métodos Numéricos...34

4.1 Método das Diferenças Finitas Explicita ...34

4.2 Simulações de Monte Carlo ...35

5 Aplicação...36

5.1 Aplicando o Modelo de Fitting Parameters...36

5.1.1 Simulações para um regime de mercado normal...36

5.1.2 Simulações para um regime de mercado nervoso...39

5.1.3 Simulações para um regime de mercado calmo...41

6 Resultados...42

6.2 Comparativo entre os modelos de Black&Scholes e Hoggaed Whalley

Wilmott...89

7 Conclusões e Pesquisas Futuras...100

7.1 Conclusões...100

7.2 Pesquisas Futuras...102

Referências Bibliográficas...104

Apêndice I...107

Apêndice I...114

Apêndice I...114

Capitulo 1

Introdução

Inicialmente, apresentamos a origem do problema que gerou a motivação da escolha do tema estudado, seguido do objetivo almejado. Na seqüência discorremos sobre a estrutura da dissertação.

1.1 Motivação para a Dissertação

Em muitas áreas de finanças que envolvem negociações de derivativos, como por exemplo, market-makers, traders ou risk manegers é de muita importância ter um

conhecimento de como apreçar um derivativo V

( )

S,t sem liquidez adequadamente.

Para se encontrar um valor de V

( )

S,t _{faz-se necessário o entendimento de algumas}

técnicas, como por exemplo, a replicação do ‘payoff’ do derivativo e o hedging para

este derivativo.

Ao estudar essas técnicas mencionadas acima e aplicá-las mediante a diferentes modelos fizemos a seguinte pergunta: qual o preço que o comprador de um derivativo sem liquidez V

( )

S,t deve pagar ao vendedor ? Que replicação ou qual

estratégia de hedging deve ser utilizada por este comprador e qual o modelo que ele

deverá utilizar para se proteger dos riscos envolvidos? Que volatilidade deve-se colocar em seu modelo? Qual o modelo mais eficiente para quando estamos em um mercado de regime “normal”, calmo ou nervoso? O que acontece quando erramos a

volatilidade de hedging? Qual o modelo mais penalizado quando isso ocorre?

Seguindo a relevância destas perguntas, consideramos uma instituição financeira que compre um derivativo de seus clientes e, no instante t₀ até o vencimento T,

essa instituição necessita adotar alguma estratégia de replicação utilizando outros ativos de liquidez no mercado para mitigar seus riscos.

Esse problema possui grande relevância para os agentes financeiros mencionados acima, pois está diretamente relacionado com a possibilidade de lucro ou prejuízo de suas operações. Pela importância na prática e na teoria acadêmica, esse tema provê a motivação para esta dissertação.

1.2 Objetivo da dissertação

O objetivo de nossa pesquisa é apresentar o problema descrito acima de forma

Desenvolvemos um algoritmo simples, exploramos bem esta situação para verificar se nossos resultados estão coerentes com o resultado de pesquisas já publicadas acerca do tema e adicionamos mais complexidade ao algoritmo no intuito de convergir com a realidade dos mercados.

Em nossas simulações, no intuito de explorar diferentes possíveis situações,

utilizamos diferentes frequências de rebalanceamento no hedging dinâmico,

utilizamos diferentes volatilidades de hedging sob regimes de mercado diferentes.

Para convergir um pouco mais com a realidade dos mercados, alteramos a volatilidade do ativo objeto para uma volatilidade estocástica e adicionamos custos de transação nos rebalanceamentos.

Através de histogramas dos resultados finais de cada situação de hedging,

buscamos compará-los de forma objetiva sob o aspecto de propriedades estatísticas e dominância estocástica.

1.2 Estrutura da Dissertação

Esta dissertação está estruturada da seguinte forma. No capítulo 1 apresentamos a motivação para o desenvolvimento da dissertação, definimos o objetivo a ser atingido com as pesquisas realizadas e descrevemos a estrutura do trabalho.

No Capitulo 2, apresentamos conceitos básicos e uma breve revisão teórica da literatura sobre o tema hedging.

No Capítulo 3, apresentamos com mais detalhes os modelos de Black&Scholes (1976), e o modelo de Hoggard Whalley Wilmott (1994), utilizados para as

comparações de estratégias de hedging.

Além dos modelos de hedging, apresentamos os modelos que utilizamos para gerar

diferentes regimes de mercado onde o hedging é executado, ou seja, os modelos

utilizados para simular a dinâmica do ativo base. Para isso utilizamos o modelo do movimento browniano geométrico, o modelo de volatilidade estocástica de Vasicek e o modelo de volatilidade estocástica empírica, ou “fitting data”.

encontrar o delta do ativo base no modelo Hoggard Whalley Wilmott utilizamos o método de diferenças finitas explicita.

No Capítulo 5, apresentamos a aplicação do modelo de volatilidade estocástica empírica.

No Capítulo 6, apresentamos o resultado de cada estratégia de hedging sob a forma

de histograma das distribuições dos resultados, o gráfico de dispersão dos P&L’s

sobre as volatilidades realizadas com diferentes volatilidades de hedging e

diferentes freqüências de rebalanceamentos, além da dominância estocástica entre os modelos.

No Capítulo 7, apresentamos de forma objetiva a conclusão de nossa pesquisa e oportunidades futuras que derivam diretamente do que foi pesquisado aqui.

Capitulo 2

Revisão Bibliográfica

Neste capitulo, no item 2.1 fazemos uma breve revisão do tema hedging e alguns

conceitos matemáticos básicos utilizados para desenvolver os modelos de hedging,

no item 2.2 apresentamos alguns trabalhos já realizados sobre este tema.

2.1 Conceitos Básicos

Assumindo primeiramente que existe oportunidade de arbitragem de volatilidade no mercado de opções, ou seja, digamos que o mercado está negociando uma opção com uma determinada volatilidade implícita e nós estamos com uma estimativa de volatilidade para o ativo objeto até o vencimento maior que a volatilidade implícita. Se nós estivermos certos, existe uma oportunidade de arbitragem que resultará em lucro. Este lucro depende de diversas variáveis, entre elas a volatilidade de hedging

utilizada no modelo, o próprio modelo utilizado para realizar o hedging da opção, a

freqüência dos ajustes, além de outras.

Em mercados organizados, um derivativo financeiro V é um instrumento no qual seu

valor depende de outras variáveis menos elaboradas, no qual iremos chamar de ativo base. S

( )

t será o vetor de preços do ativo base a cada instante de tempo t e

( )

S t

V , , é a função do derivativo de nosso interesse.

Admitimos que podemos estruturar em um portfólio Π _{sendo uma combinação de} V

e Sde forma que minimize o risco de Π. Chamaremos de

(

ut,u0,t

)

_0≤t≤T as possíveis estratégias de hedging para o portfólio Π sendo que i

t

u representa o número de

ativos de risco i, e u_t0 representa o montante investido no ativo livre de risco

existente em Π. Esta estratégia gera o seguinte fluxo de caixa até o vencimento T

de V : F1

( ) ( ) ( )

St1 ,F2 St2 ,F3 St3 ,...FN

( )

StN .

Deste modo, temos que o valor de V seja:

( )

= ( )

( )

= − − j j t j N j t t r S F e E t S V 1 , (2.1)

Ao realizar o hedging de um derivativo V na situação em que compramos a call por

uma volatilidade implícita inferior a volatilidade do ativo base (suponhamos, por enquanto, que sabemos que a volatilidade realizada do ativo base será maior que a volatilidade implícita da opção). Nesta situação, certamente ganharemos dinheiro e nosso lucro dependerá da trajetória realizada pelo ativo objeto na vida da opção, ou

seja, o fluxo de caixa Firá depender de todos os valores assumidos pelo vetor de

preços S

( )

t , ou seja, da dinâmica de S

( )

t .

Para melhor compreender a dinâmica deste P&L, vamos chamar de i

V _{o valor da}

opção que compramos com a volatilidade implícita de mercado, e a

V o valor ‘justo’

da opção incorporando uma volatilidade realizada maior ao invés da volatilidade

implícita. Nosso lucro deveria ser exatamente a i

V

V − .

S dt dX dS σ µ + = (2.2)

Ao fazer o hedging da opção comprada encontramos o primeiro problema tratado

em nosso trabalho. Qual a volatilidade de hedging iremos colocar no modelo Black&

Scholes? A marcação a mercado de nossa estratégia de hedging está resumida na

expressão (2.3): Sdt S V dt S V V r dS S V dV a a i a i ∂ ∂ − ∂ ∂ − − ∂ ∂ − (2.3)

Primeiramente, como ainda estamos trabalhando com uma forte premissa de que sabemos qual a volatilidade futura do ativo objeto, que é a volatilidade realizada, vamos trabalhar com esta volatilidade no modelo. Assim temos a marcação a mercado de nosso portfólio a cada instante de tempo dt:

Sdt S V dt S V V r dS S V dV a a a a a ∂ ∂ − ∂ ∂ − − ∂ ∂ − (2.4)

Aplicando o lema de Itô em (2.3), temos:

(

)

(

)

dt

S V S dt S V S V S SdX S V S V Sdt S V SdX S V S V dt V V r dt S V S dt S V S V S dt t V Sdt S V dt S V V r dS S V dt S V S dS S V dt t V i a i a i a i a a i a i i a i i a a i a i i i 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 2 1 ∂ ∂ − + ∂ ∂ − ∂ ∂ + ∂ ∂ − ∂ ∂ = ∂ ∂ − ∂ ∂ − ∂ ∂ + − − ∂ ∂ + ∂ ∂ − ∂ ∂ + ∂ ∂ = ∂ ∂ − ∂ ∂ − − ∂ ∂ − ∂ ∂ + ∂ ∂ + ∂ ∂ σ σ µ σ σ σ µ σ (2.5)

Então, temos a marcação a mercado de nosso P&L:

(

)

(

(

r

)

Sdt SdX

)

S V S V dt S V S L P a i a i

MtM σ σ µ− +σ

Generalizando para

σ

h,seja a volatilidade de hedging utilizada no modelo, seja ela qual for, temos o total do P&L para a vida da opção com delta hedge no mundo

Black&Scholes:

(

)

(

)

(

)

( ) dt

S V S e t S V t S V L P T t t t r h h 2 2 2 2 2 0 0 2 1 , , , , & ∂ ∂ − + −

= σ σ σ σ − − (2.7)

Ao realizar algumas simulações de possíveis trajetórias seguindo o processo (2.2) e

em cada uma delas realizar o delta hedging dinâmico na menor frequência de tempo

possível, iremos verificar que o P&L irá ser diferente para cada trajetória. Isso se deve, pois estamos quebrando uma premissa do modelo Black&Scholes que refere-se ao rebalanceamento contínuo do portfólio. Na prática, os rebalanceamentos deverão ocorrer de forma discreta, por isso ocorre esta dispersão pequena nos P&L’s o que chamaremos de erro de hedging.

Assim como o P&L das operações de hedging que estudamos, o erro de hedging

será muito importante para nossa análise.

Iremos trabalhar com o processo (2.2) em tempo discreto, ou seja:

2 1 t S t S

S µ δ σ φδ

δ = + _(2.8)

Mais adiante no capitulo 3 veremos algumas outras alterações na mudança do processo a tempo contínuo para tempo discreto.

Formando o mesmo portfólio delta neutro:

Π_t =V

(

t,S_t

)

−∆S_{t (2.9)}

Temos que a variação do portfólio a cada instante de tempo discreto δt:

δΠt =δV

(

t,St

)

−∆St (2.10)

Onde,

(

t St

)

V

(

t t St St

)

V

(

t St

)

V , = +δ , +δ − ,

δ _(2.11)

t t

t t

t

t S S

S V S S V t t V δ δ δ δ

δ −∆

∂ ∂ + ∂ ∂ + ∂ ∂ = Π 2 2 2 1 (2.12)

Vamos chamar

δ

Gtde erro de hedging, representado pela expressão:

t t t

t r

G δ δ

δ = Π − Π _(2.13)

Sabemos que δS_t2 ₌σ2S_t2φ2δ_{t, substituindo em (2.12), temos:}

(

t t

)

t t

t t t t

t S r V S

S V S S V t V

G σ φ δ δ δ

δ −∆ − −∆

∂ ∂ + ∂ ∂ + ∂ ∂

= 2 2 2

2 2

2 1

(2.14)

Se E

(

δ

G_t

)

=0, estamos na equação do modelo Black&Scholes:

0 2

1 2 2 ₌

∂ ∂ + − + ∂ ∂ t t t t S V rS rV S t V δ σ _(2.15)

Fazendo (2.13) – (2.14), chegamos ao erro de hedging:

(

)

t

t t

S V S

G σ φ δ

δ 1 2 1 2 2 2 2 2 − ∂ ∂

= _(2.16)

Assim o erro de hedging total será:

= → = T t t T G G 0 0 δ (2.17)

Mas adiante, no capítulo 3 iremos demonstrar rapidamente o modelo Balck&Scholes e iremos apresentar alguns outros modelos teóricos de hedging em que iremos

incorporar custos de transação em cada operação realizada na estratégia e analisar seu respectivo impacto na distribuição dos P&L’s.

2.2 Estratégias de hedging.

Neste item do capitulo, apresentamos resumidamente alguns trabalhos de relevância do tema tratado em nossa pesquisa.

Os primeiros estudos de hedging de opções foram estudados por Fischer Black e

Black&Scholes

[ ]

3 . A partir desse modelo, que se tornou referência nos estudos de finanças, surgiram outros modelos de maior complexidade.

Os estudos que começaram a quebrar com as premissas impostas no modelo Black&Scholes foram realizados por Thorpe

[ ]

31 e depois por Boyle e Emanuel

[ ]

6

que estudaram a distribuição dos retornos do hedged portfólio quando a freqüência

dos ajustes ocorrem em tempo discreto. Através de simulações de Monte Carlo, contatou-se que, em uma composição de portfólio comprada em opções, os P&L´s tem uma distribuição chi-quadrado com 1 grau de liberdade e média zero, ou seja, dois terços das observações apresentam valores pequenos negativos e muito próximo de zero, e um terço das observações apresentam valores grandes positivos, e o intervalo de ajustes do hedged portfólio é diretamente relacionado com a

dispersão dos P&L´s.

Um estudo de extrema importância, seguindo no raciocínio do hedging dinâmico

discreto do modelo Black&Scholes foi realizado por Henrard

[ ]

18 ,Carr

[ ]

8 com extensões de Ahmad e Wilmott

[ ]

33 onde exploraram propriedades estatísticas do

P&L do hedging dinâmico, como por exemplo, seu retorno esperado e sua

dispersão. Além disso, realizaram variações na volatilidade de hedging. O problema

de qual volatilidade utilizar no modelo é de extrema importância para realidade

operacional da estratégia de delta hedging, uma vez que dependendo da volatilidade

de hedging, o delta muda, as quantidades de rebalanceamento mudam, assim o

P&L final sofre variação de acordo com a volatilidade de hedge adotada. Através de

simulações do ativo base com a dinâmica do movimento browniano geométrico, chegaram a conclusão de que a dispersão dos P&L´s é menor quando utilizado a volatilidade realizada do ativo objeto na volatilidade de hedging do modelo ao invés

da volatilidade implícita.

A incorporação dos custos de transação nos modelos dinâmicos de hedging foi

primeiramente estudado por Leland

[ ]

23 , e depois contribuições extremamente relevantes a cerca do tema e um dos primeiros modelos não lineares para derivativos foram desenvolvidos por Hoggard, Whaley & Wilmott

[ ]

35 .

de maneira bem intuitiva. Quando se compra um ativo com custos, estamos na

realidade pagando um net price mais caro por ele, assim como quando vendemos

certo ativo com custos, vendemos mais barato, fazendo com que haja uma mudança na dispersão dos retornos do ativo objeto.

Essa mudança de dispersão é ajustada na volatilidade de hedge do modelo que

depende do sinal do gamma, ou seja, existe diferença para posições compradas e

vendidas. Portanto, o modelo de Leland só funciona para opções plain vanillas com

o mesmo sinal do gamma para todos os valores do ativo base.

Para uma alocação de portfólio onde se trabalha com derivativos exóticos ou com diferentes opções plain vanillas compradas e vendidas, precisa-se trabalhar com modelos não lineares, o modelo de Hoggard, Whalley & Wilmott

[ ]

35 funciona muito bem para este tipo de situação. Hoggard, Whalley & Wilmott chegaram a uma equação não linear para o apreçamento de uma opção considerando custos de

transação em que se é possível trabalhar com um book de opções em que o gamma

pode variar de sinal ao longo da vida das opções. Em nossa pesquisa adotamos o

modelo de Hoggard, Whalley & Wilmott como um dos modelos de hedging.

A dinâmica do ativo objeto pelo modelo Black&Scholes, o movimento browniano geométrico, também foi alvo de contestações pelo fato deste modelo apresentar uma volatilidade constante.

Um dos modelos que quebraram com esta premissa, foi o modelo de volatilidade

estocástica de Vasicek

[ ]

32 , trabalhando com modelagem de taxa de juros,

incorporou-se uma dinâmica para a volatilidade estabelecendo uma relação de equilíbrio de longo prazo. Outro estudo acerca da dinâmica da volatilidade onde os parâmetros do modelo são encontrados por “fitting data” é o modelo de Wilmott e

Oztukel

[ ]

34 .

Seguindo este raciocínio de que a volatilidade não é constante, Avellaneda,Levy e Paras

[ ]

1 estudaram o hedge de volatilidade, onde a volatilidade de hedging do

modelo não é mais determinística e sim uma “banda de certeza” em que a volatilidade do ativo objeto pode oscilar até o vencimento do derivativo. Ao utilizar este modelo, e realizar o hedging de volatilidade é necessário realizá-lo com outros

Capitulo 3

Modelos Teóricos

Neste capítulo apresentamos os modelos de hedging e os modelos em que

utilizamos para realizar as simulações do ativo objeto e gerar os diferentes regimes

de mercado para trabalharmos o hedging.

3.1 Modelos de Hedging

Nesta parte de nosso trabalho apresentamos os modelos utilizados para realizar o

hedging. Demonstramos rapidamente o modelo Black&Scholes em 3.1.1, o modelo UVM Uncertain Volatility Model em 3.1.2, o modelo de Leland em 3.1.3 e o modelo

de Hoggard Whalley Wilmott em 3.1.4.

O portfólio inicial que utilizamos para desenvolver os modelos de hedging é sempre

o mesmo, ou seja, a compra de uma opção plain vanilla européia. A diferença será a

quantidade de ativo base, ou delta, vendida. Cada modelo terá um delta particular que será respeitado.

3.1.1 O modelo de Black and Scholes (1976)

Neste capitulo relembramos o modelo original de Black&Scholes e suas premissas.

O modelo de Black&Scholes é muito importante para nossa análise, uma vez que é a base de todos os outros modelos estudados a diante.

Começando com a dinâmica do retorno de um ativo que não pague dividendos ou qualquer outro provento, o modelo assume que o retorno deste ativo segue um processo estocástico chamado de movimento browniano geométrico (2.2), já apresentado no capitulo anterior.

Na equação (2.2) apresentada dX é a aleatoriedade do modelo conhecido como

processo de Wiener que possui uma distribuição N ~

(

0, dt

)

_, µ é o ‘drift’ ou retorno

esperado e σ é o desvio padrão ou volatilidade dos retornos, dt é a variação do

tempo.

Definindo o valor de uma opção européia V como uma função V

( )

S,t , onde S é o

aplicando o lema de Itô para dV que seria a variação do valor da opção, constituindo

um portfólio Π do modo (2.9), onde∆ _{é a primeira derivada}

S V

∂

∂ _{obtida na expansão}

do lema de Itô. Desta forma iremos ‘zerar’ a aleatoriedade dX , e de acordo com

‘Arbitrage Pricing Theory’ qualquer ativo que não contenha risco (aleatoriedade)

deverá ter retorno igual a taxa de juros livre de risco, assim, igualamos a variação de nosso portfólio a variação da taxa de juros livre de risco r. Com isso obtemos a

equação diferencial parcial de Black &Scholes : 0 2 1 2 2 2

2 _{− =}

∂ ∂ + ∂ ∂ + ∂ ∂ rV S V rS S V S t V σ (3.1)

Esta formidável equação nos permite uma solução fechada simples uma vez que o

modelo adota a premissa de que os parâmetros σ e rsão constantes para qualquer

T t ≤ ≤

0 _.

Outras premissas importantes do modelo de Black&Scholes e da qual iremos relaxar mais adiantes são: Não há custos de transação e a negociação das ações é

contínua, portando podemos realizar o hedging em nosso portfólio continuamente e

a dinâmica do ativo base segue um passeio aleatório chamado de movimento browniano geométrico contínuo baseado em incrementos de distribuição Normal.

3.1.2 O modelo UVM – Uncertain Parameters

A volatilidade pode ser determinística, como utilizamos no modelo Black&Scholes e randômica no caso do modelo de volatilidade estocástica. Além destes dois modelos de volatilidade, existe o modelo de volatilidade como parâmetro incerto, sob a hipótese de que a volatilidade tem uma dinâmica em que ela oscila dentro de dois valores extremos, este é o modelo Uncertain Volatility Model UVM de Avellaneda,

Levy e Parás (1995).

Para chegar ao modelo UVM de Avellaneda, Levy e Parás (1995), mais uma vez

iremos construir o mesmo portfólio Π descrito em (2.9), mas ao invés de adotar uma

volatilidade constante σ no modelo, iremos adotar um intervalo onde a volatilidade

pode variar, no qual chamaremos de bandas de certeza. Esta banda terá uma

volatilidade mínima e uma volatilidade máxima, do modo − +

≤ ≤σ σ

σ .

Esta premissa de que a volatilidade não é constante e flutua dentro de uma banda é perfeitamente aceitável para a realidade do mercado, assim como podemos observar no gráfico 1 a dinâmica da volatilidade realizada de Itaú PN :

Gráfico1 – volatilidades realizadas para o ativo base ITUB4

Adotando dois possíveis cenários para o valor do portfólio Π, o pior cenário e o

melhor cenário, e definindo o pior cenário como sendo o cenário em que a combinação dos parâmetros no modelo produz o menor preço o qual corresponde a

mínima variação, menor incremento e maior decréscimo na variação do portfólio dΠ

para cada instante de tempo dt, assim minimizamos a equação:

{ }

∂ ∂ +

∂ ∂ =

Π _{− +}

≤

≤ 2

2 2 2 2 1 min

min

S V S t

V

d σ

σ σ σ

Como a volatilidade na equação (3.2) depende do sinal de Γ , e trabalhamos com

uma opção comprada no portfólio inicial, a mínima variação em dΠ será σ =σ−.

Resolvendo a equação, temos:

( )

0

2 1 2 2 2 2 = − ∂ ∂ + ∂ ∂ Γ + ∂ ∂ − − − − rV S V rS S V S t V σ (3.3)

Esta equação é resolvida por diferenças finitas, onde encontramos a quantidade

S V

∂ ∂

do ativo base para o hedge.

Temos uma equação parcial diferencial não linear em (3.3). A notação −

V significa

que estamos comprados na opção e estamos apreçando o derivativo no cenário mais pessimista, onde a volatilidade é baixa. Pela não linearidade, o valor do derivativo depende da estrutura do portfólio em que ele irá constituir. Se houver outros derivativos, o apreçamento será diferente. O valor de um portfólio de opções será maior que a soma individual de cada opção nele contida.

= = ≥ N i i N i i V V valor 1 1 (3.4)

O modelo UVM realmente é muito interessante ao tratar a volatilidade com parâmetro não determinístico, mas como a banda de certeza da volatilidade pode

ser grande, os spreads de compra e venda também serão grandes podendo

inviabilizar a negociação no mundo real.

Uma ferramenta para melhorar o modelo e estreitar os spreads para níveis aceitáveis é o chamado hedging estático ou Lagrangian UVM. Em nosso trabalho,

estudamos apenas o hedging dinâmico, portanto não iremos detalhar o hedging

estático. O modelo UVM é importante, pois ele juntamente com o modelo de Leland é a base do modelo Hoggard Whalley Wilmott do qual iremos apresentar na

seqüência de nossa pesquisa e o utilizamos para a estratégia de hedging a fim de

3.1.3 Modelo de Leland

O nosso grande interesse nos modelos é encontrar a quantidade, ou delta, do ativo

base que iremos negociar para realizar o hedging do portfólio até o vencimento da

opção que temos comprada. Como o hedging será feito em tempo discreto e com

custos de transação iremos estudar modelos que tratam esta realidade.

Para isso, relaxamos outra premissa do modelo de Black&Scholes que é a hipótese

de continuidade dos rebalanciamentos do portfólio Π_{. Esta hipótese não somente é}

impossível como não desejável em um mundo que existe custo de transação e o processo de difusão do ativo em questão tem uma variação finita. Nesta situação é

necessário adotar uma estratégia de hedge (como por exemplo, ajustar o portfólio a

cada n minutos, a cada nsemanas, a cada n dias e etc...).

Trabalhar em tempo discreto significa adotar a hipótese de que o tempo consiste em

uma seqüência ordenada de pontos. Iremos chamar de τ um determinado instante

de tempo em que

{

ττ∈Ν

}

. Diferentemente da notação contínua d utilizada em (2.2)

iremos adotar δ para a variação nos modelos em tempo discreto.

Alterando a dinâmica do ativo base para uma versão de tempo discreto, temos a equação (2.8) apresentada no Capítulo 2.

O termo de difusão foi alterado, temos em (2.8) φ ~N

( )

0,1 e o termo 2 1 t

φδ entra no

lugar do processo de Wiener dX .

Assim como no modelo Black&Scholes, constituímos o portfólio Π (2.9) “sem risco”

e realizamos a expansão em sua variação de valor. Como não estamos mais no mundo contínuo, não podemos mais utilizar o Lemma de Itô para a expansão, então

utilizamos a expansão de Taylor para a variação δ Π, obtendo a equação:

t t t t t t S S V S S V t V δ δ φ σ

δ −∆

∂ ∂ + ∂ ∂ + ∂ ∂ =

Π 2 2 2

2 2

2 1

(3.5)

Como φ~ N

( )

0,1 ,

( )

_φ2 ₌1

E , e para a variância de φ temos _σ2

( )

_φ2

[

( )

_φ

]

2

φ = E − E e

( )

t t

t S

S σ φ δ

δ 2 ₌ 2 2 2

(3.6)

A partir da equação (3.6) podemos começar a definir a estratégia de hedge a ser

adotada. Hoggard Whilley e Wimott (1994) sugere que a estratégia de controle seja

encontrar∆ que minimize a variância de δ Π e apreçar a opção do estilo europeu

igualando o retorno do portfólio Π com a taxa de juros livre de risco r.

Para encontrar o melhor ∆ precisamos conhecer a variância de δ Π, facilmente

encontrada em _var

[ ]

_{δΠ =}

[ ]

_δΠ2 ₋

(

[ ]

_δΠ

)

2 E

E e trabalhando com o operador esperança

de δΠe 2

Π

δ para calcular var

[ ]

δΠ os termos φ são eliminados na integração, assim Π

δ se torna uma função de V e suas derivadas. Para minimizar a variância de δΠ

encontraremos a quantidade ∆ para var

[ ]

Π =0

∂ ∂

δ

S que resultará no ∆ ótimo:

t G S V δ + ∂ ∂ =

∆ (3.7)

Na equação (3.7) o primeiro termo é derivada do modelo Black&Scholes e o segundo termo δGt seria uma correção do ∆ de Black&Scholes que oferece uma melhor redução na variância de δΠ, ou seja, oferece uma redução no erro de

hedge.

Vamos assumir que os rebalanceamentos do porfólio são ajustados em intervalos discretos, porém quanto mais ajustes fizermos em nosso portfólio para minimizar nosso erro de hedge, encontramos outro problema que na prática não poderá ser

evitado em hipótese alguma: o custo de transação.

O primeiro e mais evidente problema que encontramos ao incorporar custo de transação nas operações é que se desejamos reabalancear o portfólio o máximo possível, o custo de transação irá subir sem limites, essa estratégia seria muito cara e inviável. O segundo problema vem da natureza randômica dos custos de transação que junto com a estratégia de replicação há uma correlação fortemente ‘path-dependt’, ou seja, o custo de transação irá depender não somente do preço

trajetória do ativo objeto até a data de vencimento da opção. Ao incorporar custos de

transação em nossa estratégia, acresentamos em (3.5) os custos operacionais k .

Antes, enfatizemos os rebalanceamentos do porfólio:

Digamos que no instante t temos um valor S para o ativo base e seu respectivo

( )

S,t

∆ e no instante t′ =t+δ t temos S′,t′ com ∆′

(

S+δ S,t+δ t

)

. O número de

contratos que iremos rebalancear será ∆′−∆ . Segundo o modelo de Leland (1985)

o custo operacional é proporcional ao valor negociado do ativo base (o que faz total sentido na prática), na forma de custo=k S ∆′−∆ , aplicando Taylor em ∆′, e desprezando os termos que são prevalecidos chegamos a:

(

S t

)

∂Sφ δ t

∆ ∂ +

∆ ,

(3.8)

Então, temos :

∂Sσ S φ δ t

∆ ∂ = ∆ − ∆′ (3.9)

Onde =Γ

∂ ∆ ∂

S , portanto chegamos a equação:

custo=k Γ σ S2 δ t φ

(3.10)

Voltando na equação (3.5), incorporando (3.10) e simplificando, temos o modelo de Leland: 0 2 2 1 2 1 2 2 2 = − ∂ ∂ + ∂ ∂ Π − + ∂ ∂ = rV S V rS S V t k S t V Gt δ σ σ δ (3.11)

3.1.4 Modelo de Hoggard – Whalley – Wilmott

Uma extensão não linear do modelo de Leland, onde se possibilita trabalhar com

Considerando a dinâmica do ativo objeto (2.8) e realizando a mesma expansão feita em (3.5), admitindo que subtraímos os custos de transação na equação do valor de

Π e que não vamos ao limite δ t =0 chegamos a equação de δΠ :

ν δ µ µ φ σ φδ σ

δ S t kS

t V S V S S V S t S V

S − ∆ −

∂ ∂ + ∂ ∂ + ∂ ∂ + ∆ − ∂ ∂ = Π 2 2 2 2 2 2 1 2 1 (3.12)

Realizando o delta-hedging temos que a quantidade de ativo objeto em nosso

portfólio é dado por:

(

S S t t

)

S V δ δ + + ∂ ∂

, e o número de ativos negociados é dado por:

(

)

( )

S t

S V t t S S S V , , ∂ ∂ − + + ∂ ∂

= δ δ

ν , admitindo que a variação em δt é bem pequena,

podemos aplicar a expansão de Taylor, obtendo:

(

,

)

( )

,

( )

,

( )

, ... 2 2 2 + ∂ ∂ ∂ + ∂ ∂ + ∂ ∂ = + + ∂ ∂ t S t S V t t S S V S t S S V t t S S S V δ δ δ

δ (3.13)

Da equação (3.13), sabemos que δS =σSφδ t2 +Ο

( )

δt 1

é o termo dominante, então a quantidade de ativos comprados ou vendidos para o rebalanceamento do porfolio é aproximadamente:

( )

2

1

2 2

2 2

, S t

S V S t S S V φδ σ δ ν ∂ ∂ ≈ ∂ ∂

≈ (3.14)

Como não sabemos exatamente quantos ativos serão negociados em nosso

hedging dinâmico até o vencimento da opção, trabalhamos com o operador

esperança:

[

]

2

1 2 2 2 2 t S V S k kS

E σ δ

π ν

∂ ∂

= (3.15)

Note que

π

2

é o valor esperado de φ. Com o termo (3.15) podemos aplicar o

operador esperança para a equação (3.12):

[ ]

t

Igualando nosso valor esperado a taxa de juros livre de risco, temos a equação de Hoggard, Whalley & Wilmott:

0 2 2 1 2 2 2 2 2 2

2 _{− =}

∂ ∂ + ∂ ∂ − ∂ ∂ + ∂ ∂ rV S V rS S V t S k S V S t V πδ σ

σ (3.17)

3.2 Modelos para os processos do ativo base

Neste parte do trabalho, construímos o ambiente em que geramos os diferentes

regimes de mercado onde realizamos o hedging dos modelos apresentados.

Como sabemos, é impossível realizar previsões no mercado financeiro, pois desconhecemos completamente a dinâmica do processo gerador dos retornos dos ativos. Com isso, simulamos diferentes regimes de mercado com diferentes níveis de volatilidades realizadas para o ativo objeto em um mundo em que adotamos além do Movimento Browniano Geométrico, a hipótese de volatilidade estocástica para as trajetórias simuladas.

3.2.1 O modelo de volatilidade estocástica.

Assumir que a volatilidade tem caráter estocástico é um grande passo para convergir com a realidade e aumentar a complexidades dos modelos. Neste item do trabalho apresentamos como a volatilidade estocástica impacta nos modelos apresentados anteriormente.

Por observações empíricas podemos constatar que a premissa de volatilidade constante não é válida (Avellaneda; Levy e Parás, 1995). A volatilidade não se comporta do jeito que descreve a equação de Black&Scholes, não é constante, não é facilamente observável e nem previsível. Isso a torna, pelo seu grau de complexidade, a ‘vedete’ nos estudos das finanças modernas.

Segundo o trabalho realizado por Oztukel e Wilmott (1998), adotamos a dinâmica do ativo como dS =µSdt+σSdX₁ e assumimos que a volatilidade satisfaz:

(

S, ,t

)

dt q

(

S, ,t

)

dX2 p

dσ = σ + σ (3.18)

podemos realizar o hedging facilmente. Então, trabalhamos com duas fontes de

aleatoriedade. A primeira é vinda do ativo base, que já foi demonstrada no modelo Black&Scholes, a segunda que iremos abordar em breve é o risco de volatilidade, pois não estamos mais trabalhando com volatilidade constante. Nesse contexto, temos V

(

S,t,σ

)

. Desta maneira, para constituir o portfólio Π em (2.9) precisamos

de uma segunda opção, que chamaremos de V₂. Temos:

Π=V₁−∆₁S−∆₂V₂ (3.19)

A variação deΠ em dt será dada por:

σ σ σ σ σ ρσ σ σ σ ρσ σ d V V ds S V S V dt V q S V qS S V S t V dt V q S V qS S V S t V d ∂ ∂ ∆ − ∂ ∂ + ∆ − ∂ ∂ ∆ − ∂ ∂ + ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ + ∂ ∂ ∆ − ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ + ∂ ∂ = Π 2 2 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 1 2 2 1 2 2 2 1 2 1 2 1 2 1 2 1 (3.20)

Por termos 2 fontes de aleatoriedade dX₁ e dX₂ no modelo, existe uma correlação

ρ entre elas.

Para se eliminar todas as fontes de aleatoriedades existentes na equação (3.20),

precisamos 1 _{1 2} 2 =0

∂ ∂ ∆ − ∆ − ∂ ∂ S V S V

, para eliminarmos os temos de dS temos

0 2 2 1 ₌ ∂ ∂ ∆ − ∂ ∂ σ σ V V

e para eliminarmos os termos de dσ ,

σ σ ∂ ∂ ∂ ∂ = ∆ / / 2 1 2 V V e σ σ σ ∂ ∂ ∂ ∂ ∂ ∂ + ∂ ∂ = ∆ 1 2 1 1 1 / / V V V S V

Substituindo na equação (3.20) e igualando a variação de Π com a taxa de juros

livre de risco, chegamos a:

Encontramos em (3.21) a equação do preço do derivativo quando se admite volatilidade estocástica.

Como não trabalhamos com o hedging de volatilidade em nossa pesquisa, pois

trabalhamos apenas com uma opção comprada em todos os estudos, não detalhamos muito o modelo. O que é importante para nossa pesquisa é verificar

como os modelos de hedging se comportam quando estamos trabalhando com a

dinâmica da equação (2.2) com a volatilidade estocástica para o processo do ativo base.

3.2.1.1 O modelo de Vasicek.

Ao trabalhar com modelos de volatilidade estocástica, não mais trabalhamos com a volatilidade do ativo objeto constante. Iremos trabalhar com a seguinte dinâmica:

( )1 dW vol dt

S dS

+ =µ

(3.22)

Onde, vol é o parâmetro de volatilidade não constante. Pelo modelo de Vasicek,

temos a dinâmica da vol:

(

)

( )2

t t t t

eq vol dt vol dW

vol k

dvol= − +ξ α _(3.23)

Onde, voleq é a volatilidade de equilíbrio, ξ é a volatilidade da volatilidade e k é a velocidade com que a volatilidade converge para o equilíbrio.

Uma das grandes desvantagens do modelo Vasicek é a estimação dos parâmetros. Pelo trabalho realizado por Wilmott e Oztukel foi derivado uma forma de estimar empiricamente estes parâmetros, como veremos no item seguinte.

3.2.1.2 O modelo de fitting parameters.

O modelo de volatilidade estocástica de fitting parameters ou análise empírica de

volatilidade examina séries realizadas de mercado para extrair os parâmetros do

modelo, esse procedimento chamamos de ‘fitting data’.

ativo financeiro. No trabalho original de Wilmott e Oztukel (1998) foi utilizado uma série histórica do índice Dow Jones.

Como sugere Wilmott e Oztukel (1998), trabalhamos com volatilidades mensais dos retornos diários de Itaú PN.

Gráfico 2 – volatilidade dos retornos mensais de ITUB4

Neste modelo da dinâmica do ativo, utilizamos a premissa de que existe um estado

de equilíbrio de longo prazo para a volatilidade, no qual chamaremos de steady state

distribution e através da técnica de fitting buscamos parâmetros empíricos para o

modelo.

Primeiramente, assumimos que a dinâmica da volatilidade segue o seguinte processo:

( )

dt

( )

dX

d

σ

=

α

σ

+

β

σ

_(3.24)

Similarmente a equação (3.18), temos um termo determinístico, o ‘drift’ α

( )

σ e um termo aleatório, a volatilidade da volatilidade β

( )

σ . Ambos os parâmetros são funções da volatilidade.

Para estimar o parâmetro β

( )

σ , assim como no trabalho original de Wilmott e Oztukel (1998), assumimos que

_β

( )

_σ

₌

_φσ

γ _{onde φ γ}

, são constantes na qual determinamos empiricamente através de nossa série.

Para estimar o ‘drift’ da volatilidade assumimos a premissa que existe um estado de

equilíbrio de longo prazo para a volatilidade e a equação que governa a PDF deste

estado é a Fokker-Planck equation, em que:

( )

(

)

(

( )

)

σ σ σ σ β ∂ ∂ ∂ − ∂ ∂ = ∂

∂ P P

t P 2 2 2 2 1 (3.25)

Onde P

(

σ,t

)

é a PDF para σ.

Entretanto, podemos deduzir uma distribuição de probabilidade para o estado de equilíbrio de longo prazo extraída dos dados de nossa série empírica, devendo satisfazer:

(

( )

)

(

( )

₂

)

2 2 2 1 σ σ β σ σ α d P d d P

d _{∞ ∞}

= (3.26)

Integrando uma vez, temos

( )

(

( )

)

∞ ∞ ∞ + = P c d P d P σ σ β σ α 2 2

1 _(3.27)

Para encontrar α

( )

σ precisamos de P_∞ ou de um valor aproximado. Como estamos

interessados no comportamento de longo prazo, buscamos uma distribuição conhecida para aproximar seu valor. Segundo Wilmott e Oztukel (1998) uma solução para este problema é criar uma distribuição empírica de probabilidade plotando em gráfico a freqüência contra grupos de volatilidades realizadas e observar se podemos aproximar por uma distribuição conhecida. Deixaremos esta aplicaçao para o capitulo 5. Wilmott e Oztukel (1998) concluíram que no longo prazo, ou seja, 20 anos de dados históricos de retornos do índice S&P500 a distribuição empírica aproxima-se de uma distribuição log-normal:

2 2 2 / log 2 1 a e a P − ∞ Π = σ σ

Substituindo (3.28) em (3.27) ,temos :

( )

= − − − 2 1 2 2 2 ln 2 1 a σ σ γ σ φ σ α γ (3.29)

Portanto, a dinâmica da volatilidade para as simulações que realizamos com este

modelo é:

[ ]

dX dt

a

d γ σ φσλ

σ γ

σ φ

σ = − − − +

2 1 2 2 2 ln 2 1 (3.30) Capítulo 4 Métodos Numéricos

Neste capitulo da dissertação apresentamos os métodos numéricos utilizados em nosso trabalho.

4.1 Diferenças Finitas Explicita

Para a o modelo Hoggard Walley e Wilmott (1994), chegamos a uma Equação Diferencial Parcial na qual não temos solução analítica. Para resolver a equação (3.17) utilizamos do método numérico chamado de diferenças Finitas Explícita. O principal fator acerca deste método é delimitar as chamadas condições de contorno. Onde no vencimento da opção teremos:

(

S T

)

payoff

( )

S

Outra condição de contorno que podemos facilmente adotar é quando o ativo base assumir o valor 0, o derivativo V _{valerá 0, e para valores altos de} S(quando temos

um delta de 100%), podemos adotar:

( )

rt

Ee S t S

V , = − − (4.2)

Para resolver a equação, definimos que o ativo base pode assumir 3 valores em

uma mudança de instante SU ,SM ,SD, assim :

dt dt dt dt dt

e D e M e

U = σmax +µ _, = µ _, = −σmax +µ (4.3)

O parâmetro de probabilidade de risco ajustado para o valor de S é dado por:

−

= p dt

P_{U max}

2 1

1 σ (4.4)

P_M =1−2p (4.5)

P_D = p + _max dt

2 1

1 σ (4.6)

Onde p satisfaz:

2 1 2 _max2

2

min _{≤ p≤}

x

σ σ

(4.7)

A implementação numérica em uma notação de tempo discreto para o valor da opção dado os fluxos de caixa oriundos da estratégia de hedging é dado por:

[

j

]

n j n rdt j n j

n F e V pL

V = + − ₊₁+ ₊₁ (4.8)

Onde j

n j n j n j

n dt V dt V V

L 2 2 1 1 2 1 1 1 1 max 1 1 max

1 = − + + −

− + +

+

+ σ σ corresponde ao Γ quando

trabalhamos com notação de tempo contínuo.

0 2

0 2

1

1 2

max 2 min

1 ≥ = <

= ₊ j₊

n j

n ou p se L

L se p

σ σ

(4.9)

4.2 Simulações de Monte Carlo

O segundo método numérico que utilizamos é as simulações de Monte Carlo.

O objetivo em utilizar esta ferramenta, foi gerar suficientes trajetórias para o ativo

base e em cada trajetória realizar o hedging de acordo com cada modelo

apresentado, e por fim analisar os resultados obtidos.

Como na prática desconhecemos completamente o processo gerador dos retornos de um ativo financeiro, utilizamos três modelos diferentes.

O primeiro modelo utilizado foi o movimento browniano geométrico (2.2), depois utilizamos o modelo de Vasicek (3.22) com sua dinâmica de volatilidade (3.23), e por fim o modelo de volatilidade estocástica empírica de Wilmott e Oztukel (3.22) com a dinâmica de volatilidade (3.30), todos já apresentados.

Além de diferentes modelos, realizamos as simulações com diferentes regimes de mercado, em que iremos detalhar mais a diante no Capítulo 5.

Ao trabalhar com a dinâmica de volatilidade estocástica encontramos um problema

de correlação entre '

t t e dX

dX . Para resolver isso, recorremos a fatoração de

Cholesky e encontramos ξ₁ dt para dX_t e ξ₂ dt paraos '

t

dX .

Capitulo 5

Aplicação

5.1 Aplicando o modelo de fitting parameters

Neste item, apresentamos o processo que utilizamos para gerar a dinâmica do ativo base em três possíveis regimes de mercado: o mercado “normal”, o mercado “nervoso” e o mercado “extremamente calmo”.

No capitulo 3, demonstramos a teoria do modelo de volatilidade estocástica por

‘fitting parametes`. Primeiramente, testamos se a forma adotada por Wilmott e

Oztukel (1998) para a aleatoriedade da volatilidade, ou volatilidade da volatilidade,

( )

γ

φσ

σ

β

= estaria correta também para os dados da série de Itaú PN.

Elevando todos os termos ao quadrado da equação (3.24), obtemos

( )

2

( )

2 2

υ σ β

σ dt

d = , onde υ é uma variável aleatória com distribuição normal padrão.

Substituindo a forma de β

( )

σ na equação de

( )

dσ , chegamos a

( )

σ 2 φ2σ2γ υ2

dt

d =

utilizando o operador esperança e atribuindo escala logarítmica em todos os termos, temos:

( )

[

]

(

σ

)

ln

(

φ

)

2ln

( )

σ

lnE d 2 = 2dt + . (5.1)

5.1.1 Simulações para um regime de mercado “normal”

Neste regime de mercado, extraímos de nossa série histórica as 200 últimas observações, ou seja do dia 20/08/2010 até o dia 30/05/2011 para compor os parâmetros do modelo de volatilidade estocástica empírico e gerar nossas simulações.

Aplicando o fitting em nossa série histórica do regime de mercado “normal”

Gráfico 3 - regressão regime de mercado normal

Ao obvervar o gráfico 3, percebemos que a forma (5.1) está intuitivamente correta.

Para realizar o ‘fitting’, dividimos σ em gruposg iguais para todos os valores de σ, onde g será:

(

)

para g g

g i

g_i max min 0,1,...,

min =

− +

=σ σ σ (5.2)

Pela regressão linear feita utilizando o método de mínimos quadrados, encontramos os seguintes parâmetros do modelo:

= 0,84375 a = 1,6875 = 0,190257 b = -6,5456

Para o ‘drift’, o α

( )

σ do modelo, testamos se a nossa série aproxima-se de uma distribuição Log-Normal. Pelo ‘drift’ ser um parâmetro de longo prazo, utilizamos

Gráfico 4 – Distribuição empírica e distribuição log normal

Percebe-se que a distribuição de nossa série aproxima-se de uma distribuição log normal, na qual:

2 2

2 / log

2

1 a

e a

P

− ∞

Π

= σ

σ

σ _(5.1)

Onde σ é a média da distribuição logσ e a seria a dispersão em torno da média.

Então, temos:

( )

= 2 2 −1 − − ₂

2 ln

2 1

a

σ σ γ

σ φ σ

α γ _(5.2)

Gráfico 5 – Exemplo das trajetórias do ativo base sob o regime de mercado normal

Para a dinâmica da volatilidade, também geramos 50 possíveis trajetórias sob as condições dos parâmetros extraídos do regime de mercado ‘normal’.

No gráfico abaixo segue as simulações para a dinâmica da volatilidade:

Gráfico 6 – Exemplo da dinâmica da volatilidade da volatilidade no regime de mercado normal

5.1.2 Simulações para um regime de mercado “nervoso”

Gráfico 7 – Regressão para o regime de mercado nervoso

E os seus respectivos parâmetros encontrados:

a = -1,6855 = -0,84275 b = 4,6752 = 51,98847

No gráfico abaixo, temos 50 simulações da trajetória do ativo base em um mercado de regime nervoso:

Abaixo, temos 50 simulações para a dinâmica da volatilidade em um mercado de regime nervoso:

Grafico 9 – Exemplo da dinâmica da volatilidade da volatilidade para o regime de mercado nervoso.

5.1.2 Simulações para um regime de mercado calmo

Para este regime de mercado, adotamos que dσ é constante. Ou seja, a dinâmica

do ativo base segue o processo de movimento browniano geométrico (2.2) com uma volatilidade constante de 11%a.a.

Esta volatilidade de 11%a.a. encontramos nos períodos de 5/12/2006 até 2/01/2007.

Abaixo segue um gráfico com as últimas observações de nossa série histórica e um exemplo de simulações dos diferentes regimes de mercado juntos:

Gráfico 11 – Série histórica e “possíveis trajetórias futuras”com os 3 regimes de mercado

De posse de todas as simulações, utilizamos-as para realizar o hedging dinâmico, e

seus resultados são apresentados no capítulo seguinte.

Capitulo 6

Resultados

Nesta parte do trabalho apresentamos os resultados das estratégias de hedging.

Primeiramente, demonstramos um estudo inicial para análise de como diferentes níveis de volatilidades realizadas, diferentes volatilidades de hedging e diferentes

frequências de rebalanceamento afetam os resultados dos P&L’s.

Concluído a apresentação do estudo inicial, escolhemos uma determinada frequência de rebalanceamento, alguns níveis de volatilidades realizadas e algumas volatilidades de hedging para fazer uma comparação entre os modelos de B&S e

HWW.

Como a programação do modelo B&S é bem mais simples, realizamos o estudo inicial somente com o modelo de B&S para o hedging.

Para analisar os resultados de nossa pesquisa demonstramos desde a modelagem mais simples apresentada com o modelo Black&Scholes, geramos possíveis trajetórias pelo movimento browniano geométrico com diferentes níveis de volatilidades e realizamos o hedging dinâmico considerando diferentes frequências

de hedging a tempo discreto e com diferentes volatilidades de hedging. O objetivo

desse nosso estudo inicial é além de demonstrar a modelagem de hedging passo a

passo, conferir se o algoritmo que desenvolvemos em C está intuitivamente correto com base nos trabalhos já realizados acerca do tema e referidos no capítulo 2.

O portfólio inicial no qual realizamos o hedging será sempre o mesmo na quantidade

de derivativo, ou seja estaremos sempre comprados em 100.000 quantidades de

opções do ativo base ITUB4, com vencimento em 36 dias uteis, com strike price de

38,00 e com o ativo base valendo R$35,50. O preço pago pela opção é de R$0,60; equivalente a 24,10% de volatilidade implícita pelo modelo B&S. A quantidade inicial

vendida de ITUB4 depende do modelo adotado e do nível de volatilidade de hedging

inserida no modelo.

Nossa primeira preocupação foi verificar se de fato, ao realizar o hedging em um

mundo mais simples possível, ou seja, seguindo as premissas do modelo B&S, se

utilizarmos 24,10% de volatilidade de hedging e se gerarmos as trajetórias do ativo

objeto pelo MBG com 24,10% de volatilidade, realizando o delta hedging com um ∆t

baixo deveríamos obter uma média dos resultados próxima de zero, com dispersão próxima de zero também.

Realizando a estratégia de replicação do delta hedging com estas premissas,

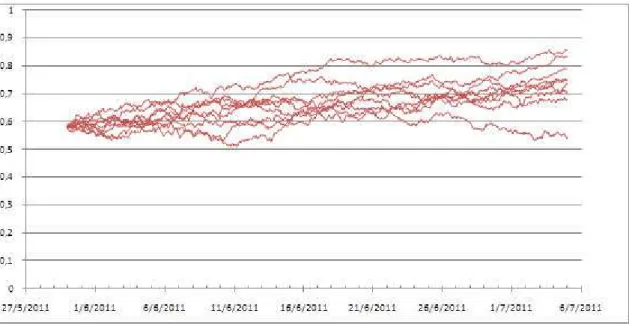
Gráfico 12 – Estrátegia de replicação com o modelo B&S com 24,10% de volatilidade de hedging,

frequência de 1 minuto nos rebalanceamentos sem custos de transação e 24,10% de volatilidade realizada pelo modelo do MBG.

Como podemos observar no gráfico acima, a replicação se torna quase perfeita quando se utilizamos o modelo B&S e suas premissas com uma freqüência de rebalanceamento de 1 minuto.

Aumentando a freqüência dos rebalanceamentos para 27 minutos, obtemos:

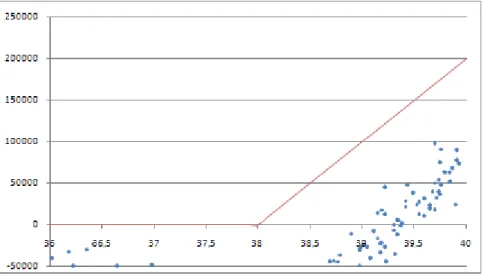
Gráfico 13 – Estrátegia de replicação com o modelo B&S com 24,10% de volatilidade de hedging,

frequência de 27 minutos nos rebalanceamentos sem custos de transação e 24,10% de volatilidade realizada pelo modelo do MBG.

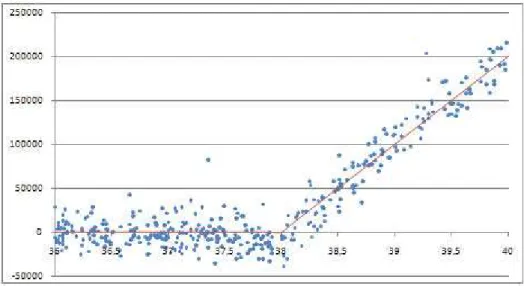
Gráfico 14 – Estrátegia de replicação com o modelo B&S com 24,10% de volatilidade de hedging,

frequência de 300 minutos nos rebalanceamentos sem custos de transação e 24,10% de volatilidade realizada pelo modelo do MBG.

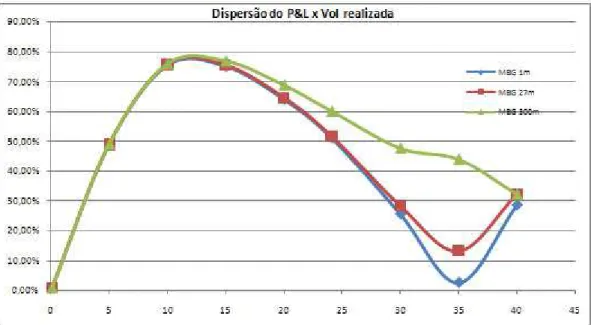
No gráfico abaixo segue o resultado das simulações do hedging com diferentes

volatilidades realizadas. No eixo y, temos a dispersão dos resultados finais do P&L sobre o prêmio pago pela opção. No eixo x, temos as volatilidades realizadas pelo ativo objeto. Utilizamos 24,10% de volatilidade de hedging no modelo B&S e

realizamos três freqüências de ajustes diferentes, com 1 minuto, com 27 minutos e com 300 minutos entre os ajustes do portfólio.

Note que quando a volatilidade realizada do ativo objeto é de 24,10% e estamos

trabalhando com 24,10% de volatilidade de hedging no modelo B&S, temos zero de

dispersão no P&L, confirmando os resultados obtidos por Black&Scholes. Quando erramos para baixo a volatilidade de hedging com a volatilidade realizada, a

dispersão dos P&L’s aumenta até o ponto de 10% de volatilidade realizada, abaixo de 10% a dispersão dos P&L’s diminui. Intuitivamente, quando a volatilidade do mercado é próxima de zero, ou seja, não há variações no preço do ativo avista, o resultado do P&L é uma perda praticamente determinística, e não importa o intervalo de hedging adotado na estratégia. Quando erramos a volatilidade para cima, a

dispersão do P&L só aumenta, ou seja, o trader nem precisaria gastar tempo e

dinheiro realizando hedge se a volatilidade do mercado for acima de 40%, por

exemplo, pois seu P&L final terá um resultado aleatório.

Note também, que cada ponto do gráfico refere-se a uma determinada distribuição com média e variância. Para detalhar mais os resultados, apresentamos essas distribuições em forma de histograma.

Primeiramente, temos os histogramas dos P&L’s do experimento realizado com o modelo B&S e suas premissas, gerando a volatilidade realizada com 24,10%; com freqüência de 1, 27 e 300 minutos nos rebalanceamentos e com 24,10% de volatilidade de hedging:

Alterando a volatilidade realizada para 15%. Abaixo temos os histogramas utilizando a frequência dos rebalanceamentos com 1, 27 e 300 minutos:

Alterando a volatilidade realizada para 10%, temos os histogramas utilizando os rebalanceamentos com 1, 27 e 300 minutos:

Alterando a volatilidade realizada para 5%, temos os histogramas utilizando os rebalanceamentos com 1, 27 e 300 minutos:

Alterando a volatilidade realizada para 0,1%, praticamente sem alteração no valor do ativo objeto. Abaixo temos os histogramas utilizando os rebalanceamentos com 1, 27 e 300 minutos:

Com uma volatilidade realizada de 35%, temos:

Com uma volatilidade realizada de 40%, temos:

Alterando a volatilidade de hedging do modelo B&S para 35% e realizando o mesmo

Gráfico 16 – Dispersão dos P&L’s pelas volatilidades realizadas com 35% de volatilidade de hedging com 1, 27 e

300 minutos de freqüência de hedging sob o modelo B&S e suas premissas.

Para cada ponto da curva, temos os histogramas para os resultados com 24,10% de

volatilidade realizada, sem custos de transação e com uma volatilidade de hedging

de 35%, com rebalanceamentos com 1, 27 e 300 minutos:

Com uma volatilidade realizada de 15%, temos:

Com uma volatilidade realizada de 10%, temos:

Com uma volatilidade realizada de 0,1%, temos:

Aumentando a volatilidade realizada para 30%, temos:

Com uma volatilidade realizada de 40%, temos:

Realizando o mesmo experimento e alterando a volatilidade de hedging do modelo