Seguimento de referência para sistemas lineares incertos sujeitos a restrições

(1)

UNIVERSIDADE_FEDERALDO RIO GRANDE DO NORTE

UNIVERSIDADEFEDERAL DORIOGRANDE DONORTE CENTRO DETECNOLOGIA

PROGRAMA DEPÓS-GRADUAÇÃO EMENGENHARIAELÉTRICA E COMPUTAÇÃO

Seguimento de Referência para Sistemas Lineares

Incertos Sujeitos a Restrições.

José Ilton Sarmento Silveira Júnior

Orientador: Prof. Dr. Carlos Eduardo Trabuco Dórea (DCA/UFRN)

Dissertação de Mestrado apresentada ao Programa de Pós-Graduação em Engenha-ria Elétrica e Computação da UFRN (área de concentração: Automação e Sistemas) como parte dos requisitos para obtenção do título de Mestre em Ciências.

(2)

UFRN / Biblioteca Central Zila Mamede Catalogação da Publicação na Fonte.

Silveira Júnior, José Ilton Sarmento.

Seguimento de referência para sistemas lineares incertos sujeitos a restrições / José Ilton Sarmento Silveira Júnior. - Natal, RN, 2016

63 f.: il.

Orientador: Prof. Dr. Carlos Eduardo Trabuco Dórea

Dissertação (Mestrado) - Universidade Federal do Rio Grande do Norte. Cen-tro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica e de Computação.

1. Controle robusto - Dissertação. 2. Rastreamento de referência - Disserta-ção. 3. Controle sob restrições - DissertaDisserta-ção. 4. Sistemas incertos - DissertaDisserta-ção. 5. Conjuntos invariantes - Dissertação. I. Dórea, Carlos Eduardo Trabuco. II. Título.

(3)

Seguimento de Referência para Sistemas Lineares

Incertos Sujeitos a Restrições.

José Ilton Sarmento Silveira Júnior

Dissertação de Mestrado aprovada em 25 de Janeiro de 2016 pela banca examinadora composta pelos seguintes membros:

Prof. Dr. Carlos Eduardo Trabuco Dórea (Orientador) . . . DCA/UFRN

Prof. Dr. Anderson Luiz de Oliveira Cavalcanti (Membro Interno) DCA/UFRN

Prof. Dr. Fábio Meneghetti Ugulino de Araújo (Membro Interno) DCA/UFRN

(4)

(5)

Resumo

Os controladores robustos, nas últimas décadas, vêm sendo muito estudados por espe-cialistas na área de controle para tratar problemas inerentes a sistemas dinâmicos sujeitos a incertezas dos seus parâmetros, como também perturbações. Mas além desses proble-mas, existe outra característica importante, presente na maioria dos processos práticos, que é a existência de restrições, as quais podem resultar de limitações nos estados do sis-tema, na entrada de controle ou na saída. Ambos os fatores citados, se não forem tratados devidamente na etapa de síntese do controlador, podem acarretar perda de desempenho do sistema controlado ou até levá-lo à instabilidade. Neste sentido, este trabalho apresenta uma proposta de um controlador robusto que utiliza a teoria de conjuntos invariantes para o rastreamento de referências constantes, garantindo que o sistema obedeça às restrições a despeito do efeito de perturbações limitadas em amplitude e de variações nos parâme-tros. Poliedros invariantes controlados são usados para garantir que as restrições sejam respeitadas tanto para o caso de um sistema com realimentação de estados quanto para com realimentação de saída. Em ambos os casos é utilizado um procedimento de reiden-tificação dos parâmetros do sistema, o qual é utilizado para reduzir o erro de rastreamento a referências constantes.

(6)

(7)

Abstract

In recent decades, robust controllers, have been studied by experts in control systems to deal with problems inherent to dynamic systems subject to disturbances and variations of its parameters. However, beyond these problems, another important characteristic that is present in most practical cases is the existence of constraints, which may result from limitations in the system states, the control input or output. Both mentioned factors, if not dealt with properly in the controller synthesis step, can cause degradation of perfor-mance of the controlled system or even lead it to instability. Thus, this work presents a proposal of a robust controller that uses the theory of invariant sets perform the refe-rence tracking, ensuring that the system complies with the constraints despite the effect of bounded disturbances and variations of parameters. Invariant Polyhedra are used to ensure compliance with the constraints to systems both with state feedback and output feedback. Reidentification procedure of system parameters is used to cancel the error of constant references tracking in both the cases.

(8)

(9)

Sumário

Sumário i

Lista de Figuras iii

Lista de Símbolos v

1 Introdução 1

2 Conjuntos Invariantes e Controle sob Restrições 3

2.1 Sistemas Lineares Sujeitos a Restrição . . . 3

2.2 Poliedros Positivamente Invariantes . . . 4

2.3 Conjuntos Invariantes Controlados . . . 5

2.3.1 Poliedros Invariantes Controlados . . . 5

2.3.2 Conjunto Invariante Controladoλ-Contrativo . . . 6

2.3.3 Máximo Conjunto Invariante Controlado . . . 6

2.4 Poliedros Invariantes para Sistemas com Modelos Incertos . . . 7

2.4.1 Máximo Conjunto∆-Invariante . . . 9

3 Rastreamento de Referências sob Restrições 11 4 Controle Robusto por Realimentação de Estados 15 5 Controle Robusto por Realimentação de Saída 19 5.1 Modelo Conhecido . . . 19

5.2 Modelo Incerto . . . 22

6 Simulações e Resultados 27 6.1 Realimentação de Estados . . . 27

6.1.1 Controle Regulatório . . . 27

6.1.2 Rastreamento de Referência . . . 29

6.1.3 Rastreamento Robusto de Referência . . . 31

6.2 Realimentação de Saída . . . 37

6.2.1 Controle Regulatório . . . 37

6.2.2 Rastreamento de Referência . . . 38

6.2.3 Rastreamento Robusto de Referência . . . 39

7 Conclusões 45

(10)

(11)

Lista de Figuras

3.1 Servosistema tipo 0 . . . 12

6.1 Poliedro Invariante Controlado . . . 28 6.2 Controle Regulatório com Realimentação de Estados . . . 29 6.3 Sinal de Controle upara o Controle Regulatório com Realimentação de

Estados . . . 29 6.4 Rastreamento de Referência com Realimentação de Estados . . . 30 6.5 Trajetória dos Estados para o Rastreamento de Referência com

Realimen-tação de Estados . . . 30 6.6 Sinal de Controleupara o Rastreamento de Referência com

Realimenta-ção de Estados . . . 30 6.7 Controle com Modelo Incerto com Realimentação de Estados . . . 31 6.8 Poliedro∆-invariante Controlado . . . 32 6.9 Controle com modelo reidentificado em Realimentação de Estados . . . . 33 6.10 Trajetória dos Estados com Rastreamento Robusto com Realimentação de

Estados . . . 33 6.11 Sinal de Controleupara controle com reidentificação com Realimentação

de Estados . . . 33 6.12 Controle com modelo reidentificado com mudança de parâmetros em k =

10 com Realimentação de Estados . . . 34 6.13 Sinal de Controleupara controle com reidentificação e mudança de

parâ-metros com Realimentação de Estados . . . 34 6.14 Controle com modelo reidentificado em Realimentação de Estados com

referência igual à 3 . . . 35 6.15 Trajetória dos Estados com Rastreamento Robusto com Realimentação de

Estados com referência igual à 3 . . . 35 6.16 Sinal de Controleupara controle com reidentificação com Realimentação

de Estados com referência igual à 3 . . . 35 6.17 Controle com modelo reidentificado em Realimentação de Estados com

referência igual à 4 . . . 36 6.18 Trajetória dos Estados com Rastreamento Robusto com Realimentação de

Estados com referência igual à 4 . . . 36 6.19 Sinal de Controleupara controle com reidentificação com Realimentação

de Estados com referência igual à 4 . . . 36 6.20 Controle Regulatório com Realimentação de Saída . . . 37

(12)

6.21 Sinal de Controle u para o Controle Regulatório com Realimentação de

Saída . . . 38 6.22 Rastreamento de Referência com Realimentação de Saída . . . 38 6.23 Trajetória dos Estados para o Rastreamento de Referência com

Realimen-tação de Saída . . . 38 6.24 Sinal de Controleupara o Rastreamento de Referência para

Realimenta-ção de Saída . . . 39 6.25 Controle com Modelo Incerto para Realimentação de Saída . . . 39 6.26 Controle com modelo reidentificado em Realimentação de Saída . . . 40 6.27 Trajetória dos Estados para o Rastreamento Robusto com Realimentação

de Saída . . . 40 6.28 Sinal de Controleupara controle com reidentificação com Realimentação

de Saída . . . 40 6.29 Controle com modelo reidentificado com mudança de parâmetros em k =

10 com Realimentação de Saída . . . 41 6.30 Sinal de Controleupara controle com reidentificação e mudança de

parâ-metros com Realimentação de Saída . . . 41 6.31 Controle com modelo reidentificado em Realimentação de Saída com

re-ferência igual à 3 . . . 42 6.32 Trajetória dos Estados com Rastreamento Robusto com Realimentação de

Saída com referência igual à 3 . . . 42 6.33 Sinal de Controleupara controle com reidentificação com Realimentação

de Saída com referência igual à 3 . . . 42 6.34 Controle com modelo reidentificado em Realimentação de Saída com

re-ferência igual à 4 . . . 43 6.35 Trajetória dos Estados com Rastreamento Robusto com Realimentação de

Saída com referência igual à 4 . . . 43 6.36 Sinal de Controleupara controle com reidentificação com Realimentação

(13)

Lista de Símbolos

A- Matriz de transição de estados,A∈Rn×n. B- Matriz de entradas,B∈Rn×m.

C- Matriz de saídas,C∈Rp×m.

x- Variáveis de estado,x∈Rn.

y- Saídas do sistema,y∈Rp.

u- Sinal de controle,u∈Rm.

V- Matriz de ponderações do sinal de controle nas restrições,V∈Rv×m.

Ω- Subconjunto no espaço de estados. λ- Taxa de contração.

ζ- Conjunto admissível a um passo de um subconjunto no espaço de estados.

C∞ - Máximo conjunto invariante controlado contido em um subconjunto no espaço de

estados.

α- Vetor de incertezas da matrizA.

β- Vetor de incertezas da matrizB.

∆A- Hipercubo formado pelas incertezas da matrizA.

∆B- Hipercubo formado pelas incertezas da matrizB.

Kp- Ganho proporcional ao erro.

K- Ganho proporcional as variáveis de estado. e- Erro da saída do sistema em relação à referência.

Ao- Matriz nominal da matriz incertaA.

Bo- Matriz nominal da matriz incertaB.

ym- Saída medida no sistema.

yo- Saída usando o modelo nominal.

ξ- Pior caso próximo passo para as variáveis de estado do sistema que obedecem as res-trições.

κ- Pior caso de saída do sistema para as variáveis de estado do sistema que obedecem as

(14)

(15)

Capítulo 1

Introdução

Os sistemas de controle desempenham um papel fundamental no desenvolvimento da engenharia e da ciência, e tornaram-se uma ferramenta de muita importância em todos os tipos de sistemas automatizados, processos industriais e de produção [Ogata 2003].

Desde o final da década de 60, a utilização e síntese de controladores robustos para sistemas lineares vem sendo muito discutida pela comunidade científica, já que estes con-troladores tem a capacidade de garantir o desempenho e a estabilidade dos sistemas pe-rante as incertezas inerentes aos modelos, além de poderem ser utilizados em sistemas multivariáveis, variantes no tempo e de ordem elevada [Nogueira 2009].

A modelagem matemática de sistemas dinâmicos é resultado da análise das equações físicas do processo e/ou obtida a partir de técnicas de identificação de sistemas. Essa mo-delagem é feita com o objetivo de representar o mais próximo possível o comportamento dinâmico do sistema real, mas devido a algumas características inerentes ao sistema, o modelo pode conter incertezas que afetam o seu comportamento.

As incertezas que afetam o modelo de um sistema podem ter sua origem em diver-sos aspectos da sua identificação, elas podem ser provenientes dos erros de modelagem, das variações paramétricas, das incertezas sobre os parâmetros por causa da precisão e das aproximações de modelagem, tais como linearização ou eliminação de dinâmicas de ordem elevadas [Langner 2004].

Além das incertezas do modelo, existe também uma outra característica importante, presente na maioria das aplicações práticas, que é a existência de restrições nos estados, no controle ou na saída do sistema. Algumas vezes, essas restrições são colocadas pro-positalmente, com o objetivo de reduzir o consumo de energia, minimizar a utilização de recursos e/ou para assegurar que algumas variáveis não ultrapassem valores críticos, como por exemplo para que um tanque não transborde [Kido 2011].

O problema de rastreamento de referência para sistemas com restrições é bem mais complexo do que para sistemas livres de restrição, onde deve existir um controlador que consiga levar o sistema ao sinal de referência sem violar as restrições durante o transitório, este problema pode ser visto detalhado em [Blanchini & Miani 2000]. Existem muitos trabalhos que resolvem o problema de rastreamento com restrições, como [Limon et al. 2008], [Chisci & Zappa 2010] e [Dórea 2004].

(16)

po-2 CAPÍTULO 1. INTRODUÇÃO

liédricos está diretamente relacionada às restrições dos sistemas físicos, pois as restrições lineares podem ser matematicamente traduzidas na forma de poliedros. A invariância dos poliedros garante que as variáveis de estado do sistema permanecerão dentro do conjunto de restrições que é o conceito conhecido como invariância controlada [Araújo 2011].

Um conjunto positivamente invariante tem a propriedade de que, para qualquer con-dição inicial pertencente ao conjunto, a trajetória dos estados de um sistema controlado permanecerá no interior do mesmo em todo o tempo, garantindo, assim, que as restrições do sistema não serão violadas [Nogueira 2009].

Existem muitos estudos e aplicações envolvendo os conjuntos invariantes, como [Olaru et al. 2010], [Pluymers et al. 2005],[Tarbouriech & Burgat 1994], [Limon et al. 2002], [Chisci et al. 2001], [Kerrigan & Maciejowski 2000], [Cannon et al. 2003], [Alamo et al. 2005], [Kolmanovsky & Gilbert 1998], mas em nenhum dos casos existe o estudo de rastreamento robusto de referência para modelos incertos.

Neste contexto, este trabalho tem como objetivo geral o estudo e aplicação dos con-ceitos de conjuntos invariantes em um controlador robusto para o controle de um sistema linear sob restrições, contribuindo nas áreas de controle de sistemas com restrição para os casos de sistemas conhecidos e incertos, tanto para realimentação de estados quanto para realimentação de saída, enfatizando o caso de realimentação de saída para sistemas incertos, no qual não existem trabalhos até então publicados, e visa os seguintes objetivos específicos:

1. Estudar os conceitos de conjuntos invariantes, em específico o conjunto poliédrico controlado.

2. Usar os conceitos adquiridos de conjuntos invariantes para implementar um con-trole para rastreamento de referência.

3. Usar os conjuntos invariantes no caso em que o modelo do sistema tenha incertezas.

4. Encontrar um método que garanta que o controle do sistema seja robusto.

(17)

Capítulo 2

Conjuntos Invariantes e Controle sob

Restrições

Um subconjunto do espaço de estado de um sistema dinâmico é dito positivamente invariante se qualquer trajetória originada deste conjunto não o deixa [Dórea 2004].

A abordagem da invariância positiva tem sido usada com sucesso na resolução de um grande número de problemas em sistemas dinâmicos com restrição. As restrições destes sistemas normalmente são provindas de limitações físicas nas variáveis de entrada e/ou saída [Dórea 2004]. O problema relativo as restrições é que devido à dinâmica do sistema, em geral, nem todas as trajetórias originadas de estados iniciais admissíveis permanecerão dentro das restrições. Já para as condições iniciais contidas em um subconjunto positiva-mente invariante no domínio admissível, as violações das restrições podem ser evitadas.

Utilizando a abordagem para o caso em que exista um controle envolvido, dizemos que um conjunto é invariante controlado ou viável se, para todas as condições iniciais escolhidas entre seus elementos, a trajetória pode ser mantida dentro do conjunto por meio de uma ação de controle apropriada [Blanchini 1999].

Existem famílias especiais de conjuntos positivamente invariantes, as duas mais im-portantes são os conjuntos elipsoidais e conjuntos poliédricos. Neste trabalho serão utili-zados os conjuntos poliédricos por representar melhor as restrições utilizadas nos sistemas dinámicos.

2.1 Sistemas Lineares Sujeitos a Restrição

Como já foi mencionando anteriormente as restrições são geralmente provindas de limitações físicas e/ou não-linearidades inerentes ao sistema. A maioria dos problemas de controle práticos são dominados por grandes limitações. Por exemplo, válvulas que apenas podem ser operadas entre completamente aberta e completamente fechada, bom-bas e compressores que têm capacidade de processamento limitadas e tanques que podem apenas manter um certo volume. Negligenciar essas restrições pode causar a degradação do desempenho do sistema ou até mesmo levá-lo à instabilidade [Tarbouriech 1991].

(18)

4 CAPÍTULO 2. CONJUNTOS INVARIANTES E CONTROLE SOB RESTRIÇÕES

x(k+1) =Ax(k) +Bu(k) y(k) =Cx(k)

(2.1) (2.2)

Onde, x(k) é a variável de estado no instante k, x∈Rn; _u₍_k₎ é o sinal de controle no instante k, u∈Rm; _y₍_k₎ é a saída do sistema no instante _k, _y_∈Rp; _Aé a matriz de transição de estados, A∈Rn×n; _B é a matriz de entradas, _B_∈Rn×m; _C é a matriz de saídas,C∈Rp×n.

A representação das restrições dos estados é dada pela equação 2.3.

Wx(k)≤ρ (2.3)

Em queW∈Rq×nsão as ponderações das variáveis de estado nas restrições e_ρ_∈Rq são os valores que restrigem o sistema.

As restrições do sinal de controle são dados pela equação 2.4.

Vu(k)≤Ψ (2.4)

Em que,Ψsão os valores que restringem os sinais de controle,Ψ∈Rv, e_V_∈Rv×m.

2.2 Poliedros Positivamente Invariantes

Como já mencionado anteriormente, um subconjunto no espaço de estados é con-siderado invariante se todas as trajetórias originadas por um estado neste subconjunto permanecerem no mesmo conjunto. Segundo Dantas (2015), existem três definições im-portantes em relação à teoria de conjuntos positivamente invariantes sobre o domínio do sistema mostrado na equação 2.1 que são:

Definição 2.1: Um conjuntoΩ⊂Rn é dito positivamente invariante em relação ao sistema dado pela equação 2.1 se∀x(0)∈Ω⊆Rn,_x₍_k₎_∈_Ω,_∀_k_≥0.

Definição 2.2:Um conjunto invarianteΩpode ser representado por poliedros

conve-xos não vazios de Rn caracterizado por _R_[_G,ρ] ={x∈Rn; _G_x_≤_ρ}, onde _G_∈Rr×n é uma matriz eρ∈Rr um vetor,_r_∈N− {0},_n_∈N− {0}.

Definição 2.3:Um conjunto não nulo e fechado, contendo a origemΩé um conjunto

λ-contrativo para o sistema dado pela equação 2.1 com x∈Ω, se para um apropriado λ∈[0,1], x(k+1)∈λΩ, ∀x∈Ω. Se o conjunto Ω é contrativo, então ele também é positivamente invariante, porém, a recíproca nem sempre é verdadeira.

(19)

2.3. CONJUNTOS INVARIANTES CONTROLADOS 5

2.3 Conjuntos Invariantes Controlados

A abordagem da invariância positiva se tornou de grande importância para os projetos de controladores para sistemas dinâmicos sujeitos a restrições. A sua importância é de-vido a sua condição fundamental para manter a estabilidade do sistema e garantir que as restrições sejam obedecidas [Blanchini & Miani 2008 apud Dantas 2015].

Um conjunto é dito invariante controlado, de acordo com Dantas (2015), pelas seguin-tes definições e teoremas:

Definição 2.4: O conjunto Ω∈Rn é dito ser invariante controlado com respeito ao sistema mostrado nas equações 2.1 e 2.2 se∀x∈Ω,∃u∈Rm:_A_x₍_k_{) +}_B_u₍_k₎_∈_Ω.

Definição 2.5: O conjuntoζ(Ω)é dito ser o conjunto admissível a um passo deΩse ζ(Ω) ={x∈Rn:_∃_u_∈Rm:_A_x₊_B_u_∈_Ω}.

ζ(Ω)é o conjunto de todos os estados que podem alcançar em um passo para o

con-juntoΩ.

Teorema 2.1: O conjuntoΩ∈Rné invariante controlado, se e somente se,_Ω_⊆_ζ₍_Ω₎. Pelos teorema 2.1 e definições 2.4 e 2.5 observamos que um conjunto é dito invariante controlado se dada uma condição inicialx(0)∈Ω, existeutal que todos os estados a um

passo deΩcontinuam dentro deΩ.

2.3.1 Poliedros Invariantes Controlados

Um poliedro convexo pode ser representado por:

Ω=R(G,ρf) ={x:Gx≤ρf},ρf ≥0 (2.5)

Então, para um conjunto poliédrico, os valores das variáveis de estado admissíveis podem ser dadas pela equação 2.6.

Gx(k)≤ρf (2.6)

e o conjunto admissível do próximo passo paraΩ, usando a equação 2.6, é dada por:

Gx(k+1)≤ρf (2.7)

Usando as equações 2.7 e 2.1 obtemos a expressão 2.8 que restringe o sistema em relação ao poliedro.

(20)

2.3.2 Conjunto Invariante Controlado

λ

-Contrativo

Muito frequentemente, uma taxa de contração, 0≤λ≤1, é imposta para um conjunto invariante controlado para garantir a convergência do estado para a origem, ou para dimi-nuir um conjunto, ao redor da origem, se existem perturbações persistentes [Dórea 2009]. A definição de conjunto invariante controladoλ-contrativo é dado por Dantas (2015), da seguintes forma:

Definição 2.6:Um conjunto fechadoΩ⊂Rné dito invariante controlado_λ-contrativo com 0<λ≤1, se∀x∈Ω,∃u∈Rn:_A_x₊_B_u_∈_λΩ.

Reescrevendo a equação 2.8, usando a nova definição de conjunto invarianteλ-contrativo, obtemos a equação 2.9, que restringe o sistema para este caso.

GAx(k) +GBu(k)≤λρf (2.9)

2.3.3 Máximo Conjunto Invariante Controlado

Suponha que os estados de um sistema como o mostrado em 2.1 e 2.2 são sujeitos a restriçõesx∈Ω. Em geral, o conjuntoΩnão é invariante. Assim, uma possível solução

para o problema restrito é restringir os estados para um conjunto invariante contido emΩ. E também é desejável que o conjunto seja o maior possível. [Dórea 1999]

Com esse intuito, Dórea & Hennet (1999) desenvolveram uma solução para este pro-blema, chamado de o máximo conjunto invariante controlado,Supremal (A,B)-Invariant Set, usando a seguinte proposição, dada por Dantas (2015) da seguinte forma:

Proposição 2.1:A família de todos os conjuntos invariantes contidos em um conjunto convexoΩé fechado em relação à operação envoltória convexo.

ComoΩé fechado por suposição, esta proposição garante a existência do elemento máximo, ou seja, um elemento que contém todos os outros elementos.

C∞(Ω)=△máximo conjunto invariante controlado contido emΩ.

C∞(Ω)é o conjunto definido pelo envoltório convexo de todos os conjuntos invariantes

de Ω. O conjunto supremo pode ser caracterizada pelas seguintes equações recursivas [Blanchini 1994]:

Ci+1=ζ(Ci)∩Ci,C0=Ω (2.10)

C∞(Ω) =lim

i→∞Ci (2.11)

Deve ser notado queCi é o conjunto de estados para o qual existe uma sequência

(21)

2.4. POLIEDROS INVARIANTES PARA SISTEMAS COM MODELOS INCERTOS7

obtido calculando i→∞. Também pode ser introduzido o conceito de λ-contratividade nas equações 2.12 e 2.13.

C∞(Ω,λ)=△máximo conjuntoλ-contrativo contido emΩ.

Substituindo nas equações 2.12 e 2.13:

Ci+1=ζ(λCi)∩Ci,C0=Ω (2.12)

C∞(λ,Ω) =lim

i→∞Ci (2.13)

2.4 Poliedros Invariantes para Sistemas com Modelos

In-certos

Nem sempre os parâmetros dos modelos dos sistemas dinâmicos são totalmente co-nhecidos, mas isso não torna impossível estimar os intervalos de valores desses parâme-tros. Os poliedros invariantes podem ser estendidos para o caso em que esses parâmetros são incertos.

Considere o sistema linear, sujeito a incertezas paramétricas, descrito pela equação 2.14:

(

x(k+1) =A(α)x(k) +B(β)u(k) y(k) =Cx(k)

(2.14)

Onde as matrizesA(α)eB(β)são funções lineares dos seus parâmetros, isto é:

A(α) =Ao+α1A1+· · ·+αpAp=Ao+∆A(α) (2.15)

B(β) =Bo+β1B1+· · ·+βqBq=Bo+∆B(β) (2.16)

Nos quais as matrizesAoeBosão os valores nominais das matrizes e os vetoresα∈

Rpe_β_∈Rqsão os parâmetros incertos do sistema que estão situados entre os intervalos:

−α_M≤α≤α_M (2.17)

−β

M ≤β≤βM (2.18)

(22)

∆A

△

=

(

A∈Rn×n;_A₌

ηA

∑

i=1

ξiAi,

ηA

∑

i=1

ξi=1,ξi≥0

) (2.19) ∆B △ = (

B∈Rn×m;_B₌

ηB

∑

j=1 µjBj,

ηB

∑

j=1

µj=1,µj≥0

)

(2.20)

OndeηA =2p, ηB =2q. Ai e Bj são as matrizes com todas as possíveis variações

máximas e mínimas dos parâmetros deA(α)eB(β).

Dórea (1997) define os conjuntos invariantes para sistemas com modelos incertos da seguinte forma:

Definição 2.7Um conjunto Ω⊂Rn é dito _∆-invariante Controlado (Invariante Con-trolado para Sistemas com Modelos Incertos) para o sistema mostrado nas equações 2.14, 2.19 e 2.20 se,∀x∈Ω, existe um vetor controle,u∈Rm, tal que_A_x₊_B_u_∈_Ω,_∀A_∈_∆_A, ∀B∈∆B.

O conjunto admissível a um passo é dado por:

ζ(Ω,∆) ={x∈Rn;_∃_u_∈Rm;_A_x₊_B_u_∈_Ω,∀A∈∆_A,∀B∈∆_B} (2.21)

Para o caso poliédrico,Ω=R[G,ρf]. Temos:

(GA)∆=

                     GA1 GA2 ... GAηA

GA1 ... GAηA

... GA1

... GAηA

                    

,(GB)∆=

                     GB1 GB1 ... GB1 GB2 ... GB2 ... GBηB

... GBηB

                    

,ρ∆_f =

                     ρf ρf ... ρf ρf ... ρf ... ρf ... ρf                      (2.22)

Onde,G∈Rg×n;₍_GA₎∆_∈R(ηAηBg)×n;₍_GB₎∆_∈_R(ηAηBg)×m;_ρ∆

f ∈RηAηBg.

Assim, o conjunto admissível a um passo é dado por:

ζ(R[G,ρf],∆) =

n

(23)

2.4. POLIEDROS INVARIANTES PARA SISTEMAS COM MODELOS INCERTOS9

2.4.1 Máximo Conjunto

∆

-Invariante

Como mencionado na Proposição 2.1, a família de todos os conjuntos invariantes contidos em um conjunto convexoΩé fechado para a operação envoltório convexo, o que

assegura a existência do conjunto máximo:

C∞(Ω,∆)=△ máximo conjunto∆-invariante contido emΩ.

Assim, podem ser obtidas as seguintes equações recursivas [Blanchini 1999]:

Ci+1=ζ(Ci,∆)∩Ci,C0=Ω (2.24)

C∞(Ω,∆) =lim

(24)

(25)

Capítulo 3

Rastreamento de Referências sob

Restrições

Muitos problemas em engenharia de controle tratam de rastreamento de forma ótima, de uma dada referência, enquanto assegura que as restrições de controle e estados são todas satisfeitas ao mesmo tempo. A obtenção de resultados teóricos sobre estabilidade, viabilidade e robustez para qualquer rastreamento restrito de referências que variam com tempo são extremamente difíceis. Então, o problema de rastreamento é geralmente res-trito apenas ao problema de otimizar o rastreamento para sinais de referência constantes [Balandat 2010].

Naturalmente, quando se fala em rastreamento de referência, se pensa em controlar o sistema calculando o sinal de controle a partir das variáveis de estado medidas. Segundo Dorf & Bishop (2008), o projeto de um controlador em variáveis de estados apresenta 3 passos.

Primeiramente é assumido que todas as variáveis do sistema possam ser medidas e utilizadas em uma lei de controle, o que, normalmente, na prática não é possível, pois geralmente não podem medir todos os estados do sistema. O segundo passo é construir um observador para estimar os estados do sistema que não possam ser medidos. O terceiro, e ultimo, passo é usar as variáveis medidas e estimadas na lei de controle.

Neste projeto, levaremos em consideração que todas as variáveis de estado são com-pletamente mensuráveis.

Existem diversas formas de rastreamento de referência. Neste projeto serão utilizados os servosistemas de tipo 0 como base.

Dado um sistema LIT na forma das equações 2.1 e 2.2 o sinal de controle de um servosistema tipo 0 pode ser calculado por 3.1

u(k) =Kpe(k)−Kx(k) (3.1)

Onde,

(26)

12 CAPÍTULO 3. RASTREAMENTO DE REFERÊNCIAS SOB RESTRIÇÕES

E Kp e K são os ganhos proporcionais ao erro e as variáveis de estado,

respectiva-mente.

O diagrama de blocos do servosistema de tipo 0 pode ser observado na Fig. 3.1:

Figura 3.1: Servosistema tipo 0

Para calcular um sinal de controleu que atenda as restrições, é necessário deixar as

equações em função do sinal de controle, então, substituindo a equação 2.1 na 2.3 obtemos 3.3.

W(Ax(k) +Bu(k))≤ρ (3.3)

A partir de 3.3 obtemos 3.4

WBu(k)≤ρ−WAx(k) (3.4)

Para fazer o sistema seguir a referência é necessária a utilização do erro dado pela equação 3.2, sabendo que a saída do sistema é dada pela 2.2 e o estado futuro sendo calculado por 2.1 obtemos 3.5.

e(k+1) =r−CAx(k)−CBu(k) (3.5)

O módulo dee(k+1)pode ser minimizado a partir da seguinte restrição:

|e(k+1)|=|CAx(k) +CBu(k)−r| ≤ι (3.6)

(27)

13

Assim|e(k+1)|pode ser minimizado minimizando-seι:

_CB_u₍_k₎₋_ι1_≤_r₋_CA_x₍_k₎

−CBu(k)−ι1≤ −r−CAx(k)

(3.8) (3.9) Juntando as equações 2.4, 3.4, 3.8 e 3.9 obtemos todas as restrições do sistema que podem ser representadas pela equação 3.10.

    WB 0 V 0 CB −1 −CB −1    

u(k)

ι ≤    

ρ−WAx(k)

Ψ

r−CAx(k)

−r+CAx(k)



  

(3.10)

O sistema de equações 3.10 garante que as restrições sejam respeitadas e minimizar o

eimplica minimizar o módulo do erro de rastreamento um passo à frente. A partir desse

sistema é possível utilizar o conceito de máximo conjunto invariante controlado, estudado no Capítulo 2, para obter o conjuntoR[G,ρf]que é o maior conjunto invariante controlado

contido emR[W,ρ]. Desta forma, obtemos o seguinte sistema de equações:

    GB 0 V 0 CB −1 −CB −1    

u(k)

ι ≤    

ρf−GAx(k)

Ψ

r−CAx(k)

−r+CAx(k)



  

(3.11)

A partir da equação 3.11 é possível calcular o sinal de controle que leva até a referência desejada, sem violar as restrições, usando programação linear. A função objetivo, no caso desse sistema, é o módulo do erro um passo à frente, minimizar o erro implica minimizar o módulo do erro de rastreamento um passo à frente. Para isso, o sistema deve obedecer às proposições mencionadas no Capitulo 2, a origem deve estar contida no conjuntoΩe a referência deve ser alcançável, ou seja, o ponto de equilíbrio(u,x), que corresponda a

y=r, deve satisfazer as restrições no estado e no controle.

O problema de otimização é descrito por :

min Z=ι

su jeito a GBu(k)≤ρ−GAx(k)

Vu(k)≤Ψ

CBu(k)−ι≤r−CAx(k)

(28)

(29)

Capítulo 4

Controle Robusto por Realimentação de

Estados

Em sistemas práticos, incertezas aparecem quando alguns aspectos dos modelos dos sistemas não são completamente conhecidos, como os valores dos parâmetros que podem variar dependendo das condições de operação do sistema. Já que os projetos dos contro-ladores dependem dos sistemas a serem controlados, se os parâmetros do controlador são calculados a partir de um modelo com parâmetros diferentes do processo real, pode acar-retar em perda de desempenho, levar o sistema à instabilidade, entre outros problemas.

Então, podemos chamar de controle robusto, um sistema de controle que é tolerante às variações dos parâmetros do processo. A robustez é muito importante, já que na prá-tica, geralmente, os modelos usados não conseguem descrever perfeitamente todas as características do processo e os processos reais são vulneráveis a perturbações externas, não-linearidades e variações das condições operacionais [Ventin 2010].

Apesar de muitas vezes alguns parâmetros dos modelos de sistemas dinâmicos não serem exatamente conhecidos, é possível determinar os valores dos intervalos em que estes parâmetros variam. O controle para tais sistemas deve ser robusto no sentido de que o objetivo especificado previamente deve ser atingido, independente dos valores destes parâmetros [Dórea 1997].

Usando o conjunto∆-Invariante é possível fazer com que o sistema de controle obe-deça todas as restrições impostas para cada uma das variações de parâmetros do sistema. Usando o conceito de máximo conjunto∆-invariante e a equação 3.11 podemos obter a seguinte equação para as restrições:



  

(GB)∆ 0

V 0

CB −1 −CB −1



  

u(k)

ι

≤



  

ρ∆_f−(GA)∆x(k)

Ψ

r−CAx(k)

−r+CAx(k)



  

(4.1)

Mas, como o sistema descrito pela equação 2.14 é incerto em relação a A e B, é necessário utilizar como valor inicial os seus valores nominais,Ao eBo, para que possa

ser calculado o sinal de controle, já que não se tem um valor exato para as matrizes (vide equações 2.15 e 2.16).

(30)

16 CAPÍTULO 4. CONTROLE ROBUSTO POR REALIMENTAÇÃO DE ESTADOS

sistema à referência, pode ser calculada resolvendo um problema de programação linear, cuja função objetivo é o erro de rastreamento e as restrições são dadas por:



  

(GB)∆ 0

V 0

CBo −1

−CBo −1



  

u(k)

ι

≤



  

ρ∆_f −(GA)∆x(k)

Ψ

r−CAox(k)

−r+CAox(k)



  

(4.2)

O problema de otimização é descrito por :

min Z=ι

su jeito a (GB)∆u(k)≤ρ∆_f−(GA)∆x(k)

Vu(k)≤Ψ

CBou(k)−ι≤r−CAox(k)

−CBou(k)−ι≤ −r+CAox(k)

Porém, só a equação 4.2 não garante o seguimento robusto de referência como po-derá ser visto no Capítulo de simulações, para que o mesmo seja garantido, é proposta a reidentificação dos parâmetros de Ae B quando for detectado que a saída do modelo nominal (yo) é diferente da saída medida (ym) no processo real, ou seja, |yo−ym| ≥χ,

ondeχé a tolerância.

Como o modelo deve ser igual ao sistema real então podemos dizer que:

ym=Cx(k) (4.3)

Substituindo ox(k)na equação 4.3 pela equação 2.1 obtemos:

ym=CAx(k−1) +CBu(k−1) (4.4)

Supondo um caso base, ondeA=

a1,1 a1,2

a2,1 a2,2

, B=

b1 b2

eC=

c1 c2 ,

te-mos:

ym = c1a1,1+c2a2,1 c1a1,2+c2a2,2

x(k−1) + (c1b1+c2b2)u(k−1) = c1a1,1x(k−1)1+c2a2,1x(k−1)1+c1a1,2x(k−1)2+c2a2,2x(k−1)2+

c1b1u(k−1) +c2b2u(k−1) (4.5)

(31)

17

ym= c1x(k−1)1 c2x(k−1)1 c1x(k−1)2 c2x(k−1)2 c1u(k−1) c2u(k−1)

       

a1,1

a2,1

a1,2

a2,2

b1 b2         (4.6)

Generalizando para qualquer tamanho deA,BeC, temos:

ym=

CTx(k−1)1 · · · CTx(k−1)n CTu(k−1)1 · · · CTu(k−1)m

                               

a1,1

...

an,1

a1,2

...

an,2

...

an,n

b1,1

...

bn,1

b1,2

...

bn,2

...

bn,m

                                (4.7)

Para que o sistema reidentificado continue dentro do poliedro∆-invariante controlado,

no processo de reidentificação devem ser adicionadas restrições que garantam que as ma-trizesA e Breidentificadas pertençam respectivamente a ∆A e ∆B vide equações 2.19 e

(32)

18 CAPÍTULO 4. CONTROLE ROBUSTO POR REALIMENTAÇÃO DE ESTADOS                                              

a1,1

...

an,1

a1,2

...

an,2

...

an,n

b1

...

bn

−a1,1

... −an,1

−a1,2

... −an,2

... −an,n

−b1

... −bn

                                              ≤                                              

max(Aa(1,1),Aa(n+1,1),Aa(2n+1,1),· · ·,Aa((ηA−1)n+1,1))

...

max(Aa(n,1),Aa(n+n,1),Aa(2n+n,1),· · ·,Aa((ηA−1)n+n,1))

max(Aa(1,2),Aa(n+1,2),Aa(2n+1,2),· · ·,Aa((ηA−1)n+1,2))

...

max(Aa(n,2),Aa(n+n,2),Aa(2n+n,2),· · ·,Aa((ηA−1)n+n,2))

...

max(Aa(n,n),Aa(n+n,n),Aa(2n+n,n),· · ·,Aa((ηA−1)n+n,n))

max(Ba(1),Ba(n+1),Ba(2n+1),· · ·,Ba((ηB−1)n+1))

...

max(Ba(n),Ba(n+n),Ba(2n+n),· · ·,Ba((ηB−1)n+n))

−min(Aa(1,1),Aa(n+1,1),Aa(2n+1,1),· · ·,Aa((ηA−1)n+1,1))

...

−min(Aa(n,1),Aa(n+n,1),Aa(2n+n,1),· · ·,Aa((ηA−1)n+n,1))

−min(Aa(1,2),Aa(n+1,2),Aa(2n+1,2),· · ·,Aa((ηA−1)n+1,2))

...

−min(Aa(n,2),Aa(n+n,2),Aa(2n+n,2),· · ·,Aa((ηA−1)n+n,2))

...

−min(Aa(n,n),Aa(n+n,n),Aa(2n+n,n),· · ·,Aa((ηA−1)n+n,n))

−min(Ba(1),Ba(n+1),Ba(2n+1),· · ·,Ba((ηB−1)n+1))

...

−min(Ba(n),Ba(n+n),Ba(2n+n),· · ·,Ba((ηB−1)n+n))

                                              (4.8)

Onde,Aa=



 

A1 ... AηA





eBa=



 

B1 ... BηB





.

O procedimento de cálculo do sinal de controle e da reidentificação dos parâmetros do sistema fica da seguinte forma:

1. Calcular o Poliedro Invariante Controlado a partir das restriçõesR[W,ρ].

2. Calcular o sinal de controle resolvendo o problema de otimização descrito, utili-zando os valores nominais das matrizesAeB,AoeBo.

3. Aplicar o sinal de controle calculado no sistema.

4. Se |yo−ym| ≥χ, resolver o sistemas de equações 4.7 e 4.8 para obter os novos

valores deAeB.

(33)

Capítulo 5

Controle Robusto por Realimentação de

Saída

Também pode ser utilizado o conjunto ∆-Invariante para que o sistema de controle obedeça todas as restrições, mas nem todos os sistemas que são invariantes controlados para realimentação de estados também o são para realimentação de saída, como também não existe um algoritmo para calcular um conjunto invariante controlado para o mesmo.

Neste Capítulo para facilitar o uso dos algortimos o conjunto invariante é normalizado para que o vetorρf tenha seus valores iguais a 1, ou sejaGx≤1.

5.1 Modelo Conhecido

Apesar de não existir um algoritmo para calcular o conjunto, é possível descobrir se um conjunto é invariante controlável para realimentação de saída (o.f.c.i).

Usando o sistema mostrado nas equaçãos 2.1 e 2.2. Considere o conjunto de saídas admissíveis associados aΩ:

Y(Ω) ={y:y=Cx para x∈Ω}. (5.1)

De acordo com Dórea (2009):

Definição 5.1: Um conjuntoΩ⊂Rn é dito invariante controlado para realimentação de saída (o.f.c.i) para o sistema mostrado nas equações 2.1 e 2.2, se,∀y∈Y(Ω),∃u∈U :

Ax+Bu∈Ω,∀x∈Ω :Cx=y.

Esta definição implica dizer que se um estado em um tempo k pertence aΩ, ondeΩé invariante controlado por realimentação de saída, tendo conhecimento dey(k)é possível obrigar o estado seguinte, x(k+1), a permanecer em Ω através do cálculo do sinal de

controle u(k)∈U. Como consequência, se o estado inicial, x(0), pertence a Ω então, através de uma realimentação de saída adequado, u(y(k)), é possível manter x(k) em

Ω∀k.

(34)

20 CAPÍTULO 5. CONTROLE ROBUSTO POR REALIMENTAÇÃO DE SAÍDA

Ω={x:Gx≤1},U ={u:Vu≤1}.

ComG∈Rg×n _e_V_∈Rv×m. O conjunto de saídas admissíveis, que é um poliedro convexo e fechado contendo a origem, é dado por:

Y(Ω) ={y:y=Cx para x:Gx≤1}. (5.2)

É possível estender aDefinição 5.1usando o conceito de taxa de contração (λ), onde um conjuntoΩéo.f.c.i.com taxa de contraçãoλse, e somente se:

∀y∈Y(Ω),∃u:G(Ax+Bu)≤λ1, Vu≤1∀x:Cx=y, Gx≤1. (5.3)

Definindo os vetoresξeφ, dados por:

ξj(y) =arg maxGjAx

su jeito a Gx≤1 (5.4)

Cx=y

φj(y) =GjAξj(y) (5.5)

Como a mesma entrada u precisa funcionar para todos os x∈Ω consistente com a saída y, então o pior caso de xpode ser calculado linha por linha. Consequentemente, a

equação 5.3 é equivalente a:

∀y∈Y(Ω),∃u:

φ(y)

0

+

GB V

u≤

λ1 1

(5.6)

Considerando agora o seguinte cone poliédrico:

Γ=

t w

∈Rg+v : _t,_w_≥0, [tTwT]

GB V

=0

(5.7)

Em quen

Ti Wi T, i=1, ...,nr

o

forma um conjunto gerador mínimo deΓ. Como

Γé pontiagudo, os elementos desse conjunto gerador mínimo são os pontos extremos de

Γ. Então, qualquer vetor

t w

∈Γ podem ser escritos como uma combinação linear positiva de vetores

Ti Wi

T

.

(35)

5.1. MODELO CONHECIDO 21

Ti Wi

φ(y)

0

≤

Ti Wi

λ1 1

, ∀y∈Y(Ω), ∀i=1, ...,nr. (5.8)

Assim é possível estabelecer o seguinte teorema [Dórea 2009]:

Teorema 5.1:O conjunto poliédricoΩ={x:Gx≤1}éo.f.c.icom taxa de contração

λse, e somente se,∀i=1, ...,nr.: g

∑

j=1Ti jGjAξj≤(

g

∑

j=1Ti j(λ)) +Wi1,

∀y,ξj,j=1,2, ...,g:Gξj≤1,−Gξj+y≤1.

(5.9)

Fazendo o teste se o conjunto invariante éo.f.c.i. e se o mesmo retornar positivo, é

possível fazer o controle por realimentação de saída. Da mesma forma que nocapítulo 4, utilizando o sistema de equações dado por 4.2 é possível fazer o controle do sistema, tendo apenas um único problema, que consiste em não ser possível obter os valores das variáveis de estado. Então, como já foi falado neste capítulo, é possível estimar o pior caso para estas variáveis utilizando as equações em 5.5, onde podem ser calculado os vetoresξe φ. Mas além desses vetores, será necessária a criação de dois novos vetores

γ+ e γ−. Considere agora a restrição |Cx(k+1)−r| ≤e, escrita em termos do modelo

conhecidox(k+1) =Ax(k) +Bu(k), resultando em:

CAx(k) +CBu(k)≤r+ι

−CAx(k)−CBu(k)≤r−ι

(5.10) (5.11)

A exemplo do vetor φ(y) em 5.5, pode-se calcular o vetor γ(y(k)) que representa o

pior caso de

CA

−CA

x(k), linha por linha:

κj(y) =arg max

CA −CA

j

x

Cx=y

Assim obtemos:

γ+(y) =CAκ1(y) (5.13)

γ−(y) =−CAκ2(y) (5.14)

(36)



  

GB 0

V 0

CB −1 −CB −1



  

u(k)

ι

≤



  

1−φ(y(k))

Ψ

r−γ−(y(k))

−r−γ+(y(k))



  

(5.15)

Desta forma, o problema de otimização é dado por:

min Z=ι

su jeito a GBu(k)≤1−φ(y(k))

Vu(k)≤Ψ

CBu(k)−ι≤r−γ−(y(k))

−CBu(k)−ι≤ −r+γ+(y(k))

5.2 Modelo Incerto

Considerando agora o caso dos modelos incertos, é possível espandir a definição de

o.f.c.i.para este caso, usando o conceito de poliedros invariantes para modelos incertos

apresentado naSessão 3.4, onde:

(

x(k+1) =A(α)x(k) +B(β)u(k) y(k) =Cx(k)

(5.16)

Então, para o caso Incerto, podemos dizer que:

Definição 5.3:Um conjuntoΩ∈Rné dito_∆-invariante controlado por realimentação de saída (o.f.c.i.) para o sistema mostrado na equação 2.14, se, ∀y∈Y(Ω), ∃u∈U :

A(α)x+B(β)u∈Ω, ∀x∈Ω:Cx=y.

Assim, dado:

Ω={x:Gx≤1},U ={u:Vu≤1}.

ComG∈Rg×n _e _V_∈Rv×m. Como a matriz C não é incerta, o conjunto de saídas admissíveis, que é um poliedro convexo e fechado contendo a origem, é dado por:

Y(Ω) ={y:y=Cx para x:Gx≤1}. (5.17)

(37)

5.2. MODELO INCERTO 23

∀y∈Y(Ω),∃u:G(A(α)x+B(β)u)≤λ1, Vu≤1∀x:Cx=y, Gx≤1. (5.18)

Definindo os vetoresξ∆eφ∆, dados por:

ξ∆_j(y) =arg max(GA)∆jx

Cx=y

φ∆_j(y) = (GA)∆_jξ∆_j(y) (5.20) Considerandoφ∆_η_B(y) =



 

φ∆(y)

...

φ∆(y)



 

ηB×1

e ξ∆_η_B(y) =



 

ξ∆(y)

...

ξ∆(y)



 

ηB×1

, ou seja, vetores

comηBrepetições do vetorφ∆(y)e do vetorξ∆(y).

Então, a equação 5.18 é equivalente a:

∀y∈Y(Ω),∃u:

φ∆_η_B(y)

0

+

(GB)∆

V u≤ λ1 1 (5.21)

Considerando agora o seguinte cone poliédrico:

Γ=

t w

∈RηBg+v : _t_,_w_≥0_, _[_tT_wT_]

(GB)∆

V

=0

(5.22)

Com o mesmo conjunto gerador do caso sem incertezas. Usando o Lema de Farkas, temos:

Ti Wi

φ∆_η_B(y)

0

≤

Ti Wi

λ1 1

, ∀y∈Y(Ω), ∀i=1, ...,nr. (5.23)

Assim é possível definir um novo teorema para o caso incerto:

Teorema 5.2: O conjunto poliédricoΩ={x:Gx≤1}éo.f.c.icom taxa contrativo

λse, e somente se,∀i=1, ...,nr.:

ηBg

∑

j=1Ti j(GA) ∆

jξ∆η_{B j} ≤( ηBg

∑

j=1Ti j(λ)) +Wi1,

∀y,ξ∆η_{B j},j=1,2, ...,ηBg:GηBξ

∆

η_{B j} ≤1,−GηBξ

∆

η_{B j}+y≤1.

(38)

Fazendo o teste se o conjunto invariante éo.f.c.i.para o caso em que os parâmetros

são incertos e se o mesmo retornar positivo, também é possível fazer o controle por reali-mentação de saída. Neste caso serão utilizadas as equações 5.20 para calcular os vetores

ξ∆ eφ∆ e utilizando a equação a seguir para calcular novos valores para oγ+_o eγ−_o. Considere agora a restrição|Cx(k+1)−r| ≤e, escrita em termos do modelo nominal x(k+1) =Aox(k) +Bou(k), resultando em:

_CA

ox(k) +CBou(k)≤r+ι

−CAox(k)−CBou(k)≤r−ι

(5.25) (5.26)

Da mesma forma do modelo conhecido, a exemplo do vetor φ(y) em 5.5, pode-se calcular o vetorγ(y(k))que representa o pior caso de

CAo

−CAo

x(k), linha por linha:

κj(y)o=arg max

CAo

−CAo

j

x

Cx=y

Assim obtemos:

γ+(y)o=CAoκ1(y)o (5.28)

γ−(y)o=−CAoκ2(y)o (5.29)

Assim o seu sistema de equações fica da seguinte forma:



  

(GB)∆ 0

V 0

CBo −1

−CBo −1



  

u(k)

ι

≤



  

1−φ∆ηB

Ψ

r−γ−_o

−r−γ+_o



  

(5.30)

Da mesma forma que no capítulo anterior, será necessário fazer a reidentificação dos parâmetros do sistema utilizando as equações 4.7 e 4.8, mas como também exige o valor do x, então será utilizado a sua estimativa do pior caso. Assim a equação 4.7 fica da

(39)

5.2. MODELO INCERTO 25

ym= CTκ(y(k−1))1 · · · CTκ(y(k−1))n CTu(k−1)1 · · · CTu(k−1)m

                               

a1,1

...

an,1

a1,2

...

an,2

...

an,n

b1,1

...

bn,1

b1,2

...

bn,2

...

bn,m

                                (5.31)

O procedimento de cálculo do sinal de controle e da reidentificação dos parâmetros do sistema fica da seguinte forma:

1. Calcular o Poliedro Invariante Controlado a partir das restriçõesR[W,ρ].

2. Testa se o sistema é o.f.c.i., caso sim, passa para o passo 3, senão não é possível

utilizar esta técnica.

3. Calcular os valores deξ(y(k))eκ(y(k))o.

4. Calcular o sinal de controle resolvendo o problema de otimização descrito, utili-zando os valores nominais das matrizesAeB,AoeBo.

5. Aplicar o sinal de controle calculado no sistema.

6. Se |yo−ym| ≥χ, resolver o sistemas de equações 4.8 e 5.31 para obter os novos

valores deAeB.

(40)

(41)

Capítulo 6

Simulações e Resultados

Neste Capítulo serão mostradas simulações de exemplos dos conceitos estudados nos capítulos anteriores, utilizando o algoritmo do máximo conjunto invariante controlado desenvolvido por Dórea (1997), bem como exemplos resolvidos utilizando o controle por realimentação de estados e por realimentação de saída. Nestes exemplos, serão tratados primeiramente sistema com controle regulatório, em que o propósito é apenas levar até o ponto de equilíbrio do sistema, e a cada passo é aumentada a complexidade do controle do sistema até a necessidade do uso de um controlador robusto.

O sistema utilizado é representado pela seguinte equação de estados:

x(k+1) =Ax(k) +Bu(k) y(k) =Cx(k)

(6.1) (6.2)

Com as matrizes A=

0.9347 0.5194

0.33835 0.831

, B=

−1.4462

−0.7012

e C=

0.5 0.5 .

O sistema é sujeito as seguintes restrições de estado e de controle respectivamente:



  

1 0

−1 0

0 1

0 −1



  

x(k)≤



  

4 4 4 4



  

(6.3)

1 −1

u(k)≤

1 1

(6.4)

6.1 Realimentação de Estados

6.1.1 Controle Regulatório

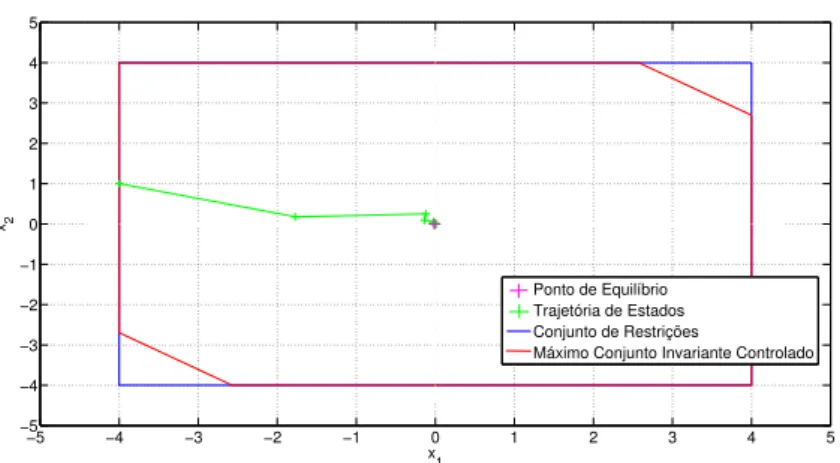
Primeiro, é aplicado o algoritmo do máximo conjunto invariante controlado às restri-ções do sistemas, usando uma taxa de contração(λ) de 0.99, obtendo o seguinte conjunto

(42)

28 CAPÍTULO 6. SIMULAÇÕES E RESULTADOS         1 0 −1 0 0 1 0 −1

0.1379 0.1510

−0.1379 −0.1510

       

x(k)≤

        4 4 4 4 0.9589

0.9589

        (6.5)

Na Fig 6.1 é mostrado o poliedro antes e depois da aplicação do algoritmo.

−5 −4 −3 −2 −1 0 1 2 3 4 5

−5 −4 −3 −2 −1 0 1 2 3 4 5 x 1 x2

Conjunto de Restrições

Máximo Conjunto Invariante Controlado

Figura 6.1: Poliedro Invariante Controlado

Após o cálculo do poliedro invariante, é utilizado um método de otimização para calcular o valor deuque leva o sistema ao ponto de equilíbrio, as restrições para o método

de otimização são dadas por:

GB −ρf

V 0

u(k)

ε

≤

−GAx(k)

Ψ

(6.6)

Onde, G=

        1 0 −1 0 0 1 0 −1

0.1379 0.1510

−0.1379 −0.1510

       

, ρf =

        4 4 4 4 0.9589

0.9589

       

e εé a variável que vai ser

minimizada para levar o sistema para o ponto de equilíbrio. O problema de otimização é descrito por:

min Z=ε

su jeito a GBu(k)−ρfε≤ −GAx(k)

Vu(k)≤Ψ

(43)

6.1. REALIMENTAÇÃO DE ESTADOS 29

Minimizando o sistema com essas restrições cuja função objetivo é igual amin z=ε, descobrimos o melhor valor de u que respeita as restrições e que leva para o ponto de

equilíbrio, o que pode ser observado nas Figs 6.2 e 6.3, parax(0) =

−4 1

.

−5 −4 −3 −2 −1 0 1 2 3 4 5

x₁

x2

Ponto de Equilíbrio Trajetória dos Estados Conjunto de Restrições

Figura 6.2: Controle Regulatório com Realimentação de Estados

0 5 10 15

−1.2 −1 −0.8 −0.6 −0.4 −0.2 0 0.2

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.3: Sinal de Controleupara o Controle Regulatório com Realimentação de

Esta-dos

6.1.2 Rastreamento de Referência

No rastreamento de referência, é utilizada a equação 3.11, que otimiza o sistema, para determinar o valor deuque minimizará o erro, obtendo os resultados mostrados nas Figs

6.4, 6.5 e 6.6, usando uma referência igual a 1 ex(0) =

0 0

(44)

30 CAPÍTULO 6. SIMULAÇÕES E RESULTADOS

0 2 4 6 8 10 12 14 16 18 20

0 0.2 0.4 0.6 0.8 1 1.2 1.4

Tempo(s)

Amplitude

Saída do Sistema Referência

Figura 6.4: Rastreamento de Referência com Realimentação de Estados

−5 −4 −3 −2 −1 0 1 2 3 4 5

x₁

x2

Ponto de Equilíbrio Trajetória dos Estados Conjunto de Restrições

Figura 6.5: Trajetória dos Estados para o Rastreamento de Referência com Realimentação de Estados

0 5 10 15

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.6: Sinal de Controleu para o Rastreamento de Referência com Realimentação

(45)

Podemos observar pelos resultados que o sistema teve um ótimo comportamento se-guindo a referência e obedecendo todas as restrições do poliedro, mas isso só ocorre quando não há qualquer influência de perturbação no sistema, o que será mostrado na próxima sessão.

6.1.3 Rastreamento Robusto de Referência

Suponhamos queA=

0.9347+α 0.5194

0.33835 0.831

, B=

−1.4462

−0.7012+β

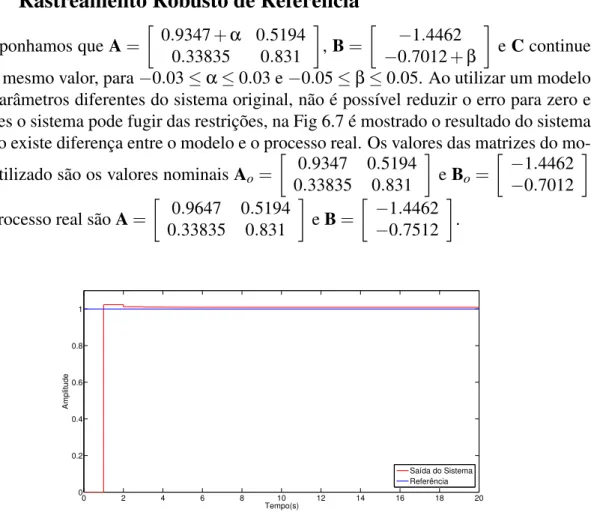
eCcontinue com o mesmo valor, para−0.03≤α≤0.03 e−0.05≤β≤0.05. Ao utilizar um modelo

com parâmetros diferentes do sistema original, não é possível reduzir o erro para zero e as vezes o sistema pode fugir das restrições, na Fig 6.7 é mostrado o resultado do sistema quando existe diferença entre o modelo e o processo real. Os valores das matrizes do mo-delo utilizado são os valores nominaisAo=

0.9347 0.5194

0.33835 0.831

eBo=

−1.4462

−0.7012

e do processo real sãoA=

0.9647 0.5194

0.33835 0.831

eB=

−1.4462

−0.7512

.

0 2 4 6 8 10 12 14 16 18 20

0 0.2 0.4 0.6 0.8 1 Tempo(s) Amplitude

Figura 6.7: Controle com Modelo Incerto com Realimentação de Estados

Então, para que as restrições não sejam violadas para todos os casos de variação de parâmetros, é calculado o máximo conjunto∆-invariante controlado, mostrado no Capí-tulo 4. Obtendo-se os valores mostrados na equação 6.8 e seu poliedro mostrado na Fig 6.8: G=         1 0 −1 0 0 1 0 −1

0.1510 0.1597

−0.1510 −0.1597

       

, ρf =

        4 4 4 4 0.9604

0.9604

(46)

−5 −4 −3 −2 −1 0 1 2 3 4 5

−5 −4 −3 −2 −1 0 1 2 3 4 5 x₁ x2

Máximo Poliedro ∆−invariante Controlado Máximo Poliedro Invariante Controlado Conjunto de Restrições

Figura 6.8: Poliedro∆-invariante Controlado

O máximo conjunto ∆-invariante controlado resolve o problema para as restrições,

mas o erro do seguidor de referência não foi resolvido, então é necessário utilizar a rei-dentificação que foi mostrada no Capítulo 4. A qual é feita pela resolução do sistema 6.9, com o resultado mostrado nas Figs 6.9, 6.10 e 6.11.

                       

CTx(k−1)1 CTx(k−1)2 CTu(k−1)

−CTx(k−1)1 −CTx(k−1)2 −CTu(k−1)

                   

1 0 0 0 0 0

0 1 0 0 0 0

0 0 1 0 0 0

0 0 0 1 0 0

0 0 0 0 1 0

0 0 0 0 0 1

−1 0 0 0 0 0

0 −1 0 0 0 0

0 0 −1 0 0 0

0 0 0 −1 0 0

0 0 0 0 −1 0

0 0 0 0 0 −1

                                                   

a1,1

a2,1

a1,2

a2,2

b1 b2         ≤                         yreal

−yreal

max(Aa(1,1),Aa(3,1))

max(Aa(2,1),Aa(4,1))

max(Aa(1,2),Aa(3,2))

max(Aa(2,2),Aa(4,2))

max(Ba(1),Ba(3))

max(Ba(2),Ba(4))

−min(Aa(1,1),Aa(3,1))

−min(Aa(2,1),Aa(4,1))

−min(Aa(1,2),Aa(3,2))

−min(Aa(2,2),Aa(4,2))

−min(Ba(1),Ba(3))

−min(Ba(2),Ba(4))

                        (6.9)

OndeAa=



  

0.9047 0.5194

0.33835 0.831

0.9647 0.5194

0.33835 0.831



  

eBa=



  

−1.4462

−0.7512

−1.4462

(47)

0 2 4 6 8 10 12 14 16 18 20

0 0.2 0.4 0.6 0.8 1

Tempo(s)

Amplitude

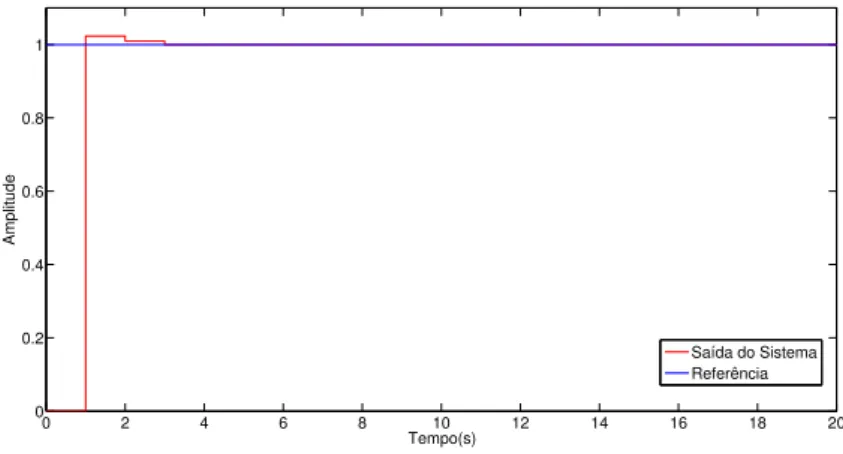
Figura 6.9: Controle com modelo reidentificado em Realimentação de Estados

−5 −4 −3 −2 −1 0 1 2 3 4 5

x₁

x2

Máximo Poliedro ∆−invariante Controlado Máximo Poliedro Invariante Controlado Conjunto de Restrições

Trajetória dos Estados Ponto de Equilíbrio

Figura 6.10: Trajetória dos Estados com Rastreamento Robusto com Realimentação de Estados

0 2 4 6 8 10 12 14 16 18 20

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4

Tempo(s)

Amplitude

Sinal de Controle

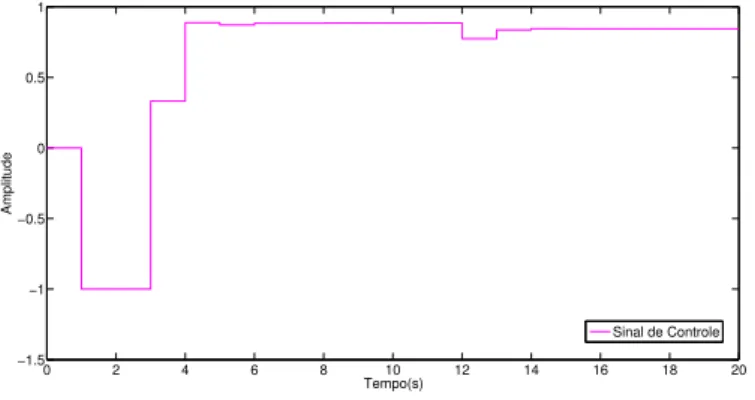
Figura 6.11: Sinal de Controle upara controle com reidentificação com Realimentação

(48)

Testando o sistema com uma variação nos seus parâmetros em k=10, onde A=

0.9047 0.5194

0.33835 0.831

eB=

−1.4462

−0.6512

obtemos o seguinte resultado:

0 2 4 6 8 10 12 14 16 18 20

0 0.2 0.4 0.6 0.8 1 1.2 1.4

Tempo(s)

Amplitude

Figura 6.12: Controle com modelo reidentificado com mudança de parâmetros em k = 10 com Realimentação de Estados

0 2 4 6 8 10 12 14 16 18 20

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.13: Sinal de Controleupara controle com reidentificação e mudança de

parâme-tros com Realimentação de Estados

Percebemos que mesmo com a variação de seus parâmetros, o sistema consegue voltar à referência, isto ocorre devido à reidentificação dos parâmetros.

(49)

0 2 4 6 8 10 12 14 16 18 20 0

0.5 1 1.5 2 2.5 3 3.5

Tempo(s)

Amplitude

Figura 6.14: Controle com modelo reidentificado em Realimentação de Estados com re-ferência igual à 3

−5 −4 −3 −2 −1 0 1 2 3 4 5 −5

−4 −3 −2 −1 0 1 2 3 4 5

X₁

X2

Máximo Poliedro ∆−invariante Controlado Máximo Poliedro Invariante Controlado Conjunto de Restrições Trajetória dos Estados Ponto de Equilíbrio

Figura 6.15: Trajetória dos Estados com Rastreamento Robusto com Realimentação de Estados com referência igual à 3

0 2 4 6 8 10 12 14 16 18 20 −1.5

−1 −0.5 0 0.5 1

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.16: Sinal de Controle upara controle com reidentificação com Realimentação

de Estados com referência igual à 3

(50)

0 2 4 6 8 10 12 14 16 18 20 0

0.5 1 1.5 2 2.5 3 3.5 4 4.5

Tempo(s)

Amplitude

Figura 6.17: Controle com modelo reidentificado em Realimentação de Estados com re-ferência igual à 4

−5 −4 −3 −2 −1 0 1 2 3 4 5 −5

−4 −3 −2 −1 0 1 2 3 4 5

X₁

X2

Máximo Poliedro ∆−invariante Controlado Máximo Poliedro Invariante Controlado Conjunto de Restrições Trajetória dos Estados Ponto de Equilíbrio

Figura 6.18: Trajetória dos Estados com Rastreamento Robusto com Realimentação de Estados com referência igual à 4

0 2 4 6 8 10 12 14 16 18 20 −1.5

−1 −0.5 0 0.5 1

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.19: Sinal de Controle u para controle com reidentificação com Realimentação

de Estados com referência igual à 4

(51)

6.2. REALIMENTAÇÃO DE SAÍDA 37

6.2 Realimentação de Saída

6.2.1 Controle Regulatório

Como já foi explicado no capítulo anterior, não existe um algoritmo que calcule um conjunto invariante controlado para o caso de realimentação de saída, mas é possível saber se um conjunto é invariante controlado para realimentação de saída (o.f.c.i.). Para o caso

do sistema mencionado no exemplo, comλ=0.99 o sistema éo.f.c.i.. Então, utilizando

a equação 6.6 mostrada na sessão anterior é possível fazer o controle regulatório, porém, no caso da realimentação de saída, ox(k)é desconhecido, então, é utilizado a equação 5.5

mostrada no capítulo anterior para encontrar o pior caso para ox, assim podemos obter a

seguinte equação:

GB −ρf

V 0

u(k)

ε

≤

−φ Ψ

(6.10)

Como não foi calculado um novo conjunto invariante, e sim testado se o conjunto era invariante controlado para realimentação de saída, então, o conjunto calculado na sessão anterior é o mesmo utilizado nesta. Para os testes o estado inicial foi o mesmo,

x(0) =

−4 1

.

−5 −4 −3 −2 −1 0 1 2 3 4 5

x 1

x2

Ponto de Equilíbrio Trajetória de Estados Conjunto de Restrições

(52)

0 5 10 15 20 25 30 35 40 45 50 −1.2

−1 −0.8 −0.6 −0.4 −0.2 0 0.2

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.21: Sinal de Controleupara o Controle Regulatório com Realimentação de Saída

6.2.2 Rastreamento de Referência

No caso do rastreamento de referência para a realimentação de saída é utilizada a equação 5.15, os resultados são mostrados nas figuras 6.26, 6.27 e 6.28, usando uma referência igual a 1 ex(0) =

0 0

.

0 5 10 15

0 0.2 0.4 0.6 0.8 1 1.2 1.4

Tempo(s)

Amplitude

Figura 6.22: Rastreamento de Referência com Realimentação de Saída

−5 −4 −3 −2 −1 0 1 2 3 4 5 −5

−4 −3 −2 −1 0 1 2 3 4 5

x₁

x2

Ponto de Equilíbrio Trajetória dos Estados Conjunto de Restrições Máximo Conjunto Invariante Controlado

(53)

6.2. REALIMENTAÇÃO DE SAÍDA 39

0 5 10 15 20 25 30 35 40 45 50 −1

−0.8 −0.6 −0.4 −0.2 0 0.2 0.4

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.24: Sinal de Controleupara o Rastreamento de Referência para Realimentação

de Saída

Neste caso, com os parâmetros conhecidos, o sistema tem ótimo desempenho, conse-guindo chegar até a referência.

6.2.3 Rastreamento Robusto de Referência

Supondo da mesma forma que para a realimentação de estados queA=

0.9347+α 0.5194

0.33835 0.831

,

B=

−1.4462

−0.7012+β

eC=

0.5 0.5 , para−0.03≤α≤0.03 e−0.05≤β≤0.05.

Os valores das matrizes do modelo utilizado são os valores nominaisAo=

0.9347 0.5194

0.33835 0.831

eBo=

−1.4462

−0.7012

e do processo real sãoA=

0.9647 0.5194

0.33835 0.831

eB=

−1.4462

−0.7512

. Usando a equação 5.15 obtemos o seguinte resultado:

0 5 10 15 20 25

0 0.2 0.4 0.6 0.8 1

Figura 6.25: Controle com Modelo Incerto para Realimentação de Saída

(54)

valores deG, ρf, Aa e Bacalculados na sessão de realimentação de estados, obtemos o

seguinte resultado:

0 5 10 15 20 25

0 0.2 0.4 0.6 0.8 1

Tempo(s)

Amplitude

Figura 6.26: Controle com modelo reidentificado em Realimentação de Saída

−5 −4 −3 −2 −1 0 1 2 3 4 5 −5

−4 −3 −2 −1 0 1 2 3 4 5

x1

x2

Ponto de Equilíbrio Trajetória dos Estados Conjunto de Restrições Conjunto Invariante Controlado Conjunto ∆−Invariante Controlado

Figura 6.27: Trajetória dos Estados para o Rastreamento Robusto com Realimentação de Saída

0 5 10 15 20 25

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4

Tempo(s)

Amplitude

Sinal de Controle

Figura 6.28: Sinal de Controle u para controle com reidentificação com Realimentação