Abordagem analítica e caracterização de contato entre superfícies

ABORDAGEM ANALÍTICA E

CARACTERIZAÇÃO DE CONTATO ENTRE

SUPERFÍCIES

Paulo Eduardo Nunes Bruel

Dissertação apresentada à escola de

Engenharia de São Carlos da Universidade

de São Paulo, como parte dos requisitos

para obtenção do título de Mestre em

Engenharia Mecânica

ORIENTADOR: Prof. Dr.Luiz Carlos Felicio

São Carlos

ii

RESUM O

BRUEL, P. E. N. (2005). Análise e Caracterização de Contato entre Superfícies. – Dissertação (Mestrado) – Escola de Engenharia de São Carlos - Universidade de São Paulo, São Carlos, 2005.

Pode-se definir o tato através da capacidade de um corpo sentir o contato, localizá-lo, reconhecer a forma e a rugosidade da superfície impactante. Normalmente, não se encontram estruturas analíticas adequadas para descrever o fenômeno. Neste trabalho, pretende-se determinar a localização dos pontos de contato entre dois corpos através da análise dos sinais resultantes das vibrações causadas pelo contato, além de estimar a geometria da superfície do objeto impactante . A descrição qualitativa do impacto é obtida através da análise de uma série de funções matemáticas que geram uma base ortogonal adequada para este tipo de evento. Assim, o contato não é considerado através de uma modelagem física tradicional, mas pela descrição das ondas geradas pelas tensões e deformações superficiais, incorporando a interação de múltiplos pontos vinculados e procedimentos de contagem estatística. Com a metodologia para estudo de impacto experimental, é efetuada a construção qualitativa do espectro de deslocamento de uma placa simplesmente apoiada sujeita à aplicação de esforços distribuídos.

ABSTRACT

BRUEL, P. E. N. (2005). Analysis and Characterization of the Contact Between Surfaces – Dissertation (Mastering) – Escola de Engenharia de São Carlos - Universidade de São Paulo, São Carlos, 2005.

The tact may be defined as the capacity of a body to locate the contact on its surface, to recognize shape of the contacting surface as well as the superficial rugosity. Usually analytical models are not able to describe the phenomenon properly. This work, proposes an approach for the contact form location between two bodies using the resultant signals analysis of the vibrations caused for the contact. In this way it is determined the target surface geometry. The qualitative description of the impact is obtained through the analysis of mathematical series that generate orthogonal basis for this sort of event. Thus, the contact is not considered through a traditional physical modeling, but by the description of the waves generated for the superficial stress and strain, incorporating the interaction of multiple entailed points and procedures of counting statistics. With a methodology for study of theoretical impact, the quantitative construction of the specter of displacement of a subject plate to the application of distributed strains is effected.

iv

AGRADECIM ENTO

Agradeço a minha avó Alda Facchina Nunes (in memória) pelo carinho e pelos anos de convivência possibilitando a realização desse trabalho.

Agradeço a Msc. Renata Nunes Bruel do Centro Tecnológico da Marinha pela colaboração e pela revisão desta dissertação.

ÍNDICE DE FIGURAS

FIGURA 2.1–REPRESENTAÇÃO TÍPICA DA ENTRADA δ(X). ...13

FIGURA 2.2-RESPOSTA EM FREQÜÊNCIA PARA SISTEMA COMPOSTO;...25

FIGURA 3.1-TRAJETÓRIA DE UM PONTO EM UM ESPAÇO DE FASE BIDIMENSIONAL...29

FIGURA 3.2-ENSEMBLE DE FUNÇÕES ALEATÓRIAS. ...32

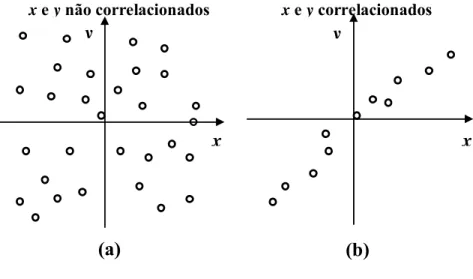
FIGURA 3.3–REPRESENTAÇÃO DE CORRELAÇÃO ENTRE VARIÁVEIS X E Y...33

FIGURA 3.4-REGRESSÃO LINEAR DE X EM Y PARA COEFICIENTES DE CORRELAÇÃO ρXY...38

FIGURA 3.5-FUNÇÃO DENSIDADE ESPECTRAL. ...39

FIGURA 3.6-FUNÇÃO DENSIDADE ESPECTRAL COM MÉDIA NÃO NULA...40

FIGURA 3.7-FUNÇÃO DENSIDADE ESPECTRAL. ...41

FIGURA 3.8–SINAIS DE SAÍDA TÍPICOS DE SISTEMAS. ...43

FIGURA 3.9–FUNÇÕES AUTOCORRELAÇÃO IDEALIZADAS. ...43

FIGURA 3.10-SISTEMA LINEAR COM DUAS ENTRADAS E UMA SAÍDA...44

FIGURA 3.11–ESQUEMA DE UM SISTEMA DINÂMICO...48

FIGURA 4.1-SISTEMAS SEPARADOS POR PAREDE ADIABÁTICA,FIXA E IMPERMEÁVEL. ...54

FIGURA 5.1–ESFORÇOS EM UM ELEMENTO DE VOLUME...72

FIGURA 6.1–ESQUEMA DO SISTEMA MODELADO. ...81

FIGURA 6.2–ESQUEMA DA DISTRIBUIÇÃO DE ESFORÇOS. ...83

FIGURA 6.3–REPRESENTAÇÃO DOS ENSAIOS...84

FIGURA 6.4-SINAL OBTIDO NO PONTO P1 DO ENSAIO ANSYS_OQ1 ...88

FIGURA 6.5–CORRELAÇÃO PARA O ENSAIO ANSYS_OQ1 NO PONTO P1...89

FIGURA 6.6–FUNÇÃO DENSIDADE ESPECTRAL PARA O ENSAIO ANSYS_OQ1 EM P1 ...89

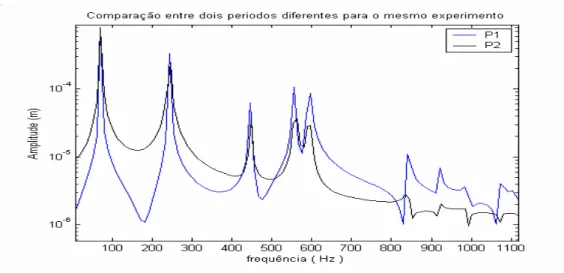
FIGURA 6.7–DESLOCAMENTO DO PONTO DE AQUISIÇÃO P1 EM ∆T1 E ∆T2...90

FIGURA 6.8–ESPECTRO DE FREQÜÊNCIAS DO SINAL EM ∆T1 E ∆T2...91

FIGURA 6.9–DESLOCAMENTOS NOS ENSAIOS ANSYS_OQ1/2/3 EM P1,P2,P3 ...93

FIGURA 6.10–AMPLITUDE NOS ENSAIOS ANSYS_OQ1/2/3 EM P1,P2,P3 ...94

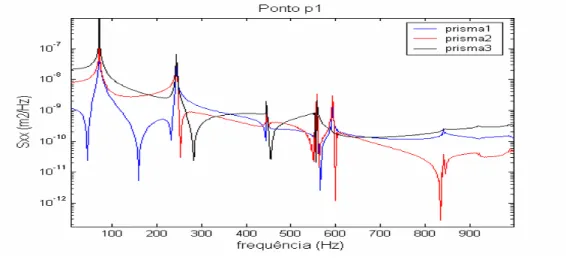
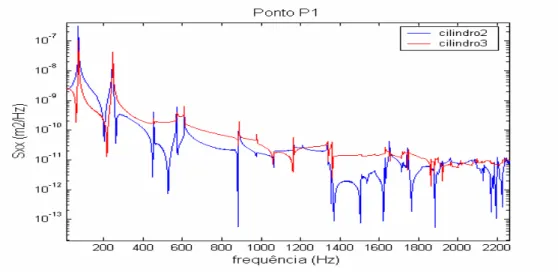
FIGURA 6.11–DESLOCAMENTOS NOS ENSAIOS ANSYS_OC2/3 EM P1 ...95

FIGURA 6.12–AMPLITUDE NOS ENSAIOS ANSYS_OC2/3 EM P1 ...95

FIGURA 6.13–FUNÇÃO DENSIDADE ESPECTRAL NOS ENSAIOS ANSYS_OC2/3 MEDIDO EM P1...96

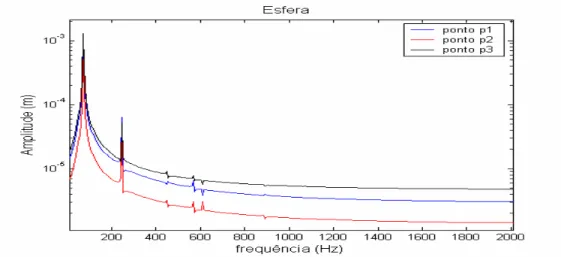
FIGURA 6.14–DESLOCAMENTOS NO ENSAIO ANSYS_OE2 EM P1,P2,P3 ...97

FIGURA 6.15–AMPLITUDES NO ENSAIO ANSYS_OE2 EM P1, P2, P3...97

FIGURA 6.16–FUNÇÃO DENSIDADE ESPECTRAL NO ENSAIO ANSYS_OE2 EM P1,P2,P3...98

FIGURA 6.17–AMPLITUDES NOS ENSAIOS ANSYS_OQ2/OC2/OE2 EM P1 ...99

FIGURA 6.18–AMPLITUDES NOS ENSAIOS ANSYS_OQ3/OC3/OE2 EM P1 ...99

FIGURA 6.19-FORÇAS HARMÔNICAS SIMULANDO O PRISMA DE 20.0MM DE LADO...102

FIGURA 6.20-AMPLITUDE NOS ENSAIOS MAM_DQ1/2/3 EM P1...105

FIGURA 6.21-AMPLITUDE NO ENSAIO MAM_DQ3 PARA FORÇAS DE 1N,2N E 10N...106

vi

FIGURA 6.23–AMPLITUDES DA SOLUÇÃO DA EQUAÇÃO HOMOGÊNEA DA PLACA...107

FIGURA 6.24–DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DQ1 EM P1...108

FIGURA 6.25–REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DQ1–1900HZ...109

FIGURA 6.26–REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DQ1-1920HZ...109

FIGURA 6.27-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DQ2 EM P1 ...110

FIGURA 6.28-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DQ2 ...111

FIGURA 6.29-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DQ2 EM P1 ...111

FIGURA 6.30-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DQ2 ...111

FIGURA 6.31-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DQ3 EM P1 ...112

FIGURA 6.32-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DQ3 ...112

FIGURA 6.33-AMPLITUDE NOS ENSAIOS MAM_DC2 EM P1 ...113

FIGURA 6.34-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DC2 EM P1 ...114

FIGURA 6.35-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DC2 ...114

FIGURA 6.36-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DP EM P1 ...115

FIGURA 6.37-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DP ...115

FIGURA 6.38-DISTRIBUIÇÃO DOS ESFORÇOS ALEATÓRIOS DO ENSAIO MAM_DA...116

FIGURA 6.39-AMPLITUDE NOS ENSAIOS MAM_DA EM P1 ...116

FIGURA 6.40-DISCRIMINAÇÃO EM NÓS DO SINAL DO ENSAIO MAM_DA EM P1 ...117

FIGURA 6.41-REPRESENTAÇÃO EM 3D E VISTA EM PLANTA DO ENSAIO MAM_DA EM P1 ...117

FIGURA 6.42–LEITURA DO SENSOR NO PONTO P1 ...118

FIGURA 6.43–MODOS DE VIBRAÇÃO DA PLACA EM FUNÇÃO DA FREQÜÊNCIA...119

FIGURA 6.44–MODOS DE VIBRAÇÃO DA PLACA EM FUNÇÃO DOS NÓS NA FREQÜÊNCIA 1725 HZ...119

FIGURA 6.45–.DISTRIBUIÇÃO DOS ESFORÇOS ALEATÓRIOS DO ENSAIO MAM_DA...120

ÍNDICE DE TABELAS

TABELA 2.1–OPERADORES LINEARES PARA DIVERSAS ESTRUTURAS. ...21

TABELA 6.1-ENSAIOS...82

TABELA 6.2-PONTOS DE AQUISIÇÃO DOS DESLOCAMENTOS DA PLACA...84

TABELA 6.3–ENSAIOS ANSYS_O ...85

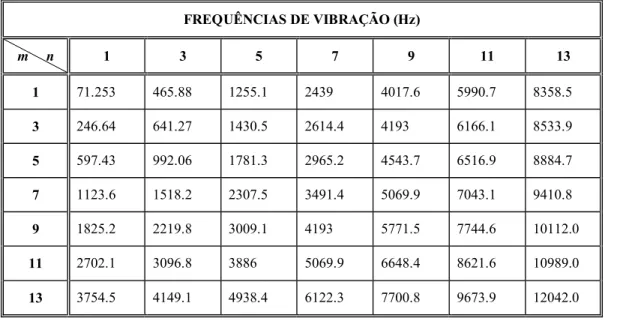
TABELA 6.4–FREQÜÊNCIAS DE RESSONÂNCIA SEGUNDO O CÁLCULO TEÓRICO...86

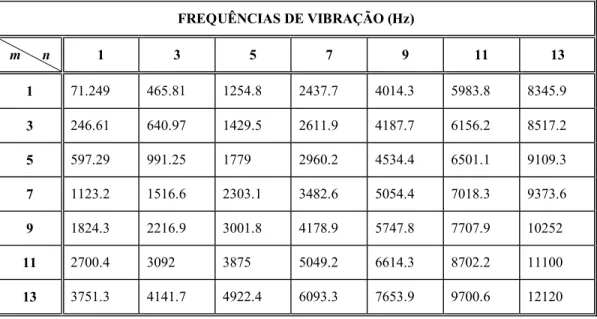
TABELA 6.5-FREQÜÊNCIAS DE RESSONÂNCIA DA MALHA COM (90X60)ELEMENTOS...87

viii

LISTA DE SÍMBOLOS

a, b Largura, Comprimento ak Coeficientes de aproximação amn, bmn Coeficiente da série de Fourier A(w) Função resposta freqüência b Coeficiente de regressão linear B Operador das condições de contorno

c Constante, Coeficiente de amortecimento, Velocidade de propagação da onda cmn Constante para o modo mn

Cxx(τ) Função autocovariância

Cxy(ω) Função covariância

d distância D Vetor coluna esi;eri Versor

E Modulo de Elasticidade Ei Energia

E[] Valor esperado de [x] E[∆2

] Soma dos quadrados dos resíduos f freqüência

gk(t) Função de aproximação

G(x|γ) Função de Green

Gxx(ω) Função densidade espectral (ω >0)

Gxy(ω) Função densidade espectral cruzada (ω >0))

Gy:x(ω) Função densidade espectral cruzada (ω >0)

h espessura

hi(τ) Função resposta impulsiva unitária

H(q,p) Função de Hamilton; operador de Hamilton Hxy Momento de torção por unidade

Hi(ω) Função resposta na freqüência

Hmn(ω) Componente mn da matriz resposta na freqüência

H(ω) Fator de ganho do sistema

I Momento de inércia da secção tranversal i, j, k variáveis inteiras

J Momento de Torção

J Vetor densidade de momento generalizado k rigidez

kB Constante de Boltzman

Kmn Constante relativa às coordenadas (x0 y0) da placa do modo mn L Operador Sturm-Lioville

m massa

mn indica o modo mn

m(r) Densidade de massa em função de r

mx, my Valor médio da variável randômica X, Y do processo estacionário x(t) e y(t)

M-1 Matriz de covariância

N Número de pontos Ni Numero de partículas

Nx, y, z.. Esforços normais por unidade de comprimento

n Variável inteira

p Momentum generalizado p(s,t) Pressão randômica estacionária px, y, z Força por unidade de área P Pressão

q Coordenada generalizada Q0, x, y Reação na quina

Q x, y Reação nas bordas do contorno

r Vetor posição nas coordenadas (x, y) ri Vetor posição nas coordenadas (xi, yi) Rxx(τ) Função autocorrelação

Rxy(τ) Função correlação cruzada

s Vetor posição nas coordenadas (x, y) si Vetor posição nas coordenadas (xi, yi) S0 Constante no domínio da freqüência

S(E) Entropia em função da energia interna Sxx(ω) Função densidade espectral

Sxy(ω) Função densidade espectral cruzada

t Variável, normalmente tempo ti Instante de tempo

T Período Ti Temperatura

Txy Esforços tangenciais por unidade de comprimento

u(x,y) Vetor deslocamento em função de (x, y) v(x,y) Vetor deslocamento em função de (x, y) v Velocidade generalizada

Vi Volume

Vx, y Esforço cortante por unidade de comprimento

x, y, z Variáveis independentes x, y, z variáveis de espaço x(t) Função espacial do tempo

Função estacionária randômica xi(t) Função entrada i

xi Ponto fixo i na coordenada x

X Variável aleatória

X(ω) Transformada de Fourier de x(t)

y(t) Função espacial no tempo; Função estacionária randômica yi Ponto fixo i na coordenada y

yi (t) Função saída i

Y(ω) Transformada de Fourier de y(t) w(r) Função resposta da variável r

Flecha; deflexão

α, β ângulos

x

εxx, yy, zz.. Componentes de deformação devido às tensões normais

ϕ Função característica

γ Vetor numero de onda, similar a ω; Parâmetro da função de Green γxy, γ xz, γyzz Componentes de deformação devido as tensões de cisalhamento

ηyx 2_(ω)

Função coerência entre y(t) e x(t) λ Vetor comprimento de onda

λi Auto valor devido as condições de contorno; valor característico

ν Coeficiente de Poisson θ

θi Constante de tempo θxy(ω) ângulo de fase

ρ Densidade

ρ(q, p) Densidade generalizada ρxy Coeficiente de autocorrelação

ρyx Coeficiente de correlação para as variáveis randômicas y,x

σ Variância; desvio padrão σx, σy Tensão normal

σyx Variância da variável aleatória X, Y ??

τ Variável temporal τxy, τ xz, τyzz Tensão de cisalhamento

ω Freqüência angular

ωmn Freqüência angular para o modo mn

Ψ Função de forma

Desvio do valor da amostra em relação ao valor predito

Ω Número dos estados acessíveis do sistema

∇ Operador diferencial

∇2

Operador Laplaciano

∇4

ÍNDICE

Resumo ________________________________________________________ ii

Abstract ________________________________________________________iii

Agradecimento __________________________________________________ iv

Índice de Figuras ________________________________________________ v

Índice de Tabelas _______________________________________________ vii

Lista de Símbolos _______________________________________________viii

Índice _________________________________________________________xi

CAPÍTULO 1 - Introdução à Teoria do Contato _______________________ 1

1.1 Introdução __________________________________________________ 1

1.2 Justificativa _________________________________________________ 2

1.3 Objetivos____________________________________________________ 3

1.4 Revisão Bibliográfica__________________________________________ 3

1.5 Apresentação Da metodologia Proposta __________________________ 7

1.5.1 Conteúdo da Dissertação ___________________________________________ 9

CAPÍTULO 2 - Desenvolvimento dos Modelos Teóricos ________________ 11

2.1 Introdução _________________________________________________ 11

2.2 Base Discreta ou Contínua ____________________________________ 11

2.3 Método de Green ____________________________________________ 12

2.3.1 Solução da Equação de Poisson com o Método de Green _________________ 16 2.3.2 Propagação das Condições Iniciais __________________________________ 18

2.4 Análise Harmônica do Movimento______________________________ 21

2.4.1 Transformada da Função de Green em Resposta em Freqüência____________ 23 2.4.2 Acoplamento Através dos Modos de Vibração _________________________ 25

CAPÍTULO 3 – Análise estatÍsca __________________________________ 28

3.1 Introdução _________________________________________________ 28

3.2 Ensemble Estatístico _________________________________________ 29

3.3 Correlação _________________________________________________ 33

xii

3.4 Função Correlação Via Espectro _______________________________ 39

3.4.1 Análise Estatística dos Sinais de Entrada e Saída do Sistema ______________ 44 3.4.2 Desenvolvimento para Excitação Distribuída __________________________ 48

CAPÍTULO 4 - Análise de Contato _________________________________ 52

4.1 Técnica para a Descrição de Contato____________________________ 52

4.1.1 Termodinâmica de Gibbs – Análise Térmica___________________________ 54 4.1.2 Abordagem Mista________________________________________________ 56

4.2 Vínculos e Condições Iniciais __________________________________ 60

4.2.1 Elaboração Estatística ____________________________________________ 62 4.2.2 Descrição Física do Contato________________________________________ 63

CAPÍTULO 5 - Modelagem do Sistema _____________________________ 67

5.1 Introdução _________________________________________________ 67

5.2 Aproximação por Autofunções_________________________________ 68

5.3 Coeficientes da Série de Fourier________________________________ 70

5.4 Modelo de placa fina _________________________________________ 71

5.5 Condições de Contorno da Placa _______________________________ 76

5.6 Método Numérico Aplicado na Equação _________________________ 79

CAPÍTULO 6 - Resultados e Conclusões ____________________________ 81

6.1 Descrição do Sistema _________________________________________ 81

6.2 Ensaios ANSYS_O___________________________________________ 85

6.2.1 Apresentação dos Resultados _______________________________________ 88 6.2.2 Análise dos Resultados __________________________________________ 100

6.3 Validação do MAM coM o ANSYS ____________________________ 101

6.3.1 Comparação dos Ensaios ANSYS_D e MAM_D ______________________ 102 6.3.2 Análise dos Resultados __________________________________________ 103

6.4 Método de Análise Modal ____________________________________ 104

6.4.1 Ensaios com o MAM ____________________________________________ 105 6.4.2 Análise dos Resultados __________________________________________ 121

6.5 Conclusões ________________________________________________ 122

6.6 Trabalhos Futuros __________________________________________ 128

CAPÍTULO 1 - INTRODUÇÃO À TEORIA DO CONTATO

1.1

INTRODUÇÃO

A descrição qualitativa do impacto é obtida através da análise de uma série de funções matemáticas que geram uma base ortogonal e descrevem adequadamente este tipo de evento, possibilitando um novo enfoque das teorias de impacto e contato que considere o amortecimento.

Através da análise de sinais provenientes de vibrações causadas pelo contato entre uma superfície previamente conhecida e um objeto desconhecido, é possível determinar a localização ou o posicionamento dos pontos de contato na superfície conhecida, estimar a geometria da superfície do objeto desconhecido e, dependendo do tipo de interação entre os corpos, outras características como a massa e o modulo de Young (E).

Com este intuito, é assumido que os modos normais de vibração, as freqüências naturais, a forma geométrica e as propriedades físicas da superfície contactada são previamente conhecidos.

Como superfícies contactadas são utilizadas chapas planas, pois são estruturas matematicamente bem conhecidas. Como agentes impactantes são utilizadas diversas formas geométricas, como quadrados, cilindros e formas pontuais, que definem a distribuição de esforços sobre a chapa. As distribuições dos esforços servem, em uma primeira aproximação, para obtenção e análise dos resultados das simulações.

2

uma série matemática convenientemente escolhida de forma a descrever o espaço amostral das soluções. A série de Fourier, por exemplo, pode gerar uma gama muito grande de funções e seus coeficientes podem ser considerados como distribuição. Em particular, pode descrever funções descontínuas no tempo e no espaço.

O grau de precisão é determinado pela sensibilidade, acuracidade e pela quantidade de sensores dispostos sobre a superfície alvo. O amortecimento não é considerado qualitativamente na análise, por causa das dificuldades experimentais para sua avaliação e não existem modelos genéricos para sua descrição, NEWLAND, D. E (1989).

Considerando os termos da série de Fourier como uma distribuição, e atribuindo-lhes um caráter estatístico, estes podem ser assumidos como eventos que, analisados individualmente são desprezíveis, mas combinados entre si através de uma série, estes termos são avaliados como uma forma de desvio padrão da função densidade espectral.

O contato entre corpos não é considerado através de uma modelagem física tradicional, mas através de uma descrição de ondas (pulsos) geradas pelas tensões e deformações superficiais.

Assim, utilizando as estruturas apresentadas, é desenvolvida uma metodologia onde a localização e a intensidade de esforços distribuídos pode ser identificada pela utilização de um único sensor (de deslocamento, por exemplo) acoplado à superfície impactada. Em paralelo são esboçados modelos de abordagem para o estudo de contato.

Esta forma de tratamento visa a elaboração de um desenvolvimento sistemático que não se preocupa com o contato em si, mas com as conseqüências do evento, restringindo-se a uma análise quantitativa que permita rápidas tomadas de decisões, onde uma avaliação simples e direta de seu efeito é suficiente.

1.2

JUSTIFICATI VA

A partir de um tratamento matemático das respostas de sistemas pretende-se determinar as possíveis condições que resultarão nestas respostas

1.3

OBJETIVOS

Com a apresentação dos fundamentos matemáticos adequados para a obtenção das soluções da equação de onda e através modelagem de estruturas mecânicas vibrantes pretende-se avaliar vínculos e contatos entre superfícies, utilizando um formalismo estatístico na análise de sinais e, principalmente, avaliar esforços e formas de contatos responsáveis pela geração de onda, utilizando, para isto, as soluções teóricas da equação de Sturm-Nioville.

Com este intuito, são apresentadas algumas propostas para o tratamento de vínculos sob a ótica de vínculos modais, para o tratamento de alguns tipos de contato dinâmico e para a criação de um ambiente de sensibilidade tátil.

Portanto, através do desenvolvimento de uma metodologia para estudo de impacto experimental e estatístico, será efetuada a construção qualitativa do espectro de deslocamento de uma placa simplesmente apoiada sujeita à aplicação de esforços distribuídos, além do reconhecimento destas distribuições.

1.4

REVISÃO BIBLIOGRÁFICA

No estudo do impacto ou do contato entre corpos säo necessários o desenvolvimento dos conceitos teóricos envolvidos e a utilização de técnicas atualizadas de processamento de sinais para uma avaliação segura dos resultados obtidos.

Teoria do Impacto e Contato

4

estudo de propagação de ondas em problemas de impacto e a avaliação da distribuição de tensão no ponto de contato.

Segundo GOLDSMITH, W. (1960), GRAFF, K.F. (1975) e STRONGE, W.J. (2000) , pode ser utilizada em estudos dinâmicos de impacto longitudinal e transversal, como por exemplo, nos estudos efetuados por Sears e Timoshenko, apesar da teoria de contato de deformação proposta por Hertz ter sido elaborada com restrições para o regime elástico e estático

Para o desenvolvimento da teoria de impacto proposta faz-se necessária a incorporação de modelos matemáticos de estruturas vibrantes e suas respectivas soluções que, de acordo com CRAIG Jr., R.R. (1981) e KALMAKOV, I.A.S. (1961), pode ser observado no modelo de uma placa plana desenvolvido por Kirchoff.

Modelos mais elaborados foram introduzidos por MINDLIN, R.D.; FOX, E.A. (1960), por REISSNER, E. (1947) e por SALERNO, V.L.; GOLDBERG, M.A. (1960), que levaram em consideração as tensões de cisalhamento transversais. A importância dessa incorporação é relativa à espessura e à presença de furos na chapa onde, no modelo da placa proposto por Kirchoff, ocorrem concentrações de tensões inadmissíveis. A solução para este modelo, com várias condições de contorno, foi apresentada, por BERGMAN, L.A.; HALL, J.K.; LUESCHEN, G.G. (1993), entre outros que adotaram o formalismo matemático das funções de Green na solução da placa vibrante. Estes modelos são muito utilizados em programas de elementos finitos (MEF) como, por exemplo, no código ANSYS-LS DYNA.

Inúmeros experimentos têm sido conduzidos para medidas de vários parâmetros de impacto (normalmente pontual), freqüentemente com objetivo de verificar uma particular teoria de colisão ou quantificar resultados. Generalizações são obtidas através de processos computacionais como o método por elementos finitos (MEF), que utiliza como fundamento, o princípio de minimização variacional, conforme pode-se observar nos trabalhos desenvolvidos por GOLDSTEIN, H. (1980) e LEECH, J.W. (1971).

impacto em vigas, placas e cascas que envolvem grandes deformações são apresentados por JONES, N.L. (1997 ).

O MEF apresenta basicamente dois tipos de tratamento para o contato:

1. Método dos Multiplicadores de Lagrange e 2. Método da Penalização.

O Método de Lagrange calcula de modo exato através de restrições impostas e é indicado quando se deseja extremizar um funcional sujeitas as restrições de contato, resultando em um aumento no número de incógnitas.

No Método da Penalização, as restrições de contato são calculadas de forma aproximada através de um fator de penalização onde se admite a penetração de um corpo no outro. O problema principal consiste em achar esse fator sem que haja o comprometimento da matriz de rigidez, tornado-a mal condicionada ou, inversamente, sem permitir penetrações inaceitáveis.

A principal desvantagem do método dos elementos finitos é o alto custo computacional envolvido nas análises, além da necessidade de se conhecer previamente os parâmetros de impacto e as características do agente impactante.

Análise de Sinais

Para a confirmação das teorias apresentadas ou para elaborações de novos procedimentos é necessário o desenvolvimento de equipamentos e ferramentas capazes de quantificar e processar sinais.

O processamento de sinais é concernente com a representação, transformação e manipulação de sinais e das informações que o constituem. Uma classe de processamento de interesse é a que envolve o problema de interpretação, onde o objetivo não é obter um sinal de saída, mas caracterizar o sinal de entrada ou extrair informações deste.

6

um caso especial de sistemas a tempo discreto. Vide, por exemplo, MIRSHAWKA, V. (1979).

No século XVIII foram introduzidos métodos para integração numérica e interpolação de funções de variáveis contínuas, desenvolvidos por Euler, Bernoulli, e Lagrange,conforme: ATKISON, K.E. (1989); LAZARINI, C.; FRANCO, N.M.B. (1996) e MIRSHAWKA, V. (1979), a mecânica racional foi desenvolvida por Euler, D´Alambert , Lagrange e Hamilton, por fim, Fourier estudando o calor, apresenta a série harmônica, estabelecendo as bases da Acústica Fisiológica e Musical.

No século seguinte, foi introduzida a teoria da elasticidade por Navier, Cauchy, Clausus e Stokes e surgiram as primeiras inovações tecnológicas como, por exemplo, o primeiro transdutor utilizado por Reiss em uma demonstração de comunicação telefônica, os microfones a carvão e o fonógrafo, iniciando o desenvolvimento da gravação e da reprodução de sinais.

No fim da primeira guerra mundial, Langevin conseguiu a detecção de um submarino através de transdutores de cristal de quartzo que funcionavam como emissores e receptores. Enfim, o processo de detecção e geração de ultra-som tem evoluído significativamente a cada dia.

O campo do processamento e aquisição de sinais sempre se beneficiou de uma estreita relação entre a teoria, a tecnologia de implementação e as aplicações práticas. Na década de sessenta, a tecnologia de processamento de sinais era quase exclusivamente analógica a tempo contínuo.

A rápida evolução de computadores e microprocessadores, juntamente com o desenvolvimento de algoritmos causou uma grande mudança na tecnologia, elevando ao primeiro plano o processamento digital.

Os aspectos fundamentais do processamento de sinais digitais são a aquisição de seqüências de dados, caracterizando um espaço amostral e a natureza do sinal a tempo discreto. Com a descoberta de Cooley and Tukey, de um algoritmo eficiente para o cálculo da transformada de Fourier, conhecido como transformada rápida de Fourier (FFT), observa-se um aumento significativo na rapidez do cálculo.Ver NEWLAND, D.E. (1993); (1989); OPPENHEIM, A.V.;SCHAFER, R.W. (1989) BENDAT, J.S.; PIERSOL, G.P. (1993)

informações sobre as características do sinal. Deve-se salientar que, na transformada de Fourier a análise é feita no domínio da freqüência.

Uma distribuição tempo-freqüência muito usada é a transformada de Fourier de curta duração que fornece uma resolução constante no tempo e na freqüência, pois fixa uma largura no domínio do tempo.

A transformada wavelet apresenta um período de análise de multiresolução, que permite alterar a largura da janela e obter uma resolução mais adequada.

Atualmente, a teoria e os métodos de análise apresentados são utilizados na otimização de estruturas, obtendo-se perfis mais esbeltos e flexíveis, visando à diminuição de peso, a prevenção de acidentes e assegurando um maior controle de sistemas, principalmente no campo da robótica YU, W(1995).

KAO, S;CHEN ,S.F. LI, YM.; WANG, G. (2003) entre outros desenvolvem pesquisas na área de superfície de contato e utilizam uma grande quantidade de sensores que atuam na região de contato e dificultam sua implementação, aumentando os custos consideravelmente.

1.5

APRESENT AÇÃO DA M ETODOL OGIA PROPOSTA

O desenvolvimento da metodologia se baseia na procura de soluções que apresentem estruturas matemáticas que facilitem a modelagem do problema e a forma de resposta. Assim, devido à dificuldade de descrever fisicamente o contato, propõe-se descrevê-lo a partir de funções ortogonais, e então, subdividir o sistema em uma série de equações desacopladas.

O modelo físico é formulado através das funções de Green ,BUTKOV, E. (1978), desenvolvidas através de séries de Fourier e resolvido utilizando o modelo dos modos normais de vibração.

8

Por construção, os modelos apresentam essencialmente as mesmas propriedades matemáticas. Os modos normais de vibração discretos são dimensionalmente finitos e apresentam uma convergência mais rápida; as séries são infinitas. Dependendo do conhecimento prévio sobre o experimento e da necessidade de detalhamento necessária, é possível escolher um método matemático mais adequado para análise.

Em trabalhos introdutórios e de caráter essencialmente acadêmico, que visam uma generalização das aplicações, opta-se por modelos contínuos que possibilitam a geração de espaços de dimensão infinita e podem ser gerados automaticamente. Além disso, as séries utilizadas convergem para uma grande variedade de funções e servem como bases para procedimentos numéricos.

Assim, através da análise dos sinais de ondas provenientes de um choque, descreve-se o evento que causou ou pode ter causado estas ondas. Para a validação do procedimento proposto também são apresentadas simulações computacionais baseadas na metodologia de elementos finitos, fundamentadas no princípio minimização variacional e que geram autovetores em uma análise modal.

Particularmente, é investigado o contato entre dois corpos, com o intuito de reconhecer a forma geométrica do objeto que entrou em contato com uma superfície que contém o sensor e cujas propriedades geométricas e físicas, as condições de vínculo e as condições iniciais são previamente conhecidas.

Neste trabalho, a aplicação dos modelos teóricos é efetuada para verificar a validade da metodologia, utilizando simplificações algébricas cabíveis, sem perda da generalidade. Portanto, apenas as tensões e deformações normais são consideradas e os demais esforços são desprezados, como por exemplo, a tensão e deformação provocadas pelo cisalhamento. Isto não chega a ser uma restrição, pois o objetivo é o reconhecimento da forma e não o dos esforços gerados. Com esse procedimento torna-se evidente a facilidade obtida em analisar apenas aspectos de interestorna-se e de simetria.

Dependendo do sistema de coordenadas adotado, as vibrações provenientes do choque de dois corpos podem ser descritas através das funções de Bessel, das funções de Legendre ou da transformada de Fourier.

o fenômeno. Como condições iniciais são consideradas apenas as ondas estabelecidas em regime.

São considerados dois tipos de contato:

ƒ Contato tipo impulso→ caracterizado por não haver um acoplamento de estruturas e considera a ação de uma força externa em cada sistema.

ƒ Contato tipo acoplamento→ caracterizado pelo acoplamento de estruturas e considera uma única estrutura enquanto houver vínculos.

Para uma generalidade completa substitui-se a palavra contato por vínculo e se necessário, o tipo de contato é especificado e considerado como um modelo de vínculo.

1.5.1

Conteúdo da Dissertação

A dissertação é composta por capítulos estruturados de modo a fornecer uma visão clara e objetiva da teoria envolvida no impacto ou contato entre corpos. Assim, após uma breve descrição histórica sobre o fenômeno de contato, é feita uma introdução à abordagem do problema propriamente dito e da interação mecânica entre corpos, além do desenvolvimento das ferramentas matemáticas que são utilizadas no modelo físico.

Para o desenvolvimento teórico da metodologia de análise do impacto entre dois corpos são utilizados os seguintes tópicos:

ƒ Critérios de convergência,

ƒ Conhecimento de Série de Funções,

ƒ Função distribuição

ƒ Modos normais de vibração,

ƒ Autovetores e autovalores,

ƒ Função de Green (convolução),

10

Dando prosseguimento à explanação dos fenômenos teóricos utilizados no trabalho, é feita uma apresentação dos instrumentos estatísticos usados para análise de sinais e como integrá-los ao modelo físico. Os tópicos desenvolvidos nesta análise são:

ƒ Halmitoniana,

ƒ Princípios probabilísticos e estocásticos,

ƒ Termodinâmica estatística

CAPÍTULO 2 - DESENVOLVIMENTO DOS MODELOS

TEÓRICOS

2.1

INTRODUÇÃO

A descrição do contato entre duas superfícies é baseada no desenvolvimento de formalismos físicos e matemáticos que justificam o tipo de abordagem adotado no trabalho.

O desenvolvimento de modelos clássicos e teóricos e suas soluções fornecem resultados que são utilizados na análise do contato, corroborando com as hipóteses assumidas.

Na parte final deste capitulo há uma abordagem na resposta em freqüência. Os fundamentais propostos neste capítulo são apresentados por BUTKOV, E. (1978) e KREYSZIG, E. (1969).

2.2

BASE DI SCRET A OU CONTÍNUA

A base gerada por modos normais discretizados é indicada em trabalhos mecânicos e repetitivos, em casos onde a geometria e as condições de contorno são complexas. As principais limitações podem ser definidas em relação ao tipo de detalhamento e as dimensões do objeto impactante.

12

questões de detalhamento e às dimensões do objeto impactante. Outro aspecto relevante é poder utilizar os conceitos de distribuição adequados para descrever o impacto. Suas limitações são condicionadas à complexidades geométricas e de contornos.

2.3

M ÉTODO DE GRE EN

O Método de Green ou Duhamel é um modelo utilizado na resolução de equações diferenciais não homogêneas, condições de contorno e condições iniciais e, normalmente, obtem-se a solução de uma integral do tipo convolução.

Sintetizando, consiste na substituição de uma entrada distribuída f(x) por uma entrada concentrada do tipo δ(γ) aplicada no ponto γ.

Considerando a equação diferencial (2-1) de Sturm-Lioville, substituindo f(x) por δ(γ) e mantendo as mesmas condições de contorno, obtém-se a função(2-2), do tipo h(x|γ).

(2-1)

onde: p(x), s(x), r(x) → funções analíticas, s(x)≥0 e r(x)≥0

λ → parâmetro

(2-2)

A equação (2-3) corresponde à solução da equação(2-2) integrada em relação a

γ.

(2-3)

onde: a≤x≤b

w(x)→ solução da equação (2-1) e

h(x|γ)→ solução da equação(2-2) soluções de funções de Green.

Pode-se, ao invés de aplicar uma entrada distribuída f(x), considerar condições iniciais ou condições de contorno específicas.

∫

=b

a

d f x h x

w( ) ( γ) (γ) γ

) ( ) | ( ) ( ) ( ) ( ) ( )

( s x w x r x h x f x

dx x dw x p dx

d

= +

− ⎥⎦ ⎤ ⎢⎣

⎡ _{λ γ}

) ( ) | ( ) ( ) | ( ) ( ) | ( )

( γ − γ +λ γ =δ −γ

⎥⎦ ⎤ ⎢⎣

⎡

x x

h x r x

h x s dx

x dh x p dx

O método de Green aplicado à equação (2-1) e a utilização de autovetores geram uma base na forma de séries, conforme Figura 2.1.

Figura 2.1 – Representação típica da entrada δ(x).

Definindo o operador linear de Sturm-Lioville L como:

(2-4)

Pretende-se resolver a equação diferencial não homogênea (2-5).

(2-5)

onde: w(x)→satisfaz as condições de contorno da forma Bw(x) = 0 B→ operador das condições de contorno no intervalo (a,b).

(2-6)

com: α1 e α2 constantes, não simultaneamente nulas e

β1 e β2 constantes, não simultaneamente nulas.

Considerando λ fixo, pode-se relacionar equação (2-1) com o problema de autovalores, sendo λ determinado de modo a satisfazer as condições de contorno (2-6).

f( x) =

δ

(x )

y(x )= h (x )

x

( )

( )

d x p dx

d

L= _⎢⎣⎡ _⎥⎦⎤−

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

= +

= +

=

) (em

) (em

2 1

2 1

b x dx

d

a x dx

d

B

β β

α α

) ( ) ( ) ( )

(x r x w x f x

14

Para condições gerais impostas sobre as funções p(x), s(x) e r(x), contínuas e reais no intervalo (a,b), o problema de Sturm-Lioville possui um número infinito de valores característicos λ.

A solução de w(x) ≠ 0 pode ser escrita sob a forma de funções características

ϕλ(x) ortogonais e possuem derivadas contínuas no intervalo considerado. As funções ϕλ são também chamadas de funções próprias ou autofunções.

As equações(2-2) e (2-6) podem ser escritas empregando os operadores L e B, de acordo com as equações(2-7).

(2-7)

Se existe o conjunto solução ϕλ(x) e, este é completo, então L pode ser

representado sob a forma da equação (2-9), que corresponde à soma de autovalores sob todo o espectro de L.

(2-8)

A solução da equação(2-2) pode, então, ser escrita conforme (2-9), onde ξλ são coeficientes de ϕλ.

(2-9)

Aplicando o operador L, tem-se:

(2-10)

Multiplicando ambos os lados por ϕλ,.(x) e integrando sobre x, obtém-se o conjunto solução (2-11), usado para determinar os coeficientes ξλ(γ).

(2-11) (a,b) x x Bh x x h x r x Lh ∈ ⊥ = − = + 0 ) | ( ) ( ) | ( ) ( ) | ( γ γ δ γ λ γ 0 ) ( ) ( = = λ λ λ ϕ λϕ ϕ B x x L

∑

λ λ λ

ϕ γ ξ

γ) ( ) ( ) |

(x x

h

∑

∑

=

λ λ λ λ λ

γ δ λϕ γ ξ ϕ γ ξ

γ) ( ) ( ) ( ) ( ) ( ) |

(x L x x x

Lh

∑

∫

λ λ λ λ λ

γ ϕ ϕ ϕ λ γ ξ b a dx x

x) ( ) ( )

( )

Se as funções características ϕλ.(x) são ortonormais tem-se:

(2-12)

Cujos coeficientes são determinados por:

(2-13)

Finalmente, obtém-se a equação (2-14) que é a solução da equação (2-7).

(2-14)

Quando a equação diferencial for da forma Lw(x)−λw(x)= f(x), onde λ é um parâmetro arbitrário, os valores de L são representados por λn e as funções

características são da forma bilinear:

(2-15)

É nesse contexto que se fala em pólos das funções de Green h(x|λ) no plano e nos casos de ressonância. No espaço das funções complexas a formula bilinear se modifica, para ter a forma (2-16):

(2-16)

E assim, as funções de Green não são mais simétricas, mas sim hermitianas sob a troca de x e γ, conforme equação h(x|γ)=h*(γ|x)

⎪⎩ ⎪ ⎨ ⎧ = ⇒ ≠ = ⇒ = ⊥ =

∫

' , ' , ' , ' , , , λ λ λ λ λ λ λ

λ _{λ λ δ}

δ λ λ δ

ϕ ϕ x xdx b a

∑

γ) ( ) ( ) | (

∑

γ) ( ) ( ) |

(

* _{x x}

x h λ γ ϕ γ ξ λ λ ) ( ) ( =

∑

γ) ( ) ( )

(x x

16

2.3.1

Solução da Equação de Poisson com o Método de Green

A modelagem de uma membrana resulta na equação de Poisson em duas dimensões (2-17), e pode ser particularizada na forma da equação (2-1) de Sturm-Lioville. As soluções são obtidas através do desenvolvimento de série dupla de Fourier. Assim, considera-se a equação diferencial parcial (2-17) não homogênea, com duas variáveis espaciais, onde f(x,y) representa uma carga externa por unidade de área aplicada em uma membrana simplesmente engastada. As condições de contorno são dadas pelas equações (2-18)

(2-17)

(2-18)

Para a força unitária concentrada agindo no ponto (γ1,γ2), representada

por δ(x-γ1)δ(y-γ2), a equação (2-17) pode ser escrita conforme equação (2-19), cuja

solução é a função de Green em duas dimensões.

(2-19)

A solução da equação diferencial parcial (2-17) pode ser obtida através da solução da integral (2-20).

(2-20)

Aplicado o operador diferencial Laplace ∇2 nas funções características normalizadas ϕmn(x,y), obtém-se:

(2-21) ) , ( ) , ( ) , ( 2 2 2 2 y x f y y x w x y x w ₌ ∂ ∂ + ∂ ∂ 0 ) , ( ) 0 , ( 0 ) , ( ) , 0 ( = = = = b x w x w y a w y w ) ( ) ( ) ; ( , ) ; ( 2 1 2 2 1 2 2 2 1 2 γ δ γ δ γ γ γ γ − − = ∂ ∂ + ∂ ∂ y x y y x h x y x h 2 1 2 1 0 0 2

1; ) ( , )

( )

,

(x y h xγ yγ f γ γ dγ dγ

Sabendo que os autovetores λmn e as funções ϕmn(x,y) são definidos de acordo

com as equações (2-22) e (2-23) respectivamente, procura-se a equação solução da

função de Green h(x|y) definida pela equação (2-24).

(2-22)

(2-23)

(2-24)

Substituindo a equação (2-24) na EDP (2-19) e integrando em relação a (x,y)

obtém-se os coeficientes Amn:

(2-25) onde: b m sen a m sen ab 2 1

2 πγ πγ

são as autofunções da série de senos de Fourier

Substituindo a equação (2-25) na equação (2-24) resulta na fórmula bilinear de Green (2-26).

(2-26)

Portanto, a solução da equação de Poisson (2-17) pode ser escrita através da série Fourier da função w(x,γ), ,equação (2-27), onde amn são os coeficientes da série,

conforme equação (2-28).

(2-27) (2-28) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −

= 2₂2 2₂2

b n a m mn π π λ b y m sen a x m sen ab y x mn π π

ϕ ( , )= 2

b y m sen a x m sen A ab y x h m n mn π π γ γ γ

γ

∑∑

= ∞ = = 1 1 2 1 2

1 ( , )

2 ) ; ( b m sen a m sen ab A b n a m mn 2 1 2 2 2 2 2

2π π ₂ πγ πγ

= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + −

∑∑

mn π π

π π

∑∑

∫∫

=a b _mn

mn f x y x y dxdy

18

2.3.2

Propagação das Condições Iniciais

O método de Green aplicado nas condições iniciais da equação harmônica (2-29) resulta em equações do tipo de D’Alembert para a propagação de onda. Sob este aspecto, pode-se considerar as funções f(x,γ) como condições iniciais de deslocamento e/ou velocidade.

No caso de deslocamentos transversais em uma corda infinita, sem forças externas aplicadas, a equação (2-29) descreve a propagação da onda, onde c é a velocidade de propagação.

(2-29)

Impõe-se que a função solução w(x,t), com condições iniciais de deslocamento w0 e velocidade v0, conforme as equações (2-30), se anule no infinito, satisfazendo a condição de contorno (2-31) para todos os valores de t.

(2-30)

(2-31)

A função w(x,t) pode ser escrita como uma superposição contínua da distribuição das condições iniciais (2-30) em vários pontos γ .

(2-32)

Onde, g1(x|γ,t) é a função de Green para o deslocamento inicial e g2(x|γ,t) para a velocidade inicial, satisfazendo as condições (2-33) e (2-34).

(2-33) 0 1 2 2 2 2 2 = ∂ ∂ − ∂ ∂ t w c x w 0 ) , ( lim = ∞

→ w x t

x

∫

∫

= g xγ t w γ dγ g xγ t v γ dγ

t x

w( , ) ₁( ; ) ₀( ) ₂( ; ) ₀( )

0 ) ; ( ) ( ) 0 ; ( 1

1 _∂ =

∂ −

= x t

t g x

x

g γ δ γ γ

(2-34)

Aplicando a transformada de Fourier em relação à x na função g1(x|γ,t) e na condição inicial do deslocamento (2-33), obtém-se a transformada das funções de Green (2-35) e (2-36), respectivamente.

(2-35)

(2-36)

Substituindo a função (2-35) na transformada da equação harmônica (2-29) resulta na EDO (2-37), cuja solução é dada pela equação (2-38).

(2-37)

(2-38)

Em t=0, obtêm-se as constantes A1 e B1:

(2-39)

Invertendo G1(k|γ,t) chega-se à solução da equação g1(x|γ,t).

(2-40)

Da mesma forma, aplicando a transformada de Fourier na função de Green da velocidade g2(x|γ,t), equação(2-34), obtém-se a solução (2-41) e as constantes A2 e B2,

{

}

) ;

( ₁

1 k t g x t

G γ =ℑ_x γ

0 ) ; ( ) ( ) 0 ; ( 2

2 _∂ =

∂ −

= x t

t g x

x

g γ δ γ γ

π γ γ 2 ) 0 ; ( 1 ik e x G = ickt ickt e B e A t k

G₁(

γ

ickt ickt e B e A t k

G₁( γ; )= ₁ + ₁ −

0 ) , | ( e 2 ) 0 , | ( 1 1 0 1 1 1 1 = − = = + = = B A dt t k dG e B A k G t ik γ π γ γ

[

]

[

]

1 x t e e e dk x ct x ct

g =

∫

∞

∞ −

− −

+ _{δ γ δ γ}

π

20

conforme equações (2-42), para t=0:

(2-41)

(2-42)

Invertendo G2(k|γ,t) chega-se à solução da equação de onda quadrada g2(x|γ,t),

igual a 1

2c no intervalo (x-ct, x+ct) e igual a zero fora dele.

[

]

{

[

] [

]

}

2 S x ct S x ct

c dk e e e k ci t x

g = ik +ct − ik −ct −ikx = − − − − +

∞ ∞ −

∫

γ γ γ

(2-43)

Substituindo as funções de Green para o deslocamento (2-40) e para a velocidade(2-43) na função (2-32), e integrando o primeiro termo obtém-se:

(2-44)

A função w(x,t) pode ser representada pela equação (2-45), onde o termo f(x-ct) representa um deslocamento com velocidade c na direção positiva de x e, g(x-ct) é um deslocamento na direção negativa de x.

(2-45)

Assim, para qualquer valor das funções f(x,t) e g(x,t) no ponto x0 e no instante t0,, estas funções de onda têm o mesmo valor em um instante posterior (t0+τ), no ponto (x0+cτ) para f(x,t) e no ponto (x0-cτ) para g(x,t), ou seja,

(2-46)

A equação (2-46) ressalta a idéia de poder descrever um evento que tenha ocorrido no ponto (x0,t0), medindo seu efeito em uma outra região num tempo posterior. Neste sentido, pode-se, por exemplo, analisar o impacto entre dois corpos através do efeito medido em um ponto qualquer do corpo impactado.

, )

;

( _{2 2}

2 ickt ickt e B e A t k

G γ = + −

π γ γ 2 ) , | ( 0 ) 0 , | ( 2 2 0 2 2 2 2 ick e B A dt t k dG B A k G ickt t = − = = + = =

[

]

_∫

w (γ) γ

2 1 ) ( ) ( 2 1 ) ,

( _{0 0 0}

) ( ) ( ) ,

(xt f x ct g x ct

w = − + +

[

] [

]

) ,

(x t f x₀ c ct₀ g x₀ c c t₀ w x₀ t₀

2.4

ANÁLISE HARMÔNICA DO M OVIM ENTO

Como o movimento harmônico é um fenômeno repetitivo, é adequado descrevê-lo substituindo a base formada pedescrevê-lo espaço e tempo por uma nova base constituída pedescrevê-los modos de vibração e freqüência.

Uma metodologia que pode ser utilizada para descrever o movimento cíclico de vibração de uma estrutura deve resolver a equação diferencial parcial (2-47).

(2-47)

onde: m e c→ coeficientes da variável x L→ operador diferencial linear

Dependendo do tipo de estrutura o operador L assume diferentes formas, conforme Tabela 2.1

Tabela 2.1 – Operadores lineares para diversas estruturas.

ESTRUTURA OPERADOR CONSTANTE

Corda 2 2 x T L ∂ ∂ −

= T→tração

Viga 4 4 x EI L ∂ ∂ =

E→módulo de elasticidade I→momento de inércia da secção transversal

Membrana ( ₂)

2 2 2 2 y x T T L ∂ ∂ + ∂ ∂ − = ∇ −

= Tcomprimento →tração por unidade de

Placa _⎟⎟

⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ + ∂ ∂ − = ∇ −

= 4 4_{4 2 2}4 ₂ 4₄

y y x x D D L D= Eh 3

12[1-ν2] :rigidez a flexão E→módulo de elasticidade v→coeficiente de Poisson h→espessura da placa ) , ( ) , ( ) , ( ) ( ) , ( ) ( ₂ 2 t r p t r Lw t t r w r c t t r w r

m + =

22

Considerando válidas as hipóteses de separação de variáveis (r,t). e que as funções Ψ(r) formam uma base completa e ortonormal, substitui-se a solução da forma (2-48) na equação (2-47)

(2-48)

Multiplicando a equação resultante (2- 49) por Ψκ(r) e integrando-a em relação

r, obtém-se as equações (2-50)

(2-49)

(2-50)

E, portanto,

(2-51)

onde: Ψj(r)→ descreve um modo de vibração para cada j; mj→massa modal ou massa generalizada;

ω→freqüência natural não amortecida;

βj=

cj

mj .

A equação (2-53) é o resultado da integral da equação (2-51). Admitindo válida a hipótese de separação de variáveis (r,t) para a entrada harmônica, pontual e unitária p(r,t) da equação (2-52) e aplicando a convolução δ(r-s).

(2-52) (2-53) ) ( ) ( ) , ( ) ( ) ( ) , ( 1 t w r t r w t w r t r w j j j j j j Ψ = Ψ =

∑

j _{+ Ψ =}

∂ Ψ ∂ + ∂ Ψ ∂

∑

∑

∑

∫

∫

_∫

(r t e r s p = iωtδ −

t i j j j j j j

j s e

m w w

Assim, é definida a função resposta em freqüência (2-55), Hj(ω), através da substituição da equação de saída (2-54) em (2-53).

(2-54)

(2-55)

Se r e s são pontos sobre a superfície do sistema, a função (2-55) pode ser escrita:como:

(2-56)

A função resposta em freqüência Hj(ω) é a medida da resposta do modo j para

uma excitação na freqüência ω.

2.4.1

Transformada da Função de Green em Resposta em Freqüência

As características dinâmicas de um sistema são definidas se as funções resposta em freqüência ou resposta ao impulso são conhecidas, devendo, portanto, ser possível transformar uma função na outra e vice versa. O método da transformada de Fourier decompõe uma função aperiódica em seu espectro de freqüências.

Em um sistema, aplicando a transformada de Fourier na entrada impulso x(t)=δ(t) e na saída transitória y(t)=h(t), obtêm-se as equações transformadas (2-57) e (2-58), respectivamente. (2-57) (2-58) t i j j

j t H s e

w ()= (ω)Ψ ( ) ω

) (

1 )

( _{2 2}

j j j j i m H ω ω β ω ω + + − = ) ( ) ( ) ( ) , , ( 1 s H r s r

H _{j j}

j j Ψ Ψ =

∑

∫

∫

= xt e dt t e dt X iωt δ iωt

π π

ω ( )

2 1 ) ( 2 1 ) (

∫

∫

= y t e dt h t e dt

Y iωt iωt

π π

ω ( )

24

onde: ω =2πf→freqüência

δ(t)→função impulso h(t)→função de Green

A equação (2-59é o resultado da integral (2-57) no tempo.

(2-59)

Em sistemas lineares, para dada uma excitação harmônica, a resposta do sistema tem a mesma freqüência da entrada. Assim, para uma excitação não harmônica com componentes na freqüência iguais a X(ω)dω, a resposta do sistema deve possuir componentes que variem na mesma faixa dω (ou banda) da freqüência. Em sistemas passivos, a freqüência depende exclusivamente de fonte excitadora.

Logo, a função resposta Y(w), equação (2-61) decorre da função harmônica excitadora (2-60).

(2-60)

(2-61)

Conforme equação (2-54), a saída y(t) pode ser escrita em termos da função resposta em freqüência H(ω). Logo,

(2-62)

Igualando as duas expressões de y(t), (2-61) e (2-62). obtém-se a transformada de Fourier do sistema e a relação H(ω),equação (2-63), entre a entrada X(ω) e saída Y(ω).

(2-63)

π ω δ

π ω

2 1 cos

) ( 2

1 )

( =

∫

∞

∞ −

t t

X

t i e d X t

x( )= (ω) ω ω

t i e d Y t

y( )= (ω) ω ω

t i e d X H t

y()= (ω) (ω) ω ω

) (

) ( ) (

ω ω ω

X Y

Y1(ω)

2A

2B

X2A(ω), Y2A(ω) _X

2B(ω), Y2B(ω)

X1(ω)

(a)

X1(ω)

Y1(ω)

Y

(

ω

)

(b)

Y1(ω)

X1(ω)

X2(ω), Y2(ω)

2.4.2

Acoplamento Através dos Modos de Vibração

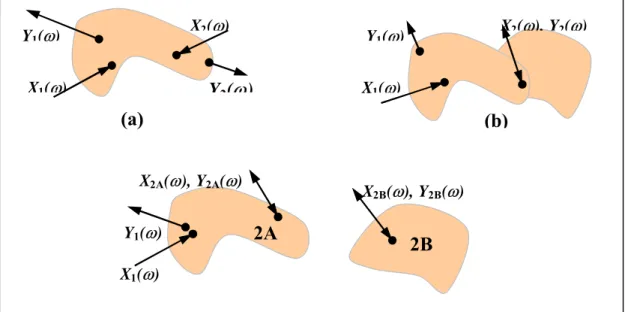
O desenvolvimento de sistema de subestruturação, foi baseado no desenvolvimento de NEWLAND, D.E. (1993), consiste no acoplamento de dois sistemas através de vínculos e sua modelagem no domínio da freqüência.

Quando os vínculos são conhecidos, é possível calcular a função resposta em freqüência de sistemas compostos, combinando as funções resposta em freqüência de cada subsistema. Para sistemas passivos, lineares e invariantes, com uma entrada harmônica X(w) e saída Y(w), a função resposta em freqüência H(w) é dada pela

equação (2-63).O vetor de saída Y →(ω) para o sistema da Figura 2.2 (a) é:

(2-64)

onde: Hjk→ função resposta freqüência para a entrada no ponto j e a saída no ponto k.

Na Figura 2.2 (b), observa-se uma entrada X1(ω) e uma saída Y1(ω) genéricas e, na conexão 2 entre os subsistemas A e B acoplados, a entrada X2(ω) é considerada como força e a saída Y2(ω) pode ser o deslocamento do ponto 2.

Figura 2.2 - Resposta em freqüência para sistema composto;

(a)→sistema simples com duas entradas e duas saídas; (b)→dois subsistemas desaclopados

e (c)→sistema acoplado

( )

( )

⎦ ⎤ ⎢

⎣ ⎡ × ⎥ ⎦ ⎤ ⎢

⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

) (

) ( )

( ) (

) ( ) (

2 1 22

21

12 11

2 1

ω ω ω

ω

ω ω

ω ω

X X

H H

H H

26 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ × ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + × + × + × + × + × − × = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 1 22 22 22 22 22 22 22 21 22 22 22 12 22 22 22 11 21 12 22 11 2 1 ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω ω X X B A B A B A B A B A B A B A B A A A A A Y Y

Desacoplando os subsistemas A e B, conforme Figura 2.2 (c), os deslocamentos Y2A(ω) e Y2B(ω) nos pontos de conexão de cada subsistema (A e B) são, por compatibilidade, iguais a Y2(ω) e, por equilíbrio, a soma das forças em cada subsistema X2A(ω) e X2B(ω) é igual a X2(ω).

(2-65)

(2-66)

A sistema de equações (2-67) e (2-68) representam os vetores de saída Y→(ω) para os subsistemas A e B da Figura 2.2 (c) respectivamente.

(2-67)

(2-68)

Rearranjando as equações (2-65) a (2-68) obtém-se o sistema de equações (2-69) e, consequentemente, a função resposta em freqüência H(ω) de acordo com as equações (2-70) a (2-73).

(2-69) (2-70)

( )

( )

[

] [

] [

]

) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 22 22 22 11 21 12 22 11

11 _{ω ω}

ω ω ω ω ω ω ω B A B A A A A A H + × + × − × = ) ( ) ( )

( _{2 2}

2 ω Y A ω Y B ω

Y = =

) ( ) ( )

( _{2 2}

2

ω

ω

ω

(2-71)

(2-72)

(2-73)

Este desenvolvimento permite concluir que, a partir das respostas do sistema à ação de um agente externo, a transformada de Fourier possibilita que os vínculos de um sistema qualquer sejam modelados no domínio da freqüência e dos modos de vibração.

) ( ) (

) ( ) ( ) (

22 22

22 12

12 _{ω ω}

ω ω

ω

B A

B A

H

+ × =

) ( ) (

) ( ) ( ) (

22 22

22 21

21 _{ω ω}

ω ω

ω

B A

B A

H

+ × =

) ( ) (

) ( ) ( ) (

22 22

22 22

22 _{ω ω}

ω ω

B A

B A

iw H

CAPÍTULO 3 – ANÁLISE ESTATÍSCA

3.1

INTRODUÇÃO

Foram desenvolvidas poucas teorias efetivas sobre o contato e são necessários modelos experimentais para descrever este tipo de fenômeno. A teoria encontra pouca aplicação prática por ser limitada e estruturada para gerar impactos pontuais.

O método dos elementos finito (MEF) é uma das principais ferramentas utilizadas para a análise de impacto. Apresenta formas para incorporar resultados teóricos e práticos às superfícies impactantes, restringidas por critérios de compatibilidade numérica, necessitando do conhecimento prévio de estruturas ensaiadas.

A proposta de uma forma alternativa para descrever o contato entre dois corpos, desenvolvida neste trabalho, é baseada na aquisição dos sinais provenientes de algum ponto do corpo impactado. A principal consideração assumida na geração do sinal é a validade das hipóteses ergótica e de invariância temporal, ou seja, os sinais obtidos através de sensores são considerados lineares e invariantes no tempo e no espaço, gerando um ensemble estatístico ou espaço amostral.

A partir destas hipóteses são deduzidas algumas relações matemáticas através das quais é possível obter características da forma de objetos impactantes. A análise se restringe ao efeito do evento.