Exemplo de dinâmica caótica em mecânica celeste

UNIVERSIDADE FEDERAL DE MINAS GERAIS

MESTRADO EM MATEM ´ATICA

EXEMPLO DE DIN ˆ

AMICA CA ´

OTICA EM MEC ˆ

ANICA

CELESTE

D´eborah da Paix˜ao Vasconcellos

Belo Horizonte - MG

D´eborah da Paix˜ao Vasconcellos

Exemplo de Dinˆ

amica Ca´

otica em

Mecˆ

anica Celeste

Disserta¸c˜ao submetida `a banca examinadora, designada pelo Programa de P´os-Gradua¸c˜ao em Matem´atica da UFMG, como requisito parcial para a obten¸c˜ao do t´ıtulo de mestre em Ma-tem´atica.

Orientador: Marcelo Domingos Marchesin

Resumo

Neste trabalho estudaremos o problema restrito de trˆes corpos de Sitnikov. Mostraremos que as solu¸c˜oes da equa¸c˜ao diferencial ordin´aria de segunda ordem que descreve o movimento do corpo de massa nula est˜ao definidas para todo o tempo e que uma solu¸c˜ao n˜ao-nula ´e necessariamente oscilat´oria, parab´olica ou hi-perb´olica quando o tempo converge para +∞ ou −∞. Caracterizaremos, no plano de condi¸c˜oes iniciais, quais s˜ao os valores que correspondem a cada uma destas solu¸c˜oes.

Abstract

In this work we will study the Sitnikov restricted three body problem. We will show that the solutions of the second order ordinary differential equation which describes the movement of the null mass body are defined for all time and that a non-null solution is necessarily oscillatory, parabolic or hyperbolic when the time goes to +∞ or −∞. We shall characterize in the plane of initial conditions what are the values that corresponds to each of this solutions.

Agradecimentos

Gostaria de agradecer inicialmente a Deus pela oportunidade que estou tendo nesta vida de estudar e lecionar.

Agrade¸co `a minha m˜ae por sempre me apoiar em todas as minhas escolhas. Desde pequena ela criou em mim o h´abito de estudar e desenvolveu em mim o gosto pelo conhecimento. Obrigada por tudo m˜ae, devo tudo o que sou e tudo o que serei a vocˆe.

Agrade¸co ao meu pai e aos meus irm˜aos Paulino e Ana Catharina por sempre fazerem meus dias mais alegres e agitados e por torcerem tanto pelo meu futuro profissional.

Agrade¸co ao Felipe, meu amor, por sempre me apoiar na vida acadˆemica e por todo o seu companheirismo.

Agrade¸co ao Marcelo, meu orientador, por toda a paciˆencia que teve comigo nestes anos de orienta¸c˜ao e por sempre me aguentar nas minhas crises existenciais. Vocˆe me ensinou demais professor e sempre me incentivou. Serei esternamente grata a vocˆe.

Agrade¸co a Capes pelos dois anos de bolsa que eu recebi, sem os quais seria imposs´ıvel me dedicar exclusivamente ao mestrado.

Agrade¸co a todos os professores que eu tive na UFMG por todo o conhecimento que vocˆes me transmitiram.

Sum´

ario

Resumo i

Abstract iii

Agradecimentos v

Introdu¸c˜ao 1

1 Defini¸c˜oes e Resultados Utilizados 5

2 Estudo qualitativo das solu¸c˜oes de x¨=−Q(x, t) 9

2.1 Q(x, t) satisfazendo certas condi¸c˜oes . . . 9

2.2 Restri¸c˜oes adicionais `a fun¸c˜ao Q(x, t) . . . 34

2.2.1 Propriedades da fun¸c˜ao sucessora . . . 54

2.2.2 Exigindo a condi¸c˜ao lim x→∞Q0(x) Z x 0 Q0(y)dy= 0. . . 70

3 O shift do espa¸co de sequˆencias como subsistema de uma aplica¸c˜ao 83 3.1 Topologia do espa¸co de sequˆencias . . . 83

3.2 O shift como subsistema de uma aplica¸c˜ao cont´ınua . . . 84

3.3 Compactifica¸c˜ao do espa¸co de sequˆencias . . . 91

3.4 O shift como subsistema de uma aplica¸c˜ao de classe C1 _{. . . 94}

4 O problema de Sitnikov 99 4.1 As equa¸c˜oes de movimento . . . 99

4.2 O shift do espa¸co de sequˆencias como subsistema da aplica¸c˜ao S−1 _{. . 113}

Considera¸c˜oes Finais 117

Introdu¸

c˜

ao

Estudaremos nessa disserta¸c˜ao o problema restrito dos trˆes corpos onde dois corpos de massas iguais (denominados prim´arios) descrevem ´orbitas el´ıpticas dadas pela solu¸c˜ao do problema dos dois corpos e o terceiro corpo de massa nula se move sobre a reta L que ´e perpendicular ao plano dos prim´arios e que passa pelo centro de massa destes. Como o terceiro corpo tem massa nula ele n˜ao influencia as ´orbitas dos prim´arios, mas seu movimento ´e influenciado por eles. Tal problema ´e conhecido como problema de Sitnikov e nosso principal objetivo ´e mostrar a existˆencia de comportamento ca´otico no movimento do corpo de massa nula.

O caso particular em que os prim´arios descrevem ´orbitas circulares foi conside-rado inicialmente por McMillan [11]. Ele encontrou a solu¸c˜ao exata das equa¸c˜oes de movimento e mostrou que a solu¸c˜ao pode ser expressa em termos das integrais el´ıpticas. Em 1922-32, Chazy [6] classificou os movimentos finais do corpo de massa nula, olhando seu comportamento assint´otico quando t → +∞. Ele declara que os movimentos poss´ıveis, neste problema, s˜ao hiperb´olicos, parab´olicos, oscilat´orios ou limitados. O problema se tornou mais importante quando Sitnikov [15] investigou o caso el´ıptico (com a excentricidade da ´orbita dos prim´arios maior que zero) e provou a possibilidade de existˆencia dos movimentos oscilat´orios previstos anteriormente por Chasy. Alekseev [1], [2] e [3] provou que no problema restrito dos 3-corpos de Sitnikov todas as combina¸c˜oes poss´ıveis dos movimentos finais previstos por Chazy de fato ocorrem e em 1973, uma prova alternativa dos resultados de Alekseev foi dado por Moser [13]. Alekseev mostra a caoticidade fazendo uma conjuga¸c˜ao to-pol´ogica entre a aplica¸c˜aoS e o shift no espa¸co de caminhos completos de um grafo e Moser mostra a caoticidade fazendo uma conjuga¸c˜ao topol´ogica entre a aplica¸c˜ao S−1 _{e o shift do espa¸co de sequˆencias (os argumentos utilizados por ele se baseiam} na existˆencia de pontos homocl´ınicos transversais). Posteriormente, alguns autores mostraram a caoticidade utilizando a transforma¸c˜ao de coordenadas de McGehhe [10] para obter um ponto homocl´ınico na origem e provar a sua transversalidade usando o m´etodo de Melnikov.

a caoticidade utilizando os teoremas de [13]. Mas as demonstra¸c˜oes e resultados obtidos pelo Alekseev para uma solu¸c˜ao de uma equa¸c˜ao diferencial ordin´aria da forma ¨x=−Q(x, t) s˜ao mais completos e mais detalhados. Ent˜ao decidimos estudar os resultados de Alekseev e utiliz´a-los para demonstrar o teorema de Moser do cap´ıtulo 3.

No cap´ıtulo 2 consideraremos uma equa¸c˜ao diferencial ordin´aria de segunda or-dem da forma ¨x =₋Q(x, t). Mostraremos que se a fun¸c˜ao Q(x, t) satisfizer certas propriedades convenientes ent˜ao podemos descrever uma solu¸c˜ao x(t) a partir de v eτ, onde x(τ) = 0 e v = ˙x(τ) ´e a velocidade no instante τ.

Mostraremos que devido a simetria do problema podemos considerar, sem perda de generalidade, apenas as velocidades iniciais n˜ao negativas e podemos considerar τ como uma vari´avel angular. Consideraremos ent˜ao o plano Φ dado por (v, τ).

Definiremos uma aplica¸c˜ao S em uma certa regi˜ao deste plano que segue uma solu¸c˜ao x(t;v, τ) com condi¸c˜oes iniciais x(τ) = 0, x(τ) =˙ v at´e seu pr´oximo zero, onde a solu¸c˜ao passa com velocidadev′ _{no instante τ}′_{, isto ´e, S(v, τ) = (v}′_{, τ}′_).

Mostraremos que a origem do plano Φ representa a solu¸c˜ao identicamente nula. Al´em disso, demonstraremos que seR+₀ ´e a regi˜ao do plano na qual a aplica¸c˜aoSest´a definida (isto ´e, as condi¸c˜oes iniciais das solu¸c˜oes que possuem um zero futuro), ent˜ao sua fronteira, Π+₀, ´e constituida de condi¸c˜oes iniciais para as quais as solu¸c˜oes cor-respondentes s˜ao parab´olicas e que o restante do planoH₀+ = Φ\ R₀+∪Π+₀ ∪ {O}

´e constitu´ıda de condi¸c˜oes iniciais para as quais as solu¸c˜oes correspondentes s˜ao hiperb´olicas.

Mostraremos que S : R+_{0 →} R−₀ ´e um difeomorfismo, onde R−₀ correspondem `as solu¸c˜oes que possuem algum zeroτ′′ <sub>< τ. Caracterizaremos, no plano Φ, quem s˜ao</sub> as regi˜oes que correspondem `as solu¸c˜oes parab´olicas, hiperb´olicas e oscilat´orias e mostraremos que tais regi˜oes s˜ao n˜ao-vazias e que, junto com a origem, elas comp˜oe todo o plano Φ.

No cap´ıtulo 3, n´os enunciaremos e demonstraremos um teorema que garante que se um homeomorfismoφdefinido no quadrado unit´ario satisfaz certas propriedades, ent˜ao ele possui a aplica¸c˜ao shift no espa¸co das sequˆencias como subsistema. Ob-teremos condi¸c˜oes alternativas a estas para o caso particular em que φ ´e de classe C1_.

No cap´ıtulo 4 estudaremos as equa¸c˜oes diferenciais obtidas no problema de Sit-nikov. Consideraremosx como sendo a coordenada da posi¸c˜ao do terceiro corpo na reta L, ondex= 0 corresponde ao centro de massa.

a fun¸c˜ao Q(x, t) do problema de Sitnikov satisfaz todas as propriedades exigidas no Cap´ıtulo 2. Consequentemente, poderemos usar todos os resultados obtidos anteriormente para a equa¸c˜ao de movimento do problema de Sitnikov.

Cap´ıtulo 1

Defini¸

c˜

oes e Resultados Utilizados

Neste cap´ıtulo, a t´ıtulo de completude, apresentaremos algumas defini¸c˜oes e alguns resultados j´a conhecidos que n´os utilizaremos ao longo desta disserta¸c˜ao.

Defini¸c˜ao 1.1. Seja x um ponto do espa¸co topol´ogico X. Uma fam´ılia Bx de

vizinhan¸cas dex´e dita uma base de vizinhan¸cas dexse toda vizinhan¸ca dexcont´em algum B ∈Bx.

Proposi¸c˜ao 1.2. Seja X ₆= _∅ um conjunto e suponha que para cada x _∈ X seja

dada uma cole¸c˜ao Bx de subconjuntos de X satisfazendo:

i) Se N ∈Bx ent˜ao x∈N;

ii) Se V cont´em algum conjunto em Bx ent˜ao V ∈Bx;

iii) SeN, M ∈B_x ent˜ao N ∩M ∈B_x;

iv) Se N _∈B_x ent˜ao existeV _∈B_x, V _⊂N tal que V _∈B_y para todo y_∈V. Definiremos como abertos os subconjuntos A _⊂X tais que para cada x _∈A existir umV _∈Bx tal quex∈V ⊂A. Os abertos assim definidos constituem uma topologia

para X relativa `a qual para todo x _∈ X a cole¸c˜ao Bx ´e a cole¸c˜ao das vizinhan¸cas

de X.

Defini¸c˜ao 1.3. Uma compactifica¸c˜ao de um espa¸co X ´e um espa¸co de Hausdorff compacto Y contendo X tal que X ´e denso em Y ( isto ´e, X =Y).

Teorema 1.4. Seja f : X → Y uma fun¸c˜ao cont´ınua bijetiva. Se X ´e compacto e

Y ´e de Hausdorff, ent˜ao f ´e um homeomorfismo.

Defini¸c˜ao 1.5. Um conjunto ´e dito de tipo Fσ se ele pode ser escrito como a uni˜ao

enumer´avel de conjuntos fechados e ´e dito de tipo Gδ se ele pode ser escrito como a

interse¸c˜ao enumer´avel de conjuntos abertos.

uma fun¸c˜ao de classeC1 _{em xe cont´ınua em t. Se (t}

0, x0)∈U, existe um intervalo

abertoJ contendot0 e uma ´unica solu¸c˜ao dex˙ =f(t, x)definida emJ e satisfazendo x(t0) =x0.

Teorema 1.7.(Continuidade das Solu¸c˜oes nas Condi¸c˜oes Iniciais e nos Parˆametros): Seja f(x, t) uma aplica¸c˜ao de classe C1 _{definida em R}n_{×R. Seja ϕ uma solu¸c˜ao}

de x˙ = f(t, x) no intervalo I = [a, b]. Ent˜ao existe um δ > 0 tal que para todo

(τ, ξ) _∈ U = _{(τ, ξ) : τ _∈ (a, b), _|ξ ₋ ϕ(x)_| < δ_} existe uma ´unica solu¸c˜ao da equa¸c˜ao x˙ = f(t, x) em I com ϕ(τ, τ, ξ) = ξ. Al´em disso, ϕ ´e cont´ınua em

V =_{(t, τ, ξ) : a < t < b, (τ, ξ)_∈U_}.

Teorema 1.8. Seja f cont´ınua num aberto Ω ⊂ R2_{. Se ϕ ´e a solu¸c˜ao m´axima}

de x˙ =f(t, x) definida em (ω₋, ω+), ent˜ao a aplica¸c˜ao g(t) = (t, ϕ(t)) tende a ∂Ω

quando t→ω_±. Isto ´e, para todo compacto K ⊂Ω existe uma vizinhan¸ca V de ω_±

tal que g(t)_∈/ K para t _∈V.

Defini¸c˜ao 1.9. Sejam (X,X, µ) e (Y,Y, ν) espa¸cos de medida. Uma aplica¸c˜ao

f : X _→ Y ´e mensur´avel se para todo B _∈ Y temos f−1_{(B) ∈ X. Dizemos}

que uma aplica¸c˜ao f : X _→ Y preserva medida se f ´e mensur´avel e se para todo conjunto mensur´avelB _∈Y temos

µ(f−1(B)) =ν(B).

Teorema 1.10. Um difeomorfismo local f : U _→ Rm _{no aberto U ⊂} Rm _{´e um}

difeomorfismo global sobre sua imagem f(U) se, e somente se, ´e uma aplica¸c˜ao injetiva.

Defini¸c˜ao 1.11. Dizemos que uma fun¸c˜ao f : U → R _{´e da ordem quande de}

g(x) :U →R _{quando x→a (e denotamos por f(x) =O(g(x)) se}

lim

x→a

f(x)

g(x) =C ∈R,

onde a _∈ U _∪∂U ou a = _∞. E dizemos que uma fun¸c˜ao f : U _→ R _{´e da ordem} pequena de g(x) :U _→R _{(e denotamos por f(x) = o(g(x)) quando x→a se}

lim

x→a

f(x) g(x) = 0,

onde a_∈U _∪∂U ou a=_∞.

Teorema 1.12. (Teorema do Ponto Fixo para Contra¸c˜oes): Sejam F _⊂ Rm _um

sequˆencia x1 = f(x0), ..., xn = f(xn−1), ... converge para um ponto a ∈ F que ´e o

´

unico ponto fixo de f.

Teorema 1.13. (Desigualdade de Bellman-Grownwall): Sejam ϕ, ψ e Ξ fun¸c˜oes

reais cont´ınuas definidas no intervalo real I : a ≤ t ≤ b. Seja Ξ(t) > 0 em I e suponha que para t∈I vale

ϕ ≤ψ(t) +

Z t

a

Ξ(s)ϕ(s)ds.

Ent˜ao em I vale

ϕ _≤ψ(t) +

Z t

a

Ξ(s)ψ(s) exp

Z t s

Ξ(u)du

ds.

Teorema 1.14. (Teorema de Dini): Se uma sequˆencia de fun¸c˜oes reais cont´ınuas

fn :M → R, definidas em um espa¸co m´etrico compacto M, converge simplesmente

para uma fun¸c˜ao cont´ınua f : M _→R_{, e, al´em disso, tem-se f1(x) ≤f2(x)≤...≤}

fn(x), ... para todo x∈M, ent˜ao a convergˆencia fn→f ´e uniforme em M.

Teorema 1.15. (Teorema dos Intervalos Fechados Encaixados): Um espa¸co m´etrico

M´e completo se, e somente se, para toda sequˆencia decrescenteF1 ⊃F2 ⊃...⊃Fn ⊃...

de subconjuntos fechados n˜ao-vaziosFn⊂M, com lim

n→∞ diˆametro Fn= 0, existe um

ponto a_∈M tal que

∞

\

n=1

Fn ={a}.

Teorema 1.16. (Teorema da Aplica¸c˜ao Inversa): Seja f : U _→ Rm_{, definida no}

aberto U _⊂ Rm_{, uma aplica¸c˜ao de classe C}k _{(k ≥ 1) tal que o seu determinante} Jacobiano seja n˜ao-nulo no pontoa_∈U. Ent˜aof ´e um difeomorfismo de um aberto

V contendo a sobre um aberto W contendof(a).

Teorema 1.17. (Teorema da Fun¸c˜ao Impl´ıcita): Seja f : U → R _{uma fun¸c˜ao de}

classe Ck _{(k ≥ 1), definida no aberto U ⊂ R}m+1_{. Se um ponto p = (x}

0, y0) ∈ U

´e tal que f(p) = c e ∂f

∂y(p)6= 0, ent˜ao existem uma bola B = B(x0, δ) ⊂ R

m _{e um}

intervalo J = (y0 −ǫ, y0 +ǫ) tais que f−1(c)∩(B ×J) ´e o gr´afico de uma fun¸c˜ao ξ:B →J, de classe Ck_{. Para todo x∈B, tem-se}

∂ξ ∂xi

(x) = ₋ ∂f ∂xi

(x, ξ(x)) ∂f

∂y(x, ξ(x))

Cap´ıtulo 2

Estudo qualitativo das solu¸

c˜

oes de

¨

x

=

₋

Q

(

x, t

)

Neste cap´ıtulo obteremos v´arios resultados a respeito das solu¸c˜oes de uma equa¸c˜ao diferencial ordin´aria da forma ¨x = −Q(x, t), onde a fun¸c˜ao Q(x, t) satisfaz cer-tas propriedades convenientes motivadas pelo problema de Sitnikov que queremos estudar.

2.1

Q

(

x, t

)

satisfazendo certas condi¸

c˜

oes

Considere a equa¸c˜ao diferencial ordin´aria, possivelmente n˜ao-autˆonoma, de 2a _ordem ¨

x=₋Q(x, t); (2.1) onde a fun¸c˜aoQ(x, t) satisfaz as seguintes condi¸c˜oes:

1 o

: Q(x, t) e todas as suas derivadas parciais de primeira ordem s˜ao cont´ınuas na regi˜ao−∞< x <+∞, −∞< t <+∞;

2 o

: Q(x, t) ´e ´ımpar em x (ou seja Q(−x, t) =−Q(x, t)) e 2π-peri´odica emt;

3 o

:Q(x, t)≥0 para todox >0 e para todot(o gr´afico de uma solu¸c˜aoxda equa¸c˜ao diferencial ´e cˆoncavo para baixo enquanto ela for positiva). Para cada x >0 existe um t tal que Q(x, t)>0;

4 o

: Existe uma fun¸c˜ao ψ(x) integr´avel em [0,_∞) tal que _|Qt(x, t)| ≤ψ(x)∀t ∈R.

Demonstra¸c˜ao. Reescrevemos a equa¸c˜ao (2.1) como

(

˙ x=y;

˙

y=₋Q(x, t).

Suponha que uma solu¸c˜ao z(t) = (x(t), y(t)) esteja definida no intervalo maximal (ω₋, ω+) comω+ <∞. ComoQ(x, t) est´a definida em todo oR2 ent˜ao, pelo teorema (1.8), lim

t→ω+|z(t)|=∞. Observemos que

Q(x, t) =

Z t

0

Qs(x, s)ds,

e ent˜ao

|y(t)˙ |=|Q(x(t), t)| ≤

Z t

0

|Qs(x(t), s)|ds≤tψ(x(t))≤ω+ψ(x(t))<∞,

Sejaω₋ < τ < ω+. Como ω+ <∞e

|y(t)| − |y(τ)| ≤ |y(t)−y(τ)|=

Z t

τ

˙ y(s)ds

≤

Z t

τ |

˙ y|ds

≤

Z t

τ

ω+ψ(x)ds= (t−τ)ω+ψ(x)≤2ω+2ψ(x),

ent˜ao lim

t→ω+|y(t)|<∞. Logo, se considerarmos a norma da soma em

R2_{, temos que}

∞= lim

t→ω+|z(t)|= limt→ω+|x(t)|+ limt→ω+|y(t)| ⇒ t→limω+|x(t)|=∞.

Suponha que lim

t→ω+x(t) = ∞. Existe um n´umero real t+ ∈ (τ, ω+) tal que x(t) ´e

positiva emI+ = (t+, ω+). Mas ent˜ao ¨x≤0 emI+. Logo,x(t) ´e uma fun¸c˜ao cˆoncava para baixo, positiva em I+ e tal que lim

t→ω+x(t) =∞, o que ´e um absurdo (uma vez

queω+ <∞). O racioc´ınio ´e an´alogo para o caso em que lim

t→ω+x(t) = −∞.

Defini¸c˜ao 2.2. Uma solu¸c˜ao x(t) de (2.1) ´e dita hiperb´olica quando t_→+_∞ se

lim

t→+∞|x(t)|=∞, t→lim+∞x(t) =˙ v∞6= 0.

´

E dita ser uma solu¸c˜ao parab´olica se

lim

t→+∞|x(t)|=∞, t→lim+∞x(t) = 0,˙

infinita de zeros convergindo para+_∞.

Analogamente, definimos solu¸c˜oes hiperb´olicas, parab´olicas e oscilat´orias quando t_{→ −∞}.

Proposi¸c˜ao 2.3. Toda solu¸c˜ao n˜ao-nula de (2.1) ´e hiperb´olica, parab´olica ou osci-lat´oria quandot →+∞ (t→ −∞).

Demonstra¸c˜ao. Suponhamos quex(t) ´e uma solu¸c˜ao n˜ao-trivial de (2.1). Se a regi˜ao t > t0 possui um n´umero infinito de zeros da solu¸c˜ao, ent˜ao esses zeros formam uma sequˆencia convergindo para +_∞e teremos assim uma solu¸c˜ao oscilat´oria. Suponha-mos que uma solu¸c˜ao possui um n´umero finito de zeros e que x(t)>0 para t≥ T. Pela 3a _{propriedade de Q(x, t) temos ent˜ao que ¨x=−Q(x, t)≤0 e,} consequente-mente, ˙x(t) ´e uma fun¸c˜ao n˜ao-crescente. Portanto,

lim

t→+∞x(t) =˙ v∞,

existe, uma vez que x(t) > 0. Se v_∞ < 0 ent˜ao x(t) seria decrescente a partir de certo momento e ter´ıamos lim

t→+∞x(t) =−∞(j´a que x(t) n˜ao muda de concavidade), o que seria um absurdo. Logo, v_∞≥0. Se v_∞ >0 ent˜ao a solu¸c˜ao ´e hiperb´olica. Resta mostrarmos que se v_∞= 0 ent˜ao teremos lim

t→+∞x(t) = ∞ e a solu¸c˜ao ser´a parab´olica. Como ˙x(t) ´e n˜ao-crescente e v_∞ = 0, ent˜ao ˙x(t)_≥ 0 e, portanto, x(t) ´e n˜ao-decrescente. Integrando (2.1), obtemos

Z t

T

Q(x(s), s)ds=

Z t

T −

¨

x(s)ds= ˙x(T)₋x(t).˙

Logo, a integral

Z ∞

T

Q(x(s), s)ds converge para ˙x(T) e

˙

x(2πn) =

Z 2π(n+1)

2πn

Q(x(s), s)ds+

Z ∞

2π(n+1)

Q(x(s), s)ds

=

Z 2π(n+1)

2πn

Q(x(s), s)ds+ ˙x(2π(n+ 1)),

para todon. Portanto,

Z 2π(n+1)

2πn

Q(x(s), s)ds = ˙x(2πn)₋x(2π(n˙ + 1)),e temos que

lim

n→∞

Z 2π(n+1)

2πn

Suponhamos que lim

t→+∞x(t) = b <∞. Ent˜ao

0 = lim

n→∞

Z 2π(n+1)

2πn

Q(x(s), s)ds= lim

n→∞

Z 2π

0

Q(x(s+ 2πn), s)ds =

Z 2π

0

Q( lim

n→∞x(s+ 2πn), s)ds =

Z 2π

0

Q(b, s)ds.

Na primeira passagem fazemos a mudan¸ca de coordenadass_7→s₋2πn e usamos o fato de queQ(x, t) ´e 2π-peri´odica na vari´avel t. Na segunda passagem usamos a 4a propriedade para garantir que o limite da integral ´e a integral do limite e o fato de queQ(x, t) ´e cont´ınua. Na terceira passagem usamos que lim

t→+∞x(t) = b <∞. Logo,

Z 2π

0

Q(b, s)ds= 0.

Como b > 0, pela 3a _{propriedade, Q(b, t) ≥ 0 para todo t e existe um r tal que} Q(b, r)>0. ComoQ(x, t) ´e cont´ınua, existe uma vizinhan¸caV dertal queQ(b, t)> 0 em V. Portanto,

Z 2π

0

Q(b, s)ds >0, o que ´e um absurdo. Logo, se v_∞= 0 ent˜ao x(t)→+∞ quando t→+∞e, portanto, x(t) ´e parab´olica.

Sejax(t;v, τ) a solu¸c˜ao de (2.1) determinada pelas condi¸c˜oes iniciais

x(τ;v, τ) = 0, x(τ˙ ;v, τ) = v. (2.2)

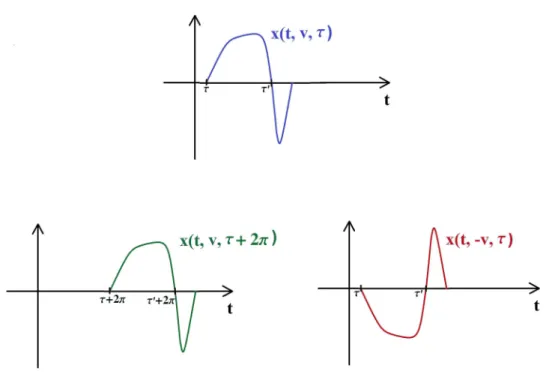
Observa¸c˜ao 2.4. Pela unicidade das solu¸c˜oes e pelo fato da fun¸c˜ao Q(x, t)ser 2π -peri´odica em t e ´ımpar em x, segue que se x(t, v, τ)´e uma solu¸c˜ao de (2.1) ent˜ao

x(t+ 2π;v, τ+ 2π)_≡x(t;v, τ), (2.3) x(t;−v, τ)≡ −x(t;v, τ), (2.4) x(t; 0, τ)_≡0. (2.5)

Veja a Figura 2.4

Figura 2.1: As solu¸c˜oes x(t;v, τ),x(t;v, τ + 2π) e x(t;₋v, τ).

da solu¸c˜ao), o que seria um absurdo. Logo, se τ′ _{< ∞, ent˜ao x(τ}′_{;v, τ) = 0.} Definimos

X(v, τ) = sup

τ <t<τ′x(t, v, τ).

Seτ′ _{=∞ent˜ao a solu¸c˜ao ´e parab´olica ou hiperb´olica quandot→ ∞e, portanto,} X = +_∞. Seτ′ _{<∞, ent˜aoX(v, τ) ´e um m´aximo local da solu¸c˜aox(t;v, τ). Como} o gr´afico dex(t;v, τ) ´e cˆoncavo para baixo parax >0, ent˜ao o conjunto dos valores de t para os quais x = X ´e um intervalo [T_∗(v, τ), T∗(v, τ)]_⊂(τ, τ′). Depois de atingir o seu m´aximo, a solu¸c˜aox(t;v, τ) come¸ca a decrescer e se torna zero quando t=τ′ _{(ver Figura 2.1). Isto significa que}

x(t;v, τ)< X(v, τ); x(t;˙ v, τ)>0 paraτ ≤t < T_∗(v, τ),

x(t;v, τ) =X(v, τ); x(t;˙ v, τ) = 0 para τ ≤T_∗(v, τ)≤t ≤T∗_{(v, τ),} x(t;v, τ)< X(v, τ); x(t;˙ v, τ)<0 paraT∗(v, τ)< t≤τ′,

(2.6)

onde a segunda e a terceira equa¸c˜oes valem somente paraτ′ _{<+∞. Para τ}′ _{= +∞} tomamos T_∗(v, τ) =T∗(v, τ) = +_∞. Definimos ainda X(0, τ)_≡0.

Figura 2.2: A solu¸c˜ao x(t;v, τ) para t_∈[τ, τ′_{] no caso em que τ}′ _<∞

2) Para v0 >0 temos que T_∗(v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)T∗(v, τ)≤_(v,τlim sup_)→(v0,τ0)T

∗_{(v, τ)≤T}∗_(v

0, τ0) (2.7)

3) SeQ(x, t)>0para todo x >0 e para todo t, ent˜aoT_∗(v, τ)_≡T∗(v, τ) e a fun¸c˜ao

T∗_{(v, τ)´e cont´ınua em todo ponto, exceto possivelmente em v = 0.}

4) Se τ for tomado em um conjunto limitado inferiormente, Q(x, t) ´e limitada su-periormente e X(v, τ)→+∞, ent˜ao

T_∗(v, τ)→+∞, T∗(v, τ)→+∞, τ′ →+∞

Demonstra¸c˜ao. Vamos come¸car demonstrando 2) no caso τ′ _{<∞. Sejam v}

0 >0 e τ′ _{<∞. Sejam t}

1 e t2 quaisquer tais que

τ < t1 < T∗(v0, τ0)≤T∗(v0, τ0)< t2 < τ′.

Por (2.6) sabemos que ˙x(t;v0, τ0)>0 para τ ≤t ≤ t1 e que ˙x(t2;v0, τ0)<0. Dado ǫ >0 arbitr´ario, o ponto (v0, τ0) possui vizinhan¸ca U0 na qual

˙

x(t;v, τ)>0 para τ _≤t _≤t1, (2.8) ˙

x(t2;v, τ)<0 e |x(t;v, τ)−x(t;v0, τ0)|< ǫ para t1 ≤t≤t2, (2.9) pela continuidade das solu¸c˜oes nas condi¸c˜oes iniciais. Por (2.8) temos queT_∗(v, τ)> t1 em U0 (pois em ˙x(T∗(v, τ);v, τ) = 0). Logo,

lim inf

Pela arbitrariedade da escolha de t1 obtemos ent˜ao T_∗(v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)T∗(v, τ). De forma an´aloga se mostra que

lim sup (v,τ)→(v0,τ0)

T∗(v, τ)_≤T∗(v0, τ0),

e a parte 2) da proposi¸c˜ao est´a demonstrada para o caso em que τ′ _{< +∞. Agora} vamos mostrar 1) no caso em queτ′ _{<∞. Por (2.8) obtemos quex(t}

1;v, τ)≤X(v, t) em U0 e, portanto, x(t1;v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)X(v, τ). Fazendo o limite quando t1 → T_∗(v0, τ0) obtemos

X(v0, τ0) = lim

t1→T∗(v0,τ0)

x(t1;v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)X(v, τ). (2.10) Por outro lado, por (2.8) e pela primeira desigualdade de (2.9), para (v, τ) _∈ U0, temost1 ≤T∗(v, τ)≤T∗(v, τ)≤t2, e, pela segunda parte de (2.9), temos que

X(v, τ) = max

t∈[t1,t2]x(t;v, τ)≤t∈max[t1,t2]x(t;v0, τ0) +ǫ=X(v0, τ0) +ǫ. Comoǫ >0 ´e arbitr´ario, segue que

lim sup (v,τ)→(v0,τ0)

X(v, τ)_≤X(v0, τ0),

e, portanto, por (2.10), temos que lim

(v,τ)→(v0,τ0)X(v, τ) =X(v0, τ0).

Ou seja, X(v, τ) ´e cont´ınua em (v0, τ0), o que conclui a demonstra¸c˜ao da parte 1) da proposi¸c˜ao no caso em que v > 0 e τ′ _{< +∞. Vamos agora considerar o caso} em que τ′ _{= ∞. Mostraremos primeiro a parte 2) da proposi¸c˜ao neste caso. Se} τ′ _{= +∞ ent˜ao X(v}

0, τ0) = +∞ e T∗(v0, τ0) = +∞. Sejam v0 > 0 e t1 arbitr´ario tal que τ < t1 < +∞. Sabemos que ˙x(t;v0, τ0) > 0 para τ ≤ t ≤ t1. O ponto (v0, τ0) possui ent˜ao uma vizinhan¸caU0 na qual ainda vale (2.8). Logo, como vimos anteriormente, temos queT_∗(v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)T∗(v, τ)≤T ∗_(v

0, τ0). Portanto, +_∞=T_∗(v0, τ0)≤ lim inf

(v,τ)→(v0,τ0)T∗(v, τ)≤_(v,τlim sup_)→(v0,τ0)T

∗_{(v, τ)≤T}∗_(v

Logo,

T_∗(v0, τ0) = lim

(v,τ)→(v0,τ0)T∗(v, τ) =(v,τ)lim→(v0,τ0)T

∗_{(v, τ) = T}∗_(v 0, τ0),

o que conclui a prova da parte 2) da proposi¸c˜ao. Vamos mostrar agora a parte 1) da proposi¸c˜ao no casoτ′ _{=∞e v}

0 >0. ComoX(v0, τ0) = ∞, por (2.10) (que segue de (2.8)), temos que

lim

(v,τ)→(v0,τ0)X(v, τ) =∞=X(v0, τ0),

e, portanto, X(v, τ) ´e cont´ınua em (v0, τ0), o que conclui a demonstra¸c˜ao da parte 1) da proposi¸c˜ao no caso em que v > 0 e τ′ _{= +∞. Para finalizar a prova da} primeira parte da proposi¸c˜ao, temos que mostrar que X(v, τ) ´e cont´ınua para v = 0. Suponhamos, por absurdo, que exista uma sequˆencia (vn, τn) → (0, τ0) tal que X(vn, τn)→α >0. Como

X(v, τ) = sup (τ,τ′₎

x(t;v, τ) = sup (τ,T∗)

x(t;v, τ),

ent˜ao existe uma sequˆenciatn tal quex(tn;vn, τn)→α, τn ≤tn< T∗(vn, τn). No

in-tervalo [τn, tn] a velocidade ˙x(t;vn, τn) ´e n˜ao-crescente e, portanto, 0≤x(t;˙ vn, τn)<

˙

x(τn;vn, τn)≤vn. Comox(τn;vn, τn) = 0, temos

x(tn;vn, τn) =

Z tn

τn

˙

x(t;vn, τn)dt≤

Z tn

τn

vndt=vn(tn−τn)

e ent˜ao

tn−τn≥

x(tn;vn, τn)

vn →

+_∞. Mas

0≤x(t˙ n;vn, τn) =vn−

Z tn

τn

Q(x(t;vn, τn), t)dt,

e se come¸carmos por umn tal que tn−2π > τn, ent˜ao teremos

Z tn

tn−2π

Q(x(t;vn, τn), t)dt≤

Z tn

τn

Q(x(t;vn, τn), t)dt≤vn →0.

Como 0≤x(t;˙ vn, τn)≤vn, a oscila¸c˜ao de x(t;vn, τn) no intervalo [tn−2π, tn] n˜ao

excede 2πvn. Mas x(tn;vn, τn)→αe, portanto, x(tn−2π+s;vn, τn)→α

uniforme-mente para 0_≤ s _≤2π, pois vn →0 e |x(tn−2π+s;vn, τn)−x(t;vn, τn)| ≤2πvn.

m´odulo 2π. Assim, a sequˆencia tn ´e limitada e, passando a uma subsequˆencia se

necess´ario, podemos assumir quetn →t0 ∈[0,2π]. Logo,

0 = lim

n→+∞

Z tn

tn−2π

Q(x(t;vn, τn), t)dt

= lim

n→+∞

Z tn−2π[₂tn_π]

tn−2π([₂tn_π]+1)

Q(x(2π

tn

2π

+s;vn, τn), s)ds

= lim

n→+∞

Z 2π

0

Q(x(tn−2π+r;vn, τn), r+tn)dr

=

Z 2π

0

Q( lim

n→+∞x(tn−2π+r;vn, τn), r+ limn→+∞tn)dr =

Z 2π

0

Q(α, r+t0)dr.

Na segunda igualdade fizemos a mudan¸ca de coordenadas t=s+ 2π

tn

2π

e na terceira fizemos a mudan¸ca de coordenadasr=s₋tn+ 2π([tn/2π] + 1). Pela

pro-priedade 3o _temos

Z 2π

0

Q(α, r+t0)dr >0, o que ´e um absurdo. Logo, X(v, τ) ´e cont´ınua parav = 0, o que conclui a prova da parte 1) da proposi¸c˜ao. Agora vamos mostrar a parte 3) da proposi¸c˜ao. Suponhamos que Q(x, t)> 0 para todo x > 0 e para todo t ∈ R _{e que T∗(v, τ) < T}∗_{(v, τ). Ent˜ao x(t;v, τ) ´e constante em [T∗, T}∗_]

e, portanto, ¨x= 0 neste intervalo. Mas ¨x=−Q(x, t)< 0. Isto ´e uma contradi¸c˜ao. Logo, T_∗(v, τ) = T∗_{(v, τ). Pela parte (2) da proposi¸c˜ao sabemos que se v}

0 > 0, ent˜ao

T_∗(v0, τ0) = lim inf

(v,τ)→(v0,τ0)T∗(v, τ) = lim sup_{(v,τ)→(v0,τ0)}T

∗_{(v, τ) = T}∗_(v 0, τ0),

e, portanto, a fun¸c˜aoT_∗(v, τ) =T∗_{(v, τ) ´e cont´ınua. Suponhamos queτ seja tomado} em um conjunto limitado inferiormente, queQ(x, t) ´e limitada superiormente e que X(v, τ) → ∞. Suponhamos ainda, por absurdo, que exista uma sequˆencia (vn, τn)

tal que

X(vn, τn)→ ∞, τn ≥a >−∞, T∗(vn, τn)→b <+∞,

onde τn ≥ a para todo n ∈ N. Logo, a≤τn ≤T∗(vn, τn)→b (ou seja, a sequˆencia

τn ´e limitada). Portanto, passando a uma subsequˆencia se necess´ario, podemos

assumir queτn →τ0 <+∞. Al´em disso, passando novamente a uma subsequˆencia se necess´ario, podemos assumir quevn →v0 6= 0, pois sev0 = 0 ter´ıamosX(v, τ)→ X(0, τ0) = 0 pela parte (1) da proposi¸c˜ao, o que seria uma absurdo. Se v0 < +_∞, ent˜ao X(v0, τ0) = lim

n→+∞X(vn, τn) = +∞ e ent˜ao x(t;v0, τ0) ´e hiperb´olica ou parab´olica. Logo, para tal solu¸c˜ao,T_∗(v0, τ0) = +∞. Mas como v0 6= 0, ent˜ao pela parte 2) da proposi¸c˜ao, temos que T_∗(v0, τ0)≤lim inf

um absurdo. Sev0 = +∞, ent˜ao por (2.2) e por (2.6) temos que

Z T∗(vn,τn)

τn

Q(x(s;vn, τn), s)ds = ˙x(τn;vn, τn)−x(T˙ ∗(vn, τn);vn, τn) = vn →+∞.

Mas, por hip´otese,Q(x, t) ´e limitada superiormente. Logo,

Z T∗(vn,τn)

τn

Q(x(s;vn, τn), s) ds ≤C(T∗(vn, τn)−τn)→C(b−τ0)<∞,

o que ´e um absurdo. Portanto, T_∗(v, τ) → +∞. Como T_∗(v, τ) ≤ T∗_{(v, τ) ≤ τ}′_, ent˜ao

T∗(v, τ)_→+_∞ e τ′ _→+_∞.

SejaQ0(x) a fun¸c˜ao dada por

Q0(x) = 1 2π

Z 2π

0

Q(x, t)dt.

A demonstra¸c˜ao do seguinte lema ´e imediata.

Lema 2.6. Se a fun¸c˜ao Q(x, t) satisfaz a propriedade 4o

para todo x > 0 e para todo t, ent˜ao

|Q0(x)−Q(x, t)| ≤2πψ(x) (2.11) Definamos a fun¸c˜ao

h(v, τ) =

            

v2 ∞ 2 +

Z ∞

0

Q0(x)dx , seX(v, τ) =∞,

Z X(v,τ)

0

Q0(x)dx , seX(v, τ)<∞,

(2.12)

onde v_∞= lim

t→∞x(t;˙ v, τ). Esta fun¸c˜ao ser´a essencial para classificarmos o compor-tamento das solu¸c˜oes quando t _→ +_∞. Chamaremos de caso conservativo o caso em que a fun¸c˜ao Q(x, t) n˜ao depende de t. Mostraremos na afirma¸c˜ao abaixo que, neste caso, a fun¸c˜aoh(v, τ) independe deτ:

Afirma¸c˜ao 2.7. No caso conservativo temos Q(x, t)_≡ Q0(x) e a fun¸c˜ao h(v, τ) ´e

dada por

h(v)≡ v 2

2 ≡ ˙ x2

2 +

Z x

0

Q0(y)dy,

Demonstra¸c˜ao. No caso conservativo temos Q(x, t) = Q(x) e, portanto, Q0(x) = Q(x). Neste caso temos X(v, τ) =X(v) e se X(v)<+_∞ temos

h(v, τ) =

Z T∗(v,τ)

τ −

¨

x(t;v, τ) ˙x(t;v, τ)dt = −x(t;˙ v, τ) 2 2

T∗(v,τ)

τ

=−x(T˙ ∗(v, τ);v, τ) 2

2 +

˙

x(τ;v, τ)2

2 =

v2 2. SeX(v) = +_∞ tamb´em obtemos o mesmo resultado. Vejamos:

h(v, τ) = v 2 ∞

2 + limy→∞

Z y

0

Q(x)dx= v 2 ∞

2 + limy→∞

Z t(y;v,τ)

τ

−x(t;¨ v, τ)dt = v

2 ∞

2 −ylim→∞ ˙

x(t(y;v, τ);v, τ)2

2 +

˙

x(τ;v, τ)2 2 = v

2 ∞

2 −tlim→∞ ˙

x(t;v, τ)2

2 +

v2 2 =

v2 2.

SejaG(t) = x(t)˙ 2

2 +

Z x(t)

0

Q0(y)dy. Temos que

˙

G(t) = 2 ˙x(t)¨x(t)

2 + ˙x(t)Q0(x(t)) =

2 ˙x(t)¨x(t)

2 −x(t)¨˙ x(t) = 0. Logo, G´e constante ao longo da solu¸c˜ao x. Como emt =τ temos

G(τ) = x˙ 2_(τ)

2 +

Z x(τ)

0

Q0(y)dy= v2

2 +

Z 0

0

Q0(y)dy= v2

2

ent˜ao G(t)_≡ v₂2.

Proposi¸c˜ao 2.8. 1) A fun¸c˜ao h(v, τ) ´e cont´ınua para todo τ e para todo v _≥ 0 e satisfaz as seguintes desigualdades

v2 2 −2π

Z ∞

0

ψ(y)dy ≤ h(v, τ) ≤ v 2

2 + 2π

Z ∞

0

ψ(y)dy. (2.13)

2) Se para todo x >0 e para todo t tivermos

0_≤q1(x)≤Q(x, t)≤q2(x), (2.14)

ent˜ao

v2 2 −

Z X(v,τ)

0

q2(x)dx≤h(v, τ)−

Z X(v,τ)

0

Q0(x)dx≤ v2

2 −

Z X(v,τ)

0

Demonstra¸c˜ao. Como ∂x

∂t = ˙x(t;v, τ)>0 na regi˜aoτ ≤t ≤T∗(v, τ), ent˜ao a fun¸c˜ao x(t;v, τ) ´e cont´ınua e mon´otona crescente em t nessa regi˜ao. Logo, a equa¸c˜ao x(t;v, τ) = y determina t(y;v, τ) como uma fun¸c˜ao mon´otona crescente em y e que ´e cont´ınua em todas as suas vari´aveis para 0 _≤ y < X(v, τ) (pelo teorema da fun¸c˜ao impl´ıcita, pois ∂x

∂t 6= 0

. Temos que

∂t ∂y =

∂t ∂x

∂x ∂y =

∂x ∂t

−1

= 1

˙

x(t(y;v, τ);v, τ), (2.16)

pois ∂

∂y(x(t(y;v, τ);v, τ)) = 1. A fun¸c˜ao ˙x(t(y;v, τ);v, τ) ´e cont´ınua nessa regi˜ao e a medida queyvaria de 0 aX(v, τ), esta fun¸c˜ao decresce dev para 0 permanecendo positiva para 0 _≤ y < X(v, τ) (pois caso contr´ario ter´ıamos uma mudan¸ca de concavidade na fun¸c˜ao). Seja V(y;v, τ) a fun¸c˜ao que fornece a velocidade com que a solu¸c˜aox(t;v, τ) passa pela altura y quando y < X(v, τ) e a fun¸c˜ao nula quando y≥X(v, τ). Ou seja,

V(y;v, τ) =

  

˙

x(t(y;v, τ);v, τ) , se 0≤y < X(v, τ),

0 , seX(v, τ)≤y <+∞. (2.17) A continuidade da fun¸c˜ao V(y;v, τ) precisa ser verificada apenas na superf´ıcie y = X(v, τ). Seja y0 = X(v0, τ0) < +∞ e seja ǫ > 0 um n´umero arbitr´ario. Como

˙

x(t(y;v, τ);v, τ)↓0 quando y ↑ X(v0, τ0), podemos escolher y1 < X(v0, τ0) = y0 tal que 0 < x(t(y˙ 1;v, τ);v0, τ0) < ǫ. Por continuidade, existe uma vinhan¸ca U0 de (v0, τ0) tal que para todo (v, τ)∈U0 valem

0<x(t(y˙ 1;v, τ);v, τ)< ǫ, y1 < X(v, τ). (2.18) O conjunto

{(y, τ, v) : y > y1, (v, τ)∈U0},

´e uma vizinhan¸ca de (y0;v0, τ0) e pelas equa¸c˜oes (2.17) e (2.18) temos queV(y;v, τ)< ǫ nesta vizinhan¸ca (uma vez que a fun¸c˜ao ´e n˜ao-crescente emy). Logo,V(y;v, τ) ´e cont´ınua na superf´ıciey=X(v, τ) e, portanto, em todo o dom´ınio de sua defini¸c˜ao. Por (2.1) e por (2.16) temos que se 0_≤y < X(v, τ) ent˜ao

∂V

∂y(y;v, τ) = ∂

∂y( ˙x(t(y;v, τ);v, τ)) = ¨x ∂t

∂y =−Q(y, t(y;v, τ)) 1

e se X(v, τ)≤y <+∞ ent˜ao ∂V

∂y(y;v, τ) = 0. Introduzimos a fun¸c˜ao

h(y;v, τ) =

            

V(y;v, τ)2

2 +

Z y

0

Q0(ξ)dξ , se 0≤y < X(v, τ),

Z X(v,τ)

0

Q0(ξ)dξ , seX(v, τ)≤y <+∞,

(2.20)

que nos ser´a ´util, uma vez que lim

y→∞h(y;v, τ) = h(v, τ). Observemos que a fun¸c˜ao h(y;v, τ) ´e cont´ınua quando V(y;v, τ) o ´e. Al´em disso, segue de (2.19) que

∂h ∂y =

  

−V Q_V1 +Q0 =Q0(y)−Q(y, t) , se 0≤y < X(v, τ),

0 , seX(v, τ)_≤y <+_∞. (2.21) Paray=X(v, τ) as duas derivadas laterais existem,

lim

y→X(v,τ)− ∂h

∂y =y→limX(v,τ)Q0(y)−Q(y, t) =Q0(X(v, τ))−Q(X(v, τ), t) e

lim

y→X(v,τ)+

∂h ∂y = 0,

mas elas n˜ao necessariamente coincidem (exceto no caso conservativo). Pelo lema (2.6) temos que

∂h ∂y

≤2πψ(y),

ondeψ(y) ´e integr´avel em [0,∞). Logo, ∂h

∂y ´e integr´avel e, portanto, existe o limite

lim

y→+∞h(y;v, τ) = h(0;v, τ) +

Z ∞

0 ∂h ∂y dy,

onde a convergˆencia ´e uniforme em v e τ. Fazendo o limite quando y _→ +_∞ em (2.20) obtemos (2.12). De fato, quando X(v, τ) = +_∞, a solu¸c˜ao x(t;v, τ) ´e hiperb´olica ou parab´olica. Logo,

lim

y→+∞V(y;v, τ) = limt→+∞x(t;˙ v, τ) = v∞. Assim,

lim

y→+∞h(y;v, τ) = limy→+∞

V(y;v, τ)2

2 +

Z y

0

Q0(ξ)dξ

= v 2 ∞ 2 +

Z ∞

0

e quandoX(v, τ)<+_∞

lim

y→+∞h(y;v, τ) =

Z X(v,τ)

0

Q0(ξ)dξ.

Portanto,

h(v, τ) = lim

y→+∞h(y;v, τ) = v2

2 +

Z X(v,τ)

0

(Q0(y)−Q(y, t))dy. (2.22)

Como a convergˆencia em (2.22) ´e uniforme e h(y;v, τ) ´e cont´ınua em todas as suas vari´aveis, ent˜ao h(v, τ) ´e cont´ınua. Pelo lema (2.6) temos que

v2 2 −2π

Z ∞

0

ψ(y)dy≤h(v, τ)≤ v 2

2 + 2π

Z ∞

0

ψ(y)dy,

(uma vez que ψ(y) _≥ 0 para todo y) o que prova (2.13). Para verificar (2.15), suponhamos que 0_≤q1(x)≤Q(x, t)≤q2(x) para todo x >0 e todot ∈R. Ent˜ao

v2 2 −

Z X(v,τ)

0

q2(x)dx≤ v2

2 −

Z X(v,τ)

0

Q(x, t)dx=h(v, τ)₋

Z X(v,τ)

0

Q0(x)dx ≤ v

2

2 −

Z X(v,τ)

0

q1(x)dx.

Observemos que, pela equa¸c˜ao (2.3), X(v, τ) ´e 2π-peri´odica em τ. De fato, se τ′ _{´e o primeiro zero de x(t;v, τ) depois de τ ent˜ao τ}′ _{+ 2π ´e o primeiro zero de} x(t+ 2π;v, τ + 2π) depois de τ + 2π (pois x(τ′ _{+ 2π;v, τ + 2π) = x(τ}′_{, v, τ) = 0).} Temos ent˜ao que

X(v, τ+ 2π) = sup

τ+2π≤t≤τ′_+2πx(t;v, τ + 2π) = sup_τ

≤t≤τ′x(t+ 2π;v, τ+ 2π) = sup

τ≤t≤τ′

x(t;v, τ) =X(v, τ).

Definimos a seguinte constante:

I=

Z ∞

0

Q0(x)dx=

Z ∞

0

Z 2π

0

Q(x, t)dt dx.

Com ela podemos particionar o plano Φ nos seguintes subconjuntos (ver Figura 2.3): {O_}=_{v = 0_}=_{(v, τ); h(v, τ) = 0_},

R0 ={(v, τ); 0< h(v, τ)<I}, Π0 ={(v, τ); h(v, τ) =I}, H0 ={(v, τ); h(v, τ)>I},

que nos auxiliar˜ao a caracterizar o comportamento das solu¸c˜oes quando t _→ +_∞. O seguinte teorema nos diz que o conjunto _{O_} corresponde `a solu¸c˜ao trivial e que seI=_∞, ent˜aoR0 = Φ\ {O}corresponde aos movimentos oscilat´orios e se I<∞, ent˜ao Π0 ´e composta somente de solu¸c˜oes parab´olicas, R0 ´e composta somente de solu¸c˜oes que voltam a passar pelo planox= 0 e H0´e composta somente de solu¸c˜oes hiperb´olicas:

Figura 2.3: Os conjuntos _{O_}, R0, Π0 e H0 no plano Φ

Teorema 2.9. O conjunto R0 ´e aberto e n˜ao-vazio e se (v, τ)∈R0, ent˜ao a solu¸c˜ao x(t;v, τ) retorna ao plano x= 0 pelo menos uma vez para t > τ. Se I=∞, ent˜ao todas as solu¸c˜oes n˜ao triviais s˜ao oscilat´orias. Se I<_∞, ent˜ao Π0 ´e fechado e n˜ao

vazio e a solu¸c˜ao x(t;v, τ) ´e parab´olica para (v, τ)_∈Π0; H0 ´e aberto e n˜ao vazio e

a solu¸c˜ao x(t;v, τ)´e hiperb´olica para (v, τ)_∈H0.

aber-tos e Π0 ´e fechado. Claramente, se I = ∞, ent˜ao Φ = {O} ∪ R0. Por (2.13) podemos obter h(v, τ) arbitrariamente grande bastando tomar v suficientemente grande. Logo, seI<∞, ent˜ao o conjuntoH0 ´e n˜ao vazio. Como h(v, τ) ´e cont´ınua eh(0, τ) = 0, ent˜ao os conjuntos R0 e Π0 s˜ao tamb´em n˜ao vazios. Pela defini¸c˜ao da fun¸c˜ao h percebemos queh(v, τ)≥I_⇔X(v, τ) =∞. Neste caso,

h−I= v∞ 2 .

Portanto, os pontos emH0 correspondem `as solu¸c˜oes hiperb´olicas e os pontos em Π0 correspondem `as solu¸c˜oes parab´olicas. Como a solu¸c˜ao ´e trivial seX(v, τ) = 0, ent˜ao temos que uma solu¸c˜ao ´e n˜ao-trivial e retorna parax= 0 ⇔ 0< X(v, τ)<∞ e, neste caso,

0< h(v, τ) =

Z X(v,τ)

0

Q0(x)dx <

Z ∞

0

Q0(x)dx=I,

uma vez que Q0(x) > 0. Ou seja, em R0 a solu¸c˜ao retorna ao menos uma vez a x= 0. Se I =_∞, ent˜ao Φ =_{O_{} ∪}R0. Neste caso, toda solu¸c˜ao que cruza x = 0 de forma crescente retorna para o planox = 0. Pela simetria (2.4) as solu¸c˜oes que cruzam o plano x = 0 de forma decrescente voltam a cruzar o plano x = 0. Logo, todas as solu¸c˜oes n˜ao triviais s˜ao oscilat´orias quando I=_∞.

Corol´ario 2.10. O conjunto _{O_{} ∪}R0 est´a contido em um disco de raio

2I+ 4π

Z ∞

0

ψ(x)dx

1/2

. Se para todo x > 0 e para todo t tivermos Q(x, t) ≤ q2(x), ent˜ao {O} ∪R0 est´a contido em um disco de raio R2 =

2

Z ∞

0

q2(x)dx

1/2

.

Se para todo x > 0 e para todo t tivermos 0 _≤ q1(x) ≤ Q(x, t), ent˜ao {O} ∪R0

cont´em um disco de raioR1 =

2

Z ∞

0

q1(x)dx

1/2

.

Demonstra¸c˜ao. Seja (v, τ) ∈ Φ tal que |v| ≥

2I+ 4π

Z ∞

0

ψ(x)dx

1/2

. Ent˜ao por (2.13) temos que

h(v, τ)_≥ v 2

2 −2π

Z ∞

0

ψ(y)dy_≥I.

Logo, (v, τ)∈({O} ∪R0)c e{O} ∪R0 est´a contido em um disco de raio

2I+ 4π

Z ∞

0

ψ(x)dx

1/2

. Suponhamos que para todo x > 0 e para todo t vale Q(x, t)≤ q2(x). Seja (v, τ)∈Φ tal que |v| ≥

2

Z ∞

0

q2(x)dx

1/2

ent˜ao por (2.15) temos que

h(v, τ)_≥ v 2

2 −

Z X(v,τ)

0

q2(x)dx+

Z X(v,τ)

0

Q0(x)dx ≥

Z ∞

0

q2(x)dx−

Z ∞

0

q2(x)dx+

Z ∞

0

Q0(x)dx=

Z ∞

0

Q0(x)dx=I.

SeX(v, τ)<_∞, ent˜ao por (2.15) temos que

h(v, τ)_≥

Z ∞

X(v,τ)

Q(x)dx+

Z X(v,τ)

0

Q0(x)dx

≥

Z ∞

X(v,τ)

Q0(x)dx+

Z X(v,τ)

0

Q0(x)dx=I.

Logo, (v, τ)∈({O} ∪R0)c e{O} ∪R0 est´a contido em um disco de raio

2

Z ∞

0

q2(x)dx

1/2

. Analogamente se mostra que (v, τ)_{∈ {}O_{} ∪}R0 e {O} ∪R0 cont´em um disco de raio

2

Z ∞

0

q1(x)dx

1/2

.

At´e agora trabalhamos apenas com o comportamento da solu¸c˜ao x(t;v, τ) para t≥τ. Utilizando argumentos semelhantes, podemos obter resultados an´alogos para t_≤τ. Para distinguir qual destes dois casos estamos mencionando, vamos utilizar os ´ındices + e₋quando estivermos tratando dos casos t_≥τ et_≤τ, respectivamente. A partir de agora denotaremos a fun¸c˜ao (2.12) por h+_{(v, τ) e a parti¸c˜ao do plano Φ} do Teorema 2.9 por

Φ =_{O_{} ∪}R+_{0 ∪}Π+_{0 ∪}H₀+.

Se a solu¸c˜aox(t;v, τ) possuir algum zero menor queτ, ent˜ao denotamos por ˜τ o zero mais pr´oximo de τ no passado e definimos X−_{(v, τ) como sendo}

X−(v, τ) =

τ <t<τ˜inf x(t;v, τ) ,

e este ´ınfimo ´e atingido no intervalo [T∗−_{(v, τ), T}−

∗ (v, τ)]. Temos ent˜ao ˙x > 0 para T−

aindaX−_{(0, τ}′_{) = 0 e h}−_{(v, τ) por}

h−(v, τ) =

            

v_−∞

2 +

Z ∞

0

Q0(x)dx , seX−(v, τ) = ∞,

Z X−(v,τ)

0

Q0(x)dx , seX−(v, τ)<∞,

onde v_−∞= lim

t→−∞x(t;˙ v, τ). Analogamente, definamos

{O_}=_{v = 0_}=_{(v, τ);h−(v, τ) = 0_}, R₀−=_{(v, τ); 0 < h−(v, τ)<I_}, Π−₀ ={(v, τ); h−(v, τ) =I_}, H₀− =_{(v, τ); h−(v, τ)>I_},

e, tamb´em obtemos que

Φ ={O} ∪R−₀ ∪Π−₀ ∪H₀−.

Os resultados anteriores todos possuem an´alogos para o caso em que analisamos o passado das solu¸c˜oes.

Pelo teorema 2.9, toda solu¸c˜ao x(t;v, τ) onde (v, τ)∈ R+₀, retorna para o plano x = 0 em algum momento τ′_{. Podemos ent˜ao definir em R}+

0 a fun¸c˜ao sucessora S:R+0 →Φ como abaixo.

Defini¸c˜ao 2.11. A aplica¸c˜ao S leva (v, τ)_∈R+₀ em (v′_{, τ}′_{)∈Φ de tal forma que} x(τ′;v, τ) = 0, x(τ˙ ′;v, τ) +v′ = 0 (2.23)

e x >0 paraτ < t < τ′ _{(ou seja τ}′ _{´e o primeiro zero da solu¸c˜ao depois de τ).} Pelo Teorema de Existˆencia e Unicidade de Equa¸c˜oes Diferenciais, a aplica¸c˜ao S ´e injetiva.

Proposi¸c˜ao 2.12. Seguindo a nota¸c˜ao apresentada anteriormente, temos

X−◦S =X+, h−◦S =h+, T_∗−◦S =T∗+, T∗−◦S=T_∗+. (2.24)

unici-dade de solu¸c˜oes temos

x(t;v′, τ′)_{≡ −}x(t;₋v′, τ′)_{≡ −}x(t;v, τ),

poisx(τ′_{;v, τ) = 0 =x(τ}′_;−v′_{, τ}′_{) e ˙x(τ}′_{;v, τ) = −v}′ _{= ˙x(τ}′_;−v′_{, τ}′_{). Logo,} X+_{(v, τ) = sup}

τ <t<τ′

x(t;v, τ) = sup

τ <t<τ′−

x(t;v′_{, τ}′_{) = − inf}

τ <t<τ′x(t;v ′_{, τ}′₎ =| inf

τ <t<τ′x(t;v

′_{, τ}′_)|=X−_(v′_{, τ}′_{) =X}−_{◦S(v, τ),}

e X−_(v′_{, τ}′_{) = X}+_{(v, τ), [T}+

∗ (v, τ), T∗+(v, τ)] = [T∗−(v′, τ′), T∗−(v′, τ′)]. Portanto, em R+₀ (dom´ınio deS), vale

h−◦S(v, τ) =h−(v′, τ′) =

Z X−(v′,τ′)

0

Q0(x) dx =

Z X−◦S(v,τ)

0

Q0(x) dx

=

Z X+(v,τ)

0

Q0(x) dx=h+(v, τ).

A proposi¸c˜ao a seguir nos garantir´a que a aplica¸c˜ao S : R+_{0 →} R−₀ ´e um difeo-morfismo que pode ser extendido a um homeodifeo-morfismo do conjunto R₀+_{∪ {}O_} no conjunto R−₀ ∪ {O}:

Teorema 2.13. Suponha que duas curvas Γe Γ′ _{cerquem o mesmo tubo de fase das}

trajet´orias de um sistema Hamiltoniano p˙ = −Hx, x˙ =Hp. Ent˜ao as integrais da

forma p dx−H dt ao longo delas s˜ao as mesmas:

Z

Γ

p dq₋H dt=

Z

Γ′

p dq₋H dt.

A forma p dq−H dt ´e chamada de integral invariante de Poincar´e-Cartan.

Proposi¸c˜ao 2.14. A aplica¸c˜ao S : R+

0 → R−0 ´e um difeomorfismo que preserva

´area. Se definirmos S(O) =O, ent˜ao a aplica¸c˜ao S :R₀+_{∪ {}O_{} →} R−_{0 ∪ {}O_} ´e um homeomorfismo que preserva ´area.

Demonstra¸c˜ao. Pelo an´alogo do teorema 2.9 temos que se (v′_{, τ}′_{) ∈ R}−

0 ent˜ao a solu¸c˜aox(t;v′_{, τ}′_{) passou porx= 0 pelo menos uma vez parat < τ}′_{. Logo,S}−1 _est´a definida para (v′_{, τ}′_{) ∈ R}−

que

(v, τ)_∈R+_{0 ⇔} 0< h+(v, τ)<I _⇔ 0< h−_◦S(v, τ)<I _⇔ S(v, τ)_∈R−₀. Portanto,S(R+₀)_⊂R−₀, e, consequentemente,S(R+₀) =R₀−eS´e bijetiva. Considere a aplica¸c˜aoF :R+_×R_×R+_×R_→R2 _{dada por}

F(v, τ, v′, τ′) = (x(τ′;v, τ),x(τ˙ ′;v, τ) +v′). Observemos que

∂F

∂(v′_{, τ}′₎(v, τ, v′, τ′) =

0 x(τ˙ ′_{;v, τ)} 1 ¨x(τ′_{;v, τ)}

!

.

Se (v0, τ0, v0′, τ0′)∈F−1(0,0), ent˜ao o determinante do Jacobiano ´e −x(τ˙ ′;v, τ) = v′ 6= 0. Logo, ∂F

∂(v′_{, τ}′₎ ´e sobrejetiva em (v0, τ0, v0′, τ0′). Pelo Teorema da Fun¸c˜ao Impl´ıcita temos ent˜ao que existem vizinhan¸cas V _⊂ R2 _{de (v0, τ0) e U ⊂} R4 _de

(v0, τ0, v0′, τ0′) e uma aplica¸c˜ao C1: ξ :R2 →R2 tais que para cada (v, τ)∈V existe um ´unicoξ(v, τ) tal que ((v, τ), ξ(v, τ))∈U eF((v, τ), ξ(v, τ)) = (0,0). Como as di-mens˜oes coincidem eξ´e obtido do difeomorfismo proveniente do Teorema da Forma Local das Submers˜oes, ent˜aoξ´e um difeomorfismo. ComoF((v, τ), S(v, τ)) = (0,0), ent˜ao ξ =S. Logo, S ´e um difeomorfismo local. Como S ´e injetiva, ent˜ao S ´e um difeomorfismo global. A equa¸c˜ao diferencial ¨x =₋Q(x, t) ´e equivalente ao sistema Hamiltoniano

˙

x=Hp, p˙=−Hx, (2.25)

onde H ´e o Hamiltoniano

H(x, p) = p 2

2 +

Z x

0

Q(y, t)dy. (2.26)

SejaG ⊂R+₀ a regi˜ao limitada pelo contorno γ ={(v(α), τ(α)} e seja SG a regi˜ao limitada por Sγ = {(v′_{(α), τ}′_{(α)}. O contorno Γ}′ _{= {(x, p, t) = (0,−v}′_{(α), τ}′_(α))} ´e obtido de Γ ={(x, p, t) = (0, v(α), τ(α))} por um shift das trajet´orias do sistema (2.25) no espa¸co de fase (x, p, t). Pelo teorema 2.13 temos que

µ(G) =

I

γ

v2

2dτ =−

I

Γ

pdx₋Hdt=₋

I

Γ′

pdx₋Hdt=

I

Sγ

(v′₎2 2 dτ

′ _=µ(SG),

propriedades similares. Seja vn →0. Ent˜ao

X−(v′_n, τ_n′) =X+(vn, τn)→X+(0, τ) = 0.

Logo, o ´unico ponto limite poss´ıvel para a sequˆencia (v′

n, τn′) =S(vn, τn) ´e um ponto

onde X− _{= 0, e, portanto, a origem O. Logo, S ´e cont´ınua em O. Analogamente,} o ´unico ponto limite poss´ıvel para a sequˆencia (vn, τn) = S−1(v′n, τn′) ´e um ponto

onde X+ _{= 0, e, portanto, a origem O. Logo, S}−1 _{´e cont´ınua em O. Portanto, S} ´e um homeomorfismo quando estendido a R+_{0 ∪ {}O_} (uma vez que ele j´a era um difeomorfismo em R+₀). Como S preserva ´area em R+₀ e {O} ´e um conjunto de medida nula emR₀+∪ {O}, ent˜ao a fun¸c˜ao Sestendida aR+₀ ∪ {O}tamb´em preserva

´area.

Um ponto S(v, τ) = (v′_{, τ}′_{) onde (v, τ) ∈ R}+

0 pode cair em um dos conjuntos H₀+, Π+₀, R+₀. Somente no ´ultimo caso ´e que podemos definir S(v′_{, τ}′_{) =S}2_{(v, τ), e} a solu¸c˜ao correspondente x(t;v, τ) retorna a Φ pelo menos duas vezes para t _≥ τ. Assim, podemos considerar a possibilidade de iterarmos a aplica¸c˜aoS.

Se (v, τ)_∈S−1(H₀+_∩R−₀), ent˜ao (v′_{, τ}′_{)∈ H}+

0 e a solu¸c˜ao x(t;v, τ) retorna a Φ exatamente uma vez para t _≥ τ e depois tende monotonicamente para o infinito, pois a solu¸c˜ao neste caso ´e hiperb´olica. Analogamente, se (v, τ)∈S−1(Π+₀ ∩R−₀), ent˜ao (v′_{, τ}′_{) ∈ Π}+

0 e a solu¸c˜ao x(t;v, τ) retorna a Φ exatamente uma vez para t ≥ τ e depois tende monotonicamente para o infinito, pois a solu¸c˜ao neste caso ´e parab´olica.

Definimos recursivamente os seguintes conjuntos para n _≥1:

        

R+

n =S−1(R+n−1∩R−0), R+ =

T∞

n=0R+n,

Π+

n =S−1(Π+n−1∩R0−), Π+ =

S∞

n=0Π+n,

H+

n =S−1(Hn+−1∩R−0), H+ =

S∞

n=0Hn+.

(2.27)

        

R−

n =S−1(R−n−1∩R+0), R− =

T∞

n=0R−n,

Π−

n =S−1(Π−n−1∩R0+), Π− =

S∞

n=0Π−n,

H−

n =S−1(Hn−−1∩R+0), H− =

S∞

n=0Hn−.

(2.28)

Proposi¸c˜ao 2.15. Mantendo a nota¸c˜ao acima, para todo n_≥1 vale

R_n+₋₁ =R+_{n ∪}Π+_{n ∪}H_n+, R−_n−1 =R−_{n ∪}Π−_{n ∪}H_n−. (2.29)

A solu¸c˜ao x(t;v, τ) ´e parab´olica, hiperb´olica ou oscilat´oria para t _{→ ∞} (t _{→ −∞}) se, e somente se, (v, τ)_∈Π+_{, H}+ _{ou R}+_{, respectivamente ((v, τ)∈Π}−_{, H}− _{ou R}−_,

respectivamente). Al´em disso,

Φ_{\ {}O_}=H+_∪Π+_∪R+ =H−_∪Π−_∪R−. (2.30)

Os conjuntos H_n+, H+, H_n−, H−, R+_n, R−_n s˜ao abertos e os conjuntos Π+_{0 ∪}..._∪Π+_n e

Π−_{0 ∪}..._∪Π_n− s˜ao fechados. Os conjuntos Π+ _{e Π}− _{s˜ao de tipo F}

σ e os conjuntos

R+ _{e R}− _{s˜ao de tipo G}

δ.

Demonstra¸c˜ao. A equa¸c˜ao R+n−1 =Rn+∪Π+n ∪Hn+ ´e equivalente a

S(R_n+₋₁) = S(R+_n ∪Π+_n ∪H_n+) = (R+_n−1∪Π+_n−1∪H_n+₋₁)∩R−₀,

uma vez que a imagem do difeomorfismo S ´e R₀−. Para n = 1 a equa¸c˜ao se reduz a S(R+₀) = R₀− uma vez que Φ\ {O}=R+₀ ∪Π+₀ ∪H₀+ e R−₀ ∩ {O}=∅. Mas pela proposi¸c˜ao (2.14) j´a sabemos que esta equa¸c˜ao ´e satisfeita. Suponhamos que a equa¸c˜ao valha para n₋1, isto ´e, que

S(R_n+₋₁) = S(R+_n ∪Π+_n ∪H_n+) = (R+_n−1∪Π+_n−1∪H_n+₋₁)∩R−₀. Ent˜ao

S(R_n+) = R+_n−1∩R−₀ = (R+_{n ∪}Π+_{n ∪}H_n+)_∩R−₀ =S(R+_n+1∪Π+_n+1∪H_n+₊₁), portanto, a equa¸c˜ao vale para todon _∈N_{. De forma an´aloga mostra-se que}

R−_n−1 =R−_{n ∪}Π−_{n ∪}H_n−. Por indu¸c˜ao temos ainda que

Φ\ {O}=R+_n ∪

n

[

k=0 Π+_k ∪

n

[

k=0 H_k+.

De fato, paran = 0 temos Φ_{\ {}O_}=R+_{0 ∪}Π+_{0 ∪}H₀+. Paran = 1 temos, por (2.29), que

Suponhamos a equa¸c˜ao v´alida paran₋1. Ent˜ao, por (2.29), temos que

Φ_{\ {}O_}=R+_{n−1 ∪}

n−1

[

k=0 Π+_{k ∪}

n−1

[

k=0

H_k+ =R+_{n ∪}Π+_{n ∪}H_n+_∪

n−1

[

k=0 Π+_{k ∪}

n−1

[

k=0 H_k+,

=Rn∪ n

[

k=0 Π+

k ∪ n

[

k=0 H+

k,

e, portanto, a equa¸c˜ao vale para todo n∈N_{. Logo,}

Φ_{\ {}O_}= lim

n→∞ R +

n ∪ n

[

k=0 Π+_{k ∪}

n

[

k=0 H_k+

!

.

Como, por (2.29),Rn⊇Rn+1 para todo n∈N, ent˜ao

lim

n→∞R +

n =

∞

\

k=0

R_k+=R+.

Logo,

Φ\ {O}=R+∪Π+∪H+. Seja (v, τ)∈H+

n. Por (2.27) temos que

S(v, τ)_∈H_n+₋₁, S2(v, τ)_∈H_n+₋₂, ..., Sn(v, τ)_∈H₀+.

Logo, parat _≥τ a solu¸c˜aox(t;v, τ) retornanvezes ao planox= 0 e depois tende ao infinito hiperbolicamente. Logo, todas as solu¸c˜oes para as quais (v, τ)_∈H+=

∞

[

n=0 H_n+ s˜ao hiperb´olicas e o maior ´ındice n para o qual (v, τ)_∈ H+

n conta o n´umero de

ze-ros de x(t;, v, τ) para t _≥ τ. Analogamente, se (v, τ)_∈Π+_{n ⊂}Π+, ent˜ao a solu¸c˜ao x(t;v, τ) ´e parab´olica. Ela assume o valor zero n vezes parat≥τ e depois tende ao infinito parabolicamente. Se (v, τ)∈R+ = Φ\({O} ∪H+∪Π+)⊂R+_n para todo n ∈ N_{, ent˜ao a solu¸c˜ao x(t;v, τ) retorna para Φ um n´umero infinito de vezes e,}

portanto, parat > τ existem infinitos zeros. Logo, a solu¸c˜ao ´e oscilat´oria. Como os conjuntosH₀+, H₀−, R+₀ eR₀− s˜ao abertos e S´e um homeomorfismo de R+_{0 ∪ {}O_} em R−_{0 ∪ {}O_}, ent˜ao, por (2.27) e por (2.28), os conjuntos H+

n, H+, Hn−, H−, R+n e R−n

s˜ao abertos e os conjuntosR+_eR−_{s˜ao de tipoG}

δ. O conjunto Π+0 ´e fechado em Φ e, portanto, Π+_{0 ∩}R−₀ ´e relativamente fechado emR−_{0 ∪{}O_}. Logo, Π+₁ =S−1_(Π+

que Π+_{0 ∪}..._∪Π+

n ´e fechado em Φ, e como

Π+ = ∞

[

n=0

Π+0 ∪...∪Π+n,

ent˜ao Π+ _{´e de tipo F}

σ. De forma an´aloga mostramos que Π−0 ∪...∪Π−n ´e fechado

em Φ e que Π−₀ ´e de tipo Fσ.

Vamos considerar a decomposi¸c˜ao do plano Φ gerado pelas parti¸c˜oes

Φ =_{O_{} ∪}R+_∪

" _∞ [

n=1 Π+_n

#

∪Π+_{0 ∪}

" _∞ [

n=1 H_n+

#

∪H₀+, (2.31)

e

Φ =_{O_{} ∪}R−_∪

" _∞ [

n=1 Π−_n

#

∪Π−_{0 ∪}

" _∞ [

n=1 H_n−

#

∪H₀−. (2.32)

Observemos que nos conjuntos Π+0 e H0+ a aplica¸c˜ao S n˜ao est´a definida e nos conjuntos Π−

0 e H0− a aplica¸c˜ao S−1 n˜ao est´a definida.

Proposi¸c˜ao 2.16. Para todo n _≥1 e para todo m_≥0, temos

        

S(R+_∩R−_{) =R}+_∩R−_, S(R+_∩Π−

m) =R+∩Π−m+1, S(R+_∩H−

m) = R+∩Hm−+1,

         S(H+

n ∩R−) = Hn+−1∩R−, S(H+

n ∩Π−m) = Hn+−1∩Π−m+1, S(H+

n ∩Hm−) =Hn+−1∩Hm++1,

(2.33)          S(Π+

n ∩R−) = Π+n−1∩R−, S(Π+

n ∩Π−m) = Π+n−1∩Π−m+1, S(Π+

n ∩Hm−) = Π+n−1∩Hm−+1.

Demonstra¸c˜ao. Um ponto (v, τ) _∈ R+ _{se a solu¸c˜ao ´e oscilat´oria quando t → ∞.} Um ponto (v, τ)_∈H+

n se a solu¸c˜ao ´e hiperb´olica e possui exatamente n zeros para

t > τ e (v, τ)_∈Π+

n se a solu¸c˜ao ´e parab´olica e possui exatamentenzeros parat > τ.

Analogamente, um ponto (v, τ)_∈R−_{se a solu¸c˜ao ´e oscilat´oria quandot→ −∞, um} ponto (v, τ)_∈H−

n se a solu¸c˜ao ´e hiperb´olica e possui exatamenten zeros parat < τ

e (v, τ) _∈Π−

n se a solu¸c˜ao ´e parab´olica e possui exatamente n zeros para t < τ. A

pr´oximo zero `a direira de τ. O car´ater da solu¸c˜ao quando t _{→ ±∞} n˜ao ´e afetado por esta aplica¸c˜ao e, portanto, os s´ımbolosR, H e Π n˜ao se alteram e temos

S(R+) =R+, S(R−) = R−.

O n´umero de zeros `a direita de τ decresce de 1 com a aplica¸c˜ao S e o n´umero de zeros `a esquerda de τ cresce de 1. Logo, o ´ındice n ´e substitu´ıdo por n−1 e o ´ındicem ´e substitu´ıdo por m+ 1. Isto ´e,

S(H_n+) =H_n+₋₁, S(Π+_n) = Π+_n−1, S(H_m−) = H_m−₊₁, S(Π−_m) = H_m−₊₁.

Teorema 2.17. Quase todas as solu¸c˜oes que s˜ao oscilat´orias para t _{→ −∞} s˜ao

tamb´em oscilat´orias para t_→+_∞e quase todas as solu¸c˜oes que s˜ao hiperb´olicas ou parab´olicas para t _{→ −∞} s˜ao parab´olicas ou hiperb´olicas para t_→+_∞.

Demonstra¸c˜ao. SeI= +_∞, temos, pelo teorema 2.9 que Φ =R+_{∪ {}O_}=R−_{∪ {}O_}. Como µ(_{O_}) = 0, ent˜ao quase todas as solu¸c˜oes s˜ao oscilat´orias quando t _→ +_∞ e quando t → −∞. Suponha que I < +∞. Pelo corol´ario 2.10 R+₀ e R−₀ est˜ao contidos em um disco de raio finito. Como R+ _{⊂ R}+

0 e R− ⊂ R−0, ent˜ao R+ e R− tamb´em est˜ao contidos em discos de raios finitos, e, portanto, tem medida de Lebes-gue finita. ComoR+_eR− _{s˜ao de tipoG}

δ(pela proposi¸c˜ao 2.15), ent˜aoR+ eR− s˜ao

mensur´aveis. De fato, como aσ-´algebra de Borel ´e gerado pelos abertos deR2_{, ent˜ao}

todo aberto pertence a ela. Como aσ-´algebra ´e fechada por interse¸c˜oes enumer´aveis, ent˜ao todo conjunto de tipo Gδ ´e Borel-mensur´avel. Como o conjunto formado por

um ´unico ponto do plano tamb´em ´e Borel mensur´avel, ent˜aoR+_{∪ {O} eR}−_{∪ {O}} s˜ao mensur´aveis. Logo, R+_{\ {}R−_{∪ {}O_}} e R−_{\ {}R+_{∪ {}O_}} s˜ao mensur´aveis e ambos possuem medida finita. Seja

Bm =R+∩(Hm−∪Π−m), m≥0.

Pela proposi¸c˜ao 2.16 temos que

S(B_m+) = S(R+_∩H_m−)_∪S(R+_∩Π_m−) = (R+_∩H_m−₊₁)_∪(R+_∩Π−_m+1) =R+∩(H_m−₊₁∪Π−_m+1) =Bm+1.