Fernanda Navarro Song
Rio Claro 2013
INSTITUTO DE BIOCIÊNCIAS - RIO CLARO
CIÊNCIAS BIOLÓGICAS
Orientador: José Silvio Govone
Trabalho de Conclusão de Curso apresentado ao Instituto de Biociências da Universidade
Estadual Paulista “Júlio de Mesquita Filho” -
Câmpus de Rio Claro, para obtenção do grau de Bacharela em Ciências Biológicas.
Rio Claro
2013
66 f. : il., figs., gráfs., tabs.
Trabalho de conclusão de curso (bacharelado Ciências Biológicas) -Universidade Estadual Paulista, Instituto de Biociências de Rio Claro Orientador: José Silvio Govone
1. Análise multivariada. 2. Componentes principais. 3. Manova. 4. Correlações canônicas. 5. Análise de correspondência. 6. Análise fatorial. I. Título.
A minha família, que nos momentos de minha
ausência dedicados ao estudo superior, sempre
fizeram entender que o futuro é feito a partir da
Agradecimentos
Agradeço primeiramente a Deus pela minha vida, saúde e por ter colocado pessoas maravilhosas nela.
Um agradecimento especial à minha mãe, por todo apoio e amor que me deu desde sempre e continua dando. Também ao meu pai, que nessas minhas indecisões da vida sempre me incentivou continuar. Agradeço ao Evandro por me ajudar sempre que possível e pelas caronas sempre muito úteis.
Ao Joaquim, que além de meu namorado é meu amigo, me ajudando mais do que o imaginável, sempre me cobrando e incentivando a fazer o que precisava. Obrigada pela paciência e amor.
Ao meu orientador, Silvio Govone, que acreditou em mim mais do que eu mesma. Agradeço pelo conhecimento transmitido, pela demasiada paciência e pela compreensão.
Às minhas queridas companheiras e amigas da República Moitinha! Andréia, Beatriz e Flávia, sou grata por dividir desse teto e paredes verdes com vocês! Gosto muito de vocês, do jeito de cada uma e das nossas ideias para o fundo que ainda não conseguimos concretizar.
Às minhas ex-companheiras de casa, Lívia e Gabriela, agradeço pelo tempo que passamos juntas e pela amizade que continuou independente de qualquer coisa! Agradeço também à Júlia, que apesar de não morar na mesma casa que eu, compartilhou de muitas histórias e conquistas! Podem ter certeza que vocês nunca serão esquecidas por mim!
CBI10! Nunca vou esquecer desses quatro anos com todos vocês! Muito obrigada pelos churrascos, festinhas juninas, gordices em geral sempre! A sala
“mito” vai perpetuar na Unesp e, é claro, no meu coração!
de vocês! Aprendi, degustei, ri, gargalhei, vendi, tive ataque de nervos, dancei, aproveitei e até conheci o amor! Muito obrigada por tudo mesmo!
Mesmo longe, a amizade de verdade continua. Cristina, Mariana, Débora, Nívea e Otávio, não passamos mais o dia-a-dia juntas, mas o apoio de longe e nossos escassos encontros me fortaleceram e ainda fortalecem todos os dias! Amo muito vocês!
RESUMO
A análise estatística multivariada, extensão da análise univariada, consiste num conjunto de técnicas estatísticas, aplicadas quando há diversas variáveis relacionadas simultaneamente, sendo todas elas, em princípio, consideradas importantes no fenômeno em estudo. É de grande aplicação a conjuntos de dados das mais diversas áreas do conhecimento, principalmente da área biológica.
Seu desenvolvimento teve um grande impulso na primeira metade do século passado. Entretanto, devido a complexidade dos cálculos matemáticos, principalmente envolvendo operações com matrizes de altas ordens, as aplicações somente se popularizaram nos dias atuais, com o desenvolvimento dos computadores e aplicativos computacionais.
Técnicas estudadas: distâncias multivariadas, componentes principais, análise fatorial, correlações canônicas, análise de correspondência, teste t² de Hotelling, análise de variância multivariada (Manova), teste de normalidade multivariada, igualdade de matrizes de variâncias e covariâncias para populações multinormais.
SUMÁRIO
1 – INTRODUÇÃO ... 8
2 – EXEMPLOS DE DADOS MULTIVAIADOS ... 9
3 – REPRESENTAÇÃO DE DADOS MULTIVARIADOS ... 13
4 – DISTÂNCIAS MULTIVARIADAS ... 15
5 – TESTES DE IGUALDADE DE MATRIZES E DE VARIÂNCIAS E COVARIÂNCIAS PARA POPULAÇÕES MULTINORMAIS ... 17
6 – TESTES DE SIGNIFICÂNCIA COM DADOS MULTIVARIADOS ... 18
6.1 – Lambda de Wilks ... 25
6.2 – Maior raiz de Roy ... 26
6.3 – Traço de Pillai ... 26
6.4 – Traço de Lawley-Hotelling ... 26
7 – UM MÉTODO PARA SE VERIFICAR A NORMALIDADE MULTIVARIADA ... 27
8 – ANÁLISE DE CORRELAÇÕES CANÔNICAS ... 33
9 – ANÁLISE DE CORRESPONDÊNCIA ... 37
10 – COMPONENTES PRINCIPAIS ... 43
11 – ANÁLISE FATORIAL ... 48
12 – CONCLUSÃO ... 65
1 - INTRODUÇÃO
Os métodos estatísticos utilizados em análises de problemas práticos são, na maioria, univariados, tratando somente da análise de uma única variável aleatória. A maior facilidade no emprego destes métodos permite com que sejam mais conhecidos e mais utilizados por profissionais das diversas áreas, que necessitam de análises estatísticas em seus dados.
A análise estatística multivariada, extensão da análise univariada, consiste num conjunto de técnicas estatísticas, aplicadas quando há diversas variáveis relacionadas simultaneamente, sendo todas elas, em princípio, consideradas importantes no fenômeno em estudo.
Seu desenvolvimento teve um grande impulso na primeira metade do século passado. Entretanto, devido a complexidade dos cálculos matemáticos, principalmente envolvendo operações com matrizes de altas ordens, as aplicações somente se popularizaram nos dias atuais, com o desenvolvimento dos computadores e aplicativos computacionais.
Tais métodos são utilizados na análise de dados em que há observações de várias variáveis correlacionadas entre si. Estes tipos de dados são muito comuns na área de ciências biológicas, abrangendo biologia, ecologia, ciências da saúde e ciências agronômicas.
Basicamente a análise multivariada procura responder as seguintes questões (Manly, 2005):
a) como as p variáveis se relacionam dentro de cada grupo?
b) os grupos diferem significativamente quanto aos valores médios das variáveis?
c) os grupos mostram quantidades similares de variação para as variáveis? d) caso os grupos sejam diferentes em termos de distribuições das variáveis, é
possível construir alguma função destas variáveis que separe os dois grupos?
2 – EXEMPLOS DE DADOS MULTIVARIADOS
Algumas aplicações de métodos multivariados foram estudadas, sendo elas, em sua maioria, relacionadas com a área de Ciências Biológicas. Em todos os casos fica claro que todas as variáveis são não-independentes umas das outras.
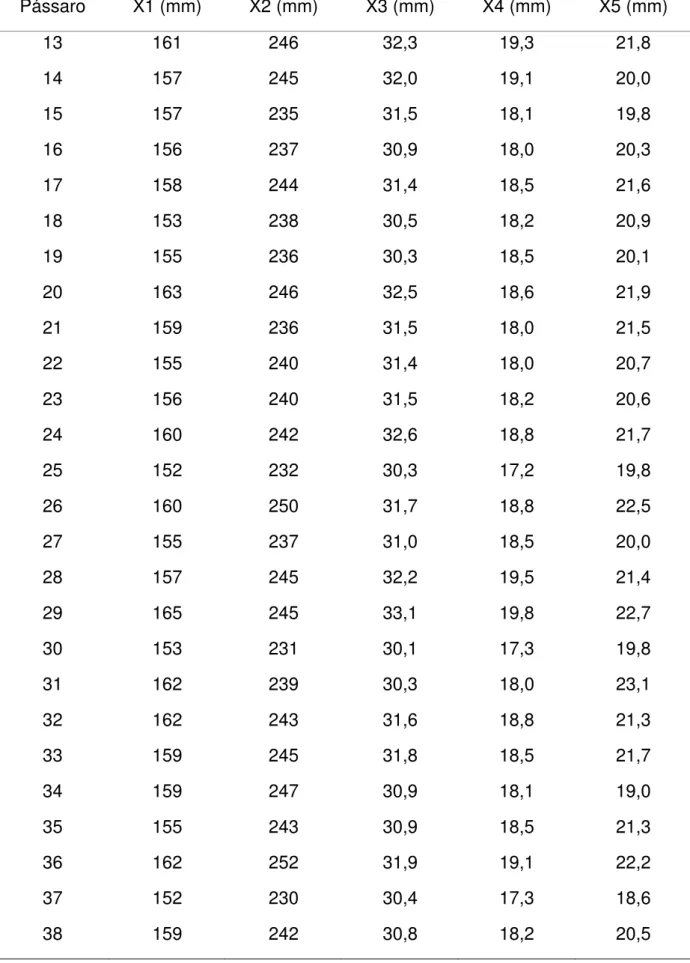
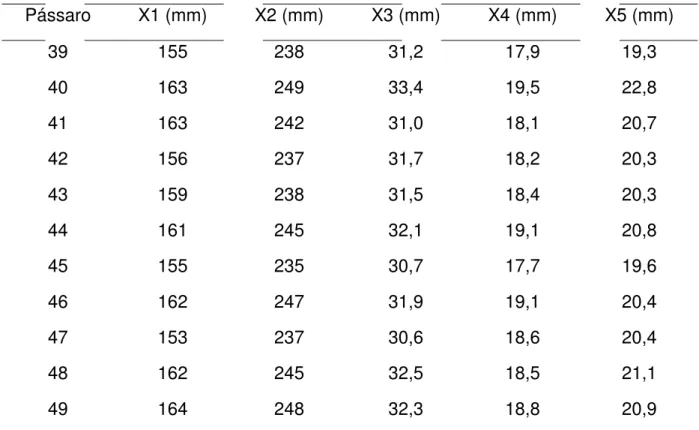
Uma das aplicações (Manly, 2008) é referente a uma tempestade que ocorreu em 1º de Fevereiro de 1898, em Rhode Island (EUA), onde diversos pardais ficaram moribundos e metade desses morreu. Com esse fato, coletaram-se dados (tabela 1) para tentar encontrar suporte para a teoria de seleção natural de Charles Darwin.
Tabela 1– Medidas do corpo de pardocas (Manly, 2008)
Pássaro X1 (mm) X2 (mm) X3 (mm) X4 (mm) X5 (mm)
1 156 245 31,6 18,5 20,5
2 154 240 30,4 17,9 19,6
3 153 240 31,0 18,4 20,6
4 153 236 30,9 17,7 20,2
5 155 243 31,5 18,6 20,3
6 163 247 32,0 19,0 20,9
7 157 238 30,9 18,4 20,2
8 155 239 32,8 18,6 21,2
9 164 248 32,7 19,1 21,1
10 158 238 31,0 18,8 22,0
11 158 240 31,3 18,6 22,0
Tabela 1– Medidas do corpo de pardocas (continuação) (Manly, 2008)
Pássaro X1 (mm) X2 (mm) X3 (mm) X4 (mm) X5 (mm)
13 161 246 32,3 19,3 21,8
14 157 245 32,0 19,1 20,0
15 157 235 31,5 18,1 19,8
16 156 237 30,9 18,0 20,3
17 158 244 31,4 18,5 21,6
18 153 238 30,5 18,2 20,9
19 155 236 30,3 18,5 20,1
20 163 246 32,5 18,6 21,9
21 159 236 31,5 18,0 21,5
22 155 240 31,4 18,0 20,7
23 156 240 31,5 18,2 20,6
24 160 242 32,6 18,8 21,7
25 152 232 30,3 17,2 19,8
26 160 250 31,7 18,8 22,5
27 155 237 31,0 18,5 20,0
28 157 245 32,2 19,5 21,4
29 165 245 33,1 19,8 22,7
30 153 231 30,1 17,3 19,8
31 162 239 30,3 18,0 23,1
32 162 243 31,6 18,8 21,3
33 159 245 31,8 18,5 21,7
34 159 247 30,9 18,1 19,0
35 155 243 30,9 18,5 21,3
36 162 252 31,9 19,1 22,2
37 152 230 30,4 17,3 18,6
Tabela 1– Medidas do corpo de pardocas (continuação) (Manly, 2008)
Pássaro X1 (mm) X2 (mm) X3 (mm) X4 (mm) X5 (mm)
39 155 238 31,2 17,9 19,3
40 163 249 33,4 19,5 22,8
41 163 242 31,0 18,1 20,7
42 156 237 31,7 18,2 20,3
43 159 238 31,5 18,4 20,3
44 161 245 32,1 19,1 20,8
45 155 235 30,7 17,7 19,6
46 162 247 31,9 19,1 20,4
47 153 237 30,6 18,6 20,4
48 162 245 32,5 18,5 21,1
49 164 248 32,3 18,8 20,9
Nota: X1 = comprimento total; X2 = extensão alar; X3 = comprimento do bico e cabeça; X4 =
comprimento do úmero; X5 = comprimento da quilha do esterno. Pássaros de 1 a 21 sobreviveram,
pássaros de 22 a 49 morreram. Fonte: Adaptado de Bumpus, H.C. (1898), Biological Lectures, 11th
Lecture, Marine Biology Laboratory, Woods Hole, MA, PP. 209-226. (Manly, 2008)
Como conclusão da aplicação de técnicas multivariadas, tem – se que:
x “Os pássaros que morreram, morreram não por acidente, mas porque eles eram fisicamente desqualificados”;
x “Os pássaros que sobreviveram, sobreviveram porque eles possuíam certas características físicas”;
x “O processo de eliminação seletiva é mais severo com indivíduos
extremamente variáveis, não importando em qual direção a variação possa
ocorrer”.
Tailândia, podendo ser o Canis lupus chanco, da China, ou o Canis lupus pallides, do subcontinente indiano).
Para tentar esclarecer os ancestrais dos cães pré-históricos, foram feitas medidas da mandíbula dos espécimes disponíveis para comparar com outras espécies (tabela 2).
Tabela 2 – Médias de medidas de mandíbulas para sete grupos caninos (Manly,
2008)
Grupo X1 (mm) X2 (mm) X3 (mm) X4 (mm) X5 (mm) X6 (mm)
Cão moderno 9,7 21,0 19,4 7,7 32,0 36,5
Chacal dourado 8,1 16,7 18,3 7,0 30,3 32,9
Lobo chinês 13,5 27,3 26,8 10,6 41,9 48,1
Lobo indiano 11,5 24,3 24,5 9,3 40,0 44,6
Cuon 10,7 23,5 21,4 8,5 28,8 37,6
Dingo 9,6 22,6 21,1 8,3 34,4 43,1
Cão pré-histórico 10,3 22,1 19,1 8,1 32,2 35,0
Nota: X1 = largura da mandíbula; X2 = altura da mandíbula abaixo do primeiro molar; X3 =
comprimento do primeiro molar; X4 = largura do primeiro molar; X5 = comprimento do primeiro ao
terceiro molar, inclusive; X6 = comprimento do primeiro ao quarto molar, inclusive. Fonte: Adaptado de
Higham, C.F.W. ET al. (1980), J. Archaeological Sci., 7, 149-165.(Manly, 2008)
Nesse primeiro momento foram apresentados brevemente alguns métodos multivariados que serão vistos mais detalhadamente nos próximos capítulos: análise de componentes principais; análise de fatores; análise de função discriminante; análise de agrupamento; correlação canônica; escalonamento multidimensional; análise de coordenadas principais; análise de correspondência.
3 – REPRESENTAÇÃO DE DADOS MULTIVARIADOS
A representação gráfica dos dados multivariados pode ser problemática visto que consegue ser apresentada em até três dimensões. Para solucionar esse problema, várias soluções foram propostas e discutidas.
Podem-se utilizar variáveis índices para reduzir o problema de representar muitas variáveis para duas ou três dimensões, mas, nesse caso, alguma diferença-chave pode ser perdida nessa redução.
Outra saída é a representação de draftsman, em que são feitos vários gráficos bidimensionais comparando os valores de cada uma das variáveis com todas as outras. Na imagem 1 temos o exemplo das pardocas (bolinhas pretas são os sobreviventes e bolinhas brancas representam os não sobreviventes). No entanto, essa técnica tem a desvantagem de não mostrar aspectos dos dados que somente seriam aparentes quando três ou mais variáveis são consideradas em conjunto.
Imagem 1 – Representação de draftsman do número de pássaros e cinco variáveis medidas (em
Na representação de pontos de dados individuais, as variáveis são medidas por um símbolo, os quais variam de acordo com elas. No exemplo citado dos cães pré-históricos da Tailândia, podemos obter as seguintes representações gráficas (imagem 2), onde visivelmente notamos a maior semelhança com o cão moderno e maior diferença com o lobo chinês. A desvantagem dessa técnica está na impressão que se capta do gráfico, que pode depender da ordem na qual os objetos são apresentados e da ordem na qual as variáveis são atribuídas aos diferentes aspectos do símbolo, além da dificuldade em se encontrar programas computacionais para produzir os gráficos. Também podemos fazer essa representação gráfica através de linhas e colunas (perfis de variáveis).
Imagem 2 – Representação gráfica de medidas da mandíbula em diferentes grupos caninos usando
(a) faces de Chernoff e (b) estrelas. Nota: X1 = largura da mandíbula; X2 = altura da mandíbula abaixo
do primeiro molar; X3 = comprimento do primeiro molar; X4 = largura do primeiro molar; X5 =
comprimento do primeiro ao terceiro molar, inclusive; X6 = comprimento do primeiro ao quarto molar,
4 - DISTÂNCIAS MULTIVARIADAS
É utilizado o conceito de distância, em que quanto mais similaridade entre as amostras, mais próximas elas estão entre si.
Para observações individuais, consideremos dois objetos (i e j) e duas variáveis (X1 e X2), apenas. Fazendo a representação gráfica (imagem 3),
conseguimos obter a distância Euclidiana entre os dois objetos (dij) através da
equação de Pitágoras:
d = x− x + x− x /
Imagem 3– A distância Euclidiana entre objetos i e j com p=2 variáveis. (Manly, 2008)
Com p=3 variáveis (X1, X2 eX3), os valores podem ser tomados como as
coordenadas no espaço para marcar as posições dos indivíduos i e j (imagem 4). O teorema de Pitágoras então fornece a distância entre os dois pontos como sendo
d = x− x+ x− x+ x− x
Imagem 4– A distância Euclidiana entre objetos i e j com p=3 variáveis. (Manly, 2008)
Com mais do que três variáveis, não é possível usar valores das variáveis como as coordenadas para marcar pontos fisicamente. Entretanto, os casos de duas e três variáveis sugerem que a distância Euclidiana generalizada
d = x− x
pode servir como uma medida satisfatória para muitos propósitos com p variáveis.
5 - TESTE DE IGUALDADE DE MATRIZES DE VARIÂNCIAS E COVARIÂNCIAS PARA POPULAÇÕES MULTINORMAIS
É um teste semelhante ao teste de Bartlett para o caso univariado. A suposição básica para a aplicação deste teste é a multinormalidade. Sejam m populações cada com p variáveis, com matrizes de variâncias e covariâncias desconhecidas, sendo ∑ a matriz da i-ésima população, i=1,2,...,m.
Hipóteses: H0: ∑ 1 = ∑ 2= ... = ∑
Ha: ∑ ≠∑ , para alguns i, j; i ≠ j; i, j = 1, 2, ..., m.
Sejam a estimativa da matriz de variâncias e covariâncias de ∑ , baseada numa amostra de tamanho da i-ésima população, i = 1, 2, ..., m, e
C =
∑ ( )∑ ( )
a média das matrizes de variância e covariância.
A estatística é
M = ∑ (n – 1) ln|c| - ∑ (n – 1) ln|C|
em que |.| representa o determinante da matriz.
Aplica-se o fator de correção:
Cor = 1 -
²!"∑
#$ ∑ #$
%
&(!)()
A estatística MC tende, quando n cresce, para a distribuição quiquadrado
com ()(!)
Aceita-se H0, ao nível de probabilidade , se MCor < Χ² tabelado. Caso
contrário, rejeita-se H0. Ex.: (Morrison, 1967).
Grupos de 32 jovens do sexo masculino e 32 do sexo feminino foram analisados quanto ao tempo de reação a um estímulo visual. Dados amostrais:
p = 2 variáveis (0,5s e 15s)
n= n= 32
m = 2 grupos (masc. e fem.)
C'*,= -4,32 1,881,88 9,180 , C56 = -2,52 1,901,90 10,060 , C = -3,42 1,891,89 9,620
Variância dos 32 valores do masculino ao estímulo 0,5s
Hipóteses: H0: ∑ masc = ∑ fem
Ha: ∑ masc ≠ ∑ fem
M = (32+32+1) ln(29,328) – 31(ln 36,123 + ln 21,741) = 2,82
Cor = 1 −6(2 + 1)(2 − 1) <2x2+ 3x2 − 1 31 +1 31 −1 62> = 0,9651
MCor = 2,72
Χ² = ?²(@$) × @ × A
; 5% = P²,B% = 7,81 > MCor
⇒ Aceitamos a hipótese de igualdade entre as matrizes de variância e covariância das populações masculina e feminina.
6 - TESTES DE SIGNIFICÂNCIA COM DADOS MULTIVARIADOS
Primeiramente estudou-se uma revisão sobre testes de significância no caso univariado, em condições de normalidade e não normalidade.
Depois dessa breve introdução, inseriu-se o caso multivariado para esses testes de significância. É possível empregar os testes para cada uma das variáveis, podendo-se analisar se há e quais delas têm valores médios diferentes. No entanto, pode ser interessante saber se todas as variáveis consideradas juntas sugerem alguma diferença também e, para isso, é necessária a aplicação de um teste multivariado.
A MANOVA (Análise de Variância Multivariada, do inglês Multivariate Analysis of Variance) consiste em uma generalização de análise de variância univariada (ANOVA), para o caso de comparação de m grupos, em que há p variáveis medidas na mesma unidade experimental, ou p medidas no tempo, referentes à mesma unidade experimental.
Vantagens do emprego da MANOVA: controla a probabilidade α de erro
tipo I, pois um único teste é realizado ao invés de m testes simultâneos; considera a correlação entre as variáveis, o que não acontece com a ANOVA, em que cada variável é analisada separadamente. Quanto mais fortemente forem correlacionadas entre si as variáveis, mais indicada será a MANOVA. No caso de baixas correlações, a ANOVA tende a ser mais recomendada.
Sejam m grupos com médias µ1, µ2, ..., µm desconhecidas.
Hipóteses: H0: µ1 = µ2 = ... = µm
Ha: µi ≠ µj, para alguns i, j = 1, 2, ..., m, i ≠ j,
µ1i
µ2i
onde µi = ....
Quando m = 2, uma possibilidade a ser utilizada, além da MANOVA, é o teste T2 de Hotelling, uma variação (o quadrado) do teste t de Student da análise
univariada, o qual pode ser definido como:
T = nn(xF − x GGG) ′C(x
F − xGGG)/(n − n)
Sendo:
n1 = número total de valores do grupo 1
n2 = número total de valores do grupo 2
x1 = vetor de médias amostrais do grupo 1
x2 = vetor de médias amostrais do grupo 2
(x1-x2)’ = vetor transposto da subtração dos vetores de médias
C-1 = inversa da matriz de covariâncias amostrais combinadas
Ao encontrar o valor T2, ele poderá ser significantemente grande,
evidenciando que os dois vetores de médias populacionais são diferentes, ou significantemente pequeno ou nulo, apresentando semelhanças entre os vetores. Para testar a hipótese nula de que a média das duas amostras é igual, é necessário transformar o número na estatística:
F = (n1+n2-p-1)T2/{(n1+n2-2)p},
em que p = número de variáveis, e compará-lo com o valor tabelado (tabela F).
Rejeitamos a hipótese de igualdade de médias entre os grupos, se F > F tabelado.
Uma aplicação feita com a estatística T² de Hotelling foi comparando grupos de idosos preservados e idosos com Doença de Alzheimer (DA) do grupo PRO-CDA (Programa de Cinesioterapia Funcional e Cognitiva em Idosos com Doença de Alzheimer), na UNESP – Rio Claro.
circunferência da cintura (cm), circunferência do quadril (cm) e RCQ (razão circunferência quadril).
Tabela 3 –Dados antropométricos de idosos com Doença de Alzheimer
Idosos Peso (kg) Altura (cm) IMC CC (cm) CQ (cm) RCQ
1 55,6 1,55 23,14 86 98 0,88
2 61 1,52 26,40 86 95 0,91
3 73,2 1,62 27,89 98 108 0,91
4 87 1,65 31,96 109 108 1,01
5 68 1,57 27,59 93 105 0,89
6 71,1 1,59 28,12 90,5 117,5 0,77
7 66,5 1,46 31,20 101 108 0,94
8 61,5 1,58 24,64 85 103 0,83
9 80,1 1,69 28,05 101 104 0,97
10 53,6 1,5 23,82 81 95 0,85
11 59,9 1,46 28,10 87 104 0,84
12 64,2 1,61 24,77 80 100 0,80
Tabela 4– Dados antropométricos de idosos saudáveis
Idosos Peso (kg) Altura (cm) IMC CC (cm) CQ (cm) RCQ
1 64,2 1,57 26,05 96 100 0,96
2 50 1,58 20,03 72 92 0,78
3 45,8 1,46 21,49 75 92 0,82
4 55,5 1,45 26,40 93 98 0,95
5 70,3 1,68 24,91 105 110 0,95
6 83,5 1,73 27,90 108 105 1,03
7 60,8 1,65 22,33 94 90 1,04
8 84,9 1,66 30,81 108 111 0,97
9 98 1,6 38,28 114 126 0,90
10 41,1 1,52 17,79 69 85 0,81
11 68,7 1,62 26,18 95 97 0,98
12 67,4 1,55 28,05 111 115 0,97
13 56,3 1,47 26,05 84 101 0,83
14 75 1,55 31,22 103 116 0,89
Tabela 4– Dados antropométricos de idosos saudáveis (continuação)
Idosos Peso (kg) Altura (cm) IMC CC (cm) CQ (cm) RCQ
16 62,5 1,44 30,14 88 110 0,8
17 70,3 1,57 28,52 98 109 0,90
18 54,1 1,45 25,73 91 103 0,88
Pelo fato de o IMC e a RCQ serem variáveis obtidas a partir das outras quatro variáveis, optou-se por utilizar apenas as quatro fundamentais: peso, altura, circunferência da cintura e circunferência do quadril.
Calculamos as médias destas quatro variáveis para cada um dos grupos de idosos:
Tabela 5 – Médias das variáveis dos dois grupos
Peso Altura CC CQ
Média idosos com DA 66,8083 1,5667 91,4583 103,7917 Média idosos saudáveis 66,0611 1,5617 95,1111 104,3889
Logo, (x1-x2) = H
66,81 − 66,06 1,57 − 1,56 91,46 − 95,11 103,79 − 104,39
J
e (x1-x2)’ = (66,81 − 66,06 1,57 − 1,56 91,45 − 95,11 103,79 − 104,39)
Para calcular a matriz C, é necessário calcular antes a variância (A) de cada variável em cada um dos grupos e a covariância (B) entre eles:
(A) s = ∑ XK − XFY− YF/n− 1
(B) COVAR = ∑ XK − XFY− YF/n− 1
onde:
n = número de variáveis
X = valor da variável do grupo de idosos com DA
XF = média das variáveis do grupo de idosos com DA
Y = valor da variável do grupo de idosos saudáveis
YF = média das variáveis do grupo de idosos saudáveis
Os resultados estão na tabela 6:
Tabela 6– Variância das variáveis dos dois grupos
Peso Altura CC CQ
Variância idosos com DA 96,5172 0,0052 81,6117 40,5208 Variância idosos saudáveis 217,8378 0,0074 181,9869 122,0163
Com estes valores podemos montar a matriz C1 do grupo de idosos com
Doença de Alzheimer da seguinte forma:
= H
96,51
0,0052
81,61
40,52 J
= H
96,51 MNQSâUQ WZSW [ W [
MNQSâUQ WZSW [ W [ 0,0052
81,61
40,52 J
=
⎝ ⎛
96,51 0,47 MNQSâUQ WZSW [ W [
0,47 0,0052
MNQSâUQ WZSW [ W [ 81,61
.
.
.
C = H
96,51 0,47 70,3 34,86
0,47 0,0052 0,24 0,11
70,3 0,24 81,61 29,3
34,86 0,11 29,3 40,52
J
Segue-se o mesmo procedimento para montar a matriz C2 para o grupo
de idosos saudáveis.
Tendo as duas matrizes (C1 e C2) é possível obter a matriz geral (média)
C de variâncias e covariâncias das variáveis:
C =[(n− 1)C(n + (n − 1)C] + n− 2)
Calcula-se a inversa da matriz C, C-1, e calcula-se os valores na fórmula
inicial do T². Realizando os cálculos obtém-se o valor de 4,64.
Com este valor encontrado, calcula-se a estatística F a partir da fórmula apresentada anteriormente, obtendo-se o valor 1,03.
O valor Ftabelado vem da tabela F-Snedecor. No exemplo apresentado
procura-se a coluna 4 (número de variáveis) e linha 25 (12+18-4-1), onde encontra-se o valor Ftab = 2,76.
F < Ftabelado, portanto aceitamos a igualdade das médias dos dois grupos,
ou seja, não há relação aparente entre as medidas antropométricas e a Doença de Alzheimer.
Nesse aspecto, a utilização de um teste multivariado se destaca aos vários univariados no controle da probabilidade α do erro tipo I, em que a
probabilidade de rejeitar incorretamente a hipótese nula é menor. Há como controlar a probabilidade total de um erro tipo I quando vários testes univariados são aplicados. Porém, há quem prefira utilizar o teste multivariado, que também tem a vantagem de levar em conta apropriadamente a correlação entre as variáveis.
Para uma única variável, o método para comparação da variabilidade entre duas amostras é o teste F (situação de normalidade) ou o teste de Levene (situação de não normalidade). Já no caso multivariado, em uma situação de normalidade, é utilizado o teste M de Box e, em uma situação de não normalidade, pode-se utilizar o teste de Van Valen.
Em algumas situações pode ocorrer um resultado não significante para o teste de Levene e um resultado significante para o teste de Van Valen, por exemplo. Isso é devido ao fato de o teste de Levene não ser direcional e também não levar em consideração a expectativa de um grupo ser menos variável que outro, o que não acontece com o teste de Van Valen, que é específico para quando há essa diferença de variação entre as amostras, enfatizando esse fato.
Quanto à MANOVA, temos quatro estatísticas alternativas usadas para testar a hipótese de que todas as amostras vêm de populações com o mesmo vetor médio.
6.1 - Lambda de Wilks: Ʌ = |W|/|T|, em que:
|W| = determinante da matriz das somas de quadrados e produtos cruzados dentro da amostra;
|T| = determinante da matriz das somas totais de quadrados e produtos cruzados.
Se Ʌ for pequeno, a variação dentro das amostras é baixa em
6.2 - Maior raiz de Roy: λ1 (alguns aplicativos computacionais usam a
expressão: λ1/(1- λ1)).
A base para este teste é que se a combinação linear das variáveis de X1 à
Xp que maximiza a razão entre a soma dos quadrados entre amostras e a soma dos
quadrados dentro das amostras é encontrada, então essa razão máxima é igual a ao autovalor λ1. Portanto, o autovalor máximo λ1 pode ser uma boa estatística para
testar se a variação entre amostras é significantemente grande, e que há, portanto, evidência de que as amostras sendo consideradas não vêm de populações com o mesmo vetor médio. O valor λ1 é comparado com um valor tabelado da tabela F.
Rejeitamos a igualdade para valores grandes de λ1.
6.3 - Traço de Pillai:
V = ∑λ/(1 +λ),
onde os λi são autovalores obtidos, i=1,2,... ,p.
Temos novamente que valores grandes de V fornecem evidências de que as amostras consideradas vêm de populações com vetores médias diferentes.
6.4 - Traço de Lawley-Hotelling:
U = ∑λ
Essa estatística é apenas a soma dos autovalores da matriz W-1B, onde
grandes valores fornecem evidência contra a hipótese nula de igualdade.
Observação:
W = matriz das somas de quadrados e produtos cruzados dentro da amostra;
T = matriz das somas totais de quadrados e produtos cruzados.
A tabela 7 fornece as estatísticas de comparação com os valores tabelados da tabela F-Snedecor, dos quatro testes analisados.
Tabela 7 – Estatísticas de testes usadas para comparar vetores médias amostrais
com testes F aproximados para evidência de que valores populacionais não são constantes (Manly, 2008)
Teste Estatística F gl1 gl2 Comentário
Lambda
de Wilks Ʌ h1 −
Ʌ
Ʌij k gl
glq p(m − 1) wt − kgl2 q + 1
w = n − 1 − vp + m2 y
t = "{p+ (m − 1)gl− 4− 5}%
Maior raiz
de Roy λ1 kglglqλ d n − m − d − 1
Se gl= 2, faça t = 1 O nível de significância obtido é um limite inferior
d = max(p, m − 1).
Traço de
Pillai V = λ/(1 + λ)
(n − m − p + s)V
{d(s − V)} sd s(n − m − p + s)
s = min(p, m − 1) = número de autovalores
positivos d = max(p, m − 1).
Traço de
Lawley-Hotelling U = λ ?
glU
(s gl) s(2A + s + 1) 2(sB + 1)
s é como no traço de Pillai
A =(|m − p − 1| − 1)2
B =(n − m − p − 1)2
Nota: Assume-se que há p variáveis em m amostras, com a j-ésima de tamanho nj, e um tamanho
Os quatro testes mostram níveis de significância similares, geralmente, o que nos dá possibilidade de utilizar qualquer um deles quando se têm a suposição de que a distribuição das p variáveis é normal multivariada com a mesma matriz covariância dentro das amostras para todas as m populações das quais as amostras foram extraídas, além da independência entre os grupos. Tais testes são considerados robustos (isto é, podem ser aplicados mesmo se as suposições não se verificarem na totalidade dos grupos ou variáveis) se os tamanhos amostrais forem aproximadamente iguais para as m amostras. No entanto, se houver alguma questão sobre essa suposição, estudos sugerem que a estatística de Pillai possa ser mais eficiente. Altas correlações entre as variáveis sugerem maior confiança no teste de Pillai; baixas correlações sugerem escolher o teste de Roy.
Apesar disso, os quatro testes costumam fornecer conclusões similares e
nenhum deles pode ser considerado “o melhor”, em geral. Cada teste capta
diferentes características das diferenças entre as médias.
Caso falhe a normalidade multivariada, podem-se usar alguns testes não paramétricos (extensões do Kruskal-Wallis e do Friedman). Caso falhe a homogeneidade das matrizes de covariância, deve-se escolher o teste de Pillai.
Na MANOVA, quando rejeita-se H0, há alguns procedimentos para se
testar a diferença entre grupos. Pode-se executar a ANOVA univariada em cada uma das variáveis para testar a diferença entre médias em cada variável separadamente (seguida, se necessário, de testes de comparação múltiplos, como o de Tukey). Outra possibilidade é aplicar a teste T2 de Hotelling dois a dois grupos.
Para comparação da variação para várias amostras, sendo verificada a normalidade multivariada, utiliza-se o teste M de Box.
A estatística M é dada pela equação
M = h |C|()/
j /|C|()/
m = número de amostras;
ni = tamanho da i-ésima amostra;
n = ∑ n = número total de observações;
Ci = covariância amostral para a i-ésima amostra;
C = matriz de covariâncias combinada
|C| = determinante da matriz Ci ,
C = (n− 1)C/(n − m)
Valores altos de M fornecem evidência de que as amostras não provêm de populações com a mesma matriz de covariâncias. Para saber se um valor M observado é significativamente grande, é necessário um teste F, calculando
F = −2b log6(M)
e encontrando a probabilidade de um valor desse tamanho ou maior para uma distribuição F com v1 e v2 graus de liberdade, em que
v = p(p + 1)(m − 1)/2
v = (v+ 2)/(c− c)
e
b = (1 − c− v/v)/v
em que
c = (2p+ 3p − 1) hn 1
− 1 − 1/(n − m)
j /{6(p + 1)(m − 1)}
e
c = (p − 1)(p + 2) h(n 1 − 1)−
1 (n − m)
Essa aproximação da equação F somente é válida para c2 > c1². Se c2 <
c1², então uma aproximação alternativa é usada, sendo o valor F calculado como
sendo
F = {2bv log6(M)}/{v+ 2blog6(M)}
em que
b = (1 − c− 2/v)/v
Esta estatística é testada contra a distribuição F com v1 e v2 gl. Uma
razão F significante é evidência de que as amostras vêm de populações com desvios médios diferentes, isto é, populações com matrizes covariâncias diferentes.
O teste de Box é sensível a não normalidade em algumas das variáveis. Caso esta situação ocorra, um teste alternativo, robusto a não normalidade, pode ser aplicado. O chamado teste de Levene, que consiste em calcular, para cada valor de cada variável, dentro de cada amostra, a diferença, em módulo, entre este valor e a mediana dos dados da correspondente variável naquela amostra. Após obtidas todas as diferenças, aplica-se qualquer um dos quatro testes: lambda de Wilks, maior raiz de Roy, traço de Pillai e traço de Lawley-Hotelling, como visto anteriormente, aos dados transformados, e um resultado significante indica que a matriz de covariâncias não é constante para as m populações amostradas.
Os testes apresentados até o momento são encontrados com facilidade em aplicativos computacionais estatísticos. Como os testes são baseados em aproximações, os resultados de um programa podem se diferenciar de outro.
7 - UM MÉTODO PARA SE VERIFICAR A NORMALIDADE
MULTIVARIADA
Umas das suposições para a aplicação da MANOVA é a normalidade multivariada em todos os grupos. Uma ideia inicial para verificar a normalidade multivariada é testar a normalidade univariada em cada grupo, para cada uma das p variáveis. Um teste muito usado é o de Shapiro-Wilk. Entretanto o fato de todas as distribuições serem normais não necessariamente implica que o vetor aleatório tenha distribuição multivariada. Pode-se falar, apenas, que a chance deste fato acontecer é muito alta.
Um teste muito simples para se verificar a normalidade multivariada quando o tamanho amostral n for relativamente grande é o teste quiquadrado, cujo procedimento segue.
Sejam p variáveis de um grupo, em que se deseja testar a normalidade multivariada. Calcula-se a estatística
d² = x− x ′Cx− x, j = 1, 2,..., n ,
a qual tem aproximadamente uma distribuição quiquadrado com p graus de liberdade, onde:
x: vetor que representa os valores observados das p variáveis no i-ésimo elemento amostral.
x: é o vetor de médias amostrais.
C: inversa da matriz de variâncias e covariâncias.
O procedimento é, então, o seguinte:
- Calcular as distâncias d² para todos os elementos da amostra e ordenar
os mesmos em ordem crescente, de forma que d²() ≤ d²() ≤ ... ≤ d²(), em que d ()
- Construir o gráfico dos pares d²(); P²(j − 1 2 )/n em que P²(j −
1 2 )/n representa a ordenada do percentil de ordem 100 (j − 1 2 )/n da distribuição quiquadrado com p graus de liberdade.
Quando o gráfico for próximo de uma reta, há indicativo de normalidade. Caso se afaste da reta, indica não normalidade.
Exemplo: Notas obtidas (de 0 a 25 pts) em 3 provas de 19 estudantes de uma disciplina. O vetor de médias e as matrizes de covariância e correlação são dadas, respectivamente, por:
xG = 19,72120,263
20,063 , C =
8,47 8,01 7,22 8,01 13,23 8,87
7,22 8,87 8,37 , R=
1 0,757 0,857
0,757 1 0,843
0,857 0,843 1
Nota-se altas correlações positivas entre as variáveis.
Os valores originais, bem como os valores necessários para a construção do gráfico Q. Q. Plot são dados na tabela 8.
Tabela 8– Teste normalidade multivariado
Aluno X1 X2 X3 dj^2
1 17,2 16,7 15,8 2,935082
2 16,8 15 17,2 2,295652
3 25 24,6 24,2 3,376142
4 19 17,5 18 1,160355
5 21 24,8 20,8 3,804392
6 15,6 13,4 16,2 3,901417
7 19 23,4 22,8 5,229576
8 22,5 24,3 23,5 1,470303
9 18,2 20,3 19,6 0,714871
10 16,7 17,5 15,7 3,338009
11 22,6 20,2 23,6 5,27213
12 22 20,6 21,9 1,396433
13 15,8 16,3 17,7 2,580905
14 15,5 17,8 17,7 2,816592
15 21,3 24,8 22,9 2,035865
16 21,2 21,5 18,9 4,050425
Tabela 8– Teste normalidade multivariado (continuação)
Aluno X1 X2 X3 dj^2
18 22,7 18,9 20,6 4,299497
19 19,6 23,3 20,7 1,874104
Média 19,72105 20,26316 20,06842
Desvio padrão 2,911391 3,637033 2,893681
O gráfico Q. Q. Plot é apresentado na imagem 5 (Mingoti, 2005).
Imagem 5– Gráfico Q. Q. Plot (Mingoti, 2005).
A disposição dos pontos, em forma aproximada de uma reta, indica a não rejeição da suposição de normalidade multivariada.
Há testes apropriados para verificar a normalidade multivariada, como os chamados testes de Jobson (1992).
8 – ANALÍSE DE CORRELAÇÕES CANÔNICAS
O primeiro exemplo de Hoteling consistiu em uma amostra de 140 crianças, em que aplicou-se testes para velocidade de leitura (X1), potência de
leitura (X2), velocidade aritmética (Y1) e potência aritmética (Y2).
O interesse era verificar se habilidade de leitura (X1, X2) está relacionada
com habilidade aritmética (Y1, Y2). Encontrou-se duas variáveis u e v, com maior
correlação possível, das seguintes combinações lineares:
u = ax+ ax
v = bx+ bx
Os valores encontrados para os coeficientes foram: a= −2,78; b = −2,44; a = 2,27; b = 1, que produziram uma correlação r = 0,62.
u: mede a diferença entre potência e velocidade de leitura,
v: idem, para aritmética.
Percebe-se que crianças com grandes diferenças entre X1 e X2 tendem a
ter grandes diferenças entre Y1 e Y2 (razoável correlação positiva).
Correlação canônica consiste numa generalização da correlação múltipla, pois nesta última, apenas uma variável Y está associada a várias variáveis X, enquanto que, na correlação canônica, várias variáveis Y (duas ou mais) estão associadas a várias variáveis X (duas ou mais).
Sejam p variáveis X1, X2, ... , Xp e q variáveis Y1, Y2, ... , Yq. Pode-se
formar r relações lineares, em que r ≤ min (p, q):
u = ax+ ax+ ⋯ + ax
u = ax+ ax+ ⋯ + ax
.
.
u = ax+ ax+ ⋯ + ax
v = bY+ bY+ ⋯ + bY
.
.
.
v = bY+ bY+ ⋯ + bY
Estas correlações são escolhidas de forma que a correlação entre u1 e v1
seja máxima; a correlação entre u2 e v2 seja máxima, sujeito a estas variáveis não
serem correlacionadas com u1 e v1; a correlação entre u3 e v3 seja máxima, sujeito a
estas variáveis não serem correlacionadas com u1, v1, u2, v2; etc.
Cada par (ui, vi) representa uma dimensão independente no
relacionamento entre os dois conjuntos de variáveis.
O primeiro par (u1, v1) tem a mais alta correlação possível, sendo o mais
importante. O segundo par (u2, v2) tem a segunda correlação mais alta, e assim por
diante.
Assemelha-se a componentes principais, exceto que aqui, a correlação é maximizada, enquanto que, em componentes principais, a variância é maximizada.
Procedimento de análise:
Seja a matriz de correlação (p + q)x(p + q):
Calculamos (B-1C’ A-1 C)qxq e os autovalores λ , considerando
|B-1 C’ A-1 C – λI|b= 0, em que I é a matriz identidade, de ordem pxq, e |.| refere-se
ao determinante da matriz.
Os autovalores são os quadrados das correlações entre as variáveis canônicas, e os correspondentes autovetores b1, b2, ... , br fornecem os coeficientes
das variáveis Y para as variáveis canônicas.
Os coeficientes da i-ésima variável canônica (ui) para as variáveis X são dados pelo elemento a = ACb
Então, u = a′X , v = b′Y , onde a′ = a, a, … a, b′= b, b, … b,
X′= x, x, … x, Y′= y, y, … y.
A suposição para a execução de tais cálculos é que X e Y estejam na forma padronizada (média zero e desvio padrão 1).
As variáveis u e v têm variâncias que dependem da escala adotada para o autovetor bi. Entretanto, podemos obter uma variância canônica escalonada ui,
com variância unitária (idem para vi). Basta calcular o desvio padrão de ui para os
dados e dividir os valores de aij pelo desvio padrão.
Barthett (1947) apresentou um teste aproximado para a significância das correlações entre u e v, como um todo. A suposição é que a distribuição das variáveis seja normal multivariada.
Χ = vn −1
2 (p + q + 3)y ln
1 −λ
n: tamanho amostral
Regra de decisão: Χ² > Χ²tab : pelo menos uma das r correlações
canônicas é significante. Caso contrário, nenhuma das correlações é significante.
O teste acima pode ser modificado para melhor aproximação quando o tamanho amostral for pequeno. Também, a contribuição de cada correlação canônica pode ser testada individualmente, porém o teste não é confiável (Bryan, M., 2005).
9 - ANÁLISE DE CORRESPONDÊNCIA
Método complementar ao teste quiquadrado de independência, utilizado para verificar a relação entre linhas e colunas numa tabela de contingência, relacionando duas variáveis categóricas.
Seja a tabela 9 em que ni,j representa a frequência absoluta da categoria i
da variável X e categoria j da variável Y.
Tabela 9
X 1 2 ... b Totais
1 n11 n12 ... n1b n1.
2 n21 n22 ... n2b n2.
... ... ... ... ... ...
A na1 na2 ... nab na.
Totais n.1 n.2 ... n.b n
Exemplo: Resultado de uma análise de 257 famílias quanto ao número de filhos e a renda familiar.
nº de filhos
Renda ($) 0 1 2 >2 Totais
< 2000 15 27 50 43 135
2000 –
5000
25 37 12 8 82
> 5000 8 13 9 10 40
Totais 48 77 71 61 257
Matriz de Correspondência: pi,j = ni,j/n
P = 0,058 0,105 0,195 0,1670,097 0,144 0,047 0,031 0,031 0,051 0,035 0,039
Matriz perfil das linhas: Dl = ni./n
Matriz perfil das colunas: Dc = n.i/n
D =
0,525 0 0
0 0,319 0
0 0 0,156 , D, =
0,187 0 0 0
0 0,299 0 0
0
0 00 0,276 00 0,237
l′ = -.
@.
…
.
0 , c′= . .@ … . 0
Seja a matriz
Esta matriz é do tipo p = .
. .K
, ou seja, os termos representam uma comparação da proporção observada no inferior de cada casela da tabela, com aquela esperada supondo independência entre as variáveis X e Y.
O posto (rank) da matriz P é dado por k = min(p − 1, q − 1). Tal matriz pode ser decomposta em seus autovalores e autovetores, chegando-se ao resultado:
P = A ∆ B′ ,
em que A = D é uma matriz de dimensão pxk, B = D, v é de dimensão qxk, u e
v são ortogonais e ∆ é uma matriz de dimensão kxk contendo os autovalores da
matriz P, ordenados em ordem decrescente.
u contém os autovetores da matriz PP′, e v, os autovetores de PP.′
Pela decomposição da matriz, as linhas de P podem ser escritas como
combinações lineares das linhas de B’ e as colunas de P podem ser escritas como
combinações lineares das colunas da matriz A.
As coordenadas principais das linhas da matriz P são definidas como:
Y = DA∆
As coordenadas principais das colunas da matriz P são
Z = D,B
∆
Como consequência desta decomposição, P pode ser expressa como função dos autovalores e das coordenadas principais, isto é,
P = P − lc′ = λab ′
, sendo
a-> i-ésima coluna da matriz A,
k = posto (P) = min(p-1,q-1)
As duas primeiras coordenadas principais das linhas e das colunas, são as que mais representam a associação entre X e Y estando relacionadas aos maiores autovalores da matriz P.
A variação total existente é chamada inércia total, e é dada por
λ,
sendo λ os autovalores não nulos da matriz ∆, i=1,2,...k.
A proporção explicada pela i-ésima coordenada principal é
λ
∑λ
Mostra-se que ∑ λ = ∑ -K¡K0 @
¡K
,
=¢
@
sendo Eij = npij representando o número esperado de observações na casela(i,j),
supondo independência entre as variáveis: E = ..K
Tabela 10– Coordenadas principais
Perfil das linhas Y1 Y2
(l1) <2000 -0,351 0,014
(l2) 2000 - 5000 0,543 0,021
(l3) > 5000 0,013 -0,089
Perfil das colunas Z1 Z2
(c1) 0 0,463 0,006
(c2) 1 0,375 -0,007
(c3) 2 -0,366 0,051
Analisando o gráfico, nota-se, pelas proximidades linhas-colunas, que:
- famílias de renda menor de 2.000 reais tendem a ter 2 ou mais filhos;
- famílias de renda entre 2.000 e 5.000 reais tendem a ter 0 ou 1 filho;
- famílias de mais de 5.000 reais de renda não se associam quanto ao número de filhos.
Um outro exemplo, Ramos et al. (2008), consiste em estudar possível associação entre dias da semana e horários de ocorrência de crimes em Belém, PA, ano de 2007, conforme noticiado pelos jornais. O resultado da análise é dado no gráfico seguinte.
Mapa perceptual da análise de correspondência das variáveis turno versus dia da semana para os
Observa-se que as terças, quartas e quintas feiras, os crimes tendem a ocorrer no período de tarde; aos domingos e sextas feiras, à noite; aos sábados, à noite e na madrugada; às segundas feiras, as maiores ocorrências acontecem na madrugada e no período da manhã.
10 – COMPONENTES PRINCIPAIS
Técnica descrita por Pearson (1901), melhorada por Hotelling (1933) e utilizada amplamente após o advento dos computadores.
Dadas p variáveis, X1, X2, ... , Xp, o objetivo da análise é encontrar
combinações e produzir índices Z1, Z2, ... , Zp que sejam não correlacionados, que
permitam descrever a variação dos dados, em que as variâncias possuem a seguinte relação:
Var (Z1) ≥ Var (Z2) ≥ ... ≥ Var (Zp)
Os índices Z são as componentes principais. Tais componentes medem
diferentes “dimensões” dos dados e as variâncias dos Zi tornam-se desprezíveis
para valores altos de i, i = 1, 2, ... , p.
Assim, poucas variáveis Z (as de variâncias não desprezíveis) descrevem a maior parte da variação do conjunto e uma economia na dimensão das variáveis é obtida.
Quanto mais correlacionadas forem as variáveis (positiva ou negativamente), melhores serão os resultados.
Dadas as p variáveis X1, X2, ... , Xp, seja a seguinte matriz de variâncias e
covariâncias:
S =
⎝ ⎜
⎛Var (X) Cov (XVar (X, X)) … Cov (X… Cov (X, X, X))
… …
Var (X) ⎠ ⎟ ⎞
As variâncias das componentes principais são os autovalores da matriz S.
Existem p autovalores, alguns dos quais podem ser zero. Autovalores negativos não são possíveis para uma matriz de covariâncias.
Sejam λ1 ≥ λ2≥ ... ≥ λp ≥ 0 os autovalores ordenados, sendo λ1 = Var (Zi)
correspondente ao i-ésimo componente principal:
Z = aX+ aX+ ⋯ + aX
Em que a, a, ... , a são os elementos do correspondente autovetor, escalonado,
de modo que ∑ a = 1.
Propriedade: ∑ λ = ∑ Var(X ) = traço da matriz
Variáveis de diferentes magnitudes podem ter diferentes influências nas componentes principais. Para evitar este fato padroniza-se as variáveis X1, X2, ... ,
Xp de forma a terem média zero e variância 1. Obtém-se a nova matriz, chamada
matriz de correlação, sendo e a correlação entre X1 e Xj:
e = §
1 e … e
… 1 … e
… … … e= 1
¨
O traço da matriz é igual ao valor p.
Portanto, o procedimento consiste em:
- Codificar X1, X2, ... , Xp para ter média zero e variância unitária. Às vezes
este procedimento não é feito quando se deseja que a importância das variáveis seja refletida em suas variâncias.
- Calcular a matriz e (ou S, dependendo do procedimento anterior).
- Encontrar os autovetores λ1, λ2, ... , λp e os correspondentes autovetores
a1, a2, ... , ap. Os coeficientes do i-ésimo componente principal são os elementos ai,
enquanto que λi é a sua variância.
Exemplo (Mingoti, 2005): Oito marcas de coxinhas são avaliadas por alguns examinadores, em relação às variáveis sabor (X1), aroma (X2), massa (X3) e
recheio (X4). As médias das notas dos examinadores, para cada marca e variável,
são dadas na tabela seguinte.
Marca Sabor Aroma Massa Recheio
M1 2,75 4,03 2,80 2,62
M2 3,90 4,12 3,40 3,52
M3 3.12 3,97 3,62 3,05
M4 4,58 4,86 4,34 4,82
M5 3,97 4,34 4,28 4,98
M6 3,01 3,98 2,90 2,82
M7 4,19 4,65 4,52 4,77
M8 3,82 4,12 3,62 3,71
Média 3,67 4,26 3,68 3,79
Desvio Padrão 0,638 0,332 0,651 0,954
Matriz de variâncias e covariâncias:
S = H
0,407 0,159 0,313 0,482 0,110 0,157 0,237 0,424 0,516 0,911
J
Os autovalores da matriz S são:
λ© = 1,7368
λ© = 0,0649
λ© = 0,0279
O traço da matriz S, dado também pela soma dos autovalores é igual a 1,852.
λ/traço = 0,9378
λ/traço = 0,0350
λ/traço = 0,0150
λª/traço = 0,0120
Juntas, explicam 97,3% da variância total do vetor original X (alta explicação).
Assim, duas componentes são suficientes para explicar as variações nas marcas.
Os autovetores gerados pelos primeiros dois autovetores são:
a« = H 0,456 0,223 0,477 0,717
J , a« = H
−0,816 −0,215 0,456 0,282
J
A primeira componente representa um índice global da qualidade da coxinha (todos os coeficientes são positivos). Assim,
Y¬ = 0,456 sabor + 0,223 aroma + 0,477 massa + 0,717 recheio
(maior importância é o recheio).
Quanto maior for o valor numérico de Y¬, maior será a qualidade da coxinha.
Os escores obtidos para as diferentes marcas são os seguintes:
M1: 5,367
M2: 6,843
M3: 6,222
M5: 8,390
M6: 5,665
M7: 8,524
M8: 7,047
Nota-se que a marca melhor classificada é a M4 e a pior, M1.
A segunda componente (de baixa explicação), contrasta sabor e aroma com massa e recheio:
Y¬ = −0,816 sabor − 0,215 aroma + 0,456 massa + 0,282 recheio
Obtém-se:
M1: -1,095
M2: -1,525
M3: -0,889
M4: -1,444
M5: -0,817
M6: -1,194
M7: -1,012
M8: -1,306
11 - ANÁLISE FATORIAL
Consiste em descrever um conjunto de p variáveis X1, X2, ... , Xp em um
número menor de índices ou fatores, bem como obter uma melhor compreensão do relacionamento entre estas variáveis.
A ideia é semelhante à de componentes principais, com a diferença de que a análise de componentes principais não é baseada em um modelo particular, o que ocorre com análise fatorial.
Spearman (1904), em estudo de correlações entre escores de testes de estudantes, observou que havia relações entre as correlações observadas. Por exemplo, seja a tabela de correlações entre escores de testes de meninos de uma escola (tabela 11):
Tabela 11 - Correlações entre escores de testes de meninos de uma escola
(Spearman, 1904)
Clássicos Francês Inglês Matemática Música Discriminação de tom
Clássicos 1 0,83 0,78 0,70 0,63 0,66
Francês 0,83 1 0,67 0,67 0,57 0,65
Inglês 0,78 0,67 1 0,64 0,51 0,54
Matemática 0,70 0,67 0,64 1 0,51 0,45
Música 0,63 0,57 0,51 0,51 1 0,40
Discriminação
de tom 0,66 0,65 0,54 0,45 0,40 1
Spearman notou que quaisquer duas linhas eram quase proporcionais se as diagonais fossem ignoradas.
Para as linhas Clássicos e Inglês:
0,83
Sugeriu, então, escrever: X = aF + e
X: i-ésimo escore após ter sido padronizado para ter média zero e desvio padrão 1, para todos os meninos
a: constante (carga fatorial)
F: fator com média zero e desvio padrão 1 para todos os meninos
e: parte de X específica para o i-ésimo teste somente
Spearman mostrou que uma razão constante entre as linhas de uma matriz de correlações segue como uma consequência dessas suposições e que, portanto, este é um modelo plausível para os dados.
var(X) = var(aF+ e) = avar(F) + var(e)
¾1 = a+ var(e), em que a representa a proporção da variância de X que
está contida no fator.
Spearman formulou uma teoria de dois fatores de testes mentais: uma parte comum a todos os testes (inteligência geral) e outra específica para o teste.
Generalizando: X = aF + aF+ … + aF+ e ,
F, F, … , F m fatores comuns, não correlacionados entre si, cada um com média zero e variância 1.
a, a, … , a cargas fatoriais para o i-ésimo teste
X i-ésimo escore do teste com média zero e variãncia 1
e fator específico somente para o i-ésimo teste, com média zero e não correlacionado com quaisquer dos fatores
a+ a+ … + a comunalidade de X (parte da variabilidade de X relacionada aos fatores comuns)
var(e) especificidadede X (parte da variância não relacionada aos fatores comuns)
Pode-se mostrar que a correlação entre X e X é:
r = aa + aa+ … + aa
Dois escores podem ser altamente correlacionados se possuem altas cargas nos mesmos fatores.
Em particular:
r = a+ a + … + a ≤ 1
−1 ≤ a ≤ 1 (somente m ˂ p termos)
Seja n indivíduos, cada um com valores na p variáveis. O procedimento é:
x Passo 1: Determinar a, as cargas dos fatores provisórios.
Inicia-se de maneira semelhante às componentes principais e despreza-se as componentes após as m iniciais (m ≤ p), sendo estas m componentes tomadas
como sendo os m fatores. Tais fatores não são correlacionados entre si.
Os fatores provisórios não são únicos. Se F, F, … , F são fatores provisórios, então as combinações lineares deles da forma
F∗ = dF+ dF+ … + dF , i = 1, 2, … , p
podem ser construídas de modo a serem não correlacionadas entre si e explicarem os dados tão bem quanto os fatores provisórios.
x Passo 2: Rotação de fator.
x Passo 3: Calcular os escores dos fatores.
Estes são os valores dos fatores rotacionados F∗, F∗, … , F∗ para cada um dos n indivíduos para os quais os dados estão disponíveis.
A escolha do número m de fatores (m ≤ p) é, de certa forma, subjetiva.
Uma regra grosseira consiste em escolher m como sendo o número de autovalores maiores que a unidade na matriz de correlação dos escores do teste. Um fator associado a um autovalor menor que a unidade responde por pouca variação nos dados.
As comunalidades aumentam com o aumento de m. Entretanto, as comunalidades não são alteradas por rotação do fator.
Há vários métodos de rotação de fatores. Um método muito usado é o varimax, que consiste num trabalhoso método numérico de maximização e pode ser encontrado na literatura.
Tal método é baseado na suposição que a interpretabilidade do fator j pode ser medida pela variância dos quadrados de suas cargas do fator, isto é, a variância de a, a, … , a.
Se esta variância for grande, então os valores a tendem a ser próximos de zero ou próximos de 1 (isto é bom para discriminar, pois a próximo à zero implica que X não é fortemente relacionado a F); um grande valor (positivo ou
negativo) de a significa que X é determinado, em grande parte, por F. A rotação varimax maximiza a soma das variâncias para todos os fatores.
Uma maneira de se fazer a análise fatorial é começar com análise de componentes principais e usar os primeiros componentes principais como fatores não rotacionados.
O método é como segue:
Z = bX+ bX+ … + bX , i = 1, 2, … , p
em que os b são dados pelos autovetores da matriz de correlações.
Esta transformação de X para Z é ortogonal, de forma que o relacionamento inverso é:
X = bZ+ bZ+ … + bZ , i = 1, 2, … , p
Para uma análise fatorial, apenas m ˂ p das componentes principais são
retiradas, em que m é o número de autovalores “grandes”, de forma que as
equações se tornam:
X = bZ+ bZ+ … + bZ+ e , i = 1, 2, … , p
em que e é uma combinação linear das componentes principais Z! a Z.
O próximo passo consiste em escalonar os componentes principais Z, Z, … , Z para que suas variâncias sejam unitárias.
Para tal, Z deve ser dividido por °λ, em que λ é o correspondente
autovalor na matriz de correlações e representa a variância de Z. Então:
X = °λbF+ °λbF+ … + °λbF+ e
em que
F
=
±°λ , i = 1, 2, … , p
O modelo de fatores não rotacionados é, então:
X = aF+ aF+ … + aF+ e ,
a = °λb ; i = 1, 2, … , p ; j = 1, 2, … , m
Após algum tipo de rotação, como o varimax, têm-se uma nova solução:
X = gF∗+ gF∗+ … + gF∗+ e
Os valores do i-ésimo fator não rotacionado são os valores do i-ésimo componente após eles terem sido escalonados para terem variância 1.
Os valores dos fatores rotacionados são dados pela equação matricial:
F∗ = XG(G′G)
em que F∗ matriz nxm contendo os valores para os m fatores
rotacionados em suas colunas, com uma linha para cada uma das linhas originais dos dados;
X matriz (nxp) dos dados originais para as p variáveis e n
observações, com as variáveis X padronizadas;
G matriz (pxm) das cargas dos fatores rotacionais dados pela equação
X = gF∗+ gF∗+ … + gF∗+ e (mostrada acima).
Cita-se, a seguir, as seguintes observações finais:
a) Há muitas opções de análise nos programas computacionais, o que pode causar confusão nos iniciantes no assunto.
b) A análise fatorial não funciona para todas as situações. Há conjuntos de dados em que não se chega a conclusões razoáveis. c) A análise vista é chamada análise fatorial exploratória, pois ela
inicia sem nenhuma suposição sobre o número de fatores existentes ou a natureza destes fatores.
d) Existe uma outra análise, chamada análise fatorial confirmatória, que requer que o número de fatores e a estrutura dos fatores seja especificada inicialmente. A mesma pode ser usada para testar teorias sobre a estrutura dos dados.
Exemplo: Porcentagens da força de trabalho empregados em 9 grupos de indústrias de 30 países da Europa (Manly, 2005) (tabela 12).
Tabela 12
País Grupo AGR MIN FAB FEA CON SER FIN SSP TC
Bélgica EU 2,6 0,2 20,8 0,8 6,3 16,9 8,7 36,9 6,8
Dinamarca EU 5,6 0,1 20,4 0,7 6,4 14,5 9,1 33,3 7,0
França EU 5,1 0,3 20,2 0,9 7,1 16,7 10,2 33,1 6,4
Alemanha EU 3,2 0,7 24,8 1,0 9,4 17,2 9,6 28,4 5,6
Grécia EU 22,2 0,5 19,2 1,0 6,8 18,2 5,3 19,8 6,9
Irlanda EU 13,8 0,6 19,8 1,2 7,1 17,8 8,4 25,5 5,8
Itália EU 8,4 1,1 21,9 0,0 9,1 21,6 4,6 28,0 5,3
Luxemburgo EU 3,3 0,1 19,6 0,7 9,9 21,2 8,7 29,6 6,8
Países
baixos EU 4,2 0,1 19,2 0,7 0,6 18,5 11,5 38,3 6,8
Portugal EU 11,5 0,5 23,6 0,7 8,2 19,8 6,3 24,6 4,8
Espanha EU 9,9 0,5 21,1 0,6 9,5 20,1 5,9 26,7 5,8
Reino Unido EU 2,2 0,7 21,3 1,2 7,0 20,2 12,4 28,4 6,5
Áustria AELC 7,4 0,3 26,9 1,2 8,5 19,1 6,7 23,3 6,4
Finlândia AELC 8,5 0,2 19,3 1,2 6,8 14,6 8,6 33,2 7,5
Islândia AELC 10,5 0,0 18,7 0,9 10,0 14,5 8,0 30,7 6,7
Noruega AELC 5,8 1,1 14,6 1,1 6,5 17,6 7,6 37,5 8,1
Suécia AELC 3,2 0,3 19,0 0,8 6,4 14,2 9,4 39,5 7,2
Tabela 12 (continuação) (Manly, 2005)
País Grupo AGR MIN FAB FEA CON SER FIN SSP TC
Albânia Leste 55,5 19,4 0,0 0,0 3,4 3,3 15,3 0,0 3,0
Bulgária Leste 19,0 0,0 35,0 0,0 6,7 9,4 1,5 20,9 7,5
República Tcheca / Eslováquia
Leste 12,8 37,3 0,0 0,0 8,4 10,2 1,6 22,9 6,9
Hungria Leste 15,3 28,9 0,0 0,0 6,4 13,3 0,0 27,3 8,8
Polônia Leste 23,6 3,9 24,1 0,9 6,3 10,3 1,3 24,5 5,2
Romênia Leste 22,0 2,6 37,9 2,0 5,8 6,9 0,6 15,3 6,8
USSR (antiga) Leste 18,5 0,0 28,8 0,0 10,2 7,9 0,6 25,6 8,4
Iugoslávia (antiga) Leste 5,0 2,2 38,7 2,2 8,1 13,8 3,1 19,1 7,8
Chipre Outro 13,5 0,3 19,0 0,5 9,1 23,7 6,7 21,2 6,0
Gibraltar Outro 0,0 0,0 6,8 2,0 16,9 24,5 10,8 34,0 5,0
Malta Outro 2,6 0,6 27,9 1,5 4,6 10,2 3,9 41,6 7,2
Turquia Outro 44,8 0,9 15,3 0,2 5,2 12,4 2,4 14,5 4,4
Nota: AGR, agricultura, florestal e pesca; MIN, mineração e exploração de pedreira; FAB, fabricação;
FEA, fornecimento de energia e água; CON, construção; SER, serviços; FIN, finanças; SSP, serviços sociais e pessoais; TC, transportes e comunicações. Os dados para os países individuais são para vários anos, de 1989 a 1995. Dados do Euromonitor (1995), exceto para Alemanha e Reino Unido, em que valores mais razoáveis foram obtidos do United Nations Statistical Yearbook (2000). Fonte:
Adaptado do Euromonitor (1995), European Marketing Data and Statistics, Euromonitor Publications,
London; e de United Nations (2000), Statistical Yearbook, 44th issue, U.N. Department of Social
Tabela 13 – A matriz de correlação para porcentagens de empregados em nove
grupos industriais em 30 países na Europa na forma diagonal inferior, calculada dos dados na tabela 12. (Manly, 2005)
AGR MIN FAB FEA CON SER FIN SSP TC
AGR 1,000
MIN 0,316 1,000
FAB -0,254 -0,672 1,000
FEA -0,382 -0,387 0,388 1,000
CON -0,349 -0,129 -0,034 0,165 1,000
SER -0,605 -0,407 -0,033 0,155 0,473 1,000
FIN -0,176 -0,248 -0,274 0,094 -0,018 0,379 1,000
SSP -0,811 -0,316 0,050 0,238 0,072 0,388 0,166 1,000
TC -0,487 0,045 0,243 0,105 -0,055 -0,085 -0,391 0,475 1,000
Nota: As variáveis são as porcentagens de empregados em AGR, agricultura, florestal e pesca; MIN,
mineração e exploração de pedreira; FAB, fabricação; FEA, fornecimento de energia e água; CON, construção; SER, serviços; FIN, finanças; SSP, serviços sociais e pessoais; TC, transportes e comunicações (Manly, 2005).
Tabela 14 – Autovalores e autovetores para dados de emprego europeu na tabela
12. (Manly, 2005)
Autovetores
Autovalores X1 AGR X2 MIN X3 FAB X4 FEA X5 CON X6 SER X7 FIN X8 SSP X9 TC
3,111 0,512 0,375 -0,246 -0,315 -0,222 -0,382 -0,131 -0,428 -0,205
1,809 -0,024 0,000 0,432 0,109 -0,242 -0,408 -0,553 0,055 0,516
1,495 -0,278 0,516 -0,503 -0,292 0,071 0,064 -0,096 0,360 0,413
1,063 0,016 0,113 0,058 0,023 0,783 0,169 -0,489 -0,317 -0,042