UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA
DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL
Transporte Térmico em Nanofitas de
Grafeno-Nitreto de Boro
Isaac de Macêdo Félix
-Transporte Térmico em Nanofitas de
Grafeno-Nitreto de Boro
Dissertação apresentada ao Programa de Pós-Graduação em Física do Departamento de Física Teórica e Ex-perimental da Universidade Federal do Rio Grande do Norte, como requisito de obtenção do título de Mestre em Física.
Orientador: Prof. Dr. Luiz Felipe Cavalcanti Pereira
-Félix, Isaac de Macêdo.
Transporte térmico em nanofitas de grafeno-nitreto de boro / Isaac de Macêdo Félix. - Natal, 2016.
xxii, 100f: il.
Orientador: Prof. Dr. Luiz Felipe Cavalcanti Pereira. Dissertação (Mestrado) - Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Física.
1. Dinâmica molecular de não-equilíbrio. 2. Super-redes BNC. 3. Transporte térmico de fônons. 4. Materiais
termoelétricos. I. Pereira, Luiz Felipe Cavalcanti. II. Universidade Federal do Rio Grande do Norte. III. Título.
Catalogação da Publicação na Fonte
“ Somos o que repetidas vezes
fazemos. A excelência, portanto, não é
Agradecimentos
Muitas pessoas colaboraram para a realização de mais essa etapa em minha vida,
algu-mas de forma técnica, outras de maneira pessoal. Nenhuma lista de agradecimentos é
completa, mas a lista que segue expresso meu mais nobre sentimento de reconhecimento.
A Deus, pela sua constante presença em minha vida. Fazendo os desafios se tornarem fáceis quando a vida os apresentam difíceis.
"Porque eu estou bem certo de que nem a morte, nem a vida, nem os anjos, nem os principados, nem as coisas do presente, nem do
porvir, nem os poderes, nem a altura, nem a profundidade, nem
qualquer outra criatura poderá separar-nos do amor de Deus, que
está em Cristo Jesus, nosso Senhor."
(Romanos 8:38-39)
A minha família, que me permitiu nascer e me criar num lar digno onde nunca me faltou incentivo e afeto. Com vocês aprendi muito sobre a vida. Do caráter à ternura. São mais que teoria. São exemplos.
A minha namorada, pelos incentivos, compreensão e companheirismo. E ao sorriso, que transforma minhas agitações em afagos.
Também desejo expressar meus agradecimentos ao meu ex-orientador, o Prof. Dr. Luis Alberto Terrazos Javier (UFCG/CES), quem me direcionou à Física da Matéria Condensada, e a todos os professores que outrora fizeram parte da minha vida estu-dantil, no ensino superior e na educação básica. Que Deus os recompense pelo amor e dedicação ao ensino.
Aos meus amigos, colegas do grupo de pesquisa e colegas de pós-graduação, pelas ajudas e incentivos. Em especial a Silas e a César, pessoas que tenho um enorme apreço e sentimento fraternal.
Aos funcionários da UFRN, principalmente aos que compõem o DFTE, que estiveram nos bastidores da minha formação, facilitando questões burocráticas (a todos da Coor-denação e da secretária do DFTE), proporcionando um ambiente digno para trabalhar (aos funcionários da limpeza e do serviço de manutenção), cuidando da alimentação (aos funcionários do RU) e facilitando o acesso ao "cérebro" da UFRN (aos funcionários da Biblioteca Zila Mamede). Muito obrigado pelos serviços prestados!
O desenvolvimento científico não acontece sem investimentos e incentivos. Agradeço a Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) que financiou essa pesquisa.
Resumo
A capacidade de manipular propriedades térmicas de super-redes pode ajudar na des-coberta de materiais mais promissores para aplicações na nanotecnologia. Por meio de simulações de dinâmica molecular de não-equilíbrio, investigamos o transporte térmico em nanofitas de grafeno-nitreto de boro (nanofitas BNC), revezando periodicamente quantidades equivalentes de grafeno e nitreto de boro ao longo do seu comprimento, nomeando de período de rede o tamanho de cada par de domínio (grafeno-nitreto de
boro). Este trabalho revela que a condutividade térmica nessa super-rede varia não-monotonicamente com o período de rede, podendo dessa forma ser controlada de acordo com os domínios de grafeno e nitreto de boro. Isso possibilita identificar o período de rede que fornece a menor condução de calor nessa super-rede. Nesse sentido, para nanofitas com período de rede de3,43 nm, registramos uma condutividade térmica de
∼89 W/m·K. Este valor é muito menor do que o encontrado para grafeno e nitreto de boro isolados. O transporte térmico em nanofitas BNC é dominado por vibrações na sua rede cristalina (fônons). Associamos o comportamento não-monotônico da con-dutividade térmica dessa super-rede com o transporte térmico de fônons coerentes e incoerentes. Por meio da densidade de estados vibracionais (VDOS) e da dispersão de fônons analisamos seu espectro vibracional.
The ability to manipulate thermal properties of superlattices can help in fin-ding the most promising materials for applications in nanotechnology. Through non-equilibrium molecular dynamics simulations, we investigate the thermal transport in graphene-boron nitride nanoribbons (BNC nanoribbons), alternating periodically equi-valent amounts of graphene and boron nitride along its length, by naming the size of each domain pair (graphene-boron nitride) a lattice period. This work shows that the thermal conductivity in BNC nanoribbons varies non-monotonically for different lattice periods, which can thus be controlled according to the domains of graphene and boron nitride. This allows the identification of a lattice period that provides the lowest heat conduction in these superlattices. Accordingly, for nanoribbons with lat-tice period 3,43 nm, we find a thermal conductivity of ∼ 89 W/m·K. This value is much lower than the value found for both graphene and boron nitride isolated. The thermal transport in BNC nanoribbons is dominated by vibrations in their crystal lat-tice (phonons). We associate this non-monotonic behavior of the thermal conductivity of this super-lattice with the thermal transport of coherent and incoherent phonons. Through the density of vibrational states (VDOS) and phonon dispersion we analyze its vibrational spectrum.
Lista de Abreviaturas
BNC grafeno-nitreto de boro
COSERN Companhia Energética do Rio Grande do Norte DOE Departamento de Energia dos Estados Unidos GULP General Utility Lattice Program
IEA Agência Internacional de Energia
LAMMPS Large-scale Atomic/Molecular Massively Parallel Simulator
MD dinâmica molecular
LLNL Lawrence Livermore National Laboratorie
NASA National Aeronautics and Space Administration
NEMD dinâmica molecular de não-equilíbrio NPT ensemble isotérmico-isobárico
NVE ensemble microcanônico
NVT ensemble canônico
RTG gerador termelétrico de radioisótopo USB barramento serial universal
VACF função de autocorrelação da velocidade VDOS densidade de estados vibracionais
Constante Símbolo Valor
Constante de Boltzmann kB 1,38×10−23 J/K
Constante de Planck h 6,62×10−34 J·s
Constante de Planck reduzida ~ 1,05×10−34 J·s
Fator de Lorentz (elétrons livres) L 2,44×10−8 J2/K2·C2
Massa do elétron me 9,11×10−31 kg
Carga elementar e 1,60×10−19 C
Lista de Tabelas
2.1 Parâmetros do potencial Tersoff otimizados para interações C-BN. . . . 45 4.1 Listagem do número de átomos por período de rede. . . 62 4.2 Listagem das medições do livre caminho médio efetivo dos fônons Λph
e da condutividade térmica κ∞ (no limite termodinâmico) para cada período de rede λ. . . 68
1.1 Esquema do dispositivo original criado por Seebeck no descobrimento do que se tornaria conhecido como termoeletricidade. O dispositivo consistia de dois metais diferentes conectados, AB e K. Quando uma
junção foi aquecida (B), um campo magnético foi induzido, fazendo a
agulha da bússola (N S) orientar-se de acordo com a conformidade. . . 3
1.2 Obtenção do efeito Seebeck para um fio condutor sujeito a um gradiente de temperatura. Quando os portadores de cargas são negativos o sentido do campo elétrico é paralelo ao fluxo de calor. Quando os portadores de cargas são positivos o sentido do campo elétrico é antiparalelo ao fluxo de calor. . . 4 1.3 Efeito Seebeck na junção de dois materiais distintos, A e B. Quando
esses materiais são submetidos a um gradiente de temperatura, os por-tadores de cargas se movem, do lado quente para o frio, devido ao fluxo de calor imposto ao sistema. O resultado é uma diferença de potencial induzido, Eq. (1.3). . . 5 1.4 Esquema de um termopar: Os condutores A e B são compostos por
materiais diferentes,TM é a temperatura que se pretende medir eTAé a
temperatura ambiente. A combinação específica de A e B resultará em
um coeficiente Seebeck SAB(T) e permitirá resolver a Eq. (1.3) afim de
medir TM a partir da tensão obtida com o voltímetro V. . . 6
1.6 (a) Esquema de funcionamento do relógio Seiko Thermic: A tensão é gerada a partir da dispersão dos portadores de cargas nos módulos ter-moelétricos, durante a condução de calor do pulso do utente para o ambiente (setas vermelhas). (b) Módulos termoelétricos: Nesse reló-gio foram utilizados dez módulos termoelétricos conectados em série e confeccionados com telureto de bismuto (Bi2Te3). . . 8
1.7 O diagrama ηT ×ZT marca a menor (ηmin) e a maior (ηmax) eficiência
termoelétrica para um suposto material termoelétrico com 1 ≤ ZT ≤
2,62à temperatura ambiente (300 K). Nesse contexto, para ηC = 0,80
os possíveis valores de ηT variam de∼ 20 a ∼ 35 %. . . 10
1.8 Otimização da figura de mérito ZT em termos da concentração de
por-tadores de carga n e da condutividade térmica κ. (a) Acima temos
o comportamento típico da figura de mérito (linha tracejada). Vemos que semicondutores fortemente dopados normalmente são bons materi-ais termoelétricos. Abaixo vemos que a maximização do fatorS2σ exige
um valor para κentre ke e kph. (b) Exemplo de ZT e da condutividade
térmica κe versus n para Bi2Te3. Abaixo, vemos que a contribuição
eletrônica da condutividade térmica (curva roxa) é uma função de n.
Associando com o diagrama acima, quando κph = 0,8, o máximo ZT
está no ponto 1. Ao diminuir κph, ZT aumenta para o ponto 2.
Dimi-nuindo n e mantendo κph temos um aumento adicional em ZT, ponto
3. . . 12 1.9 Cadeia diatômica unidimensional formada por uma célula unitária com
parâmetro de redea, composta por partículas do tipoαe do tipoβ, com
massas mα emβ, respectivamente, conectados por uma mola com
cons-tante elástica K. Como a célula unitária desse sistema é unidimensional
o vetor de onda do espaço recíproco é dado por k =±π
a. Os termosuj
e vj denotam, respectivamente, os deslocamentos dos átomos de tipo α
mente da diferença entre as massas dos átomos que a cadeia diatômica compreende. . . 15 1.11 Nos modos acústicos, dois átomos de um mesmo sítio da rede de Bravais
vibram com uma ligeira diferença de fase. Nos modos ópticos, eles estão em oposição de fase. . . 16 1.12 Estruturas cristalinas: (a) Grafeno. (b) Nitreto de Boro. . . 18 1.13 (a) Filme BNC com espessura atômica (região retangular cinza). (b)
Periodicidade em uma monocamada BNC com domínios controlados de grafeno e nitreto de boro. (c) e (d) Circuitos elétricos finos, flexíveis e com litografia. A parte escura é feita com grafeno e a parte clara é feita com nitreto de boro. . . 19 1.14 Modelo de uma nanofita BNC com largura fixa Ly, revezando
periodi-camente domínios equivalentes de grafeno e nitreto de boro ao longo de seu comprimento Lx. Cada par de domínio (grafeno-nitreto de boro)
nomeamos período de rede, e é representado por λ. . . 20
2.1 Esquema da mudança da posição e da velocidade do i-ésimo átomo de
um sistema com o incremento temporal δt. . . 24
2.2 Representação dos ensembles NVE (microcanônico), NVT (canônico) e
NPT (isotérmico-isobárico). . . 36 2.3 Descrição qualitativa do potencial de Lennard-Jones (a) e do potencial
de Coulomb. . . 41 2.4 Representação das ligações atômicas para: (a) Ligação de alongamento,
(b) Ligação angular e (c) Ligação com torção. . . 42 2.5 Descrição qualitativa dos potenciais harmônicos de alongamento e
vi-bração (a) e distorções angulares (b). . . 42 2.6 Potencial para descrever rotações de átomos em torno de uma ligação
usando o ângulo diedro. . . 43 2.7 Maneira como uma partícula cruza o limite da célula de simulação e
2.8 (a) Na convenção de mínima imagem as partículas interagem com as mais próximas N −1imagens vizinhas. (b) Um truncamento esférico é utilizado para as contribuições de curto alcance para a energia potencial. 47 2.9 Fluxograma dos procedimentos básicos de uma simulações MD. . . 49 3.1 Ilustrando a lei de Fourier. Quando submetemos certo material a um
gradiente de temperatura um fluxo de calor surge da região quente para a região fria e sua magnitude dependerá da condutividade térmica do material. . . 53 3.2 Divisão da célula de simulação periódica em n caixas na direção x. As
caixas 0 e n são chamadas caixa fria e a caixa n/2 é chamada caixa quente. As caixas têm geometrias idênticas e possuem mesma quanti-dade de átomos, além de satisfazer condições de contorno periódicas. . 56 3.3 Simulação de uma nanofita BNC com período de rede λ = 0,86 nm e
comprimento total Lx ∼48 nm (sistema com 8960 átomos equilibrado à
300 K, com um passo de integração fixo dt = 0,5 fs). (a) Temperatura
entre as camadas quentes e frias em função do tempo de simulação. (b) Fluxo de calor versus tempo de simulação. Nos momentos iniciais da simulação o fluxo de calor apresenta um comportamento transiente, tornando-se estacionário no decorrer da simulação. Assim, quanto maior (suficiente) o tempo de simulação, menores serão as incertezas do fluxo de calor no sistema. . . 57 3.4 Ilustração do perfil de temperatura. Quando a simulação atinge o
es-tado estacionário é possível determinar o gradiente de temperatura do sistema. No método de Müller-Plathe esse gradiente é dado pela média aritmética de ∇xT1 e ∇xT2. Geralmente, o gradiente de temperatura
é calculado na região onde foi estabelecido a temperatura do sistema (região branca). . . 58 3.5 VDOS para uma nanofita BNC com período de rede λ= 0,86 nm (160
mente ao longo do eixo-xde forma periódica. A soma de dois domínios
consecutivos (um de grafeno e um de nitreto de boro) é nomeadoperíodo de rede e é representado por λ. Sua larguraLy é fixa (∼5 nm), mas seu
comprimento Lx cresce periodicamente cada vez que replicamos λ. . . . 62
4.2 A amostras de nanofitas BNC com diferentes períodos de rede (λ) mas
tamanhos idênticos (Lx = 6,86 nm). . . 64
4.3 Dependência da condutividade térmica (κ) com o tamanho (Lx) e com o
período de rede (λ) das nanofitas BNC. A condutividade térmica cresce
a medida que o comprimento de cada amostra aumenta. Além disso, ela apresenta valores diferentes para amostras de tamanhos idênticos, mas períodos de rede distintos. . . 65 4.4 (a) Ajustes (linhas cheias) nas medições apresentadas no diagrama da
Fi-gura 4.3 por meio da Eq.(4.1). (b) Ajuste extrapolado até1µmpara es-timar o comportamento deκno limite termodinâmico (κ∞). Vemos que
a dependência da condutividade térmica com comprimento das amostras ocorre até determinado tamanho. Assim, para nanofitas suficientemente longas, a dependência de κ com seu comprimento Lx desaparece. . . 67
4.5 (a) Condutividade térmica (κ∞) e (b) livre caminho médio efetivo dos
fônons (Λph) versus período de rede (λ). Comparando essas figuras,
vemos que existe uma forte relação deκ∞ comΛph. Vemos também que
o comportamento deΛph(quadrados vermelhos), e consequentemente de
4.6 Representação qualitativa do comprimento de coerência dos pacotes de onda (curvas vermelhas). (a) Quando o período de rede é menor do que o comprimento dos pacotes de onda, os fônons não "sentem" as interfaces que conectam os diferentes domínios de grafeno e nitreto de boro. (b) Quando o período de rede é da ordem do comprimento dos pacotes de onda, começa a predominar o transporte térmico de fônons incoerentes. Esse é o período de rede que fornece a menor condutividade térmica da super-rede. (c) Quando o período de rede é maior do que o tamanho dos pacotes de onda, o comportamento corpuscular (quase-partícula) dos fônons predomina. Como resultado, há um aumento da condutividade térmica, devido a diminuição da densidade de interfaces. . . 70 4.7 VDOS projetada nos grupos atômicos de cada períodos de rede. A
contribuição dos átomos de boro (curvas vermelhas) aumenta de acordo com λ para uma frequência de ∼ 48 THz. No entanto, a VDOS dos
carbonos (curvas pretas) e dos nitrogênios (curvas azuis) têm pequenas variações. . . 72 4.8 VDOS total para cada período de rede λ das nanofitas BNC. Para
do-mínios equivalentes de grafeno e nitreto de boro (λ), temos a mesma
intensidade de vibração da rede, não importando o seu número de áto-mos Nλ. . . 73
4.9 (a) A célula unitária para nanofitas BNC com período de rede λ = 0,86 nm(retângulo com linha azul tracejada ) possui 8 átomos não equi-valentes: quatro átomos de carbono, dois de boro e dois de nitrogênio, que são separados entre si por uma distância a= 1,43Å (parâmetro de rede). (b) Primeira zona de Brillouin para as nanofitas BNC (retângulo com linha azul cheia) com os pontos de alta simetria (e coordenadas) Γ (0,0,0), X 1
2,0,0
, Y 0,1 2,0
e M 1 2,
1 2,0
lho representam os modos acústicos longitudinal (LA), transversal (TA) e flexural (ZA). Os dois primeiros apresentam dispersão linear enquanto o terceiro apresenta dispersão quadrática entorno do pontoΓ. A maioria dos modos ópticos apresentam pouca dispersão, dando origem a picos na VDOS. . . 75 4.11 Dispersão de fônons para nanofitas BNC com diferentes períodos.
Sumário
Lista de Abreviaturas x
Constantes Física xi
Lista de Tabelas xii
Lista de Figuras xiii
1 Introdução 1
1.1 Materiais Termoelétricos . . . 2
1.1.1 Breve Histórico . . . 2
1.1.2 Fundamentos . . . 3
1.1.3 Aplicações . . . 5
1.1.4 Limites e Desafios . . . 8
1.1.5 Otimizando ZT . . . 10
1.2 Vibrações da Rede e Transporte de Calor . . . 12
1.2.1 Modelo Diatômico Unidimensional . . . 13
1.3 Motivação da Pesquisa . . . 17
1.3.1 Grafeno e Nitreto de Boro . . . 18
1.4 Nossa Proposta . . . 20
2 Dinâmica Molecular 21 2.1 Equação de Movimento . . . 21
2.1.1 O Formalismo Lagrangeano . . . 21
2.1.2 O Formalismo Hamiltoniano . . . 23
2.2 Algoritmo de Integração . . . 23
2.2.1 Algoritmo de Verlet . . . 24
2.2.2 Algoritmo Velocity Verlet . . . 25
2.3 Conservação de Energia . . . 27
2.4.1 Revisão . . . 32 2.4.2 Ensembles Estatísticos . . . 35
2.5 Inicialização e Termalização . . . 36 2.5.1 Termostato de Nosé-Hoover . . . 37 2.5.2 Cadeias de Nosé-Hover . . . 39 2.6 Potenciais Interatômicos . . . 40 2.6.1 Potenciais intermoleculares . . . 40 2.6.2 Potenciais intramoleculares . . . 41 2.6.3 Campo de Força . . . 43 2.7 Condições de Contorno Periódicas . . . 45 2.8 Convenção de Mínima Imagem . . . 46 2.9 Executando uma Simulação MD . . . 47 2.10 Software LAMMPS . . . 50
2.10.1 Descrição do software . . . 50
3 Transporte de Calor e Fônons 52
3.1 Lei de Fourier . . . 52 3.2 Método NEMD . . . 54 3.2.1 O Método Direto . . . 55 3.2.2 O Método Reverso . . . 55 3.3 Espectro Vibracional de Fônons . . . 59 3.3.1 Densidade de Estados Vibracionais . . . 59
4 Transporte Térmico em Nanofitas BNC 61
4.1 Nanofitas BNC . . . 61 4.1.1 Protocolo de Simulação . . . 63 4.2 Resultados e Discussão . . . 63
4.3 Perspectivas . . . 78
5 Conclusão 79
Referências Bibliográficas 81
A Ferramentas Matemáticas para o Capítulo 2 91
A.1 Prova reversa da Eq. (2.32) . . . 91 A.2 Propriedade Simplética do Algoritmo Velocity Verlet . . . 93
A.3 Prova da Eq. (2.48) . . . 95 A.4 Prova do Teorema de Trotter . . . 97
Introdução
Na última conferência das Nações Unidas sobre as Mudanças Climáticas, que ocorreu de 30 de novembro a 11 de dezembro de 2015 em Paris, Brasil e Estados Uni-dos apresentaram uma declaração conjunta reconhecendo a necessidade de acelerar o emprego de energias renováveis para substituir atuais formas de obtenção de eletrici-dade. Dados apresentados em novembro do mesmo ano pela IEA (International Energy Agency) mostram que cerca de 70% da eletricidade do mundo é gerada por usinas que
trabalham a partir de combustíveis fósseis [1]. Tipicamente isso envolve processos de queima de combustível para aquecer a água que é então convertida em vapor. Em seguida, esse vapor é usado para mover uma turbina que gera eletricidade. As turbinas mais eficientes são capazes de atingir um rendimento de aproximadamente 60% [2], os outros 40% são rejeitados na forma de calor para o ambiente. Isso resulta em cerca de 15 TWh de energia desperdiçada a cada ano1 [3].
1.1. Materiais Termoelétricos Capítulo 1. Introdução
outros 95% são transformados em calor2. Estes são alguns casos, dentre inúmeros, em que o calor é considerado um incômodo e, portanto, essa energia é naturalmente desperdiçada.
Se o calor rejeitado nos dispositivos citados acima pudesse de alguma maneira ser recuperado de forma útil, seria possível aumentar a eficiência desses dispositivos. Há uma classe de materiais que permitem esse efeito. Estamos nos referindo aos ma-teriais termoelétricos, ou simplesmente termoelétricos. Esses materiais são capazes de
converter calor em eletricidade. Descobertos há quase 200 anos, os termoelétricos des-pertam o interesse de cientistas do mundo inteiro, principalmente na construção de dispositivos que reduzem o desperdício de energia térmica.
1.1
Materiais Termoelétricos
1.1.1
Breve Histórico
Em 1820, o físico alemão Thomas Johann Seebeck criou um dispositivo capaz de gerar um campo magnético por meio da aplicação de calor. Sua maquineta era bastante simples, envolvendo apenas dois metais diferentes (Figura 1.1). Quando o calor foi aplicado a uma das junções entre os dois metais, um campo magnético foi gerado. Ele observou este campo magnético através de uma bússola no meio do circuito que, por aplicação de calor, orientava a agulha da bússola. Seebeck chamou este fenômeno de
efeito termomagnético [4, 5].
Seebeck não associou no momento a forma como o campo magnético realmente era criado. Mais cedo, naquele mesmo ano, o cientista dinamarquês Hans Christian Oersted mostrou que uma corrente elétrica podia gerar um campo magnético. Foi Oers-ted quem esclareceu como o dispositivo de Seebeck realmente funcionava e denominou o fenômeno como efeito termoelétrico [5]. Hoje, este fenômeno é muitas vezes referido
simplesmente comoefeito Seebeck.
A
B
S
N
K
Figura 1.1: Esquema do dispositivo original criado por Seebeck no descobrimento do que se tornaria conhecido como termoeletricidade. O dispositivo consistia de dois metais diferentes conectados, AB e K. Quando uma junção foi aquecida (B), um
campo magnético foi induzido, fazendo a agulha da bússola (N S) orientar-se de acordo
com a conformidade.
Crédito: ClipArt ETC.
metais diferentes, Peltier aplicou uma corrente elétrica. Ele constatou que, dependendo do sentido dessa corrente, o calor pode ser absorvido ou rejeitado pela junção [6]. Tal fenômeno ficou conhecido como efeito Peltier.
1.1.2
Fundamentos
Seebeck e Peltier observaram a ocorrência do efeito termoelétrico em experiên-cias compostas por uma junção de condutores diferentes. Tais efeitos também estão presentes em condutores individuais. Se um fio de metal, por exemplo, é submetido a um gradiente de temperatura, com aquecimento e esfriamento em extremidades opos-tas (Figura 1.2), os portadores de cargas irão se mover, do lado quente para o frio, devido ao fluxo de calor imposto ao sistema. A concentração de elétrons (ou bura-cos) no extremo com menor temperatura produz um campo elétrico, que induz uma diferença de potencial elétrico ao longo do comprimento do fio [7]. A razão entre a dife-rença de potencial e a difedife-rença de temperatura é conhecida comocoeficiente Seebeck, representado aqui por "S". Matematicamente, esse coeficiente pode ser escrito como:
S =−∆V
1.1. Materiais Termoelétricos Capítulo 1. Introdução
_
+
_
baixa densidade
de elétrons
alta densidade
de elétrons
Campo Elétrico
Temperatura
alta
Temperatura
baixa
elétrons
Fluxo de calor
+
baixa densidade
de buracos
alta densidade
de buracos
Campo Elétrico
buracos
Fluxo de calor
Figura 1.2: Obtenção do efeito Seebeck para um fio condutor sujeito a um gradiente de temperatura. Quando os portadores de cargas são negativos o sentido do campo elétrico é paralelo ao fluxo de calor. Quando os portadores de cargas são positivos o sentido do campo elétrico é antiparalelo ao fluxo de calor.
onde∆V é a diferença de potencial elétrico induzido pela diferença de temperatura∆T. O coeficiente Seebeck é uma função da temperatura, portanto, deve ser tecnicamente representado como S =S(T). Para calcular a diferença de potencial elétrico ao longo de um gradiente de temperatura, deve-se resolver a seguinte integral:
∆V =
Z T1 T0
S(T) dT. (1.2)
Seguindo a mesma linha de raciocínio da experiência original realizada por Seebeck consideremos como exemplo a junção de dois materiais distintos,AeB, como mostra a
Figura 1.3. Esses materiais têm diferentes coeficientes Seebeck, isso leva a uma variação do acúmulo de carga nos extremos das junções desses materiais. Isto significa que, se queremos calcular a diferença de potencial elétrico induzido não podemos simplesmente usar a Eq.(1.2). A tensão entre os dois materiais será dada como∆VAB = ∆VA−∆VB,
o que conduz a uma forma modificada da Eq.(1.2):
∆VAB =
Z T1 T0
(SA(t)−SB(t)) dT =
Z T1 T0
SAB(T) dT. (1.3)
V
− −
− − −
material
A
material
B
fluxo de calor
− −
− − − − −
−
Figura 1.3: Efeito Seebeck na junção de dois materiais distintos,A eB. Quando esses
materiais são submetidos a um gradiente de temperatura, os portadores de cargas se movem, do lado quente para o frio, devido ao fluxo de calor imposto ao sistema. O resultado é uma diferença de potencial induzido, Eq. (1.3).
calor pode ser absorvido, ou rejeitado, pela junção será dada por:
Qp = (ΠA−ΠB)IT = ΠABIT, (1.4)
ondeΠA eΠB são os coeficientes Peltier para os materiais A eB, respectivamente, eI
é a corrente elétrica. O coeficiente Peltier está relacionado com o coeficiente Seebeck pela seguinte relação:
Π =T S. (1.5)
1.1.3
Aplicações
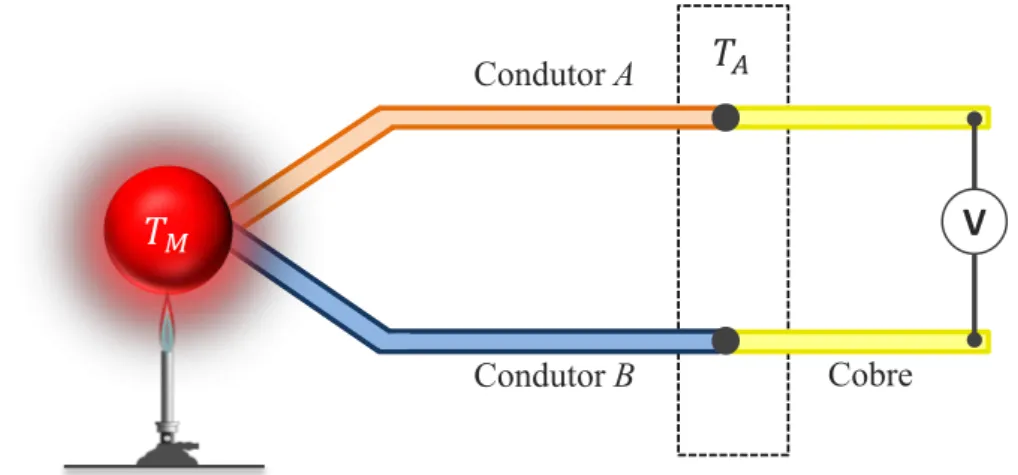
Existem diversos dispositivos que funcionam por meio do efeito termoelétrico. A aplicação mais simples é a do efeito Seebeck para medições de temperatura por um equipamento conhecido comotermopar. O desenho básico de um termopar é ilustrado
na Figura 1.4 e é semelhante à da junção de metais diferentes apresentado na seção anterior (Figura 1.3). Os termopares são populares para a medição da temperatura, porque eles são relativamente baratos, tem boa sensibilidade e geralmente podem ope-rar em vasta escala de temperatura. A acessibilidade de uso desse dispositivo é tão facilitada, que existem multímetros que vem com a opção termopar.
tempera-1.1. Materiais Termoelétricos Capítulo 1. Introdução
𝑇
𝐴Cobre
Condutor
B
Condutor
A
𝑇
𝑀V
Figura 1.4: Esquema de um termopar: Os condutores A e B são compostos por ma-teriais diferentes, TM é a temperatura que se pretende medir e TA é a temperatura
ambiente. A combinação específica de A e B resultará em um coeficiente Seebeck SAB(T) e permitirá resolver a Eq. (1.3) afim de medir TM a partir da tensão obtida
com o voltímetroV.
tura. O esquema de funcionamento de um módulo termoelétrico é mostrada na Figura 1.5 (a). Esta técnica tem sido usada pela NASA na exploração espacial ao longo de décadas, sob o uso de geradores termoelétricos de radioisótopos (radioisotope thermo-electric generator - RTGs). Os RTGs operam essencialmente com encapsulamento de
um material radioativo dentro de um cilindro termoelétrico. À medida que o material radioativo decai, calor é emitido nos módulos termoelétricos e convertido em eletri-cidade. A meia-vida típica para muitos isótopos radioativos é da ordem de décadas, tornando-se possível gerar eletricidade durante muitos anos. Os RTGs utilizados nas sondas Voyager, lançadas em 1977, continuam operando quase 40 anos mais tarde [8].
Nos últimos anos, os termoelétricos começaram a encontrar aplicações mais acessíveis e práticas, não necessitando de uma viagem espacial para usufruir das suas vantagens. Dispositivos que usam o efeito Peltier, por exemplo, oferecem o potencial de substituir técnicas tradicionais de arrefecimento, como condensadores e compressores de forma mais eficiente. Eles têm sido usados para criar uma variedade de dispositivos interessantes e com pouco peso, tais como refrigeradores portáteis e dissipadores de calor de dispositivos eletrônicos de alta performance. A operação termoelétrica de um refrigerador Peltier é ilustrada na Figura 1.5 (b).
Tipo B
dissipador de calor
dissipador de calor
𝑖
− +𝑖
(a)
(b)
F
L
U
X
O
D
E
C
A
L
O
R
Tipo A
fonte de calor
+ + + + +
− − − − − − − − +
+ +
Tipo B
Tipo A
+ + + + +
− − − − − − − − +
+ +
arrefecimento
Figura 1.5: Módulos termoelétricos, operando como (a) um dispositivo Seebeck gerador de energia elétrica e (b) um dispositivo Peltier para refrigeração.
CampStove, que colhe parte do excesso de calor produzido pela queima de madeira para
gerar energia elétrica através de módulos termoelétricos integrados. Essa eletricidade é usada para alimentar um ventilador elétrico que funciona como um fole soprando a lenha para queimar mais intensamente. Com o fogo mais forte, tem-se menos fu-maça, tornando-o muito mais seguro para usá-lo em ambientes fechados. O excesso de eletricidade produzida também pode ser usado para carregar baterias de dispositivos eletrônicos via porta USB. Para oCampStove, a companhia promete reduzir a
necessi-dade de combustível em 50%, fumaça tóxica em cerca de 94% e emissões de monóxido de carbono em 91%, quando comparado a versão rústica desse dispositivo [9]. Con-siderando que bilhões de pessoas ainda dependem de fogões a lenha para cozinhar e não têm acesso a fontes de energias confiáveis [10, 11], está claro que dispositivos como esse têm a capacidade de melhorar a vida dessas pessoas e, inclusive, agredir menos a natureza.
O efeito termoelétrico despertou a "sede" de converter calor desperdiçado em ele-tricidade útil. Já existem dispositivos termoelétricos que podem funcionar até mesmo com calor humano. É o caso do relógio de pulso Thermic fabricado pela empresa
1.1. Materiais Termoelétricos Capítulo 1. Introdução
(a)
(b)
Figura 1.6: (a) Esquema de funcionamento do relógio Seiko Thermic: A tensão é gerada a partir da dispersão dos portadores de cargas nos módulos termoelétricos, durante a condução de calor do pulso do utente para o ambiente (setas vermelhas). (b) Módulos termoelétricos: Nesse relógio foram utilizados dez módulos termoelétricos conectados em série e confeccionados com telureto de bismuto (Bi2Te3).
Crédito: Seiko Watch Corporation.
1.1.4
Limites e Desafios
Como vimos, dispositivos que funcionam a partir do efeito termoelétrico podem levar a algumas aplicações bem interessantes. Tais dispositivos são máquinas térmi-cas, portanto, obedecem as leis da termodinâmica. Se considerarmos como exemplo um módulo termoelétrico que absorve uma quantidade de calor Q para fornecer uma
quantidade de energiaE operando sem qualquer perda de calor (caso ideal), podemos
determinar sua eficiência máxima como:
η = E
Q. (1.6)
Outra forma de se fazer isso é usando a relaçãoZT, conhecida comofigura de mérito. O
termoZT é um parâmetro adimensional e define a eficiência de conversão termoelétrica
de um material. Matematicamente, ele é expresso como:
ZT = S
2σT
κ , (1.7)
em que S é o coeficiente Seebeck do material (discutido na seção 1.1.2), σ é a
con-dutividade elétrica, κ é a condutividade térmica e T é a temperatura da operação
eletricidade, ao passo que outros materiais, tais como madeira, plástico, vidro e ce-râmica são tipicamente bons isolantes térmicos e elétricos. A Eq. (1.7) nos diz que os melhores termoelétricos são bons condutores de eletricidade, no entanto, não são bons condutores de calor. Para entender a natureza por trás da condutividade elétrica, basta analisar a forma como os portadores de carga se movem no material. Materiais com muitos portadores de carga livres tais como metais e semicondutores fortemente dopados, tem boa condutividade elétrica. Já materiais como vidro não têm elétrons livres, portanto, são considerados isolantes elétricos. A condutividade térmica normal-mente ocorre por duas vias. A primeira é a contribuição dos elétrons, por isso que a maioria dos metais são bons condutores de calor e eletricidade, a segunda vem da maneira como os átomos do material vibram em sua rede. Assim, a condutividade térmica é matematicamente escrita como uma soma algébrica:
κ=κe+κph. (1.8)
Nesta equação,κe é a contribuição eletrônica para condutividade térmica eκph a
con-tribuição vibracional da rede, que será discutida de maneira mais detalhada à frente. Usando a Eq. (1.8) podemos reescrever a Eq. (1.7) como:
ZT = S
2σT
κe+κph
. (1.9)
Esta equação ilustra os principais parâmetros que devem ser otimizados, a fim de aumentar ZT. Em princípio, um material é considerado um "bom" termoelétrico
quando ZT ≥ 1à T = 300 K. Trataremos a Eq. (1.9) com mais detalhes na próxima
seção.
A eficiência máxima de um dispositivo termoelétrico (ηT) pode ser escrito em
termos de ZT como [13]:
ηT =
TQ−TF
TQ √
1 +ZT −1
√
1 +ZT +TF
TQ
=ηC √
1 +ZT −1
√
1 +ZT + TF
TQ
, (1.10)
em queTQ eTF são as temperaturas da fonte quente e fria, respectivamente. O termo
(TQ−TF)/TQ representa a eficiência de Carnot,ηC. Essa equação é plotada para uma
1.1. Materiais Termoelétricos Capítulo 1. Introdução
pela diferença de temperatura, recorrente de ηC. A outra é que a eficiência de
dispo-sitivos termoelétricos normalmente assume valores relativamente baixos. Para se ter uma ideia, a maior figura de mérito já registrada foi ZT = 2,62 à uma temperatura de923 K, atribuída a condutividade térmica extremamente baixa (0,23 W/m·K) do seleneto de estanho (SnSe) [14]. Se a figura de mérito de SnSe tivesse sido obtida à 300 K, de acordo com a Figura 1.7, a máxima eficiência termoelétrica conseguida por esse material, seria de aproximadamente 35 %, se ηC atingisse 0,80 (80 %). Como
resultado disso, vemos que os termoelétricos tornam-se atraentes apenas para aplica-ções de dispositivos em que a conversão de energia termoelétrica está dentro do limite aceitável (nesse caso, em torno 35%), podendo ser usado como um meio de aumentar a eficiência global de outros processos.
0 1 2 3 4
ZT
0 10 20 30 40 50 60
ηΤ(%)
0,80 0,60 0,40 0,20 ηC
ηmax
2,6
1
ηmin
Figura 1.7: O diagramaηT ×ZT marca a menor (ηmin) e a maior (ηmax) eficiência
ter-moelétrica para um suposto material termoelétrico com1≤ZT ≤2,62à temperatura ambiente (300 K). Nesse contexto, para ηC = 0,80 os possíveis valores de ηT variam
de∼ 20 a ∼ 35 %.
1.1.5
Otimizando
ZT
Eq. (1.9) mostramos que ZT pode ser melhorado através da elevação do fator S2σ e
da diminuição da condutividade térmica κ. Uma das abordagens mais simples para
otimizarZT é começar trabalhando com um material de baixa condutividade térmica e
em seguida aumentar a sua condutividade elétrica, através da adição de portadores de carga (processo conhecido comodopagem). No entanto, há uma interdependência entre
S, σ e κque torna este processo um pouco complicado. Para metais e semicondutores
fortemente dopados, o coeficiente Seebeck pode ser escrito como [15, 16]:
S = 2 3
k2 B
e~2m
∗T π 3n
2/3
, (1.11)
em que e, n e m∗ são, respectivamente, a carga, a concentração e a massa efetiva dos portadores de carga. A concentração desses portadores está relacionada com a condutividade elétrica σ por:
σ=neµ, (1.12)
onde µé a mobilidade elétrica dos portadores. Essas duas últimas equações mostram
que um material com baixa concentração de portadores de cargas produz um elevado coeficiente Seebeck, mas uma baixa condutividade elétrica. A interdependência entre estas propriedades são plotadas na Figura 1.8 [15, 17]. Não levaremos em conta as unidades das grandezas porquê queremos fazer apenas uma abordagem qualitativa. Note que a Figura 1.8 (a) destaca a relação inversa entre o coeficiente Seebeck S e a condutividade elétrica σ, dando origem a um fator de potência máxima S2σ [17].
Além disso, quando a concentração de portadores aumenta a condutividade térmica total κ também aumenta. Isso se deve a contribuição dos elétrons κe dada pela lei de
Wiedemann-Franz [16, 18]:
κe=neµLT =σLT, (1.13)
ondeLé o fator de Lorentz. A Figura 1.8 (b) ilustra a interdependência entren,κeZT
(paraBi2Te3). A curva roxa representa a contribuição dos elétrons para condutividade
térmica κe que a partir da Eq. (1.13), é uma função da concentração de portadores
de carga. Para um sistema com κph = 0,8 o máximo ZT é mostrado no ponto 1. Se
essa condutividade térmica diminui para κph = 0,2, mas mantém a concentração de
portadores, isso leva a um aumento de ZT, mostrado no ponto 2. O máximo ZT,
1.2. Vibrações da Rede e Transporte de Calor Capítulo 1. Introdução
𝑍
(figu
ra
de
mé
rito
)
𝜅𝑒
𝜅𝑝ℎ
(a)
𝑛 (concentração de portadores)
𝜅
(c
on
du
tiv
ida
de
t
ér
mic
a)
isolantes semicondutores metais
²𝜎 𝜎
𝜅𝑒
𝜅𝑝ℎ= 0,8
𝜅𝑝ℎ= 0,2
(1) (2) (3)
(b)
𝑛 (concentração de portadores)
Figura 1.8: Otimização da figura de méritoZT em termos da concentração de
portado-res de cargan e da condutividade térmicaκ. (a) Acima temos o comportamento típico
da figura de mérito (linha tracejada). Vemos que semicondutores fortemente dopados normalmente são bons materiais termoelétricos. Abaixo vemos que a maximização do fatorS2σ exige um valor paraκentrek
e ekph. (b) Exemplo deZT e da condutividade
térmicaκe versus n para Bi2Te3. Abaixo, vemos que a contribuição eletrônica da
con-dutividade térmica (curva roxa) é uma função den. Associando com o diagrama acima,
quandoκph = 0,8, o máximoZT está no ponto 1. Ao diminuirκph,ZT aumenta para
o ponto 2. Diminuindon e mantendo κph temos um aumento adicional em ZT, ponto
3.
Fonte: Adaptadas de (a) Rowe, (2005) e (b) Snyder; Toberer, (2008).
um ponto fundamental para obtenção de bons termoelétricos: Podemos aumentar ZT
simplesmente reduzindoκph, enquanto as propriedades elétricas pode ser reguladas por
meio do ajuste da concentração de portadores [15]. Esse entendimento está motivando muitos estudos sobre formas de reduzirκph em diversas estruturas.
1.2
Vibrações da Rede e Transporte de Calor
Vimos na seção anterior queZT é incrementado à medida que diminuímosκph.
claro no final da seção 1.1.4 por meio da Figura 1.7. Qualquer adicional para ZT
é importante, pois, isso pode proporcionar dispositivos termoelétricos mais eficientes. Assim, entender como diminuir a condutividade térmica vibracional de uma rede (κph)
é um passo determinante para otimizar sua figura de mérito. No entanto, devemos primeiro entender como se dá o transporte de calor em sua estrutura.
1.2.1
Modelo Diatômico Unidimensional
Consideremos um sistema constituído por uma cadeia diatômica unidimensional com átomos do tipo α e de tipo β, com massas mα e mβ, respectivamente, ocupando
posições alternadas, em que cada átomo interage com os seus dois vizinhos mais pró-ximos. Este modelo representa um cristal diatômico unidimensional simples. Vamos considerar também a interação entre esses átomos como sendo harmônica, isto é, a força entre dois átomos será proporcional à distância entre eles. Para este exemplo específico, podemos levar em conta apenas os deslocamentos longitudinais desses átomos. Com imposição dessa condição de contorno periódica no eixo-x, podemos então calcular os
diferentes modos de vibração deste sistema e considerar que cada par consecutivo de átomos forma uma célula unitária, como mostra a Figura 1.9.
...
...
𝑗−1 𝑗 𝑗 𝑗+1
(tipo ) (tipo )
𝐾
(célula unitária)
𝑎
k = ±𝜋𝑎
(vetor do espaço recíproco)
𝑚 𝑚
Figura 1.9: Cadeia diatômica unidimensional formada por uma célula unitária com parâmetro de rede a, composta por partículas do tipo α e do tipoβ, com massas mα
e mβ, respectivamente, conectados por uma mola com constante elástica K. Como a
célula unitária desse sistema é unidimensional o vetor de onda do espaço recíproco é dado por k =±π
a. Os termosuj evj denotam, respectivamente, os deslocamentos dos
1.2. Vibrações da Rede e Transporte de Calor Capítulo 1. Introdução
As equações de movimento dos átomos tipo α e tipo β são dadas,
respectiva-mente, por:
mαu¨j =−K(2uj−vj−vj−1), (1.14)
mβ¨vj =−K(2vj−uj+1−uj), (1.15)
onde K é uma constante de ligação (tipo mola) e uj e vj denotam os deslocamentos
dos j-ésimos átomos tipo α e tipo β, respectivamente. Como as Eqs. (1.14) e (1.15)
são lineares, suas soluções podem ser descritas como uma combinação linear de autova-lores (automodos vibracionais) periodicamente espaciais, respeitando as condições de contorno estabelecidas anteriormente:
uj =Aei(ωt−kx), (1.16)
vj =Bei(ωt−kx), (1.17)
em queωé a frequência angular de oscilação ao longo do sistema,ké o número de onda e
xé sua posição na cadeia. Substituindouj evj nas Eqs. (1.14) (1.15), respectivamente,
e resolvendo-as obtemos:
A(ω2−2Ω2α) + 2BΩ2αcos(ka/2) = 0, (1.18)
B(ω2−2Ω2β) + 2AΩ2βcos(ka/2) = 0, (1.19)
onde definimosΩj =
q
K
mj. Resolvendo esse problema de autovalores temos a relação
entre a frequência e número de onda, conhecida como relação de dispersão [18]:
ω2+(k) = (Ω2α+ Ω2β) +
s
(Ω2
α+ Ω2β)2−4Ω2αΩ2βsin 2
ka
2
, (1.20)
ω2−(k) = (Ω2α+ Ω2β)−
s
(Ω2
α+ Ω2β)2−4Ω2αΩ2βsin 2
ka
2
. (1.21)
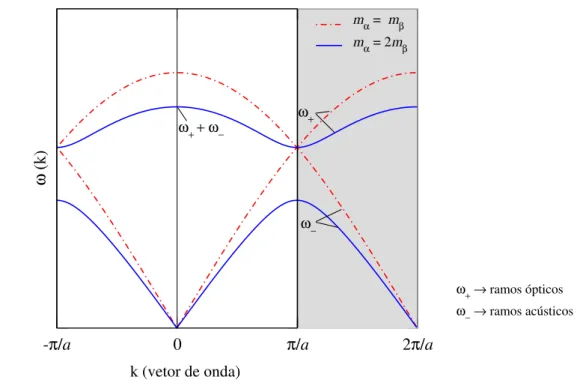
A partir dessas equações vemos que não há diferença entre suas soluções para um nú-mero de onda k e um número de onda k + 2π
a , como mostra a Figura 1.10. Assim,
podemos restringir essa análise apenas para valores entre −π
a e π
a que definem a
pri-meira zona Brillouin do nosso sistema. Note que há uma abertura (gap) na faixa de
te-remos estados degenerados na vizinhança dos pontos −π
a e π
a. Assim, podemos dizer
que há uma relação de dispersão maior para o caso mα = 2mβ.
-π/a 0 π/a 2π/a
k (vetor de onda)
ω
(k)
mα = mβ mα = 2mβ
ω+ ω+ + ω−
ω−
ω+→ ramos ópticos ω−→ ramos acústicos .r
Figura 1.10: Relação de dispersão para uma estrutura linear diatômica. Vemos que o tamanho da abertura na faixa de frequência angular depende diretamente da diferença entre as massas dos átomos que a cadeia diatômica compreende.
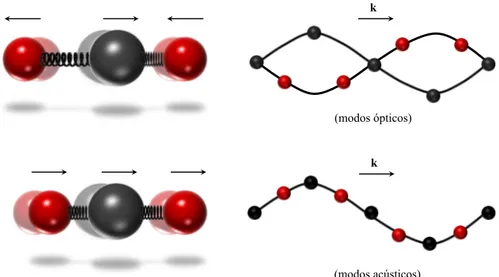
Este modelo diatômico simples revela dois tipos de modos de vibração: o modo acústico e o modo óptico [18]. A fim de ter uma descrição da diferença entre esses modos, podemos olhar mais de perto o modo óptico no centro da zona de Brillouin, k = 0, e perceber que a frequência angular é ω =q2(Ω2
α+ Ω2β). Resolvendo o sistema
linear das Eqs. (1.16) e (1.17) para A=−B teremosuj =−vj, o que significa que os
dois átomos de cada sítio da rede estão se movendo em fases opostas, como mostra a Figura 1.11. Por outro lado, nos modos acústicos os dois átomos de um mesmo sítio da rede estão normalmente se movendo na mesma direção. Em geral, a condutividade térmica de um material se deve aos modos acústicos, devido ao grande comprimento de onda e alta dispersão.
Transporte Térmico de Fônons
1.2. Vibrações da Rede e Transporte de Calor Capítulo 1. Introdução
+
+
+
+
+
– –
– –
+
+
+
+
+
–
–
–
–
(modos acústicos) (modos ópticos)
k
k
Figura 1.11: Nos modos acústicos, dois átomos de um mesmo sítio da rede de Bravais vibram com uma ligeira diferença de fase. Nos modos ópticos, eles estão em oposição de fase.
uma forma de energia, o aquecimento de um átomo aumenta sua vibração. Além disso, a vibração de um único átomo afeta e é afetada pelas vibrações dos átomos vizinhos. Como resultado, se o calor for aplicado em um lado de um sólido, ele irá se propagar ao longo do material por meio das vibrações e interações entre os átomos. Estas vibrações são frequentemente descritas como ondas [19]. Estas ondas, ou vibrações da rede, em sólidos são normalmente referidas comofônons3.
A descrição acima é relativamente simples, mas suficiente como ponto de par-tida, porque nos permite discutir o transporte de calor através do contexto de fônons que, como partículas, podem ser espalhados e/ou desviados. Na ausência de qualquer espalhamento e/ou deflexão, um fônon irá se propagar sempre na mesma direção e com velocidade constantevg. A duração de tempo que fônons podem viajar sem obstáculos
é chamado detempo de vida dos fônonsτph. Podemos escrever a condutividade térmica
de uma rede em termos deτph como [19]:
κph=
1 3CVv
2
gτph, (1.22)
expressar a Eq. (1.22) é escrevendoΛph =vgτph,
κph =
1
3CVvgΛph, (1.23)
onde Λph é chamado livre caminho médio dos fônons, e significa o percurso que um
fônon faz sem encontrar obstáculos.
Na Eq. (1.23) vemos queκph é diretamente proporcional a Λph. Assim,
modifi-cando a estrutura cristalina de um material, adicionando átomos, defeitos ou interfaces, por exemplo, é possível reduzir o livre caminho médio dos fônons Λph de modo a
en-contrar valores menores para condutividade térmica κph. Recentemente, essa trama
se tornou uma maneira bastante viável de encontrar materiais com boa performance termoelétrica [15, 20, 21, 22, 23, 24].
1.3
Motivação da Pesquisa
Nos últimos anos, os termoelétricos parecem ter ganhado um "novo corpo". A nanoestruturação é uma das principais estratégias usadas atualmente para melhorar as propriedades termoelétricas dos materiais. Isso se deve a dois motivos principais: o confinamento quântico de portadores, que leva a um aumento da energia entre a banda de valência e a banda de condução, e a dispersão de fônons, que leva a diminuição do livre caminho médio Λph [25, 26]. Na verdade o interesse de termoelétricos em
nanoescala surgiu no início dos anos 90 pelo trabalho pioneiro de Hicks e Dresselhaus [27]. Esta proposta impulsionou o aumento do número de artigos e patentes com base em nanosistemas termoelétricos e duas décadas depois os nanotermoelétricos, como também são chamados, estabeleceram firmemente uma subclasse na física da matéria condensada [28].
Recentemente as propriedades termoelétricas do grafeno têm sido investigadas devido ao seu potencial em converter calor em eletricidade [29, 30]. Um problema particular que essa nanoestrutura enfrenta, à respeito da termoeletricidade, é devido a alta condutividade térmica observada nesse material [31, 32]. A condutividade térmica do grafeno à temperatura ambiente é dominada por vibrações da rede (fônons). Assim, reduzirκph no grafeno por meio de modificações na sua estrutura pode transformá-lo
1.3. Motivação da Pesquisa Capítulo 1. Introdução
algumas abordagens que combinam grafeno com monocamadas de nitreto de boro he-xagonal4 (h-BN) têm sido estudadas para fins termoelétricos [33, 34], tendo em vista, sobretudo, que sua condutividade térmica também é dominada por fônons. Quando se considera que heteroestruturas de grafeno-nitreto de boro podem ser sintetizadas [35, 36], fica claro o motivo da especulação científica acerca dessa nanoestrutura.
1.3.1
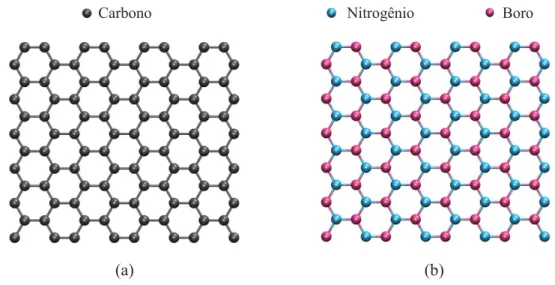
Grafeno e Nitreto de Boro
O grafeno é uma das formas alotrópicas do carbono, onde os átomos ocupam os sítios de uma rede cristalina hexagonal, formando uma monocamada. O nitreto de boro possui uma estrutura cristalina semelhante à do grafeno, sendo um composto químico binário formado por átomos de boro e nitrogênio que se alternam ocupando a sua rede cristalina, como mostra a Figura 1.12. Os parâmetros de rede desses materiais são muito próximos5 (
∼1,43Å), com uma diferença de apenas 2%.
(b)
(a)
Carbono
Nitrogênio
Boro
Figura 1.12: Estruturas cristalinas: (a) Grafeno. (b) Nitreto de Boro.
Apesar da semelhança entre suas estruturas cristalinas, existem diferenças mar-cantes entre o grafeno e o nitreto de boro. O grafeno possui a maior condutividade térmica já observada em um material (∼ 5000 W/m·K) [31, 32] e é um
semicon-4Nesse trabalho, quando o leitor ver o termo
nitreto de boro, deve-se entender como monocamada de nitreto de boro hexagonal, h-BN.
dutor de gap nulo com excelentes propriedades de transportes à temperatura
ambi-ente [37]. O nitreto de boro apresenta uma condutividade térmica relativamambi-ente alta (∼400 W/m·K) [38] e é um isolante com gap direto de ∼5 eV [39].
Recentemente, dois grupos de pesquisas liderados por cientistas da Rice Uni-versity, sintetizaram independentemente monocamadas de grafeno e nitreto de boro (BNC) [35, 36], Figura 1.13 (a). Em suas pesquisas eles observaram que monocamadas BNC podem ser produzidas com quantidades controladas de grafeno e nitreto de boro, Figura 1.13 (b). Como resultado direto desse estudo, o grupo liderado por Pulickel M. Ajayan observou que essas monocamadas podem ser usadas para construção de circuitos elétricos finos, flexíveis e inclusive litografados [35], Figuras 1.13 (c) e (d).
BNC film
Graphene
h-BN
(a)
(b)
(c)
(d)
10 μm
Figura 1.13: (a) Filme BNC com espessura atômica (região retangular cinza). (b) Pe-riodicidade em uma monocamada BNC com domínios controlados de grafeno e nitreto de boro. (c) e (d) Circuitos elétricos finos, flexíveis e com litografia. A parte escura é feita com grafeno e a parte clara é feita com nitreto de boro.
1.4. Nossa Proposta Capítulo 1. Introdução
1.4
Nossa Proposta
Nesse trabalho simulamos nanofitas BNC adotando o padrão de periodicidade usado na sintetização de monocamadas BNC proposta por Liu et al. (2013) [35], Figura 1.13 (b). A ideia principal é analisar o transporte térmico de fônons dessa super-rede, assumindo domínios equivalentes de grafeno e nitreto de boro, como ilus-tra a Figura 1.14. Compreender o ilus-transporte térmico de fônons dessa super-rede é de importante relevância para sua utilização na construção de nanodispositivos 2D e oferece novas perspectivas sobre as propriedades de transporte térmicas de materiais bidimensionais à base de grafeno. O nosso estudo com nanofitas BNC foi realizado por meio de simulações de dinâmica molecular de não-equilíbrio. Nos próximos dois capítulos apresentaremos uma revisão teórica dos conceitos mais relevantes abordados nessa pesquisa.
λ
𝐿
...
...
𝐿
Figura 1.14: Modelo de uma nanofita BNC com largura fixa Ly, revezando
periodica-mente domínios equivalentes de grafeno e nitreto de boro ao longo de seu comprimento
Lx. Cada par de domínio (grafeno-nitreto de boro) nomeamos período de rede, e é
Dinâmica Molecular
Dinâmica molecular (MD) é uma técnica computacional utilizada para calcular propriedades de equilíbrio e de transporte de sistemas clássicos de muitos corpos. Este método baseia-se no fato de que as trajetórias das partículas que compõem um sis-tema são previstas integrando suas equações de movimento, de acordo com a segunda lei de Newton. Assim, dadas inicialmente as posições e velocidades de um conjunto de partículas que interagem mutuamente entre si, sob certas condições, esse método integra numericamente suas equações de movimento, proporcionando novos conjun-tos de posições e velocidades para cada etapa de tempo. As trajetórias obtidas para essas partículas permitem calcular várias propriedades do sistema, através de médias estatísticas.
2.1
Equação de Movimento
Conhecer as equações de movimento das partículas (segunda lei de Newton) que compõem um sistema clássico é um passo fundamental para conhecer seu estado, a partir de uma simulação MD. Existem várias maneiras de determinar essas equações. A seguir, apresentamos duas formas bem sugestivas de se fazer isso.
2.1.1
O Formalismo Lagrangeano
Em um sistema isolado de N partículas com coordenadas r = (r1,r2, ...,rN) e
momentosp= (p1,p2, ...,pN), escrevemos o Lagrangeano L(r,r˙) como:
2.1. Equação de Movimento Capítulo 2. Dinâmica Molecular
ondeV(r)é a energia potencial do sistema1 e
K(˙r)é sua energia cinética, dada por:
K(˙r) =
N
X
i=1
1 2mir˙
2
i. (2.2)
Podemos determinar a força resultante sobre a i-ésima partícula, Fi, causada pela
interação de todas as outras partículas do sistema, como:
Fi = ∇riL, (2.3)
= ∇ri[K(˙r)−V(r)], (2.4)
= −∂V(r)
∂ri
. (2.5)
Fazendo uso da equação de Euler-Lagrange [40],
d dt
∂L ∂r˙i
−
∂L ∂ri
= 0, (2.6)
teremos:
d dt
∂L ∂r˙i
=
∂L ∂ri
. (2.7)
Usando a Eq. (2.1) e resolvendo as derivadas obtemos:
d dt
∂K(˙r)
∂r˙i
=−∂V(r)
∂ri
. (2.8)
Fazendo uso da Eq. (2.2) encontramos:
d dt
∂ ∂r˙i
mir˙2i
2
=−∂V(r)
∂ri
, (2.9)
∴ mir¨i =−∂V(r)
∂ri
. (2.10)
Por fim, substituindo a Eq. (2.10) na Eq. (2.5) encontramos a segunda lei de Newton:
Fi =mir¨i. (2.11)
1O cálculo de
V(r)pode ser realizado através da chamada Mecânica Molecular, onde é definida
Note que se resolvermos a equação diferencial de segunda ordem, Eq. (2.11), podemos prever as velocidades das partículas e suas respectivas trajetórias como uma função do tempo. Esse é o objetivo de uma simulação em MD.
2.1.2
O Formalismo Hamiltoniano
Novamente vamos considerar um sistema deN partículas com coordenadas r= (r1,r2, ...,rN) e momento p = (p1,p2, ...,pN). Agora, escrevemos sua energia total,
ou seu Hamiltoniano H(r,p), como sendo a soma da energia cinética mais a energia potencial:
H(r,p) =
N
X
i=1
p2 i
2mi
+V(r). (2.12)
Note que, derivando o Hamiltoniano da Eq. (2.12) por p e r obtemos as equações de Hamilton [40]:
∂H(r,p)
∂pi = pi
mi
= ˙ri, (2.13)
∂H(r,p)
∂ri
= ∂V(r)
∂ri
=−Fi =−p˙i. (2.14)
Da Eq. (2.13) temos, pi = mir˙i. Substituindo na última igualdade da Eq. (2.14)
obtemos mais uma vez a segunda lei de Newton:
Fi =mir¨i. (2.15)
Portanto, para prever a dinâmica das partículas como uma função do tempo pode-mos resolver as equações diferenciais de primeira ordem (2.13) e (2.14), ou resolver a equação diferencial de segunda ordem (2.15). Particularmente, existem algoritmos computacionais que resolvem essa equação para um número suficiente de partículas. É isso que vamos ver na próxima seção.
2.2
Algoritmo de Integração
Em MD as coordenadas de cada átomo são atualizadas a cada passo de tempo
δt, de ordem muito pequena (pico ou femtosegundos, por exemplo), de acordo com a
dinâmica clássica (newtoniana). A Figura 2.1 esquematiza a mudança da posiçãori e
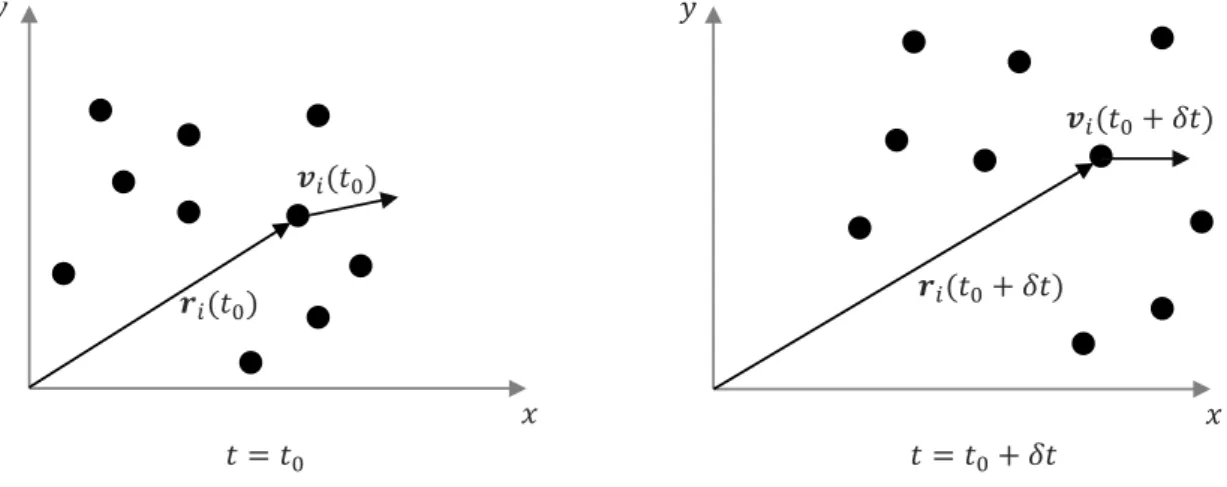
2.2. Algoritmo de Integração Capítulo 2. Dinâmica Molecular
de um algoritmo eficiente para integrar as equações de movimento desse sistema. Em simulações MD um dos mais requisitados é o algoritmo de Verlet [41, 42], que será abordado a seguir.
𝒓𝑖 𝑡0
𝒗𝑖 𝑡0
𝒓𝑖 𝑡0+ 𝛿𝑡
𝒗𝑖 𝑡0+ 𝛿𝑡
𝑡 = 𝑡0+ 𝛿𝑡
𝑡 = 𝑡0
Figura 2.1: Esquema da mudança da posição e da velocidade doi-ésimo átomo de um
sistema com o incremento temporal δt.
2.2.1
Algoritmo de Verlet
A ideia básica do algoritmo de Verlet é escrever duas expansões em série Taylor para as posições ri das partículas, uma para frente e outra para trás no tempo:
ri(t+δt)≈ri(t) + ˙ri(t)δt+
1
2!¨ri(t)δt
2+ 1
3! ...r
i(t)(δt3) +· · · , (2.16)
ri(t−δt)≈ri(t)−r˙i(t)δt+
1
2!¨ri(t)δt
2
− 3!1...ri(t)(δt3) +· · · . (2.17)
Onder˙i(t)e¨ri(t)são, respectivamente, as velocidadesvi e as aceleraçõesai das
partí-culas. Usando a segunda lei de Newton escrevemos as Eqs. (2.16) e (2.17) como:
ri(t+δt)≈ri(t) +vi(t)δt+
1 2mi
Fi(t)δt2+
1
6bi(t)(δt
3) +
O(δt4), (2.18)
ri(t−δt)≈ri(t)−vi(t)δt+
1 2mi
Fi(t)δt2−
1
6bi(t)(δt
3) +
O(δt4). (2.19)
Somando as Eqs. (2.18) e (2.19) obtemos:
ri(t+δt) +ri(t−δt) = 2ri(t) +
1
mi
Fi(t)δt2+O(δt4), (2.20)
∴ ri(t+δt) = 2ri(t)−ri(t−δt) + 1
mi
A Eq. (2.21) é a expressão utilizada para calcular as novas posições dos átomos em uma simulação MD utilizando o algoritmo de Verlet. A utilização de ri(t−δt) no
cálculo das posições no tempot+δttorna esse método reversível temporalmente. Além
disso, o método apresenta a conservação de energia do sistema mesmo com δt longos
[41, 42].
Agora, subtraindo as Eqs. (2.18) e (2.19) obtemos:
ri(t+δt)−ri(t−δt) = 2vi(t)δt+O(δt4), (2.22)
∴ vi(t) = ri(t+δt)−ri(t−δt)
2δt +O(δt
2). (2.23)
A Eq. (2.23) é usada para atualizar as velocidade dos átomos em uma simulação MD que utiliza o algoritmo de Verlet. Portanto, as Eqs. (2.21) e (2.23) compõem o algoritmo de Verlet [41]:
ri(t+δt) = 2ri(t)−ri(t−δt) +
1
mi
Fi(t)δt2+O(δt4),
vi(t) =
ri(t+δt)−ri(t−δt)
2δt +O(δt
2).
(2.24)
2.2.2
Algoritmo Velocity Verlet
O esquema original do algoritmo de Verlet, Eqs. (2.24), não controla as ve-locidades de forma plenamente satisfatória. Além disso, as condições iniciais de um sistema normalmente são dadas no mesmo instante de tempo,ri(0) evi(0), entretanto,
no algoritmo de Verlet precisamos das posições no presente intervalo de tempo, ri(0),
e no anterior, ri(−δt). Há também algumas preocupações sobre erros de
arredonda-mento que podem surgir na aplicação das Eqs. (2.24) [43]. No entanto, um algoritmo equivalente, que armazena posições, velocidades e acelerações ao mesmo tempo em que, também, minimiza erros de arredondamento pode ser construído.
Consideremos a Eq. (2.19) no próximo passo de tempo:
ri(t) =ri(t+δt)−vi(t+δt)δt+
1 2mi
2.2. Algoritmo de Integração Capítulo 2. Dinâmica Molecular
Adcionando a Eq. (2.25) na Eq. (2.18) e resolvendo para vi(t+δt), obtemos:
✘✘✘ri(t+✘✘δt) =
✘✘✘ri(t+✘✘δt)−vi(t+δt)δt+
1 2mi
Fi(t+δt)δt2− · · ·
(2.26) +
vi(t)δt+
1 2mi
Fi(t)δt2+· · ·
,
(2.27)
vi(t+δt)δt✁✁ = vi(t)δt+
1 2mi
[Fi(t) +Fi(t+δt)]δt✁2.
∴ vi(t+δt) =vi(t) + 1
2mi
[Fi(t) +Fi(t+δt)]δt. (2.28)
As Eqs. (2.18) e (2.28) formam um novo algoritmo conhecido como algoritmo velocity Verlet [43]:
ri(t+δt) = ri(t) +vi(t)δt+
1 2mi
Fi(t)δt2
vi(t+δt) =vi(t) +
1 2mi
[Fi(t) +Fi(t+δt)]δt.
(2.29)
O algoritmo velocity Verlet, Eqs. (2.29), é equivalente ao algoritmo de Verlet original, Eqs. (2.24), e produz as mesmas trajetórias. Só que ele envolve duas fases com uma avaliação das forças (aceleração) entre elas. Assim, para um passo de tempo
r(t),v(t),a(t) → r(t+δt),v(t +δt),a(t +δt), podemos codificar esse algoritmo da seguinte forma:
inicialização para N passos:
%atualiza metade do passo de tempo das velocidades:
vi(t+δt
2) =vi(t) + 1 2mi
Fi(t)δt
%atualiza um passo de tempo completo das posições:
ri(t+δt) =ri(t) +vi(t+1
2δt)δt %calcula novas acelerações/forças.
%atualiza metade do passo de tempo das velocidades:
vi(t+δt) =vi(t+δt
2) + 1 2mi
Fi(t+δt)δt
A estabilidade numérica, conveniência e simplicidade fazem do algoritmo ve-locity Verlet uma atraente ferramenta para estudos de simulação MD. Vários outros esquemas têm sido propostos na literatura, como o algoritmo leap-frog [44, 45] e o algoritmo de Beeman [46] . Todos eles têm a mesma precisão e devem reproduzir os
mesmos resultados.
2.3
Conservação de Energia
Podemos fazer o esquema de integração numérica do algoritmo velocity Verlet de maneira mais formal e provar que ele é simplético, ou seja, conserva a dinâmica Hamiltoniana.
2.3.1
Propriedade Simplética
O estado de um sistema clássico, a qualquer instante de tempo, também pode ser determinado através da especificação de um conjunto completo de posições e momentos de seus átomos. Alternativamente, podemos coletar todo o conjunto de posições e momentos em um único vetor X = (r1, . . . ,rN;p1, . . . ,pN), chamado de vetor espaço de fase. Um estado clássico de um sistema corresponde a um único ponto do espaço
de fase. O espaço de fase é, assim, a união de todos os possíveis estados clássicos de um sistema. Podemos escreverX na forma matricial:
X=
r
p
. (2.30)
Usando as equações de Hamilton na Eq. (2.30) obtemos:
˙
X=
0 1
−1 0
∂H
∂X. (2.31)
Ou, usando uma forma mais compacta2,
˙
X=M ∂H
∂X, (2.32)
2.3. Conservação de Energia Capítulo 2. Dinâmica Molecular
temos anotação simplética das equações de Hamilton. Podemos dizer que a Eq. (2.32)
é uma transformação canônica, seM e a matriz jacobiana J obedecem:
M=J†MJ
. (2.33)
A Eq. (2.33) é conhecida como propriedade simplética. Se essa propriedade for
obe-decida, o integrador numérico exibe o resultado correto das propriedades do sistema. Assim, ele é dito simplético3.
2.3.2
Das Equações de Hamilton ao Algoritmo Velocity Verlet
Podemos escrever as equações de Hamilton, Eqs. (2.13) e (2.14), em termos das coordenadas generalizadas (q = q1, q2, ..., qN) e momentos generalizados (p =
q1, q2, ..., qN):
˙
qα =
pα
mα
= ∂H
∂pα
,
(2.34) ˙
pα =Fα=−
∂H ∂qα
.
Agora, vamos escrever a evolução temporal de um vetor espaço de fase4,
Γ(q, p), em
queq e p dependem do tempo: dΓ(p, q)
dt = 3N X α=1 ∂Γ ∂qα ˙
qα+
∂Γ ∂pα ˙ pα , (2.35) = 3N X α=1 ∂Γ ∂qα ∂H ∂pα −
∂Γ ∂pα ∂H ∂qα , (2.36)
= [Γ,H]q,p, (colchete de Poisson) (2.37)
≡ iLΓ. (2.38)
OndeL é o operador de Liouville, definido por:
iL= 3N X α=1 ∂ ∂qα ∂H ∂pα −
∂ ∂pα ∂H ∂qα . (2.39)
3No Apêndice A.2 mostramos que o algoritmo velocity Verlet satisfaz a propriedade simplética. 4Nessa nova notação escrevemos o espaço de fase
Da Eq. (2.38) obtemos para os vetores do espaço de fase:
dΓ
dt =iLΓ, (2.40)
dΓ
Γ =iLdt, (2.41)
ln
Γ Γ0
=iLt, (2.42)
Γ =eiLtΓ0. (2.43)
Ou,
q(t)
p(t)
=eiLt
q0
p0
. (2.44)
A Eq. (2.44) mostra como o sistema evolui ao longo do tempo usando o operador de Liouville.
Encontrada a fórmula da evolução temporal, o objetivo agora é conseguir criar um regime de propagação com um passo de tempo discreto∆t em vez de t. Podemos
escrever o operador de Liouville como a soma de dois operadores independentes:
iL= N X α=1 ∂H ∂pα ∂ ∂qα − N X α=1 ∂H ∂qα ∂ ∂pα . (2.45)
Se considerarmos agora as equações de Hamilton, Eqs. (2.34), obtemos:
iL= N X α=1 pα mα ∂ ∂qα − N X α=1 Fα ∂ ∂pα , (2.46) ou
iL=iL1 +iL2. (2.47)
Em geral, iL1 eiL2 não comutam 5. Isto significa que,
eiLt=eiL1t+iL2t
6
=eiL1teiL2t , (2.48)