DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL PROGRAMA DE PÓS
-
GRADUAÇÃO EM FÍSICAE
VOLUÇÃO DA EXCENTRICIDADE DOS SISTEMAS
BINÁRIOS COM COMPONENTE EVOLUÍDA
.
F
LODOALDO DE
L
IMA
S
IMÕES
N
ETO
NATAL
-
RN
E
VOLUÇÃO DA EXCENTRICIDADE DOS SISTEMAS
BINÁRIOS COM COMPONENTE EVOLUÍDA
.
Dissertação de Mestrado apresentada ao Programa de
Pós-Graduação em Física do Departamento de Física Teórica e Expe-rimental da Universidade Federal do Rio Grande do Norte como requisito parcial para a obtenção do grau demestreem Física.
Orientador: José Dias do Nascimento Júnior
NATAL
-
RN
• A minha família, pelo amor incondicional e por sempre acreditar e me apoiar em todas as minhas escolhas;
• Ao Prof. José Dias do Nascimento Júnior, pela orientação durante este trabalho; • A todos os professores do DFTE que contribuiram de forma direta ou indireta para
a minha formação acadêmica;
• Ao colega Jefferson Soares que me ajudou em vários momentos da iniciação cientí-fica e também durante a construção deste trabalho;
• Aos vários colegas que dividiram a sala Mário Schenberg e ajudaram a manter um ambiente agradável nas horas do café;
• As colegas Crislane Souza, Juliana Cerqueira e Noélia, cujo companherismo e várias horas de estudo foram fundamentais para enfrentar (e vencer) as disciplinas obri-gatórias da pós-graduação;
• Aos professores José Ronaldo Pereira da Silva (UERN) e José Renan de Medeiros (DFTE/UFRN), pelas correções e sugestões, que contribuiram para o melhoramento deste trabalho;
• Ao grupo de astrofísica;
• Aos funcionários da PPG-Física, DFTE e CCET; • À CAPES, pelo apoio financeiro.
por
Flodoaldo de Lima Simões Neto
Resumo
No presente estudo, é revisitada a teoria que prevê a circularização por efeito da maré dos sistemas binários, contendo componente evoluída. Tais sistemas sofrem inter-ações gravitacionais que tendem a sincronizar o período orbital com o perído de rotação e tornar as órbitas circulares (Zahn 1977, 1989, 1992). Seguindo a teoria de Zahn, foi cal-culada, neste trabalho, a integral que descreve a variação da excentricidade em um sis-tema binário sob a influência da força de maré e foram comparados os resultados teóricos das integrais com observações recentes para 260 sistemas binários com elementos orbitais publicados. Os resultados descritos aqui confirmam por um lado o sucesso da teoria Zahn, sob a luz dos novos dados e novos modelos evolutivos e, por outro, aponta para a neces-sidade de uma melhor descrição do papel da convecção nessa teoria.
by
Flodoaldo De Lima Simões Neto
Abstract
On this study we have revisited the predicted tidal circularization theory in close binary systems with a evolved component. Close binaries suffer tidal interactions that tend to synchronize periods and circularize the orbits (Zahn 1977, 1989, 1992). According to Zahn’s theory we compute the integral that give us the variation of the eccentricity in a binary under the influence of tidal force and we compare the integral results with new observations for 260 binary systems with orbital solutions. Our results confirm the success of the Zahn’s theory with a new data and new stellar evolutionary models, on the other hand, our results points to the need for a better description of the role of convection on this theory.
2.1 Órbita individual de cada estrela de um sistema binário e a órbita relativa do sistema. O semi-eixo maior da órbita relativa de M1 em torno de M2 é a soma dos semi-eixos das órbitas de cada estrela em volta do centro de massa (C.M.). Os índices 1 e 2 referem-se às estrelas primária e secundária,
respectivamente. . . 5 2.2 Para uma normal n inclinada com relação ao plano orbital a um ângulo i
em relação a linha de visão do observador, então a velocidade de rotação projetada é v sini. . . 7 2.3 A geometria de Roche, mostrando as superfícies equipotenciais em um
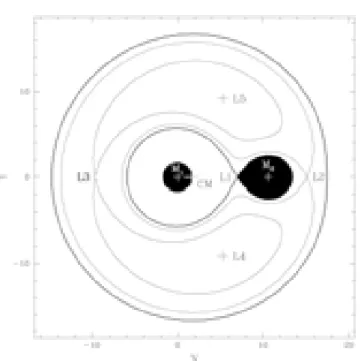
sis-tema binário. Quando nenhuma das componentes,M2 ouM1, preenche o interior do contorno mostrado (Lóbulo de Roche), o sistema não está tro-cando massa. Quando uma das componentes evoluiu e expandiu o sufi-ciente para preencher seu Lóbulo de Roche, o material flui através L1 (o primeiro ponto de Lagrange) para a outra estrela. Quando ambos os lóbu-los são preenchidos, é provável que no sistema de contato ocorra mistura entre os materiais das componentes. Envoltórios comuns transbordam em ambos os lóbulos, e o material traportado que passa de L2 pode deixar o sis-tema, geralmente levando momentum angular. (Fonte da figura: Barblan et. al (1998)) . . . 12
1.3M⊙( Figuras retiradas do livroStellar Structure and EvolutionRudolf
Kip-penhahn & Alfred Weigert, 1994) . . . 14
3.1 Representação das protuberâncias de maré em um sistema binário. A região escura representa a deformação devido a interação gravitacional entre as componentes. . . 16 3.2 Torques na componente primária do sistema binário. O circulo a esquerda
é a componente primária do sistema binário e o ponto a direita representa a componente secundária (figura retirada do artigotidal dissipation in binary system, Zahn em 2008). . . 18
4.1 Diagrama H-R contendo todas as estrelas encontradas na literatura. Os cir-culos abertos representam as estrelas binárias que não foram consideradas nesse trabalho por estar na sequência principal, os círculos pretos repre-sentam estrelas estudadas e são consideradas evoluídas e os triângulos são estrelas que ainda não possuem todos os dados necessários para o estudo da evolução da ecentricidade. . . 27 4.2 Diagrama H-R contendo todas as estrelas estudadas neste trabalho com os
erros da temperatura e da luminosidade. . . 28 4.3 Evolução da profundidade do envoltório convectivo (em massa)
represen-tado em função do logaritmo temperatura efetiva. Os traços representam respectivamente as massas: 1.0M⊙ (linha sólida), 1.2M⊙ (pontos), 1.5 M⊙
(traço curto), 2.0 M⊙ (traço longo), 2.5 M⊙ (pontos - traço curto), 3.0 M⊙
(pontos - traço longo) e 4.0M⊙(traço curto - traço longo). Nesta figura os
círculos abertos representam os valores da Mzc das componentes primárias das estrelas binárias. Os traçados foram calculados para [Fe/H] = 0.. . . 30
5.1 A excentricidade dos sistemas binários em função do logarítmo do período orbital para todos os sistemas binários descritos na tabela. Os pontos fecha-dos representam as componentes primárias fecha-dos sistemas binários. Os val-ores são provenientes de diversos autval-ores, como mostra a tabela A e B (en-contradas no apêndice) . . . 33
foi calculado comf = 1. Os pontos fechados representam as componentes
primárias dos sistemas binários com componente evoluída.. . . 35 5.3 Figura da evolução teórica prevista da taxa de excentricidade versus a
ex-centricidade obtida por métodos observacionais. Para essa figura utiliza-se os valores dos envoltórios convectivos emf′
= M Menv
2/3
α
2
4/3
. Os pontos fechados representam as componentes primárias dos sistemas binários com componente evoluída. . . 36 5.4 Figura de comparação entre o resultado teórico e observacional,
normali-zado. No eixo X é mostrada a referência da estrela na base apresentada
nesse trabalho. Para todas as componentes primárias, comf = 1. . . 37
5.5 Figura de comparação entre o resultado teórico e observacional, normali-zado. No eixo X é mostrada a referência da estrela na base apresentada
nesse trabalho. Para essa figura utiliza-se os valores dos envoltórios con-vectivos, comf′
=MM
env 2/3
α
2
4/3
. . . 38
1 Introdução 1
2 Propriedades dos sistemas binários 4
2.1 Parâmetros orbitais dos sistemas binários . . . 4
2.1.1 Semi-eixo maior. . . 5
2.1.2 A excentricidade orbital . . . 5
2.1.3 O período orbital . . . 6
2.1.4 O tempo de passagem pelo periastro. . . 6
2.1.5 Inclinação da órbitai . . . 6
2.1.6 Velocidade de rotação projetada . . . 6
2.2 Leis de Kepler . . . 7
2.3 Parâmetros estelares . . . 8
2.3.1 Temperatura efetiva (Tef f) . . . 8
2.3.2 Luminosidade (L) . . . 9
2.3.3 Sistemas de magnitudes . . . 9
2.3.4 Tipo espectral . . . 10
2.4 Classificação dos sistemas binários . . . 10
2.4.3 Classificação do segundo estado evolutivo . . . 13 2.5 Envoltório convectivo . . . 13
3 Aspectos teóricos dos efeitos de maré 15
3.1 Teoria de Marés . . . 16 3.2 Evolução da excentricidade orbital via forças de maré . . . 17 3.2.1 O Valor da integralI(t) . . . 24
4 Dados observacionais das estrelas binárias com componente evoluída 25
4.1 Os modelos evolutivos e estatus evolutivo . . . 25 4.2 A profundidade do envoltório convectivo . . . 27
5 Resultados e discussões 31
5.1 Período e excentricidade nos sistemas binários . . . 31 5.2 Evolução da excentricidade devido as forças de maré . . . 32
6 Perspectivas 40
A Tabela 42
B Constantes físicas e astronômicas 58
INTRODUÇÃO
"A mente crédula (...) experimenta um grande prazer em acreditar em coisas es-tranhas, e quanto mais estranhas forem, mais facilmente serão aceitas; mas nunca leva em consideração as coisas simples e plausíveis, pois todo mundo pode acreditar nelas."
Samuel Butler,Characters(1667-9)
Estrelas binárias são pares de estrelas unidas por uma força de atração gravita-cional e em órbita em torno de um centro de massa comum às duas componentes. As ob-servações astronômicas estimam que 60 - 70%das estrelas em nossa Galáxia fazem parte de sistemas binários ou múltiplos1. Além dessa grande frequência, as estrelas binárias
fornecem parâmetros fundamentais, como a massa e raios das componentes, com maior precisão e guardam importantes características da sua formação. Portanto é importante determinar as propriedades desses sistemas e assim entender melhor um dos principais componentes de nossa Galáxia.
Os primeiros pares de estrelas duplas já eram observadas há pelo menos 3 séculos. Por volta de 1775, William Herschel começou a catalogar estrelas duplas. Grande parte dos astrônomos desse período supunham que todas as estrelas possuíam o mesmo brilho
1Um sistema múltiplo contém 3 ou mais estrelas ligadas por força gravitacional
intrínseco e, portanto, pares com brilho bastante diferentes deveriam estar distantes. Em 1804, Herschel confirmou a teoria2proposta por John Michell (1767), que muitas dessas
es-trelas possuíam vínculos físicos entre elas (órbitas elípticas como previstas pela gravitação de Newton), e para diferenciá-las das estrelas duplas as nomeou de estrelas binárias.
O filho de Herschel continuou a catalogar as estrelas duplas e atualmente, devido ao trabalho de vários pesquisadores, o número atual de sistemas binários tem crescido ano após ano. No entanto, atualmente ainda existem poucas estrelas com seus elementos orbitais completamente determinados.
As primeiras binárias astrométricas catalogadas foram Sirius e Procyon e o movi-mento senoidal delas foi traçado por Friedrich Wilhelm Bessel, por volta de 1844. A primeira binária espectroscópica catalogada foi a componente de maior brilho do sistema Mizar, em 1889 por Antonia C. Maury em Harvard. Ela reconheceu a linha de absorção Ca II K (cálcio ionizado), que se dividia em duas componentes, com separação variável. No mesmo ano, H.C. Vogel reportou mudanças periódicas no comprimento de onda do es-pectro da estrela Algol, mostrando ser um sistema binário eses-pectroscópico de linha única. As bases físicas do estudo evolutivo estelar foram desenvolvidas inicialmente por Gamow (1939), quando foi descoberto que as gigantes vermelhas representam uma fase de evolução, em que o combustível para a fusão do hidrogênio se esgota no centro da estrela. Dessa forma a vida na sequência principal de uma estrela é proporcional à quan-tidade deste combustível (em massa) dividido pela respectiva taxa de consumo (lumi-nosidade), levando a uma relação de tempo de vida na sequência principal de aproxi-madamente1010anos(M/M
⊙)
−2,5. Para os sistemas binários o estudo segue a mesma base desenvolvida para estrelas simples.
Em 1953, Otto Struve identificou o paradoxo de Algol. Esse paradoxo consiste no fato de que um número considerável de sistemas binários, a maioria eclipsantes (ex.: Algol), é composto por uma estrela mais evoluída (uma gigante vermelha) que também é a estrela menos massiva. Gerard P. Kuiper, em 1941, sugeriu que poderia haver trans-ferência de massa entre as componentes unidas (lóbulos de Roche) dos sistemas binários. Atualmente o estudo dos sistemas binários é composto por um grande número de com-plexos fenômenos astrofísicos.
Um dos importantes aspectos da evolução dos sistemas binários é sua evolução dinâmica devido à força de maré. É esse fenômeno que atua sobre a estrela causando a
circularização da órbita e modificando os parâmetros do sistema. Nos dias atuais aborda-se o problema da interação entre as componentes, mais especificamente baaborda-seado na teoria de maré desenvolvida por Jahn Paul Zahn e colaboradores (1966, 1977, 1989 e 1992). A deformação de uma estrela binária deve-se à atração gravitacional de sua companheira que induz uma mudança de fase dos bojos de maré. A distribuição assimétrica da massa exerce um torque sobre a estrela, levando a uma troca de momentum angular entre a sua rotação e movimento orbital, como veremos nos capítulos seguintes.
Sistemas binários espectroscópicos mostram uma transição crítica entre órbitas circulares e com períodos curtos e órbitas excêntricas com longo períodos. De maneira geal, o período orbital (Porb) cresce com a idade nas estrelas da sequência principal. Essas
observações são explicadas por interações dissipativas de maré. A teoria de marés em equilíbrio supõe equilíbrio hidrostático instantâneo e atribui a dissipação da energia aos movimentos convectivos turbulentos no interior da estrela (Zahn 1966, 1977).
A teoria foi confirmada e calibrada por Verbunt & Phinney (1995) através do es-tudo comparativo com estrelas binárias contendo uma gigante vermelha. O período pred-ito para a transição de estrelas binárias do tipo Solar com idades da ordem de1010anosé Pcirc = 2dias (Goodman & Oh, 1997). Devido à grande influência do mecanismo de cir-cularização pela força de maré, existe uma grande discrepância entre as observações e a teoria.
O objetivo principal nesta dissertação é aplicar a teoria de Zahn para estrelas evoluídas com diferentes profundidades de envoltório convectivo. Para este objetivo foi construída uma base composta por 260 sistemas binários para os quais conhecemos os parâmetros orbitais do sistema (excentricidade e período orbital) e os parâmetros funda-mentais evolutivos (massa das componentes, luminosidade, temperatura efetiva, idade e profundidade da zona convectiva).
PROPRIEDADES DOS SISTEMAS BINÁRIOS
"Astronomia incita a alma a olhar para as alturas e nos leva a partir deste mundo para o outro. "
Platão
Neste capítulo serão apresentados importantes parâmetros físicos para o estudo e especificação de um sistema binário. Primeiramente serão abordados os aspectos físicos relativos à órbita e em seguida discutidos os parâmetros relativos ao estado evolutivo das componentes do sistema binário.
2.1
Parâmetros orbitais dos sistemas binários
Nos sistemas binários, as duas estrelas do sistema estão ligadas devido a ação de uma força gravitacional que varia na razão inversa do quadrado da distância entre as componentes, como descrito na Lei da gravitação universal. Cada estrela se move ao longo de uma elipse que tem o centro de massa (C.M.) do sistema em um dos focos.
Para uma completa descrição do movimento orbital de um sistema binário são usados os seguintes parâmetros.
2.1.1
Semi-eixo maior
O semi-eixo maior da órbita, a, determina o comprimento da órbita do sistema binário1. Geometricamente, o semi-eixo maior de um sistema binário é:
b1+b2+d2+d1 =b1+d1+b2+d2 = (a1+a2)2 = 2a. (2.1) ondea1 = b1 +d1 e a2 = b2 +d2. Portanto a = a1 +a2, ondea1 ea2 são os semi-eixos maiores da órbita relativa de uma estrela em relação a outra.
Figura 2.1: Órbita individual de cada estrela de um sistema binário e a órbita relativa do sistema. O semi-eixo maior da órbita relativa deM1 em torno deM2 é a soma dos semi-eixos das órbitas de cada estrela em volta do centro de massa (C.M.). Os índices 1 e 2
referem-se às estrelas primária e secundária, respectivamente.
2.1.2
A excentricidade orbital
A excentricidade, e, da órbita de um sistema binário é um valor compreendido entre 0 e 1, onde 0 representa uma órbita circular e tende a 1 quanto maior for a diferença entre o semi-eixo maior da elipse. Matematicamente a equação que define a excentrici-dade de uma elipse é:
e2 = 1− b
2
a2 (2.2)
Ondebé o semi-eixo menor da elipse. De uma forma geral podemos classificar a
forma da órbita, para sistemas fechados, da seguinte maneira:
Tabela Seção cônica
Excentricidade Seção Cônica e = 0 órbita circular 0 < e < 1 órbita Elíptica e = 1 órbita Parabólica
Para órbitas abertas, no caso de órbitas de asteróides, temose >1e a seção cônica será uma hiperbóla. Mas esse tipo de descrição não é aplicado para sistemas binários.
2.1.3
O período orbital
O período orbital, Porb, é definido como tempo necessário para que as
compo-nentes de um sistema binário percorram toda sua órbita. Esse tempo pode ser de algumas horas para alguns sistemas e até de alguns milhares de anos para outros.
2.1.4
O tempo de passagem pelo periastro
Periastro é o ponto de maior aproximação entre as duas componentes do sistema binário. Para fins observacionais, o tempo de passagem pelo periastro (T) é adotado como
sendo o referencial de partida para a contagem do período orbital.
2.1.5
Inclinação da órbita
i
Representa a inclinação da órbita em relação ao plano da eclíptica (plano em que a componente primária gira em torno da componente secundária). Dependendo do ângulo, a estrela poderá apresentarmovimento aparente progressivo(se0◦
≤ i ≤ 90◦) ou,movimento
aparente retrógrado(se90◦
< i≤180◦).
2.1.6
Velocidade de rotação projetada
como a medida do alargamento Doppler das linhas espectrais de uma estrela e nos dá sua velocidade de rotação a menos de um fator de projeçãosini2.
Figura 2.2: Para uma normalninclinada com relação ao plano orbital a um ânguloi em
relação a linha de visão do observador, então a velocidade de rotação projetada é v sini.
Outra importante observável é a velocidade radial, que é medida espectroscopi-camente devido ao deslocamento das linhas. A partir da velocidade radial, também pode-mos definir os parâmetrosK1eK2(também medida em km s−1) que são assemi-amplitude
da velocidade radialpara as componentes primárias e secundária, repectivamente.
2.2
Leis de Kepler
Com os parâmetros orbitais definidos, podemos descrever geometricamente as órbitas de um sistema binário a partir das três leis de Kepler. Entre 1609 e 1618, Johannes Kepler publicou suas Leis a partir de observações precisas da órbita de Marte, cuidadosa-mente feita por Tycho Brahe. Com base nisso descreveu o formato da órbita dos planetas em volta do Sol como uma elipse (primeira Lei), explicou como os planetas se movem em torno do Sol (segunda Lei) e obteve uma relação entre a extensão da órbita e seu período (terceira Lei).
Historicamente, essas leis representam um importante avanço na Astronomia. Elas permitiram um cálculo muito mais preciso das posições nas tabelas astronômicas
e introduziram um conceito revolucionário: um fenômeno físico pode simplesmente ser descrito por equações matemáticas.
Kepler usou suas leis para descrever órbitas de planetas em torno do Sol, mas essas leis são aplicáveis a qualquer sistema que gira em torno de um centro de massa comum. As leis podem ser descritas da seguinte forma:
• Primeira lei (lei das órbitas): Todos os planetas se movem em órbitas elípticas tendo o sol em um dos focos.
• Segunda lei (lei das áreas): Uma linha unindo qualquer planeta ao Sol varre áreas iguais em períodos de tempo iguais.
• Terceira lei (lei dos períodos): O quadrado do período de qualquer planeta orbitando o Sol é proporcional ao cubo da distância média entre o planeta e o Sol.
2.3
Parâmetros estelares
Trata-se aqui de diversos parâmetros que caracterizam fisicamente as estrelas per-tencentes aos sistemas binários.
2.3.1
Temperatura efetiva (
T
ef f)
A temperatura efetiva (medida na escala Kelvin) descreve a temperatura superfi-cial da estrela. Supondo que a estrela se comporta como umcorpo negro, podemos usar a
lei de Stefan-Boltzmannpara encontrar a temperatura efetiva na superfície da estrela:
Tef f4 =
I σ
1/4
(2.3)
Onde I é a potência emitida por unidade de área e σ é a constante de
2.3.2
Luminosidade (
L
)
A luminosidade descreve a energia total irradiada pela superfície da estrela (em todas as direções e em todos os comprimentos de onda) por unidade de tempo (segundos), assumindo que a estrela é esférica e irradia como um corpo negro. Logo, a luminosidade é definida pela relação:
L= 4πR2σTef f4 (2.4)
Onde R é raio da estrela medido em unidade de raios solares R⊙.
2.3.3
Sistemas de magnitudes
O sistema mais usado é o sistema UBV, desenvolvido por Harold Lester Johnson e William Wilson Morgan em 1951, que define magnitude aparente em três bandas espec-trais: U de ultravioleta, B de blue (azul), e V de visual (amarelo). Essas magnitudes têm seus comprimentos de onda efetivos em 3600 Å, 4200 Å e 5500 Å.
A magnitude aparente de uma estrela mede seu brilho aparente, que depende da distância. Para comparar os brilhos intrínsecos de duas estrelas, usa-se uma medida de brilho que independe da distância. Para isso, é definida a magnitude absoluta (M) como a magnitude teórica que a estrela teria se estivesse a 10 parsecs de um observador na Terra. É descrita pela seguinte relação:
MV =V −5logD(pc) + 5 +Av. (2.5) MB =B−5logD(pc) + 5 +Av. (2.6)
Onde D é a distância do observador até a estrela em parsecs e Av representa a
2.3.4
Tipo espectral
A classificação espectral é feita de acordo com as linhas presentes no espectro da estrela. Essas linhas correspondem às linhas de absorção dos átomos no interior da estrela. Historicamente a sequência de classificação é definida como: O, B, A, F, G, K e M. De uma forma geral, pode-se dizer que:
• Estrela de tipo O: São estrelas que possuem linhas de hidrogênio fracas. São estrelas com azul mais intenso;
• Estrela de tipo B: Possuem linhas intensas de hidrogênio, mas apresentam também linhas de absorção do hélio;
• Estrela de tipo A: Possuem as linhas mais intensas do hidrogênio e não apresentam linhas do hélio;
• Estrela de tipo F: As linhas de elementos mais pesados que o hélio tornam-se inten-sas;
• Estrela de tipo G: As linhas de metais e as linhas de hidrogênio possuem a mesma intensidade;
• Estrela de tipo K: As linhas principais presentes no espectro são de elementos neu-tros;
• Estrela de tipo M: As linhas de moléculas aparecem no espectro.
2.4
Classificação dos sistemas binários
Atualmente os sistemas binários são classificados devido: (a) como eles são des-cobertos e estudados; (b) ao seu estado físico atual; (c) e ao seu estado evolutivo. Em seguida será feito um resumo sobre cada um dos classificadores.
2.4.1
Classificação por método de descobrimento
• Sistemas binários visuais: São sistemas que estão suficientemente separados para se-rem resolvidos por telescópios. Normalmente os períodos são longos (20 a 700 anos). • Sistemas binários astrométricos: São sistemas onde as componentes estão bastante próximas, mostrando apenas uma imagem que muda de orientação com o período orbital ou move-se periodicamente no céu.
• Sistema binário eclipsante: Uma estrela do sistema, periodicamente, passa em frente a sua companheira eclipsando-a parcialmente ou completamente. Então, variando, temporariamente, a luminosidade recebida em nosso referencial.
• Sistemas binários de espectro: São sistemas onde o espectro de uma única imagem mostra duas linhas com duas estrelas de diferentes tipos espectrais. Não há desloca-mento Doppler observado no espectro.
• Sistemas binários espectroscópicos: São sistemas descobertos por efeito Doppler (vari-ação das linhas espectrais) de uma ou das duas componentes do sistema. O efeito Doppler observado é produto de uma combinação da velocidade radial do centro de massa do sistema binário e da variação resultante do movimento orbital de cada componente em torno do centro de massa. Esse movimento é tal que quando uma das estrelas se afasta de nós, apresenta-se um desvio positivo no comprimento de onda das linhas do espectro. E quando a outra componente se aproxima, apresenta um desvio negativo no comprimento de onda das suas linhas espectrais. Os sistemas binários espectroscópicos podem ser subdivididos em: sistema binário espectroscópico de linha única(SB1) onde apenas uma das linhas do espectro do sistema é vista. Sis-tema binário espectroscópico de linha dupla(SB2), onde as duas linhas são distinguíveis. Existem também osSistema binário espectroscópico de linha tripla(SB3) com três linhas observadas. É importante mencionar que a determinação de sistemas binários es-pectroscópicos deve-se aos avanços da astronomia espectroscópica, para medidas confiáveis da velocidade radial das estrelas.
2.4.2
Classificação por estado físico
O limite de Roche é definido como sendo a região do espaço ao redor de uma es-trela, pertencente a um sistema binário, na qual o material orbital está gravitacionalmente vinculado a essa estrela.
Figura 2.3: A geometria de Roche, mostrando as superfícies equipotenciais em um sistema binário. Quando nenhuma das componentes,M2 ouM1, preenche o interior do contorno mostrado (Lóbulo de Roche), o sistema não está trocando massa. Quando uma das com-ponentes evoluiu e expandiu o suficiente para preencher seu Lóbulo de Roche, o material flui através L1 (o primeiro ponto de Lagrange) para a outra estrela. Quando ambos os lóbulos são preenchidos, é provável que no sistema de contato ocorra mistura entre os materiais das componentes. Envoltórios comuns transbordam em ambos os lóbulos, e o material traportado que passa de L2 pode deixar o sistema, geralmente levando momen-tum angular. (Fonte da figura: Barblan et. al (1998))
• Sistemas separados3: Nenhum dos sistemas preenche o limite de Roche.
• Sistema Semi-separado4: Onde um dos limites é preenchido.
• Binárias de contato5: As duas componentes preenchem seus limites de Roche.
2.4.3
Classificação do segundo estado evolutivo
Atribuir ao sistemas binários o seu lugar em um cenário evolutivo é o mais in-certo dos métodos, mas também é aquele que oferece uma compreensão mais física. Essas classes são nomeadas por um protótipo (por exemplo: estrelas Beta Lyrae, variáveis Al-gol e as estrelas V 471 Tauri). Muitas vezes, o protótipo não é muito típico de sua classe. Existem pelo menos 50 classes nominadas na literatura, muitas reconhecidas apenas por especialistas.
2.5
Envoltório convectivo
Segundo a teoria de evolução estelar, após a exaustão do hidrogênio no centro da estrela, acontece a queima do hélio no núcleo, a estrela deixa assim a sequência principal. Para uma estrela com massa da ordem de 1M⊙ há o desenvolvimento da zona
convec-tiva externa após 7,0 x109 anos. Nesta fase a estrutura da estrela passa de menos de 1% convectiva para uma estrela de aproximadamente 80% convectiva.
Dependendo da camada da estrela, a energia pode ser transportada por convecção ou radiação. Nas camadas internas, a energia gerada no interior da estrela é transportada por radiação. Nas camadas mais externas, ocorre a convecção, onde o plasma mais quente é transportado para superfície e o plasma mais frio desce até o fundo da região convectiva. Na figura 2.4 é mostrada a evolução de uma estrela de 1,3 M⊙, na esquerda é
re-presentado o traçado evolutivo calculado por Thomas em 1967. No eixo horizontal temos o logarítmo da temperatura e no eixo vertical o logarítmo da luminosidada. Nesse traçado são indicados momentos evolutivos dessa estrela, onde: A ao C, a estrela segue o ramo da sequência principal; C a D, o ramo das subgigantes; D onde a estrela entra no ramo das gigantes vermelhas.
Ainda na figura 2.4, a direita é mostrada a representação da evolução da região interna da estrela de 1,3 M⊙. Onde o eixo horizontal mostra o tempo de vida da estrela
(em giga anos) e eixo vertical a profundidade (em massa) da estrela. Nota-se que no início da vida da estrela ela é praticamente radiativa (representada pela região tracejada), nesse momento a estrela está queimando o hidrogênio do núcleo.
na figura). Portanto, é observado que para estrelas ditas evoluídas temos uma efetiva zona (ou camada) convectiva superficial.
Muitos fenômenos estão relacionados com as envolvidos nas camadas convecti-vas. Será tratada neste trabalho a influência da evolução da convecção superfical sobre o efeito de maré do ponto de vista evolutivo.
Figura 2.4: A direita: Traço evolutivo de uma estrela de 1.3M⊙, calculado por Thomas
em 1967. A esquerda: A evolução da estrutura interna de uma estrela de 1.3M⊙( Figuras
ASPECTOS TEÓRICOS DOS EFEITOS DE MARÉ
"O estudo das estrelas binárias é a estrada real para nossa compreensão da evolução estelar. "
Henry Norris Russel
Devido a interação gravitacional1 entre as componentes do sistema binário há o
surgimento de protuberâncias na direção da linha que une os seus centros de massa, que são denominadas protuberâncias de maré2. Essa interação que produz as protuberâncias
nas componentes é chamada de efeito de maré3, essas protuberâncias são mostradas na
figura 3.1.
Com o surgimento das protuberâncias de maré, outro fenômeno atua em cada estrela: o torque de maré. Originalmente discutido por Darwin (1879) 4, este fenômeno
modifica o momentum angular das componentes do sistema binário quando a rotação não está sincronizada com o movimento orbital do sistema binário, levando a um estado de sincronização, ou seja, o período orbital é igual ao período rotacional.
1Citando a lei da gravitação universal:Os corpos se atraem na razão direta de suas massas e na razão inversa do quadrado da distância entre
elas.
2Do inglês: tidal bulges. 3Do inglês: Tidal effect
4No contexto do estudo do sistema planeta-satélite
Figura 3.1: Representação das protuberâncias de maré em um sistema binário. A região escura representa a deformação devido a interação gravitacional entre as componentes.
Outro fator resultante da interação de maré é a redução da excentricidade da ór-bita da estrela (ou circularização), pois devido à falta de simetria da órór-bita(e6=0) há vari-ações de energia cinética no movimento orbital das componentes, levando o sistema a estabilizar-se quando a energia cinética for mínima, ou seja, tornando a órbita da estrela circular (excentricidade igual a 0).
Para a análise teórica dos efeitos descritos, deve-se levar em conta a distribuição de massa, a excentricidade, período orbital do sistema binário, além do raio da compo-nente primária.
Neste capítulo, será estudada a circularização5 por efeito de maré, com base na
teoria da circularização desenvolvida por Zahn (1966, 1977, 1989). Testaremos esta teoria para as componentes primárias dos sistemas binários totalmente convectivos (modeliza-ção) e para o sistema cujas componentes dos sistemas possuam diferentes envoltórios convectivos.
3.1
Teoria de Marés
Como já foi discutido, devido à atração gravitacional entre as componentes do sistema binário, há o surgimento de marés nas superfícies das estrelas. A teoria distingue dois tipos de marés: Marés de equilíbrio, que consistem em uma fricção turbulenta, ou seja, a interação entre o movimento convectivo e o fluxo da maré (Zahn, 1966); eMarés dinâmicas, que consistem em um amortecimento radiativo no envoltório radiativo da es-trela (Zahn, 1977).
Em estrelas que possuem uma região convectiva externa, o mecanismo de fricção turbulenta atua com mais intensidade (Zahn, 1989). Essa teoria é confirmada por obser-vações que mostram que a maioria dos sistemas binários próximos, com órbita circular, possui uma componente com envoltório convectivo (Zahn, 1966).
No modelo de Zahn (1966), cada componente possui marés que induzem um atraso de fase do campo externo da força. Isso ocorre por efeito da viscosidade turbu-lenta no envoltório convectivo. Assim, esse desalinhamento dos bojos de maré em relação à linha que une os dois centros de massa irá introduzir um torque resultante entre as com-ponentes. Isso fará com que este torque favoreça uma mudança no momentum angular das componentes individuais, cujos efeitos serão refletidos em uma variação dos elemen-tos orbitais do sistema binário.
Uma importante consideração na teoria de marés é a descrição da distribuição das camadas internas de uma estrela. Esta consideração separa o estudo em dois modelos: os modelos para estrelas do tipo tardio6 (com tipos espectrais F, G, K e M), as quais são
constituídas basicamente de um centro radiativo e um envoltório convectivo, e os modelos para estrelas do tipo precoce7 (com tipos espectrais O, B e A), constituídas de um centro
convectivo e um envoltório radiativo.
3.2
Evolução da excentricidade orbital via forças de maré
Considerando um sistema binário com órbita quase circular com semi-eixo maior
a, períodoPorb e excentricidadee. As forças de maré na estrela primária com massaM1 e raioR1 causadas pela estrela secundária de massaM2, podem ser decompostas em marés estáticas e marés variáveis.
Segundo Phinney (1992), a maré estática distorce o equipotencial da superfície em uma altura aproximada de (M2/M1)(R41/a3), mas como ela é estática não há deslocamento ou dissipação na estrela primária.
Na figura 3.2, é mostrada a representação das forças que atuam sobre os bojos formados na componente primária do sistema binário. OndeM representa a componente
Figura 3.2: Torques na componente primária do sistema binário. O circulo a esquerda é a componente primária do sistema binário e o ponto a direita representa a componente secundária (figura retirada do artigotidal dissipation in binary system, Zahn em 2008).
primária e m a componente secundária, f1 e f2 as forças aplicadas sobre os bojos, α a variação do ângulo da linha que une as duas componentes,Ωo movimento de rotação da estrela primária eω o movimento orbital do sistema. Como as forças aplicadas sobre as
protuberâncias são diferentes o movimento de rotaçãoΩtente a sincronizar com o orbital
ω.
A maré variável é mais facilmente visualizada do ponto de vista de um obser-vador que está na superfície da componente primária do sistema. No curso da órbita, o observador verá a componente secundária variar a uma distância de aproximadamente
±ae. Mas como descrito pela segunda lei de Kepler, a velocidade orbital angular varia
com o inverso quadrado da distância a estrela secundária, enquanto a companheira rota-ciona a uma velocidade constante de 2π/Porb. Assim a estrela secundária oscilará para
frente e para trás por um angulo de≈emedido em referência do céu observado.
Portanto, as marés variáveis proporcionam deslocamentos horizontais e verticais na amplitudeξde:
ξ ≈
M1
M2
r4
a3
e, (3.1)
maior.
ξ varia com a frequência orbital Ωb = 2π/Porb, portanto, a superfície da estrela
primária deve se mover a uma velocidadeu≈Ωbξ, e possuir um gradiente de velocidade:
∇u ≈ Ωbξ/r. (3.2)
Pode-se assumir inicialmente que há uma viscocidade superficial ν diferente de
zero apenas na superfície da estrela de espessuraH e densidade ρ, distância r entre as
componentes. Então a taxa de dissipação viscosa de energia no movimento orientado pela variação da maré é dada pela seguinte equação:
˙
Ediss ≈ 4πr2Hρν|∇u|2. (3.3)
Se a estrela primária for convectiva na superfície, a viscosidade mais importante será a viscosidade superficial, que é:
ν = νsuper ≈HvH, (3.4)
ondevH é a velocidade do movimento do envoltório convectivo. Substituindo a
equação do gradiente da velocidade (3.2) na equação (3.3), tem-se:
˙
Ediss ≈ 4πr2HρνΩ2bξ 2
r2. (3.5)
Usando a equação para viscosidade superficial (3.4):
˙
Ediss ≈ 4πH2ρvHΩ2bξ2. (3.6)
E finalmente usando a variação da amplitude das marés (3.1), na equação (3.6) encontra-se:
˙
Ediss ≈ 4πρvHH2Ω2b
M1
M2
2
r8
a6
e2. (3.7)
angular (conservado durante a evolução da estrela):
Ee = 1
2GM2M1
e2
a. (3.8)
Pode-se relacionar a frequência orbital com as massas das componentes dos sis-temas binário e substituir na equação (3.7). Usando a relação do centro de massa:
M1d1 =M2d2, (3.9)
onde M1 eM2 são, respectivamente, as massas das componentes primárias e se-cundárias ed1ed2 são as distâncias das componentes do sistemas binários até o centro de gravidade. Em um sistema binário, deve haver equilíbrio entre as forças gravitacional e centrífuga para que exista uma órbita estável. Portanto:
GM1M2 (d1+d2)2
=M1d1Ω21 =M2Ω22d2, (3.10)
onde G é a constante gravitacional e Ω1 e Ω2 são as velocidades angulares das componentes primária e secundária, respectivamente.
Para que as duas estrelas permaneçam em fase, ou seja, se mantenham em ve-locidade constante ao centro de gravidade, devemos terΩ1 = Ω2 = Ωb e para que (3.10)
também seja válida, devemos ter as condições mostradas em (3.9), que são as duas estrelas orbitando em torno do centro de massa do sistema. UsandoΩ1 = Ω2 = Ωb:
GM1M2 (d1+d2)2
=M1d1Ω2b. (3.11)
ExplicitandoΩb
Ω2b = GM1M2 (d1+d2)2
1
M1d1
. (3.12)
A relação (3.9) fornece:
M1 =
(M2d2)
d1
SomandoM2 nos dois lados da igualdade:
M1+M2 =M2
d2
d1 + 1
= M2
d1
d2+d1 1
. (3.14)
Que é igual a:
M2
d1
= M1+M2
d1+d2
. (3.15)
Usando a equação (3.15) na equação (3.12):
Ω2 = G(M1+M2) (d1+d2)3
. (3.16)
Com a relação geométrica entre os semi-eixos maiores e a distância de cada com-ponente até o centro de massa do sistema e substituindo na equação anterior, têm-se:
d1+d2 =a. (3.17)
E substituindo na equação (3.16):
Ω2 = G(M1+M2)
(a)3 . (3.18)
Finalmente a taxa de dissipação da energia:
˙
Ediss ≈ 4πρvHH2G(M1+M2)
(a)3
M1 M2 2 r8 a6
e2. (3.19)
FazendodEe/dt=−Ediss˙ e usando (3.8): dEe
dt =
1 2
GM2M1
a 2e
de dt =
GM2M1
a e
de
dt. (3.20)
Calculando a igualdade mostrada anteriormentedEe/dt=−Ediss˙ , obtemos a taxa
de dissipação de energia negativa na equação:
GM2M1
a e
de
dt =−4πρvHH
2G(M1+M2) (a)3
M1 M2 2 r8 a6
Cancelando os termos que aparecem nos dois lados da igualdade e explicitanto a excentricidade:
−1
e de
dt = 4πρvHH
2(M1+M2)
M1M2
M1 M2 2 r8 a8 . (3.22)
Na camada convectiva de uma estrela de luminosidadeL, o fluxoF =L/(4πr2)é transportado por convecção,F ≈ρv3
H. Portanto a frequência da turbulência81/τf turbé:
1
τf turb ≈ vH
H ≈
L
4πr2ρH3
1/3
. (3.23)
Substituindo a equação anterior na equação (3.22), encontra-se que o tempo de circularização é dado por:
1
τc =−
1 e de dt = L
4πr4ρH
1/3
4πρH3
M1
M1+M2
M2 M2 M1 2 r a 8 . (3.24)
A massa da camada viscosa é dada por Mcv = 4πρr2H e pode ser substituindo em (3.24), Phinney (1992) usa a equação anterior e calcula o tempo de circularização para componente primária. Para uma gigante vermelha, Phinney descreve a seguinte equação para a escala de tempoτc na qual a circularização deve ocorrer:
1
τ ≡
dlne
dt (3.25)
= f
L MenvR2
1
1/3
Menv M1
M2
M1
M1 +M2
M1 R a 8 . (3.26)
OndeM1,LeR1 representam, respectivamente, a massa, a luminosidade e o raio da estrela com maré dissipativa (geralmente a maior gigante ou subgigante). Menv é a
massa do envoltório convectivo,M2 é a massa da estrela companheira, ea é o semi-eixo maior da órbita da binária. f é um número adimensional dependente de características
da viscosidade e convecção da estrela. Na seção 5.2 será discutido o valor def.
No artigo de Verbunt e Phinney (1995), a equação para a escala de tempo na qual a circularização ocorre é reescrita como:
1
τc
≡ dlne
dt ≈ −1,7f
Tef f
4500K
4/3
Menv M⊙
2/3
M⊙ M1
M2
M1
M1+M2
M1
R a
8
anos−1.(3.27)
Para encontrar a variação total da excentricade deve-se resolver a equação integral (3.26) para o tempo de vidatda estrela:
∆lne =
Z t
0
dt′
τc(t′). (3.28)
Ao aplicar essas equações em sistemas binários é necessário especificar o sistema estudado. Neste trabalho serão tratados sistemassemi-separadose sistemasseparados.
Para estudar o efeito da circularização em sistemas binários separados, foi reagru-pada a equação (3.27) e (3.28) em partes que são independentes das órbitas e partes onde há influência da força de maré.
I(t) ≡ Z t
0
Tef f(t′
) 4500k
4/3
Menv(t′
)
M⊙
2/3
R(t′
)
R⊙ 8
dt′
. (3.29)
Conforme a evolução da estrela.
Resolvendo a integral da equação (3.27) e fazendo q ∝ M2/M1 e aplicando a ter-ceira lei de Kepler para relacionar o semi-eixo maior a ao período orbital Porb, é
encon-trada:
∆ln(e) = −1,7×10−5f
M1
M⊙ −11/3
q(1 +q)−5/3I(t) (P
orb)
3.2.1
O Valor da integral
I
(
t
)
A integral I(t) é definida pela equação (3.29). Observa-se que o valor dela au-menta com a evolução da estrela, portanto, seu valor pode ser integrado ao longo de traçados evolutivos de estrelas.
Segundo Verbunt (1995), o tratamento analítico é uma boa aproximação paraI(t) por duas razões: é possível fazer boas estimativas com maior velocidade e os traçados evolutivos são normalmente compostos por poucos pontos, impossibilitando assim uma integração numérica direta e algumas vezes os autores não publicam a massa do núcleo ou pontos finais.
Usando a relaçãoL/L⊙ = (Mc/0.16M⊙)7.3, e a equação:
L L⊙
= 4πR 2σT4
4πR2
⊙σT⊙4
= R
R⊙ ≈
T⊙ T
2s
L L⊙
(3.31)
encontramos R/R⊙ = (Mc/0.16M⊙)4.7. Com dt = 0.007c2dMc/Le resolvendo a
integral, têm-se:
I = 7,6×108
R R⊙
6,51
DADOS OBSERVACIONAIS DAS ESTRELAS BINÁRIAS
COM COMPONENTE EVOLUÍDA
"Todo grande progresso da ciência resultou de uma nova audácia da imaginação.".
John Dewey
Com o objetivo de confrontar os resultados do modelo proposto por Zahn (1966) é apresentado neste trabalho uma base de dados composta por 260 sistemas binários com parâmetros orbitais e estruturais determinados. As estrelas selecionadas possuem tipo espectrais de F até K (componente primária). Neste capítulo serão apresentados os mode-los evolutivos utilizados no presente trabalho e as principais características evolutivas e estruturais das estrelas que compõem a base estudada.
4.1
Os modelos evolutivos e estatus evolutivo
Neste trabalho foram utilizados dois conjuntos de modelos evolutivos para o es-tudo dos sistemas binários. Para o diagrama H-R, foram utilizados os traçados de Claret (2004), onde o modelo estelar é calculado para a metalicidade Solar (Z = 0,02eX = 0,70).
As massas estelares calculadas no modelo estão entre 0.8M⊙e 125M⊙. Os modelos foram
calculados desde a pré-sequência principal (PMS) até a exaustão de carbono no núcleo, para as estrelas mais massivas. As temperaturas dos modelos mais massivos foram cor-rigidas para ventos estelares, enquanto os modelos de menor temperatura efetiva são cal-culados usando o tratamento das equações de estado (CEFF1).
Esse modelo fornece informações necessárias para o estudo da evolução de marés para sistemas binários, pois como já foi descrito, a escala de tempo necessária a sincroniza-ção e circularizasincroniza-ção para estrelas depende não somente da massa, raio e temperatura das componentes como também da profundidade do envoltório convectivo.
Uma vez que os modelos de Claret não fornecem a massa do envoltório convec-tivo, foram utilizados os modelos de do Nascimento et al. (2000), calculados a partir do código evolutivo TGEC. Esse modelo fornece uma descrição dos envoltórios convectivos, em função da massa da estrela para massas entre 1.0M⊙ e 4.0M⊙. O método utilizado
para encontrar a massa do envoltório convectivo das componentes primárias do sistema binário será descrito detalhadamente ao longo seção 4.2.
A temperatura efetiva de uma estrela e sua luminosidade possuem uma relação, e essa relação é comumente ilustrada em um diagrama bidimensional chamadodiagrama Hertzsprung-Russel (ou diagrama H-R), onde o eixo vertical representa a luminosidade e o eixo horizontal sua temperatura efetiva (normalmente a temperatura é mostrada em escala logarítmica); por razões históricas a temperatura decresce para direita.
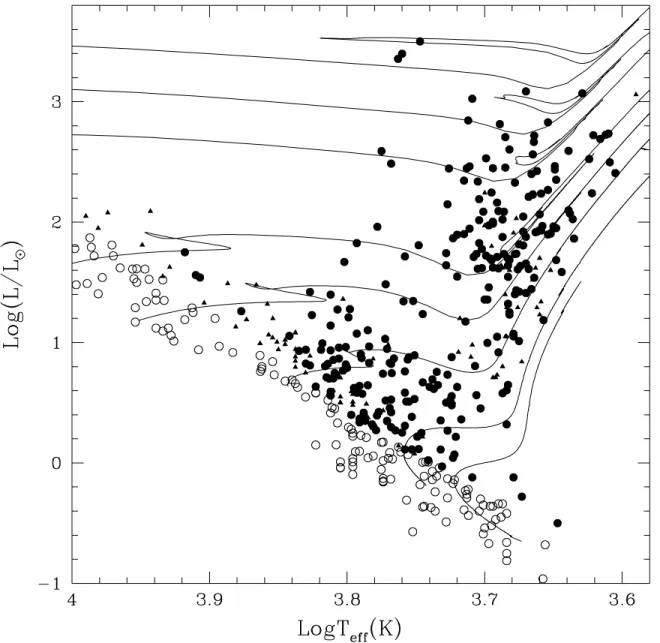
Através dos traços evolutivos é possível estudar o estado evolutivo da compo-nente primária (geralmente a mais brilhante) do sistema binário e também é possível obter os valores teóricos das massas da componente primária. O diagrama H-R com vários sis-temas binários encontrados na literatura está representado na figura 4.1. Nessa figura estão representados o modelos para: 0.8M⊙, 1.0M⊙, 1.49M⊙, 2.0M⊙, 2.51M⊙, 3.98M⊙,
5.01M⊙e 6.31M⊙. Os modelos aqui apresentados foram calculados por Claret (2004). Na
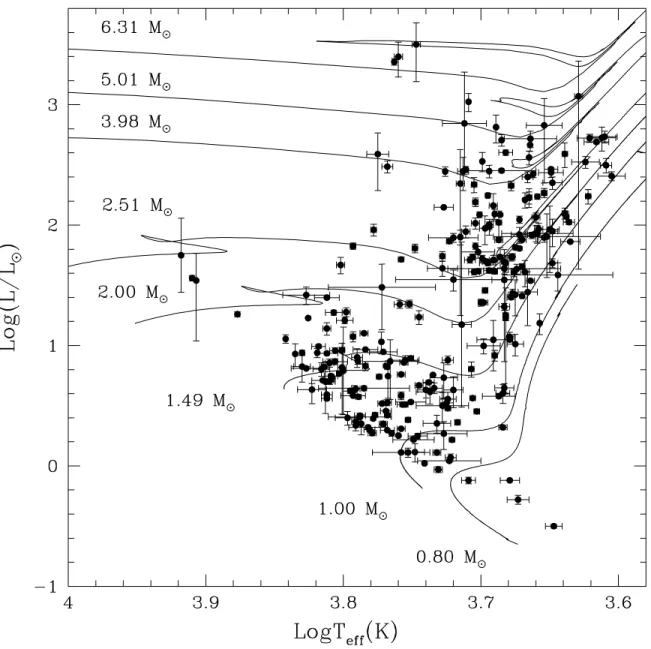
figura 4.2 são apresentadas as 260 componentes primárias selecionadas para este trabalho.
1Em 1973 Eggleton, Faulkner e Flannery definiram a equação de estado EFF, que envolve descrições químicas para o interior das
Figura 4.1: Diagrama H-R contendo todas as estrelas encontradas na literatura. Os cir-culos abertos representam as estrelas binárias que não foram consideradas nesse trabalho por estar na sequência principal, os círculos pretos representam estrelas estudadas e são consideradas evoluídas e os triângulos são estrelas que ainda não possuem todos os dados necessários para o estudo da evolução da ecentricidade.
4.2
A profundidade do envoltório convectivo
Para a determinação da profundidade do envoltório convectivo em função da temperatura efetiva (Tef f) da componente primária e sua massa (M1) utiliza-se uma
Figura 4.2: Diagrama H-R contendo todas as estrelas estudadas neste trabalho com os erros da temperatura e da luminosidade.
do envoltório convectivo em função do logaritmo da temperatura efetiva, com base nos traçados evolutivos calculados por do Nascimento et al. (2000).
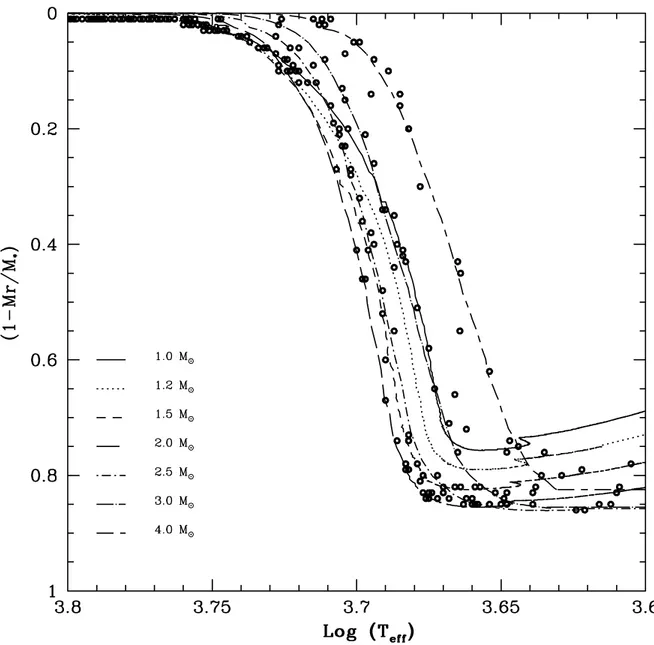
Os valores resultantes estão expostos na tabela B no apêndice deste trabalho. O diagrama obtido com o resultado para todas as componentes primárias, e suas respectivas massas dos envoltórios convectivos (Mzc) é mostrado na figura 4.3.
binárias com componente evoluída está distribuída entre valores de Mzc de aproximada-mente 0.1 (1% convectiva) até valores de Mzc de aproximadaaproximada-mente 0.85 (85% convectiva). Tais valores representam uma larga diferença estrutural, reflexo da evolução ao longo do ramo das gigantes vermelhas (RGB2).
Figura 4.3: Evolução da profundidade do envoltório convectivo (em massa) representado em função do logaritmo temperatura efetiva. Os traços representam respectivamente as massas: 1.0M⊙ (linha sólida), 1.2M⊙ (pontos), 1.5M⊙(traço curto), 2.0M⊙(traço longo),
2.5 M⊙ (pontos - traço curto), 3.0 M⊙ (pontos - traço longo) e 4.0 M⊙(traço curto - traço
RESULTADOS E DISCUSSÕES
"É mais frequente que a confiança seja ger-ada pela ignorância do que pelo conheci-mento: são os que conhecem pouco, e não os que conhecem muito, os que afirmam tão positivamente que este ou aquele problema nunca será solucionado pela ciência. "
Charles Darwin, introdução, The
de-scent of man(1871)
No presente capítulo, serão apresentados os resultados da análise do comporta-mento da excentricidade em função do período orbital e comparado com os valores obti-dos quando utilizamos o formalismo proposto por Zahn (1966, 1977, 1989) e Verbunt & Phinney (1995).
5.1
Período e excentricidade nos sistemas binários
Uma evidência para o processo a longo prazo da circularização pode ser obtida através de uma comparação sistemática entre os valores da excentricidade do sistema binário em função de seu período orbital. Uma importante série de trabalhos descreveu os
aspectos gerais (tratamento estatístico) bem como os aspectos relacionados com questões dinâmicas. Entre outros, é importante citar Alexander (1973), Wilson e Stother (1975), Alladin e Parthasarathy (1978), tais trabalhos relacionados com questões dinâmicas.
Para relacionar os valores das excentricidades dos sistemas binários com seus períodos orbitais, foi utilizado 260 sistemas binários (listados na base encontrada no apen-dice A). Essa amostra possui sistemas binários que vão desde o tipo espectral F até K, e 5 sistemas binários de diferentes tipos espectrais. A amostra estudada foi observada por diferentes configurações instrumentais. O objetivo neste trabalho foi de compor a base mais larga possível e depois restringir ao tipo espectral e classe de luminosidade interes-sada. Deve-se ressaltar que o estudo abordado nesse trabalho é importante, pois com uma amostra completa é possível comparar importantes características de diferentes sistemas binários e diferentes escalas de tempo.
A figura 5.1 mostra a excentricidade dos sistemas binários em função do logarítmo do período orbital. O comportamento encontrado nessa figura é discutido por diversos autores, entre outro podemos citar Mermilliod&Mayor (1992) e Duquennoy et al. (1992). Basicamente é mostrado que a partir de um dado período orbital (aproximadamente um período de 10 dias) as órbitas dos sistemas binários são essencialmente circulares, ou seja, apresentame≤0,2. Para um período orbital longo (Porb≥1000 dias), não existem órbitas
circulares. Na próxima seção serão discutidos os possíveis fatores evolutivos que podem causar uma diminuição da excentricidade.
5.2
Evolução da excentricidade devido as forças de maré
Com o intuito de confrontar os resultados previstos com a teoria de Zahn e o comportamento observacional apresentado na figura 5.1, à luz da metodologia desen-volvida no artigo de Verbunt e Phinney (1995) foram novamente calculadas neste trabalho as equações fundamentais do efeito de maré. Foi utilizada a equação encontrada no capí-tulo 3, que é obtida a partir das equações de Zahn:
∆ln(e) =−1,7×10−5 f
M1
M⊙ −11/3
M1
M2
1 + M1
M2
−5/3
×7,6×108
R R⊙
6,51
Figura 5.1: A excentricidade dos sistemas binários em função do logarítmo do período or-bital para todos os sistemas binários descritos na tabela. Os pontos fechados representam as componentes primárias dos sistemas binários. Os valores são provenientes de diversos autores, como mostra a tabela A e B (encontradas no apêndice)
Os parâmetros estruturais e orbitais utilizados na equação acima foram definidos nos capítulos anteriores. A partir dessa equação foi determinado o valor da evolução da excentricidade dos sistemas binários sobre o tempo de vida da estrela. Os resultados são mostrados nas figuras 5.2 e 5.3.
modelos utilizados para descrever a evolução das componentes dos sistemas binários: o parâmetrof. Esse parâmetro descreve a física da convecção e possui um valor
adimen-sional. Fisicamente o valor def depende da descrição física dos processos convectivos e
viscosos. Zahn (1977) e Verbunt e Phinney (1995) utilizamf = 1(estrela completamente convectiva) para a situação em que o tempo de circularização (τc) for menor que o período
orbital (Porb). No tratamento clássico, Zahn (2008) definef como:
f =
M1
Menv
2/3 α
2
4/3
. (5.2)
Verbunt (1995) estabelece para a equação (3.18) que a Menv ≈ M1 e usa f = 1,01 (α/2)4/3 ondeαé o parâmetro de mistura1. Esse é um parâmetro livre e usado para
calibrar os raios de estrelas evoluídas. Suas características dependem, fundamentalmente, da massa da estrela e algumas outras propriedades. Por ser um parâmetro livre, oα
de-pende do modelo e vários autores usam diferentes valores. Zahn (1989) usa α = 2,0 e
f = 1, ou seja, Zahn fixa a estrela como sendo totalmente convectiva durante todo o ramo
das gigantes vermelha (RGB), tal simplificação não é totalmente verdadeira.
Neste trabalho utiliza-se o código TGEC e o valor de f foi calculado para cada
estrela em função de seu estado evolutivo. Assim, foram calculadas as massas dos en-voltórios convectivos das componentes primárias dos sistemas binários e aplicadas na equação (5.2). Portanto para cada componente primária é encontrado o valor def
indi-vidualmente.
Na figura 5.2 é mostrado o resultado da evolução da excentricidade para f = 1 (caso padrão) e na figura 5.3 apresentamos o resultado da evolução da excentricidade em função do tempo, levando-se em consideração o parâmetrof calculado particularmente
para cada estrela.
Observa-se na figura 5.2 e na figura 5.3 uma aglomeração de estrelas na região que vai de 5 até 0. Estas estrelas já estão circularizadas e a equação da evolução da excentrici-dade (5.1) não influencia de forma significativa na mudança desse conjunto de estrelas. É importante observar que essas duas figuras, de forma geral, concordam com a figura 5.1, e que a abcissa nas figuras 5.2 e 5.3 são resultados da solução numérica da equação 5.1 para os casos:
Figura 5.2: Figura da evolução teórica prevista da taxa de excentricidade versus a excen-tricidade obtida por métodos observacionais. Nessa figura o valor def foi calculado com f = 1. Os pontos fechados representam as componentes primárias dos sistemas binários
com componente evoluída.
Figura 5.3: Figura da evolução teórica prevista da taxa de excentricidade versus a excen-tricidade obtida por métodos observacionais. Para essa figura utiliza-se os valores dos envoltórios convectivos em f′
= M Menv
2/3
α
2
4/3
Figura 5.4: Figura de comparação entre o resultado teórico e observacional, normalizado. No eixoX é mostrada a referência da estrela na base apresentada nesse trabalho. Para
todas as componentes primárias, comf = 1.
Nas figuras 5.4 e 5.5 é apresentada a diferença entre os dois casos calculados. Os valores foram normalizados para uma melhor comparação e análise da diferença entre a evolução prevista da excentricidade para f = 1e a evolução prevista da excentricidade comf variando respectivamente com o valor dos envoltórios convectivos.
Figura 5.5: Figura de comparação entre o resultado teórico e observacional, normalizado. No eixoX é mostrada a referência da estrela na base apresentada nesse trabalho. Para
essa figura utiliza-se os valores dos envoltórios convectivos, comf′
= M Menv
2/3
α
2
4/3
.
em situações muito similares ao obtido quando é calculada com a massa do envoltório convectivo para cada estrela. Portanto não é encontrada uma diferença significativa na distribuição da posição de cada objeto quando compara-se o cálculo comf = 1ouf
PERSPECTIVAS
"Nada é mais digno de nosso patrocínio que o fomento da ciência e da literatura. O conhecimento é, em todo e qualquer país, a base mais segura da felicidade pública."
George Washington, discurso no Con-gresso, 8 de janeiro de 1790.
No presente trabalho, os resultados obtidos mostram que a descrição da evolução da excentricidade com base na teoria de Zahn, para sistemas binários com componentes evoluídas, não leva em conta a evolução da convecção. Tal resultado aponta para a ne-cessidade de um refinamento no que diz respeito a influência evolutiva do envoltório convectivo na evolução da força de maré destes sistemas.
Os sistemas binários pertencentes à sequência principal mostrados por Torres (2010) possuem valores precisos dos parâmetros físicos e podem ser utilizados com vín-culos físicos aos processos evolutivos. No entanto alguns desses sistemas não possuem parâmetros orbitais definidos que são essenciais para o teste da teoria de Zahn. Certa-mente, com a obtenção desses parâmetros poderão ser realizados novos testes para essa teoria.
Para o futuro próximo, será possível enriquecer os resultados obtidos nesse tra-balho com os seguintes pontos:
• Estender esse trabalho para diversos estágios evolutivos ao longo do ramo das gi-gantes vermehas (RGB), com o objetivo de estudar a circularização em vários mo-mentos da evolução estelar;
• Refazer o presente trabalho à medida que mais parâmetros orbitais forem surgindo na literatura;
• Os elementos químicos na superfície nos mostram os vínculos da evolução da con-vecção e desempenham um fator fundamental na evolução estelar, portanto um es-tudo da abundância de elementos leves nas componentes dos sistemas binários é importante para entender a influência do efeito de maré sobre esses elementos e estudar as escalas tempos associados a evolução da excentricidade;
• O estudo do momentum angular dos sistemas binários com componente evoluída, traz a perspectiva de visualizar a influência da convecção na evolução do momen-tum angular.
TABELA
Nas tabelas A e B estão descritos os parâmetros físicos e orbitais necessários para o estudo feito neste trabalho. Para questões comparativas a profundidade do envoltório convectivo foi repetido nas duas tabelas. Os 260 sistemas binários estão descritos da seguinte forma:
Tabela A : Parâmetros físicos das componentes primárias dos sistemas binários.
• Ordem : número estrela na base do trabalho;
• Nome: em HD, número que identifica a estrela no catálogo Henry-Draper; • T.E.: Tipo espectral;
• Magnitude Visual: Brilho visual de uma estrela; • Erro na Magnitude visual;
• B-V: Correção Bolométrica; • Erro na Correção Bolométrica;
• Paralax: Distância da estrela medido por Paralax; • Erro na Paralax;
• Log L: Luminosidade da estrela em escala logarítmica;
• Erro na Luminosidade;
• LogTef f: Temperatura superficial da estrela;
• Erro na Temperatura;
• Mzc: Profundidade do envoltório convectivo (em massa solar).
Tabela B : Parâmetros orbitais e físicos dos sistemas binários.
• Ordem : número estrela na base do trabalho;
• Mzc: Profundidade do envoltório convectivo (em massa solar); • R1: Raio da componente primária (em raio solar);
• M1: Massa da componente primária (em massa solar); • M2: Massa da componente secundária (em massa solar); • Porb: Período orbital (em dias);
• e: excentricidade orbital;
• K1: semi-amplitude da velocidade radial da estrela primária;
• K2: semi-amplitude da velocidade radial da estrela secundária;
A.
Tabela
44
A.
Tabela
45
A.
Tabela
46
A.
Tabela
47
A.
Tabela
48
A.
Tabela
49
A.
Tabela
50
A.
Tabela
51
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
Tabela B: Parâmetros orbitais e físicos dos sistemas binários.
Ref. Nome Mzc RaioR1 M1 M2 Porb e K1 K2 Vsini (R⊙) (M⊙) (M⊙) (dias)
-CONSTANTES FÍSICAS E ASTRONÔMICAS
Constantes físicas e astronômicas usadas no textos estão listadas aqui com seus respectivos valores em unidades S.I.
Constantes físicas
Constante gravitacional = 6,673×10−11N m2/kg2
Constante de Stefan-Boltzmann (σ) = 5,67×10−8W/m2/K4
Constantes astronômicas
Unidade Astronômica = 149 597 871 464 m Parsec = 3,086×1016m
Características Solares
Massa = 1,9884×1030kg Raio = 695,970×106 m
Luminosidade = 3,85×1026W Temperatura efetiva = 5778 K Idade = 4,6×109 anos
Período Rotacional = 25 - 35 dias
Alexander, M. E. The Weak Friction Approximation and Tidal Evolution in Close Binary Systems. Astrophysics and Space Science, vol. 23, ed. 2, pág. 459,1973.
Alladin, S. M.; Parthasarathy, M. Tidal disruption and tidal coalescence in binary stellar systems. Royal Astronomical Society, Monthly Notices, vol. 184, pág. 871,1978.
Barblan, F.; Bartholdi, P.; North, P.; Burki, G.; Olson, E. C. Physical parameters of the Algol system TZ Eridani from simultaneous analysis of Geneva 7-colour light curves. Astronomy and Astrophysics Supplement, vol. 132, pág. 367,1998.
Claret, A. New grids of stellar models including tidal-evolution constants up to car-bon burning. I. From 0.8 to 125 M⊙ at Z=0.02. Astronomy and Astrophysics, vol.424,
pág. 919,2004.
Darwin, G. H. A tidal theory of the evolution of satellites. The Observatory, vol. 3, pág. 79.1879.
do Nascimento, J. D., Jr.; Charbonnel, C.; Lèbre, A.; de Laverny, P.; De Medeiros, J. R. Lithium and rotation on the subgiant branch. II. Theoretical analysis of observations. Astronomy and Astrophysics, vol. 357, pág. 931,2000.
Gamow, G. Physical Possibilities of Stellar Evolution. Physical Review, vol. 55,
sue 8, pág. 718,1939.
Goodman, Jeremy; Oh, Siang Peng. Fast Tides in Slow Stars: The Efficiency of Eddy Viscosity, Astrophysical Journal, vol .486, pág. 403,1997.
Kippenhahn, Rudolf; Weigert, Alfred. Stellar Structure and Evolution. Springer-Verlag Berlin Heidelberg New York, pág. 314,1994.
Mazeh, Tsevi; Goldberg, Dorit; Duquennoy, Antoine; Mayor, Michel. On the mass-ratio distribution of spectroscopic binaries with solar-type primaries. Astrophysical Journal, vol. 401, no. 1, pág. 265,1992.
Phinney, E. S. Pulsars as Probes of Newtonian Dynamical Systems. Philosophical Transactions: Physical Sciences and Engineering, vol. 341, ed. 1660, pág. 39,1992.
Torres, G.; Andersen, J.; Giménez, A. Accurate masses and radii of normal stars: Modern results and applications. Astronomy and Astrophys, pág. 67,2010.
Verbunt, F.; Phinney, E. S. Tidal circularization and the eccentricity of binaries con-taining giant stars. Astronomy and Astrophysics, vol.296, pág. 709,1995.
Wilson, R. E.; Stothers, R. On angular momentum transfer in binary systems. Royal Astronomical Society, Monthly Notices, vol. 170, pág. 497,1975.
Zahn, J. -P. Les marées dans une étoile double serrée (suite et fin). Annales d’Astrophysique, vol. 29, pág. 565,1966.
Zahn, J. -P. Les marées dans une étoile double serrée (suite). Annales d’Astrophysique, vol. 29, pág. 489,1966.
Zahn, J. -P. Les marées dans une étoile double serrée. Annales d’Astrophysique, vol. 29, pág. 313,1966.
vol. 265, no. 1, pág. 115,1992.
Zahn, J.-P. Tidal dissipation in binary systems. EAS Publications Series, vol. 29, pág. 67,2008.
Zahn, J.-P. Tidal evolution of close binary stars. I - Revisiting the theory of the equili-brium tide. Astronomy and Astrophysics, vol. 220, no. 1-2, pág. 112,1989.
Zahn, J.-P. Tidal friction in close binary stars. Astronomy and Astrophysics, vol. 57, no. 3, pág. 383,1977.