PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA APLICADA E ESTATÍSTICA
Daniel de Souza Grilo
Sobre a Integração Indefinida de Funções
Racionais Complexas: teoria e
implementação de algoritmos racionais
Sobre a Integração Indefinida de Funções
Racionais Complexas: teoria e
implementação de algoritmos racionais
Dissertação apresentada ao
Pro-grama de Pós-graduação em
Ma-temática Aplicada e Estatística
da Universidade Federal do Rio
Grande do Norte, para a obtenção
de Título de Mestre em Matemática
Aplicada, na Área de Computação
Algébrica.
Orientador: Nir Cohen
Grilo, Daniel de S.
Sobre a Integração Indefinida de Funções Racionais Complexas: teoria e implementação de algoritmos racio-nais
162 páginas
Dissertação (Mestrado) - Programa de Pós-graduação em Matemática Aplicada e Estatística da Uni-versidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Departamento de Matemá-tica.
1. Integração indefinida
2. Funções racionais
3. Algoritmos
I. Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Departamento de Ma-temática. Programa de Pós-graduação em Matemática Aplicada e Estatística.
Comissão Julgadora:
Prof. Dr. Prof. Dr.
Examinador Interno Examinador Externo
Agradecimentos
À Alma Mater e ao PPgMAE/UFRN que me abençoaram e nutriram tanto com saber quanto com trabalho.
Em seguida, agradeço a todos os mestres que contribuíram para o meu co-nhecimento acadêmico, em especial aqueles que me influenciaram diretamente na elaboração deste trabalho. Nominalmente, os Professores Doutores Nir Cohen, Ed-gar Silva Pereira, Roberto Hugo Bielschowsky, Marcelo Ferreira Siqueira e Vilmar Trevisan.
Agradeço ainda aos coordenadores e vice-coordenadores do PPgMAE/UFRN de todos os tempos, pela disposição nobre em cuidar de um programa de pós-graduação. Uma missão nada trivial. Em especial, agradeço às Professoras Dou-toras Carla Almeida Vivacqua e Elaine Gouvea Pimentel, por todo o suporte dado.
Resumo
Apresentamos algoritmos de integração indefinida de funções racionais sobre subcorpos dos complexos, a partir de uma abordagem algébrica. Estudamos o algoritmo local de Bernoulli e algoritmos racionais de integração para a classe de funções em questão, a saber, os algoritmos de Hermite; Horowitz-Ostrogradsky; Rothstein-Trager e Lazard-Rioboo-Trager. Estudamos também o algoritmo de Ri-oboo para conversão de logaritmos envolvendo extensões complexas para funções arco tangente reais, quando estes logaritmos surgem da integração de funções racionais com coeficientes reais. Concluímos fornecendo pseudocódigos e códigos para implementação no software Maxima relativos aos algoritmos estudados neste trabalho, e, além disso, a algoritmos para cálculo de mdc de polinômios; decompo-sição em frações parciais; fatoração livres de quadrados; cálculo de subresultantes, entre outros algoritmos acessórios ao trabalho. Será também apresentado no apêndice o algoritmo de Zeilberger-Almkvist para integração de funções hiperex-ponenciais, bem como seu pseudocódigo e código para Maxima. Como alternativa aos algoritmos de Rothstein-Trager e Lazard-Rioboo-Trager, apresentamos ainda um código para o algoritmo de Bernoulli para denominadores livres de quadrados; e outro para o algoritmo de Czichowski, ainda que este não seja estudado em detalhes no trabalho, devido às bases teóricas necessárias para o seu entendimento, as quais se encontram fora do escopo deste trabalho.
Diversos exemplos são fornecidos de modo a demonstrar o o funcionamento dos algoritmos de integração deste trabalho.
Abstract
We present indefinite integration algorithms for rational functions over sub-fields of the complex numbers, through an algebraic approach. We study the local algorithm of Bernoulli and rational algorithms for the class of functions in concern, namely, the algorithms of Hermite; Horowitz-Ostrogradsky; Rothstein-Trager and Lazard-Rioboo-Trager. We also study the algorithm of Rioboo for conversion of logarithms involving complex extensions into real arctangent functions, when these logarithms arise from the integration of rational functions with real coef-ficients. We conclude presenting pseudocodes and codes for implementation in the software Maxima concerning the algorithms studied in this work, as well as to algorithms for polynomial gcd computation; partial fraction decomposition; squarefree factorization; subresultant computation, among other side algorithms for the work. We also present the algorithm of Zeilberger-Almkvist for integration of hyperexpontential functions, as well as its pseudocode and code for Maxima. As an alternative for the algorithms of Rothstein-Trager and Lazard-Rioboo-Trager, we yet present a code for BenoulliŠs algorithm for square-free denominators; and another for CzichowskiŠs algorithm, although this one is not studied in detail in the present work, due to the theoretical basis necessary to understand it, which is beyond this workŠs scope.
Several examples are provided in order to illustrate the working of the inte-gration algorithms in this text
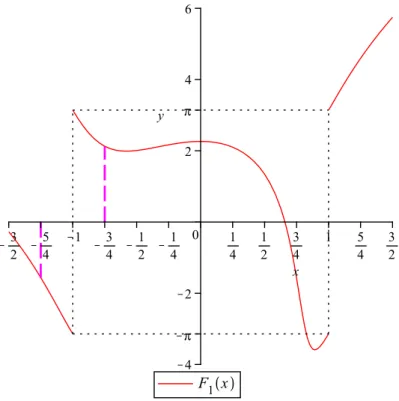
4.1 Gráfico de � próximo do intervalo [⊗5/4,⊗3/4]. . . 68
4.2 Gráfico da forma descontínua de ∫� =�1(�). . . 70
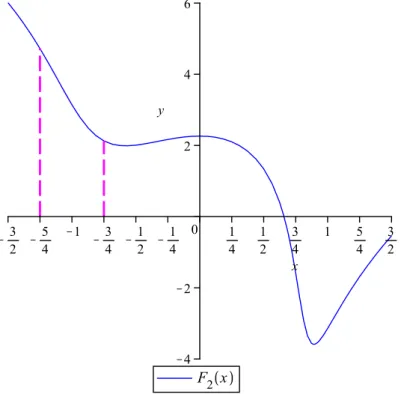
4.3 Gráfico de ∫� =�2(�). . . 72
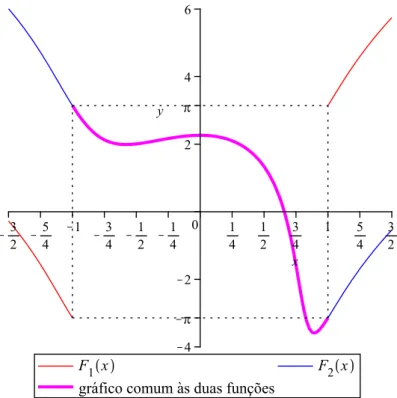
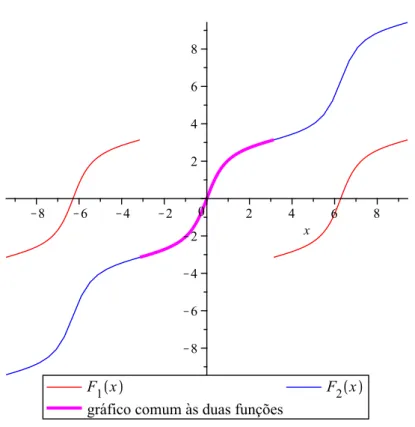
4.4 Comparação das formas contínua e descontínua de∫�. . . 73
1 Introdução 1
1.1 Motivação e Objetivos do Trabalho . . . 1
1.2 Histórico do Problema Abordado . . . 2
1.3 Visão Geral dos Capítulos e Seções . . . 6
1.4 Esclarecimentos Acerca do Presente Texto . . . 8
2 Noções Preliminares 11 2.1 Resultantes e Sequências de Restos Polinomiais . . . 11
2.1.1 Resultantes e Subresultantes . . . 11
2.1.2 Sequências de Restos Polinomiais . . . 15
2.2 Fatoração Livre de Quadrados . . . 18
3 Integração Indefinida de Funções Racionais Complexas 25 3.1 O Algoritmo de Bernoulli . . . 25
3.1.1 Exemplos . . . 28
3.2 O Algoritmo de Hermite . . . 29
3.2.1 Versão Original do Algoritmo de Hermite . . . 29
3.2.2 Versão Quadrática do Algoritmo de Hermite . . . 30
3.2.3 Versão Linear do Algoritmo de Hermite . . . 31
3.2.4 Exemplos . . . 33
3.3 O Algoritmo de Horowitz-Ostrogradsky . . . 36
3.3.1 Exemplos . . . 38
3.4 O Algoritmo de Rothstein-Trager . . . 39
3.4.1 Exemplos . . . 47
3.5.1 Exemplos . . . 54
4 Integração Indefinida de Funções Racionais Reais 59 4.1 O Algoritmo de Rioboo para Funções Racionais Reais . . . 60
4.1.1 Exemplos . . . 67
5 Pseudocódigos e Códigos em Maxima 79 5.1 Funções para Manipulação de Polinômios . . . 80
5.1.1 Group . . . 80
5.1.2 LC . . . 81
5.1.3 Mon . . . 81
5.1.4 Parts . . . 82
5.1.5 RPoly . . . 82
5.2 MDC de Polinômios e Resultantes . . . 83
5.2.1 PDiv . . . 83
5.2.2 PPsDiv . . . 84
5.2.3 GCD . . . 85
5.2.4 ExGCD . . . 86
5.2.5 HExGCD . . . 87
5.2.6 HFExGCD . . . 88
5.2.7 DioExGCD . . . 88
5.2.8 DioHExGCD . . . 89
5.2.9 DioHFExGCD . . . 90
5.2.10 SubRes. . . 91
5.2.11 Normalize . . . 93
5.3 Fatorações e Frações Parciais . . . 94
5.3.1 LFactor . . . 94
5.3.2 SQFR . . . 94
5.3.3 PFrac . . . 96
5.4 Hermite e Horowitz . . . 97
5.4.1 HermO. . . 97
5.4.2 HermQ. . . 98
5.4.4 HorOstro . . . 101
5.5 Logaritmos . . . 102
5.5.1 Bern . . . 102
5.5.2 RothTra . . . 105
5.5.3 LaRiTra . . . 106
5.5.4 Czi . . . 108
5.6 Conversão Real . . . 110
5.6.1 Classic . . . 110
5.6.2 Rioboo . . . 110
5.6.3 Rioboo2 . . . 111
5.7 Manipuladores de Extensões Algébricas . . . 112
5.7.1 NoSolve . . . 112
5.7.2 DomSolve . . . 113
5.7.3 LinSolve . . . 113
5.7.4 QuadSolve . . . 114
5.7.5 CubeSolve . . . 114
5.7.6 Solve . . . 115
5.7.7 RHS . . . 117
5.7.8 SolveSys . . . 117
5.7.9 Extensions . . . 118
5.7.10 VerifyRatSols . . . 118
5.8 Montagem de Integrais de Funções Racionais . . . 119
5.8.1 RealLog . . . 119
5.8.2 ComplLog . . . 121
5.8.3 InertLog . . . 123
5.8.4 GenList . . . 124
5.8.5 IRF . . . 125
6 Considerações Finais 131 6.1 A Integração de Funções Elementares . . . 131
6.2 O Cenário da Computação Algébrica . . . 132
6.3 Referências em Computação Algébrica . . . 133
Introdução
1.1
Motivação e Objetivos do Trabalho
O problema da integração indefinida de funções é, como conhecemos, aquele de encontrar uma função cuja derivada seja precisamente aquela função que se integra. Por isto, este também é chamado de problema da antiderivação. O primeiro contato que se tem com este problema geralmente se dá durante os cursos de Cálculo. Nesta ocasião, o estudante, via de regra, é apresentado a diversas técnicas de integração que, na maior parte das vezes, necessitam de uma medida de intuição e heurística para que possam ser utilizadas de maneira apropriada. Não raro, o processo de integração acaba por depender fortemente de uma mudança de variável adequada, ou se resume à detecção de algum padrão do integrando que indique qual expressão dentro de uma tabela de integrais é a solução do problema.
Porém, quando queremos automatizar processos com eficiência através de implementações em máquinas, apesar de podermos desenvolver códigos heurísticos, o mais desejável é que se busque por algoritmos de terminação finita que não contem com recursos que seriam próprios do uso da razão, e que possam ser bem delimitados por um conjunto finito de tarefas sequenciadas.
A intenção é expor uma teoria introdutória sobre o problema (e resolução) da integração indefinida de funções à luz da Computação Algébrica, utilizando algo-ritmos que são usados ainda hoje em diversos Sistemas de Computação Algébrica (doravante CAS Ů do inglês, Computer Algebra System). A resolução
algorít-mica do problema da integração de funções racionais é o ponto de partida para se entender como buscar uma solução, nas mesmas condições, para o problema mais geral da integração de funções elementares Ů uma classe de funções que engloba o conjunto das funções racionais.
Os algoritmos abordados neste trabalho, com exceção do algoritmo de Ber-noulli, são classificados como algoritmosracionais, no sentido de que, no curso de sua execução, não requerem fatorações completas do denominador do integrando e evitam introduções de constantes algébricas desnecessárias à resolução do pro-blema, tanto na representação final da integral, quanto durante os cálculos. Além disso, a base de seu funcionamento são as operações de corpo, isto é, as quatro operações aritméticas básicas aplicadas, neste contexto, a polinômios. Isto é per-cebido de maneira muito forte nos constantes cálculos de mdc entre polinômios que serão realizados.
O desenvolvimento teórico do presente trabalho baseia-se em conceitos da teoria de Álgebra Abstrata. No que concerne a esta teoria, o que for omitido aqui poderá ser encontrado entre os capítulos de I a IV, VII e IX de [16].
1.2
Histórico do Problema Abordado
Segundo M. Ostrogradsky [26], tanto Newton quanto Leibniz tentaram desenvol-ver métodos de integração indefinida para funções racionais reais, sem obterem êxito completo. A abordagem utilizada por Leibniz consistia em fatorar o de-nominador do integrando sobre os reais, realizar a decomposição completa em frações parciais e integrar parcela a parcela. Ele obteve sucesso em calcular a integral de quaisquer termos com denominadores lineares (a menos de uma po-tência) na decomposição em frações parciais, mas não conseguiu o mesmo para os denominadores quadráticos de maneira completa.
Acta Eruditorum de 1703, o que se acredita ser o algoritmo de terminação finita mais antigo para a integração de funções racionais de que se tem registro [21, Cap. IX, p. 353], o qual é lecionado ainda hoje em grande parte dos cursos de Cálculo. Infelizmente, este método, apesar de bastante simples, apresenta uma dificul-dade computacional proibitiva, que acaba por fazer com que, na prática, ele não seja utilizado com frequência. A dificuldade em questão é a necessidade de se saber a fatoração completa do denominador do integrando sobre os reais (o que, não raro, pode recorrer a expressões envolvendo muitas extensões algébricas) e decompor o integrando em frações parciais completas com esta dada fatoração (o que requer muitas operações aritméticas envolvendo diversos termos algébricos distintos). Por outro lado, além de uma importância histórica, este método possui uma importância teórica que motiva o seu estudo. Ele é capaz de explicitar a integral de uma função racional com coeficientes reais como sendo a soma en-tre uma parte racional real Ů uma função racional real que dispensa quaisquer extensões algébricas com unidade imaginária Ů, e outra parte transcendental real Ů formada por somas de logaritmos e arcos tangentes de polinômios com coeficientes reais. Desse modo, a integral de uma função racional real obtida pelo método de Bernoulli é ainda contínua no intervalo de definição do integrando, de modo que o Teorema Fundamental do Cálculo pode ser aplicado corretamente para o cálculo da integral definida da função original, qualquer que seja o inter-valo de integração. O método possui ainda uma variante para funções racionais com coeficientes complexos em geral, em qual caso, a parte racional vem a ser ainda uma função racional complexa e a parte transcendental pode ser expressa apenas como uma combinação linear com coeficientes complexos de logaritmos de polinômios com coeficientes complexos.
o método expressa a parte transcendental como sendo a integral não calculada de um novo integrando racional completamente determinado e cujo denominador é livre de quadrados (dito de outro modo, todas as suas raízes possuem multipli-cidade 1). Este era o método ensinado nas escolas russas naquela época e está presente em textos de Análise russos mais antigos [10, Cap. VIII, ğ2]. Foi redes-coberto por E. Horowitz no século XX, que também apresentou detalhadamente um estudo sobre a sua complexidade [13], razão pela qual o método recebe, hoje, o nome de algoritmo de Horowitz-Ostrogradsky.
Porém, no restante do mundo, outros métodos foram descobertos e ensinados. Um método notável também descoberto no século XIX é o algoritmo de Hermite. Foi publicado em 1872 [12].
Essencialmente, tanto o método de Ostrogradsky quanto o método de Her-mite produzem os mesmos resultados. A diferença é que o primeiro condiciona o problema da integração à resolução de um sistema linear para explicitar tanto a parte racional quanto o integrando da parte transcendental, enquanto o segundo, originalmente, utiliza fatorações livres de quadrados do denominador, decomposi-ção em frações parciais do integrando e a resoludecomposi-ção de uma equadecomposi-ção diofantina de polinômios para Şretirar partesŤ do integrando a cada passo e construir a parte a parte racional sucessivamente, deixando aquilo que não pode ser ŞretiradoŤ para formar o integrando da parte transcendental (este processo ocasiona suces-sivas reduções de potência do denominador de cada parcela das frações parciais, razão pela qual o método de Hermite é chamado de redução). O modo como cada algoritmo trabalha reflete apenas na forma final da expressão, mas não na validade.
Duas melhorias podem ser feitas ao método de Hermite. A primeira dispensa a necessidade de se decompor o integrando em frações parciais e é conhecida como versão quadrática do método de Hermite. A segunda dispensa ainda a necessidade prévia de se conhecer a fatoração livre de quadrados do denominador Ů esta é calculada a cada passo do processo Ů, sendo conhecida como versão linear do mesmo método e foi proposta por D. Mack [22]. Tais nomenclaturas derivam da própria complexidade destas versões [2, Cap. 2, ğ2]. Mantêm, contudo, o caráter de redução.
completas do denominador e calculem de maneira satisfatória a parte racional da integral utilizando somente operações de corpo (isto é, sem introduzir novas extensões algébricas no corpo de constantes, nem introduzindo funções transcen-dentais como logaritmos ou arcos tangentes), eles não são capazes de resolver definitivamente o problema da integração indefinida de funções racionais, uma vez que só são capazes de fornecer a parte transcendental da integral em termos de um novo integrando racional. O problema da integração indefinida da parte transcendental sem fatoração completa permaneceria em aberto por mais de um século e só viria a ser resolvido recentemente. Em registro, o primeiro método para a integração da parte transcendental sem fazer uso de fatorações completas do denominador do integrando foi descoberto de maneira independente por M. Rothstein [31] e B. Trager [34]. A proposta deste método é descobrir o menor número de extensões que deve ser feita ao corpo de constantes original do inte-grando, de modo que a integral possa ser expressa como uma combinação linear de logaritmos de polinômios cujos coeficientes (tanto da combinação quanto dos polinômios) pertencem à nova extensão. Uma vez descobertas as extensões neces-sárias (as quais são as raízes de um polinômio obtido por cálculo de resultantes), os polinômios que aparecem como argumentos dos logaritmos são determinados por cálculos de mdc a partir das extensões.
Uma melhoria ao método de Rothstein-Trager foi descoberta e publicada por D. Lazard e R. Rioboo [17] e, de maneira independente, também por Trager, apesar de ele não tê-la publicado formalmente [11, Cap. 11, ğ5]. A ideia por trás desta melhoria Ů conhecida como algoritmo de Lazard-Rioboo-Trager Ů é utilizar subresultantes para calcular de modo quase direto os argumentos que aparecem nos logaritmos da parte transcendental, dispensando cálculos de mdc envolvendo novas constantes algébricas.
Em 1995, uma alternativa aos métodos de Rothstein-Trager e Lazard-Rioboo-Trager utilizando bases de Gröbner seria proposta por Czichowski [9].
por exemplo, quando a integral possui extensões complexas. Felizmente, em con-formidade com o próprio algoritmo e Bernoulli, Rioboo mostrou em [28] um método para expressar a integral de uma função racional com coeficientes reais como sendo também uma função com coeficientes reais, utilizando, tanto quanto possível, somente operações de corpo e, se necessário, anexando minimamente extensões reais ao corpo de constantes. Tanto quanto o método de Bernoulli, o processo não gera novas singularidades (denominadores polinomiais não constan-tes), o que significa que integral encontrada é, ainda, contínua no intervalo de definição do integrando original. A ideia é agrupar pares conjugados de logaritmos complexos que apareçam na expressão complexa da integral e convertê-los em uma combinação linear envolvendo um logaritmo e funções arcos tangentes, onde os argumentos de cada parcela são polinômios e todos os coeficientes na expressão são reais. Obtemos, novamente, uma função contínua no intervalo de definição do integrando e, dessa forma, também é possível calcular a integral definida de uma função racional de maneira correta, sem recorrer a métodos aproximativos, e sim utilizando de maneira direta o Teorema Fundamental do Cálculo, do mesmo modo que no algoritmo de Bernoulli.
O ponto importante de se combinar os algoritmos racionais mencionados é que, do mesmo modo como comparamos os algoritmos de Hermite e Horowitz, o resultado final é essencialmente o mesmo do algoritmo de Bernoulli, tanto no caso de integração de funções com coeficientes complexos, quanto no caso de funções com coeficientes estritamente reais, porém a forma deste resultado costuma ser consideravelmente mais simples, se comparada àquela fornecida pelo método de Bernoulli.
1.3
Visão Geral dos Capítulos e Seções
com operações de corpo para obter os resultados desejados. Além de estarmos interessados em resultados mais simples, a razão para isto reside no fato de querermos diminuir a complexidade dos algoritmos, mas isto não será tratado com detalhes neste texto Ů nosso foco será demonstrar como os métodos funcionam, e não analisar seu desempenho.
No capítulo2, estudaremos brevemente conceitos envolvendo resultantes, sequên-cias de restos de polinômios e fatorações livres de quadrados. Apesar destes conteú-dos estarem presentes em certos textos de Álgebra, não são comumente estudaconteú-dos, de modo que sua exposição é razoável no presente texto. São fundamentais para embasar teoricamente os capítulos posteriores.
No capítulo 3 apresentaremos os algoritmos racionais e não heurísticos para a integração de funções racionais. Como introdução, apresentaremos o algoritmo de Bernoulli. Em seguida, estudaremos os algoritmos de Hermite; de Horowitz-Ostrogradsky; de Rothstein-Trager; e Lazard-Rioboo-Trager. Optamos por omitir uma apresentação detalhada do algoritmo de Czichowski devido à demanda teórica para o seu entendimento.
Complementando o terceiro capítulo, o capítulo4 será dedicado ao problema da integração definida de funções racionais com coeficientes reais, onde explicita-remos o algoritmo clássico e o algoritmo de Rioboo para conversão de logaritmos complexos em uma combinação de funções arco tangente envolvendo apenas extensões reais, conforme mencionado na seção 1.2.
Apresentaremos, no capítulo 5, códigos para implementação no software Ma-xima (software livre copyleft do CAS pioneiro Macsyma) que possibilitam a
construção de um programa para integração de funções racionais sobre subcorpos dos complexos. Os principais são baseados em pseudocódigos presentes em [2, Caps. 1, 2], os quais também são apresentados juntamente com seus respectivos códigos no presente trabalho. Aqui, também apresentaremos um código para o algoritmo de Czichowksi.
no capítulo 5.
Ao longo do trabalho serão apresentados exemplos que ilustram o funciona-mento dos algoritmos de integração e dos códigos fornecidos no capítulo5.
No apêndice A, apresentaremos o algoritmo de Zeilberger-Almkvist para a integração de funções hiperexponenciais. Trata-se de um algoritmo aplicado a funções cuja derivada logarítmica seja uma função racional e que é sempre capaz de encontrar a integral de uma função dessa forma quando a mesma pode ser expressa como um múltiplo racional seu. Dentre outras classes de funções, pode ser aplicado a funções racionais, mas diferente dos demais algoritmos estudados, este nem sempre é capaz de obter uma solução para esta classe de funções. Além de apresentar este algoritmo, também forneceremos os pseudocódigos e os códigos para implementação em Maxima relativos ao mesmo.
1.4
Esclarecimentos Acerca do Presente Texto
Antes de prosseguirmos, alguns esclarecimentos são válidos.
1. A sigla ŞDFUŤ indica Şdomínio de fatoração únicaŤ. A função cont(�) indica o conteúdo do polinômio �, isto é, o mdc de seus coeficientes, enquanto que pp(�) indica a parte primitiva, definida como sendo �/cont(�). cl(�) indica o coeficiente líder do polinômio �, isto é, o coeficiente (não nulo) do termo �grau(p) em �. A função pquo(�,�) indica o pseudoquociente da
pseudodivisão de � por �, enquanto prem(�,�) indica o pseudo-resto da mesma pseudodivisão, isto é, equivalem respectivamente ao quociente e resto da divisão de cl(�)δ+1� por �, onde Ó = max(
⊗1,grau(�)⊗grau(�)). Note que pquo(�,�) e prem(�,�) são polinômios cujo domínio de coeficientes é o mesmo que o de � e � não sendo necessário recorrer a um corpo de frações, caso o domínio original não seja um. Subscritos �como em ppx, clx, contx
e premx irão indicar que os argumentos destas funções serão tratados como
polinômios na variável �.
2. � é a unidade imaginária, isto é, �2 =⊗1.
de uma multiplicação por elemento do corpo de coeficientes, ou seja, apenas o grau e a relação entre os coeficientes é importante. Isto quer dizer que a expressão � = mdc(�,�), por exemplo, indica que � é um dos possíveis mdc para � e �.
4. Dados dois polinômios � e �, estes são ditos primos entre si, relativa-mente primos, ou coprimos, se grau(mdc(�,�)) = 0. Uma fração redu-zida é aquela em que o numerador e o denominador são primos entre si. Uma fração própria é aquela em que o grau do numerador é menor que o grau do denominador.
5. Não estamos interessados nos valores dos logaritmos que aparecem durante este trabalho, mas nas suas propriedades algébricas. Isto quer dizer que, sempre que o leitor se deparar com um logaritmo complexo, poderá fixar qualquer valor para o mesmo, dentro do conceito de ramos de um logaritmo complexo. Além disso, como a variável de integração será sempre complexa, não utilizaremos o valor absoluto sobre o argumento dos logaritmos na integral, ficando implícita a existência de uma parte real e outra imaginária na fórmula da integral. Por outro lado, caso se deseje uma resposta para uma variável de integração real, supondo que o integrando seja uma função racional com coeficientes reais, poderemos, da mesma forma, empregar os algoritmos aqui estudados e simplesmente substituir os argumentos dos logaritmos pelos seus valores absolutos no final.
6. Quando quer que haja denominadores mônicos, estaremos supondo que o nu-merador e o denominador da fração tenha sido multiplicado pelo inverso do coeficiente líder do denominador para efeitos de simplificação dos cálculos.
7. Os exemplos apresentados seguirão a notação dos códigos e pseudocódigos apresentados no capítulo 5.
Noções Preliminares
2.1
Resultantes e Sequências de Restos
Polino-miais
2.1.1
Resultantes e Subresultantes
Estudamos agora as resultantes e subresultantes. A resultante ente dois polinômios é uma ferramenta que auxilia na detecção de seus fatores comuns, ou mesmo na detecção de raízes comuns entre os mesmos que estejam no fecho algébrico do corpo de constantes dos polinômios. As subresultantes de um par de polinômios, por sua vez, possuem uma relação especial com qualquer sequência de restos polinomiais gerada por este par e possuem uma importante propriedade algébrica envolvendo homomorfismos sobre anéis de polinômios induzidos a partir do anel de coeficientes em questão. Utilizaremos os conceitos de resultante e subresultante ao estudarmos os algoritmos de Rothstein-Trager e Lazard-Rioboo-Trager.
Definição 2.1.1. Seja � um anel comutativo e �,� ∈ �[�]\ ¶0♢. Escrevamos
� = �m�m +≤ ≤ ≤�1�+�0 e � =�n�n+≤ ≤ ≤�1�+�0, onde �m ̸= 0, �n ̸= 0 e pelo
�(�,�) = ⎛ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁
�m ≤ ≤ ≤ ≤ ≤ ≤ ≤ ≤ ≤ �1 �0
...
�m ≤ ≤ ≤ ≤ ≤ ≤ ≤ ≤ ≤ �1 �0
�n ≤ ≤ ≤ �1 �0
... ...
...
�n ≤ ≤ ≤ �1 �0
︀ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︂ ︀ ⎫ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ n linhas ⎫ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ m linhas
onde as �-linhas são repetidas � vezes e as �-linhas são repetidas � vezes. A resultante entre � e � é o determinante de �(�,�) e é indicada por res(�,�).
A seguir, enunciamos alguma propriedades algébricas das resultantes.
Lema 2.1.1 ([11], Cap. 9, ğ5). Sejam� um anel comutativo, �,� ∈�[�] polinô-mios de graus � e � respectivamente e �∈� não nulo.
1. res(�,�) = �n;
2. res(�,�) = 0;
3. res(�,�) = (⊗1)mnres(�,�);
4. res(��,�) =�nres(�,�);
5. res(�k�,�) = �k
0res(�,�) para � >0, onde �0 é o termo independente de �;
Lema 2.1.2 ([15] Cap. IV ğ8, [11] Cap. 9 ğ5). Sejam � um anel comutativo, Ð1, . . . ,Ðm,Ñ1, . . . ,Ñn�,�∈� com� ̸= 0,� ̸= 0, e polinômios �=�(�⊗Ð1)≤ ≤ ≤(�⊗
Ðm) e �=�(�⊗Ñ1)≤ ≤ ≤(�⊗Ñn) em �[�]. Então,
res(�,�) =�n�m
m ︁ i=1 n ︁ j=1
(Ði⊗Ñj) = �n m
︁
i=1
�(Ði) = (⊗1)mn�m n
︁
j=1
�(Ñj).
Corolário 2.1.1 ([15] Cap. IV ğ8). Suponha que � seja um domínio de
integri-dade. Seja � o corpo quociente de � e � o fecho algébrico de �. Então, dados
quaisquer �,� ∈�[�]\ ¶0♢,
res(�,�) = 0⇐⇒ ∃Ò ∈� tal que �(Ò) =�(Ò) = 0.
O Corolário 2.1.1 acima nos diz que dois polinômios em um domínio de integridade � possuem raízes comuns no fecho algébrico do corpo quociente de � se e só se a resultante entre eles é nula.
Proposição 2.1.1 ([15] Cap. IV ğ8). Seja � um anel comutativo. Para quais-quer �,� ∈ �[�] de grau positivo, existem à,á ∈ �[�], com grau(à) < grau(�) e
grau(á)<grau(�) tais que res(�,�) = à�+á �.
Em outras palavras, o Proposição 2.1.1 nos diz que a resultante de dois po-linômios se encontra no ideal gerado por estes. Consequentemente, se � é um DFU, então a resultante de dois polinômios em �é nula se e só estes se possuem um fator comum não trivial. Formalmente temos o resultado abaixo.
Corolário 2.1.2 (Critério de Sylvester, [11] Cap. 7 ğ3, [2] Cap. 1 ğ4). Suponha que � seja um DFU. Então, dados quaisquer �,� ∈�[�]⊗ ¶0♢,
res(�,�) = 0⇐⇒grau(mdc(�,�))>0.
Apresentamos agora as subresultantes, que são polinômios obtidos a partir de submatrizes da matriz de Sylvester. Sua definição formal segue abaixo.
Definição 2.1.2. Sejam � um anel comutativo, �,� ∈�[�]\ ¶0♢, �= grau(�),
� = grau(�), � a matriz de Sylvester de � e �, e � um inteiro tal que 0 ⊘ � < min(�,�). Seja j� a matriz �+�⊗2� por �+� obtida deletando-se de �:
1. as linhas de �⊗� + 1 até � (i.e. as � últimas linhas correspondentes a �),
2. as linhas de �+�⊗� + 1 até �+� (i.e. as � últimas linhas de �).
Além disso, para 0 ⊘ � ⊘ � seja j�i a matriz quadrada obtida deletando-se as
coluna �+�⊗�⊗�. A �-ésima subresultante de � e � é definida por
�j(�,�) = j
︁
i=0
det(j�i)�i ∈�[�].
É evidente que grau(�j(�,�)) ⊘ � para cada �. Quando �j(�,�)< � dizemos
que�j(�,�) édefectiva, eregular em caso contrário. Além disso,0�0 =�, donde
�0(�,�) = res(�,�).
Encerrando esta subseção, explicitamos o seguinte resultado a respeito das su-bresultantes (e, consequentemente, das resultantes), o qual revela uma importante propriedade sobre as mesmas.
Proposição 2.1.2 ([23] ğ7.8). Sejam � e � anéis comutativos, à : � ⊃ � um
homomorfismo de anéis, à:�[�]⊃�[�]o homomorfismo de anéis de polinômios
induzido por à, isto é, satisfazendo
à︁︁�j�j
︁
=︁
à(�j)�j, (2.1)
e �,� ∈�[�]\ ¶0♢. Se grau(à(�)) = grau(�) então
à(�j(�,�)) =à(cl(�))grau(q)⊗grau(σ(q))�j(à(�),à(�))
para 0⊘� <min(grau(�),grau(à(�)).
Em outras palavas, a Proposição 2.1.2 nos fornece um modo de calcular �j(à(�), à(�)) a partir de �j(�,�), quando pelo menos um dos coeficientes
lí-deres de � ou � não é levado em 0. Ainda, se o homomorfismo à não diminui o grau de � e de �, isto é, grau(à(�)) = grau(�) e grau(à(�)) = grau(�), ou se ambos � e� são mônicos, então as subresultantes �j(�,�), na verdade, comutam
com o homomorfismoà. Ou seja, passamos a ter:
à(�j(�,�)) =�j(à(�),à(�))
teremos o homomorfismo à :K[�]⊃K(Ð) que é a identidade sobre K⊖Ce leva � emÐ, e mostraremos que, para calcular as subresultantes�j(�,�⊗Ð�)∈K(Ð)[�],
onde �,�,�∈K[�] e Ð é uma extensão algébrica sobreK, podemos simplesmente calcular �j(�,�⊗��)∈K[�][�] e utilizar
�j(�,�⊗Ð�) = �j(�,�⊗à(�)�) =à(�j(�,�⊗��)),
evitando, assim, cálculos sobre extensões algébricas do corpo de constantes K para se obter �j(�,�⊗Ð�).
2.1.2
Sequências de Restos Polinomiais
Nesta seção, estudamos as sequências de restos polinomiais, que generalizam o algoritmo de Euclides para o cálculo de mdc. Nosso principal objetivo será de-senvolver um método eficiente para o cálculo de resultantes e subresultantes. Ao longo desta seção, � será um domínio de integridade.
Definição 2.1.3. Sejam �,� ∈ �[�] com � ̸= 0 e grau(�) ⊙ grau(�). Uma Sequência de Restos Polinomiais (SRP)para�e �é uma sequência(�i)i⊙0
em �[�] satisfazendo
1. �0 =�, �1 =�,
2. Para �⊙1,
Ñi�i+1 =
⎧ ︁ ︁ ︁ ︁
0 se �i = 0
prem(�i⊗1,�i) se �i ̸= 0
onde (Ñi)i⊙1 é uma sequência de elementos não nulos de �.
Pela definição de SRP, é evidente que �i+1 = 0 ou grau(�i+1)<grau(�i) para
�⊙1. Portanto, uma SRP sempre possui uma quantidade finita de elementos não nulos, e se �i ̸= 0, �j ̸= 0, grau(�i) = grau(�j) e �,� ⊙1, então � =�. Em outras
palavras o grau é estritamente decrescente na sequência, de modo que só �0 e�1
A escolha de diferentes Ñi na Definição 2.1.3 origina tipos diferentes de SRP.
A SRP euclidiana é obtida tomando-seÑi = 1 para todo�, e é simplesmente a
sequência de pseudo-restos sucessivos de�e�, obtidos de modo semelhante ao que teríamos no algoritmo de Euclides em um domínio euclidiano. Outro exemplo de SRP é aSRP primitiva, obtida quando definimosÑi = cont(prem(�i⊗1,�i))∈�.
Definição 2.1.4. Sejam�,� ∈�[�]. Dizemos que�ésemelhantea�se existem
Ð,Ñ ∈�\ ¶0♢ tais que Ð� =Ñ�.
A similaridade é uma relação de equivalência. O seguinte resultado aponta para o fato importante de que, se � é um DFU, então o último elemento não nulo de uma SRP do par �,� ∈�[�] é semelhante a mdc(�,�).
Proposição 2.1.3 ([2] Cap. 1 ğ5). Suponha que � seja um DFU e sejam �,� ∈ �[�] com � ̸= 0 e grau(�) ⊙ grau(�). Seja (�0,�1, . . . ,�k,0, . . .) uma SRP
qualquer de � e � com �k ̸= 0. Então mdc(�i,�i+1) é semelhante a mdc(�j,�j+1)
para quaisquer 0⊘�,� ⊘�. Em particular (fazendo �= 0, � =�), temos que �k é
semelhante a mdc(�,�).
Portanto, toda SRP de � e � contém mdc(�,�) (a menos de um elemento multiplicativo pertecente ao domínio de coeficientes).
Dada uma SRP qualquer de � e �, o teorema abaixo mostra que toda su-bresultante não nula de � e � é semelhante a algum elemento da SRP e traz fórmulas explicitas para os coeficientes de similaridade, isto é, mostra como as subresultantes de� e � podem ser recuperadas a partir de qualquer SRP gerada por �e �.
Teorema 2.1.1 (Teorema Fundamental das SRP, [11] Cap. 7 ğ3, [27]). Sejam
� e � ̸= 0 polinômios em �[�] com grau(�)⊙ grau(�), e seja (�0,�1, . . . ,�k,0. . .)
uma SRP de � e � com �k ̸= 0. Para � = 1, . . . ,�, sejam �i = grau(�i) e �i o
coeficiente líder de �i. Então, para qualquer � em ¶0, . . . ,grau(�)⊗1♢,
�j(�,�) =
⎧ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁
Öi�i se � =�i⊗1 ⊗1,
ái�i se � =�i,
onde
Öi = (⊗1)φi�i1⊗⊗1ni⊗1+ni
i⊗1 ︁ j=1 ︀ ︀ ︀ ⎛ ︁ Ñj
�l+nj⊗1⊗nj j
︀ ︀
1+nj⊗ni⊗1
�nj⊗1⊗nj+1
j
︀ ⎥ ︀
ái = (⊗1)σi�nii⊗1⊗ni⊗1 i⊗1 ︁ j=1 ︀ ︀ ⎛ ︁ Ñj
�l+nj⊗1⊗nj j
︀ ︀
nj⊗ni
�nj⊗1⊗nj+1
j
︀
︀ (2.2)
e
ãi = i⊗1
︁
j=1
(�j⊗�i⊗1+ 1)(�j⊗1⊗�i⊗1+ 1), ài = i⊗1
︁
j=1
(�j⊗1⊗�i)(�j ⊗�i). (2.3)
A SRP das subresultantes de � e � é uma SRP que satisfaz Öi = 1 no
teorema anterior. É obtida através das seguintes regras de recursão:
�0 =�, �1 =�, Ó1 =⊗1, Ñ1 = (⊗1)γ1+1
e ⎧
︁ ︁
Ói+1 = (⊗cl(�i))γiÓi1⊗γi
Ñi+1 =⊗cl(�i)Óγi+1i+1
para � ⊙ 1, onde Òi = grau(�i⊗1)⊗grau(�i). Sua propriedade principal é dada
pelo seguinte resultado.
Teorema 2.1.2 ([4] ğ7, [7,27]). Sejam � e � polinômios em �[�]com grau(�)⊙ grau(�) e (�0,�1, . . . ,�k,0, . . .) a SRP das subresultantes de � e �, com �k ̸= 0 e
�i = grau(�i) para�= 1, . . . ,�. Então,
∀� ∈ ¶0, . . . ,grau(�)⊗1♢, �j(�,�) =
⎧ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁ ︁
�i se � =�i⊗1⊗1
ái�i se � =�i
0 caso contrário
onde ái é dado pela fórmula 2.2.
de � e �, temos que se grau(�k) > 0 então � e � possuem um fator comum, de
modo que res(�,�) = 0. Senão, pelo Teorema 2.1.2 temos que �0(�,�) = �k se
grau(�k⊗1) = 1, ou �0(�,�) = ák�k, se grau(�k⊗1) > 1. No segundo caso, como
Ök= 0, o cálculo de ák fica simplificado, pois 2.3 se torna
àk = k⊗1
︁
j=1
�j⊗1�j
e, portanto,
(⊗1)σk = k⊗1
︁
j=1
(⊗1)nj⊗1nj
No produto acima, um fator ⊗1 so aparece se ambos �j⊗1 e �j forem ímpares.
Além disso, como grau(�k) = 0, �k =�k e a equação 2.2 se torna
ák = (⊗1)σk� nk⊗1⊗1
k
k⊗1
︁
j=1
︀ ︀
⎛ ︁
Ñj
�l+nj⊗1⊗nj j
︀ ︀
nj
�nj⊗1⊗nj+1
j
︀ ︀.
Por outro lado, se grau(�)<grau(�), podemos calcular a SRP de � e �e utilizar a fórmula 3 do Lema 2.1.1: res(�,�) = (⊗1)grau(p) grau(q)res(�,�).
Na subseção 5.2.10, fornecemos um pseudocódigo, juntamente com um código para implementação no Maxima do algoritmo das subresultantes.
2.2
Fatoração Livre de Quadrados
A fatoração livre de quadrados é um tipo especial de fatoração capaz de agrupar as raízes de um polinômio de acordo com a sua multiplicidade, mas de maneira que não seja necessário saber quais são estas raízes (e nem mesmo a fatoração irredutível do polinômio em questão). Isto é, o fator de potência� em uma fatora-ção livre de quadrados contém todas as raízes (considerando o fecho algébrico do polinômio) de multiplicidade�, mas este fator não se decompõe completamente em termos de suas raízes (a menos que haja só uma raiz).
tam-bém utiliza esta fatoração em certo ponto.
Definição 2.2.1. Sejam � ∈ �[�] e pp(�) =
n
︁
i=1
�ei
i a fatoração em fatores
irredutíveis de sua parte primitiva, onde �i ⊙1 para cada �. Definimos a parte
livre de quadrados de � como sendo
�* =
n
︁
i=1
�i
e para cada� ∈Z, �⊙0, definimos a�-deflação (ou �-ésima deflação, e apenas
deflação quando �= 1) de � como sendo
�⊗k = n
︁
i=1
�max(0,ei⊗k)
i =
n
︁
i♣ei>k �ei⊗k
i .
Em outras palavras a �-deflação diminui em � unidades a multiplicidade de cada raiz, mas apenas enquanto a potência da respectiva raiz não se tornar negativa. Observe que �⊗0 = pp(�). Além disso, convencionamos �⊗ = �⊗1 ou seja,
�⊗ =
n
︁
i=1
�ei⊗1 i .
Pela Definição 2.2.1, temos que �⊗i+j = (�⊗i)⊗j, para quaisquer �,�
⊙ 0, e, por-tanto,
�⊗k+1 = (�⊗k)⊗. (2.4)
Além disso,
�*�⊗ = pp(�). (2.5)
As equações (2.4) e (2.5) combinadas fornecem
�⊗k+1 = � ⊗k
(�⊗k)*, para �⊙0. (2.6)
uma vez a menos. Além disso, a recíproca vale se�tem característica 0, de modo que, se � for primitivo, passamos a ter
�⊗ = mdc
︃
�,�� ��
︃
(2.7)
e, desta forma, �* pode ser calculado através de 2.5. As demais deflações de �
podem ser calculadas recursivamente através de 2.4.
Lema 2.2.1 ([2], Cap. 1, ğ6). Sejam � um DFU, �,� ∈ �[�]\� e � > 0 um
inteiro. Então,
1. �n+1 ♣� =⇒�n ♣mdc(�,��/��),
2. se � é irredutível e � tem característica 0, então �n ♣ mdc(�,��/��) =⇒ �n+1 ♣�.
Sejam�um DFU e�uma indeterminada sobre�. As considerações anteriores nos permitem concluir que é mais fácil calcular partes livres de quadrados e deflações do que calcular a fatoração em fatores irredutíveis de um polinômio em �[�]. Isto nos motiva a definir um tipo especial de fatoração.
Definição 2.2.2. Um polinômio �∈�[�] é dito livre de quadrados, ou livre de fatores quadráticos se não existe �∈�[�]\� tal que �2 ♣� em �[�].
Ou seja, um polinômio é livre de quadrados quando sua fatoração em fatores irredutíveis sobre �, ou sobre qualquer extensão de � tem todos os expoentes iguais a 1.
Definição 2.2.3. Seja � ∈ �[�]. Uma fatoração livre de quadrados (flq)
de � é uma fatoração da forma � =
k
︁
i=1
�ii onde cada �i é livre de quadrados e
mdc(�i,�j) = 1 para�̸=�.
Uma vez que os elementos de �, vistos como elementos de �[�], são sempre
livres de quadrados por definição, e que � = cont(�) pp(�), se pp(�) =
k
︁
i=1
�ii é a flq de pp(�), então
�= (cont(�)�1)
k
︁
i=2
é uma flq de �. Portanto, só precisamos nos preocupar em calcular a flq da parte primitiva de um polinômio. Além disso, se � possui característica 0, a flq de � separa as suas raízes pelas multiplicidades, agrupando em �i aquelas com
multi-plicidade �, pois qualquer raiz de � deve ser raiz de exatamente um destes �i (os
�i são coprimos).
Proposição 2.2.1 ([2], Cap. 1, ğ7, [25]). Sejam�∈�[�]\�,pp(�) =
n
︁
i=1
�ei i uma
fatoração em fatores irredutíveis de pp(�), � = max(�1, . . . ,�n) e �i =
︁
j♣ej=i �j
para 1⊘�⊘�. Então,
1. �⊗k = m
︁
i=k+1
�ii⊗k =�k+1�k2+2. . . �mm⊗k para qualquer � ⊙0.
2.
�i =
�⊗i⊗1*
�⊗i* para1⊘�⊘�. (2.8)
3. pp(�) = ︁m
i=1
�ii é uma fatoração livre de quadrados de pp(�).
Temos, portanto, uma maneira de calcular os fatores de uma flq de um polinô-mio em termos de suas deflações e vice-versa. Além disso, se �tem característica 0, conseguimos o seguinte algoritmo para calcular a parte primitiva de um po-linômio: como vimos na subseção anterior, vale em �[�] a equação (2.7), isto é, �⊗1 =�⊗ = mdc(�,��/��), o que nos dá �1 = (�⊗0)* =�* = pp(�)/�⊗.
Indutiva-mente, se temos (�⊗k)* e�⊗k+1, então conseguimos calcular
mdc︁
(�⊗k)*,�⊗k+1︁= mdc(�
k+1≤ ≤ ≤�m,�k+2�2k+3≤ ≤ ≤�mm⊗k⊗1) = (�⊗k+1)*,
e �k+1 e �⊗k+2 podem ser obtidos respectivamente por 2.8 e 2.6. Seguimos até
encontrar o primeiro�inteiro positivo tal que�⊗k+1 ∈�, em qual caso teremos�⊗k livre de quadrados, com�=�⊗1 e�m =�⊗k. Ou seja, conseguimos oalgoritmo
de Musser, que encontra uma flq para � utilizando apenas operações racionais e cálculos de mdc em �[�].
chamado algoritmo de Yun [36]. Mantendo a notação, a ideia é considerar a seguinte sequência de polinômios:
�k = m
︁
i=k
(�⊗�+ 1)��i ��
(�⊗k⊗1)*
�i
=︁m
i=k
(�⊗�+ 1)�k≤ ≤ ≤�i⊗1
��i
���i+1≤ ≤ ≤�m para � ⊙1. (2.9)
O lema abaixo traz algumas propriedades desta sequência.
Proposição 2.2.2 ([2] Cap. 1, ğ7, [36]). Com a notação acima,
mdc((�⊗i⊗1)*,�
i)∈�,
��⊗i⊗1/��=�⊗i�
i, (2.10)
e com �i como definido na Proposição 2.2.1,
�i⊗
�(�⊗i⊗1)*
�� =�i�i+1 (2.11)
para 1⊘�⊘�.
Temos que (�⊗i⊗1)* =�
i(�⊗i)
*
e mdc((�⊗i)*,�
i+1) = 1, donde concluímos, por
(2.11) que
mdc
︃
(�⊗i⊗1)*,�
i⊗
�(�⊗i⊗1)*
��
︃
=�i. (2.12)
Esta é a base para o algoritmo de Yun, o qual descrevemos a seguir.
Novamente, suponha que � é primitivo. Temos que �⊗ = mdc(�,��/��) e, portanto,
�⊗0* =�* = pp(�)/�⊗ e�1 =
��/��
�⊗ por (2.10).
Indutivamente, se temos �⊗k⊗1* e �
k, �k pode ser calculado através de (2.12), e
�k+1 e �⊗k* são obtidos respectivamente por (2.11) e (2.8). Seguimos até que
�k = ��⊗k⊗1*/��, quando temos que �⊗k⊗1 é livre de quadrados, com � = � e
�k=�⊗k⊗1 =�⊗k⊗1*. Na subseção5.3.2, fornecemos um pseudocódigo, juntamente
com um código para implementação no Maxima do algoritmo de Yun.
característica 0 e � ∈ �[�] \� é primitivo e livre de quadrados então, pelo item 1 da Proposição 2.2.1, mdc(�,��/��) = �⊗ = 1, pois, neste caso, � = 1. Reciprocamente, se mdc(�,��/��) = 1 então � = �⊗0 é livre de quadrados. Ou seja,
Teorema 2.2.1 ([11], Cap. 8, ğ2). Sejam � um DFU de característica 0 e �∈ �[�]\� um polinômio primitivo. Então, � é livre de quadrados se e só se
grau
︃
mdc
︃
�,�� ��
︃︃
= 0.
Integração Indefinida de Funções
Racionais Complexas
Apresentamos agora algoritmos de integração de funções racionais sobre um sub-corpo dos complexos (portanto, de característica 0). O primeiro algoritmo a ser apresentado é o algoritmo de Bernoulli, que é comumente estudado nos cursos de Cálculo, mas não costuma ser o método utilizado pelos CAS da atualidade. Seguimos com o algoritmo de Hermite e suas variantes e o algoritmo de Horowitz-Ostrogradsky. Ambos são capazes de expressar a integral de uma função racional como sendo a soma entre uma função racional e a integral de uma função racional própria cujo denominador é livre de quadrados. Finalizamos apresentando os algo-ritmos de Rothstein-Trager e de Lazard-Rioboo-Trager, que efetivamente calculam a integral deixada pelos últimos algoritmos, expressando-a como uma combinação linear de logaritmos com certas propriedades desejáveis, como veremos.
3.1
O Algoritmo de Bernoulli
Seja � = �/� ∈ R(�) uma função racional reduzida com coeficientes reais. A divisão polinomial nos permite expressar � =�+�/�, onde �,�∈R[�], com �/� reduzida e própria. Seja
�=
n
︁
i=1
(�⊗�i)ei m
︁
j=1
(�2+�
a fatoração em fatores irredutíveis de � sobre os reais, com todos �i,�j,�j ∈ R e
�i,�j inteiros positivos. Decompondo � em frações parciais completas, temos
� =�+ n ︁ i=1 ei ︁ k=1 �ik
(�⊗�i)k
+︁m
j=1
fj
︁
k=1
�jk�+�jk
(�2+�
j�+�j)k
(3.1)
onde todos �ik,�jk,�jk ∈ R. Portanto, pela linearidade da integração, ∫ � é a
soma das integrais das parcelas do lado direito da equação (3.1). A integral de �∈R[�] é fácil de ser calculada, pois � é um polinômio. Para as outras parcelas, temos:
︁ �
ik
(�⊗�i)k
= ⎧ ︁ ︁ ︁ ︁
�ik(�⊗�i)1⊗k/(1⊗�) se � >1
�1klog(�⊗�i) se � = 1
(3.2)
e, notando que �2j ⊗4�j < 0, uma vez que �2+�j�+�j é irretdutível sobre os
reais,
︁ �
j1�+�j1
(�2+�
j�+�j)
=�j1
2 log(�2+�j�+�j)
+2�︁j1⊗�j�j1
4�j⊗�2j
arctg
⎛ ︁
2�+�j
︁
4�j ⊗�2j
︀ ︀
e para � >1,
︁ �
jk�+�jk
(�2+�
j�+�j)k
= (2�jk⊗�j�jk)�+�j�jk ⊗2�j�jk (�⊗1)(4�j⊗�2j)(�2+�j�+�j)k⊗1
+︁ (2�⊗3)(2�jk⊗�j�jk)
(�⊗1)(4�j ⊗�2j)(�2+�j�+�j)k⊗1
. (3.3)
A regra explicitada por (3.3) pode ser aplicada recursivamente sobre a integral do lado direito desta equação, até que atinjamos � = 1. Assim, completamos o algoritmo de Bernoulli.
isto é � = ︁
i=1
(�⊗�i)ei, onde os �i pertencem ao fecho algébrico de K. Temos a
seguinte decomposição em frações parciais completas de �:
� =�+
n
︁
i=1
ei
︁
k=1
�ik
(�⊗�i)k
. (3.4)
Basta, então, aplicar (3.2) para cada termo cada termo próprio do lado direito. Esta abordagem é equivalente a expandir� em sua série de Laurent em todos os seus polos finitos, uma vez que, em �=�i, a série de Laurent é
� = �iei (�⊗�i)ei
+≤ ≤ ≤+ �i2 (�⊗�i)2
+ �i1 (�⊗�i)
+≤ ≤ ≤
onde os �ij são os mesmos que em (3.4). Portanto, podemos perceber esta
abor-dagem como a expansão do integrando em série em torno de seus polos (incluíndo ∞), seguida de integração termo a termo da série e interpolação, através da soma de todos os termos polares, obtendo, assim, a integral de (3.4).
Dada a natureza desta variante do método de Bernoulli de se basear em ex-pansão de séries, dizemos que sua abordagem é local. Em termos computacionais, a inconveniência deste método reside no fato de sermos levados a computar exten-sões de números algébricos sobreKque não necessariamente precisam aparecer na integral, a saber, os coeficientes da série de Laurent, além de precisarmos realizar cálculos de frações parciais envolvendo estes números algébricos. No Exemplo 3.1.2 a seguir, realizamos cálculos em Q(�) e obtemos o resultado final a partir deste corpo, mas existe uma integral que pode ser expressa inteiramente sobre Q(�). Por outro lado, certas integrais não são possíveis de serem expressas sem a introdução de novas extensões algébricas constantes, como ∫��/(�2
⊗2), a qual necessita da extensão √2. Portanto, de maneira geral, é possivel que precisemos introduzir novas extensões algébricas de K em algum momento.
Na subseção5.5.1, um código para implementação no Maxima do algoritmo de Bernoulli aplicado a integrandos reduzidos, próprios e com denominadores livres de quadrados.
3.1.1
Exemplos
Exemplo 3.1.1 (extraído de [2], Cap 2, ğ1). Seja � = 1/(�2 + 1)2 ∈ Q(�).
Observe que o denominador já está fatorado em fatores irredutíveis sobre R, e portanto, � já está decomposta em frações parciais. Portanto, nas fórmulas do algoritmo de Bernoulli, com � = 1, �= 1, �1 =�12= 0 e �1 =�12 = 1, temos
︁ 1
(�2+ 1)2 =
2� 4(�2+ 1) +
2�� 4(�2+ 1) =
� 2(�2+ 1) +
1
2arctg(�).
Exemplo 3.1.2 (extraído de [2], Cap 2, ğ1). Seja � = 1/(�3 +�) ∈ Q(�). O denominador se fatora em fatores irredutíveis em Rna forma �3+�=�(�2+ 1). Portanto, temos a seguinte decomposição em frações parciais de �:
1 �3 +� =
1 � ⊗
� �2+ 1.
Seguindo as fórmulas do algoritmo de Bernoulli temos
︁ 1
�3 +� = log(�)⊗
1
2log(�2+ 1). (3.5)
Se tivéssemos escolhido fatorar � sobre os complexos, a fatoração em fatores irredutíveis do denominador ficaria �3+�=�(�+�)(�⊗�), e a decomposição em frações parciais seria
1 �3+� =
1 � ⊗
1/2 �+� ⊗
1/2 �⊗�.
Portanto, uma representação alternativa para a integral de� seria
︁ 1
�3+� = log(�)⊗
1
2log(�+�)⊗ 1
2log(�⊗�).
des-necessários na representação da integral de �, enquanto que a representação (3.5) evita esta introdução. Isto motivará o algoritmo de Rothstein-Trager, a ser estu-dado mais adiante.
3.2
O Algoritmo de Hermite
Como vimos na seção 3.1, se � ∈ K(�), onde K é um subcorpo dos complexos, podemos expressar
︁
� = � � +
m
︁
i=1
Òilog(�i) (3.6)
onde �,�,�1, . . . ,�m ∈K[�] e Ò1, . . . ,Òm ∈K. No lado direito, a fração �/�∈K(�)
é chamada de parte racional da integral, sendo o restante a parte logarítmica ou transcendental, como já mencionamos no Capítulo1. Oalgoritmo de Hermite permite encontrar completamente a parte racional da integral de �, enquanto expressa a parte logarítmica implicitamente por ∫�/�, onde �/� ∈ K(�) é uma fração reduzida, própria e de denominador livre de quadrados.
3.2.1
Versão Original do Algoritmo de Hermite
Novamente, seja � = �/� ∈ K(�) uma fração reduzida. Valendo-nos da divisão euclidiana, escrevamos � = �+ �/�, onde �,� ∈ R[�], com �/� própria. Seja � = �11≤ ≤ ≤�kk a flq de �. A decomposição em frações parciais em relação a esta fatoração é
� =�+︁k
i=1
�i
�i i
onde cada �i ∈ K[�] e vale 0, ou grau(�i) < grau(�ii). Como no algoritmo de
Bernoulli, reduzimos o nosso problema a integrar cada uma das parcelas próprias por vez no lado direito da equação acima. Observando ainda que, como cada �i é livre de quadrados e, portanto, temos que mdc(�i,�′i) = 1, se � > 1 então
para encontrar à,á ∈K[�] tais que
�i
1⊗� =à�
′
i+á �i
com grau(à) < grau(�i). Logo, grau(à�i′) < grau(�i2) ⊘ grau(�ii) e, portanto,
grau(á)<grau(�ii⊗1). Multiplicando ambos os lados por (1⊗�)/�ii, temos
�i
�i i
=⊗(�⊗1)à�
′
i
�i i
+ (1⊗�)á �ii⊗1 .
Adicionando e subtraindo à′/�ii⊗1 no lado direito, temos
�i �i i = ︃ à′
�ii⊗1 ⊗
(�⊗1)à�′
i
�i i
︃
+ (1⊗�)á ⊗à′ �ii⊗1
.
Finalmente, integrando ambos os lados,
︁ �
i
�i i
= à �i⊗1
i
+︁ (1⊗�)á ⊗à′ �i⊗1
i
. (3.7)
Uma vez que grau((1⊗�)á⊗à′)<grau(�ii⊗1), o integrando à direita em (3.7) é semelhante ao da esquerda, porém com a potência do denominador reduzida em uma unidade. De maneira semelhante ao algoritmo de Bernoulli, podemos repetir esta fórmula recursivamente à direita, até que a potência do denominador seja 1. Quando atingimos esta condição, obtemos �i,�i,�i ∈K[�] tais que grau(�i)<
grau(�i) e�i/�ii = (�i/�i)′+�i/�i, para cada �. Portanto, obtemos �,ℎ∈K(�) tais
que � = �′ +�+ℎ, onde ℎ é uma fração própria cujo denominador é livre de quadrados (é o produto dos �i) e, ∫ ℎ é a parte logarítmica da integral de �. A
parte racional, portanto, é �+∫ �.
3.2.2
Versão Quadrática do Algoritmo de Hermite
Uma variante do algoritmo de Hermite nos permite chegar ao mesmo resultado sem a necessidade de se computar a decomposição em frações parciais de �. Descrevemos esta variante a seguir.
já seria livre de quadrados), definamos�=�/�kk. Como mdc(��k′,�k) = 1, podemos
utilizar o algoritmo de Euclides estendido para calcular à,á ∈K[�] tais que
�
1⊗� =à��
′
k+á �k
e grau(à)<grau(�k). Multiplicando ambos os lados por (1⊗�)/(��kk), temos
� ��k
k
= (1⊗�)à�k′
�k k
+ (1⊗�)á ��kk⊗1 .
Logo, adicionando e subtraindo à′/�kk⊗1 do lado direito, temos
� ��k
k
=
︃
à′
�kk⊗1 ⊗
(�⊗1)à�′
k
�k k
︃
+(1⊗�)á ⊗�à′ ��kk⊗1 . Finalmente, integrando dos dois lados:
︁ �
��k k
= à �kk⊗1 +
︁ (1⊗�)á ⊗�à′
��kk⊗1 .
Novamente, a integral à direita é similar à integral à esquerda, com a redução de potência em uma unidade no denominador. O processo segue recursivamente até que se obtenha um denominador livre de quadrados.
Como o expoente dos fatores livres de quadrados é reduzido em uma unidade em cada passo, no pior dos casos, o número de passos de redução e 1+2+≤ ≤ ≤+(�⊗1), o que tem complexidade �(�2) e, portanto, chamamos esta variante deversão
quadrática do método de Hermite.
3.2.3
Versão Linear do Algoritmo de Hermite
Uma última variante do algoritmo de Hermite é fornecida a seguir e é devida a D. Mack [22]. Nela, não precisamos calcular nem a decomposição em frações parciais do integrando, nem, a priori a fatoração livre de quadrados de seu denominador (esta última sendo computada ao longo do processo).
![Figura 4.1: Gráfico de � próximo do intervalo [⊗5/4, ⊗ 3/4].](https://thumb-eu.123doks.com/thumbv2/123dok_br/15640300.110906/82.892.233.690.289.775/figura-gráfico-de-próximo-do-intervalo.webp)