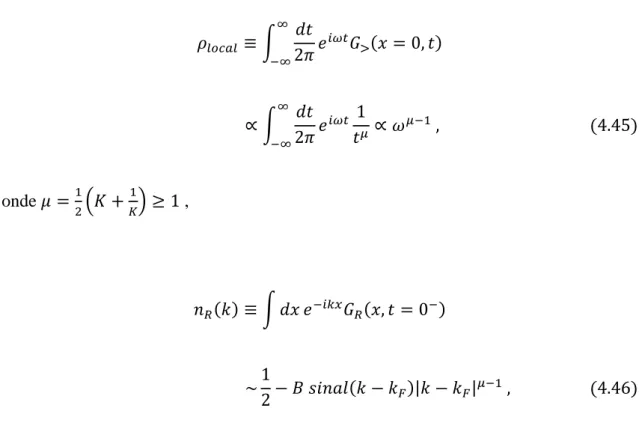UNIVERSIDADE FERERAL DO RIO GRANDE DO
NORTE
DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL - DFTE
DISSERTAÇÃO DE MESTRADO
Pareamento BCS em um Líquido de Luttinger em 1D
Por
Ronivon Lourenço Eneias
Rio Grande do Norte-RN, Brasil.
DISSERTAÇÃO DE MESTRADO
Por
Ronivon Lourenço Eneias
Pareamento BCS em um Líquido de Luttinger em 1D
Orientador
Prof. Dr. Álvaro Ferraz Filho
Dissertação apresentada ao Programa de
Pós-graduação em Física da
Universidade Federal do Rio Grande do
Norte como parte dos requisitos para
Agradecimentos
Agradeço primeiramente a Deus pela vida concedida e por me dar força e
dedicação para prosseguir nos momentos mais difíceis.
Um especial agradecimento à minha mãe por ter acreditado em meu potencial
diante de todas as dificuldades neste longo caminho percorrido.
À minha querida esposa e filho pela paciência, apoio e incentivo constantes.
Obrigado!
Aos meus irmãos e irmãs, por estarem sempre ao meu lado nos momentos
difíceis.
Agradeço ao meu orientador professor Dr. Álvaro Ferraz Filho por me orientar e
pela amizade e dedicação demostrada durante a realização deste trabalho de mestrado.
Resumo
Neste trabalho investigamos o efeito de um termo de emparelhamento do tipo
BCS para férmions livres sem spins, com propensão a formar um condensado de pares
em uma dimensão 1+1. Utilizando a técnica de bosonização vamos explorar a possível
condição de existência de quasipartículas em um estado supercondutor. Embora não
haja nenhuma quebra espontânea de simetria quiral o propagador de 1-partícula
fermiônica é massivo e de fato assemelha-se a função de Green de 1-partícula de uma
fermions, with a propensity to form a condensate of pairs in a 1+1 dimension. Using
Abstract
In this work we investigate the effect of a BCS-type pairing term for free spinless
the of bosonization technique we explore the possible condition of existence of
quasiparticles in a superconducting state. Although there is no spontaneous breaking of
chiral symmetry the propagator of one-particle fermion is massive and, in fact,
Sumário
1 Introdução 1
2 Bosonização 3
2.1 Linearização do Espectro...3
2.2 Operador Densidade...6
2.3 Bosonização do Hamiltoniano com Relação de Dispersão Linear...9
2.4 Por que os Fatores de Klein São Depois Ignorados?...14
2.5 Dicionário de Bosonização...15
3 Supercondutores de Alta Temperatura 20
3.1 Diagrama de Fase de Supercondutores de Alta Temperatura...22
4 Líquido de Luttinger 27
4.1 O modelo de g-ologia...27
4.2 Bosonização da Interação...31
4.3 Diagonalização do Hamiltoniano...34
4.4 O Hamiltoniano em Termos dos Campos e ...36
5 Pareamento BCS em um Líquido de Luttinger em 1D 43
5.1 Hamiltoniano e Lagrangiano do Modelo...43
5.2 Densidades de Hamiltoniano e Lagrangiano Bosonizados...45
5.3 Refermionização da Densidade de Lagrangiana e Funções de Correlação...50
1
Capítulo 1
Introdução
Os cupratos supercondutores se notabilizam por possuírem propriedades
metálicas anômalas acima da temperatura crítica e uma fase supercondutora do tipo-d
em baixas temperaturas. Em dopagens ótimas e em baixas dopagens os experimentos de
ARPES (“Angle-resolved photoemission spectroscopy”) demonstram a ausência de
quasipartículas na fase metálica. Na fase supercondutora do tipo-d encontramos, por sua
vez, a presença de pares de elétrons, nas regiões anti-nodais, e quasipartículas usuais,
nas regiões nodais no espaço de momento. Se em , parece estarmos lidando com
um estado metálico não-líquido de Fermi, por outro lado à presença de quasipartículas
nodais na fase supercondutora do tipo-d demonstra que se há separação de carga e spin
acima de , esse graus de liberdade se recompõem por completo na fase
supercondutora. Essa observação põe em questão o caráter do estado supercondutor.
Nosso ponto de partida é o modelo de Tomonaga-Luttinger (TL) que é o estado de
referência para um líquido de não-Fermi. Levando-se em conta que nos cupratos
uniformemente nas regiões anti-nodais no espaço de momenta, nós formulamos um
modelo mínimo que descreve essa situação.
Nosso objetivo é investigar diretamente o efeito que esses pares produzem em um
líquido de TL.
Usando métodos de bosonização vamos explorar a condição de existência de
Capítulo 2
Bosonização
Neste capítulo vamos trabalhar com um método que descreve com exatidão
propriedades de baixas-energias de sistemas unidimensionais. Um método bastante
conhecido é chamado de bosonização e é uma ferramenta muito usada, especialmente,
em uma dimensão. Uma forma prática de apresentarmos esse método é fazermos uma
aplicação em um modelo específico.
2.1 Linearização do Espectro
A descrição dessa técnica tem sido sujeita a muitas revisões ao longo dos anos.
Podemos citar os trabalhados de (Emery, 1979; Sólyom. 1979; Schulz, 1995; Voit,
1995; Von Delft e Schoeller, 1998; Gogolin et al. 1999; Schonhammer. 2002; Senechal,
2003; T. Giamarchi, 2004). Para descrevermos o método vamos considerar inicialmente
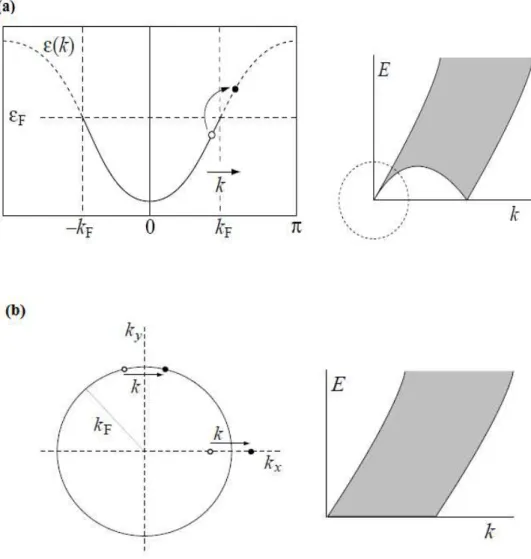
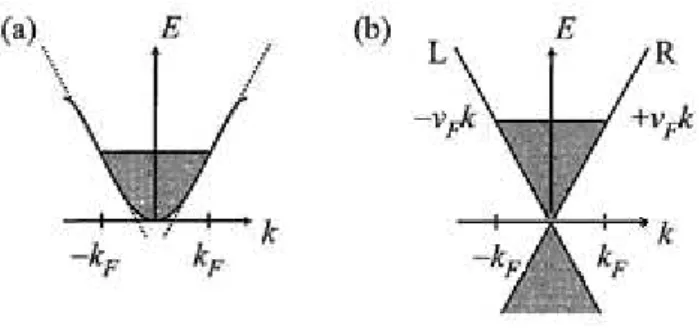
férmions sem spins. Como podemos ver na figura 2.1.1 às excitações de
partícula-buraco do sistema têm um espectro aproximadamente linear, e são, essencialmente,
excitações bem definidas, com energia e momento, também, bem definidos. Vamos
substituir o modelo original por um modelo efetivo em que o espectro seja puramente
Figura 2.1.1. Espectro das excitações de partícula buraco para sistemas em uma dimensão em (a) e para duas dimensões em (b). Em uma dimensão, ao contrário do que ocorre em dimensões mais elevadas, tem ambos à energia e momento bem definidos, para um q pequeno [2].
espectro de energia também para . Isso nos faz introduzir dois tipos de férmions: os
férmions que se movem à direita e os que se movem à esquerda nas vizinhanças de
, respectivamente. Com isso o Hamiltoniano do sistema torna-se
∑
Figura 2.1.2. O modelo original de férmions com banda curva em (a) e substituído por um modelo de férmions com espectro linear em (b). Isso força a introduzir dos tipos de férmions (férmions que se movem à direita (R) e à esquerda (L)). O espectro é agora estendido a todos os valores de k, levando a um número infinito de estados com energia negativa. Um corte no momento pode ser necessário para que o modelo seja bem definido [1].
partículas que se movem à esquerda. Para evitarmos uma notação muito carregada,
vamos usar a conversão , para , e , para . Note que (2.1)
é equivalente ao Hamiltoniano de Dirac em uma dimensão. Similarmente, o mar de
Fermi onde todos os estados abaixo do potencial químico ( ) estão preenchidos é
substituído aqui por um „mar de Dirac‟ onde o número de estados com energia negativa
( ) estão completamente preenchidos.
Embora os dois sistemas da figura 2.1.2 sejam diferente para grandes diferenças
de momentos, eles são bem parecidos para baixas energias de excitação. Note que
falar-se em um espectro linear é simplesmente equivalente a falar-falar-se em densidades de estado
constantes, que é uma aproximação muito comum para férmions em 1D. Podemos
agora, por exemplo, escolher as partículas que se movem para a esquerda e ver que as
excitações de partícula-buraco são agora dadas por
Vemos com isso que as excitações de partícula-buraco são totalmente independentes de
definido e uma energia bem definida . Uma vez que as excitações de
partícula-buraco do sistema são bem definidas, podemos tentar reescrever (2.1) nessa base. Essa
base é sem dúvida muito especial. Primeiramente, somente excitações coletivas se
manifestam em uma dimensão. A densidade de flutuações é, portanto, uma base natural
a ser usada.
2.2 Operador Densidade
Na verdade, a densidade de flutuações é, essencialmente, uma superposição de
excitações partícula-buraco. Essas oscilações de cargas são descritas pelo operador
densidade, ̂ dado por
̂ ∑
Em função do número infinito de estados ocupados em (2.1) (ver figura 2.1.2),
precisamos ter cuidado na definição do operador densidade para evitarmos infinitos.
Para fazermos isso, se introduz o ordenamento normal de produtos de operadores
. Os operadores de destruição no produto ordenado normal (com respeito a
um dado vácuo) são colocados à direita e os operadores de criação à esquerda. Para dois
operadores A e B que são uma combinação linear de operadores de criação e destruição
é fácil checarmos que o ordenamento normal dos operadores é equivalente a
subtrairmos o produto desses operadores do seu valor médio no estado fundamental:
| |
A densidade ordenada normal, por exemplo, é definida com
Onde usamos a notação para operadores de criação de uma partícula do tipo à
direita ou do tipo , no ponto x. A componente de Fourier ̂ da
densidade é definida como
̂ ∑ ̂
e é dada por
̂ ∑
̂ ∑[ ⟨ | | ⟩]
que define o operador ̂ . Como é usual ̂ ̂ uma vez que ̂ é real. |
é o estado fundamental de (2.1). Isto é, ele é o mar de Dirac onde todos os estados com
energia negativa estão ocupados. A subtração do valor médio (ou seja, o ordenamento
normal) em (2.7) garante que os elementos de matriz do operador densidade sejam
finitos, apesar do número infinito de estados ocupados.
Agora vejamos como fica o comutador desses operadores. Entre partículas de
ramos diferentes o comutador é, obviamente, zero
[ ̂ ̂ ]
Para partículas do mesmo ramo, temos
[ ̂ ̂ ] ∑ [ ]
∑( )
Poderíamos fazer apenas uma simples mudança de variável no segundo termo de (2.9) e
acharmos que este comutador se anularia. Isso na verdade não é possível, devido ao
número infinito de estados ocupados. Os operadores de densidade sem o ordenamento
normal contêm infinitos e (2.9) é, de fato, a subtração de dois infinitos. Só podemos
fazer essa mudança de variável no ordenamento normal da densidade
[ ̂ ̂ ] ∑( )
∑(⟨ | | ⟩ ⟨ | | ⟩)
∑(⟨ | | ⟩ ⟨ | | ⟩)
Uma vez que temos o produto de ordenamento normal à mudança de variável pode ser
feita com segurança. O último termo é facilmente avaliado e nos dá
[ ̂ ̂ ] ∑(⟨ | | ⟩ ⟨ | | ⟩)
Levando-se em conta que ⟨ | | ⟩ , se o estado estiver ocupado e zero em
qualquer outra região, chegamos facilmente ao resultado
[ ̂ ̂ ]
O resultado (2.12) é crucial. Ele mostra que por causa do número infinito de estados
de um fator de normalização, aos operadores de bósons. As flutuações de carga têm um
comportamento de operadores de destruição e de criação de bósons.
2.3 Bosonização do Hamiltoniano com Relação de Dispersão
Linear
Os operadores de densidade podem ser identificados com os operadores de
destruição e criação para bósons. Agora podemos definir os operadores de criação e de
destruição para e como
√
√
e para e
√
√
Observe que os operadores de bósons somente são definidos para .
Para que esses operadores de bósons possam ser usados, precisamos mostrar que
claro, que a nova base é completa. Vamos começar com o hamiltoniano. Pode-se
calcular novamente o comutador do Hamiltoniano com os operadores de bósons usando
regras de anti-comutação dos operadores fermiônicos. Assumindo que ,
[ ] ∑ [ ]
∑
Resultado semelhante pode ser obtido com , que nos leva ao comutador com
. Se assumirmos, por um momento, que a base gerada pelos os operadores é
completa, o resultado (2.17) define completamente o Hamiltoniano na base de bósons.
Isto é fácil de se checar, pelas as relações de comutação e o operador desejado que
satisfaz as regras de comutação (2.17) é, portanto
∑ | |
Esta fórmula é muito importante para a representação de bósons, pois nos mostra que,
contrariamente às expectativas, o termo cinético é quadrático em termos destes
operadores.
Os operadores de uma única partícula podem ser determinados pelo mesmo
método. Primeiro, deve-se introduzir um operador para cada tipo de férmion. Seja
o operador de destruição de férmion, movendo-se à direita, no ponto x e o
operador de destruição de 1 férmion movendo-se à esquerda, também no ponto x. Isto
[ ̂ ]
√ ∑ [ ]
onde é dada por
√ ∑
e a transformada de Fourier
∫
O anticomutador dos operadores fermiônicos no espaço de momento é então
{ }
Considere agora a função de correlação, no mesmo instante de tempo, no estado
fundamental, por exemplo, para
⟨ ⟩ ∫ ∫ ⟨ ⟩ ⏟ ∫
A integral em (2.23) é mal definida quando . Para removermos essa indefinição,
vamos introduzir um fator de convergência | |. Com isso, temos que
Chegamos em um resultado análogo para . Em resumo, temos que
⟨ ⟩
e, semelhantemente,
⟨ ⟩
Note que, no limite , também temos
⟨ ⟩
Assim, um operador fermiônico escrito diretamente em termos de operadores de bósons
e que produz a mesma relação de comutação é
∑ ̂
As fórmulas de (2.13) a (2.16), (2.18) e (2.28) podem ser tomadas, por assim dizer,
como um dicionário relativo à representação fermiônica para bósons. Isso é uma mera
mudança de base, embora, evidentemente, essa mudança aparenta ser altamente não
trivial. A esperança é que essa nova base seja melhor para diagonalizar o problema.
Uma vez que (2.28) dá o operador de um único férmion, qualquer operador fermiônico
composto pode ser agora em princípio escrito na linguagem de bósons.
As fórmulas acima são fisicamente corretas. Infelizmente, é fácil ver que (2.18) e
unidade. Por outro lado, e conservam o número de férmions da cada tipo uma vez
que eles são simplesmente flutuação de densidade de (2.13) a (2.16). Para reproduzir
todos os estados possíveis do espaço de Fock fermiônico original, é necessário
introduzir dois tipos de operadores adicionais (um para cada tipo de férmion) que muda
o número total de férmions. Tais operadores são conhecidos, na linguagem de teoria de
campo, como „fatores de Klein‟. Daremos uma explicação mais detalhada na próxima
seção, por que os fatores de Klein podem ser deixados de lado.
Ao invés de trabalharmos diretamente em termos dos operadores de bósons é
conveniente introduzirmos dois campos e definidos por
∑ ( | | ) ⁄ | | ⁄ (
)
∑ ( | | )
⁄
| | ⁄ (
)
Estritamente falando, deveríamos tomar o limite . Mantermos finito é uma boa
maneira para reintroduzirmos uma largura de banda finita nesse modelo. Os campos e
satisfazem as regras de comutação
[ ]
onde tomamos o limite e então Similarmente
[ ]
O resultado (2.32) mostra que o momento conjugado para o campo é
simplesmente dado por
usando (2.32) obtemos (para )
[ ]
√
[ ]
√
é, portanto, parte das flutuações de densidade para no ponto x.
contem a diferença entre férmions à direita e à esquerda e é simplesmente o operador
corrente em um sistema unidimensional. O Hamiltoniano pode ser reescrito em termos
desses novos campos
∫ [ ]
Usando-se todas as fórmulas acima, fica-se rigorosamente estabelecida à relação
em bósons e férmions.
2.4 Por que os Fatores de Klein São Depois Ignorados?
Em muitos trabalhos, os fatores de Klein são assumidos implicitamente, mas os
autores não se dão o trabalho de escrevê-los explicitamente. Em alguns outros casos eles
são, inclusive, simplesmente ignorados. Isso é usualmente correto se o objetivo for
calcular funções de correlações da forma
Para um Hamiltoniano que conserva separadamente cada ̂ , os valores esperados desse
portanto de e , de modo que o último pode ser comutado com cada outro e os
operadores e são combinados para dá um, ou seja, . É claro, que é
preciso ter-se o cuidado de acompanhar os sinais de menos que surgem nesse processo.
Mas há varias maneiras de fazermos isso, por exemplo, adicionando-se o então chamado
„módulozero‟ com propriedades adequadas para os campos bosônicos. Além disso, para
bósons livres os campos bosônicos fazem com que somente funções de correlações
contendo um número igual de e sejam diferente de zero, por causa da invariância
do Hamiltoniano bosônico.
2.5 Dicionário de Bosonização
Considere um campo escalar sem massa livre, cujo hamiltoniano é dado por
∫ [ ]
onde o campo bosônico em 1D, é definido para , como
∫
√ | |
[ ] | | ⁄
∫ | |
√ | |
[ ] | | ⁄
onde é um fator de convergência infinitesimal, é o campo canonicamente
conjugado. Esses operadores obedecem às relações de comutação, no limite ,
temos
[ ]
[ ]
Como férmions, temos partículas bosonicas em 1D que se movem ou para a direita ou
para a esquerda.
[ ∫
]
∫ √ | |
| | ⁄ | |
Pode-se verificar que
[ ] {
[ ]
Vamos trabalhar agora com algumas funções de correlação, considere primeiro
⟨ ⟩
∫
√ | |∫
√ | |⟨ ⟩(
)
∫ | | ( )
Vamos considerar um conjunto de operadores muito comuns quando se usa
bosonização. Esses operadores contêm um campo escalar no argumento de uma
exponencial. Frequentemente, precisamos calcular o valor esperado dos produtos desses
operadores, ou seja, ⟨ ⟩. Usando a identidade
⟨ ⟩
onde ⟨ ⟩ é simplesmente o valor esperado do estado fundamental. Fazendo o
cálculo de , encontramos
com isso, por exemplo, para , temos
⟨ ⟩
⁄
Quando fazemos a passagem da teoria de Fermi para a teoria de Bose uma
fórmula muito importante é
onde e são constantes a serem determinada. Para determinar as constantes e
⟨ ⟩
⟨ ⟩
⟨ ⟩ ⟨ ⟩
Isso implica que devemos ter √ ⁄ e √ e então temos o operador (2.53)
dado por
√ √
Isso significa que qualquer função de correlação do campo fermiônico, calculado no
vácuo de Fermi com um dado “cut-off” , é reproduzida pelo operador bosônico dado
no lado direito, se caculado no vácuo bosônico com o mesmo “cut-off”. Dado este
operador de equivalência, podemos substituir qualquer campo fermiônico pelo seu
corespondente bosônico. Às vezes, isso requer algum cuidado, mas esta é a ideia geral.
Vamos considerar agora o operador ̅ definido por
̅
̅ √ √
[ √ ]
√
onde o fator de ⁄ na exponencial vem do comutador (2.46).
Finalmente para fechar essa seção segue mais um resultado muito importante, que usa a
expansão do produto de operadores definido por
[ ]
Mais detalhes desse cálculo será dado no capítulo 5, aqui segue o resultado
√
Isso fecha o capítulo em que resolvemos o modelo de Luttinger sem interação e
Capítulo 3
Supercondutores de Alta Temperatura
A supercondutividade foi considerada um grande mistério científico durante boa
parte do século passado. Descoberta em 1911, ela só explicada microscopicamente em
1957, e, assim mesmo, uma grande quantidade de teorias e estudos experimentais
sugiram depois dessa descoberta. Em 1950, Ginzburg e Landau apresentaram uma
teoria que explicava a supercondutividade fenomenologicamente como uma quebra
espontânea de simetria. A teoria microscópica da supercondutividade foi formulada por
Bardeen, Cooper e Schrieffer e ela é conhecida hoje em dia como à teoria BCS. A base
da teoria BCS é a interação de um “gás” de elétrons de condução com ondas elásticas de
uma rede cristalina (fônons). Como sabemos dois elétrons no vácuo repelem-se
mutuamente pela força coulombiana, mas em um supercondutor abaixo da temperatura
critica existe uma atração resultante entre os dois elétrons que, assim, formam o
chamado par de Cooper. Cada par de Cooper é formado por dois elétrons de momenta e
polarização de spins opostas. Além do emparelhamento dos elétrons, a
supercondutividade também requer uma fase coerente de longo alcance entres os pares
interação elétron-fônon, enquanto que a fase coerente entre os pares de Cooper é
estabelecida pela superposição das suas funções de onda. Nos supercondutores
convencionais, o acoplamento da função de onda pode mediar à fase coerente, pois a
distância média entre os pares de Cooper é muito menor do que o comprimento de
coerência (o tamanho de um par de Cooper).
O efeito que desempenhou um papel decisivo em mostrar o caminho para a
correta teoria da supercondutividade em metais é conhecido com efeito isotópico. Um
estudo de diferentes isótopos de supercondutores de mercúrio estabeleceu uma relação
entre a temperatura critica e a massa correspondente do isótopo; encontrou-se a
relação ⁄ que acabou mostrando-se válido, para a maioria dos supercondutores convencionais. Mesmo hoje em dia o efeito isotópico serve com um
indicador do mecanismo de fônons da supercondutividade. Após o surgimento da teoria
desenvolvida por Bardeen, Cooper e Schrieffer, os cientistas que estavam trabalhando
nessa área entre 1960 e 1970 puderam calcular em mais detalhe as consequências da
teoria BCS, até os novos materiais supercondutores serem descobertos. Em 1986,
Bednorz e Müller [3] surpreenderam o mundo cientifico com a descoberta da
supercondutividade de alta temperatura em compostos cerâmicos de óxido de cobre (os
cupratos). Já em 1987 eles receberam o Prêmio Nobel pela sua descoberta. Os dados
experimentais obtidos nos cupratos supercondutores indicam que esses compostos
exibem um tipo de supercondutividade não convencional. O fato mais surpreendente é
que a supercondutividade de alta temperatura ocorre em óxidos que são condutores
muito pobres em dopagem mais elevadas. A primeira reação da maioria dos cientistas
que trabalhavam no campo da supercondutividade foi pensar que deveria haver um novo
mecanismo, porque a supercondutividade mediada por fônons é improvável à
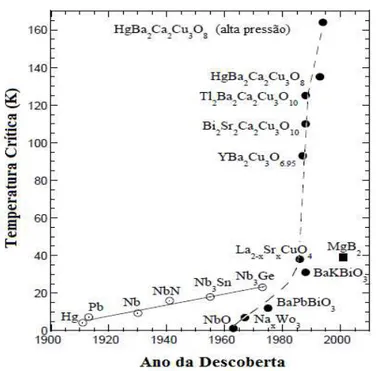
Figura 3.1. A evolução temporal das temperaturas críticas dos supercondutores desde a descoberta da supercondutividade em 1911. A linha sólida mostra a evolução de dos supercondutores metálicos. A linha tracejada para a evolução dos óxidos supercondutores [4].
diversos cupratos, em função do ano da descoberta, bem como algumas temperaturas
criticas de alguns supercondutores convencionais. Todos os compostos
supercondutores podem ser classificados em dois grupos: convencionais e não
convencionais. A Supercondutividade em supercondutores convencionais é descrita
pelas equações da teoria BCS. As propriedades dos supercondutores não convencionais
são definitivamente diferentes dos seus análogos convencionais.
3.1 Diagrama de Fase dos Supercondutores do Tipo d
de Alta Temperatura
Os cupratos supercondutores mais comuns são os que têm planos de cobre e
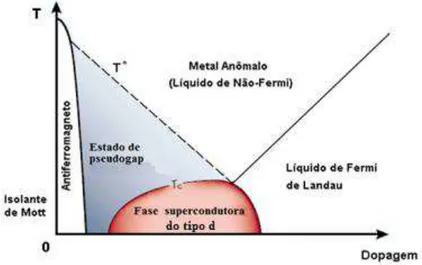
Figura 3.1.1. Diagrama de fase típico dos cupratos supercondutores do tipo d.
figura 3.1.1 mostra o diagrama de fase típico dos cupratos dopados de buracos. Quando
a dopagem é próxima de zero, os materiais desse tipo possuem exatamente um elétron
por cada sítio da rede cristalina. Portanto, na classificação da teoria de banda de esses
sistemas teriam banda semicheia, e assim um comportamento metálico. Mas, na verdade
não é isso o que ocorre. Tais sistemas são isolantes de carga com um “gap” de excitação
correspondente consideravelmente grande, da ordem de . Como em sua fase
isolante eles são antiferromagnéticos, esses materiais são classificados como isolantes
de Mott.
Quando removemos alguns elétrons dos planos , isto é, quando dopamos
esses compostos de modo a que os portadores de carga sejam buracos, temos uma
grande variedade de novos estados quânticos que surgem desse processo. Daí a grande
dificuldade em desenvolver-se uma teoria que descreva todas essas fases de uma
maneira unificada. Os cupratos quando submetidos a certo percentual de dopagem
podem se tornar condutores e, em seguida, em dopagem mais elevadas, abaixo de certa
temperatura de transição, supercondutores do tipo d, como podemos observar na figura
dopagem no sistema: a região classificada com subdopada e a outra região conhecida
como superdopada. Existe uma temperatura de transição máxima para a fase
supercondutora, em certa dopagem característica. Nesse ponto específico, dizemos estar
em uma dopagem ótima. Na região superdopada, medidas experimentais apontam que a
fase metálica que se manifesta em altas temperaturas é consistente com a teoria
tradicional do líquido de Fermi de Landau [5], ou seja, observa-se a existência de
quasipartículas bem definidas além de outras propriedades diretamente relacionadas a
esse modelo. Agora, na região subdopada, a fase metálica em altas temperaturas é
altamente anômala e, definitivamente, não se encaixa dentro dessa caracterização. Por
essa razão, essa fase é conhecida como, líquido de Não-Fermi. Nessa fase os
experimentos de ARPES (“Angle-resolved photoemission spectroscopy”) revelam
evidencias da existência de uma superfície de Fermi coerente em 2d bem definida, e, ao
mesmo tempo, indicam a ausência de quasipartículas bem definidas, acima de .
Se voltarmos à fase de isolante de Mott e agora doparmos esse sistema levemente
com buracos, isto é, se removermos poucos elétrons do sistema, surge uma nova fase
eletrônica conhecida como estado de pseudogap. Nessa fase, o ordenamento de quase
longo alcance antiferromagnético do estado isolante de Mott desaparece completamente
e também existem fortes evidências experimentais de uma abertura de “gap” de spin
sem nenhuma quebra espontânea de simetria no sistema. Recentemente, nos
experimentos de ARPES também foram observados que esses sistemas levemente
dopados podem apresentar “gap” de carga ao longo de certas direções preferencias no
espaço de momenta e, portanto seriam metais muito pobres com a superfície de Fermi
truncada [6]. Isso indicaria que a fase de pseudogap é influenciada pela proximidade
,
Figura 3.1.2. O espectro ARPES acima e abaixo da temperatura de transição . A figura mostra com nitidez os picos de quasipartículas no supercondutor abaixo de [7].
O protótipo de um líquido de não Fermi é um líquido de Tomonaga-Luttinger que
também não tem quasipartículas bem definidas apesar de ser metálico, como veremos
no capítulo 4. De fato, já em 1987, logo após a descoberta dos supercondutores, Phil
Anderson [8] propôs um estado de TL bidimensional como estado de referência básica
para a supercondutividade nos cupratos ter origem magnética e não fonônica,
observam-se pares de buracos e quasipartículas na faobservam-se supercondutora do tipo d. A figura 3.1.2
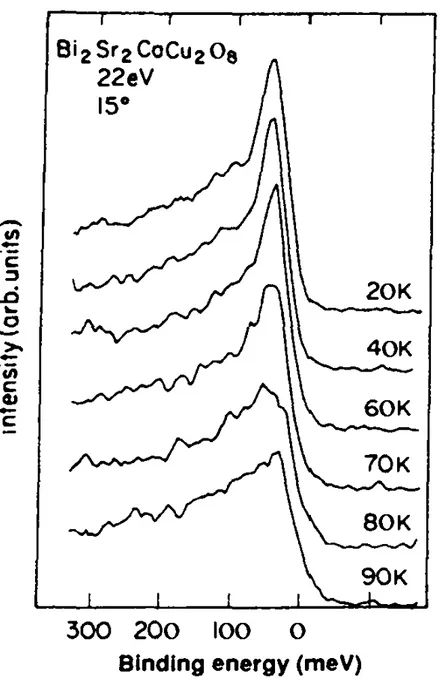
mostra o espectro ARPES do composto Bi2Sr2CaCu2O8 cuja temperatura de transição é
[9]. Essa figura mostra à intensidade do feixe, em unidades arbitrária, em
função da energia de ligação para algumas temperaturas. A energia de ligação mede, na
verdade, a diferença de energia, relativa ao nível de Fermi. Além disso, a intensidade do
feixe é diretamente proporcional à função de distribuição de Fermi. A figura 3.1.2
mostra também que existe um pico de quasipartículas próximo ao ponto zero, isto é, no
nível de Fermi. Quando a temperatura é aumentada o pico diminui e quase desaparece
por completo em , indicando com isso a ausência de quasipartículas para
. Se as quasipartículas são instáveis na fase metálica anômala por que elas aparentam
se recompo e passam a ser bem definidas na fase supercondutora? Para entendemos
melhor essa questão investigamos no nosso trabalho como se dá o emparelhamento de
partículas em um líquido de Tomonaga-Luttinger. Apesar do caráter qualitativo e da
unidimensionalidade do nosso modelo, nós mostramos que a presença de um “gap”
supercondutor nos leva naturalmente a um propagador de 1-particula com sinais
Capítulo 4
O Líquido de Tomonaga-Luttinger em
1D
Neste capitulo vamos introduzir e resolver um modelo mais emblemático para
elétrons em baixa dimensionalidade. O modelo de TL (Luttinger, 1963) foi introduzido,
construído a partir do trabalho de Tomonaga (Tomonaga, 1950), para descrever o
comportamento de um líquido de Fermi interagente em uma dimensão. A solução exata
do modelo foi obtida primeiramente por Mattis e Lieb (1965) e, posteriormente, usada
por Luther e Peschel (1974) para calcular as funções de correlação de uma partícula.
Finalmente, o conceito de líquido de Luttinger foi introduzido de maneira rigorosa e
abrangente por Haldane (Haldane, 1981). Esse conceito de líquido de Luttinger engloba
a maior parte da física simples de um sistema unidimensional e é o ponto de partida
para estudo de situações mais complexas.
Vamos primeiro considerar o Hamiltoniano que descreve férmions em um sistema
unidimensional sem interação, como vimos no capitulo 2. No caso mais simples em que
as interações são fracas, podemos nos concentrar nas propriedades de baixa-energia do
sistema e, portanto, vamos lidar apenas com excitações próximas à superfície de Fermi,
que, em uma dimensão, consiste de apenas dois pontos e . Nesse caso
podemos, simplesmente, linearizar a relação de dispersão próxima a esses dois pontos.
O Hamiltoniano do sistema como sabemos é
∑
O que acontece longe da superfície de Fermi não é realmente importante para
processos de baixa energia. Podemos usar um cuttof arbitrário para cortarmos o
espectro e evitarmos grandes transferências de momento. Vamos escolher de tal
forma que a nossa linearização se restrinja apenas ao intervalo e
. Como já temos o termo cinético (capítulo 2), agora precisamos
definir as interações para nosso novo modelo. Para férmions sem spin a interação típica
é dada por
∫
O operador densidade pode ser escrito usando os férmions que se propagam para a
esquerda ou para à direita. Os operadores de férmion de uma única-partícula são
√ ∑ √ ∑ √ ∑
Figura 4.1.1 Processos de baixa energia que o operador densidade é capaz de produzir. A componente desse operador produz excitações partícula buraco no mesmo ramo, enquanto que a transporta uma partícula de um lado para o outro da superfície de Fermi. Para o espectro linearizado esses dois processos corresponde, respectivamente, aos termos e
[1].
Apenas uma parte do operador atuando próxima a superfície de Fermi é importante para
as propriedades de baixa-energia. A expressão (4.3) mantém apenas essas partes
importantes. O operador densidade torna-se assim
o operador densidade pode ser reescrito com
̂ ∑
Ambos e têm que estar perto de um dos pontos de Fermi. Esses processos são
mostrados na figura 4.1.1
∑
onde para férmions que se propagam a direita e para férmions que se
propagam a esquerda.
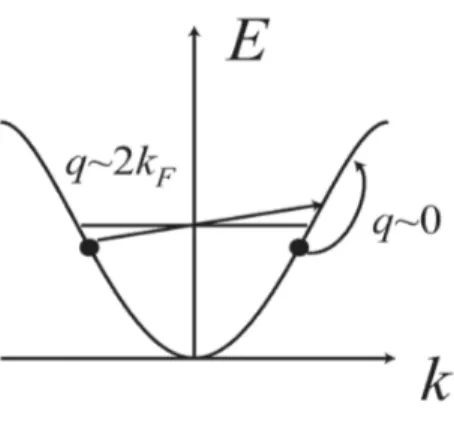
Os processos de espalhamento mais interessantes são aqueles que ocorrem quando
as partículas se situam próximo aos pontos de Fermi. Isso significa que todos os
momentos na expressão (4.6) estão próximos de ou . Isso nos permite
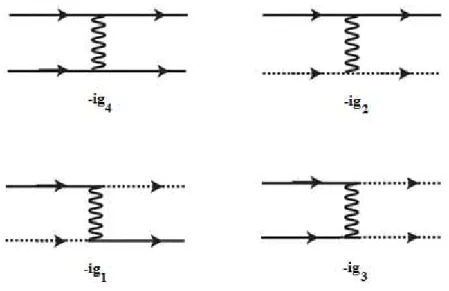
classificar as interações em quatro diferentes processos mostrados na figura 4.1.2. O
primeiro processo da figura 4.1.2 é o acoplamento de férmions que se situam do
mesmo lado de um dos pontos de Fermi. O segundo processo é o acoplamento de
férmions que se situam em lados diferentes desses pontos de Fermi. Entretanto, apesar
dessa interação, cada férmion permanece no seu próprio ramo da superfície de Fermi.
Essa interação de baixa transferência de momento é associada ao processo de
espalhamento frontal (“forward scattering”). O acoplamento , chamado de
acoplamento “para trás” (“backscattering”), corresponde ao espalhamento de ordem de
entre as partículas, que agora podem mudar de ramo. Finalmente, para o caso
específico em que o sistema se encontra exatamente em uma banda semicheia, podemos
ter ainda, os processos de interação do tipo Umklapp, descritos pelo acoplamento
que, em outras situações, viola a conservação de momento do sistema a menos de um
vetor da rede reciproca. No processo produzido por dois elétrons em um mesmo
ramo interagem entres si e se mudam para o outro ramo.
O modelo de g-ologia não pode ser resolvido exatamente no seu caso mais geral
possível. No entanto, no caso particular em que , há conservação de
Figura 4.1.2. Os processos importantes de baixa energia da interação podem ser divididos em quatro setores. A linha cheira representa férmions com momento próximo a (férmions que se propagam para a direita) e a linha pontilhada representa férmions com momento próximo a (férmions que se propagam para a esquerda). A notação g para denotar as diferentes interações é conhecida como g-ologia.
, esse modelo recebe um nome especial e passa a ser chamado de modelo de
Tomonaga-Luttinger. Esse modelo será resolvido nesse capítulo pelo método de
bosonização.
4.2 Bosonização da Interação
Representando o termo de interação em termos dos operadores de densidade, a
contribuição da interação da hamiltoniana pode ser escrita como
∑
∑ (
∑ ̂ ̂ ̂ ̂
Quando trabalhamos com teoria de segunda quantização, frequentemente
precisamos calcular comutadores de operadores que são polinômios de
operadores de bósons ou de férmions da teoria. Esse tipo de calculo é feito facilmente
usando identidades elementares na álgebra de comutadores. Uma das identidades
básicas mais usadas é a seguinte
[ ̂ ̂] [ ̂] ̂ ̂[ ̂]
Até agora, o que temos feito é reescrever a parte de interação do hamiltoniano em
termos dos operadores de densidade. No entanto, o que queremos é chegar a uma
representação em que estes operadores, ao invés dos operadores originais, representem
os graus de liberdade fundamentais da teoria. Como a definição dos operadores ̂
envolve o produto de dois operadores de férmions, esperamos que os operadores de
densidade possam, eventualmente, representar excitações bosônicas.
Essa conexão explícita entre os operadores fermiônicos e os operadores bosônicos
foi feita no capítulo 2, para , temos que se
√ ̂
√ ̂
e para
√ ̂
onde mais uma vez . É fácil verificar que os novos operadores de bósons e
obedecem agora à relação de comutação canônica habituais. Expressando o termo de
interação em termos desses operadores e , temos então que
∑
̂ ̂ ̂ ̂
∑ [ ̂ ̂ ̂ ̂ ]
[ ̂ ̂ ̂ ̂ ]
∑ (
A parte livre do hamiltoniano foi reescrita no capitulo 2, em termos dos operadores e
:
∑
(
Finalmente, usando (4.12) e adicionando a contribuição da interação , nós obtemos
o hamiltoniano efetivo
∑
( ( ̅ ̅ ̅ ̅
onde ̅ ⁄ e ̅ ⁄ . Assim, vemos que o modelo de Tomonaga-Luttinger
4.3 Diagonalização do Hamiltoniano
A hamiltoniana (4.13) é quadrática e, portanto, pode ser resolvida exatamente via
uma transformação de Bogoliubov. Vemos de (4.13) que consiste de termos da forma
e que violam a conservação do número total de excitações.
Convém então expressarmos em termos de “novos” operadores de bósons ,
definidos como . Vamos assumir que e são reais e que
dependem somente do valor absoluto de . Note que esses novos operadores satisfazem
também a relação de comutação bosônica
[ ]
logo,
[ ] (
e isso significa que ( . Os coeficientes e podem ser expressos então
como e respectivamente. Os operadores pode ser, portanto, escritos
como
que invertendo, obtemos
Fazendo
∑
( ̅ ̅ ̅ ̅
Substituindo as equações (4.17 a) e (4.17 b) na expressão acima temos
∑
̅ ̅ ̅ ̅
̅ ̅ ̅ ̅
onde
.
Para que o hamiltoniano seja diagonal os termos fora da diagonal devem ser iguais à
zero, com isso
̅ ̅
o que implica em
̅
√ ̅ ̅
̅
√ ̅ ̅
Definindo-se √ ̅ ̅ , o hamiltoniano pode ser escrito na forma
diagonal como
∑| |
(
Com isso, podemos afirmar que é exatamente solúvel o modelo de
Bogoliubov.
4.4 O Hamiltoniano
em Termos dos Campos
e
Como vimos no modelo TL apenas os processos e são considerados
explicitamente. Os termos de interação associados a podem ser escrito em linguem
de bósons como
̂ ̂
(
e um termo similar pra férmions que se propagam para a esquerda:
̂ ̂
(
a soma desses dois termos, é assim a contribuição de para o termo de interação e,
portanto, nos leva ao resultado
∫
Adicionando esse ultimo termo na equação (2.36) do capitulo 2, vemos que o efeito de
é, basicamente, renormalizar a velocidade das excitações, que se torna assim
Procedendo-se da mesma forma com a contribuição de
Portanto, podemos ver que o hamiltoniano se torna quadrático mesmo com um termo
não-trivial de interação. Isso é o que torna a técnica de Bosonização tão interessante
quando lidamos com um sistema unidimensional. Resolver o problema com interação
não é assim tão mais difícil do que lidarmos com um sistema descrito por um
hamiltoniano livre. Contrariamente ao processo , que somente modifica a velocidade
, o processo altera o peso relativo dos termos e no hamiltoniano. O efeito
resultante pode ser absolvido em dois novos parâmetros. Assim podemos reescrever
nosso hamiltoniano quadrático na forma
∫
onde tem dimensão de velocidade, é um parâmetro adimensional. Então temos
( ̅ ̅
(
̅ ̅
que pode ser resolvido com
( ̅
(
̅
̅ ̅ ̅ ̅ )
Podemos notar que de maneira bastante geral que para uma interação repulsiva
̅
e para interação atrativa ̅ . Podemos ver também como o
método de Bosonização é extraordinário em 1D, pois para férmions sem spin,
diagonalizamos o hamiltoniano com interação e em 1D com uma certa facilidade.
A física do modelo TL é descrita, portanto por excitações bosônicas livres.
4.4 Funções de Green
Vamos iniciar o estudo das funções de Green para explorarmos as propriedades de
uma única partícula (do modelo TL). A função de Green é definida como
⟨ | { }| ⟩
⟨ | { }| ⟩ ⟨ | | ⟩
onde e é o operador de ordenamento
temporal. A representação bosônica dos operadores fermiônicos das duas espécies de
férmions, associados aos ramos direito e esquerdo do modelo de TL, pode ser escrito
como
√ √ √
onde
√ ∑
√
⁄ e é um “cutoff” de ultravioleta. Podemos usar a
que diagonaliza , e usando a identidade , onde ,
fazendo os cálculos para , temos que
√ √ √ [ ] onde √ ∑ √ ⁄ ( [ ]
Considere agora o cálculo do comutador acima
[ ] ∑ √ √ ⁄ [ ] ⏟ ∑ [ ]
onde usou-se que , onde é um numero inteiro. Tomando o limite e
fazendo , temos que
[ ] (
√ ( √
√ [ ]
A dependência no tempo do operador é obtida facilmente usando evolução temporal
de um operador, com isso temos que
√ ∑ √ ⁄ √ ∑ √ ⁄
Depois de tomar o limite termodinâmico , a função de Green avançada para o
ramo positivo definida como ⟨ ⟩ , obtemos que
e para o ramo negativo, seguido o mesmo procedimento, temos
Finalmente a função de Green avançada é dada por
A função de Green tem um ramo de corte e não um polo simples o que indica a
Figura 4.4.1 A função número de ocupação de momentos tem uma não-analiticidade em vez da habitual descontinuidade do líquido de Fermi em . Esse é um sinal que não existem quasipartículas em uma dimensão.
densidade de estado local e a distribuição do momento de sistema em uma dimensão ver
figura 4.4.1
∫
∫
onde ,
∫
| |
onde é uma constante. Podemos ver que a densidade local de estados tende a zero
quando . A distribuição de momento não possui uma descontinuidade em
indicando a inexistência de quasipartículas. Entretanto,
natureza metálica do líquido de Luttinger. Em contraste se
| o sistema é
Capítulo 5
Emparelhamento BCS em um Líquido
de Luttinger em 1D
A proposta deste capítulo é analisar como um termo de interação do tipo BCS
afeta diretamente as propriedades de uma única partícula na hamiltoniana de Tomonaga
e Luttinger no espaço 1D, pois não há uma teoria, até o momento, para a
supercondutividade em um liquido de Luttinger. Vamos usar o método de bosonização
introduzido no capitulo 2 para fazer essa análise. Por simplicidade, vamos considerar
férmions, sem spins, livres na presença de um condensado de quasipartículas em um gás
de elétrons em uma dimensão.
5.1 Hamiltoniano e Lagrangiano do Modelo
A densidade de hamiltoniano nas vizinhanças à esquerda e a direita dos dois
pontos de Fermi de férmions livres sem spins, com propensão a formar um condensado
de pares de quasipartículas, é dada por
( √ ) ( √ )
onde é a velocidade de Fermi, e a compressibilidade do condensado. Os campos
, e se fazem necessários para evitar uma quebra de simetria. Claramente,
tomamos aqui, por simplicidade, a velocidade do superfluido como a velocidade de
Fermi [10]. A densidade de hamiltoniana pode ser escrita em termos do campo
fermiônico de Nambu, definido com
e usando-se também que
̅
Podemos analisar cada termo da densidade de hamiltoniano separadamente, e depois de
um pouco de álgebra, vamos reescrevê-los como
̅
e
( √ ) ( √ ) ̅ ( √ )
Portanto, a densidade de hamiltoniana, em termos dos operadores de campo de Nambu,
torna-se
As matrizes são definidas em termos das bem conhecidas matrizes de Pauli , e
A densidade de lagrangiana correspondente a hamiltoniana (5.6) é dada por
Podemos escrever o termo entre parênteses na forma compacta usando o campo de
Nambu . Fazendo isso temos
̅
e usando o fato de que o momento conjugado do campo é dado por
Substituindo (5.8) e (5.9) na densidade de lagrangiana (5.7), temos
̅ [ ] ̅ ( √ )
Aqui nós levamos, explicitamente em conta, o fato de que o campo de fase
associada ao gap é diferente de zero para evitar a quebra espontânea de simetria em 1 D.
Note que, a densidade de lagrangiano é invariante a uma transformação quiral global
, ̅ ̅ e √ . Ela também possui uma
simetria global do tipo U(1), , ̅ ̅ .
5.2 Densidades de Hamiltoniano e Lagrangiano
A técnica de bosonização nos permite resolver exatamente esse modelo de
lagrangiana. Vamos trabalhar diretamente com os campos bosônicos e para isso
introduzimos os dois campos e tais como em [2]
√ √
e
√ √
Note que já estamos ignorando o fator de Klein. No primeiro termo do lado direito
da densidade hamiltoniana (5.8) vamos usar a expansão de produto de operadores
(“OPE”, em inglês). Considere o produto de dois operadores onde
é uma constante real. Quando o produto diverge, pois os operadores não
estão em ordenamento normal. Podemos, por exemplo, escolher o ramo positivo e,
portanto, temos que
√
e, por definição, a expansão de produtos de operadores, por exemplo, para é
dada por
[ ]
Usando a identidade encontrada na
referência [2], podemos escrever a equação (5.15), como
[ √ √ ⟨ ⟩
[ √ ]
[
√
]
√
onde, na segunda linha, o argumento da exponencial foi expandido até a primeira ordem
em e, na terceira linha, nós tomamos o limite . Para o ramo negativo, temos um
resultado parecido que pode ser obtido usando a mesma técnica, e com isso temos que
Definindo-se os campos duais como
e
podemos reescrever os campos e em termos desses novos campos,
obtemos
Substituindo (5.21) e (5.22) em (5.17) e (5.18) respectivamente, e somando-se os termos
( ) ( )
Ainda falta bosonizarmos o termo ̅ (
√ ) , o que é feito usando-se as
definições dos campos fermiônicos (5.12) e (5.13). Por fim, substituindo-se as
equações (5.21) e (5.22), ficamos com o termo de emparelhamento na forma
bosonizada, como
̅ ( √ )
√
√
Vamos definir o momento conjugado do campo simplesmente como
Finalmente, a densidade de hamiltoniano bosonizada, em termos dos novos campos,
torna-se
( ) ( ) [ ]
√
√
Com isso, segue-se imediatamente que a densidade de lagrangiano é então
[ ] [ ]
√ √
A densidade de lagrangiano bosonizada e na forma diagonal fica então
[ ] [ ]
√ √
Esta é a teoria de campo de Sine-Gordon para e uma teoria de campo livre e
sem massa para . O espectro de Sine-Gordon é conhecido exatamente, e neste caso
como √
é maior do que √ , está diretamente associado a um férmion com
massa. Em outras palavras, com era de se esperar, os férmions adquirem “massa” na
presença de um termo de interação do tipo BCS. Entretanto, em uma dimensão 1+1, isso
ocorre sem qualquer quebra espontânea de simetria.
5.3 Refermionização da Densidade de Lagrangiana e
Funções de Correlação
Com a finalidade de tornar a discursão no final da seção anterior mais clara,
vamos refermionizar o campo de bóson de Sine-Gordon. Primeiro realizamos uma
√ ̃
agora substituindo (5.33) na densidade de lagrangiano (5.32), temos
[ ( ̃) ( ̃) ] [ ]
(√ ̃)
Vamos somar e subtrair ( ̃) ( ̃) da equação acima, temos com isso
[ ( ̃) ( ̃) ] [ ] (√ ̃)
[ ( ̃) ( ̃) ]
Para iniciarmos a refermionização da densidade de lagrangiano. Definimos
inicialmente os novos campos fermiônicos tais como
̃
√ √ ̃
̃
√ √ ̃
Assim, o novo campo de Nambu ̃ é tal que
̃ ̃
̃
Note que, com essas definições
̃̅ ̃ ̃ ̃ ̃ ̃ ̃
̃
̃ ̃ ̃
̃
̃ ̃ ̃ ̃
√ ̃ ̃ √ ̃ ̃
√ ̃ ̃
Mas, por definição, ̃ ̃ ̃ o que nos leva imediatamente a
̃̅ ̃ (√ ̃)
Agora temos que refermionizar o termo
( ̃) ( ̃) .
Considere ̃̅ ̃ usando a técnica de expansão de produto de operadores e usando
uma transformação conforme.
̅
segue-se que
̃̅ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̅ ̃
̃ ̅
Mas, esse tipo de cálculo já foi feito anteriormente e o resultado final é facilmente
obtido. Seguindo-se os mesmos passos encontramos que
̃ ̃
√ ̃
e
̃ ̅ ̃ ̅
√ ̅ ̃ ̅
Então,
̃̅ ̃
√ ̃ √ ̅ ̃ ̅
Agora, usando a definição dada em [2],
̅
̅
segue-se que
̃̅ ̃
√ ̅ ̃ ̃ ̅
√ ̅ ̃ ̃ ̅
√ ( ̃ ̃ )
Considere agora, ̃̅ ̃ . Seguindo o mesmo procedimento é fácil chegarmos
ao resultado
̃̅ ̃
√ ̃
Podemos concluir de (5.50) e (5.51) que
̃̅ ̃ ̃̅ ̃ ( ̃̅ ̃ ) ( ̃̅ ̃ )
(
√ ̃) √ ̃
[ ( ̃) ( ̃) ]
[ ( ̃) ( ̃) ]
ou seja,
̃̅ ̃ ̃̅ ̃ [ ( ̃) ( ̃) ]
Multiplicando ambos os lados por,
, temos que
̃̅ ̃ ̃̅ ̃ [ ( ̃) ( ̃) ]
Levando-se esse resultado na densidade de lagrangiana, obtemos
[ ( ̃) ( ̃) ] [ ] ̃̅ ̃
O termo,
( ̃) ( ̃) da densidade de lagrangiana precisa ser
refermionizado, para isso basta notar que
[ ( ̃) ( ̃) ] ( ̃) [ ( ̃) ( ̃) ]
̃ ̃
[ ( ̃) ( ̃) ]
Como sabemos que
̃ ( ̃) ̃ ̃ ̃ ̃
̃̅ ̃
Finalmente, a densidade de lagrangiano em termos dos novos campos fermiônicos
̃̅ ̃ [ ]
( ̃̅ ̃) ( ̃̅ ̃ )
Apesar não haver quebra espontânea de simetria o férmion físico torna-se massivo
e passa a possuir um gap BCS característico do condensado. Além disso, existe uma
auto interação fermiônica atrativa como resultado da contribuição do emparelhamento
produzida pelo condensado. Embora seja um bóson livre sem massa, pelo teorema de
Coleman [11], ele não é um modo de Goldstone. Para esclarecermos isso, vamos
discutir a seguir, a relação de simetria quiral dos campos fermiônicos antigos e os
resultantes. Sob uma transformação quiral as componentes direita e esquerda do campo
Naturalmente, se o propagador anômalo for diferente de zero ele
viola a quiralidade. Para calcularmos esse propagador, nós vamos expressar o campo
original em termo do campo livre e do campo fermiônico ̃, como feito em [12], é
̃
̃
onde,
√
√
Então o propagador anômalo fica da forma
̃ ̃
̃ ̃
Note que e ̃ se dissociam um do outro exatamente e pela
condição de neutralidade [2]. Assim, a parte da assimetria quiral do propagando
anômalo fermiônico se anula.
̃ ̃
No teorema de Coleman, o comportamento de férmions bilineares tais como a
função de correlação de pares devem ser anular para
̃ ̃ ̃ ̃
̃ ̃ ̃ ̃
O segundo termo do lado direito se aproxima de uma constante para | | grande. Então
precisamos nos preocupar com o primeiro termo. Usando-se
e, o nosso resultado conhecido da teoria de bosonização chegamos que
| |
e portanto,
| |
| |
Isso é um decaimento de lei de potencia. Isso está de acordo com o fato de não pode
haver quebra de simetria continua em dimensão 1+1.
| |
Finalmente, vamos considerar o propagador de única partícula
para férmions livres que se propagam para a direita
ostrando novamente um decaimento de lei de potência para grandes distâncias o comportamento de (5.
mas o | | , enquanto que ̃ ̃ é o propagador de
um férmion massivo, e, portanto tem o comportamento | |para o | | grande, onde
é a massa. Então, 71) é
| | | |
m . Entretanto o termo
exponencial apesar disso atenua esse comportamento em grandes distâncias. O
propagador de uma partícula continua sem polo simples e continua também a possuir
um ramo de corte, sinalizando a ausência de ordenamento de longo alcance em uma
dimensão. No entanto, o “gap” introduz uma “massa” no propagador de uma
partícula que está completamente dissociado do campo , e isso faz com que essa
Conclusão
Levando-se em conta que ainda não há uma teoria de supercondutividade em um
líquido de Luttinger, nós formulamos um modelo que descreve um gás de elétrons em
uma dimensão na presença de um termo de interação do tipo BCS. Usando o método de
bosonização, uma ferramenta muito utilizada para sistemas em 1D, e uma
transformação apropriada para dois campos bosônicos, o modelo resultante é
basicamente uma teoria de Sine-Gordon para um desses campos associados e uma teoria
de campo livre, sem massa, para o campo de fase. Para explicamos o significado físico
dessa teoria efetiva refermionizamos o campo de bóson de Sine-Gordon e o férmion
físico adquire massa sem qualquer quebra espontânea de simetria. Para averiguarmos
isso nós calculamos o propagador anômalo e encontramos que ele se anula confirmando
a não violação da simetria quiral. Nós mostramos que ambas as funções de correlação
de pares e o propagador fermiônico de uma partícula obedecem a um comportamento de
lei de potência para grandes distâncias. Esse comportamento, que é típico de um líquido
de TL em uma dimensão, sinaliza também a ausência de um ordenamento de longo
alcance. Porém, esse comportamento de lei de potência para o propagador é atenuado
para grandes distâncias por um fator exponencial que é função do “gap” supercondutor.
Como a magnitude do “gap” é diferente de zero, ele introduz, com isso, uma “massa” no
propagador de uma partícula. Isso, automaticamente, dá um caráter de quasipartícula
mesmo se o estado normal de referência é um líquido de TL, podem haver excitações de
1-particulas que se assemelham as excitações de quasipartículas na presença de um gap
supercondutor. A fase metálica otimamente dopada, e a fase pseudogap dos cupratos
supercondutores se notabilizam pelas suas inúmeras propriedades não convencionais e
pela ausência de quasipartículas bem definidas para . Em contraste, na fase
supercondutora, apesar de haverem pares de Cooper em profusão, as propriedades
supercondutoras são visivelmente não BCS, especialmente, na região de baixa
dopagem. Como vimos, os nossos férmions efetivos se assemelham bastante com as
quasipartículas convencionais. Essa situação de certo modo é retratada facilmente em