Estabilidade de Liapunov e derivada radial

(1)

Estabilidade de Liapunov e derivada radial

Gerard John Alva Morales

TESE APRESENTADA

AO

INSTITUTO DE MATEM ´ATICA E ESTAT´ISTICA

DA

UNIVERSIDADE DE S ˜AO PAULO

PARA

OBTENÇ ÃO DO TÍTULO

DE

DOUTOR EM CIˆENCIAS

Programa: Matem´atica Aplicada

Orientador: Prof. Dr. Manuel Valentim de Pera Garcia Durante o desenvolvimento deste trabalho o autor recebeu

aux´ılio financeiro do CNPq.

(2)

Estabilidade de Liapunov e derivada radial

Esta tese corresponde `a reda¸c˜ao final devidamente corrigida e defendida por Gerard John Alva Morales, e aprovada pela Banca Examinadora.

S˜ao Paulo, 31 de Outubro de 2014

Banca Examinadora:

Prof. Dr. Manuel Valentim de Pera Garcia (Orientador) -IME-USP

Prof. Dr. F´abio Armando Tal -IME-USP

Prof. Dr. Ricardo dos Santos Freire Jr. -IME-USP

Prof. Dr. Ricardo Miranda Martins -IMECC-UNICAMP

(3)

Dedico este trabalho a:

(4)

Agradecimentos

Agrade¸co:

A minha fam´ılia, pelo apoio moral, pelos ensinamentos, pelo carinho, pela confian¸ca e pela for¸ca incondicional que me proporcionaram em todo momento; em particular durante este per´ıodo no doutorado. Meu carinho e especial considera¸c˜ao para: Isadora Silva Alva Morales, Adriana Maria Silva Morales, Marco Ascenci´on Alva Castillo, Mercedes Georgina Morales de Alva e Miriam Edith Alva Morales.

A meu orientador, Prof. Dr. Manuel Valentim de Pera Garcia, pela aceita¸cão como seu aluno de doutorado no programa de matemática aplicada em momentos cr´ıticos na minha forma¸cão académica, pela generosidade em compartilhar comigo a matemática sutil que ele estuda, pela orienta¸cão e pelas valiosas sugestões que tornaram poss´ıvel esta tese. À Profa. Dra. Sônia Regina Garcia, pelas corre¸cões do português e sugestões que deram maior estética a este trabalho.

As sugestões da banca examinadora durante a defesa de esta tese o qual permitiu considerável melhoramento na reda¸cão da mesma.

Aos amigos, Prof. Dr. Jorge Manuel Sotomayor Tello, pela cama-radagem proporcionada em momentos de descontra¸cão no IME, FEA-USP durante a homenagem à Profa. Dra. Marilda Sotomayor e pelas con-versa¸cões sobre equa¸cões integro-diferenciais singulares, Prof. Dr. Alexan-dre Patriota Galvão, pelas conversa¸cões de caracter filosófico durante repeti-das tardes de café, Dr. Pedro Losco Takecian, pela cordialidade e pelas sugestões técnicas sobre Ubuntu, ambiente onde preparei esta tese.

A hospitalidade dos departamentos de matem´atica e matem´atica apli-cada do IME-USP que facilitaram o desenvolvimento desta tese, e o aux´ılio financeiro do CNPq.

(5)

Resumo

Apresentaremos uma classe de energias potenciais Π _∈ C∞_(Ω,R_{) que} s˜ao s−decid´ıveis e que admitem fun¸c˜oes auxiliares de ˇCetaev da forma

h∇jsΠ(q), q_i,q_∈Ω_⊂Rn _{que s˜ao} _s₋_resistentes.

(6)

Abstract

We will present a class of potential energies Π ∈ C∞(Ω,R_{) that are} s₋decidable and that admit auxiliary functions of ˇCetaev of the form_h∇jsΠ(q), q_i, q_∈Ω_⊂Rn _{which are}_s₋_resistant.

(7)

Conte´

udo

1 Introdu¸c˜ao 9

2 Preliminares, o problema e um lema 13

2.1 Fun¸c˜oess-decid´ıveis . . . 13

2.2 Formula¸c˜ao do problema . . . 14

2.2.1 O problema . . . 16

2.3 Lema fundamental . . . 17

3 Cones tangentes e s-resistˆencia 21 3.1 O coneZs−1 . . . 21

3.2 Construindo o cone_Ks . . . 23

3.3 s-resistˆencia de Ps . . . 34

4 Aplica¸c˜oes da s-resistˆencia de Ps 39 4.1 Instabilidade do equil´ıbrio segundo Liapunov . . . 39

4.1.1 Hip´oteses (H1)−(H3) . . . 39

4.1.2 Hip´oteses (H₁1)₋(H3) . . . 40

4.1.3 Hip´oteses (H2 1)−(H3) . . . 41

4.2 An´alise da hip´otese (H1) . . . 42

4.3 Existência de trajetórias assintóticas . . . 46

(8)

(9)

Cap´ıtulo 1

Introdu¸

c˜

ao

Neste trabalho, estamos interessados em estudar a estabilidade segundo Liapunov de um equil´ıbrio (q0, p0) ∈ Rn×Rn do sistema mecˆanico comn

graus de liberdade, cuja dinˆamica ´e governada pelo sistema hamiltoniano

XH(q, p)



 

 

˙

q = ∂H_∂p(q, p)

˙

p=₋∂H_∂q(q, p)

com hamiltoniana H(q, p) = T(q, p) + Π(q), (q, p)_∈ Ω_×Rn, onde Ω _⊂Rn ´e uma vizinhan¸ca aberta de q0. Admitiremos que a energia cin´eticaT(q, p)

é uma forma quadrática definida positiva na variávelp, assim, podemos ver que os equil´ıbrios deste sistema, isto é, os pontos tais queXH(q0, p0) = (0,0),

s˜ao os pontos (q0,0), em queq0 ´e um ponto cr´ıtico de Π.

O teorema de Dirichlet-Lagrangeafirma que, se emq0a energia potencial

Π tem um m´ınimo estrito local, ent˜ao o equil´ıbrio (q0,0) do sistema XH ´e

est´avel.

O seguinte exemplo com 1 grau de liberdade com hamiltoniana definida em R_×R

T(q, p) = 1 2p

2_, _{Π(q) =}

e−1/q2cos(1/q) , q 6= 0

0 , q = 0

mostra que a rec´ıproca do teorema de Dirichlet-Lagrange é falsa, pois neste caso a origem (q0,0) = (0,0) é estável mas Π(q) não tem m´ınimo emq0= 0.

Apesar deste exemplo, a situa¸cão de sistemas com um grau de liberdade (n = 1) é a única em que a estabilidade do equil´ıbrio é caracterizada de forma completa por propriedades da energia potencial.

(10)

10 CAPÍTULO 1. INTRODUÇ ÃO

De fato, se n = 1, a origem (0,0) é estável segundo Liapunov se, e só se, existem sequências (q+_n) e (q_n−), convergentes para 0, (q_n+) estritamente decrescente, (q−

n) estritamente crescente, tais que Π(qn+) > 0 e Π(q−n) > 0

(para uma demonstra¸c˜ao veja [LHR]).

Em termos topológicos, esta condi¸cão para n = 1 pode ser reescrita assim, “ para sistemas com um grau de liberdade, a origem (0,0) é estável segundo Liapunov se, e só se, existe um sistema fundamental de vizinhan¸cas da origem, (Un), tal que Π(q)>0,∀q∈∂Un, para todon∈N”.

Durante algum tempo acreditou-se que a condi¸cão acima caracterizasse a estabilidade da origem para o caso geral de sistemas comngraus de liber-dade, entretanto, embora esta seja efetivamente uma condi¸cão suficiente para a estabilidade da origem, ela não é necessária, conforme se vê pelo exemplo abaixo, devido a Laloy (1977), para o caso de dois graus de liberdade.

Considere em R2_×R2_,_T_{(q, p) =} 1

2(p21+p22) e Π(q) a fun¸c˜ao

Π(q1, q2) =

     e− 1

q21 cos(1

q1)−e

−1

q22q2

2+ cos(q12)

, q1q2 6= 0

0 , q1q2 = 0.

Note que, na verdade, Π ´e de classeC∞. Aqui, o equil´ıbrio (q0,0) = (0,0)

do sistema XH ´e est´avel, mas na reta {q2 = q1}, tem-se para q1 6= 0,

Π(q1, q1) =−q12e−1/q

2 1 <0.

Nos dois exemplos anteriores Π é uma fun¸cão C∞, mas não anal´ıtica, de fato, todas as derivadas de Π em 0 anulam-se. No contexto de fun¸cões anal´ıticas o problema da estabilidade de Liapunov de um equil´ıbrio está discutido em [P].

Neste trabalho estudamos um problema que na literatura (ver por exem-plo [LHR]) é conhecido como inversão do teorema de Dirichlet-Lagrange e consiste em estabelecer condi¸cões suficientes sobre a energia potencial para nosso sistemaXH que garantam a instabilidade do equil´ıbrio (q0,0) = (0,0)

deste sistema hamiltoniano.

Existem muitos trabalhos relevantes abordando este problema (por ex-emplo [LP], [MN], [GT] e [FGT]), mas o problema ainda n˜ao tem uma completa solu¸c˜ao para o caso geral den graus de liberdade.

Um dos primeiros resultados nesta dire¸c˜ao foi mostrado pelo pr´oprio A.M. Liapunov, e mostra que: se a matriz hessiana de Π em q0 mostra que

Π não tem m´ınimo nesse ponto, então (q0,0) é um equil´ıbrio instável do

sistema XH. Utilizando a linguagem de jatos pontuais, introduzida por A.

(11)

11

ordem 2 de Π em q0 mostra que a energia potencial Π n˜ao tem m´ınimo em

q0, então o equil´ıbrio(q0,0) do sistema hamiltoniano XH é instável.

Na classe de energias potenciais Π que admitem jatos de ordens_≥2 no ponto cr´ıtico q0, a generaliza¸c˜ao natural deste resultado ´e a:

Conjectura (Liapunov-Barone)

Se para algum natural s _≥ 2, o jato de ordem s de Π em q0 mostra que

a energia potencial Π n˜ao tem m´ınimo em q0, ent˜ao o equil´ıbrio (q0,0) do

sistema hamiltoniano XH ´e inst´avel.

No caso em que o jato de ordem sde Π é um polinômio homogêneo, no contexto dengraus de liberdade, o artigo [MN] mostra, usando a teoria da variedade estável, que, o equil´ıbrio (q0,0) do sistemaXH, é instável.

No artigo [GT] mostrou-se que esta conjectura é verdadeira no contexto de 2 graus de liberdade, e em [FGT] mostrou-se parcialmente, que a con-jectura é verdadeira no contexto geral de ngraus de liberdade. Nestes dois resultados usaram-se fun¸cões auxiliares como ferramenta básica.

Tanto no trabalho [MN] como em [GT] e [FGT] demonstrou-se não ape-nas a instabilidade de (q0,0), mas a existência de trajetórias assintóticas

para esse equil´ıbrio.

Outro resultado cl´assico neste problema ´e um teorema de ˇCetaev que garante a instabilidade de (q0,0) se existe uma componente conexa do

con-junto Π−1₍_−∞_,_{0) aderente a}_q

0 em que a derivada radial de Π,h∇Π(q), qi,

´e estritamente negativa (se Π tem essa propriedade diremos que Π ´e um potencial de tipo ˇCetaev).

Neste trabalho consideramos uma questão que relaciona estas duas for-mas de abordar o problema da inversão do teorema de Dirichlet-Lagrange, mais precisamente, admitiremos que jsΠ mostra que q0 não é ponto de

m´ınimo de Π e que jsΠ é um potencial de tipo ˇCetaev (isto é, suporemos que a derivada radial de js_Π, _h∇_js_{Π(q), q}_i _{é estritamente negativa numa}

componente conexa de (jsΠ)−1(−∞,0)), e procuramos determinar situa¸c˜oes em que isto garantisse que Π ´e um potencial de tipo ˇCetaev (e portanto a instabilidade de (q0,0) fica provada).

Conseguimos assim determinar uma classe de energias potenciais em que a instabilidade da origem ´e garantida por jatos.

O resultado central do trabalho (veja o Teorema 4.1.1) afirma, em lin-guagem um pouco livre (para defini¸cões precisas veja a se¸cão 2.1) que se a energia potencial Π : Ω_→ R_{, Ω}_⊂Rn _{aberto com 0} _∈_{Ω, é suficientemente} regular e tem um ponto cr´ıtico na origem, com Π(0) = 0, satisfaz:

(H1) Paraℓ≤s−1, jℓΠ(q)≥0 para q numa vizinhan¸ca da origem.

(12)

12 CAPÍTULO 1. INTRODUÇ ÃO

(H3) Existeε >0 tal que

{q_∈Rn_|_js_Π(q)_<_0,_|_q_|_{< ε}_{} \ {}₀_{} ⊂ {}_q _∈Rn_|h∇_js_{Π(q), q}_i_<_0,_|_q_|_{< ε}_}_.

Ent˜ao Π ´e um potencial de tipo ˇCetaev.

Isso mostra que nos sistemas XH em que as energias potenciais

satis-fazem (H1), (H2) e (H3) o ponto (0,0) ´e inst´avel segundo Liapunov, o que

justifica nossa afirma¸c˜ao anterior sobre caracterizar uma classe de potenciais em que a instabilidade ´e garantida por jatos.

Os resultados obtidos neste trabalho garantem além da instabilidade da origem do sistema XH, a existência de trajetórias assintóticas à origem de

XH.

As hip´oteses (H2) e (H3) feitas sobre Π s˜ao, em um sentido que expomos

no texto, bastante naturais neste contexto. Já a hipótese (H1) parece, à

primeira vista, um pouco restritiva demais, porém mostramos na se¸cão 4.2 que, enfraquecendo um pouco essa hipótese, a conclusão do nosso resultado central não se mantem.

(13)

Cap´ıtulo 2

Preliminares, o problema e

um lema

O objetivo deste cap´ıtulo é apresentar nosso problema e também apre-sentar um lema que será fundamental no resto do trabalho.

2.1 Fun¸

c˜

oes

s

_{-decid´ıveis}

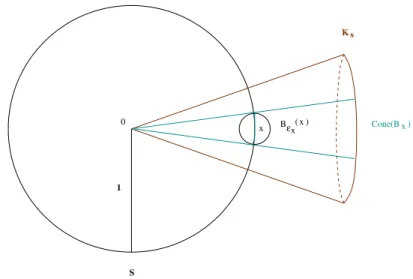
No espa¸co euclidiano (Rn_,_{| · |}_{) com a norma usual, consideramos uma} vizinhan¸ca aberta da origem Ω e denotamos por B(q0, ε) o conjunto aberto

B(q0, ε) ={q∈Rn| |q−q0|< ε}.

Quando q0 = 0, simplesmente denotaremos esta bola por Bε.

Como é usual, para fun¸cões f, g : Ω _→ R _{em que} _g(q) ₆_{= 0 se} _q ₆_{= 0, a} nota¸cão f =o(g) em 0 significa que

lim

q→0

f(q) g(q) = 0.

Defini¸cão 2.1.1 Sejam s um natural não nulo eΩ uma vizinhan¸ca aberta da origem de Rn_{. Dizemos que uma fun¸c˜}_ao _f _{: Ω}_→R _{tem jato pontual de} ordems na origem, se existe um polinômio de grau menor ou igual as, que denotamos por js_f_{, tal que}

f(q) =jsf(q) +o(_|q_|s).

Observa¸cão 2.1.2 E simples ver que existe no m´´ aximo um polinômio que satisfaz estas condi¸cões e, se f for de classe Cs, então f tem jato pontual de ordem sna origem ejs_f _{é o polinˆ}_{omio de Taylor de ordem}_s_de _f _em_0.

(14)

14 CAP´ITULO 2. PRELIMINARES, O PROBLEMA E UM LEMA

Denotemos porJs(Ω,R_{) o conjunto das fun¸c˜oes} _f _{: Ω}_→ R_{, com}_f_{(0) = 0,} que admitem jato pontual de ordemsna origem.

Diremos quef tem um m´ınimo forte (respectivamente um m´aximo forte) na origem se existeε >0 tal que f(x)>0 (respectivamente f(x)<0) para todox_∈(Ω_{\ {}0_})_∩Bε; diz-se quef tem um m´ınimo fraco (respectivamente

um m´aximo fraco) na origem se existe ε >0 tal que f(x) _≥0 (respectiva-mentef(x)≤0) para todox∈Ω∩Bε e existe uma sequˆencia (xk),xk 6= 0,

comxk →0 ef(xk) = 0.

Nestes casos diz-se quef tem extremo forte, ou extremo fraco, na origem. Se f n˜ao tem extremo forte ou fraco na origem, diremos quef tem sela na origem.

Diz-se que as fun¸cões f : Ω _→ R _e _g _{: Ω} _→ R _{têm mesmo} compor-tamento em rela¸cão a extremo na origem se f e g tiverem ambas m´ınimo forte (respectivamente máximo forte) na origem, ou ambas tiverem m´ınimo fraco (respectivamente máximo fraco) na origem, ou ambas tiverem sela na origem.

Defini¸cão 2.1.3 Uma fun¸cão f _∈ Js_(Ω,_R₎ _é _{s-decid´ıvel se, para cada}

fun¸c˜ao g ∈ Js(Ω,R₎ _{tal que} _js_f ₌ _js_{g, tem-se que ambas as fun¸c˜}_oes _f eg possuem o mesmo comportamento em rela¸c˜ao a extremo na origem.

Denotamos por Ds_(Ω,_R_{) a classe de fun¸c˜oes} _f _∈ _Js_(Ω,_R₎ _{s-decid´ıveis na}

origem. Uma consequência direta desta defini¸cão é que, se f ∈ Ds(Ω,R_), então na origem 0, f tem extremo forte ou uma sela, conforme se vê na observa¸cão abaixo.

Observa¸c˜ao 2.1.4 Se f _∈ Jr_(Ω,_R₎ _e _jr_f _{tem na origem um extremo}

brando, ent˜ao f /_∈Dr_(Ω,_R_{). Para ver isto, basta supor, sem perda de}

gen-eralidade que jrf tem m´ınimo fraco e considerar a fun¸c˜ao g(q) :=jrf(q) +

|q_|2r _∈ Jr(Ω,R_{); observemos que enquanto} _jr_f _{tem m´ınimo fraco,} _g _tem m´ınimo forte na origem; e se considerarmosg(q) :=jr_f(q)_−|_q_|2r_∈_Jr_(Ω,_R_),

g tem uma sela na origem (ou m´aximo, caso f ≡0).

Mais detalhes acerca des-decidibilidade podem ser vistos em [B] ou [G].

2.2 Formula¸

c˜

ao do problema

Sejam dois números naturais k e s, com 2 _≤ k < s, e consideremos fun¸cões f ∈Js(Ω,R_{) cujo primeiro jato n˜}_{ao nulo é o de ordem k. Então o} jato de ordemsde f na origem, pode ser escrito da seguinte forma

(15)

2.2. FORMULAC¸ ˜AO DO PROBLEMA 15

onde, para cada ℓ∈ {k, ..., s},fℓ(q) =jℓf(q)−jℓ−1f(q). Note que fℓ ´e um

polinômio ℓ₋homogêneo (isto é, fℓ(λq) =λℓfℓ(q), para todo λ ∈R e para

todo q _∈Rn_{), chamada parte homogˆenea de grau} _ℓ _de _js_f_{. Veja ainda que} fk =jkf.

Estamos interessados em energias potenciais cujo jato de ordemsmostra que esta fun¸cão não têm m´ınimo na origem, mais precisamente isto é for-malizado na defini¸cão abaixo.

Defini¸cão 2.2.1 Dada uma fun¸cão f ∈ Js(Ω,R_{), dizemos que o jato} _js_f mostra quef não tem m´ınimo na origem se, para cada fun¸cãog_∈Js(Ω,R₎ com js_f ₌_js_{g, tem-se que} _g _n˜_{ao tem m´ınimo na origem.}

Observa¸c˜ao 2.2.2 Note que o fato dejs_f _{mostrar que} _f _n˜_{ao tem m´ınimo}

na origem não implica quef és-decid´ıvel, por exemplo, sej2f(x, y) =−x2, claro que esse jato mostra que f não tem m´ınimo na origem, mas f não é 2-decid´ıvel, pois j2_f _{tem m´}_{aximo n˜}_{ao estrito na origem. Entretanto se o}

primeiro jato n˜ao nulo de f na origem tem m´ınimo fraco nesse ponto ejs_f

mostra que f não tem m´ınimo na origem, é simples ver que f é s-decid´ıvel e tem sela na origem.

Ser´a de fundamental importˆancia estudar o comportamento da derivada radial de js_{Π na origem,} _P

s(q) :=h∇jsΠ(q), qi; em geral, as fun¸c˜oes jsΠ e

Psn˜ao tˆem o mesmo comportamento em 0, como pode ser visto no seguinte

exemplo

Exemplo 2.2.3 Consideremos um polinˆomio

f(q1, q) := (aq1−b|q|2)2+c|q|4, com a >0, b >0, c >0, b2>8c.

e onde q:= (q2, ..., qn). Notemos que

∂f ∂q1

= 2a(aq1−b|q|2)

∂f ∂qj

=

−4abq1+ (4b2+ 4c)|q|2

qj, j= 2, ..., n

assim, a derivada radial _h∇f(q), q_i= _∂q∂f 1q1+

Pn

j=2 ∂q∂fjqj, escreve-se como

h∇f(q), q_i= 2a2q1−

3b 2a|q|

22 −b

2₋_8c

2

|q_|4.

´

(16)

A fun¸c˜aoh∇f(q), qi, foi utilizada por ˇCetaev para mostrar o seguinte resul-tado de instabilidade

Teorema 2.2.4 (N.G. ˇCetaev [1936])

Suponha que Bε ⊂Ω, para algum ε >0 e que o sistema hamiltoniano XH

satisfaz as propriedades

1. Θ =_{q _∈Bε|Π(q)<0} 6=∅

2. 0_∈∂Θ

3. h∇Π(q), qi<0, ∀q∈Θ

ent˜ao o equil´ıbrio(q, p) = (0,0)´e instavel.

Uma demonstra¸cão deste resultado pode ser vista, por exemplo, em [LHR]. Se uma energia potencial Π satisfaz as condi¸cões deste teorema diremos que Π é um potencial do “tipo ˇCetaev”.

O que faremos neste trabalho ser´a determinar se Π ´e um potencial do “tipo ˇCetaev”a partir de propriedades dejs_{Π. Mais precisamente,}

descreve-mos este problema a seguir.

2.2.1 O problema

Supondo quejsΠ é uma energia potencial do tipo ˇCetaev, será verdade que Π também é uma energia potencial do tipo ˇCetaev?

Esta quest˜ao, sem outras hip´oteses, tem uma resposta negativa, mesmo quando js_{Π mostra que Π n˜}_{ao tem m´ınimo na origem, e um exemplo}

mostrando isto ser´a apresentado em algum detalhe no cap´ıtulo 4.

A fim de trabalhar no contexto das energias potenciais Π_∈Js_(Ω,_R_{) que}

n˜ao apresentam m´ınimo na origem, consideramosPs(q) :=h∇jsΠ(q), qie os

conjuntos semi-alg´ebricos

As:={q ∈Ω|jsΠ(q)<0}, Cs:={q ∈Ω|Ps(q)<0}

e vamos supor que a energia potencial Π_∈Js_(Ω,_R_{) satisfaz:}

(H1) jℓΠ(q)≥0 numa vizinhan¸ca da origem 0∈Ω, seℓ≤s−1;

(H2) jsΠ mostra que Π n˜ao tem m´ınimo na origem 0∈Ω;

(17)

2.3. LEMA FUNDAMENTAL 17

Claro que (H3) mostra que jsΠ ´e um potencial do tipo ˇCetaev.

Nosso principal resultado ´e:

Teorema.

“ Se Π satisfaz as hipóteses (H1)−(H3), então Π é um potencial de tipo

ˇ

Cetaev ”.

Mostraremos tamb´em que, enfraquecendo um pouco a hip´otese (H1) esse

resultado deixa de ser verdadeiro.

2.3 Lema fundamental

Nesta se¸cão colocamos em evidência a importância da hipótese (H3), o

que será crucial na constru¸cão feita no próximo cap´ıtulo.

Seγ : [0, ρ]→Rn_{´e uma curva alg´ebrica tal que}_{γ(0) = 0 e}_γ(t)₆_{= 0 para} todo t_∈(0, ρ]; denotamos por rγ a semi-reta tangente aγ na origem. Para

detalhes técnicos acerca de curvas algébricas e conjuntos semi-algébricos referimos a [M].

Lema 2.3.1 Suponha que Π ∈Js(Ω,R₎ _{satisfaz a hip´}_otese _(H₃₎ _{e seja} _γ _: [0, ρ]_→ Rn _{uma curva alg´ebrica tal que} _{γ(0) = 0} _e _γ(t) _∈_A_s _se _t_∈_{(0, ρ].} Ent˜ao js_Π_|

rγ tem m´aximo local estrito na origem.

Demonstrac¸˜ao

Sejav6= 0 o versor deγ em 0+. Como jsΠ ´e um polinˆomio de graus, existe ε >0 tal que uma das seguintes possibilidades acontece:

(a) jsΠ(λv)>0, para todo λ_∈(0, ε) (b) js_{Π(λv) = 0, para todo} _λ_∈_{(0, ε)}

(c) jsΠ(λv)<0, para todo λ∈(0, ε)

eλv,λ_∈R+_{, é uma parametriza¸cão de}_r_γ_{. Mostremos que as possibilidades} (a) e (b) não ocorrem.

1. Suponha que (a) ocorre. Tome q = ε₂v, ent˜ao jsΠ(q) > 0 e escolha δ >0 tal que1jsΠ(x)≥0, para todo x tal que|x−q|< δ. Seja agora Σδ(q) o disco de dimens˜ao n−1 centrado em q de raio δ, ortogonal

a v. Tomando ent˜ao o tronco de cone ∆ de v´ertice 0 e base Σδ(q),

veja que, como v ´e o versor de γ em 0+ e, para t > 0, γ(t) ∈ As,

1

Neste ponto pode-se garantirjsΠ(x)>0 emB(q, δ), preferimos a desigualdade branda

(18)

resulta que existe um ponto p no interior de ∆ tal que jsΠ(p) < 0. Considere a semi-reta de origem 0 que passa por pe note que, comop está no interior de ∆ existe exatamente um ponto w dessa semi-reta que está em Σδ(q). Claro que pé um ponto do interior do segmento

0we, comojsΠ ´e um polinˆomio,jsΠ(p)<0 ejsΠ(w)_≥0, resulta que existetu ∈(0,1) tal que o pontou:=tuw do segmento 0w satisfaz,

(i) jsΠ(tw)_≥0, setu ≤t≤1;

(ii) existeρ >0 tal quejs_Π(tw)_<_{0, se}_t

u−ρ < t < tu.

Portanto u_∈As\ {0} e _dtdjsΠ(tw)|t=tu ≥0. Como

d dtj

s_Π(tw)

t=tu

=

∇jsΠ(tuw), w=

1 tu

Ps(u)

resulta Ps(u) ≥ 0. Isso contraria a hip´otese (H3), e mostra que (a)

n˜ao pode acontecer.

2. Suponha que (b) ocorre. Tome outra vezq= ₂εve agora escolha Σ1(q)

o disco de dimens˜ao n₋1 centrado em q de raio 1, ortogonal a v. Se existe uma sequˆencia de pontos (qk) ⊂Σ1(q)\ {q}, qk → q, tais que

jsΠ(qk) < 0 ent˜ao q ∈ As\ {0}, e como jsΠ(λv) = 0, se λ ∈ (0, ε),

resulta

Ps(q) =

ε 2

∇jsΠ(ε 2v), v

= ε 2

d dλj

s_Π(λv)

λ=ε

2 = 0

contrariando outra vez a hip´otese (H3). Se isso n˜ao acontece, existe

δ >0 tal quejs_Π(x)_≥_{0, para todo} _x_∈_Σ

δ(q), aplicamos o raciocinio

do item (a) contrariando a hip´otese (H3) tamb´em neste caso. Assim,

(c) ocorre (ver Figura 2.1).

(19)

2.3. LEMA FUNDAMENTAL 19

. r

γ

A

γ Cs

s

0

ε n−1 R

B_ε

Figura 2.1: A hip´otese (H3)

0

γ A 4

C4

r γ y

Figura 2.2: Sem a hip´otese (H3)

Notemos que sem a hip´otese (H3) o resultado enunciado no lema acima

´e falso, para ver isto considere, emR2_{, Π(x, y) = (y}₋_x2_)(y₋_3x2_{) e a curva} γ(t) = (t,2t2_), _t_≥_{0. ´}_{E imediato ver que} _γ _{´e tangente em 0}+ _{ao semi-eixo}

x≥0 e Π(γ(t)) =−t4 enquanto Π(x,0) = 3x4 (ver Figura 2.2).

Além disso, é interessante destacar que o Lema 2.3.1 apresenta apenas conclusões sobre o sinal de jsΠ em semi retas tangentes a curvas em As e

n˜ao em Cs, o exemplo a seguir esclarece este ponto.

Considere emR3_{o polinˆ}_omio_f_{(x, y, z) = (x}₋_8z2₎2_+z4₋_y6_{, no semi-eixo} y≥0 este polinômio satisfazf(0, y,0) =−y6, isto é, este semi-eixo menos a origem está contido no conjuntof−1₍_−∞_,_{0). Notemos que a derivada radial}

F(x, y, z) =_h∇f(x, y, z),(x, y, z)_i, ´e um polinˆomio que pode ser escrito como

(20)

r γ

γ C 6

B

A 6

y

x B_ε

ε

0

Figura 2.3: γ ⊂C6\A6 n˜ao satisfaz a conclus˜ao do Lema 2.3.1

notemos tamb´em que no conjunto

B:={(x, y, z)∈R3_|₍₁₂₋√_14)z2_≤_x_≤_{(12 +}√_14)z2_, ₋_az2_≤_y_≤_az2_} onde [(4 +√14)2_{+ 1]}16 < a <2, o polinˆomio

G(x, y, z) := 2[x₋(12 +√14)z2][x₋(12₋√14)z2]

satisfaz G((12±√14)z2,±az2, z) = 0 e como F(x, y, z) < G(x, y, z) re-sulta que vale a inclus˜ao B _⊂ C6, onde C6 ´e a componente conexa de

F−1₍_−∞_,_{0) que cont´em o semi-eixo} _y _≥ _{0. Por outro lado, nas curvas}

((12±√14)z2,±az2, z) da fronteira de B vˆe-se que

f(12±√14)z2,±az2, z=(4±√14)2+ 1−a6z8z4,

daqui, se ε = [(4−

√ 14)2

+1]18

a

3

4 temos que f((12±

√

14)z2,±az2, z) > 0 para todo 0< z < ε, portanto

(A6\ {0})∩Bε⊂B∩Bε

onde A6 ´e a componente conexa de f−1(−∞,0) que cont´em o semi-eixo

y≥0. Mostramos, de fato, a inclus˜ao

(A6\ {0})∩Bε ⊂C6∩Bε.

Mas note que, a curva γ(t) = ((12 +√14)t2, at2, t), t _≥ 0 ´e tangente em 0+ _{ao semi-eixo} _z _≥_0, _{γ(0) = 0, e vale} _{F(γ(t)) =} ₋_6a6_t12_{, e se}_λv _{´e a}

(21)

Cap´ıtulo 3

Cones tangentes e

s

_-resistˆ

_encia

Neste cap´ıtulo ser´a construido um cone positivo _Ks ⊂ Rn de v´ertice

na origem, no qual terá sentido apresentar nosso resultado principal de s₋resistência. Entendemos como cone de vértice na origem a um conjunto M _⊂ Rn _{tal que para cada} _q _∈ _M _{e todo} _λ _∈ R _tem-se _λq _∈ _M; _M _será chamado cone positivo se esta propriedade vale para todo λ≥0.

Lembremos que, a menos de men¸cão expl´ıcita em contrário, Ω será uma vizinhan¸ca aberta da origem de Rn _e _Js_(Ω,R_{) representa o conjunto das} fun¸cões de Ω em R_{, de classe} _C2 _{e que tem jato pontual de ordem} _s_{em 0.}

Lembremos tamb´em que, a energia potencial Π _∈ Js(Ω,R_{) satisfaz as} hip´oteses:

(H1) jℓΠ(q)≥0 numa vizinhan¸ca da origem 0∈Ω, seℓ≤s−1;

(H2) jsΠ mostra que Π n˜ao tem m´ınimo na origem 0∈Ω;

(H3) existeε >0 comBε⊂Ω, tal que (As\ {0})∩Bε⊂Cs◦∩Bε.

3.1 O cone

Z

_s₋₁

Como no cap´ıtulo anterior, se Π _∈ Js(Ω,R_{) ent˜ao denotemos} _P_s_{(q) =}

h∇js_{Π(q), q}_i _{e por}_A

s e Cs os conjuntos semi-alg´ebricos

As:={q∈Ω|jsΠ(q)<0}, Cs:={q∈Ω|Ps(q)<0}.

Lembremos que se γ : [0, ρ] → Ω ´e uma curva alg´ebrica com γ(0) = 0 e γ(t)₆= 0 se 0< t_≤ρ, denota-se por rγ a semireta tangente a γ em 0+.

Uma consequˆencia direta do Lema 2.3.1 ´e o seguinte

(22)

22 CAP´ITULO 3. CONES TANGENTES E S-RESIST ˆENCIA

Corolário 3.1.1 Se Π ∈ Js(Ω,R₎ _{satisfaz a hip´}_otese _(H₃₎ _{e, além disso,} jsΠé o primeiro jato que mostra que Π não tem m´ınimo na origem, então, para toda curva algébrica γ : [0, ρ]_→Rn _{tal que} _{γ(0) = 0} _e_γ_(t)_∈_A_s_{\ {}₀_} se 0 < t ≤ρ, tem-se que Πℓ|rγ ≡ 0 para todo ℓ ≤ s−1 e Πs(q) <0 para

cadaq _∈rγ\ {0}.

Demonstrac¸˜ao

Seja uma curva alg´ebricaγ : [0, ρ]_→Rn _{tal que} _{γ(0) = 0 e}_γ_(t)_∈_A_s_{\ {}₀_} se 0< t≤ρ; parametrizemos a semi-retarγ={τ q0} comτ ≥0 para algum

q0∈rγ\ {0}. Do Lema 2.3.1 segue que

jsΠ(q)<0, ∀q∈(rγ\ {0})∩Bε0

para algum 0< ε0 <1. UsandojsΠ =Pℓ≤s−1Πℓ+ Πs e a homogeneidade

das fun¸c˜oes Πℓ, podemos escrever

jsΠ(τ q0) =

X

ℓ≤s−1

τℓΠℓ(q0) +τsΠs(q0).

Suponha, por absurdo, que para algum ℓ _≤ s₋1, Πℓ|rγ 6= 0, tomemos

ℓ0 = min{ℓ≤s−1 : Πℓ|rγ 6= 0}, então Πℓ0|rγ é uma fun¸cão homogênea de

grauℓ0, portanto ou Πℓ0|rγ tem m´ınimo estrito em 0 ou tem m´aximo estrito

em 0. No primeiro caso Πℓ0(q0) > 0 e j

s_{Π(τ q}

0) = τℓ0Πℓ0(q0) +o(|q0|

s_),

dondejs_Π_|

rγ tem m´ınimo estrito local em 0, contrariando o Lema 2.3.1. No

segundo caso jℓ0_{Π mostra que Π n˜}_{ao tem m´ınimo na origem, contrariando} a hip´otese, pois ℓ0 < s.

Observa¸c˜ao 3.1.2 Considere

Zs−1 :=

s−1

\

ℓ=k

q_∈Ω

Π_ℓ(q) = 0 \ {0}.

Observemos que, Zs−1 ⊂(js−1Π)−1({0}) e, da homogeneidade das fun¸c˜oes

Πℓ, segue queZs−1∪ {0} ´e um cone de v´ertice em0.

Observa¸cão 3.1.3 O Corolário3.1.1, mostra que seΠ_∈Js_(Ω,_R₎ _e _js_Π _é

o primeiro jato que mostra queΠ n˜ao tem m´ınimo na origem, ent˜ao existe pelo menos uma semi-retar_⊂Zs−1 de origem em 0 tal que Πs(q)<0 para

(23)

3.2. CONSTRUINDO O CONE _KS 23

Proposi¸c˜ao 3.1.4 Suponha que Π satisfaz as hip´oteses (H1)−(H3), seja

uma semi-reta r_⊂Zs−1 de origem em0 e denotemos por ∆r `a componente

conexa de Zs−1 que cont´emr. Se Πs(q0)<0para algum q0 ∈r\ {0}, ent˜ao

Πs(q)<0 para todoq ∈∆r\ {0}.

Demonstrac¸˜ao

Da conexidade de ∆r, basta mostrar que Πs(q)6= 0 para todoq ∈∆r\ {0}.

Suponha por absurdo que, para algum q1 ∈ ∆r \ {0}, vale Πs(q1) = 0.

Notemos primeiro que na reta ℓ = {tq0|t ∈ R} tem-se Πs(tq0) = tsΠs(q0),

assim o ´unico ponto de ℓ onde Πs anula-se ´e a origem, portanto q1 ∈/ ℓ.

Tomemos ent˜ao q∗ _{o ponto do segmento} _q₀_q₁ _{mais afastado de} _q₁ _{tal que}

Πs(q∗) = 0 e Πs(q) < 0 se q est´a no segmento q0q∗ \ {q∗}. Ent˜ao, pelas

observa¸c˜oes precedentes, q∗ ₆= 0, e temos que q∗ _∈ As\ {0} e jsΠ(q∗) = 0,

contrariando (H3).

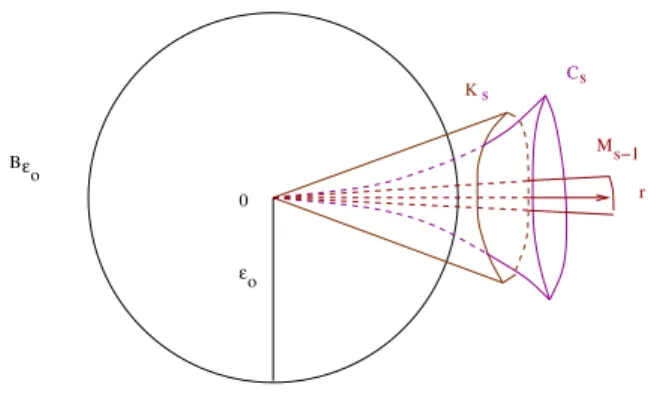
3.2 Construindo o cone

_K

_s

Se r ⊂ Zs−1 ´e uma semi-reta de origem em 0 e q ∈ r\ {0} um ponto

fixado, podemos considerar aqui o hiperplano [r]⊥ _{ortogonal a} _r _{que passa}

por q. Vamos construir um cone fechado Kr ⊂Rn contendo r e de v´ertice

na origem; simplesmente consideramos uma bola fechadaB ⊂[r]⊥de centro em q e raio δ >0, com B_∩Zs−1 ⊂∆r, e definindoKr como

Kr :=

[

x∈B

Lx, Lx:={λx|0≤λ}.

Este cone fechado será útil no futuro para uma constru¸cão mais sofisticada.

Proposi¸c˜ao 3.2.1 Suponha que Π satisfaz as hip´oteses (H1)−(H3), seja

uma semi-reta r _⊂ Zs−1 de origem em 0 tal que Πs(q) < 0 para todo q ∈

r\ {0} e considere a componente conexa ∆r de Zs−1 que cont´em r. Ent˜ao

existe um cone fechado Kr⊂Rn de v´ertice na origem tal que

1. r_{\ {}0_{} ⊂}(Kr)◦,

2. Πs(q)<0 para todoq ∈Kr\ {0},

(24)

K r

∆r r

0

B R

n−1

Figura 3.1: O cone Kr e o cone ∆r⊂Zs−1.

Demonstrac¸˜ao

Fixemos um pontoq0 ∈r\{0}e escolhamos um n´umero 0< δ0 <1 pequeno

o suficiente tal queB_∩Zs−1⊂∆r, ondeB⊂[r]⊥´e a bola fechada de centro

emq0 e raioδ0>0 de [r]⊥; como feito acima, o conjunto Kr dado por

Kr:=

[

x∈B

Lx, Lx:={λx|0≤λ}

é de fato um cone fechado de vértice em 0 e como vale Lq0 = r, segue então o item 1. Como Πs(q0) < 0, da continuidade da fun¸cão Πs segue

que eventualmente diminuindoδ0>0, se necess´ario, tem-se Πs(x)<0 para

todox _∈B, e sendo Πs uma fun¸c˜ao homogˆenea tem-se que Πs(q)<0 para

todo q ∈ Lx \ {0} e todo x ∈ B, consequentemente Πs(q) < 0 para todo

q_∈Kr\{0}, isto mostra o item 2. Para obter o item 3, note que, comoKre

Zs−1 são cones de vértice na origem, então, sey∈Kr∩Zs−1,ty∈Kr∩Zs−1,

para todot >0, assim tomandot⋆ = |q0|

|y|, tem-se t⋆y∈B∩Zs−1, portanto

Kr∩Zs−1 =

[

x∈B

(Lx∩Zs−1) =

[

x∈B∩Zs−1 Lx.

ComoB∩Zs−1⊂∆r, resulta da conexidade de ∆r quey∈∆r, concluindo

a demonstra¸c˜ao (ver Figura 3.1).

Observa¸c˜ao 3.2.2 A Proposi¸c˜ao 3.2.1 diz que, para cada semi-reta r _⊂ Zs−1 de origem em 0 tal que Πs(q) < 0 para todo q ∈ r\ {0}, o cone Kr

(25)

Corol´ario 3.2.3 Suponha que Π satisfaz as hip´oteses (H1)−(H3), e

con-sidere uma semi-reta r_⊂Zs−1 de origem em 0 tal que Πs(q)<0 para todo

q _∈r_{\ {}0_}, e seja ∆r a componente conexa de Zs−1 que cont´em r. Ent˜ao

existe um cone Ks⊂Rn de v´ertice na origem tal que

(a) ∆r\ {0} ⊂(Ks)◦.

(b) Seq_∈∂_Ks\{0}existeℓ∈ {k,· · · , s−1}tal queΠℓ(q)>0eΠj(q) = 0

para j < ℓ.

(c) Πs(q)<0 para todoq ∈ Ks\ {0}.

Demonstrac¸˜ao

Da Proposi¸c˜ao 3.1.4, temos que para cada semi-reta ˜r_⊂∆r de origem em 0

tem-se Πs(q)<0 para todoq∈r˜\{0}e da Proposi¸c˜ao 3.2.1, existe um cone

fechadoK˜r⊂Rnde v´ertice na origem com as propriedades l´a descritas, isto

´e:

1. r_{\ {}0_{} ⊂}(Kr)◦,

2. Πs(q)<0 para todoq ∈Kr\ {0},

3. Kr∩Zs−1 ⊂∆r.

Definamos o conjunto Ks como sendo

Ks:=

[

˜

r⊂∆r

Kr˜.

Seja q ∈ Ks\ {0} arbitr´ario, ent˜ao q ∈ Kr˜\ {0} para alguma semi-reta

˜

r _⊂∆r, tal que ˜r\ {0} ⊂Kr◦˜; daqui segue que, Πs(q)<0 e al´em disto, para

cadaλ_≥0 valeλq_∈Kr˜; isto mostra o item (c) e queKs´e de fato um cone

de v´ertice em 0.

Notemos que para todo ˜r _⊂ ∆r, o conjunto Sr˜⊂∆r(K˜r)

◦ _{´e aberto e}

S

˜

r⊂∆r(K˜r)

◦ _{⊂ K}_s_{, portanto} S

˜

r⊂∆r(Kr˜)

◦ _⊂ ₍_K_s₎◦_{, e daqui obtemos as}

seguintes inclus˜oes (∆r\ {0}) =

[

˜

r⊂∆r

(˜r_{\ {}0_})_⊂ [

˜

r⊂∆r

(Kr˜)◦ ⊂(Ks)◦,

o que mostra o item (a).

Agora note que _Ks∩Zs−1 =S˜r⊂∆rK˜r∩Zs−1 e, pela Proposi¸c˜ao 3.2.1

Kr˜∩Zs−1 ⊂∆r\ {0}, assim

(26)

r _∆r

0 R

n−1

F i

K s

Figura 3.2: O cone _Ks e algum coneFi⊂∂Ks\ {0} (k≤i≤s−1).

ComoZs−1 =Zs−1∪ {0}, ´e claro que se q ∈Zs−1 e q6= 0, ent˜ao q ∈Zs−1,

o que mostra que∂_Ks∩Zs−1∩Bδ =∅, para todoδ >0.

Portanto, seq _∈∂_Ks e q= 0, ent˜ao6 q∈(Zs−1)c, e como

(Zs−1)c =

s−1

[

ℓ=k

q _∈Ω

Π_ℓ(q)6= 0

vem que, para todoq_∈∂_Ks\{0}, existeℓ1 ∈ {k, ..., s−1}tal que Πℓ1(q)6= 0. Podemos considerar o menor destes n´umerosℓ1(q) := min{ℓ1∈ {k,· · · , s−

1}|Πℓ1(q)6= 0}, e definir subconjuntosFℓ⊂∂Ks\ {0} da forma

Fℓ:=

n

q ∈∂Ks\ {0}

ℓ1(q) =ℓ o

, ℓ∈ {k, ..., s−1}.

Note que (ver Figura 3.2)

s−1

[

ℓ=k

Fℓ = (∂Ks\ {0}).

Proposi¸cão 3.2.4 Suponha queΠ satisfaz as hipóteses(H1)−(H3). Então

existem ε > 0 e m > 0 tal que o cone Ks ⊂ Rn dado no Corol´ario 3.2.3

satisfaz:

(i) js−1_Π(q)_≥ m

(27)

(ii) Ps−1(q)≥(s−1)m₂|q|s−1, ∀q ∈(∂Ks\ {0})∩Bε.

Demonstrac¸˜ao

Tem-se que ∂_Ks ´e um cone de v´ertice na origem. Seja S a esfera de centro

na origem e raio 1; o conjunto∂_Ks∩S ´e compacto.

Se x ∈ ∂Ks∩S ent˜ao x ∈ Fℓ para algum ℓ ∈ {k, ..., s−1} e portanto

Πℓ(x)>0. Existeεx >0 tal que Πℓ(q)>0 para todoq∈(∂Ks∩S)∩Bεx(x);

podemos definir Bx= (∂Ks∩S)∩Bεx(x) e considerar

mx= min q∈Bx{

Πℓ(q)}>0

Se Cone(Bx) ´e o cone de v´ertice na origem gerado porBx, eq∈Cone(Bx),

q 6= 0, ent˜ao (ver Figura 3.3)

jℓΠ(q) =jℓ−1Π(q) + Πℓ(q)≥Πℓ(q) =|q|ℓΠℓ

q

|q|

≥mx|q|ℓ.

Para s > ℓ+ 1, escrevendo js−1Π =jℓΠ +j_ℓs−1Π, vem j_ℓs−1Π = Πℓ+1+...+

Πs−1, e portanto jℓ(j_ℓs−1Π) = 0. Seq ∈Cone(Bx),q 6= 0, ent˜ao

js−1Π(q) =jℓΠ(q) +j_ℓs−1Π(q)_≥mx|q|ℓ+j_ℓs−1Π(q),

e como jℓ(js_ℓ−1Π) = 0 existeρx>0 tal que se 0<|q|< ρx ent˜ao

|j_ℓs−1Π(q)| ≤ mx

2 |q|

ℓ_.

Assim, se 0<_|q_|< ρx e q ∈Cone(Bx), tem-se

js−1Π(q)≥ mx

2 |q|

ℓ_.

A fam´ılia_C=_{Bεx(x)|x∈∂Ks∩S}´e uma cobertura por abertos de∂Ks∩S.

Seja_{Bεx1(x1), Bεx2(x2), ..., Bεxr(xr)}uma subcobertura finita deCtal que

∂Ks∩S ⊂Bεx1(x1)∪Bεx2(x2)∪...∪Bεxr(xr).

Como Bxi = (∂Ks∩S)∩Bε_xi(xi),i∈ {1, ..., r}, segue que

∂_Ks∩S ⊂Bx1∪Bx2 ∪...∪Bxr.

Notemos que xi ∈∂Ks∩S,i∈ {1, ..., r}, ent˜ao pelo procedimento anterior,

para cada i _{∈ {}1, ..., r_} existem mxi >0, ρxi > 0 e ℓi ∈ {k, ..., s−1} tais

que, se 0<_|q_|< ρxi e q∈Cone(Bxi) tem-se

js−1Π(q)_≥ mxi

2 |q|

(28)

Consideremos agora os n´umeros

m:= min_{mx1, ..., mxr}>0, ρ:= min{ρx1, ..., ρxr}>0,

e seja q ∈∂Ks, q 6= 0; ´e claro que xq = _|q_q_| ∈ S e como ∂Ks ´e um cone de

v´ertice na origemxq= _|q_q_| ∈∂Ks, logoxq∈∂Ks∩S, portantoxq ∈Bε_xiq(xiq)

para algum iq ∈ {1, ..., r}, consequentemente tem-se que xq ∈ Bxiq; e al´em

disso observemos que q = |q|xq ∈ Cone(Bxiq). Assim, se 0 < |q| < ρ

obtemos

js−1Π(q)≥ mxiq

2 |q|

ℓiq _≥ m

2|q|

ℓiq_.

Portanto, se 0< ε′ <min_{ρ,1_}tem-se

js−1Π(q)≥ m

2|q|

ℓiq _≥ m

2|q|

s−1_, _∀_q_∈_(∂_K

s\ {0})∩Bε′,

o qual mostra o item (i) emBε′.

Para ver o item (ii) note que, como js−1Π(q) =Ps−2

ℓ=kΠℓ(q) + Πs−1(q),

podemos escrever a seguinte estimativa

Πs−1(q)≥

m 2|q|

s−1₋

s−2

X

ℓ=k

Πℓ(q), ∀q∈(∂Ks\ {0})∩Bε′.

Pela hip´otese (H1) vale jℓΠ(q) ≥ 0 se k ≤ ℓ ≤ s−1 e q ∈ Bε′; e como

jℓΠ(q) =jℓ−1Π(q) + Πℓ(q) =Piℓ=−k1Πi(q) + Πℓ(q), podemos escrever

Πℓ(q)≥ − ℓ−1

X

i=k

Πi(q), ∀q ∈Bε′, k+ 1≤ℓ≤s−1

Dado q _∈ (∂_Ks\ {0})∩Bε′ temos que tq ∈ ∂K_s \ {0} para todo t > 0.

Como vale _ℓ₊₁ℓ < ℓ_ℓ+1₊₂ para cada ℓ_∈N_{, temos que} k

k+1 = mink≤ℓ≤s−1{ℓ+1ℓ }.

Consideremos 0< t < _k₊₁k , as estimativas dadas acima e a identidade

Ps−1(q) =h∇js−1Π(q), qi=

s−1

X

ℓ=k

(29)

para mostrar as seguintes desigualdades

Ps−1(tq) =

s−2

X

ℓ=k

ℓtℓΠℓ(q) + (s−1)ts−1Πs−1(q)

≥

s−2

X

ℓ=k

ℓtℓΠℓ(q) + (s−1)ts−1

m

2|q|

s−1₋

s−2

X

ℓ=k

Πℓ(q)

=

s−2

X

ℓ=k

(ℓtℓ₋(s₋1)ts−1)Πℓ(q) + (s−1)ts−1

m 2|q|

s−1

=

s−3

X

ℓ=k

(ℓtℓ₋(s₋1)ts−1)Πℓ(q) + ((s−2)ts−2−(s−1)ts−1)Πs−2(q)

+(s−1)ts−1m 2|q|

s−1

≥

s−3

X

ℓ=k

(ℓtℓ−(s−1)ts−1)Πℓ(q)−((s−2)ts−2−(s−1)ts−1) s−3

X

ℓ=k

Πℓ(q)

+(s₋1)ts−1m 2|q|

s−1

=

s−3

X

ℓ=k

(ℓtℓ₋(s₋2)ts−2)Πℓ(q) + (s−1)ts−1

m 2|q|

s−1

.. .

= (ktk−(k+ 1)tk+1)Πk(q) + (s−1)ts−1

m 2|q|

s−1

= (k−(k+ 1)t)Πk(tq) + (s−1)

m 2|tq|

s−1_.

Daqui, como Πk(tq) =jkΠ(tq)≥0 e 0< t < _k₊₁k resulta

Ps−1(tq)≥(s−1)

m 2|tq|

s−1_, _∀_q _∈_(∂_K

s\ {0})∩Bε′, 0< t <

k k+ 1 Portanto, se ε= _k₊₁k ε′ _{obtemos o afirmado}

Ps−1(q)≥(s−1)

m 2|q|

s−1_, _∀_q _∈_(∂_K

s\ {0})∩Bε.

(30)

K s

Cone(B x )

x Bε_x( x )

1 0

S

Figura 3.3: Um pontox_∈∂_Ks∩S e o coneCone(Bx).

Corolário 3.2.5 Suponha que Π satisfaz as hipóteses (H1)−(H3). Então

existeε >0 tal que o cone_Ks⊂Rn dado no Corol´ario3.2.3, satisfaz:

(i)′ _js_Π(q)_>₀ _{para cada}_q _∈_(∂_K

s\ {0})∩Bε,

(ii)′ _P_s_(q)_>₀ _{para cada} _q_∈_(∂_K_s_{\ {}₀_}₎_∩_B_ε_.

Demonstrac¸˜ao

Do item (c) dado no Corol´ario 3.2.3, tem-se que Πs(q) < 0 para cada q ∈

Ks\ {0}; logo vale Πs(_|q_q_|) =|q|−sΠs(q)<0 para cada q∈ Ks\ {0}, e como

a esfera∂B1 de raio 1 ´e compacta, existem constantes M1>0,M2>0 tais

que

−M1≤Πs

q

|q_|

≤ −M2, ∀q∈(Ks\ {0}).

Da Proposi¸c˜ao 3.2.4, item (i), existem uma constante uniforme m > 0 e o n´umero 0< ε′ _<_{1 tais que}

js−1Π(q)≥ m

2|q|

s−1_, _∀_q_∈_(∂_K

s\ {0})∩Bε′.

Assim, para cadaq _∈(∂_Ks\ {0})∩Bε′ resulta

jsΠ(q) =js−1Π(q) + Πs(q)≥

m 2|q|

s−1₋_M

1|q|s =|q|s−1

m

2 −M1|q|

e considerandoε1 = min{ε′,₂m_M1}obtemos o afirmado no item (i)

′_{, em}_B_ε

(31)

Analogamente, da Proposi¸c˜ao 3.2.4, item (ii), existe 0< ε′′ <1 tal que

Ps−1(q)≥(s−1)

m 2|q|

s−1_, _∀_q_∈_(∂_K

s\ {0})∩Bε′′,

logo, para cada q_∈(∂_Ks\ {0})∩Bε′′ obtemos

Ps(q) = Ps−1(q) +sΠs(q)≥(s−1)

m 2|q|

s−1₋_sM 1|q|s

= _|q_|s−1h(s₋1)m

2 −sM1|q|

i

,

e considerando ε2 = min{ε′′,(s₂−_sM1)1m} obtemos o afirmado no item (ii)

′_{, em}

Bε2. Agora tomeε= min{ε1, ε2}.

Observa¸c˜ao 3.2.6 Do Corol´ario 3.2.3, temos que, se o conjunto Ms−1 :=r ⊂Zs−1

Π_s|₍_r_\{₀_}₎<0 6=∅

for conexo, ent˜ao Ms−1 = ∆r para alguma semi-reta r ⊂ Ms−1 de origem

em 0. O conjunto Ms−1 ´e de fato um cone positivo de v´ertice na origem e

ser´a chamado de cone tangente ao conjunto As, pois, para qualquer curva

alg´ebrica γ: [0, ρ]_−→Ωcomγ(0) = 0eγ(t)_∈As\ {0}se0< t≤ρ, tem-se

que rγ ⊂Ms−1.

Admitindo que o cone tangente Ms−1 ao conjunto As ´e constituido por

uma ´unica componente conexa, temos a seguinte consequˆencia

Corol´ario 3.2.7 Suponha que Π satisfaz as hip´oteses (H1)−(H3), e seja

r uma semi-reta de origem0 contida em Ms−1. SeA˜s eC˜s s˜ao,

respectiva-mente as componentes conexas de As eCs que cont´em r\ {0} eKs ´e o cone

dado pelo Corol´ario3.2.3, ent˜ao existe 0< ε0<1 tal que

( ˜Cs\ {0})∩Bε0 ⊂(Ks)◦∩Bε0. Demonstrac¸˜ao

Do Lema 2.3.1, o cone tangente a ˜As\ {0}´e

Ms−1 ={r⊂Zs−1| Πs|(r\{0})<0}

e satisfaz a inclus˜aoMs−1 ⊂A˜spoisjsΠ|(r\{0}) = Πs|(r\{0})para cada

(32)

do item (b) segue que a fronteira ∂Ks\ {0} n˜ao ´e tangente aAs\ {0} pois

(∂_Ks\ {0})∩Zs−1∩Bε=∅ para todoε >0.

Al´em disto, do item (i)′ dado no Corol´ario 3.2.5, existe 0 < ε1 <1 tal

que js_Π(q) _> _{0 para cada} _q _∈ _(∂_K

s\ {0})∩Bε1, assim, diminuindo ε1 se necess´ario, obtemos

( ˜As\ {0})∩Bε1 ⊂(Ks)◦∩Bε1

e, como do item (c) dado no Corol´ario 3.2.3, vale Πs(q) < 0 para cada

q_{∈ K}s\ {0}, tem-se

Πs(q)<0, ∀q ∈(∂A˜s\ {0})∩Bε1.

Pela hipótese (H3) vale a inclusão ( Ãs \ {0}) ∩Bε1 ⊂ C˜s ∩Bε1, conse-quentemente vale Ps(q) < 0, para todo q ∈ (∂A˜s \ {0}) ∩Bε1, e como Ps(q) =h∇jsΠ(q), qi satisfaz a igualdade (dada na próxima se¸cão, no Lema

3.3.1)

Ps(q) = (s−1)jsΠ(q)− s−2

X

ℓ=k

jℓΠ(q) + Πs(q)

utilizando a hip´otese (H1) obtemos daqui que

Ps(q)≤Πs(q), ∀q∈(∂A˜s\ {0})∩Bε1.

Lembremos que como_Ks ´e um cone positivo de v´ertice na origem, fechado,

existem constantesM1>0 eM2 >0 tais que

−M1≤Πs

q

|q|

≤ −M2, ∀q∈(Ks\ {0}).

Seja agora uma fun¸c˜aoo(|q|s_{), esta fun¸c˜ao satisfaz lim}

q→0 o(|q|

s₎

|q|s = 0, isto ´e,

paraM2>0 existe 0<ε˜1 < ε1 tal que

o(_|q_|s₎

|q|s

<

M2

2 , ∀q∈Bε˜1. Daqui, seq∈(Ks\ {0})∩Bε˜1 tem-se

Πs(q) +o(|q|s) =|q|s

h

Πs

q

|q_|

+o(|q|

s₎

|q_|s

i

(33)

Cs Ks

r M

ε Bε

0 o

o

s−1

Figura 3.4: O conjunto Cs e o cone Ks.

consequentemente, como para cada q _∈(∂A˜s\ {0})∩B˜ε1 existe uma semi-reta contida em (_Ks)◦∩B˜ε1 passando pela origem e porq, vale que

Πs(q) +o(|q|s)≤ −

M2

2 |q|

s_,

∀q _∈(∂A˜s\ {0})∩Bε˜1.

Assim, usando a desigualdade

Ps(q)≤Πs(q), ∀q∈(∂A˜s\ {0})∩Bε˜1 resulta que

Ps(q) +o(|q|s)≤ −

M2

2 |q|

s_,

∀q_∈(∂A˜s\ {0})∩Bε˜1.

Al´em disto, do item (ii)′ dado no Corol´ario 3.2.5, existe 0 < ε2 < 1 tal

que Ps(q) > 0 para cada q ∈ (∂Ks\ {0})∩Bε2, assim, se considerarmos ε0 = min{ε2,ε˜1}, obtemos (ver Figura 3.4)

( ˜Cs\ {0})∩Bε0 ⊂(Ks)◦∩Bε0.

Observa¸c˜ao 3.2.8 A desigualdade

Ps(q) +o(|q|s)≤ −

M2

2 |q|

s_, _∀_q_∈_(∂_A_˜

s\ {0})∩Bε˜1

vista no Corol´ario 3.2.7 mostra uma propriedade do polinˆomio Ps no

(34)

Esta propriedade refere-se à resistência do sinal de um polinômio num con-junto. Neste caso tem-se claramente que o sinal dePs(q)+o(|q|s)é o mesmo

que o dePs(q) em(∂A˜s\ {0})∩B˜ε1, isto ´e, o sinal de Ps(q) “resiste”a per-turba¸c˜oes de ordemo(|q|s₎ _{no conjunto}_(∂_A˜_s_\{₀_}₎_∩_B_ε_˜

1 em uma vizinhan¸ca da origem.

Observa¸c˜ao 3.2.9 Se Ms−1 ´e constituido por mais de uma componente

conexa, aplicamos a cada componente o corol´ario 3.2.7.

3.3 s

_-resistˆ

_{encia de}

P

_s

Come¸camos esta se¸c˜ao dando a seguinte estimativa para Ps

Lema 3.3.1 Se Π _∈Js_(Ω,_R_{), ent˜}_ao _js_{Π(q) =} Ps

ℓ=kΠℓ(q) e sua derivada

radial Ps(q) :=h∇jsΠ(q), qi satisfazem a seguinte igualdade:

Ps(q) = (s−1)jsΠ(q)− s−2

X

ℓ=k

jℓΠ(q) + Πs(q).

Demonstrac¸˜ao

Como Πℓ é uma fun¸cão homogênea para todo ℓ ∈ {k, ..., s}, obtemos do

teorema de Euler quePs(q) =Psℓ=kℓΠℓ(q), e a igualdade segue diretamente.

Admitindo que os conjuntosAse Cs, assim como o coneMs−1 tangente

ao conjuntoAs, s˜ao todos constituidos por uma ´unica componente conexa,

o seguinte resultado de crucial importˆancia ´e obtido:

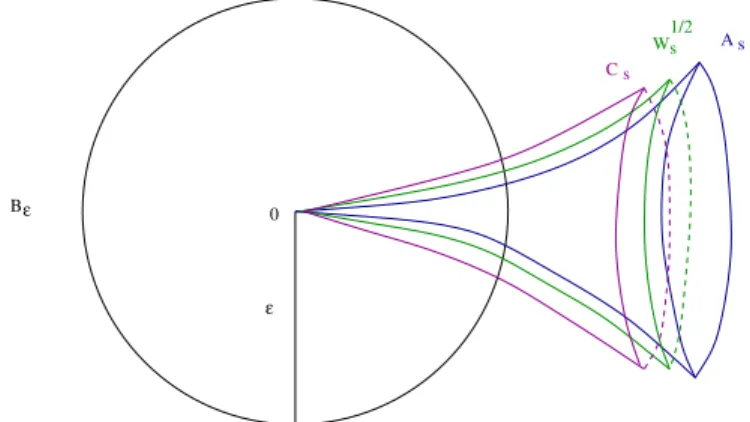
Proposi¸cão 3.3.2 Suponha queΠ satisfaz as hipóteses(H1)−(H3). Então

existem0< ε <1e um conjunto semi-alg´ebricoWs⊂Bε tais que 0∈∂Ws,

e:

1. (As\ {0})∩Bε⊂Ws◦⊂Ws\ {0} ⊂(Cs)◦∩Bε.

2. Πs(q)<0para todoq∈Ws\{0}e, ademais, existem constantesα >0

e β >0 tais que:

(a) Se q_∈∂Ws\ {0}, ent˜aojsΠ(q)≥ −αΠs(q);

(35)

3.3. S-RESIST ˆENCIA DE PS 35

Demonstrac¸˜ao

Consideremos a seguinte fam´ılia a um parˆametro de conjuntos semi-alg´ebricos

Wλ

s :={q∈Ω|Q(q, λ)<0}, ondeQ(q, λ)∈R[q, λ] s˜ao polinˆomios definidos

como

Q(q, λ) := (s₋1)jsΠ(q) +λh₋

s−2

X

ℓ=k

jℓΠ(q) + Πs(q)

i

.

Observemos que estes polinˆomios satisfazem o seguinte:

(i) Q(q,0) = (s−1)jsΠ(q) para todoq∈Ω, o qual mostra queW0

s =As;

(ii) Q(q,1) =Ps(q) para todo q ∈Ω, mostrando que Ws1 =Cs;

(iii) ∂Q_∂λ(q, λ) = ₋Ps−2

ℓ=kjℓΠ(q) + Πs(q) para todo q ∈ Ω, daqui que,

uti-lizando a hip´otese (H1), obtemos

∂Q

∂λ(q, λ)<Πs(q)<0, ∀q ∈ Ks\ {0}, ∀λ∈[0,1],

onde_Ks ´e o cone construido no Corol´ario 3.2.7 (e que tem a estrutura

dada no Corol´ario 3.2.3).

Consideremos 0 < ε0 < 1 dado no Corol´ario 3.2.7; do item (iii), sendo as

fun¸c˜oes Q(q,_·) decrescentes, para todo q _∈ (_Ks\ {0})∩Bε0 temos que, a fam´ılia Wλ

s ´e crescente emλ, isto ´e; se 0< λ1 < λ2 <1 valem as seguintes

inclus˜oes

(As\ {0})∩Bε0 ⊂ W

λ1

s ∩Bε0 ⊂ W

λ2

s ∩Bε0 ⊂Cs∩Bε0

Para algum n´umero 0< ε < ε0<1, consideremos o conjunto semi-alg´ebrico

Ws:=Ws1/2∩Bε, ´e claro que 0∈∂Ws e que Ws ⊂Bε satisfaz o item 1. ´E

claro tamb´em que, da inclus˜ao

Ws\ {0} ⊂Cs∩Bε⊂(Ks)◦∩Bε

e do Corol´ario 3.2.3, tem-se que Πs(q)<0 para todoq∈Ws\{0}. Daqui, se

q _∈∂Ws\{0}, ent˜aoQ(q,1/2) = 0, de onde obtemos a seguinte desigualdade

(s₋1)jsΠ(q) =₋(1/2)h₋

s−2

X

ℓ=k

jℓΠ(q) + Πs(q)

i

≥ −(1/2)Πs(q)

(36)

C s

Ws A s

0

ε B_ε

1/2

Figura 3.5: O conjuntoWs e as-resitˆencia.

Por outro lado, seq_∈Ws\{0}, ent˜aoQ(q,1/2)≤0, de onde conseguimos

a segunda desigualdade

Ps(q) = Q(q,1) =Q(q,1/2) +Q(q,1)−Q(q,1/2)

≤ (1/2)h₋

s−2

X

ℓ=k

jℓΠ(q) + Πs(q)

i

≤ (1/2)Πs(q)

mostrando o item 2-(b) comβ = 1₂ (ver Figura 3.5).

Consideremos a seguinte

Defini¸cão 3.3.3 Seja U ⊂ Ω um conjunto aberto com 0 ∈ ∂U e f um polinômio de grau menor ou igual a s tal que f(0) = 0 e f(q) < 0 para cadaq _∈U. Dizemos que f é s-resistente em U _{\ {}0_}, se para toda fun¸cão h∈Js(Ω,R₎ _com _js_h_≡_{0, existe} _ε₌_ε(h)_>₀ _{tal que}_f_{(q) +}_h(q)_<₀ _para cadaq _∈(U _{\ {}0_})_∩Bε.

Podemos agora, apresentar nosso resultado principal em termos de s-resistˆencia.

Teorema 3.3.4 Se Π satisfaz as hip´oteses (H1)−(H3), e se Ws ´e o

con-junto dado na Proposi¸c˜ao3.3.2, ent˜ao

(37)

3.3. S-RESIST ˆENCIA DE PS 37

(ii) Existe 0< ε2 <1 tal que, Ps ´e s-resistente em(Ws\ {0})∩Bε2.

Demonstrac¸˜ao

Consideremos 0< ε0<1 obtido na Proposi¸c˜ao 3.3.2, tal que

Πs(q)<0, ∀q ∈Ws\ {0} ⊂Cs∩Bε0 ⊂(Ks)◦∩Bε0.

Como em qualquer curva alg´ebricaγ : [0,1)→Wscomγ(0) = 0,γ(t)6= 0 se

t >0, tem-se que 0 ´e ponto de m´aximo de Πs|γ, existe 0< ε1=ε1(ε0)< ε0

tal que

Πs(q)≤ −ε0|q|s, ∀q∈Ws\ {0} ∩Bε1.

Na vizinhan¸ca Bε0, a fun¸c˜ao Π pode ser escrita, por hip´otese, da seguinte forma

Π(q) =jsΠ(q) +o(|q|s), q ∈Bε0,

ondeo(_|q_|s_{) ´e uma fun¸c˜ao cont´ınua satisfazendo lim}

q→0 o(|q|

s₎

|q|s = 0, portanto

|o(|q|s)|< αε0 2 |q|

s_, _∀_q_∈_B

ε1\ {0}.

Assim, do item 2-(a) dado na Proposi¸c˜ao 3.3.2, podemos obter, para todo q _∈(∂Ws\ {0})∩Bε1 a seguinte desigualdade

Π(q) =jsΠ(q) +o(|q|s)≥ −αΠs(q) +o(|q|s)> αε0

2 |q|

s_,

o que mostra o item (i), para ε1 ≤ αε₂0.

Considere agora 0< ε1<1, obtido na Proposi¸c˜ao 3.3.2. Sabemos que

Πs(q)<0, ∀q∈Ws\ {0} ⊂Cs∩Bε1 ⊂(Ks)◦∩Bε1

e, como na prova do item anterior, existe 0< ε2 =ε2(ε1)< ε1 tal que

Πs(q)≤ −ε1|q|s, ∀q∈Ws\ {0} ∩Bε2.

Seja agora h _∈Js(Ω,R_{) uma fun¸c˜ao definida em}_B_ε₁ _⊂_{Ω, tal que}_js_h_≡_0; por defini¸c˜ao h(q) =o(_|q_|s_),_q _∈_B

ε1, portanto,

|h(q)_|< βε1 2 |q|

s_, _∀_q _∈_B

(38)

Assim, do item 2-(b) dado na Proposi¸c˜ao 3.3.2, podemos obter, para todo q_∈(Ws\ {0})∩Bε2 a seguinte desigualdade

Ps(q) +h(q)≤βΠs(q) +h(q)≤ −

βε1

2 |q|

s_,

mostrando o item (ii) para ε2 ≤ βε₂1, isto ´e, mostra-se a s-resistˆencia de

Ps(q) :=h∇jsΠ(q), qi no conjunto (Ws\ {0})∩Bε2.

Observa¸cão 3.3.5 Considere a componente conexa Θ do conjunto Bε2 ∩ Π−1((−∞,0))que contém o cone tangente (Ms−1\ {0})∩Bε2. Obtemos da Proposi¸cão 3.3.2 que

Θ∩(∂Ws\ {0})∩Bε2 =∅

e, como(Ms−1\{0})∩Bε2 ⊂Θ∩Ws∩Bε2 6=∅, da conexidade deΘ, obtemos a inclus˜ao

Θ⊂Ws∩Bε2 ⊂(Ws\ {0})∩Bε2. Portanto, Ps ´e s-resistente emΘ.

Corol´ario 3.3.6 Suponha que Π = jsΠ +R satisfaz as hip´oteses (H1)−

(H3), e que exista a fun¸c˜ao ∇R(q) =o(|q|s−1). Se Ws ´e um conjunto dado

na Proposi¸c˜ao 3.3.2, ent˜ao existe 0 < ε3 < 1, tal que h∇Π(q), qi <0 para

todoq ∈(Ws\ {0})∩Bε3.

Demonstrac¸˜ao

Considerando a fun¸c˜aoh(q) :=_h∇R(q), q_i, temos

h∇Π(q), q_i=Ps(q) +h(q)

e o resultado segue das-resistˆencia da fun¸c˜ao Ps dada no Teorema 3.3.4.

(39)

Cap´ıtulo 4

Aplica¸

c˜

oes da

s

_-resistˆ

_encia

de

P

_s

Neste cap´ıtulo usaremos nosso resultado sobre s-resistência do cap´ıtulo anterior para obter uma resposta positiva à conjectura de Liapunov apre-sentada no Cap´ıtulo 1 para energias potenciais Π_∈Js(Ω,R_{) que satisfazem} as hipóteses (H1)−(H3). Variantes das hipóteses (H1)−(H3) serão

apre-sentadas e veremos em que medida aconjectura de Liapunov ´e ainda v´alida.

4.1 Instabilidade do equil´ıbrio segundo Liapunov

Estudemos aqui a estabilidade segundo Liapunov do equil´ıbrio (q0, p0) =

(0,0)∈Rn_×Rn_{, com} _n_≥_{2 graus de liberdade, cuja dinˆ}_{amica ´e governada} pelo sistema hamiltoniano

XH(q, p)



 

 

˙

q = ∂H_∂p(q, p)

˙

p=−∂H ∂q(q, p)

com hamiltoniana H(q, p) = T(q, p) + Π(q), (q, p) _∈ Ω_×Rn _{onde Ω}_⊂ Rn é uma vizinhan¸ca aberta da origem. Suporemos que a energia cinética é da forma T(q, p) := 1₂hp, B(q)pi, sendo B(q) uma matriz simétrica definida positiva, de clase C2(Ω,Rn2_).

4.1.1 Hip´oteses (H₁₎₋₍H₃₎

No que segue, dizer que o sistema hamiltonianoXH satisfaz as hip´oteses

(H1)−(H3) ser´a equivalente a dizer que a energia potencial Π ∈Js(Ω,R)

(40)

40 CAPÍTULO 4. APLICAÇ ÕES DAS-RESIST ÊNCIA DE PS

satisfaz as hip´oteses (H1)−(H3). Admitiremos tamb´em que, se Π(q) =

jsΠ(q) +R(q), ent˜ao _∇R(q) ´e de ordem o(_|q_|s−1) em uma vizinhan¸ca da origem.

Teorema 4.1.1 Se o sistema hamiltoniano XH(q, p) satisfaz as hip´oteses

(H1)−(H3), ent˜aoΠ ´e uma energia potencial do tipo ˇCetaev e, portanto, o

equil´ıbrio(q, p) = (0,0) deste sistema ´e inst´avel segundo Liapunov.

Demonstrac¸˜ao

Sejaε >0, o n´umero dado no item (ii) do Teorema 3.3.4, tal que Bε⊂Ω.

Temos deste resultado, a existˆencia do conjuntoWs:=Ws1/2∩Bε6=∅com

0 _∈ ∂Ws tal que Ps(q) := h∇jsΠ(q), qi ´e s-resistente em (Ws\ {0})∩Bε;

além disso, na prova do Teorema 3.3.4 foi mostrado que se Θ é a componente conexa de Π−1((_−∞,0))_∩Bε que contém o cone tangente Ms−1∩Bε, vale

a inclus˜ao

Θ_⊂Ws∩Π−1((−∞,0))∩Bε⊂(Ws\ {0})∩Bε,

diminuindoε se necess´ario. Portanto, do Corol´ario 3.3.6, resulta

h∇Π(q), qi<0, ∀q∈Θ.

Agora vai-se apresentar, nas se¸cões 4.1.2 e 4.1.3, casos particulares do teorema 4.1.1. De um ponto de vista formal não haveria necessidade de fazer a demonstra¸cão da instabilidade da origem nestes casos, visto serem casos particulares do nosso teorema principal, mas optamos por apresentar demonstra¸cões expl´ıcitas para cada caso pois, além de serem mais simples do que a do Teorema 4.1.1, ilustram técnicas e procedimentos usuais nesta ´

area, podendo eventualmente vir a ser usadas em outras situa¸c˜oes no futuro.

4.1.2 Hip´oteses (H1

1)−(H3)

Aqui substituimos nossa hip´otese (H1) pela seguinte hip´otese

(H1

1) Πℓ≥0 numa vizinhan¸ca da origem 0∈Ω, seℓ≤s−1.

Corol´ario 4.1.2 Se o sistema hamiltoniano XH(q, p) satisfaz as hip´oteses

(H₁1)₋(H3), ent˜ao o equil´ıbrio(q, p) = (0,0)deste sistema ´e inst´avel segundo

(41)

4.1. INSTABILIDADE DO EQUIL´IBRIO SEGUNDO LIAPUNOV 41

Demonstrac¸˜ao ´

E claro que a hipótese (H₁1) implica na hipótese (H1), então com as hipóteses

(H1

1)−(H3), podemos obter tamb´em um n´umero ε > 0 e um conjunto

Ws := Ws1/2∩Bε de maneira similar ao feito na Proposi¸c˜ao 3.3.2. Neste

caso particular o conjunto_Ws1/2´e obtido como um elemento da fam´ılia a um

parˆametro _Wλ

s ={q ∈Ω|Q(q, λ)<0}de conjuntos semi-alg´ebricos, onde

Q(q, λ) := (s−1)jsΠ(q) +λh

s−2

X

ℓ=k

(ℓ−(s−1))Πℓ(q) + Πs(q)

i

, λ∈[0,1].

Paraε >0 pequeno suficiente, o conjuntoWs :=Ws1/2∩Bε, de fato, satisfaz

a Proposi¸c˜ao 3.3.2 com constantes α= ₂₍_s1₋₁₎ eβ = 1₂.

4.1.3 Hip´oteses (H2

1)−(H3)

Aqui substituimos nossa hip´otese (H1) pela seguinte hip´otese

(H₁2) Existeν ∈ {k, ..., s−1} tal que numa vizinhan¸ca da origem Πr ≥0 e

Πℓ≤0, se k≤r ≤ν eν+ 1≤ℓ≤s−1 e, al´em dissojs−1Π≥0.

Corol´ario 4.1.3 Se o sistema hamiltoniano XH(q, p) satisfaz as hip´oteses

(H2

1)−(H3), ent˜ao o equil´ıbrio(q, p) = (0,0)deste sistema ´e inst´avel segundo

Liapunov.

Demonstrac¸˜ao ´

E claro que as hip´oteses (H₁2)−(H3) implicam nas hip´oteses (H1)−(H3),

então de maneira similar ao feito na Proposi¸cão 3.3.2 conseguimos aqui também um número ε > 0 e um conjunto Ws := Ws1/2 ∩Bε, onde Ws1/2

neste caso particular, ´e obtido como um elemento da fam´ılia a um parˆametro

Wsλ ={q∈Ω|Q(q, λ)<0}comλ∈[0,1], de conjuntos semi-alg´ebricos, onde

Q(q, λ) =νjsΠ(q) +λh

ν−1

X

r=k

(r₋ν)Πr(q) + s−1

X

ℓ=ν+1

(ℓ₋ν)Πℓ(q) + (s−ν)Πs(q)

i

Para εpequeno suficiente, o conjunto Ws := Ws1/2∩Bε tamb´em satisfaz a

Proposi¸c˜ao 3.3.2 com constantes α= s₂−_νν e β = s−₂ν.