Me^ania Qu^antia no Espao de Fase:
I. Formula~ao de Weyl-Wigner
(QuantumMehanisinPhaseSpae: I.TheWeyl-WignerFormalism)
Marelo A.Marhiolli
InstitutodeFsiadeS~aoCarlos,Universidadede S~aoPaulo,
CaixaPostal369, 13560-970S~aoCarlos,SP,Brasil
E-mail: marelo marhbol.om.br
Reebidoem01deabril,2002. Aeitoem03deoutubro,2002.
Nasultimas deadas onstata-seum resentenumerodeartigosem diversas areasdaFsia
de-diadosadesenvolvereapliaroformalismodeWeyl-Wignernosmaisdiferentessistemasfsios. A
possibilidadedeaprofundarmososnossosonheimentossobreoprinpiodainertezae
reuperar-mosaMe^aniaClassianolimite~!0,fazomqueadesri~aodaMe^aniaQu^antianoespao
defaseganheadavezmaisadeptos. Nessesentido,estetrabalhotempornalidadeapresentarum
onjuntobasioderesultadosquearaterizamoformalismoemquest~ao,possibilitandoaoleitoro
aessoas ideiasprinipaisdeorrentesdestefasinantetema.
Thelastdeadeshavewitnessedaneverinreasingnumberofartilesinnumerousphysialareasof
researhdediatedtodevelop andapplythe Weyl-Wignerformalisminonnetion withavariety
of dierent physial systems. The possibility of deepening our understandingof the unertainty
prinipleandreuperatingClassialMehanisinthe~!0limitexplainstheinreasingabundane
of adepts of the phase-spae desription of Quantum Mehanis. In this favorable ontext, the
present workaims at introduing a basi set of results that haraterize the formalism at issue,
allowingthereadertohaveaesstothemainideasemanatingfromthisfasinatingtheme.
I Introdu~ao
Oformalismoque iremosdesenvolveronsidera
es-senialmente umsistema qu^antio onstitudo deuma
uniapartulademassaM exeutandoummovimento
unidimensional, nos quais Q e P s~ao os respetivos
operadoresposi~aoe momentum, edestituda de spin
(movimentorotaionalintrnseo). Comotais
operado-ressatisfazem arela~aode omuta~ao[Q;P℄=_{~1,a
posi~ao eomomentum destapartulan~ao podem ser
simultaneamentemedidos(prinpiodeinerteza);
on-sequentemente,n~aoepossveldenirumadistribui~ao
de probabilidadesgenunanoespao defaseassoiada
ao operadordensidade(t)quedesreveas
proprieda-desfsiasdapartula. Nessesentido,arepresenta~ao
daMe^aniaQu^antianoespaodefaseeproblematia
e nadatrivial. Entretanto, tais diuldadesforam
su-peradas om o ferramental matematio desenvolvido
por Weyl-Wigner [1, 2℄ em que a fun~ao distribui~ao
de Wigner desempenha um papel ruial: esta possui
propriedadesmatematiasquepermitemarateriza-la
omoumapseudo-distribui~ao(ouquase-distribui~ao),
tivosparadeterminados sistemasqu^antios(o quen~ao
epermitido no sentidolassio da deni~ao de
distri-bui~oes de probabilidades). Alem disso, a fun~ao de
Wignerpermiteestabeleeronex~oesentreaMe^ania
ClassiaeaMe^aniaQu^antiaatravesdolimite~!0,
proedimento esse muito utilizado no estudo de
siste-masaotiossemilassios[3,4℄. Defato,asaplia~oes
desteformalismos~aoinumeraseseestendempor
dife-rentes areasda Fsia [5℄, sendo que atransi~ao para
sistemastridimensionaiseainlus~aodospinpodemser
feitassemmudanasoneituais.
Nos ultimos anos, belssimos experimentos
envol-vendoareonstru~aode algunsestadosdoampo
ele-tromagnetio [6℄ ou mesmo de estados assoiados ao
movimento do entro-de-massa de ons 9
Be +
aprisio-nadosemuma armadilhade Paul[7℄foram realizados
om suesso e as respetivas reonstru~oes feitas por
intermediodafun~aodeWigner. Posteriormente,
algu-maspropostasteoriasparaamedidadiretadafun~ao
deWignertambemforamapresentadas[8,9℄e
orres-pondem aexperimentosdeeletrodin^amiaqu^antiade
reen-trabalhovamosnosatersomenteemrealizarumestudo
preliminardaformula~aodeWeyl-WignerdaMe^ania
Qu^antia no espao de fase, visando a ompila~ao de
um material basio que permita ao leitor
aprofundar-senotema oumesmoserviromoumomplementoas
disiplinasdos ursosde pos-gradua~aoem Fsia,
sa-tisfazendo assimos diferentes programasexistentesno
pas.
Os topios abordados est~ao dispostos omo segue:
nase~ao 2deduzimosuma express~aoque permite
ma-pearumoperadorgenerionoespaodefaseatravesde
primeirosprinpiosemMe^aniaQu^antia(MQ).Esta
express~aoeinterpretadaomosendoumaexpans~aona
formaintegraldeumabasedeoperadoresnesteespao,
ujosoeientesrepresentamatransformadadeWeyl
assoiadaaooperadorgenerioemquest~ao. Alemdisso,
obtemos um onjunto razoavel de propriedades para
os elementos onstituintes da expans~ao e mostramos
que a fun~ao de Wigner e um aso partiular de um
formalismo mais geral introduzido por Weyl-Wigner.
Na se~ao 3alulamos as transformadas de Weyl das
rela~oesde omuta~aoeantiomuta~ao paradois
ope-radores tambem arbitrarios, no qual mostramos que
tais express~oes reuperam resultados ja estabeleidos
emMe^ania Classia(MC) nolimite ~!0. Istonos
permite realizar um estudo da evolu~ao temporal da
fun~aodeWignerpormeiodomapeamento noespao
defasedaequa~aodevonNeumann-Liouville,onforme
desritonase~ao4. Talequa~aonoslevaaobteruma
express~aogeralpara aderivada temporal assoiadaao
valor medio de um observavel qualquer que, no aso
partiulardosoperadoresmomentum eposi~ao,
repre-sentaatransformadade Weyldasequa~oesde
Ehren-fest da formula~aousual daMQ. Finalmente,
realiza-mos o limite ~ ! 0 nessas equa~oes om o objetivo
dereuperarasequa~oeslassiasdeHamiltondaMC.
Nase~ao5apresentamosasonsidera~oesnaisedias
de leitura para aqueles quequeiram se aprofundar no
tema. Algumasse~oess~aoomplementadasom
exem-plosquevisamilustrareenriqueerateoriasubjaente.
Estematerialfoioriginalmenteonebidonaforma
deapostilaeseuonteudoministradonoprimeirourso
de ver~ao sobre topios em Metodos Matematios da
Fsia: Introdu~ao ao grupo de rota~oes
tridimensio-nais,estadosoerenteseaformula~aodeWeyl-Wigner
daMe^aniaQu^antianoespao defase,realizadopelo
grupode teoria do Departamento de Fsia e Ci^enia
dos Materiais (DFCM), do Instituto de Fsia de S~ao
Carlos (IFSC-USP), noperodode 21 a 30 de janeiro
deste ano e sob a oordena~ao do Prof. Esmerindo
Bernardes. A apostila foi utilizadapelos alunosomo
material didatio e as duvidas que surgiramao longo
do urso,serviram-me para remodelar oseu onteudo
de modo a transformar osexerios em exemplose a
inluir novosparagrafosque atendessem as
neessida-desdospartiipantes,ulminandoassimnestetrabalho.
Porultimo,gostariademenionarqueadisposi~aodos
topiosealgumaspassagensmatematiasforam
basea-dasnasrefer^enias[10,11℄,asquaisindioomoleitura
omplementaraopresentetexto.
II Preliminares Algebrios
Iniialmente vamos araterizar a inematia
qu^antia dosistema fsio desritona introdu~ao, por
intermedio das rela~oes de omuta~ao assoiadas aos
operadoresfQ;P;1g,ouseja,
[Q;Q℄=[P;P℄=[Q;1℄=[P;1℄=0 e [Q;P℄={~1_ : (1)
Taisoperadoresobedeem a algebradeWeyl-Heisenberg, sendo queosautovetoresorrespondentess~ao denidos
pelasequa~oesdeautovalores
Pjpi=pjpi; Qjqi=qjqi; 1jpi=jpi; 1jqi=jqi: (2)
d
As bases dos autovetores fjpig e fjqig satisfazem as
rela~oesdeompletezaeortonormaliza~aoque s~ao
da-das,respetivamente,por
Z
1
1
dpjpihpj=1; Z
1
1
dqjqihqj=1; (3)
e
hpjp 0
i=Æ(p p 0
); hqjq 0
i=Æ(q q 0
); (4)
sendo Æ(x) a fun~ao delta de Dira. Alem disso,
tambemonheemosoprodutoesalar
hqjpi= 1
p exp
_ {
~ pq
; (5)
quepermiteonetarosdiferentesespaosdos
autove-toresjpiejqimedianteatransforma~aodeFourier
jpi= Z
1
1 dq
p
2~ exp
_ {
~ pq
jqi: (6)
De posse dessas informa~oes, omearemos ent~ao a
desrever a formula~ao de Weyl-Wigner da Me^ania
Qu^antianoespaodefase.
Considere um operador arbitrario F tal que seja
F
Z
1
1 dp
0
dp 00
dq 0
dq 00
jq 00
ihq 00
jp 00
ihp 00
jFjp 0
ihp 0
jq 0
ihq 0
j
= Z
1
1 dp
0
dp 00
dq 0
dq 00
2~
exp
_ {
~ (p
00
q 00
p 0
q 0
)
hp 00
jFjp 0
ijq 00
ihq 0
j; (7)
noqualutilizamosasrela~oesdeompleteza (3)eoprodutoesalar(5). Introduzindoasnovasvariaveis
2p=p 0
+p 00
; 2q=q 0
+q 00
; u=p 00
p 0
; v=q 00
q 0
;
omjaobianoigualaum,
dp 0
dp 00
dq 0
dq 00
=J
p 0
;p 00
p;u
| {z }
=1 J
q 0
;q 00
q;v
| {z }
=1
dpdqdudv=dpdqdudv;
d
ent~ao aidentidade (7) pode ser esrita omo uma
re-presenta~aointegraldooperadorF,istoe,
F= Z
1
1 dpdq
2~
f(p;q)(p;q): (8)
A fun~ao f(p;q)edenominada transformada de Weyl
dooperadorFomrela~aoaosoperadoresmomentum
eposi~ao,noqualedadapor [12,13℄
f(p;q)= Z
1
1 duexp
_ {
~ qu
hp+u=2jFjp u=2i:
(9)
NotequeseFforumoperadorhermitiano,ent~aof(p;q)
eumafun~aoreal. Porsuavez,(p;q)representauma
base de operadoresnoespaode faseeujaexpress~ao
temaseguinteforma:
(p;q)= Z
1
1 dvexp
_ {
~ pv
jq+v=2ihq v=2j: (10)
A express~ao (8) pode ser interpretada omo sendo a
deomposi~aodooperadorFemumabasede
operado-res,sendo asomponentes (p;q) oselementos dessa
base. Alem disso, tambem mostra que se for
onhe-ida a transformada de Weyl de um dado operador,
este pode ser prontamente determinado. Em
ontra-partida,umavezonheidoooperadorF,a
orrespon-dente transformada de Weyl e obtida atraves da Eq.
(9). Existem outrasbases estudadas naliteraturaque
apresentam diferentes virtudes para o mapeamento e
quepodemserdisutidasdamesmamaneiraomo
ze-mosomabasedeWeyl. Umestudo detalhadodessas
bases e enontrado na refer^enia [14℄, no qual e feita
umaompara~aoentreelas.
Exemplo 1 O proedimento matematio realizado para mapear o operador F n~ao e unio. Ao utilizarmos
on-venientemente as rela~oes de ompleteza (3) e as demais propriedades estabeleidas no primeiro paragrafo desta
se~ao, obtemos uma representa~ao integral equivalente a Eq. (8), mas agora om express~oes alternativas para a
transformada de Weylf(p;q)e abasede operadores(p;q), istoe,
f(p;q) = Z
1
1 dvexp
_ {
~ pv
hq v=2jFjq+v=2i; (11)
(p;q) = Z
1
1 duexp
_ {
~ qu
jp u=2ihp+u=2j: (12)
Taisexpress~oes,emonjuntoomasEqs. (9)e(10),permitemdemonstrarqueosprojetoresdeposi~aoemomentum
podemser esritos,respetivamente,omo
jqihqj = Z
1
1 du
2~ exp
_ {
~
u(q Q)
=Æ(q Q); (13)
jpihpj = Z
1
dv
2~ exp
_ {
~
v(p P)
Asintegra~oesnasvariaveisuevnoslevamaobterfun~oesdeltade Dira formais,ujosigniadoestaassoiado
om a a~ao da fun~ao delta e a substitui~ao do argumento por um operador, n~ao uma variavel. De posse desses
resultados e om oauxlio da rela~ao de Baker-Hausdor 1
, aforma simetria de (p;q)e prontamente obtida e
dada por
(p;q)= Z
1
1 dudv
2~ exp
_ {
~
[u(q Q)+v(p P)℄
: (15)
Em onsequ^enia aos resultadosdelineadosateopresente momento, torna-sefailveriar queatransformada de
Weyladmiteaforma ompata f(p;q)=Tr[F(p;q)℄.
ExisteummetodoalternativomuitoeleganteparaseaharooperadorFapartirdesuatransformadadeWeyl.
Paratanto,onsidereiniialmente aexpress~aodooperador(p;q)esritaomo
(p;q)= Z
1
1 dudv
2~ exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
exp
_ {
~ uv
2
: (16)
Emseguida,veriquequeaigualdade
~
2_{
2
pq exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
= _ {
~ uv
2 exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
noslevaaobter ointegrandodaEq. (16)atravesdaopera~ao
1
X
k =0 1
k!
~
2_{
2
pq
k
exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
= 1
X
k =0 1
k!
_ {
~ uv
2
k
exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
;
ouseja,
exp
~
2_{
2
pq
exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
= exp
_ {
~ uv
2
exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
:
Agora,inserindoesseresultadonaexpress~aopara(p;q)hega-sea
(p;q) = exp
~
2_{
2
pq
Z
1
1 dudv
2~ exp
_ {
~
u(q Q)
exp
_ {
~
v(p P)
= 2~ exp
~
2_{
2
pq
Æ(q Q)Æ(p P); (17)
oqualpermite-nosesreveraexpress~aoparaooperadorFomo
F = Z
1
1
dpdqf(p;q)
exp
~
2_{
2
pq
Æ(q Q)Æ(p P)
= Z
1
1 dpdq
exp
~
2_{
2
pq
f(p;q)
Æ(q Q)Æ(p P); (18)
sendoasegundaigualdade obtidaporintermediodarela~aoauxiliar
Z
1
1
dxf(x)
d m
dx m
Æ(x)
=( 1) m
d m
dx m
f(x)
x=0
=( 1) m
Z
1
1 dx
d m
dx m
f(x)
Æ(x):
1
SeAeBs~aodoisoperadoresquen~aoomutamequesatisfazemasondi~oes
[A;[A;B℄℄=[B;[A;B℄℄=0;
ent~ao
e A+B
=e A
e B
e 1
2 [A;B℄
=e B
e A
e 1
2 [A;B℄
Note que para enontrarmos tal operador, a partir de sua transformada de Weyl, devemos em um primeiro
momento alular
exp
~
2_{
2
pq
f(p;q)
edepoissubstituirasvariaveisqeppelosrespetivosoperadoresQeP,omaressalvadeesrevermososoperadores
posi~ao aesquerda dosoperadoresmomentum. Esteproedimentoemuitoutil quandosetrabalhaomprodutos
simples deQ eP, e aressalvada ordemdosoperadoresgarante aompleta simetriza~aodo operadorresultante
[10℄.
Exemplo 2 Comoaplia~ao do metodoestabeleido noparagrafoanterior, onsiderequeatransformada de Weyl
seja onheida edada pela fun~ao f(p;q)=g(q)p n
. Assimsendo, temosque
exp
~
2_{
2
pq
g(q)p n
= 1
X
k =0 1
k!
~
2_{
k
k
q k
g(q)
k
p k
p n
= n
X
k =0
n
k
~
2_{
k
k
q k
g(q)p n k
;
no qual
n
k
n!=k!(n k)!denota osoeientes binomiais. A segundaigualdade foi obtida omo auxlio da
rela~ao
k
p k
p n
= n!
(n k)! p
n k
(kn);
levando-nos a transformar a soma innita em uma soma nita. Ao substituirmos esse resultado na Eq. (18) e
realizando asintegra~oesomouidado depreservaraordemdos operadores posi~aoe momentum,hega-se a
F= n
X
k =0
n
k
~
2_{
k
d k
dQ k
g (Q)P n k
: (19)
Em seguida, vamos demonstrar queooperador Ftambempode ser esritoomo
F= 1
2 n
n
X
l=0
n
l
P l
g (Q)P n l
: (20)
Paratanto,reorreremosiniialmenteasrela~oesjaestabeleidasna literaturapara osoeientesbinomiais,
n
l
l
k
=
n
k
n k
l k
e
n k
X
m=0
n k
m
=2 n k
;
de modo aobtermosumaexpress~ao intermediaria paraooperador Fmediante osseguintepassos:
F = 1
2 n
n
X
k =0
n
k
2 n k
~
_ {
k
k
Q k
g (Q)P n k
= 1
2 n
n
X
k =0 n k
X
m=0
n
k
n k
m
~
_ {
k
k
Q k
g (Q)P n k
:
Agora,realizando atroadendies m=l komklnnasegundasoma,obtem-se
F = 1
2 n
n
X
k =0 n
X
l=k
n
k
n k
l k
~
_ {
k
k
Q k
g (Q)P n k
= 1
2 n
n
X
l=0 l
X
k =0
n
l
l
k
~
_ {
k
k
Q k
g (Q)P n k
= 1
2 n
n
X
l=0
n
l
l
X
k =0
l
k
~
_ {
k
k
Q k
g (Q)P l k
| {z }
P l
g (Q)
P n l
= 1
2 n
n
X
n
l
P l
g (Q)P n l
Note que na tereira igualdade utilizamos a rela~ao de omuta~ao [P;g (Q)℄ = {~_ d
dQ
g (Q), o que permitiu-nos
mostrararela~ao
P l
g (Q)= l
X
k =0
l
k
~
_ {
k
d k
dQ k
g (Q)P l k
:
Por ultimo, resta-nos somente menionar ofato de que aEq. (20) possui uma express~ao analtia fehada quee
dada por
F= 1
2 n
fffg (Q);Pg;Pg;;Pg
| {z }
nantiomutadores
; (21)
em que fA;Bg = AB+BA orresponde ao antiomutador entre os operadores A e B. Para deduzirmos tal
express~ao,basta reorrermos arela~ao de omuta~ao supraitadaparaveriarmosque
fffg (Q);Pg;Pg;;Pg
| {z }
n antiomutadores =
n
X
l=0
n
l
P l
g (Q)P n l
;
levando-nos assimaoresultadodesejado.
d
Jaafun~ao daMe^ania Classiaqueorresponde
aooperadorF,podeserenontradaporintermedioda
transformada de Weyl deste operador realizando-se o
limite~!0,
f
l
(p;q)= lim
~!0
f(p;q): (22)
Notequef(p;q)n~aoeaquantidadelassiaassoiada
aooperadorqu^antioF,massomenteumafun~aoque,
emgeral,podeserexpressaomoumaseriedepot^enias
em ~. Portanto, oproedimento ~! 0eruial para
obtermosf
l (p;q).
No formalismo desenvolvido ate o presente
mo-mento, (p;q)desempenhaumpapelimportantepois
trata-sedeumelemento quepermitemapear
operado-resnoespaodefase. Comotal,estetambempodeser
expandidonumabasedeoperadoresomo
(p 0
;q 0
)= Z
1
1 dpdq
2~
f(p;q)(p;q);
no qualf(p;q) =2~ Æ(p p 0
)Æ(q q 0
). Emseguida,
vamos exibir uma serie de propriedades para (p;q)
que ser~ao muito uteis nodeorrer dotrabalho. Dessa
forma,vamosiniiaromoselementosdematriz
(i)hq 0
j(p;q)jq 00
i = exp
_ {
~ p(q
0
q 00
)
Æ
q q
0
+q 00
2
; (23)
(ii)hp 0
j(p;q)jp 00
i = exp
_ {
~ q(p
0
p 00
Æ
p p
0
+p 00
2
; (24)
(iii)hq 0
j(p;q)jp 0
i = p
2~ exp
_ {
~ p
0
q 0
exp
~
2_{
2
pq
Æ(p p 0
)Æ(q q 0
): (25)
As Eqs.(23) e (24)podem ser demonstradas de imediatoom oauxlio das deni~oes estabeleidas para (p;q)
e o produto esalar (5). Consequentemente, ao onsiderarmos q 00
= q 0
e p 00
= p 0
, tais express~oes se reduzem a
hq 0
j(p;q)jq 0
i=Æ(q q 0
)ehp 0
j(p;q)jp 0
i=Æ(p p 0
),respetivamente. Comrela~aoademonstra~aodaEq.(25),
estarequeroauxliodaEq.(17)ealgunsuidadosdeorrentesdoaluloomoveremosabaixo:
hq 0
j(p;q)jp 0
i = 2~ exp
~
2_{
2
pq
hq 0
jÆ(q Q)Æ(p P)jp 0
i
= 2~ exp
~
2_{
2
pq
Z
1
1 dq
00
hq 0
jÆ(q Q)jq 00
ihq 00
jÆ(p P)jp 0
i
= 2~ exp
~
2_{
2
pq
Æ(p p 0
) Z
1
1 dq
00
p
2~ exp
_ {
~ p
0
q 00
Æ(q q 00
)Æ(q 0
q 00
)
= p
2~ exp
_ {
p 0
q 0
exp
~ 2
Æ(p p 0
)Æ(q q 0
Asintegra~oesdooperador(p;q)nasvariaveispeqresultamem
(iv) Z
1
1 dp
2~
(p;q)=jqihqj (26)
e
(v) Z
1
1 dq
2~
(p;q)=jpihpj: (27)
Taisresultadosnoslevamaosprojetoresdosestadospartiularesdoonjuntodeautovetoresdosoperadoresposi~ao
e momentum. Como deorr^enia dessas propriedades, vamos retornar a deni~ao da transformada de Weyl do
operadorF,ouseja,f(p;q)=Tr[F(p;q)℄ . AoonsiderarmosF=(operadordensidadeassoiadoaumsistema
fsio),obtemosformalmente adeni~aodafun~aodeWigner[2℄
W(p;q)= Z
1
1 dvexp
_ {
~ pv
hq v=2jjq+v=2i: (28)
Assim,para=j ih j, aspropriedades(26)e(27)assumemaseguinteforma:
Z
1
1 dp
2~
W(p;q)=j (q)j 2
e Z
1
1 dq
2~
W(p;q)=j(p)j 2
: (29)
Logo, ao integrarmos a fun~ao de Wigner em uma das variaveis do espao de fase, reuperamos as densidades
de probabilidadesassoiadasas respetivas fun~oes deonda (q)e (p). Estaeuma araterstiapartiular de
W(p;q)en~aoseestendepara asdemais quase-distribui~oesde probabilidades[16,17℄. Outraspropriedadesser~ao
abordadasnasproximasse~oes.
Exemplo 3 Vamosalular afun~ao deWignerassoiada aon-esimo estadodoosilador harm^onio
unidimensi-onal desritopelo operador densidade=jnihnj eujafun~ao de ondae dadapor
n
(q)=hqjni= 1
p
p
2 n
n!b exp
q 2
2b 2
H
n
(q=b); (30)
em que H
n
(x) denota os polin^omios de Hermite e b 2
=~=m!. Para tanto, devemos iniialmente reorrer a Eq.
(28) eproederomoaluloda integral delineado abaixo:
W
n
(p;q)= 2( 1)
n
p
2 n
n! exp
q 2
b 2
+ b
2
p 2
~ 2
Z
1
1 dv
2b exp
"
v
2b _ {
bp
~
2 #
H
n
v
2b q
b
H
n
v
2b +
q
b
:
Substituindo avariavel x= v
2b _ {
bp
~
nointegrando,obtem-seaexpress~ao intermediaria
W
n
(p;q)= 2( 1)
n
p
2 n
n! exp
q 2
b 2
+ b
2
p 2
~ 2
Z
1
1 dxe
x 2
H
n
x+
q
b +{_
bp
~
H
n
x
q
b _ {
bp
~
:
Agora,om oauxlio da rela~ao [18℄
Z
1
1 dxe
x 2
H
m
(x+y)H
n
(x+z)= p
2 n
m!z n m
L (n m)
m
( 2yz) (nm)
sendo L (m)
n
(x) os polin^omios de Laguerre assoiados, aintegra~ao pode ser efetuada de imediato, levando-nos ao
resultadonal
W
n
(p;q)=2( 1) n
exp
q 2
b 2
+ b
2
p 2
~ 2
L
n
2
q 2
b 2
+ b
2
p 2
~ 2
: (31)
Esta fun~ao eomumente enontradaem livrostextossobre
Optia Qu^antia[19-22℄sobaforma ompata
W
n
()=2( 1) n
e jj
2
L
n (2jj
2
); (32)
om =
q
b +{_
bp
~
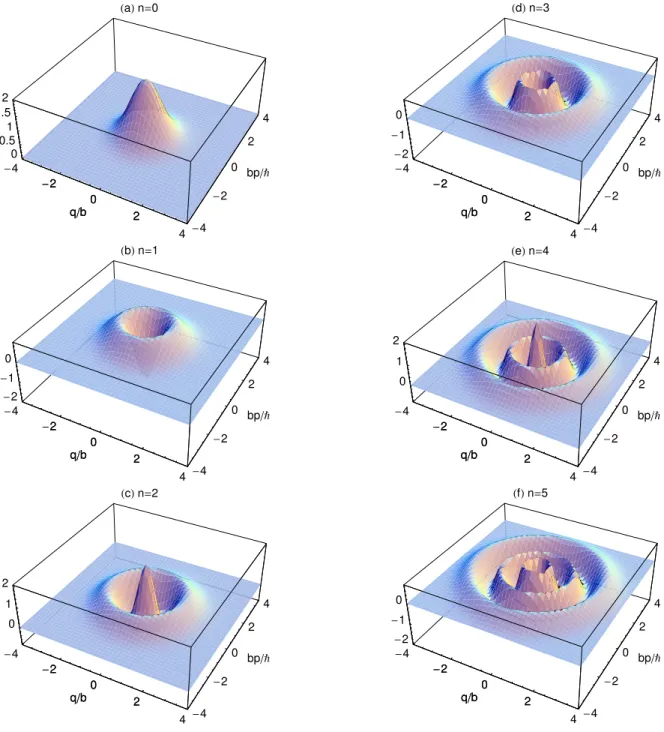
. A gura 1 mostra os graos da fun~ao de Wigner W
n
(p;q) versus
q
b ;
bp
~
para o estado
fundamental (a) n=0 e osino primeiros estados exitados (b)-(f) n=1;:::;5do osilador harm^onio
unidi-mensional. Note que a fun~ao assume valores negativos no espao de fase e este importante fato esta assoiado
ao arater qu^antio do operador densidade em quest~ao.
E importante salientarmos que a fun~ao W
1
(p;q) foi
re-onstrudareentementepelo grupodoNIST emum belo experimento envolvendoons 9
Be +
aprisionados em uma
armadilhadePaul[7 ℄. Nase~aoIV,retomaremosnovamentenestepontoaodisutirmosaspropriedadesdafun~ao
a
n
0
4
2
0
2
4
qb
4
2
0
2
4
bp
0
0.5
1
1.5
2
2
0
2
qb
b
n
1
4
2
0
2
4
qb
4
2
0
2
4
bp
2
1
0
2
0
2
qb
c
n
2
4
2
0
2
4
qb
4
2
0
2
4
bp
0
1
2
2
0
2
qb
d
n
3
4
2
0
2
4
qb
4
2
0
2
4
bp
2
1
0
2
0
2
qb
e
n
4
4
2
0
2
4
qb
4
2
0
2
4
bp
0
1
2
2
0
2
qb
f
n
5
4
2
0
2
4
qb
4
2
0
2
4
bp
2
1
0
2
0
2
qb
Figura1. Asguras1(a)-(f)orrespondemaos graosdeWn(p;q) versus q
b e
bp
~
paran=0;:::;5. Os valoresnegativos
dafun~aodeWignerest~aoompreendidosnointervalo 1
~ W
n (p;q)
1
~
eassoiadosaoaraterqu^antiodoestado de
numero.
Paranalizarmosestase~ao,resta-nossomentemenionaraspropriedadesrelativasaotraodooperador(p;q)
edoprodutodestes operadores,omanalidadede obtermosexpress~oesanaltiaspara atransformadade Weyl
dasrela~oesdeomuta~aoeantiomuta~ao. Reorrendoadeni~aodaopera~aotrao,temos que
(vi) Tr[(p;q)℄=1; (33)
(vii) Tr[(p
1 ;q
1 )(p
2 ;q
2
)℄=2~Æ(p
1 p
2 )Æ(q
1 q
2
); (34)
(viii) Tr[(p
1 ;q
1 )(p
2 ;q
2 )(p
3 ;q
3 )℄=2
2
exp
2_{
~ [(q
1 q
3 )(p
2 p
3 ) (q
2 q
3 )(p
1 p
3 )℄
A demonstra~aodaEq.(34)eimediatadesdequeutilizamosapropriedade(23),ouseja, Tr[(p 1 ;q 1 )(p 2 ;q 2 )℄ = Z 1 1 dq 0 hq 0 j(p 1 ;q 1 )(p 2 ;q 2 )jq 0 i = Z 1 1 dq 0 dq 00 hq 0 j(p 1 ;q 1 )jq 00 ihq 00 j(p 2 ;q 2 )jq 0 i = Z 1 1 dq 0 dq 00 exp _ { ~ (q 0 q 00 )(p 1 p 2 ) Æ q 1 q 0 +q 00 2 Æ q 2 q 0 +q 00 2 :
Agora,substituindoasnovasvariaveisq 0 +q 00 =2x 1 eq 0 q 00 =x 2
naexpress~aoaimaom
dq 0 dq 00 =J q 0 ;q 00 x 1 ;x 2
| {z }
=1 dx 1 dx 2 =dx 1 dx 2 ;
nalizamososalulosomosegue:
Tr[(p
1 ;q 1 )(p 2 ;q 2 )℄ = Z 1 1 dx 1 dx 2 exp _ { ~ x 2 (p 1 p 2 ) Æ(q 1 x 1 )Æ(q 2 x 2 )
= 2~Æ(p
1 p 2 )Æ(q 1 q 2
): 2
Demaneiraanaloga,temosqueademonstra~aodaEq.(35)exigeuidadosadiionais,umavezque
Tr[(p
1 ;q 1 )(p 2 ;q 2 )(p 3 ;q 3 )℄ = Z 1 1 dq 0 dq 00 dq 000 hq 0 j(p 1 ;q 1 )jq 00 ihq 00 j(p 2 ;q 2 )jq 000 ihq 000 j(p 3 ;q 3 )jq 0 i = Z 1 1 dq 0 dq 00 dq 000 exp _ { ~ [p 1 (q 0 q 00
)+p
2 (q
00
q 000
)+p
3 (q 000 q 0 )℄ Æ q 1 q 0 +q 00 2 Æ q 2 q 00 +q 000 2 Æ q 3 q 000 +q 0 2 :
Agora,designandoq 0 +q 00 =2x 1 ,q 00 +q 000 =2x 2 eq 000 +q 0 =2x 3 om dq 0 dq 00 dq 000 =J q 0 ;q 00 ;q 000 x 1 ;x 2 ;x 3
| {z }
=2 2 dx 1 dx 2 dx 3 =2 2 dx 1 dx 2 dx 3 ; obtemos
Tr[(p
1 ;q 1 )(p 2 ;q 2 )(p 3 ;q 3
)℄ = 2 2 Z 1 1 dx 1 dx 2 dx 3 Æ(q 1 x 1 )Æ(q 2 x 2 )Æ(q 3 x 3 ) exp 2_{ ~ [(x 1 x 3 )(p 2 p 3 ) (x 2 x 3 )(p 1 p 3 )℄ = 2 2 exp 2_{ ~ [ (q 1 q 3 )(p 2 p 3 ) (q 2 q 3 )(p 1 p 3 )℄ : 2
Consequentemente,ao identiarmosnovamente F omooperadordensidade , novaspropriedadesassoiadasa
fun~aodeWignersurgemnaturalmente: aprimeirarefere-seasuanormaliza~ao,
Z
1
1 dpdq
2~
W(p;q)=1; (36)
enquantoqueasegundapropriedadereeteailiidade daopera~aotrao,
Tr( 1 2 ) = Z 1 1 dp 1 dq 1 dp 2 dq 2 (2~) 2 W 1 (p 1 ;q 1 )W 2 (p 2 ;q 2
)Tr[ (p
1 ;q 1 )(p 2 ;q 2 )℄ = Z 1 1 dp 1 dq 1 dp 2 dq 2 2~ W 1 (p 1 ;q 1 )W 2 (p 2 ;q 2 )Æ(p 1 p 2 )Æ(q 1 q 2 ) = Z 1 1 dp 1 dq 1 2~ W 1 (p 1 ;q 1 )W 2 (p 1 ;q 1 )
= Tr(
2
1
) : (37)
III O mapeamento das rela~oes de omuta~ao e antiomuta~ao
Paraenontrarmosatransformada deWeyldas rela~oesde omuta~ao eantiomuta~aoentre doisoperadores
arbitrariosA e B em MQ,torna-se neessario estudar iniialmente a transformada deWeyl do produto AB. O
pontodepartidaearepresenta~aointegral(8),istoe,
AB = Z 1 1 dp 1 dq 1 dp 2 dq 2 (2~) 2 A(p 1 ;q 1 )B(p 2 ;q 2 )(p 1 ;q 1 )(p 2 ;q 2 ) = Z 1 1 dpdq 2~
f(p;q)(p;q); (38)
noqualf(p;q)=Tr[AB(p;q)℄. Assim,substituindoaprimeiraigualdade daequa~aoaimaem f(p;q),amos
om
f(p;q) = Z 1 1 dp 1 dq 1 dp 2 dq 2 (2~) 2 A(p 1 ;q 1 )B(p 2 ;q 2
)Tr[ (p
1 ;q 1 )(p 2 ;q 2 )(p;q)℄ = 2 2 Z 1 1 dp 1 dq 1 dp 2 dq 2 (2~) 2 A(p 1 ;q 1 )B(p 2 ;q 2 )exp 2_{ ~ [ (q 1 q)(p 2 p) (q 2 q)(p 1 p)℄ : (39)
Pararesolvermosessa integraldevemos,em prinpio, realizaratroade variaveisp=p
2
peq=q
2
q, oque
noslevaa
f(p;q)=2 2 Z 1 1 dp 1 dq 1 dpdq
(2~) 2 A(p 1 ;q 1
)B(p+p;q+q)exp 2_{ ~ [p(q 1 q) q(p 1 p)℄ :
Agora,expandindoafun~aoB(p+p;q+q)emuma seriedeTaylornasproximidadesdospontos(p;q),obtem-se
B(p+p;q+q)= 1 X n=0 1 n! p p +q q n
B(p;q)=exp p p +q q
B(p;q):
Estarela~aopermite-nosveriaraigualdade
exp 2_{ ~ [p(q 1 q) q(p 1 p)℄ exp p p +q q
B(p;q)=
exp 2_{ ~ [p(q 1 q) q(p 1 p)℄ exp " ~ 2_{ p ! q q ! p !# B(p;q)
que e fundamental para os nossos propositos. Note que as variaveis pe qforam substitudas pelos operadores
difereniais ~ 2_{ q e ~ 2_{ p
, respetivamente, atuando na primeira exponenial. Este fato justia a taquigraa
utilizadanoladodireitodaigualdade eassetasindiamosentidodeatua~aodosoperadoresdifereniais. Logo,a
transformadadeWeylf(p;q)podeserreesritaomosegue:
f(p;q) = 2 2 Z 1 1 dp 1 dq 1 dpdq
(2~) 2 A(p 1 ;q 1 )exp 2_{ ~ [p(q 1 q) q(p 1 p)℄ exp " ~ 2_{ p ! q q ! p !# B(p;q) = 2 2 Z 1 1 dp 1 dq 1 2~ A(p 1 ;q 1 ) Z 1 1 dpdq
2~ exp 2_{ ~ [p(q 1 q) q(p 1 p)℄
| {z }
= 2 ~ 2 2 Æ(p 1 p)Æ(q 1 q) exp " ~ 2_{ p ! q q ! p !# B(p;q) = Z 1 1 dp 1 dq 1 A(p 1 ;q 1 )Æ(p 1 p)Æ(q 1 q)exp " ~ 2_{ p ! q q ! p !# B(p;q)
= A(p;q)exp " ~ ! ! !#
EsseresultadonoslevaaonluirqueatransformadadeWeyldoprodutodeoperadoresABn~aoeigualaoproduto
das transformadasA(p;q)B(p;q), massimuma fun~aomais ompliadaque depende detodasasordensem~ do
operadorpseudo-diferenial loalizadoentre asfun~oes A(p;q)e B(p;q). Em geral,tal operadoredenotado pelo
smbolo?introduzidoporGroenewold[23℄,
?exp "
~
2_{
p !
q
q !
p !#
;
oqualrepresentaumadeforma~aopseudo-diferenialassoiativadoprodutoordinarioA(p;q)B(p;q). Dessemodo,
aEq.(40)tambempodeserenontradanaliteraturasobaforma[24℄
f(p;q)=A(p;q)?B(p;q); (41)
ujasaplia~oesemfsiaseestendemdesdeoestudodemodelossemilassioseaotiosateasideiasdegeometria
n~ao-omutativaemgravita~aoqu^antia[25℄. Outrasaplia~oesdoproduto-?einforma~oesteniasmaisdetalhadas
podemserobtidasnasrefer^enias[26, 27℄.
AtransformadadeWeyldasrela~oesdeomuta~aoeantiomuta~aodeorremagoraprontamentedaEq.(40),
[A;B℄ 2_{ sin
~
2
(A)
p
(B )
q
(A)
q
(B )
p
A(p;q)B(p;q); (42)
fA;Bg 2 os
~
2
(A)
p
(B )
q
(A)
q
(B )
p
A(p;q)B(p;q): (43)
Nessas express~oes,as fun~oes seno eossenodevem serinterpretadasformalmente omoa serieorrespondente a
ada umdeles,respetivamente. Alem disso, osndies AeB empregadosnosoperadoresdifereniaisindiam as
transformadas deWeylemque osoperadoresatuam,araterizandoassimnuma mudana denota~ao.
Alternati-vamente,utilizandoanota~aodeGroenewold,taisexpress~oesadquiremoseguinteaspeto:
[A;B℄ A(p;q)?B(p;q) B(p;q)?A(p;q); (44)
fA;Bg A(p;q)?B(p;q)+B(p;q)?A(p;q): (45)
Note queasEqs.(42)e(43)s~aoseriesem~ eostermos deordemmaisbaixarepresentadospor
_ {~
(A)
p
(B )
q
(A)
q
(B )
p
A(p;q)B(p;q) e 2A(p;q)B(p;q);
respetivamente. Consequentemente,aserieassoiadaatransformadadeWeylde 1
_ {~
[A;B℄omeaomopar^enteses
dePoissondastransformadasdeWeyldeAeB;enquantoqueaserieassoiadaa 1
2
fA;Bg,iniiaomoproduto
dastransformadasdeWeyldeAeB. Assim,onsiderandoolimite~!0,amos om
lim
~!0 1
_ {~
[A;B℄ !
(A)
p
(B )
q
(A)
q
(B )
p
A
l (p;q)B
l
(p;q); (46)
lim
~!0 1
2
fA;Bg ! A
l (p;q)B
l
(p;q): (47)
Istonosmotivaaprourarolimitedoanalogolassiodaequa~aodevonNeumann-Liouville,ouseja,veriar
seadin^amiaqu^antiatendeadin^amialassianolimite~!0.
IV A din^amia qu^antia
Vamosonsiderarumsistemafsioqualquerdesritopelooperadordensidade(t)=j (t)ih (t)j,emquej (t)i
representa umestadopurodosistema. OalulodovalormediodeumoperadorFefeitopeladeni~aousualda
MQ,
hFi
t
=Tr[(t)F℄=h (t)jFj (t)i; (48)
ouatravesdosresultadosobtidosateopresente momento,
hFi
t =
Z
1
dpdq
2~
om W(p;q;t) sendo a fun~ao de Wigner para um tempo t arbitrario. Assim, antes de prosseguirmos om a
desri~aodadin^amiadosistema,vamosapresentaralgumaspropriedadesadiionaisparaafun~aodeWigner. As
duasprimeiraspropriedadesreferem-seaoalulodaquase-distribui~aoporintermediodasEqs.(10)e(17),istoe,
(i)W(p;q;t) = Z
1
1 dv
2~ exp
_ {
~ pv
(q v=2;t)
(q+v=2;t)
= Z
1
1 du
2~ exp
_ {
~ qu
(p+u=2;t)
(p u=2;t) (50)
e
(ii)W(p;q;t) = 2~ exp
~
2_{
2
pq
Tr[(t)Æ(q Q)Æ(p P)℄
= p
2~ exp
~
2_{
2
pq
exp
_ {
~ pq
(p;t)
(q;t)
: (51)
Comoooperadordensidadeehermiteano,afun~aoW(p;q;t)erealeonsequentemente,
W(p;q;t)= p
2~ exp
~
2_{
2
pq
exp
_ {
~ pq
(p;t) (q;t)
: (52)
AtereirapropriedadedeorredadesigualdadedeCauhy-Shwarz,istoe,
jW(p;q;t)j 2
Z
1
1 dv
2~
j (q v=2;t)j 2
Z
1
1 du
2~
j (q+u=2;t)j 2
= 1
(~) 2
: (53)
AdesigualdadejW(p;q;t)j 2
h
(h=2~)impliaqueafun~aodeWignerediferentedezeronumaregi~aoujaarea
doespao defaseemenorouiguala h
2
[21℄. Portanto,tal fun~aotrazembutida ainforma~ao basiadoprinpio
deinerteza: esta n~aopodeserloalizadatanto em pquanto emq, oque noslevaaonluirqueasdistribui~oes
deltadeDiraest~aodesartadasnesteontexto. Defato,esteespaodefasen~aoeapenasumaoutrarepresenta~ao
doespaodefaselassio,massimumrepresentantelegtimodeumespaodeestadosomsuaestruturaelulada
devidoaoprinpiode inerteza[10℄. Alemdisso,afun~aodeWignerW(p;q;t)podeassumirvaloresnegativos,o
quejustiaatermosdesignado dequase-distribui~ao.
IV.1 A equa~ao de von Neumann-Liouville
Aevolu~aotemporaldafun~aodeWignereumaonsequ^eniaimediatadaequa~aodevonNeumann-Liouville
paraooperadordensidade(t),
t (t)=
1
_ {~
[H;(t)℄ ; (54)
noqual Heohamiltonianodo sistema queindepende dotempo. De fato,realizando-seatransformada de Weyl
destaequa~aoobtemosomoresultado
t
W(p;q;t)= 2
~ sin
~
2
(H)
q
(W)
p
(H)
p
(W)
q
H(p;q)W(p;q;t); (55)
sendo H(p;q) a transformada de Weyl do operador H. Para resolver essa equa~ao, vamos denir o operador
Liouvillianoqu^antio
L(p;q)= 2_{
~ sin
~
2
(H)
q
(W)
p
(H)
p
(W)
q
H(p;q);
oqualpermite-nosreesreveraEq.(55)daseguinteforma:
t
W(p;q;t)= _{L(p;q)W(p;q;t): (56)
Asolu~aoformaldestaequa~aoedadapor
Nestaexpress~ao,observamosqueadepend^eniaem~dafun~aodeWignerW(p;q;t)eprovenientededuasfontes:
W(p;q;t
0
)eL(p;q).
Paraumsistemafsioqualquer,ujaformamapeadadooperadorhamiltonianoseja
H(p;q)= p
2
2m
+V(q); (58)
afun~aodeWignerW(p;q;t)obedeeaequa~aodiferenialparial[21℄
t +
p
m
q
dV(q)
dq
p
W(p;q;t)= 1
X
k =1 ( 1)
k
(2k+1)!
~
2
2k
d 2k +1
V(q)
dq 2k +1
2k +1
p 2k +1
W(p;q;t); (59)
aqualeprontamente obtidaatravesdaEq. (56). Aoxarmos~=0nesta equa~ao, oque eequivalente a
onsi-derarmos umaevolu~aolassiaparaW(p;q;t), veriamos queestareuperaaequa~aodeLiouville daMe^ania
EstatstiaClassia,
t +
p
m
q
dV(q)
dq
p
W(p;q;t)=0:
Portanto,oladodireitodaEq. (59)podeserinterpretadoomoumtermoadiionalqueintroduzorre~oesqu^antias
aequa~aodeLiouvilleClassia.
Exemplo 4 Aomplexidade emresolver aequa~ao diferenial parial(59) estadiretamente assoiada a natureza
daenergiapotenialV(q)dosistemafsioqueestamosabordando. Reentemente,algunssistemassujeitosa
poten-iaisdo tipoMorse,Poshl-Teller eosiladorharm^oniomodiado(OHM),foraminvestigados esuasrespetivas
fun~oesde Wigneraluladas atravesdas fun~oesde onda paraosestadosestaionarios [28 , 29 ℄. Por exemplo, ao
onsiderarmos
V(q)= 8
>
<
>
: D
h
1 e q
2
1 i
; D>0 e 1
>0 (Morse)
V
0 osh
2
(aq); V
0 =~
2
a 2
=m e a>0 (Poshl-Teller)
~ 2
2
2m
(q) 2
2(q)tanh(q)
; >0 (OHM)
temos que
d 2k +1
V(q)
dq 2k +1
= 8
>
<
>
:
4D 2
2
k
e 3q=2
sinh
q
2
kln2
; 8q (Morse)
2V
0
a P
1
m=1 ( 1)
m
(2am) 2(k +1)
e 2aqm
; q0 (Poshl-Teller)
2~ 2
3
m P
1
m=1 ( 1)
m
(2m) 2k
[1+2(k qm)℄e 2qm
; q>0 (OHM)
para k 1, o que nos leva a obter diferentes ontribui~oes em ordens de ~ para ada potenial em quest~ao. Em
partiular, as fun~oes deWigner parat
0
=0podemser enontradasnasrefer^enias supraitadas, restandoapenas
realizar um estudo detalhado aera da evolu~ao temporal lassiae omo asdiferentes ontribui~oesde ~ afetam
tal evolu~ao.
Emseguida,iremosinvestigarolimite ~!0deL(p;q). Paratanto, vamosdenirooperador
$
q !
p
p !
q
eintroduzirumpar^ametroadimensionalnoLiouvillianoqu^antiodeformaareesrev^e-loomosegue:
L
(p;q)=
2_{
~ sin
~
2 $
H(p;q):
Supondoqueafun~aoH(p;q)n~aodependade~, aexpans~aoem seriedepot^eniasdooperador
L
(p;q)=
2_{
~ "
~
2 $
1
3!
~
2
3
$
3
+ #
H(p;q);
permite-nosrealizarolimite!0onformeoproedimento
limL
(p;q)=_{ $
H(p;q)=L
sendoL
0
(p;q)umoperadorlassio. Nessesentido,aevolu~aotemporal(56)temporsolu~ao
W
0
(p;q;t)=exp[ {L_
0
(p;q)(t t
0
)℄W(p;q;t
0
); (60)
ouonsiderandoumpassoanterior,
W
0
t =
H
q W
0
p H
p W
0
q
=fH;W
0
g (61)
em que fH;W
0
g representa o par^enteses de Poisson das fun~oes H(p;q) e W
0
(p;q;t). Dessa forma, a Eq.(60)
desrevea evolu~ao lassia do objeto qu^antio W(p;q;t
0
). Em suma, a introdu~ao do par^ametro nos leva a
tratardeformaindependenteoslimites~!0nafun~aodeWignerenasuaevolu~aotemporal[11℄.
Exemplo5 Considereooperadorhamiltoniano do osiladorharm^onio unidimensional
H= P
2
2m +
1
2 m!
2
Q 2
; (62)
assimomo asuaforma mapeada
H(p;q)= p
2
2m +
1
2 m!
2
q 2
; (63)
aqualindependede ~. Paraalularmos aevolu~ao temporalda fun~aode WignerW
n
(p;q;t)atraves daEq. (57),
devemos emprinpio estabeleer umaexpress~aoformal paraooperadorLiouvilliano qu^antioL(p;q) assoiado ao
sistema fsioemestudo,quepara onossoasoedado por
L(p;q)={!_
q
b
(bp=~) bp
~
(q=b)
=L
0
(p;q) b 2
=~=m!
: (64)
Notequeesteoperadorn~aopossuiqualquerdepend^eniaem~,levando-nosassimaumaevolu~aolassiadafun~ao
de Wignerqu^antiaW
n
(p;q)parat
0 =0,
W
n
(p;q;t)=exp[ {tL_
0
(p;q)℄W
n
(p;q); (65)
omW
n
(p;q)dado pelaEq. (31). Emseguida,vamos realizaratransforma~ao de variaveis
q
b
=Re()=ros
bp
~
=Im()=rsin
om (
r 2
= q
2
b 2
+ b
2
p 2
~ 2
=jj 2
=artan
b 2
~ p
q
=artan h
Im()
Re() i
na Eq. (65), o qual permite-nos obter um resultado importante. Para tanto, devemos iniialmente reorrer as
rela~oesauxiliares
(bp=~) =sin
r +
os
r
e
(q=b)
=os
r sin
r
;
de maneiraareesreverooperador lassioL
0
(p;q) omoL
0
()={!_
. Consequentemente,temos que
W
n
(r;t)=exp
_ {!t
W
n
(r)=W
n
(r) =) W
n
(p;q;t)=W
n
(p;q); (66)
ou seja, a fun~ao de Wigner assoiada ao autoestado do operador hamiltoniano (62) n~ao evolui temporalmente.
Estefato pode ser expliadoomoauxlio do operador evolu~ao temporal
U(t)=exp
_ {t
~ H
=e _ {!t=2
R(!t); (67)
noqual R(!t)=exp _{!ta y
a
refere-se aooperador rota~ao,sendo
a= 1
p
2 r
m!
~ Q+_{
P
p
e a
y
= 1
p
2 r
m!
~ Q _{
P
osoperadores aniquila~ao eria~ao,respetivamente. Dessaforma, aoalularmosafun~ao deWigner W
n (p;q;t)
por intermedio da Eq. (50),
W
n
(p;q;t) = Z
1
1 dv
2~ exp
_ {
~ pv
hq v=2jU(t)jnihnjU y
(t)jq+v=2i
= Z
1
1 dv
2~ exp
_ {
~ pv
h
e _
{!t(n+1=2)
hq v=2jni ih
e _
{!t(n+1=2)
hnjq+v=2i i
= Z
1
1 dv
2~ exp
_ {
~ pv
n
(q v=2)
n
(q+v=2)
= W
n (p;q);
veriamos queooperador evolu~ao temporal introduzapenasuma fase global e estan~ao apresenta nenhuma
on-tribui~aoparaoalulo. De maneiraanaloga, omesmopode ser onstatado paraaEq. (51),
W
n
(p;q;t) = p
2~ exp
~
2_{
2
pq
exp
_ {
~ pq
hpjU(t)jnihnjU y
(t)jqi
= p
2~ exp
~
2_{
2
pq
exp
_ {
~ pq
h
e _
{!t(n+1=2)
hpjni ih
e _
{!t(n+1=2)
hnjqi i
= p
2~ exp
~
2_{
2
pq
exp
_ {
~ pq
n (p)
n (q)
= W
n (p;q);
orroborando assimomoresultadoobtido anteriormente.
Agora,paraenontrarmosumaexpress~aoassoiadaaderivadatemporaldovaloresperadodeumobservavelF,
bastalembrarmosdaEq.(49). Comisso,temosque
d
dt hFi
t =
Z
1
1 dpdq
2~
f(p;q)
t
W(p;q;t)
= {_ Z
1
1 dpdq
2~
f(p;q)[L(p;q)W(p;q;t)℄
= {_ Z
1
1 dpdq
2~
[L(p;q)f(p;q)℄W(p;q;t)
= 2
~ Z
1
1 dpdq
2~ sin
~
2
(H)
q
(f)
p
(H)
p
(f)
q
H(p;q)f(p;q)W(p;q;t); (68)
d
noqualatereira igualdadefoiobtidaatravesda
inte-gra~aoporpartes elembrandoque W(p;q;t) seanula
noslimites p(q)!1. Empartiular, ao
onsiderar-mososoperadoresmomentumeposi~ao,amosom
d
dt hPi
t =
Z
1
1 dpdq
2~ H
q
W(p;q;t) (69)
e
d
dt hQi
t =
Z
1
1 dpdq
2~ H
p
W(p;q;t); (70)
as quais representam a transformada de Weyl das
equa~oesdeEhrenfestdaformula~aousualdaMe^ania
Qu^antia. Para ~ ! 0, a fun~ao de Wigner e
equi-valente ao produto Æ(p p
0
)Æ(q q
0
) e as express~oes
paraH
l (p
0 ;q
0 ),
dp
0
dt =
H
l
q
0 e
dq
0
dt =
H
l
p
0
: (71)
Resumindo, nesta ultima se~ao onseguimos
reu-peraraMe^ania Classiae asequa~oes fundamentais
que governam a evolu~ao temporal de valores medios
dos observaveis fsios atraves de um proesso limite
formal, oqualpermiteobter uma desri~ao doespao
defaselassioapartirdeumespaodefasequ^antio.
V Considera~oes Finais
Oobjetivoentraldestetrabalhoeapresentaruma
por-lidade nos diversos ramos da Fsia. Para tanto,
uti-lizamos de alguns oneitos matematios que s~ao
ge-ralmente ensinados nos ursos de Me^ania Qu^antia
da gradua~ao e pos-gradua~ao, de modo a ompilar
um texto didatio e rigoroso aera da formula~ao de
Weyl-WignerdaMe^aniaQu^antianoespaodefase,
possibilitando ao leitor uma rapida assimila~ao e um
eventual aprofundamento no tema. De fato, para os
leitoresavidos por informa~aoreomendoaleitura das
refer^enias[16,17℄emaisreentemente,oexelente
li-vrodeW.P.Shleih[21℄quetrazumnumerorazoavel
de aplia~oes em
Optia Qu^antia. Em suma, espero
que otexto aquiapresentado umpra sua nalidadee
sirva de inentivo para alunos e professores na busa
inessantepornovos onheimentos.
Agradeimentos
Oautorgostariadeagradeeroonvitefeitopelo
Prof. Esmerindo Bernardes (IFSC-USP) para
minis-trar umdostopiosabordadosnourso de ver~aoeao
inentivoonstante emesreverestematerial,aoProf.
DiogenesGaletti(IFT-UNESP)pela leiturauidadosa
eomentariospertinentes,alemdoapoionaneiro
pro-piiadopelaFAPESPatravesdosproessos01/11209-0
e00/15084-5.
Refer^enias
[1℄ H.Weyl,Z.Phys.46,1(1927).
[2℄ E.Wigner,Phys.Rev.40,749(1932).
[3℄ A.M.O. deAlmeida,Sistemas Hamiltonianos: Caose
Quantiza~ao,EditoradaUniamp,Campinas,segunda
edi~ao(1991).
[4℄ M.C.Gutzwiller,ChaosinClassialandQuantum
Me-hanis,Springer-Verlag,NewYork(1990).
[5℄ Y.S.Kim e M.E.Noz, Phase Spae Piture of
Quan-tumMehanis(GroupTheoretialApproah),Leture
Notes inPhysis SeriesVol. 40, WorldSienti,
Sin-gapore(1991).
[6℄ D.T. Smithey,M. Bek, M.G. Raymere A. Faridani,
Phys.Rev.Lett.70,1244(1993).Vertambem:Ulf
Le-onhardt,MeasuringtheQuantumStateofLight,
Cam-bridge,NewYork(1997).
[7℄ D. Leibfried, D.M. Meekhof, B.E. King, C. Monroe,
W.M.ItanoeD.J.Wineland,Phys.Rev.Lett.77,4281
(1996).
[8℄ L.G.LutterbaheL.Davidovih,Phys.Rev.Lett.78,
2547(1997).
[9℄ R.L. de Matos Filho e W. Vogel, Phys. Rev. A 58,
R1661(1998).
[10℄ D.Galetti,Me^aniaQu^antianoEspaodeFase,
No-tasdeauladaIIIEsolaMarioShenbergdo
Departa-mentodeFsiadaUFPB,Jo~aoPessoa(1996).
[11℄ M.C. Tijero, Aproxima~oes Semilassias nos
Proes-sos de Colis~oes At^omio-Moleulares, Tese de
douto-ramento apresentada no Instituto de Fsia Teoria
(UNESP),IFT-T.004/94(1994).
[12℄ H.Weyl,TheTheory ofGroupsandQuantum
Meha-nis,Dover,NewYork(1950).
[13℄ B.Leaf,J.Math.Phys.9,65e769(1968).
[14℄ N.L. Balaz e B.K. Jennings, Phys. Rep. 104, 347
(1984).
[15℄ W.H.Louisell,QuantumStatistialPropertiesof
Radi-ation,JohnWiley&Sons,NewYork(1990).
[16℄ M.Hillery,R.F.O'Connell,M.O.SullyeE.P.Wigner,
Phys.Rep.106,121(1984).
[17℄ H-W.Lee,Phys.Rep.259,147(1995).
[18℄ I.S. GradshteyneI.M. Ryzhik,Table of Integrals,
Se-ries,andProduts,AademiPress,SanDiego(1980).
[19℄ M.O. Sullye M.S. Zubairy, Quantum Optis,
Cam-bridgeUniversityPress,NewYork(1997).
[20℄ M. Orszag, Quantum Optis, Springer-Verlag, Berlin
(2000).
[21℄ W.P.Shleih,QuantumOptisinPhaseSpae,
Wiley-VCH,Berlin(2001).
[22℄ W. Vogel, D-G. Welsh e S. Wallentowitz, Quantum
Optis: AnIntrodution,Wiley-VCH,Berlin(2001).
[23℄ H.Groenewold,Physia12,405(1946).
[24℄ T.Curtright,T.UematsueC.Zahos,Generating all
Wignerfuntions,hep-th/0011137v2(2001).
[25℄ L.Castellani, Class.Quant.Grav.17,3377(2000).
[26℄ N.C. Dias e J.N. Prata, Causal Interpretation and
QuantumPhase Spae,quant-ph/0110062(2001).
[27℄ O.V. Man'ko, V.I. Man'ko e G. Marmo, J. Phys. A:
Math.Gen.35,699(2002).
[28℄ A. Frank, A.L.Riverae K.B.Wolf,Phys.Rev.A 61,
054102(2000).
[29℄ G.W. Bund eM.C. Tijero, Phys.Rev. A 61, 052114