Um Calulo Aproximado do Poder das Pontas
Anapproximatetreatmentforthestrenghtofthepoints
G. F. LealFerreira
FCM,IFSC,USP
CP369,13560-970, S~aoCarlos,SP
Reebidoem27defevereiro,2002. Aeitoem3deabril,2002.
Caluloaproximadodopotenialedadensidadedeargadeumondutorquaseilndrioeletrizado
e realizado seguindo metodo desenvolvido por Maxwell em seu Treatise para ondutores quase
esferios. Com isso, e possvel obter rela~oes diretasentre densidade de arga e urvatura para
asossimples. Oplanoarregado,levementeorrugado,etambemabordado.
Anapproximatetreatmentofthepotentialandofthehargedensityofaquasi-irularonduting
ylinder is arried outalong the line proposed by Maxwell inhis `Treatise ' for quasi-spherial
ondutors. Thisallows usto establish relations between hargedensity andurvatureinsimple
ases. Theslightlyorrugatedhargedplaneisalsotreated.
I Introdu~ao
Antigamente, o ensino da Eletrostatia dava muita
aten~ao ao estudo dos ondutores eletrizados.
Ilus-trando oque se hama de `o poder das pontas'
gu-ravamesmootorniqueteeletrioemque,asemelhana
dotorniquetehidrodin^amio,quegiraomaeje~aode
agua, aquele giraaoserligado aumafonte de tens~ao.
Aeletriidadeseaumulanaspontas,oampoeletrio
ioniza o area repuls~ao entre asargas da ponta eas
ionizadasdemesmosinalfazotorniquetegirarem
sen-tido oposto ao da ponta, omo se fosse movido, pela
rea~aoao`ventoeletrio'[1℄riadopelaponta.
Mais geralmente, o `poder das pontas' signia a
preferenial aumula~aode arganasregi~oesdemaior
urvaturadasuperfiedoondutoreletrizado,fatoque
pode seronstatado experimentalmente om oauxlio
do `plano de prova' [2,3℄- um diso maleavel,
manu-seado om um isolante, que se aplia a superfie do
ondutor, emvariadasregi~oesdamesma. Doponto de
vistateorio,ajustia~aodopoderdaspontasemais
difilporqueexigeorrelaionaremgeralafun~ao
po-tenial nasvizinhanasdoondutoromas
proprieda-desgeometriasdasuperfie. Aquifaremosuma
abor-dagem bem mais modesta ao problema, aproveitando
umasolu~aoaproximadadadaporMaxwellemseu
Tre-atise [4℄ do potenial de um ondutor quase esferio,
adaptadaaquiparaoasodeilindrosquaseirulares,
prourandoobteradensidadedeargaerelaionando-a
omaurvatura,que, nopresenteaso,eunia.
II Solu~ao aproximada: o
poten-ial
Asolu~ao aproximadaproposta noTreatise [4℄,
adap-tadaaonossoaso,easeguinte.
Sejaoilindro`quaseirulardeequa~aopolar,r e
; <<,
r=a(1+"f()) (1)
emque"epequenoomparadoom1eaeoraiomedio
(ouseja, R
f()d=0). Admitiremosquef()e
su-ientementeregularequeerepresentadoporumaserie
deFourier
f()= 1
X
n=1 (h
n
osn+g
n
senn) (2)
Comosolu~aogeraldaEqua~aodeLaplae,o
poten-ialriado pelo ondutor arregadopode serexpresso
por
V(r;)=V
0 +A
0 log
r
a +"
1
X
n=1 A
n
osn+B
n senn
r n
(3)
emqueV
0
eopotenialdoondutore"maraaqueles
termos que se anulam quando o ondutor e
Na superfie do ondutor (e no seu interior),
V(r;)=V
0
etambempodemosesrever
log r
a
=log(1+"f())'"f() (4)
ComoosomatoriodaEq. 3jaontem";o
denomi-nadorr n
podeseraproximadoparaa n
eobtem-se
0="A
0 f()+
1 X n=1 " a n (A n
osn+B
n
senn); (5)
outendoemontaaEq.2
0= 1 X n=1 [(A 0 h n + A n a n
)osn+(A
0 g n + B n a n
)senn℄ (6)
deonde,porargumentosonheidos,obtem-se
A n a n = A 0 h n (7) e B n a n = A 0 g n (8)
Em duas dimens~oes, o potenial do ondutor n~ao
determinaasolu~aonoespao: eadensidadedearga,
A
0
,queofaz.
III A densidade de arga
Adensidadedearga,, noCGS,eobtidode
4=
V
n
(9)
ndesignandoaquianormalaoondutor. Adire~aode
neadire~aoder diferemdeum^anguloque,em
radi-anos, eda ordemde ", e omo os" '1 "
2
2
, para "
pequeno,e,ent~ao,podemostomaradire~aodenomo
sendoader. Ent~ao,aproximadamente,
4= V r = A 0 r +" 1 X n=1 n r n+1 (A n osn+B n senn) (10)
Desenvolvendo-se1=r, omr dadonaEq. 1,omo
a(1 "f())enosomatoriofazendo-ser n !a n ,vem 4= A 0 a [1 " 1 X n=1 (h n
osn+g
n
senn)℄+" 1 X n=1 n a n+1 (A n
osn+B
n
senn) (11)
d
esubstituindo-seosvaloresdeA
n eB
n
dadosnasEqs.
7e8,vem
4= A 0 a [1 " 1 X n=1 (1 n)(h n
osn+g
n
senn)℄;
(12)
equa~ao que mostra que o somatorio efetivamente se
iniiaemn=2,ouseja,queotermoparan=1 `que
daaposi~aodoentro demassa doondutor, suposto
dedensidade uniforme,em rela~aoaorigem' [4℄
pode-riasereliminadoapriori daEq. 2. AEq. 11tambem
mostraque parauma densidade deargapositiva,
0 ,
A
0
enegativo. ReesrevemosaEq. 11omo
=
0 [1+"
1
X
n=2
(n 1)(h
n
osn+g
n
senn)℄ (13)
om = A =4a.
IV O raio de urvatura
Oraiodeurvatura,R ,emoordenadaspolaresedado
por[5℄ R= (r 2 +r0 2 ) 3=2 r 2 +2r0 2 rr00 (14)
onder0er00signiamderivadasprimeiraesegundaem
rela~aoa:Paraaaproxima~aode1a. ordemdonosso
alulo, vamos tomarr 2
'a 2
(1+2"f()), r0'"af0(
),r0 2
'0;rr0'a(1+"f())"af00()' "a 2
f00(),
demaneiraqueRe
R=
a(1+3"f())
1+2"f() "f00()
'a[1+"(f()+f00())℄ (15)
outendoem ontaaEq. 2
R=a[1 " X n=2 (n 2 1)(h n
osn+g
n
senn)℄ (16)
AurvaturaKiguala1=Re
K=K
0 [1+"
1 X n=2 (n 2 1)(h n
osn+g
n
senn)℄ (17)
V Disuss~ao
V.1 Casos \puros"
Casos \puros"s~aoaquidenidosomoaquelesem
queum unionomparee nadeforma~aodoilindro,
seja ele m. Disutiremos oaso em que ela e dotipo
osm omm par. osm tem mperodosangulares,
ada um ompreendendo ^angulo de
p
= 2=m. As
pontasestar~aoem
pk
=2k=me, entreelas, os
va-les (depress~oes) em
vk
= (2k+1)=m, 0 k
(m 1)=2. Com
r=a(1+"osm) (18)
tem-se paraadensidadedeargaeparaaurvatura
=
0
[1+"(m 1)osm℄eK=K
0 [1+"(m
2
1)osm℄
(19)
Esrevemostambemaexpress~aodopotenialV(z),
sendoz=r a;
V(z;)=V
0 4
0
a[log(1+ z
a ) "(
1
1+ z
a )
m
osm℄
(20)
Na verdade, a urvaz() que faz V(z) na Eq. 20
igualaV
0
soedadapelaEq.17naordemde". Em
or-denssuperioresde"," 2
," 3
,et.,apareer~aoharm^onios
de ordemm1,m2,et. Permaneeremosem
pri-meiraordem.
Comparando-seadepend^eniaangularder, eK
omm,v^e-sequeelaemais forteparaK,depoispara
e,emgeral,maisfraaparar.Dovalorde nasEq.
19 v^e-se que adiferena entre as densidades de arga
naspontasenosvalesede2
0
"(m 1),istoe,aumenta
om oestreitamento do perodo, quando aspontas
-am, relativamente, mais aguadas. Tambem dasEq.
19v^e-seque,aproximadamente,vale arela~ao
()
0 =(
K()
K
0 )
1
m+1
(21)
mostrando queparaoasopuropode-seesreveruma
rela~ao direta entre a densidade e a urvatura. Por
exemplo, param=2,quandooilindro eelptio,
te-mos () 3 p
K() e () r(). Na Fig. 1
mos-tramos r=a, =
0
eK =K
0
para esse aso,m =2;om
"=0;1enaFig. 2,param=4;om"=0;05:
V.1.1 Plaaplana levementeorrugada
Para um dado valor de m, o perodo angular e
p
=2=m,omovistoaima,eoaroorrespondente,
l,e
l= 2a
m
(22)
Como em 1 a
ordem todas as grandezas tem esse
unioperodo,soneessitamosdoqueoorrenoperodo
emtornodaorigem, =m=m,paradesrever
asgrandezastomemosneleoarox,orrespondendoa
=x=a:Teremos
m= mx
a =
2x
l
(23)
Faamos,agora,oraioareserenosmantenhamos
nasvizinhanasdasuperfiedoilindro. Devemos
fa-zer tambem m reser para que l se mantenha nito,
Eq. 22. Teremos uma superfiepratiamente plana,
levemente orrugada, isto e, "a = b
0
<< l. A Eq.20
paraopotenial,naaproxima~aoz<<a,e
V(z;)=V
0
4a
0 z
a +
4
0
a"osm
1+m z
a
(24)
Figura1. Graopolar parar();()e K();
normaliza-dosaunidade,parar()=1+0;1os2. Traoheiopara
r();pontilhado para() -quenesse aso oinide omo
der()-,etraejadoparaK():
Figura 2. O mesmo que na Fig.1, para r() = 1 +
0;05:os4:
Em primeiro lugar, notemos, ao passarmos da
solu~aoilindroasolu~aoplano,queestaherdadaquela
aondi~aodeamponulonointeriordoilindro
(essen-ialmente z negativo). Para orrigirmosisso, devemos
p^or2 em vez de 4 naEq.23,om oquesubtramos
oampo2
0
aoprimeirotermodaEq.23eobrigamos
queosegundoaneleoprimeiroparaznasuperfiedo
ilindro. Fazendo-seassubstitui~oesvalidasparaoaso
a!1, ques~ao a"!b
0
, m ! 2x=l, m=a!2=l,
tem-senalmente
V(z;x)=V
0 2
0 z+
2
0 b
0 os2
x
l
1+ 2z
para a qual vale aobserva~ao do tipo feita abaixoda
Eq.19.
V.2 Caso geral
NasFigs. 3e 4 mostramos () e K(),
normali-zados, parar=a =1+0;05:(os2+0;5:os3)e nas
Figs.5 e6,para r=a =1+0;05:(os2+0;5:os3+
0;25:os4):Figs.3e5s~aograospolares,
inluindo-setambem osder()=a,enquantoasFigs. 4e6s~ao
graos artesianos. V^e-se que maximos e mnimos
de () e K() se orrelaionam perfeitamente,
sem-preom K()mais proeminente. Alias, ()esta,em
geral,mais proximode r()doquede K(),porem, a
determina~ao der()dependeda loa~aoda origeme
e,emtermospratios,menosaessvel.
Figura3. Mesmasonven~oes,parar()=1+0;05:(os2+
0;5os3):
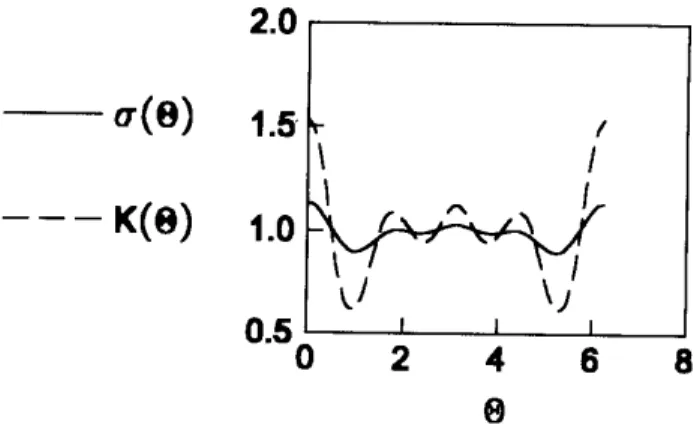
Figura4. Graoartesiano paraompara~aoentre()e
K();normalizados, para r() daFig.3. Traoheio para
Figura5. Mesmas onven~oes dosoutros graos polares,
parar()=1+0;05:(os2+0;5os3+0;25os4):
Figura6.ComonaFig.4, parar()daFig.5.
Agradeimentos
O autor agradee a bolsa de produtividade do
CNPq, e, muito espeialmente, ao arbitro deste que,
paientemente,orrigiuinumerosenganosemformulas
navers~aooriginalmentesubmetida.
Refer^enias
1. G. Castelfranhi, Fisia Sperimentale e Appliata,
Vol.II,EditoreUlrioHoepliMilano,1948,Cap.XVI
2. P.FleuryeJ.-P.Mathieu,
Eletrostatique,Courants
Continues, Magnetostatique,
Editions Eyrolles, 1962,
Cap. III.
3. E.Perua,FsiaGeneralyExperimental,TomoII,
EditorialLabor,1953,Cap. IV.
4. J. C. Maxwell, A Treatise on Eletriity and
Mag-netism,DoverPubl.,1954,Cap.9,se~ao145a.
5. Andre Delahet, Geometrie Dierentielle, ole~ao
quesais-je? n o