Avanços no estudo de complexidade em linguagem regular de autômatos celulares elementares

(1)

UNIVERSIDADE PRESBITERIANA MACKENZIE

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM

ENGENHARIA EL´

ETRICA

Wander Lairson Costa

Avan¸cos no estudo de complexidade em linguagem regular de

autˆ

omatos celulares elementares

(2)

UNIVERSIDADE PRESBITERIANA MACKENZIE

PROGRAMA DE P ´

OS-GRADUAC

¸ ˜

AO EM

ENGENHARIA EL´

ETRICA

Wander Lairson Costa

Avan¸cos no estudo de complexidade em linguagem regular de

autˆ

omatos celulares elementares

Disserta¸cão de Mestrado apresentada ao Programa de Pós-Gradua¸cão em Engenharia Elétrica, como parte das Exigências para Obten¸cão do Grau de Mestre em Engenharia Elétrica, na Area´ de Concentra¸cão em Engenharia da Computa¸cão.

Orientador: Pedro Paulo Balbi de Oliveira

(3)

(4)

(5)

AGRADECIMENTOS

Agrade¸co primeiramente a Deus, por guiar meus passos e a meus pais, Maria das Dôres Costa e Marcelo Damas da Costa, que me ensinaram que a fé realmente move montanhas e por terem-me mostrado o verdadeiro significado da palavra caráter, além do apoio incondicional mesmo nos momentos mais dif´ıceis.

Agrade¸co ao meu irmão, C´ırio Wandery Costa, por entender os incontáveis finais de semana que não pudemos estarmos juntos.

Agrade¸co ao corpo t´ecnico e docente da Universidade Presbiteriana Mackenzie. Agrade¸co tamb´em aos colegas de curso, que sempre me incentivaram, em especial agrade¸co aos meus amigos Israel Florentino dos Santos e Ad´ılson Eduardo Spagiari.

(6)

ABSTRACT

Cellular automata are totally discrete systems that act locally in a simple and deter-ministic way, but whose resulting global behavior can be extremely complex. The set of possible global configurations in one finite time step for a CA can be described by a regular language, which in turn can be represented by a finite automaton, more precisely the so-called process graph, in which all states are initial and final. Here, we study the temporal evolution complexity of the elementary cellular automata (i.e., one-dimensional, binary, with radius 1), and related previous works are revisited and discussed, indicating problems and their consequences. We also start up a novel approach for the problem, substituting the process graph based representation that describes the configuration at each time step by adjacency matrices derived from them. In fact, we extend the classical adjacency matrix notation, as they cannot fully represent process graphs. With this new notation, we show that it is possible to obtain the algorithm to generate a process graph for an arbitrary finite time step for each of the rules at study. In conclusion, although advancing the limit graph problem, it still remains open, and we provide suggestions for further research.

(7)

RESUMO

Autômatos celulares são sistemas totalmente discretos que agem localmente de forma simples e determin´ıstica, mas cujo comportamento global resultante pode ser extrema-mente complexo. O conjunto de poss´ıveis configura¸cões globais em um passo de tempo t

finito para um autômato celular pode ser descrito por uma linguagem regular, a qual por sua vez pode ser representada por meio de um autômato finito, mais precisamente, pelo chamado grafo de processo, em que todos os estados são iniciais e finais. Estuda-se aqui a complexidade da evolu¸cão temporal dos autômatos celulares elementares (i.e., unidimen-sionais, binários, de raio 1), e trabalhos anteriores são revisitados e discutidos, no quais apontam-se problemas e suas consequências. Também inicia-se uma nova abordagem para o problema, substituindo a representa¸cão dos grafos de processo que descrevem a configura¸cão a cada passo de tempo por matrizes de adjacência deles derivadas. De fato, estende-se a nota¸cão clássica de matriz de adjacência, já que ela se mostra insuficiente para descrever completamente os grafos de processo em questão. Com essa nova nota¸cão, mostra-se que é poss´ıvel obter o algoritmo que gere o grafo de processo de tempot para cada uma das regras estudadas. Conclui-se que, embora houve avan¸cos para o problema do grafo limite, este ainda permanece aberto, e sugestões para continua¸cão da pesquisa são dadas.

(8)

Sum´

ario

1 Introdu¸c˜ao 1

2 Autˆomatos celulares 5

2.1 Autˆomatos celulares elementares . . . 6

2.2 Equivalˆencia dinˆamica de regras . . . 8

2.3 Classifica¸c˜ao dos autˆomatos celulares . . . 13

2.4 Linguagens formais . . . 15

2.5 Autˆomatos finitos e linguagens regulares . . . 16

2.6 Grafos de processo . . . 19

2.7 Evolu¸c˜ao de um autˆomato celular . . . 19

2.8 Configura¸c˜ao inicial de um autˆomato celular . . . 22

2.9 Fun¸c˜oes NetCAStep, TrimNet eMinNet . . . 23

3 Complexidade de linguagens regulares de autˆomatos finitos elementares 26 3.1 Revisitando [Trafaniuc, 2004] e [Miki, 2006] . . . 27

3.2 Problemas encontrados no trabalho de [Trafaniuc, 2004] . . . 35

3.3 Comportamento limite da regra 184 . . . 39

3.4 Nova tabela de complexidade de regras . . . 42

4 Constru¸cão do grafo de processo por meio de matrizes de adjacências 50 4.1 Representa¸cão de grafos de processo em forma matricial . . . 50

4.1.1 Matrizes de adjacˆencias . . . 50

4.1.2 Matrizes de adjacˆencia de evolu¸c˜ao temporal . . . 52

4.2 Algoritmo do grafo de processo de tempo t para a regra 184 . . . 55

4.3 Padrão de forma¸cão das matrizes de adjacências de evolu¸cão temporal . . . 59

5 Conclus˜ao 61

Referˆencias bibliogr´aficas 66

A Algoritmos para gerar o grafo de processo de tempot para as 26 regras

(9)

Lista de Figuras

1.1 Convergˆencia da regra 8 para configura¸c˜ao limite. . . 2

1.2 Evolu¸c˜ao da regra 184. . . 3

2.1 Condi¸c˜ao de contorno peri´odica . . . 7

2.2 Evolu¸c˜ao temporal de um autˆomato celular unidimensional. . . 8

2.3 Exemplo de esquema de numera¸c˜ao de Wolfram para ACs unidimensionais 9 2.4 Transforma¸c˜ao de complemento. . . 10

2.5 Transforma¸c˜ao do tipo reflex˜ao. . . 10

2.6 Regra 30. . . 13

2.7 Regra 86. . . 13

2.8 Classes dinˆamicas dos ACs . . . 14

2.9 Autˆomato finito representado como um grafo orientado. . . 18

2.10 Grafo de transi¸c˜ao de estados . . . 22

2.11 Configura¸c˜oes iniciais do AF . . . 23

2.12 Grafo de processo representando configura¸c˜oes iniciais . . . 23

2.13 Exemplo de sa´ıda das fun¸c˜oes NetCAStep, MinNet e TrimNet . . . 25

3.1 Sequência de utiliza¸cão das fun¸cões NetCAStep,MinNet e TrimNet. . . 28

3.2 Grafos de processo para 4 passos de tempo da regra elementar 11. . . 29

3.3 Convergˆencia da regra 8 para o grafo de processo limite. . . 29

3.4 AF determin´ıstico limite da regra 128. . . 30

3.5 Algoritmo de sele¸c˜ao de regras . . . 31

3.6 Grafos de processo de t et+ 1 para a regra 128. . . 32

3.7 Subgrafos de t+ 1 que possuem o mesmo n´umero de n´os do grafo de t. . . 32

3.8 Subgrafos de t+ 1 que se encaixam perfeitamente em t. . . 33

3.9 Opera¸c˜ao de diferen¸ca entre t e os subgrafos do passo anterior. . . 33

3.10 Grafo limite da regra 184 . . . 34

3.11 Compara¸cão de encadeamento das fun¸cões NetCAStep, MinNet eTrimNet 36 3.12 Sequência de grafos de processo da regra 32. . . 37

3.13 Sequˆencia de grafos de processo da regra 128. . . 37

(10)

3.16 Deslocamento da regra 184 na configura¸c˜ao limite . . . 40

3.17 Grafo limite da regra 184 em condi¸cão de contorno não periódica. . . 41

3.18 Sequˆencia de AFs da regra 32. . . 46

3.24 AFs limite. . . 49

4.1 Grafo direcionado. . . 51

4.2 Representa¸c˜ao em matriz de adjacˆencia. . . 51

4.3 Grafo de processo representado atrav´es de um grafo direcionado. . . 53

4.4 Representa¸cão em matriz de adjacência de evolu¸cão temporal. . . 53

4.5 Grafos de processo para os cinco primeiros passos de tempo da regra 184. . 55

4.6 Estrutura adicionada . . . 56

4.7 Estrutura exclu´ıda . . . 56

4.8 Estrutura adicionada em nota¸c˜ao matricial. . . 56

4.9 Estrutura exclu´ıda em nota¸c˜ao matricial. . . 56

(11)

Lista de Tabelas

2.1 Aplica¸c˜ao de regra local. . . 9

2.2 Autˆomatos celulares elementares dinamicamente equivalentes . . . 12

3.1 Tabela de complexidade de linguagens regulares (1/3). . . 43

4.1 Regra 184. . . 57

(12)

1 Introdu¸c˜

ao

Autômatos celulares (ACs) são sistemas discretos que apresentam um comportamento local extremamente simples, mas cujo comportamento global pode ser complexo ao ponto de eles poderem ser equivalentes a uma máquina de Turing universal [Wolfram, 1984a]. Ele é caracterizado por um reticulado de células cujos estados posteriores dependem dos estados atuais de si próprias e de suas vizinhas. Este tipo de comportamento, que é local-mente simples mas globallocal-mente complexo dá origem à chamada computa¸cão emergente, e é a base da utiliza¸cão dos ACs na modelagem de diversos sistemas naturais.

A vizinhan¸ca das células de um AC pode ser definida por um raio centrado na célula em questão, de forma a englobar todas as células dentro do raio. Um AC elementar possui raio igual a 1 e conjunto de estados{0,1}, o que permite a defini¸cão de um espa¸co de 256 regras poss´ıveis, que são usualmente identificadas por um número entre 0 e 255 [Wolfram, 1984b]. Este trabalho estuda um subconjunto dos ACs elementares, que consiste em 26 regras estudadas em [Trafaniuc, 2004] e [Miki, 2006].

O comportamento limite de ACs pode ser descrito por meio de linguagens formais, a partir das cadeias ou palavras formadas por seu alfabeto [Lewis e Papadimitriou, 2008]. A classe mais simples de linguagens formais é a das linguagens regulares, que pode ser gerada por uma gramática regular ou pelas chamadas expressões regulares. Qualquer linguagem regular pode ser reconhecida por um autômato finito (AF), que é uma modalidade de reconhecedor de linguagem com memória restrita. As linguagens regulares são o tipo mais simples de linguagem na hierarquia de Chomsky.

(13)

anterior e da fun¸cão de transi¸cão da regra. Estas fun¸cões estão descritas na Se¸cão 2.9.

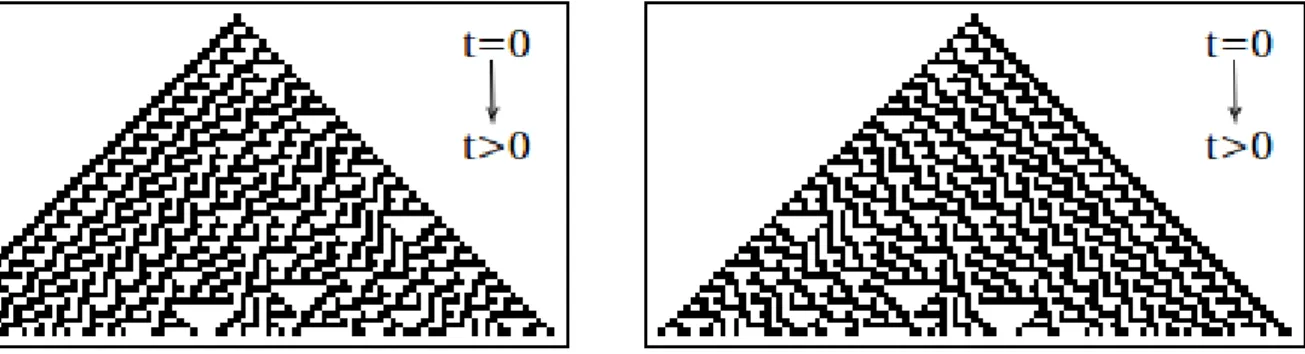
Trafaniuc (2004) e Miki (2006) estudaram, em seus respectivos trabalhos, a complexi-dade de ACs elementares por meio da análise da evolu¸cão dos sucessivos grafos de processo para diferentes instantes de tempo. Uma questão que ficou aberta nesses trabalhos foi a eventual convergência dos grafos de processo para o comportamento limite da regra quando t 7→ ∞. Por exemplo, na Figura 1.1 são mostrados os sucessivos grafos de pro-cesso da evolu¸cão temporal da regra elementar 8, onde após dois passos de tempo o seu grafo limite é atingido; em cada grafo, a liga¸cão entre dois nós representa uma transi¸cão de estados entre eles, a partir do s´ımbolo 0, em vermelho, ou 1, em preto (outros aspectos da nota¸cão de grafos de processo utilizada neste trabalho é apresentada na Se¸cão 2.8). Na Figura 1.2 são apresentados os grafos de processo da regra elementar 184, a qual não converge para a configura¸cão limite, apesar de se saber que seu comportamento limite pode ser expresso por uma linguagem regular [Miki, 2006].

t = 1 t = 2 t= 3

Figura 1.1: Convergˆencia da regra 8 para configura¸c˜ao limite.

(14)

t= 1 t= 2 t= 3

t= 4 t= 5 t= 50

t= 100

(15)

O Cap´ıtulo 2 apresenta referencial te´orico sobre os ACs, linguagens formais e com-portamento limite.

O Cap´ıtulo 3 descreve os trabalhos anteriores, aponta os problemas neles encontrados e discute novos resultados obtidos.

O Cap´ıtulo 4 descreve uma nova abordagem por meio de matrizes de adjacência. A obten¸cão do grafo de processo de tempo t pode ser conseguida por meio de uma nova nota¸cão de matrizes de adjacência em rela¸cão ao respectivo grafo de processo.

(16)

2 Autˆ

omatos celulares

´

E comum na natureza encontrar sistemas cujo comportamento global é extremamente complexo, ainda que as partes que os formam sistemas sejam simples. A complexidade é gerada pelo efeito cooperativo de componentes com regras locais simples. Muito foi descoberto sobre a natureza dos componentes em sistemas f´ısicos e biológicos, mas pouco é conhecido sobre os mecanismos pelos quais tais componentes agem cooperativamente para gerar o comportamento global observado [Wolfram, 1984a].

Autômatos Celulares (ACs) podem ser vistos como uma classe de sistemas dinâmicos que atua em um reticulado infinito cujo tempo, espa¸co e estado são todos discretos e os estados de cada célula podem ser obtidos a partir de um conjunto finito de estados poss´ıveis [Jiang, 2001].

ACs são, fundamentalmente, as representa¸cões matemáticas mais simples de uma classe muito maior dos chamados sistemas complexos, termo que se refere a qualquer sistema dinâmico formado por inúmeros componentes, possivelmente simples, que inter-agem de forma não linear com os outros. Assim, ACs têm se provado serem idealiza¸cões extremamente úteis do comportamento dinâmico de muitos sistemas complexos reais, in-cluindo flu´ıdos f´ısicos, redes neurais, sistemas dinâmicos moleculares, economia, entre outros [Ilachinski, 2002]. Por causa de sua simplicidade subjacente, ACs são máquinas conceituais poderosas com as quais se estuda padrões generalizados de forma¸cão. Eles já forneceram ideias cruciais sobre auto-organiza¸cão de rea¸cões qu´ımicas, sistemas de di-fusão, crescimento de cristais, forma¸cão de padrões de conchas e fenômenos em fluxo de tráfego veicular, para citar alguns exemplos. Em um lado mais prático, ACs fornecem a base de algoritmos importantes de criptografia [Nandi, Kar e Chaudhuri, 1994], gera¸cão de padrões [White e Engelen, 1993], entre outros. Existem até mesmo algumas sérias especula¸cões de que ACs possam fornecer a espinha dorsal de uma f´ısica fundamental radicalmente discreta [Ilachinski, 2002].

(17)

processa-mento não são separadas uma da outra, e que fossem massivamente paralelos e capazes de se autorreparar e reproduzir dado o material base necessário. Segundo sugestões de Stanislaw Ulam, von Neumann visualizou um universo discreto consistindo de uma grade bidimensional de máquinas de estado finito, chamadas células, interconectadas interna-mente umas com as outras [Kari, 2005]. O autômato originalinterna-mente descrito por von Neumann é um vetor uniforme infinito bidimensional de células, onde cada célula é conec-tada pelos seus quatro vizinhos ortogonais. As primeiras estruturas estudadas eram em sua maioria de uma ou duas dimensões, apesar de dimensões maiores também terem sido consideradas [Sarkar, 2000].

Dois tópicos imediatos surgiram a partir do trabalho de von Neumann. O primeiro, em sua maior parte na década de 60, era uma discussão sobre a constru¸cão de autômatos autorreplicantes. O segundo foi uma tentativa de capturar mais da essência de autor-replica¸cão por meio de estudos matemáticos de propriedades detalhadas de ACs. Durante o curso da década de 60 foram encontradas constru¸cões mais simples de ACs capazes de autorreplica¸cão e computa¸cão universal. No in´ıcio da década de 60 foram notadas algu-mas caracter´ısticas gerais incrivelmente simples de ACs que acreditava-se serem relevantes para autorreplica¸cão - e foram estudadas com um formalismo técnico mais elaborado. Ex-istiram também várias constru¸cões de ACs cujo comportamento mostrou caracter´ısticas particularmente simples, talvez relevantes, para a autorreplica¸cão [Wolfram, 2002].

(18)

2.1 Autˆ

omatos celulares elementares

Um AC unidimensional consiste de uma grade bi-infinita (podendo tamb´em ter tamanho

N, para o caso finito), onde existe uma fun¸cão de transi¸cão φ : Zr 7→ Σ, que deter-mina a dinâmica do AC, onde r representa o raio (inteiro) de vizinhan¸ca do AC e Σ é o conjunto de estados poss´ıveis de uma célula. Um AC com raio r tem vizinhan¸ca (−r,−r+ 1, . . . , r−1, r), de maneira que cada vizinhan¸ca consiste de 2r+ 1 células.

Um AC elementar ´e um AC unidimensional com conjunto de estados Σ = {0,1} e raio r= 1 [Kari, 2005].

Em ACs unidimensionais uma configura¸cão inicial genérica será tipicamente atra´ıda para uma condi¸cão de equil´ıbrio a qual é chamada de atrator [Li, 1987]. Atratores rep-resentam pontos de equil´ıbrio em sistemas dinâmicos, e, no caso de ACs, reprep-resentam configura¸cões estáveis quandot7→ ∞. O conjunto de atratores de um AC representa sua configura¸cão limite.

Embora teoricamente um autômato unidimensional possa ser interpretado como uma linha bi-infinita, na prática existe uma quantidade fixa de células e é necessário adotar uma condi¸cão de contorno para as células nos extremos. Um possibilidade é adotar uma condi¸cão de contorno fixa, onde escolhe-se um determinado valor para os vizinhos não existentes das células da extrema direita e esquerda. Outra possibilidade é adotar uma condi¸cão de contorno periódica, onde o vizinho da direita da última célula é a primeira célula, e vice-versa, conforme ilustrado na Figura 2.1.

A evolu¸cão de um autômato unidimensional pode ser visualizada por meio de uma grade bidimensional onde cada linha representa uma configura¸cão global em um determi-nado instante de tempo discreto, conforme visualizado na Figura 2.2, onde a cor preta representa um estado em 0 e a cor branca um estado em 1.

Existem 23 _{= 8 poss´ıveis padr˜oes de estados dentro de uma vizinhan¸ca para ACs} elementares. Como cada combina¸c˜ao pode resultar nos valores 0 ou 1, podem existir, portanto, 223

= 256 ACs elementares. A regra local pode ser formalizada como:

xt_i+1 =φ(xt_i−1, xti, x t

(19)

Figura 2.1: Condi¸cão de contorno periódica: a última célula é ligada à primeira, formando um anel [Chua, Yoon e Dogary, 2002].

(20)

ondext

i é o estado da célula ino instante t em que a regra local atua, eφ é a fun¸cão que executa a regra local. A Tabela 2.1 mostra como é aplicada a regra local. As regras locais para ACs elementares podem ser descritas por um número binário de oito bits, codificado pelo resultado das oito combina¸cões de vizinhan¸ca da regra local{xi−1, xi, xi+1}[Wolfram, 1983]. No caso da Figura 2.3, este número é o número 9010, e este autômato é chamado deregra 90. Neste texto, a menos que explicitamente dito o contrário, a referência a um AC por meio do número de sua regra se diz respeito a um AC elementar.

xi−₁ x_i x_i+1 φ

1 1 1 0

1 1 0 1

1 0 1 0

1 0 0 1

0 1 1 1

0 1 0 0

0 0 1 1

0 0 0 0

Tabela 2.1: Aplica¸c˜ao de regra local.

111 0

110 1

101 0

100 1

011 1

010 0

001 1

000

0

=

90

Figura 2.3: Exemplo de esquema de numera¸c˜ao de Wolfram para ACs unidimensionais [Wolfram, 1983].

2.2 Equivalˆ

encia dinˆ

amica de regras

(21)

Transforma¸cão de complemento (ou conjuga¸cão): Nesta transforma¸cão todos os es-tados são complemenes-tados, ou seja, troca-se 0 por 1 e vice-versa, tanto nas viz-inhan¸cas quanto nos bits de sa´ıda, conforme exemplificado na Figura 2.4, onde mostra-se a vizinhan¸ca original, depois a opera¸cão de complemento e, finalmente, o resultado depois das vizinhan¸cas serem reordenadas.

Vizinhan¸ca 111 110 101 100 011 010 001 000

φ 0 1 1 0 1 1 1 0

Complemento 000 001 010 011 100 101 110 111

φ 1 0 0 1 0 0 0 1

Reordenado 111 110 101 100 011 010 001 000

φ 1 0 0 0 1 0 0 1

Figura 2.4: Transforma¸c˜ao de complemento.

Transforma¸cão por reflexão: Nesta transforma¸cão o estado do vizinho da direita é trocado com o estado do vizinho da esquerda, ou seja, o valor do estado do vizinho da esquerda passa a ser o valor do vizinho da direita e vice-versa. A Figura 2.5 ilustra o processo.

Vizinhan¸ca 111 110 101 100 011 010 001 000

φ 0 1 1 0 1 1 1 0

Reflex˜ao 111 011 101 001 110 010 100 000

φ 0 1 1 0 1 1 1 0

Reordenado 111 110 101 100 011 010 001 000

φ 0 1 1 1 1 1 0 0

(22)

Transforma¸cão conjunta: Neste caso é realizada uma opera¸cão conjunta de composi¸cão (independente de ordem) das duas opera¸cões anteriores.

(23)

Representante Regras

da classe equivalentes

0 255 1 127 2 16,191,247 3 17,63,119 4 223 5 95 6 20,159,215 7 21,431,87 8 64,239,253 9 65,111,125 10 80,175,245 11 47,81,117 12 68,207,221 13 69,79,93 14 84,143,213 15 85 18 183 19 55 22 151 23 24 66,189,231 25 61,67,103 26 82,167,181 27 39,53,83 28 70,157,199 29 71 30 86,135,149 32 251 33 123 34 48,187,243 Representante Regras

35 49,59,115 36 219 37 91 38 52,155,211 40 96,235,249 41 97,107,121 42 112,171,241 43 113 44 100,203,217 45 75,89,101 46 116,139,209 50 179 51 54 147 56 98,185,227 57 99 58 114,163,177 60 102,153,195 62 118,131,145 72 237 73 109 74 88,173,229 76 205 77 78 92,141,197 90 165 94 133 104 233 105 106 120,169,225 Representante Regras

108 201 110 124,137,193 122 161 126 129 128 254 130 144,190,246 132 222 134 148,158,214 136 192,238,252 138 174,208,244 140 196,206,220 142 212 146 182 150 152 188,194,230 154 166,180,210 156 198 160 250 162 176,186,242 164 218 168 224,234,248 170 240 172 202,216,228 178 184 226 200 236 204 232

(24)

As Figuras 2.6 e 2.7 mostram a evolu¸cão de duas regras locais equivalentes por uma transforma¸cão de reflexão. Nota-se pelas figuras que a evolu¸cão de uma é o espelho da outra.

Figura 2.6: Regra 30. Figura 2.7: Regra 86.

Estudar as classes de equivalência mostra-se importante porque regras locais equiva-lentes apresentam o mesmo padrão de complexidade de evolu¸cão.

2.3 Classifica¸c˜

ao dos autˆ

omatos celulares

Wolfram (1983) dividiu os ACs elementares em quatro classes segundo a complexidade do padrão tipicamente gerado pelo seu comportamento dinâmico, a partir de configura¸cão inicial aleatória, conforme descrito a seguir:

Classe 1 A evolu¸c˜ao leva a um estado nulo, ou seja, em que as condi¸c˜oes iniciais levam ao mesmo estado uniforme.

Classe 2 A evolu¸cão leva a um conjunto de estruturas de ponto-fixo ou periódicas. Classe 3 A evolu¸cão leva a um padrão caótico.

Classe 4 A evolu¸c˜ao apresenta longos transientes, que envolvem estruturas localizadas complexas.

Os atratores nas classes 1, 2 e 3 são análogos, respectivamente, aos atratores de ponto fixo, ciclo limite e caóticos encontrados em sistemas dinâmicos cont´ınuos. A Figura 2.8 mostra exemplos de ACs das quatro classes de complexidade.

(25)

Figura 2.8: Classes dinˆamicas dos ACs [Wolfram, 1984b]. (a) classe 2, (b) classe 1, (c) classe 3 e (d) classe 4.

Regras Nulas A configura¸c˜ao limite ´e formada somente por 0s ou somente por 1s.

Regras Ponto-Fixo A configura¸cão limite não se altera ao reaplicar a regra do autômato celular.

Regras Ciclo Duplo A configura¸cão limite não se altera ao reaplicar a regra do autômato celular duas vezes.

Regras Periódicas A configura¸cão limite não se altera à aplica¸cão da regra N vezes; com o tamanho do ciclo N independente ou fracamente dependente do tamanho do reticulado.

Regras Complexas Embora a dinˆamica limite possa ser peri´odica, o intervalo tran-siente pode ser extremamente longo e, tipicamente, este intervalo cresce mais que linearmente com o tamanho do sistema.

(26)

2.4 Linguagens formais

A teoria dos autômatos é o estudo dos dispositivos de computa¸cão abstratos, ou máquinas. Antes de existirem computadores, na década de 1930, Alan Turing estudou uma máquina abstrata que tinha todas as caracter´ısticas dos computadores atuais, pelo menos no que se refere ao quanto eles poderiam calcular. O objetivo de Turing era descrever com exatidão o limite entre o que uma máquina de computa¸cão podia fazer e aquilo que ela não podia fazer.

Nas décadas de 1940 e 1950, tipos de máquinas mais simples, que hoje são conhecidas como autômatos finitos, foram estudados por diversos pesquisadores. Esses autômatos, propostos originalmente no contexto de modelagem matemática do cérebro, se mostraram extremamente úteis para uma grande variedade de propósitos. Também no final dos anos 50, o linguista N. Chomsky, iniciou o estudo de gramáticas formais gerativas, as quais guardam relacionamentos estreitos com os autômatos abstratos [Hopcroft, Motwani e Ullman, 2002].

Linguagens regulares estão entre os tópicos mais antigos em teoria de linguagens for-mais. O estudo formal de linguagens regulares e AFs é datado do in´ıcio da década de 40, quando máquinas de estado finito foram utilizadas para modelar conjuntos de neurônios por McCulloch e Pitts. Desde então, linguagens regulares têm sido extensivamente es-tudadas. Resultados das primeiras investiga¸cões são, por exemplo, o teorema de Kleene estabelecendo a equivalência de expressões regulares e AFs, a introdu¸cão de autômatos com sa´ıda por Mealy e Moore e a introdu¸cão de AFs não determin´ısticos por Rabin e Scott [Rozenberg e Salomaa, 1997].

O elemento básico de uma linguagem é o alfabeto, um conjunto finito de s´ımbolos utilizados para formar as cadeias pertencentes à linguagem. Por exemplo, o alfabeto Σ ={0,1} contém os s´ımbolos 0 e 1, e todas as cadeias formadas a partir deste alfabeto só poderão conter estes s´ımbolos.

(27)

denotado por Σ+_{, e o conjunto de todas as cadeias, incluindo a cadeia vazia, sobre um} alfabeto Σ ´e denotado por Σ+S

{ε} = Σ∗

. O comprimento de uma cadeia é o número de s´ımbolos que a forma. Logo, o comprimento da cadeiaabcd é 4. Denota-se o compri-mento de uma cadeia w por |w|; portanto, |101| = 3 e |ε| = 0. Alternativamente, por meio de um isomorfismo natural, uma cadeia w ∈ Σ∗

pode ser considerada uma fun¸c˜ao

w:{1, . . . ,|w|} 7→Σ; o valor de w(j), onde 1≤j ≤ |w|, é o s´ımbolo que ocupa a j-ésima posi¸cão em w [Lewis e Papadimitriou, 2008].

D´a-se o nome de linguagem a qualquer conjunto de cadeias sobre um alfabeto Σ, ou seja, a qualquer subconjunto de Σ∗

. Portanto, Σ∗

, ε e Σ são linguagens. Sendo uma linguagem simplesmente um tipo particular de conjunto, pode-se especificar linguagens finitas enumerando-se todas as suas cadeias. Por exemplo, {aba, czr, d, f} é uma lin-guagem sobre{a, b, . . . , z}. Entretanto, quando as linguagens são infinitas, não é poss´ıvel listar todas as cadeias [Lewis e Papadimitriou, 2008]. Assim, especifica-se linguagens in-finitas da seguinte forma: L={w∈W: W⊂Σ∗

}. Linguagens infinitas tamb´em podem ser representadas pelos sistemas que as reconhecem.

2.5 Autˆ

omatos finitos e linguagens regulares

Segundo Hopcroft, Motwani e Ullman (2002), um AF ´e definido por uma qu´ıntupla

A= (Q,Σ, δ, q0,F), onde:

A ´e o nome associado ao AF.

Q ´e um conjunto finito de estados.

Σ ´e um conjunto finito de s´ımbolos de entrada

δ é uma fun¸cão de transi¸cão do tipo δ : Q×Σ 7→ Q. A fun¸cão de transi¸cão toma um estado e um s´ımbolo de entrada e retorna um novo estado. δ também é chamada de tabela de transi¸cão de estados.

q0 ´e o estado inicial.

(28)

O autômato atua lendo s´ımbolos de uma fita de entrada onde cada posi¸cão na fita contém um s´ımbolo. O autômato come¸ca seu processamento no estado inicialq0 e, a cada s´ımbolo lido da fita de entrada, a fun¸cão de transi¸cão δ : Q×Σ 7→ Q define um novo estado como o estado atual. Quando o processamento da fita de entrada termina, se o estado atual for um dos estados pertencentes ao conjuntoF de estados finais, a entrada é considerada aceita, caso o contrário, a entrada é rejeitada. Por exemplo, considere o seguinte AF:

M ={Q={A, B},

Σ = {0,1},

δ ={A×07→A;A×17→B;B×07→A;B×17→B}, q0 =A,

F={B}}

Neste caso, o estado inicial é o estado A, e o conjunto de estados finais é formado pelo estado único B. É fácil verificar que este autômato aceita qualquer cadeia sobre o alfabeto {0,1} que termine com o s´ımbolo 1. Considere a cadeia 00101. O autômato come¸ca no estadoA e lê o primeiro s´ımbolo 0, a fun¸cãoδ possui uma entradaA×07→A, então o autômato consome o s´ımbolo 0, avan¸ca a fita de entrada e permanece no estado

A. Novamente um 0 é lido, então o estado A é mantido e avan¸ca-se a fita de entrada. Agora o s´ımbolo 1 é lido, a entrada correspondente na tabela de transi¸cão éA×17→B, então o autômato vai para o estado B. O próximo s´ımbolo da entrada é o 0, e a entrada correspondente na tabela de transi¸cão éB×07→A, então o autômato vai para o estado

A. O último s´ımbolo de entrada é o s´ımbolo 1, então o autômato vai para o estado B. Como toda a entrada foi consumida e o estado atualB pertence ao conjunto de estados finaisF, a cadeia de entrada 00101 é aceita.

AFs também podem ser representados graficamente através de um grafo orientado. Os estados são representados pelos nós do grafo e os arcos representam as transi¸cões de estado. O estado inicial possui uma seta de entrada e os estados finais possuem um c´ırculo duplo. A Figura 2.9 mostra graficamente o autômato anterior.

(29)

A

B

1

0

1

Figura 2.9: Autˆomato finito representado como um grafo orientado.

objetivo, ou seja, cada entrada da tabela de transi¸cão possui a formaδ:Q×Σ7→Q. Nos AFs não determin´ısticos, cada entrada na tabela de transi¸cão é da formaδ:Q×Σ7→2Q_,

ou seja, para um dado estado e um s´ımbolo de entrada, o n´umero de poss´ıveis transi¸c˜oes pode ser maior que um [Rozenberg e Salomaa, 1997].

A mecânica básica de um AF é simples. O processamento em um autômato não determin´ıstico é análogo ao da versão determin´ıstica, exceto que, quando existe uma ambiguidade na transi¸cão (i.e., mais de um estado objetivo para uma dada entrada), o autômato se replica, tomando o caminho dosnestados objetivos. A entrada é considerada aceita se, ao final do processamento, pelo menos uma instância das cópias geradas está em um estado final.

O conjunto de cadeias reconhecidas por um autômato forma a linguagem do autômato. SejaM um autômato,L(M) constitui sua linguagem. A classe de linguagens reconhecidas por AFs são as linguagens regulares. Linguagens regulares podem também ser represen-tadas por meio das chamadas expressões regulares.

Sejam as opera¸c˜oes:

Uni˜ao A+B ={x|x∈A oux∈B}

Concatena¸c˜ao AB ={xy|x∈A e y∈B}

Fechamento de Kleene A∗

= {x1x2. . . xk|k ≥ 0 e cada xi ∈ A}. Adicionalmente também pode-se utilizar a nota¸cão A+, que é equivalente a AA∗

.

Uma cadeia R é considerada uma expressão regular [Sipser, 1996] se ela é:

(30)

2. ∅ (a linguagem vazia)

3. ε (a cadeia vazia)

4. R1+R2, onde R1 e R2 são expressões regulares e a opera¸cão + representa a união de duas linguagens representadas pelas expressões

5. R1R2, ondeR1 e R2 são expressões regulares e R1R2 representa a concatena¸cão das duas linguagens expostas

6. R1

∗

, ondeR1´e uma express˜ao regular eR1

∗

denota o fechamento de Kleene aplicado sobre R1

Por exemplo, a expressão regular do autômato da Figura 2.9 é (0 + 1)∗

11∗

.

2.6 Grafos de processo

Uma importante subclasse das linguagens regulares ´e a classe de linguagens de pro-cesso.

Defini¸cão Linguagens regulares de processo são um subconjunto das linguagens regulares em que dada uma cadeiaw∈L, qualquer subcadeia de w também está em L.

Defini¸cão O grafo de processo de uma linguagem de processo L é o grafo formado per-mitindo o AF m´ınimo associado M(L) iniciar em qualquer estado e marcando todos os estados como de aceita¸cão.

Todos os estados de um grafo de processo são, então, estados iniciais e de aceita¸cão.

Claramente linguagens regulares de processo são um conjunto menor do que linguagens regulares. Por exemplo, a linguagem L = {0011} só pode ser representada por uma linguagem regular, pois as subcadeias de 0011 não fazem parte de L.

2.7 Evolu¸c˜

ao de um autˆ

omato celular

(31)

que o AC é formado por N células. O conjunto dos estados de todas as células de um reticulado do AC em um dado passo em sua evolu¸cão temporal é chamado deconfigura¸cão global, e um subconjunto dos estados destas células define uma configura¸cão local.

Linguagens formais consistem do conjunto de cadeias formadas a partir de cadeias de s´ımbolos em um alfabeto finito Σ de acordo com regras gramaticais definidas. Conjuntos de configura¸cões de ACs podem assim ser considerados como linguagens formais, com cada cadeia na linguagem representando uma configura¸cão do AC. Tais conjuntos infinitos de configura¸cões são então completamente especificados por conjuntos finitos de regras gramaticais [Wolfram, 1984b].

O conjunto de configura¸c˜oes poss´ıveis em um AC unidimensional depois de t passos de evolu¸c˜ao pode ser representado por um conjunto Ω(t) _{[Wolfram, 1984b].}

O seguinte exemplo, retirado de [Wolfram, 1984b], ilustra o processo de gera¸cão do AF que representa o conjunto de configura¸cões poss´ıveis Ω(t)_após_t_{itera¸cões. A constru¸cão do} AF se baseia no grafo de De Bruijn [Bruijn, 1946], [Powley, 2009], [McIntosh, 2009]. Um grafo de De Bruijn com m s´ımbolos é um grafo direcionado representando sobreposi¸cões entre sequências de s´ımbolos, onde cada estado possui m arestas chegando e m arestas deixando o estado. Toda regra unidimensional pode ser inicialmente representada por um grafo de De Bruijn de 4 estados, em que somente as transi¸cões mudam para cada regra.

Considere a constru¸cão do conjunto Ω(1) _{gerado por um passo de tempo na evolu¸cão} do AC elementar com uma regra localφ dada por (regra número 76):

1117→0,1107→1,1017→0,1007→0,0117→1,010 7→1,001 7→0,000 7→0 (2.2)

O valora(1)_i de uma célula na posi¸cãoina configura¸cãoA(1) =φA(0) ∈Ω(1)_{depende da} vizinhan¸ca de três células (a(0)_i−₁, a

(0) i , a

(0)

(32)

associa um s´ımbolo com cada arco deg. Cada poss´ıvel caminho através deg corresponde a uma configura¸cão particular A(0)_{. O sucessor} _A(1) _{de cada configura¸cão inicial é dado} pela sequência de s´ımbolos associada com os arcos no caminho. As sequências de s´ımbolos obtidas seguindo todos os caminhos poss´ıveis através deg assim correspondem a todas as poss´ıveis configura¸cões A(1), obtidas depois de 1 passo de tempo na evolu¸cão do AC da Equa¸cão 2.2. O conjunto completo Ω(1) _{pode assim ser representado pelo grafo} _g_{. Está} claro que nem todas as poss´ıveis sequências de 0s e 1s podem aparecer nas configura¸cões de Ω(1)_{. Por exemplo, não existe um caminho em} _g _{que inclui a sequência 111, e assim} nenhuma configura¸cão em Ω(1) _{pode conter blocos de células 111.}

(33)

00

01

10

11

001 7→

0

000 7→

0

011 7→

1

010 7→

1

101 7→

0

100 7→

0

110 7→

1

111 7→

0

Figura 2.10: O grafo de transi¸cão de estados g para um AF não determin´ıstico que representa as configura¸cões obtidas depois de um passo de tempo na evolu¸cão do AC com a regra número 76. Poss´ıveis sequências de valores de células são representadas por caminhos poss´ıveis pelo grafo. Os nós no grafo são rotulados por pares de valores iniciais das células; os arcos então correspondem a triplas de valores iniciais das células. Cada tripla é mapeada sob a regra 76 para um valor particular da célula. O grafo com arcos rotulados por estas células correspondem a todas as configura¸cões poss´ıveis obtidas depois de um passo de tempo [Wolfram, 1984b].

2.8 Configura¸c˜

ao inicial de um autˆ

omato celular

(34)

A

0 ,

1

Figura 2.11: Poss´ıveis configura¸cões iniciais representadas por um AF determin´ıstico. É trival perceber que o autômato aceita qualquer sequência de 0s e 1s.

Figura 2.12: Grafo de processo representando as poss´ıveis configura¸cões iniciais. Arcos vermelhos representam transi¸cões em 0 e arcos pretos representam transi¸cões em 1.

Neste trabalho, o estado inicial dos AFs determin´ısticos apresentados é o primeiro estado, também destacado por um c´ırculo preenchido (sólido), enquanto os demais estados possuem um c´ırculo vazio.

2.9 Fun¸c˜

oes

NetCAStep

,

TrimNet

e

MinNet

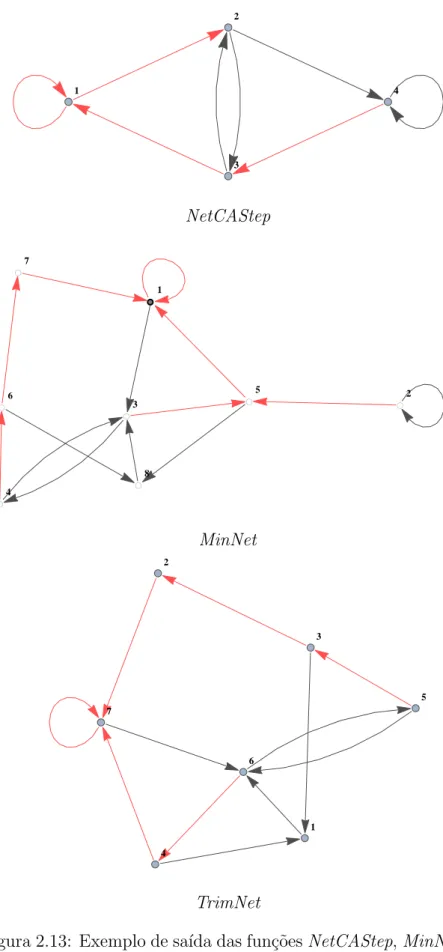
NetCAStep, TrimNet e MinNet [Wolfram, 2002] são fun¸cões desenvolvidas no Math-ematica para gerar AFs que representam a evolu¸cão para um passo de tempo de um AC unidimensional.

(35)

(configura¸c˜ao inicial).

A fun¸cão NetCAStep gera como sa´ıda uma lista de transi¸cões de estados correspon-dente a um grafo de processo. Sobre a lista de transi¸cões de estado resultante da fun¸cão NetCAStep é aplicada a fun¸cão MinNet, que, por sua vez, gera um AF determin´ıstico m´ınimo equivalente ao autômato gerado por NetCAStep, em que o último estado é o estado inicial e todos os estados são finais.

A fun¸c˜ao TrimNet faz a transforma¸c˜ao do AF de sa´ıda da MinNet em um grafo de processo determin´ıstico m´ınimo.

(36)

1

2

3

4

NetCAStep

ç

8

ç

3

ç

7

1

ç

6

ç

5

ç

4

ç

2

MinNet

1 6

2

7

3

4

5

TrimNet

(37)

3 Complexidade de linguagens regulares de autˆ

omatos

finitos elementares

O conjunto de poss´ıveis configura¸cões globais de um AC elementar sempre pode ser representado por um AF para um passo de tempo finito. Para o casot→ ∞, o conjunto de configura¸cões globais nem sempre pode ser representado por um AF, pois a configura¸cão limite de uma regra não necessariamente é regular. Diversos trabalhos trataram de estudar e caracterizar o comportamento limite de ACs.

O comportamento limite de um AC pode ser definido por uma linguagem formal den-tro da hierarquia de Chomsky. Hurd (1987) apresentou exemplos de ACs para os quais o conjunto limite era uma linguagem não regular. Exemplos adicionais foram apresen-tados em [Hurd, 1990b]. Hurd (1987) também provou que o problema de determinar se uma dada cadeia aparece no conjunto limite de um AC é indecid´ıvel. Uma prova alter-nativa utilizando uma abordagem topológica foi demonstrada por [Culik II, Pachl e Yu, 1989]. Hurd (1990a) provou que é poss´ıvel construir um AC cuja linguagem limite não é recursivamente enumerável.

Culik II e Yu (1988) formalizaram a classifica¸cão de ACs proposta por [Wolfram, 2002]. Com a formaliza¸cão, conseguiram provar que é indecid´ıvel determinar a qual classe um determinado AC pertence, e que ACs que em geral evoluem para um estado quiescente não necessariamente possuem comportamento limite descrito por uma linguagem regular.

Jiang (2001), utilizando dinâmica simbólica e teoria de linguagens formais, provou que o conjunto limite da regra 122 é, pelo menos, sens´ıvel ao contexto. Zhisong e Yi (2005) provaram que o comportamento limite da regra 22 não é regular.

Kürka e Maass (2000) analisaram a probabilidade do aparecimento de determinadas estruturas conforme t 7→ ∞ para as regras 18, 54, 62 e 184, e também compararam este conceito probabil´ıstico com o conceito de atratores, tanto do ponto de vista topológico quanto de teoria de medidas.

(38)

3.1 Revisitando [Trafaniuc, 2004] e [Miki, 2006]

O encadeamento das fun¸c˜oes NetCAStep,MinNet eTrimNet rende um grafo de pro-cesso que representa o conjunto de configura¸c˜oes globais para um passo de tempo finito, conforme ilustra a Figura 3.1.

Conforme avan¸cam-se os passos de tempo, a tendência é que o conjunto de con-figura¸cões fique mais restrito e, como consequência, o grafo torne-se mais complexo. A Figura 3.2 mostra os grafos de processo de 4 passos de tempo para a regra 11. Nota-se que, com o passar do tempo, o número de estados e transi¸cões aumenta, em decorrência da maior restri¸cão de configura¸cões poss´ıveis. Wolfram (1984b) propôs este aumento de complexidade do grafo como medida de complexidade da regra, ou seja, a complexidade da regra é proporcional ao aumento do número de estados e transi¸cões dos grafos dos sucessivos passos de tempo. Wolfram (1994) construiu uma tabela contendo a rela¸cão do número de estados e arestas das regras do espa¸co elementar (agrupadas pelas classes de equivalência) para os cinco primeiros passos de tempo e, quando poss´ıvel, para o grafo limite, além da expressão de crescimento dos nós e arestas para t >5.

Conforme já mencionado, o conjunto de configura¸cões globais de uma regra unidimen-sional parat <∞ de um AC sempre pode ser representada por um grafo de processo. É importante ressaltar que esta abordagem limita-se à condi¸cão de contorno não periódica. Para condi¸cão de contorno periódica, este grafo pode não existir para uma determinada regra, mesmo existindo na condi¸cão de contorno não periódica. A Se¸cão 3.3 apresenta uma prova de que em condi¸cão de contorno periódica, o comportamento limite da regra 184 não pode ser representado por um grafo de processo.

Pode-se imaginar que, para os casos em que a configura¸cão limite de um AC possa ser representada por um grafo de processo, a execu¸cão do encadeamento das fun¸cões NetCAStep,MinNet eTrimNet por um per´ıodo suficiente de tempo levará ao grafo limite, conforme se exemplifica na Figura 3.3. Mas existem regras em que esta convergência não ocorre, como a regra 128 (Figura 3.13), mesmo seu comportamento limite sendo conhecido [Wolfram, 1984b] (Figura 3.4).

(39)

In´ıcio

Entrada: - NDFA - n´umero da regra do AC

NetCAStep

Sa´ıda: - autˆomato

finito n˜ao determin´ıstico

Gerar para o pr´oximo passo de tempo?

MinNet

finito de-termin´ıstico

TrimNet Entrada: - DFA

Sa´ıda: - grafo de processo

sim n˜ao

(40)

T

₌

1 T

₌

2 T

₌

3 T

₌

4

Figura 3.2: Grafos de processo para 4 passos de tempo da regra elementar 11.

T

=

1 T

=

2 T

=

3

(41)

ç

3

ç

2 1

Figura 3.4: AF determin´ıstico limite da regra 128.

[Trafaniuc, 2004] e, posteriormente, de [Miki, 2006].

[Trafaniuc, 2004] procurou isolar aquelas regras que possuem crescimento estruturado, ou seja, em que se pode observar estruturas comuns nos sucessivos passos de tempo. Primeiramente, sobre as 256 regras elementares, foi aplicado um algoritmo para sele¸c˜ao de regras que apresentam grafos com complexidade crescente a cada passo de tempo. O algoritmo ´e ilustrado na Figura 3.5.

O algoritmo divide as regras em dois grupos [Trafaniuc, 2004]:

Grupo 1: Regras que apresentam crescimento de complexidade no AF limite a cada passo de tempo, e o método é interrompido após 5 passos de tempo.

Grupo 2: Regras que deixam de apresentar crescimento de complexidade no AF em at´e 5 passos de tempo.

(42)

In´ıcio

Regra de AC elementar

NetCAStep, MinNet, TrimNet

Autˆomato para o passo de tempo t+ 1

Autˆomato

t+ 1 ´e o mesmo quet?

Regras grupo 2 N´umero da

itera¸c˜ao ´e 5?

Regras grupo 1

sim n˜ao

Figura 3.5: Algoritmo de sele¸c˜ao de regras [Trafaniuc, 2004].

(43)

1. Gerar os grafos das regras de transi¸c˜ao, para 2 passos de tempo consecutivos, t e

t+ 1, de uma regra do espa¸co elementar (Figura 3.6).

Figura 3.6: Grafos de processo det et+ 1 para a regra 128.

2. Gerar todos os poss´ıveis subgrafos do passo de tempo t+ 1 que tenham o mesmo n´umero de estados que o grafo do passo de tempo t (Figura 3.7).

Figura 3.7: Subgrafos de t+ 1 que possuem o mesmo n´umero de n´os do grafo de t.

(44)

Figura 3.8: Subgrafos de t+ 1 que se encaixam perfeitamente em t.

4. Realizar uma opera¸cão de diferen¸ca entre o grafo det e todos os subgrafos de t+ 1 selecionados no passo três, com o mesmo número de nós. O subgrafo que apresentar a menor diferen¸ca no número de transi¸cões de estados é selecionado. No caso de empate, o primeiro subgrafo é selecionado (Figura 3.9).

Figura 3.9: Opera¸c˜ao de diferen¸ca entret e os subgrafos do passo anterior.

(45)

dos grafos de processo de acordo com o passo de tempo, sendo apresentado o método de obten¸cão do grafo de processo de passo t para cada uma. O trabalho chegou à conclusão que são necessárias duas propriedades para caracteriza¸cão do grafo de processo de uma regra [Trafaniuc, 2004]:

1. O crescimento do n´umero de estados do grafo de processo deve ser proporcional ao passo de tempo, ou seja, o n´umero de estados cresce a cada passo de tempo.

2. Os grafos de processo para passos de tempo distintos devem possuir uma rela¸c˜ao de crescimento, conforme descrito anteriormente.

Trafaniuc (2004) reconstruiu a tabela de complexidade de [Wolfram, 1994], preenchendo novas lacunas na tabela. Também encontrou alguns valores divergentes em rela¸cão à tabela original, embora não tenha mencionado nada em rela¸cão a tal discrepância. Miki (2006), posteriormente, identificou que a descri¸cão da fun¸cão MinNet estava errada em [Wolfram, 2002], que apontava o primeiro estado como sendo o estado inicial no autômato gerado pela fun¸cão, mas na verdade o último estado é o que representa o estado inicial, e atribuiu a esse fato como poss´ıvel causa das diferen¸cas entre as tabelas de [Trafaniuc, 2004] e [Wolfram, 1994]. Realmente, a sa´ıda da fun¸cão MinNet possui o último estado como estado inicial, mas este não é o motivo da discrepância em rela¸cão à tabela de Wolfram, como será visto mais adiante.

Miki (2006) automatizou o processo manual de análise de crescimento de AFs desen-volvido por Trafaniuc (2004) por meio de uma opera¸cão de diferen¸ca de grafos. Com os resultados, o trabalho passou a focar na análise da regra 184, com o objetivo de se obter o autômato limite, o qual foi constru´ıdo manualmente como referência, conforme mostra a Figura 3.10.

ç ç ç ç

Figura 3.10: Grafo limite da regra 184 segundo [Miki, 2006].

(46)

fizesse essa transforma¸cão de simetria, não conseguiu, assim, encontrar o AF limite da regra 184 partindo-se dos AFs intermediários.

Por meio da automa¸cão do processo de análise, [Miki, 2006] conseguiu obter as ex-pressões de crescimento das regras 11, 14, 35, 50, 70 e 81, que [Trafaniuc, 2004] não tinha conseguido, deixando aberto, portanto, 4 regras do conjunto original das 26, sendo elas as regras 23, 56, 98 e 172.

3.2 Problemas encontrados no trabalho de [Trafaniuc, 2004]

Tanto [Trafaniuc, 2004] quanto [Miki, 2006] basearam seus respectivos trabalhos nas fun¸cões NetCAStep, MinNet e TrimNet. Acontece que Trafaniuc (2004) usava a sa´ıda da fun¸cão NetCAStep como entrada para a fun¸cão TrimNet, cuja sa´ıda era usada como entrada da fun¸cãoMinNet, que então realimentava a fun¸cão NetCAStep. Como primeira consequência (conforme já apontado em [Miki, 2006]), Trafaniuc (2004) trabalhou com AFs determin´ısticos, e não com grafos de processo como descreveu. Trafaniuc (2004) realimentou a fun¸cão NetCAStep com a sa´ıda da fun¸cão MinNet, enquanto Miki (2006) utilizou a sa´ıda da fun¸cão TrimNet para realimentar a fun¸cão NetCAStep. A Figura 3.11 mostra o encadeamento de chamadas das fun¸cõesNetCAStep,MinNet eTrimNet da forma utilizada pelos dois trabalhos.

De acordo como está descrito em [Wolfram, 2002], nenhuma das duas formas estaria correta e, teoricamente, o modo como foram executadas leva a um comportamento in-definido, sendo a forma como apresentada na Figura 3.1 o modo correto de encadeá-las e realimentá-las.

Diante deste problema das chamadas das fun¸cões, os resultados da tabela de [Wolfram, 1994] reconstru´ıda por [Trafaniuc, 2004] poderiam estar incorretos, então a tabela foi nova-mente refeita neste trabalho. A nova tabela e a discussão dos resultados são apresentados na Se¸cão 3.4.

(47)

Entrada:

- grafo de

processo

- n´umero da

regra do AC

NetCAStep Sa´ıda: - autômato finito não determin´ıstico Entrada: - autômato finito não determin´ıstico TrimNet Sa´ıda:

- grafo de

processo

Entrada:

- grafo de

processo MinNet Deseja gerar o autômato para o próximo instante? Sa´ıda: - autômato finito de-termin´ıstico não sim Entrada:

- grafo de

processo

- n´umero da

regra do AC

NetCAStep Sa´ıda: - autômato finito não determin´ıstico Entrada: - autômato finito não determin´ıstico TrimNet Sa´ıda:

- grafo de

processo Deseja gerar o autˆomato para o pr´oximo instante? Entrada:

- grafo de

processo MinNet Sa´ıda: - autômato finito de-termin´ıstico sim não In´ıcio Entrada: - NDFA - número da regra do AC

NetCAStep

finito n˜ao determin´ıstico

Gerar para o pr´oximo passo de tempo? MinNet Sa´ıda: - autˆomato finito de-termin´ıstico TrimNet Entrada: - DFA Sa´ıda: - grafo de processo

sim n˜ao

Trafaniuc (2004) Miki (2006) Forma correta

Figura 3.11: Compara¸cão de como as fun¸cões NetCAStep, MinNet e TrimNet são chamadas em [Trafaniuc, 2004] (à esquerda), [Miki, 2006] (no centro) e como é a forma correta de executá-las (à direita).

(48)

regras 32 (Figura 3.12) e 128 (Figura 3.13), repara-se que ambos são muito semelhantes, mas a regra 128 é selecionada pelo algoritmo, enquanto a regra 32 é descartada.

T ₌1 T₌ 2 T ₌3 T₌4 T₌5

Figura 3.12: Sequˆencia de grafos de processo da regra 32.

T₌1 T₌ 2 T ₌3 T₌ 4 T₌ 5

Figura 3.13: Sequˆencia de grafos de processo da regra 128.

Nota-se que ambas as regras possuem grafos de processo com a mesma estrutura geral: uma pequena estrutura parcialmente recorrente é formada e existe uma sequência de transi¸cões que parte desta estrutura e retorna à mesma, com a distância deste caminho aumentando a cada passo de tempo.

(49)

para realizar a opera¸cão de diferen¸ca de grafos, utilizada na implementa¸cão do algoritmo de sele¸cão de regras de [Trafaniuc, 2004] (descrito na Se¸cão 3.1). O algoritmo original utilizava a antiga versão do pacote Combinatorica, mas testes mostraram que a versão mais recente da fun¸cão, integrada ao núcleo doMathematica, apresenta o mesmo compor-tamento. A Figura 3.14 mostra a opera¸cãoGraphDifference entre dois grafos de processo de passos de tempo consecutivos da regra 32.

Figura 3.14: Fun¸c˜aoGraphDifference para dois grafos de processo adjacentes da regra 32.

A Figura 3.15 mostra o que ocorre quando se muda a numera¸c˜ao dos v´ertices do primeiro grafo.

Repara-se que, apesar de os vértices terem sido renomeados, trata-se ainda do mesmo grafo, mas a opera¸cão resulta em uma diferen¸ca menor entre os grafos de referência para o segundo caso. É exatamente essa dependência da nomea¸cão de vértices que faz com que a implementa¸cão do algoritmo de sele¸cão de regras (Se¸cão 3.1) gere falsos negativos, uma vez que o algoritmo acaba selecionando o subgrafo errado como o menor subgrafo entre dois grafos de passos adjacentes.

Para contornar este problema, seria necessário um algoritmo que, dado um grafo G, reordenasse seus vértices de tal forma a gerar a menor diferen¸ca com um grafo de referência

G′

(50)

Figura 3.15: Fun¸c˜aoGraphDifference para dois grafos de processo adjacentes da regra 32 com os v´ertices do primeiro grafo renomeados.

3.3 Comportamento limite da regra 184

Miki (2006) analisou a regra elementar 184. O comportamento limite desta regra pode ser dividido em trˆes partes, dependendo da configura¸c˜ao inicial [Miki, 2006]:

• Configura¸cão inicial com número de 1s igual ao número de 0s (#1s = #0s), implica em configura¸cão limite com 0s e 1s intercalados.

• Configura¸cão inicial com número de 1s maior que o número de 0s (#1s > #0s), implica em configura¸cão limite com forma¸cão de grupos de 1s, intercalados por blocos 01.

• Configura¸cão inicial com número de 0s maior que o número de 1s (#1s < #0s), implica em configura¸cão limite com forma¸cão de grupos de 0s, intercalados por blocos 10.

(51)

periódica (CCNP), o conjunto das configura¸cões limites em uma condi¸cão de contorno não é o mesmo na outra. Por exemplo, a cadeia 1001 não faz parte da configura¸cão limite da regra 184 em CCP, pois é simplesmente a cadeia 0011 deslocada, mas é válida em CCNP sobre um fundo de 0s, pois representa 1s separados por blocos de 0s.

Com base na descri¸cão do comportamento limite da regra 184 acima, Miki (2006) construiu um AF que seria o AF limite da regra 184 (em CCNP, Figura 3.10). Mas este AF não aceita, por exemplo, a cadeia 011, que faz parte da linguagem limite e, portanto, não descreve o comportamento limite da regra.

Figura 3.16: Deslocamento da regra 184 na configura¸cão limite. Na figura, quadrados em preto representam 0s, e quadrados em azul representam 1s. O bloco de 1s é deslocado à esquerda a cada aplica¸cão da regra.

A Figura 3.17 mostra o que acredita-se ser o grafo de processo que representa o comportamento limite da regra 184 para CCNP, gerado manualmente a partir da descri¸c˜ao de seu comportamento limite dado anteriormente. Importante observar que este grafo de processo somente descreve o comportamento limite da regra 184 em CCNP, pois ´e imposs´ıvel representar o comportamento limite da regra em CCP por meio de um grafo de processo, conforme demonstrado a seguir.

Proposi¸cão 3.1 Não é poss´ıvel representar o comportamento limite da regra 184 por meio de um grafo de processo para condi¸cão de contorno periódica.

Prova Seja L a linguagem limite da regra 184 em CCP, e G o grafo de processo que reconhece L. Como w = 000101 ∈ L, também v = 100010 ∈ L, uma vez que v é igual a w a menos de um deslocamento à direita; logo v também é reconhecida por G. Como

v′

(52)

grafos de processo,v′

também é reconhecida por G; entretanto,v não pode pertencer aL, porquev′

é a cadeia 11000 deslocada, e sabe-se que essa cadeia não faz parte do conjunto limite da regra 184 em CCP. Portanto, G não pode ser um grafo de processo.

Em busca de evidências de que o grafo da figura 3.17 representa de fato o compor-tamento limite da regra 184 em CCNP, primeiramente foram geradas todas as cadeias limites a partir de todas as combina¸cões de configura¸cões iniciais de tamanho 20, e então foi verificado se o grafo aceitaria cada configura¸cão limite gerada. Além disso, foram aplicadas todas as configura¸cões inválidas de tamanho 10 para verifica¸cão quanto a falsos positivos. Todos os testes foram executados com sucesso. Assim, embora não haja um prova formal de que este grafo de processo seja realmente o comportamento limite da regra 184 em CCNP, há fortes evidências que levam a tal conclusão.

1

10

2

4 5

3 6

7

8

9

11

12

13

Figura 3.17: Grafo limite da regra 184 em condi¸cão de contorno não periódica.

3.4 Nova tabela de complexidade de regras

(53)

nas sa´ıdas da fun¸cão MinNet, então tratam-se de AFs determin´ısticos e não grafos de processo. As Tabelas 3.1, 3.2 e 3.3 apresentam os novos resultados.

Em cada tabela, existe uma divisão de duas subtabelas, à esquerda são mostradas as simula¸cões de [Wolfram, 1994], enquanto à direita estão as simula¸cões deste trabalho. Novos resultados são a soma dos resultados presentes em [Trafaniuc, 2004], [Miki, 2006] e neste trabalho.

Um ponto importante é que, para algumas regras em que os resultados de [Wolfram, 1994] e [Trafaniuc, 2004] coincidiram, houve divergências neste trabalho. Um exemplo é a regra 38, onde Wolfram e Trafaniuc obtiveram os mesmos resultados mas este trabalho obteve valores diferentes.

Outra questão é com rela¸cão às regras 32, 128, 136, 160, 168, e 224. Estas têm o número de estados e arestas do AF limite apresentados em [Wolfram, 1994] mas não há qualquer registro de como seus AFs limite foram obtidos. O AF determin´ıstico da regra 128 está em [Wolfram, 1984b] e é mostrado na Figura 3.4 (embora no texto original não haja descri¸cão como este foi obtido), mas não há qualquer ind´ıcio de onde os outros grafos vieram.

Baseado no comportamento limite da regra 128, no presente trabalho foi desenvolvida uma técnica manual para inferir o AF determin´ıstico limite das outras regras. A técnica parte da observa¸cão do papel das estruturas parcialmente recorrentes dos grafos dos su-cessivos passos de tempo, observando a evolu¸cão dos grafos, para assim inferir o caso limite.

(54)

Tabela 3.1: Tabela de complexidade de linguagens regulares (1/3).

(55)

(56)

(57)

ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç

Figura 3.18: Sequˆencia de AFs da regra 32.

ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç

ç ç ç ç ç ç ç ç ç ç ç ç ç ç

(58)

ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç ç

(59)

9 7 8 3 1 6 5 4 2 16 15 13 1 11 9 12 7 5 10 3 1 8 6 4 2 25 24 2 23 21 20 18 17 19 14 13 11 16 9 15 8 6 5 12 3 1 10 7 4 2 36 35 33 34 32 31 29 28 30 27 26 25 23 22 21 24 17 16 15 13 20 11 19 10 18 9 7 6 5 14 3 1 12 8 4 2

49 48 46

47 45 44 42 41 43 40 39 38 36 35 34 37 33 32 31 30 28 27 26 25 29 20 19 18 17 15 24 13 23 12 22 11 21 10 8 7 6 5 16 3 1 14 9 4 2

(60)

ç 4 ç 3 ç 2 1 ç 3 ç 2 1

Regra 32 Regra 128

ç 3 ç 2 1 ç 9 ç 8 ç 2 ç 7 ç 6 ç 5 ç 4 ç 3 1

Regra 136 Regra 160

ç 4 ç 3 ç 2 1 ç 4 ç 3 ç 2 1

Regra 168 Regra 224

Figura 3.24: AFs limite.

(61)

4 Constru¸c˜

ao do grafo de processo por meio de

ma-trizes de adjacˆ

encias

Qualquer grafo pode ter uma representa¸cão matricial. Para AFs, é necessário ainda definir uma forma de representar os estados iniciais e finais. No caso de grafos de processo, esta informa¸cão é irrelevante, pois todos os estados são iniciais e finais.

Wang e Wang (2011) propuseram uma representa¸cão matricial alternativa para ACs, a qual é baseada na própria evolu¸cão do AC.

Neste cap´ıtulo, é proposta uma nova abordagem para o problema, por meio da análise das matrizes de adjacência correspondentes aos grafos de processo das respectivas regras do espa¸co elementar. Porém, como será visto adiante, não é poss´ıvel representar comple-tamente um grafo de processo utilizando a nota¸cão clássica de matrizes de adjacência. É proposta, então, uma nova nota¸cão que, dada a matriz de adjacência, é poss´ıvel construir integralmente o grafo da respectiva matriz.

O texto então deduz o algoritmo de forma¸cão do grafo de processo de tempo tpara a regra 184; e então finaliza com uma breve descri¸cão dos padrões de forma¸cão de matrizes das mesmas regras estudadas em [Trafaniuc, 2004]. O motivo de escolher a regra 184 para ilustrar o processo se deve ao fato de ser uma regra que já foi extensivamente estudada em [Trafaniuc, 2004] e [Miki, 2006]. No Apêndice A os algoritmos para todas as 26 regras estudadas são apresentados.

4.1 Representa¸c˜

ao de grafos de processo em forma matricial

4.1.1 Matrizes de adjacˆencias

Uma matriz de adjacência, algumas vezes também chamada de matriz de conexões, representa os estados e transi¸cões de grafos em forma matricial, rotulando as linhas e colunas com os vértices do grafo. As linhas e colunas representam, respectivamente, os estados de origem e destino do grafo1_.

1_{No caso de grafos n˜}_{ao direcionados, n˜}_{ao existe distin¸c˜}_{ao de estados origem e destino, mas somente}

(62)

A representa¸cão de um grafo direcionado G com n vértices se dá por uma matriz M

de dimensão n×n. O valor da posi¸cão aij da matriz M será 1 se existir uma transi¸cão do estado i para o estado j. A Figura 4.1 mostra um grafo direcionado e a Figura 4.2 mostra a matriz de adjacência correspondente.

1

2

3

Figura 4.1: Grafo direcionado.

    

0 1 1 1 0 0 0 1 1

    

Figura 4.2: Representa¸c˜ao em matriz de ad-jacˆencia.

Embora matrizes de adjacência possam representar grafos direcionados simples, não é poss´ıvel representar completamente um grafo de processo, dado que:

1. ´E poss´ıvel haver mais de uma transi¸c˜ao do estado i para o estado j, ∃i, j.

2. Nos ´ındices da matriz não está codificado o valor da transi¸cão, que é o valor esperado na fita de entrada. Observe que a solu¸cão de criar um mapeamento f : L 7→ aij que associa o valor do arco ao ´ındice da matriz é inviável devido à possibilidade de existir mais de uma transi¸cão por par de estados (i, j).

Para ilustrar a dificuldade de se representar grafos de processo utilizando matrizes de adjacência, considere o grafo de processo da Figura 2.11. A matriz de adjacência deste autômato seria uma matriz 1×1 com valora1,1 = 1. Porém, perde-se a informa¸cão de que existem duas transi¸cões reflexivas no grafo de processo. Mais ainda, não existe qualquer men¸cão ao valor das transi¸cões.

(63)

A próxima se¸cão introduz uma nota¸cão alternativa de matrizes de adjacência que contorna as dificuldades apresentadas.

4.1.2 Matrizes de adjacˆencia de evolu¸c˜ao temporal

Uma matriz de adjacência de evolu¸cão temporal é uma nota¸cão de matriz de ad-jacência para representar grafos de processo que possui uma rela¸cão de isomorfismo entre a matriz e sua representa¸cão em grafo. Formalmente, dado o conjunto de matrizes de adjacência de evolu¸cão temporal M e o conjunto de grafos de processo G, existe uma transforma¸cão T : G 7→ M e uma transforma¸cão T−₁

: M 7→ G [Costa e de Oliveira, 2012].

O elemento chave para conseguir essa rela¸cão de isomorfismo é encontrar uma repre-senta¸cão do conjunto de transi¸cões e seus respectivos valores em um número real que possa ser codificado nos ´ındices da matriz, e que possa ser decodificado quando for aplicada à transforma¸cão T−₁

. Formalmente, dado o conjunto de transi¸c˜oes L do estado i para o estadoj,∀i, j, encontrar uma rela¸c˜ao η:L7→ ℜ que seja bijetora.

A resposta para esta questão está em criar um mapeamento dos valores poss´ıveis de transi¸cões para o conjunto de números naturais L 7→ N e então codificar os valores das transi¸cões em um número binário. Cada bit do número binário corresponde a um valor de transi¸cão. Se o valor nok-ésimo bit for 1, existe uma transi¸cão (mapeada no conjunto dos naturais) de valor k do estado de origem para o estado destino em questão. A opera¸cão

η de codifica¸cão dos arcos Lem um número natural é o polinômio de base 2:

η(Lij) =

X

∀k∈(Lij7→N)

2k (4.1)

(64)

base 2, poderia-se trabalhar com outras bases. Todavia, a única implica¸cão na mudan¸ca de base é a quantidade de d´ıgitos necessária para representar um dado conjunto 2L _de

poss´ıveis combina¸cões de transi¸cões e, do ponto de vista de arquitetura computacional, a base 2 é a base mais natural para se trabalhar. A Figura 4.3 mostra o grafo da Figura 4.1, agora representado como um grafo de processo (repare que agora existe um valor para cada transi¸cão), e a Figura 4.4 mostra a matriz de adjacência de evolu¸cão temporal correspondente.

1

2

3

0

1 ₁

0

Figura 4.3: Grafo de processo representado atrav´es de um grafo direcionado.

    

0 1 1 2 0 0 0 2 1

    

Figura 4.4: Representa¸cão em matriz de ad-jacência de evolu¸cão temporal.

A transforma¸cão de um grafo de processo em uma matriz de adjacência de evolu¸cão temporal é executada por meio do Algoritmo 4.1, onde ψ(n) = matriz nula n×n.

Algoritmo 4.1 Algoritmo para gerar a matriz de adjacˆencia de evolu¸c˜ao temporal a partir de um grafo de processo.

n ←Length(Q) {n´umero de estados} A←ψ(n)

for all i, j ∈Q do if Lij 6=∅ then

Aij ←η(Lij) end if

end for

O algoritmo atua criando uma matrizAn×n, ondené o número de estados do grafo de processo e atribuindo à posi¸cão Aij o valor da fun¸cão η(Lij),∀i, j, onde Lij é o conjunto de transi¸cões de ipara j.

(65)

um grafo de processo é baseado na representa¸cão binária dos valores dos ´ındices da matriz. Por exemplo, se no ´ındice A1,2 existir o valor 3, então existe uma transi¸cão em 0 e uma transi¸cão em 1 do estado1 para o estado 2, pois 20_{+ 2}1 _{= 3. O Algoritmo 4.2 mostra o} processo de gera¸cão do grafo de processo a partir de uma matriz de adjacência de evolu¸cão temporal. O algoritmo pressupõe a existência de uma fun¸cão MakeTransition(i,j,m) que cria uma transi¸cão emm do estado i para o estado j.

Algoritmo 4.2 Algoritmo para gerar o grafo de processo a partir de uma matriz de adjacˆencia de evolu¸c˜ao temporal.

for i= 1 to n do for j = 1 ton do

if Aij 6= 0 then repeat

q ← ⌊Aij ÷2⌋

r ←M od(Aij,2) if r6= 0 then

n ←0

while 2n_≤_A ij do

n←n+ 1

end while

MakeTransition(i, j, n−1) end if

untilq 6= 0 end if

end for end for

(66)

4.2 Algoritmo do grafo de processo de tempo

t

_{para a regra 184}

Esta se¸cão mostra como utilizar a nota¸cão de matriz de adjacência de evolu¸cão tem-poral para deduzir um algoritmo que gere o grafo de processo de uma regra do espa¸co elementar para um passo de tempo discreto t qualquer. Em particular, aqui é deduzido o algoritmo para gerar a matriz de evolu¸cão temporal para a regra 184 e, a partir desta, poderá ser aplicado o Algoritmo 4.2 para obten¸cão do grafo de processo.

Baseado nos resultados de Trafaniuc (2004), Miki (2006) estudou extensivamente o padrão de crescimento da regra 184 através da análise dos grafos de processo gerados pelos sucessivos passos de tempo. Conforme relatado anteriormente, no caso estudou-se os grafos de processo gerados dentro dos 5 primeiros passos de tempo. A Figura 4.5 mostra os grafos de processo da regra 184 gerados para os 5 primeiros passos de tempo. A nota¸cão de grafo é a mesma da Figura 2.12.

T =1 T= 2 T =3 T=4 T=5

Figura 4.5: Grafos de processo para os cinco primeiros passos de tempo da regra 184.

Utilizando o método apresentado na Se¸cão 3.1, sua conclusão foi a de que a cada passo de tempo, sempre existia uma mesma estrutura de grafo sendo adicionada e uma sendo exclu´ıda, e essas estruturas eram invariantes no tempo. As Figuras 4.6 e 4.7 mostram, respectivamente, as estruturas adicionada e exclu´ıda dos sucessivos grafos de processo da regra 184.

´