Projeteis om Resist^enia do Ar
Quadratia na Veloidade
Theballistiproblemwithsquareveloityairresistane
G. F. LealFerreira
guilhermif.s.usp.br
InstitutodeFsiadeS~aoCarlos,USP
CaixaPostal 369,13.560-970,S~aoCarlos, S.P.
Reebidoem2deMaio2001. Aeitoem26deJunho2001
Asolu~aoaproximadadoproblemadomovimentodeprojetilomresist^eniadoar quadratiana
veloidade,obtidaem1719porJohannBernoulli,eomparadaomsolu~oesintegradas
numeria-mentea partirdeuma primeiraintegral analtia daveloidade horizontal em termosdo^angulo
queovetorveloidadefazomahorizontal,eeveriadaseradequada,pelomenosate^angulosde
tirodeate20 Æ
. Comelaresultadoss~aoobtidosemalgunsasospratiosdeinteresse(t^enis,futebol
eoutros) qued~aoelementosaoprofessorde fsia naarea,paradelimitaroque depratiotemo
seuensinoemquearesist^eniadoareignorada.
Comparing approximate solutionof the ballistiproblem withair resistane proportional to the
squareoftheveloity,obtainedbyJohannBernoulliin1719,withnumerialonesobtainedthrough
ananalytial solution expressing the horizontal omponent of the veloity in terms of the angle
betweenthetangent tothetrajetoryandthehorizontalaxis,itisfoundittobesuÆientlygood
for shootingangles sohigh as20 Æ
. Results ofpratial interestare thenalulated (football and
tennis gameamong otherases) whih may give elementsto the physis teaher in this area, of
knowinghowgoodishisteahingusuallyignoringairresistane.
I Introdu~ao
O estudo do movimento dos projeteis (ideal) no
en-sinode Me^aniaeimportante porseroprimeiroaso
{ fora talvez o do movimento irular uniforme -, de
omposi~ao de movimentos noplano. Entretanto, em
que situa~oes pode este estudo idealizado serapliado
apratiaemqueoarimp~oeresist^eniaaomesmo? No
queapresentamosaseguir,prouramosfamiliarizarum
pouooprofessoromoproblemadaresist^eniadoar
de forma a lhe permitir delimitar o alane dos seus
ensinamentos. Paraveloidadesda ordemdem/s, ate
suientemente inferiores a veloidade do som, a
re-sist^enia doarebemrepresentada omo proporional
ao quadrado da veloidade, estabeleida por Newton
[1℄. Para projeteis propriamente ditos (bala de fuzil
ou de anh~ao), a resist^enia e mais ompliada pela
emiss~ao de ondas e, por isso, nos restringiremos ao
aso sub-s^onio mais simples. Por outro lado, o aso
daresist^eniadoarproporionalaveloidade,embora
tratavelanalitiamente,n~aoerealista.
Johann Bernoulli (daqui em diante J. Bernoulli;
uma brevssimanotabiograasobre afamosafamlia
Bernoulli e feita na se~ao 6) em 1719 obteve uma
solu~ao aproximada do problema [2℄, valida para
tra-jetoriasahatadas,istoe,om^angulodetiro pequeno.
Qu~ao grande pode este ser, a solu~ao de J. Bernoulli
mantendo-serazoavelmenteboa? Pararesponderaesta
perguntadeve-sedispordeumasolu~aomelhor,de
pre-fer^enia`exata'. Aonteequesepodeobterum
resul-tadoanaltiopara aveloidadehorizontal doprojetil
noasoemquest~ao,emfun~aodo^anguloqueovetor
ve-loidadefazomahorizontal. Comohojedispomosdas
failidadesdeintegra~aonumeriaproporionadapelos
omputadores, a integra~ao para se obter os espaos
perorridospodeserobtidalogo. Comistoveriamos
que para ^angulos de tiro de 20 Æ
, asolu~ao de J.
Ber-noullieboa e,possivelmente,oemesmopara ^angulos
maiores.
Aanalisedoproblemaemuitosimpliadapelofato
de sepoderaferir a`ondut^ania' domeio ao projetil
(ondut^aniaomoinversoderesist^enia)emunidades
deomprimento-oomprimentodeondut^ania,x
-,
eda sepoder denirdist^aniaspormeio dex
, alem
detambempormeiodaoutraunidadenaturaldo
pro-blema, o alaneideal x
0
. Istonos permitiraestudar
avaria~aodarela~aoalanereal/alaneidealatraves
As express~oes teorias, saidas de tratamentos
o-nheidos na literatura [2-4℄ e usadas na analise a
se-guir,est~aodeduzidasnosAp^endies,I eII.Nase~aoII
adaptamosaquelasexpress~oesaosnossosns.
II Prepara~ao
Os prinipais resultados da analise teoria s~ao a
ex-press~aodaveloidadedoprojetilvemfun~aodo^angulo
que o seu vetor veloidade faz om a horizontal (ver
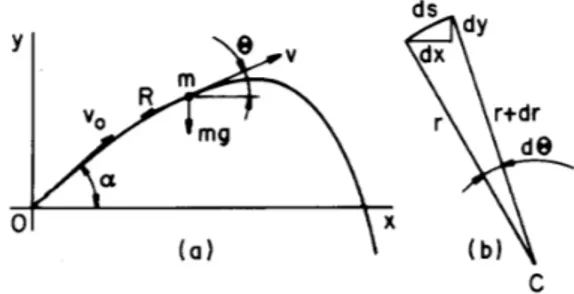
Fig.1,tiradade[1℄),
v 2
()=
v 2
0 os
2
h
1 2v
2
0 kos
2
g
(() ())
i
os 2
(1)
resultado tirado da Eq.A11, e as equa~oes
determi-nandoosdesloamentoshorizontal,x,evertial,y,Eqs.
A13-A14,
x()= Z
v
2
()d
g
; (2)
y()= Z
v
2
()tgd
g
: (3)
Outroresultado,estenoAp^endieII,eaaproxima~ao
deJ.Bernoulli(1719)[2℄,validaparatrajetorias
aha-tadas,Eq. A19,
y=xtg x
2
g
2v 2
0 os
2
F(z) (4)
om,Eq. A20,
z= 2kx
m
: (5)
NasEqs. 1e4,ev
0
s~aoo^angulodetiroea
velo-idadeiniialeg aaelera~aodagravidade. NaEq. 5
meamassaekeooeienterelaionandoaforade
resist^eniaR eoquadradodaveloidade,
R=kv 2
; (6)
oqualpodeseranalisadonosseguintestermos:
k= CA
2
ar
(7)
sendo
ar
adensidadedoar ('1;3kg/m 3
),A ase~ao
doprojetilperpendiular atrajetoriaeC um fatorde
forma que para uma esfera lisa e ' 0,4 [5℄. A
de-pend^enia quadratiadaresist^eniado arfoideduzida
por Newton, pelo momento na unidade de tempo
o-muniadopelo projetilaoar[1℄.
Figura1: a)Esboodatrajetoriadeumprojetildemassa
m, lanadoom^angulo detiro e veloida iniial v0, e
v sendoo^anguloomahorizontal num pontogenerio da
mesma. b)esboo doelementode trajetoriads,sendo ro
raiodeurvatura.
A fun~ao () naEq. 1eF(z) na Eq. 4s~ao,
res-petivamente,A12eA21,
()=0;5
sen
os 2
+0;5ln
1+sen
1 sen
; (8)
F(z)= e
z
1 z
0;5z 2
: (9)
Paraz, Eq.5,iguala zero,F(0) =1eatrajetoria
da Eq.4 torna-se ideal. V^e-se que m=k na Eq.5 tem
a dimens~ao de omprimento, o que permite denir o
omprimentodeondut^aniax
=m=k:
Assim, para k = 0, x
! 1. Maior resist^enia
resulta em menor x
. Uma outra unidade natural do
problemaeoalanehorizontalidealx
0
,quepelaEq.2
e
x
0 =
v 2
0 sen2
g
: (10)
Com o valor de x
0
=2 na equa~ao da trajetoria ideal,
enontra-seovalordaalturamaxima,y
m ,
y
m =
x
0 tg
4
(11)
quepermiteaproximadamente estimaromo ahatada
eatrajetoria,y
m =x
0 <<1:
AtravesdaEq.10,podemossubstituirv 2
0
=gnasEqs.
2e3emtermosdex
0
,obtendo-se
x()
x
0
= 0;5ot Z
d
h
1 x
0
x
(otg)(() ()) i
os 2
; (12)
y()
x
0
= 0;5ot Z
tgd
h
1 x0
x
(ot)(() ()) i
os 2
em que`ot' signiaotangente.
III O alane horizontal
Podemosestimaraimport^aniadaresist^eniadoarno
movimentodoprojetilestudandoomovariaarela~ao
entreoalanehorizontalreal,x
r
,eoalane
horizon-tal ideal, x
0
, omaresist^enia. Paraisto,integram-se
asEqs.12e13atequeaultimadasduasseanule(ouna
pratia,troquedesinal). Istooorrepara umvalorde
,
m
= ,negativo,om>1etantomaiorquanto
menorforx
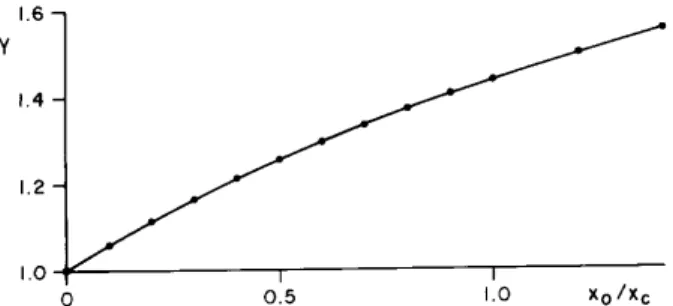
. NaFig. 2mostramosx
r =x
0
omofun~ao
de x
0 =x
, rulosheios, e naFig. 3, omo fun~ao
do mesmo x
0 =x
, para =20 Æ
. Naverdade,x
r =x
0 e
temdepend^eniafraaom,ompequeno. Esta
independ^eniadex
r =x
0
ompodesersuspeitadapela
rela~ao validana aproxima~aoJ. Bernoulli, Eq.4, que
em fun~aodex
0 ex
e
y
x
0 =
x
x
0 tg
1 x
x
0 F
2x
x
; (14)
daqualsetira
x
r
x
0 =
1
F
2x
r
x
(15)
independentedeequepermiteaobten~aodarela~ao
entre x
r =x
0 e x
0 =x
. Para isto, o valor de u =
2x
r =x
que satisfaz a Eq.15 e esrito omo u =
2:(x
r =x
0 ):(x
0 =x
) e da alula-se x
0 =x
para ada
x
r =x
. Na Fig. 2 tambem mostramos este resultado
da aproxima~aode J.Bernouilli, porrulosvazados.
Vemosqueoaordoentreestaeasolu~ao`exata'e
bas-tante razoavel, forneendovalores dex
r =x
0
umpouo
superioresdoqueaexata. PelaFig. 2vemosquepara
x
0 =x
igual a 0,5 e 1, x
r =x
0
e era de 0,76 e 0,62,
aproximadamente. O primeiro valor, x
0 =x
=0,5, vai
seronsiderado,omertaarbitrariedade,omoaquele
paraoqualaresist^eniadoaromeaaserimportante.
Figura 2: Alane real/alane ideal, xr=x0, em fun~ao
do par^ametro alane ideal/omprimento de ondut^ania,
x0=x, aluladoa partirdas Eqs. 12 e13, vertexto, em
rulosheios,ealuladoomaaproxima~aoJ.Bernoulli,
Æ
Figura3: omofun~aodex
0 =x
obtido das Eq.12e 13.
-e o^anguloomqueoprojetil atingeoeixohorizontal
=20 Æ
.
IV Trajetorias J. Bernoulli
O bom resultado proporionado pela aproxima~ao J.
Bernoullinos animaaobter dela, Eq. 14, trajetorias,
de formabem mais simples doque pelas exatas, Eqs.
12e13. EsrevendoaEq. 14omo
y
x
0 =
x
x
0 tg
1 x
x
0 F
2 x
0
x
x
x
0
; (16)
mostramosnaFig. 4(noteadiferenaentreasesalas
vertialehorizontal)trajetoriasaluladasparax
0 =x
igual a 0, 0,23, 0,53 e 0,93 e = 20 Æ
. V^e-se que a
alturamaximaideal, y
m
,Eq. 11,esoera de 9%do
alane horizontal ideal, x
0
, no presente aso,
justi-andooeptetode`ahatada'.
Figura4: Trajetorias J.Bernoulli, Eq.14,parax0=x =0,
0,23,0,53e0,93e=20 Æ
.
V Alguns asos pratios
Adotamosnonaldase~ao3oriteriosegundooqual
aresist^enia doar setorna importante quandox
0 =x
e 0,5. Vamos agora tomar algunsprojeteis familiares
esferiosparaaquilatarmossuasperformanesfrentea
resist^eniadoar. Antes, porem,alulemos ovalor de
x
,dadopelaEq. 7,omC=0,4,
ar
=1,3kg/m 3
x
=
8m
(0;4)D 2
(1;3) =
4;9m
D 2
(17)
a)Jogodetenis. Aboladetenis`pesa'erade2onas
etemodi^ametrode2,5polegadas[6℄. 1ona=28,35ge
1polegada=2,54m. Obteramosx
=69m,masomo
a bola de tenis e bastante rugosa, C deve ser maior,
vamos dizer0,6. Com isto x
eera de 46 m. Como
aquadradetenispara jogodesimplestem 42pes[6℄,
ou seja 14 m pode-sedizer que mesmo para lanes
longos aresist^enia doar n~aoe determinante nojogo
detenis.
b) Jogo defutebol: abola defuteboltemera de
71 m de permetro e456 gde `peso' [7℄. Usando
es-tes valores na Eq. 16 obtemos x
=44 m. portanto
para hutesde 22 m dealane ideal,orrespondendo
aveloidadeiniial de 18,3 m/s, a resist^enia do are
importante.
Estudemos agora os orpos massivos (n~ao oos).
Paraestes orpos,aEq. 17podeserexpressaem
ter-mosdadensidade edodi^ametroD doprojetilomo
x
=2;56D; (18)
mostrandoquearesist^eniatendeasermaisimportante
para menores D. Tomemos um solido bem leve, por
exemplooisopor (poli-estirenoexpandido) uja
densi-dadenoarfoipornosestimadaem0,033g/m 3
ou33
kg/m 3
. Para D= 4 m = 0,04 m, obtemos para x
,
Eq. 18,3,8m. Portanto,paraoprojetildeisopora
re-sist^eniadoarseraimportanteparaalanes.superiores
a1,9m,orrespondendoaumaveloidadeiniialde5,4
m/s, ou seja, pratiamente 20 km/h (o isopor paree
seromaterialindiado paraoestudo da inu^eniada
resist^eniadoarparaveloidadesdem/s). Coma
den-sidadeusual, istoedaordemdeg/m 3
, x
seriaera
de 30 vezes maior e aresist^enia do ar n~ao sera
usu-almente importante. Nesta situa~ao se enquadram as
experi^eniasques~aorealizadasnolaboratorioemaulas
de Me^ania. Mas sepequenos desvios do
omporta-mento ideal quiserem ser tomados em onsidera~ao a
seguinte aproxima~aoevalida ate x
0
= 0;1, extraida
daFig.2,
x
r
x
0
=
1 0;61 x
0
x
: (19)
VI Nota bibliograabrevssima
Varios Bernoulli's, ao longo de gera~oes durante os
seulos 17 e 18, se destaaram em estudos de
Ma-tematia, Fsia e Teoria das Probabilidades [6℄. Os
dois primeiros foram Jakob, mais velho, e Johann,
irm~aos,masquenemporissoviveramsempreem
har-monia. OBernoullidoteoremadeBernoullida
Hidro-din^amiaeDaniel,lhodeJohann.
Agradeimentos
O autor agradee a bolsa de produtividade do
C.N.Pq e aoarbitro deste poralgumas de suas
suges-t~oes. E a olega Profa. Mariangela T. de Figueiredo
pelaleitura atenta.
Ap^endie I - Resultado Analtio
SeguiremosdepertoaRef. [2℄,havendoporemum
pequenoerrodesinalnasuaEq. 74,Cap.1,
orrespon-dendo a nossa Eq. 11 abaixo. A Ref. [3℄ tambem
apresenta este estudo, porem om erro mais
impor-tante nessamesmaexpress~ao,Eq. 8.8, Cap. IV.
Coin-id^enia. A Ref. [4℄ tambem apresentatratamento do
problemageraldaresist^eniadependentedaveloidade,
mas, omo dissemos, seguiremos a Ref. [2℄.
Natural-mentequeomplia~oesoutrasomoadepend^eniada
resist^enia doar, omaaltura do projetil, atravesda
densidadedoarvariavel,n~aoser~aoonsideradasaqu.
Preliminarmente, pela deni~ao de raio de
urva-turartemos,verFig.1.ae1.b,que
1
r =
d
ds
; (A1)
em que eo^angulo queo vetorveloidadefazoma
horizontal e dseoelemento de aro. Poroutro lado,
tambemsabemosque
1
r =
d 2
y
dx 2
1+
dy
dx
2
3=2
; (A2)
sendox ey asoordenadas artesianasdos pontos da
urva. V^e-sefailmentequepodemosp^or
1
r =
d 2
y
dx 2
os 3
: (A3)
Aaelera~aoentrpetaev 2
=r,sendovaveloidade,
oupelaEq. A1
v 2
r = v
2 d
ds
(A4)
eusandoaequa~aodaforaentrpeta,ommamassa,
verFig. 1a,
mv 2
r
= mv 2
d
ds
=mgos (A5)
resultando
v 2
d
ds
= gos (A6)
ouainda,omov=ds=dt;
d
=
gos
E interessante que uma primeira integra~ao sera
possvelatravesdavariavelv
x
=vos:
Comeandoporesrevera2aleinadire~ao
horizon-tal
m dv
x
dt
= Ros= kv 2
os (A8)
sendoR=kv 2
aforaderesist^enia,esubstituindodt
daEq.7,temos
dv
x
d =
kv 3
mg
(A9)
emultipliandoedividindooladodireitoporos 3
dv
x
v 3
x =
kd
mos 3
(A10)
que e uma equa~ao diferenial integravel em v
x e ,
obtendo-se
v 2
x =v
2
os 2
=
v 2
0 os
2
1 2k v
2
0 os
2
mg
(() ())
(A11)
em que
()= Z
0 d
os 3
=0;5
sen
os 2
+0;5ln
1+sen
1 sen
;
(A12)
sendoev
0
o^angulodetiroeveloidadeiniiais,
res-petivamente. Foi por meio databela deintegraisda
Ref. [6℄quedetetamososerros menionados. Comv
x
naEq.11,dx edy podem serobtidosdedx=dsos
edy=dssen eusando-seaEq.6tem-se
x()= Z
v
2
d
g
; (A13)
y()= Z
v
2
tgd
g
: (A14)
Ap^endie II - Aproxima~ao de J.
Bernoulli
A dedu~aoda aproxima~aode J.Bernoulliomea
onsiderandoasEqs. A9eA6obtem-se
dv
x
v
x =
kv 2
d
mg os =
kds
m
(A15)
equa~aoquepodeserintegrada
v
x =v
x0 e
k s=m
(A16)
sendov
x0
aomponente x da veloidadeiniial. Para
trajetoriasahatadassx,demaneiraque
v
x =x_
= v
x0 e
k x=m
=x_
0 e
k x=m
(A17)
epelas Eqs. A3, A5 eA17 hega-sea, jaomo sinal
deigualdade,(os1)
d 2
y
dx 2
= g
_ x 2
= ge
2k x=m
_ x 2
0
; (A18)
equa~ao esta que integrada om y = 0 para x = 0 e
dy=dx)
0
=tgda
y(x)=xtg
gx 2
2v 2
0 os
2
F(z) (A19)
om
z= 2kx
m
(A20)
F(z)= e
z
1 z
0;5z 2
(A21)
Notequepara z=0,meiosemresist^enia,F(0)=1:
Referenes
[1℄ S.TimoshenkoeD.H.Young,DinamiaAvanzada,
Li-breriaHahette,BuenosAires,Cap.1,se~ao4.
[2℄ Omesmo,Cap.1,se~ao12.
[3℄ T.vonKarmaneMaurieBiot,MathematialMethodas
in Engineering,MGraw-Hill Book Co., N.York, 1940,
Cap.IV,se~ao8.
[4℄ JohnL.SyngeeByronA.GriÆth,Priniplesof
Meha-nis,MCGraw-Hill BookCo., 1959,pag.142.
[5℄ VitorL.Streeter, Me^ania dosFluidos,MGraw-Hill
doBrasil,1974,pg.261.
[6℄ EnylopaediaBritania,ed.1969.
[7℄ Leopoldo Sant'Ana, Regras de Futebol Ilustradas, Cia.
BrasilEditora,S~aoPaulo,1968.
[8℄ HandbookofChemistryandPhysis,55 th
Edition,