Descoberta de preço nas opções de Petrobrás

(1)

FUNDAÇÃO GETULIO VARGAS

ESCOLA DE ECONOMIA DE SÃO PAULO

YURIE YASSUNAGA SUZUKI

DESCOBERTA DE PREÇO NAS OPÇÕES DE

PETROBRÁS

SÃO PAULO

(2)

YURIE YASSUNAGA SUZUKI

DESCOBERTA DE PREÇO NAS OPÇÕES DE

PETROBRÁS

Dissertação apresentada ao Programa de Mestrado Proﬁssional da Escola de Economia de São Paulo da Fundação Getúlio Vargas, como requisito para a obtenção do título de Mestre em Economia.

Área de concentração: Finanças Quantitativas.

Orientador:

Prof. Dr. Pedro Luiz Valls Pereira

(3)

Suzuki, Yurie Yassunaga.

Descoberta de Preço nas Opções de Petrobrás / Yurie Yassunaga Suzuki. - 2015.

40 f.

Orientador: Pedro Luiz Valls Pereira

Dissertação (MPFE) - Escola de Economia de São Paulo.

1. Mercado financeiro - Modelos econométricos. 2. Mercado de opções. 3. Ações (Finanças). 4. Petrobrás. 5. Sistemas de recuperação da informação. I. Pereira, Pedro Luiz Valls. II. Dissertação (MPFE) - Escola de Economia de São Paulo. III. Título.

(4)

YURIE YASSUNAGA SUZUKI

DESCOBERTA DE PREÇO NAS OPÇÕES DE

PETROBRÁS

Dissertação apresentada ao Programa de Mestrado Proﬁssional da Escola de Economia de São Paulo da Fundação Getúlio Vargas, como requisito para a obtenção do título de Mestre em Economia.

Área de concentração: Finanças Quantitativas.

Data da Aprovação: 12/08/2015

Banca Examinadora:

Prof. Dr. Pedro Luiz Valls Pereira

(Orientador) FGV-EESP

Prof. Dr. Marcelo Fernandes

FGV-EESP

Prof. Dr. Marcelo Cunha Medeiros

(5)

Agradecimentos

(6)

RESUMO

Este trabalho tem como objetivo estudar o comportamento do mercado de ações e opções de Petrobrás utilizando a metodologia de price discovery (descoberta de preços). A partir

de dados de alta frequência de ambos os mercados, fornecidos pela BM&FBOVESPA, os modelos econométricos utilizados nessa metodologia foram estimados e as medidas

de Information Share (IS) e Component Share (CS) foram calculadas. Os resultados das

análises indicaram dominância do mercado à vista no processo de descoberta de preços, dado que, para este mercado, foram observados valores acima de 66% para a medida IS e acima de 74% para a medida CS. Análises gráﬁcas da função resposta ao impulso indicaram, também, que o mercado à vista é o mais eﬁciente.

(7)

ABSTRACT

This work aims to study market behavior involving Petrobras’ stock and options mar-kets applying price discovery methodology. Using high-frequency data, provided by BM&FBOVESPA, econometric models used in this methodology were estimated and measures of Information Share (IS) and Component Share (CS) were calculated. The results of the analyzes indicated dominance of the spot market in the process of price discovery, since, for this market, were observed values over 66% for IS and above 74% for CS. Graphical analysis of the impulse response function indicated that the spot market is more eﬃcient than the option market.

Keywords: high frequency data; price discovery; information share; component share;

(8)

Lista de ilustrações

Figura 1 – Preço da ação no mercado à vista e preço implícito nas opções, entre 08/abr/13 e 30/dez/13, para a frequência de 5 minutos.. . . 20

Figura 2 – Gráﬁco de dispersão do preço da ação no mercado à vista e preço implícito nas opções, entre 08/abr/13 e 30/dez/13, para a frequência

de 5 minutos. . . 20 Figura 3 – Preço da ação no mercado à vista e preço implícito nas opções, no dia

10/abr/13, para a frequência de 5 minutos. . . 21 Figura 4 – Gráﬁco de dispersão do preço da ação no mercado à vista e preço

implícito nas opções, no dia 10/abr/13, para a frequência de 5 minutos. 21

Figura 5 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência de 1 minuto / número de lags = 5). . . 30 Figura 6 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência

de 1 minuto / número de lags = 10). . . 31 Figura 7 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência

de 15 minutos / número de lags = 20). . . 31 Figura 8 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência

(9)

Lista de tabelas

Tabela 1 – Estatísticas descritivas para os preços da ação no mercado à vista e no mercado de opções, entre abril e dezembro de 2013. . . 22 Tabela 2 – Estatísticas descritivas para os log-retornos dos preços da ação no

mercado à vista e no mercado de opções, entre abril e dezembro de 2013. 22 Tabela 3 – Coeﬁcientes da regressão do modelo VEC - frequência 1 minuto(Desvios

padrão das estimativas entre parêntesis). . . 27 Tabela 4 – Coeﬁcientes da regressão do modelo VEC - frequência 5 minutos(Desvios

padrão das estimativas entre parêntesis). . . 27 Tabela 5 – Coeﬁcientes da regressão do modelo VEC - frequência 10 minutos

(Desvios padrão das estimativas entre parêntesis). . . 28 Tabela 6 – Coeﬁcientes da regressão do modelo VEC - frequência 15 minutos

(10)

Lista de abreviaturas e siglas

VMA Vector Moving Average Model

VAR Vector Auto Regressive Model

VEC Vector Error Correction Model

IS Information Share

(11)

Sumário

1 Introdução. . . 11

2 Conceitos Teóricos . . . 14

2.1 Teste de Raiz Unitária . . . 14

2.2 Modelo de Médias Móveis Vetorial (VMA) . . . 15

2.3 Modelo Autorregressivo Vetorial (VAR) . . . 15

2.4 Cointegração e Modelo com Correção de Erros (VEC) . . . 15

2.4.1 Metodologia de Engle-Granger . . . 17

2.4.2 Metodologia de Johansen. . . 17

3 Metodologia . . . 18

3.1 Dados de Mercado . . . 18

3.2 Descoberta de Preço . . . 19

3.2.1 Information Share (IS) . . . 24

3.2.2 Component Share (CS) . . . 25

4 Resultados . . . 26

4.1 Estimação do modelo VEC . . . 26

4.2 Análises de Price Discovery . . . 28

5 Conclusão . . . 38

(12)

11

1 Introdução

Cada vez mais, estudos envolvendo análises de dados de alta frequência vem sendo realizados no mercado ﬁnanceiro. No cenário externo, o mercado de trading de alta

frequência é bem desenvolvido, e a literatura já produzida sobre este assunto é bastante ampla. No mercado brasileiro, as negociações em alta frequência representam uma esfera relativamente nova se comparada ao mercado internacional, e tem despertado o interesse para estudos relacionados à microestrutura de mercado no âmbito nacional.

A expansão de plataformas de negociação, o desenvolvimento e aprimoramento da tecnologia, são fatores que ajudam a promover eﬁciência e melhorar a difusão da informa-ção nos ambientes de negociainforma-ção, além de promover incentivos para atrair investidores. No cenário de negociações em alta frequência, pode haver investidores interessados em identiﬁcar, para ativos transacionados em diferentes mercados, em qual deles uma nova informação é incorporada mais rapidamente. Neste sentido, a literatura de price discovery

(descoberta de preços) pode ser utilizada na identiﬁcação do mercado dominante, que lidera a formação de preços.

A metodologia envolvendo a descoberta de preços baseia-se no conceito de que existe um preço comum (ou fundamental) a diferentes mercados em que um ativo é transacionado. A literatura mais conhecida relacionada ao tema é o trabalho desenvolvido por Hasbrouck (1995), que busca a identiﬁcação do mercado onde a incorporação de novas informações ocorre mais rapidamente. O Information Share (IS) é deﬁnido como a

proporção da contribuição relativa de cada mercado na variância do preço comum.

A segunda métrica mais frequentemente utilizada é a Component Share (CS),

desenvolvida por Gonzalo e Granger(1995), que propuseram um método de decomposição de séries de preços cointegradas em um componente permanente e um componente transi-tório, utilizando os coeﬁcientes de correção de erros do vetor de cointegração. Gonzalo e Granger (1995) mostraram que o componente permanente é uma combinação linear de todas as séries de preço no sistema de cointegração. No contexto de price discovery, as

primeiras aplicações desse modelo surgiram com os estudos de Booth et al. (1999), Chu et al. (1999) e Harris et al. (2002), que propuseram que uma série de preços com maior peso na combinação linear move-se mais próxima do preço eﬁciente e, portanto, contribui mais para a descoberta de preço.

A utilização da literatura de price discovery em estudos envolvendo ativos

(13)

Capítulo 1. Introdução 12

observaram os preços das ações da Petrobrás e da Vale, negociadas nos mercados doméstico e americano (ADRs), e notaram que o mercado internacional é o mais importante para a descoberta de preços. Booth et al. (1999) avaliaram o processo de descoberta de preços na Alemanha para o índice DAX e contratos de futuros e de opções sobre o índice, concluindo que os dois primeiros apresentam maiores valores de IS em comparação com o mercado de opções.

Alguns estudos voltados para a análise do mercado cambial, comparando o mercado

spot com o mercado futuro, também podem ser encontrados na literatura. Sulzbach et

al. (2012) usando as operações do primeiro vencimento dos contratos futuros de câmbio Real/Dólar da BM&FBovespa testaram se as transações impuseram efeitos informativos sobre os preços. Os resultados apontaram para a existência de informação assimétrica no mercado futuro de câmbio brasileiro, indicando que aproximadamente 50% da variação do preço eficiente é resultado da informação privada contida no fluxo de ordem. Além disso, a análise do fluxo de ordem permitiu a estimação das taxas de chegada de ordens de agentes informados e não informadas no mercado, utilizadas para calcular a probabilidade de uma transação ser informativa (PIN). Altos valores de PIN implicam spreads mais amplos que reduzem a liquidez do mercado. O resultado de 1,53% indica que o mercado de câmbio brasileiro é bastante líquido, o que impõe menores custos aos agentes menos informados que chegam ao mercado. Santos et al. (2014) estudaram a formação de preços no mercado cambial brasileiro comparando o dólar à vista com o futuro. Com base nas medidas calculadas, concluíram que o mercado futuro domina a descoberta de preços e é mais eficiente. Outras análises envolvendo mercados emergentes foram realizadas por Boyrie et al. (2012), que trabalharam com as moedas brasileira, sul-africana e russa. No estudo, eles observaram que o mercado futuro é mais importante do que o à vista na descoberta de preços para o real brasileiro, ao contrário do que ocorre para o rublo russo, onde o mercado à vista é dominante. Para o rand sul-africano, os resultados foram inconclusivos. Estudos realizados observando-se a paridade euro/dólar e iene/dólar mostram resultados de dominância do mercado à vista (Cabrera et al., 2009), apesar de outros trabalhos indicarem que essa característica de liderança nem sempre é observada ao avaliar diferentes períodos de tempo (Rosenberg e Traub, 2006).

(14)

Capítulo 1. Introdução 13

importante fonte para a descoberta de preços.

O objetivo deste trabalho é estudar o comportamento do mercado de opções brasileiro na descoberta de preços. A metodologia de price discovery será aplicada a dados

de alta frequência das ações e opções de Petrobrás, fornecidos pela BM&FBOVESPA (Bolsa de Valores, Mercadorias e Futuros de São Paulo), para o período de abril a dezembro de 2013. Os resultados obtidos indicam dominância do mercado à vista na descoberta de preços, com relação ao mercado de opções.

A estrutura do trabalho será organizada da seguinte maneira: O capítulo 2 possui caráter introdutório, apresentando uma abordagem geral sobre os modelos de séries temporais e demais técnicas utilizadas neste estudo. O capítulo seguinte apresenta o detalhamento da metodologia empregada no trabalho, com a descrição dos dados e das medidas de price discovery utilizadas. O capítulo 4 exibe os resultados obtidos em cada

(15)

14

2 Conceitos Teóricos

O objetivo deste capítulo é discursar sobre alguns conceitos que envolvem mode-lagem de séries temporais. As teorias podem ser exploradas com maiores detalhes nas respectivas referências, citadas ao longo do texto.

2.1 Teste de Raiz Unitária

Uma série temporal {yt}, t= 1,· · ·, n é dita estritamente (ou fortemente) estacio-nária se os vetores aleatórios (yt1,· · · , ytk) e (yt1+s,· · · , ytk+s) têm a mesma distribuição

conjunta, para qualquer s, com k um inteiro positivo e (t1,· · · , tk) uma coleção de k inteiros positivos. Esta é uma condição forte e difícil de ser veriﬁcada empiricamente, levando à utilização de uma versão mais fraca de estacionariedade. Assim, uma série temporal {yt} é dita estacionária fraca (ou estacionária de segunda ordem) se a média de

yt e a covariância entre yt e yt−l forem invariantes no tempo, com l um inteiro arbitrário. Isto é:

i) E[yt] =µ(constante);

ii) V ar[yt] =σ2 (constante); iii) Cov[yt, yt−l] não depende de l.

Uma estatística utilizada para veriﬁcar a condição de estacionariedade é o teste de raíz unitária ou teste de Dickey-Fuller Aumentado (ADF), cujo modelo é dado por:

∆yt =ψ0+βyt−1+

q X

i=1

ψi∆yt−i+et,

com ∆yt=yt−yt−1 e et um processo de inovações.

Para que o modelo seja estacionário, β deve ser menor do que 1. Se β = 1, então

existe uma raíz unitária e yt é não estacionária. A hipótese nula é de que a série é não estacionária (H0:β = 1 contra H1: β <1). A estatística do teste é dada por:

DF = βb−1 std(βb),

com _βb _{obtido pelo método de mínimos quadrados.}

(16)

Capítulo 2. Conceitos Teóricos 15

2.2 Modelo de Médias Móveis Vetorial (VMA)

Um modelo VMA(q) é uma generalização vetorial de um modelo de médias móveis

escalar, de forma que

yt=µ+et+ψ1et−1+ψ2et−2+· · ·+ψqet−q

=µ+

q X

i=0

ψiet−i, (2.1)

em que µ é um vetor de dimensão n×1 de constantes, ψi, i= 0,· · · , q, é uma matriz de coeﬁcientes de dimensão n×n eet−i é um vetor de ruídos brancos.

2.3 Modelo Autorregressivo Vetorial (VAR)

Denotamos por VAR(p), a generalização vetorial de um modelo autoregressivo de ordem p, deﬁnido como

yt =κ+φ1yt−1+φ2yt−2+· · ·+φpyt−p+et

=κ+

p X

i=1

φiyt−i+et, (2.2)

em que κ é um vetor de dimensão n×1 de constantes, φi, i= 1,· · · , p, é uma matriz de dimensão n×n de coeﬁcientes autorregressivos e et é um vetor de ruídos brancos, ou seja

E(et) = 0 E(e′tes) = Ωδts,

com Ω uma matriz positiva deﬁnida.

Dessa forma, um modelo VAR(p) é um sistema em que cada variável é descrita por uma

constante, p lags da própria variável e p lags de cada uma das outras variáveis do modelo

(Hamilton, 1994).

2.4 Cointegração e Modelo com Correção de Erros (VEC)

O conceito de cointegração foi introduzido porEngle e Granger(1987) e diz respeito à dinâmica de evolução de séries temporais que apresentam uma relação de equilíbrio de longo prazo.

As componentes de um vetor de séries temporaisyt são ditas cointegradas de ordem d, b (yt ∼ CI(d,b)), se:

(17)

Como exemplo, dada uma série não estacionária yt, se a série de diferenças yt−yt−1

for estacionária, então a série yt é integrada de ordem 1 ou I(1). Dessa forma, sobre a série de diferenças, diz-se que é integrada de ordem 0.

ii) Existe um vetorα (6=0) tal que zt=α⊤yt∼I(d−b), b > 0. O vetorα é chamado de vetor de cointegração.

Assim, um conjunto de séries temporais integradas é cointegrado se existir uma combinação linear entres essas séries que seja estacionária. Por exemplo, duas séries temporais y1 e y2 (não estacionárias) são cointegradas se existirem α1 e α2 tais que a

combinação linear dada por 2.4 seja estacionária.

z=α1y1+α2y2 = (α1 α2) y1 y2

!

, (2.3)

z é chamado de desequilíbrio, pois captura o desvio de um equilíbrio de longo prazo,

e (α1, α2) é o vetor de cointegração.

A tendência de reversão à uma tendência estocástica comum entre as variáveis é expressa em termos de correção de erros. No caso de n séries temporais, representadas

pelo vetor yt e comβ sendo uma matriz de vetores de cointegração (em que cada coluna corresponde a uma relação especíﬁca), os erros no tempo t são dados por β⊤_y

t e as velocidades de ajuste com que as séries corrigem o desequilíbrio são dadas pela matriz α.

Estes vetores são incorporados no modelo, no tempo t, através do termo de correção de erros: αβ⊤_y

t−1 (=Cyt−1).

Adicionando-se o termo de correção de erros a um modelo VAR nas diferenças, obtem-se um modelo VEC:

∆yt=Cyt−1+

q X

i=1

Γi∆yt−i+et. (2.4)

Portanto, o modelo VEC nas diferenças pode ser transformado em um modelo VAR nos níveis das variáveis, conforme abaixo:

yt=yt−1+Cyt−1+

q X

i=1

Γi∆yt−i+et

= (Id+ Γ1+C)yt−1+ (−Γ1+ Γ2)yt−2+· · ·+ (−Γq)yt−(q+1)+et =A1yt−1+A2yt−2+· · ·+Aq+1yt−(q+1)+et

= q+1

X

i=1

(18)

O posto da matrizC, conhecida como matriz de longo prazo, determina o número

de relações de cointegração entre as variáveis do vetor yt. Se a matriz tem posto completo, então o sistema yt é estacionário nos níveis. Caso o posto seja zero, o sistema é estacionário nas diferenças. Na literatura existem duas metodologias principais para identiﬁcar relações de cointegração: a metodologia de Engle-Granger e a metodologia de Johansen. Ambas serão descritas a seguir e maiores detalhes sobre os testes e a estimação dos parâmetros podem ser obtidos em Hamilton (1994).

2.4.1 Metodologia de Engle-Granger

Engle e Granger(1987) desenvolveram um teste para identiﬁcar relações simples de cointegração. O teste consiste em fazer uma regressão de uma componente deytnas demais componentes do vetor e realizar um teste de raíz unitária nos resíduos dessa regressão. Se a hipótese nula de não-estacionariedade dos resíduos for rejeitada, então as séries em yt são cointegradas. O teste de Engle-Granger apresenta algumas limitações:

i) É possível a identiﬁcação de apenas uma relação de cointegração, dentren−1 possiveis

(num conjunto de n variáveis podem existir atén−1 vetores de cointegração);

ii) A escolha da componente de yt que será a variável dependente da regressão é, geralmente, arbitrária e a troca da variável implica em uma mudança na relação de cointegração, indicando que a relação é única, caso o posto da matriz de longo prazo seja um, a menos de regra de normalização;

iii) Por ser um procedimento realizado em dois passos, com uma primeira regressão para estimar os resíduos e uma segunda para testar a raíz unitária, os erros na primeira estimação são transferidos para a segunda.

2.4.2 Metodologia de Johansen

A técnica apresentada por Johansen foi desenvolvida para análise de sistemas multivariados. Consiste em veriﬁcar o número de relações de cointegração com base no teste das hipóteses: H0:r ≤R vs H1: r > R, onde r representa o número de relações de

cointegração (ou seja, o posto da matriz de impacto C =αβ⊤_).

(19)

18

3 Metodologia

3.1 Dados de Mercado

Para a realização deste estudo foram utilizados dados de alta frequência, dis-ponibilizados pela Diretoria de Controles Internos, Compliance e Riscos Corporativos

da BM&FBOVESPA, dos mercados de ações e opções de ações da empresa Petrobrás (PETR4), de abril a dezembro de 2013, totalizando um histórico de 183 dias.

Foram coletadas todas as informações de ordens enviadas para o livro de ofertas em cada um dos mercados. As bases de dados foram tratadas com o auxílio do software SAS Enterprise Guide.

Conforme esperado, observa-se nos dados que o mercado de ações é negociado em uma frequência maior que o mercado de opções. Em estudos deprice discovery (descoberta

de preço) cujas análises envolvem mercados com diferentes frequências de negociação, algumas suposições e ajustes são necessários, como a deﬁnição de intervalos de preço de acordo com a frequência observada no mercado menos líquido. Dessa forma, as análises foram realizadas considerando-se frequências de 1 minuto, 5 minutos, 10 minutos e 15 minutos.

Para este estudo, foi adotado um conceito usual na literatura de descoberta de preços para a comparação entre os dois mercados, que corresponde ao bid-ask midpoint,

obtido a partir da seguinte relação entre os preços de bid (compra) e ask (venda):

midP = best_bid+best_ask

2 , (3.1)

em que

midP corresponde ao valor domidpoint;

best_bid corresponde ao melhor preço de compra;

best_ask corresponde ao melhor preço de venda.

As séries demidpoints foram obtidas para cada mercado e para a comparação entre

eles foram utilizados o preço no mercado à vista e o preço da ação implícito nas opções, obtido a partir da relação entre opções de compra (call) e venda (put) na paridadeput-call:

St =Ct(K, T)−Pt(K, T) +P Vt(Dt, T)) +Ke−r(t,T)(T−t), (3.2) em que

(20)

Capítulo 3. Metodologia 19

Ct(K, T) é o preço da call com strike K e vencimento T, no instante t;

Pt(K, T) é o preço da put com strike K e vencimentoT, no instante t;

P Vt(D(t, T)) é o valor presente dos dividendos, no instante t;

r(t, T) é a taxa de juros para o prazo T.

A tabela 1 exibe as estatísticas descritivas de ambas as séries de preços, para diferentes frequências de dados. Observa-se que os preços da ação no mercado à vista são, em média, maiores que os preços implícitos da ação no mercado de opções, para todas as frequências analisadas1_{. Os valores das medianas também indicam a existência dessa}

diferença, sendo a distância entre os preços maior do que a observada quando comparados os valores médios (3 ticks e 2 ticks, respectivamente).

A tabela 2 exibe as estatísticas descritivas para as séries de retornos dos preços. Neste caso, os valores observados para as médias são da ordem de 10−6 _{e iguais a zero}

para as medianas. Para ambos os mercados e em todas as frequências amostrais (exceto para o mercado à vista na frequência de 1 minuto), observa-se leve assimetria positiva. Os valores de curtose maiores que 3 indicam que os retornos apresentam distribuição com caudas mais pesadas que a distribuição Normal.

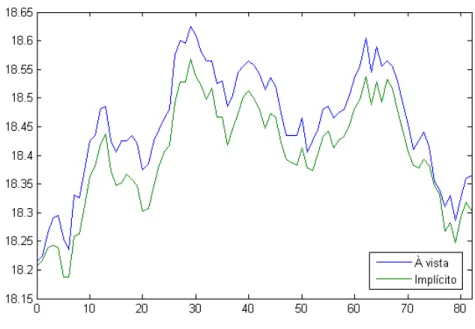
A figura1ilustra o preço da ação no mercado à vista e o preço implícito nas opções, na frequência de cinco minutos, para todo o período avaliado. Para uma visualização mais detalhada, específica para uma data, a figura 3apresenta um exemplo do comportamento das séries de preços no dia 10/abr/2013. Nota-se a existência de um movimento conjunto,

mas observam-se, também, divergências de preços em alguns momentos, dependendo da velocidade de ajuste a novas informações em cada mercado. Pelos diagramas 2e 4, que correspondem aos gráﬁcos de dispersão das séries para todo o período amostral e para a data de 10/abr/2013, respectivamente, também pode-se notar que, em geral, os preços apresentam um movimento conjunto ao longo do tempo.

3.2 Descoberta de Preço

A literatura relacionada a modelos de descoberta de preço compartilha o princípio de que existe um preço eﬁciente comum a todos os mercados em que um ativo é transacionado. Dessa forma, os preços para um mesmo ativo podem divergir no curto prazo (devido a fricções no mercado) mas estão conectados a um valor fundamental para o qual convergirão no longo prazo. Tais séries de preços são, portanto, cointegradas e prestam-se a análises empíricas utilizando modelos de correção de erros (VEC), sob a suposição de que as

1 _{A rigor, deve-se realizar um teste de igualdade de médias para se fazer essa observação. Porém,}

(21)

Figura 1 – Preço da ação no mercado à vista e preço implícito nas opções, entre 08/abr/13

e 30/dez/13, para a frequência de 5 minutos.

(22)

Figura 3 – Preço da ação no mercado à vista e preço implícito nas opções, no dia 10/abr/13,

para a frequência de 5 minutos.

(23)

Estatísticas 1 minuto 5 minutos 10 minutos 15 minutos À vista Opção À vista Opção À vista Opção À vista Opção Média 18,17 18,15 18,16 18,14 18,16 18,14 18,16 18,14 Mediana 18,21 18,18 18,20 18,17 18,20 18,17 18,21 18,18 Desvio Padrão 1,451 1,446 1,449 1,444 1,449 1,444 1,449 1,444

Tabela 1 – Estatísticas descritivas para os preços da ação no mercado à vista e no mercado de opções, entre abril e dezembro de 2013.

Estatísticas 1 minuto 5 minutos 10 minutos 15 minutos

À vista Opção À vista Opção À vista Opção À vista Opção

Média -1,6E-06 2,9E-06 -6,3E-06 -1,4E-05 -1,3E-05 -2,8E-05 -7,4E-06 -3,0E-05

Mediana 0 0 0 0 0 0 0 0

Desvio Padrão 0,001 0,001 0,002 0,002 0,003 0,003 0,003 0,003

Assimetria -0,06 2,46 0,31 0,47 0,21 0,04 0,34 0,08

Curtose 57,64 279,65 12,55 29,95 10,05 15,89 9,72 11,58

Tabela 2 – Estatísticas descritivas para os log-retornos dos preços da ação no mercado à vista e no mercado de opções, entre abril e dezembro de 2013.

séries de preços compartilham de um preço eﬁciente comum, representado por um passeio aleatório.

Considere um ativo negociado em dois mercados cujos preços são dados pelo vetor (p1t, p2t). Assume-se que cada série de preços é integrada de ordem 1, isto é, apresentam um componente que segue um processo de passeio aleatório. Assume-se, também, que as diferenças de preços são covariância-estacionárias. Portanto, os preços podem ser descritos a partir de uma representação de um modelo de médias móveis vetorial (VMA):

∆pt= Ψ(L)et, (3.3)

em que et é um vetor de perturbações não correlacionadas com média zero e matriz de covariância Ω, e Ψ é um polinômio no operador lag.

Embora os preços sejam não estacionários, a diferença entre eles é estacionária. Dessa forma, os preços são cointegrados de ordem 1 e o vetor β = (1,−1) 2 _{é um vetor}

de cointegração, isto é, β′_p

t é estacionário. Deﬁnindo Ψ(1) como a soma dos coeﬁcientes VMA, o fato de β′_p

t ser estacionário implica que β′Ψ(1) = 0 e também que as linhas de Ψ(1) são idênticas. Intuitivamente, Ψ(1)et representa o impacto de longo prazo de uma perturbação em cada preço. As linhas idênticas indicam que este impacto de longo prazo

2 _{O vetor}_β _{pode ser diferente de (1}_,_{−1). Neste trabalho,}_β _{será estimado para as amostras de dados}

(24)

é o mesmo em ambos os preços. Denotando ψ como a linha comum de Ψ(1), utilizando

a representação proposta por Stock e Watson (1988), os preços podem ser escritos da seguinte forma:

pt=p0+ψ t X

s=1 es

!

ι+ Ψ∗₍_L₎_e

t, (3.4)

em que p0 é um vetor de constantes, ι é um vetor unitário e Ψ∗₍_L_{) é uma matriz de}

polinômios do operador lag.

O primeiro termo do lado direito da equação 3.4 é um vetor de valores iniciais, representando as diferenças não estocásticas entre os preços. O segundo termo captura o componente aleatório que é comum a todos os preços (preço fundamental). O último termo corresponde aos resíduos com média zero e covariância-estacionários.

Suponha que existe uma representação autorregressiva (VAR) não estacionária de ordem K para os níveis de preço:

A(L)pt=κ+et, (3.5)

A(L) = I−A1L−A2L2−. . .−AKLK.

Como descrito na seção 2.4, um modelo VAR nos níveis pode ser representado como um modelo VEC nas diferenças:

∆pt=α(β′pt−1−Eβ′pt) + Γ1∆pt−1+ Γ2∆pt−2+. . .+ ΓK−1∆pt−K+1+et, (3.6)

com αβ′ ₌₋_A_{(1) e Γ}

j =−PKi=j+1Ai, paraj = 1, . . . , K −1.

A partir da estimação do modelo VEC, pode-se identiﬁcar os parâmetros do modelo VAR e, utilizando-se um procedimento de programação dinâmica, é possível obter os coeﬁcientes do modelo VMA. Maiores detalhes sobre o procedimento de simulação para o cálculo da representação VMA podem ser encontrados em Hamilton(1994).

Nas seções a seguir, serão apresentadas as medidas de descoberta de preço abordadas neste estudo: information share(IS) ecomponent share (CS). Ambas são derivadas a partir

das estimativas de uma forma reduzida do modelo VEC.

Sobre a medida IS, Hasbrouck(1995) propôs que a contribuição de um mercado para a descoberta de preços pode ser medida pela proporção da variância nas inovações do preço eﬁciente comum que é explicada pelas inovações daquele mercado.

(25)

3.2.1 Information Share

(

IS

)

A equação3.4 apresenta um termo aleatório comum a todos os preços. Segundo Hasbrouck (1995), o componente ψet é a inovação do preço eﬁciente, cuja variância é dada por ψΩψ′_{. Supondo que} _p

t representa os preços em n mercados diferentes e que ej,t é a inovação no j-ésimo mercado. Se Ω é diagonal (ou seja, as inovações do mercado são não

correlacionadas), então cada um dos n termos de ψΩψ′ _{representam a contribuição para a}

inovação de um mercado em particular. A medida IS é dada por:

ISj =

ψ2

jΩjj

ψΩψ′, (3.7)

em que ψj corresponde ao j-ésimo elemento deψ. IS indica a proporção da variância do preço eﬁciente que é explicada por cada mercado, sendo utilizada para determinar qual deles se move primeiro no processo de descoberta de preço.

Esta medida é baseada no conceito de que os resíduos do modelo VMA são não correlacionados. Porém, se as inovações forem correlacionadas entre os mercados, então Ω não é diagonal e, portanto, a medida deve ser ajustada. Segundo Hasbrouck, uma maneira de aprimorar a medida é aplicando a decomposição de Cholesky sobre a matriz Ω (Ω = F F′_{). Assim, a medida IS é dada por:}

ISj =

[ψF]_j2

ψΩψ′ , (3.8)

em que [ψF]_j representa oj-ésimo elemento da matriz ψF. A decomposição impõe uma

hierarquia que maximiza o conteúdo informacional do primeiro mercado e minimiza o do segundo. Limites inferiores e superiores para as medidas de IS podem ser obtidos, permutando-se a ordem (hierarquia) dos mercados.

Outra forma de se calcular a medida IS é deﬁnindo-se a média dos valores para cada hierarquia, conforme Santos et al. (2014):

ISj =

([ψF1]j)

2

ψΩψ′ + (

[ψF2]j)

2

ψΩψ′

2 , (3.9)

A desvantagem desta abordagem é que quando os resíduos são altamente cor-relacionados, a distância entre os limites inferior e superior pode ser grande, conforme documentado em algumas literaturas de price discovery (Hasbrouck,2003). Uma

alterna-tiva proposta por Hasbrouck (1995) para contornar o problema é aumentar a frequência amostral dos dados, o que nem sempre é possível devido à restrições de disponibilidade de informações, por exemplo. Fernandes e Scherrer (2013) propuseram uma medida alterna-tiva, com base na decomposição espectral de Ω, utilizada nos casos em que as inovações são altamente correlacionadas:

ISj =

[ψS]_j2

(26)

em que S = VΛ1/2_V′_, _V _{é a matriz dos autovetores de Ω e Λ é a matriz (diagonal) de}

autovalores.

3.2.2 Component Share

(

CS

)

Gonzalo e Granger (1995) propuseram um método de decomposição de séries cointegradas em um componente permanente e um componente transitório, utilizando os coeficientes de correção de erros. O componente permanente é interpretado como o preço eficiente comum aos mercados e o componente transitório reflete os desvios devido às fricções no mercado. Gonzalo e Granger (1995) mostraram que o componente permanente é uma combinação linear dos preços de cada mercado. De acordo com a literatura, séries de preços com pesos maiores na combinação linear movem-se mais próximas do preço eficiente e, portanto, contribuem mais para a descoberta de preços. Assim, a contribuição de um mercado para a descoberta de preços é seu peso normalizado na combinação linear entre os preços. Desse modo, a medida CS é definida como:

CSj =

α⊥,j

α⊥,j+α⊥,i

, (3.11)

em que o vetor (α⊥,j, α⊥,i) é ortogonal ao vetorα, que representa a velocidade de ajuste do modelo VEC.

Valores baixos deα indicam que o mercado é pouco sensível aos desvios em relação

ao equilíbrio (dado pelo termo β′_p

t−1 do modelo VEC) e implicam maior participação na

composição do preço permanente.

Algumas literaturas, como Baillie et al. (2002) eJong (2002), associam os pesos com a matriz de impacto de longo prazo Ψ(1), de modo que:

CSj =

ψj

ψj+ψi

, (3.12)

(27)

26

4 Resultados

Neste capítulo serão exibidos os principais resultados obtidos com as estimações dos modelos VEC. Também serão apresentadas as análises referentes às medidas de price discovery, descritas na seção 3.2 e calculadas neste trabalho. As análises foram realizadas

para as frequências de 1 minuto, 5 minutos, 10 minutos e 15 minutos.

Para efeito deste estudo, denota-se o preço no mercado à vista porP e o preço da

ação implícito nas opções por IP.

As análises e gráﬁcos foram executados e gerados com o auxílio do software

MATLAB.

4.1 Estimação do modelo VEC

Esta seção discorre sobre os resultados da estimação do modelo VEC. A primeira etapa consistiu em veriﬁcar a existência de cointegração entre as duas séries de preços, foram realizados os testes de cointegração de Engle-Granger e de Johansen. A hipótese nula do teste de Engle-Granger é de que não há relação de cointegração entre as variáveis testadas. Para todas as frequências estudadas, veriﬁcou-se rejeição da hipótese nula, o que indica que as séries de preços P eIP são cointegradas. Utilizando a metodologia de

Johansen, cuja hipótese nula do teste é de que o posto de cointegração é igual a r (neste

caso, r = 0 ou 1), os resultados foram concordantes, observando-se em todos os casos a não rejeição da hipótese nula (para r= 1) de existência de cointegração.

Os resultados de ambos os testes conﬁrmam a intuição de que o preço da ação no mercado à vista e o preço implícito da ação no mercado de opções apresentam uma relação de cointegração. A análise utilizando a metodologia de Engle-Granger apresentou resultados para o p-valor que indicam a rejeição da hipótese nula de inexistência de cointegração, em todas as frequências avaliadas. O teste realizado a partir da metodologia de Johansen produziu resultados indicando que o número de relações de cointegração existentes é igual a 1 e, portanto, as séries de preços são cointegradas.

Observada a existência de relação de cointegração entre os preços, seguiu-se a análise com a estimação dos parâmetros do modelo VEC (3.6), comc0 =β′pt. O modelo foi estimado para todas as frequências de dados (1, 5, 10 e 15 minutos) e considerando-se diferentes defasagens para as séries de preços (5, 10 e 20 lags). Os parâmetros estimados

α, β e c0, bem como a correlação dos resíduos e o número de observações utilizadas em

(28)

Capítulo 4. Resultados 27

lag = 5 lag = 10 lag = 20

À vista Opção À vista Opção À vista Opção

α -0,0088 0,0231 -0,0071 0,0198 -0,0053 0,0169

(0,0014) (0,0044) (0,0014) (0,0044) (0,0014) (0,0044)

β 1,0000 -1,0021 1,0000 -1,0021 1,0000 -1,0021

(0,0001) (0,0001) (0,0001)

c0 -0,0051 -0,0051 -0,0051

(0,0004) (0,0004) (0,0004)

Correl. contemporânea resíduos 0,55 0,55 0,55

Num. observações 69157 69152 69142

Tabela 3 – Coeﬁcientes da regressão do modelo VEC - frequência 1 minuto(Desvios padrão das estimativas entre parêntesis).

lag = 5 lag = 10 lag = 20

α -0,0155 0,0455 -0,0104 0,0401 -0,0063 0,0381

(0,0060) (0,0127) (0,0063) (0,0129) (0,0067) (0,0132)

β 1,0000 -1,0021 1,0000 -1,0021 1,0000 -1,0021

(0,0003) (0,0003) (0,0003)

c0 -0,0051 -0,0051 -0,0051

(0,0009) (0,0009) (0,0009)

Tabela 4 – Coeﬁcientes da regressão do modelo VEC - frequência 5 minutos(Desvios padrão das estimativas entre parêntesis).

minutos, respectivamente. 3

A literatura deprice discovery usualmente adota o vetor (1;−1) para representar

o parâmetro β. Neste estudo, optou-se por estimar o valor de β para as amostras de

dados utilizadas. Para todas as frequências de dados e defasagens analisadas, observou-se a relação (1;−1,003) para o vetor de cointegração β.

O parâmetroαrepresenta a velocidade de ajuste ao equilíbrio. Os resultados obtidos

nas estimações dos modelos indicam existência de correção dos erros, porém os valores baixos são um indicativo de que a correção ocorre lentamente. Para o caso dos dados com frequência de cinco minutos, por exemplo, aproximadamente 1,1% do desequilíbrio é

ajustado no primeiro intervalo de cinco minutos.

(29)

lag = 5 lag = 10 lag = 20

α -0,0165 0,0702 -0,0066 0,0709 -0,0054 0,0647

(0,0120) (0,0207) (0,0128) (0,0214) (0,0142) (0,0223)

β 1,0000 -1,0020 1,0000 -1,0020 1,0000 -1,0020

(0,0004) (0,0004) (0,0004)

c0 -0,0049 -0,0049 -0,0049

(0,0013) (0,0013) (0,0013)

Tabela 5 – Coeﬁcientes da regressão do modelo VEC - frequência 10 minutos (Desvios padrão das estimativas entre parêntesis).

lag = 5 lag = 10 lag = 20

α -0,0106 0,0990 -0,0034 0,0919 0,0082 0,0815

(0,0187) (0,0285) (0,0205) (0,0299) (0,0228) (0,0323)

β 1,0000 -1,0020 1,0000 -1,0020 1,0000 -1,0020

(0,0005) (0,0005) (0,0005)

c0 -0,0050 -0,0050 -0,0050

(0,0016) (0,0016) (0,0016)

Tabela 6 – Coeﬁcientes da regressão do modelo VEC - frequência 15 minutos (Desvios padrão das estimativas entre parêntesis).

4.2 Análises de

Price Discovery

Nesta seção serão apresentadas as análises de price discovery descritas na seção

3.2 deste trabalho. A exibição dos resultados será realizada em duas partes: a primeira, abordando os resultados e análises obtidos para a frequência amostral de 1 minuto; a segunda, contemplando os resultados para as demais frequências utilizadas no estudo.

Denotaremos por IS1 a medida deinformation share calculada via decomposição

espectral e por IS1 a medida obtida utilizando-se a decomposição de Cholesky (vide

subseção 3.2.1). A medida component share será referida nas análises porCS.

A medida IS1 permite a obtenção de limites inferior e superior para o valor de

information share. No entanto, conforme já descrito anteriormente, dependendo do nível

(30)

No _de _lags CS IS1 IS2

5 74,4 25,6 69,5 30,5 _{[63,7 ; 92,9]}78,3 _{[7,1 ; 36,3]}21,7

10 75,4 24,6 70,5 29,5 78,1 21,9

[62,7 ; 93,5] [6,5 ; 37,3]

20 77,0 23,1 72,0 28,0 _{[60,5 ; 94,3]}77,4 _{[5,7 ; 39,5]}22,6

Tabela 7 – Medidas de price discovery para a frequência de 1 minuto (em %).

Ainda assim, neste estudo tais parâmetros foram calculadas, a ﬁm de obter uma análise comparativa entre as diferentes medidas, apresentada ao longo desta seção.

Análises para a frequência amostral de 1 minuto

A tabela 7 exibe os resultados das avaliações para a frequência amostral de um minuto. Considerando o caso em que foram estimadas cinco defasagens, a comparação entre os valores de todas as medidas indica que o mercado à vista para as ações da Petrobrás é dominante em relação ao mercado de opções (este resultado é consistente com a intuição baseada na liquidez e tamanho dos mercados. Embora o mercado de opções de Petrobrás represente um dos mais líquidos dentre as opções negociadas no Brasil, o mercado de ações ainda é o mais transacionado). De acordo com o valor deCS, o mercado

à vista contribui com uma participação de 74,4% na composição do preço permanente.

Pela medida IS2, observa-se que 69,5% da variância do preço eﬁciente é explicada pelo

mercado à vista. A medida IS2 corresponde ao critério adotado por Santos et al.(2014), e

os valores apresentados entre colchetes correspondem aos limites inferior e superior, obtidos a partir da mudança de hierarquias deﬁnida por Hasbrouck (1995). Neste caso, também nota-se a dominância do mercado à vista, pelo valor calculado para a medida (78,3%

contra 21,7%). Avaliando as diferentes defasagens, observa-se consistência na indicação de dominância do mercado à vista. Os valores de CS variam entre 74,4% e 77%, e os valores de IS1 apresentam variação entre 69,5% e 72%, indicando que os resultados são robustos

às variações nos lags.

(31)

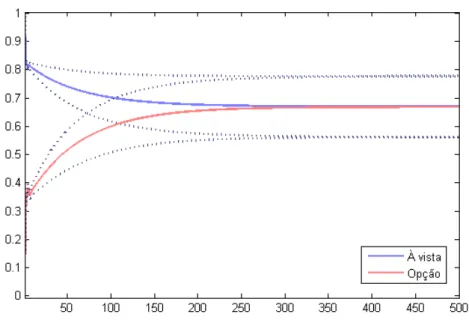
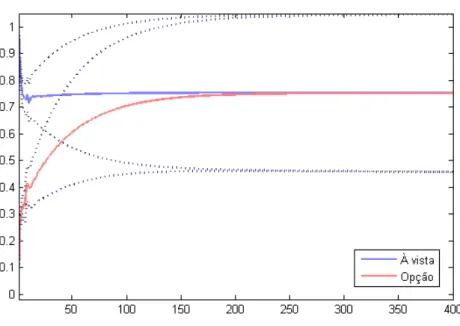
Figura 5 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência de 1 minuto / número de lags = 5).

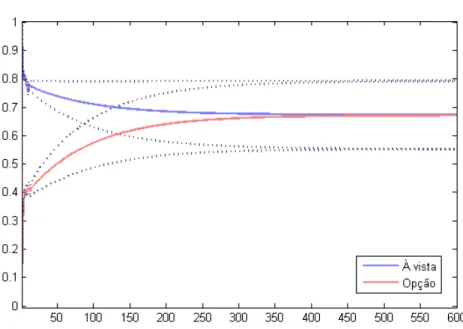
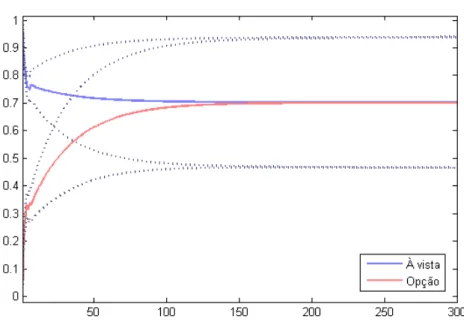
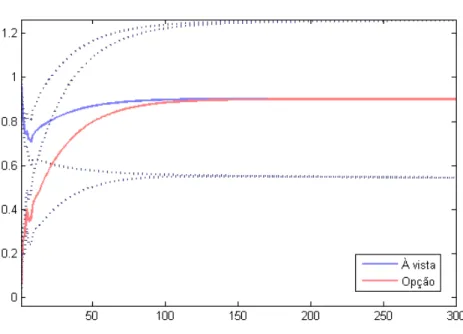
é igual a 10 (ﬁgura 6), observa-se a convergência a partir de 90 minutos. E observando-se a ﬁgura 7, para 20 defasagens, nota-se que os preços atingem o equilíbrio a partir de 100 minutos após o choque.

(32)

Figura 6 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência de 1 minuto / número de lags = 10).

(33)

5 75,4 24,6 66,7 33,3 _{[79,7 ; 97,5]}88,6 _{[2,5 ; 20,3]}11,4

10 79,3 20,7 69,1 30,9 87,8 12,3

[77,3 ; 98,2] [1,8 ; 22,7]

20 84,5 15,5 72,2 27,8 _{[73,5 ; 99,0]}86,2 _{[1,0 ; 26,5]}13,8

Tabela 8 – Medidas de price discovery para a frequência de 5 minutos (em %).

Análises para as demais frequências amostrais (5, 10 e 15 minutos)

Os resultados das avaliações para a frequência amostral de cinco minutos são exibidos na tabela 8. Para todos os casos de defasagens considerados, assim como para a frequência amostral de 1 minuto, os valores obtidos indicam uma dominância do mercado à vista com relação ao mercado de opções. As estimativas deCSmostram que a contribuição do mercado à vista na composição do preço permanente varia entre 75,4% e 84,5%,

de acordo com as defasagens consideradas. No caso da medida IS1, o mercado à vista

explica entre 66,7% e 72,2% da variância do preço eﬁciente. Para a medida IS2, os valores

apresentam-se dentro do intervalo entre 86,2% e 88,6%.

Para a frequência de dados de 10 minutos (tabela9), os resultados observados para todas as medidas e para todas as defasagens utilizadas, reﬂetem a dominância do mercado à vista comparado ao mercado de opções. Os valores de CS concentram-se entre 80,8%

e 90,9%, os de IS1 entre 67,2% e 72,3%, e os deIS2 estão no intervalo entre 88,3% e

90,9%.

Por ﬁm, analisando os dados na frequência de 15 minutos, conﬁrma-se a caracte-rística de mercado dominante para o mercado de ações frente ao de opções. Os valores das medidas de price discovery variam dentro do intervalo de 88,3% e 94,7% para oCS,

de 69,4% a 72% para o IS1, e de 89,4% a 91,6% para o IS2 (conforme apresentado na

tabela 10).

(34)

5 80,8 19,2 67,2 32,8 _{[82,8 ; 98,9]}90,9 _{[1,1 ; 17,2]}9,1

10 89,7 10,3 71,7 28,3 88,9 11,1

[78,2 ; 99,7] [0,3 ; 21,8]

20 90,9 9,1 72,3 27,7 88,3 11,8

[76,7 ; 99,8] [0,2 ; 23,3]

5 88,3 11,7 69,4 30,7 _{[83,6 ; 99,7]}91,6 _{[0,3 ; 16,4]}8,4

10 93,4 6,6 71,5 28,5 90,6 9,4

[81,4 ; 99,9] [0,1 ; 18,6]

20 94,7 5,3 72,0 28,0 89,4 10,6

[78,8 ; 99,9] [0,1 ; 21,2]

(35)

Figura 9 – Função resposta ao impulso entre abril e dezembro de 2013 (Frequência de 5 minutos / número de lags = 10).

(36)

(37)

(38)

(39)

38

5 Conclusão

Os resultados das análises deprice discovery aplicadas ao preço da ação da Petrobrás

no mercado à vista e ao preço da ação implícito no mercado de opções mostraram evidências de que o mercado à vista domina o processo de descoberta de preços. Este indicativo é condizente com a intuição de que mercados que apresentam maior liquidez, transparência nas negociações e cujo conhecimento é mais amplo, são mais favoráveis ao ingresso de mais investidores, incluindo os de alta frequência.

A característica de dominância do mercado de ações foi observada em diferentes frequências amostrais. A medida de information shareindicou que o percentual da variação

no choque do preço fundamental que é originado no mercado à vista encontra-se dentro do intervalo entre 66% e 72%, contra 34% a 28% para o mercado de opções. Já os valores obtidos para a medida component share indicaram que o mercado de ações responde por

74% a 95% da composição do preço fundamental, dependendo da frequência amostral adotada, enquanto o mercado de opções responde por 26% a 5%.

Em geral, com a avaliação do comportamento das funções de resposta ao impulso, observou-se que a convergência entre os preços até atingirem o equilíbrio ocorre a partir de 120 minutos, nas análises para frequências menores, e a partir de 75 minutos para frequências amostrais de 1 minuto. As análises gráﬁcas destas funções indicaram, também, que o preço no mercado à vista está sempre mais próximo do preço permanente e, em geral, recupera o equilíbrio mais rapidamente, indicando maior eﬁciência com relação ao mercado de opções.

Pesquisas futuras podem ser realizadas comparando-se diferentes períodos de dados, para observar se as estimativas obtidas são consistentes se comparadas com períodos de crises ou alta volatilidade no mercado. Além disso, estudos de price discovery envolvendo

outras ações do mercado brasileiro também podem ser interessantes, a ﬁm de veriﬁcar se existe algum comportamento padrão envolvendo esses mercados. De modo geral, a aplicação de análises para dados de alta frequência no mercado brasileiro ainda é pouco empregada, podendo ser amplamente explorada. Espera-se que este trabalho possa contribuir para a literatura de price discovery e estimule a realização de novos estudos envolvendo,

(40)

39

Referências

BAILLIE, R. T.; BOOTH, G. G.; TSE, Y.; ZABOTINA, T. Price discovery and common factor models. Journal of financial markets, Elsevier, v. 5, n. 3, p. 309–321, 2002.

BOOTH, G. G.; SO, R. W.; TSE, Y. Price discovery in the german equity index derivatives markets. Journal of Futures Markets, Wiley Online Library, v. 19, n. 6, p.

619–643, 1999.

BOYRIE, M. E. de; PAVLOVA, I.; PARHIZGARI, A. Price discovery in currency markets: Evidence from three emerging markets. International Journal of Economics and Finance,

v. 4, n. 12, p. p61, 2012.

CABRERA, J.; WANG, T.; YANG, J. Do futures lead price discovery in electronic foreign exchange markets? Journal of Futures Markets, Wiley Online Library, v. 29, n. 2,

p. 137–156, 2009.

CHAKRAVARTY, S.; GULEN, H.; MAYHEW, S. Informed trading in stock and option markets. The Journal of Finance, Wiley Online Library, v. 59, n. 3, p. 1235–1258, 2004.

CHU, Q. C.; HSIEH, W.-l. G.; TSE, Y. Price discovery on the s&p 500 index markets: An analysis of spot index, index futures, and spdrs. International Review of Financial Analysis, Elsevier, v. 8, n. 1, p. 21–34, 1999.

ENGLE, R. F.; GRANGER, C. W. Co-integration and error correction: representation, estimation, and testing. Econometrica: journal of the Econometric Society, JSTOR, p.

251–276, 1987.

FERNANDES, M.; SCHERRER, C. M. Price discovery in dual-class shares across multiple markets. 2013.

GONZALO, J.; GRANGER, C. Estimation of common long-memory components in cointegrated systems. Journal of Business & Economic Statistics, Taylor & Francis, v. 13,

n. 1, p. 27–35, 1995.

HAMILTON, J. D. Time series analysis. [S.l.]: Princeton university press Princeton, 1994.

HARRIS, F. H. deB; MCINISH, T. H.; WOOD, R. A. Security price adjustment across exchanges: an investigation of common factor components for dow stocks. Journal of Financial Markets, Elsevier, v. 5, n. 3, p. 277–308, 2002.

HASBROUCK, J. One security, many markets: Determining the contributions to price discovery. The journal of Finance, Wiley Online Library, v. 50, n. 4, p. 1175–1199, 1995.

HASBROUCK, J. Intraday price formation in us equity index markets. The Journal of Finance, Wiley Online Library, v. 58, n. 6, p. 2375–2400, 2003.

(41)

Referências 40

JOHANSEN, S. Estimation and hypothesis testing of cointegration vectors in gaussian vector autoregressive models. Econometrica: Journal of the Econometric Society, JSTOR,

p. 1551–1580, 1991.

JONG, F. D. Measures of contributions to price discovery: a comparison. Journal of Financial markets, Elsevier, v. 5, n. 3, p. 323–327, 2002.

MURAVYEV, D.; PEARSON, N. D.; BROUSSARD, J. P. Is there price discovery in equity options? Journal of Financial Economics, Elsevier, v. 107, n. 2, p. 259–283, 2013.

PATEL, V.; PUTNIN¸ Š, T. J.; MICHAYLUK, D. Price discovery in stock and options markets. Available at SSRN 2506712, 2014.

ROSENBERG, J. V.; TRAUB, L. G. Price discovery in the foreign currency futures and spot market. FRB of New York Staff Report, n. 262, 2006.

SANTOS, F. E. d. L. A.; GARCIA, M. G. P.; MEDEIROS, M. C. Price discovery no mercado de câmbio brasileiro: o preço é formado no mercado à vista ou futuro? Instituto de Pesquisa Econômica Aplicada (Ipea), 2014.

STOCK, J. H.; WATSON, M. W. Testing for common trends. Journal of the American statistical Association, Taylor & Francis, v. 83, n. 404, p. 1097–1107, 1988.