Aprendizagem de Eletromagnetismo via Programa~ao
e Computa~ao Simbolia
LearningEletromagnetismViaProgrammingandSymboliComputation
D. T. Alves
, J. V. Amaral y
, J.F. MedeirosNeto z
UniversidadeFederaldoPara,
Departamentode Fsia,Rua AugustoCorr^ea,1
66075-110, CaixaPostal479,Belem,PA,Brasil
E. S. Cheb-Terrab x
Centre forExperimentalandConstrutiveMathematis
DepartmentofMathematis andStatistis,SimonFraserUniversity
BurnabyMountainCampus,Burnaby,BCCanadaV5A1S6
eUniversidadedo EstadodoRiode Janeiro, InstitutodeFsia,
Rua S~aoFranisoXavier, 524,20550-013Riode Janeiro, RJ,Brasil
Reebidoem20deabril,2002. Aeitoem26dejunho,2002.
Relatamosaexperi^eniadeutilizarprograma~aoemMapleomoferramentade aprendizagemdo
estudantenumursobasiodeteoriaeletromagnetia. Areditamosqueesterelatopossaserutil a
quemdesejarutilizaroomputadoromoinstrumentopedagogionoensinodeFsia.
We desribe anexperieneinusing programming inMaple asa student'stool for thelearning of
introdutoryeletromagneti theory. Webelievethatthispaperanbeofuseforthoseinterested
inusingomputersasapedagogialtool.
I Introdu~ao
Denomina-se omputa~ao algebria (CA) a
mani-pula~ao de smbolos matematios - feita no
omputa-dor-deaordoomasregrasabstratasdamatematia
simbolia. Entre os mais onheidos softwares que
permitem este tipo de manipula~ao est~ao oMaple 1
e
o Mathematia 2
. Nestes sistemas de CA
enontram-se implementadas, por exemplo, regras de algebra,
trigonometria e alulo, de modo que pesquisadores
e estudantes podem derivar, integrar, obter a solu~ao
de equa~oes difereniais, simpliar express~oes,
repre-sentar graamente ampos esalares, vetoriais e
ur-vas parametrias. Alem dos omandos usuais, esses
sistemas de CA permitem um fail e rapido
desen-volvimento de programas matematios, atraves de um
repertorio vasto de fun~oese opera~oes. Poressas
a-raterstias,autiliza~aodaCAtemseintensiadoa
ada dia, assumindo um papel ada vez mais
impor-tantetanto napesquisaquantonaedua~ao[1-9℄.
Pesquisadorese estudantes podem utilizar um
sis-tema de CA basiamente de duas formas: usando os
omandosquejaseenontramdisponveisnosistema,
ouonstruindo(programando)aspropriasferramentas
ou sequ^enia de opera~oes matematias que julguem
neessarias.
Empesquisa podemosusarosomandos e fun~oes
ja implementados na resolu~ao de problemas difeis
de serem resolvidos sem o auxlio da omputa~ao
algebria. Caso neessitemos de ferramentas que n~ao
estejamdisponveis,podemosprogramarnovos
oman-dos, tomando omo base os omandos e fun~oes ja
daniloufpa.br
y
jairamaralyahoo.om.br
z
jfmnufpa.br
x
eterrabem.sfu.a
1
http://www.maplesoft.om
implementados, uma vez que eles est~ao aessveis ao
usuarionumsistemadeCAtpio,omooMaple. Esta
possibilidadededesenvolverprogramasapartirdosja
existentes e uma pratia usual e que failita
enorme-menteaprograma~aoemCA.
Por outro lado, no proesso de aprendizagem, o
aluno pode usaros omandos e fun~oes ja
implemen-tados, por exemplo, ao explorar a solu~ao de uma
dadaequa~ao,alterandoseuspar^ametroseobtendo
as-simnovas solu~oes. Dessa forma, epossvel examinar
um grande numero de exemplos em urto espao de
tempo. Emadi~ao,muitosdosgraospodem ser
ani-mados, sendoaanima~ao uma ferramenta pedagogia
poderosa, n~ao disponvelnos livros-texto e de grande
valia na ilustra~ao de proessosdin^amios. Esse tipo
deutiliza~aodaCAemedua~aoehojeemdiaomum
[6,7℄. Ousodaprograma~aoemCAomoinstrumento
de aprendizagem, entretanto,ebemmenosdifundido.
Neste trabalho,desrevemosnossa experi^eniaom
ousodosomandosdeMapleebasiamentedasua
lin-guagem de programa~ao omo instrumentos de
apren-dizagem em um urso de introdu~ao a teoria
eletro-magnetia. Tendo emvista estaaprendizagem,
enten-demosqueaprograma~aodeveserfeitapeloaluno(que
atuariaomoagentedeonstru~aodeseuproprio
on-heimento), e n~ao pelo professor. Diferentemente do
pesquisador, que programa objetivando onstruir
fer-ramentasn~ao disponveisnossistemas deCA, oaluno
programavisandoaprender,onstruindooproprio
o-nheimento.
EsteusodaCA gerouum ambiente extremamente
positivodeaprendizado,explorandoaexpress~aode
on-eitosabstratoseasequ^eniaalgortmiadepassosna
resolu~ao de problemas atraves da linguagem de
pro-grama~ao do sistema Maple. Como as linguagens de
omputa~ao s~ao preisas e n~ao ambguas, de aordo
omValente [4℄ oaluno que representa aresolu~ao de
umproblemasegundoumprogramadeomputador,tem
uma desri~ao formal e preisa dessa resolu~ao,
apu-randoseuentendimentosobreaestruturalogiadetoda
uma lasse de problemas semelhantes ao que ele esta
tratando.
Mais ainda, orientar o aluno a se onentrar na
sequ^enia logia que leva a solu~ao de um problema
-apontodeserapazderiarprogramasquesimulem
talsequ^enia-semterquedesviaraaten~aoomevitar
os\errosdeontas",aelerounotavelmenteotempode
matura~ao dosoneitos. As teniasdeprograma~ao
tambem trazem, de um modo geral, um divertimento
onretoparaalunosqueoptaramporareasdei^enias
exatas e tenologias, resultando num inentivo
adi-ional aoproessodeaprendizado. Finalmente,a
pos-sibilidade de experimentar osprogramasfeitos em
di-versos problemas, seguida da orre~ao eajuste desses
programas,ajudouonretamenteaidentiar os
pon-tosn~aoentendidosdateoria. Osuessodeadaajuste
resultou num estmulo onreto e tangvel para ada
passoafrentedadopeloalunonainorpora~aodonovo
onheimento.
Durante o urso implementamos, via CA, varios
programas,dentreosquaisvariossugeridosemedi~oes
modernas de livros destinados ao urso de Fsia de
gradua~ao. Porexemplo, podemos itar o tradiional
Fsia, de Resnik, Hallidaye Krane [10℄, que trazao
nal dos aptulos uma olet^anea de problemas para
seremresolvidosviaprograma~ao 3
.
Quanto a estruturado urso,as aulas para alunos
degradua~aoemQumiaeEngenhariaCivildaUFPA
foramministradasdaformausual,via\quadronegro",
mas om os alunos dispondo de omputadores (tr^es
alunos poromputador, em media), equipados om o
sistema Maple. Os alunos tinham aesso failitado
aos omputadores fora do horario de aula, enquanto
que, durante o tempo de aula, uma parte importante
transorreuomosalunostrabalhandoefetivamenteno
omputador,omoprofessorassistindoosdiversos
gru-pos.
Finalmente,aberessaltarqueaapresenta~aodeste
trabalho n~ao tem por objetivo veriar, em termos
estatstios, a ei^enia pedagogia do uso da
pro-grama~ao via omputa~ao algebria omo ferramenta
de aprendizagem. Isso so poderia ser obtido atraves
darepeti~aodaexperi^eniaomvariasoutrasturmas.
Onossoobjetivoonsisteemmotivaraaplia~aodesta
tenia a quem tiver interesseno uso do omputador
emedua~ao.
Orestantedesteartigoestaorganizadoomosegue.
Nase~aoII,relatamosaexperi^eniaemtrabalharom
alunosque,aoiniodourso,n~aotinhamtidoqualquer
ontatoomumsistemadeCA.Nase~aoIII,damos
al-guns exemplosdametodologiausadadurante ourso.
Nase~aoIV,expomosde maneiraresumidaospontos
queahamosmaisimportantesdestaexperi^enia.
II Primeiras aulas: omandos
basios e no~oes de
pro-grama~ao
Consideremosumprofessorquedaraaulasparauma
turma de gradua~ao, ujos alunos n~ao tenham tido
qualquerontatoprevioomCA. Ele poderia
tar,nessasondi~oes,qualaviabilidadedeonduzirum
ursobaseadoemomputa~aoalgebria.
Trabalhando omalunosdegradua~ao,totalizando
43 alunos - 29 do urso de Engenharia Civil e 14 do
urso deBahareladoem Qumia,divididosem3
tur-masomerade14alunosemadauma-observamos
que apenas uma aulafoi suiente paraque osalunos
adquirissem erta familiaridade om a sintaxe basia
doMapleeomeassemafazeralulosporsiproprios,
tornando-se aptos a ja utilizar o omputador no
pro-essodeaprendizagem.
Oproedimentoadotadonessaprimeiraaulafoiode
oloaroalunoemontatoomalgunsdosomandose
regrasbasiasdasintaxedoMaple,mostrandotambem
omofazeraluloselementares,usarvariasdasfun~oes
ja implementadas, omo as fun~oes trigonometrias,
os operadores de deriva~ao, integra~ao, et. Tambem
mostramos omo realizar graos em duas e tr^es
di-mens~oes (vide Figs. 1e 7). Ao nal da aula,
sugeri-mos aosalunosveriaromoepossvelexpandir esse
onheimentoatravesdaop~aoHelp,ofereidapelo
sis-tema. Oprofessorpode guiarosalunosnesse primeiro
ontato om o Maple, tomando tambem omo base
as se~oes-guiaparanovosusuarios(New User'sTour),
disponveisnoHelp.
Aposumprimeiroontatoomosomandosea
sin-taxe basia, mostramosao aluno,numa segundaaula,
omoelepodeonstruirferramentasporsiproprio,
uti-lizando a linguagem de programa~ao do sistema. Ao
nal da aula sugerimos varios exerios relaionados
omaonstru~aodepequenosprogramas.
Foram,portanto,neessarias2aulas(2horasada)
para que os alunos adquirissem erta familiaridade
mnimaomosomandosbasiosdoMapleeno~oesde
programa~ao.
Eimportanteressaltarquetaisno~oesja
permitemaoalunorealizaralulos,experimentos
om-putaionais e pequenos programas, uteis no proesso
de aprendizagem. Novasferramentasetenias foram
sendo gradativamente introduzidas durante o urso,
onformeaneessidade.
Oonteudoministrado foiousual, enontradonos
livrossobreoassunto,porexemplo[10,11,12℄. Alguns
exemplos, entretanto, foram extrados de livros mais
avanadosomo,porexemplo,[13℄.
III Aplia~oes a aprendizagem
de eletromagnetismo
Nesta se~ao, expomos varias aplia~oes de
pro-grama~ao via CA na aprendizagem de oneitos
rela-ionadosom a teoriaeletromagnetia, iniiando om
os oneitos de ampos esalares e vetoriais. Numa
primeiraetapadesseproessodeaprendizagem,o
estu-danteeapresentadoasdeni~oesdeampoesalare
ve-torial. Asaber,umampoesalarrealeumafun~ao
que mapeia ada ponto ~r doespao lR 3
num numero
(~r)2lR. Umampovetorialreal~veumafun~aoque
mapeia ada ponto ~r do espao numvetor~v(~r), ujas
omponentes s~aofun~oesreais de~r. Logono iniode
umursobasiodeeletromagnetismo,oalunosedepara
omessesdoistiposdeampo,tantooesalar,atraves
do potenial eletrio V, quanto ovetorial, atravesdo
ampo eletrio ~
E. Numa segunda etapa do proesso,
taisoneitos,aindan~aoamadureidos,podemser
ma-terializados na implementa~ao de uma serie de
exem-plosde tais fun~oes matematias, dispostas em forma
de rotinas omputaionais. Por exemplo, podemos
pedir ao aluno que implemente omputaionalmente
as seguintes fun~oes: (x;y;z) = 1= p
x 2
+y 2
+z 2
,
~v
1
(x;y)=x ^
i+y ^
j,~v
2
(x;y)=y ^
i+x ^
j,~v
3
(x;y)=y ^
i x ^
j
e~v
4
(x;y)=(sen (x)+1) ^
j, queresultam nasseguintes
rotinas:
> phi := (x,y,z)->1/sqrt(x^2+y^2+z^2);
> v1 := (x,y,z)->[x,y,0℄;
> v2 := (x,y,z)->[y,x,0℄;
> v3 := (x,y,z)->[y,-x,0℄;
> v4 := (x,y,z)->[0,sin(x)+1,0℄;
Durante a elabora~ao de tais rotinas, o aluno
amaduree os oneitos de ampo esalar e vetorial,
perebendo que o input das fun~oes , ~v
1 , ~v
2 , ~v
3 e
~v
4
e do mesmo tipo, a saber uma sequ^enia de tr^es
numeros reais x;y;z. Quanto aos outputs, osdo
ope-rador s~aoobjetos tipof(x;y;z), portanto esalares,
enquantoosdosoperadores~v
1 ,~v
2 e~v
3 e~v
4
s~aoobjetos
tipo [f
1
(x;y;z);f
2
(x;y;z);f
3
(x;y;z)℄ 4
, logo vetoriais.
Numatereiraetapa,taisrotinaspodemserusadas,por
exemplo,noaprendizadodo meanismode onstru~ao
degraosdeamposvetoriais. Numprimeiroinstante,
expliamosoneitualmenteomodesenhargraos
as-soiadosaamposvetoriais: paraadaampo,deve-se
esolherumonjunto depontos e,emada ponto,
de-senharovetorassoiado,deaordoomafun~aodada.
Emseguida,pedimosaosalunosque,usandolapise
pa-pel,semqualquerauxliodoomputador,onstruamos
graosparavariosamposvetorias,dentreeles~v
1 ,~v
2 ,
~v
3 e~v
4
,gerandograosrudimentaresparaosreferidos
ampos. Expliamosque,numproedimento
semelhan-te,soquemaiseiente,oomputadorgeraumgrande
onjuntodepontos 5
ealulaovetorassoiadoaada
ponto. Fazendousodasfun~oes(rotinas)~v
1 ,~v
2 ,~v
3 e~v
4
queelespropriosimplementaramomputaionalmente,
podem agora, usando o omando \eldplot" gerar os
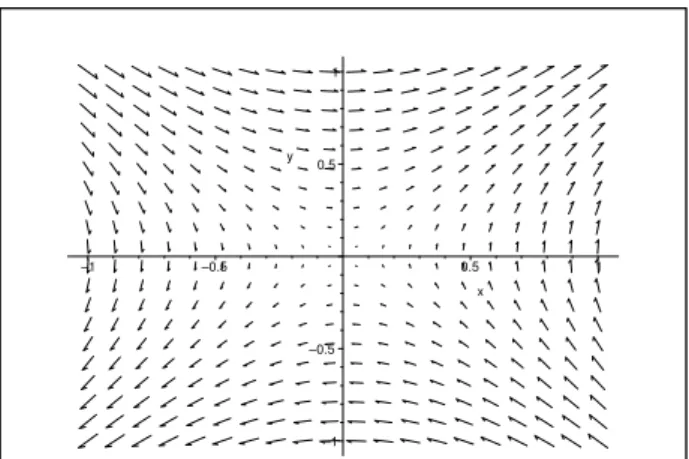
graosbidimensionaismostradosnasFigs. 1,2,3e4:
> fieldplot([v1(x,y,z)[1℄,v1(x,y,z)[2℄℄,x=-1..1,y=-1..1);
> fieldplot([v2(x,y,z)[1℄,v2(x,y,z)[2℄℄,x=-1..1,y=-1..1);
> fieldplot([v3(x,y,z)[1℄,v3(x,y,z)[2℄℄,x=-1..1,y=-1..1);
> fieldplot([v4(x,y,z)[1℄,v4(x,y,z)[2℄℄,x=-1..1,y=-1..1);
d
A proximaetapa doaprendizado onsiste na
om-para~aodosgraosonstrudosomlapisepapel,aos
obtidosviaomputador,resultandonoaperfeioamento
daapaidadedoalunoemdesenharoumesmousara
imagina~aoparavisualizargraosdeamposvetoriais.
Menionaremos agora oproessode aprendizagem
relaionado om as aplia~oes do operador diferenial
~
r. Os oneitos de gradiente, divergente erotaional
frequentemente onfundem os alunos, pois misturam
opera~oesvetoriaisedifereniais. Oproessode
apren-dizagemdautiliza~aoedosigniadofsio-matematio
da atua~ao detal operador pode ser feitoatravesdas
seguintesetapas. Numaprimeiraetapa,asequ^eniade
opera~oes matematiasligadas omaatua~ao do
gra-diente,dodivergenteedorotaionaleexposta,usando,
porsimpliidade,oordenadasartesianas:
~
rf = f
x ^
i+ f
y ^
j+ f
z ^
k; (1)
~
r~v = v
x
x +
v
y
y +
v
z
z
; (2)
~
r~v =
v
z
y v
y
z
^
i+
v
x
z v
z
x
^
j+
v
y
x v
x
y
^
k: (3)
d
Numa segunda etapa, a m de xar as opera~oes
aimadesritas,oalunopodeorganizaros
proedimen-tos matematios em rotinas omputaionais,
onstru-indo rotinas simples, que gerem o gradiente de uma
fun~aoesalar,assimomo odivergentee orotaional
de uma fun~ao vetorial (todos, por simpliidade, em
oordenadas artesianas). Tais omandos,
denomina-dos\grad",\div"e\rot",podemseronstrudosomo
segue 6
:
> grad := f -> [diff(f,x),diff(f,y), diff(f,z)℄;
> div := v -> diff(v[1℄, x) + diff(v[2℄, y) + diff(v[3℄, z);
> rot := v -> [diff(v[3℄, y) - diff(v[2℄, z),
diff(v[1℄, z) - diff(v[3℄, x),
diff(v[2℄, x) - diff(v[1℄, y)℄;
d
5
OspontosgeradospeloMaplenarealiza~aodeumdadograo,podemservisualizados,sendotalvisualiza~aointeressanteparao
aluno.
6
Ao realizar a tarefa, o aluno deve pereber que,
apesar de onstrudos a partir de um mesmo
ope-rador vetorial, os proedimentos atuam em fun~oes
distintas. O input do omando \grad" sera do tipo
f(x;y;z),enquantooinputdosomando\div"e\rot"
ser~ao fun~oes vetoriais, representadas no Maple por
[f
1
(x;y;z);f
2
(x;y;z);f
3
(x;y;z)℄. Tambemveriaque
osoutputsresultantesdaatua~aodoomando\div"s~ao
objetos tipof(x;y;z), enquanto \grad"e\rot" geram
objetos tipo [f
1
(x;y;z);f
2
(x;y;z);f
3
(x;y;z)℄. Numa
tereiraetapa,oalunotestaasrotinaselaboradas.
Es-olhe varios exemplos simples de ampos esalares e
vetoriais e alula sem o uso do omputador, o
gra-diente, o divergente e o rotaional, omparando em
seguida om os resultados geradospelas rotinas
om-putaionais. A seguirorrige,seneessario,asrotinas,
de modoaforneeremosresultadosorretos. Tal
pro-essoresultanaxa~aodosproedimentosmatematios
por parte do aluno. Numa etapa nal desse ilo de
aprendizagem,relaionadoomaxa~aodasopera~oes
matematias envolvidas, oaluno pode usaras rotinas
poreleonstrudas,ejatestadas,parainiiarumoutro
ilodeaprendizagem,porexemplo,busandoarela~ao
entreodivergenteeorotaionaldeumampovetorial
e oseu omportamento espaial. Neste sentido,
suge-rimos aos alunos a realiza~ao de graos para varios
amposvetoriaise,em seguida,queprourassem
rela-ionarodivergenteeorotaionaldessesampos,
toma-dos na origem (~r = ~
0), om o omportamento
espa-ialdos ampos proximos a esse ponto. Na tabela 1,
enontram-seresumidasalgumasdasobserva~oesfeitas
pelos alunos.
–1
–0.5
0.5
1
y
–1
–0.5
0.5
1
x
Figura1. Graoparaafun~aovetorial~v1(x;y)=x ^
i+y ^
j:
Campo Figura ( ~
r~v)( ~
0) ( ~
r~v)( ~
0 ) Observa~oesdosalunos
~ v
1
1 2
~
0 \todososvetoressaemdaorigem"
~ v
2
2 0
~
0 \vetoresentramesaemdaorigem"
~ v
3
3 0 -2
^
k \vetoresgiramemtornodaorigem"
~ v
4
4 0
^
k \vetoresadireita maioresdoqueaesquerda"
. . . . .
. . . . .
Tabela 1: Naprimeira oluna est~ao identiados varios ampos vetoriais ja denidos no texto. Na segunda oluna enontra-se a
numera~aoorrespondente asguraspresentes notexto. Nastereiraequarta olunasenontram-serespetivamente odivergente e
rotaionaldeadaampo,tomadosnaorigem.Naquintaolunaest~aoasobserva~oesfeitaspelosalunosaoanalisaremoomportamento
dosamposproximosaorigem.
Apos analisarem varios exemplos, os alunos
omeam a pereber que o ~
r ~v(~r) e uma medida
de quanto o ampo vetorial ~v se \espalha" (ou
di-verge)deumpontoemquest~ao[13℄. Demodoanalogo,
perebeque ~
r~v(~r)eumamedidadequantooampo
vetorial ~v \gira ao redor" de um ponto em quest~ao
[13℄. Em seguida, inlumos na disuss~ao os ampos
em 3D 7
eapresentamosformalmente asinterpreta~oes
geometriasdodivergenteedorotaional,relaionadas
om ouxo eairuita~ao dosampos (vide, por
ex-emplo, [11, 12℄ ). Chamou nossa aten~ao o fato de
os alunos, atraves da experimenta~ao omputaional,
inturem previamente tais rela~oes, antes que elas
fos-semdisutidasformalmente.
–1
–0.5
0.5
1
y
–1
–0.5
0.5
1
x
Figura2. Graoparaafun~ao~v2(x;y)=y ^
i+x ^
j:
–1
–0.5
0.5
1
y
–1
–0.5
0.5
1
x
Figura3. Graoparaafun~ao~v
3
(x;y)=y ^
i+x ^
j:
–1
–0.5
0.5
1
y
–1
–0.5
0.5
1
x
Figura4. Graoparaafun~ao~v4(x;y)=(sen(x)+1) ^
j:
O ilo de aprendizagem do uso e do signiado
dos operadoresdivergente e rotaional, portanto,
pas-soupeloproessode \intui~ao"e\desoberta" do
sig-niadodessesoperadorespormeiodaexperimenta~ao
omputaional. O signiado fsio-matematio da
atua~ao de tais operadores nos ampos eletrio e
magnetio, o que resulta nas equa~oes de Maxwell, e
a proxima etapa do aprendizado. O aluno, ja om
boa perep~ao do signiado de tais operadores, tem
ondi~oes de entender que: (i) ~
r ~
E = =
0
sig-nia que a \medida de quanto o ampo eletrio
es-palha" (ou diverge) de um ponto dado, e dada pela
densidadedearga naqueleponto; (ii)odivergentedo
ampomagnetioserigualazero,emqualquerposi~ao
eem qualquerinstante,india aaus^eniana natureza
da arga magnetia, ou do monopolo magnetio; (iii)
~
r ~
E= ( ~
B=t)signiaquea\medidadequanto
oampoeletriogira"aoredordeumpontoedadapela
varia~aodoampomagnetioomotemponesseponto;
(iv) de modo analogo ~
r ~
B =
0 ~
J +
0
0 (
~
E=t)
signiaque\amedida dequanto oampomagnetio
epelavaria~aodoampoeletrioomotemponaquele
ponto.
Comointuito de estimularosalunos n~ao somente
a hegar num resultado, mas a explorar o resultado
obtido, interpretando-o e veriando suas implia~oes
fsias,sugerimosque,aposaresolu~aodevarios
ios, eles explorassem seus resultados, utilizando as
varias ferramentas existentes no Maple. Para ilustrar
algunsdesses exerios,soliitamosque osalunos
al-ulassem o potenial eletrioV e o ampo eletrio ~
E
gerados por uma esfera isolante de raio R = 1, om
entronaorigemeuniformementearregadaom
den-sidade de arga = 1. Considerando-se V(1) = 0 e
usando-seosistemagaussianodeunidades(4"
0 =1),
obtem-se,em oordenadasesferias:
V(~r) = 8
<
: 2
3 r
2
+2; se r<1
4
3r
; se r1
(4)
~
E(~r) = 8
<
: 4
3
~r; se r<1
4
3 ^ r
r 2
; se r1
(5)
Em seguida, soliitamos que programassem uma
fun~ao esalar que representasse o potenial e outra
fun~ao vetorial que representasseo ampo eletrio do
modeloemquest~ao,emoordenadasartesianas. Como
resultado,obtivemos:
> V := (x,y,z) ->
if evalf(sqrt(x^2 + y^2 + z^2)) < 1 then
-2/3*Pi*(x^2 + y^2 + z^2) + 2*Pi
else
(4*Pi)/3*(1/sqrt(x^2 + y^2 + z^2))
fi;
> E := (x,y,z) ->
if evalf(sqrt(x^2 + y^2 + z^2)) < 1 then
[4*Pi/3*x, 4*Pi/3*y, 4*Pi/3*z℄
else
[4*Pi/3*x/(x^2 + y^2 + z^2)^(3/2),
4*Pi/3*y/(x^2 + y^2 + z^2)^(3/2),
4*Pi/3*z/(x^2 + y^2 + z^2)^(3/2)℄
fi;
Nosproedimentosaima,osmapeamentosVeElevam
tr^esnumerosouvariaveissimboliasdadas-
representa-dosporx,y,z-novalordoamporespetivo.
Ressalta-mosparaosalunosanaturezadiferentedosresultados
detaismapeamentos. Noasodoprograma\V",o
re-sultadoeumesalar,enquantoqueoresultadode\E"
vememformadeumobjetoomestruturadotipo\[,
, ℄",portanto, umvetor. Comtais programasoaluno
pode ter instantaneamente o potenial e oampo em
qualquerpontodoespao,oquepermiteaele,por
ex-emplo, tentar responder, iniialmente sem o
omputa-dor, perguntas sobre oomportamentodesses ampos
num dado ponto, e logo em seguida veriar sua
re-spostaomoprogramafeitoporele.
Usandoarela~ao r= p
x 2
+y 2
+z 2
, podemos
> V1 := r -> if evalf(r) < 1 then -2/3*Pi*(r^2) + 2*Pi else 4/3*Pi*1/r fi;
> E1 := r-> if evalf(r) < 1 then 4/3*Pi*r else 4/3*Pi/r^2 fi
d
As rotinas V1 e E1 reebem omo entrada um
numero n~ao-negativo r (oordenada radial), gerando,
respetivamente, osvalores do potenial e do modulo
doampoeletrioparaadist^aniadada.
Pedimos aos alunos que, usando lapis e papel,
esboassemosgraosdetaisfun~oes,omparando-os,
em seguida,omosobtidosusandooomando plotdo
Maple (Figs. 5 e 6). O aluno pode ainda fazer, por
exemplo,z=0egerarograodeV(x;y;0),usandoo
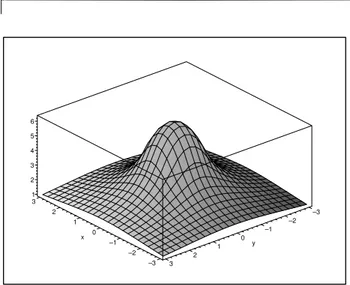
omando plot3d(verFig. 7).
1
2
3
4
5
6
0
2
4
6
8
10
r
Figura 5. Graopara opotenialV (eixovertial)omo
fun~ao de r, gerado por uma esfera uniformemente
ar-regadaderaioR=1.
0
1
2
3
4
2
4
6
8
10
r
Figura 6. Graopara omodulodoampo ~
E (eixo
verti-al)omofun~aoder,geradoporumaesferauniformemente
–3
–2
–1
0
1
2
3
x
–3
–2
–1
0
1
2
3
y
1
2
3
4
5
6
Figura 7. Grao para a fun~ao V(x;y;0) para uma
es-ferauniformementearregadaderaioR=1,omentrona
origem. Talgrao,numase~aodeMaple,podesergirado,
permitindoavisualiza~aodaguraporvarios^angulos.
Seguindooursoomessalinhadetrabalho,varios
outros topios foram abordados, inluindo ampos e
poteniais magnetios, hegando ate as equa~oes de
Maxwell. Dando sequ^enia a este trabalho,
onside-ramos o seguinte exerio, inspirado em um
proble-ma sugerido na refer^enia [10℄: partindo dos ampos
~
E = E
m
(sen!t)(senkx) ^
j, ~
B = B
m
(os!t)(oskx) ^
k,
pede-se (a) mostrar que estes satisfazem as eqs. de
MaxwellseE
m
estiverrelaionadoomB
m
demaneira
apropriada e ! estiver relaionada om k tambem de
maneira onveniente e determinar estas rela~oes; (b)
alularovalorinstant^aneodovetordePoynting.
Comeemospelo item (b), porsero mais simples.
Umarotinasimplesparadeterminarovetorde
Poynt-ingedadaabaixo:
> poy := (E,B) -> (1/mu[0℄)*
[ E[2℄*B[3℄ - E[3℄*B[2℄,
E[3℄*B[1℄ - E[1℄*B[3℄,
E[1℄*B[2℄ - E[2℄*B[1℄ ℄;
Aentradadedadosdarotinaaimadeveseresrita
naforma de um parde vetores,sendo queo primeiro
delesdeverepresentar oampoeletrio. Como
exem-plode utiliza~ao darotina aima, determinemoso
ve-tordePoyntingassoiadoaosampos ~
Ee ~
B propostos.
Denindoiniialmente,noMaple,osampos:
determinamosent~aoovetordePoyntingassoiado:
> poy(E,B);
(1=
0
)[Emsin(kx)sin (!t)Bmos(kx)os(!t); 0; 0℄
Resultousurpreendenteparaosalunosnotarqueum
proedimento destetipopodeserusadopara
determi-narovetordePoyntingassoiadoaqualqueronjunto
( ~
E; ~
B), bastandoparaissomudarapenasaforma
fun-ionalnadeni~aodosampossemterquesedeterna
veria~aodeerrosdeontausuaisaos^omputosfeitos
omanetaepapel. Comomenionadonaintrodu~ao,
issopermitiu ao alunoseonentrarnos oneitos
en-volvidos, deixando o momento de pratiar \ontas a
m~ao" apenas para veriar - em algum momento do
proesso-queoprogramafeitofunionaorretamente.
Oitem(a)podeserresolvidousando-seumarotina
quetesteos amposeletrio ~
E emagnetio ~
B, as
den-sidadesde argaeorrente ~
j dadas,veriando seo
onjuntodestasvariaveiseoun~aosolu~aodasequa~oes
deMaxwell. Arotinaqueexeutataltarefausaos
pro-gramas feitospelos alunos\rot" e\div", usados
ante-riormente,eseesreveemtermosdestesomo:
> maxwell := (E, B, rho, j) ->
if simplify(expand(div(expand(E)) - rho/epsilon[0℄)) = 0
and simplify(div(expand(B))) = 0
and simplify(expand(rot(expand(E)) + diff(expand(B), t))) = [0,0,0℄
and simplify(expand(diff(expand(mu[0℄*epsilon[0℄*E), t) +
expand(mu[0℄*j)-expand(rot(expand(B))))) = [0,0,0℄
then
return "O onjunto dado e soluao das equaoes de Maxwell"
else
return "O onjunto dado NAO e soluao das equaoes de Maxwell"
fi;
d
Narotinaaima, aentradadedadosdeveserfeita
na seguinte sequ^enia: primeiro oampoeletrio,
de-poisomagnetio,aseguiradensidadede argae,por
ultimo, a densidade de orrente. Uma das limita~oes
da rotina aima oorre quando se trabalha om
am-pos gerados por distribui~oes disretasde argas, por
exemplo o ampo de uma arga pontual q loalizada
naorigem: =qÆ(~r). Arotina trabalha deforma
er-rada om distribui~oes deste tipo, sendo tal limita~ao
originadaem suasimpliidade. OsoftwareMaple
per-mite aonstru~ao de rotinasmais omplexas, apazes
detrabalharomexpress~oesdeamposedistribui~oes
deargabem maisompliadas.
Foiinstrutivoressaltarparaosalunosomoa
ons-tru~ao previa dos omandos div e rot tinham agora
usos multiplos, e permitiam expressar as equa~oes de
Maxwell\dentrodeumprograma",demaneiraid^entia
aquelas obtidas om o uso de lapis e papel. O aluno
podeaseguirveriarqueoonjunto ~
E, ~
Bproposto
ini-ialmentenolivro(om=0, ~
j= ~
0eEm,Bm,!,k
ar-bitrarios)n~aoesolu~aodasequa~oesdeMaxwell. Para
istobastouintroduzirnoMapleasorrespondentes
ex-press~oesdos ampos eletrioemagnetio edas
densi-dadesdeargaeorrente:
> E := [0, Em*sin(k*x)*sin(omega*t), 0℄:
> B := [0, 0, Bm*os(k*x)*os(omega*t)℄:
> rho := 0:
Usandooomando\maxwell",obtemos:
> maxwell(E, B, rho, j);
Oonjuntodado N ~
AOesolu~aodas equa~oesde Maxwell
A seguir, sugerimos veriar que, esolhendo as
onstantesEm,Bm, ! ekadequadamente,por
exem-plo: E
m =a=
p
0
0 ; B
m
=a; !=k= p
0
0
,ondeae
umaonstantearbitraria,asnovasfun~oess~aosolu~oes
aeitaveis:
> Em := a/sqrt(mu[0℄*epsilon[0℄):
> Bm := a:
> omega := k/sqrt(mu[0℄*epsilon[0℄):
> maxwell(E, B, rho, j);
Oonjunto dadoe solu~ao dasequa~oesde Maxwell
A ideia motivadora para esta experi^enia
omputa-ional tambem foi que os alunos pudessem onstatar
que os programas onstrudos para resolver problemas
espeos podem tambem ser usados para soluionar,
x
z
y
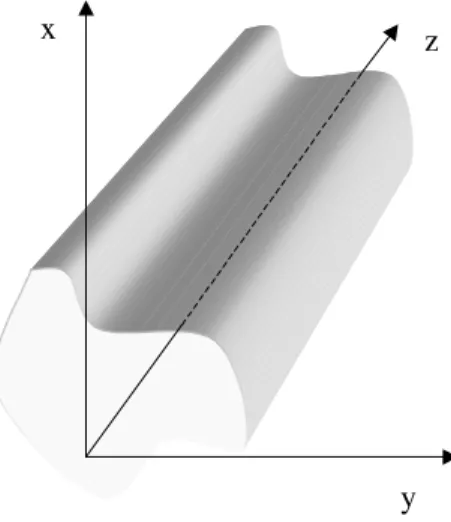
Figura8. Guiadeondas.
Vejamos,agora,umexemplomaisomplexo: ondas
eletromagnetiasonnadas nointeriorde umguiade
ondas,onsideradoomoumondutorperfeito(Fig. 8).
As ondi~oes deontornona paredeinterna s~aodadas
por: ~ E jj = ~ 0; B ?
=0: (6)
Conentrando o foo em ondas monoromatias,
propagando-seaolongo dotubo, temosque asformas
generiasde ~
E e ~
B s~aodadaspor[13℄:
~
E(t;x;y;z) = ~
E
0 (x;y)e
i(k z !t)
;
~
B(t;x;y;z) = ~
B
0 (x;y)e
i(k z !t)
;
(7)
onde a nota~ao omplexa foi introduzida, pela
van-tagem que ha em manipular exponeniais em
om-para~ao om senos e ossenos. Os vetores ~ E 0 e ~ B 0
podem ser esritos em termos de suas ompontentes
daseguinteforma:
~ E 0 =E x ^ x+E
y ^ y+E
z ^ z ~ B 0 =B x ^ x+B
y ^ y+B
z ^ z:
(8)
E possvel mostrarque asubstitui~ao de (8) em (7) e
estasnasequa~oesdeMaxwell,resultaemqueas
om-ponentesE x ,E y ,B x ,B y
podemseresritasemtermos
dasomponentesE
z eB
z
,daseguinte forma[13℄:
E x = i ! 2 0 0 k 2 k E z x +! B z y ; (9) E y = i ! 2 0 0 k 2 k E z y ! B z x ; (10) B x = i ! 2 0 0 k 2 k B z x ! 0 0 E z y ;(11) B y = i ! 2 0 0 k 2 k B z y +! 0 0 E z x ;(12)
sendo que as omponentes B
z e E
z
obedeem as
seguintesequa~oesdifereniais:
2 x 2 + 2 y 2 +! 2 0 0 k 2 B z
=0; (13)
2 x 2 + 2 y 2 +! 2 0 0 k 2 E z
=0; (14)
ujas solu~oes devem levar em onsidera~ao as
ondi~oesdeontornodadasem(6).
Eimportantelevar
oalunoaobservarqueaexist^eniadeomponentesde
ampo eletrioe magnetio ao longo da dire~ao z
re-vela queaondaquesepropaganoguia-de-onda n~aoe
transversal 8
. SeE
z
=0aondadenomina-se
transverso-eletria(TE);seB
z
=0,transverso-magnetia(TM).
Num primeiro momento, portanto, o aluno entra
em ontatoom essa sequ^enia logia de ideias a
res-peito do problema da propaga~ao de ondas
eletro-magnetias num guia-de-ondas. Num segundo
mo-mento,taisideias,aindan~aoamadureidas,assimomo
a sequ^enia de opera~oes matematias desritas nas
formulas(9), (10),(11)e(12), podem serorganizadas
peloalunoemrotinasomputaionais. Aelabora~aode
taisrotinaspermiteaoalunoxar,renareamadureer
osoneitos teoriosenvolvidos,assim omo melhorar
seuentendimentosobreasequ^eniadeopera~oesusadas
noproblema. Dessemodo,podemossoliitaraoaluno
que implemente um par de rotinas simples, tais que,
dadasasomponentesB
z eE
z
(solu~oesdasequa~oes
(13)e(14)),sejamgeradasautomatiamenteas
ompo-nentes restantesdosampos ~
E e ~
B. Taisrotinas,aqui
denominadas\guiaE"e\guiaB", esritasomo:
> guiaE := (X,Y) ->
[(I/((omega)^2*mu[0℄*epsilon[0℄-k^2))*(k*diff(X,x)+omega*diff(Y,y)),
(I/((omega)^2*mu[0℄*epsilon[0℄-k^2))*(k*diff(X,y)-omega*diff(Y,x)),X℄
*exp(I*(k*z-omega*t));
> guiaB := (X,Y) ->
[(I/((omega)^2*mu[0℄*epsilon[0℄-k^2))*(k*diff(Y,x)
-(omega)*mu[0℄*epsilon[0℄*diff(X,y)),
(I/((omega)^2*mu[0℄*epsilon[0℄-k^2))*(k*diff(Y,y)
+(omega)*mu[0℄*epsilon[0℄*diff(X,x)),Y℄
*exp(I*(k*z-omega*t));
d
permitem o alulo automatio, respetivamente, dos
ampos ~
E e ~
B dados em (7). A entrada das rotinas
onsiste das express~oes para E
z e B
z
, representadas,
respetivamente,porXeY.Asadadoprogramaeda
forma\[,,℄",representandoosvetores ~
Eou ~
B parao
modeloemquest~ao.
y
x
z
a
b
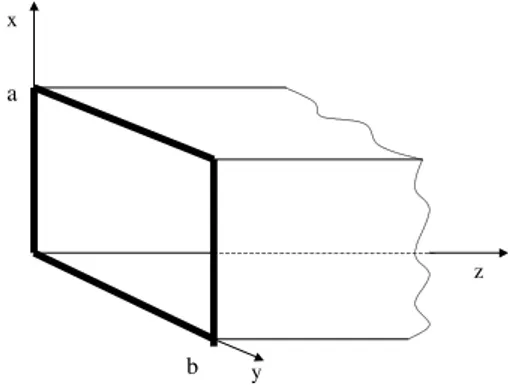
Figura9. Guiadeondasretangular.
Num tereiro momento do proesso de
aprendiza-gem sobre o guia-de-ondas, o aluno, apos elaborar as
rotinas \guiaE" e \guiaB", preisa testa-las e
orrigi-las,asoneessario. Paraissoelepodebusarsolu~oes
partiulares simples 9
dessas equa~oes e, em seguida
alular, usando o lapis e o papel, as omponentes
restantes dadas pelas formulas (9), (10), (11) e (12).
Emseguida,deveveriarseosresultadosobtidos
pe-losomandos \guiaE"e\guiaB" est~ao de aordoom
osresultadosqueele proprioalulou. Talproessode
testagemexigetreinodealulos,alemdexartambem
todaasequ^eniamatematiadoproblemaemquest~ao.
Atestagemnaldosomandos\guiaE"e\guiaB"passa
aindapelousodeoutroomandoonstrudopeloaluno,
oomando\maxwell",omoqualsepodeveriar se
o onjunto de ampos obtido satisfaz as equa~oes de
Maxwell. Desse modo espera-se que todo o onjunto
de ampos eletrio e magnetio gerado pelas rotinas
\guiaE"e\guiaB",ujas entradassejam amposE
z e
B
z
quesatisfaamaseqs. (13)e(14),sejatalque:
> maxwell(guiaE(Ez,Bz),guiaB(Ez,Bz),0,[0,0,0℄);
\O onjuntodadoesolu~aodasequa~oesdeMaxwell"
ouseja,satisfaaasequa~oesdeMaxwell. Numquarto
momento, fehando-seoiloiniial deaprendizagem,
osprogramasfeitosetestadospodemserviragorapara
satisfazer a uriosidade do aluno, de modo que ele
possa testar varias solu~oes para ampos eletrios e
magnetios em guias-de-onda, sem o desestmulo de
ter que realizarlongos alulos para testarada ideia.
Comoumexemplo,oalunopodetestartaisrotinaspara
oasodeondastransverso-eletriasnumguiadeondas
retangular, onformemostrado na Fig. 9. Neste aso
E
z
=0,eaeq. (13),resolvidaviametododesepara~ao
devariaveiselevando-se emonsidera~aoasondi~oes
deontornodadasem(6), resultaem[13℄
B
z =B
0 os
mx
a
os
ny
b
; (15)
onde m e n s~ao inteiros n~ao-negativos, e a seguinte
rela~aodeveserobedeida:
k= s
! 2
0
0
2
m 2
a 2
+ n
2
b 2
:
(16)
Usando-seasrotinas\guiaE"e\guiaB",pode-se
alu-lar,apartirdasomponentesE
z eB
z
,osampos ~
E e
~
B. Denimosiniialmente,noMaple, asomponentes
Ez eBz:
> Ez := 0:
> Bz := B[0℄*os((1/Pi*(-n^2*Pi^2+omega^2*mu[0℄*epsilon[0℄*b^2-k^2*b^2)^(1/2)
*a/b)*Pi*x/a)*os(n*Pi*y/b):
Usamosent~aoarotina\guiaE"parageraroampo ~
E ompleto:
> E := guiaE(Ez,Bz);
oquedara:
E:= "
i!B
0 os
mx
a
sin( ny
b )n
(! 2
0
0 k
2
)b
; i!B
0 msin
mx
a
os ny
b
(! 2
0
0 k
2
)b
; 0 #
e i(k z !t)
: (17)
Usandoarotina\guiaB"parageraroampo ~
B ompleto:
9
> B := guiaB(Ez,Bz);
resultando em:
B := "
ikB
0 msin
mx
a
os ny
b
(! 2
0
0 k
2
)b ;
ikB
0 os
mx
a
sin ny
b
n
(! 2
0
0 k
2
)b
;B
0 os
mx
a
os
ny
b
#
e i(k z !t)
: (18)
As ondi~oesdeontorno(6),que,espeiamentepara esteproblema,podemseresritasomo
E
y
(t;0;y;z)=E
y
(t;a;y;z)=E
x
(t;x;0;z)=E
x
(t;x;b;z)=0 (19)
B
x
(t;0;y;z)=B
x
(t;a;y;z)=B
y
(t;x;0;z)=B
y
(t;x;b;z)=0; (20)
podemserfailmenteveriadasfazendo-se:
> subs(x=0,E[2℄),subs(x=a,E[2℄),subs(y=0,E[1℄),subs(y=b,E[1℄),
subs(x=0,B[1℄),subs(x=a,B[1℄),subs(y=0,B[2℄),subs(y=b,B[2℄);
d
oqueresultaem:
0;0;0;0;0;0;0;0
Isso india que todas asondi~oes s~ao satisfeitas.
Fi-nalizando o proesso de testagem da solu~ao para o
ploblema do guia retangular, o aluno pode apliar o
omando \maxwell",por ele ontrudoem etapa
ante-riordourso,paraveriarqueoonjunto deampos
dadosem (17)e(18)satisfazasequa~oes deMaxwell.
Casoeleproedafazendo:
> maxwell(E,B,0,[0,0,0℄),
obtera:
\OonjuntodadoN ~
AOesolu~aodasequa~oesde
Maxwell"
Talresultadopode,aprinpio, ausarsurpresano
es-tudante. Entretantodeverapereberqueasexpress~oes
(17) e (18), para um k generio, de fato n~ao
satis-fazem as equa~oes de Maxwell. O aluno devera, em
sua testagem, levar em onsidera~ao a rela~ao (16) e
proederatestagemomosegue:
> zz := k =
sqrt(omega^2*epsilon[0℄*mu[0℄-pi^2*(m^2/a^2)+(n^2/b^2)):
> maxwell(subs(zz,E),subs(zz,B),0,[0,0,0℄);
obtendo:
\Oonjuntodadoesolu~aodasequa~oesdeMaxwell"
d
Dessa forma, o alunoteria ompletado atestagem
eaanalise deuma dasinumerassolu~oesrelaionadas
omguias-de-onda. Vale menionarnovamentequetal
proessode investiga~ao e o ultimo estagio de um
i-lo de aprendizado baseado no amadureimento e na
xa~ao de oneitos atravesda onstru~ao de rotinas
omputaionais.
IV Comentarios nais
grama~ao - omo ferramenta auxiliar na
aprendiza-gem,oalunoebeneiado pelofato deossistemas de
CA possurem uma vasta bibliotea de omandos
im-plementados(deriva~ao, integra~ao, et...), o que
per-miteaeleonentrar-semaisdiretamentenosoneitos
teoriosutilizados. Porexemplo,quandooaluno
ons-troiumprogramaquegeraogradientedeumafun~ao,
elepreoupa-seapenasomadeni~aodegradienteem
termosdaatua~aode derivadas(aspetoteoriamente
relevante),emvezdeterquepreoupar-seomterque
programaraopera~aodederiva~aoemsimesmaouom
usualdeaprendizagemdemaneirapartiularmente
in-teressante. Num primeiro momento, os oneitos s~ao
enuniados e veriados, podendo-se ja fazer uso dos
reursosdisponveisnossistemasdeCA, taisomo
re-ursosgraoseaapaidadedefazerontassimbolias
utilizandoregrasmatematiasabstratas.
Num segundo momento, os oneitos - ainda n~ao
amadureidos - s~ao organizadosem sequ^enias logias
deopera~oes matematias, eorganizadosemformade
rotinas omputaionais, num sistema de CA. Essa
se-gundapartepermiterenar,xar,eateestenderesses
oneitosalemdoslimitesomqueforamapresentados.
Exerita,ainda,outroaspetofundamentaldoproesso
deaprendizagem: odomnioompletodarepresenta~ao
abstratado problema,semoqualeimpossvel
organi-zarosoneitosemrotinasomputaionais.
Entre os estudantes de i^enias exatas e
te-nologias,estaatividadede\programa~ao"tambem
in-lui tipiamente um divertimento e induz a intera~ao
entre alunos, uma vez que a atividade se faz em
pe-quenos grupos. O ingrediente humano adiiona um
aspeto subjetivo positivo e importante a atividade.
Alem disso, oaspetode olabora~ao,t~ao util na
ar-reira ienta, passa a ser um fator importante para
o suesso do grupo, durante as atividades de
pro-grama~ao.
Numtereiromomento,ogrupotestaosprogramas
elaborados,aumentando aompreens~ao dosoneitos,
xandoasideiaseveriandoaneessidadedeorre~ao
dos programas, omparando, nos asos mais simples,
alulosfeitossem ousodoomputador omosfeitos
pelasrotinasimplementadas.
O ilo se feha num quarto momento, quando os
programasfeitosetestados(motivodeorgulhoe
auto-inentivo para os alunos-autores) s~ao repentinamente
perebidos omo potentes ferramentas para satisfazer
auriosidade(investiga~ao)emrela~aoaostemas
rela-ionados. Assim,oalunotemagoraaoportunidadede
imaginarvaria~oes,pratiasouteorias,de topios
es-tudados, sem odesestmulo da perspetivade ter que
realizar \longas ontas passveis de erro" para ada
ideia. O que observamos foi que varios alunos
par-tiram para a experimenta~ao de onjeturas riativas
epossveisderiva~oesteoriasdosoneitos ensinados,
muitas vezes resultando em novasideias, que por sua
vezs~aotambemprogramaveis,reomeandoassimo
i-lo.
Um detalhe adiional - n~ao menos importante
-desteilodeaprendizagemonsistenaveloidadeom
queosalunoss~aoapazesdetestarsuaspropriasideias,
uma vez queoprograma para analisa-las foi feitopor
eles mesmos. A resposta dos programas vem - em
tempo real - quase instantaneamente. Isso permite
onentrar,num lapsopequeno detempo,umnumero
grandederespostas,tratandodiversosaspetosdeum
mesmotema, omoingrediente emoional positivode
Notamosqueestaaumula~aorapidaderesultados
fa-ilitanotoriamenteodesenvolvimentoda\intui~ao"dos
alunosemrela~aoaosassuntosestudados. Este
desen-volvimentorapidodaintui~aonospareeun~aousualse
omparado omo oque oorreem mediaem ilos de
aprendizagemquen~aoinluemaprograma~aodos
on-eitosensinados. Tambemnospareeuaimadamedia
o interesse pelo onteudo da disiplina, assim omo a
preis~aonousodalinguagemmatematia.
Baseadonaexperi^eniaquerelatamos,areditamos
queousodeprograma~aoviaomputa~aosimboliae
umaferramentadegrandevalianosproessosde
apren-dizagem.
Agradeimentos
Os autores agradeem aos professores Jesse
Car-valho Costa, Benedito Ferreira e Manoel Reinaldo
Filho, daUFPA, pelas refer^eniasforneidas.
Agrade-em,espeialmente,aoprofessorLusCrispino(UFPA)
pela leitura rtia deste texto e pelas valiosas
dis-uss~oes sobre o tema. Finalmente, a um
agradei-mento a todos os alunos que partiiparam desta
ex-peri^enia.
Refer^enias
[1℄ M. Lang-Lazi, I. Diospatonyi, D. Petz, Z. Vizian e
G.Fetter,Computerandmultimediainhemial
engi-neering eduation, Comp.Chem. Eng. 23, S637-S640
(1999);
[2℄ B.Amrhein,O.Gloor eR.E. Maeder,Visualizations
for mathematis ourses based on a omputer algebra
system,J.Symb.Comp.23,5-6,447-452(1997);
[3℄ A.I.Beltzer,A.L.Shenkman,UseofSymboli
Compu-tation in Engineering-Eduation, IEEE Traansations
onEduation,38,2,177-184(1995);
[4℄ J. A. Valente, Computadores e onheimento:
repen-sando aedua~ao,Uniamp,Campinas(1993);
[5℄ Willi-Hans. Steeb, Quantum Mehanis using
Com-puterAlgebra,WorldSienti,Singapura(1994);
[6℄ WillianE.Baylis,Theoretialmethodsinphysial
si-ene:anintrodutiontoproblemsolvingwithMapleV,
Birkhauser,1994;
[7℄ G.Baumann, Mathematia intheoretial physis:
se-leted examples from lassial mehanis to fratals,
Spring-Verlag,1996;
[8℄ K.R.Hunt,B.R.Hunt,R.L.Lipsman,J.E.Osborn
eC.J.StukDierential equation with Maple,Wiley,
NovaYork(1995);
[9℄ K.R.Hunt,B.R.Hunt,R.L.Lipsman,J.E.Osborn
e C.J.Stuk Dierential equation with Mathematia,
Wiley,NovaYork(1995);
[10℄ D. Halliday, R. Resnik, K. S. Krane, Fsia, 3, 4 a
[11℄ H. Moyses Nussensveig, Curso de Fsia Basia, 3,
1 a
edi~ao, Editora Edgard Bluher Ltda., S~ao Paulo
(1997);
[12℄ E. Purell,Curso de Fsia de Berkeley,2,1 a
edi~ao,
PrentieHall,NewJersey (1999);
[13℄ D. J. GriÆths, Introdution to Eletrodynamis, 3 a