Análise Perturbativa de Campos Fermiônicos com Auto-Interação Quártica Acoplados...

UNIVERSIDADE DE SÃO PAULO

"

INSTITUTO DE FíSICA

Análise  Perturbativa de  Campos  

Fermiônicos  com Auto­Interação  

Quártica Acoplados  a  um  Campo 

de  Chern­Simons 

Van Sérgio Alves

(,

Tese de Doutorado

submetida  ao  Instítuto  de  Físíca  da 

Universidade  de  São  Paulo 

li:

ç

ORIENT

_{ADOR. Prol. Dr. Marcelo Otavio Cam, a Gomes}

.

.

tL'U

{!

' o

?

BANCA EXAMINADORA

Prol, DL Carlos Farina de Souza (UFRJ)

t>

ａ

ｲＣＮＺｾｦＡｲＮ＠

Carlos Eugênio Imbassahy Carneiro (IFUSP)

ｃｊｱｪｨｾ＿ｪ＠

Ｚ＾［Ｎ､ＭｾｲＺＡｊＺＺ［＠

Pro[  DL  Eduardo  Cantera  Marino  (UFRJ) 

ｏＺｾＮＮ＠

Prol, Dr. Josif Frenkel (IFUSP)

'o

ｾＺｾＨＧＮｲＮｳ＠

ＬＬｾ＠ ",0,t'

Prol. Dr. Marcelo Otavio Caminha Gomes (IFUSP)

Ｎｾ＠ ｾ....o Ç.,tJ  

ｾ＠ ｾＢｴＬ＠

.'

,0

ｾ＠

o· '?,.<:J:'

q' ｻｬｾ＠ São  Paulo 

1998 -

-1-SBI-IFU$P

1111111111

_305M810T2855

_{Ｑｉｉｉｮｬｬｾｉｉｾｉｾｉｉ｛}

IIM1

_{ｾｉｉｉ＠}

.,-- I

S?:JJ·'ll{

Pc

ＧＭ｜Ｍ］ｴｾ＠

ｾ＠

J)

...eX.

i

FICHA CATALOGRÁFICA

Preparada pelo Serviço de Biblioteca e Informação

do Instituto de Fisica da Universidade de São Paulo

Alves, Van Sérgio

Análise Perturbativa de Campos Fermiônicos com Auto-Interação Quártica Acoplados a um Campo de Chern-Simons. São Paulo, 1998.

Tese (Doutoramento) - Universidade de São Paulo. Inslttuto de Física - Departamento de Física Matemática

Orientador: Prol. Dr. Marcelo Otavio Caminha Gomes Area de Concentração: Física de Partículas e Campos

Unitermos: 1. Análise Perturbativa; 2. Teoria de Campos em 2 + 1 D;

3. Teoria de Chern-Simons; 4. Modelos Fermiônicos; 5. Grupo de Renormalização.

USP/IF/SBI-062198

ABSTRACT

In thls work a theory of fermlonk fields coupled through l:\ quartic s(>]f

interae-tion and also interacting with a  Chern­Sirnons field (CS) ís perturbutlve)y anaJyzed.  Up two loops.  renormalization gmup  parametcrs were  calculated  using  dimensional 

renormalization as  a  tool  to  render  finite  the  Feynrnan  amplitudes.  For  the  theory  wjth just  aue  flavo! (N =

])1 

we ycrífied  that  operators  with  dimensíon (d) lower  or equal  to three have  an  anomalous dimension which  decreases  as  a  functíon 

Df 

the 

CS

parameter 

(o:);

that indicates a  better ultraviolet bchavior.  The  theory  presents  the origin  as  the oul:.'  fixed  poínt  "'hkh tllrns Qut  to  be infrared  stable.  For the case 

N

> 

Ｑｾ＠ using a method af l'eductioll of coupling parameters. wr. reuud. in 10l,vcRt order.  a  Une  of fixed  points,  \Ve  "cl'ified  that of o 

> 

ar the theory  is stabln in  tht' infrared.  In the renormalization proct"SS of operators wíth d = .:1. \\'I? fotmd  a Um'ar cümbinatiol1 

RESUMO

Neste truballlO fazt'tuo!i uma <H1álise perturbath1t para fél'mions com

auto-interação  quárticn1  acoplados  com  um  campo  de  Chern­Simons {CS). Calculamos 

as  funções  do  grupo  de  rcnormalização até  a  ordem  de  2­loopsj  válidas no  limite de  baixas  energias:  usando  a  reguladzação  dimensional  para  tornar  as  amplitude.>;  de  Feynaman finitas.  Para a  teoria  com  único  sabor (N = 1)t  verificamos  que opera-dores  com  dimensão (d) três  adquirem  uma  dimensão  anômala  que 

é 

UIna função  decrescente  do  parâmetro  de 

CS

(aL que  indica  um  melhor  comportamento ultrá-violeta.  Essa  teoria  apresenta  apenas:  a  orígem  como  ponto  fixo,  que 

é 

estável  no 

ｩｮｦｲ｡ｾｶ･ｲｭ･｝ｨｯＮ＠ Para o  caso  (:Y 

> 

1})  usaudo  o  método  de  redução das  constantes  de  acoplamento:  encontramos:  em  ordem  mais  baixa,  uma  linha de  pontos fixos  pa-ra qualquer  "alor do acoplamento quártico.  Verficamos  que  para (l'

> 

_{á c} a  teoria é  estável  no infra­vermelho.  ::\0 proccsso  dc  rcnormalização de  operadores com ri = 4,  encontramo!'i  uma  combinação  lineal'  dos  operadores ('ÔfP'1!-'),

(vnf'f

e (-0''(II'/f;)2 cuja  dimensão também diminui como  função  de Ct. 

,

j

'll!-l:i!gre 8p SgjUOJ Sl"Iljtqtu

Agradecimentos

Ao Prof, Dr. Marcelo Otavio Caminha Gomes pela orientação e pelas discussões no decorrer deste trabalho,

Ao Prof. Dr. Adilson José da SiJva,

Aos meus pais, irmãos e sobrinhos: i\'lanoel Augusto. Maria José, Claúdia Lúcia. Jan Claúdioj Laura Cinthya; Carlos Augusto. Ronaldo Bentesj Daniellc. Marcellc1 Edésio .1únior: Van Claúdio e Pedro Henrique, pelo apoio c amor que nos une,

A Silvallil Perez por estar presente em todos os momentO$)

Aos amigos. em especial ao Sérgio Vizeu. Luis lvlalucafJH!, Francisco Pena. Rênio l\{endes, Luiz Cláudio. Paulo Valente, Paulo Barros. Alexandre. Akira, IGeber, Cris-pino e Angela. 

Aos  colegas  do  Departamento  de  Física  da  Cniversidade  Federal  do  Pará,  nas  figuras  da  Prafa.  Fátima ｂ｡ｲ｡ｉｬ｡ｾ＠ Paulo  de  Tarso e em  especial  ao  Prof.  Dr..José  filIaria  FUardQ Bassalo,  pelo  apoio e confiança. 

Conteúdo

Introdução

8

1 O Modelo de Gross-Neveu Acoplado Com um Campo de

Chern- 

Simons  14  

1.1  Apresentação do 2\Iodclo  .  .  .  .. ,  .  ,  ,  ,  .  ,  .  ,  ,  .. ,  .  ,  ,  H 

1.2  Estrutura Gerai da Série  Perturbatíva .   15  

1.2.1  As  Regras dE' ｆ･ｾＭｮｭ｡ｮ＠ .  ,  .  ,  .  15  

1.2,2  Contagem d{'  Potência dos Diagrama." de  Feynrnan e  a  Regula­ 

I'Ízaçâo . , ... , ... , .. , , , 16  

1.3  O  Grupo de Renonualízação e à Teoria Efetiya ,  22  

lA  As  Funções do  Grupo de  Rcnonnalização  28  

1.4.1  Função de  Doís Pontos  .  .   32  

1.4.2  Funções  de  Quatro Pontos   45  

1.5  Pontos Fixos  e Dimensões anômalas de  OperadOl'efi  Compostos  ,  ,  ,  .  ,  5] 

2   O Modelo Fermiônico Com Simetria U{lV) Acoplado Com um Campo  

de ChernwSimons 

60  

2,1  O  l,.,lodelo  Como uma Teoria Efetiva e  o Grupo de Rcnormalização .  60   2.2  As Funções do Grupo de Renormalizaçâo  .  .  .  .   63  

2.3  Pontos Fixos e  Hedução das Consr,ant(>$  de  Acoplamento   67  

2:1  Dimensões Anômalas de  Operadores Composto."   71  

Discussões  

77  

A   Notação no Espaço de Minkowski  79  

,

6  

A,I Representação e Propriedades das Matrízes de Dirac. , 79

A,2 Parâmetros de Feynrnan e a Regularização Dimensional 81

B Simetrias do lVlodelo

83

C Diagramas de 1-Loop 88

C.l Função de Dois Pontos

88

C,l.l Ordem 9 , 88

C.1.2 Ordem a . 89

C.2 Tensor de

Polarização. 91

C.3 Função de Quatro Pontos 93

D Diagramas de 2-Loops

95

D.1 Funções de Quatro Pomos

95

E Operadores Compostos 112

F Geração Dinâmica de Massa no Modelo

ｇｲｯｳｳｾｎ･ｶ･ｵ＠

na Expansão

122 F

*

J Quebra de Paridade, . 123

Referências

130

,

7

Introdução

Nos últimos anos, teorias efetivas de campos tem sido extensivamente estudadas. Esse interesse deve-se não apenas a suas potenciaís aplicações, mas também por nos proporcionar uma nova maneira de se obter informações [1, 2, 3}, Esses estudos têm levado a urna mudança conceitual na teoria quântica de campos [4], e em particular sobre a questão da rcnormalizabilidade.

Originalmente fi idéia da rcnormalização era remover os infinitos dos cálculos

per-turbativos e surgiu nos anos quarenta como uma resposta  para as  diflculdades  encon-tradas  no  tratamento  teórico  dos  resultados  experimentais.  obtidos  por  Lamb  [51  e 

Rabi  [6]:  referentes 

à 

estrutura fina  e  hipcrfina do atômo  de hidrogênio.  No  entanto 

a questão do porque a ｮ｡ｴｵｲｾｚｈ＠ seria descrita  por uma teoria  rellormalizávcl  não era  enfocada [4],  Devemos recordar que anterior ao de::;envolvimento  da teoria de  renor-malização , Fermi, na década de trinta; descm'olveu uma teoria de campos, envolvendo 

uma interação  corrente  x  corrente.,  na tentativa de  cxplkar o decaimento  beta.  Por 

muitos anos a.lguns  cálculos que envolvem a teoria das interações fracas  foram feitos  com êxito, usando C&'ia teoria de quatro férmlons que é não renonnalizável (no sentido 

de 

contagem de potênciM 

[7])-Embora a  renormaHzabilidade não  seja um principio físico  fundamental 

!n

o 

re-querimento  de  que  a  natureza  deva  ser  descrita  por  teorias  renormalizáveis  impõe  restrições sobre  uma  ,­ariedarie  de  teorias  físicas  que  podemos Ｈｾｯｮｳｩ､｣ｲ｡ｲＬ＠ Essas  res-trições não seriam todavia lle<:essárias  se  a  teoria fmlS(' consjderada como uma teoria 

efetiva. 

Uma tAoria efetiva  de campos contêm  um  número  infinito  de  termosj incluindo 

aqueles rellOrmalizáveis, que correspondem aos termos com dimensão menor ou igual a 

dimensão do espaço­­tempo.  De ｦ｡ｴｯｾ＠ conl5idere a ação no espaço­tempo D­dimensional 

ｾ＠

s

=

J

dD:r I:gi Oi(X) ,

,

onde tJi(x) referem-se a operadores constituidos de campos básicos e suas derivadas. gi são as respectivas constantes de acoplamento e a soma é sobre todos os operadores que são permitidos por considerações de simetria [2]. A parametrização da forma

S

-t SA, onde A é um corte ultravioleta, nos leva a interpretar SA como uma ação efetiva, válida no regime de baixas energias, ou seja, para E

< <

A. Podemos então imaginar SA vindo de uma teoria fundamental da seguinte maneira: separamos o campo em partes de baixa (B) e alta (.4) frequência, isto

é,

cp

=

1>B

+

tPA'

de modo que podemos escrever

!

'nÇJB

VifJ..\

eiS(OB.,z,A) =

J

'DcPB ei S,d4>B) ,

onde eiS... {,pR) = IVcjJ.4,ci5 {OB,ó A). Como os campos remanescentes em 5.\ pertencem à região onde E

<

A, podemos expandi-la cm termos de operadores lot:ais, ou seja,

S.I =

J

dDT

I:

9i Oi(") .

•

No sistema de unidades naturais. se um operador Oi possuir dimensâo de massa

[Oi] = Edi, onde di é a sua dimensão canônica, entâo [9i] = ED-dó. Definindo uma

constante de acoplamcnto adimensional ),i = Ad;-D .rJi, podemos estimar, para

pro-cessos em uma escala de energia E, a magnitude de cada termo contido na ação SA

usando apenas argumentos dimensionais. Assim,

J

dDx Oi"" Ed,-D. de modo que o

i-ésimo termo será da ordem ),i(*)di-D. Aqui podemos distinguir três casos: (i) di

>

D,

este termo torna-se menos importante para baixas energias, e dizemos que este termo é não renormalizável (ou ｩｲｲ｣ｨｾｙ｡ｮｴ｣ＩＺ＠ (ii) di = D é importante em todas as escalas de energia e é dito renormalizáycl (011 marginal): (iii) di

<

D, o operador correspondente

é importante para processos em baixas energias e ele é dito super-nmormalizável (ou relevante) ;

Interações não renormalizáveis se caracterizam por possuirem uma constante de acoplamento com dimensão negativa, em unidades de massa. Se A for o parâmetro de escala de massa que caracteriza o acoplamento de um vértice não renonnalizáycl,

,

9

então: podemos obter uma teoria efeüra, não como uma expansão nos operadores) como nos _{referimos acimar} mas como uma expansão no inverso da potência A. Assim, os contra-termos induzidos pelo processo de rCllormaJização vêm acompanhados de

potências da forma

ＨｬｭＢｲＮｾｨＩＩＬ＠

onde m é a massa da partícula, p o momento externo. dh) é o grau de divergência superficial de um gráfico de Feynmau e n a n-ésima ordem de perturbação. Embora essa..q teorias gerem um número infinito de contra-termos, se (m,p)

«

A o efeito das potências maiores em (m/i será atenuado,

Partindo desta ｰ･ｲｳｰ･｣ｴｪｶ｡ｾ＠ modelos nào renormalizáveis tem adquirido um novo

enfoque, pois eles podem tornar-se fisicamente relevantes no regime de baixas energias

[1], O ponto é que se a escala de energia for pequena o bastante, as ambigllidades devído aos estados virtuais de alta energia nào são significativos. !'\"O intervalo de

energía onde isso acontece a teoria é tratada como uma tcoria rellormalizável. Em outras situações: onde nào há restrições quanto ao número de campos

fer-ｭ￭￴ｮｩ｣ＨＩｳｾ＠ o comportamento ultraYÍoleta das funções dc Grc(!O nas interaçôes quárticas

pode Ser melhorado. Realmente, incorporando os efeitos de polarização de vácuo e rea-grupanuo a série perturbativa em potência de ［ｾＮＢＮ＠ inturaçÕCR do tipo ｇｲｯｳｳｾＺＺ｜ｩ･ｶ･ｵ＠ [8, 9] ou tipo Thirring [lO) 11. 12] tornam-se rcnonnalizáveis. ;\ia linguagem da mecânica estatística poderíamos dizer que os operadores de quatro férmiol1R tornam-se relevan-tes. EstE''s resultados tem motivado uma série de invcfltigações sobre as propriedades

dessas teorias [13, 14, 15, J6,

l7J.

Ao lado da expansão

k.

em (2+1) dimensões tem sído conjecturado [18] que cxi!tte

urna outra possibilidade de melhorar o comportamento ullravíolcta das amplitudes de Feynmau_l através do açoplumento de férmions com o campo de Chero-Shnolls. Em

parte) esta conjectura vem do fato de que em duas dimensões espaeiais o grupo de rotações 80(2) é abeHano; e assim não existem1 em princípio, restrições aos valores

que o apio pode assumir, A transmuração de spin poderia então ocasionar um melhor

comportamento u]travlo]f>la da teoria.

No contexto da mecânica quãntica ob.letos tom Sphl fracionário, denominados

de anyons) e sua correspondente estatística foram inieiahnente estudadas por Lei-nam; e Myrheim

[19J

e posteriormente por Wilczek

[20J.

Como sabemos, a estatística

das partículas tem um papel fundamental na determinaçào das propriedades de um

,

sistema de muítos corpos. Partículas convencionais são classificadas em bósons ou férmions, se elas obedecem a estatística de Bose-Einstcín ou de Ferrni-Dirac, respec-tivamente.

É

bem conhecido que a função de onda de muitos corpos é simétrica pela permutação de duas partículas bosônicas e anti-simétrica para férmions idênticos. Es-ses estudos, referidos anteriormente, sobre as propriedades de: partículas imersas num espaço ｢ｩｾ､ｩｭ･ｮｳｪｯｮ｡ＡＺ＠ tem nos mostrado que existe um mecanismo que pode converter

bÓSOJls em férmions, quando se acopla uma intéração via potencial de Chern-Sunons [21, 22]. A título de ilustração, podemos interpretar a interação neste sístema como tubos de fluxos magnéticos, de raio infinitesimal. acompanhando cada partícula. Este mecanismo é baseado no efeito Aharanov-Bõhm [231 26], isto é. fi. função de onda de

dois anyons adquire uma fase ei_{1l'Ct quando as duas "partículas" são trocadas. O fator}

de fase eirru (O

<

a:

<

1) define a estatística fracionária dos anyons, de maneira que

existe um tipo de interpolação estatística, ou seja, para a = Ocorrespondc a férmions livres (de spin ｾＩ＠ e para (] = 1 corrcsponde a oosons livres (de spin O). ema revisão sobre anyons pode SCr cuenntrada na referência [24].

O

conceito de ｌｾｴ｡ｴ￭ｳｴｩ｣｡＠ fracionária tem sido últil no estudo da física da matéria

condensada, particularmente na tentativa de se obter boas explicações teóricas para o efeito Hall quântico :25], que ocorrem em sistemas que exibem uma geometria planar e podem em principio ser descritos por modelos de teoria quântica de campos (além de possíveis conexões no entendimento da teoria da sllpercondutividade COm alto valor

da temperatura crítica ,26. 27. 28.

20.

30. 31]).

I\o contexto da temia quântica de campos, a transmutação Fermi-Bose pode ser simulada pela introdução de um campo de gauge de Chern-Simons 132, 33], que ｩｮｴ･ｲ｡ｾ＠

ge com a matéria via uma corrente conservada. Deste modo o termo de Chern-Simons

(CS) produz uma interação de longo akance entre as partíeula::; carregadas, que pode ser interpretada como mudando a estatística, transformando bósons e férmions em

anyollS. Uma outra pl't'uliaridade consist.e na existência de campos vetarias massivos sem a quebra da simetria de gauge [34, 3ã}. De fato, o termo de CS quando acoplado com um termo de :Vla.'-"'\YE'll fornece uma massa para o fÓtOll1 já na aproximação de

árvore.

Na ausência do termo de ｾ｜ｩｲ｡ｸｷ･ｬｬＬ＠ não existem graus de liberdade dinâmicos

,

11

associados ao campo de gaugc, embora. a interação de longo alcance que muda a

estatística

persista, Neste caso, o termo de

as

pode ser interpretado corno um campo auxiliar, já que o seu propagador não possui um conteúdo de partícula. Este termo surge naturalmente em sistemas planaresr mais especificamente, quando se calcula o

tensor de polarização para fêrmions massiyos. Realmente. ao usarmos a representação de duas ｣ｯｭｰｯｮ･ｮｴ･ｳｾ＠ surgc uma parcela antí-símétrica que corrcspond(' ao tenno

de Chern-Simons induzido' [361, Como mostrado em [101 o te'mo de

CS

pode ser gerado ､ｩｮ｡ｭｩ｣｡ｭ･ｮｴ･ｾ＠ em teorias com férmions de massa nula) quando se acopla minimamente um campo de gauge .-1;! com a matéria) apenas se a simetria de paridade

é

quebrada.

Do que foi dito aciInaj é natural imaginar que para O

< (}:

<

1 exista um

a

c na qual quando Q -4

ar

ocorra uma transição de fase, de um sistema tipo férmion para tipo bóson, ou \'íce-yersa. For outro lado, é sabído que operadores de campos adquírem uma dimensão anômala deyido às coneções radiativas. Podemos entào obter ínfor-mações sobre a influência do tenno de CS. no que se refere a renorrnalizabiHdade da teoriaj através do cálculo das dimensões anômalas dos op<:radores de campo" incluindo os compostos. Em ｰ｡ｲｴｩ｣ｵｬ｡ｲｾ＠ a dimensão anômala do operador (t,f;t};}2 foi calculada em ｾＱＸ｝ｾ＠ onde foi usado um corte para regularizar as amplitude.;:; de Fe.vnman, O re-sultado obtido no trabalho acima indica que a dimensão anômala deste operador é uma funçã.o decrescente do parâmetro 0:2• Ao mesmo tempo que a função beta do

6

acoplamento de Gross-NeVCtí POSSU! um ponto fixo não trivial para

0';

= 1 o que leva o operador (ill-p)!< a torn8N:i€ marginal para este v'dlor de Ü:. Nos.ws resultados,

entretanto, confirmam apenas em parte esta conjectura [37\.

Parte deste trabalho dedica-se ao estudo de um proeedimcnto perturbativo

ade-quado para modelos com auto-jnteração quártica fenniõnica. Eic esta dividido em doís capltnlos e seís apendic('_". ｾｯ＠ primeiro capitulo estudaremos o modelo de Gross-Neveu massivo acoplado com um termo de

CS.

Após uma brcyc apresentação do modelo e suas simetrias. discutiremos a não renormalizabilidade da teoria e a construção da teoria. ･ｦ･ｴｩｶ｡ｾ＠ assim como o método da regularizaç.ão utilizada neste trabalho. A

se-guir ･ｮｃｏｊｌｴｲ｡ｲ･ｭｯｾ＠ a equação do grupo de renormalizà(,:ào que as funções de vertices, 'veJa o Ｇｾ｡ｬ｣ｵｊｯ＠ do tensor de polarização que se em:ontra !LO apêndice C desta tese,

71

.

com N linhas externas do tipo férmion deverão satisfazer, Calcularemos as funções do grupo de renormalização até a ordem de 2-1oops, e mostraremos que neste ca'5O (de

um único sabor) existe apenas um ponto fixo infravermelho ｰＮｳｴ￡ｶ｣ｬｾ＠ que ê o trivial. Obteremos também as dimensões anômalas do campo básico yf; e de alguns opera-dores  compostos.  No  segundo  Càpítulo  estenderemos  a  discussão  para a  situação de 

N (N

>

1)  campos fermiônicos  áÇQplaclos  com  o  tenno de CS, Neste  caso  teremos  duas constantes de acoplamento, e para estudarmos a natureza dos pontos fixos utiliza-remos o método da redução das cantantes de  acoplamento proposto por Zimmermann  [38].  Mostraremos que existe  uma  linha de  pontos fixos,  além daquele  trivial,  o  que  não ocorre para o caso onde N = L  Discutiremos as dimensões anômalas para alguns  operadores compostos e seu  comportamento como uma função  de 0:.  Devemos espe-rar algumas  diferenças  qualitatíuls e quantitativas em  relação  ao  caso  de  um  único  saborI pois como  sabemos,  quando 

N

torna­se grande,  mudanças  drásticas  ocorrem 

em  teorias quárticas fcrrniônicas.  tais  como  a questão da  rcnormalizabilidade.  c  em  particular) com  uma int.eraçâo  tipo Thirring,  haverá geração dinâmica de  massa para  os férmions  [11].  Nas  discussoos  apresentaremos um  resumo  dos  resultados obtidos e 

possíveis extensões a  este trabalho.  Nos apéndices enéontram­se a notação e tabelas  de  integrais que  utilizaremos  no  decorrer  deste  trabalho,  assim.  como  os  cálculos  de  alguns  diagramas rcfcnmtes aos modelos considerados. 

13  

Capítulo 1

o

Modelo de Gross-Neveu

Acoplado Com um Campo de

Chern-Simons

1.1 Apresentação do Modelo

o

modelo de ｇｲｯｳｳＭｾ･ｙ･ｵ＠ maSSl\U em (2

+

1) dimensões ;u-:opiarlo com um campo de Chern-Slrnons é dado pt:>la segumte densidade de Lagrangeana.

1 - . - -") 1 "l

ｾ＠ -_{- 4'irG:} _ _;:-Jl"OF _{ｉｴｖｾＢｬＡＩ＠} ' ｾ＠ "(I'",,,}.!'> _Up - ｬｮＩｾ￭ＧＮＮＮＮｌ＠ _' 'l!1",JI..h!1_{,'. ＢＧｾ＠ fi G{.,f;w)- - 2.\ (Dw4")',} (1.1)

ｾ＠ ｾ＠ I 'f/

onde Fllv ;;;; Df.!Al' - 81'Aw l' é um campo fermiônko de massa rn cum duas

componen-tes, A/l o campo de Chern-Simons e À o parâmetro de fixação de gangc. Xcstc caso_l a

interação de ｇｲｯｳｳＭｾ･ｶ･ｵ＠ é a mais geral auto-int.eração qlHírtica fermiônica invarian-te de Lorentz, uma vez Q1H' a interação vetorial tipo ThitTing não é independente e

satisfaz a relação; (tPj.J'1/'f : = -3 :

(..p1jJ)2

:.

)Jo próximo capítulo analizaremos o

caso de N campos fcrmiônÍCos.

Note que em D = 3 11 teoria âCima1 possui o acop)amemo G com dimensão

::v1a..<;5a-1, e de acordo com o critério de contagcm dí! potência ti. teoria é nào

rc-normalizávcl [39, 40, 42]. Isto significa, como vcremos na seção IA, que o número

INo sistema de unidades naturais (c =

tt

= 1), a dlJl\cnsão da densulade de Lagrangeana em unidades de ｭ｡ｳｾ｡＠ é

[eJ

= D. onde D é 11 dimensào do espaço-tempo. Logo. h/;] = ｛ｾ｝＠

=

11:;1

=

IApJ "'" Dil, O que implica qut' [u] =;} .', D e [G] = 2 - D.

,

de ｣ｯｮｴｲ｡ｾｴ･ｲｭｯｳ＠ necessários para tornar as amplitudes de Feynman firiitas aumenta com a ordem de perturbação em G,

O modelo descrito por {l.1} é jnvariante peja simetria de conjugação de carga

(C). No ･ｮｴ｡ｮｴｑｾ＠ a presença do termo de Chem-Simons. assim Como o termo de

massa, quebram explicitalIlfmte as simetrias de paridade (P) c reversão temporal (7),

contrariamente ao caso das simetrías

PT

e

C'PT

que não sâo violadas [34] (para maiores detalhes veja o apêndice

B).

O modelo apresenta também uma simetria de

gauge local, pois pelas transformações

Ap(x) -> Ap(x)

+

ope(",),

e

ｾＨｸｽ＠

--+

et9_{(x; '<p(x) .}

a Lagrangeana muda apenas por uma derivada total

.c --)-

L

+

4!n

é W() 8ó (F,lIJ 9(;r)),

mantendo a ação clássica invariante,

1.2 Estrutura Geral da Série Perturbativa

1.2.1 As Regras de Feynman

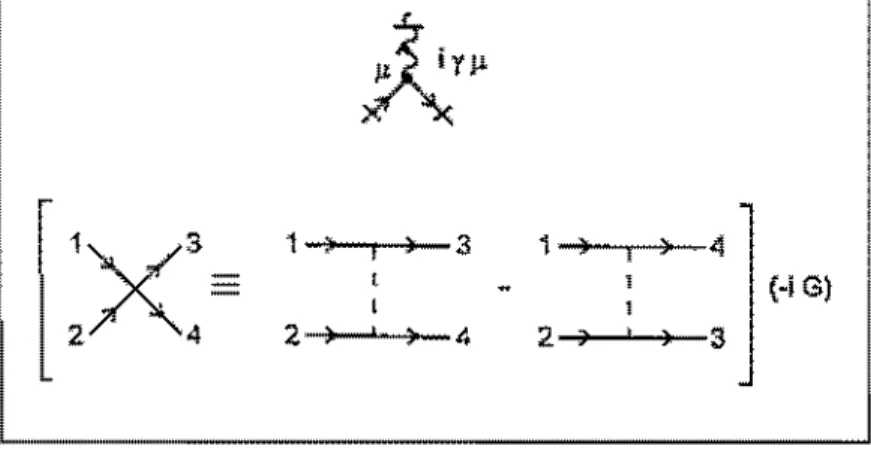
A teoria de perturbação aproxima as amplitudes de espalhamento por uma série de diagramas de Feynman que mostram sub-processos entre os estados iniciais e finais. Podemos construir a série perturbatíva da teoría (1.1) através das regras para os vértices de interação mostradas na figura abaixo. Por cOllveniência introdúzimos a linha tracejadat que chamaremos::t partir de agora de linha auxiliar G.V l para darificar a estrutura tensorial do vértice fermíôn1co.

Os propagadores da teoria livre são obtidos facilmente se aplicarmos a equaçào de Euler-Lagrange em (1.1). Para o campo de Chern-Símous, obtemos a seguinte equação de movimento

11)

a

'v

1 "' '" . _(1.2)

ｾＭ I! 1>"fl

+

:-Ep>.vu _{ｾＧＺＱ＠}

=]"

,\ 21i'{x

,

15

ｾｲｾ＠

,

1

_,

I ) 3

1. , 4]

(-i G)

,

[:x:=

2 , _> 4 2. 'J I ) 3

Figura LI: Regras de Feynman para os vértice da teoria (1,1). A linha ondulada representa o propagador de

CS

e a linha cheia o propagador fermiônlco,

ｪＮｾｦ｜ＨｫＩ＠

= 2no:

ｴￍＧｑ＾Ｎｫｾ＠

_ iA kPk o _(1.:l)

k' k,j

o que nos mostra que este propagador nào possui um conteúdo de partícula. urna vez que não apresenta pólo, :\0 decorrer deste trabalho ｩｲ･ｭｯｾ＠ adotar {} gauge de Landau

À

-+

O. A escolha deste gauge leva a um melhor comportamento infravermelho das

funções de Green 134,

44),

De maneira análoga podemos obter o propagador do férmíon. que é dado por

SP(k) =

V

i (IA)

-m

1.2.2 Contagem de Potência dos Diagramas de Feynman e a

Regularização

o

comportamento ultra-vioLet.A. de um gráfico de fl\ynman .l é gun::rnado. de acordo

com o critério de contagem de potências. pelo grau de divergência superficial d(',!}, Os diagramas calculados com as regras de Feynman acima possuem)

d{'y) = DL - 11._1 - nF . (1.5)

onde L é o número de loops: nA e nF são os números de linhas interna.., do tipo Ap e

fermiônica: respectivamente, e D é a dimensão do espaço-tempo.

Podemos escrever (1.5) em termos do número de linhas externas dos campos 'IjJ e Ali! NF , IV..\. respectivamente. usando a relação de ｅｵｾ･ｲ＠ e as relações topológicas

I , 1 \" 2

,,·1 ",

n

"F

L =n.-\+np-""

+

l ｾ＠ Ai ｮａ］ｾｬｾＬ＠ jYFif.llP:=L.,.Vll ,

a

onde F = V

e

+

ｬＬｾＬ＠ é o mImem total de yértices em um diagrama de Fcynman,

v:

e

1/:;

sâo os números de linhas do campo

.4

p e do campo ti: chegando no vértíce u, respectivamente. Usando as relações adma: a equação (L5} toma a forma

d(-y)

D

....

(D::

1 111'.1

+

N

F

+

ＲＩｖｾＱ＠

+

1/';)] -

Dl'

a

3 ..··N" Sy+li; (1.6)

para D = 3.

Os diagramas são dito;:;: superficialmente divergentes quando db) ｾ＠ 0, então de acordo com (1.6) são superficialmente divergentes; por exemplo)

0.,

diagramas mostrados nas figuras ＱＮＲｾ＠ 1ＬＳｾ＠ IA e 1,5. Para remo"er essas divergências devemos usar

algum esquema de renorm<lllzação. Por outro lado, os contra-termos são construídos para cancelar as divergências das funções de Grecn de )V pontos, de maneira que sua estrutura está intimamc<ute relacionada com o grau de divergência superficial, Ivlais precisamente. de acordo

com o

teorema

de

\'Tcinberg

[45],

um contra-termo

C("y)

de wn gráfico I' será. um polinômio 110S momentos externos, de gnlll igual ao grau de

divergência ::.npcrficial dh). Isto

é

uma propriedade geral da teoria da renormalização, onde os contra-termos induúdos são locais (-lO, 461.

Portanto até 2-1oops. com relação à função de doís pontos para {) férmion (NA = O

e NF = 2), os contra-termos induzioos pt:los diagramas de Feynman serão proporcio-nais a: 'In c

p,

que cOl'respondem aos diagramas de ordem (t e (,/'1 (são linearmente divergentes); m2 _{ｾ＠ m}

'fi

_{e p2, que correspondem aos diagramas ､ｾ＠ ordem G e Gn (são}

quadraticarnente di\'crgentes); ｭＳｾ＠ m2

p.

_{m p2 e}

p

_{p2. referentes aos diagramas de} ordem

G

2 _{(são cubicamente divergentes). Com reJação à função de quatro pontos}2 ;:Por comodidade adotamos uma representação comiem;.ada onde p represf'.uta quaisquer dos mo-mentos externos .

.

-17

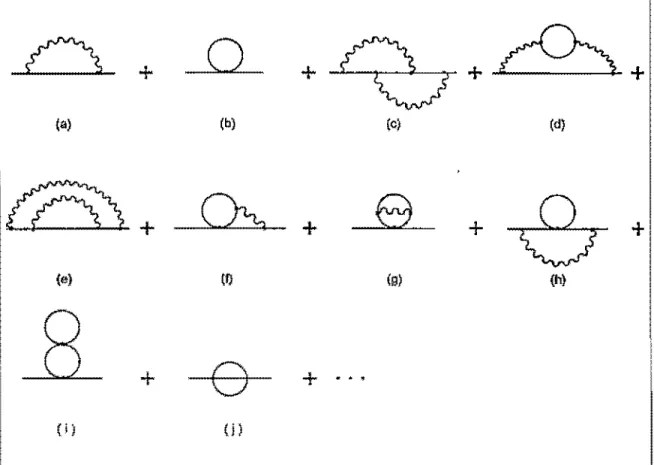
t::\

₊

o

+

r ,

ｾ＠

,

ＫｾＫ＠

ia) ib) (c) (d)

CÀ,

e

ｾＫ＠

+

+

-6r

+

(e) iQ (9) (h)

R

₊

_O

+ ...

(q

(j)

Figura 1.2: Diagramas com

N,4,

= O e :\'F = 2: que contribuem para a função de dois pontos do férmion. Os diagramas (b), (1), (9), (h), (i) e (j) representam de fato uma família de diagramas.

e 1'1F = 4) \ os ｃｮｴｲ｡ｾｴ･ｮｮｯｳ＠ induzidofl serão pro!)orcionais a; constante, que

corres-pondem aos diagramas dr ordem Gn e G(l2 (são loga:ritirnicamcnte divergentes); m e

P,

gerados pelos diagramas de ordem G)· e

VQ

{são linearmente divergentes}: m2 ,

m

p

e

r

l gerados: pelos diagramas de ordem G3 (são quadraticamente divergentes).

Como podemos obsenl1r. diagramas logaritimieamente ､ｩｮｾｲｧ｣ｮｴ･ｳ＠ {d{"y) ;;;; O)

indu-zirão contrawterm05 <:OnSlllntcS. 05 linearmente div€l'gentf's induzirio contra-termos

com dimensão de massa c assim por diam c, Desta forma. com relação a função de dois pontos para o férmioll. os termos S('!1l derivadas poderiam ::;er ab:mrvido." numa

repararnctrização da massa, os de urna derivada numa fE'parametrização do campo, e os com duas e ttês deri\'adas são novos contra-termos diferentes das interações já contidas em (l.I). Semelhantemente: para a função ､Ｈｾ＠ quatro ｰＰＱｬｴｏｾ＠ os termos sem

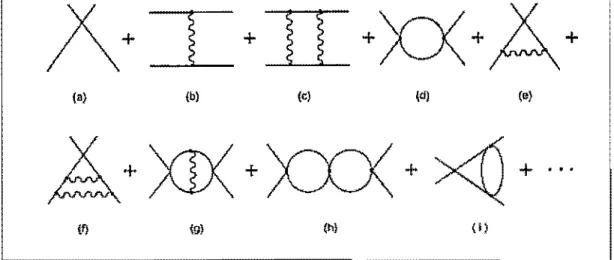
ｾ＠

)\+ I+I[+XX+A+

{'I {bl {oi {di _('I

A+

)CD(

+

XXX

+

><Q

+".

Ｈｾ＠ (o) (h) {' }

Figura 1.3: Diagramas com

NA =

O e

N F =

4, que contribuem para a função de

quatro pontos, Os diagramas

(e),

(d),

(e),

(I),

(g), (h)

e

(i)

representam uma família

de diagramas,

derivada poderiam ser absorvidos numa repararnetrização da const.ante de

acoplamen-to

G, e os de uma ou mais derivadas sâo nOvo.', contra-termOR induzidos, Q1lC por sua

vez requereriam a introdução de novos tipos de interações da forma ]{\

{'/f;

ｾ＼ｊＬＩＨｬｩｊｬｪｊｽＬ＠

K

₂

(ij,8

21/I)(J)1/t).

etc,,, . Note entretanto que como a interação de CS é

renorma-lizâvel, um aumento na ordem de perturbação no seu acoplamento nào altera o grau

de divergência superficial dos diagramas. Contrariamente, inscrçõp.s extras de

ope-radores (ij}'l/l)2 fazem com que a amplítude se torne mais divergente, nos levando a

ter que adicionar, para tornar as amplltudes de Feynman finitas, contra-termos com potência cada vez maiores de momento. Isto é urna característica de teorias não re-normaUzáveis3: onde necessitamos fazer infinitas ｭ･､ｩ､｡ｾ＠ para fixar os contra-termos, diminuindo assim o poder de predição da teoria com ti, ordem, de perturbação,

Em teoria quântica de

campos prcdsarnos especificar

a

maneira

pela qual as

par-ceias finitas dos diagramas de Feynman sâo determinadas. já que existe uma am-bíguidade na sua definição, ::\a teoria de perturbação. a prescrição para remover as divergências

corresponde

a escolber um esquema dI? renormalização

que

regule as "!::5e por teoria renormalizâycl por -COntagem de potênda entendemos lltIuela. em que todos 05

contraAermo$ induz.idos pelo procedimento de renormahzação, podem ser absorvidos por uma rede-nnição dos parâmetros originais da teoria, e não pelo fnto da constante de acoplamento ser adimen-sional, a teoria de Yukawa em (3+ l)D com acoplamento ｱＬｾｾｬＯＧＮＧ＠ é não renormalizável. Pois em l-loop há a indução do contra-termo 6'1 para cancelar a divergência logaritimicn.

,

19

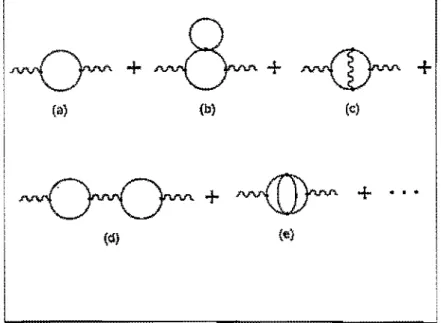
ｾＫｾＫｾＫ＠

(') (b) (o)

ｾＫｾＫ

...

(.)

(O)

Figura 1.4: Diagramas com NA = 2 e Xp = O, que contribuem para a função de dois

pontos do campo AI"

integrais e que subtraia ús infinitos de maneira sistemática.

A questão de qual regulador devemos usar não tem a príori uma resposta em

teoria quântica de campos, Em princípio qualquer método pura retirar os infinitos

pode ser ｵｴｩｬｩｺ｡､ｯｾ＠ entretanto. na prática alguns mêtodos são mais convenientes que

outros. l\"este trabalho adotaremos a regularização dimensional [47] juntamente com o esquema de subtração minimal

[47] 

[48]. Em muitas situçÕ€s este é o método mais conveniente pois nào destrói nenhuma relaçâo algébrica entre as funções de Green, em particular as identidades de VVard. _\lêm de preservar a invariância de Poincaró na teoria regularizada e também as simetrias de gauge. nos permíte calcular as funções do grupo de renormalização de maneira relatl\'amente simples. como veremos na próxima seção. Outros métodos como o 'cut-oW' e o dE' Pauli-Viliars desuoem a invariância de gauge. embora () segundo preservE' àS identidades de ｜｜ｾ｡ｲ､＠ na QED. Entretanto,

como observado em [49] a regularização com um simples :'cut-off"' leva a ambiguídades associado ao fluxo de momento nos gráficos de FeYllman. Xo contexto das teorias efetivas, o uso da reguJarizaçào dimensional ê quase que obrigatório para garantir que contra-term'JS de ordem mais elevadas possam ser desprezados (50).

A idéia deste esquema é baseada no fato de que as dh'ergéncias ultravioletas

primi--

₂₀

+

A+A+

",

(b (o)

A+M+A+

(d) (.) Ｈｾ＠

Figura 15: Diagramas com X. \ = 1 e .\"F = 2, que contribuem para a função de três

pOntos.

ti'ras dos diagramas de Fe-ynmúu. qm' adn":m uos "loops" de: integração. são t-liminadas

quando se vai para uma dimensão D do pspaço-tempo pequena. o bastante para tornar tal amplitude conycrgemc. As integrais clt! Feynrnan sào então definidas como funções analíticas elo espaço-tempo ｄＭ､ｩｭｾｮＵｩｯｮ￠ｬＮ＠ e os infinitos aparecem como

síngularida-des da  forma  ｾＮ＠ onde €  = 3 ­ D. quando D -t 3  [51].  Assim.  numa.  determinada 

ordem de perturbação. a função de  Green G(€) conterá pólos em tê, de modo que  pode  ser expandida ('!ll Ｕ｣ｲｩｴｾ＠ de Laurem 

G,

G'-i Gi

-G(r) =  -f+-'-. + ... +-+G(f) (1.7)

é'­'  E 

onde G(f} é finito  para é  _..,  0,  Os contra·termoR sâo então construídos (k manpira a 

subtrair os tel'llloS de  pólo em G(e:}.  deixando G(E) corno a função de Green subtraída. 

Como COIl1{'lHildo adma.  na  regularização dimensional  os  pólos ocorrelll nas 

inte-grais de  Fe)'nmaIl  quando  D  (dimensào do espaço­ternpo  na  teoria regularizada)  for  igual  a  trÊ's.  Por  outro tado.  de  acordo  com  [52];  os  pólos  de  um  gráfico  genérico  ;'  apar()cem na fonna r( ­ ､ｾＧｬＩＮ＠ isto é.  para "alores onde ­ ､ｾＩ＠ = 0,  ­1. ­2. _...  Usando  (1.5)  para L = 1 rucontramo.s d(-.}

= 

3 ­ nA ­ np. Entretanto, para construirmo!' um  diagrama de l­Ioop dl'\"emos  ter no  mínimo 

. 

11..­­1 +nF::::: 2.  o que nos leyaria a dh') = L 

21 

portantn livre de pólo. Por outro lado, as divergências logaritimicas (dh-J = O), que em geral estão contidas nos gráficos de I-Ioop; são ímpares na variável de integração, e portantol se anulam por integração simétrica. Consequentcmente. uma característica

desta regularização em três dimensões f: o faLo que as integrais de Feynman em l-loop, que são formalmente diycrgentes por contagem de potência. são de fato finitas uma vez que nenhum póio ocorre quando D = 3. A"iSim, ao usarmos esta regularização os diagramas efetivamente ､ｩｙｦｾｲｧ･ｮｴ･ｳ＠ são aqueles fi. partir de ＲｾｬｯｯｰｳＮ＠

1.3 O Grupo de Renormalização e a Teoria Efetiva

1;ma prescrição de renorma1ização consiste em usarmos um procedimento de regu-larização que isole os infinitos dos diagramas de Feynman c uma maneira sísternátka de remo\'(:r as divergências e definir os parâmetros renormalízados da teoria, isto

é

r

especificar uma escala d€' momento /1. na qual as sublrações dos infinitos são feit.a..s. Entretanto, quando adotamos o formalismo de contra-termos e sltbtrações. existe umá liberdade em como separar a Lagraugcana nào renormalizada numa ｰ｡ｲｴＨｾ＠

renorma-lizada e a outra que contêm os contra-termos. Embora esta arbitrariedade não ｬ･ｶｾ＠

a nenhuma consequência física, pois todos os procedimentos dc\'crão levar ao méSmO

resultado, eles podem diferir na definição dos parâmetros da teoria. Existe portanto uma simetria associada com a invariância das amplitudes renormalizadas quando se muda o ponto de subtração p. ou seja) um grupo de t.ransformações envolvendo 11 que deixam os resultados físicos inalterados, Essas transformações são chamadas de grupo de renormalização (GR). e dependendo da escolha das condições de renormalização empregada, existe uma "ariedade de formas de equações do

GR

{53], "Cma das prin-cipais utilidades da equaçào do GR é na discussão do comportamento assintótico de uma teoria quântica de (;ampos para pequenos e grandes momentos,

Para modelos renoTInalizáycis. a equação ､Ｈｾ＠ fHoot't-\"Veinberg {-lIL 48] é a equação do G R que

é

derivada do esquema de subtração minimal. Esta equação é frequen-temente chamada de equação independente da massa. pois as funções do grupo de renormalizaçãú que aparecem na equaçào sào Independentes dOR parâmetros de massa da teoria.

Por simplicidade, ignoremos inicialmente a uno ｮｾｮｯｲｉｈ｡ｬｩｺ｡｢ｩｬｩ､｡､･＠ da teoria,

tma-22

ginando que a renormalização da massa e das constantes de acoplamento em

(1.1) 

sejam suficientes para tornar as funções de Green bem definidas, Para derivarmos a equação de t'Hooft-\\'einberg é conveniente introduzirmos as constantes de acopla-mentos e o parâmetro de renonnalização tt através das relações G -t G jJt e O: -t (X p/,

G possui dimensão de luyerso de massa e ( = 3-Dê tomado zero no final dos cálculos. Partimos em seguida da relação usual entre as funções de vértice fermiônicas não re-normalizadas de N pontos (gráficos IPI), r{N) {Pi, G, 0:, m,c), com a renorrnaHzada

ｲｾＢｩＩＨｐｩｬ＠ G Rr ctn, mnd1). onde Pi representa os N momentos Pb]12. "·,PN, dada por

(N) , _

-!f

(N),

r

(p"G,a,m,€) - ｺｾ＠

(I",e)r

_n (p"Gn,CfR,m",,,) ,

(L8)

onde o subescrito

R

significa uma quantidade renormaHzada. e USJlmos também o fator de renormaUzaçào

ｚｾ＠

para (:ada linba externa

fermiônicR.

Obviamente

ｲｾｾＩ＠

possuí um limite finito quando f -+ O...\. equação do GR é obtida de maneira muito simples

se notarmos que rCl\<) em (1.8) é independente d.e /1. para G. lY. m e (: fixos, ísto ê

ＬＬｾｲＨｓＩ＠

= O =

ＨＬＬｾｺＭＧｴＩｲＨｎＩ＠

,

ｚｾＧｬＧｦＱｾｉＧＨＢＩ＠

_(L9)

ｾ､＠ _I' ｾ､＠ 1!J R T ! f ! d H

I' I'

Se expressarmos a dcriyada total do lado direito em termos de derivadas parciais,

d

= ｾ｟＠

e

...L _ _ _ _ _

e eG

R ｾ＠ ｟ｾ＠

en

n _ "__

e

ｾ＠ +_ ... ..._

amn

a

d" ai' eG

R

e"

aI' afrR aft &m

n

obtemos a seguinte equação

a

a

e

a

"

1

,I")

_(UO)

li-a +111.6 ｾ＠ ＫｉＳｇｾｇ＠

+(Ju-;;;--}'h

f R =0,

[

_ti UfJ!n U R uo.ll

onde4

arl

_{8ra . e} 1 Dln Z1/J

I3c(G, a)

=

ｉｉｾｱＢ

a"

('n(G, a) = I' aI' , mó(G,Lt)

="

aI" '

'i(G, a) =

21'8;'-(Lll)

As expressões acima são chamadas de funções do grupo de renonnalização, e nos informam como os parâmet,ros G, G: e m se comportam quando fazemos urna mudança '-'A partir deste momento. salvo o contrário, para não sobrecarregar a noração, r!N). G, n c m ｲ･ｦ･ｲ･ｭｾｳ･＠ a quantidades renonnalízadas.

,

no ponto de subtração 11, Em (1.11)

fJa

e fla são as funções beta do acoplamento G c a, respectivamente,

É fácil \"erificar que se definirmos G ...,

f

j.l. onde 9 faz o papel de constante de acoplamento adimensional e A é um parâmetro massivo,

r

OV)(pil9, 0:, m, J-L) satisfará

a equação

18 8\

l

A-_DA

+

_"Dg

g--)' r(NI(p _L .g.fr.m li) _{. . 1}

=

O ( 1.12)

Somando (1.10) c (1.12) tomos

[A!A

+f.L;p

+mÓ:

_m

+!39: +1'10;0'

_g

-N'l']

r(N)(pi>g,

a.m,

1')

=

O, (1.13)

onde agora

/J

-t

i3

,...

9 = ｊＮｌｾＬ＠ Observe que {} que: fizemos f01 fixar

.:3

_g em ordem

mais baixa como sendo igual li g. !'\enhurna Qlltra implicação ocorre com as funções

do GR uma vez que A entra !la expansão penurb}Hi"a apenas na combinação

Ã,

de maneira que todas as contribuições do termo de derivada em relação li ,\ são

eliminadas. Entretanto. a introdução do parâmetro massivo :\ nos pcrmjtirá construir uma teoria efcti"a de uma. maneira consistente. ｾｏｩｃＡ＠ também que () procedimento acima é dependente da. razão entre dojs parâmetros HI.a5sivos

X.

de maneira que as funções do grupo de renormalização terão a forma

/:1

= .B(g,a:,X),

J

=

ó(g,a, ';:) e

; = ')'(g. a,

X).

Por outro lado. modelos não renormalizáveÍs requerem uma consideração espedal uma vez que a forma da lagrangeana efeth'a muda com a ordem de perturbação. Assim, rigorosamente falando, a equação (1.8) c portanto (L13) só serão verdadeiras no caso onde 9 = O, Para 9

#

O a teoria é não rcnormalizá\'el e o lado direito de (L13) não é de fato verificada em todas as ordens ､Ｈｾ＠ pertllrbação. uma vez que

existem contribuições para r(2} c r(4) que nào podem ser absorvidas em redefinições dos parâmetros de massa, fl1nção de onda e constante de acoplamento, corno vimos na seção 1.4. Neste caso r(2) receberá contribuições. além daquelas já contidas em

(1.8). da forma

,

g ,) 3

r(2} _{,..., Dl ｾ｜ｮｰＭ}

₊

_!J..

_(D,

_mp'

+

_{D, pp')}

+

_O(Y

₎

_{T ... •}

/\.2 - "

_A'

,

24

que advêm da contribuição dos diagramas 1.2(/) e

1.2(j)

respectivamente (Dl,

D.

e

D3

contém as divergências ｾＩＮ＠ Analogamente, para r(4) temos

g'l g3 . g4

r(4) ｾ＠ Bl ;\,"

p+

E, :\3(m

p+p')

+

0(:\4)

+ ...

corrcspolldendo aos diagramas 1.3(g), 1.3(i}, etc ....

Portanto) o lado direito de (1.13) seria proporcional a esses novos contra-termos para N =

2

e N =

4,

respectivamente. tornando a equação do G R muito díficil de ser analisada, Contudo: se nos limitarmos à análise na região onde o parâmetro massivo A seja muito maior que qualquer momento externo e a massa do fél'mion (m,Pj

«

A), de maneira que os efeitos desses novos contra-termos possam ser efetivamente desprezados, as funções de GrC€ll ainda satisfariam (aproximadamente) a seguinte equação

ａｾ＠

Ｋｉｬｾ＠

ＫＢｭｾ

ＭＫＮＸｧｾ＠

Ｋｩｊｯｾ＠

-N7]

r(NI(pi,g, cun, j') '"

° ,

(1.14)

｛

uA uf! um ug Vü

onde o símbolo ｾ significa igualdade na região onde todos os contra-termos djf{'rentes

daqueles já contidos em (1.1) podem ser desprezados.

No entanto,

é

bem <:onhecído que em 1-1oop [21, 431, ú acoplamento do campo

de

CS

com férmions produz uma parcela ímpar por paridade na correção quântica da função '(OIT A/,(x)A"()J)IO) (com ou sem o termO de CS presente inicialmente na lagrangeana). Por outro lado: como "crificado nas referências [54, 55;, em ＲＭＱｯｯｾ＠ não

existe correção para a parcela ímpar por paridade, no crí.1culo do tensor de polariza-ção. A partir desses rC5tlltados, Coleman e Hill pron'trarn que em uma ampla classe de

teorias6 _{em três dimensões, todas as correções para () termo de}

_CS

_{::;5.0 ídcnticamonte}

nulas

[56],

a não ser àquela prm"eníente de l-loop. Em particularl eles enfati:turam

que o resultado é válido mesmo que interações não ｲ･ｮｯｲｲｮ｡ｬｩｺ￡ｶｴｾｩｳ＠ estejam presf'ntes na lagrangeanat desde que usemos urna regularização que preserve a iuvariância de

gauge e de Lorentz, Extensões ､ｅＧｾｴ･＠ teorema podem ser encontradas mUi referências

[57].

::'Veja a equação dezoito do apêndice C,

60 teorema foi demonstradQ em condições bastante gerais. onde o campo abeliano de CS interage com c.ampos escalares e espiuorials.

,

?-_{_v}

Em outras palavras. o teorema nos diz que a função beta do acoplamento de C8 é identicamente nula

(ô

_o

=

O)

de maneira que podemos escrever (1.14) como

O

8

iJ

a

]

A

+1

1 /1 +6711

+P'[)g -N7

r(N)(J!i,g,a,m,IJ) "'0 , (1.15)

[

_oA

₀

₈₁₇₁

m

Usando a equação acima juntament.e com ajuda da ｡ｵ￡ｬｩｳｾ＠ dimensional podemos

obter o comportamento assintótico de r(N)" Designando por dimf{NJ a dimensào

canônica7 _{de r(Nj e como ela é urna função homogênea nas variáveis dimensionais Pü}

1 A e jl., então por uma mudança de escala da forma

(Pi,

m j A,

p)

---r S (Pi, m,A! fl).,

temos

(N) ( . " .) _ d;mr(X; r[N) (p"\ )

r

sp" sm. .ｾｌ｜Ｎ＠ sp, g, a - S tl fn.. : /1, g, (t (1.16)

Usando o teorema de Euler para funçôes homogêneas podemos obter que a equação do GR que r(N) dcvcni satisfazer pela mudum,:a de escala adma será

Ｌ｜ｾ＠

+

ｊＱｾ＠

+.,"'- +

ｭｾｬ＠

r(NI = (dimrl,vJ) r lN) . ( 1.17)

｛

8A 8/1 iJs Bm

Esta por sua vez pode SE'T combinada com (1.15) para obtermos urna outra equaçâo que relacione n escala 8 com uma mudança em m e [f (mas não em

/-1.),

isto é,

dim

ｲｉＢｾＩ＠

+

3 "'-

+

m (ó(q) -

ｉＩｾ＠

-

N

"I(q.

O)]

r'i'l) = O (1.18)

[-s"'-

_iJs 9_ôg .

am,

.,

1Por definição,

ＨＲ

ＭＩｄｉｩ［ｾ＠_{" \Pl+P'1'T· .. +PN 'COXp"p2, .. ·,P.\'} , ) a,N) ( ) ₌

ldD.

_Xl'" dD _x",e ｾｩｌＺＮＬｰＧ _ｾ＠

x ｻｏｉｔｴＺＧＨｸ､Ｎ｟ＮｗＨｔｾＩｾＨｘＮｙＫＡＩ _{o ,} ..:t3(:t'j\")IO>CON ,

onde ú subescrito CON quer dizer conexa. Púr análise dimensional fiO obtêm facilmente que

､ｩｭｇｾＩｾ＠ "'" ]I: d_v - DiV + D. Como a dimensão de r(!I,'1 é a mesma que a das função de

Gre-cn conexas, porêm com as linllas externas amputadas, então

d· rU\'l _{1111 =} d' _{Im GON} a(N)

+

_{l\' ;;;;;;} ,,- II _ｊｾ＠"d_{V ,}

com dlJl =

,

26

que expressa o fato de que uma mudança em 8 déve ser compensada por uma mudança

em m j 9 e um fator multipJicatívo. A discussão da equação acima é simplificada se introduzirnlos a constante de acoplamento efetiva (também chamada de carga gene-ralizada) 0(9, s) e a massa efetiva m(g, s), definidas como

a-

_am

s

%8

(9, s)

ｾ＠

,13(1/) s as

(9,8)

ｾ＠ m(ó -1) (1.19) com as condições

!l(g,

1)

ｾ＠ 9 m(g, 1) =

m.

(1.20) Usando estas definições, a solução de (1.18) pode ser escrita como [8, 40]

r(N)(S Pi, m,

g,

D:,

/1,)

= sélmrpq

･ｾｎ

f

ｾ

'(YJ.,xj r(X'(pi' m(m, s),

IHg;

'<;)j a, jJ) _(1.21)

Esta forma de solução é às vezes usada para analisar o comportamento assÍntôtico da amplitude de Fe:;:nman ｲｾｖｽ＠ quando s -t oc" Para este propósito devemos conhecer

as propriedades de 9(9, s) e d·u dimensão anômala i:oIno uma função do parâmetro

8. Vemos então que H menos do fator multiplicativo1 o comportamento assint.ótico

da teoria

é

gO'.'emado por [}(g)s) e Ú1.(g)

5).

Note inicialmente que na teoria livre

fi

= I = § = 0, e o efeito sobre r{N) devido a uma transformação de escala nos

parâmetros massivos é dado simplesmente pela dimensão canônica de r(N). Note

também que se part.isscmos de urna teoria sem massa, a densidade de lagrangcana seria invariante por essa transformação de em-;ala. no entanto, o mesmo não acontece com as funções de Green nma "CZ que em geral {'J não

é

nulo. Por outro fado, a tCoria assintótica será iuvariaute de escala para algnm 'Valor de g* de 9 se

{3(g*)

= O (isto

t\

g* é um ponto fixo da teoria) e rn = O. Neste caso, para momentos não excepcionai:f' I

a solução de (1.18) para J' constante e não nulo será

r(N) (51';, g, Q, m, /L) ｓ､ＡｭｲｕＢＩｾｽ｜Ｇ＿ＨｧﾷＮＨｴｬ＠ r(N){Pi) g") (1,

m

=

O:,u)

ｳｬｊｾｎＨ､ＬＧＫＷｻＹＧ ,o)) ｲＨｎＩＨｐｩｾ＠

9'\

0:₁ m =

O,,u) ,

_(1.22)

8Numa região euclidiana os momentos são ditos não excepcionais quando nenhuma soma dos Pi

for igual a zero 139, 40).

.

27

de onde vemos que a dimensão canônica dírnr(N) é modificada por um fator adicional de -''1(g*,cr) para cada N campos. de modo que 7(g*,rx) desempenha o papel da dimen.lião anômala do campo 1/) [58}.

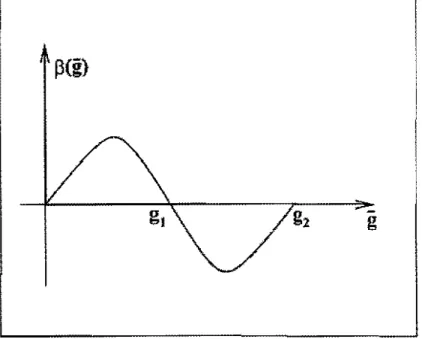
A solução de (1.19) requer o conhecimento de lJ(g), que pode ser obtida através da teoria de perturbação, Os pontos fixos da teoria são particularmente importantes uma vez que na criticalidadc (m O) fi. teoria é invariante de escala, conforme (1.22).

Suponha então que o valor da constante de acoplamento efetiva

!J

est.eja próximo de um dos zeros não trivial de beta (a origem

é

sempre um zero de beta), então podemos escrever, supondo que beta possua zeros simples

Er

s

:5

(09, s) = P(!!) '" (9 - g*)6'(g*) (1.23)

cuja solução é

9

...

g* =

ＨｾＩ

8'(g')

sendo

c

uma constante de integração. Portanto. dependendo do sinal de p'(g*) temos as seguintes situações: 1) para

.8/

(g")

<

0, então

9

-).

r/

quando s -). 00, ou se,la.

o ponto fixo é estáyel no uitnn"Íoleta: 2) para !f(y")

>

O. temos que

li

---)

g'" St'

S

-+

ｾ＠ e o ponto fixo é estável no infravermelho. A natureza desses pontos fixos estão exemplificada.s na figura 1.6.

1.4 As Funções do Grupo de Renormalização

Os coeficientes Ó,

,B

(! '} na equação (1.14) são obtidos taltuh:mdo a ação dos

operadores diferenciais sobre as funções de yértkcs de dois e quatro pontos. Para a função de dois pontos, rP1(p) = _[SP(p)],l = i(p - m) -;- l:, onde E representa as inserções de auto-energia. ternos que até a segunda ordem nos acoplamentos

r(21(p) í(p - rn)

+

Ｚｾ＠

p.'li21

+

Q

p/l1'1

+

,,'(I ....

T}

p." 1;2)

2

+

ｾｾＨｊ＠

-T}p."'Ij21

+

ｾＲＨＱ＠

T}I"'Iá'l,

(1.24)

" _e b - , li2). •

00d

e o

}l:TIlte d O 'E ---7 esta su entend'HI "O. ...:a expressa0 aCima I l 1- = 1ｾ＠ ...ｾ［Ｉｾ＠

denotam amplitudes de Fej'nmzm rpgularizadas. 05 diagramas associados a IJ2}, lf),

,

28

l

P(g}

-g,

g,

_g

Figura 1.6: Exemplos da natureza dos pontos fixos. A origem c o ponto 92 são pontos fiXos infravermelho cst.áycL enquanto que 91 representa um pouto fixo ultra,"ioleta

•

estável.

e

li

2) estão mostrados nas figuras 1.6. L7 e 1.8 respecüyamentc,

r

é um operador

que remove o termo de pólo nas amplitudes sobre a qual ele ar,ua. Como mencionado anteriormente. as amplitude ｉｾＲＱ＠ e [fi que estão assodadas à diagramas de I-Ioop são

finitas.

Analogamentt\ a funçào de quatro pontos,

ate

a terceira ordem nos acoplamentos

é

dada por (omitimos aqui as contribuições que por contagem de potência sâo fhítas, assim como os índkes espinoriais)

4 , . 9 ,g ｾ＠ Hl ,g 2 (·1), 9 :! 2f ! t)

r(

I(p"p,,)Ja,p,)

11

_[

-',\

ｾ＠

,\

ap

I,

-r A,/1

l,

-r ,\ n (I-T)I'

I"

I . '

+

_ＬｾＬ＠

a (I - T) I'" 1,;")

+

Ｚｾｉ＠

(1 - TJ p" Ij,j)

1

(1.25)

sendo novamente que as ampHtudes de ｬＭｾｯｯｰ＠ ｊｾｾ［＠ e

4

1) são finitas devido ao uso da regularização ､ｩｭｾｾｳｩｯｮ｡ｬＬ＠

De uma maneira geral, de acordo com (1.7). se I:'\'l representar uma amplitu-de regularizada amplitu-de ]\f linhas externas do tipo fcrmiônka. então. f"squematlcamente.

I _i (N'

'=

_po 'I _Oi (N)

+

fi' _TUta(I') _• d ' ,

l c mun€lfH que a operaçao

(1 - T) flX< iN)

,

(1- T) ･ｸｾｬｮｬＭＧ＠ (póloiN)

+

ｦｩｮｩｴ｡ｾｎﾻＩ

(1 - T) (pÓIO!N)

+

finita!N)

+

x In /l Res!N)

+

O(f))

ｦｩｮｩｴ｡ｾｎＩ＠

+

:1: lu f-L Res;N) , _(1.26)

onde _{ｒ･ＸｾｎＩ＠} representa o resíduo de diagramas de N pontos, que são dados pelos coeficientes do termo ｾＮ＠

Para a função de dois pontos eles possuem a seguinte estrutura

Resl') = m A3+ Fi B3 Resl') = -i

(m'

A,

+

m Fi B4

+

O(p'))

e

Res;') = -

(m'.4

5

+

TIl' )I B,

+

O(p'))

onde ａｾｳ＠ e ｂＺＭｾ＠ são constantes numéricas. Para a função de quatro pontos temos,

Res(4) _{-2 3,} ·C R O)_{eS-t -(mC,}

+

_{O(p)) , e ｒ･ｳｾＱＩ＠ = i(m'C,}

+

_{0(7")) ,}

3

(1.27) onde C? são constantes numéricas.

Deste modo, (1.24) e (1.25) podem ser escritas como

r(2)(p) i(p - m)

+

ｾ＠ ｊＱｦｉｾＲＩ＠

+

Cl:jlf1J2)

+

(1'2 ｛ｦｩｮｩｴ｡ｾＲＩ＠

+

2 InlL(rn .43

+

)lB3 )]

+

ｾ＠

Q [finita\2) - 2i Infl(m'.4,

+

m FiB,)]

+

o

g- [fi· (" ? I ( ' 4 ' ., B )]

+

1\2 mta;:; - ｾ＠ n f-L m . 5

+

m p 5 (1.28)

e

ri') (Pl, P2, P3, p.,) fl,f -i _A 9

+

9 _A o: I{ ](4) ₁

+

L

_}\2 flf ](-1) _{2 . \}

+

9 0;2 [finita(-l)-₃

2

[

,

2i C3 In 11]

+

ｾＲ＠

o:

｛ｦｩｮｩｴ｡ｾﾷＱＩ＠

- 2 m C4 In

III

ＺｾＺ＠

[finita(')

+

2i m' C5 In

1'1]

(1.29)

-30

Usando as expansões

(5 = LÓiJyinj (1.30)

iJ

J

'''i

L

"ii,j gj

a

(l.31)

i,j

e

(3 =

í:,

(3i,j gi

a

j , (1.32) i,j

substituindo (1.28) e (1.29) em (1.l4) e agrupando os termos proporcionais a m e

p

obtemos9

.5

1,0 =

.5

0,1 = "It.{l = ｾｲｏＮｬ＠

O:

(1.33)

6

0., = -2;(A,

+

B,) • ")(1,2 ｾＭｩｂｊＬ＠ (1.34)

_

m

m

61.1

A

(A, +B,)

,

tU = ｾ A B4 (1.35)

m

2

m'

8

2,0 =

2í={A.+B.)

,

")2,0 = i .1\2 B5 (1.36)

13'.0 = 1, (30.1

=

/3 ,

=

/3'.0 - /30.'

=

O , (1.37)

"

tA,?

= -4i B3 ｾ＠

2 C

il , (1.38)

4

TTl _B.

= ?,' m

C. _

_(1.39)

/h,l

_{- A" .\."}

e

2 2

m m

(3.,0 _{= 2}

_A2

_{C. +4í}

_.\.'

_Bs

(1AO)

­­;:­.,..­­­­c­­­:­­­­­-!iNote que at.é  a Ordl'fll  qut' estamos indo 000 existe mistura entre as comrihuições de f3 com l' e 

Ó, OU  séja, as funções J ｾＬ＠ '}  são completamente determinadas pela função de nktice de  dois  pontos, 

,

31  

Assim, para encontrarmos as funções do grupo de renormalização precisamos dos coeficientes Ah

Ri

e

C

i (i = 3,4,5). Isto será feito nas pr6ximas seções,

".

('I (bl (el

Figura L 7: Diagramas de ordem 0:2 que contribuem para para a auto--energia do

férmion.

1.4.1 Função de Dois Pontos

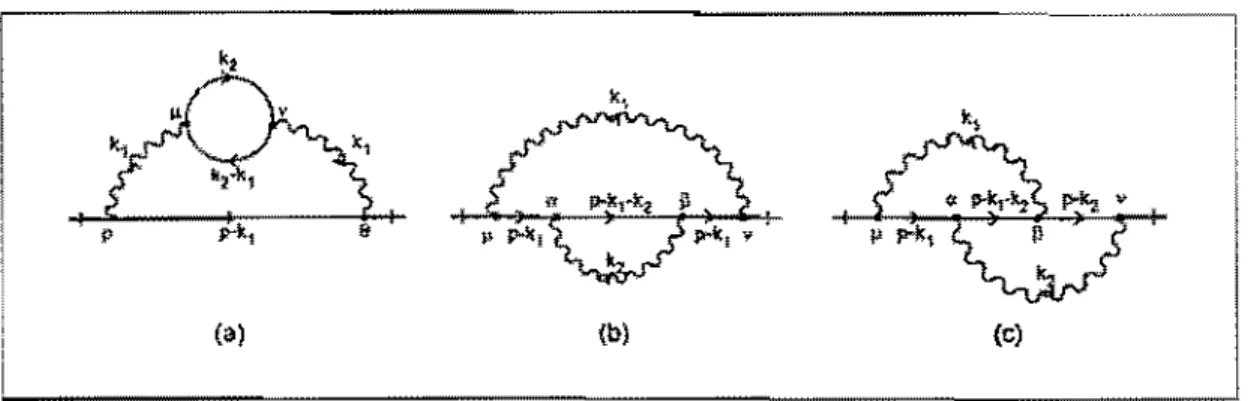
Ordem Q,2

Nesta ordem temo!'> três diagramas que contribuem para a auto-energia do férmioll:

que estão mostrados na figura 1.7, Como eles divergem linearmente no ultra-violeta; podemos usar a segulllte ､･｣ｯｉｰｯｳｩｾ￣ｯ＠ para a paroela de póio1

Parte de Pólo = (A3(;) m

+

B,(i) ]i) _(1.41)

c

onde i = a! b, c representam as três contríbuições para a ｡ｵｴｾ･ｮ･ｲｧｩ｡Ｌ＠ Para i = a, que

corresponde ao diagrama (a) da figura 1.7. temos a seguinte forma analítica)

>

J.

d'k, d'k, [ i

'l

J1

21 _{(a) ＭＴ［ｲｾｦ＠ >. t}

_o

_---

_{ｾＮｴｴ＠ 'Y}

PIi

/la

ＱＱｬｾｧＨＲｩｔＩｊＨＲｲＮｹ＠ .

p-Vl-m'

í)

k'

kO

.)'

i I I

X

T

r ₍ f - - (1.42)

f2 -

m

V2 -

Vl

-

m

kr

k"f

T

onde o sÍLal negativo refer-se ao ［ＧｬｯｻＩｰｾｾ＠ fcrmiônico. c o símbolo Reg significa. que a

expressão acima deve estar regularizada, Para obtermos apenas a parcela d(! pólo

podemos escrever (1.42) tomO.