Modelagem Matemática e Computacional de fenômenos eletrocinéticos em meios porosos carregados eletricamente

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exatas e da Terra

Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Aldemir Cirilo da Silva

Modelagem Matem´

atica e Computacional

de Fenˆ

omenos Eletrocin´

eticos em Meios

Porosos Carregados Eletricamente

Orientador:

Prof. Dr. Sidarta A. Lima

(2)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exatas e da Terra

Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Aldemir Cirilo da Silva

Modelagem Matem´

atica e Computacional

de Fenˆ

omenos Eletrocin´

eticos em Meios

Porosos Carregados Eletricamente

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Es-tat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

Orientador:

Prof. Dr. Sidarta A. Lima

(3)

Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.

Silva, Aldemir Cirilo da.

Modelagem matemática e computacional de fenômenos eletrocinéticos em meios porosos carregados eletricamente / Aldemir Cirilo da Silva. - Natal, 2013.

83 f. : il.

Orientador: Prof. Dr. Sidarta Araujo de Lima

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Matemática Aplicada e Estatística.

(4)

(5)

(6)

Agradecimentos

Elaborar uma disserta¸cão de mestrado não é uma tarefa fácil, exige muito trabalho e esfor¸co. Foi necessária muita dedica¸cão para chegar até aqui. Nesse momento de grande felicidade e realiza¸cão na minha vida, não poderia deixar de agradecer as contribui¸cões de algumas pessoas que conviveram comigo nesses anos de mestrado.

Agrade¸co primeiramente a Deus, por ser minha fortaleza nas horas mais dif´ıceis, por est´a sempre ao meu lado, pelo fato de me amar e permitir que o ame.

Aos meus pais, Maria Dalva e Valmir Vicente, por acreditar que s´eria capaz de terminar esse trabalho, pelas for¸cas que me deram e pela cria¸c˜ao que tive.

Quero expor aqui minha imensa gratidão ao meu orientador Sidarta Araújo de Lima, pela disponibilidade de me orientar e por ter tido tanta paciência ao longo desse mestrado.

Obrigado a minha fam´ılia, em especial aos meus irmãos Almir e José Jaizon, as minhas irmãs Lucyella e Jucyelle, pelo apoio que me derão nas horas que mais precisei e a minha noiva Juliana pelas palavras de incentivo e for¸ca.

Agrade¸co aos meu colegas de mestrados Anna Rafaella, Antonio Marcos, Elisângela, Fabio, Ivanildo, Josemir, Marcio, Maria Jucimeire, Paulo e a todos os outros que aqui não citei o nome, por serem prestativos nas horas que mais necessitei, pelas inúmeras vezes que estudamos juntos e por todas as angustias e alegrias que compartilhamos.

Gostaria de expressar meus agradecimentos a todo o corpo docente do Pro-grama de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica (PPGMAE), pelas disci-plinas ministradas e as dúvidas tiradas, e aos funcionários do Centro de Ciências Exatas e da Terra (CCET) pelos seus servi¸cos nas horas necessárias.

Tamb´em gostaria de agradecer a CAPES pelo apoio financeiro atrav´es da bolsa de estudo.

(7)

Resumo

Neste trabalho apresentamos uma modelagem matemática e computacional de fenômenos eletrocinéticos em meios porosos carregados eletricamente. Consideramos o meio poroso composto por três diferentes escalas (nanoscópica, microscópica e ma-croscópica). Na escala microscópica o dom´ınio é composto por uma matriz porosa e uma fase sólida. Os poros são preenchido por uma fase aquosa composta por solutos iônicos totalmente diluidos, e a matriz sólida consiste de part´ıculas carregadas eletricamente.

Inicialmente apresentamos o modelo matemático que governa a dupla camada elétrica com o intuito de quantificar o potencial elétrico, densidade de carga elétrica, adsor¸cão de ´ıons e adsor¸cão qu´ımica na escala nanoscópica. Em seguida, derivamos o modelo microscópico, onde a adsor¸cão de ´ıons devido a dupla camada elétrica e as rea¸cões de protona¸cão/deprotana¸cão e potencial zeta obtidos na modelagem nanoscópica, surgem na escala microscópica através de condi¸cões de interface no problema de Stokes e equa¸cões de Nerst-Planck que governam respectivamente o movimento da solu¸cão aquosa e o trans-porte dos ´ıons. Desenvolvemos o processo de upscaling do problema nano/microscópico, utilizando a técnica de homogeneiza¸cão de estruturas periódicas, deduzindo o modelo macroscópico com os respectivos problemas de células para os parâmetros efetivos das equa¸cões macroscópicas. Considerando um meio poroso argiloso consistindo de placas da argila caulinita distribu´ıdas paralelamente, reescrevemos o modelo macroscópico numa versão unidimensional.

(8)

Abstract

In this work we present a mathematical and computational modeling of elec-trokinetic phenomena in electrically charged porous medium. We consider the porous medium composed of three different scales (nanoscopic, microscopic and macroscopic). On the microscopic scale the domain is composed by a porous matrix and a solid phase. The pores are filled with an aqueous phase consisting of ionic solutes fully diluted, and the solid matrix consists of electrically charged particles.

Initially we present the mathematical model that governs the electrical double layer in order to quantify the electric potential, electric charge density, ion adsorption and chemical adsorption in nanoscopic scale. Then, we derive the microscopic model, where the adsorption of ions due to the electric double layer and the reactions of pro-tonation/deprotana¸c˜ao and zeta potential obtained in modeling nanoscopic arise in mi-croscopic scale through interface conditions in the problem of Stokes and Nerst-Planck equations respectively governing the movement of the aqueous solution and transport of ions. We developed the process of upscaling the problem nano/microscopic using the homogenization technique of periodic structures by deducing the macroscopic model with their respectives cell problems for effective parameters of the macroscopic equations. Con-sidering a clayey porous medium consisting of kaolinite clay plates distributed parallel, we rewrite the macroscopic model in a one-dimensional version.

(9)

Sum´

ario

1 Introdu¸c˜ao 1

2 Modelagem Nanosc´opica 6

2.1 Modelagem da Dupla Camada El´etrica . . . 7

2.2 Modelagem Matemática dos Fenômenos de Adsor¸cão . . . 9

2.2.1 Adsor¸c˜ao na Camada Dupla . . . 9

2.2.2 Rea¸cão de Protona¸cão/Deprotona¸cão . . . 9

2.3 Solu¸c˜ao Anal´ıtica do Modelo Nanosc´opico . . . 10

2.3.1 Equa¸c˜ao de Poisson-Boltzmann . . . 11

2.3.2 Caso Unidimensional da Adsor¸c˜ao na Camada Dupla . . . 13

2.3.3 Solu¸c˜ao Anal´ıtica Para Potencial Zeta ζ . . . 14

2.4 Sum´ario da Modelagem Nanosc´opica . . . 15

3 Modelagem Microscópica 17 3.1 Rea¸cões de Ioniza¸cão no Bulk . . . 18

3.2 Rea¸c˜oes de Eletr´olise no Bulk . . . 18

3.3 Modelo Microsc´opico . . . 19

3.3.1 Hidrodinˆamica . . . 20

3.3.2 Equa¸c˜ao do Transporte dos Solutos . . . 20

3.4 Modelo Reduzido nas Vari´aveis Prim´arias . . . 21

3.4.1 Equa¸c˜ao do pH . . . 21

3.4.2 Conserva¸c˜ao da Carga El´etrica . . . 21

3.4.3 Condi¸c˜oes de Interface . . . 22

3.5 Sum´ario do Modelo em Duas Escalas . . . 23

4 Homogeneiza¸c˜ao 25 4.1 Processo de Homogeneiza¸c˜ao . . . 25

4.2 Adimensionaliza¸c˜ao dos Parˆametros do Problema . . . 26

4.3 Normaliza¸c˜ao . . . 28

4.4 Expans˜ao Assint´otica . . . 29

4.5 Variáveis Não-Oscilatórias . . . 31

4.6 Problema de Fechamento Microsc´opico . . . 31

4.7 Equa¸c˜ao do Transporte Macrosc´opico . . . 32

4.8 Conserva¸c˜ao da Carga Macrosc´opica . . . 33

4.9 Lei de Darcy Macrosc´opica . . . 34

(10)

4.11 Resumo do Modelo em Trˆes Escalas . . . 36

5 Simula¸c˜oes Computacionais Aplicados `a Solos Argilosos 38 5.1 Meios Porosos Argilosos . . . 38

5.1.1 Caracteriza¸c˜ao Minerol´ogica dos Meios Porosos Argilosos . . . 38

5.1.2 Origem da Carga El´etrica da Argila . . . 39

5.1.3 Caulinita . . . 42

5.2 Modelo Multiescala Unidimensional . . . 42

5.2.1 C´alculo dos Parˆametros Efetivos . . . 42

5.2.2 Sum´ario do Modelo Multiescala Unidimensional . . . 43

5.3 Resultados Computacionais . . . 44

5.3.1 Simula¸c˜oes Num´ericas na Camada Dupla . . . 44

5.3.2 An´alise dos Parˆametros Efetivos . . . 50

6 Discretiza¸cão Numérica por Elementos Finitos 52 6.1 Formula¸cão Fraca do Problema . . . 52

6.2 Formula¸c˜ao Discreta . . . 54

7 Resultados Numéricos 57 7.1 Simula¸cões Numéricas Unidimensionais . . . 57

8 Conclus˜oes e Proposta de Trabalhos Futuros 63

Referˆencias Bibliogr´aficas 65

A Solu¸c˜ao Num´erica Para o Potencial ζ 68

B Equa¸c˜ao de Helmholtz-Smoluchowski 69

(11)

Lista de Figuras

2.1 Descri¸cão da Adsor¸cão de Contra–Íons na Dupla Camada Elétrica.

(Modi-ficado de [31], [33]). . . 7

3.1 F´ısica do Problema Microsc´opico. (Modificado de [31], [33]). . . 17

3.2 Descri¸cão das Rea¸cões de Eletrólise no Bulk. . . 19

3.3 Dom´ınio Microsc´opico. (Modificado de [31], [33]). . . 19

4.1 As três escalas do problema acoplado e aplica¸cão da técnica de homoge-neiza¸cão na escala macroscópica [30], [31]. . . 25

4.2 Dom´ınio Ωε _{de uma fam´ılia de modelos} _{ε-pertubado [30]. . . 26}

5.1 Ensaios microgr´aficos para uma caulinita [17]. . . 39

5.2 Estrutura minerol´ogica da caulinita [18]. . . 40

5.3 Composi¸c˜ao das camadas TO ou 1:1 da caulinita [16]. . . 41

5.4 Geometria da part´ıcula da caulinita com estrutura composta de planos de siloxano/hidroxila e liga¸c˜oes rompidas nas extremidades [31], [32]. . . 41

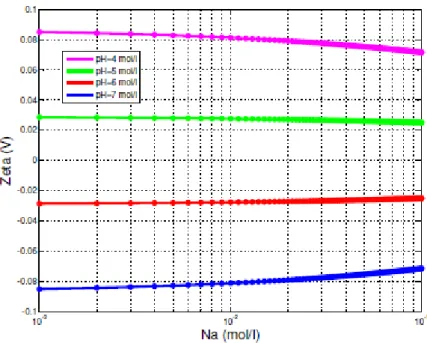
5.5 Potencial zeta em fun¸c˜ao da salinidade para diferentes valores do pH. . . . 46

5.6 Potencial zeta em fun¸c˜ao do pH para diferentes valores da salinidade. . . . 46

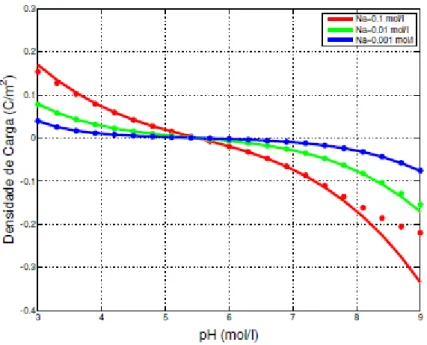
5.7 Densidade de carga em fun¸cão da salinidade para diferentes valores dopH. 47 5.8 Densidade de carga em fun¸cão do pH para diferentes valores da salinidade. 47 5.9 Adsor¸cão qu´ımica de H+ _{em fun¸cão da salinidade para diferentes valores} dopH. . . 48

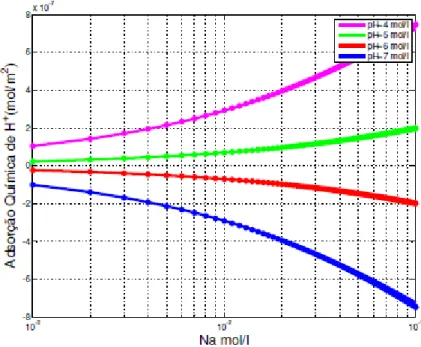
5.10 Adsor¸c˜ao qu´ımica deH+ em fun¸c˜ao dopH para diferentes valores da sali-nidade. . . 48

5.11 Adsor¸c˜ao deN a+ _{em fun¸c˜ao da salinidade para diferentes valores do}_pH_{. . 49}

5.12 Adsor¸c˜ao deN a+ em fun¸c˜ao do pH para diferentes valores da salinidade. . 49

5.13 Condutividade Eletroosm´otica em fun¸c˜ao dopH para diferentes valores da salinidade para porosidadeη = 0.5. . . 50

5.14 Condutividade Eletroosm´otica em fun¸c˜ao dopH para diferentes valores da salinidade para porosidadeη = 0.75. . . 51

6.1 Descri¸cão do Algoritmo para Solu¸cões Numéricas. . . 56

7.1 Evolu¸cão da Concentra¸cão de Sódio para pH = 4.0 nos Eletrodos. . . 58

7.2 Evolu¸c˜ao do pH da Solu¸c˜ao Eletrol´ıtica. . . 58

7.3 Evolu¸c˜ao do Potencial El´etrico. . . 59

7.4 Evolu¸c˜ao da Press˜ao. . . 59

(12)

7.6 Evolu¸c˜ao do pH da Solu¸c˜ao Eletrol´ıtica. . . 61

7.7 Evolu¸c˜ao do Potencial El´etrico. . . 62

7.8 Evolu¸c˜ao da Press˜ao. . . 62

(13)

Lista de Tabelas

(14)

Cap´ıtulo 1

Introdu¸c˜

ao

Meios Porosos carregados eletricamente são caracterizados pela existência de um excesso de carga elétrica superficial na part´ıcula sólida. Diversos materiais naturais, sintéticos e biológicos, tais como, meios porosos argilosos, pol´ımeros, tecidos biológicos e cartilagens apresentam um excesso de carga elétrica na part´ıcula sólida. Tal desbalan¸co de carga dão origem a diversas intera¸cões de natureza f´ısico-qu´ımica e eletroqu´ımica com con-sequências em inúmeros problemas que surgem nos dom´ınios das engenharias e ciências aplicadas. Dentre as diversas aplica¸cões, evidenciamos o movimento de fluidos em re-servatórios de petróleo e gás, aqu´ıferos, estabilidade de po¸cos de petróleo, utiliza¸cão de argilas expansivas como barreira de conten¸cão em aterros sanitários, processos de des-contamina¸cão de solos, inchamento de materiais poliméricos, análise de tecidos biológicos hidratados como cartilagens e o disco invertebral, bem como eletro-remedia¸cão em solos contaminados [1], [26], [30].

Neste trabalho apresentamos uma modelagem matemática e computacional multiescala do escoamento de fluidos e transporte de solutos iônicos em meio porosos carregados eletricamente. Considerando o meio poroso na escala microscópica composto por uma matriz porosa e uma fase sólida, os poros são preenchidos por uma fase aquosa composta por solutos iônicos diluidos no solvente, por sua vez a matriz sólida consiste de part´ıculas de um material com excesso de carga elétrica na superf´ıcie exterior. Como proposta de disserta¸cão de mestrado, o objetivo é derivar um modelo matemático e com-putacional multiescala para a descri¸cão de processos eletrocinéticos em meios porosos car-regados eletricamente. Para a deriva¸cão do modelo multiescala na escala macroscópica, fazemos uso da técnica de upscaling denominada homogeneiza¸cão de estruturas periódicas [2], [4], [26], [30].

(15)

bulk. No ânodo ocorre a oxida¸cão da água que produz hidrogênio H+ _{e gás oxigênio} _O 2.

Por outro lado, no cátodo acontece uma rea¸cão de redu¸cão gerando hidroxilasOH− _{e gás}

hidrogˆenio H2 [11]. Consequentemente, para uma part´ıcula s´olida carregada

negativa-mente, fenômenos eletroosmótico, eletromigrativos e eletrodifusivos impulsionam os ´ıons H+ _{em dire¸cão ao interior da amostra criando uma frente ácida que se move na dire¸cão do}

cátodo. Reciprocamente, para uma part´ıcula sólila carregada positivamente, fenômenos eletrocinéticos impulsionam os ´ıons OH− _{em dire¸cão ao interior da amostra criando uma}

frente alcalina que se move na dire¸c˜ao do ˆanodo [4].

De um ponto de vista da modelagem computacional, diversos trabalhos fo-ram publicados com o intuito de simular numericamente fenômenos eletrocinéticos em meios porosos carregados eletricamente, fazendo uso de uma abordagem puramente ma-croscópica [2], [7], [41], [42]. Neste trabalho propomos a utiliza¸cão da técnica de ho-mogeneiza¸cão de estruturas periódicas para desenvolver uma modelagem multiescala do problema. A teoria de homogeneiza¸cão na análise multiescala de equa¸cões diferenciais parciais iniciaram na década de 70 com os trabalhos de Bensoussan e colaboradores [42]. As principais aplica¸cões da técnica de pertuba¸cão assintótica, consistem na dedu¸cão do modelo macroscópico a partir da descri¸cão dos problemas nas pequenas escalas do pro-blema [30]. Neste contexto, diferentemente da modelagem macroscópica, postula-se o sistema de equa¸cões diferenciais nas escalas inferiores, e fazendo uso de uma expansão asintótica das variáveis de interesse, o modelo matemático macroscópico é deduzido rigo-rosamente, sob a hipótese de separa¸cão de escalas e periodicidade do meio poroso. Além disso, a técnica permite derivar os respectivos parâmetros efetivos do modelo, calculados a partir da solu¸cão de equa¸cões diferenciais postadas nas células periódicas [3], [5], [42]. Os primeiros resultados aplicados as engenharias obtidos durante a década de 80, con-sistiam em derivar modelos multiescala para o acoplamento hidro-dinâmico e transporte de solutos em meios porosos. Trabalhos desenvolvidos por Sanchez-Palencia e colabora-dores possibilitaram derivar a Lei de Darcy a partir da homogeneiza¸cão do problema de Stokes postulado na escala do poro [42]. Posteriomente, pesquisas cient´ıficas publicadas por Auriault e colaboradores permitiram derivar modelos multiescalas para o transporte de solutos em meios porosos. Auriault e Adler discutiram os regimes assintóticos do pro-blema do transporte de solutos não reativos para diferentes valores do número de Péclet, mostrando a forte dependência entre o coeficiente de difusão macroscópica e a velocidade de Darcy quando o regime é fortemente convectivo [7]. Auriault e Lewandowska incorpo-raram os efeitos de adsor¸cão na modelagem multiescala via técnica de homogeneiza¸cão, derivando um modelo para o transporte reativo considerando dois n´ıveis de porosidade. Este trabalho permitiu derivar com acurácia o problema de fechamento para os coefici-entes de parti¸cão, que governa a adsor¸cão dos solutos na superf´ıcie da part´ıcula sólida [9], [42]. Além disso, Auriault e Lewandowska fizeram algumas combina¸cões de ordens de magnitude dos três números adimensionais: o número de Péclet que mede a razão de conveçcão/difusão nos poros, o de Damkohler que é a razão de adsor¸cão/difusão na superf´ıcie da part´ıcula sólida e o terceiro número adimensional representando o gradiente de tempo da concentra¸cão em rela¸cão à difusão nos poros. O objetivo desta pesquisa foi investigar a influência competitiva dos diferentes fenômenos microscópicos sobre o caráter da equa¸cão governante macroscópica [9].

(16)

de homogeneiza¸cão de estruturas periódicas foi aplicada para a modelagem multiescala do acoplamento eletro-qu´ımico-hidro-mecânico em meios porosos argilosos expansivos. A modelagem permite descrever o fluxo de contaminantes e remedia¸cão de solos por técnica de eletrocinética em argilas compactadas em aterros sanitários. Esse modelo foi derivado, com a expansão da descri¸cão da escala dos poros que consiste da eletro-hidrodinâmica con-sistindo do problema de Stokes modificado juntamente com as equa¸cões de Nernst-Planck e o problema de Poisson-Boltzmann que governa o movimento de fluidos, transporte de ´ıons e eletrostática locais na solu¸cão eletrol´ıtica respectivamente. Para as simula¸cões computacionais, foi considerado um arranjo microscópico estratificado para a argila mont-monilonita. Dessa forma os problemas de célula foram resolvidos analiticamente [35].

Posteriormente, Lima et al., desenvolveram uma nova modelagem em três es-calas, nanoscópica, microscópica e macroscópica, para meios porosos carregados eletri-camente, com o objetivo de descrever o acoplamento entre os fluxos eletroosmótico e transporte de solutos iônicos em meios argilosos carregados eletricamente, considerando fenômenos de adsor¸cão eletroqu´ımica na interface da part´ıcula sólida [30], [31]. Esta for-mula¸cão permitiu estabelecer um elo entre os diferentes fenômenos eletroqu´ımicos nas três escalas do problema, considerando o acoplamento na nanoescala com a microescala devido aos fenômenos de adsor¸cão que ocorrem na vizinhan¸ca da part´ıcula sólida. Utilizando a técnica de homogeneiza¸cão de estruturas periódicas, para o acoplamento entre a escala microscópica e macroscópica, foi poss´ıvel derivar o sistema de equa¸cões na escala de Darcy. A liga¸cão entre as duas últimas escalas acontece por causa dos parâmetros efetivos, que se obtém resolvendo os problemas de células de forma computacional. Por sua vez, Igreja, desenvolveu uma modelagem em três escalas (nano-micro-macro), onde os parâmetros nanoscópicos são obtidos analiticamente utilizando o método de pertuba¸cão local [26]. Diferentemente de Lima et al., Igreja derivou os parâmetros efetivos analiticamente, re-duzindo consideravelmente o custo computacional e gerando um modelo macroscópico localmente pertubado onde a não linearidade fica restrita ao problema macroscópico evi-tando o processo sucessivo de downscaling em cada passo macroscópico [26], [30], [31]. Além disso, considerando a hipótese de estacionaridade no modelo multiescala, o sistema de equa¸cões foi discretizado pelo método de Galerkin fazendo uso de um algoritmo se-quencial, incorporando os efeitos hidrodinâmicos ao sistema não linear do transporte dos ´ıons por um pós-processamento. O sistema do transporte foi linearizado pelo método de

Picard.

Neste trabalho, propomos uma modelagem matemática em três escalas (na-noscópica, microscópica e macroscópica) do acoplamento eletroqu´ımico em um meio po-roso argiloso adotando técnica de homogeneiza¸cão de estruturas periódica. As argilas são caracterizadas por possuirem uma nanoestrutura cristalina formada por lâminas te-traédricas e octaédricas. A lâmina tetraédrica é composta por um cátion de sil´ıcio (Si4+₎

cercado por quatro átomos de oxigênio (O2−_{), já a lâmina octaédrica é formada por um}

c´ation de alum´ınio (Al3+_{) circundado por seis agrupamento de hidroxila (OH}−_{) ou por}

´atomos de oxigˆenio (O2−_{) [24], [34]. Na nossa pesquisa abordamos o grupo das}

(17)

Poisson-Boltzmann. Incorporamos ao modelo nanoscópico as rea¸cões de protona¸cão/deprotona¸cão entre o fluido e a superf´ıcie da part´ıcula carregada eletricamente. Na escala microscópica o movimento da solu¸cão aquosa é governado pelo problema de Stokes e o transporte dos solutos por equa¸cões do tipo Nernst-Planck. As equa¸cões microscópicas são suplemen-tadas por condi¸cões de contorno de deslizamento na componente tangencial do campo de velocidade e de adsor¸cão para o transporte das espécies. A partir dos modelos na-noscópico/microscópico desenvolvemos a homogeneiza¸cão do problema derivando o mo-delo na escala de Darcy. Complementando o trabalho de mestrado desenvolvido por Igreja [26], onde as simula¸cões numéricas foram obtidas em regime estacionario, nesta disserta¸cão propomos a exten¸cão para o caso transiente onde o coeficiente de retarda-mento nas equa¸cões parabólicas tornam as equa¸cões mais não lineares, que por sua vez, torna a discretiza¸cão do modelo macroscópico consideravelmente mais complexo. Posteri-ormente, discretizamos o modelo macroscópico via método de elementos finitos utilizando o método de Galerkin, em seguida o sistema de equa¸cões macroscópicas não lineares são linearizadas usando método de Picard, permitindo resolver o sistema de equa¸cões não li-neares iterativamente. Finalmente os resultados computacionais foram obtidos utilizando código in house, desenvolvido em fortran, com o objetivo de descrever a dependência do potencial elétrico e a carga elétrica da part´ıcula sólida com pH da solu¸cão bulk, devido ao acoplamento eletroqu´ımico ocorrido na nanoescala e microescala, que dão origem a fenômenos eletroosmótico, eletromigrativos e eletrodifusivos. O modelo matemático e numérico permite descrever o processo de eletroremedia¸cão dos solos argilosos carregados eletricamente, onde propomos simula¸cões para o caso unidimensional considerando uma microestrutura estratificada.

De um ponto de vista organizacional, além do cap´ıtulo introdutório, o texto é constitu´ıdo de 7 cap´ıtulos:

• No cap´ıtulo 2, descrevemos o modelo matemático que governa a dupla camada elétrica com o intuito de quantificar o potencial elétrico, densidade de carga e ad-sor¸cão de ´ıons. Em seguida incluimos uma rea¸cão de protana¸cão/deprotana¸cão para o cálculo da adsor¸cão qu´ımica.

• No cap´ıtulo 3, descrevemos o modelo microscópico. Postulamos o problema de Stokes para a hidrodinâmica da solu¸cão aquosa combinada com uma condi¸cão de deslizamento na componente tangencial da velocidade para incorporar os efeitos do deslizamento da dupla camada elétrica. Para o transporte de ´ıons utilizamos uma equa¸cão do tipo Nernst-Planck para cada uma das espécies. A adsor¸cão de ´ıons devido a dupla camada elétrica e as rea¸cões de protana¸cão/deprotana¸cão obtidas na modelagem, surgem na escala microscópica através de condi¸cões de interface.

• No cap´ıtulo 4, realizamos a homogeneiza¸cão do problema deduzindo o modelo ma-croscópico com os problemas de células para os parâmetros efetivos das equa¸cões macroscópicas.

(18)

• No cap´ıtulo 6, mostramos a discretiza¸cão numérica do modelo macroscópico via ele-mentos finitos, onde utilizamos o método de Galerkin para derivar a formula¸cão vari-acional do problema. Logo em seguida, obtemos a formula¸cão discreta do problema e adotamos o método interativo de Picard para resolu¸cão do modelo variacional.

• No cap´ıtulo 7, realizamos simula¸cões numéricas para o caso transiente com pH variável no caso unidimensional, onde essas simula¸cões tem por objetivo demonstrar a remedia¸cão de solos contaminados.

(19)

Cap´ıtulo 2

Modelagem Nanosc´

opica

(20)

(a) (b)

Figura 2.1: Descri¸cão da Adsor¸cão de Contra–Íons na Dupla Camada Elétrica. (Modifi-cado de [31], [33]).

2.1 Modelagem da Dupla Camada El´

etrica

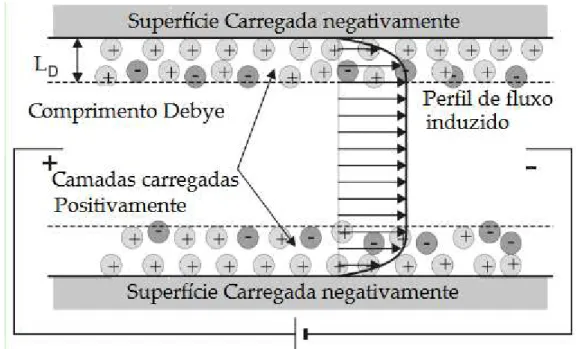
Seja Ωl _{o dom´ınio nanoscópico na dire¸cão normal à superf´ıcie da part´ıcula}

sólida ocupado por uma solu¸cão eletrol´ıtica (ver fig.2.1), e denotando Cb a concentra¸cão

total de cátions ou ânions na solu¸cão bulk, definida como uma solu¸cão eletricamente neutra, a condi¸cão de eletroneutralidade na solu¸cão bulk é dada na forma [40]

Cb =CN ab+CHb =CClb+COHb, (2.1)

onde Cib (i = H+, N a+, Cl−, OH−) representa a concentra¸cão de cátions ou ânions no

bulk.

DenotandoE,ϕ o campo el´etrico e potencial el´etrico na camada dupla respec-tivamente, considerando a teoria de Gouy-Chapman [14], [25] temos que

(

∇ ·E =₋ q

eǫ0eǫr

,

E =−∇ϕ, em Ωl_, (2.2)

onde_eǫ0,eǫrsão a permissividade do vácuo e a constante dielétrica da água respectivamente

e q a densidade volum´etrica de carga definida na forma

q=

4

X

i=1

ziCi, i= (N a+, H+, Cl−, OH−), (2.3)

com Ci a concentra¸c˜ao dos ´ıons em (mol/m3) na camada dupla e zi a valˆencia dos ´ıons.

Pela condi¸cão de equil´ıbrio termodinâmico temos que a igualdade entre os potenciais eletroqu´ımicos dos ´ıons na solu¸cão eletrol´ıtica e fluido bulk é válida [19], [36]. Portanto, igualando as respectivas expressões para os potenciais termodinâmicos, obtemos a rela¸cão de Boltzmann que permite modelar a concentra¸cão dos ´ıons na camada dupla Ci a partir

(21)

Ci = Cibexp (∓ϕ), i= (N a+, H+, Cl−, OH−), (2.4)

ondeϕ =F ϕ/RT é o potencial elétrico adimensional e{F, R, T}são constante de Faraday, constante universal dos gases ideais e temperatura absoluta respectivamente.

Substituindo a distribui¸cão de Boltzmann (2.4) e a condi¸cão de eletroneutra-lidade (2.1) na defini¸cão da densidade volumétrica de carga (2.3), obtemos

q =F Cb[exp (−ϕ)−expϕ] =−2F Cbsinhϕ. (2.5)

Combinando o resultado acima com a equa¸c˜ao (2.2), obtemos a equa¸c˜ao de Poisson-Boltzmann na forma

△ϕ= 2F Cb

e

ǫ0eǫr

sinhϕ, em Ωl. (2.6)

A equa¸cão (2.6) é suplementada por condi¸cões de contorno na superf´ıcie da part´ıcula sólida Γf s e na interface da camada dupla e fluido bulk. Na superf´ıcie do sólido

o campo el´etrico equilibra a densidade de carga superficial, e portanto

∇ϕ_·n=₋ σ

e

ǫ0eǫr

, sobre z = 0. (2.7)

Na solu¸cão bulk o campo elétrico é nulo, logo consideramos uma condi¸cão limite de Newman homogênea na forma

∇ϕ_·n= 0, sobre _kz_{k ≫}LD, (2.8)

ondeLD := (eǫ0eǫrRT /2F2Cb)1/2denota o comprimento de Debye que mede a espessura

ca-racter´ıstica da camada dupla (ver figura 2.1(b)) [28]. Podemos observar que na superf´ıcie da part´ıcula surge uma restri¸c˜ao entre os valores da densidade σ eq devido a condi¸c˜ao de compatibilidade do problema. Portanto, utilizando (2.7) e (2.2), obtemos

σ =₋_eǫ0eǫr∇ϕ

z=o

=₋_eǫ0eǫr

Z

Ωl△

ϕdΩl ₌₋

Z

Ωl

qdΩl_. _(2.9)

Portanto o comportamento do potencial elétrico na nanoescala é governado pelo problema de Poisson-Boltzmann (2.6) juntamente com as condi¸cões de interface (2.7) e (2.8) na forma

        

△ϕ= 2F Cb

eǫ0eǫr

sinhϕ, em Ωl = (0, LD),

∇ϕ_·n =₋ σ

e

ǫ0eǫr

, em z = 0,

∇ϕ_·n = 0, em z _≫LD.

(22)

2.2 Modelagem Matem´

atica dos Fenˆ

omenos de

Ad-sor¸c˜

ao

Uma etapa fundamental da modelagem multiescala de fenômenos eletroqu´ımicos em meios porosos carregados eletricamente, consiste na descri¸cão dos fenômenos de ad-sor¸cão eletroqu´ımica que ocorrem no dom´ınio da camada dupla. Nesta se¸cão propomos a modelagem de fenômenos de adsor¸cão eletroqu´ımica que ocorre na interface fluido/sólido.

2.2.1 Adsor¸

c˜

ao na Camada Dupla

Devido ao excesso de carga elétrica na superf´ıcie da matriz sólida, fenômenos de atra¸cão e repulsão elétrica surgem com o intuito de assegurar a eletroneutralidade local na camada dupla dada pela expressão (2.9). Tais fenômenos dão origem a uma nuvem de contra-´ıons na vizinhan¸ca da part´ıcula sólida caracterizando um processo de adsor¸cão elétrica (ver fig 2.1). A densidade de ´ıons adsorvidos na camada dupla relativa a concentra¸cão bulk é definida por

Γi±: =

Z

Ωl

(Ci± −C_ib)dΩl, i= (N a+, H+, Cl−, OH−). (2.11) Fazendo uso da distribui¸cão de Boltzmann (2.4), a defini¸cão acima para a adsor¸cão elétrica é reescrita na forma

Γi± =C_ib

Z

Ωl

(exp (∓ϕ)−1)dΩl. (2.12)

2.2.2 Rea¸

c˜

ao de Protona¸

c˜

ao/Deprotona¸

c˜

ao

Nesta subse¸cão apresentamos um modelo matemático para descrever a de-pendência do excesso de carga elétrica superficial e adsor¸cão qu´ımica que ocorre na su-perf´ıcie da part´ıcula sólida em termos do pH e salinidade da solu¸cão aquosa [13], [27], [34]. Seguindo o mesmo procedimento descrito por Lima e Igreja [26], [31], neste trabalho propomos uma única rea¸cão de protona¸cão/deprotana¸cão, com o objetivo de modelar a de-pendência da carga elétrica superficial e adsor¸cão qu´ımica em termos dopH e salinidade da solu¸cão aquosa. Dessa forma assumimos uma única rea¸cão de protona¸cão/deprotona¸cão representada na forma

(> M ₋OH)−12 +H+⇋(> M −OH₂)+

1

2, (2.13)

onde (> M) representa os cátions ou ânions residentes na microestrutura mineralógica do sólido. Fazendo uso da lei de a¸cão das massas, definimos a constante de equil´ıbrio K1

associada a rea¸c˜ao qu´ımica acima, como sendo a raz˜ao entre o produto da molaridade dos constituintes resultantes dos reagentes e dos produtos [10], [23]

K1 :=

γ

{(>M−OH2)+ 12_}

γ

{(>M−OH)−12_}CH0+

(23)

onde γi ´e a densidade superficial em (mol/m2) (i=M −OH, M−OH2).

A densidade superficial m´aximal de s´ıtios ´e dada na forma, ΓM AX :=γ_{₍_>M₋_OH₂₎+ 1

2_}+γ_{₍_>M₋_OH₎− 1

2_}, (2.15)

onde {i}=γi/ΓM AX é a concentra¸cão superficial adimensional da espécie i.

Além disso, a concentra¸cão dos cátions H+ _{na interface da part´ıcula sólida}

C_H+

0 quantificada pela rela¸c˜ao de Boltzmann

C_H+

0 = CHbexp −ζ

, (2.16)

onde ζ = F ζ/RT é o potencial zeta adimensional definido como o potencial elétrico na superf´ıcie da part´ıcula sólidaϕ(z= 0). Partindo da expressão (2.14) e usando a defini¸cão da densidade superficial máxima, obtemos

γ

{(>M−OH)−12_} =

ΓM AX

1 +K1C_H+ 0

e γ

{(>M−OH2)+ 12_} =

ΓM AXK1C_H+ 0

1 +K1C_H+ 0

. (2.17)

Utilizando as equa¸c˜oes (2.17) deduzimos a express˜ao que governa a densidade superficial de ´ıons H+ _{quimicamente adsorvidos}

γH+ :=

γ

{(>M−OH2)+ 1₂

}−γ{(>M−OH)−12_}

= ΓM AX 2

K1CH+0 −1

K1CH0++ 1

!

. (2.18)

Além disso, a densidade de carga elétrica superficial é obtida imediatamente na forma

σ:=F γH+ =

FΓM AX

2

K1CH+ 0 −1

K1CH+ 0 + 1

!

. (2.19)

Fazendo uso da rela¸cão (2.16), as expressões (2.18) e (2.19) permitem calcular a densidade superficial de carga elétricaσe adsor¸cão qu´ımicaγH+ em termos do potencial

zeta, pH e salinidade da solu¸cão aquosa. Além disso, podemos observar que os valores de σ e γH+ dependem da constante de equil´ıbrio K₁ e da densidade máxima de s´ıtios

ΓM AX. Tais parˆametros s˜ao fortementes dependentes das propriedades f´ısico-qu´ımicas

da microestrutura mineralógica da matriz sólida. De um ponto de vista experimental, a constante de equil´ıbrio e densidade máxima de s´ıtios podem ser calculados através de experimentos de titula¸cão que permitem construir as curvas da adsor¸cão qu´ımica γH+ em

fun¸c˜ao do pH para uma dada concentra¸c˜ao salina [27], [30], [31].

2.3 Solu¸c˜

ao Anal´ıtica do Modelo Nanosc´

opico

(24)

2.3.1 Equa¸c˜

ao de Poisson-Boltzmann

Considerando uma part´ıcula sólida homogênea com uma carga elétrica su-perficial uniformemente distribu´ıda, a equa¸cão de Poisson-Boltzmann é reduzida a uma forma unidimensional. Considerando o dom´ınio unidimensional nanoscópico Ωl= (0, LD)

na dire¸cão normal à superf´ıcie da part´ıcula sólida, a equa¸cão (2.6) juntamente com as condi¸cões de contorno (2.7) e (2.8) são reduzidas à forma

            

d2_ϕ

dz2 =

2F Cb

e

ǫ0eǫr

sinhϕ, em Ωl = (0, LD),

dϕ

dz = 0, em z ≫LD,

dϕ dz =−

σ

eǫ0eǫr

, em z = 0.

(2.20)

A restri¸cão entre valores da densidade σ e q devido a condi¸cão de compatibi-lidade do problema de Poisson-Boltzmann é dada por

σ=₋_eǫ0eǫr

dϕ dz z=0

=₋_eǫ0eǫr

Z LD

0

d2_ϕ

dz2dz =−

Z LD

0

qdz.

Assim o comportamento do potencial elétrico na camada dupla é governado pela equa¸cão de Poisson-Boltzmann unidimensional (2.20(a)) juntamente com as condi¸cões de interface (2.20(b)) e (2.20(c)). Para derivarmos a solu¸cão anal´ıtica do problema uni-dimensional reescrevemos (2.20(a)) na forma auni-dimensional

d2_ϕ

dz2 = sinh (ϕ), (2.21)

onde z:=z/LD. Multiplicando (2.21) por 2dϕ/dz e utilizando a regra da cadeia obtemos

d dz dϕ dz 2

= 2d

dz[cosh (ϕ)]. (2.22)

Integrando (2.22) a partir de um ponto arbitr´ario z := z/LD no interior da

camada dupla at´e um ponto δ na solu¸c˜ao do bulk, temos que

Z δ z d dz dϕ dz 2 = 2 Z δ z d

dz(cosh (ϕ)).

Fazendo a integra¸cão e assumindo que os efeitos da camada dupla são restritos a uma fina camada de espessura média LD na vizinhan¸ca da part´ıcula sólida (ver figura

2.1), consequentemente na solu¸c˜aobulk em um pontoδ _≫LD suficientemente distante da

(25)

dϕ dz 2 z

= 2 cosh (ϕ)

z −1 ! . (2.23)

Usando o fato que sinh (ϕ/2) = [(coshϕ−1)/2]1/2 e que cosh (ϕ)≥1, ∀ ϕ ∈ ℜ, derivamos a seguinte express˜ao

dϕ

dz =−2 sinh

ϕ 2

. (2.24)

Reordenando a express˜ao acima, temos que

−dz = dϕ

2 sinh ϕ₂ =

dϕ

exp ϕ₂−exp −₂ϕ. (2.25) Integrando a partir da superf´ıcie da part´ıcula onde z = 0 e um ponto z da camada dupla, e usando o fato que ϕ(z= 0) =ζ, obtemos

−

Z z

0

dz =

Z ϕ ζ

dϕ

exp ϕ₂−exp −₂ϕ, (2.26) onde ζ := F ζ/RT é o potencial zeta adimensional na parede da part´ıcula sólida. Para solu¸cão do problema acima propomos a seguinte mudan¸ca de variáveis

t= exp

ϕ 2

e dt= exp

ϕ 2

dϕ

2 ⇐⇒ dϕ= 2dt

t . (2.27) Portanto, substituindo (2.27) em (2.26) derivamos a express˜ao

−z z 0 =

Z exp(ϕ

2) expζ₂

2dt t t₋1_t =

Z exp(ϕ

2) expζ₂

2dt t2₋₁.

Usando o fato que 2 t2₋₁ =

1 (t₋1) −

1

(t+ 1), temos que

−z=

Z exp(ϕ₂)

expζ₂

dt t−1 −

Z exp(ϕ₂)

expζ₂

dt

t+ 1 = ln (|t−1|)

exp(ϕ₂)

expζ₂

−ln (_|t+ 1_|)

exp(ϕ₂)

expζ₂

e consequentemente

−z = lnexp

ϕ 2 −1

−lnexp

ζ 2 −1 −

−lnexp

ϕ 2 + 1

+ lnexp

(26)

Reordenando os termos, obtemos a express˜ao

exp (z) = tanh

ϕ 4

× 1

tanhζ₄ .

Considerando que ζ e ϕ tem o mesmo sinal, usando o fato que tanh(x) ≥

1 _∀x_{∈ ℜ}podemos expressar o potencial el´etrico na camada dupla em fun¸c˜ao do potencial zeta “ζ” e do comprimento de Debye “LD” temos que

ϕ = 4RT

F arctanh

tanh F ζ 4RT ×exp − z LD . (2.29)

Usando (2.20(c)) e (2.29) deduzimos uma rela¸c˜ao entre σ e ζ.

σ = eǫ0eǫrRT F LD

sinh

F ζ 2RT

=p8_eǫ0eǫrRT Cbsinh

F ζ 2RT

. (2.30)

Supondoσconhecido, o sistema algébrico gerado pelas equa¸cões (2.29) e (2.30) estabelece nosso modelo nanoscópico em fun¸cões das variaveis {ϕ, ζ}. Como a carga su-perficial σ e o potencial ζ variam fortemente em fun¸cões do pH e salinidade da solu¸cão eletrol´ıtica, o fechamento do sistema de equa¸cões está restrito a constru¸cão de tal de-pendência [27].

2.3.2 Caso Unidimensional da Adsor¸

c˜

ao na Camada Dupla

Partindo da equa¸c˜ao (2.11), reescremos a adsor¸c˜ao unidimensonal na forma

Γi± =C_ib

Z z=LD

z=0

(exp (_∓ϕ)₋1)dz. (2.31) Sabendo que z :=z/LD e invocando o resultado (2.25), temos que

−dz = dϕ

2 sinh ϕ₂ =

dϕ

exp ϕ₂₋exp −₂ϕ.

Fazendo uso do resultado acima efetuando uma mudan¸ca de vari´avel de inte-gra¸c˜ao em (2.31) obtemos o resultado

Γi± =−C_ibL_D

Z ϕ=0

ζ

"

exp (∓ϕ)−1 exp ϕ₂−exp −₂ϕdϕ

#

=

=CibLD

Z ζ ϕ=0

"

exp _∓ϕ₂ exp _∓ϕ₂₋exp _±ϕ₂ exp ϕ₂₋exp −₂ϕ dϕ

#

=

=_±2CibLD

Z ζ ϕ=0

exp

∓ϕ₂

dϕ= 2CibLD

2 exp

∓ϕ₂

ζ z=0

=

= 2CibLD

exp

∓_2RTF ζ

−1

(27)

2.3.3 Solu¸

c˜

ao Anal´ıtica Para Potencial Zeta

ζ

Para obten¸cao da solu¸cão anal´ıtica do potencialζ, fazemos uso de uma técnica de pertuba¸cão assintótica em (2.19) e (2.30). Agrupando as respectivas equa¸cões obtemos o sistema nanoscópico em termos da densidade de carga superficial σ e do potencial zeta na forma

        

σ=p(8_eǫ0eǫrRT Cb) sinh

ζ 2

,

σ= FΓM AX 2

K1CHbexp −ζ

−1 K1CHbexp −ζ+ 1

!

.

(2.33)

Igualando as duas equa¸cões acima obtemos uma equa¸cão algébrica não linear em termo do potencial zeta

K1CHbexp −ζ−1

K1CHbexp −ζ

+ 1

!

= 2ΛpCbsinh

ζ 2

, (2.34)

onde Λ =p(8_eǫ0eǫrRT)/FΓM AX e Cb =CHb+CN ab.

Com o objetivo de deduzir uma solu¸c˜ao anal´ıtica pertubada, propomos as seguintes mudan¸cas de vari´aveis

x= exp −ζ e h = (K1CHb)−1 = 10(pH−ke), (2.35)

sendo pH = ₋log (CHb), K1 = 10ke com ke o ponto isoel´etrico definido como o valor

do pH onde a carga superficial ´e nula. Sabendo que sinh(t) = (exp(t)−exp(−t))/2, a equa¸c˜ao (2.34) pode ser reescrito na forma

x−h= Λ

r

Cb

x (x+h) (1−x). (2.36) Observando a express˜ao (2.35) percebemos que para valores de pH > ke

te-remos h > 1. Por outro lado, considerando pH < ke obtemos h < 1. Estes resultados

permitem afirmar que x ∈ [0,(ke−pH) ln 10]. Agora, considerando o ponto isoel´etrico

ζ = 0 em (2.34), obtemos CHb = K1−1. Comparando este resultado com (2.35) vem que

pH =ke. Al´em disso, para ζ = (ke−pH) ln 10, substituindo em (2.35) temosx=h, logo

de (2.36) temos que

Λ

r

Cb

x 2h(1−h) = 0, (2.37) o qual valida a aproxima¸c˜ao para valores Cb ≪ 1. O pr´oximo passo baseia-se na

(28)

u:= x−h

h . (2.38)

Substituindo a defini¸c˜ao (2.38) em (2.36) obtemos

u= Λ

s

Cb

h(1 +u)(2 +u) [1−h(1 +u)]. (2.39) Agora, expandindo a parcela não linear da expressão acima em Série de Taylor e desprezendo os termos não lineares, temos que

u≈2Λ

r

Cb

h (1−h−hu)≈2Λ

r

Cb

h (1−h)−2Λ

r

Cb

h hu. (2.40) Logo

1 + 2ΛphCb

u_≈ 2Λ h

p

Cbh(1−h). (2.41)

Dessa forma obtemos uma representa¸cão para o parâmetro pertubativo u em fun¸cão de Cb e pH dada por

u_≈ 1−h h

2Λ√hCb

1 + 2Λ√hCb

. (2.42)

Substituindo a defini¸cão (2.38) em (2.42) e considerando as mudan¸cas de variáveis (2.35), obtemos a expressão semi-anal´ıtica para o potencial ζ dada na forma

ζ _{≈ −}

"

lnh+ ln 1 + 1−h h

2Λ(hCb)

1 2

1 + 2Λ(hCb)

1 2

!#

. (2.43)

O resultado acima representa a solu¸c˜ao pertubada para o potencial ζ em fun¸c˜oes do pH e CN ab.

2.4 Sum´

ario da Modelagem Nanosc´

opica

O modelo nanosc´opico desenvolvido neste cap´ıtulo consiste em dados as cons-tantes _{F, R, T,_eǫ0,eǫr, K1,ΓM AX}, para valores e unidades das constantes ver apˆendice

C, juntamente com o pH e a salinidade _{CHb, CN ab} podemos calcular o potencial zeta

atrav´es da equa¸c˜ao

ζ ≈ −

"

lnh+ ln 1 + 1−h h

2Λ(hCb)

1 2

1 + 2Λ(hCb)

1 2

!#

(29)

onde ζ :=F ζ/RT,Cb =CHb+CN ab, h= (K1CHb)−1 e Λ =

p

(8_eǫ0eǫrRT)/FΓM AX.

De posse do valor deζ obtido na equa¸cão acima podemos calcular as incógnitas do modelo nanoscópico

                                                                      

ϕ = 4RT

F arctanh

tanh F ζ 4RT ×exp − z LD ,

C_H+

0 =CHbexp −ζ

,

σ = (8_eǫ0eǫrRT Cb)1/2sinh

ζ 2

,

γH+ =

ΓM AX

2

K1CH+ 0 −1

K1CH+ 0 + 1

!

,

ΓH+ = 2C_HbL_D

exp

− F ζ

2RT

−1

,

ΓN a+ = 2C_{N ab}L_D

exp

− F ζ

2RT

−1

,

ΓOH− = 2C_OHbL_D

exp F ζ 2RT −1 ,

ΓCl− = 2C_ClbL_D

exp F ζ 2RT −1 . (2.45)

As simula¸cões computacionais na escala nanoscópica das equa¸cões (2.44) e (2.45) que relacionam (ϕ, σ,Γi, γH+) em fun¸cões de (ζ, C_b, C_ib) dependem das propriedades

(30)

Cap´ıtulo 3

Modelagem Microsc´

opica

Neste cap´ıtulo apresentamos a modelagem matemática para o movimento dos fluidos e transporte de solutos na escala microscópica considerando a existência de ele-trodos na fronteira exterior da amostra (ver figura 3.1). Para a deriva¸cão das equa¸cões na escala do poro, assumimos as part´ıculas sólidas carregadas eletricamente, considera-das r´ıgiconsidera-das e incompress´ıveis com matriz porosa saturada por uma solu¸cão aquosa salina. Rea¸cões eletroqu´ımicas de ioniza¸cão, hidrólise e eletrólise dão origem a quatro ´ıons nonova-lentes (N a+_{, H}+_{, Cl}−_{, OH}−_{) dissociados na fase aquosa. Para modelagem do movimento}

da solu¸cão aquosa e transporte dos ´ıons, postulamos a equa¸cão de Stokes que governa a eletrohidrodinâmica do fluido e equa¸cões de Nernst-Planck do cont´ınuo para o movimento dos solutos iônicos, juntamente com condi¸cão de interface para o deslizamento dos ´ıons na camada dupla e adsor¸cão eletro-qu´ımica das espécies na interface fluido/sólido modela-dos no cap´ıtulo anterior. O sistema de equa¸cões microscópico/nanoscópico, possibilitará posteriormente o upscaling do problema para a escala macroscópica utilizando a técnica de homogeneiza¸cão.

(31)

3.1 Rea¸c˜

oes de Ioniza¸

c˜

ao no

Bulk

A existência de ´ıons parcialmente ou completamente dissociados em uma solu¸cão eletrol´ıtica pode ser descrito pela teoria de ioniza¸cão que propõe o equil´ıbrio eletroqu´ımico entre ´ıons e moléculas não ionizadas [15]. Por exemplo, o cloreto de sódio (N aCl) quando dissolvido em uma solu¸cão aquosa se comporta como eletrólitos fortes, e portanto ocorre dissocia¸cão completa da molécula na forma

N aCl _→N a+₊_Cl−_. _(3.1)

Por outro lado, a molécula da água é caracterizada por ser um solvente que apresenta uma pequena condutividade elétrica. Tal caracter´ıstica é consequência do fenômeno denominado auto-ioniza¸cão representado pela seguinte rea¸cão de hidrólise [15], [23]

H2O ⇋H++OH−. (3.2)

Considerando o equil´ıbrio termodinâmico da solu¸cão aquosa, a lei de a¸cão de massas é válida. Portanto o produto iônico da água é dado na forma

KW :=CHbCOHb, (3.3)

onde CHb eCOHb são as concentra¸cões molares dos solutosH+ eOH− na solu¸cão aquosa.

Para condi¸cões padrão de temperatura e pressão, o valor t´ıpico do produto iônico éKW ∼=

10−14_(mol/l)2 _logo

CHbCOHb = 10−14(mol/l)2. (3.4)

3.2 Rea¸c˜

oes de Eletr´

olise no

Bulk

A existência de eletrodos no exterior da amostra dão origem a fenômenos de eletrólise na vizinhan¸ca dos ânodos e cátodos (ver figura 3.2) [11]. No ânodo ocorre a oxida¸cão da água que produz hidrogênio H+ _{e gás oxigênio} _O

2

• Anodo (+): 2Hˆ 2O−4e− →O2 ↑+4H+.

Enquanto que no cátodo acontece uma rea¸cão de redu¸cão gerando hidroxilas OH− _{e gás}

hidrogˆenio H2 [11]

• C´atodo (-): 2H2O+ 2e− →H2 ↑+2OH−.

As rea¸cões eletroqu´ımicas descritas acima descrevem o processo de eletrólise de uma solu¸cão aquosa na presen¸ca de eletrodos. É importante ressaltar que a rea¸cão no ânodo produz uma acidifica¸cão da solu¸cão aquosa enquanto que no cátodo ocorre uma basifica¸cão. Consequentemente, para uma part´ıcula sólida carregada negativamente, fenômenos eletroosmótico, eletromigrativos e eletrodifusivos impulsionam os ´ıons H+ _em

(32)

Figura 3.2: Descri¸cão das Rea¸cões de Eletrólise no Bulk.

3.3 Modelo Microsc´

opico

Seja ΩM = Ωs ∪Ωf ⊂ ℜ3 o dom´ınio microsc´opico ocupado por um meio

poroso bif´asico constitu´ıdo por uma fase s´olida Ωs e uma fase fluida Ωf com interface

fluido s´olido Γf s (ver figura 3.3(a)). O dom´ınio ocupado pela fase s´olida consiste de

part´ıculas sólidas carregadas eletricamente com uma carga elétrica superficial distribu´ıda uniformemente na superf´ıcie da fase sólida, considerada r´ıgida e incompress´ıvel (ver figura 3.3(b)). O dom´ınio Ωf consiste da matriz porosa completamente preenchida por uma

solu¸cão eletrol´ıtica considerada incompress´ıvel composta por quatro ´ıons nonovalentes (N a+_, _H+_,Cl−_, _OH−_{). Considerando a hipótese de solu¸cão dilu´ıda onde os solutos se}

encontram completamente dissolvidos na fase l´ıquida, o movimento do fluido é obtido pelas equa¸cões da eletrohidrodinâmica e o transporte dos ´ıons na solu¸cão intersticial pelas equa¸cões de Nernst-Planck do cont´ınuo [29], [41].

(a) (b)

(33)

3.3.1 Hidrodinˆ

amica

Para deriva¸cão do modelo microscópico para eletrohidrodinâmica, considera-mos o fluido newtoniano, incompress´ıvel e efeitos inerciais de conveçcão e gravitacionais desprez´ıveis. Portanto o modelo matemático para o movimento da solu¸cão aquosa no dom´ınio microscópico é dado pelo clássico problema de Stokes na forma

∇ ·v= 0,

µf△v− ∇p= 0, em Ωf, (3.5)

onde v é a velocidade do fluido, pa pressão termodinâmica e µf a viscosidade do fluido.

3.3.2 Equa¸c˜

ao do Transporte dos Solutos

Denotando t o tempo caracter´ıstico associados ao movimento dos ´ıons pro-duzidos através das rea¸cões de ioniza¸cão, hidrólise e eletrólise. O transporte dos ´ıons é governado por equa¸cões de conveçcão/eletro-difusão de Nernst-Planck [29], [41]

∂Ci

∂t +∇ ·(Civ) = ∇ ·

DiCi

RT ∇µi

+ ˙mi, (3.6)

onde Ci,Di e µi (i=N a+,H+,Cl−,OH−) representam a concentra¸c˜ao molar, o

coefi-ciente de difusão dos solutos e o potencial termodinâmico eletroqu´ımico respectivamente, com ˙mi um termo de produ¸cão de massa de ´ıons H+ e OH− devido a hidrólise da água.

Portanto ˙mi = 0 para (i=N a+, Cl−).

O potencial termodinâmico eletroqu´ımico µi é dado pela seguinte expressão

µi(T, P, Ci, φ) =µ0i(T, P) +RT ln(Ci) +

ziF φ

RT . (3.7)

Combinando as express˜oes (3.6)-(3.7) obtemos as equa¸c˜oes do transporte dos solutos na forma

                  

∂CN ab

∂t +∇ ·(CN abv)− ∇ ·

DN a ∇CN ab+CN ab∇φ= 0,

∂CHb

∂t +∇ ·(CHbv)− ∇ ·

DH ∇CHb+CHb∇φ+ ˙m= 0,

∂CClb

∂t +∇ ·(CClbv)− ∇ ·

DCl ∇CClb−CClb∇φ

= 0, ∂COHb

∂t +∇ ·(COHbv)− ∇ ·

DOH ∇COHb−COHb∇φ

+ ˙m = 0,

em Ωf, (3.8)

onde φ =F φ/RT é o potencial elétrico adimensional devido a existência de eletrodos no exterior da amostra.

´

(34)

3.4 Modelo Reduzido nas Vari´

aveis Prim´

arias

Nesta subse¸cão uma versão simplificada do modelo microscópico (3.8) é obtida eliminando as variáveis secundárias _{CClb, COHb, ˙m}, reformulando o transporte dos ´ıons

nas variáveis primárias relativa as concentra¸cões {CN ab,CHb}e potencial elétricoφ. Para

tanto considerando as expressões (2.1) e (3.4) reescrevemos o modelo microscópico (3.8) em uma forma reduzida denominada equa¸cão do pH e conserva¸cão da carga elétrica.

3.4.1 Equa¸c˜

ao do

pH

A equa¸c˜ao do pH consiste em eliminar o termo de fonte ˙m derivando as equa¸c˜oes do transporte dos ´ıons em termos da diferen¸ca entreH+_e_OH−_{. Fazendo uso da}

expressão para o produto iônico da água (3.4), subtraindo as equa¸cões (3.8(b))-(3.8(d)) obtemos a equa¸cão não linear para o transporte dos ´ıons H+ _{dada por}

∂(ΘCHb)

∂t +∇ ·(ΘCHbv)− ∇ ·

h b

DH ∇CHb+CHb∇φ

i

= 0, (3.9)

com DbH :=DH +

DOHKW

C2

Hb

e Θ = 1₋ KW C2

Hb

.

3.4.2 Conserva¸

c˜

ao da Carga El´

etrica

Com o objetivo de eliminar as concentra¸c˜oes dos ˆanions CClb e COHb e obter

uma equa¸c˜ao adicional nas vari´aveis _{CN ab, CHb}, reescrevemos os fluxos total dos ´ıons

em termos da corrente el´etrica If definido na forma [30], [31]

If :=F

˜

JNa+˜JH−J˜Cl−˜JOH

,

onde J˜i := C_ibv−D_i ∇C_ib±C_ib∇φ

, (i = N a+_{, H}+_{, Cl}−_{, OH}−_{) denota o fluxo total}

convectivo eletro-difusivo dos solutos iˆonicos.

Partindo da defini¸cão acima e utilizando as equa¸cões de Nernst-Planck (3.8) juntamente com as condi¸cões de eletroneutralidade (2.1) e produto iônico da água (3.3), deduzimos a equa¸cão da conserva¸cão da carga em regime estacionário

∇ ·If = 0,

If =A∇C_{N ab}+B∇C_Hb+C∇φ, (3.10) onde

A:=F (DN a−DCl),

B :=F

DH −DCl+

(DOH −DCl)KW

C2

Hb

, (3.11)

C :=F

(DN a+DCl)CN ab+ (DH +DCl)CHb+

(DOH −DCl)KW

CHb

(35)

3.4.3 Condi¸

c˜

oes de Interface

Para complementar o modelo microscópico (3.5) e (3.8), as equa¸cões deduzidas são suplementadas por condi¸cões de contornos na interface fluido/sólido Γf s. Sob hipótese

de camada dupla fina onde o tamanho caracter´ıstico da camada dupla ´e suficientemente inferior ao comprimento de Debye l _≪LD, o movimento dos ´ıons e adsor¸c˜ao dos solutos

na camada dupla (dom´ınio nanoscópica), são modelados na escala microscópica através de condi¸cões de interface. Portanto o movimento dos ´ıons na camada dupla são incorpo-rados no problema de Stokes considerando uma condi¸cão de deslizamento na componente tangencial da velocidade dada pela equ¸ca¸cão Helmholtz-Smoluchowski [38]. Portanto, denotando n e τ os vetores normais exterior e tangente à superf´ıcie do sólido Γf s, temos

que

v·τ =Vslip,

v·n= 0, sobre Γf s,

onde Vslipdenota um campo escalar definido na interface Γf s que governa o salto da

com-ponente tangencial da velocidade [20]. Para calcularmos Vslip tomamos a m´edia

trans-versal da velocidade eletroosmótica unidimensional do problema de Stokes modificado na dire¸cão tangencial à superf´ıcie da part´ıcula sólida (ver apêndice B). Dessa forma obtemos a equa¸cão de Helmholtz-Smoluchowski para a velocidade de deslizamento tangencial [28], [34], [37]

Vslip=v·τ =−KE∇φ·τ, com KE =−e

ǫ0eǫrζ

µf

, sobre Γf s, (3.12)

onde KE desempenha o papel de uma condutividade eletroosm´otica. Al´em disso, a

condi¸c˜ao de interface para transporte dos ´ıons, consideramos que a adsor¸c˜ao qu´ımicaγH+

é exclusiva aos ´ıons de hidrogênio, enquanto que a adsor¸cão elétrica na camada dupla Γié

comum a todos os solutos iônicos. Dessa forma, as condi¸cões de interface part´ıcula/poro para equa¸cões de Nernst-Planck são representadas por uma condi¸cão de Newmann não homogênea na forma [8]

−DN a ∇CN ab+CN ab∇φ·n =

∂ΓN a

∂t ,

−DH ∇CHb+CHb∇φ·n=

∂ΓH

∂t + ∂γH

∂t ,

−DCl ∇CClb−CClb∇φ

·n= ∂ΓCl ∂t ,

−DOH ∇COHb−COHb∇φ

·n= ∂ΓOH ∂t .

sobre Γf s, (3.13)

´

(36)

Ao invocar as leis constitutivas para as adsor¸cões reconstru´ıda a partir da modelagem nanoscópica (2.44)-(2.45), fazendo uso das condi¸cões de eletroneutralidade (2.1) e hidrólise da água (3.3), reformulamos as condi¸cões de contorno (3.13) em termos de variáveis primárias [30], [31]

        

−DN a ∇CN ab+CN ab∇φ

·n= ∂ΓN a ∂t ,

−DbH ∇CHb+CHb∇φ

·n= ∂

∂t(γH + ΓH −ΓOH), A_∇CN ab+B∇CHb+C∇φ·n= 0.

sobre Γf s,

3.5 Sum´

ario do Modelo em Duas Escalas

Dadas as constantes {µf, KW, DN a, DH DCl, DOH, F, R, T}, as fun¸c˜oes {Θ,

b

DH,B}dependente deCHbe{Γi,γH+,C}dependentes de{C_{N ab},C_Hb}, o modelo descrito

em duas escalas (nanoscópica/microscópica) consiste em achar os campos microscópico

{v, p,CN ab, CHb,CClb,COHb, φ,If, JNa, JH} satisfazendo

                                        

∇ ·v= 0,

µf△v− ∇p= 0,

∂CN ab

∂t +∇ ·(CN abv) +∇ ·JNa= 0, ∂(ΘCHb)

∂t +∇ ·(ΘCHbv) +∇ ·JH = 0,

∇ ·If = 0,

JNa=−DN a ∇CN ab+CN ab∇φ,

JH =−DbH ∇CHb+CHb∇φ,

If =A∇C_{N ab}+B∇C_Hb+C∇φ, COHb=

10−14

CHb

,

CClb =CN ab+CHb−COHb.

em Ωf, (3.14)

Com as respectivas condi¸c˜oes de interface fluido/s´olido

                

v·τ =−KE∇φ·τ,

v_·n = 0,

JNa·n=α₁ ∂CN ab

∂t +β1 ∂CHb

∂t ,

JH·n=α₂ ∂CN ab

∂t +β2 ∂CHb

∂t ,

If ·n= 0,

sobre Γf s, (3.15)

onde DbH := DH +

DOHKW

C2

Hb

, Θ = 1− KW

C2

Hb

(37)

KE =−e

ǫ0eǫrζ

µf

, α1 =

∂ΓN a

∂CN ab

, β1 =

∂ΓN a

∂CHb

, (3.16)

α2 =

∂ΓH

∂CN ab

+ ∂γH ∂CN ab −

∂ΓOH

∂CN ab

, β2 =

∂ΓH

∂CHb

+ ∂γH ∂CHb −

∂ΓOH

∂CHb

, (3.17)

com o potencial zetaζ e adsor¸c˜oes eletroqu´ımica obtidas a partir da modelagem deduzida na escala nanosc´opica

                                                            

ζ ≈ −

"

lnh+ ln 1 + 1−h h

2Λ(hCb)

1 2

1 + 2Λ(hCb)

1 2

!#

,

C_H+

0 =CHbexp −ζ

,

γH =

ΓM AX

2

K1CH0+ −1

K1CH0+ + 1

!

,

ΓH = 2CHbLD

exp

− F ζ

2RT

−1

,

ΓN a = 2CN abLD

exp

−_2RTF ζ

−1

,

ΓOH = 2COHbLD

exp F ζ 2RT −1 ,

ΓCl = 2CClbLD

exp F ζ 2RT −1 , (3.18)

onde ζ :=F ζ/RT,Cb =CHb+CN ab, h= (K1CHb)−1 e Λ =

p

(38)

Cap´ıtulo 4

Homogeneiza¸

c˜

ao

De posse do modelo microscópico derivado no cap´ıtulo anterior, neste cap´ıtulo demonstraremos o procedimento de upscaling do modelo derivado na escala do poro (fi-gura 4.1). Para tanto, fazemos uso da técnica de homogeneiza¸cão de estruturas periódicas para deduzir o sistema de equa¸cões efetivas na escala macroscópica (figura 4.1) [42]. A metodologia consiste em, considerando o meio poroso macroscópico com uma microes-trutura periódica, definimos um parâmetro de pertuba¸cão assintótica ε :=l/L, onde l e L representam respectivamente a dimensão caracter´ıstica microscópica e macroscópica. Uma das hipóteses para assegurar a validade da teoria de homogeneiza¸cão consiste em assumir ε_≪1, ou seja, l _≪Lgarantindo a hipótese de separa¸cão de escala nas variáveis espaciais o que permite definir dois sistemas de coordenadas para cada escala. Neste cap´ıtulo discutimos o processo de upscaling do problema, apresentamos a adimensiona-liza¸cão e normaadimensiona-liza¸cão das equa¸cões, e em seguida postulamos uma expansão assintótica das variáveis do problema com o objetivo de obter o modelo macroscópico com os respec-tivos problemas de células na escala microscópica e nanoscópica [5], [8].

Figura 4.1: As três escalas do problema acoplado e aplica¸cão da técnica de homogeneiza¸cão na escala macroscópica [30], [31].

4.1 Processo de Homogeneiza¸c˜

ao

(39)

Ωε _{= Ω}ε f

S

Ωε

s, onde Ωεf e Ωεs representam respectivamente o dom´ınio do fluido e s´olido,

juntamente com a condi¸c˜ao Γε

f s na interface fluido/s´olido ε-pertubados. O dom´ınio Ωε

é reconstru´ıdo pela replica¸cão de uma micro célula Yε_{. De uma maneira semelhante, os}

subdom´ınios Ωε

f e Ωεs juntamente com a interface Γεf s s˜ao dadas pela uni˜ao dos dom´ınios

de c´elulas adjacentes Yε

f eYsε e interfaces∂Yf sε respectivamente [30], [31] . Cada dom´ınio

elementar é congruente a célula unitáriaY composta de subdom´ıniosYf eYs, com interface

∂Yf s. Comε= 1 observamos o fenˆomeno na escala do poro, onde o dom´ınio Ω mostra alto

grau de heterogeneidade. O dom´ınio homogeneizado ou macrosc´opico ´e obtido fazendo o ε_→0, limite na qual a heterogeneidade tende a zero (ver figura 4.2).

Figura 4.2: Dom´ınio Ωε _{de uma fam´ılia de modelos} _{ε-pertubado [30].}

A hip´otese de sepera¸c˜ao de escalas l _≪ L nos induz a observar o problema parametrizado por dois sistemas de coordenadas x e y, onde x = (x1, x2, x3) denota a

vari´avel macrosc´opica que descreve o meio homogeneizado e y= (y1, y2, y3) a coordenada

microscópica da ordem de grandeza das heterogeneidades. Tais variáveis espaciais são relacionadas na forma y = x/ε. O escalonamento mostra que as distâncias na escala macroscópica são amplificada pelo fator 1/ε na escala microscópica.

4.2 Adimensionaliza¸c˜

ao dos Parˆ

ametros do Problema

O processo de adimensionaliza¸cão consiste em reescrever o sistema de equa¸cão em termos das variáveis de referência. Para tanto, vamos seguir o procedimento proposto por Auriault [5]. Denotando “ref”para as grandezas de referência e “_∗” para as grande-zas adimensionalizadas, as variáveis adimensionais das equa¸cões do modelo microscópico (3.14)-(3.17) são dadas na forma

x∗ = x

L; v

∗ ₌ v

Vref; p

∗ ₌ p

Pref; C

∗

N ab=

CN ab

C_{N a}ref; C_Hb∗ = CHb

C_Href; t

∗ ₌ t

tref; φ

∗ ₌ φ

φref; ζ

∗ ₌ ζ

φref; Db

∗

H =

b

DH

;

∇∗ = 1

L∇; I

∗

f =

If

I_fref; J

∗

Na=

JNa

J_{N a}ref; J

∗

H =

JH J_Href; α∗_i = αi

αref_i ; β

∗

i =

βi

(40)

Definimos os n´umeros adimensionais

QL=

µfVref

prefL

; PLN a =

L2

DN atref

; PLH =

L2

DHtref

; P eN a =

VrefL

DN a

; P eH =

VrefL

DH

;

Daα1 =

αref₁ L DN atref

; Daβ1 =

β₁refC_HrefL DN aCN areftref

; Daα2 =

αref₂ C_{N a}refL DHCHreftref

; Daβ2 =

β₂refL DHtref

;

B∗ ₌

DH −DCl

DN a−DCl

+(DOH −DCl)KW (DN a−DCl)CHb2

C_Hbref

C_{N ab}ref ; (4.1) C∗ ₌ (DN a+DCl)CN ab

(DN a−DCl)CN abref

+ (DH +DCl)CHb (DN a−DCl)CN abref

+ (DOH −DCl)KW (DN a−DCl)CN abrefCHb

.

Inserindo os n´umeros adimensionais no modelo microsc´opico, obtemos o mo-delo adimensionalizado na forma

                            

∇∗_·_v∗ _{= 0,}

QL△∗v∗− ∇∗p∗ = 0,

PLN a

∂C∗

N ab

∂t∗ +P eN a∇ ∗

·(C_{N ab}∗ v∗) +_∇∗_·J∗Na= 0, PLH

∂(ΘC∗

Hb)

∂t∗ +P eH∇ ∗

·(ΘC_Hb∗ v∗) +_∇∗_·J∗H = 0,

∇∗_·_I∗

f = 0,

J∗

Na=−(∇∗CN ab∗ +CN ab∗ ∇∗φ∗),

J∗

H =−DbH∗ (∇∗CHb∗ +CHb∗ ∇∗φ∗),

I∗

f =∇∗CN ab∗ +B∗∇∗CHb∗ +C∗∇∗φ∗.

em Ωf, (4.2)

As condi¸c˜oes de interface adimensionalizada s˜ao dadas por

                

v∗_·

τ =ULζ∗∇∗φ∗·τ,

v∗_·_n_{= 0,} J∗

Na·n=Daα1α

∗

1

∂C∗

N ab

∂t∗ +Daβ1β

∗

1

∂C∗

Hb

∂t∗ , J∗

H·n =Daα2α

∗

2

∂C_{N ab}∗

∂t∗ +Daβ2β

∗

2

∂C_Hb∗ ∂t∗ , I∗

f ·n = 0.

sobre Γf s, (4.3)

No modelo adimensional (4.2)-(4.3), o n´umero QL quantifica a raz˜ao entre a

for¸ca de viscosidade e o gradiente de pressão macroscópico no problema de Stokes. O número de Péclet P ei (i =N a, H) quantifica a razão entre efeitos convectivo e difusivo.

Por sua vez, os n´umeros de Damkholer Daαi e Daβi (i = 1, 2) quantificam a raz˜ao entre

a adsor¸c˜ao dos ´ıons na interface fluido/s´olido e os efeitos difusivos, e UL =

K_Erefφref

VrefL