Construção e análise de códigos esféricos com boas taxas binárias.

Uma Publiação daSoiedade BrasileiradeMatemátiaApliadaeComputaional.

Construção e análise de ódigos esférios om boas

taxas binárias 1

L.R.B. NAVES 2

, IFRJ - Instituto Federal do Rio de Janeiro, Campus Volta

Redonda,27213-100VoltaRedonda,RJ,Brasil

C. TOREZZAN 3

, Fauldade de Ciênias Apliadas, UNICAMP -

Universi-dadeEstadualdeCampinas,13484-350Limeira,SP,Brasil

S.I.R. COSTA 4

, Departamento de Matemátia, UNICAMP - Universidade

EstadualdeCampinas13081-970Campinas,SP,Brasil

Resumo. Neste trabalho onsideramos a distribuição de um onjunto disreto

de pontossobre a superfíie de uma esfera eulidiana unitária, omo propósito

de onstruiródigosesférios parao anal Gaussiano. Apresentamos famílias de

ódigos esférios estruturados, que podem ser onstruídas em tempo linear para

dimensõesparesesuperam,paraalgunsparâmetros,olimitanteinferiordeShannon

paraataxabináriadeinformação.

Palavras-have. Matemátiadisreta,Códigosesférios,taxabinária.

1. Introdução

Um ódigoesfério éum onjunto nito de pontos sobre aesfera unitáriado

R

R

R

n

.

Vamos denotarpor

C

(M, n, ρ)

um ódigosobre aesferaunitária

S

n

−

1

_⊂

_R

_R

_R

n

, om

M

pontos, osquaispossuemdistâniaeulidianamínimaaoquadradoiguala

ρ

.

Oproblema de aloar pontos sobre asuperfíie de uma esfera eulidianatem

atraído a atenção de matemátios, engenheiros e ientistas em geral, devido sua

amplagamadeapliaçõesemdiversasáreas[8℄.

Demodogeral,aonstruçãodeódigosesfériosenvolveabusaporuma

on-guraçãode

M

pontossobre

S

n

−

1

queotimizaertosparâmetrosdeinteresse,que

podemser: distâniamínimaentrepontos,raiodeobertura,kissingnumber,

ener-giamédia,oeiente dequantização,dentreoutros. A esolhadoparâmetroaser

otimizadovaidependerdesuaapliação.

1

Trabalho apresentado no Congressode Matemátia Apliadae Computaional - Sudeste

-2011.

2

ligia.navesifrj.edu.br-BolsistadoCNPQ.

3

ristiano.torezzanfa.uniamp.br.

4

Emteleomuniações,pontosaloadossobreasuperfíiedeumaesferaunitária

sãoutilizadosparaaomuniaçãoatravésdeumanalGaussianoesãoa

generali-zaçãonaturalparaaonheidamodulaçãophaseshiftkeying (PSK),queutilizaos

vértiesdeumpolígonoregularinsritonairunferêniaunitáriado

R

R

R

2

.

Para este propósito é desejável maximizaro númerode pontos sobre a esfera,

alémdeonstruiródigosquetenhamalgumaestruturaadiionalquepermitalidar

omaomplexidadede odiaçãoedeodiação. Nestesentido,onstruções

es-truturadassãopriorizadasemrelaçãoàsoluçõesobtidasviamétodosdeotimização

numéria.

O problema de maximizar o número de pontos sobre uma superfíie esféria

sujeitoaestaremafastadosdeumadistânia

d

éequivalenteaoproblemade

empa-otar omaiornúmerodehapéusesfériosomângulode aberturaentral iguala

2arcsen(d/2)

(Figura1).

Figura1: Dozehapéusesfériosrelaionadosaoódigo

C

(12,

3,

2

−

2/

√

5)

.

Quandoadistania

ρ

deresee/ouadimensão

n

aumenta,onúmerodepontos

M

podetornar-searbitrariamentegrande. Quandoneessário,aomparaçãoentre

ódigosesfériosdistintoséfeitaatravésdemedidasquerelaionamosparâmetros

(M, n, ρ)

. A densidade deempaotamento do ódigoé uma dessas medidas e

ex-pressa afraçãoda áreadasuperfíie esfériaqueéoupadapeloshapéus. Outra

medidausualétaxadeinformaçãobinária(outaxadeinformação),queédenida

por:

R

:= lim sup

log

2

(M

)

n

.

Comoodesaodeenontraródigos esfériosótimoséaindaumproblemaem

aberto [8℄, adesoberta delimitantes para funções querelaionam osparâmetros

(M, n, ρ)

, ou deonstruçõesexplíitas para osmesmos parâmetros,onstituem-se

emimportantesontribuiçõesparaestaárea.

Chabautyem1953 [2℄ eShannonem1959[7℄apresentaram deforma

indepen-denteumlimitante inferiorpara

R

omofunçãode

ρ

dadopor:

Embora este sejao melhorlimitante inferior onheidoaté o momento para a

taxa de informação de ódigos esférios, sua dedução é baseada em argumentos

existeniaisquenãoauxiliamnaonstruçãoefetivadeódigos.

Umaabordagemonstrutivafoiapresentada em[6℄,onsiderandoódigos

esfé-riosonstruídosemtempopolinomial,ujataxadeinformação

R

pol

(ρ)

obedee

R

pol

(ρ)

≥

0.5R

CS

(ρ).

P. Solée J.C.Belore [10℄, baseadosna existêniade alguns empaotamentos

retiulados, apresentaram a onstrução deódigos esférios em tempo polinomial

queatingem ataxa

R

L

:=

−

0.5 log

2

(ρ)

emostraramque, paravaloresde

ρ

sui-entementepequenos,

R

CS

(ρ)

−

R

L

(ρ) =

O(ρ

2

₎

.

Nestetrabalhoapresentamosumafamíliadeódigosesfériosquepodeser

ons-truídaemtempolinearetem,paravaloresde

ρ

nãoassintotiamentepequenos,taxa

deinformaçãobináriaaimadolimitanteinferiordeShannon. Aonstruçãoutiliza

umafolheaçãodaesferaunitáriaemtorosplanaresbaseadaem[9℄.

Este trabalho estádividido da seguinte forma: naseção 2,apresentamos uma

rápidarevisãosobreaonstruçãodeódigosesfériosemamadasdetoros,baseados

em[8℄e[9℄;naseção3,apresentamosumamaneiradeesolherostorosetambémde

preenhê-losquepossibilitaaonstruçãoemtempolinear;naseção4,apresentamos

umomparativoentrenossaonstruçãoeoslimitantesmenionadosanteriormente.

2. Códigos esférios em amadas de toros

Dada uma dimensão

k

≥

2

e

ρ

∈

(0,

2]

,

ρ

=

d

2

, seja

C

(k, ρ)

um ódigo esfério

k-dimensional qualquer, om distânia mínima ao quadrado maior ou igual a

ρ

.

Oódigoesfério emamadas detoros denotadopor

C

T

(2k, ρ)

éonstruído em 2

etapas,omosegue[9℄e[8℄:

•

Etapa1-Seleionamosospontosem

C

(k, ρ)

quepossuemsomenteoordenadas

não negativas. Vamos denotareste subódigopor

C

(k, ρ)

+

. Cadaponto

c

=

(c

1

, . . . , c

k

)

∈ C

(k, ρ)

+

dene umtoroplanar

T

c

naesfera unitária

S

2

k

−

1

. É

interessanteque

C

(k, ρ)

+

tenhaboadensidadeem

S

k

−

1

e,sepossível,alguma

propriedadealgébriaougeométria.Paraestepropósito,podemosonsiderar

um

C

T

(k, ρ)

ouqualqueródigoesfériok-dimensionalonheido.

•

Etapa2-Paraadatoro

T

c

denidopor

C

(k, ρ)

+

,determinamosumonjunto

nito depontos

Y

Tc

om

Y

Tc

⊂

P

c

,para

P

c

=

{

x

∈

R

R

R

k

: 0

≤

x

i

≤

2πc

i

}

, tal

que

k

Φ

c

(y)

−

Φ

c

(x)

k ≥

d,

∀

x, y

∈

Y

Tc

. Onde

Φ

c

(y) = (c

1

(cos(

y

1

c

1

), sen(

y

1

c

1

)), . . . , c

k

(cos(

y

k

c

k

), sen(

y

k

c

k

))).

Uma boaopçãopara

Y

T

c

onsisteem onsiderarpontos dealgumretiulado

k

−

dimensional onheido.

Pode-se demonstrarque, sejam

T

b

e

T

c

dois torosplanares,para

b

e

c

vetores

Figura2: Construçãodetoroplanaremdimensão

4

.

dadapor [9℄:

d(T

b

, T

c

) =

k

c

−

b

k

= (

k

X

i

=1

(c

i

−

b

i

)

2

)

1

/

2

.

Adistâniaentre doispontosnomesmotoro

T

c

édadapor:

d(Φ

c

(u),

Φ

c

(v)) = 2(

k

X

i

=1

c

2

i

sen

2

(

u

i

−

v

i

2c

i

))

1

/

2

eélimitadaemtermosde

k

u

−

v

k

.

Seja

c

= (c

1

, c

2

, . . . , c

k

)

,

k

c

k

= 1

, e sejam

u, v

∈

P

c

. Seja

d

k

=

k

u

−

v

k

e

d

2

k

=

k

Φ

c

(u)

−

Φ

c

(v)

k

. Então

2

π

d

k

≤

sen

₂

dk

_c

ξ

dk

2

c

ξ

d

k

≤

d

2

k

≤

sen

dk

₂

dk

2

d

k

≤

d

k

onde

ξ

=

argmin

i

(c

i

)

[9℄.

Existe,portanto,umadeformaçãonadistâniaquandosaímosdo

P

c

⊂

R

R

R

k

para

o

T

c

⊂

R

R

R

2

k

.

3. Construção e análise de ódigos esférios

Considerandoasduasetapasparaaonstruçãodeódigosesfériosemamadasde

toros expliitadasna seção anterior, analisaremosnessa seção diferentes

possibili-dadesparaaesolhadosubódigonaprimeiraetapa. Manteremosasegundaetapa

onformefoi desrita, esolhendopara

Y

Tc

o retiulado

D

k

reesalado de modo a

atingiradistâniadesejadanoódigo.

Aspossibilidadesdeonstruçãoanalisadaspara primeiraetapaestão divididas

3.1. Análise de subódigo om

k

elementos

Podemosonsiderarpara aprimeira etapa, osubódigoonstruído apartir das

k

permutaçõesdovetor

c

i

(t) =

ei

+

te

k

ei

+

te

k

,em que

e

= (1,

1, . . . ,

1)

∈

R

R

R

k

,

t >

0

e

e

i

éo

i-ésimovetoranniodo

R

R

R

k

. Cadavetor

c

i

(t)

deneumtoroplanarsobre

S

2

k

−

1

.

Podemosestabeleerentãooseguinteresultado.

Proposição 3.1. Para ada

ρ

,

0

< ρ <

2

, há ao menos

k

vetores unitários em

S

k

−

1

,omoordenadaspositivas,taisqueoquadradodadistâniaentredoisdestes

vetoresémaior que

ρ

.

Demonstração. Peladenição aima,há

k

vetores

c

i

(t)

∈

R

R

R

k

. A distâniaao

qua-dradoentrevetoresdotipo

c

i

(t)

supraitadoédadapor:

k

c

i

(t)

−

c

j

(t)

k

2

=

2

kt

2

_{+ 2t}

_{+ 1}

ondeaequação

2

kt

2

+2

t

+1

=

ρ

temsempreumasoluçãorealpositivadadapor

¯

t(ρ) =

−

ρ

+

p

ρ(k(2

−

ρ) +

ρ)

kρ

.

Seja

c

min

a menoroordenadade

c

i

(¯

t)

, aimagemda apliação

Φ

de qualquer

onjunto disretonointeriordaaixa

P

ci

(¯

t

)

omdistâniamínima

d

k

≥

2c

min

arcsen

√

_ρ

2c

min

(3.1)

seráumódigoesférioem

S

2

k

−

1

omdistâniamínimaaoquadrado

ρ

.

Assim,nasegundaetapadeonstrução,paraadaumdos

k

torosdenidospor

c

i

(¯

t)

onsideramosospontos doretiuladoobtidoreesalandooretiulado

D

k

por

umfator

d

k

√

2

,onde

d

k

édadopor(3.1).

Como todos os vetores

c

i

são simétrios porpermutações ílias de suas

o-ordenadas, é suiente onstruiruma amada doódigo e tomar aspermutações

íliasdasoordenadasdospontosenontradosparaobtertodooódigo.

Comoum exemplodesta onstruçãoonsidere

k

= 3

e

ρ

= (0,

3)

2

. Neste aso

teremos

¯

t

= 2.34719

etrêstorosdenidospelosvetores

c

1

(¯

t) = (0.710045,

0.497913,

0.497913)

,

c

2

(¯

t) = (0.497913,

0.710045,

0.497913)

e

c

3

(¯

t) = (0.497913,

0.497913,

0.710045)

. Temos

d

k

= 0.304734

epodemosonsiderarumretiuladoreesaladode

D

3

pelofator

d

k

/

√

2

.

As palavras ódigo em ada umdos três toros serãoa imagemdos pontos do

retiulado

d

k

√

2

D

3

na aixa

P

ci

(¯

t

)

pela função

Φ

ci

. Nesteaso, adatoroterá

1605

pontoseteremos

M

= 4815

pontosnoódigoesfério. Ataxadeinformaçãodeste ódigoé

R

= 2.03889

. Paraestes parâmetros,oslimitantes deShannonede Solé

3.2. Construção de subódigos om

k

!

elementos

Umapossibilidadedemelhoraronúmerode pontosnosubódigosem aumentar a

omplexidadedeodiaçãoétomandoas

k!

permutaçõesdovetor

c

i

(t) =

p

+

te

k

p

+

te

k

,

onde

e

= (1,

1, . . . ,

1)

∈

R

R

R

k

,

t >

0

e

p

éovetor

(0,

1,

2, ..., k

−

1)

do

R

R

R

k

.

Entretanto,nesteaso,amedidaqueaumenta-seonsideravelmenteonúmerode

pontosnosubódigo,diminuem-seosvalorespossíveisaseonsiderarparadistânia

mínimaemdimensõesmaiores. Porexemplo,paraumsubódigoobtidoapartirde

c

i

(t)

nadimensão

k

= 6

teremos

k! = 720

torosmas, parageraródigosomestes

toros,devemoslimitaravaloresde

ρ <

0.19

2

.

Como um exemplo desta onstrução, tomemos

k

= 3

e

ρ

= (0.3)

2

. Teremos

¯

t

= 1.59629

,emque

t

¯

ésoluçãopositivadaequação

ρ

=

2

kt

2

_{+ (k}

2

₋

_k)t

₊

k

3

3

−

k

2

2

+

k

6

.

Ospontosdosubódigoserãoas

3! = 6

permutaçõesdovetor

c

i

(¯

t) = (0.33863,

0.55076,

0.76289).

Teremos

d

k

= 0.31079

e novamente na segunda etapa onsideraremos na aixa

P c

i

(¯

t)

dearestasommedidas

2πc

i

(¯

t)

umretiuladoreesaladode

D

3

porumfator

d

k

√

2

.

Aspalavrasódigoemadaumdosseistorosserãodadaspelaimagemde

Φ

ci

do

retiulado

d

k

√

2

D

3

naaixa

P

ci

(¯

t

)

. Cadatoroterá

1120

pontoseteremos

M

= 6720

pontos noódigoesfério. Ataxade informaçãoserá

R

= 2.11904

,queésuperior

àtaxaobtidanoexemplodasubseçãoanteriorparaosmesmosvaloresde

ρ

e

n

.

Asduaspossibilidadesanalisadasnassubseçõesanterioresresultamemódigos

quepodemserfailmenteonstruídos,alémdeteremboataxadeinformaçãobinária

paraalgunsparâmetroseterembaixaomplexidadedeodiaçãoedeodiação.

Entretanto é possível ainda aumentar o número máximo de pontos repetindo de

formaiterativaaonstruçãoanteriorbaseadanaseguinte observação.

É fáil pereber que osvetores

c

i

obtidospelo método desrito nas subseções

anteriorespertenem,respetivamente,aoshiperplanos

x

1

+

x

2

+

...

+

x

k

=

1 +

kt

√

kt

2

_{+ 2t}

_{+ 1}

e

x

1

+

x

2

+

...

+

x

k

=

(k

−

1)k

+ 2kt

2

r

kt

2

_{+ (k}

2

₋

_k)t

₊

k

3

3

−

k

2

Partindo daideia de que em qualquerdos doismétodos temos pontos em um

úniohiperplano,podehavermaisdeumhiperplanoque,aointereptaraesferado

R

R

R

k

,forneçavetoresunitáriosomoordenadaspositivas.

Natentativadeobtermosresultadosaindamelhores,propomosumaonstrução

quetomasuessivoshiperplanosparalelosomvetoresunitáriosno

R

R

R

k

paradenir

ostoros, ao invés deum únio hiperplano omo foi feitoaté agora. Isso permite,

em geral,aumentaronúmerode pontos noódigopara umvalor xadode

ρ

sem

omprometerdemasiadamenteaomplexidadedeonstrução. Essaonstruçãoserá

detalhadanapróximaseção.

4. Construção de ódigos esférios por vetores

uni-tários em hiperplanos paralelos

Pararealizaressaonstruçãoonsideraremos,omooprimeirohiperplano

Π

1

,aquele

obtidopelo métododesritonasubseção3.1.,em quetemos vetoresunitários

c

i

(t) =

e

i

+

te

k

e

i

+

te

k

,

satisfazendo

x

1

+

x

2

+

...

+

x

k

=

1 +

kt

√

kt

2

_{+ 2t}

_{+ 1}

=

α

1

.

Apartirdeste hiperplano

Π

1

,edeaordoomadistânia

d

=

√

_ρ

estabeleida

é possível obter um novohiperplano

Π

2

paralelo a

Π

1

e distante deste ovalor

x

.

Ovalor

x

éfáildeserobtidobastandoparaissoobservarquevetoresunitáriosde

diferentes hiperplanosdevemnomínimoestardistantesovalor

d

.

Paraoasoemque

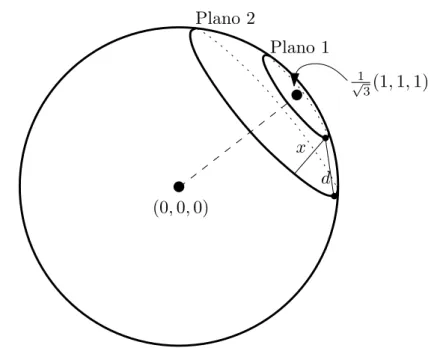
k

= 3

,umailustraçãodesteproessoéapresentadanagura

3. Cadahiperplano(quenesteasoéumplano)ortaoprimeirootanteemírulos

paraobtervetoresunitáriosdeoordenadaspositivas.

Adistânia

x

entre os(hiper)planoséobtidaporrelaçõestrigonométrias

sim-plesepodeserexpressapor

x

=

d sen(

θ

2

+

arccos(1

−

y))

,emque

d

éadistânia

mínima do ódigoe

y

é adistânia entre ospontos

P

0

=

1

√

k

(1,

1,

· · ·

,

1)

∈

R

R

R

k

e

P

i

=

√

αi

_k

(1,

1,

· · ·

,

1)

∈

R

R

R

k

(

P

i

é o ponto do hiperplano

Π

i

que possui todas as

oordenadasiguaisepositivas).

Obtidoovalor

x

,onovoplano

Π

2

serádenido por

Π

2

:

x

1

+

x

2

+

. . .

+

x

k

=

α

1

−

x

√

k.

Nestenovoplanotomaremos,semprequepossível,vetoresunitáriosom

oordena-daspositivas,osquaisdistem entresi

d

=

√

_ρ

. Prosseguimosassimsuessivamente

enquantohouveremplanosparalelosa

Π

i

, distantes de

Π

i

ovalor

x

, queforneçam

vetoresunitáriosomoordenadaspositivas. Teremosassimmaispontosno

subó-digoe,onsequentemente,maistoroseumnúmeromaiordepontosno

CT

(2k, ρ)

. Utilizandoestemétodoforamonstruídosalgunsódigosesfériospara

diferen-tes valores de

ρ

, partindo de vetores no

R

R

R

3

x

d

Plano 1

Plano 2

1

√

3

(1

,

1

,

1)

(0

,

0

,

0)

Figura 3: Esfera

S

2

intereptada por dois planos. A interseção são írulos no

quadrante positivo.

provenientes de diferentes planos. Cada vetor gerou umtoro e depois, ada toro

planotri-dimensionalfoipreenhidoompontosdoretiulado

D

3

. Oresultadofoi

a obtenção de ódigos esférios no

R

R

R

6

om boas taxasbinária onformeos dados

apresentadosnatabela 1.

Tabela1: Comparaçãoentreastaxasbináriasdeódigosesfériosno

R

R

R

6

om

limi-tantes inferioresparaváriasdistâniasmínimas.

d M Taxa Shannon Patri

0.5 194. 1.26665 1.04655 1.

0.4 997. 1.66024 1.35137 1.32193

0.3 7357. 2.14082 1.75338 1.73697

0.2 81095. 2.71789 2.32918 2.32193

0.1

3.50004

×

10

6

3.62316 3.32373 3.32193

0.01

4.30642

×

10

11

6.44128 6.64387 6.64386

Omesmométododeonstruçãofoiusadoparaseobteródigos

C

T

(2k, ρ)

para

k

= 4,

5

e

6

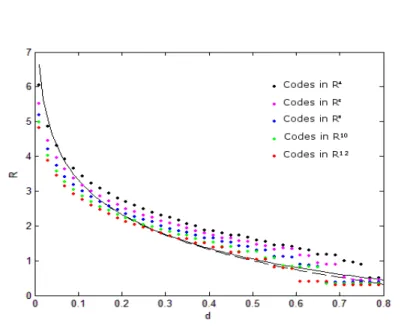
. Nagura4,apresentamosresultadosobtidospara ataxade

informa-çãobináriaonsiderando-sediferentes valoresde

ρ

emforma degráo. Podemos

Figura4: Comparaçãoentrealgunsódigosesfériosonstruídos(pontosisolados)

e oslimitantes para taxade informaçãobinária (Shannon: urva ontínua. Solé:

urvapontilhada) emfunçãode

ρ

.

5. Conlusão

Nestetrabalhoonsideramosadistribuiçãodeumonjuntodepontossobrea

super-fíiedeumaesferaeulidianaunitária,omopropósitodeonstruiródigosesférios

para oCanal Gaussiano. Apresentamosfamilias deódigosesfériosestruturados,

que podem seronstruídosem tempolinearpara dimensõespares e superam, em

algumas dimensõeseparadistânia mínimanão muitopequenas, olimitante

infe-riordeShannonparaataxade informaçãobinária. Essaonstruçãoébaseadana

folheação daesferaunitáriaportorosplanares, propostaem[8℄ easontribuições

prinipaisdeste trabalhoreferem-seàmaneiradeobterostorosutilizandovetores

depermutaçãounitários

R

R

R

k

.

Abstrat. Inthispaperwedealswiththeonstrutionofspherialodesfor the

Gaussian hannel. We present familiesof struturedspherial odes, designed in

layersofattori, thatanbe onstrutedinlinear timeforevendimensions and

improves, for ertain parameters, the lower bound for the binary rate given by

Shannon.

Keywords. Disretemathematis,spherialodes,binaryrate.

Referênias

[1℄ M. Berger,B.Gostiaux, DierentialGeometry: Manifolds, Curvesand

[2℄ C. Chabauty,Résultats surl'empilement dealottes égalessur une périsphère

de

R

R

R

n

et orretionàun travail antérieur,C.R. Aad.Si. Ser. A, 236,1953,

1462-1464.

[3℄ J.H. Conway, N.J.A. Sloane, Sphere pakings, lattiesand groups, Springer

Verlag,GMW290,2003.

[4℄ S.I.R. Costa, M.M. Alves, E. Agustini, R. Palazzo, Graphs, tesselations and

perfetodesonattori,IEEETransationsonInformation Theory,50, Ot.

2004,2363-2377.

[5℄ T.Erison,V.Zinoviev,CodesonEulideanspheres,North-Holland,

Amster-dam, 2001.

[6℄ G.Lahaud,J.Stern,Polynomial-timeonstrutionofodes.IISpherialodes

andthekissingnumberofspheres,IEEETrans.Inform.Theory,40,No.4,1994,

1140-1146.

[7℄ C.E. Shannon, Probabilityof errorfor optimal odes in a Gaussian hannel,

BellSyst.Teh. J.,38,1959,611-656.

[8℄ C.Torezzan,Códigosesfériosemtorosplanares,Tesededoutorado,

IMECC-Uniamp,2009.

[9℄ C. Torezzan, S.I.R. Costa, & V.A. Vaishampayan, Spherial odes on torus

layers,InternationalSymposium onInformationTheory,Seul,Coreia,2009.

[10℄ P.Solé,J.C.Belore,ConstrutivespherialodesneartheShannonbound,

The Seventh International Workshop on Coding and Cryptography, Paris,