Zeros de polinômios característicos e
estabilidade de métodos numéricos
SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP
Data de Depósito: 15 de fevereiro de 2008
Assinatura:
Zeros de polinômios característicos e estabilidade de métodos
numéricos
Vanessa Avansini Botta
Orientador:José Alberto Cuminato
Tese apresentada ao Instituto de Ciências Matemáticas e de Computação - ICMC/USP, como parte dos requisitos para
obtenção do título de Doutor em Ciências de Computação e Matemática Computacional.
Agradecimentos
N
Odecorrer deste trabalho, em meio a tantas descobertas, muitas dificuldades surgiram etambém muitas alegrias floresceram. E nestes momentos inesquecíveis, a colaboração
de algumas pessoas incomparáveis foi de extrema importância para a conclusão desta tese, que representa uma grande conquista.
Então, agradeço sinceramente: À Deus, por tudo.
Aos meus familiares e amigos, que sempre me acolheram nos momentos mais difíceis. Ao meu marido, Fabio, pela paciência e amor que sempre me dedicou.
A todos os professores que sempre me ajudaram, em especial ao Prof. Dr. Dimitar Kolev Dimitrov, pela disposição nos momentos em que precisei.
Ao Prof. Dr. José Alberto Cuminato, pela orientação deste trabalho, pela confiança e atenção. Ao Prof. Dr. Messias Meneguette Junior, em especial, pela orientação deste trabalho, pela
atenção, dedicação e paciência.
A todos que de alguma forma contribuíram para a realização deste trabalho.
Resumo
A
Teoria das equações diferenciais faz parte de uma área daMate-mática muito rica em aplicações. Os métodos numéricos para a solução de equações diferenciais ordinárias são, da mesma
forma que as próprias equações, fontes importantes de problemas a serem pesquisados. Como destaque tem-se os métodos multiderivadas de passo
múltiplo, que são importantes na solução de problemas stiff. Os métodos numéricos mais conhecidos para a solução desses problemas são os BDF,
que compõem, para L = 1, a família dos métodos (K, L) de Brown. Al-gumas questões relacionadas à estabilidade dos métodos (K, L)ainda não
foram solucionadas como, por exemplo, uma conjectura de Jeltsch. Para analisá-la, é necessário estudar o comportamento dos zeros dos polinômios
característicos associados aos métodos(K, L). Neste trabalho é apresentado um estudo sobre zeros de polinômios com o objetivo de demonstrar a
vali-dade da conjectura de Jeltsch paraK ≤K∗
L. As regiões de estabilidade para
alguns valores deKeLfixos são apresentadas e também é utilizada a teoria
das order stars para mostrar algumas propriedades dos métodos(K, L). Por-tanto, este trabalho apresenta um estudo sobre os métodos(K, L)de Brown
e usa uma ferramenta pouco utilizada na literatura, que são as order stars, para demonstrar alguns resultados.
Palavras-chave: métodos(K, L)de Brown, estabilidade de métodos numéri-cos, zeros de polinômios característinuméri-cos, order stars.
Abstract
T
He theory of differential equations is part of one area ofMathe-matics very rich in applications. The numerical methods for the
solutions of ordinary differential equations are, in the same way as the equations themselves, important sources of problems to be studied. As
prominence one has the multiderivative multistep methods which are impor-tant for the solution of stiff problems. The best known numerical methods
for the solutions of these kind of problems are the BDF methods, which is part of the family of the Brown (K, L) methods with L = 1. Some
ques-tions about stability of the (K, L) methods has not been solved yet as, for example, a conjecture by Jeltsch. In order to tackle this open problem, it
becomes necessary to study the behavior of the zeros of the characteristic polynomials associated to the (K, L)methods. In this work a study of the
zeros of the characteristic polynomial is carried out aiming at proving Jeltsch conjecture forK ≤K∗
L. Regions of stability is shown for some fixed values
ofK andL, as well as the use of order stars techniques are applied to show some properties of (K, L) methods. Therefore, this work presents a study
of Brown’s(K, L)methods, that makes use of a tool that seems not to have been used very often in the literature, the order stars, in order to prove the
main results.
Key words: Brown (K, L)methods, stability of numerical methods, zeros
of characteristic polynomials, order stars.
Sumário
Agradecimentos i
Resumo ii
Abstract iii
1 Introdução 1
2 Zeros de Polinômios 11
2.1 Resultados clássicos sobre zeros de polinômios . . . 11
2.1.1 Localização dos zeros . . . 11
2.2 Análise da Conjectura 1.2 . . . 15
2.2.1 Limitante para os zeros . . . 15
2.2.2 Polinômio reflexivo . . . 15
2.2.3 Caso geral . . . 20
2.2.4 Condições adicionais . . . 24
3 Métodos(K, L)de Brown 30 3.1 Introdução . . . 30
3.2 Order stars . . . 35
3.2.1 Conceito geral . . . 38
3.2.2 Order stars para os métodos de passo múltiplo . . . 41
3.3 Propriedades dos métodos de Brown e order stars . . . 43
3.3.1 Order stars para os métodos(K, L) . . . 44
3.3.2 Comportamento dos zeros dos polinômios característicos . . . 48
3.3.3 Resultados sobre zero-estabilidade . . . 49
3.3.4 Regiões de estabilidade . . . 51
4 Considerações Finais 58 4.1 Sobre zeros de polinômios . . . 58
4.2 Sobre os métodos(K, L)de Brown . . . 60
Referências Bibliográficas 63
Lista de Figuras
1.1 Soluçõesu(x)ev(x). . . 3
2.1 Comportamento dos zeros dePγ(z) = (1 +γ)z3+ 3z2+ 3z+ 1,0≤γ ≤1.2. . . 18
2.2 Comportamento dos zeros dePγ(z) = (1 +γ)z4+ 2z3+ 2z2+ 2z+ 1,0≤γ ≤1. 19 2.3 Comportamento dos zeros dePγ(z) = (2.2 +γ)z3+ 6z2+ 6z+ 2.2,0≤γ ≤2. . 19
2.4 Comportamento dos zeros dePγ(z) = (1 +γ)z3+ 2z2+ 2z+ 1,0≤γ ≤1. . . . 20
2.5 Comportamento dos zeros dePγ(z) = (1.5 +γ)z3+ 2z2+ 2z+ 1.5,0≤γ ≤1. . 20
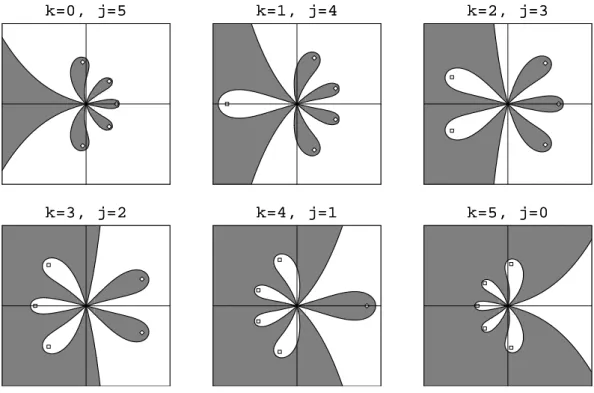
3.1 Order stars da aproximação de Padé . . . 38
3.2 Order star do BDF de 2 passos . . . 44
3.3 Order star do BDF de 3 passos . . . 44
3.4 Order star do BDF de 4 passos . . . 44
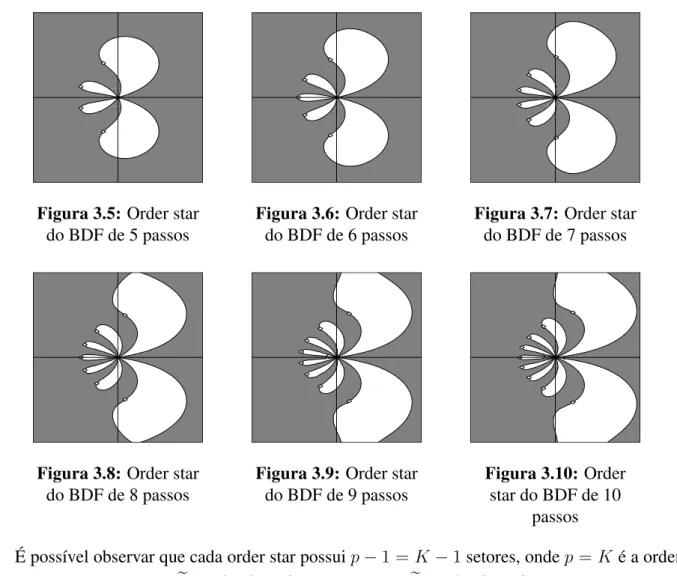
3.5 Order star do BDF de 5 passos . . . 45
3.6 Order star do BDF de 6 passos . . . 45
3.7 Order star do BDF de 7 passos . . . 45
3.8 Order star do BDF de 8 passos . . . 45
3.9 Order star do BDF de 9 passos . . . 45
3.10 Order star do BDF de 10 passos . . . 45
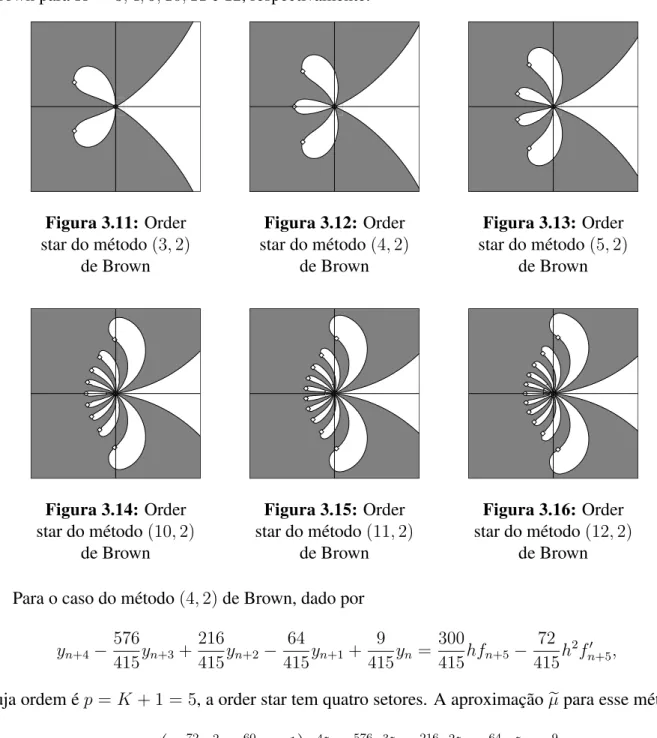
3.11 Order star do método(3,2)de Brown . . . 46
3.12 Order star do método(4,2)de Brown . . . 46
3.13 Order star do método(5,2)de Brown . . . 46
3.14 Order star do método(10,2)de Brown . . . 46
vii
3.15 Order star do método(11,2)de Brown . . . 46
3.16 Order star do método(12,2)de Brown . . . 46
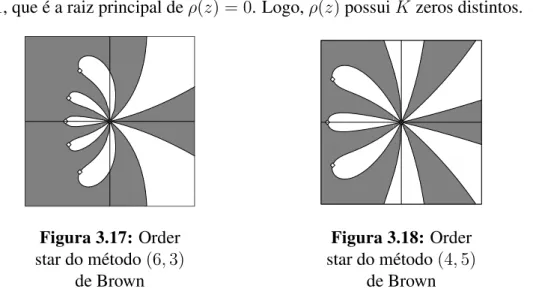
3.17 Order star do método(6,3)de Brown . . . 49
3.18 Order star do método(4,5)de Brown . . . 49
3.19 Zeros deρ(z)paraK = 3eρ′ (z)paraK = 4,L= 1 . . . 50
3.20 Zeros deρ(z)paraK = 3eρ′(z)paraK = 4,L= 2 . . . 50
3.21 Zeros deρ(z)paraK = 3eρ′ (z)paraK = 4,L= 3 . . . 50
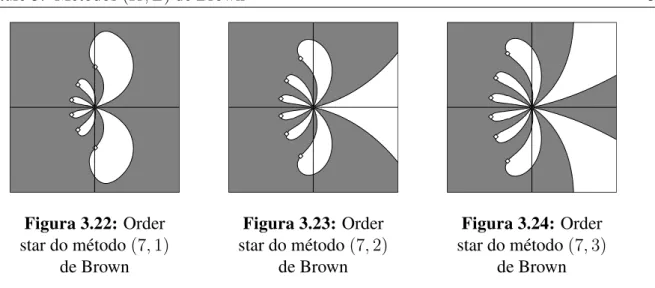
3.22 Order star do método(7,1)de Brown . . . 52
3.23 Order star do método(7,2)de Brown . . . 52
3.24 Order star do método(7,3)de Brown . . . 52
3.25 Curvas soluções paraw+ ew−para o método BDF de 2 passos . . . 52
3.26 Região de estabilidade do método BDF de 2 passos . . . 53
3.27 Região de estabilidade do método BDF de 3 passos . . . 53
3.28 Região de estabilidade do método BDF de 4 passos . . . 53
3.29 Regiões de estabilidade para os métodos de Brown paraL= 1eK = 2, ...,6 . . . 54
3.30 Curvas soluções do método(2,2)de Brown . . . 55
3.31 Região de estabilidade do método(2,2)de Brown . . . 55
3.32 Região de estabilidade do método(3,2)de Brown . . . 55
3.33 Região de estabilidade do método(4,2)de Brown . . . 55
3.34 Regiões de estabilidade para os métodos de Brown paraL= 2eK = 3, ...,10 . . . 56
3.35 Curvas soluções do método(2,3)de Brown . . . 56
3.36 Região de estabilidade do método(2,3)de Brown . . . 57
3.37 Região de estabilidade do método(3,3)de Brown . . . 57
3.38 Região de estabilidade do método(4,3)de Brown . . . 57
3.39 Região de estabilidade do método(2,4)de Brown . . . 57
3.40 Região de estabilidade do método(3,4)de Brown . . . 57
C
APÍTULO1
Introdução
A teoria das equações diferenciais tem sido muito utilizada nas últimas décadas, pois é uma área rica em aplicações não somente na Matemática mas também em outras ciências, como na Física e na Engenharia, por exemplo.
Neste trabalho, o enfoque principal será em questões relacionadas aos métodos numéricos para a solução de equações diferenciais ordinárias, com destaque para os métodos multiderivadas de passo múltiplo, que foram originalmente introduzidos com o intuito de obter métodos com menor número de passos e melhor precisão. A análise desses métodos desenvolveu-se paralelamente aos avanços em problemas stiff, que surgem quando são modelados fenômenos que envolvem repentinas mudanças de dinâmica ou variações bruscas como, por exemplo, em situações que envolvem reações nucleares e circuitos elétricos, entre outras. Esses fenômenos são, em geral, modelados por sistemas de equações diferenciais ordinárias lineares na forma
y′ =Ay+φ(x), (1.0.1)
onde Aé uma matriz de ordem mcujos autovalores λi, i = 1, . . . , m, são distintos eφ(x) é um
vetorm-dimensional.
Os problemas stiff surgem quando a distância entre o maior e o menor autovalor da matrizAé muito acentuada, sendo necessário o uso de dois valores muito diferentes deh(tamanho do passo) para manterz =λh(obtida a partir da equação testey′ =λy) dentro da região de estabilidade do
método numérico.
Capítulo 1. Introdução 2
A solução geral da equação (1.0.1) é
y(x) = m
X
i=1
kieλixvi+ψ(x),
ondevi é o autovetor correspondente ao autovalorλi,i= 1, . . . , m.
Assumindo queRe(λi)<0,i= 1, . . . , m, segue que
lim
x→∞
m
X
i=1
kieλixvi = 0.
O termo
m
X
i=1
kieλixvi é chamado de solução transiente e ψ(x) recebe o nome de solução de
estado estacionário.
O exemplo a seguir ilustra as dificuldades presentes quando tenta-se obter uma solução apro-ximada do problema por métodos numéricos.
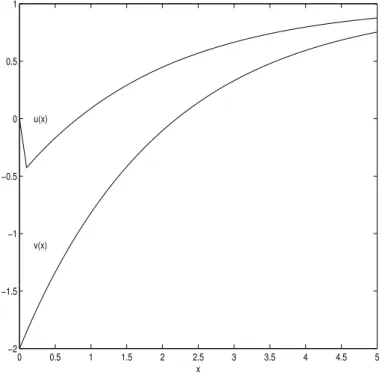
Exemplo 1.1. Sejamy=
u v
!
,A= −2000 999,75
1 −1
!
eφ= 1000,25 0
!
.
A equação (1.0.1) toma a forma
u v
!′
= −2000 999,75
1 −1
!
u v
!
+ 1000,25 0
!
.
A condição inicial a ser utilizada é
u(0)
v(0)
!
= 0
−2
!
.
Os autovalores da matrizA sãoλ1 = −2000,5e λ2 = −0,5, e, portanto, a solução exata é
dada por
u(x) = −1,499875e−0,5x+ 0,499875e−2000,5x+ 1
e
v(x) =−2,99975e−0,5x−0,00025e−2000,5x+ 1.
A Figura 1.1 mostra o gráfico das soluçõesu(x)ev(x).
Na tentativa de obter uma solução aproximada do problema por métodos numéricos, uma difi-culdade que surge é que, comoλ1eλ2 têm magnitudes muito diferentes, a necessidade de manter
z = λh dentro da região de estabilidade leva a dois valores muito distintos de h, pois z = λ1h
exigehmuito pequeno ez =λ2hpermite uma passo maior. Portanto, o fato de alguns autovalores
Capítulo 1. Introdução 3
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
−2 −1.5 −1 −0.5 0 0.5 1
x u(x)
v(x)
Figura 1.1:Soluçõesu(x)ev(x).
Os problemas onde os autovalores têm Re(λ) grande mas positiva também terão z fora da região de estabilidade absoluta do método, mas estes casos não são interessantes, pois a solução exata cresce exponencialmente de qualquer forma (assim como o erro), não justificando o mesmo cuidado das situações em queRe(λ)<0.
De maneira geral, ao analisar a solução transiente e a solução de estado estacionário, as seguintes características podem ser observadas:
1. seRe(λi) < 0, i = 1, . . . , m, está garantida a existência da solução de estado estacionário
ψ(x);
2. se |Re(λi)| assume um valor pequeno para algumi = 1, . . . , m, como é o caso de λ2 do
Exemplo 1.1, obtém-se um vasto intervalo de integração para alcançar o estado estacionário, pois quanto menor|Re(λi)|o decaimento exponencial dado poreλixserá mais lento;
3. se|Re(λi)|assume um valor grande para algumi= 1, . . . , m, por exemploλ1 =−2000,5,
será necessário usar tamanho de passo pequeno para manter a estabilidade do método numéri-co;
4. quanto maior o quociente maxi=1,2,...,m|Re(λi)|
mini=1,2,...,m|Re(λi)|
, maior o esforço computacional gasto; este quociente recebe o nome de razão de stiffness.
Logo, a seguinte definição pode ser apresentada:
Definição 1.1. O sistema linear (1.0.1) é chamado de stiff se, parai = 1, . . . , m, Re(λi) < 0e
Capítulo 1. Introdução 4
Portanto, os métodos numéricos mais adequados para a solução de problemas stiff são aqueles que possuem grande região de estabilidade absoluta, pois assim existe maior liberdade na escolha do tamanho do passo.
Por possuírem boas propriedades de estabilidade, como grandes regiões de estabilidade abso-luta, os métodos multiderivadas de passo múltiplo são indicados para resolver problemas stiff.
Existem muitos problemas que requerem a utilização de métodos numéricos com boas pro-priedades de estabilidade. Portanto, o estudo da estabilidade de métodos numéricos é uma área que possui grande potencial em pesquisa.
Uma classe de métodos multiderivadas de alta ordem, chamada de métodos(K, L)de Brown, foi apresentada em Brown (1977) e caracteriza-se por possuir uma grande subclasse de métodos A-estáveis. A construção explícita e a dedução de algumas propriedades importantes desta classe foram apresentadas por Jeltsch e Kratz (1978).
Os métodos(K, L)de Brown são definidos por
K
X
i=0
αiyn+i = L
X
j=1
βjhjf(j
−1)
n+K ,
onde as constantesαi eβj são escolhidas de modo a maximizar a precisão do método.
Os coeficientesαi eβj são dados por
αi = (−1)K−i
K i
!
(K−i)−L, i = 0, . . . , K−1,
αK = −(α0+α1+. . .+αK−1),
βj =
(−1)j
j!
KX−1
i=0
(−1)K−i K
i
!
(K−i)j−L, j = 1, . . . , L.
A constante do erro é representada por
CK+L =
(−1)LK!
(K+L)!.
Tais coeficientes foram obtidos em Jeltsch e Kratz (1978) através de representações matriciais, descritas a seguir:
D1L+1×K IL+1×L+1
D2K×K 0K×L+1
!
α β
!
= ΘL+K+1×1,
ondeα= (α0, α1, ..., αK−1)T, β = (β0, β1, ..., βL)T,Θé a matriz nula,Ir×ré a matriz identidade
de ordemreDL+K+1×K =
D1 D2
T
é definida pordi,j =
(j −K)i
i! , para 0≤i ≤ L+K
Capítulo 1. Introdução 5
Quando L = 1, a classe de métodos de Brown e os métodos BDF (Backward Difference
Formulae) representam a mesma classe de métodos, sendo este aspecto não verificado por Jeltsch em seus estudos. A seguir este fato é mostrado através das fórmulas de interpolação de Newton (nós simples), no caso em queL= 1, e de Hermite (nós múltiplos), paraL≥2. Maiores detalhes a respeito dessas fórmulas de interpolação podem ser encontrados em Hairer e Wanner (1996).
Uma representação para os métodos(K, L)de Brown paraL= 1pode ser encontrada por meio
da fórmula de interpolação de Newton nos pontos xn+1, xn, ..., xn+1−K, derivando o polinômio
resultante no pontoxn+1. De fato, das diferenças divididas, segue que
s= 1 f1
∇f1
s= 0 f0 ∇
2
f1
2!
∇f0 ∇
3
f1
3!
s=−1 f−1 ∇
2 f0 2! ∇4 f1 4!
∇f−1 ∇
3
f0
3! ...
s=−2 f−2
∇2
f−1
2! ...
∇f−2 ...
s=−3 f−3 ...
... ...
ondex=xn+sh,f1 =f(xn+h)e∇j denota aj−ésima diferença para trás.
Então
f(xn+sh) = f1 + (s−1)∇f1+ (s−1)s∇ 2f
1
2! + (s−1)s(s+ 1)
∇3f 1
3!
+(s−1)s(s+ 1)(s+ 2)∇
4f 1
4! +...
Substituindof pory,
y(xn+sh) = y1+ (s−1)∇y1+ (s−1)s∇ 2y
1
2! + (s−1)s(s+ 1)
∇3y 1
3!
+(s−1)s(s+ 1)(s+ 2)∇
4y 1
4! +...
Derivando no pontos= 1, segue que
hfn+1 =
K X j=1 1 j∇ jy
n+1, (1.0.2)
Capítulo 1. Introdução 6
Para encontrar os coeficientes para alguns valores fixos deKdos métodos(K,1), basta utilizar
a expressão (1.0.2). Por exemplo, paraK = 2, segue, de (1.0.2),
hfn+1 = 2 X j=1 1 j∇ jy
n+1 =∇yn+1+
1 2∇
2y
n+1 =∇yn+1+
1
2(∇yn+1− ∇yn)
= 3
2∇yn+1− 1
2∇yn= 3
2(yn+1−yn)− 1
2(yn−yn−1) = 3
2yn+1−2yn+ 1 2yn−1.
Portanto, o método(2,1)de Brown é definido por
3
2yn+1−2yn+ 1
2yn−1 =hfn+1.
ParaL= 2a mesma idéia do casoL= 1pode ser aplicada, mas considerando a fórmula de
in-terpolação de Hermite nos pontosxn+1(nó duplo),xn, xn−1, ..., xn+1−K (nós simples) e derivando
o polinômio resultante duas vezes emx=xn+1. Então, das diferenças divididas,
s= 1 f1
hf′
1
s= 1 f1 hf1′ − ∇f1
∇f1
hf′
1−∇f1−12∇2f1
2!
s= 0 f0 ∇
2
f1
2!
hf′
1−∇f1−12∇2f1−13∇3f1
3!
∇f0 ∇
3
f1
3! ...
s=−1 f−1 ∇
2
f0
2! ...
∇f−1 ...
s=−2 f−2 ...
... ...
Logo
f(xn+sh) = f1+ (s−1)hf1′ + (s−1)2(hf
′
1− ∇f1) + (s−1)2s
hf′
1− ∇f1− 12∇2f1
2!
+(s−1)2s(s+ 1)hf
′
1− ∇f1− 12∇2f1−13∇3f1
3! +...
Substituindof pory,
y(xn+sh) = y1+ (s−1)hy1′ + (s−1)2(hy
′
1− ∇y1) + (s−1)2s
hy′
1− ∇y1− 12∇2y1
2!
+(s−1)2s(s+ 1)hy
′
1− ∇y1 −12∇2y1− 13∇3y1
Capítulo 1. Introdução 7
Derivando duas vezes no pontos= 1e considerandoy′′(x
n+1) = gn+1, segue que
h2
2 gn+1 =
K
X
i=1
1
i
!
hfn+1−
K
X
j=1
K
X
i=j
1
i
!
∇jy n+1
j . (1.0.3)
Tal expressão foi usada por Hairer e Wanner (1996) para representar os "second derivative BDF methods (SDBDF)". Para encontrar alguns coeficientes dos métodos(K,2)de Brown para valores
fixos deK basta utilizar a expressão (1.0.3).
O mesmo procedimento pode ser usado para determinar as expressões para outros métodos
(K, L) para valores fixos deL, bastando utilizar a interpolação de Hermite nos pontos xn+1 (nó
de multiplicidadeL), xn, xn−1, ..., xn+1−K (nós simples) e derivar o polinômio resultanteLvezes
em x = xn+1. Além disso, alguns coeficientes para valores fixos deK eLdos métodos (K, L)
encontram-se em Meneguette (1987). Portanto, de maneira geral, os métodos (K, L) de Brown podem ser chamados de "multiderivative BDF methods (MDBDF)".
Jeltsch, em uma série de artigos, estudou os métodos(K, L) e provou alguns resultados
as-sintóticos como, por exemplo, o comportamento desses métodos quandoK cresce e Lfica fixo, quandoKestá fixo eLcresce e apresentou também o resultado:
Teorema 1.1. Os métodos(K, L)de Brown são stiff-estáveis se, e somente se, sãoA0e fortemente
estáveis.
Um resultado interessante demonstra queA0-estabilidade dos métodos(K, L)está relacionada
ao polinômio
ργ(z) = (αK+γ)zK+αK−1zk−1+...+α0,
comγ um parâmetro real variando de0a∞eρ0(z)sendo o polinômio característico do método
(K, L)que fornece a zero-estabilidade. Esse resultado parece uma forte indicação de que é possível refazer o teorema anterior sem a exigência daA0-estabilidade. Conjectura-se, então,
Conjectura 1.1. Todos os métodos(K, L)de Brown são stiff-estáveis se, e somente se, são zero-estáveis.
Ou, equivalentemente, "um método(K, L)zero-estável é stiff-estável".
No caso dos métodos BDF tal resultado é válido, pois Hairer e Wanner (1983) mostraram que tais métodos são zero-estáveis paraK ≤6e tambémA0-estáveis.
Em Meneguette (1987), demonstrou-se que os coeficientes deργ(z)são positivos, satisfazendo,
1. 0< α0 < α1 < ... < αK−1 masαK < αK−1, paraK ≤KL;
Capítulo 1. Introdução 8
onde
KL = min
2L+1+ 1,3
L+1
2L + 2, ...,
(L+ 1)L+1
LL +L
e
K∗
L= min
2L+ 1,3
L+1
2L+1 + 2, ...,
(L+ 1)L+1
2LL +L
.
Seγ > αK−1−αK, todos os zeros deργ(z)encontram-se no disco unitário, como conseqüência
do Teorema de Eneström-Kakeya. Se0< γ < αK−1−αK, o comportamento dos zeros ainda não
é conhecido. De uma maneira geral, a seguinte conjectura pode ser estabelecida:
Conjectura 1.2. SejaP(z) =anzn+an−1zn−1+...+a0um polinômio tal que
0< a0 ≤a1 ≤...≤an−1 ean < an−1,
cujos zeros encontram-se no disco unitário, e P′(z) com os coeficientes ordenados. Então, os
zeros do polinômio
Pγ(z) = (an+γ)zn+an−1zn−1 +...+a0
encontram-se no disco unitário, para todoγ >0.
Esse é um problema que encontra-se em aberto em Meneguette (1994). A origem dessa conjec-tura está relacionada aos polinômios característicos associados aos métodos(K, L)de Brown, mas sua formulação é válida para um polinômio qualquer que satisfaz as condições descritas acima.
Através dessa conjectura, muitos problemas sobre estabilidade dos métodos(K, L)de Brown podem ser resolvidos, como o resultado que afirma que, para K ≤ KL, os métodos (K, L) de
Brown são stiff-estáveis. Portanto, um dos principais objetivos deste trabalho é o estudo da estabi-lidade dos métodos(K, L)de Brown, pois muitas questões relacionadas à estabilidade desta classe
de métodos ainda não foram exploradas. O foco principal é a análise das conjecturas, sendo que, para estudá-las, são utilizados resultados clássicos da literatura, como o Teorema de Eneström-Kakeya, por exemplo. Além disso, a construção das regiões de estabilidade para alguns valores fixos de K e L dos métodos (K, L) é um item importante para a solução de alguns problemas.
Convém lembrar que o estudo da Conjectura 1.2 é importante nas questões de estabilidade dos métodos(K, L), mas também é significativo na área de zeros de polinômios.
Outra ferramenta que tem extrema importância nas questões relacionadas à estabilidade são as order stars, que foram introduzidas por Wanner et al. (1978), através das quais é possível descrever ordem, estabilidade e suas relações como propriedades de certas funções complexas. A teoria das order stars ainda é pouco conhecida e divulgada, pois seu desenvolvimento é recente quando comparado a outras áreas.
Capítulo 1. Introdução 9
zeros dePγ(z)encontram-se em
|z| ≤1 + 1
n−1.
Em seguida é mostrada a validade da Conjectura 1.2 no caso em que o polinômioP(z)é
refle-xivo, estabelecendo uma condição sobreγpara que o polinômioPγ(z), sujeito apenas às condições
de P(z)ter seus zeros no disco, cujos coeficientes satisfazem as desigualdades descritas na
con-jectura, tenha também seus zeros no disco unitário. Esta consideração representa um caso crítico da conjectura, poisP(z)possui todos os seus zeros sobre o círculo unitário e qualquer perturbação dos coeficientes poderia fazer os zeros saírem do disco unitário. Mas, como é possível observar no Capítulo 2, a perturbação no coeficiente dominante faz com que os zeros dePγ(z)permaneçam no
disco unitário. Além disso, é analisada a Conjectura 1.2 no caso em que os coeficientes de P(z)
satisfazem algumas condições adicionais, como, por exemplo, quando são verdadeiras as seguintes desigualdades:
pai <(p−1)ai+1, i = 0,1, ..., n−2, epan >(p−1)an−1,
ondepé um número inteiro positivo,p > 1. Nesse caso, a Conjectura 1.2 é válida. Portanto, no Capítulo 2, é realizado um estudo da Conjectura 1.2 no caso geral, não necessariamente no caso em que os polinômios analisados são os polinômios característicos associados aos métodos(K, L)
de Brown, sendo esse caso objeto de estudo do Capítulo 3. ParaK ≤K∗
L, os coeficientes deρ(z)satisfazem
2αj < αj+1 e2αK > αK−1.
Portanto, no Capítulo 3, mostra-se que a Conjectura 1.2 é verdadeira para K ≤ K∗
L, sendo
P(z) = ρ(z), ou seja, o polinômio característico associado ao método (K, L) de Brown, onde
K eLsão fixos. Através desse resultado segue que a Conjectura 1.1 é válida paraK ≤K∗
L, que é
um resultado de significativa importância na área.
Além disso, no Capítulo 3, é apresentado um estudo sobre order stars, trazendo uma genera-lização desse conceito para o caso dos métodos(K, L)de Brown, que são métodos multiderivadas de passo múltiplo, sendo o caso dos métodos lineares de passo múltiplo analisado em Iserles e Norsett (1984).
A teoria das order stars é uma ferramenta que será muito utilizada na análise das questões de estabilidade dos métodos(K, L). Por exemplo, através das order stars, prova-se que os zeros
dos polinômios característicos associados aos métodos (K, L)são distintos. Outras propriedades
Capítulo 1. Introdução 10
Portanto, é dado um enfoque diferente às propriedades já conhecidas dos métodos(K, L)de
Brown, demonstrando-as através das order stars, e também através desta ferramenta mostra-se que os zeros dos polinômios característicos associados aos métodos (K, L) são distintos, que é um
C
APÍTULO2
Zeros de Polinômios
Este capítulo traz uma revisão bibliográfica sobre localização de zeros de polinômios e tam-bém um estudo da conjectura apresentada no capítulo anterior. Primeiramente são apresentados resultados clássicos sobre a localização de zeros de polinômios, assunto que será muito utilizado na análise das conjecturas objetos de estudo desta tese. Em seguida, uma seção traz uma análise da Conjectura 1.2, onde, primeiramente, é determinado um limitante para os zeros de Pγ(z).
De-pois é mostrada a validade da conjectura no caso em que o polinômio é reflexivo. Em seguida, uma análise da conjectura no caso em que os coeficientes dePγ(z)satisfazem algumas condições
adicionais é apresentada.
2.1
Resultados clássicos sobre zeros de polinômios
Nesta seção são apresentados resultados importantes que delimitam regiões onde estão loca-lizados os zeros de polinômios. Esses resultados foram muito importantes para o desenvolvimento da pesquisa, pois para determinar a zero-estabilidade de um método numérico é preciso analisar a quantidade de zeros no disco unitário.
2.1.1
Localização dos zeros
Os teoremas apresentados a seguir são resultados clássicos da literatura e indicam regiões onde estão localizados os zeros de um polinômio. Um estudo detalhado do assunto encontra-se em Botta (2003), Marden (1966) e Milovanóvic et al. (1994).
Capítulo 2. Zeros de Polinômios 12
A seguir é apresentado um resultado clássico sobre a localização dos zeros de um polinômio, que é o Teorema de Eneström-Kakeya, que encontra-se em Marden (1966).
Teorema 2.1 (Eneström-Kakeya). Seja P(z) =
n
X
i=0
aizi um polinômio cujos coeficientes ai,
i= 0,1, . . . , n, satisfazem
0< a0 ≤a1 ≤. . .≤an.
Então,P(z)possui seus zeros em|z| ≤1.
No próximo teorema é determinado um anel que contém todos os zeros de um polinômio. Este resultado, que é um caso mais abrangente do Teorema de Eneström-Kakeya, encontra-se em Anderson et al. (1979).
Teorema 2.2. SejaP(z) =
n
X
i=0
aizi um polinômio tal que n ≥ 1e ak > 0 parak = 0,1, ..., n.
Considerando
α= min
0≤k<n
ak
ak+1
eβ = max
0≤k<n
ak
ak+1
,
todos os zeros deP(z)encontram-se no anelα ≤ |z| ≤β.
São utilizadas também as fórmulas de Vieta, que determinam relações entre os zeros de um polinômio e seus coeficientes, dadas por:
z1z2. . . zn = (−1)n
a0
an
z1z2. . . zn−1+. . .+z2z3. . . zn = (−1)n−1
a1
an
... z1 +z2+. . .+zn = −
an−1
an
,
ondez1, z2, . . . , znsão os zeros do polinômioP(z) = n
X
i=0
aizi.
Existem muitos resultados que relacionam os zeros de um polinômio com os de sua derivada. O resultado a seguir, que encontra-se em Marden (1966), recebe o nome de Teorema de Gauss-Lucas e representa uma generalização do Teorema de Rolle.
Teorema 2.3 (Gauss-Lucas). Os zeros da derivada de um polinômio estão contidos na região convexa fechada formada pelos zeros desse polinômio.
Como conseqüência do Teorema de Gauss-Lucas tem-se o seguinte resultado.
Capítulo 2. Zeros de Polinômios 13
A seguir é analisado um algoritmo, chamado de algoritmo de Schur, e alguns resultados sobre a quantidade de zeros no disco unitário, sendo tal abordagem apresentada em Marden (1948).
Suponha agora que o polinômioP(z) =
n
X
i=0
aizi,ai ∈IR, tenhap(p≤n) zeros em|z| ≤1.
Associado a ele considere o polinômio
P∗(z) = znP
1
z
=a0zn+a1zn−1+. . .+an=a0
n
Y
j=1
(z−zj∗),
sendo seus zerosz∗
k, em relação ao disco unitário, os inversos dos zeroszkdeP(z), isto é,zk∗ =
1
zk
.
Logo, qualquer zero deP(z) que possui módulo um é também zero deP∗(z)e se P(z)não
tem zeros em |z| = 1, P∗(z) também não tem zeros em
|z| = 1. Além disso, se P(z) possuip zeros em|z|<1, entãoP∗(z)possuin
−pzeros em|z|<1. Seja agora a seqüência de polinômios
Pj(z) = n−j
X
k=0
a(kj)zk,
ondeP0(z) =P(z)e
Pj+1(z) =a(0j)Pj(z)−a(nj−)jP
∗
j(z),
comj = 0, ..., n−1. Então,
ak(j+1) =a0(j)a(kj)−a(nj−)jan(j−)j−k. (2.1.1)
Em cada polinômioPj(z)o termo constantea(0j)é representado porδj. Assim,
δj+1 =|a(0j)|2− |a (j)
n−j|2 =a
(j+1) 0 ,
comj = 0, ..., n−1.
Os próximos resultados relacionam a quantidade de zeros dePj(z)ePj∗(z)em relação ao disco
unitário e são muito utilizados na análise da Conjectura 1.2.
Lema 2.1. SePj tempj zeros em|z| ≤1e seδj+1 6= 0, entãoPj+1 tem
pj+1 =
1
2{n−j−[(n−j)−2pj]sinal(δj+1)}
zeros em|z| ≤1. Além disso,Pj+1 tem os mesmos zeros em|z|= 1quePj.
Capítulo 2. Zeros de Polinômios 14
Teorema 2.5. Se|a0| <|an|, P(z)tem todos os seus zeros no disco unitário se, e somente se,P1∗
tem também todos os seus zeros em|z| ≤1.
A demonstração desse resultado segue do Lema 2.1.
Proposição 2.1. Se os coeficientes deP(z)são todos reais e se0 < an < an−1 < ... < a1 < a0,
então todos osa(kj)dados por (2.1.1) são reais e0< a(nj−)j < a
(j)
n−j−1 < ... < a (j)
0 , paraj = 1, .., n.
Através desse resultado é possível determinar a quantidade de zeros dos polinômiosP∗
j(z)no
disco unitário, como decorrência do Teorema de Eneström-Kakeya.
A seguir tem-se o critério de Schur-Cohn, que determina a quantidade de zeros de um polinômio no interior do círculo unitário através de condições expressas em termos dos coeficientes deP(z).
Teorema 2.6 (Critério de Schur-Cohn). SejaP(z) =
n
X
i=0
aizi. Se os determinantes
∆k =
a0 0 . . . 0 an . . . an−k+1
a1 a0 . . . 0 0 . . . an−k+2
..
. ... . . . ... ... . . . ... ak−1 ak−2 . . . a0 0 . . . an
an 0 . . . 0 a0 . . . ak−1
an−1 an . . . 0 0 . . . ak−2
..
. ... . . . ... ... . . . ...
an−k+1 an−k+2 . . . an 0 . . . a0
, k = 1,2, ..., n,
são diferentes de zero, então P(z)não possui zeros em|z| = 1epzeros em|z| < 1, ondepé o
número de variação de sinal da seqüência1,∆1, ...,∆neai representa o complexo conjugado de
ai,i= 0,1, ..., n.
Como tal condição envolve o cálculo de determinantes de matrizes de altas ordens, sua utiliza-ção será limitada.
A seguir é apresentado o critério de Hurwitz. SejamP(z) =
n
X
i=0
aizi e os determinantes
Dk=
a1 a3 . . . a2k−1
a0 a2 . . . a2k−2
0 a1 . . . a2k−3
0 a0 . . . a2k−4
... ... . . . ...
0 0 . . . ak
,
k = 2, . . . , neD1 =a1.
Capítulo 2. Zeros de Polinômios 15
Teorema 2.7. Se todos os determinantes Dk são positivos, o polinômioP(z)tem somente zeros
com parte real negativa.
Definição 2.1. Os polinômios reais cujos zeros estão localizados no semi-plano esquerdo são chamados de polinômios de Hurwitz.
Esse critério pode ser utilizado para mostrar que os zeros de um polinômio encontram-se no disco unitário fazendo a transformação r = 1 +z
1−z, que mapeia o interior do disco unitário no semi-planoRe(z)<0.
2.2
Análise da Conjectura 1.2
Nesta seção é abordado um estudo da Conjectura 1.2. Na primeira subseção é encontrado um limitante para os zeros de Pγ(z). Depois é analisado o caso em queP(z)é um polinômio
refle-xivo, com a apresentação de alguns exemplos. Em seguida, considerando um polinômio sujeito a algumas condições sobre seus coeficientes, é mostrada a validade da Conjectura 1.2.
2.2.1
Limitante para os zeros
Do Teorema 2.2, segue que
β = max
0≤k<n
ak
ak+1
= an−1
an+γ
.
Mas como P′(z) possui os coeficientes ordenados, então P′
γ(z) também possui. Logo,
n(an+γ)>(n−1)an−1.
Portanto, do Teorema 2.2, segue que os zeros dePγ(z)encontram-se em
|z| ≤β = an−1
an+γ
< n
n−1 = 1 + 1
n−1.
Então, os zeros do polinômioPγ(z)encontram-se em
|z|<1 + 1
n−1.
2.2.2
Polinômio reflexivo
Agora é analisado o caso em que o polinômioP(z)é um polinômio reflexivo, isto é,
Capítulo 2. Zeros de Polinômios 16
onde
a0 ≤a1 ≤...≤an−1 ean−1 > an.
Mas comoP(z)satisfaz as hipóteses da Conjectura 1.2, segue que
a0 < a1 =a2 =...=an−1 ean−1 > an.
Convém lembrar que os coeficientes apresentados acima são quaisquer, somente satisfazendo as condições da Conjectura 1.2 comP(z)um polinômio reflexivo.
Através desta pesquisa foi possível chegar a um resultado mais amplo, não sendo necessário es-tabelecer queP′(z)tenha seus zeros no disco. Além disso, seP(z)está sujeito a estas condições,
seus zeros encontram-se sobre o disco unitário, sendo, portanto, um caso crítico da conjectura, já que qualquer perturbação dos coeficientes acarretaria numa perturbação dos zeros. Portanto, a seguir é exibida a demonstração de que, para qualquer γ > 0, o polinômio Pγ(z), sujeito às
condições da Conjectura 1.2, possui seus zeros no disco unitário, e é encontrada uma condição sobreγ para que o polinômioPγ(z), sujeito apenas à condição deP(z)(cujos coeficientes
satis-fazem a ordenação acima) possuir todos os seus zeros no disco, tenha também seus zeros no disco unitário.
SejaP(z) =
n
X
i=0
aizi um polinômio que possui todos os seus zeros no disco unitário tal que
ai =an−i, ai >0 (i= 0,1,2, ..., n),
onde
a0 < a1 =...=an−1ean−1 > an.
Sejam
P1∗(z) =
n−1
X
i=0
a(1)i zn−1−i
(relacionado àP(z)) e
P∗
1,γ(z) = n−1
X
i=0
a(1)i,γzn−1−i
(relacionado àPγ(z)), onde os coeficientesa(1)i ea
(1)
i,γ, i = 0, ..., n−1, são dados pela expressão
(2.1.1).
Seγ > 0, segue que|a0| < |an+γ|. Caso contrário, tal hipótese é considerada. Assim, o
Teorema 2.5 pode ser utilizado paraPγ(z).
Observe que
|a(1)n−1,γ|=|a
(1)
n−2,γ|=...=|a
Capítulo 2. Zeros de Polinômios 17
Resta analisar a relação existente entre|a(1)0,γ|e|a(1)1,γ|:
|a(1)0,γ| − |a(1)1,γ|=|γ|(γ+ 2an−an−1).
Se|a(1)0,γ| ≥ |a(1)1,γ|, os coeficientes deP∗
1,γ(z)estão ordenados e então, pelo Teorema de
Eneström-Kakeya, os zeros deP∗
1,γ(z)encontram-se no disco unitário. Mas para que isso ocorra é necessário
que
|γ|(γ+ 2an−an−1)≥0⇔γ ≥an−1 −2an.
Portanto, paraγ ≥an−1−2an, o polinômioPγ(z)possui os zeros no disco unitário.
No caso do polinômio reflexivo estar sujeito às condições da Conjectura 1.2, isto é, sendoP(z)
um polinômio cujos zeros encontram-se no disco unitário eP′(z)com os coeficientes ordenados,
segue que
2an−an−1 ≥0,
sendon >1.
Logo, para qualquerγ >0, os coeficientes deP∗
1,γ(z)estão ordenados.
Para analisar o caso em queγ < an−1−2an, observe que
|a(1)0,γ| − |a(1)n−1,γ| = γ(γ+ 2an−a1) =|γ|(γ+ 2an−an−1)<0.
Portanto,|a(1)0,γ|<|a(1)n−1,γ|.
Utilizando uma das relações das fórmulas de Vieta, dada por
ζ1ζ2...ζn−1 = (−1)n−1
a(1)n−1,γ
a(1)0,γ ,
ondeζi,i= 1, ..., n−1, são os zeros deP1∗,γ(z), tem-se
|ζ1ζ2...ζn−1|=
(−1)
n−1a (1)
n−1,γ
a(1)0,γ
,
ou seja,
|ζ1|.|ζ2|...|ζn−1|>1,
de onde é possível concluir que pelo menos um dos zeros de P∗
1,γ(z) encontra-se fora do disco
unitário.
Portanto, os zeros dePγ(z)encontram-se no disco unitário quandoγ ≥an−1−2an.
Capítulo 2. Zeros de Polinômios 18
Proposição 2.2. SejaP(z)um polinômio reflexivo que possui seus zeros no disco unitário cujos coeficientes satisfazem
0< a0 < a1 =a2 =...=an−1ean−1 > an.
Os zeros dePγ(z) =P(z) +γznencontram-se no disco unitário quandoγ ≥an−1−2an.
A seguir são apresentados alguns exemplos que ilustram os resultados obtidos.
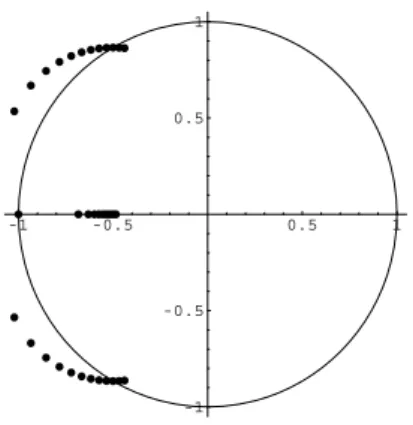
Exemplo 2.1. Seja
P(z) =z3 + 3z2+ 3z+ 1,
cujos zeros encontram-se no disco unitário (z =−1). O polinômio
Pγ(z) = (1 +γ)z3+ 3z2+ 3z+ 1
possui todos os seus zeros no disco quando γ ≥ an−1 −2an = 1, como é possível observar na
Figura 2.1.
-1 -0.5 0.5 1
-1 -0.5 0.5 1
Figura 2.1:Comportamento dos zeros dePγ(z) = (1 +γ)z3+ 3z2+ 3z+ 1,0≤γ ≤1.2.
Nesse caso, o polinômioPγ(z) = (1 +γ)z3 + 3z2+ 3z+ 1, paraγ = 0.1,0.2, ...,1.2, possui
um zero real e dois complexos. Quando γ = 1, os zeros complexos encontram-se sobre o círculo
unitário e à medida queγ aumenta, os zeros dePγ(z)entram no círculo.
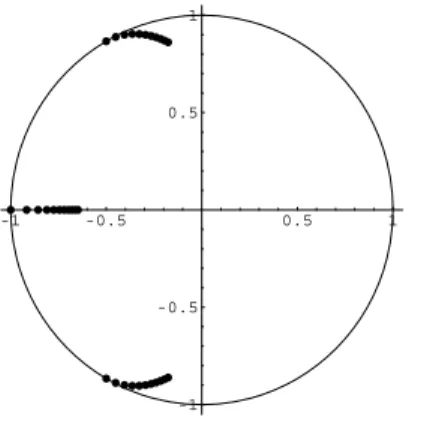
Exemplo 2.2. Seja
P(z) =z4+ 2z3+ 2z2+ 2z+ 1,
cujos zeros encontram-se no disco unitário. O polinômio
Pγ(z) = (1 +γ)z4+ 2z3+ 2z2 + 2z+ 1
possui todos os seus zeros no disco quandoγ ≥0, como está ilustrado na Figura 2.2, cujos pontos
Capítulo 2. Zeros de Polinômios 19
-1 -0.5 0.5 1
-1 -0.5 0.5 1
Figura 2.2:Comportamento dos zeros dePγ(z) = (1 +γ)z4+ 2z3+ 2z2+ 2z+ 1,0≤γ ≤1.
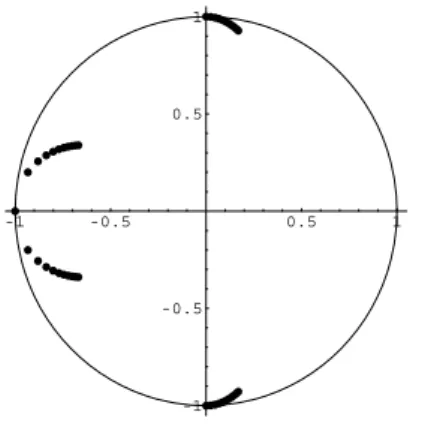
Exemplo 2.3. Seja
P(z) = 2.2z3+ 6z2+ 6z+ 2.2,
cujos zeros encontram-se no disco unitário. O polinômio
Pγ(z) = (2.2 +γ)z3+ 6z2+ 6z+ 2.2
possui todos os seus zeros no disco quandoγ ≥1.6, como pode ser visto na figura a seguir, onde
os pontos representam os zeros dePγ(z) = (2.2 +γ)z3+ 6z2+ 6z+ 2.2paraγ = 0,0.2,0.4, ...,2.
-1 -0.5 0.5 1
-1 -0.5 0.5 1
Figura 2.3:Comportamento dos zeros dePγ(z) = (2.2 +γ)z3 + 6z2+ 6z+ 2.2,0≤γ ≤2.
Exemplo 2.4. Seja
P(z) = z3 + 2z2+ 2z+ 1,
cujos zeros encontram-se no disco unitário. O polinômio
Pγ(z) = (1 +γ)z3+ 2z2+ 2z+ 1
Capítulo 2. Zeros de Polinômios 20
-1 -0.5 0.5 1
-1 -0.5 0.5 1
Figura 2.4: Comportamento dos zeros dePγ(z) = (1 +γ)z3 + 2z2+ 2z+ 1,0≤γ ≤1.
Exemplo 2.5. Seja
P(z) = 1.5z3+ 2z2+ 2z+ 1.5,
cujos zeros encontram-se no disco unitário. O polinômio
Pγ(z) = (1.5 +γ)z3+ 2z2+ 2z+ 1.5
também possui todos os seus zeros no disco, paraγ >0, poisP′(z)tem seus coeficientes
ordena-dos. A Figura 2.5 apresenta os zeros dePγ(z)para0≤γ ≤1.
-1 -0.5 0.5 1
-1 -0.5 0.5 1
Figura 2.5:Comportamento dos zeros dePγ(z) = (1.5 +γ)z3 + 2z2+ 2z+ 1.5,0≤γ ≤1.
Através dessa abordagem, existem fortes indícios da validade da Conjectura 1.2, pois como já foi mencionado anteriormente, este caso seria um caso crítico da conjectura, sendo que a pertur-bação no coeficiente dominante faz com que os zeros dePγ(z)entrem no disco unitário.
2.2.3
Caso geral
Uma das hipóteses da Conjectura 1.2 é que os coeficientes da derivada deP(z)estão ordenados. Então,
Capítulo 2. Zeros de Polinômios 21
sendon >1.
Portanto,
an−1−2an≤0. (2.2.1)
Outra hipótese da Conjectura 1.2 é que os zeros deP(z)encontram-se no disco unitário. Então, através das fórmulas de Vieta, segue que
|z1z2. . . zn|=|z1||z2|...|zn| ≤1⇒
a0
an ≤
1⇒a0 ≤an ⇒a0 < an+γ,
ondeγ >0.
Suponha que2a0 < a1 e serão analisados os coeficientesaj em (2.1.1).
Paraj = 1, tem-se:
a(1)0 = a20−a2n a(1)1 = a0a1−anan−1
a(1)2 = a0a2−anan−2
...
a(1)n−1 = a0an−1 −ana1.
Observe quea(1)n−1 <0, pois
a(1)n−1 =a0an−1−ana1 <2a0an−a1an<0.
Além disso,
a(1)1 −a(1)2 =a0(a1−a2) +an(an−2−an−1)<0
a(1)2 −a(1)3 =a0(a2−a3) +an(an−3−an−2)<0
... a(1)n−2−a
(1)
n−1 =a0(an−2 −an−1) +an(a1−a2)<0.
Então,
a(1)1 < a(1)2 < ... < a(1)n−1 <0.
Logo,
|a(1)1 |>|a(1)2 |> ... >|a(1)n−1|. (2.2.2)
De maneira análoga dos coeficientes deP∗
1(z), segue que
|a(1)1,γ|>|a(1)2,γ|> ... >|a(1)n−1,γ|. (2.2.3)
É utilizado o Teorema 2.5 para analisar o comportamento dos zeros de Pγ(z), pois como
Capítulo 2. Zeros de Polinômios 22
Sejam
P∗
1(z) = a (1)
n−1+a (1)
n−2z+. . .+a (1) 0 zn
−1
P1∗,γ(z) =a(1)n−1,γ +a
(1)
n−2,γz+. . .+a
(1) 0,γzn
−1.
Sabe-se que as relações (2.2.2) e (2.2.3) são válidas. Resta analisar a relação entre os coefi-cientesa(1)1 ,a(1)0 ,a(1)1,γ ea(1)0,γ.
Considere os seguintes casos:
1. |a(1)1 | ≤ |a(1)0 |e|a(1)1,γ| ≤ |a(1)0,γ|:
Como|a(1)1 | ≤ |a(1)0 |, entãoa(1)1 −a(1)0 ≥0.
Assim,
|a(1)1,γ| ≤ |a(1)0,γ| ⇔ a(1)1,γ −a(1)0,γ ≥0⇔γ2+ (2an−an−1)γ+a(1)1 −a (1) 0 ≥0
⇔ γ(γ+ 2an−an−1)≥0⇔γ ≥an−1−2an.
Logo, como γ > 0 e a desigualdade (2.2.1) é válida, segue que esse caso é satisfeito para qualquerγ, o que já era de se esperar, pois os coeficientes deP∗
1(z)estão ordenados.
Por exemplo, considere o polinômio
P(z) = 0.9 + 2z+ 2.4z2+ 2z3,
que satisfaz as condições da Conjectura 1.2. O polinômio
P1∗(z) = −1.84−3z−3.19z2
possui seus coeficientes ordenados. Então,Pγ(z) = P(z) +γz3 tem também todos os seus
zeros no disco unitário, paraγ >0.
Observe que a condiçãoγ ≥an−1−2ané a mesma encontrada no caso do polinômioP(z)
ser reflexivo, que foi um caso analisado na subseção anterior.
2. |a(1)1 |<|a(1)0 |e|a(1)1,γ|>|a(1)0,γ|:
Como|a(1)1 |<|a(1)0 |, entãoa(1)1 −a(1)0 >0. Logo,
|a(1)1,γ|>|a0(1),γ| ⇔ a(1)1,γ −a(1)0,γ <0⇔γ2+ (2an−an−1)γ+a(1)1 −a (1) 0 <0,
que não possui solução paraγ >0, pois todos os coeficientes são positivos.
Portanto, esse caso é impossível de ocorrer.
Capítulo 2. Zeros de Polinômios 23
Nesse caso, os coeficientes deP∗
1,γ(z)estão ordenados e assim, pelo Teorema de
Eneström-Kakeya, segue que os zeros deP∗
1,γ(z)encontram-se no disco unitário e, conseqüentemente,
os zeros dePγ(z)também estão em|z| ≤1.
4. |a(1)1 |>|a(1)0 |e|a(1)1,γ|>|a(1)0,γ|:
Esse caso ainda está sendo pesquisado.
É possível observar, através de testes numéricos, que os coeficientes dos polinômiosP∗
j,γ(z)
têm as mesmas características dos coeficientes deP(z)ePγ(z), ou seja,
|a(1j,γ)|>|a2(j,γ)|> ... >|a(nj−)j,γ|e|a
(j) 0,γ|<|a
(j) 1,γ|.
Então, o problema se resumiria a determinar a raiz deP∗
n−1,γ(z) = a
(n−1) 1,γ +a
(n−1)
0,γ z = 0, que
tudo indica ter módulo menor ou igual a um.
Para polinômios de grau menor ou igual a três, fica fácil mostrar que a conjectura é válida. De fato, paran = 1, o resultado é óbvio, pois a única raiz dePγ(z) = 0é
z =−a a0
1+γ
.
Paran = 2, é necessário analisar o que ocorre com a raiz de P∗
1,γ(z) = a
(1) 1,γ +a
(1)
0,γz = 0,
de acordo com o Teorema 2.5. Observe primeiramente que, como P(z)tem seus zeros no disco,
P∗
1(z)também tem, e então|a (1) 0 | ≥ |a
(1) 1 |. Mas
|a(1)0,γ| − |a(1)1,γ|=γ2 + (2a2−a1)γ+|a(1)0 | − |a (1) 1 |>0,
paraγ >0.
Portanto,P∗
1,γ(z)tem seu zero no disco e, pelo Teorema 2.5,Pγ(z)também tem.
Paran= 3, é preciso analisar o que ocorre com a raiz deP∗
2,γ(z) = a
(2) 1,γ +a
(2) 0,γz = 0.
Observe que
|a(2)0,γ| − |a(2)1,γ|=|a(1)0,γ−a(1)2,γ||a(1)0,γ+a2(1),γ| − |a(1)1,γ|.
Mas
|a(1)0,γ +a(1)2,γ| − |a(1)1,γ|=−(a0+a3+γ)(P(−1)−γ)≥0.
Logo,
Capítulo 2. Zeros de Polinômios 24
Portanto,P∗
2,γ(z)tem seu zero no disco unitário e, pelo Teorema 2.5,Pγ(z)também tem.
Para polinômios de grau maior que três, um dos problemas que surge é somente em relação ao sinal dos coeficientes deP∗
j,γ(z), j = 2, ..n−1. Se for possível mostrar que todos são positivos,
não existiria dificuldade em provar a Conjectura 1.2, pois, neste caso, sabe-se que
|a(1j,γ)|>|a2(j,γ)|> ... >|a(nj−)j,γ|,
paraj = 1, ..., n−j, e
|a(0n,γ−1)|>|a(1n,γ−1)|.
Portanto, um desafio agora é mostrar que os coeficientes deP∗
j,γ(z),j = 2, ..n−1, são todos
positivos.
A próxima subseção traz uma análise que inclui o último caso apresentado, sendo possível provar a validade da Conjectura 1.2 quando os coeficientes deP(z)satisfazem algumas condições
adicionais, sendo o caso geral objeto de estudos futuros.
2.2.4
Condições adicionais
A análise apresentada nesta seção está baseada no Teorema 2.5, pois se|a0|< |an|, P(z)tem
todos os seus zeros no disco unitário se, e somente se, o mesmo ocorre comP∗
1(z). Caso não seja
conhecido o comportamento dos zeros deP∗
1(z), é possível usar o mesmo resultado para analisar
os zeros deP∗
2(z), ou seja, se|a (1)
n−1|<|a (1)
0 |,P1∗(z)tem todos os seus zeros no disco unitário se, e
somente se,P∗
2(z)também tem. Continuando esse raciocínio, é preciso analisar o que ocorre com
o zero do polinômioP∗
n−1(z) =a (n−1) 1 +a
(n−1) 0 z.
Considere o polinômio P(z), cujos zeros encontram-se no disco unitário e seus coeficientes satisfazem
a0 < a1 < ... < an−1 > an
e
pai <(p−1)ai+1, i = 0,1, ..., n−2, epan >(p−1)an−1,
ondepé um número inteiro positivo,p > 1.
Sejam os polinômios
Pj∗(z) = a(nj−)j +a
(j)
n−j−1z+...+a (j) 0 zn
−j
e
Pj,γ∗ (z) =a(nj−)j,γ +a
(j)
n−j−1,γz+...+a
(j) 0,γzn
−j,
relacionados, respectivamente, aos polinômios P(z) e Pγ(z), cujos coeficientes são obtidos da
Capítulo 2. Zeros de Polinômios 25
Como o polinômioP(z)tem todos os seus zeros no disco unitário (por hipótese da Conjectura
1.2), segue, pelo Teorema 2.5, que todos os polinômiosP∗
j(z)também têm.
Resta analisar o que ocorre com os zeros dos polinômiosP∗
j,γ(z).
Já foi visto que, paraj = 1,
a(1)1 < a(1)2 < ... < a(1)n−1. (2.2.4)
Comoa(1)n−1 <0, pois
a(1)n−1 =a0an−1−ana1 <
p−1
p a1an−1−ana1 =a1
p−1
p an−1−an
<0,
então, de (2.2.4) segue quea(1)i <0parai= 1,2, ..., n−1.
Portanto,
|a(1)1 |>|a(1)2 |> ... >|a(1)n−1|.
Da mesma forma que os coeficientes deP(z), os coeficientes deP∗
1(z)satisfazem
p|a(1)n−i|<(p−1)|an(1)−i−1|, parai= 1,2, ..., n−2,
e
p|a(1)0 |>(p−1)|a(1)1 |.
De fato,
pa(1)0 −(p−1)a(1)1 = p a20−an2−(p−1) (a0a1 −anan−1)
= a0(pa0−(p−1)a1) +an((p−1)an−1 −pan)<0.
Então,
pa(1)0 −(p−1)a(1)1 <0⇒pa(1)0 <(p−1)a(1)1 <0⇒a(1)0 <0.
Portanto,
p|a(1)0 |>(p−1)|a(1)1 |.
Além disso, parai= 1,2, ..., n−2, segue que
pa(1)n−i−(p−1)a
(1)
n−i−1 = p(a0an−i−anai)−(p−1) (a0an−i−1−anai+1)
Capítulo 2. Zeros de Polinômios 26
Portanto, parai= 1,2, ..., n−2,
p|a(1)n−i|<(p−1)|a
(1)
n−i−1|.
De maneira análoga é possível provar que o mesmo ocorre com os coeficientes do polinômio P∗
1,γ(z).
Paraj = 2,
a(2)1 > a(2)2 > ... > a(2)n−2. (2.2.5)
Comoa(2)n−2 >0, pois
a(2)n−2 =a (1) 0 a
(1)
n−2−a (1)
n−1a (1) 1 >
(p−1)
p a
(1) 1 a
(1)
n−2−a (1)
n−1a (1) 1 =a
(1) 1
p−1
p a
(1)
n−2−a (1)
n−1
>0,
então, de (2.2.5) segue quea(2)i >0parai= 1,2, ..., n−2. Portanto,
a(2)1 > a(2)2 > ... > a(2)n−2.
Da mesma forma que os coeficientes deP∗
1(z), os coeficientes deP
∗
2(z)satisfazem
pa(2)n−i <(p−1)an(2)−i−1, parai= 2, ..., n−2,
e
p|a(2)0 |>(p−1)|a(2)1 |.
De fato,
pa(2)0 −(p−1)a(1)2 = p(a(1)0 )2 −(a(1)n−1)2
−(p−1)(a(1)0 a(1)1 −a(1)n−2a (1)
n−1)
= a(1)0 pa(1)0 −(p−1)a(1)1 +a(1)n−1
(p−1)a(1)n−2−pa (1)
n−1
>0.
Então,
pa(2)0 −(p−1)a(2)1 >0⇒pa(2)0 >(p−1)a(2)1 >0⇒a(2)0 >0.
Portanto,
pa(2)0 >(p−1)a(2)1 .
Além disso, parai= 2, ..., n−2,
pa(2)n−i−(p−1)a
(2)
n−i−1 = p
a(1)0 a(1)n−i−a
(1)
n−1a (1)
i−1
−(p−1)a(1)0 a(1)n−i−1−a (1)
n−1a (1)
i
= a(1)0 pa(1)n−i−(p−1)a
(1)
n−i−1
Capítulo 2. Zeros de Polinômios 27
Portanto, parai= 2, ..., n−2,
p|a(1)n−i|<(p−1)|a
(1)
n−i−1|.
De maneira análoga prova-se que o mesmo ocorre com os coeficientes do polinômioP∗
2,γ(z).
Como hipótese de indução, suponha que, paraj qualquer,
ai(j)>0, paraj = 0,1, ..., n−j, a1(j) > a(2j)> ... > a(nj−)j,
pa(0j)>(p−1)a1(j)epan(j−)i <(p−1)a
(j)
n−i−1, parai=j, ..., n−2.
A seguir é verificado o que ocorre paraj+ 1(j = 2, ..., n−3).
Parai= 1, .., n−j,
ai(j+1)−a(i+1j+1) = a0(j)a(ij)−a(nj−)ja
(j)
n−j−i−a
(j) 0 a
(j)
i+1+a (j)
n−ja
(j)
n−j−i−1
= a(0j)a(ij)−a(i+1j)+a(nj−)ja(nj−)j−i−1−a(nj−)j−i>0.
Observe também que
an(j−+1)(j+1) = a(0j)an(j−)(j+1)−an(j−)ja(1j)> p−1 p a
(j) 1 a
(j)
n−(j+1)−a (j)
n−ja
(j) 1
> a(1j)
p−1
p a
(j)
n−(j+1)−a (j)
n−j
>0.
Portanto,
a1(j+1) > a(2j+1) > ... > an(j−+1)(j+1) >0.
A desigualdadepa(0j+1) >(p−1)a(1j+1)é verdadeira, pois
pa(0j+1)−(p−1)a(1j+1) = p(a(0j))2−(a(nj−)j)2
−(p−1)a(0j)a1(j)−a(nj−)ja
(j)
n−j−1
= a(0j)pa(0j)−(p−1)a(1j)+a(nj−)j
(p−1)a(nj−)j−1−pa (j)
n−j
>0.
Então, da desigualdade acima é possível concluir quea(0j+1) >0.
Além disso, parai=j+ 1, ..., n−2,
pa(nj−+1)i −(p−1)a
(j+1)
n−i−1 = p
a(0j)a(nj−)i−a
(j)
n−ja
(j)
i−j
−(p−1)a(0j)a(nj−)i−1−a (j)
n−ja
(j)
i−j+1
= a(0j)pa(nj−)i−(p−1)a
(j)
n−i−1
+a(nj−)j
(p−1)ai(−j)j+1−pai−j
Capítulo 2. Zeros de Polinômios 28
Portanto, parai=j + 1, ..., n−2,
pa(nj−+1)i <(p−1)a
(j+1)
n−i−1.
De maneira análoga prova-se que o mesmo ocorre com os coeficientes do polinômioP∗
j+1,γ(z).
Resta analisar o polinômioP∗
n−1,γ(z) = a
(n−1) 1,γ +a
(n−1) 0,γ z.
Observe que
a(1n−1) = a(0n−2)a1(n−2)−a1(n−2)a(2n−2) > p−1 p a
(n−2) 1 a
(n−2) 1 −a
(n−2) 1 a
(n−2) 2
= a(1n−2)
p−1
p a
(n−2) 1 −a
(n−2) 2
>0.
Portanto,a(1n−1) >0.
Além disso,
pa(0n−1)−(p−1)a1(n−1) = p(a0(n−2))2−(a2(n−2))2−(p−1)a(0n−2)a(1n−2)−a1(n−2)a(2n−2)
= a(0n−2)pa0(n−2)−(p−1)a(1n−2)+a2(n−2)(p−1)a1(n−2)−pa(2n−2) > 0.
Logo,a(0n−1) >0.
Para analisar o que ocorre coma(0n−1)−a(1n−1), observe que
a(0n−1)−a(1n−1) = (a(0n−2)−a(2n−2))(a(0n−3)+a(3n−3))...(a(1)0 + (−1)na(1)n−1)
(a0+ (−1)n+1an)((−1)nan+ (−1)n−1an−1+...+a0). (2.2.6)
Já foi visto que, paraj = 2,3, ..., n−1,
0< a(0j) = (a0(j−1))2−(an(j−−(1)j−1))2 = (a0(j−1)−a(nj−−(1)j−1))(a0(j−1)+a(nj−−(1)j−1)).
Então,a(0j−1)−an(j−−(1)j−1) >0ea0(j−1)+an(j−−(1)j−1) >0.
Em (2.2.6), é possível observar que(−1)na
n+ (−1)n−1an−1+...+a0 =P(−1).
Além disso,P(−1)≥0paranpar eP(−1)≤0paranímpar. Então, de (2.2.6),
a(0n−1)−a(1n−1) ≥0.
Portanto,P∗
n−1(z)tem seu zero no disco unitário.
No caso do polinômioPn−1,γ(z), a mesma demonstração é usada para provar quea(n
−1) 0,γ >0e
Capítulo 2. Zeros de Polinômios 29
Além disso,
a(0n,γ−1)−a(1n,γ−1) = (a(0n,γ−2)−a(2n,γ−2))(a(0n,γ−3)+a(3n,γ−3))...(a(1)0,γ+ (−1)na(1)n−1,γ)
(a0+ (−1)n+1(an+γ))((−1)n(an+γ) + (−1)n−1an−1 +...+a0)
= (a(0n,γ−2)−a2(n,γ−2))(a(0n,γ−3)+a(3n,γ−3))...(a(1)0,γ+ (−1)na(1)n−1,γ)
(a0+ (−1)n+1(an+γ))((−1)nγ+P(−1)) ≥0.
Logo,a(0n,γ−1)−a1(n,γ−1) >0eP∗
n−1,γ(z)tem seu zero no disco unitário e, como conseqüência do
Teorema 2.5,Pγ(z)também tem.
Portanto, esta é a demonstração do seguinte resultado:
Proposição 2.3. SejaP(z) =
n
X
i=0
aizium polinômio cujos zeros encontram-se no disco unitário e
os coeficientes satisfazem
0< a0 < a1 < ... < an−1 > an, pai <(p−1)ai+1, i = 0,1, ..., n−2, epan >(p−1)an−1,
ondepé um número inteiro positivo. Então, o polinômioPγ(z) = P(z) +γzn,γ >0, possui todos
os seus zeros no disco unitário.
Esse é um dos principais resultados obtidos neste trabalho, pois além de ser inédito, será im-portante para dar suporte à Conjectura de Jeltsch, pois no caso dos métodos(K, L)de Brown, para K ≤K∗
L, os coeficientes deρ(z)satisfazem
2αj < αj+1 e2αK > αK−1,
como foi citado anteriormente.
Portanto, no caso dos polinômios característicos relacionados aos métodos(K, L)de Brown,
segue que a Conjectura de Jeltsch é válida paraK ≤K∗
L.
No próximo capítulo tem-se maiores detalhes a respeito da Conjectura 1.1.
C
APÍTULO3
Métodos
(
K, L
)
de Brown
Neste capítulo são apresentadas algumas propriedades dos métodos(K, L)de Brown e é
uti-lizada a teoria das order stars para analisá-las, como, por exemplo, as questões de estabilidade. Primeiramente são apresentadas propriedades importantes relacionadas aos métodos (K, L) de
Brown. A segunda seção traz algumas definições e resultados sobre order stars, pois tal ferramenta será muito utilizada no decorrer deste capítulo. Depois são apresentadas algumas características dos métodos de Brown e são provados alguns resultados importantes através das order stars.
3.1
Introdução
Os métodos(K, L) de Brown, introduzidos por Brown (1977), formam uma classe de
méto-dos multiderivadas de passo múltiplo para a solução de equações diferenciais ordinárias. Foram introduzidos como métodos com menor número de passos e melhor precisão para a solução de problemas. Tais métodos possuem boas propriedades de estabilidade, como grandes regiões de estabilidade absoluta. Por esse motivo, os métodos multiderivadas são indicados para resolver problemas stiff.
Como já foi visto anteriormente, os métodos(K, L)de Brown são representados por
K
X
i=0
αiyn+i = L
X
j=1
βjhjf(j
−1)
n+K ,
Capítulo 3. Métodos(K, L)de Brown 31
onde as constantes αi e βj são escolhidas de modo a obter a máxima precisão. A construção
explícita desta classe de métodos pode ser encontrada em Jeltsch e Kratz (1978). Os coeficientesαi eβj são dados por
αi = (−1)K−i
K i
!
(K−i)−L, i = 0, . . . , K
−1,
αK = −(α0+α1+. . .+αK−1),
βj =
(−1)j
j!
KX−1
i=0
(−1)K−i K
i
!
(K−i)j−L, j = 1, . . . , L.
A seguir são apresentados alguns resultados sobre os métodos(K, L), cujo estudo detalhado pode ser visto em Meneguette (1987).
Teorema 3.1. Os métodos(K, L)de Brown têm ordem de consistênciap=K+L−1.
Observe que, como K, L ≥ 1, estes métodos têm ordem pelo menos um. Logo, são sempre consistentes para quaisquer valores deK eL.
Se os métodos(K, L)têm ordemp, então
ρ(ez)−
L
X
j=1
zjσj(ez) =
∞ X
j=p+1
Cjzj, Cp+1 6= 0,
onde ρ(ξ)e σj(ξ)são os polinômios característicos relacionados aos métodos(K, L) de Brown,
dados por
ρ(ξ) =
K
X
i=0
αiξi (3.1.1)
e
σj(ξ) =βjξK, j= 1,2, ..., L. (3.1.2)
Para analisar a convergência de métodos lineares de passo múltiplo, basta verificar se o método é consistente e zero-estável, sendo este um resultado clássico de Dahlquist. No caso de métodos multiderivadas de passo múltiplo, este resultado também é válido.
Um método é zero-estável quando os zeros do polinômioρ(ξ)encontram-se no disco unitário
e os zeros de módulo um são simples. Além disso, diz-se que um método numérico é fortemente estável quando é zero-estável e temz = 1como a única possibilidade para os zeros de módulo um. Para analisar a convergência dos métodos(K, L), basta analisar a zero-estabilidade, pois como
já foi visto, são sempre consistentes.
Além do conceito de zero-estabilidade, existem outros conceitos de estabilidade, que são: A-estabilidade, A(α)-estabilidade, A0-estabilidade e stiff-estabilidade. Tais conceitos diferem da