UNIVERSIDADEFEDERALDO RIO GRANDE DO NORTE PROGRAMA DEPÓS-GRADUAÇÃO EMENGENHARIAELÉTRICA
Máquina de Vetores-Suporte Intervalar
Adriana Takahashi
Orientador: Prof. Dr. Adrião Duarte Dória Neto Co-orientador: Prof. Dr. Benjamín René Callejas Bedregal
Tese de Doutorado apresentada ao
Pro-grama de Pós-Graduação em Engenharia Elétrica da UFRN, área de concentração: Engenharia de Computação como parte dos requisitos para obtenção do título de Doutor em Ciências.
Adriana Takahashi
Tese de Doutorado
Prof. Dr. Adrião Duarte Dória Neto (orientador) . . . UFRN/DCA
Prof. Dr. Benjamín René Callejas Bedregal (co-orientador) . . . UFRN/DIMAp
Prof. Dr. Jorge Dantas de Melo . . . UFRN/DCA
Prof. Dr. Aarão Lyra . . . UnP
Prof. Dra. Renata Hax Sander Reiser . . . UFPel
Aos meus orientadores, professores Adrião e Benjamin, sou grata pela orientação e paciên-cia.
Aos colegas do departamento.
As máquinas de vetores suporte (SVM - Support Vector Machines) têm atraído muita atenção na área de aprendizagem de máquinas, em especial em classificação e reconhe-cimento de padrões, porém, em alguns casos nem sempre é fácil classificar com precisão determinados padrões entre classes distintas. Este trabalho envolve a construção de um classificador de padrões intervalar, utilizando a SVM associada com a teoria intervalar, de modo a modelar com uma precisão controlada a separação entre classes distintas de um conjunto de padrões, com o objetivo de obter uma separação otimizada tratando de imprecisões contidas nas informações do conjunto de padrões, sejam nos dados iniciais ou erros computacionais.
A SVM é uma máquina linear, e para que ela possa resolver problemas do mundo real, geralmente problemas não lineares, é necessário tratar o conjunto de padrões, mais conhecido como conjunto de entrada, de natureza não linear para um problema linear, as máquinas kernels são responsáveis por esse mapeamento. Para a extensão intervalar da SVM, tanto para problemas lineares quanto não lineares, este trabalho introduz a definição de kernel intervalar, bem como estabelece o teorema que valida uma função ser um kernel, o teorema de Mercer para funções intervalares.
The Support Vector Machines (SVM) has attracted increasing attention in machine learning area, particularly on classification and patterns recognition. However, in some cases it is not easy to determinate accurately the class which given pattern belongs. This thesis involves the construction of a intervalar pattern classifier using SVM in association with intervalar theory, in order to model the separation of a pattern set between distinct classes with precision, aiming to obtain an optimized separation capable to treat impreci-sions contained in the initial data and generated during the computational processing.
The SVM is a linear machine. In order to allow it to solve real-world problems (usu-ally nonlinear problems), it is necessary to treat the pattern set, know as input set, trans-forming from nonlinear nature to linear problem. The kernel machines are responsible to do this mapping. To create the intervalar extension of SVM, both for linear and nonlin-ear problems, it was necessary define intervalar kernel and the Mercer’s theorem (which caracterize a kernel function) to intervalar function.
Sumário i
Lista de Figuras iii
Lista de Tabelas iv
1 Introdução 1
1.1 Apresentação e motivação . . . 1
1.2 Objetivos . . . 2
1.3 Trabalhos relacionados . . . 2
1.4 Organização do Trabalho . . . 3
2 Máquinas de Vetores-Suporte 5 2.1 Máquina de Vetores-Suporte Linearmente Separável . . . 6
2.1.1 Hiperplano Ótimo para Classes Linearmente Separáveis . . . 10
2.2 Máquina de Vetor de Suporte Não Lineares . . . 12
2.2.1 Hiperplano Ótimo para Classes Não Linearmente Separáveis . . . 12
2.2.2 Função Kernel . . . . 15
2.3 Considerações . . . 17
3 Matemática Intervalar 18 3.1 Representação de Intervalos . . . 19
3.2 Operações Aritméticas Intervalares . . . 19
3.3 Propriedades Algébricas Intervalares . . . 20
3.4 Ordem Intervalar . . . 21
3.5 Função Intervalar . . . 21
3.5.1 Metrica intervalar emIRn . . . . 21
3.5.2 Integral Interval . . . 23
3.6 R-vetoide e espaço R-vetoide intervalar . . . 23
3.6.1 Produto interno intervalar . . . 24
4 Otimização usando Análise Intervalar 26
4.1 Otimização Linear . . . 26
4.1.1 Funcional de Lagrange . . . 27
4.1.2 Condições de Kuhn-Tucker . . . 28
4.2 Otimização Linear usando Computação Intervalar . . . 28
4.2.1 Otimização com restrições . . . 29
4.2.2 Condições de John . . . 30
5 Kernel Intervalar 31 5.1 Mapeamento Função Kernel Intervalar . . . 33
5.2 Construção de Kernel Intervalar . . . 34
5.2.1 Fazendo Kernels de kernels . . . 36
5.3 Alguns Kernels Intervalares . . . 37
5.3.1 Extensão Intervalar do Kernel Gaussiano . . . . 37
5.3.2 Extensão intervalar do Kernel Polinomial . . . . 38
6 Máquina de Vetores-Suporte Intervalar 39 6.1 Máquina de Vetores-Suporte Intervalares Linearmente Separáveis . . . . 39
6.2 Máquina de Vetor de Suporte Intervalares Não Separáveis . . . 44
7 Implementações Computacionais e Resultados 48 7.1 Implementações Computacionais e Resultados . . . 48
7.1.1 Método Intervalar: Gradiente . . . 50
7.1.2 Algumas variações: . . . 50
7.1.3 Método Intervalar: Adatron . . . 50
7.1.4 Método Intervalar: Perceptron Dual . . . 51
7.2 Resultados de testes . . . 53
7.2.1 Resultados da SVMI . . . 53
7.2.2 Conjunto de treinamento intervalar . . . 54
8 Conclusões 57 8.1 Possibilidades de trabalhos futuros . . . 58
2.1 Hiperplano de separação (w,b) para um conjunto de treinamento
bidi-mensional. . . 6
2.2 Hiperplano ótimo com máxima margemρode separação dos padrões lin-earmente separáveis. . . 7
2.3 Interpretação gráfica da distância x até o hiperplano ótimo para o caso bidimensional. . . 8
2.4 Mapeamento de características. . . 12
2.5 (a) O ponto(xi,di)se encontra na região de separação, mas do lado cor-reto. (b) O ponto(xi,di)se encontra na região de separação, mas do lado incorreto. (c) O ponto (xi,di) se encontra fora da região de separação, mas do lado incorreto. . . 13
6.1 Ilustração do hiperplano ótimo intervalar. . . 40
6.2 Interpretação da distância de X até p hiperplano ótimo. . . . 41
7.1 Treimanento de uma SVMI . . . 49
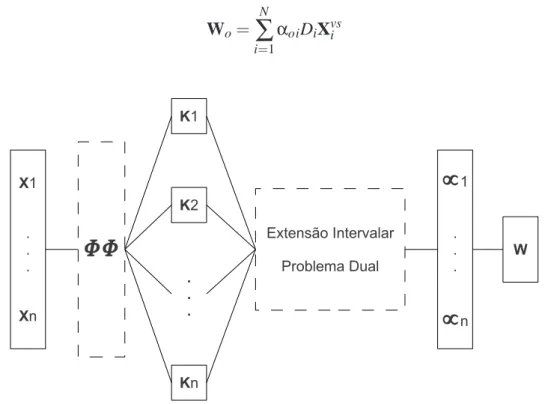
7.2 Topologia da SVMI . . . 53
2.1 Principais kernels utilizados nas SVMs . . . . 16
7.1 Tabela de resultados da SVMI . . . 53
7.2 Tabela de resultados da SVMI . . . 54
7.3 Problema das espirais . . . 54
7.4 Problema das espirais intervalar . . . 54
7.5 Matriz intervalar do problema das espirais intervalar para o kernel linear . 55 7.6 Matriz intervalar do problema das espirais intervalar para o kernel linear . 55 7.7 Matriz kernel do problema das espirais para o kernel polinomial . . . . . 55
7.8 Matriz intervalar do problema das espirais intervalar para o kernel poli-nomial . . . 55
7.9 Matriz kernel do problema das espirais para o kernel gaussiano . . . . 56 7.10 Matriz intervalar do problema das espirais intervalar para o kernel gaussiano 56
Introdução
1.1
Apresentação e motivação
As máquinas de vetores suporte (SVM - Support Vector Machines) têm atraído muita atenção nos últimos anos devido a sua eficiência, comparada com outros tipos de redes neurais, em aplicações que requerem aprendizado de máquina e por estar bem fundamen-tado na teoria de aprendizado estatístico [Stitson et al. 1996, Pontil & Verri 1997]. A SVM pode ser usada para resolver problemas de classificação e regressão linear. Burges [Burges 1998] apresenta um tutorial sobre a SVM que trata de problemas de classificação de padrões, e em [Stitson et al. 1996, Hearst 1998], mostram-se problemas de regressão, fazendo da SVM uma abordagem abrangente para diversas aplicações que envolvem prob-lemas de modelagem de dados empíricos.
obtidos através de um problema de otimização com restrições. Uma generalização deste conceito é utilizado para o caso não linear.
O problema de classificação de padrões, que originou a formulação da SVM, pode ser resolvido por muitos outros classificadores, porém, a grande vantagem da SVM sobre outros classificadores está no hiperplano ótimo que consegue obter uma máxima margem de separação entre classes. Entretanto, mesmo com todas as vantagens e eficiência da SVM como um classificador, existem alguns casos onde não é tão simples determinar oti-mamente a separação entre classes distintas através de um hiperplano, seja por utilizar um conjunto de treinamento com informações imprecisas ou inconsistentes, ou por problemas de erros de arredondamentos de valores durante a execução da máquina para encontrar o hiperplano, ou por problemas de truncamento ou aproximação de procedimentos.
1.2
Objetivos
Ojetivando a diversidade e os pontos fortes da SVM, o desenvolvimento deste es-tudo está focado na construção de uma teoria intervalar aplicada à SVM, abordando os princípios teóricos da SVM e da teoria intervalar sob a nova modelagem da SVM inter-valar, que será chamado resumidamente de SVMI. Essa nova modelagem tende a oferecer uma precisão, herdada de conceitos da matemática intervalar, para controlar erros com-putacionais, que poderá advir de ruídos durante a aquisição dos dados de treinamento, imprecisão e informações faltosas nos dados de entrada.
A contribuição científica desde estudo está em oferecer uma formalização deste novo modelo para o mundo científico, tanto de Redes Neurais, quando de qualquer outra área, que pretende obter um controle de erros computacionais, ou analisar o desempenho de métodos que gerem resultados com uma dada precisão, utilizando como classificador uma SVMI.
1.3
Trabalhos relacionados
As áreas mais comuns de aplicações da SVM estão em: reconhecimento de caracteres, reconhecimento de imagens, detecção de faces em imagens e categorização de textos [Boser et al. 1992, Burges 1998, Ganapathiraju 2002, Hearst 1998, Joachims 1998, Lima 2004, Pontil & Verri 1997, Stitson et al. 1996], e entre diversos problemas de regressão [Stitson et al. 1996, Hearst 1998].
clas-sificação de duas ou mais classes [Hsu & Lin 2002], ou estudos unindo SVMs a outras teorias, como lógica Fuzzy, máquinas de vetores de suporte fuzzy (MVSF) ou do inglês
Fuzzy Support Vector Machines (FSVM) [Lin & Wang 2002].
Pesquisas mostram a SVM utilizando análise intervalar. Zhao [Zhao et al. 2005] de-senvolveu uma extensão intervalar da SVM para classificação de padrões que estivessem incompletos. Através de experimentos e análises de resultados, Zhao, concluiu que o método proposto classifica novos padrões mesmo com informações incompletas, e com a utilização do conhecimento à priori pode ser reduzido os atributos em relação ao custo durante o processo de classificação.
Existe também um outro estudo na teoria de aproximação, onde, Lingras [Lingras & Butz 2004] propõe o uso de duas técnicas de classificação, a SVM e teoria Rough Set, onde, busca-se interpretar o resultado da classificação da SVM em termos intervalares ou rough sets e explora-se tais vantagens. Hong [Hong & Hwang 2005] propõe utilizar SVM para regressão intervalar, partindo de uma análise de regressão fuzzy. Em [Do & Poulet n.d.] propõe-se uma análise de dados intervalares para métodos baseados no
ker-nel. Angulo e autores [Angulo et al. 2007] utilizam análise intervalar sobre a SVM para
o caso linear. A SVM desenvolvida neste trabalho consiste em uma extensão (essen-cialmente intervalar), caracterizando-se entre outros aspectos, pelo uso de uma métrica caracterizando-se do usual para tratamento intervalar dos dados.
1.4
Organização do Trabalho
Este trabalho está organizado em capítulos da seguinte forma:
• Capítulo 1: traz uma breve introdução da SVM, bem como a motivação de realizar este estudo, os objetivos juntamente com as contribuições que se pretende alcançar e alguns trabalhos relacionados na área e nesta proposta.
• Capítulo 2: mostra a fundamentação teórica da SVM para os casos de classes linear-mente separáveis e não linearlinear-mente separáveis, com o objetivo de um embasamento teórico bem esclarecido para um melhor entendimento da proposta deste estudo.
• Capítulo 3: apresenta a fundamentação teórica da abordagem intervalar, objeti-vando apresentar os conceitos básicos da matemática intervalar que serão utilizados na construção de uma máquina SVM intervalar.
otimização com restrições. Será mostrado também os fundamentos da otimização com uso da análise intervalar, necessário para encontrar o hiperplano que satisfaça as condições de otimização intervalar e as propriedades da SVM.
• Capítulo 5: formalismo da extensão intervalar de kernels, bem como o teorema que valida funções a serem consideradas válidas para serem kernels.
• Capítulo 6: este capítulo descreve os aspectos teóricos baseados nos capítulos an-teriores, e uma definição inicial para o caso linearmente separável, detalhando com um algoritmo e a aplicação de exemplos para apresentar alguns resultados já obti-dos.
• Capítulo 7: implementações de métodos iterativos intervalares para o treinamento de uma SVMI.
Máquinas de Vetores-Suporte
As máquinas de vetores suporte, referenciado em inglês como Support Vector
Ma-chines (SVM), constituem numa técnica fundamentada na Teoria de Aprendizado
Estatís-tico visando a proposição de técnicas de aprendizado de máquina que buscam a maximiza-ção da capacidade de generalizamaximiza-ção e a minimizamaximiza-ção do risco estrutural [Haykin 2001]. A maximização da capacidade de generalização em técnicas de aprendizado de máquina é a capacidade da máquina na classificação eficiente perante o conjunto de treinamento, e a minimização do risco estrutural é a probabilidade de classificação errônea de padrões ainda não apresentados à máquina.
Na literatura é encontrado o termo máquinas de vetor de suporte ligado a proble-mas de classificação e regressão [Hearst 1998, Lima 2004, Stitson et al. 1996], e o termo vetores-suporte ou ainda, vetores de suporte utilizado para encontrar um hiperplano ótimo de separação, responsável pela separação de classes, ou uma função de separação com margem máxima entre classes distintas. A teoria que define rigososamente os conceitos e demonstrações matemática da função do hiperplano ótimo é a teoria de aprendizado estatístico, tratado por Vapnik como dimensão Vapnik-Chervonenkis, ou simplemente di-mensão VC [Haykin 2001, Lorena & Carvalho 2003, Semolini 2002]. Essa didi-mensão é de fundamental importância, pois, sua estimativa correta garante o aprendizado de maneira confiável, em outras palavras, a dimensão VC engloba o princípio de minimização de risco estrutural, que envolve a minimização de um limite superior sobre o erro de general-ização, tornando a máquina com uma habilidade alta para generalizar padrões ainda não apresentados.
2.1
Máquina de Vetores-Suporte Linearmente Separável
O problema de classificação binária, problema de classificação inicial tratado pela SVM, trata da classificação de duas classes, sem perda de generalidade, através de um hiperplano ótimo à partir de um conjunto de treinamento linearmente separável. Um conjunto de treinamento é dito linearmente separável se for possível separar os padrões de classes diferentes contidos no mesmo por pelo menos um hiperplano [Haykin 2001, Semolini 2002].
Considere o conjunto de treinamento{(xi,di)}Ni=1, onde xié o padrão de entrada para
o i-ésimo exemplo e di é a resposta desejada, di={+1,−1}, que representa as classes
linearmente separáveis.
A equação que separa os padrões através de hiperplanos pode ser definida por:
wT ·x+b=0 (2.1)
onde, wT·x é o produto escalar entre os vetores w e x, em que x é um vetor de entrada
que representa os padrões de entrada do conjunto de treinamento, w é o vetor de pesos ajustáveis e b é um limiar também conhecido como bias.
A Figura 2.1 mostra o hiperplano de separação (w,b)em um espaço bidimensional para um conjunto de treinamento linearmente separável.
A equação (2.1) pode ser reescrita por:
(
wT·xi+b≥0, se di= +1
wT·xi+b<0, se di=−1
(2.2)
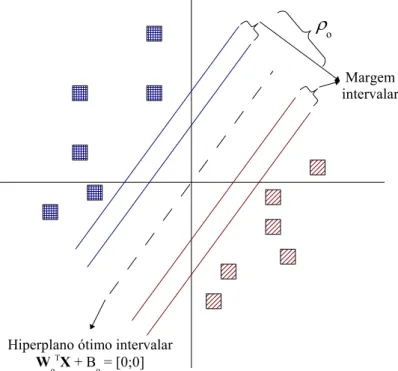
A margem de separação, distância entre o hiperplano definido na equação (2.1) e o ponto mais próximo de ambas as classes, é representado porρ. O objetivo de uma SVM é encontrar um hiperplano que separe o conjunto de treinamento sem erro e maximize a margem de separação, sobre essa condição, o hiperplano é referido como hiperplano ótimo. A Figura 2.2 ilustra o hiperplano ótimo para um espaço de entrada bidimensional.
Figura 2.2: Hiperplano ótimo com máxima margemρo de separação dos padrões
linear-mente separáveis.
Considerando que wo e bo representam os valores ótimos do vetor peso e do bias,
respectivamente, a equação (2.1) do hiperplano pode ser reescrita para o hiperplano como:
wTo·xo+bo=0 (2.3)
A função discriminante
fornece uma medida algébrica de distância r entre x e o hiperplano(wo,bo)que pode ser
representado por:
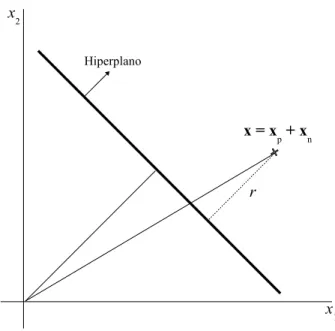
x=xp+xn (2.5)
onde, xp é a projeção normal de x sobre o hiperplano ótimo e xn é o vetor normal com
distância r, onde,
xn=r·
wo
kwok
(2.6)
A Figura 2.3 ilustra a distância r entre x e o hiperplano(wo,bo), onde, r é positivo se
x estiver no lado positivo do hiperplano ótimo caso contrário será negativo.
Figura 2.3: Interpretação gráfica da distância x até o hiperplano ótimo para o caso bidi-mensional.
Considerando g(xp) =0
g(x) = wTo·xo+bo = r· kwok
(2.7)
onde, através da equação (2.7) é obtido a distância r
r= |g(x)|
kwok
O conjunto de treinamento é linearmente separável se woe bosatisfazer a restrição (
wTo ·xi+bo≥+1, se di= +1
wTo ·xi+bo≤ −1, se di=−1
(2.9)
onde, os parâmetros woe bosão obtidos somente através do conjunto de treinamento.
A equação (2.9) pode ser reescrita por:
di(wTo ·xi+bo)≥1 (2.10)
O pontos(x,d), onde a equação (2.10) é satisfeita para o sinal de igualdade são deno-minados de vetores-suporte, e são esses pontos que influenciam diretamente na localiza-ção do hiperplano ótimo de máxima margem, pois, esses pontos estão mais próximos da superfície de decisão.
Considerando um ponto x(s) vetor-suporte de classe positiva d(s) = +1, então por definição:
g(x(s)) =wTo·x(s)+bo−1 para di= +1 (2.11)
Da equação (2.8), a distância do vetor de suporte x(s) até o hiperplano ótimo é dado por:
r= wTo·x(s)+bo
kwok =
( +kw1
ok se d
(s)= +1
−kw1ok se d
(s)=
−1 (2.12)
onde, o sinal positivo indica que x(s) pertence ao lado positivo do hiperplano ótimo e o sinal negativo o contrário. Considerando ρ a margem de separação máxima entre duas classes de um conjunto de treinamento, então:
ρ= 2r= kw2ok (2.13)
Logo, a equação (2.13) mede a distância entre os hiperplanos da equação (2.10), da mesma forma que a distância entre os hiperplanos wT ·x+b=0 e wT ·x+b=1 ou
2.1.1
Hiperplano Ótimo para Classes Linearmente Separáveis
O hiperplano ótimo definido para os parâmetros w e b que satisfaçam as desigualdades da equação (2.10), pode ser reescrito como:
di(wT·xi+b)≥1 (2.14)
O objetivo da SVM é encontrar um procedimento computacional que, utilizando o conjunto de treinamento{(xi,di)}Ni=1encontra o hiperplano ótimo sujeito às restrições da
equação (2.14). Este problema pode ser resolvido através do problema de otimização com restrições, minimizando a função custoΦem relação ao vetor de peso w e satisfazendo as restrições da equação (2.14)
Φ(w) = 1
2w
T
·w (2.15)
A partir da função custo Φ da equação (2.15) pode ser formulado o problema de otimização com restrições, denominado de problema primal:
Minimizar: 12wT ·w
Sujeito as restrições: di(wT ·xi+b)≥1, para i=1, ...,n
(2.16)
Este é um problema clássico em otimização de programação quadrática [Hearst 1998] sob o aspecto de aprendizado de máquina. O problema de otimização analisado sob o ponto de vista de otimização de função quadrática pode ser resolvido introduzindo uma função lagrangiana, definida em termos de w e b:
J(w,b,α) =1
2 kwk
2
−
N
∑
i=1
αi(di(wT ·x+b)−1) (2.17)
onde, osαisão denominados de multiplicadores de Lagrange não-negativos.
O problema passa a ser então a minimização da equação (2.17) em relação a w e b e maximização deαi, com αi≥0. Os pontos ótimos desta esquação são obtidos
diferen-ciando a equação (2.17) em relação a w e b e igualando os resultados a zero, obtendo as condições de otimização:
Condição 1: ∂J(w,∂wb,α) =0
Condição 2: ∂J(w,∂bb,α) =0 (2.18)
resultado:
w=∑N
i=1αidixi ∑N
i=1αidi=0
(2.19)
Substituindo a equação (2.19) em (2.17), obtém-se o problema dual de otimização:
Maximizar: ∑Ni=1αi−12∑Ni=1∑Nj=1αiαjdidjxTi ·xj
Sujeito as restrições:
(
(1)αi≥0,i=1, ...,N
(2) ∑Ni=1αidi=0
(2.20)
Tendo encontrado os multiplicadores de Lagrange ótimos, representados porαoi,
pode-se calcular o vetor de peso ótimo woatravés da equação (2.19):
wo= N
∑
i=1
αoidixi (2.21)
O valor do bias ótimo boé encontrado utilizando os pesos ótimos woencontrados na
equação (2.21) e descrito como:
bo=1−wTo ·x(s)para d(s)=1 (2.22)
O problema dual (2.20) é formulado totalmente em termos dos padrões de treina-mento, além disso, a equação a ser maximizada da equação (2.20) depende somente dos padrões de entrada. O hiperplano ótimo depende somente dos vetores de suporte, consi-derados os padrões mais significativos do conjunto de treinamento. Os multiplicadores de Lagrangeαo>0 (diferentes de zero) são justamente os padrões de entrada com margem
igual a 1, chamados de vetores de suporte.
O hiperplano ótimo é expresso em termos do conjunto de vetores de suporte descrito pela função sinal como:
f(x) =sgn( NSV
∑
i=1
diαoixT ·x+bo) (2.23)
Os padrões de entrada que não são vetores de suporte não influenciam na função de decisão da escolha do hiperplano ótimo pela da SVM.
2.2
Máquina de Vetor de Suporte Não Lineares
O problema de classificação binária, onde, classes distintas são não linearmente se-paráveis no espaço original, mas, com um mapeamento não linear através de um produto interno kernel transforma o espaço original em um espaço de características de dimensão maior, e, o problema que era não linearmente separável no espaço original passa-se a ser linearmente separável no espaço de características é representado pela SVM não linear-mente separável ou SVM para classes linearlinear-mente separáveis no espaço de características. O espaço de características, mencionado acima, corresponde a uma representação do conjunto de treinamento, um mapeamento do espaço de entrada original em um novo espaço utilizando funções reaisϕi, ...,ϕM. A Figura 2.4 ilustra esse conceito.
Figura 2.4: Mapeamento de características.
Para a construção da SVM no caso não linear, a idéia depende de duas operações matemáticas. Primeiro: o mapeamento não linear do vetor de entrada para um espaço de características de alta dimensionalidade. O teorema que trata dessa operação é o teorema de Cover [Haykin 2001], onde, as funções ϕi são não lineares e a dimensionalidade do
espaço de características M é suficientemente alta. Segundo: a construção de um hiper-plano ótimo para separação das características descobertas no primeiro, uma vez que o teorema de Cover não procura o hiperplamo ótimo de separação. A fundamentação desta última operação está na teoria da dimensão VC que busca o princípio da minimização do risco estrutural [Haykin 2001, Lorena & Carvalho 2003, Semolini 2002].
2.2.1
Hiperplano Ótimo para Classes Não Linearmente Separáveis
treinamento, possivelmente gerará erros de classificação. O objetivo da SVM neste caso é encontrar um hiperplano que minimiza a probabilidade de erro de classificação junto com o conjunto de treinamento.
Existem alguns casos onde, não é necessário fazer um mapeamento de características no conjunto de treinamento. Esses casos são tratados pela SVM linear com margens de separação entre classes suaves ou flexíveis (soft), pois, poderão existir pontos(xi,di)que
violarão a equação (2.14).
Esta violação pode ocorrer em três diferentes situações descritas a seguir:
• O ponto (xi,di) se encontra dentro da região de separação e no lado correto da
superfície de decisão, ilustrado na Figura 2.5 (a). Neste caso, houve uma escolha incorreta do hiperplano.
• O ponto(xi,di) se encontra dentro da região de separação e no lado incorreto da
superfície de decisão, ilustrado na Figura 2.5 (b). Neste caso, houve uma escolha incorreta do hiperplano de margem maior.
• O ponto (xi,di) se encontra fora da região de separação e no lado incorreto da
superfície de decisão, ilustrado na Figura 2.5 (c).
Figura 2.5: (a) O ponto(xi,di)se encontra na região de separação, mas do lado correto.
(b) O ponto(xi,di)se encontra na região de separação, mas do lado incorreto. (c) O ponto (xi,di)se encontra fora da região de separação, mas do lado incorreto.
Para tratar desses problemas introduz-se uma variável não negativa {ξi}1≤i≤N na
definição do hiperplano de separação:
As variáveisξisão denominadas de variáveis soltas, e medem os desvios dos pontos (xi,di) para a condição ideal de separação de classes. Quandoξi satisfazer 0≤ξi≤1
o ponto encontra-se dentro da região de separação mas do lado correto da superfície de decisão. Quandoξi>1 o ponto encontra-se do lado incorreto do hiperplano de separação.
Os vetores-suporte são os pontos que o resultado da equação (2.24) é igual a 1−ξi
mesmo que ξi >0. Ao retirar um padrão do conjunto de treinamento em que ξi>0 a
superfície de decisão tem possibilidade de mudança, porém, ao retirar um padrão em que
ξi=0 e o resultado da equação (2.24) for maior que 1 a superfície de decisão permanecerá
inalterada.
O objetivo é encontrar um hiperplano de separação onde o erro de classificação in-correta seja mínimo perante o conjunto de treinamento, podendo ser feito minimizando a equação:
Φ(ξ) = N
∑
i=1
I(ξi−1) (2.25)
em relação ao vetor peso w, sujeito à restrição da equação do hiperplano de separação da equação (2.24) e a restrição sobre wTw. A função I(ξ−1)é uma função indicadora, definida por:
I(ξ−1) = (
0 seξ≤0
1 seξ>0 (2.26) A minimização de Φ(ξ) é um problema de otimização não convexo de classe NP-completo não determinístico em tempo polinomial. Para fazer este problema de otimiza-ção matematicamente tratável, aproxima-se a funotimiza-çãoΦ(ξ)por:
Φ(ξ) = N
∑
i=1
ξi (2.27)
Para a simplificação de cálculos computacionais a função a ser minimizada em relação ao vetor peso w segue:
Φ(w,ξ) =1
2w
T
·w+C
N
∑
i=1
ξi (2.28)
onde, o parâmetro C controla a relação entre a complexidade do algoritmo e o número de amostras do conjunto de treinamento classificados incorretamente, sendo denominado de
parâmetro de penalização.
equação (2.28) satisfaz os princípios de minimização do risco estrutural.
O problema de otimização em sua representação primal para encontrar o hiperplano ótimo de separação para classes não linearmente separáveis pode ser escrito como:
Minimizar: 12wT ·w+C∑Ni=1ξi
Sujeito as restrições:
(
(1) di(wT·xi+b)≥1−ξi, para i=1, ...,N
(2)ξi≥0,∀i=1, ...,N
(2.29)
Utilizando o método dos multiplicadores de Lagrange, pode-se formular o problema de otimização primal em seu correspondente problema dual de maneira similar à descrita na seção 2.1.
Maximizar: ∑Ni=1αi−12∑Ni=1∑Nj=1αiαjdidjxTi ·xj
Sujeito as restrições:
(
(1) ∑Ni=1diαi
(2) 0≤αi≤C para i=1, ...,N
(2.30)
onde, C>0 é especificado pelo usuário.
A principal diferença entre o caso de classes linearmente separáveis, seção 2.1, e o caso de classes não linearmente separáveis é qua a restriçãoαi≥0 é substituída por uma
mais forte 0≤αi≤C.
O vetor de pesos ótimos woé calculado da mesma maneira do caso de classes
linear-mente separáveis, equação (2.21). O bias ótimo b também segue um procedimento similar ao descrito anteriormente, equação (2.22).
Existem casos também onde, é necessário mapear o espaço de entrada não linear para um espaço de características. Para realizar esse mapeamento, as funções kernel ou pro-duto do núcleo interno são utilizadas e que serão apresentados a seguir.
2.2.2
Função Kernel
Existem muitos casos onde não é possível dividir satisfatoriamente os padrões do conjunto de treinamento através de um hiperplano, mesmo observando as variáveis soltas. Para a realização desta tarefa é feito um mapeamento no domínio do espaço de entrada do conjunto de treinamento para um novo espaço, o espaço de características, usando uma função kernel apropriada.
Um kernel k é uma função que recebe dois pontos xi e xj do espaço de entrada e
computa o produto escalarϕT(xi)·ϕ(xj)no espaço de características.
representado por:
k(xixj) =ϕT(xi)·ϕ(xj) (2.31)
Adaptando a equação (2.21) envolvendo um espaço de características, pode ser rees-crito como:
w= N
∑
i,j=1
αidiϕT(xi)·ϕ(xj) (2.32)
onde, o vetor de características ϕ(xi) corresponde ao padrão de entrada xi no i-ésimo
exemplo.
Dessa forma, pode ser usado o produto interno k(xi,xj)para construir um hiperplano
ótimo no espaço de características sem ter que considerar o próprio espaço de caracterís-ticas de forma explícita, observe a equação (2.32) em (5.1):
N
∑
i,j=1
αidik(xi,xj) (2.33)
A utilização de kernels está na simplicidade de cálculos e na capacidade de representar espaços muito abstratos.
As funçõesϕdevem pertencer a um domínio em que seja possível o cálculo de pro-dutos internos. No geral, utiliza-se o teorema de Mercer para satisfazê-las. Segundo o teorema, os kernels devem ser matrizes positivamente definidas, isto é, ki j =k(xi,xj),
para todo i,j=1, ...,N, deve ter auto-vetores maiores que 0.
Alguns kernels mais utilizados são: os polinomiais, os gaussianos ou RBF (Radial
Basis Function) e o sigmoidais.
Kernel Função k(xi,xj) Comentários
Polinomial (xTi ·xj+1)p p é especificado a priori pelo usuário
RBF e(− 1
2σ2kxi−xjk 2)
a largura deσ2é especificada a priori pelo usuário Sigmoidal tanh(β0xTi ·xj+β1) teorema de Mercer satisfeito somente paraβ0eβ1
Tabela 2.1: Principais kernels utilizados nas SVMs
2.3
Considerações
Algumas considerações deste capítulo.
Para a SVM linear existem algumas particularidades:
• O problema dual é formulado somente com os padrões de treinamento.
• O hiperplano ótimo é definido somente pelos vetores de suporte, que são os padrões mais significativos.
• Os vetores de suporte são os multiplicadores de Lagrange diferentes de zero para
α>0.
• Os padrões de entrada que não são vetores de suporte não influenciam a definição do hiperplano ótimo.
• Essa máquina oferece solução única e ótima, ao contrário de outras máquinas.
Algumas particularidades para o caso não linear:
• No caso de classes não linearmente separáveis a restriçãoαi≤0 é substituída por
uma mais forte 0≤αi≤C.
• O vetor de pesos ótimos wo é calculado da mesma maneira do caso de classes
linearmente separáveis, wo=∑Ni=1αoidixi.
Matemática Intervalar
A matemática intervalar, assim como a matemática “clássica”, é uma ciência que es-tuda medidas, relações de quantidade e grandezas e possui diversos ramos, por exemplo, a aritmética intervalar, que estuda as propriedades dos números intervalares (intervalos) e suas operações. O histórico do desenvolvimento da matemática intervalar não é muito recente, possuindo diversos estudos realizados a mais de cinco décadas atrás. Norbert Wiener, considerado o “pai” da cibernética, em 1914, introduziu a análise de medida de aproximações [Kreinovich et al. 1998]. Na década de 30, Young publicou um estudo [Young 1931] em que dava regras para cálculos com intervalos e outros conjuntos de números reais. Outras publicações foram feitas nas décadas posteriores, mas foi com Ra-mon E. Moore [Moore 1966], na década de 60, que a matemática intervalar ficou mais difundida na computação, devido principalmente à sua abordagem de computação inter-valar, e das técnicas para problemas computacionais.
Sistemas computacionais podem ser descritos como um conjunto finito de processos que envolvem operações matemáticas para uma determinada função. O uso da matemática intervalar em sistemas computacionais consiste em buscar soluções mais eficientes para problemas computacionais, como a criação de modelos computacionais que reflitam de forma fidedigna a realidade, e também a escolha de técnicas de programação adequadas para desenvolvimento de softwares científicos a fim de minimizar erros do resultado.
ini-ciais na forma de intervalos, computando-os, onde, cada intervalo contém um indicativo máximo de erro, antes de ser introduzido na computação.
A seguir, serão abordado alguns conceitos fundamentais da aritmética intervalar en-contrados na literatura em [Acióly 1991, Santos 2001, Hayes 2003, Kreinovich et al. 1998, Kulisch 1982, Kulisch & Miranker 1981, Lyra 2003, Moore 1966, Young 1931].
3.1
Representação de Intervalos
A motivação de pesquisas computacionais no desenvolvimento do campo intervalar vem da impossibilidade de representar uma informação computacional igual à informação original. Por exemplo, informações do tipo imagem, como discutida anteriomente, são representadas por funções contínuas, e na discretização, existe uma perda de informações, e a utilização intervalar possibilitará uma maior manipulação dos erros na aquisição da imagem.
A noção de intervalos foi traçada inicialmente por Arquimedes quando estimou dois valores paraπ, e que garantia que esse intervalo continha o valor deπ.
A representação de intervalos no conjunto dos números reaisR é denotado pelo par
ordenado de números reais X= [x1; x2](ou X = [x,x]), tal que x1≤x2, e x1e x2∈R, e se
Rrepresenta o conjunto de todos os números reais, então, X ={x∈R|x1≤x≤x2}.
Considerem as descrições deste estudo as letras maiúsculas como pontos do conjunto de intervalos reais, por exemplo, seguindo a definição acima, a letra X representa o ponto do conjunto dos intervalos de reais e x1 é denominado de ínfimo e x2 denominado de
supremo. O conjunto intervalar dos números reais será denotado comoIR.
A representação de um número real exato é dado como X = [x1; x2], em que, x1 = x2, ou seja, seja X =4, logo, 4= [4; 4]. Este tipo de intervalo é chamado de intervalo
degenerado.
3.2
Operações Aritméticas Intervalares
Sejam X = [x1; x2] e Y = [y1; y2], onde, X e Y ∈IR. As operações aritméticas, tais
como, adição, subtração, multiplicação e divisão emIRsão definidas sobre os extremos
de seus intervalos.
1. Adição Intervalar:
2. Pseudo Inverso Aditivo Intervalar:
−X= [−x2;−x1]
3. Subtração Intervalar:
X−Y = [x1−y2; x2−y1]
4. Multiplicação Intervalar:
X∗Y = [min{x1y1; x2y1; x1y2; x2y2}; max{x1y1; x2y1; x1y2; x2y2}]
5. Pseudo Inverso Multiplicativo Intervalar: 0∈/X X−1=1/X = [1/x2; 1/x1]
6. Divisão Intervalar: 0∈/Y
X/Y = [min{x1/y2; x2/y2; x1/y1; x2/y1}; max{x1/y2; x2/y2; x1/y1; x2/y1}]
7. Quadrado Intervalar:
X2=
[x2
1; x22], se 0≤x1 [x2
2; x21], se x2≤0 [0,max{x21; x22}], senão
3.3
Propriedades Algébricas Intervalares
Sejam X , Y , Z ∈IR. As propriedades algébricas para as operações anteriores são,
fechamento, comutativa, associativa, elemento neutro, subdistributiva, e monotônica.
1. Fechamento:
• Se X , Y ∈IR, então X+Y ∈IR
• Se X , Y ∈IR, então X∗Y ∈IR
2. Comutativa:
• X+Y =Y+X
• X∗Y =Y∗X
3. Associativa:
• X+ (Y+Z) = (X+Y) +Z
• X∗(Y∗Z) = (X∗Y)∗Z
4. Elemento Neutro:
• X+ [0; 0] = [0; 0] +X=X
• X∗[1; 1] = [1; 1]∗X=X
5. Subdistributiva:
6. Inclusão Monotônica:
Sejam X , Y , Z e W ∈IR, tais que, X ⊆Z e Y ⊆W .
• X+Y ⊆Z+W
• −X ⊆ −Z
• X−Y ⊆Z−W
• X∗Y ⊆Z∗W .
• 1/X ⊆1/Z, se 06∈Z
• X/Y ⊆Z/W , se 06∈W
3.4
Ordem Intervalar
Na literatura encontramos diversas formas de definição de ordens (parciais) para in-tervalos. As mais conhecidas são, ordem de Moore [Moore 1966], ordem de Kulisch & Miranker [Kulisch & Miranker 1981], ordem da Informação [Acióly 1991] e ordem da Teoria dos Conjuntos.
Para X,Y ∈IR, tem-se que:
1. Ordem de Moore: X <Y = [x1; x2]<[y1; y2]⇔x2<y1
2. Ordem de Kulisch-Miranker: X ≤Y = [x1; x2]≤[y1; y2]⇔x1≤y1e x2≤y2
3. Ordem da Teoria dos Conjuntos: X <Y = [x1; x2]≤[y1; y2]⇔[x1; x2]⊆[y1; y2]⇔ y1≤x1e x2≤y2. Logo[x1; x2]≤[y1; y2].
4. Ordem da Informação: X ≤Y = [x1; x2] ≤[y1; y2] ⇔ [y1; y2]⊆ [x1; x2] ⇔ x1 ≤ y1e y2≤x2. Logo,[x1; x2]≤[y1; y2].
3.5
Função Intervalar
Sejam F :IR→IRe f :R→R. Dizemos que F representa f ou que f é representado
por F , denotado por f ⊆F, se:
∀X ∈IR,∀x∈X temos que f(x)∈F(X)
A extensão dessa definição de função para X⊂IRme Y⊂IRné feita de forma natural.
3.5.1
Metrica intervalar em
IR
nmétrico. A distância mais utilizada é a distância Euclidiana. Para o caso intervalar, pode ser visto como subconjunto deR2suas métricas naturais seguindo:
Definição 1 (Metrica de Moore) [Moore 1979] Seja DM:IRn×IRn→R, definido, para cada X= (X1, . . .,Xn),Y= (Y1, . . . ,Yn)∈IRncomo:
DM(X,Y) = s
n
∑
i=1
max((Xi−Yi)2,(Xi−Yi)2).
Para n=1, DM(X,Y) =max(|X−Y|,|X−Y|). Como cada métrica, esta definição
determina a noção de continuidade para funções intervalares [Acióly & Bedregal 1997]. Essa métrica não é estritamente intervalar, ou seja, a distância entre dois intervalos não é um intervalo, mas um número real, o que não parecem ser natural quando visto intervalos como representação de um número desconhecido real. Por exemplo, se só sabermos que um objeto A está em uma cidade C e uma pessoa B está em uma cidade D, mas não saber a sua posição exata nas cidades, não é realista que nós podemos fornecer a real distância entre A e B, mas apenas um intervalo. Isto motivou [Trindade et al. 2008] introduzir a noção de métricas intervalares e, particularmente, métrica intervalar para
IR, chamado de distância essencialmente intervalar, que não perde as características da
métrica Euclidiana quando se trata de números reais ou intervalos degenerados. Este trabalho usará essa extensão intervalar de distância paraIRn.
A distância essencialmente intervalar é uma função DT B :IRn×IRn→IR definido
por
DT B(X,Y) = [min{d(x,y)|x∈X and y∈Y},max{d(x,y)|x∈X and y∈Y}]1
Definição 2 (Norma vetorial intervalar) Seja a norma de um número real a distância
entre o ponto e a origem, a norma para um intervalo2, X ∈IRé definido por
kXk=
[X,X], if X >0
[|X|,|X |], if X <0
[0,max{|X |,|X|}], senão
A definição geral da norma intervalar baseada na distância essencialmente intervalar
é
1A distância d : Rn×Rn → R é a distância Euclidiana, i.e. d(x,y) =
rn
∑
i=1k
xi−yik, ∀x =
(x1, . . . ,xn),y= (y1, . . . ,yn)∈Rn.
2Note que essa definição de norma intervalar é diferente da definição usual de norma intervalar, eg.: a
kXk= pDT B(X1,[0,0])2+...+DT B(Xn,[0,0])2 = pkX1k2+...+kX
nk2
3.5.2
Integral Interval
Definição 3 (Integral Interval) Seja F :R→IRuma função intervalar contínua e X ∈ IR. Para integral intervalar F limitado em[X,X]é definido [Moore 1966, Moore 1979,
Moore et al. 2009]
Z X
X
F(t)dt= [ Z X
X F(t)dt, Z X
X
F(t)dt]
onde, F(t) =F(t)e F =F(t).
3.6
R-vetoide e espaço R-vetoide intervalar
Uma vez que, operação aritmética intervalar não é um campo, então também não é um espaço vetorial. A fim de considerar as propriedades do espaço vectorial para intervalos, essa definição será relaxada.
Definição 4 (R-Vetoide) [Kulisch 2008] Seja
R
= (R,+,∗)um aneloide com 0 e 1 como elementos identidade aditivo e multiplicativo, respectivamente,V
= (V,⊕)um grupoidee·: R×V →V . Então(
R
,V
,·)é um espaço R-vetoide se satisfaz as seguintes condições: 1. Comutatividade de soma vetorial: X⊕Y=Y⊕X;2. Vetor identidade: X⊕0=X;
3. α·0=0 e 0·X=0;
4. 1·X=X;
5. −(X⊕Y) = (−X)⊕(−Y); 6. −(α·X) = (−α)·X=α·(−X).
onde−α=−1∗αe−1 é o único elemento em R tal que(−1)∗(−1) =1.
Elementos de V são chamados de vetoides e elementos de R são chamados de es-calares. Neste trabalho, vetores são distinguidos dos escalares pelo negrito.
Note que todo espaço vetorial em um espaço R é um R-vetoide.
Definição 5 (Matriz Interval) [Moore et al. 2009] Uma matrix X de ordem m×n é uma matriz intervalar se cada elemento da matriz for um intervalo. O intervalo na linha i e coluna j é denotado por Xi,j. Um vetor intervalar é uma matriz intervalar de dimensão
m×1. Será adotado a notaçãoMIRm,npara o conjnto de matrizes intervalares de ordem
As operações aritméticas entre matrizes intervalares e intervalos com matrizes inter-valares são como o caso real, mas considerando a aritmética intervalar. Será considerado o mesmo símbolo para operadores similares emIReMIRm,n, i.e. em vez de⊕também
será usado+e em vez de∗também será usado·. Na adição, considere a seguinte exten-são de subconjunto relacionado com intervalos: seja X,Y∈MIRm,n, X⊆Y se Xi,j⊆Yi,j
para algum i=1, . . . ,m e j=1, . . . ,n.
Definição 6 Um espaço R-vetoide (
R
,V
,·) é um espaço intervalar R-vetoide quando R=IRe V =MIRm,npara alguns m,n∈N.Proposição 3.6.1 [Kulisch 2008] Seja m,n≥1,
I R
= (IR,+,·)o aneloide de intervalose
M I R
= (MIRm,n,+)o grupoide de matrizes intervalares de ordem m por n. Então(
I R
,M I R
,·), onde·:IR×MIRm,n→MIRm,n é um espaço R-vetoide intervalar. Naadição esse espaço R-vetoide intervalar também satisfaz a seguinte propriedades:
1. Distributividade de adição por um escalar: (α+β)·X⊆α·X⊕β·X;
2. Distributividade de soma vetorial: α·(X⊕Y)⊆α·X⊕α·Y;
3.6.1
Produto interno intervalar
Definição 7 (Produtoide interno) Seja(
R
,V
,·)um R-vetoide. Um mapeamentoh·,·i:V×V →R é um produtoide interno se para cada X,Y∈V , satisfazer as seguintes pro-priedades:
1. Comutatividade: hX,Yi=hY,Xi. 2. Homogeneidade:hα·X,Yi=α·(X,Y)
3. Positividade: hX,Xi ≥0 andhX,Xi=0 iff X=0.
Um espaço R-vectoide juntamente com um produtoide interno é chamado um espaço interno produtoide.
Proposição 3.6.2 Seja (
I R
,M I R
m,n,·) um espaço R-vetoide intervalar e uma apli-cação intervalar (função intervalar)h·,·i:MIRm,n×MIRm,n→Rdefinido porhX,Yi= n
∑
i=1 m
∑
j=1
Xi,j·Yi,j (3.1)
3.6.2
Autovetoide intervalar
Definição 8 (Autovetoide intervalar) Seja uma matriz intervalar quadratica A de
or-dem M∈R, um autovetoide é definido por:
Aui=λiui (3.2)
Otimização usando Análise Intervalar
Este capítulo apresenta conceitos sobre a teoria de otimização utilizado para encontrar o hiperplano ótimo de separação de classes através da SVM. As conceituações sobre o problema de otimização "clássico"foram extraídas de [Bazaraa et al. 1993, Haykin 2001, Lorena & Carvalho 2003, Luenberger 1984] e para o problema de otimização usando análise intervalar foram extraídas de [Bliek et al. 2001, Hanses & Walster 1992, Kearfott 1996].
Será apresentado nas seções seguintes otimização de função com restrições, no con-texto "clássico"e intervalar, onde, restrição intervalar é uma tecnologia alternativa de-senvolvida para conjuntos contínuos, geralmente não lineares, associados com restrições sobre números reais. O termo restrição intervalar (interval constraints) é frequentemente associado com a propagação e técnicas de buscas desenvolvidas em inteligência artificial e métodos para análise intervalar [Bliek et al. 2001].
4.1
Otimização Linear
Para o problema de otimização considere:
Minimizar: f(x), x∈Ω⊆Rn
Sujeito a: gi(x)≤0 , i = 1, ..., k hj(x)≤0 , j = 1, ..., m
(4.1)
onde, f :Ω⊆Rn→R é a função objetivo, gi :Ω⊆Rn→R e hj:Ω⊆Rn →R são
utilizados para definir as restrições funcionais. A solução do problema (4.1) é denotado por:
A solução do problema de otimização será o ponto x∗ ∈F tal que não exista outro
ponto x∈F com f(x)< f∗(x), denominado de mínimo global.
Um problema de otimização onde a função objetivo é quadrática e as restrições line-ares, é denominado de problema de otimização quadrático, ou se a função objetivo for convexo e as restrições também, é denominado de problema de otimização convexo. O caso do problema de otimização do treinamento da SVM, a função objetivo é convexa e quadrática e as restrições lineares, sendo um problema de otimização convexo quadrático. Para encontrar a solução para este tipo de problema utiliza-se a função de Lagrange, para restrições de igualdade e a condição de Kuhn Tucker para restrições de desigualdades [Hanses & Walster 1992, Haykin 2001, Martinez & Santos 1995, Semolini 2002].
4.1.1
Funcional de Lagrange
Em problemas com restrições é necessário construir uma função que englobe a função objetivo juntamente com as restrições e que sua estacionalidade defina a solução. O fun-cional de Lagrange pode resolver este problema definindo como uma combinação linear a função objetivo e cada uma das restrições associando ao multiplicadores de Lagrange.
L(x,α) = f(x) + m
∑
j=1
αihi(x) (4.2)
onde,αisão os multiplicadores de Lagrange.
Se L(x,α)for uma função convexa em x, a condição necessária para que o ponto x∗ seja mínimo de f(w), sujeito a restrição hjé igualando o gradiente da L em relação a x e
aα:
∂L(x∗,α∗)
∂x =0
∂L(x∗,α∗)
∂α =0
(4.3)
Uma forma mais geral do problema de otimização que satisfaz tanto restrições de igualdades quanto de desigualdades pode ser generalizada da definição para otimização com restrições de igualdades, dado por:
L(x,α,β) = f(x) + k
∑
i=1
αigi(x) + m
∑
j=1
βihi(x) (4.4)
4.1.2
Condições de Kuhn-Tucker
Dado o problema de otimização pela equação (4.1) com domínio convexo, a solução necessária para o ponto x∗ser ótimo é a existência deα∗eβ∗que satisfaz:
∂L(x∗,α∗,β∗)
∂x =0
∂L(x∗,α∗,β∗)
∂β =0
α∗
igi(x∗) =0, i=1, ...,k gi(x∗)≤0, i=1, ...,k
α∗≥0, i=1, ...,k
(4.5)
O tratamento do funcional de Lagrange para problema de otimização convexo fornece a um problema de dual que diversas vezes é mais simples de ser resolvida do que o problema primal [Martinez & Santos 1995].
4.2
Otimização Linear usando Computação Intervalar
Muitos autores tem considerado a computação intervalar para resolver problemas de otimização linear, aplicando métodos intervalares com métodos de programação li-near para encontrar uma solução ótima do problema de otimização ou a partir de uma solução aproximada obtem-se um vetor que contém a solução exata, para mais detalhes ver [Moore 1979].
Dado A sendo uma matriz m×n com m<n, de coeficientes intervalares. Dado B e P sendo vetores intervalares de m e n dimensão, respectivamente. O objetivo é encontrar
um vetor intervalar Z que contenha o conjunto de soluções do problema de otimização linear, para cada b∈B, p∈P, Ar∈A.
Por conveniência, será denominado, neste estudo, otimização intervalar, a otimização que fizer uso de conceito da análise intervalar.
Para o problema de otimização intervalar considere:
Maximizar: Q(x) = (p,x)
Sujeito a: Arx=b ou Arx≦b
0≦x
(4.6)
onde,(p,x)é o produto interno de um vetor real p e x, b é um vetor real e Aré uma matriz
intervalar.
obtidos usando um método de otimização. Dado S sendo o conjunto de índice de todas variáveis bases da solução aproximada z∗. Para a condição ser suficientemente com-putável do conjunto de todas as soluções de (4.6) tem um mesma base com z∗. Denotado por x′ o vetor de m dimensão consistindo de componentes bases de um vetor x de n di-mensão. Assim, x′= (xi1, ...,xim onde S={i1, ...,im}. Similarmente, denotado por x′′
um vetor de n−m dimensão consistindo de todos os componentes não bases de x. Seja A′r uma matriz m×m consistindo de colunas bases de Ar e A′′ uma matriz (n−m)×m
consistindo de colunas não bases de Ar e assim por diante.
Suponha que z∗ é a solução de A′rz′=b′ para algum A′r ∈A′, b′∈B′, assume-se que todo A′r∈A′, são não singular. Dado Z′ sendo o conjunto de todas soluções z′ para todo
A′r ∈A′, b′ ∈B′. Assim, z′∗ é uma solução aproximada de A′rz′ =b′. Dado Y sendo a aproximação da inversa da matriz A′∗r que é usado na computação de z8.
Logo, o conjunto de soluções de um problema linear da equação (4.6) para todo b∈B, p∈P, Ar∈A é contido no vetor intervalar Z computado através de:
Zi′=z∗i +q[−1,1], para componentes bases de Z
Z′′=0, para componentes não bases de Z (4.7)
onde, q=kY kkA′z∗−Bk)/(1−R).
Se w(A) e w(B) são pequenos, o limite de Z pode ser refinado. Para encontrar o vetor intervalar mais estreito do conjunto de soluções para a equação (4.6) computa, para
k=1, ...2:
Zk+1=Zk∩ {Y B+ (I−YA′)Zk} (4.8) A equação (4.8) na sequencia de iterações contem no vetor intervalar os componentes bases da solução de (4.6).
Para determinar se o conjunto de todas as soluções tem uma mesma base como z∗, é testado Z′≧0 e denota a transposta das matrizes A′e A′′ por A′T e A′′T, respectivamente. Seja P′ e P′′ sendo componentes bases e componentes não bases, respectivamente, do vetor de coeficientes da função objetivo, o vetor intervalar V é encontrado e contem o conjunto de soluções de A′rTv=p′para todo A′r∈A′e todo p′∈P′. Caso A′′TV−P′′≧0, então o conjunto de soluções tem uma mesma base z∗.
Para o valor máximo de Q(x), possui Q(z)∈(P,Z).
4.2.1
Otimização com restrições
Minimar: f(x)
Sujeito a: pi(x)≤0(i=1, ...,m) qi(x) =0(1=1, ...,r)
(4.9)
onde, f(x) é diferenciável e as funções de restrições pi(x) e qi(x) são continuamente
diferenciáveis.
Assumindo um intervalo inicial X o objetivo é encontrar um mínimo de f(x) ∈X
sujeito as restrições.
4.2.2
Condições de John
Para resolução do problema de otimização com restrições é utilizado a condição de John:
u0▽f(x) +∑mi=1ui▽p(x) +∑ri=1vi▽q(x) =0 uipi(x) =0
qi(x) =0 ui≥0
(4.10)
onde, u e v são multiplicadores de Lagrange.
Para a resolução do problema de otimização pode ser considerado o uso do método de Newton, onde, ui≥0 e os vetores x, u e v da condição de John são escritos em termos do
vetor t.
Rk(t)
u0▽f(x) +∑mi=1ui▽p(x) +∑ri=1vi▽q(x) uipi(x)
qi(x)
Kernel Intervalar
Os métodos kernels têm sido considerado um poderoso atalho computacional em aprendizado de máquinas devido ao desempenho, generalização e adaptação em resolver problemas diversos [Abe 2005, Bishop 2006, Hofmann et al. 2008]. Uma vasta variedade de algoritmos em aprendizagem de máquina fazem uso desses métodos, tais como, em máquinas de vetores suporte, redes neurais, algoritmos de agrupamentos, análise de com-ponentes principais, entre outros.
Uma característica marcante dos métodos de aprendizagem de máquina que utilizam kernel é formular um problema em um novo espaço. A SVM, visto para classificação de padrões, é uma máquina linear cujo objetivo é encontrar um hiperplano que separe as classes distintas da melhor forma possível. Uma característica que torna a SVM para uso geral é tratar da dimensionalidade do espaço de entrada, mapeando o conjunto de entrada por meio de uma função que projeta uma imagem linear em um novo espaço. Em outras palavras, o espaço de entrada de um problema não linear é mapeado através da função kernel para um outro espaço, o espaço de características, dado pela relação:
k(x,x′) =hφ(x)·φ(x′)i (5.1)
Neste capítulo foi desenvolvido uma extensão intervalar de kernels, de modo que, definindo as funções intervalares que mapeiam o espaço de entrada e as funções kernels intervalares, o espaço de características é encontrado implicitamente.
Considere um conjunto de treinamento {(X1,Y1), . . . ,(XN,YN)} ⊆(X×Y)N, onde,
o i-ésimo exemplo Xi∈X⊆IRn de um espaço n-dimensional pertence a um rótulo ou
classeY={[−1,−1],[+1,+1]}(classificação binária), para todo i=1, . . . ,N e N ∈N.