Métodos de pontos interiores aplicados ao problema de regressão pela norma Lp

(1)

M´

etodos de pontos interiores aplicados ao problema

de regress˜

ao pela norma

_Lp

Daniela Renata Cantane

Orientador: Prof. Dr. Aurelio Ribeiro Leite de Oliveira

Disserta¸c˜ao apresentada ao Instituto de Ciˆencias

Matem´aticas e de Computa¸c˜ao - ICMC-USP, como parte

dos requisitos para obten¸c˜ao do t´ıtulo de Mestre em

Ciências - Área: Ciências da Computa¸cão e Matemática

Computacional.

(2)

`

(3)

Agradecimentos

`

A Deus, por estar sempre aben¸coando minha vida e iluminando meus caminhos

du-rante toda essa caminhada.

Aos meus pais, Cidinha e Carlinhos e aos meus irm˜aos, Daniel e Diego, pelo apoio e

incentivo aos meus estudos. Agrade¸co por estarem sempre presentes em minha vida.

Ao meu namorado, Daniel, pela compreens˜ao nos momentos que estive ausente, pelo

seu amor, carinho e amizade durante todos estes anos.

Ao meu orientador, pela paciˆencia e dedica¸c˜ao ao longo do desenvolvimento do

pro-jeto e por ter me concedido esta oportunidade.

Aos professores e funcion´arios da USP que contribuiram para a minha forma¸c˜ao de

uma forma em geral.

`

As minhas amigas “irm˜azinhas”, Aline, Lilian, Kelly, Cec´ılia, Glaucia e Sˆonia que

sempre estiveram dispostas a ajudar quando necessitei.

`

A FAPESP - Funda¸cão de Amparo e Apoio à Pesquisa do Estado de São Paulo,

(4)

Resumo

Neste trabalho a fam´ılia de m´etodos de pontos interiores barreira logar´ıtmica ´e

desen-volvida para o problema de regress˜ao pela norma Lp e a estrutura matricial resultante ´e

explorada objetivando uma implementa¸c˜ao eficiente. Apresentamos alguns conceitos sobre

métodos de pontos interiores necessários para o desenvolvimento do método e

descreve-mos um método de convergência quadrática previamente conhecido. Uma implementa¸cão

em Matlab dos m´etodos de pontos interiores desenvolvidos ´e comparada com uma

imple-menta¸cão do método quadrático existente, obtendo desempenho computacional superior.

Abstract

In this work the family of logarithmic barrier interior point methods is developed

for the norm Lp fitting problem and the resultant matrix structure is exploited in order to have an efficient implementation. We introduce some concepts about interior point

methods necessary for the development of the method and describe a previously known

quadratic convergent problem. An implementation in Matlab of the interior point methods

developed is compared with an implementation of the known quadratic method obtaining

(5)

Conte´

udo

Resumo iv

Abstract iv

1 Introdu¸c˜ao 1

2 M´etodos de Pontos Interiores 4

2.1 Conceitos Iniciais sobre Pontos Interiores . . . 4

2.1.1 Otimiza¸c˜ao Linear . . . 4

2.1.2 Otimiza¸c˜ao N˜ao Linear . . . 6

2.1.3 Convexidade . . . 8

2.2 M´etodo de Newton . . . 8

2.2.1 M´etodo de Newton para uma vari´avel . . . 9

2.2.2 Método de Newton para várias variáveis . . . 9

2.3 M´etodo de Pontos Interiores Primal-Dual . . . 10

2.3.1 M´etodo Primal-Dual Afim-Escala . . . 10

2.3.2 M´etodo Primal-Dual Cl´assico . . . 14

2.4 M´etodo de Pontos Interiores Barreira Logar´ıtmica . . . 16

2.4.1 Crit´erio de Convergˆencia . . . 19

2.4.2 Inicializa¸c˜ao . . . 19

2.5 M´etodo de Pontos Interiores Barreira Logar´ıtmica Preditor-Corretor . . . . 20

(6)

3.2 M´etodos Pr´e-Existentes . . . 26

3.2.1 Métodos de Relaxa¸cão por Coluna para o problema de norma m´ınima 26 3.2.2 Método GNCS . . . 27

4 Métodos de Pontos Interiores Aplicados ao Problema de Regressão pela Norma Lp 38 4.1 Método Barreira Logar´ıtmica . . . 38

4.1.2 Pontos Iniciais . . . 44

4.1.3 Algumas Considera¸c˜oes . . . 45

4.2 M´etodo Preditor-Corretor . . . 45

4.3 M´etodo Primal-Dual Barreira Logar´ıtmica . . . 50

4.4 M´etodo Primal-Dual Preditor-Corretor . . . 57

4.5 Regress˜ao Polinomial . . . 63

5 Resultados Computacionais 68 6 Conclus˜oes e Perspectivas Futuras 97 6.1 Conclus˜oes . . . 97

(7)

Lista de Tabelas

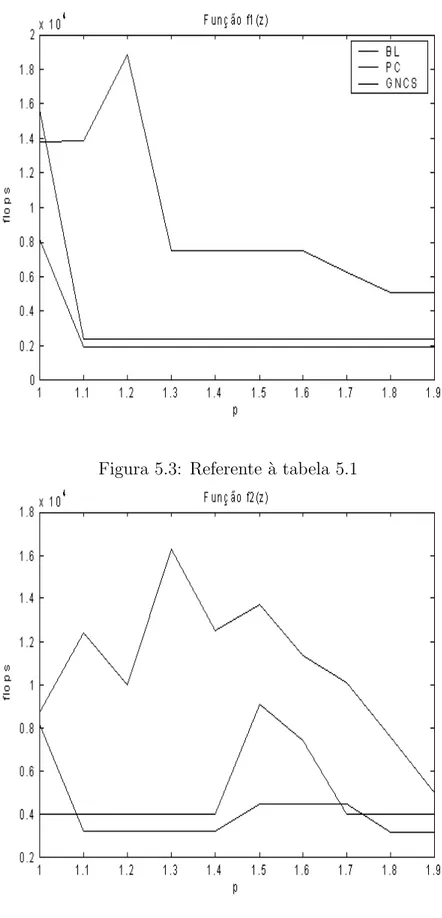
5.1 Resultados computacionais utilizando a fun¸c˜ao f1(z). . . 71

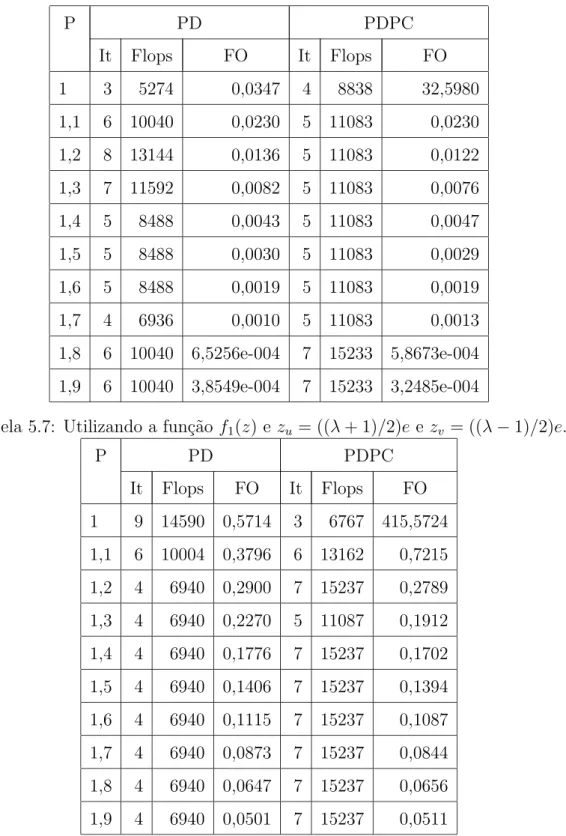
5.2 Resultados computacionais utilizando a fun¸c˜ao f2(z). . . 71

5.3 Utilizando a fun¸c˜ao f1(z): zu =u, zv =v. . . 73

5.4 Utilizando a fun¸c˜ao f2(z): zu =u, zv =v. . . 73

5.5 Utilizando a fun¸c˜ao f1(z) e zu =zv =e. . . 74

5.6 Utilizando a fun¸c˜ao f2(z) e zu =zv =e. . . 74

5.7 Utilizando a fun¸c˜ao f1(z) e zu = ((λ+ 1)/2)e e zv = ((λ−1)/2)e. . . 75

5.8 Utilizando a fun¸c˜ao f2(z) e zu = ((λ+ 1)/2)e e zv = ((λ−1)/2)e. . . 75

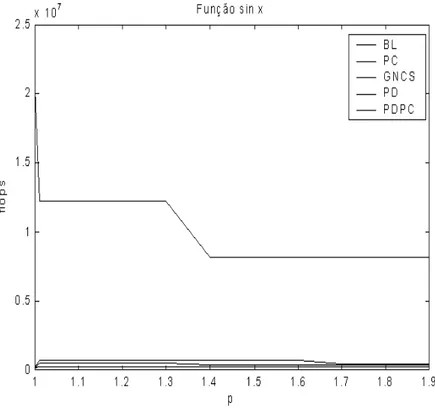
5.9 Resultados computacionais utilizando a fun¸c˜ao sinx. . . 85

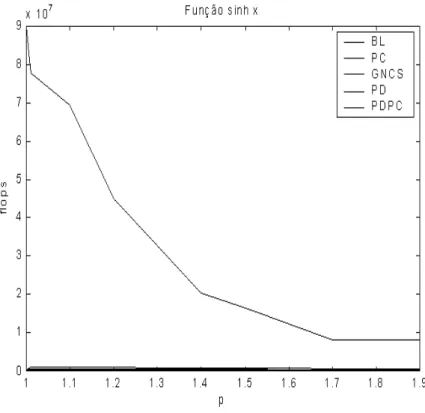
5.13 Resultados computacionais utilizando a fun¸c˜ao sinhx. . . 87

5.17 Resultados computacionais utilizando a fun¸c˜ao lnx. . . 89

(8)

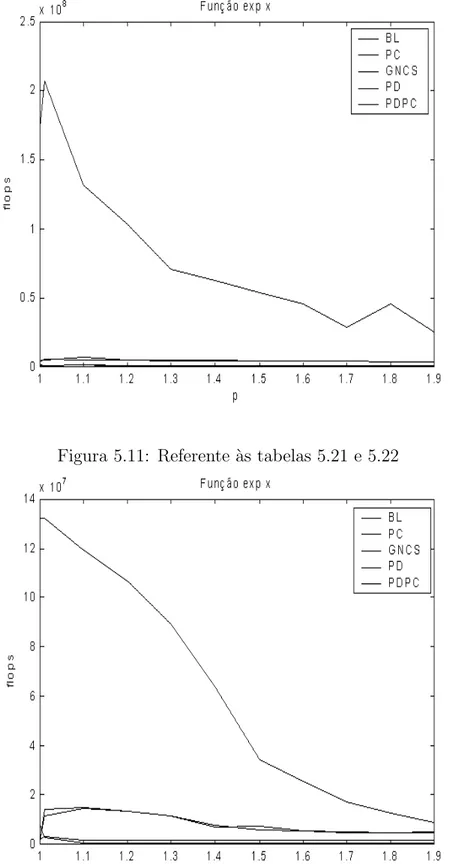
5.24 Resultados computacionais utilizando a fun¸c˜ao expx. . . 92

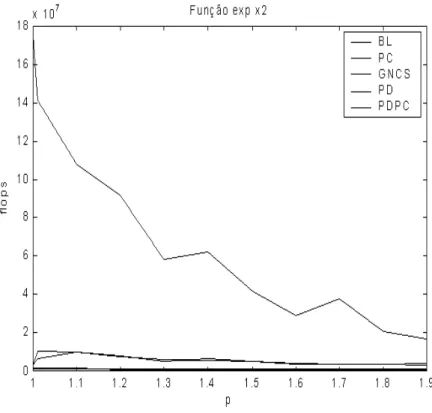
5.25 Resultados computacionais utilizando a fun¸c˜ao expx2_{. . . 93}

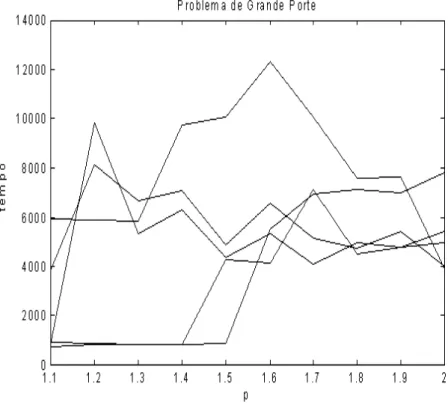
5.29 Resultados computacionais utilizando o problema de grande porte. . . 95

5.30 Resultados computacionais utilizando o problema de grande porte. . . 95

(9)

Cap´ıtulo 1

Introdu¸

c˜

ao

Desde o surgimento dos métodos de pontos interiores para otimiza¸cão linear, códigos

computacionais baseados nessas id´eias vem se apresentando como alternativas eficientes

para solu¸c˜ao de problemas de grande porte [1, 10, 15, 19].

Uma linha de pesquisa importante nesta ´area considera classes espec´ıficas de

proble-mas e explora as particularidades da estrutura matricial com o objetivo de obter

imple-menta¸cões ainda mais eficientes, inclusive para problemas com restri¸cões lineares e fun¸cão

objetivo n˜ao linear [5, 20, 21, 22, 23, 24, 25].

O objetivo deste trabalho consiste no desenvolvimento dos m´etodos de pontos

in-teriores para o problema de regressão pela norma Lp, 1< p < 2, no estudo da estrutura matricial resultante e na implementa¸cão eficiente do método desenvolvido. Os resultados

obtidos serão comparados com uma implementa¸cão do método proposto em [13].

Dada uma classe de problemas, a forma padr˜ao para o desenvolvimento de um m´etodo

de pontos interiores consiste na aplica¸cão do método de Newton às condi¸cões de

otimali-dade desconsiderando as restri¸cões de capaciotimali-dade. O método resultante é essencialmente

(10)

al-dos m´etoal-dos de pontos interiores, o m´etodo preditor-corretor [16].

A etapa seguinte desta abordagem consiste na explora¸c˜ao eficiente da estrutura

matri-cial do problema. ´E sempre importante lembrar que a resolu¸c˜ao de um sistema linear, em

geral sim´etrico, consiste no passo mais caro, em termos computacionais, de cada itera¸c˜ao

dos m´etodos de pontos interiores. Desta forma, a explora¸c˜ao da estrutura matricial pode

levar a métodos de pontos interiores mais eficientes que os métodos genéricos aplicados

a um problema particular. As idéias desenvolvidas em [20, 21] para os problemas de regressão L1 e L∞ também podem ser adaptadas a este problema devido à semelhan¸ca

das estruturas matriciais com o problema de regress˜ao Lp.

O problema de regress˜ao

min

x∈IRm kAx−bk

p p

onde A = [a1, . . . , an] ∈ IRm×n, b ∈ IRn e n > m, tem in´umeras aplica¸c˜oes em diversas

áreas de ciências e engenharias. As normas mais utilizadas são as normas L1, L2 e L∞. A

normaL2 ´e muito popular entre outros motivos por permitir uma solu¸c˜ao direta. Por sua

vez a norma L1 permite diminuir o efeito de pontos discrepantes enquanto que a norma

L∞ garante prote¸c˜ao contra o pior caso.

O m´etodo IRLS iteratively reweighted least-squares [17] foi por muito tempo a ´unica

alternativa prática para a resolu¸cão deste problema para outros valores de p. Mais recen-temente este método foi aperfei¸coado, no que diz respeito à robustez, através da inclusão

de uma busca linear [13]. No mesmo trabalho, foi tamb´em proposto um novo m´etodo

que apresenta caracter´ısticas similares aos m´etodos de pontos interiores. Este m´etodo

apresentou resultados computacionais superiores ao IRLS.

Ambos m´etodos apresentados em [13] tˆem uma importante desvantagem: a busca

linear ´e computacionalmente cara. Isto nos motivou o estudo dos m´etodos de pontos

interi-ores aplicados a este problema que obt´em resultados computacionais superiinteri-ores, repetindo

(11)

No Cap´ıtulo 2, descrevemos alguns conceitos sobre m´etodos de pontos interiores.

Descrevemos também o método de Newton que será utilizado para o desenvolvimento dos

m´etodos de pontos interiores barreira logar´ıtmica, primal-dual e preditor-corretor.

No Cap´ıtulo 3, apresentamos o problema de regressão pela norma Lp e o método de convergência quadrática GNCS, desenvolvido em [13], que será utilizado para

com-pararmos com o m´etodo de pontos interiores desenvolvido no cap´ıtulo seguinte.

Desenvolvemos, no Cap´ıtulo 4, os m´etodos de pontos interiores barreira logar´ıtmica,

primal-dual e preditor-corretor nos quais s˜ao aplicados ao problema de regress˜ao pela

norma Lp e as estruturas matriciais resultante s˜ao estudadas.

No Cap´ıtulo 5, apresentamos os resultados computacionais obtidos em nossos m´etodos

e comparamos com os resultados do m´etodo existente apresentado no Cap´ıtulo 3.

No Cap´ıtulo 6, apresentamos as conclus˜oes e perspectivas futuras do nosso trabalho

(12)

Cap´ıtulo 2

M´

etodos de Pontos Interiores

Neste cap´ıtulo, descrevemos conceitos sobre pontos interiores, m´etodo de Newton,

m´etodos barreira logar´ıtmica, primal-dual e preditor-corretor que ser˜ao aplicados ao

pro-blema de regress˜ao Lp.

2.1 Conceitos Iniciais sobre Pontos Interiores

Antes de descrevermos os m´etodos de pontos interiores, devemos caracterizar o que

é um problema de otimiza¸cão linear, um problema de otimiza¸cão não linear e um ponto

interior em problemas desse tipo.

Os problemas de otimiza¸cão linear derivam da constru¸cão de uma representa¸cão

matem´atica para um problema real em que se quer minimizar ou maximizar uma fun¸c˜ao

objetivo linear, ao mesmo tempo em que as vari´aveis est˜ao sujeitas a determinadas

res-tri¸cões também lineares. Para os problemas de otimiza¸cão não linear, temos uma fun¸cão

objetivo não linear e_\ou restri¸cões não lineares. Um ponto interior é aquele em que todas as variáveis se encontram estritamente dentro de seus limites.

2.1.1 Otimiza¸

c˜

ao Linear

(13)

min ct_x

sa Ax =b

x_≥0

(2.1)

onde A é uma matriz, x é um vetor coluna de variáveis primais, b e c são vetores de constantes.

Esta formula¸cão é denominada problema primal e está associada ao problema dual

max bt_y _⇔ _max _bt_y

sa At_y_≤_c _sa _At_y₊_z ₌_c

y livre z _≥0, y livre

(2.2)

onde y é um vetor coluna de variáveis duais ez é a variável de folga complementar.

Na forma padrão, x > 0 é um ponto interior no problema primal e z > 0 é um ponto interior para o problema dual. No problema primal Ax = b; x > 0 é um ponto interior fact´ıvel e no problema dual At_y₊_z ₌_c_; _{z >}_{0 é um ponto interior fact´ıvel.}

Um outro conceito que será utilizado para a constru¸cão de métodos de pontos

in-teriores é o gap. Ogapé a diferen¸ca entre os valores das fun¸cões objetivo para o primal e

o dual de um mesmo problema, ou seja, γ = ct_x₋_bt_y _{[30]. ´}_{E poss´ıvel mostrar que para}

um ponto primal e dual fact´ıvel, o gap´e dado por γ =ct_x₋_bt_y ₌_zt_x_.

Por último, é poss´ıvel determinar as condi¸cões de otimalidade. Um dado ponto (x, y, z) é ótimo para os problemas primal e dual se e somente se as seguintes condi¸cões são

satis-feitas [2]:

(i) Primal fact´ıvel: Ax=b, x _≥0;

(14)

nota¸cões X = diag(x) e Z = diag(z) são utilizadas e XZe = 0 equivale à

xizi = 0, i= 1, . . . , n.

2.1.2 Otimiza¸

c˜

ao N˜

ao Linear

Agora, veremos a formula¸cão de um problema de otimiza¸cão não linear [3]. Em geral,

um problema de otimiza¸cão não linear é da forma:

min f(x) sa h1(x) = 0

...

hm(x) = 0

g1(x)≤0

...

gp(x)_≤0

x_∈Ω,

onde as fun¸c˜oes f, hi e gi s˜ao cont´ınuas e normalmente _∈C2 e Ω_⊂IRn_.

Devido ao fato de que em nosso trabalho utilizaremos problema com restri¸c˜ao de

igualdade, ser˜ao abordadas somente as condi¸c˜oes de otimalidade relativa ao mesmo.

Seja o problema

min f(x) sa h(x) = 0

(2.3)

onde h(x) ´e um vetor de restri¸c˜oes de igualdade.

A fun¸c˜ao Lagrangiana associada ao problema ´e dada por

L(x, y) =f(x) +yth(x).

A fun¸c˜ao Lagrangiana torna o problema irrestrito.

(15)

(i) Condi¸c˜oes necess´arias de 1a _ordem:

Derivando a fun¸c˜ao Lagrangiana com rela¸c˜ao ax e a y, obtemos

∇L(x, y) =

              

∇f(x) +

m

X

i=1

yi_∇hi(x) = 0

hi(x) = 0, i= 1, . . . , m. x_∈IRn_.

Este sistema fornece os candidatos a ponto ´otimo.

(ii) Condi¸c˜ao necess´aria de 2a _ordem:

Um pontox∗

satisfazendo as restri¸cõesh(x) = 0 é chamadoponto regular(ponto candidato a ótimo) das restri¸cões se os vetores gradientes _∇h1(x∗),∇h2(x∗), . . . ,

∇hm(x∗

) forem linearmente independentes.

Um conjunto de restri¸c˜oes de igualdade h(x) = 0 define um subconjunto do IRn

chamado de hipersuperf´ıcie. Em um ponto regular x∗

da hipersuperf´ıcie definida

por h(x) = 0 o plano tangente ´e dado por:

M =_{y_{| ∇}th(x∗

)y = 0_}

onde

∇h(x∗

) =

      

∇h1(x∗)

...

∇hm(x∗

)

      

.

Temos que f e h _∈ C2. Seja x∗

um ponto regular das restri¸cões h(x) = 0 e um ponto extremo local (m´ınimo ou máximo) de f(x) sujeito à restri¸cão h(x) = 0. Então existe um vetor yt _∈_IRn _{| ∇}_f₍_x∗

) +yt_∇_h₍_x∗

) = 0, ondey ´e o vetor multipli-cador de Lagrange.

Considere M =_{y _{| ∇}t_h₍_x∗

)y = 0_}. Ent˜ao a matriz L(x∗

) = F(x∗

) +yt_H₍_x∗

)

´e semidefinida positiva em M, isto ´e,

(16)

(iii) Condi¸c˜ao suficiente de 2a _ordem:

Seja x∗

regular tal que_∇f(x∗

) +yt_∇_h₍_x∗

) = 0. Suponha queL(x∗

) =F(x∗

) +

yt_H₍_x∗

) seja definida positiva em M, isto ´e,

ytL(x∗

)y >0, _∀y_∈M.

Ent˜ao x∗ _{´e o ponto de m´ınimo local sujeito a}_h

i(x) = 0.

2.1.3 Convexidade

Defini¸c˜ao 2.1.1 (Conjuntos Convexos) SejaΩ_⊂IRn_,_Ω_{´e dito convexo se o segmento}

de reta que une quaisquer dois pontos de Ω est´a contido em Ω, ou seja, _∀x1, x2 ∈ Ω,

λx1+ (1−λ)x2 ∈Ω, λ∈[0,1].

Defini¸cão 2.1.2 (Fun¸cões Convexas) Sejaf :S_→E1, ondeSé um conjunto convexo

não vazio em En. A fun¸cão f é dita convexa em S se

f(λx1+ (1−λ)x2)≤λf(x1) + (1−λ)f(x2)

para todo x1, x2 ∈S e λ∈(0,1).

Se para todo λ_∈(0,1)e x1 6=x2 vale a desigualdade estrita então a fun¸cão é denominada

estritamente convexa.

Defini¸cão 2.1.3 (Fun¸cões Côncavas) A fun¸cão f : S _→ E1 é denominada côncava

(estritamente cˆoncava) em S se ₋f ´e convexa (estritamente convexa) em S.

2.2 M´

etodo de Newton

Os métodos de pontos interiores consistem na aplica¸cão do método de Newton às

condi¸c˜oes de otimalidade desconsiderando as desigualdades e partindo de um ponto

inte-rior [30]. Para tanto, apresentaremos o m´etodo de Newton para uma vari´avel e a seguir

para várias variáveis. Para mais detalhes sobre o método de Newton e suas caracter´ısticas

(17)

2.2.1 M´

etodo de Newton para uma vari´

avel

Sejax_∈Ω tal queφ(x) = 0. Para encontrarmos o valor dexutilizamos aproxima¸cões sucessivas da fun¸cão φ(x) em torno dos pontos x0_{, x}1_{, . . . , x}k_{, até que o ponto} _xk _{seja tal}

que φ(xk₎_≈_{0. Vamos utilizar a f´ormula de Taylor em torno do ponto} _x0_:

0 = φ(x) =φ(x0) +φ′

(x0)(x₋x0) + φ

′′

(x0₎

2! (x−x

0₎2₊_{. . . .}

Aproximamos φ(x1_{) at´e o termo linear da s´erie, ou seja,}

0_≃φ(x0) +φ′

(x0)(x1₋x0)_⇒x1 =x0₋ φ(x

0₎

φ′₍_x0₎.

Podemos aplicar esta f´ormula para obter x1 _{e depois calcular o valor de}_xk

sucessiva-mente, até que φ(xk₎_≃_{0. Assim, constru´ımos o método de Newton para uma variável:}

Dado x0

Para k= 0,1, . . ., fa¸ca

dk ₌₋φ(xk) φ′₍_xk₎ xk+1 ₌_xk₊_dk

At´e convergir (ou seja,φ(xk₎_≃_0).

2.2.2 M´

etodo de Newton para v´

arias vari´

aveis

Seja x _∈ IRn _{tal que} _φi₍_x_{) = 0, para} _i _{= 1}_,₂_{, . . . , n}_{. Novamente, para encontrarmos}

o valor de x utilizamos aproxima¸c˜oes sucessivas da fun¸c˜ao φ(x) em torno dos pontos

x0_{, x}1_{, . . . , x}k_{, at´e que o ponto} _xk _{seja tal que}_φi₍_xk₎_≃_{0. Aplicando a f´ormula de Taylor}

para v´arias vari´aveis em torno de x0_:

0 = φi(x) =φi(x0) +h_∇φi(x0)it(x₋x0) +. . . , parai= 1, . . . , n,

onde

   

∂φi(x)

∂x1

...

(18)

Aproximando φi(x1_{) at´e o termo linear da s´erie, obtemos}

0_≃φi(x1) =φi(x0) +h_∇φi(x0)it(x1₋x0), para i= 1, . . . , n,

ou seja,

−φ1(x0) = [∇φ1(x0)]t(x1−x0)

...

−φn(x0_{) = [}_∇_φn₍_x0_)]t₍_x1₋_x0₎_.

Sejam J(x0_{) =}       

[_∇φ1(x0)]t

... [_∇φn(x0_)]t

      

a matriz Jacobiana e F(x0_{) =}       

φ1(x0)

...

φn(x0₎       

. Ent˜ao,

−F(x0_{) =} _J₍_x0₎₍_x1₋_x0₎_⇒_x1 ₌_x0₋_[_J₍_x0_)]−1_F₍_x0₎_.

Constru´ımos, assim, o método de Newton para várias variáveis:

Dado x0 _∈_IRn

Para k= 0,1, . . ., fa¸ca

dk ₌₋_[_J₍_xk_)]−1_F₍_xk₎ xk+1 ₌_xk₊_dk

At´e convergir.

2.3 M´

etodo de Pontos Interiores Primal-Dual

Nesta se¸c˜ao, veremos os m´etodos de pontos interiores primal-dual afim-escala [18] e

primal-dual cl´assico.

2.3.1 M´

etodo Primal-Dual Afim-Escala

(19)

aplicar o método de Newton ao sistemaF(x, y, z) = 0 formado pelas condi¸cões de otimali-dade desconsiderando (x, z)_≥0, resolvendo os problemas primal e dual simultaneamente. Sejam x0_{, y}0_{, z}0_,₍_x0_{, z}0₎_>_{0 um ponto interior. Temos que} _F₍_x0_{, y}0_{, z}0_{) é dado por}

F(x0, y0, z0) =

      

Ax0 ₋b At_y0₊_z0₋_c

X0Z0e

       =₋       

r0p r0

d r0a

       .

Utilizando o método de Newton para várias variáveis, obtemos

(x1, y1, z1) = (x0, y0, z0)₋[J(x0, y0, z0)]−1_F₍_x0_{, y}0_{, z}0₎_,

onde J(x0_{, y}0_{, z}0_{) =}       

A 0 0

0 At _I

Z0 ₀ _X0        .

Assim, d0 _{ser´a dado por}

d0 =

      

A 0 0

0 At _I

Z0 ₀ _X0       

−1

      r0 p r0 d r0 a        =        dx0 dy0 dz0        .

Reescrevendo o sistema acima e por facilidade de nota¸c˜ao ignorando o ´ındice 0 temos,

      

A 0 0

0 At _I

Z 0 X

              dx dy dz        =        rp rd ra        . (2.4)

Resolvendo o sistema (2.4), obtemos as dire¸c˜oesdx, dy e dz. Assim, temos o sistema

Adx=rp (2.5)

Atdy+dz =rd (2.6)

(20)

Agora, da Equa¸c˜ao (2.6), obtemos

At_dy₊_X−1₍_ra₋_Zdx_{) =}_rd

⇒At_dy₋_X−1_Zdx₌_rd₋_X−1_ra.

Definindo D=X−1_Z_{, obtemos}

At_dy₋_Ddx₌_rd₋_X−1_ra

⇒dx=D−1₍_At_dy₋_rd₊_X−1_ra₎_.

Substituindo a ´ultima equa¸c˜ao em (2.5), temos

AD−1₍_At_dy₋_rd₊_X−1_ra_{) =}_rp

⇒(AD−1_At₎_dy ₌_rp₊_AD−1_rd₋_AD−1_X−1_ra

⇒dy= (AD−1_At₎−1₍_rp₊_AD−1_rd₋_AD−1_X−1_ra₎_.

Temos que AD−1_At _{tem dimensão} _m_, _posto₍_A_{) =}_m_{, é simétrica e definida positiva.}

Podemos escrever

AD−1_At₌_LLt_,

ou seja, podemos calcular a decomposi¸c˜ao de Cholesky de AD−1_At_{. A ordem de escolha}

dos pivôs da diagonal não altera a estabilidade numérica.

A estrutura esparsa de AD−1_At _{n˜ao varia com as itera¸c˜oes. Portanto, podemos}

uti-lizar a mesma sequˆencia de pivˆos obtidas por alguma eur´ıstia de reordenamento [] em

todas as itera¸cões reduzindo o enchimento (elementos não nulos em L que são nulos em

AD−1_At_{) da matriz na decomposi¸c˜ao de Cholesky. A matriz} _AD−1_At _{´e permutada uma}

´

unica vez antes de iniciar as itera¸c˜oes.

Podemos resumir estes c´alculos como se segue.

(21)

Dados (x0_{, y}0_{, z}0_{) interior e} _τ _∈₍₀_,₁₎

Para k= 0,1, . . ., fa¸ca

rpk = b−Axk rdk = c−Atyk−zk rak = −XkZke

dyk _{= [}_A₍_Dk₎−1_At_]−1_[_rk

p +A(Dk)

−1_rk

d−A(Dk)

−1₍_Xk₎−1_rk a] dxk _{= (}_Dk₎−1_[_At_dyk₋_rk

d + (Xk)

−1_rk a] dzk _{= (}_Xk₎−1_[_rk

a−Zkdxk]

ρp = min

dxi<0

− xi

dxi

ρd = min

dzi<0

−_dzizi

α_pk = min_{1, τ ρp_} α_dk = min_{1, τ ρd_}

xk+1 = xk+αk_pdxk (α_pk ´e tal que xk+1 >0)

yk+1 = yk+αk_ddyk

zk+1 = zk+αk_ddzk (αk_d ´e tal que zk+1 >0) At´e convergir.

Observa¸c˜ao 2.3.1 Dados x0 _e_z0 _{interiores, o tamanho do passo} _α_{´e calculado de forma}

que xk+1 _e _zk+1 _{permane¸cam interiores (}_y _{´e livre). Este m´etodo n˜}_{ao necessita de um}

ponto inicial fact´ıvel.

Crit´erio de Convergˆencia

(i) Factibilidade primal: kb−Axk

kb_k+ 1 ≤ǫ;

(ii) Factibilidade dual: kc−A

t_y₋_z_k

kc_k+ 1 ≤ǫ;

(22)

Ponto Inicial

Para o problema primal, temos [16]:

˜

x = At(AAt)−1_b

⇒Ax˜=b, x0_i = max_{xi, ǫ˜ 1},

ǫ1 = max

(

−min ˜xi, ǫ2, k

b_k₁ ǫ2kAk1

)

,

ǫ2 = 100.

Agora, para o problema dual:

y0 = 0,

z_i0 =

        

ci+ǫ3 seci ≥0;

−ci seci _{≤ −}ǫ3;

ǫ3 se−ǫ3 ≤ci ≤0,

ǫ3 = 1 +kck1.

2.3.2 M´

etodo Primal-Dual Cl´

assico

O método primdual afim-escala não é um método eficiente porque permite que

al-guns produtos xizi se aproximem de zero muito rapidamente [30]. Consequentemente, as dire¸cões calculadas nestas condi¸cões são muito distorcidas e o método progride

lenta-mente, podendo inclusive n˜ao convergir.

Para evitar esta dificuldade, é acrescentada uma perturba¸cão µàs condi¸cões de com-plementaridade [16, 30]. No lugar de xizi = 0 temos agora xizi =µ, i= 1, . . . , n.

No m´etodo primal-dual resolvemos o seguinte sistema n˜ao-linear

            

Ax=b, x_≥0

(23)

Aplicando o m´etodo de Newton temos o seguinte sistema linear       

A 0 0

0 At _I

Z 0 X

              dx dy dz        =        rp rd rc        =       

b₋Ax c₋At_y₋_z

µe₋XZe

       .

Podemos calcular as dire¸c˜oes exatamente como no m´etodo primal-dual afim-escala,

basta substituir ra porrc. Em particular, o Jacobiano ´e o mesmo.

M´etodo primal-dual cl´assico

Dados τ, σ _∈(0,1) e (x0_{, y}0_{, z}0_{) interior ou (}_x0_{, z}0₎_>₀

Para k=0,1,. . . , fa¸ca

µk = σγ k n rk_p = b₋Axk rk_d = c₋Atyk₋zk rk_c = µke₋XkZke dyk = hA(Dk)−1_Ati−1h_rk

p +A(Dk)

−1_rk

d−A(Zk)

−1_rk c

i

dxk = (Dk)−1h_At_dyk

−r_dk+X−1_rk c

i

dzk = (Xk)−1h_rk

c −Zkdxk

i

ρp = min

dxk i<0

( − x k i dxk i )

ρd = min

dzk i<0

( − z k i dzk i )

(24)

At´e convergir.

Observa¸c˜ao 2.3.2 Se tomarmosµk= 0 temos o m´etodo afim-escala. Considereσ = √1

n

e τ = 0,99995. Temos queγ se reduz a cada itera¸c˜ao, portantoµse reduz a cada itera¸c˜ao. Assim, quando k _{→ ∞}, µ_→0.

Observa¸cão 2.3.3 Dependendo da escolha deτ eσobtemos resultados teóricos e práticos com respeito à eficiência do método. Uma varia¸cão importante ocorre quando γk _< _1.

Neste caso utiliza-seµk ₌_σ(γk)2

n . Existem motiva¸c˜oes te´oricas que justificam esta escolha

[27].

2.4 M´

etodo de Pontos Interiores Barreira Logar´ıtmica

Descreveremos agora o método de pontos interiores barreira logar´ıtmica [3, 7] o qual utilizaremos para desenvolver o nosso método aplicado ao problema de regressão pela

norma Lp.

Seja o problema de programa¸c˜ao n˜ao linear:

min f(x)

sa g(x)_≤0

h(x) = 0

x_∈Ω.

Inserimos a variável de folga s uma vez que neste método trabalhamos apenas com restri¸cões de igualdade:

min f(x)

sa g(x) +s= 0

h(x) = 0

(25)

Agora, relaxamos a restri¸cãos_≥0 inserindo-a na fun¸cão objetivo através do parâmetro barreira µ, com µ_→0

minf(x)₋µ n

X

i=1

ln(si)

sa g(x) +s= 0

h(x) = 0.

A fun¸c˜ao Lagrangiana ´e dada por

L=f(x)₋µ n

X

i=1

ln(si) +πt(g(x) +s) +λth(x),

onde π eλ s˜ao os multiplicadores de Lagrange.

Aplicando as condi¸c˜oes de otimalidade, obtemos

∇L

|{z} =J(x,π,λ,s)

=          

∇f(x) +πt_∇_g₍_x_{) +}_λt_∇_h₍_x₎ g(x) +s

h(x)

Sπ           =           0 0 0 µe           . (2.8)

onde S ´e a matriz diagonal cujos elementos diagonais s˜ao os elementos de s.

Utilizando o m´etodo de Newton, chegamos a

         

∇2_f₍_x_{) +}_πt_∇2_g₍_x_{) +}_λt_∇2_h₍_x₎ _∇_g₍_x₎ _∇_h₍_x_{) 0}

∇g(x) 0 0 I

∇h(x) 0 0 0

0 S 0 π

                    dx dπ dλ ds           = =₋          

∇f(x) +πt_∇_g₍_x_{) +}_λt_∇_h₍_x₎ g(x) +s

h(x)

−µe+Sπ

(26)

Agora, calculamos os passos αp e αd, correspondentes as variáveis primais e duais respectivamente, onde s e π permane¸cam estritamente positivas. Os passos αp e αd são calculados a fim de preservarem a interioridade de todas as variáveis restritas do problema.

Sejam

ρp = min

dsi<0

−_dsisi

e

ρd= min

dπi<0

−_dπiπi

.

Assim, o passo α ´e dado por:

α= min_{1, τ ρp, τ ρd} (2.10)

Conhecendo as dire¸c˜oes e os passos, todas as vari´aveis do problema podem ser

atualizadas por:

xk+1 ₌_xk₊_αdx,

sk+1 ₌_sk₊_αds, _(2.11)

πk+1 ₌_πk₊_αdπ, λk+1 =λk+αdλ.

A atualiza¸cão do parâmetro barreira é dada por

µk+1 = µ

k

β , onde β >1. (2.12)

Resumimos agora o m´etodo barreira logar´ıtmica.

(27)

Dados xinterior, (s, π)>0, λ,µ e β >1. Para k=0,1,. . . , fa¸ca

Calcule o vetor gradiente da Lagrangiana (2.8). Calcule a matriz Hessiana e resolva o sistema (2.9). Calcule o passo α dado por (2.10).

Atualize as vari´aveis (x, s, π, λ) e o parˆametro barreiraµdados por (2.11) e (2.12) respectivamente.

At´e convergir.

2.4.1 Crit´

erio de Convergˆ

encia

O critério de convergência é dado por:

k∇L_k< ǫ,

onde _∇L´e dado por (2.8).

2.4.2 Inicializa¸

c˜

ao

Considere o problema original na forma

minf(x)₋µXln(s) sag(x) +s = 0

h(x) = 0.

Inicialize o vetor x, as variáveis de folga s > 0 tal que g(x) + s = 0, o parâmetro barreira µ, o parâmetro β e os multiplicadores de Lagrange, onde π =µS−1_e_{. Escolha o}

(28)

2.5 M´

etodo de Pontos Interiores Barreira Logar´ıtmica

Preditor-Corretor

Descreveremos agora o m´etodo de pontos interiores barreira logar´ıtmica

preditor-corretor [4] o qual tamb´em utilizaremos para desenvolver o m´etodo aplicado ao problema

de regress˜ao pela norma Lp.

Nos m´etodos de pontos interiores, resolvemos um sistema n˜ao linear dado pelas

condi¸c˜oes de otimalidade e este sistema pode ser resolvido pelo m´etodo de Newton. O

método de Newton possui uma dificuldade, ele garante apenas convergência local, isto é,

convergência a partir de um ponto inicial que está suficientemente próximo da solu¸cão.

Para ampliar a região de convergência dos métodos de pontos interiores é necessário

combiná-los com algum outro método que possua propriedades de convergência global

satisfat´orias.

Uma variante do m´etodo de Newton ´e dada por:

ˆ

xk =xk₋(_∇2f(xk))−1

∇f(xk)

xk+1 = ˆxk₋(_∇2f(xk))−1

∇f(ˆxk).

Dadoxk_{, um passo regular de Newton ´e realizado para obter ˆ}_xk _{e utilizando a mesma}

Hessiana obt´em-se xk+1 _{a partir de ˆ}_xk_{. Este m´etodo de Newton de dois passos quando}

aplicado às condi¸cões de otimalidade é conhecido como método preditor-corretor [4].

Temos que, no m´etodo barreira logar´ıtmica apenas os termos lineares de primeira

ordem s˜ao modelados. Agora, no m´etodo barreira logar´ıtmica preditor-corretor,

(29)

seguinte forma:          

∇2_f₍_x_{) +}_πt_∇2_g₍_x_{) +}_λt_∇2_h₍_x₎ _∇_g₍_x₎ _∇_h₍_x_{) 0}

∇g(x) 0 0 I

∇h(x) 0 0 0

0 S 0 π

                    dx dπ dλ ds           = =₋          

∇f(x) +πt_∇_g₍_x_{) +}_λt_∇_h₍_x₎ g(x) +s

h(x)

−µe+Sπ+dSdΠe

          (2.13)

onde dS e dΠ s˜ao matrizes diagonais cujos elementos s˜ao ds e dπ respectivamente.

No m´etodo barreira logar´ıtmica preditor-corretor, primeiramente tomamos um passo

afim em que o parâmetro barreira µ = 0. Então, o parâmetro barreira e os termos de segunda ordem podem ser obtidos a partir dos resultados do passo afim, e o lado direito

de (2.13) pode ser calculado.

A diferen¸ca fundamental entre o m´etodo barreira logar´ıtmica e o m´etodo barreira

logar´ıtmica preditor-corretor está na forma de calcular a dire¸cão de busca, que é obtida

resolvendo dois sistemas lineares em cada itera¸c˜ao, onde a matriz dos coeficientes ´e a

mesma e os lados direitos s˜ao distintos.

Resolvemos primeiro o sistema

         

∇2_f₍_x_{) +}_πt_∇2_g₍_x_{) +}_λt_∇2_h₍_x₎ _∇_g₍_x₎ _∇_h₍_x_{) 0}

∇g(x) 0 0 I

∇h(x) 0 0 0

0 S 0 π

         

| {z }

(30)

=₋          

∇f(x) +πt_∇_g₍_x_{) +}_λt_∇_h₍_x₎ g(x) +s

h(x)

Sπ           (2.14)

que equivale ao sistema linear (2.9) com µ= 0.

Agora, resolvemos o segundo sistema linear

         

∇2_f₍_x_{) +}_πt_∇2_g₍_x_{) +}_λt_∇2_h₍_x₎ _∇_g₍_x₎ _∇_h₍_x_{) 0}

∇g(x) 0 0 I

∇h(x) 0 0 0

0 S 0 π

         

| {z }

W           dx dπ dλ ds           = =₋          

∇f(x) +πt_∇_g₍_x_{) +}_λt_∇_h₍_x₎ g(x) +s

h(x)

−µe+Sπ+ ¯dSd¯Πe

          . (2.15)

Podemos observar que temos a mesma matriz nos dois sistemas lineares. A diferen¸ca

entre eles est´a apenas no vetor do lado direito, ou seja, a presen¸ca do termo n˜ao linear ¯

dSd¯Π e do parâmetro barreira µ. Assim, a fatora¸cão da matriz W do sistema (2.14) não é afetada em (2.15).

O método barreira logar´ıtmica preditor-corretor reduz o número de itera¸cões em

rela¸c˜ao ao m´etodo barreira logar´ıtmica, mas exige que dois sistemas lineares sejam

re-solvidos em cada itera¸c˜ao. No entanto, como a matriz ´e a mesma nestes dois sistemas, os

cálculos utilizados para a decomposi¸cão são efetuados uma única vez.

O cálculo dos passos primais e duais, αp e αd respectivamente, assim como a atu-aliza¸cão das variáveis são equivalentes aos apresentados na se¸cão anterior para o método

(31)

Descreveremos agora um resumo do m´etodo barreira logar´ıtmica preditor-corretor.

M´etodo barreira logar´ıtmica preditor-corretor

Dados xinterior, (s, π)>0, λ,β >1. Para k=0,1,. . . , fa¸ca

Resolva o sistema (2.14).

Entre com o parâmetro barreira µe as corre¸cões não lineares. Resolva o sistema (2.15).

Calcule o passo α dado por (2.10).

Atualize as vari´aveis (x, s, π, λ) e o parˆametro barreiraµdados por (2.11) e (2.12) respectivamente.

At´e convergir.

(32)

Cap´ıtulo 3

O Problema de Regress˜

ao

_L

_p

Apresentamos neste cap´ıtulo o problema de regressãoLp e o método proposto em [13] com o objetivo de compararmos com os métodos de pontos interiores que desenvolvemos

para o mesmo problema.

3.1 O Problema de Regress˜

ao pela Norma

_Lp

O problema de regress˜ao

min

x∈IRm kAx−bk

p

p (3.1)

onde A = [a1, . . . , an] ∈ IRm×n, b ∈ IRn e n > m, tem in´umeras aplica¸c˜oes em diversas

áreas de ciências e engenharias. As normas mais utilizadas são as normas L1, L2 e L∞. A

normaL2 ´e muito popular entre outros motivos por permitir uma solu¸c˜ao direta. Por sua

vez a norma L1 permite diminuir o efeito de pontos discrepantes enquanto que a norma

L∞ garante prote¸c˜ao contra o pior caso. Os dois ´ultimos problemas podem ser

formula-dos por programa¸c˜ao linear e os m´etoformula-dos de pontos interiores aplicaformula-dos a estes problemas

permitem a explora¸c˜ao da estrutura matricial do problema de forma bastante eficiente

[20, 21].

O problema é teoricamente interessante, pois é uma extensão de um problema de

(33)

diferenciável de 1a _{ordem (mas não diferenciável de 2}a _{ordem) quando 1} _{< p <} _{2 e até}

um problema diferenci´avel de 2a _{ordem quando} _p_{= 2.}

O objetivo deste trabalho consiste na aplica¸c˜ao de m´etodos de pontos interiores ao

problema de regress˜ao Lp

minimize _kr_kp_p (3.2)

sujeito a Ax+r=b,

onde 1< p <2.

Este problema pode combinar as propriedades de regress˜ao das normas 1 e 2 de forma

apropriada para cada aplica¸c˜ao.

Definindo r=u₋v, u_≥0 e v _≥0, podemos reescrever o problema (3.2) da seguinte forma:

minimize

n

X

i=1

(ui+vi)p (3.3)

sujeito a Ax+u₋v =b, (u, v)_≥0.

Ao transformarmos o valor absoluto em diferen¸ca de vari´aveis n˜ao negativas, _kr_kp_p =

n

X

i=1

|ui₋vi_|p, temos que incluir a restri¸c˜aoU V e = 0. No entanto, essa restri¸c˜ao pode ser ignorada se fizermos _kr_kp_p =

n

X

i=1

|ui₋vi_|p =

n

X

i=1

(ui+vi)p, pois sempre existe um ponto fact´ıvel com valor da fun¸c˜ao objetivo menor ou igual tal que ui = 0 ou vi = 0 para

i = 1, . . . , n, ou seja, U V e = 0 ´e verificado na otimalidade. Por exemplo, dados os vetores u e v, calculamos o m´ınimo e o m´aximo de seus elementos (m1 = min(u, v) e

m2 =max(u, v) respectivamente). Logo ap´os, calculamos a diferen¸ca entre eles, ou seja,

m2−m1 e assim teremos um vetor da diferen¸ca e um vetor nulo.

(34)

p = 1 temos exatamente o modelo de regress˜ao L1 resultando em um problema de

otimiza¸c˜ao linear.

3.2 M´

etodos Pr´

e-Existentes

3.2.1 M´

etodos de Relaxa¸

c˜

ao por Coluna para o problema de

norma m´ınima

O método desenvolvido em [8] é um método de relaxa¸cão de coluna para calcular a

solu¸cão da norma Lp de um sistema de equa¸cões lineares inconsistentes. Aten¸cões

especi-ais s˜ao dadas em cada um dos casos: p= 1, 1< p <2, 2< p <_∞ e p=_∞.

Neste artigo, é assumido que o sistema linear Ax = b é inconsistente e que a ma-triz Aé grande, esparsa e desestruturada. Neste caso, geralmente os elementos não nulos de A são armazenados por linha, depois de uma ordena¸cão por linha, ou por coluna, de-pois de uma ordena¸cão por coluna. Consequentemente, é conveniente resolver o problema

por um método de relaxa¸cão por linha ou por um método de relaxa¸cão por coluna. A

itera¸cão básica de um esquema de uma relaxa¸cão por linha (coluna) é percorrer as linhas

(colunas) de A.

Este artigo concentra-se no método de relaxa¸cão por coluna. A itera¸cão básica de

cada método é composta de n passos. No j-ésimo passo, para j = 1,2, . . . , n, somente

xj é modificado na tentativa de reduzir o valor da fun¸cão objetivo, enquanto todas as outras variáveis são mantidas fixas. Utiliza-se o método de relaxa¸cão de Gauss-Seidel

para resolver a equa¸c˜ao normal At_Ax₌_At_b_.

A situa¸cão é mais complicada quando 1 < p < 2. Neste caso, a segunda derivada de F(x) = _kAx₋b_kp não é definida nos pontos onde o vetor residual Ax−b tem

(35)

aproxima¸c˜ao hiperb´olica da forma

H(x) =

(_m X

i=1 h

(at_ix₋bi)2 +ǫ2ip/2

)1/p ,

onde at

i denota a i-´esima linha de A eǫ ´e uma constante positiva.

N˜ao realizamos experimentos computacionais com este m´etodo uma vez que somente

uma variável é atualizada a cada itera¸cão, devendo convergir muito lentamente. O artigo

[8] n˜ao apresenta resultados num´ericos.

3.2.2 M´

etodo GNCS

Vamos agora descrever o m´etodo desenvolvido em [13] para o problema de regress˜ao

pela norma Lp como segue. O método, referido como GNCS, é um método de Newton globalizado que usa as condi¸cões de folgas complementares para o problema da normaLp. O conteúdo e as nota¸cões desta se¸cão estão de acordo com o artigo [13], com exce¸cão da

utiliza¸c˜ao da matriz A no lugar de At_.

Considere o problema de regress˜ao (3.1). Sejam r o vetor residual r = Ax₋ b e

σ = sgn(r) o seu sinal. A fun¸c˜ao objetivo ´e denotada em termos de r por φ(r) = _kr_kp_p

(= ψ(x)) e o gradiente _∇φ(r), quando ele existe, ´e denotado por g =p(_|r_|)p−1

σ.

Para 1 < p < 2, o método tradicional para resolver (3.1) é o método (IRLS) iter-ativo de quadrados m´ınimos [17]. As dire¸cões de descida utilizadas por este método são

derivadas da equa¸cão não linear ψ(x) = 0. Esta é a condi¸cão de otimalidade para (3.1) quando 1 < p < 2 mas não quando p = 1. Quando p = 1 o progresso torna-se lento ao longo da dire¸cão de descida, pois não tentamos satisfazer as condi¸cões de otimalidade

diretamente e, portanto, acredita-se que esta ´e a causa do desempenho insatisfat´orio do

(36)

em [13] que o GNCS é mais rápido que o tradicional método IRLS quando pé quase ou igual a 1.

Em [13] tamb´em ´e apresentado um procedimento de busca linear que explora a

es-trutura da fun¸cão objetivo e impede res´ıduo nulo em cada itera¸cão. O método GNCS

apresenta-se melhor que o m´etodo IRLS e se reduz ao m´etodo de Coleman e Li [6] quando

p= 1.

Sabemos que a norma Lp ´e diferenci´avel e estritamente convexa para 1 < p < _∞

desde que A tenha posto completo. Ent˜ao, a solu¸c˜ao ocorre no ponto onde o gradiente

∇ψ(x) = At_g _{´e nulo. Supomos que existe um ponto com} _ri ₆_{= 0, 1} _≤ _i _≤ _n_{. Isto ´e}

equivalente a

At₍_D₎−2_r_{= 0}_, _(3.4)

onde D = diag(_|r_|)(2−p)/2_{, pois (3}_._{4) ´e a equa¸c˜ao normal para o seguinte sistema de}

quadrados m´ınimos:

(D)−1_Ax_{= (}_D₎−1_b.

Suponhamos que as linhas da matriz Z constituem uma base para o espa¸co nulo de

A, isto ´e, At_Z _{= 0. Podemos escrever (3}_._{4) da seguinte forma equivalente}

g₋Ztw= 0. (3.5)

O número de equa¸cões é n, que é equivalente ao número de variáveis (x, w) (note que x_∈IRm _e _w_∈_IRn−m_).

Seja Dk

r =diag

rk

e denote λk₌_Zt_wk_{. Temos que}

g₋Zt_w₌_p₍_|_r_|₎p−1₋_Zt_w₌_p₍_|_Ax₋_b_|₎p−1₋_Zt_w_{= 0}_.

Derivando em rela¸c˜ao a (x, w),

p(p₋1)(_|Ax₋b_|)p−2_A

(37)

Assim, para qualquer ponto (xk_{, w}k_{) o passo de Newton para a equa¸c˜ao acima ´e}

definido por

p(p₋1)diag rk

p−2

A,₋Zt h_dxk_{, dw}kit ₌₋h_gk₋_λki _(3.6)

⇒At₍_p₋₁₎_diag rk

−1

diag

p rk

p−1

Adx=AtZdw

| {z } =0

−At_gk₊_At_λk

| {z } =0

.

Assim, a dire¸cão de Newton para a variável xé

dxk=₋ 1

p₋1

AtD_rk−1diag gk

A

−1

Atgk.

Agora, condideramos o seguinte sistema n˜ao linear de equa¸c˜oes

Dr(g₋Ztw) = 0. (3.7)

Quando p = 1 esta é a condi¸cão de folga complementar para uma solu¸cão e λ é o vetor multiplicador dual. Quando 1< p <2, (3.7) é a condi¸cão de otimalidade para (3.1) se Dr é não singular.

Como a solu¸cão para (3.5) é sempre uma solu¸cão para (3.7) e uma solu¸cão para (3.7) é uma solu¸cão para (3.5) se para qualquer ri = 0, λi = 0, podemos calcular uma solu¸cão de (3.1) satisfazendo (3.7) e a condi¸cão λi = 0 se ri = 0.

(38)

Supomos agora que o Jacobiano de Dr(g ₋Zt_w_{) existe para (}_xk_{, w}k_{) e ´e n˜ao}

sin-gular. Seja

Dk_λ =diagpσk._∗gk₋σk._∗λk

onde ._∗´e a nota¸c˜ao do Matlab que representa o produto dos componentes dos vetores.

Temos que

Dr(g₋Ztw) =diag rk

h

p(_|Ax₋b_|)p−1

−Ztwi.

Derivando Dr(g₋Zt_w_{) com rela¸c˜ao a (}_xk_{, w}k_{), obtemos}

h

p(_|Ax₋b_|)p−1

−Zt_wi_A₊_diag rk

p(p−1)diag rk

p−2

A₋Zt

⇒ p rk

p−1

−λ

A+diag rk

(p−1)diag p rk

p−1

diag rk −1

A₋Zt

⇒hgk₋_λ₊_diag_gk₍_p₋₁₎i_A₋_Dk rZt

⇒diaggkp₋gk+gk₋λ

| {z }

=Dk λ

A₋Dk rZt.

Ent˜ao o passo de Newton para (3.7) ´e definido por

h

DλkA,−DkrZt

i h

dxk, dwkit =₋hDkr

gk₋λki (3.8)

⇒Dk

λAdxk−DrkZtdwk−Dkrλk =−Dkrgk

⇒At_Dk

λAdxk−AtDkr(Ztdwk+λk)

| {z } =0

=₋At_Dk rgk.

Daqui obtemos

At_Dk r

−1

Dk

λAdxk =−Atgk, (3.9)

ou, equivalentemente,

dxk =₋

AtD_rk−1Dk_λA

−1

Atgk. (3.10)

Foi demonstrado em [6] que, quando p = 1, At₍_Dr₎−1

(39)

vizinhan¸ca da solu¸cão, sob algumas hipóteses não degeneradas.

Consideremos o caso em que 1 < p < 2. Se não há res´ıduo nulo na solu¸cão, isto é, _|r∗

| > 0, (D∗

r)

−1

D∗

λ ´e definida positiva desde que D

∗

λ = (p−1)diag(|g

∗

|) e supomos que A tem posto completo. Assim At_Dk

r

−1

Dk

λA tamb´em ´e definida positiva quando

xk_{, w}k_{aproxima-se de (}_x∗

, w∗

). Portanto a dire¸c˜ao de Newtondxk _{torna-se uma dire¸c˜ao}

de descida para ψ(x) na vizinhan¸ca da solu¸c˜ao.

Se existe algum r∗

i = 0, a matriz Jacobiana de (3.7) ´e singular na solu¸c˜ao quando

1< p < 2 porque g∗

i =λ

∗

i = 0. No entanto, nesses pontos a matriz Jacobiana do sistema

original (3.4) também não existe. Portanto, este problema não surge quando consideramos (3.7) no lugar de (3.5). Se existe um res´ıduo nulo na solu¸cãox∗

´e dif´ıcil obter convergˆencia

quadrática, então obtemos a convergência linear.

J´a que At_Dk r

−1

Dk

λA n˜ao pode ser definida positiva distante de uma solu¸c˜ao, a

globaliza¸cão do passo de Newton (3.9) é necessária.

Para p = 1 em [6], o m´etodo de Newton ´e globalizado definindo uma matriz di-agonal Dk

θ tal que At

Dk r

−1

Dk

θA muda deAt

Dk r

−1

Apara At_Dk r

−1

Dk

λA pr´oximo a

uma solu¸c˜ao e substituindo Dk

λ porDθk quando a dire¸c˜ao ´e calculada por (3.8).

Assim, o passo pode ser considerado como solu¸c˜ao da seguinte equa¸c˜ao

h

D_θkA,₋Dk_rZti hdxk, dwkit =₋Dk_rgk₋λk. (3.11) Portanto,

dxk =₋

AtD_rk−1Dk_θA

−1

Atgk. (3.12)

(40)

onde Dk

λ =diag(gk−λk).

Portanto, θk _{mede a satisfa¸c˜ao da condi¸c˜ao de folga complementar e a viabilidade}

dual do problema da norma L1

θk= η

k

γ+ηk, (3.14)

onde ηk _{= max}

(

max

(

|Dk

r(gk−λk)| φ(r0₎

)

,maxnmaxn_|λk_{| − |}gk_|,0oo

)

e 0 < γ < 1 (na

implementa¸cão γ = 0.99), ou seja, ηk _{é o máximo da viola¸cão da condi¸cão de folga}

com-plementar (Dr(g₋λ) = 0) e da viabilidade dual (_|λ_{| ≤ |}g_|). Note que_|g_|=_|p(_|r_|)p−1_|₌_e

quando p = 1. Neste caso, θ = 0 (ou η = 0) é uma condi¸cão de otimalidade necessária e suficiente (para uma discussão mais detalhada veja [6]).

Agora consideramos o caso em que 1 < p < 2. Sabemos que a dire¸cão definida pelo método IRLS leva a convergência global, então definimos uma matriz diagonal Dθ

tal que a dire¸cão obtida trocando Dλ por Dθ seja a mesma dire¸cão do método IRLS e que localmente converge para Dλ. Assim,Dθ é uma matriz diagonal cuja diagonal é uma

combina¸c˜ao convexa dos componentes de diag(pgk_{) e} _Dλ_. Dk_θ =

diag(θk)diag

pσkgk+diage₋θkDk_λ

(3.15)

= diag pgk−

e₋θk._∗λk

.

e

θk=ηke./γ gk

+ηke

, (3.16)

onde 0< γ <1, et_{= [1}_{, . . . ,}_1]_∈_IRn _{e o escalar}_ηk _{´e definido em (3}_._14).

Quando p= 1, (3.15) ´e igual ao definido em (3.13) e portanto Dk

θ definido por (3.16)

é equivalente ao definido por (3.14). Além disso,xé ótimo se e somente se existeλ=Zt_w

tal que η = 0.

A matriz diagonal Dk

(41)

Lema 3.2.1 Suponha 0< γ < 1. Seja Dk

θ definido por(3.15). Ent˜ao Dθk satisfaz

(p₋1)diag gk ≤ Dkθ

≤(p+ 1)diag gk . (3.17)

Demonstra¸c˜ao: Pela defini¸c˜ao (3.15)

Dk_θ =diag pgk−

e₋θk._∗λk

.

Da defini¸c˜ao de θ (3.16)

ηk_e₋_θk₌_γθk_._∗ gk ⇒ λk − gk

._∗e₋θk_≤_γθk_._∗ gk . Assim, λk ≤ gk +γ

θk._∗ gk

./e₋θk

≤ e₋θk._∗ gk

+γθk.∗ gk

./e₋θk

≤ e₋(1₋γ)θk._∗gk./e₋θk.

Portanto,

(p₋1)diag gk ≤ Dkθ

≤(p+ 1)diag gk . •

Definimos τk _{como sendo}

τk = max τ,1₋ η

k γ+ηk

!

(3.18)

com o objetivo de incluir uma medida de otimalidade para p= 1. Note que, quandonηko

converge para zero, nτko _{converge para um. Quando} _p _{= 1 o procedimento da busca}

linear para GNCS ´e equivalente ao usado em [6].

Para IRLS ˇαk _{´e uma constante} _p₋_{1. Para GNCS com} _dk _{definido por (3}_._{12), ˇ}_αk

(42)

Lema 3.2.2 Supomos dk ₌ _Adxk_{, onde} _dxk _{´e definido por} ₍₃_._{12). Ent˜}_{ao o tamanho do}

passo αˇk _{definido por}

ˇ

αk=₋ g

kt_dk

dkt_diag₍_p₍_|_rk_|₎p−2₎_dk (3.19)

satisfaz

p₋1_≤αˇk _≤p+ 1.

Demonstra¸c˜ao: De (3.12),

dxk₌₋_At_Dk r

−1

Dk θA

−1

At_gk _⇒_At_Dk r

−1

Dk

θAdxk =−Atgk

⇒gk₌₋_Dk r

−1

Dk

θAdxk ⇒gk =−

Dk r

−1

Dk θdk.

Assim,

ˇ

αk=₋ d

kt_Dk r

−1

Dk θdk dkt_diag₍_p₍_|_rk_|₎p−2₎_dk

De (3.17),

(p₋1)d

kt_Dk r −1 diag gk dk dkt_diag₍_p₍_|_rk_|₎p−2₎_dk ≤αˇ

k

≤(p+ 1)d

kt_Dk r −1 diag gk dk dkt_diag₍_p₍_|_rk_|₎p−2₎_dk .

Logo,

p₋1_≤αˇk _≤p+ 1.

•

Computacionalmente, em vez de resolver um sistema linearn_×n(3.11) para calcular (dxk_{, dw}k_{), pode-se preferir calcular} _dxk _{resolvendo o problema de quadrados m´ınimos} n_×m

(Dk)−1_Adxk ₌

−Dkgk,

onde Dk ₌_Dk r

Dk θ

−11/2

. Portanto,         

At_Dk−2_r_{= 0}_,

At_Dk−2_Adxk ₌₋_At_Dk_gk_, dk₌_Adxk_.

(43)

Uma vez que dk₌_Adxk _{´e calculado,} _λ _{pode ser atualizado por}

λk+1 _←D_rk−1Dk_θdk+gk. (3.21)

O m´etodo GNCS pode ser resumido como segue.

Dado o ponto inicial r0 ₌_Ax0₋_b _com _|_r0_|_>_{0 e} _λ0_.

Passo1: Calcular θk _{por (3}_._{16) e} _gk ₌_p₍_|_rk_|₎p−1_σk_.

Sejam Dk

r =diag

rk

, Dk

θ =diag

pgk−

e₋θk_._∗_λk

.

Defina Dk _{= (}_Dk r(Dkθ)

−1₎1/2_;

Passo2: Calcule a dire¸c˜aodk _por

          

At_Dk−2_r_{= 0}_,

AtDk−2Adxk=₋AtDkgk, dk₌_Adxk_;

Atualize λk+1_:

λk+1 _←Drk

−1

Dkθdk+gk.

Passo3: Calculeτk _{por (3}_._18).

Use o procedimento de busca linear descrito a seguir.

Atualize rk+1 _←_rk₊_αk_dk_, _k_←_k_{+ 1.}

V´a para o passo 1.

Observa¸cão 3.2.1 A desvantagem deste método é que a busca linear é cara.

(44)

Dados τk_, _βf _∈₍₀_,_1), _dk_, _rk_{, ˇ}_αk_,_ρb _>_{0 (p.ex. 10}6_{) e} _αk

i definido por =

(

α_ik:αk_i =₋r

k i dk

i

, rk_idk_i <0

)

.

Passo1: Sejaαk

∗ = min(r

k₊_αk

idk) comg(rk+αk∗d

k₎t_dk _≥_{0. Se}

φ(rk+1)_≤φ(rk) +βfαk_∇φ(rk)tdk, (3.22) onde rk+1 ₌_rk₊_αk_dk _{´e satisfeito com} _αk

∗, sejaα

k

#←max n

αk

i : 0≤αki < αk∗

o

e defina

αk _←αk_#+τk(αk∗ −α

k

#)

e retorna; caso contr´ario, continua;

Passo 2: Se (3.22) não é satisfeito com αk_{= 1, vá para o passo 3.}

Caso contr´ario, estabele¸ca

αk_←

  

1, se min

rk+dk >0; αk

#+τk(1−αk#), caso contr´ario,

onde αk

# ←max n

αk

i : 0≤αki <1

o

, retorna;

Passo 3: Seja

αk _←

  

ˇ

αk_, _{se min}

rk+ ˇαkdk >0; αk

#+τk(ˇαk−αk#), caso contr´ario,

onde αk

# ←max n

αk

i : 0≤αki <αˇk

o

, retorna.

Crit´erio de Convergˆencia

O critério de convergência utilizado em [13] é dado por:

|φ(rk+1₎₋_φ₍_rk₎_|

φ(rk+1₎ < ǫ ou η

k_{< ǫ.} _(3.23)

(45)

nossos métodos de pontos interiores de uma forma mais eficiente, o critério de convergência

utilizado neste trabalho ser´a dado por:

Dkr(λk−g)

(46)

Cap´ıtulo 4

M´

etodos de Pontos Interiores

Aplicados ao Problema de Regress˜

ao

pela Norma

_L

_p

Neste cap´ıtulo, desenvolvemos uma fam´ılia de m´etodos de pontos interiores para o

problema de regressão Lp: o método barreira logar´ıtmica, o método primal-dual e a variante preditor-corretor.

4.1 M´

etodo Barreira Logar´ıtmica

O problema (3.3) tamb´em pode ser escrito como

min

n

X

i=1

(ui+vi)p (4.1)

sa Ax+u₋v₋b = 0, (u, v)_≥0.

A fun¸c˜ao objetivo ´e denotada em termos de u e v por φ(u, v) =

n

X

i=1

(ui+vi)p, o gradiente _∇φ(u, v) ´e denotado por

G=

  

Gu Gv

(47)

onde Gui =Gvi =p(ui+vi)

p−1 _e

∇2φ=

   ∇Gu ∇Gv   ,

onde _∇Guij = ∇Gvij =

    

p(p₋1)

(ui+vi)2−p, se i=j,

0, se i₆=j

´e uma matriz diagonal denotada por

G2.

Como temos um problema de otimiza¸cão não linear, usamos a forma padrão para

desenvolver um método de pontos interiores: aplicamos o método de Newton às condi¸cões

de otimalidade. Assim, temos min n X i=1

(ui+vi)p₋µ n

X

i=1

ln (ui)₋µ n

X

i=1

ln (vi)

sa Ax+u₋v₋b= 0,

onde µ >0 ´e o parˆametro barreira (µ_→0).

A Lagrangiana ´e dada por

L=

n

X

i=1

(ui+vi)p₋µ n

X

i=1

ln (ui)₋µ n

X

i=1

ln (vi) +yt(Ax+u₋v₋b),

onde y ´e o multiplicador de Lagrange.

Aplicando as condi¸c˜oes de otimalidade, obtemos

∇L

|{z}

J(x,y,u,v)

=          

At_y Ax+u₋v₋b

(G₋µU−1 ₊_Y₎_e

(48)

Reescrevendo as duas ´ultimas equa¸c˜oes de (4.2),

∇L

|{z}

J(x,y,u,v)

=          

At_y Ax+u₋v₋b

U(G+Y)e V(G₋Y)e

          =           0 0 µe µe           .

Utilizando o M´etodo de Newton, chegamos a

         

0 At ₀ ₀

A 0 I ₋I

0 U G+Y +U G2 U G2

0 ₋V V G2 G−Y +V G2

                    dx dy du dv           =           r1 r2 r3 r4           , (4.3) onde

r1 = −Aty,

r2 = −Ax−u+v+b,

r3 = −U(G+Y)e+µe e

r4 = −V(G−Y)e+µe.

Resolvendo o sistema (4.3), obtemos as dire¸c˜oesdx, dy, du, dv. Assim, temos o sistema

Atdy=r1 (4.4)

Adx+du₋dv=r2 (4.5)

U dy+ [G+Y +U G2]du+U G2dv=r3 (4.6)

−V dy+V G2du+ [G−Y +V G2]dv=r4. (4.7)

Da Equa¸c˜ao (4.6),

U dy+ [G+Y +U G2]du+U G2dv=r3

⇒[G+Y +U G2]du=r3−U dy−U G2dv

⇒du= [G+Y +U G2]

−1