Caminhantes aleatórios com perfil de memória binomial

CENTRO DE CIÊNCIAS EXATAS E DA TERRA DEPARTAMENTO DE FÍSICA TEÓRICA E EXPERIMENTAL

PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA

C

AMINHANTES

A

LEATÓRIOS COM

P

ERFIL DE

M

EMÓRIA

B

INOMIAL

R

M

B

D

C

AMINHANTES

A

LEATÓRIOS COM

P

ERFIL DE

M

EMÓRIA

B

INOMIAL

Dissertação de Mestrado apresentada ao Programa de

Pós-Graduação em Física do Departamento de Física Teórica e

Expe-rimental da Universidade Federal do Rio Grande do Norte como

requisito parcial para a obtenção do grau deMestreem Física.

Orientador: Prof. Dr. João Medeiros de Araújo Co-orientador: Prof. Dr. Ananias Monteiro Mariz

Catalogação da Publicação na Fonte. UFRN / SISBI / Biblioteca Setorial Centro de Ciências Exatas e da Terra – CCET.

Diniz, Rebecca de Moura Braz.

Caminhantes aleatórios com perfil de memória binomial / Rebecca de Moura Braz Diniz. - Natal, 2016.

xi, 66 f.: il.

Orientador: Prof. Dr. João Medeiros de Araújo. Coorientador: Prof. Dr. Ananias Monteiro Mariz.

Dissertação (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciências Exatas e da Terra. Programa de Pós-Graduação em Física.

1. Física – Dissertação. 2. Caminhadas aleatórias – Dissertação. 3. Memória binomial – Dissertação. 3. Não-markovianos – Dissertação. 4. Expoente de Hurst – Dissertação. 5. Superdifusão – Dissertação. 6. Log-periodicidade – Dissertação. I. Araújo, João Medeiros de. II. Mariz, Ananias Monteiro. III. Título.

Minhas Raízes

José Carlos Braz Diniz Rosilene Maria de Moura Braz Diniz Filipe de Moura Braz Diniz

Meus Ramos

Agradeço primeiramente ao Deus todo poderoso do Universo, o qual tem me dado forças para tocar este trabalho em frente.

Aos meus pais Braz Diniz e Rose Diniz que sempre se sacrificaram para oferecer-me a oferecer-melhor educação. Ao oferecer-meu irmão Filipe Diniz por ser oferecer-meu espelho e ouvir oferecer-meus pensamentos. Ao meu amado esposo Roosevelt Gomes muito obrigada por me manter emocionalmente centrada nos objetivos da vida. Aos meus filhos do coração Arthur e Thomas.

A minha amiga Heloisa Onias, constante em minha vida. A meus amigos que de uma forma ou de outra me incentivaram no caminho da ciência.

Ao meu orientador Prof. João Medeiros de Araújo por me acolher nessa jor-nada com muita paciência e atenção, me norteando no campo da pesquisa. Ao meu co-orientador Prof. Ananias Monteiro Mariz pelas conrversas produtivas e valiososinsights. Ao Programa de Pós-Graduação em Física da Universidade Federal do Rio Grande do Norte, desde os funcionários de serviços gerais até o coordenador da pós-graduação por todo suporte fornecido.

Agradeço ao Prof. Marcos Costa, chefe do Laboratório de Microscopia do Instituto do Cérebro da UFRN, do qual sou funcionária, pela compreensão e apoio que facilitaram o empenho nessa empreitada.

Grande tem sido o interesse nas difusões anômalas, pois se apresentam nas mais diversas áreas do conhecimento. A introdução de perfil de memória no caminhante ale-atório torna-o numa dinâmica estocástica não-markoviana, cujas correlações temporais podem criar superdifusão, persistencia e log-periodicidade. Apresentamos uma revisão da literatura sobre os perfis de memória e introduzimos nosso modelo. O modelo de me-mória binomial pode selecionar diferentes regiões de perda de meme-mória, desde a inicial até a recente. Dessa forma, investigamos o impacto da posição da perda de memória no comportamento superdifusivo do caminhante aleatório e unificamos muitos dos resulta-dos da literatura. Obtivemos que memórias iniciais geram maior superdifusão medidas pelo coeficiente de Hurst, enquanto que memórias recentes tendem a diminuir a superdi-fusão, tornando mais caminhantes adeptos da difusão normal. Também investigamos o regime de memória curta inicial, com desvio padrão tendendo a zero. Observamos log-periodicidade para alguns caminhantes sugerindo regimes diferentes de comportamento log-periódico, incluindo aqueles considerados de difusão normal. Uma particularidade do modelo binomial são os resutados extremamente simétricos para o diagramaHxr.

Palavras-chave: Caminhadas Aleatórias, Memória Binomial, Não-markovianos, Expoente de Hurst, Superdifusão, Log-periodicidade.

Great has been the interest in anomalous diffusion because they are present in se-veral areas of knowledge. The introduction of a memory profile in random walk environ-ment give them a non-Markovian stochastic dynamics, whose temporal correlations may create superdiffusion, persistence and log-periodicity. We present an overview of memory profile literature and introduce our model. The binomial memory model can select diffe-rent memory loss regions, from the old to the recent one. Thus, we investigate the impact of memory loss location on superdiffusive behavior of a random walker and unify some literature results. We verify that old memory generates higher superdiffusion measured by the Hurst coefficient, while recent memory tends to decrease superdiffusion, causing more walkers to undergo normal diffusion. We also investigate the short initial memory region, with zero tending standard deviation. We observe log-periodicity for some wal-kers suggesting different regions of log-periodic behavior, including those considered as normal diffusion. A particularity of the binomial model is an extremely symmetric result toHxrdiagram.

Keywords: Random Walk, Binomial Memory, Non-Markovian, Hurst Coefficient, Superdiffu-sion, Log-periodicity.

1.1 "A difusão cria desenhos abstratos belos e misteriosos- Microsoft, Temas do

Windows [1] Permissão de Uso em A. . . 2

2.1 Classificação da difusão pelo expoente de Hurst, adaptada de [2] . . . 8

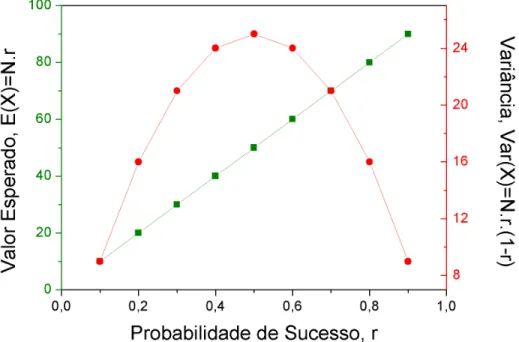
2.2 Valor Esperado e Variância de uma distribuição binomial com r variando de0,1a0,9, sendo o número totalN = 100constante. . . 11

2.3 Distribuição Binomial de 102 _{eventos com probabilidadervariando de0,1} a0,9. O valor esperado E(X)e a variânciaV ar(X)estão identificados em cada gráfico. . . 12

2.4 Distribuição Binomial para diferentes valores de Número totalN. . . 13

2.5 Esquema de caminhada aleatória unidimensional. . . 14

3.1 Perfil de Memória do Elefante para uma caminhada de 10 passos . . . 17

3.2 Resultados para o primeiro 3.2a e segundo momento 3.2b do perfil de me-mória do elefante em função do tempo. Vê-se uma mudança no comporta-mento do sistema parap > 3/4. . . 19

3.3 Difusão para o Elefante. O Expoente de Hurst apresenta região de superdi-fusão parap >3/4. [3] . . . 20

conservadores. Paraf = 1reduz-se ao caso do elefante. Adaptação de [4] . 22

3.5 Oscilações log-periódicas na posição média. Maiores são as amplitudes para baixos valores de p, com f fixo. Adaptado de[4] . . . 23

3.6 Expoente de Hurst num diagrama de fasefxpmostrando regiões de super-difusão log-periódica e super-difusão normal. Adaptado de [5] . . . 24

3.7 Perfil de Memória Alzheimer diluído pela sequência binária Thue-Morse paraf = 0.2numa caminhada de500passos. A sequência apresenta uma

diluição de50%. . . 26

3.8 Coeficiente de Hurst para o perfil de memória Alzheimer diluído pela sequência de Fibonacci dentro da fração f de memória lembrada.

Adap-tado de [6]. . . 27

3.9 Perfil de Memória Alzheimer diluído pela sequência de Fibonacci paraf = 0.2 numa caminhada de 500 passos. A sequência apresenta uma diluição

próxima de100%para longas caminhadas. . . 28

3.10 Perfil de memória gaussiano. Centrado sempre no meio da caminhada, e largura varia com o numero de passos.σ =σ0t. Reproduzido de [7] . . . 29

3.11 Coeficiente de Hurst para o perfil de memória gaussiano. Pequenas largu-ras originam superdifusão entre os reformadores. Reproduzido de [7] . . . 31

3.12 Log-peridiocidade para reformadores com perfil de memoria gaussiano. Reproduzido de [7] . . . 32

3.13 Perfil de Memória Exponencial. Quanto maior λ mais recente a memória

lembrada. . . 33

3.14 Coeficiente de Hurst para o perfil de memória recente exponencial. Quanto menos memória recente (λ grande) mais próximo do movimento

browni-ano. Reproduzido de [8] . . . 34

nas colunas. . . 38

4.2 Medida da difusão das caminhadas aleatórias com memória binomial atra-vés do Coeficiente de Hurst para diferentes posições de memória represen-tadas pelo parâmetrorda distribuição binomial . . . 41

4.3 Sobreposição espelhada do coeficiente de Hurst mostrando que existe uma simetria para reformadores (p < 0.5, espelhados em r′) e conservadores

(p >0.5emr). . . 42

4.4 Diferença percentual na simetria do Coeficiente de Hurst . . . 43

4.5 Investigando o comportamento do Coeficiente de Hurst versus tempo para um perfil de memória gaussiano próximo do ponto crítico. Em destaque no gráfico o aparecimento da superdifusão em reformadores. . . 44

4.6 Investigando o comportamento superdifusivo do perfil de memória bino-mial quandor_→0, através do Coeficiente de Hurst versus tempo. . . 46

4.7 Investigando o comportamento superdifusivo do perfil de memória bino-mial para feedback positivo em comparação com o caso da memória de elefante. . . 48

5.1 Escolha de conjunto(p, r)para investigar log-periodicidade. . . 50

5.2 Plot semi-log da posição versus tempo para os valores selecionados na fi-gura 5.1.Vê-se claramente em (a) um comportamento log-periódico e per-sistência induzida por amnésia parap= 0.1, r = 0.2. Em (b)p= 0.9, r = 0.2

alta persistencia e em destaque um comportamento periódico. Em (c)p = 0.1, r = 0.8e (d)p = 0.9, r = 0.8não vemos log-periodicidade como consta

na literatura para memória recente. . . 51

p = 0.9, r = 0.1 é mostrado normalizado por (a)1/t1/2 _{e (b)1/t}H_{. O estado}

p= 0.9, r = 0.2é mostrado normalizado por (c)1/t1/2 _{e (d)1/t}H_{. O}

compor-tamento periódico aparece apenas na normalização porH. . . 52

5.4 Plot log-log da posição quadrática para diferentes posições de memória. Vemos oscilação para valores de memória inicial. . . 53

5.5 Plot log-log da variância para diferentes valores de posição de memóriar.

parar = 0.2temos uma memória inicial. Parar= 0.8temos uma memória

recente. . . 53

5.6 Log-periodicidade para diversos valores de p para r pequeno. Ve-se que a amplitude do movimento cai com p. A log-periodicidade some e votla. . . 55

5.7 Posição do caminhante aleatório para r=0.6, flutuações atrapalham as osci-lações que desaparecem a medida que aumentap . . . 56

5.8 Regimes distintos para posição do caminhante aleatório para r=0.8 (memó-ria recente). . . 57

Agradecimentos i

Epígrafe ii

Resumo iii

Abstract iv

Lista de Figuras v

1 Introdução 1

2 Caminhantes Aleatórios 4

2.1 Difusao Normal e Difusão Anômala . . . 4

2.2 Modelos Estocásticos e Processos Não-Markovianos . . . 8

2.3 A Distrtibuição Binomial . . . 10

2.4 Caminhante Aleatório . . . 14

3 Caminhante Aleatório com Perfil de Memória 16

3.2 O Modelo de Memória Alzheimer . . . 20

3.2.1 O Modelo de Memória Alzheimer Diluído . . . 25

3.3 O Modelo de Memória Gaussiana . . . 28

3.4 O Modelo de Memória Exponencial . . . 32

3.5 Outros modelos . . . 34

4 Caminhante Aleatório com Perfil de Memória Binomial 36 4.1 O Modelo de Memória Binomial . . . 37

4.2 Métodos e Resultados . . . 39

4.2.1 Classificação da Difusão pelo Expoente de Hurst . . . 39

4.2.2 Diagrama de Fase no Regime0.1< r <0.8 . . . 40

4.2.3 O Modelo de Memória Gaussiana e o casor = 0.5 . . . 43

4.2.4 Diagrama de Fase no Regimer _→0 . . . 45

4.2.5 Diagrama de Fase para Feedback Positivo . . . 47

5 Análise da Log-periodicidade 49 5.1 Log-periodicidade no caminhante aleatório com memória binomial . . . 49

5.2 Log-periodicidade para perfis de memória inicial . . . 54

5.3 Log-periodicidade para perfis de memória recenter= 0.6er= 0.8 . . . 54

5.4 Considerações finais sobre Log-periodicidade . . . 57

6 Conclusões e Perspectivas 58 6.1 Principais resultados . . . 58

6.2 Perspectivas de futuro . . . 59

A Permissão de Uso de Imagem 64 A.1 Pacote de Temas do Windows [9] . . . 64

APÊNDICES 64

INTRODUÇÃO

A difusão pode ser vista como o movimento de um conjunto de partículas saindo, em geral, de um região de alta concentração para uma região de baixa concentração. Difu-são é, por exemplo, como uma gota concentrada de corante se dilui chegando a preencher todo um copo de água, ou como a fumaça que sai de uma chaminé desaparece na atmos-fera, ou como um enxame de abelhas sai à procura de flores, ou ainda como um montante de ações lançadas por uma empresa são vendidas e revendidas na bolsa de valores até estarem divididas entre vários acionistas.

O tema ”difusão” inspira desde trabalhos científicos até obras de arte como o recentemente lançado pacote de imagens gratuito para área de trabalho do computador; ”A difusão cria desenhos abstratos belos e misteriosos” afirma a empresa Microsoft como descrito na Figura 1.1.

Podemos olhar para o movimento macroscopicamente através da difusão ou abor-dar o problema investigando cada partícula e sua trajetória peculiar, cheia de idas e vindas aleatórias como proposto pelo modelo de caminhantes aleatórios.

Por muito tempo acreditou-se que era uma nova abordagem para o movimento browniano que explicava microscopicamente a difusão normal. Contudo é possível acres-centar um perfil de memória ao caminhante, transformando o problema numa dinâ-mica não-markoviana com difusão anômala que podemos medir através do coeficiente de Hurst.

Ao acrescentar um perfil de memória não uniforme, dizemos que o caminhante

Figura1.1: "A difusão cria desenhos abstratos belos e misteriosos- Microsoft, Temas do Windows [1] Permissão de Uso em A.

Neste trabalho estudamos um modelo capaz de selecionar a memória inicial, cen-tral ou recente com apenas um parâmetro; o modelo de memória binomial. Temos ainda outro parâmetro para tendência do caminhante de repetir a decisão lembrada. Esses dois parâmetros geram um ensemble de estados com dinâmicas difusivas ricas para discussão, e que conseguem unificar muitos dos resultados apresentados na literatura.

CAMINHANTES ALEATÓRIOS

Neste capitulo iremos revisar conceitos importantes para entender o trabalho como difusão normal e sua classificação pelo expoente de Hurst, modelos estocásticos e processos não-markovianos. Em seguida discutiremos conceitos estatísticos importantes para a distribuição binomial e faremos uma introdução às caminhadas aleatórias.

2.1 Difusao Normal e Difusão Anômala

Movimento Browniano refere-se ao que Robert Brown observou em 1827: grãos de pólen sobre um solvente viscoso descrevendo um movimento frenético e aleató-rio. Simplesmente não podiam repousar calmamente, eles "zigue-zagueavam", observou Brown. Percebeu ainda que ocorria para diversos tipos e tamanhos de partículas, inclusive inorgânicas, nas mais variadas viscosidades de solvente. Convencendo-se da natureza fí-sica do problema e não biológica, Brown lança uma teoria sugerindo uma abordagem molecular [15]. Naquela época, as teorias atomico-moleculares estavam mal estabelecidas e eram alvos de críticas entre o meio científico. Foi Einstein em seu ano miraculoso 1905 que explicou o movimento browniano usando a abordagem molecular.

Comumente, a equação da difusão é obtida através da equação diferencial para a conservação da massa,₋∂ρ/∂t=_{−∇ ·}~ J~, com a suposição de uma dependência linear do

fluxo com o gradiente de concentração,−J~=₋D_∇ρ, sendoDé o coeficiente de difusão. No caso em queDnão tem dependência espacial, temos assim a equação da difusão [16]:

∂ρ

∂t =D ~∇

2_{ρ (2.1)}

Einstein conseguiu obter a mesma equação de difusão considerando partículas ao invés de meios contínuos e assumindo que as partículas se movimentam de maneira ale-atória. A ideia consiste em supor que as partículas executem movimentos independentes e que os movimentos da mesma partícula em diferentes intervalos de tempo também se-jam processos mutuamente independentes. Dessa forma, Einstein mostra que a equação unidimensional de difusão para partículas é dada por:

∂n ∂t =D

∂2_n

∂x2 (2.2)

Sendon(x, t)é o número de partículas por unidade de volume. As deduções de Einstein tangenciam as relações modernas de Chapman-Kolmogorov, teorias de cadeias marko-vianas e até caminhantes aleatórios. De forma elegante, ele conclui que a posiçãoxdas

partículas em movimento browniano obedece à seguinte relação:

hx2_i= 2Dt (2.3)

Que veio a se tornar uma das mais famosas equações de Einstein pois, com a pre-cisão habitual da época, era possível observar o deslocamento quadrático no microscópio e ver a linearidade no tempo. Tal fato causou grande impacto no meio científico pois usando a mal estabelecida teoria atômico-molecular, foi possível concluir algo facilmente observável e mensurável [16]. Einstein também aponta que a solução da equação de di-fusão para a distribuição de partículas n(x, t) obedece a uma distribuição gaussiana ou

normal padrão:

n(x, t) = _√N0 4πDtexp

−x2

4Dt (2.4)

normal. Existem vários formalismos para abordar um sistema com difusão normal, como a teoria de Langevin que aborda o hamiltoniano do sistema, e a equação de Fokker-Plank deduzida das relações de Chapman-Kolmogorov para cadeias markovianas [17]. Todos os formalismos chegam ao mesmo resultado de dependência linear do desvio quadrático médio e distribuição gaussiana para as partículas.

Muitos fenômenos não podem ser descritos pelos formalismos acima. Por exem-plo, em 1926 Richardson [18] mostrou que as correntes turbulentas da atmosfera causam uma difusão com desvio quadrático não linear, de fato_h△x2_{i ∼ t}3_{, um comportamento}

super balístico. O deslocamento é mais rápido e não é proporcional ao tempo. Já em 1975 Scher e Montroll [19] estudaram o movimento de cargas num meio amorfo submetido a um campo elétrico. Essas cargas podem ficar presas nas imperfeições do meio por tempo indeterminado e depois serem liberadas por flutuações térmicas. Tal tendência cria um movimento mais lento do que o linearmente dependente do tempo mostrado por Einstein no movimento browniano. Foi então chamado de subdifusão.

Difusão anômala é toda difusão que não é normal. Uma possível classificação dos tipos de difusão pode ser a seguinte:_h△x2_{i ∼t}µ_{, ou mais precisamente:}

µ >1 _→ Superdifusão

µ= 1 _→ Difusão Normal (2.5)

0< µ <1 _→ Subdifusão

Outra classificação frequentemente usada e que abordaremos nesse trabalho foi feita por Harold Hurst quando estudava as enchentes do rio Nilo [20]. Inspirado na his-tória bíblica "sete anos de fartura e sete anos de penúria", Hurst procurou uma forma empírica de medir correlação em eventos aleatórios. Hurst lançava as bases para a criação de um modelo de auto-similaridade para correlação serial. Mandelbrot [21] solidificou o modelo para a estimativa do parâmetro H (em homenagem ao Hurst) através de uma aná-liseR/S (range cumulative rescaled divided by standard deviation). Esse método foi aplicado

atmosféri-cas, na variação do diâmetro dos fios da indústria textil [21], no fluxo de água dos rios [22], na frequência de terremotos da geofísica [23], no estudo de fractais [24], dentre outros.

O modelo de auto-similaridade diz que um processoX(t)na reta real é

autosimi-lar se ao mudar a escala temporal por um fatora >0, todas as distribuições de dimensões

finitas mudam por um fatoraH _{[21], preservando conservando suas propriedades}

estatís-ticas. Matematicamente temos uma função homogênea de grau H:

X(at)∼=aHX(t) (2.6)

Dessa importante propriedade segue a relação para a variância[21]:

hX(t)2_{i − h}X(t)_i2 _∝t2H (2.7)

SendoH é o coeficiente de Hurst. Note que no gráfico log-log da equação 2.7

ob-temos uma reta cuja inclinação é2H. Esse é exatamente o método utilizado neste trabalho

para medir o coeficiente de Hurst. Temos ainda que, no limite assintótico,< x2 _>≃t2H_{, o}

que tornaria mais simples a obtenção deH, contudo, conforme discutiremos no capítulo

4, preferimos a abordagem da variância.

Na Figura 2.1 vemos a classificação da difusão pelo coeficiente de Hurst, onde a inclinação da reta no gráfico log-log é2H. Basicamente consideramos os possíveis valores

deH:

1

2 < H <1 → Superdifusão

H = 1

2 → Difusão Normal (Movimento Browniano) (2.8)

0< H < 1

Figura2.1: Classificação da difusão pelo expoente de Hurst, adaptada de [2]

2.2 Modelos Estocásticos e Processos Não-Markovianos

Uma variávelX(t)é dita estocástica quando obedece a duas regras[25]:

• A cada instante de tempot, ela pode assumir um conjunto de valores.

• Existe uma probabilidadeP(X)associada a cada um dos valores do conjunto.

Note que não estamos no regime determinístico onde cada instante de tempo está associado a um único valor deX(t)por uma lei de movimento bem conhecida. Se X(t)

Por outro lado, em um processo estocástico, as leis do movimento são dadas por probabilidades para um conjunto de valores. O que faz a partícula decidir por um dos valores é tratado como probabilidade, e a variável é dita aleatória. É impossível prever onde a partícula estará em determinado instante, é possível apenas dizer qual a chance dela estar em determinado lugar. Comumente as probabilidades dos estados são obtidas por frequências após a realização de vários eventos e médias.

Uma propriedade importante de uma variável estocástica é ser contínua se seu conjunto de valores for descrito por funções contínuas como, por exemplo, a velocidade de uma partícula em movimento browniano. Ou a variável estocástica pode ser discreta se seu conjunto de valores for enumerável, por exemplo o número de moléculas que reagem em uma mistura.

Outra propriedade é como a distribuição de probabilidade dos possíveis estados se comporta dependendo do estado atual. SejaXt a posição atual de uma partícula que

teve a seguinte sequencia de posições anteriores:

X0, X1, X2, ..., Xt−1, Xt (2.9)

Num processo markoviano, a probabilidade de um estado futuro Xt+1 depende

apenas do estado atual, independente de seus estados anteriores. Matematicamente po-demos descrever um processo markoviano por probabilidades condicionais [26], sejaium

estado atual ej o estado futuro, temos a seguinte relação:

P(Xt+1 =j|Xt=i, Xt−1 =it−1, ..., X0 =i0) = P(Xt+1 =j|Xt=i) = pij (2.10)

Portanto, a probabilidade da partícula ir para o estadoXt+1 =j condicionado ao

conjunto de estados anteriores da equação 2.9 é igual a probabilidade de ir para o estado

Xt+1 = j condicionado apenas ao estado atual Xt = i. Para uma análise aprofundada

os processos markovianos são conhecidos por não apresentarem memória ou apresenta-rem memória de curto alcance, pois os estados anteriores não são relevantes para o estado futuro[27].

De forma análoga, um processo não-markoviano é um processo que tem memória, onde o estado futuro depende dos estados por onde a partícula esteve. No capitulo 3 descreveremos a literatura sobre caminhantes aleatórios com memória, pois o processo não markoviano é fundamental neste trabalho.

2.3 A Distrtibuição Binomial

A distribuição binomial tem seu nome devido as duas possibilidades que um evento pode assumir (direita ou esquerda, sucesso ou fracasso, sim ou nao). Cada ten-tativa é independente das demais; A probabilidade de sucessor a cada tentativa

perma-nece constante e independente das demais[28]; Dessa forma, a probabilidade binomial do número de sucessosk numa sequência deN tentativas é dada por:

P(k) =

N k

rk(1₋r)N−k_{, (2.11)}

Sendo N k

é a combinação do número total de eventos e do número de sucessosk,

er é a probabilidade de sucesso. Comumente é usada a notaçãop, q para essa

probabili-dade contudo, quando apresentarmos o modelo de memória binomial para o caminhante aleatório, usaremosp, qpara representar outras variáveis. Portanto estamos apresentando

agora a probabilidade binomial com a terminologiar, spara probabilidade de sucesso.

Sendo X uma variável aleatória binomialmente distribuída, o valor esperado é

dado por:

E(X) = N r , (2.12)

distribui-ções centradas em diferentes posidistribui-ções, já no caso de número total variável, a medida em queN aumenta, o centro se desloca para valores maiores deX. Se quisermos investigar a

largura (2σ) da distribuição vejamos a variância dada por:

V ar(X) =σ2 =N r(1₋r), (2.13)

Notamos que, assim como o valor esperado, a variância também depende do nú-mero totalN e a probabilidade de sucessor. Diferente da função gaussiana explanada na sessão 3.3, a largura da distribuição não é um parâmetro livre, é determinada pela escolha deN e r. Na figura 2.2 temos os valores esperados e variâncias para uma distribuição

deN = 102 _{eventos com probabilidader variando de 0,1a 0,9. Vemos mais claramente}

que o parâmetro r está associado a posição central da distribuição, a medida que r

au-menta temos um aumento linear do Valor Esperado. Percebemos ainda que a Variância é simétrica em relação ar = 0.5, sendo mais larga nessa região central e mais estreita nas

estremidades (rpróximo de0e de1).

A fim de melhor entender como a distribuição binomial depende deN er,

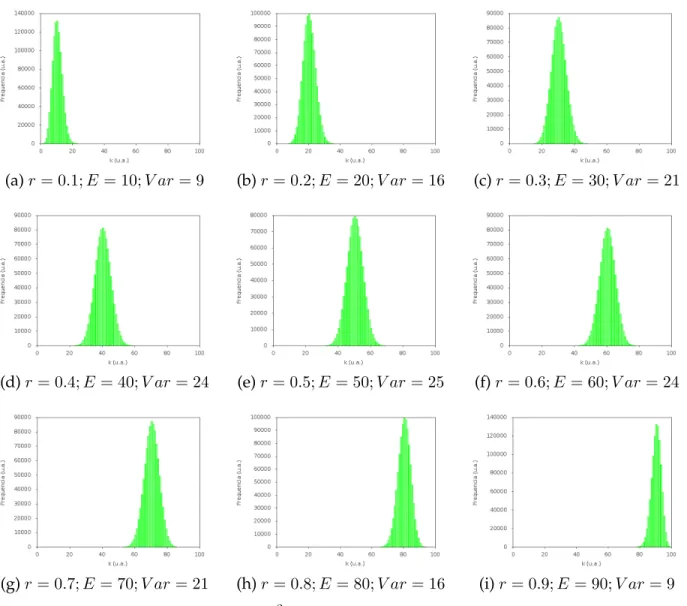
pode-mos observar a influência der pelo gráfico 2.3, no qual temos a mesma distribuição de N = 102_{eventos com probabilidadervariando de0,1em 2.3a a0,9em 2.3i.}

(a)r= 0.1;E= 10;V ar= 9 (b)r = 0.2;E = 20;V ar= 16 (c)r = 0.3;E = 30;V ar= 21

(d)r= 0.4;E = 40;V ar= 24 (e)r= 0.5;E = 50;V ar= 25 (f)r= 0.6;E = 60;V ar= 24

(g)r= 0.7;E= 70;V ar = 21 (h)r = 0.8;E = 80;V ar= 16 (i)r = 0.9;E = 90;V ar= 9

Figura2.3: Distribuição Binomial de102 eventos com probabilidader variando de0,1a0,9. O

valor esperadoE(X)e a variânciaV ar(X)estão identificados em cada gráfico.

Uma mudança emrsignifica um deslocamento da distribuição indicado pelo

Va-lor EsperadoE(X), e uma variação na largura relacionado com a VariânciaV ar(X).

Am-bos estão identificados em cada gráfico. Percebemos que a posição central da distribuição em 2.3a comr= 0.1éE(X) = 10e em 2.3i comr = 0,9éE(X) = 90, vemos portanto um

aumento do valor esperado quando o parâmetroraumenta, ou seja, um deslocamento da

Vemos também uma simetria do valor esperado em torno de r = 0,5, notamos

que os gráficos 2.3a e 2.3i são simétricos em relação ak = 0.5, possuindo ainda a mesma

variância. Assim como 2.3b e 2.3h.

Avaliemos agora a influência do número total N na distribuição binomial. Se

mantivermos constante a probabilidaderenquanto aumentamos o número total de

even-tosN como mostrado na figura 2.4, vemos que a distribuição aparentemente tende para uma função delta quandoN cresce. Note que a largura da distribuição tem um aumento

absoluto porém esse crescimento não acompanha o crescimento deN e a distribuição se

estreita como dito anteriormente. O teorema do limite central assegura que a distribuição tende para uma gaussiana no limite em queN tende para o infinito [7].

(a)N = 101;r= 0.5 (b)N = 102;r= 0.5 (c)N = 103;r= 0.5

Figura2.4: Distribuição Binomial para diferentes valores de Número totalN.

Uma boa medida para a largura relativaσrda distribuição [29] é :

σr =

σ E(X) =

p

N r(1₋r) N r =

r s r 1 √ N (2.14)

Vemos que a largura relativa da distribuição diminui com√N, como mostrado na

Figura 2.4.

A versatilidade da função binomial a torna uma ferramenta muito interessante, pois no limite deN _{→ ∞}er _→ 0de forma queN r seja constante, pode-se transformar

a binomial numa distribuição de poisson[28]. E no limite deN _{→ ∞}a binomial torna-se

Abordaremos mais da distribuição binomial na sessão 2.4, onde vemos que natu-ralmente o caminhante aleatório é binomialmente distribuído. Já no capítulo 4 apresenta-remos o modelo de memória binomial.

2.4 Caminhante Aleatório

A teoria de caminhantes aleatórios descreve o movimento de uma partícula, cha-mada caminhante, que a cada instante de tempo dá um passo de comprimentol numa direção aleatória. Numa caminhada unidimensional como mostrada na Figura 2.5, o cami-nhante pode dar um passo para direita com probabilidadep, ou um passo para a esquerda

com probabilidadeq = 1₋p.

Figura2.5: Esquema de caminhada aleatória unidimensional.

Sendo n1 o número de passos para a direita en2 o número de passos para a

es-querda, apósN passos, a posição do caminhante é dada por [29] :

X = (n1−n2)l (2.15)

A probabilidade do caminhante darn1 passos para a direita e em seguidan2

pas-sos para esquerda é dada por:

p.p.p . . . p.p.p.q.q.q . . . q.q.q=pn1_qn2 (2.16)

Contudo, a posiçãoXapósN =n1+n2 passos pode ser alcançada após qualquer

apósN passos é dada pela distribuição binomial:

P(X) = N! n1!n2!

pn1_qn2 (2.17)

Ferreira[4] mostra que podemos chegar na expressão de Einsteinσ2 _{= 2tD como}

resultado da equação de difusão para probabilidade binomial do caminhante aleatório

∂p(x,t)

∂t = D ∂2_p(x,t)

∂x2 , ondep(x, t)é a probabilidade de encontrar a partícula na posição xno

instante de tempot. Dessa forma chegamos a expressão para o coeficiente de difusão do caminhante aleatório:

D= 2p(1₋p) (2.18)

Segundo Ferreira, a difusão é um processo natural e espontâneo e se dá de uma região de mais alta concentração para baixa concentração, como conseqüência da segunda Lei da Termodinâmica, assim como o calor flui de uma fonte de mais alta temperatura para uma região de baixa temperatura a fim de alcançar o equilíbrio termodinâmico, ou seja, maximizar a entropia do sistema.

CAMINHANTE ALEATÓRIO COM PERFIL DE MEMÓRIA

O movimento browniano é um excelente exemplo de processo estocástico marko-viano pois o movimento da particula não depende de sua história. A cada instante a par-ticula tem igual probabilidade de se mover nas direções possíveis, independente de onde ela tenha vindo ou quantas vezes tenha visitado aquela posição. O movimento browniano é conhecido por ter uma difusão normal como apresentado na sessão 2.1. Nosso interesse nesse capitulo é revisar a literatura e elucidar a seguinte questõ: como a memória pode afetar o movimento? Continuaremos tendo difusão normal?

3.1 O Modelo de Memória dos Elefantes

Ao estudar o sistema estocástico não-markoviano, Trimper e Schutz[30] propuse-ram um modelo de caminhada aleatória unidimensional com memória uniforme de todos os passos dados. O modelo foi chamado de Perfil de Memória dos Elefantes, pois consta no senso comum que os elefantes sempre se lembram de tudo. A dinâmica estocástica funciona da seguinte maneira:

• Sem perda de generalidade, o primeiro passo é sempre para a direita; X0 = 0 e

σ0 = +1, ondeX0 é a posição eσ0 é o passo, ambos no instante inicial.

• Num instante discreto de tempo t, o caminhante escolhe um momento passado 0< t′ _{< t}. Essa escolha se dá por sorteio e todos os instantes de tempo possuem igual

probabilidade de serem sorteados já que o perfil de memória é uniforme.P(t′_{) = 1/t}

• Escolhido o evento passado, o caminhante tem probabilidade pde repetir o evento

lembrado σt = σt′ e probabilidade complementar1−pde fazer o opostoσ_t = −σ_t′.

Ondeσ =_±1é o passo unidimensional.

Da definição segue-se que a posição em determinado instante de tempo do cami-nhante é dado por:

X(t) = X0+

X

t′

σt′ (3.1)

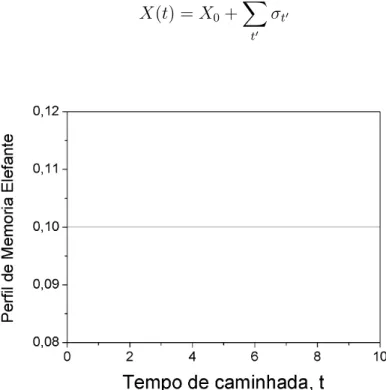
Figura3.1: Perfil de Memória do Elefante para uma caminhada de 10 passos

O perfil de memória uniforme do elefante está exemplificado na Figura 3.1 para uma caminhada de 10 passos. A fim de decidir o 11o _{passo, ocorre um sorteio dentre}

os 10passos dados. Este sorteio segue o perfil de memória, sendo, no caso do Elefante,

um perfil uniforme pois todos os10passos tem igual probabilidade de serem sorteados.

Tendo selecionado o evento a ser lembrado, o caminhante pode repetir ou fazer o oposto do evento lembrado seguindo o parâmetrop.

Analisando o modelo proposto, nota-se que no casop= 1/2, a probabilidade de ir

p = 1 tem-se um regime balístico pois, independente do evento passado escolhido, o

passo será sempre o mesmo. Em [30], os caminhantes com p < 1/2 foram chamados

de reformadores pois tem uma maior chance de fazer o oposto de suas decisões, já os caminhantes comp > 1/2foram chamados de conservadores por terem maior chance de

repetir suas decisões.

Silva et al. [3] resolveram numericamente o problema do caminhante aleatório com memória do elefante, reproduzimos seus resultados mostrados na Figura 3.2. Na Fi-gura 3.2a vemos que a média da posição do caminhante é zero parap < 3/4, por mais

longa que seja a caminhada. Intuitivamente é possível compreender que para os refor-madores, que tendem a fazer o oposto de suas decisões, permaneçam na mesma posição pois num instante dão um passo para a direita e depois para a esquerda. Contudo, alguns dos chamados conservadores também não tem deslocamento significativo. A persistência em ir numa direção possui um efeito macroscópico apenas a partir de p = 3/4, quando

a média da posição deixa de ser nula como vemos na Figura 3.2a. Quanto mais longa a caminhada, mais os efeitos são aparentes. Similarmente na Figura 3.2b notamos uma mu-dança no comportamento no segundo momento, ou seja, a média quadrática da posição. A inclinação da reta está associada ao coeficiente de Hurst, conforme será explicado na sessão 4.2.1.

O modelo do elefante tem resultado teórico exato[30] para o segundo momento da distribuição:

< xt2 > =

t

3₋4p; sep <3/4 (3.2)

= t

ln(t); sep= 3/4 (3.3)

= t

4p−2

(4p₋3)Γ(4p₋2); sep > 3/4 (3.4)

(a) Primeiro momento

(b) Segundo momento

Figura 3.2: Resultados para o primeiro 3.2a e segundo momento 3.2b do perfil de memória do elefante em função do tempo. Vê-se uma mudança no comportamento do sistema parap >3/4.

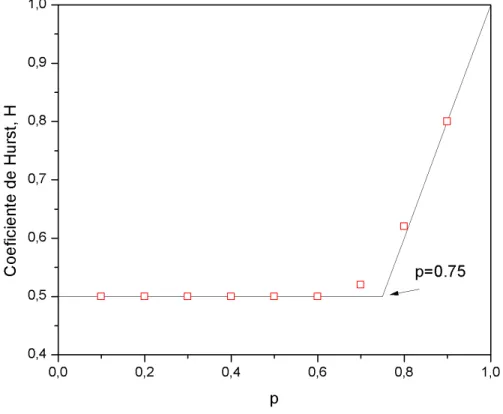
crescente parap > 3/4até que o casop = 1 entre no regime balístico (H = 1), conforme

o caso markoviano sem influência da memória. Esses resultados estão de acordo com os previamente apresentados para primeiro e segundo momento do sistema.

Figura3.3: Difusão para o Elefante. O Expoente de Hurst apresenta região de superdifusão para

p >3/4. [3]

3.2 O Modelo de Memória Alzheimer

Cressoniet al[31] adaptaram o modelo do elefante para estudar a perda de memó-ria recente. O modelo foi chamado de Alzheimer pela similaridade com a patologia que causa amnésia dos últimos anos de vida. Nesse modelo, o caminhante lembra apenas de uma fraçãof de sua caminhada de caminhada inicial. A dinâmica estocástica similar a do

• Como usual, podemos considerar o primeiro passo sempre para a direita; X0 = 0e

σ0 = +1, ondeX0 é a posição eσ0 é o passo, ambos no instante inicial.

• Num instante discreto de tempo t, o caminhante escolhe um momento passado 0< t′ _{6 f t}onde_{0< f 6 1}. Essa escolha se dá por sorteio e todos os instantes de tempo

dentro da região lembrada possuem igual probabilidade de serem sorteados já que o perfil de memória é uniforme. P(t′_{) = 1/f t}

• Escolhido o evento passado, o caminhante tem probabilidade pde repetir o evento

lembrado σt = σt′ e probabilidade complementar1−pde fazer o opostoσ_t = −σ_t′.

Ondeσ =_±1é o passo unidimensional.

No caso limite temos quef = 1reduz o problema ao caso do elefante, efpequeno

restringe a porção de memória inicial que é lembrada, gerando grande perda de memória recente. Vemos na Figura 3.4 um exemplo do perfil de memória para o casof = 0.4e uma

caminhada de 10 passos em 3.4a.

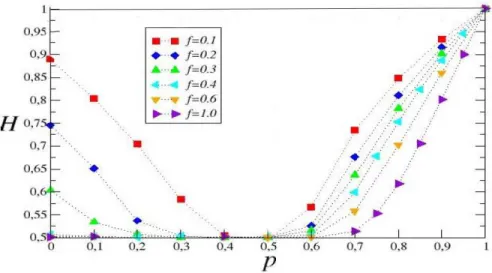
Na Figura 3.4b Ferreira[4] reproduz os resultados para o modelo de memória Alzheimer. Observe que a perda da memória recente gera um aumento na superdifu-são para os conservadores (p > 1/2). Além disso temos o aparecimento de superdifusão

para os reformadores (p < 1/2). Note que quanto maior a perda de memória (fpequeno), maior é a superdifusão em ambos os lados.

(a) Perfil de Memória Alzheimer paraf = 0.4numa caminhada de10

pas-sos

(b) Difusão para o Alzheimer

Figura3.4: Resultados para o perfil de memoria Alzheimer 3.4a. O Expoente de Hurst 3.4b apre-senta região de superdifusão tanto para reformadores quanto para conservadores. Para f = 1

reduz-se ao caso do elefante. Adaptação de [4]

Figura3.5: Oscilações log-periódicas na posição média. Maiores são as amplitudes para baixos valores de p, com f fixo. Adaptado de[4]

É interessante perceber que as oscilações mostradas na Figura 3.5 tendem a au-mentar com o tempo, ou seja, o caminhante persiste numa direção e depois volta na di-reção oposta, em seguida muda a didi-reção novamente e vai cada vez mais longe até que em determinado momento sua caminhada é unicamente numa direção. Se olharmos a janela temporal de106 _a107 _{passos paraf = 0.3ep = 0.0na Figura 3.5, temos}

persisten-cia, uma caminhada praticamente numa única direção para um caminhante reformador comp = 0.0 probabilidade de repetir o passo. Caso não houvesse a perda de memória,

tal caminhante teria difusão normal similar ao movimento browniano, que tem igual pro-babilidade de ir em todas as direções. A mudança da esperada difusão normal para um regime superdifusivo log-periódico devido à perda de memória foi chamado de "quebra espontânea de simetria"[5].

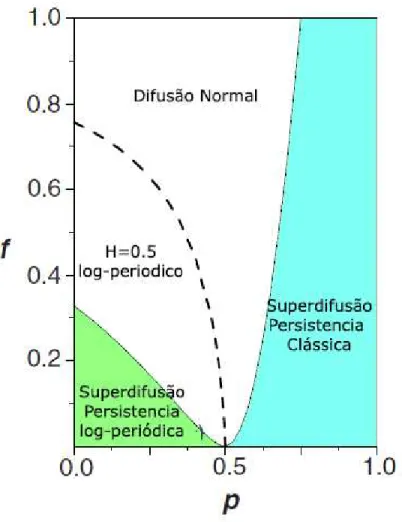
mostrados no diagrama da figura 3.6. Cada par de valores (f,p) pode apresentar:

1. difusão normal (não-persistente),

2. H=0.5 log-periódica,

3. superdifusão (persistência) e

4. superdifusão (persistência) log-periódica.

Figura3.6: Expoente de Hurst num diagrama de fasefxpmostrando regiões de superdifusão

log-periódica e difusão normal. Adaptado de [5]

dependendo do valor de f. Assim como não apresentam nenhuma periodicidade para

perfil de memória próximo do elefante (f _→1).

A log-periodicidade foi mais facilmente observada para reformadores com maio-res tendência a fazer o oposto de sua escolha comop = 0.1, e para caminhadas onde se

tem memória apenas dos primeiros passos comof = 0.1. Há uma tendência a

desapa-recer a medida que aumenta-se of oup, ou seja, à medida que se tem mais memória da caminhada ou um perfil mais conservador na tomada de decisão.

3.2.1 O Modelo de Memória Alzheimer Diluído

Nesse modelo Ferreira et al[6] propõem diluir a porção de memória lembrada do modelo Alzheimer de 3 formas diferentes:

• Aleatória com densidade dada pelo parâmetro0< d < 1.

• Sequência binária Thue-Morse. Tal sequência gera um padrão com50%de diluição.

• Sequencia de Fibonacci que gera perto de100%de diluição.

O perfil de memória ainda é uniforme, os instantes lembrados possuem igual pro-babilidade de serem escolhidos, porém a quantidade e a distribuição dentro da porçãof

é dada pelas diluições acima. A dinâmica estocástica segue exatamente como no caso anterior.

Na primeira situação ganhamos um novo parâmetrodque mede o grau de

dilui-ção uniforme dentro da região de interesse, sendod= 0nada diluído, Alzheimer comum,

ed = 1nenhuma memória. Os resultados de [6] mostram que a diluição aleatória

uni-forme não apresenta mudança qualitativa para o comportamento do caminhante. Vemos as mesmas curvas independente do valor de diluição para cada porção f de memória

lembrada.

A sequência binária Thue-Morse é uma sequência de zeros e uns, formada a partir da negação e concatenação começando pelo valor nulo. Começando com "0", negação do

Figura3.7: Perfil de Memória Alzheimer diluído pela sequência binária Thue-Morse paraf = 0.2

numa caminhada de500passos. A sequência apresenta uma diluição de50%.

"0110". E repete novamente: negação do valor anterior "1001", concatenação "01101001". E

assim segue até preencher toda a região de interesse. Os dígitos de valor nulo correspon-dem a posições de memória que não serão lembrados, enquanto que os dígitos unitário corespondem a posições de memória lembradas. Pela construção da sequência temos sem-pre a mesma quantidade de zeros e uns correspondendo a uma diluição de50%. Vemos

na figura 3.7 uma caminhada de500passos e a distribuição de memória dentro da porção f = 0,2seguindo a sequência Thue-Morse.

Esta sequência se diferencia do caso de diluição aleatória uniformed= 50%pois a

sequência de Thue-Morse permanece a mesma durante toda a caminhada. A medida que o caminhante toma suas decisões a quantidade de memória aumenta mas as posições de memória lembradas são as mesmas acrescidas de mais algumas. Já no caso diluição alea-tória, a cada passo temos uma nova distribuição de memória porém com mesma diluição

d= 50%. Contudo, essa diferença também não causa mudança qualitativa na caminhada.

Vemos as mesmas regiões de superdifusão como no modelo Alzheimer clássico.

Figura3.8: Coeficiente de Hurst para o perfil de memória Alzheimer diluído pela sequência de Fibonacci dentro da fraçãof de memória lembrada. Adaptado de [6].

caso de diluição: sequência de Fibonacci, explicada adiante. Temos um comportamento balístico para reformadores e conservadores exceto para p = 1/2 onde o sistema cai no caso markoviano (H = 1/2). Tal comportamento denota que a caminhada independe

da probabilidade de repetir o passo, exibe persistência acentuada, o caminhante segue sempre numa direção.

A sequência de Fibonacci é formada pela soma dos dois termos anteriores:

Fn =Fn−1+Fn−2; F1 = 1, F2 = 1; n= 1,2,3... (3.5)

Especificamente são os termos:

1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584... (3.6)

den-sidade de posições é maior no início. Vemos na figura 3.9 uma caminhada de500 passos

para uma distribuição de fibonacci dentro da fração f = 0.2. São poucas as posições

lembradas e a maior parte se concentra nos passos iniciais. Ferreira et al cita que em

3276800 passos dados apenas 33posições de memória foram acessíveis para f = 1.0, o

que representa uma diluição próxima de100%e mais concentrada nos primeiros passos

da caminhada.

Figura3.9: Perfil de Memória Alzheimer diluído pela sequência de Fibonacci paraf = 0.2numa

caminhada de 500 passos. A sequência apresenta uma diluição próxima de 100% para longas caminhadas.

3.3 O Modelo de Memória Gaussiana

σ =σ0t (3.7)

Essa largura começa emσ0e evolui no tempo, aumenta a medida que mais passos

são dados. A distribuição gaussiana utilizada por eles foi:

P(t′_)∝exp−(t′−t/2) 2

2(σ0)2t2

(3.8)

Sendoté tempo atual ou número de passos dados para a caminhada

unidimensio-nal de passo unitário et′é o instante lembrado. A probabilidade foi normalizada

levando-se em consideração a necessidade de truncar o perfil para excluir manualmente valores de

t′ _<0e_t′ _{> t}, pois correspondem a situações irreais onde o caminhante se lembra de um

passo anterior ao inicio da caminhada, e a um passo futuro que ainda não foi dado.

Figura3.10: Perfil de memória gaussiano. Centrado sempre no meio da caminhada, e largura varia com o numero de passos.σ =σ0t. Reproduzido de [7]

cami-nhada, de forma que sempre está na metade dos passos dados. E largura também evolui no tempo. Esse modelo sugere que o caminhante tem maior facilidade de se lembrar dos eventos ocorridos na metade de sua vida, e lembrar de cada vez mais eventos.

A dinâmica estocástica funciona como as anteriores:

• Sem perda de generalidade, o primeiro passo é sempre para a direita; X0 = +0;

σ0 = +1;

• Num instante discreto de tempo t, o caminhante escolhe um momento passado 0< t′ _{< t}. Essa escolha se dá por sorteio com uma probabilidade gaussiana eq:3.8.

• Escolhido o evento passado, o caminhante tem probabilidade pde repetir o evento

lembrado σt = σt′ e probabilidade complementar1−pde fazer o opostoσ_t = −σ_t′.

Ondeσ =_±1é o passo unidimensional.

Nosso parâmetro de interesse éσ0 que controla a largura do perfil de memória no

inicio da caminhada. Paraσ0 pequeno o caminhante lembra apenas os eventos centrais,

não tem memoria dos primeiros passos. Paraσ0 grande, a caminhada tende ao caso da

memória do elefante. O efeito da falta de memória incial está mostrado na figura 3.11.

Para o valor σ0 = 0.282a difusão ocorre como no caso do perfil de memória

ele-fante, difusão normal parap < 3/4e superdifusão parap >3/4. Já para o valorσ0 = 0.052

temos superdifusão para os reformadores como apresentado pelo modelo Alzheimer de perda de memoria recente. O mesmo ocorre para os demais valores. Borges et alcita que não encontraram o ponto crítico, a partir do qual passa a existir a PIA (persistencia indu-zida por amnésia) descrita na sessão 3.2, mas que corresponde a larguras estreitas assim como reportado anteriormente.

Tal comportamento sugere que a posição da memória não é a condição para o aparecimento da PIA, e sim grandes perdas de memória. Não apenas perda de memó-ria recente, mas grandes perdas de memómemó-ria em qualquer região induzem PIA, sendo a quantidade de memória que influencia a caminhada dos reformadores. Quanto menos o caminhante se lembra, maior sua persistência gerando superdifusão.

re-Figura3.11: Coeficiente de Hurst para o perfil de memória gaussiano. Pequenas larguras originam superdifusão entre os reformadores. Reproduzido de [7]

sultados. Concordamos que larguras estreitas de memória geram aumento na superdifu-são, contudo a posição da memória também é relevante, segundo nosso estudo.

Também foi observada a log-periodicidade para caminhadas de reformadores e baixas larguras como mostrado na figura3.12. Temos uma caminhada dep = 0.1para os

valores deσ0 = 0.001eσ0 = 0.052, foi necessário mudar a escala do gráfico para observar

Figura3.12: Log-peridiocidade para reformadores com perfil de memoria gaussiano. Reproduzido de [7]

3.4 O Modelo de Memória Exponencial

Os efeitos da memória recente são estudados porAlves et al[34] quando propõem um perfil de memória exponencial dado por:

P(t′_{, t) =Aexp}−λ(t−t′)

t (3.9)

Sendo t é o número de passos dados e t’ a possível escolha. A exponencial positiva parat′seleciona a memória recente. Vemos na Figura 3.13 um perfil de memória para uma

caminhada de100passos e3valores deλ. Quanto maiorλmais restringe a memória aos

últimos passos dados, enquanto queλpequeno voltamos ao caso da memória do elefante.

Figura3.13: Perfil de Memória Exponencial. Quanto maiorλmais recente a memória lembrada.

funciona a correlação entre a exponencial e fraçãof de memória recente, porém citamos

aqui apenas para explicar a dinâmica estocástica, que é similar as anteriores mudando apenas a distribuição de memória. De forma que num instante discreto de tempot, o

ca-minhante escolhe um momento passado(1₋f t)< t′ _{< t}onde_{0< f < 1}. Essa escolha se

dá por sorteio com uma probabilidade exponencial.

O efeito da memória recente está mostrado na Figura 3.14. Quando λé pequeno

temos um perfil de superdifusão similar ao caso do elefante, à medida queλ aumenta, a

superdifusão vai diminuindo se aproximando do movimento browniano, de forma que cada vez mais conservadores apresentam difusão normal. Ou seja, quanto mais recente a memória menor a superdifusão. A memória dos últimos passos leva a uma difusão normal.

Figura3.14: Coeficiente de Hurst para o perfil de memória recente exponencial. Quanto menos memória recente (λgrande) mais próximo do movimento browniano. Reproduzido de [8]

apresentada no modelo de memória do elefante, indicando que a memória dos primeiros passos aumenta a superdifusão.

Chamamos atenção ao não aparecimento da Persistencia Induzida por Amnésia descrita no modelo de Alzheimer na sessão 3.2. Isso indica que a memória recente ou de curto alcance não altera o comportamento dos reformadores. Esse fato não está de acordo com nossos resultados. Como veremos no próximo capítulo, ao selecionar a memória recente com o nosso modelo binomial obtivemos superdifusão tanto para conservadores como para reformadores.

3.5 Outros modelos

onde o caminhante chamado de "macaco” pode dar um passo unitário e unidimensional para os lados ou pode dar um pulo de tamanho qualquer para um lugar preferido. Tal caminhada apresenta subdifusão (H<1/2) mesmo com pulos de tamanho não fixo, mas a tendência a voltar para lugares específicos limita a caminhada. O problema tem solução exata apresentada mais tarde no mesmo ano [36].

Serva[37] sugere um modelo de caminhante aleatório com memória da posição mais distante. A caminhada funciona como movimento browniano e o caminhante apenas tem acesso a memória quando chega na posição mais distante da caminhada, onde ele pode decidir ir adiante ou retroceder baseado no parâmetro γ. Esse parâmetro diz se

o caminhante é audacioso ou temeroso. Os resultados mostram regime de subdifusão encabeçado pelos temerosos, já os audaciosos se distribuem em regime de superdifusão e regime de difusão balística.

CAMINHANTE ALEATÓRIO COM PERFIL DE MEMÓRIA BINOMIAL

A memória dos primeiros passos (de longo alcance) foi amplamente estudada na literatura como nos perfis do elefante [30] e Alzheimer [31]. Por outro lado, são poucos os estudos que exploram a ausência da memória inicial da caminhada como no estudo do perfil de memória gaussiano [33] e a memória recente como no caso exponencial [34]. O perfil de memória binomial permite variar a posição da memória, de forma que com um único modelo é possível estudar a memória de longo e curto alcance com apenas um parâmetro.

Neste estudo, privilegiamos a posição da memória e não a quantidade da mesma como no caso gaussiano. O perfil binomial ainda tem a vantagem de ser distribuído den-tro do intervalo de interesse, enquanto que a gaussiana tem suas extremidades arbitraria-mente excluídas.

Além disso, nos limites certos discutidos na sessão 2.3 podemos transformá-la numa distribuição de Poisson ou normal, o que deixa nosso modelo versátil e abrangente, pois com um único modelo pode-se abordar diferentes perfis de memória. Essas possibi-lidades, no entanto, não foram abordadas neste trabalho. Apresentamos nesse capítulo o modelo de memória binomial como processo estocástico não-markoviano e os principais resultados, comparando-os com a literatura previamente apresentada no capítulo 3.

Acrescento ainda que propomos um modelo que possui simetria, portanto, por Ansatz, esperamos bons resultados, afinal amamos simetrias!

4.1 O Modelo de Memória Binomial

Considere o modelo de caminhadas aleatórias unidimensionais e passos unifor-mes e unitários. Em um dado instante, o caminhante pode lembrar de um único evento de seu passado. Tal evento foi contemplado por um sorteio com probabilidade dada por uma função densidade de probabilidades binomial como na equação 4.1:

P(t′_{) =}

N t′

rt′

(1₋r)N−t′

, (4.1)

Sendot′representa o instante de tempo da caminhada, ou eventos, e_Né o número

total de passos dados até o momento. A dinâmica estocástica ocorre como nos modelos anteriormente apresentados. Em t = 0, o primeiro passo é dado arbitrariamente para

a direita sem perda de generalidade: X(t = 0) = +1. Em seguida tem-se o sorteio do

instantet′ a ser lembrado seguindo o perfil binomial dado pela equação 4.1. A direção do

passo em tempo atual será a mesma do instante lembrado com probabilidade pou será

oposta com probabilidade1₋p.

De acordo com o que foi dito anteriormente, o parâmetropestá no intervalo[0,1]

e representa a probabilidade de repetição do passo lembrado. Os caminhantes com 0 < p <0.5são chamados reformadores pois têm maior chance de mudarem suas escolhas de

passo. Já o caminhantes com 0.5 < p < 1 são chamados conservadores pois tem maior

chance de repetir as escolhas de passo no instante lembrado.

A fim de entender melhor o perfil de memória binomial, repetimos a discussão feita na sessão 2.3, agora no contexto de memória. Uma possível interpretação parar

se-ria a probabilidade de lembrar de uma memóse-ria recente. Dessa forma, a dualidade que origina o perfil binomial para o perfil de memória seria a procura por uma memória mais recente ou a procura por uma memória mais antiga, com probabilidadesre1₋r respec-tivamente. Para uma baixa probabilidade de acessar um lembrança recente,r pequeno,

(a)N = 101;r= 0.3 (b)N = 101;r = 0.5

(c)N = 102;r = 0.3 (d)N = 102;r= 0.5

(e)N = 103_{;r = 0.3 (f)N = 10}3_{;r= 0.5}

(g)N = 104_{;r= 0.3 (h)N = 10}4_{;r= 0.5}

Figura4.1: Perfil de memória binomial parar = 0.3er = 0.5nas linhas, e à medida que o tempo

binomial centrada em altos valores.

Podemos ver pela Figura 4.1 que, à medida que o número de passos aumenta, a distribuição se rearranja para o novo valor de passos, ou seja, há uma mudança no for-mato do perfil de memória. Na primeira linha da figura vemos as distribuições iniciais de memória para diferentes caminhadas com diferentes posições de memória (relaciona-das ao parâmetro r). Para valores baixos de r temos memórias iniciais, enquanto que para valores altos der temos memórias recentes. Nas colunas da figura 4.1 observa-se a

mudança na distribuição ao longo da caminhada, à medida que o número de passos vai aumentando. Como visto na sessão 2.3, a largura relativa diminui com√N, condensando

a memória.

4.2 Métodos e Resultados

Via simulação computacional, foram realizadas 106 _{caminhadas de 10}6 _passos

para cada combinação dos parâmetro de feedbackpe posição de memóriar. As

simula-ções ocorreram por acesso remoto ao cluster disponível no Departamento de Física Teórica e Experimental, escritas em linguagem computacional C e disparadas paralelamente. Uti-lizamos o gerador aleatório binomial disponível na biblioteca gratuitaNumerical Receipes

in C[38]. A classificação da difusão da caminhada foi dada pelo Expoente de Hurst.

4.2.1 Classificação da Difusão pelo Expoente de Hurst

O coeficiente de Hurst pode ser calculado, conforme descrito em [2], através da análise do comportamento temporal da variância da posição do caminhante. Durante a caminhada, armazenamos a posição em cada instante de tempo a fim de adquirir um gráfico de_hx2_{i − hxi}2 _{versust na escala logarítmica. Os valores médios dehx}2_{i ehxi}

fo-ram obtidos para uma média de106 _{caminahdas. O coeficiente angular do ajuste linear}

pelo método de minimus quadradus corresponde a 2H. Este mesmo coeficiente poderia

ser obtido através da análise apenas do valor médio quadrático, pois no limite assintó-tico (número grande de passos) temos que_hx2_{i ∼t}2H_{. Contudo, em nossas simulações, a}

linear sem precisar de correções log-periódicas. Segundo [7] os resultados são similires e bem sucedidos quando analisados pelo valor médio quadrático ou pela variância. Auto-matizamos o processo para obter o coeficiente de Hurst pela inclinação da reta no gráfico logaritmico da variância versus tempo.

4.2.2 Diagrama de Fase no Regime0.1< r <0.8

A partir do método discutido aqui é possível traçar o diagrama de fase para nosso modelo. Estamos interessados em identificar para quais valores específicos de posição de memória binomial o sistema exibe persistência. Na figura 4.2 podemos ver a medida da difusão das caminhadas aleatórias com memória binomial através do Coeficiente de Hurst para diferentes posições de memória representadas pelo parâmetrorda distribuição

bino-mial. Note querpróximo de0estamos lidando com a memória mais inicial da caminhada

ou memória dos primeiros passos, já pararpróximo de1estamos lidando com a memória

recente ou memória dos últimos passos dados.

Observamos regimes de superdifusão para todas as posições de memória, tanto para feedback negativo (reformadores) como para feedback positivo (conservadores). A superdifusão tende a aumentar à medida querdiminui, ou seja, a superdifusão está

pre-sente para a maioria dos valores de feedback para a memória inicial(r = 0.1)enquanto

que aparece apenas nas extremidades nas memórias mais recentes(r= 0.8). Observamos

que quanto mais recente a memória mais normal é a difusão.

Tal comportamento difusivo já era esperado para conservadores (p >0.5), devido

à persistencia, há constância na escolha do passo. Particularmente é mais intuitivo avaliar o casop= 1, pois como o caminhante sempre vai repetir a escolha, deve caminhar sempre na mesma direção, resultando um comportamento limítrofe balístico para o coeficiente de Hurst (H = 1), indepedente da posição da memória. Outra situação bem conhecida

é o casop = 0.5, onde independe o perfil de memória pois a probabilidade em todas as

direções é a mesma sempre. Nesse caso, espera-se o regime difusivo normal (H = 0.5),

como no movimento browniano. Os casos intermediários0.5< p <1obviamente devem

Figura4.2: Medida da difusão das caminhadas aleatórias com memória binomial através do Co-eficiente de Hurst para diferentes posições de memória representadas pelo parâmetror da

distri-buição binomial

O mesmo comportamento superdifusivo para os ditos reformadores (p <0.5) que

tomam decisões diferentes a cada escolha não é intuitivo. Conforme descrito no capítulo 3, este resultado também apareceu no perfil de memória gaussiano, no qual foi associado a lacunas de memória. No nosso modelo acreditamos que a largura estreita da memória contribui pois a largura relativa da binomial diminui com√Ncomo mostrado na equação

2.14. Analisemos o caso p = 0, onde o caminhante sempre escolherá o lado oposto ao

sorteado na memória; Acontece que a memória estreita sempre sorteia na mesma região de forma que o caminhante sempre fará diferente da região sorteada mas seus passos serão na mesma direção. Dessa forma, parap= 0teremosH = 1, e, pelo mesmo princípio

de continuidade usado anteriomente, devemos ter algum grau de superdifusão nas curvas em0< p <0.5. Segundo a figura 4.2, quanto mais inicial a memória maior a superdifusão.

O mais interessante, contudo, foi observarmos uma simetria em torno de p= 0.5

Figura4.3: Sobreposição espelhada do coeficiente de Hurst mostrando que existe uma simetria para reformadores (p <0.5, espelhados emr′_{) e conservadores (p >0.5emr).}

memória. A fim de investigar melhor esta simetria, espelhamos o gráfico 4.2 como mos-trado na figura 4.3. Nota-se que os valores para conservadores com os reformadores so-brepostos são bem próximos. A diferença em % encontra-se na figura 4.4. Vemos que

praticamente todas as curvas são simetricas em até 2% e não identificamos nenhum

pa-drão coerente nessas diferenças.

Tal simetria torna o modelo muito vantajoso por permitir reduzir as simulações pela metade, reduzindo o tempo de obtenção dos resultados em futuros estudos. Acredi-tamos que a simetria deve-se às propriedades simétricas da função binomial e ao grande número de passos da simulação. Embora a medida da difusão anômala pelo coeficiente de Hurst tenha valores simétricos, o comportamento da caminhada tem propriedades di-ferentes dependendo do estado(p, r)do caminhante. Uma análise da log-periodicidade

Figura4.4: Diferença percentual na simetria do Coeficiente de Hurst

4.2.3 O Modelo de Memória Gaussiana e o casor= 0.5

Na sessão 3.3 discutimos o perfil de memória gaussiana cuja distribuição é sem-pre centrada no meio da caminhada e a largura é o parâmetro de interesse. Vimos que para larguras estreitas, o caminhante aleatório apresenta superdifusão para reformado-res e conservadoreformado-res, já para larguras maioreformado-res o movimento tende ao modelo do elefante. Enquanto que no modelo gaussiano tem-se um estudo da influência da largura sobre o comportamento difusivo, no modelo binomial apresentamos a influência da posição da memória sobre o comportamento difusivo. No modelo binomial não obtemos o resultado do modelo do elefante, estamos no regime de superdifusão para conservadores e refor-madores.

Na equação 3.7 sobre o modelo gaussiano temos que o desvio padrão é σg =σ0t,

enquanto na equação 2.13 do modelo binomial temos que σb =

p

sejam dinâmicas diferentes, pois uma evolui linearmente comN e a outra com√N,

po-demos mostrar que o modelo binomial está no regime de larguras da gaussiana que apre-sentam superdifusão para conservadores e reformadores.

Reproduzimos o modelo gaussiano com o objetivo de encontrar o ponto crítico em que a largura deixa de gerar superdifusão para reformadores. Na figura 4.5 temos o Coeficiente de Hurst versus tempo para diferentes valores de largura da distribuição de memória gaussiana. Note que achamos o ponto crítico pois para larguras maiores do que

σ0c = 0.125tem-se difusão normal, já para larguras menores do queσ0c = 0.125o sistema

exibe persistência para reformadores.

Figura4.5: Investigando o comportamento do Coeficiente de Hurst versus tempo para um per-fil de memória gaussiano próximo do ponto crítico. Em destaque no gráfico o aparecimento da superdifusão em reformadores.

σb =

1 2

√

t (4.2)

σg = σ0t (4.3)

Sabemos que, dependendo do valor de σ0, a largura binomial é inicialmente

su-perior a largura da gaussiana. Mas, esperamos que a partir de certo tempo críticotc, a

largura gaussiana passe a ser superior a binomial de forma que, pelo resto da caminhada

t > tc, o perfil de memoria binomial tem largura inferior ao perfil de memória gaussiano.

Igualando as larguras temos:

σb(tc) =σg(tc) =

1 2

√

tc = σ0tc (4.4)

σ₀2t2_{c −} 1

4tc = 0 (4.5)

tc =

1 4σ2

0

(4.6)

Aplicamos agora nosso σ0c = 0.125 encontrado numericamente e temos que

tc = 16. Significa que a partir do passo 16 a largura da binomial r = 0.5se torna

infe-rior a largura da gaussiana crítica, estando na região que o modelo gaussiano apresenta superdifusão para reformadores. Ora, numa caminhada de106 _{passos, consideramos os}

primeiros16passos desprezíveis. E como a binomialr= 0.5possui a maior largura como

mostrado na Figura 2.2, consideramos nosso modelo binomial de acordo com o modelo gaussiano.

4.2.4 Diagrama de Fase no Regimer_→0

Um resultado deveras interessante surge quando fazemosr_→0. A superdifusão

se acentua visto que cada vez mais valores do parâmetro de repetição do passo apresen-tamH > 1/2como mostrado na figura 4.6. O gráfico tende a estreitar lembrando o caso

visto, tal perfil restringe a lembrança a um intervalo 0 < f < 1, num primeiro modelo

diluído por um padrão aleatório, ou seja, dentro da fraçaof de memória apenas uma

por-centagem de densidade controlada é lembrada, é um excelente exemplo de gerador ale-atório de padrão estocástico[6]. Um segundo modelo não aleale-atório e aproximadamente

100%diluído é apresentado pela seqüencia numérica de Fibonacci.

Figura4.6: Investigando o comportamento superdifusivo do perfil de memória binomial quando

r_→0, através do Coeficiente de Hurst versus tempo.

Embora a fração f possa selecionar partes da memória a ser lembrada, sempre

inclui a porção inicial mesmo com a diluição, de forma que a comparação com o modelo binomial se dá apenas para valores derbaixos que incluem essa memória inicial. Além

disso, é difícil definir uma largura para a distribuição do perfil de Memória Alzheimer Diluído por não ser uma distribuição contínua, o melhor parâmetro para comparação é o própriof. Ainda assim temos resultados bastante parecidos com o modelo de Alzheimer

perdas de memória do passado recente. Esse fenômeno foi denomidado deamnestically induced persistence.

Como já vimos, Borges et al. [33] mostra que a persistência em feedback negativo também ocorre para memória centrada no meio do seu modelo gaussiano dependendo do valor da largura e conclui que não apenas "grandes perdas de memória do passado recente” mas sim "grandes perdas de memória” causam aamnestically induced persistence. No nosso modelo binomial mostramos que "onde” essas grandes perdas de memória ocor-rem influenciam aamnestically induced persistence, reforçando que existe uma ligação entre comportamento do sistema e danos na memória.

Por limitação numérica não conseguimos fazer r _→ 0 mais do que mostrado na

figura 4.6. Contudo, temos razões para acreditar que o comportamento do gráfico tende a ficar cada vez mais estreito lembrando o caso do perfil de memória Alzheimer diluído com a sequência de Fibonacci mostrado na figura 3.8 na página 27, onde apenas o casop= 0.5

apresenta difusão normal, enquanto todos os demaispapresentam difusão balística.

4.2.5 Diagrama de Fase para Feedback Positivo

É sem dúvida intuitivo que a probabilidade maior de repetir o passo leve a com-portamentos de persistência. Na figura 4.7 temos os já apresentados resultados do Expo-ente de Hurst para as probabilidades de repetição do passo que privilegiam a repetição

(p > 0.5)e temos também o resultado exato do modelo clássico da memória do elefante

visto na sessão 3.1. Neste modelo o caminhante pode lembrar igualmente de qualquer instante anterior. Vemos que para valoresr _≤ 0.3o sistema apresenta uma superdifusão

mais elevada do que o caso clássico do elefante, enquanto que parar >0.3o sistema apre-senta superdifusão menor. Isso nos leva a acreditar que os primeiros passos são decisivos para o deslocamento da caminhada, e exercem maior influência na difusão do sistema.

Figura 4.7: Investigando o comportamento superdifusivo do perfil de memória binomial para feedback positivo em comparação com o caso da memória de elefante.