Variação temporal da volatilidade e precificação de derivativos

(1)

FUNDAÇÃO GETULIO VARGAS

ESCOLA DE ECONOMIA DE SÃO PAULO

RODRIGO MINORU MARTINHO GOTO

VARIAÇÃO TEMPORAL DA VOLATILIDADE E

PRECIFICAÇÃO DE DERIVATIVOS

(2)

Goto, Rodrigo Minoru Martinho.

Variação temporal da volatilidade e precificação de derivativos / Rodrigo Minoru Martinho Goto. – 2016.

69 f.

Orientador: Prof. Dr. Afonso de Campos Pinto.

Dissertação (mestrado) - Escola de Economia de São Paulo.

1. Processo estocástico. 2. Derivativos (Finanças). 3. Taxas de juros. I. Pinto, Afonso de Campos. II. Dissertação (metrado) – Escola de Economia de São Paulo. III. Título.

(3)

RODRIGO MINORU MARTINHO GOTO

VARIAÇÃO TEMPORAL DA VOLATILIDADE E

PRECIFICAÇÃO DE DERIVATIVOS

Data da Aprovação: 05 / 08 / 2016

Banca Examinadora:

Prof. Dr. Afonso de Campos Pinto

(Orientador) FGV - EESP

Prof. Dr. Marcos Antonio Botelho

FGV - EESP

Prof. Dr. Takashi Yoneyama

(4)

(5)

Agradecimentos

Muito especialmente ao ilustríssimo professor Marcos Antonio Botelho, por toda paciência, dedicação, disponibilidade, parceria, proﬁssionalismo, com certeza um fator determinante deste sucesso. Muito obrigado.

Ao meu orientador professor Afonso Campos Pinto, por seus conselhos e sua dedica-ção.

Aos meus chefes Cleber Drobnicki, Luiz Gambale e Jorge Bolla pela compreensão e por todo apoio ﬁnanceiro em nome do Banco J.P. Morgan.

À Jane Mara Julião dos Santos por me acolher e possibilitar a realização deste sonho.

À Maíra Lúcia Julião dos Santos pelo companheirismo, parceria, incentivo e compre-ensão.

Ao Yuri Medeiros e André Panariello pelo incentivo e ajuda.

Á minha familia, em especial aos meus pais, à minha irmã e meus amigos, por me entender e compreender a minha ausência.

(6)

(7)

RESUMO

Este trabalho apresenta uma abordagem ao estudo de robustez estruturada do modelo de Black-Scholes que permite não só levar em conta as incertezas nas determinações dos parâmetros envolvidos (volatilidade σ e taxa livre de riscor) como também dar conta de hipóteses simplificadoras do modelo tais como assumir que σ é invariante no tempo (em detrimento da heterocedasticidade inerente ao processo). A originalidade desta abordagem está em formular a equação de Black-Scholes como uma equação diferencial ordinária abstrata e transpor para o contexto de operadores lineares em espaços normados de dimensão infinita técnicas de perturbações estruturadas para sistemas determinísticos de dimensão finita. Estas incertezas no modelo são formuladas como sendo uma perturbação aditiva variante no tempo aplicada aos coeficientes da equação de Black-Scholes, cada um separadamente ou todos de uma vez só, para se obter uma quantificação da robustez. Esta quantificação é feita através de uma medida de robustez estabelecendo um limitante superior para a “magnitude” (norma) da diferença entre a realização histórica da precifi-cação do derivativo e a precifiprecifi-cação teórica fornecida pelo modelo desde que a norma da perturbação não ultrapasse esta medida. No final do trabalho, este resultado é aplicado no estabelecimento desta medida de robustez no caso da variação temporal da volatilidade de uma opção de compra europeia.

Palavras-chave: Equação de Black-Scholes, preciﬁcação de derivativos,

(8)

ABSTRACT

This work brings out an approach to the study of structured robustness for the Black-Scholes model that allows for not only accounting for the uncertainties on the determination of the parameters involved (volatility σ and risk-free rate of interest r) as well as for simplifying hypotheses such as the assumption that σ is time-invariant (in disregard of the heterocedasticity that is proper to the process). The originality of this approach comes from formulating the equation of Black-Scholes as an abstract ordinary differential equation and transfer to the context of linear operators in infinite dimensional normed spaces some techniques of structured perturbations on finite dimensional deterministic systems. These uncertainties on the model are formulated as being a time-varying additive pertubation applied to the coefficients of the Black-Scholes equation, each one separately or all at once, in order to obtain a quantification of robustness. Such quantification is done by means of a measure of robustness by establishing an upper bound for the “magnitude” (ultimately, the norm) of the difference from the actual precification of the derivative and the theoretical precification given by the model since the norm of the perturbation does not exceed this measure. At the end or this work, this result is applied to establishing such measure of robustness in the case of the temporal variation of volatility for an European call option.

Keywords: Black-Scholes equation, preciﬁcation of derivatives, heterocedasticity,

(9)

Lista de ilustrações

Figura 1 – Evolução do preço da PETR4 . . . 57

Figura 2 – Escolha do Rho . . . 58

Figura 3 – Condicionamento ponderado do erro da PETRH11 . . . 59

Figura 4 – Condicionamento ponderado para diferentes alphas . . . 60

Figura 5 – PETRH11: Teórico x Real . . . 61

Figura 6 – Erro entre o preço Teórico e o Real . . . 61

(10)

Lista de tabelas

(11)

Lista de abreviaturas e siglas

DRE Equação Diferencial de Riccati

OP Problema de Controle Ótimo Linear-Quadrático

HS Sistema Hamiltoniano

CS Sistema acoplado

CP Condicionamento Ponderado

EDP Equação Diferencial Paricial

(12)

Sumário

1 Introdução . . . 12

2 Preliminares . . . 18

2.1 Derivativos e o modelo de Black-Scholes . . . 18

2.2 Representação da equação de Black-Scholes como EDO abstrata . . . 19

2.3 Semigrupos . . . 21

3 Uma medida de robustez para o modelo de Black-Scholes . . . 28

3.1 Formulação do erro via perturbações estruturadas . . . 28

3.2 Técnica do escalonamento . . . 30

3.3 Condicionamento do erro . . . 32

4 Determinação da norma do operador Lα . . . 37

4.1 Resolução do problema de controle ótimo . . . 38

4.2 Equação de Riccati . . . 41

4.3 Sistema hamiltoniano . . . 43

5 Aplicação: medida da robustez da volatilidade . . . 47

5.1 Operadores adjuntos e normas . . . 48

5.2 Algoritmo via sistema hamiltoniano . . . 53

5.3 Aplicação a uma opção europeia . . . 57

6 Considerações Finais . . . 63

Referências . . . 65

Anexos

67

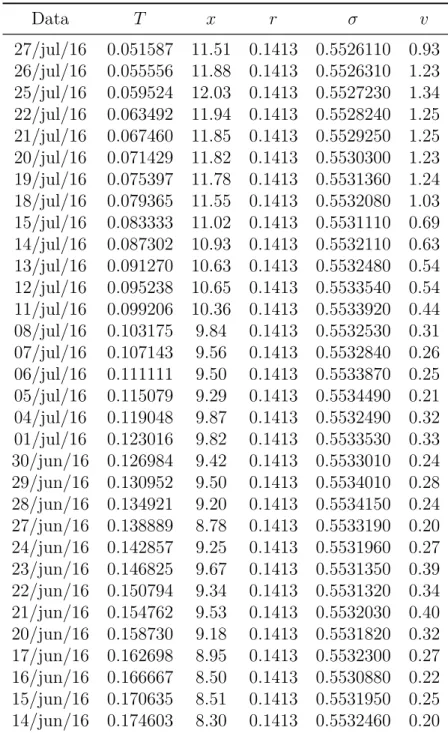
ANEXO A Tabela de Parâmetros . . . 68

(13)

12

1 Introdução

Em (BOTELHO; PRITCHARD, 1995) e (BOTELHO, 1994), foi feito um estudo de robustez da controlabilidade de sistemas determinísticos em dimensão finita assumindo as incertezas como perturbações estruturadas. Relembre-se que por incertezas estruturadas se quer dizer que o estudo de robustez é feito através de uma técnica que permite analisar de uma única vez tanto um como alguns ou todos os parâmetros que constituem os coeficientes da equação diferencial que define o modelo. Embora aquele trabalho de Controle estivesse inserido no contexto de modelos determinísticos, percebemos que sua técnica poderia ser adaptada e reelaborada para que pudéssemos contribuir de maneira original ao abordar

quantitativamente a questão da robustez do modelo de Black-Scholes para a preciﬁcação

de derivativos, particularmente no que diz respeito à questão da heterocedasticidade na essência da dinâmica de tais instrumentos financeiros. Assim, percebemos que esta técnica nos permitiria responder através de uma abordagem determinística às incertezas (inclusive de naturezas estocásticas) tanto na volatilidade quanto na taxa livre de risco, isoladamente ou em conjunto e na forma como elas são assumidas pelo modelo de Black-Scholes. Assim, a robustez do modelo de Black-Scholes poderia ser reformulada nos seguintes termos: assumindo que as incertezas nos parâmetros do modelo são representadas como uma perturbação de “magnitude” γ no alcance dos valores destes parâmetros, até que valor deγ podemos garantir que a diferença entre o resultado da precificação provida pelo modelo e o preço histórico efetivamente realizado esteja dentro de um intervalo de tolerância aceitável? Por exemplo, no que diz respeito à hipótese do modelo estabelecer que a volatilidade do instrumento base na precificação do derivativo é invariante no tempo, a presença da heterocedasticidade passa a ser considerada como uma perturbação dependente do tempo d(t) de “magnitude”γ.

(14)

Capítulo 1. Introdução 13

num cenário livre de risco é igual à taxa de juros livre de risco r) e com volatilidade σ constante (σ2 _{é referida como sendo a taxa de variância do preço da ação). Em outros}

termos, é assumido de início que a variabilidade do retorno percentual num curto intervalo de tempo ∆t é a mesma independentemente do preço da ação, ou seja, um investidor hipotético tem o mesmo grau de incerteza do retorno percentual quando o preço da ação é x como também quando o preço é 5x. Esta hipótese sugere que o desvio padrão da mudança ∆S no preço da ação num curto período de tempo deve ser proporcional ao preço da ação, o que leva a um modelo do comportamento do preço da ação essencialmente da forma

dS =µSdt+σSdz ou, equivalentemente, dS

S =µdt+σdz.

Claro está que as hipóteses de r e σ constantes deveriam ser relaxadas, dado o mundo ﬁnanceiro real, e, por exemplo, até mesmo existem trabalhos onde r e σ são assumidos como funções conhecidas de t (cf. Hull). O objetivo desta dissertação é inovar na perspectiva ao abordar a questão das incertezas nestes parâmetros como um estudo de robustez do modelo de Black-Scholes no que se refere areσ. Por questão das incertezas nos parâmetros estamos querendo dizer questões sobre se eles deveriam ser assumidos como variantes no tempo ou mesmo se temos incertezas oriundas de simpliﬁcações ou hipóteses simplicadoras, imprecisões nos cálculos, falhas nos bancos de dados ou observações que levam à mensuração destes parâmetros.

Em linhas bastante gerais, a técnica de abordagem privilegiada neste trabalho consiste em representar a equação diferencial parcial de Balck-Scholes como uma equação diferencial ordinária abstrata através da introdução do operador diferencial matricial

A=

 

ˆ

A 0

0 Aˆ

  ,

com domínio _D(A) denso num espaço de Banach, em termos do que podemos chamar de operador de Black-Scholes

ˆ A=₋1

2σ

2_x2 ∂2

∂x2 −r x

∂ ∂x −I

!

(aqui, O representa o operador nulo e I o operador identidade) definido em um domínio denso em um espaço de Banach. A razão de considerarmos artificialmente uma matriz 2_×2 na construção do operador é para reservarmos uma entrada (mais especificamente, a entrada a11 da matriz-operador A) para dar conta de perturbações no parâmetro σ e

outra entrada (a22) para perturbações no parâmetror. Isto possibilita adaptar a técnica de

(15)

uma, mas cada uma podendo ser eventualmente considerada em contexto topológico diferente.

O problema com perturbações estruturadas dando conta das incertezas assume então a seguinte forma:

dZ

tt =AZ+

2

X

k=1

DkFk(CkZ(t), t) , t_∈[0, T] e Z(0) =Vo, em correspondência ao problema nominal não-perturbado

dV

dt =AV , t∈[0, T] e Z(0) =Vo.

A partir daí, a estratégia básica começa por achar uma representação da solução do problema resultante tendo como função incógnita o erro E : [0, T]_{→ D}(A) deﬁnido, para cada t _∈[0, T], por

E(t) = Z(t)−V(t) : [0,∞) → R2×1

x _7−→ E(t) (x)

com

E(t) (x) = (Z(t)₋V(t)) (x) =Z(t, x)₋V(t, x) , _∀x_≥0,

que portanto associa a cada preço do ativo-basex_≥0 fixado as diferenças Z(t, x)₋V(t, x) no preço do derivativo ao longo do horizonte temporal [0, T]. Em seguida, por reformular a expressão desta solução em termos de solução de uma equação funcional do tipoH(u) =u. A limitação no valor do “tamanho” γ da perturbação nos parâmetros fica assim associada à condição para que H seja uma aplicação contrativa a fim de se garantir a existência de solução u para esta equação funcional através do Teorema do Ponto Fixo de Banach.

Papel preponderante nesta linha de procedimentos acaba ficando com as normas de alguns operadores que vão sendo introduzidos ao longo do processo. Particular protagonismo é desempenhado por um certo operador L, uma espécie de análogo do operador de entrada-saída no contexto do Controle determinístico, de forma que nosso resultado estabelecendo uma medida de robustez para o modelo de Black-Scholes ficaria sendo expresso por uma proposição estabelecendo que se o “tamanho” γ da perturbação que responde pelas incertezas é tal que γ._||L_||<1, então existe um número positivo K tal que||E(T)||< K. No entanto, os estudos apresentados aqui dão um passo adiante ao introduzirmos um grau de liberdade extra através de um escalonamento artificial dado por funções contínuas arbitrárias α: [0, T]_→]0,_∞)_×]0,_∞) que acabam repercutindo na determinação de cada uma das normas dos operadores envolvidos. Com isto, a proposição principal da dissertação acaba sendo estabelecida na seguinte forma mais geral: dado qualquer peso α contínuo positivo, se γ._||Lα_|| < 1, então existe um número positivo Kα tal que

(16)

primeiro lugar, abre uma nova linha de investigação em otimização nos termos do problema de se procurar por um peso α∗ _{tal que}

||Lα∗|| seja um mínimo (ou, de maneira mais fraca,

um ínﬁmo), o que ampliaria o “tamanho da robustez” dos iniciais valores de γ tais que 0 < γ < _||L_||−1 _{para agregar os novos valores do intervalo} _||_L_||−1 _≤ _{γ <} _||_Lα∗||−1. Em

segundo lugar, permite que se substitua a tarefa de se determinar os valores exatos de_||L_||e das normas constitutivas deK, que são bem soﬁsticadas e difícies, pela tarefa mais simples de se estabelecer primeiro estimativas para os valores de ||Lαo|| e Kαo com αo(t)≡(1,1)

para depois escolher um α de maneira a melhorar a precisão destas estimativas na forma de _||Lα_||e Kα menores.

O modelamento da precificação de derivativos em termos estocásticos tem uma história de pouco mais de um século. Em 1900, Louis Bachelier formalizou algumas das incertezas em Théorie de la spéculation, introduzindo o movimento browniano na área de finanças, um grande avanço no estudo de apreçamento de derivativos que com certeza contribuiu para anos mais tarde Fisher Black e Myron Scholes (1973) precificarem uma opção europeia sugerindo um portfolio livre de risco em “The Pricing of Options and Corporate Liabilities”.

O modelo apresentado por Black e Scholes é considerado um dos melhores trabalho em ﬁnanças, pois tem sido amplamente adotado como referência de apreçamento de opções do tipo europeia. No entanto, para implementar o modelo é preciso assumir algumas premissas, muitas delas irrealista, como por exemplo a taxa livre de risco re a volatilidade σ são consideradas constantes.

Devido ao fato de que muitas dessas premissas não representarem a realidade, a robustez do modelo de Black-Scholes é constantemente abordado em diversos estudos e debates, muitos desses trabalhos são conhecidos como extenssões do modelo de Black-Scholes.

Em (HULL; WHITE, 1987) mostram em seus resultados que o preço obtido pela equação de Black e Scholes estão frequentemente a acima do “preço justo”de uma opção do tipo europeia com volatilidade estocástica e essa frequência aumenta para opções com vencimentos mais longos.

(MERTON, 1976) obteve resultados similares anos antes, quando estudou o pro-blema de descontinuidade, existência de saltos(“jumps”), no processo dos preços dos ativos objetos. Em seus resultados, Merton observou uma tendência do modelo de Black-Schole de preciﬁcar do “preço justo” as opções que estão deep-in-the-money, deep-out-the-money e para vencimento de curto prazo1_.

(17)

Abordando tanto parâmetros estocástico como descontinuidades(jumps) no processo

dos preço, André C. Maiali em (MAIALI, 2006) obteve resultados promissores para estratégia dinâmica de hedging para portfólios com posições vultosas, mostrando ser

uma estratégia mais eficiente em relação a estrategia originada do modelo de Black-Scholes conhecida como delta-neutra. No entando, para portfólios com posições de volumes financeiro menores, não apresenta um ganho significatido devido a complexidade de implementação do modelo sugerido.

Estudando o impacto em uma estratégia dehedging quando a volatilidade é

des-conhecida e é mal especificada, (KAROUI; JEANBLANC-PICQUÈ; SHREVE, 1998) demostram em seu trabalho que caso a volatilidade for má especificada e esta dominar a verdadeira volatilidade , então o valor do auto-financimaneto do hedging do portfólio mal especificado excede o valor da opção no vencimento. Obtendo resuldado semelhan-tes, (MARTINI, 1995) utilizou de métodos de semigrupos para resolver o problema da volatilidade mal especificada.

Um importante resultado para o desenvolvimento dessa dissertação, foi obtido em (GAXIOLA; SANTIAGO, 2012), neste trabalho Santiado e Gaxiola consideraram a equação de Black-Scholes como sendo um problema de Cauchy e mostraram que o operador diferencial de segunda ordem ˆAu=ax2_D2_u₊_bxDu₋_bu_com_{a, b}_∈_R_{e deﬁnido no espaço}

de Schwartz é um operador gerador de C0-semigrupo.

Os capítulos seguintes dessa dissertação estão estruturados da seguinte forma. No capítulo 2, estabelecemos o roteiro de conhecimento preliminar, com resumos dos principais pontos teóricos necessários para o desenvolvimento tais como a resolução analítica do modelo de Black-Scholes e a sua representação na forma de equação diferencial ordinária abstrata.

No capítulo 3, o principal resultado desta dissertação é apresentado ao quantiﬁ-carmos a robustez do modelo de Black-Scholes introduzindo de maneira implćita uma medida de sua robustez no que concerne às incertezas nas hipóteses e nas determinações algorítmicas de seus parâmetros (α e r).

Conforme se pode perceber pela descrição geral deste resultado como foi menci-onado acima, um papel preponderante neste estudo de robustez é desempenhado pela norma do operador Lα. Assim, no capítulo 4, apresentamos o algoritmo que fornece uma caracterização da norma deste operador através da introdução de um problema de controle ótimo linear quadrático.

(18)

são deixadas para os anexos.

Finalmente, no capítulo 6 apresentamos a conclusão deste trabalho bem como as pesquisas futuras.

O conteúdo desta dissertação é original num sentido forte por duas razões. Primeiro, sua concepção parte da iniciativa de aplicar técnicas da área de Controle Determinístico para apresentar uma medida de robustez para os parâmetros estruturais que aparecem no clássico modelo de Black-Scholes, o qual diz respeito à dinâmica de fenômenos que são estocásticos por natureza. Como a fonte desta iniciativa está apenas na consideração dessas técnicas, o trabalho é original num primeiro sentido pelo fato de não se originar em alguma pesquisa na literatura de Finanças Quantitativas. Em particular, esta característica do trabalho acaba sendo um fator que trouxe alguma dificuldade em se produzir uma revisão bibliográfica suficientemente abrangente sem incorrer em afastamentos do foco do que foi efetivamente desenvolvido nesta dissertação — em outras palavras, a investigação desenvolvida aqui não está atrelada propriamente a uma relação com a literatura padrão desta área de pesquisa.

(19)

18

2 Preliminares

2.1 Derivativos e o modelo de Black-Scholes

Uma opção é um contrato de direito sobre um ou mais ativos, o qual outorga ao detentor o direito (mas não a obrigação) de comprar ou vender o(s) ativo(s), também conhecido como ativo base ou ativo objeto, por um valor previamente acordado no início do contrato. As opções são derivativos ﬁnanceiros e o seu preço bem como suas características estão vinculados ao ativo base.

O detentor do uma opção deve pagar um prêmio v ao vendedor(lançador) do derivativo, o prêmio é o valor pago pelo direito de comprar ou vender o(s) ativo(s) em uma data futura a um preço previamente acordado, também conhecido como preço da opção, o prêmio pode ser estimado através da equação de Black-Scholes.

A equação de Black-Scholes(2.1) é uma equação diferencial parcial(EDP) linear e parabólica que depende do preço do ativo objeto x e do tempo t, além dessas variáveis , a equação também têm como parâmetros a volatilidade σ e a taxa livre de risco r. Black e Scholes utilizaram da estratégia de delta hedging e realizando ohedging continuamente no

tempo, chegaram na seguinte EDP de segunda ordem:

∂v

∂t(t, x) + 1 2σ2x2

∂2_v

∂x2(t, x) +rx

∂v

∂x(t, x)−rv(t, x) = 0 (2.1) Para utilizar o modelo de Black-Scholes é necessário obedecer as premissas abaixo:

1. A taxa de juros livre de risco é conhecida e constante ao longo do tempo.

2. O preço do ativo segue um passeio aleatório, com distribuição lognormal e volatilidade constante dos retornos diários.

3. O ativo não paga dividendos ou outros benefícios.

4. A opção é do tipo européia.

5. Não há custos de transação.

6. É possível negociar qualquer quantidade fracionária do ativo.

7. Não há impedimentos à venda a descoberto.

(20)

Capítulo 2. Preliminares 19

A equação de Black-Scholes admite uma solução analítica explícita, uma das ma-neiras de se obter esta solução é, primeiro fazendo mudanças de variáveis para transformar o problema envolvendo a equação diferencial parcial em um problema de valor inicial envolvendo a equação do calor; depois, este problema é resolvido usando-se transformada de Fourier e a solução ﬁca sendo

vo(t, x) = xφ(g(t, x))₋Ke−r(T −t)φ(g(t, x)) , (2.2) onde

φ(z) =Z ∞ z e

−η2

2 dη

e

g(t, x) = ln   x K 

+ (T −t)  r+

σ2

2

 

σ√T ₋t

2.2 Representação da equação de Black-Scholes como EDO

abs-trata

Vamos considerar a equação de Black-Scholes no contexto do seguinte problema de Cauchy:            ∂v ∂t =−

1 2σ2x2

∂2_v

∂x2 −rx

∂v

∂x +rv , (t, x)∈]0, T[×(0,∞) v(T, x) = ϕ(x) , x >0.

(2.3)

Aqui, σ é a volatilidade do ativo, r _∈ R é a taxa de juros livre de risco, ambos

assumidos comos sendo invariantes no tempo ao longo do horizonte [0, T], e T > 0 é o tempo de maturidade do derivativo. No caso deste ser um modelo para uma opção de compra européia,v(t, x) representa o preço (valor) da opção como função do tempo t e do preço x do ativo. Sobre a função ϕ, exigimos que ela seja uma função mensurável. Por exemplo, no caso desta opção dar ao seu detentor o direito de comprar um ativo num tempo especiﬁcado T por um preço K, a funçãoϕ seria dada por ϕ(x) = max_{x₋K,0_}. É nosso propósito escrever esta equação como uma equação diferencial ordinária abstrata em termos de operadores em espaços de funções na forma

dV(t)

dt =AV(t) (2.4)

Seja o operador linear ˆA dado por

ˆ

Av=₋1 2σ

2_x2∂2v

∂x2 −r x

∂v ∂x −v

!

(21)

densamente deﬁnido no espaço de Banach Lp_(0,_∞_{), com o domínio}

D( ˆA) = So , (2.6)

onde _So denota o espaço de Schwartz com a norma do supremo,

So ={f ∈C∞(0,∞) ; ∀ α, β ∈N , sup x |x

α_Dβ_f(x)

|<_∞}. (2.7) De posse do operador ˆA, vamos introduzir o operador linear (sendo 0 o operador identicamente nulo)

A=

 

ˆ

A 0

0 Aˆ



 (2.8)

densamente deﬁnido no espaço de Banach

X =Lp(0,∞)×Lp(0,∞). (2.9)

O fato do operador linear A ser construído como uma matriz 2_×2 é para permitir perturbações estruturadas, reservando a entrada a11 da matriz para perturbações dando

conta de incertezas na volatilidade (σ) e a entradaa22 para perturbações dando conta de

incertezas na taxa livre de risco (r).

A rigor, a equação diferencial abstrata (2.4) resulta de mudarmos o ponto de vista para olhar o preço ui(t, x) da opção (denotandoV = [u1 u2]⊤) não como uma função de

duas variáveis 0 ≤t _≤T e x >0, mas sim da seguinte forma:

(i) Fixamos t _∈ [0, T] e introduzimos a função (ui)t : (0,_∞) _→R deﬁnida, para

cada t ﬁxado, pondo

(ui)t (x) =ui(t, x) , _∀x >0.

Isto resulta numa família de funções{(ui)t}t∈[0,T] da variável x. Na verdade, temos

aqui uma família de variáveis aleatórias, dada a natureza estocástica do preço do ativo, a variável x. Porém, isto não precisará ser levado em conta em nossos estudos, uma vez que a heterocedasticidade do preço do ativo estará camuﬂada como incerteza conﬁgurada através de uma perturbação determinística dependente do tempo d(t).

(ii) A partir daí, introduzimos a funçãoui : [0, T]→X dada por ui(t) = (ui)t , _∀t _≥0,

onde X é um espaço de Banach tal como (C[0,_∞),_||._||∞) ou, o que será o nosso caso,

(Lp_(0,_∞_),_||_._||_{p) com} _p_{= 2.}

(iii) Finalmente, introduzimos o vetor-coluna

V(t) =

 

u1(t)

u2(t)

 =

 

(u1)t

(u2)t

(22)

que deﬁne a função V(t) : (0,_∞)_→R2×1 que associa a cada _{x >}0 o vetor-coluna _V(t)_x

dado por

V(t) x=

 

(u1)t(x)

(u2)t(x)

 =

 

u1(t, x)

u2(t, x)

  .

O fato do operador matricial linearA envolver operadores diferenciais que, como tais, não são limitados, vamos tomar o domínio do operador A como sendo

D(A) = So× So, (2.10)

onde _So é o espaço de Schwartz com a norma do supremo introduzido acima.

Note que neste formalismo o operador A:_D(A)_→X é deﬁnido como sendo dado por AV =   ˆ A 0

0 Aˆ

 .   u1 u2   ,

denotando A(V(t)) simplesmente por AV e identiﬁcando V(t) = (u1(t), u2(t)) ∈ D(A)

com o vetor coluna [u1 u2]⊤ por isomorﬁsmo.

Desta forma, a equação (2.4) na verdade signiﬁca a descrição redundante

             ∂u1

∂t =− 1 2σ2x2

∂2_u 1

∂x2 −rx

∂u1

∂x +ru1

∂u2

∂t =− 1 2σ

2_x2∂2u2

∂x2 −rx

∂u2

∂x +ru2 .

Porém, este acaba sendo um preço a pagar em troca de se conﬁgurar perturbações independentes na estrutura (i.e., nos parâmetros constitutivos dos coeﬁcientes) da equa-ção de Black-Scholes. De qualquer forma, este ônus pode ser minimizado, por exemplo restringindo-se o _D(A) de maneira a incorporar condições de fronteira ou na maturidade T diferentes para cada equação.

2.3 Semigrupos

A representação de uma solução de problemas abstratos na forma

dE

dt =AE+g(t) , E(0) =Eo ∈ D(A) , A dado em (2.8), é formalizada usando-se o conceito de semigrupo como ferramenta fundamental.

Seja X um espaço de Banach. Uma família _{U(t)_}t≥0 de operadores lineares

limitados em X é chamada de semigrupo fortemente contínuo (ou Co-semigrupo)

se e somente se (sse) as seguintes propriedades são satisfeitas:

(23)

(S2) U(0) =I.

(S3) Para cadau_∈X, U(t)u é contínua na topologia de X em t= 0.

Lembramos que, se X eY são espaços normados, um operador linear U :X _→Y é limitado sse existe M _≥0 tal que _||U x_{|| ≤}M_||x_|| , _∀ x_∈X.

Para operadores lineares em geral (possivelmente não-limitado), costumamos es-peciﬁcar como operador linear o par (_D(U), U), onde _D(U)_⊆X é um subespaço de X, chamado de domínio do operador, e U :_D(U)_→Y é uma transformação linear. No caso de operadores lineares limitados, este preciosismo pode ser ignorado, uma vez que pode ser provado que o domínio _D(U) do operador linear limitado pode ser extendido para o espaço todo X. Porém, para operadores lineares não-limitados (como é o caso de operadores diferenciais, por exemplo), este resultado de extensão não acontece e precisamos tomar cuidado em especiﬁcar o domínio do operador.

Vamos denotar por _B(X) a classe dos operadores lineares limitados de X nele mesmo. É sabido que _B(X) é um espaço de Banach com a norma, chamada norma do operador,

||U_|| = sup_{||U x_|| ; x_∈X com _||x_||= 1_}

(2.11)

= sup

(

||U x_||

||x_|| ; x∈X ex6= 0

)

Temos o seguinte resultado (v. (MCBRIDE, 1987) e (RENARDY; ROGERS, 2006)) da teoria clássica estabelecendo uma estimativa para _||U(t)_||:

Teorema 2.3.1 Se _{U(t)_}t≥0 é um semigrupo fortemente contínuo de operadores lineares limitados em um espaço de Banach X, então o limite

lim t→∞log

||U(t)_||

t =ωo

existe ou tende a _−∞. Além disso, para cada γ > ωo, existe uma constante Mγ tal que

||U(t)|| ≤Mγexp(γt).

Chamamos de gerador infinitesimal de um semigrupo {U(t)}t≥0 fortemente

contínuo de operadores lineares limitados em um espaço de Banach X ao operador A :X _→X deﬁnido por

Au= lim t→0+

U(t)u−u

t , ∀ u∈X, (2.12)

(24)

Teorema 2.3.2 ((RENARDY; ROGERS, 2006), p. 236) Se A é um gerador infi-nitesimal de um semigrupo fortemente contínuo, então _D(A) é denso em X e A é um operador fechado.

Um operador (_D(A), A) é fechado sse seu gráﬁco

Γ(A) = _{(x, Ax) ; x_{∈ D}(A)_{} ⊂}X_×Y

é um conjunto fechado do espaço-produtoX_×Y (os espaços em pauta vêm da formulação A :X_→Y). O signiﬁcado de um operador ser fechado pode ser percebido pela seguinte caracterização: Um operador (_D(A), A) éfechado sse, sempre que existe uma sequência

(xn) em _D(A) tal que xn_→x eAxn_→f, então x_{∈ D}(A) e Ax=f.

O seguinte teorema dá as condições necessárias e suﬁcientes para que um operador seja o gerador inﬁnitesimas de um Co-semigrupo:

Teorema 2.3.3 (Hille-Yosida) Seja A um operador em um espaço de Banach X.

Então,

A é o gerador infinitesimal de um semigrupo fortemente contínuo _{U(t)}t≥0 satisfa-zendo _||U(t)_{|| ≤}Mexp(ωt)

se e somente se as seguintes 2 condições são verificadas:

(i) _D(A) é denso em X e A é um operador fechado.

(ii) Todo número real λ > ω está no conjunto resolvente deA e

||R(λ, A)n_{|| ≤} M

(λ₋ω)n , ∀ n ∈N,

onde estamos usando a notação R(λ, A)= (λI△ ₋A)−1_.

Dizemos que_{U(t)_}t≥0 é um semigrupo de classe Co(M, ω) quando for satisfeita a

relação

||U(t)|| ≤Mexp(ωt).

A demonstração deste teorema não somente fornece a existência de um semigrupo, como também fornece uma maneira prática de aproximá-lo, qual seja,

U(t) = lim n→∞

I₋ t nA

−n ,

o que corresponde ao esquema de diferenças

u(t+h)₋u(t)

(25)

para resolver a equação ˙u=Au.

Como em última análiseAé um operador diferencial, é de se esperar que (λI−A)−1_,

o operador inverso de (λI −A), seja um operador integral. Acontece que os operadores integrais são muito bem comportados, de maneira que pode ser provado que (λI₋A)−1 _∈

B(X), ou seja, (λI−A)−1 _{é um operador linear limitado.}

Por outro lado, de

U(t) = lim n→∞

I₋ t nA

−n

= lim n→∞

I ₋ t nA

−1!n

= lim n→∞

n t

n

tI−A

−1!n

temos ideia de como aparece em cena o operador (λI −A)−1 _{, com} _λ₌_n/t _acima.

Vamos a seguir passar a provar que nosso operadorAdeﬁnido por (2.8) é o gerador inﬁnitesimal de um Co-semigrupo, o qual nos permite obter a expressão da solução do nosso modelo abstrato. Para isto, vamos começar considerando a equação de Black-Scholes como o seguinte problema de Cauchy (2.3):

           ∂u ∂t =−

1 2σ2x2

∂2_u

∂x2 −rx

∂u

∂x +ru , (t, x)∈]0, T[×(0,∞) u(x, T) = ϕ(x) , x_≥0.

Em (GAXIOLA; SANTIAGO, 2012), González-Gaxiola e Santiago mostraram que o operador ˆA, associado à equação de Black-Scholes e deﬁnido por (2.5), é o gerador inﬁnitesimal de um Co-semigrupo _{Uˆ(t)_}t≥0 . Essencialmente, o procedimento naquele

trabalho passa por introduzir como que uma mudança de variáveis nos parâmetros, fazendo

ζ = 1 σ2

r₋ 1 2σ

2

e deﬁnindo um operador _A¯_{através de}

¯

Au:=x2 ∂

2

∂x2u+ (2ζ+ 1)x

∂

∂xu−(2ζ+ 1)u , com _D( ¯A) =_So. É fácil ver que

1

2σ2A¯=−Aˆ

e provado que _A¯_{pode ser escrito como}

¯

A= (B +ζ)2₋(1 +ζ)2 ,

ondeBé o gerador de umCo-grupo e(B+ζ)2_{é a notação para a composição}₍_B₊_ζ₎_◦₍_B₊_ζ₎_.

A prova de que_{A, e consequentemente}¯ _{A, geram um semigrupo}ˆ _{_Uˆ₍_t₎_}_t_≥₀ _em_S_o _{é expressa}

(26)

Lema 2.3.1 (González-Gaxiola & Santiago) Seja (V(t)u) (x) = u(xet₎ _{para todo} u_{∈ S}o , x≥0 e t ∈R. Então, ||V(t)||= 1 para todo t e {V(t)}t∈R é um Co-grupo em S_o

com gerador

Bu =x ∂ ∂xu

e domínio _D(B) =_S(0,_∞) =_So.

Teorema 2.3.4 (González-Gaxiola & Santiago) O operadorAˆ, com domínio_D( ˆA) =

So, é o gerador infinitesimal de um Co-semigrupo de operadores{Uˆ(t)}t≥0 em So dado por ( ˆU(t)u) (x) =

Z ∞ −∞e

−12s 2

V

s√σ2_t ₊

r₋ 1 2σ2

t

u

(x)ds , (2.13)

para cada u_{∈ S}o , t≥0 e x≥0.

Em particular, foi mostrado em (GAXIOLA; SANTIAGO, 2012) que no caso particular de Lp(R), 1_≤_{p <}_∞_, _{(lembramos que} _S_o _{é um subespaço denso de}_Lp(R)_{), o}

Co-semigrupo gerado porAˆ é o chamadosemigrupo do calor dado por

( ˆU(t)f) (x) = √1

4πt

Z ∞ −∞e

−(x−y)2

rt _f(y)dy _(2.14)

e também foi mostrado que, para todo t >0, tem-se

||Uˆ(t)_{|| ≤}1 , (2.15)

de forma que cada Uˆ(t)é um operador linear limitado em Lp₍_R₎_.

Este caso do semigrupo do calor é especialmente interessante porque, conforme consta na Introdução, a equação de Black-Scholes e condições de fronteira para uma opção de compra européia formalizado como o de encontrar uma função F _∈C2_{(]0, T}_[_×_]0,_∞₎₎_∩

C([0, T]_×[0,_∞))satisfazendo

∂F

∂t(t, x) + 1 2σ2x2

∂2_F

∂x2(t, x) +rx

∂F

∂x(t, x)−rF(t, x) = 0 ,

para (t, x)_∈]0, T[_×]0,_∞), e sujeito às condições

F(t,0) = 0 , lim x→∞

F(t, x)

x = 1 , F(T, x) = max{x−K,0} ,

pode ser transformado numa equação do calor com condição inicial.

No caso de nosso operador (2.8)

A=

 

ˆ

A 0

0 Aˆ

  ,

(27)

Proposição 2.3.1 Seja X =_So× So. O operador A dado por (2.8) é o gerador

infinite-simal do Co-semigrupo _{U(t)_}t≥0 ⊆ B(X) dado por

U(t) =

 

ˆ

U(t) 0 0 U(t)ˆ



 , (2.16)

onde nUˆ(t)o

t≥0 é o Co-semigrupo gerado pelo operador de Black-Scholes

ˆ A.

Prova: Sejau= [u1 u2]⊤ ∈X. Então,

U(t)u=

 

ˆ U(t)u1

ˆ U(t)u2

  ,

de forma que

lim t→0+

U(t)u₋u

t = limt→0+

        ˆ

U(t)u1−u1

t

ˆ

U(t)u2−u2

t         =      ˆ Au1 ˆ Au2      . Como _  ˆ Au1 ˆ Au2  =   ˆ A 0

0 Aˆ

 .   u1 u2 

=Au ,

o resultado segue.

Do fato de que _D( ˆA) = _So é denso em Lp(0,∞) segue que D(A) é denso em X.

Para provar isto, vamos deﬁnir _|||._|||:X _→R _pondo

|||u_|||=X2

k=1

||uk|| , ∀u= [u1 u2]⊤∈X , (2.17)

que reconhecidamente deﬁne uma norma em X. Mais que isto, temos que se (Y,_||._||Y)é

um espaço de Banach, então (Y _×Y _×Y,_|||._|||) também é um espaço de Banach.

Proposição 2.3.2 _D(A) é denso em X =Lp_(0,_∞₎_×_Lp_(0,_∞_).

Prova: Seja [f g]⊤ _∈_X_{. Como} _D_{( ˆ}_A) _{é denso em} _Lp_(0,_∞_), _{existem sequências} _(fn)_e (gn) de elementos em _D( ˆA) tais que

||fn₋f_{|| →} 0,

||gn−g|| → 0,

quando n _{→ ∞}. Temos que, com a norma dada por (2.17),

|||   fn gn  −   f g 

(28)

de forma que [f g]⊤_{é o limite de uma sequência de elementos de}

D( ˆA)_{× D}( ˆA) =_D(A).

A relevância de introduzirmos aqui o conceito de semigrupo é que ele nos permite dar uma representação da solução do problema abstrato de valor inicial da forma:

du

dt =Au+g(t) , u(0) =uo ∈ D(A) , (2.18)

com g _∈ C([0, T];X), onde o operador A é o gerador inﬁnitesimal de um semigrupo fortemente contínuo _{U(t)_}t≥0. Uma solução (clássica) de (2.18) é, por deﬁnição, uma

função u_∈C([0, T];X)_∩C([0, T];_D(A)) que satisfaz (2.18).

Teorema 2.3.5 (Teorema de representação) Seja u uma solução clássica de (2.18). Então, u é representado pela fórmula

u(t) = U(t)uo+

Z t

0 U(t−s)g(s)ds. (2.19)

Nosso objetivo aqui será apresentar uma representação da solução da equação

dE

dt =AE+f(t, E(t)) , (f contínua) , sujeita à condição inicial E(0) = 0_∈X, como sendo

E(t) =

Z t

0 U(t−s)f(s, E(s))ds , (2.20)

(29)

28

3 Uma medida de robustez para o modelo de

Black-Scholes

Vamos aqui estabelecer o principal resultado desta dissertação, que quantiﬁca a robustez do modelo de Black-Scholes ao introduzir de maneira implícita uma medida de sua robustez no que concerne às incertezas nas hipóteses e nas determinações algorítmicas de seus parâmetros (σ e r).

3.1 Formulação do erro via perturbações estruturadas

EmX =L2₍₀_{, T}₎_×_L2₍₀_{, T}₎_,_{que é um espaço de Hilbert (espaço métrico completo}

com a norma oriunda do produto interno usual deste espaço), vamos considerar o seguinte sistema perturbado da equação de Black-Scholes:

            

dZ

dt =AZ+

2

X

k=1

DkFk(CkZ(t), t), t_∈[0, T],

Z(0) =Vo _{∈ D}(A)

(3.1)

Formular o sistema em X signiﬁca que a solução da equação diferencial abstrata é entendida como sendo uma função Z : [0, T] _→ X que associa a cada t _∈ [0, T] uma

função Z(t) : (0,_∞)_→R2×1 _{na classe} _D₍_A_{) =}_S

o× So.Os operadores Dk eCk são dados do problema e são operadores (matrizes formais 2_×qk epk_×2, respectivamente, com cada

pk, qk_{∈ {}1,2_}) deﬁnidos em_D(A)e servem para descrever quais entradas da matriz formal

A são perturbadas. No capítulo 4 estaremos identiﬁcando estes operadores matriciais para o caso de perturbação apenas na volatilidade do ativo base no modelo de Black-Scholes.

Para dar conta das incertezas estruturadas, cada aplicação Fk :Rpk×1

×[0, T]_→

Rqk×1 é assumida como satisfazendo a condição de Lipschitz, no sentido de que existe um

número positivo γk tal que

||Fk(x, t)₋Fk(y, t)_{|| ≤}γk_||x₋y_|| para quaisquer x, y _∈Rpk×1

. (3.2)

Estaremos denotando

γ = max_{γ1, γ2}. (3.3)

(30)

Capítulo 3. Uma medida de robustez para o modelo de Black-Scholes 29

perturbado (3.1) acima e V : [0, T]_→X é a solução do sistema nominal

           dV

dt =AV, t∈[0, T], V(0) =Vo ∈ D(A)

(3.4)

Derivando ambos os membros (_E˙ _{= ˙}_Z₋_V˙_{), obtemos o seguinte problema de valor}

inicial (PVI)              dE

dt =AE+

2

X

k=1

DkFk(CkZ(t), t) , t_∈[0, T] ,

E(0) = 0

(3.5)

De acordo com a expressão (2.19), a solução do pvi (3.5) é dada por

E(t) =Z(t)₋V(t) =

Z t

0 U(t−s) 2

X

k=1

DkFk(CkZ(s), s)

!

ds

ou seja,

Z(t) =V(t) +

Z t

0 U(t−s) 2

X

k=1

DkFk(CkZ(s), s)

!

ds (3.6)

Denotando

CkV(_·) = yk(_·) , CkZ(·) = vk(·) ,

que são funções de [0, T]emRpk×1, podemos expressar a nova representação para a solução

do pvi como sendo

vk(t) = yk(t) +Ck

Z t

0 U(t−s) 2

X

k=1

DkFk(vk(s), s)

!

ds , (3.7)

para cada t _∈[0, T].

Neste ponto, com o propósito de condensar a formalização, vamos introduzir o operador Lk deL2₍₀_{, T}₎ _em _L2₍₀_{, T}₎_{) deﬁnido por}

Lkv (t) = Ck

Z t

0 U(t−s) 2

X

k=1

DkFk(vk(s), s)

!

ds , (3.8)

bem como o operador _F˜ _{deﬁnido por}

˜

F v (t) :=

2

X

k=1

DkFk(v(t), t) (3.9)

de forma a escrevermos a equação (3.7) na forma condensada

(31)

3.2 Técnica do escalonamento

Com o propósito de permitir uma certa ﬂexibilidade na estrutura que possibilite estudos de aperfeiçoamento dos resultados, vamos considerar funções reais positivas e contínuas αk(_·) : [0, T] _→ R+ , com _k _{= 1}_,₂,e multiplicá-las em ambos os membros de

(3.7), resultando no sistema de equações

αk(t)vk(t) =αk(t)yk(t)+ (3.11)

+αk(t)Ck

Z t

0 U(t−s)

1

αk(s)

2

X

k=1

Dkαk(s)Fk 1 αk(s)

αk(s)vk(s), s

!!

ds,

para k = 1,2.

Com o propósito de condensar o formalismo ainda mais, vamos denotar

vα(_·) =

 

α1(·)v1(·)

α2(·)v2(·)

 =

 

α1(·)C1Z(·)

α2(·)C2Z(·)

 

yα(_·) =

 

α1(·)y1(·)

α2(·)y2(·)

 =

 

α1(·)C1V(·)

α2(·)C2V(·)

 

e introduzir os seguintes novos operadores:

( Cα ) Considere a aplicação Cα(_·) : [0, T] _→ X tal que, a cada t _∈ [0, T], associa a

aplicação

Cα(t) : X _−→ L2₍₀_,_∞₎_×_L2₍₀_,_∞₎

u _7−→ Cα(t)u

com Cα(t)u deﬁnido, para cada u= (u1, u2)∈L2(0,∞)×L2(0,∞), por

(Cα(t)u) (x) =

      

α1(t)x2

∂2_u 1

∂x2

α2(t)x2

∂2_u 2 ∂x2        . (3.12)

( Dα ) Considere a aplicação Dα(·) : [0, T] → X tal que, a cada t ∈ [0, T], associa o operador

Dα(t) : R2×1 _−→ R2×1

µ _7−→ Dα(t)µ com Dα(t)µdeﬁnido por

Dα(t)µ=

"

1

α1(t)

D1

1

α2(t)

D2 #  µ1 µ2  = 2 X k=1 1

(32)

( Fα ) Considere a aplicaçãoFα :R2×1_×[0, T]_→R2×1 _{deﬁnida por}

Fα(µ, t) :=

 

α1(t)F1(α1(t)−1µ1, t)

α2(t)F2(α2(t)−1µ2, t)



. (3.14)

e seja o operador Fα˜ :X _→X deﬁnido, para cada g _∈X, por

˜

Fαg (t) =Fα(g(t), t) , _∀ t_∈[0, T].

Proposição 3.2.1 Fα˜ satisfaz a condição de Lipschitz com γ,

||Fαg˜ ₋Fαh˜ _{|| ≤}γ._||g₋h_|| , _∀ g, h_∈X.

Prova. Dados quaisquer g = (g1, g2) and h= (h1, h2) em X, temos

P2

i=1

RT

0 |αi(t)Fi(αi(t)−1gi(t), t)−αi(t)Fi(αi(t)−1hi(t), t)| 2

dt_≤ =P2

i=1

RT

0 αi(t)2|Fi(αi(t)−1gi(t), t)−Fi(αi(t)−1hi(t), t)| 2

dt

≤P2

i=1γ2

RT

0 |gi(t)−hi(t)|2dt

de onde o resultado segue.

Com a introdução destas novas aplicações, a equação (3.11) passa a ser expressa na seguinte maneira mais condensada

vα(t) =yα(t) +Cα(t)Z t

0 U(t−s)Dα(s)( ˜Fαvα)(s)ds . (3.15)

Finalmente, vamos introduzir um novo operador de entrada-saídaLα: considere o operador

Lα : X _−→ X

µ _7−→ Lαµ

com Lαµ: [0, T]_→R2×1 _{deﬁnido por}

Lαµ(t) =Cα(t)Z t

0 U(t−s)Dα(s)µ (s)ds . (3.16)

Com isto, temos por ﬁm (3.15) expressa da seguinte forma:

vα =yα+Lα

˜

Fαvα

. (3.17)

(33)

3.3 Condicionamento do erro

Em conexão com a expressão paraE(T),

E(T) =

Z T

0 U(T −s)Dα(s) ˜Fα(vα(s), s)ds

vamos introduzir o operador linear Mα :X _−→R2×1 pondo

Mαu:=

Z T

0 U(T −s)Dα(s)u(s)ds , ∀ u∈X. (3.18)

Temos que este operador linearMα é limitado. De fato, para cadaw_∈X,

||Mαw||2 ≤

_R_T

0 ||U(T −s)Dα(s)w(s)||ds

2

≤ e2µT _R_T

0

P2

j=1αj(s)−1Djwj(s)

ds

2

, para algum µ_∈R_,

≤ e2µT P2

j=1||Dj||.(maxsαj(s)−1).R0T ||wj(s)||ds

2

≤ e2µT_._(max

j||Dj||).(max{maxsαj(s)−1}) 2T2.||w||2X onde ﬁzemos uso das desigualdades

P2

j=1aj

2

≤ 2P2

j=1a2j ,

_R_b

a|f(t)|dt

2

≤ (b₋a)Rb

a|f(t)|2dt

,

que resultam da desigualdade de Cauchy-Schwartz em diferentes espaços de medidas.

Uma vez estabelecido que Mα é uma aplicação linear limitada, tomamos a norma

||Mα_||= sup_{||Mαu_|| ; _||u_||= 1_} . (3.19)

É fácil ver que o operador adjundoM∗

α :R2×1 −→X é dado por

(M∗

αµ)(t) =

 

α1(t)−1(D1)⊤U(T −t)∗µ

α2(t)−1(D2)⊤U(T −t)∗µ



 , ∀µ∈R2×1. (3.20)

Sendo assim, a existência de solução E(_·) para o problema (3.5) é equivalente à

existência de algum vα tal que

vα =yα+Lα( ˜Fαvα) , (3.21)

onde yα é ﬁxado, e o estado ﬁnalE(T) é dado por

E(T) = Mα( ˜Fαvα) (3.22)

(34)

Teorema 3.3.1 Suponha que

γ < 1

kLα_k

Então, temos que

||Z(T)−V(T)|| ≤ ₁γkMαk

−γ_kLα_kkyαk (3.23)

onde yα =Cα(·)Vo(·) e cada aplicação Vo(t) : (0,∞)→L2([0, T]×R+;R2×1) é definida

por

(Vo(t)) (x) :=

 

vo(x, t) vo(x, t)



 , ∀ x >0 ,

e é fixada com vo(x, t) sendo a solução da equação de Black-Scholes para condições inicial e de fronteira fixadas.

Proof. Parayα ﬁxado, deﬁna o operador Hα deX nele mesmo pondo

Hαu=yα+Lα( ˜Fαu) _∀u_∈X

Temos, para cada g, h_∈X,

kHαg−HαhkX = kLα( ˜Fαg−F˜αh)k

≤ kLα_k._kFαg˜ ₋Fαh˜ _k

≤ kLα_kγ_kg₋h_k

Uma vez que_kLα_kγ <1, segue queHα é uma contração estrita. Consequentemente, resulta do clássico Teorema da Aplicação Contrativa da Análise Funcional que existe um único ponto ﬁxo

¯

u= (¯u1,u¯2)∈X tal que Hαu¯= ¯u.

Sendo assim, deﬁna v _∈X pondo vi(t) =αi(t)−i 1u¯i(t). Então, vα =yα+Lα( ˜Fαvα)

e

kvα_{k ≤ ||}yα_||+_||Lα_||._||Fαvα˜ _||

≤ ||yα_||+_||Lα_||γ _||vα_||

de onde (1_{− k}Lα_kγo)_kvα_{k ≤ k}yα_k, uma vez que_kLα_kγo <1. Desta forma,

||vα_{|| ≤} 1

1_{− ||}Lα_||γ||yα|| .

Por outro lado, a equação (3.22) permite escrever

||E(T)_||R2×1 ≤ ||Mα||.γ.||vα||

e o resultado segue.

Vamos nos referir ao limitante superior

fα(γ) = γ ||Mα||

(35)

como condicionamento ponderado.

Um aspecto bem-vindo do teorema 3.3.1 é a presença da função-peso α= (α1, α2)

que, por um lado, possibilita um aperfeiçoamento na condição γ_||Lα|| < 1, que pode

eventualmente ser satisfeita mesmo quando γ_||L_{|| ≥}1, e, por outro lado, abre uma frente

de investigação com estudos de otimização com o propósito de obter a melhor escolha do peso α que minimize o valor de fα(γ). Porém, estes estudos não fazem parte do escopo de

presente trabalho.

Resta agora a questão sobre a obtenção das normas envolvidas em (3.24).

Com respeito à norma _||yα_||=_||CαVo_||, temos facilmente (v. (3.12)) que

||CαVo_||:=

v u u t 2 X k=1 Z T 0

αk(t)x2 ∂2

∂x2vo(t, x)

2 dt. (3.25)

Com respeito à norma de operador ||Mα||, vamos nos contentar por ora apenas

com uma estimativa. Porém, note que a presença dos pesos αk’s permite a obtenção de

estimativas menos conservadoras.

Proposição 3.3.1 A norma dada por (3.19) satisfaz

||Mα_{|| ≤}qβT

onde

β = max

  

max

0≤s≤T

1

α1(s)

!2

, max

0≤s≤T

1

α2(s)

!2  

Prova: Sejau_∈X tal que ||u_||=||u1||L2 +||u₂||_L2 = 1 e considere

Mαu=

Z T

0 U(T −s)Dα(s)u(s)ds∈

R2×1 _.

Das deﬁnições de U(t), (cf. (2.16)), e de Dα(s)u(s) , (cf. (3.13)), temos

U(T ₋s)Dα(s)u(s) =

        ˆ

U(T ₋s) 1 α1(s)

u1(s)

ˆ

U(T ₋s) 1 α2(s)

u2(s)

        ,

onde ˆU(T ₋s)uk(s) é dado por (cf. (2.14))

ˆ

U(T ₋s)uk(s) = q 1

4π(T ₋s)

Z ∞ −∞e

−(x−s)2

(36)

Assim, para Mαu dado por

Mαu=         Z T 0 ˆ

U(T ₋s) 1

α1(s)

u1(s)ds

Z T

0

ˆ

U(T ₋s) 1 α2(s)

u2(s)ds

        ,

vamos tomar a norma euclidiana emR2 :

||Mαu_||:=

  2 X k=1 Z T 0 ˆ

U(T ₋s) 1 αk(s)

uk(s)ds

2 

1/2

(3.27)

Analisemos, para dada k = 1,2 :

Z T 0 ˆ

U(T ₋s) 1

αk(s)uk(s)ds

2 . Temos que Z T 0 ˆ

U(T ₋s) 1

αk(s)uk(s)ds

2 = Z T 0 1

αk(s)Uˆ(T −s)uk(s)ds

2

≤ β_k2

Z T 0 ˆ

U(T ₋s)uk(s)ds

2 , onde

βk= max

0≤s≤T

1

αk(s) >0.

Por outro lado,

Z T 0 ˆ

U(T ₋s)uk(s)ds

2 ≤ Z T 0

Uˆ(T −s)uk(s) ds !2 ≤ Z T 0

Uˆ(T −s)

.|uk(s)|ds !2 ≤ Z T 0

Uˆ(T −s) 2 ds ! . Z T

0 |uk(s)| 2

ds

!

≤ T

onde ﬁzemos uso da desigualdade segue da desigualdade de Cauchy-Schwartz para integrais e do fato que

Uˆ(t)

(37)

Voltando a (3.27),

||Mαu_{|| ≤}

 

2

X

k=1

βk2

Z T

0

ˆ

U(T ₋s)uk(s)ds

2 

1/2

≤ β₁2T +β₂2T1/2

≤

max

k=1,2β 2

k

1/2√

T .

(38)

37

4 Determinação da norma do operador

L

_α

Vamos aqui prover uma caracterização da norma do operadorLα introduzindo um

problema de controle ótimo linear quadrátco. Para motivar o método, vamos considerar o seguinte sistema artiﬁcial

˙

x(t) = Ax(t) +Dα(t)u(t) , x(0) = 0 (4.1)

y(t) = Cα(t)x(t) (4.2)

onde A , Cα e Dα são aqueles deﬁnidos em nosso estudo acima.

Dado qualqueru_∈X, a saída y é dada em X por

y(t) = Cα(t)

Z t

0 U(t−s)Dα(s)u(s)ds

de forma que podemos escrever

y = Lαu

ky_k = _||Lαu_{|| ≤ k}Lα_k._ku_k.

Isto permite que escrevamos_kLα_k−2 _{= sup}_A _{, com}

A={ρ >0 ; _ku_k2₋ρ_ky_k2 _≥0, _∀u_∈X _},

onde y(t) =Cα(t)x(t) (x é a solução de (4.1)). Note que y também depende da entradau

, uma vez que o estado do sistema é uma função da entrada.

Sendo assim, podemos introduzir o seguinte Problema Linear Quadrático de Con-trole Ótimo no espaço X, o qual iremos nos referir como problema (OP):

Minimizar (propriamente ou não) o funcional Jρ(.) dado por

Jρ(u) =_ku_k2₋ρ_ky_k2 (4.3)

sujeito à restrição:

˙

x(t) = Ax(t) +Dα(t)u(t) , x(0) =ϕ , t_∈[0, T] (4.4) y(t) = Cα(t)x(t)

Uma notação mais esclarecedora para o funcional-custo deveria serJρ(u;ϕ,[0, T]),