Programação linear e planejamento da empresa agrícola

FUNDAÇAO GETúLIO VARGAS

ESCOLA BRASILEIRA DE ADMINISTRAÇAO PÜBLICA CURSO DE MESTRADO EM ADMINISTRAÇÃO PÜBLICA

Pot)' Reis

" PROGRj\H/\Cl~O tIN!3AR E ~~N'JEJJu"fENTO

-'---

-DA EMPRESA AGR!COLA 11

Monografia apresentada

-

a Escola Brasileira de Adminis tração Pública para a obten-ção do grau de Mestre em

Ad-ministraç~o Pública.

Rio de J3neirc~ 1978 .

. ~---~--.,---~.

FUNDAÇÃO GETOLIO VARGAS

ESCOLA BRASILEIRA DE ADMINISTRAÇÃO POBLICA CURSO DE MESTRADO EM ADMINISTRAÇÃO PÚBLICA

" PROGRAMAÇÃO LINEAR E PLANEJAMENTO DA EMPRESA AGRíCOLA "

MONOGRAFIA DE MESTRADO APRESENTADA POR

Poty Reis

E APROVADA EM

~!

/

O~

/

/7l-r

PELA COMISSÃO JULGADORA.

_.~t~@

0--%~,---NEWTON DE MELLOr.q"UELHO, PhD.,

Di-EDJ UNDO DA FONTOURA 'Livre Docente, UFPEL.

/f~

~'t)

{t-F

;3p'---cC---cfcILIO A. F. BERNDSEN,

l.601.da

e Ffâv.[a H (!.fena

à memôJz.-ta de meu PadIL-tnho e gfLande a.m-tgo

Mon~enhon

caSTABILE HIPPOLYTO

Pno;(:ono;(:âll.-tO Apo~,tÕP.-tC.O, A. I.

P.

. AGRADECIMENTOS

Cumpro o dever de apresentar sinceros agradecimentos às Instituições e pessoas seguintes:

- A

Empresa Brasileira de Pesquisa Agropecu~ria­

EMBRAPA, por me haver proporcionado a oportunidade de realizar o curso de Mestrado.

- Ao Ministério da Agricultura, pela bolsa de estudos que me foi concedida.

- Ao Prof. Dr. Newton de Mello QUELHO, incentivador e Diretor de Estudos.

- Aos meus nobres amigos, Drs. Fernando Borges de Sou za ESTÃCIO e José Manuel Coelho Verella BARROCAS, cienti$tas do Centro de Estudos de Economia Agriria do Instituto GULBENKIAN de Ciências, da Fundação Calouste GULBENKIAN, de Lisboa, pela orien

tação bibliogrifica, pelo estimulo e interesse no ~xito des~e tra

,

balho. ,;

- Ao Prof. Dr. Edmundo da Fontoura GASTAL, cujas cri ticas e sugestões enriqueceram este estudo.

- Ã Sra. Wanda Xavier BASTOS, da Fundação Getúlio Var . gas, pelo apoio e assistência constante.

- Ao Prof. Dr. Diego DIAS, pelos dados complementares e indispensaveis

ã

elaboração da parte pratica do estudo.

- Ao Dr. Heitor Amaral OLIVEIRA, Chefe do

Departamep-~ to de Projetos Especiais da EMBRAPA,pela leitura dos originais e pelas valiosas sugestões oferecidas.

- Ao Dr. Gustavo PIMENTEL, do Departamento de Métodos Quantitativos - DMQ - EMBRAPA, pela orientação e assessoria nos programas de computador.

cAPírüLO I

CAPITULO II

CONTEÚDO

P âgin a

Lista dos Quadros Lista das Figuras

• • • • • • • • • • • • e • • • • • e~ • • • • • •

...

9

10

IlE S LJIvIO •••• , ••••••• , •••••••••••• , . . . 12

o PROBLEMA E SUA U1PORTÂNCH. 1 . 1. In t )~ o U.lJ ç ã o ... tio • • • • • • .. • • • • .. • • • • • • • ,. • • • • • 1 5 1.2. O MGtodo da Programaçno Linear . . . 18

1.3. Objetivos do Trabalho . . . 19

1.4. Material e M~todos . . . 20

1.5. Revisão da Literatura . . . • . . . 21

1.6. Alcance c Limitações do Trabalho ... 24

2.1. IntroJ-llçno . . . .. 2.2. ÃJgebra d~ Programaç5o Linear . . . . 2.2.1. Representação.vetorial . . . . 2.2.2. Espaço das soluções . . . . 28 31 32 35 2.2.2.1. Conjuntos c poliedros convexos .... 35

2.2.3. O Mctodo ~~impJex ₄₁

CAPíTULO 111

Pagina

2.2.3.2. Aplicação Pratica do Algorítmo Sim

plex . . . 44

2.2.3.3. Degeneresc~ncia . . . SS

2.2.4. Dualidade . . . 57

APLICAÇÃO DO M~TODO DA PROGRAMAÇÃO LINEAR

3.1. Introdução... 64

3.2. A Empresa, seus Recursos e Limitações. 6S 3.3. Rendimentos e Preços . . . 67 3.4. Alocação e Uso dos Fatores . . . 68 3.5. Resultado Anterior da Empresa ... 71 3.6. Formulação do Prob lema para Programação 73 3.7. Resolução e Interpretação... 76

3.8. Simulação . . . 78

CON C L lJSO E S . . . e e . . . . . . . to ; e c c • 86

BIBLIOGRAFIA ANEXOS:

...

~

...

"

...

"

..

89

LISTA DOS QUADROS

Página

Quadro Q.II.l. - Primeira Iteração do Simplex . . . 47 Quadro Q.II.2. - Segunda Iteração do Simplex . . . 51 Quadro Q.II.3. - Terceira Iteração do Simplex . . . 52 Quadro Q.III.l. - Rendimentos Obtidos e Preços Unitários no

Ano AgrIco1a 1976/77 . . . 68 Quadro Q.III.2. - Quadro das Exig~ncias de Insumos por Ati

vidade e Respectiva Margem Bruta 69 Quadro Q.III.3. - Demonstrativo da Composição dos Encargos

variáveis

...

70

Quadro Q.III.4. - Resultado das Atividades da Empresa no Ano AgrIco1a 1976/77 . . . 72 Quadro Q.III.5. - Quadro das Relações Tecnológicas Fundamc~

tais ... 74

10

LISTA DAS FIGURAS

Página

Figura 1. - (la)lb) Coincid~ncia dos vetores de base com os eixos coordenados • • • • c • • • • • • • • • • • • • • • • • • • • • • • • 34

Figura 2 .

-

Combinação linear positiva de x e y

...

36

Figura 3.

-

Combinação linear convexa de x e y

...

'"

...

36

Figura 4.

-

In terse cção de conj un tos convexos

...

38

Figura 5.

-

Perfil e invólucro de um polígono convexo

...

38

Figura 6.

-

Poliedro convexo

...

38

11

RESUMO

Este trabalho tem por objetivo o estudo do m~todo da Programação Linear e de sua aplicação no planejamento da empresa agrIcola, tendo em vista a demonstração de sua import~ncia como instrumento analItico no processo de tomada de decisões.

Inicialmente ~ feita uma abordagem sobre a problem~t!

ca da programaçao e seus fundamentos, sendo examinados os princi pais conceitos sobre os quais o assunto se baseia. A discussão ~

encaminhada no sentido de chamar a atenção para o fato de que, em vista das pressões a que esti submetida a agricultura no estigio con temporâneo do desenvol vimen to, - que lhe exigem me lhores nI veis de desempenho traduzidos em Indices mais elevados de produtivida-de, - generalizou-se o consenso sobre a conveniência de se dar maior atenção

i

programação das atividades do setor agrIcola, tanto a nIvel de Região como no ~mbi to de sua irea empresarial. Entre os virias modelos gerados com o objetivo de oferecer respostas aos prob lemas de organi zaçãa da produção, otimi zação de res uI tados c racionalização do uso dos fatores, o da Programação Linea~ ~ co!?-_ siderado o mais geralmente aceito pela comunidade cientIfica, por sua estrutura teóric.él sofisticada e pela capacidade de dar Yespo~

tas exatas e diretas a questões de maior complexidade.

minada no Capítulo 11. De maneira sumária sao abordados os seus fundamentos matemáticos e discutidos os principais teoremas sobre conjuntos convexos, corno elementos do espaço das soluções possi-veis. A álgebra do algorÍtmo Simplex ~ abordada em sua forma ardi nária, com a demonstração dos passos sucessivos do algoritmo, at~

o encontro do v~rtice característico da solução otima.

No Capítulo 111 os conceitos teoricos da Programação Linear sao aplicados aos dados de uma empresa agricola, com a fi , nalidade de demonstrar a operacionalização do algoritmo Simplcx !

través de programas de computador.

CAPITULO I

O PROBLEMA E SUA IMPORTÂNCIA

1.1. In trodução

A agricultura brasileira contepor~nea, ante o extraor dinirio desenvolvimento que empolgou o país nos ~ltimos anos, tem sido cada vez mais exigida e pressionada no sentido de melhorar a sua atuação e de elevar os seus níveis de desempenho. Em função disso, passou a enfrentar urna s~rie de problemas de transformação e de adaptação, cujas soluções exigem, além da ampliação de suas possibilidades tecno16gicas, ainda o concurso de outros elementos de juízo, corno organização da produção e planejamento da ativida de agrícola. E isso porque, tendo transicionado - em seu segmento empresarial - de um estado tradicional para uma condição de merea do, onde suporta custos, encargos e concorr~ncias crescentes, a !

gricultura transformou-se num neg6cio como outro qualquer, com le gítimas aspirações a rendas mais elevadas.

Por outro lado o agricultor, -como qualquerempres~rio,

face aos modernos me ios de com uni cação que lhe proporciona r mn novas

experi~ncias Je relacionamento com o mercado, tem consci~ncia de

que o seu prob lema COllS is te na bus ca d a maior renda pos s í ve 1 par3

o seu negócio, de formas a remunerllr (lO máximo o seu capi tal e o

blemas de opção, para a solução dos quais o seu conhecimento dos estados da natureza e dos determinantes econ6micos - que t~m ori gem em circunstâncias rlhcias ao seu âmbito de influência - nao são, geralmente, suficientes para a tomada da melhor decisão. Exis te, aliás, um consenso entre os teóricos e pesquisadores, de que este

6

um problema universal e de que mais do que novas tecnolog! as de produção - pelo menos em tempo imediato - o produtor carece de orientação e auxílio sobre como organizar e planejar da forma mais conveniente as atividades de seu estabelecimento, com base em técnicas já conhecidas. Diz PEREIRA (62,63) que "a.6 .6oüc..i:taçõe..6

que. o aglLic..u.t:tOlL dilLige.

ã

Ciê.l1ua AglLonômic..a inc..ide.m agolLa tI1ai,~

.60blLe. a l1a:tulLe.za dM a:tividade..ó a que. de.ve. dalL plLiolLidade. e. .6obJl..e.

a 60lLma c..omo de.\.Je. c..ombinalL 0.6 me.io.6 de. plLodução" do que sobre qual

quer outro aspecto da técnica de produzir.

Realmente, hoje em dia, tendo presente o estágio atual da tecnologia agrícola, os problemas puramente técnicos da produ çao, aqueles que se referem ao. "como" produzir, não são os que mais afligem o agricultor e nem se constituem em fatores limitan

tes do desenvolvimento e do melhor desempenho da agricultura con temporânea. De uma maneira geral, as modernas técnicas cul turais, a mecanização, os fertilizantes e defensivos, a genética aplicada possibilitando a obtenção de novas cultivares, constituindo sist~

mas tecnológicos de diversos níveis, vulgarizados e postos

à

dis posição dos agricultores, possibilitam um considerável ailllento quantitativo e qualitativo da produção agrícola. O atual desenvol vimento da pesquisa física e biológica, mantém crescente esse qU! dro de possibilidades, assegurando a continuidade da capacidade de produção da agricultura.

Assim, outros componentes de juízo, no quadro de doci soes da administração da empresa rural, assumem maior relevância do que aqueles referentes a técnicas isoladas de produç~o, em si. São os problemas relacionados com o que e em que quantidade prod~

zir, onde e como colocar a produç50 no mercado, como enfrentar as variações dos preços dos produtos e o agravamento dos custos dos insumos e de como dimensionar a intensidade das atividades da em presa ugrícola, tendo em vista a remuneração mais conveniente do esforço e do risco. (1). Decorre daí que os métodos tradicionais

de tomar decisões no setor agrícola deverão ceder lugar, em bre ve, ao planejamento acurado das atividades, objetivando o encontro de soluções para as questões ant~s formuladas.

De fato', o planejamento e programação da agricul tura como um todo e, em particular, da organização para a produção a nIvel de empresa agrícola, tem se generalizado em quase todo mun do nas Gltimas d~cadas, incluindo virios países em desenvolvimen to. A partir dos anos 50, modelos de planejamento e de program~

çao t~m sido desenvolvidos e adaptados em institutos e laborat6 rios, visando a obtenção de f6rmulas que conduzam

à

elevação do rendimento da empresa, quer pela melhor alocação dos recursos dis. ponIveis e pela mais conveniente combinação dos fatores ,quer pela

pragmática seleção de atividades. Tal ~ a importância'dessa mo delIstica, que hoje o planejador dificilmente prescindiri dela.

Um mecanismo dial~tico estabelecido entre o cientista e a realidade pragmitica, fez com que a pesquisa gerasse e puze~

se

à

disposição dos planejadores um conjunto de métodos de I")Yogr_~

mação que vai desde modelos cuja rotina se situa no âmbito das so luções ari tm~ticas, at~ os que incluem instrumentais analíticos aI ta-mente sofisticados. Nos Estados Unidos da América foi criado um método de programação denominado "Programme Planing", generali zado depois na Inglaterra e nos Países Escandinavos e que em Portugal foi vu).:. garizado por Henrique de BARROS (9), sob o título de Programação Planeada. O M~todo dos Modelos (62,63) foi desenvolvido em "Braunschweig" e "Bad-Kreusnach", Alemanha, tendo hoje grande apli cação em países da Eu~opa Central. Outros métodos de planejamento da empresa agrícola, como o dos Orçamentos, o das Comparações e o Método Escandinavo, t~m sido aplicados com resultados positivos por extensionistas e planejadores. Nenhum deles, no entanto, ati!!. ge o grau de precisão e o rigor científico do denominado Método da Programação' Linear. b, pois, de s te G1 timo e de sua ap 1 i cação aos problemas da empresa agrícola. que este trabalho se ocuV~·

Mário PEREIRA na "Apresentação" elo trabalho de reYn~l1ldo

Borges de Souza IST.li.CJO C;2) - Técn:i ca$ de Prog.ran~1<'Jio~,

near - .sl~plicaç~ aos .Êroh]$.!11a~-y.s:onoillj..co~s_.~~~!~:.;.':.l.

1.2. O Método da Programação Linear

Dentre os vários métodos e processos aperfeiçoados com o objetivo de equacionar e de dar solução aos problemas de decisão na área econômica, o da Programação Linear

é

possivelmente o mais rIgoroso e exato, sendo também o mais aceito pela comunidade Clcn tífica. No âmbito da administração das empresas agrícolas, a sua aplicação tornou-se uma prática padronizada, sendo tida atualmen te como clássica (74).

A Programação Linear

é

um método matemático desenvol vido na área da Pe~quisa Operacional (67,32), e que consiste na otimização - maximização ou minimização - de uma função linear de "n" variáveis x" (j = 1,2, ... , n), s uj ei tas a wna série de res trições

J

igualmente lineares. Para DORF.MAN (29), o núcleo do problema da Programação Linear reside no estabelecimento de um conjunto de e quações, que devem especificar as quantidades de fatores disponí-veis e de produtos a serem gerados, em funç~o dos níveis tecno16-glCOS dos diferentes processos de produção. ~, pois, uma simp1ifi caça0 formal do processo de produção, que conduz ~ descoberta de elementos importantes para o quadro de decisões da administração da empresa (53,22).

O desenvolvimento da economia matemática e das mo der nas técnicas de administração associado ao aperfeiçoamento dos e quipamentos eletrônicos de cálculo propiciaram, nos últimos anos, o desenvolvimento ü:l6rico da Programação Linear e de sua aplica-ção aos problemas concretos da realidade econômica. No que se re fere específicamente ã agricultura, o seu emprego tem feito gra~

des progressos, tanto a nível macroeconômico - principalmente em programação regional - como no âmbito da gestão da empresa agríc~

la.A es te ní ve 1 o mé todo da Programação Linea r se res Urile a um prob lema de administração, isto

é,

de decidir quanto alocar de recursos limi tados como terra, mão-de-obra, ~gua, energia, etc., a cada ativi-dadc(2J - cultura ou criação - a uin nível tecnol6gico determina

Neste estudo o termo atividade é ellllHcgado no exato senti r10 - q"e - . 1 : : . I·r .. ~n\T C~NDL"n r48) r.Sl'1ir'TO (7'»

-u a l! se 1 e.1 81 em J;l\LIl e H 1:1\ l e L .t\\...,J. ~'L. ,

isto e, como um "phoc.eõ/.)(J e,f,pec.lfJJ..·c.o pa/w, oú:t:eh pILodu.toõ

do, de formas a ob ter-se uma margem bruta máxima ou um mínimo cus to de produção.

De uma maneira geral, o m6todo da Programação Linear

~ convenientemente empregado no setor agrícola (48,32) na solução de problemas que objetivam:

a) - a racionalização do uso dos fatores de produção e a combinação ótima das atividades;

b) - a determinação da melhor proporção entre os pr~

dutos destinados ao mercado, visando o máximo in gresso para o agricultor;

c) - encontrar a melhor combinação de insumos, de for mas a reduzir ao mínimo os custos da produção a

grícola;

d) - a determinação, nos níveis micro e macroeconômi cos, das disponibilidades de produção agropasto-ril, da localização e da distribuição das cultu ras;

e) - a solução de outros problemas relacionados com a organização empresarial e territorial de zonas relativamente homog~neas do ponto de vista agro~

~ . conomlCO.

1.3. Objetivos do Trabalho

Este trabalho tem dois principais objetivos. Imprimc,l

1'0 lugar um objetivo maior, eminentemente acad~mico, que tem em

vista - embora de forma limitada - a apresentação e a discussão dos fundamentos matomáticos da Programação Linear e do algorítmo de cálculo denominado 'Simplex, em sua forma ordinária. Esta ~ a parte fundamental do trabalho, a sua área nuclear e substantivD c cujo mGrito demora no exaustivo compendiar, visando a síntese de

Wlla mat~ria extraordinariamente complexn.

princípios da programaçao matemática a um caso concreto, com o uso de programas de corputador. Procura-se demonstrar com a m~ni

pulação e tratamento dos dados de um estabelecimento agrícola di versificado, que o agricultor, embora aja racionalmente ao compor o seu quadro de decisões - o que o leva is vezes muito próximo da otimização da utilidade - no seu resultado final, obtido pela tra dicional seleção de atividades e alocação de recursos, poderá en contrar-se em situação muito aqu~m da ótima, isto

i,

poderá acon tecer - e quase sempre acontece - que o seu volume de ingressos e a.conseqUente margem do negócio esteja aqu~m do possível de ser obtido com o mesmo esf5rço e com o mesmo risco.

YANG (79) salienta ser fora de dúvida que os agricu1. tores de todas as partes, inclusive de regiões menos

das, se prendem a um plano geral de aproveitamento de

desenvolvi-suas

tCY-ras, mio-de-obra e outros recursos, assim como para a combinação e seleção de suas atividades e. tarefas diárias, sem que no entan to os ponham por escrito e traduzidos em valores monet~rios.O pr~

blema não ~, portanto, a completa aus~ncia de mo plano de ativida des para a empresa agrícola, que de uma ou de outra forma existe sempre, mas sim o estabelecimento do melhor plano, que conduza ao máximo resultado provável, ante um quadro de alternativas poss!-veis. Por outro lado DORFMAN (29) lembra, por exemplo, que um pro dutor pode obter um máximo benefício,sem que isso im~lique na li

tilização da quantidade total de seus recursos. O problema,

PO!

tanto, geralmente reside na combinação precisa e adequada desses fatores.

Neste trabalho procura-se evidenciar que através da programaçao das atividades da empresa agrícola pela técnica da Programaçâo Linear e em função de suas propriedades relevantes diante de problemas complexos,

é

possível proporcionar ao agricu! tor elementos para uma melhor gest50 dos recursos disponívejs na propriedade, bCTiI como o mais elevado benefício do seu negócio.

1.4. Materia] e Métodos

todos e práticas de aplicaç~o de programas lineares. Não obstante a considerável bibliografia existente hoje sobre Programação Li-near e mais especIficamente sobr~ ~ua aplicação i agricultura e i empresa agricola (conforme pesquisa de THROSBY (74) e orientaç~o

de ESTÁCIO (32,33,3·4) e de BARROCAS (6,7,8), quer porumaquestão de tempo, quer por quest6es de inacessibilidade a maior parte de la, a pesquisa limitou-se iquela disponivel, principalmente

ã

clâs sica, que se encontra relacionada no final deste trabalho.

No que se refere ao exerci cio de aplicação prática da teoria da ProgrMlação Linear, o material básico foi obtido por uma amostragem intencional - do tipo "judgement samplc" - entre. várias propriedades conhecidas de uma região do Rio Grande do Sul denominada Baixada Sulriograndense, tendo-se elegido aquela que por seus aspéctos positivos e negativos pareceu melhor adaptar-se ao estudo, em termos de autenticidade. Com base nos dados declar~

dos pelo produtor e complementação de indices adequados, equacio-nou-se um probléma de Programação Linear onde foram consideradas as atividades mais relevantes que tradicionalmente são executadas na propriedade, devidamente relacionadas com as restriç6es a que

os processos estão sujeitos.

o

cálculo do sistema linear, resultante de um jogo de matrizes, foi efetuado em computador IBM 370/145 do Departamento

de Métodos Quantitativos da Empresa Brasileira de Pesquisa Agrop~

cuária - EMBRAPA -, ut.ilizando-se o Ma:themo,:t-tc.a-f.. Pn.oghamllJ-tl1g SIj~ .:tem X - MPSX.

Em torno da função objetivo obtida pelo programaMPSX, simulou-se a inclusão de uma nova atividade com o incremento na di.?, ponibilidade de um recurse, observando-se suas consequenClBS. ~ .

1. 5. Revisão da Li teratura

Registra a literatura (53, 67,76) que matemáticos dos Séculos XVII e XVIII, entre os quais NEWTON, LEIBNIZ, LAGRANGE, BERNOUILLI e EULER, trGbolh;mdo nos cálculos infini tesimaJ e da~;

variaç6es, conhcciélTI1, sem dúvida, a possibilidade da aplicaç:ío de métodos de otimização a problemas de programaç5o matem~tica.SIMO~

um problema pioneiro sobre programas lineares aplicados a questão

pragm~tica dos transportes.

No entanto, é no período da 2~ Grande Guerra - 1939 a 1945 - que se aplicg pela primeira vez o método da Programaç50 Li near para resolver problemas de transporte para a Força Aérea dos Estados Unidos da América. A partir de então, a Teoria Matemática da Programação Linear e sua aplicação aos problemas da atividade econômica, experimentaria considerável progresso. STIGLER (71), em 1945, solucionou através de programas lineares o problema de regi mes alimentares ótimos. Mas é só em 1947 que G.B. DANTZIG formula em termos matemáticos o problema geral da Programação Linear a brindo, dessa forma, a possibilidade de sua aplicaç~o a vários r! mos da atividade econômica. Em 1949 DANTZIG (24) desenvolve e ape~

feiçoa o algoritmo de cálculo denominado Simplex, que resolve o problema da escolha de bases e simplifica o cálculo dos sistemas lineares. No mesmo ano, Von NEUMAN, citado por SIMONNARD (67) e

por KOOP~~NS (53), obtém os primeiros resultados teóricos sobre o

problema da dualidade dos programas lineares e sobre os critérios básicos da Teoria dos Jogos.

Na década de 50 vários pesquisadores de diferentes e~

tidades, entre as quais a "RAND Corporation" e o "Graduate School of Indus tri aI Adminis tra tion", do "Carnegie I ns ti tu t of Te elmo! o

gy", colaboraram no desenvol vimento da Teoria Matemática da Pro gramação Linear e no aperfeiçoamento e simplificaç~o dos proce! 50S de c~lculo. Entre outros salientaram-se pOT suas grandes con tribuições DANTZ I G (23,24), DANTZ I G e ORCHAIW-HA YS (27), CIlJ\RNES e colaboradores (19) ,"FISIlER e SHRUBEN (36), WOLFE (78) e o teórico KOOPMANS (53). Em 1956,FORD e FULKERSON (37) aprimoraram a aplic~

A partir da d~cada de 60, com o aperfeiçoamento dos equipamentos eletr6nicos, verificou-se um vigoroso impulso no de senvolvimento da Programação Linear tanto no campo teórico e área das soluções computacionais, com DANTZIG (25,26) e ORCIlARD-IIAYS (61), como ainda no terreno da difusão e aperfeiçoamento de sua a plicação prática, com os clássicos VAJDA (76,77), DORFMAN e colabo radores (28), GASS (39,40); HADLEY (45,46), SIMONNARD (67), ALLEN (2), SORDET (70), BOULDING e SPIVEY (15), SMYTHE e JOHSON (68), a lêm de outros.

Em Portugal e no Brasil, vários autores contribuiramp~

ra o entendimento e a vulgarização dos fundamentos matern~ticos da Programação Linear, como MURTEIRA (59), ESTÁCIO (32,34), FERIU:IRA

(35) e EHRLICH (31), assim como para a aplicação prática do m~t~

do aos problemas econ6micos e da administração, como MOACIR (5'1), Serra COSTA (20), PUCCINI (65), Girão BARROSO e Von ELLENRIEDER

(10) .

No campo específico da aplicação da Programação Li ncar a problemas de economia e administração rural, segundo ESTÃ CIO (32), os introdutores do m~todo nessa área foram HILDRET e REITER, com um estudo sobre rotação de culturas em uma empresa a grícola. KING (52) em 1953 e BOLES (14) em 1955, aplicaram a t~c­ nica da Programação Linear ao planejamento da empresa rural, bus

cando a maximização dos resultados e a mais eficiente combinação dos recursos. Em 1958, HEADY e CANDLER (48) introduziram concei tos fundamentais para a adequação do m~todo aos problemas da agr! cultura, contribuindo para seu efetivo emprego nessa 5rea da ati-vidade humana. EST.r\CIO (32,34), 1961 e 1964, elélbor01.1 uma obra di dática completa sobre as técnicas matemáticas da Progranwção Li near e a sua aplicação aos problemas de gestão da empresa. BARRO CAS (6,7), 1962 e 1965, contribuiu para a aplicação de t~cnicas

de linearização de funções-objetivo parcialmente não lineares e para a programaç8o em númcros hlteiros e sua aplicação aos probl~

mas da exploração agrícola.

No Brasil, nos campos acad~mico e ap]ica~o do m~todo

da Programação Line ar nos ctor ngr f co la, C11 con trnm-sc t 1'(1b aJ h()~;

grfcola; de SUGAI (72), 1967, que estuda o planejamento b5sico do Sítio da Economia da Universidade FecJeral de Viçosa pela aplic~

ção da Programaç~o Linear; de OLIVEIRA (60), 1971, com programas lineares para estabelecer a combinação da exploração florestal com outras atividades do estabelecimento agrfcola; de MUELLER (58),

1975, que com base em modelos de Programação Linear empreendeu e

xercícios de simulação para estudar problemas da pecu6ria de cor

te no Brasil Central; de PRAZERES (64), 1976, que através de pr.9.. gramas lineares identifica a combinação de explorações que maximi , zam o ingresso da empresa agrícola, por nível de renda e a níveis

alternativos de tecnologia . •

Na década de 70, novas e importantes contribuições fQ ram oferecidas nas áreas teórica e prática de aplicação da Pro gramação Linear i atividade agrícola. BITNEY (13), 1970, desenvol veu estudos visando ampliar a 5rea de aplicação da ProgrDmaç~o Li near e para tornar o m6todo mais simples e acessível i

compreen-são do extensionista e do próprio produtor agrícola. HEADY (49) e BAKER (5), 1971, buscam o aperfeiçoamento do método como instru mento de planejamento e decisão no âmbito da administração rural. HARDAKER (47), 1972. colaborou no aperfeiçoamento dos métodos com putacionais, visando a redução dos tempos para a solução dos pr~

gramas lineares aplicados

à

gestão da empresa rural. BARROCAS (8),

1977, contribuiu para o estudo do problenw da seleção e obtenção

de bases iniciais nos programas lineares.

1.6. Alcance e Limitações do Trabalho

Este trabalho deve ser entendido como uma dissertação introdutória sobre os ftmdamcntos em que se baseiam os programas lineares aplicados ao planejamento da unidade agrIcola produtora. A discussão desenvolvida limita-se, assim, à área vestibular da

teoria clássica da Programação Linear, mas com suficiente profun-didade para dar suporte ao exemplo de aplicação desenvolvic1fJ no Capítulo rIr.

Apesar do rc~spalclo tcóri co de profundidade eiil que se buscou firmar o argumento, COlll fonLe élil DANTZIG (23.24,2S,26) ,Dj\J:'!

TZIG e ORCIlAHD-IIAYS (27), VAJDA (76,77), lWMAKINE (66), MÁLTZEV

e ACHER (1) entre outros, o ellfoque matem5tico desenvolvido neste trabalho, tendo em vista o nível pr~~estabe1ecido para o discurso cientifico, se resume a um exercfclo de 51gebra linear pouco mais que elementar, onde se procurou exercitar uma metodologia e veri ficar sua adequação para o tipo de estudo realizado. A ressalva feita ~ oportuna porque, com a ampliação de suas áreas de dOJllínio e aplicação, a Teoria Matemáti ca da Programação Linear evoluiu co~

sideravelmente em profundidade e extensão, tal sua importância co mo instrumento eficãz de planejamento.

Conforme referên cia anterior, o aperfeiçoamen to dos equipamentos eletr6nicos, reduzindo os tempos de cálculo e permi-. tindo a rápida inversão de matrizes de grande nÚTIlerodeelementos, tem estimulado o desenvolvimento de algoritmos sofisticados para problemas de considerável complexidade. Hoje os cientistas e pes-quisadores perseguem não apenas as soluções 6timas, mas sim solu

ções pôs-6timas, pela programação paramétrica e com avançado re quinte matemático teórico. Diante dessa problemática, considera-se este trabalho como limitado a um djscurso prelimin,:n' sohre a teoria introdutória,e sem maior alcance nos profundos domínios a tuais da Programação Linear.

No que se refere ao exemplo de aplicação do método a uma empresa agrícola, desenvolvido no Capitulo 111, o estudo está limi tado pela fatalidade universal de grande parte dos es tudos em agricultura: a pouca confiabilidade na consistência das informa-ções obtidas. De fato, solicitados a declarar valores monetários relativos a seus neg6çios, os produtores geralmente n~o dispõem de outros registros que não a memória. Reconhece-se, portaIlto,as imperfeições decorrentes da qualidade dos dados, embora, para o exemplo, perfeitamente ajustáveis ao algoritmo Simplex, assim co mo o questionável grau de aderência ~ realidade,d05 coeficicrttes

com eles geradOs.

Isso, todavia, nao resulta em perda de subst~ncia ou na diminuição da validade da discuss50 em torno do método da Pro gramação Line ar ap li cnc10 aos pr ob lemas da empre s a agrí cal a: em }JT2:

meiro lugar porque, como se desej ;~va, trabalhou-se com dados nao hipotét:icos, oriundos de UIll;) rcnli(bde, ql1:!]quer que seja n sua

trabalho, em sua parte py~tica,

6

demonstrar a rotina metodo16gi-ca para a maximizaç50 dos resultados de um estabelecimento agrrc~

CAP!TULO 11

FUNDAMENTOS TEdRICOS DA PROGRAMACÃO LINEAR ---~"-? -

-2.1. In troduç :io

O problema da Programaç~o Linear fundamenta-se na existência de wn certo l1tunero "m" de bens "i", (i=1,2, ... ,m), ou fatores de produç~o, disponíveis em quantidades limitadas, que de vem ser combinados convenientemente sob um processo de produç~o

de nível tecnológico conhecido, para a obtenç~o de um produto fi nal desejado (67,48).

Esse processo de produção, com o qual se objetiva a

obtenç~o de wn bem final a partir da combinaç~o de recursos em

proporç6es fixus, ~ o que em Programação Linear se define como a tividade (48,32). Assim, o vetor definido pela combinação tecnoló gica dos coeficientes "a·" (i=I,2, ... ,m) para a produção do arroz:

1

terra, mão-de-obra, capital, igua, etc., ~ o que deve ser entendi do como atividHde arroz.

Algumas hipóteses estão implícit.as no conceito de ati vidade em Programação Lineéu. Seguindo de p(;rto HEADY e CANDLER (48), DORPMAN (29) e ES']']\CIO (:')2), autores que interprettJm os po.? tulados b5sicos dn teoria, tem-se que a combinução de fator(;s no processo prochJtivo desenvolve-se sob os pressupostos de f.ir/e'(ulidc..

tendidas:

üne. a/L-i dad e: admite-se que entre os meios de ~Jrodução e as qlta!~

tidades de produto ocorra uma relação linear, qua_~

quer que seja o seu nfvel de intensidade; isso sig nifica dizer que os coeficientes de produção e o

rendimento dos meios e fatores produtivos empreg~

dos são constantes conhecidas;

cüv-i.6-ibLf..-idade.: tanto os recursos para a produção - meios - como o

produto,apresentam divisibilidade infinita: pode-se cultivar 7,325 hectares de arroz, por

utilizar 15,570 jornadas de trabalho e 180,17 sacos de produto;

exemplo, colher

qualquer níunero (finito) de atividades pode ser e fetuado simult~neamente, sem que se alterem as prQ porçoes dos recursos usados em cada processo prod~

tivo.

Considera-se tamb6m implfcita a suposição de que nao

-existe interdepend~ncia entre as atividades desenvolvidas em uma empresa, isto é, pode-se desenvolver a atividade A sem que isso lm

plique necessariamente na pTática das atividades B, C ou D.

Admita-se agora que no quadro das possibilidades téc nicas de produção de uma empresa, onde existam "A." atividades aI

J

ternativas e independentes, sejam conhecidas as pToporç6es entre seus coeficientes tecno16gicos, as limitações dos recursos disP2 nfveis e os reSll1tados a serem obtidos. Nestas condições, como sa lientam ESTÁCIO (32) e GASS (39), o processo de aplicação da PTO gramação Linear se reswne na determinação dos nfveis de intensid~

de de cada atividade, de maneiras que se possa compor um programa de produção que deteTmine um resultado global 6timo.

Denominando, genericamente:

a.· =- coeficientes t6cnicos de produção (i==1,2, ... ,m;

:t.]

j=1,2, ... ,n);

x. - níveis de intensidade das atividades(j=1,2 .... ,

J

b· = níveis dos recursos disponíveis (i=1,2, ... ,m),

1

pode-se representar o rToblema em suo forma standard:

AX

=

b (I)

onde

A = [a ..

J

= matriz dos coeficientes técnicos 1J

X =' {x.} = matri z coluna dos n1veis

..

de intensidade J

b = . {b. } = matriz coluna dos n1veis

..

de recursos. 1

m

Observe-se que no espaço R dos recursos limitados ' i ' , os vetores-coluna "a." da matriz'{A} representam as Im' com

J

ponentes aI·' a

Z· ' · · · ' a . do processo produtivo ou atividade'j',

J J mJ

Essa atividade produz ou consome o bem ' i ' , Como diz SIMONNARD

(67) podé-se considerar, então, 'a . .' como quantidades algébricas:

1J

positivas se ' j ' produz ' i ' e negativas se consome ' i ' .

Explicitando (I) em sua forma matricial, obtem-se o

sistema básico do cá.lculo dos programas lineares:

alI a₁₂ a_ln Xl b_l

a

Zl a2Z aZn x Z b2

.

. . .

.

. . . .

.

.

.

. . .

.

=

(I I)

. . .

.

. . .

.

. . .

. .

a

ml a m2 a mn X n b m

e cuja solução e - X

=

A -1 b.

Representando-se os resultados c. (J·=1,2, ... ,n) de ca

J

-da ativi-dade' j I por um vetor-linha c == (c

l ' c2 I . . . ,cn), tem-se

que o problema consistir5 em determinar os níveis de intensidade

"x." das ativiuades "A." da forma standardAX=b e com as

restri-_J J

çoes x_j ~ O, que produzmn um rcsul t auo final ótirno Z =: cX, ou

n

Z

₌

- . I ,",' c. x ..

j J J

'"

2.2. Álgebra da Programação Linear

Os conceitos anteriormente emitidos permitem a formu-lação do seguinte postulado b~sico da Programação Linear (32): se existe uma função

f(X) = f(x

l , x2' •.. ,x , ... ,x n n+m ) (IV)

cujos componentes "x." forem não negativos, x.~O, e que possam sa

J J

tisfazer um determinado número de condições da forma

g. (xl' X

z ...

x )

=

b.

1 n +1ll 1 (V)

então ~ possIvel determinar-se os valores da combinação gica

n+m

V a .. x. = b. (VI)

L..J 1J J 1

j=l

que otimi 2am, tornando máxjmo ou mínima, a função linear

n

=

_'-

_"

.>.-I

j~l

que ~ a função objetivo.

c.x.

J J

••• +c X +

n n •• ~ +

(VII)

c ... x _{n·m n+m}

tecnoló

=

A expressão (VI) representa a forma condensada das funções I f' e I gi I quando estas são lineares, resumindo o segui!?:

te sistema de equações da forma standard AX

=

b:

a X + a x ....

ml 1 m2 2 .

.

.

.

+ a x

In n

+ a x

2n n =

=

+ a x

=

b

mn n m

Nos casos pr5ticos de formulaç~o de problemas de Pro gromaçao Linear, as expressões (V) e (VI) apresentam-se geralme~

te sob a iorma de desigualdades:

n

,-'

...:..; a ij xj ~ b i . ( IX) j=l

DANTZIG (23,26) na resolução de programas lineares r~

solveu essa dificuldade lançando m~o de x _n+1 . (i=l ,2, ... ,m) vari5 veis auxiliares, ou variãveis de folga, nao negativas x +' ~O, cu

n 1

jo objetivo ~ facilitar a transformação das inequações de (IX) em igualdades:

n+m

j=l

a .. x.+x .

1J J n+1

=

b. 1 (X)

Em consequ5ncia, o sistema de equaçoes assume a se-guinte forma:

+ a x + x In n n+ 1

.

. . .

.

. .

.

. . .

. .

.

.

.

.

. . .

. .

. . . ...

+x n+m

=

=

=

b

m

( XI)

Sob o ponto de vista alg~brico, a solução de DANTZIG consistiu em transformar (I), em termos matriciais, para a forma

x

(A,1) (x

m) = b (XI1)

onde I ~ uma matriz identidade e os "x " correspondem às variáveis

TIl

de folga em forma de vetores de base, conforme se verá na discus são a segld r. Em flmção de (XI) é possível determinar-se os valo res das vari5veis Xl'

vo (VII).(11,22,26).

x'j'

L.

.. . ,x , que satisfazem a funç~o

n objeti

tiva "A." pode ser representado ou definido vetorialmente num es J

paço K-dimensional, por um sistema de escalares dispostos em ccr ta ordem e que constituem as suas coordenadas (51,61). O pI8cesso produtivo do arroz, por exemplo, que envolve "ai" recursos combi nados sob uma tecnologia dada, pode ser representado por um

ve-tor-coluna da forma

p

=

a

TIl

Então, um conjunto de atividades "A." formado por 'n' vetores, P2.

. J

de ser entendido com um espaço vetorial sobre um campo F de esca lares. A matriz A

=

[aijJ de AX=b,

é

um exemplo de espaço veto-rial.

Consideração especial, por sua import~ncia nesta dis cussao, merecem os denominados vetores de base. D~-se o nome de vetores de base àqueles vetores que, num espaço ou sub-espaço K-dimens ional, ap res en tam uma componen te igual à uni c1 ade e as demais n - 1 nulas:

e_l

=

( I, O , O , O )

e₂ = ( O, I, O , O )

e₃ = ( O , O , 1 , O ) (XI I I)

...

e = ( O, O, O,

...

1 )

TIl

A proprie dade fundamental atribuída a (XI I I)

-

que pode ser logo identificada como uma matriz identidade Im -

é

que

todo vetor pertencente a um espaço K-dimensional pode ser expre~

SO, de li.'lla maneira única, como uma combinação ljnear e homogên(~a

de vetores de base (59,55,32). Num espaço tri-dimensional o VEtor 5

J = 4

pode ser representado como a seguinte combinação linear de veto-res de base

1 O O

j

₌

5 O + 4 1 + 6 O

O O 1

=

5e_l+4e₂+6e₃ •

Os vetores de base apresentam ainda as propriedades de coincidirem com os eixos coordenados do espaço e de possuirem uma longitude igual i unidade, como se v~ nas Figs. la e lb.

---,

I

I I

,

I

,

Fig. la.

,

,

' I

Os vetores de base sao ditos linearmente :indc.pende~

teso O conceito de independ~ncia linear ~ importante para o desen volvimento da exposição te6rica da programação. Diz-se que 'n' v~

tores P

l , P2, ... 'Pn de um espaço K são linearmente independentes, se existem 'n' escalares ~l' ~2""'~n num campo F, tais que a relação ~lPl+ ~2P2 + .... + ~nPn

=

O. Por outro lado, o nGmero m5 ximo de vetores independentes num espaço K-dimensional

6

igual i

dimensão do espaço (55).

Nwn espaço de K dimensões, a16m dos vetores de base, qualquer conjunto de K vetores independentes forma uma base e,por conseguinte, um sistema de refer~ncia (55,32,67,39).

De "acordo com os conceitos anteriormente formu~ados,o

sistema de equações (XI) pode ser rcpTcscntudo na forma vetorial

"P", num espaço K-dimensional (39), onde os "P." são formados

pe-J_

los vetores co1una a .. (j=1,2, ... ,n+m) e "PO" e o vetor coluna

b. (i-=1,2, .•• ,m):

1

a_lj b l a

2j b2

P.

=

P

=

J o

a _mj b _m

Daí resulta, então que

+ P x + ... + P x (XIV)

n n n+m n+m

ou, de forma reduzida,

n+m

P

=

"\.' _{P .x ..}

o ,.;....J

J J (XV) j=l

2.2.2. Espaço das Soluções

Os programas lineares de muitas vari~veis, como acon tece na maior parte dos casos pr~ticos, apresentam soluções com plexas em função da amplitude do espaço em que se

verificam.KJ\Uf-MANN (50) e ESTÁCIO (32), definem .6olução pO.6.6Zve..l para wn progra ma linear, como wn conjunto de "n+m" quantidades de x. (x. ~ O)

_ _ J J

que satisfazem a relaçao AX = b. Por .6oluçao de.. ba.óe.. entende-se um conjunto de Iml _{quantidades x. (x.}

> O) e de Inl

1 1 quantidades

x. (x. = O),

J J que também satisfazem AX

=

b. Em termos vetoriais, wna solução de base pode ser definida por um vetor-solução:

com I n I componentes iguais a zero e Im I componentes maiores do que zero e que satisfazem a relação (XIV). Uma .6olução ô;tl.ma

é

enten-dida como uma solução de base que otimiza, maximizando ou minimi-zando a função objetivo (VII) .(32,50,26).

2.2.2.1. ConjUntOs e Poliedros Convexos

~ um conjunto convexo. Para definir conjunto convexo, vamos acom-panhar MURTEIRA (59) em alguns conceitos preliminares. Admita-se inicialmente, um espaço euclidiano Rm e ponha-se x = (xl ,x

Z.- .. ,xm) e Y

=

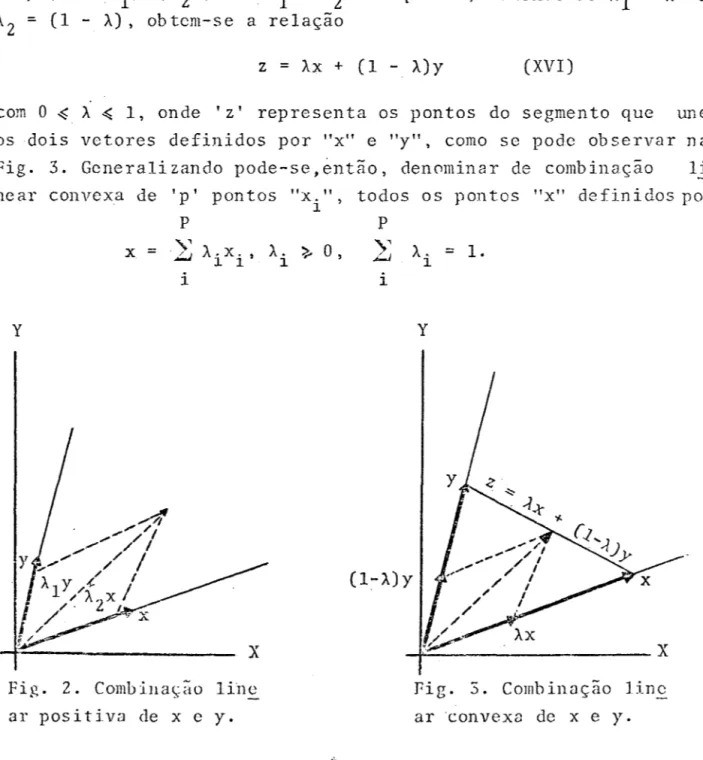
(Yl'YZ'··· ,y) como dois vetores pertencentes ao referido es _m -paço m-dimensional. A combinação linear de "x" e "y" ~ um vetor "Ix + "Zy, onde os escalares "1 e "2 são números reais e arbi trá rios. Pela combinação linear positiva de "x" e "y", obtem-se qual quer ponto do ângulo formado pelos raios direcionais de "x" e "y",

(Fig. Z).

Denomina-se combinação linear convexa dos vetores "x" e "y", C 0111 Àl >--O,À 2 ~O e "1 + ),Z

=

1 quando, fazendo-se Àl

=

À e

"2

=

(1 - À), obtem-se a relação

Z

=

Àx + (1 - À)y (XVI)

com O ~ " ~ 1, onde IZl representa os pontos do segmento que une os dois vetores definidos por "x" e "y", como se pode observar na Fig. 3. Generalizando pode-se,~ntão, denominar de combinação li neal' convexa de Ip I pontos "x" todos os pontos "x" definidos por

i '

p

x - . .k.J ",' À. x. , 1 1

i

Y

Fig. 2. Comb i1lação line ar positiva de x e y.

À.

1

p

>,:. O, _{k I}

Y

i

À.

=

L

1

Y

Em função das definições anteriores, pode-se di zer que

conjunto convexo "C"

é

um conjunto que contendo dois pontos con

têm igualmente o segmento que os une. Se "xl" pertence a "C'. e

"xZ" tamb ém pe rtence a "C", com O ~. À ~ I, en tão a comb in ação I i

near convexa de "x " e "x " também pertence a "C". Algébricamente

1 Z

se tem:

Xl C C, x

2 ~ C

O

<

À ~ 1

-Generalizando, pode··se assurür que um conjunto "C" e

convexo se, e somente se, toda combinação linear convexa de 'p'

pontos de "C"

é

também um ponto de "C", (59, 67, 54). Em termos aI

gêbricos, vem:

x. 1 L 1 P

~

1

E: C

~ O

1..=1

1

(i=1,2 ... p)

(i=l,Z ... p)

1

Lx. E: C

1 1

Os conj untos convexos apresentam algumas propriedades

relevantes para o entendimento teórico do espaço das soluções dos

programas lineares. Estas propriedades, sob a forma de hipóteses

ou de teoremas, são discutidas e demonstradas por DANTZIG (26),

SIMONNARD (67), MURTElRA (59), KAUFMANN (50) e MÁLTZEV (56),

en-tre outros autores. Com base nessa bibliografia enumeramos, sem

maiore s demons trações, as seguin tes propri edade s que julgamos ma is

importantes para o entendimento das soluções em Programação Linear:

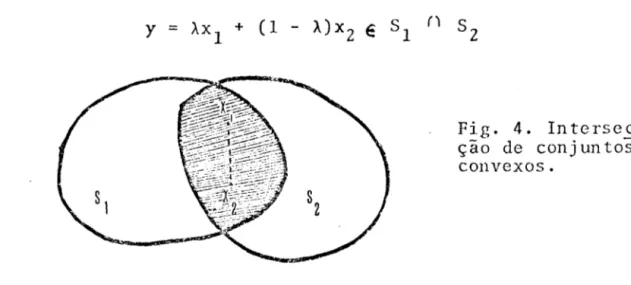
1. A intersecção de um conjunto convexo ou de

quer número de conjuntos convexos

é

também, e

junto convexo. Realmente, se SI e S2 são dois

(Fig. 4) e se x

1 ,xZ E SI n S2' então x1 ,x2 E

sequen temen te:

.

-por Sl so,

conjuntos

SI e x_l ,x₂

qual-um con

Fig. 4. Intersec ção de conjuntos convexos.

2. Define-se 'ponto extremo' de um conjllJlto convexo S,

como todo ponto que não pode ser representado como uma combinação

linear convexa de dois pontos distintos de S, isto &, um ponto do

conjunto que não pertence a qualquer segmento unindo dois pontos

quaisquer desse conjunto, verificando y = ÀX

l + (1-À)x2, com

O~À~l.

3. O conjunto de pontos extremos A, B, ••. ,E (Fig.S),

"

cons ti tui o perfil convexo S de S. Ao mesmo tempo o conj W1 to das

combinações lineares convexas de 'p' pontos extremos xi (i=1,2 ,

... ,p) consti tui o invólucro (IJ convexo desses pontos. Num espaço

R2 o invólucro convexo se configura como LLl1 polígono (fig.S) e num

espaço R3 como wn poliedro convexo, (Fig.6).

y

____

"x

F ' , ] g. S. 1) e r f'"1 "1_ e 1n ' vo.tu -'

era de um polí~ono co~

vexo

Fig.6. Poliedro Convexo ')t.Z

4. Sendo dado um conjunto convexo 5, sólido e limit0

m . ,

do, de um espaço R , e uma funcional linear qualquer 'ax, com 'x'

m

-pertencente a R , entao existem dois hiperplanos de apoio a S que sao paralelos a ax

=

O. Hiperplano de apoio a S é um hiperplano que con têm pe lo menos um pon to extremo de S. (2) .

5 . Sendo dado um conjunto convexo S, sólido e limita do, o hiperplano ~

,..,

xi e um hiperplano de apoio aS.

-i

6. Um conjunto convexo sólido é igual

à

intersecção de seus suportes, isto é, dos semi-espaços que o contém.(SO,67).

o

que foi até aqui discutido, e cujas demonstrações se encontram na bibliografia citada, permite se conceituar sem maiores problemas os cones poliédricos convexos, que são figuras fundamentais para a compreensão dos espaços das soluções dos prQ gramas lineares. Denomina-se cone a um conjunto C de pontos 'x' tais que se 'x' pertence a C e se l >0, então lx também pertence a C. Cone convexo

é

um conjunto ele combinações lineares posi tivas de um número fini to de pontos aI' a 2 ' ... ,a_k, formando um

to C de elementos 'x' tais que

k x.

=

_...

y

i=l

À. a.

1 1 com l. . 1 ~O .

conju~

Pode-se também dizer que a intersecção de um número finito de se-mi-espaços sólidos forma o cone convexo C. A figura resultante

da interse cção de wn nlill1Cro fini to de semi -espaços sólidos, cuj os

-hiperplanos geradores passam pela origem, e o que se denomina co ne poliédrico convexo. O poliedro convexo é um conjunto convexo no espaço RID, cujo invólucro está formado por um número finito ele pontos extremos. Enquanto o poliedro convexo pode ser definido co mo o ambiente convexo de um número finito de pontos, o cone poli~

drico convexo se define como o ambiente convexo de um nlUl1erO fini to de raios.(39,67,26).

(2) Em termos vetoriais, sendo lia" e "x" dois vetores no espa ço m-dimensional, denomina-se hipefLpCaJ10 a um conjunto de

veton~s "X" que satisfazem a DX=C, onde "c" é um numero

Para o estudo da programaçao, nos poliedros convexos apresentam maior interesse os pontos que venham a ser vértices; e nos cones poliédricos convexos os raios que venham a ser arestas.

(67). O conhecimento destes últimos é de relevância para o estudo das soluções em Programação Linear, uma vez que as soluções ditas degeneradas ocorrem ao longo de suas arestas,ao em vez de num pon to extremo ou vértice.

Estas considerações teóricas sobre cones e poliedros convexos tem real significado para este estudo, porque o conjunto das combinações lineares posi tivas dos vetores "a." da matriz [A],

J

constitui um cone poliédrico convexo. Então existira uma solução para AX = b, em variaveis não negativas, se, e somente se, a ex tremidade do vetor "b" for um ponto do cone poliédrico convexo.

(67,26) •

Na solução dos programas lineares, as consequências praticas dessas considerações resumem-se nos seguintes teoremas:

1. O conjunto das soluções de base, ou admissíveis de base, de um programa linear, é um conjunto

xo K.

conve

2. Se existem r < m vetores P

l , P2, ... ,Pr linearmente independentes tais que xlP

l + xZP2 + ... + xrPr = PO,com x_r ~ O, então o ponto X = (xl' xZ, ... x

r , ... O, ••. ,O)éextremo de K.

3.

4.

Para que X = (x 1 ' x_{2 ' ... , xn )} sej a pon to extremo de K,

_,

é

ne cess ário e suficiente que pelo menos 'm' de suas componentes sej am não nulas (x. > O) •

J

n+m

A função linear objetivo z(X)

=

_I c·x. , cujo do

J J

j=l

2.2.3.

Q

Método Simp1ex

Sob o ponto de vista' mutemático, o problema da Progr~

mação Linear pode ser entendido como, sendo dado um conjunto con vexo definido por um conj un to linear convexo d~ res trições num es paço euclidiano K-dimensiona1, determinar, entre todos os pontos que pertencem ao conjunto convexo, um sub conjunto de pontos que otimizem uma função objetiva 1inear~(59,43). A otimização consis te, como foi dito anteriormente, em maximizar ou minimizar a refe

~ rida função objetivo.

Num espaço bi-dimensional as soluções de programas li neares não oferecem maiores dificuldades, podendo ser obtidas, in c1usive,gráficamente. Os problemas da realidade econômica, no en tanto, envolvem grande número de variáveis e de restrições, que constituem espaços multidimensionais, o que torna extremamente complexo o encontro e identificação de soluções ótimas. Essas di ficu1dades levaram DANTZIG a desenvolver um método expedido de cá1 culo denominado Simp1ex, cujo a1gorítmo veio simplificar conside-ravelmente o esforço das soluções.

O método Simplex é um a1gorítmo iterativo convergente, (26,55,32), que na determinação da solução ótima pesquisa sucessi vamente os vários pontos extremos do poliedro convexo das solu-ções possíveis, passando em cada iteração de um vértice para ou tro, até a determinaç~o de um ponto 'z' ótimo, me1hor,(maior ou

*

menor)do que todos os z anteriores.

Recorde-se aqui, com MURTElRA (59), que em face dos teoremas expostos na seção anterior, havia-se fixado principalme~

te que: 1) há pelo menos um ponto extremo do conjunto convexo das soluções possíveis K, no qual a função z

=

~c.x. assume um va

~ J J

-lor ótimo; 2) cada solução possível corresponde a um ponto extre-mo do poliedro convexo K; 3) cada ponto extreextre-mo do poliedro conv~

xo das soluções possíveis K está associado a 'm' vetores linear mente independentes.

2.2.3.1. Fundamentos do A1gorítmo Simplex

poia-se no seguinte teorema fundamental da Programação Linear: --"Sendo dado um prob lema de Programação Linear sob a forma s tandard AX=b, se ~le admite ao menos um programa finito, admite ao menos um programa de base; e se ele admite ao menos um programa otimal finito, admite também ao menos um programa otimal de base".O enu!!. ciado supra torna relativamente simples o entendimento da discus sao que se segue.

Seja, pois, o ponto extremo de um conjunto convexo K , em um espaço Rm, a solução possível X = (xl' x₂' ...• x

n) e o con junto de 'm' vetores P

i linearmente independentes,PI , P2,·· .,Pm a que está associado esse ponto. Se essa solução fôr a solução pos sível de base

x

=

(O, ••• ,O, ••• ,x

_n

_{+l ' xn+2 ' · · · 'xn+m) (XVI I)}

com x . >

°

(i=I,2 ••. m) , e com n+J.

n+m

Po =

_...

y

P.x. _{J. J.} (XVI I I) i=n+l

n+m

então Z _{= Zo =}

~

c.x.

..:..J J. J. (XIX)

.i=n+l

é o valor da função objetivo nessa solução de base.

Como os n+i vetores "P." são linearmente independe!!. J.

tes e formam, assim, uma base, qualquer vetor P.(j=I,2, ... ,n) pode

_ J

ser obtido e expresso em funçao desses vetores de base, como uma combinação linear dos mesmos:

ros reais, da matriz te.

n+m

~

P

l

= ~ i=n+l

x .. P.

J.J J. (XX)

Observe-se que em (XX) os coeficientes "x_ij" sao núme não todos nulos, e que podem ser obtidos pela inversão quadrada da base admissível, conforme se discute

SIMONNARD (67), GASS (39,40) e BARROCAS (8), lembram que o grande problema na solução dos programas lineares sempre co!!. sistiu na obtenção de uma base inicial lógica, capaz de permitir a evolução segura pelos domínios do espaço das soluções. O número de soluções de base para um sistema de 'm' equações (espaço das restrições) e 'n'

=

n+m variáveis (espaço das soluções), é igual ao número de combinações de 'n' elementos tomados "m" a "m":

n!

(XXI) m! (n - m)!

Conforme comenta Serra COSTA

(20),

isso daria um número muito grande desse tipo de soluções na medida em que se e

levam os valores de 'n', tornando impossível distinguir-se ,a pri~

ri, uma solução ótima entre as soluções de base. O métodoSimplex, desenvolvido por DANTZIG e que veio solucionar o problema imedia to de uma solução de partida, consiste em assumir inicialmente uma solução de base igual. a zero, onde se considera que to dos os recursos estão ociosos (8, 32);

z

=

z

=

o

,..,

c.x. ... J J

j

=

O (XXII)

A partir dessa solução inicial, por combinação linear dos vetores "P." com os vetores de base e sob certos cri térios a

J

diante comentados, passa-se sucessivamente para outros vértices do poliedro convexo das soluções possíveis, aumentando (no caso de maxiinização)em cada i teração o valor da função objetivo z == cX. O va

lor de 'z' assim obtido e qualquer que seja a base considerada,

é

único, e nao se repete em nenhuma outra iteração. em virtude da finitude dos elementos 'n' e 'm'

(20).

Dada, pois, uma base inicial admissível, como a matriz quadrada, B, formada pelos vetores linearmente independentes P

I , P₂,··. ,Pm' uma nova solução de base pode ser tentada pela intro

dução,na referida base,de um vetor P. = '~x .. P., que não fazia

I J J..:..J 1J 1

i

parte dela (43,39). Para tanto, basta multiplicar-se P. por um es

J

-calar

e,

subtraindo-se, a seguir,de P ,o produto obtido, o que,em

o

n+m

'--'P = 7' (x. - ex .. ) P. + ep ..

o .;;...J 1 lJ ~ J

(XXI I

1)

i=n+l

Fazendo e

=

Xi , o vetor P. desaparece do segundo mem

1

x .. lJ

bro de

(XXIII),

dando lugar

à

introdução de "Pj" na base. Tem-se, pois, que desde que x. - ex .. >

o

e e >

o

aplicados aos 'm' coefi

1 lJ

cientes de

(XXIII),

constituiu-se uma nova base, alcançando-se um , novo ponto extremo do poliedro convexo, com uma nova solução

i' > z

_o'

ou seJ' a

m

z =

z'

=

l

c. (x.

-

ex .. ) + eco

(XXIV)

1 1 lJ _J

i=l

=

z + S(c.

-

z.) •

o _{J J}

o

critério para identificar qual vetor "P." deverá

J

ser indicado para entrar na base,no caso dos problemas de maximi-zação e de acordo com a técnica de CHARNES (18),é observar-se no quadro do Simplex, aquele que corresponde ao menor valor z.-c.<O.

~ ~ ~ J J

Para a salda de um vetor "P." da base, o cri terio e que o valor de

1

e

=

e

_o

=

min°

i

X.

1

x· . lJ

o

seja também o menor (32). Nesta relação, o elemento "x .. " que pro

" l J

-duz o menor valor positivo de 'e~

ê

denominado elemento 'pivô', e aparece no quadro do Simplex dentro de uma área tracejada, con forme se fará notar adiante. O exemplo de cômputo do Simplex que se segue (3), visa esclarecer melhor os conceitos expendidos.

2.2.3.2. Aplfcação P"ráticado Algorítmo Simp"lex

Seja solucionar, pelo método Simplex, o seguinte pro blema de Programação Linear: Maximizar a função:

"-Z (m~x) = 5x

l + l2x2 + 7x3 + 2x4

1

(XXV)

sujeito

-

a~ seguintes restrições: .

xl + 4x 2 + 2x 3 + x 4 ~ 33

3x

l + 2x2 + x3 + 5x4 ~ 75 _(XXVI) 7x

1 + x2 + 5x3 + 2x4 ~ 78 2x + 4x

2 + 5x + x4 ~ 49

.1 3

Inicialmente, no preparo do problema matemático para o algorítmo Simplex, introduz-se as variáveis de folga ou auxilia res não negativas xn+i~ O, (i=1,2,. .. ,m)no caso x

5' x6' x7 e x8' a fim de transformar em igualdades as inequações dos "b.", confor

1

-me o explicitado em (X). Observe-se que o nú-mero de variáveis de folga a serem introduzidas são no máximo iguais ao número

sional do espaço das restrições 'm'.

dimen

Em consequência, o sistema (XXVI) assume a forma:

Xl + 4x2 + 2x3 + x4 + x5

=

33

3x

I + 2x2 + x3 + 5x4 + x6

=

75 _{(XXVI I)} 7x

I + x2 + 5x + 2x3 4 + X 7 = 78 2x

1 + 4x2 + 5x3 + x4 + x8

=

49 e a função objetivo (XXV) passa a ser escrita da forma

(XXVIII)

Z (m~x) = 5x

I + 12x2 + 7x3 + 2x4 + OX5 + OX6 + OX7 + OX8

o que satifaz a condição x _n+l . ~

o.

As 'm' (no caso )fi

=

4) variáveis auxiliares que foram

'-..

triz identidade Im , (Im

₌

B) , referida em (XII) :

I O O O

O I O O

P

_s

= _{, P 6}

₌

P

7

=

P

s

=

O· O • I O

O O O I

Esses vetores "P." t que s ao linearmente independen tes ,

1

vao constituir a primeira solução de base, que inicia o método de DANTZIG. Tendo-se assumido anteriormente que nesta solução

ini-cial

então o vetor

m

X'

~ x.P. =

1 1

i

P

=

o

33 75 78 49

P

o = b. 1 (XXIX)

pode ser representado como uma combinação linear dos vetores de base:

(XXX)

Observe-se que nesta solução inicial de base tem-se as primeiras In' variávei.s "x

j " iguais a zero (xl=x2=x3=x4=0) e as

'm' variáveis auxiliares assumindo x

5

=

33; x6

=

75; x7

=

78 e x8 = 49. Como isso quer dizer que todos os recur~os estão ociosos nesta solução inicial, o valor da função objetivo Z(max) é,

natu-ralmente,zero. i

Com os elementos acima considerad6s, pode-se cons-truir o quadro da primeira iteração do Simplex. (Ver Quadro

Q. I I. 1) .

Quadro Q. I I . 1. . Primeira Iteração do Simp1ex

C

j 5 12 7

BASE C

P

_Pl

P₂ P

3 o

P_{5 O 33 1}

r---'

I ₄ I ₂

I I

I I

L ______ .1

lo

P

6 O 75 3 2 1

P_{7 O 78 7 1 5}

P

8 O 49 2 4 5

z. O O O O

J

z. - c.

O -5 -12 -7

J J

2 O O

P₄ P₅ P₆

1 1 O

5 O 1

2 O O

1 O O

O O O

-2 O O