Instituto de Físia de São Carlos
Departamento de Físia e Informátia
Modelo de Anderson de dois anais
João Vítor Batista Ferreira
Tese apresentada ao Instituto de Físia de
São Carlos, Universidade de São Paulo, para
obtenção do Título de Doutor em Ciênias:
Físia Básia
Orientador: Prof. Dr. Valter L. Líbero
São Carlos
Nozières e Blandin generalizaram o Modelo Kondo através da inlusão de mais graus de
liberdade. Eles investigaram um sistema formado de uma impureza magnétia em um metal
hospedeiro, onsiderando a estrutura orbital da impureza, ampo ristalino e interações
spin-órbita. EstesistemaérepresentadopeloHamiltonianodeKondoMultianal: ainteraçãoentrea
impurezaloal e abanda de ondução éfeita via anais (ada analrepresenta um onjunto de
númerosquântiosbemdenidos). Nozières e Blandinmostraramo apareimento de umponto
xoanmalo noregime de aoplamento nito.
Esseponto xoanmalo podeexpliar oomportamento não-líquidode Fermideompostos
de terras-raras e atinídeos. Cox e olaboradores usaram o Hamiltoniano Kondo
Quadrupo-lar para representar sistemas de férmions pesados em urânio e óxidos superondutores de alta
temperatura, osquaispodemser mapeadosemumModeloKondo de doisanais.
Como o Modelo Kondo tradiional (um anal) é o limite de baixa temperatura do Modelo
Anderson,é interessantetambém generalizareste últimopara inluir maisanais.
Nestatese nósmostramosqueomesmoproedimento trivial, oqualgeneraliza o
Hamiltoni-ano Kondo, não funiona parao Modelo de Anderson. Nós usamosum Hamiltoniano proposto
por Cox para representar o Modelo de Anderson de dois anais. Usando a transformação de
Shrieer-Wol nósdemonstramos queesteHamiltoniano éequivalenteaoHamiltonianoKondo
dedoisanaisembaixastemperaturas. Enalmente,nósapliamos oGrupodeRenormalização
Numério para investigar os níveis de mais baixa energia, a susetibilidade magnétia e o alor
Nozières and Blandin generalized the Kondo Model by inluding more degrees of freedom.
They investigated a system made of magneti impurity in a metal host, onsidering impurity
orbital struture, rystalline eld and spin-orbit interations. This system is represented by
multihannel Kondo Hamiltonian: the interation between loal impurity and ondution band
is done via hannels (eah hannel represents a set of well dened quantum numbers). They
showed thatanomalous xedpoint appears atnite oupling.
The anomalous xed point an explain the non-Fermi Liquid behaviour of rare earths and
atinides ompounds. Cox et al used a quadrupolar Kondo Hamiltonian for uranium
heavy-fermion materials and high-temperature superonduting oxides, whih an be mapped to a
two-hannelKondo Model.
Sine Kondo Model is a low temperature limit of Anderson Model, would be interesting to
generalize thislast one inluding manyhannels.
Inthisthesisweshowthatthesametrivialproedure,whihgeneralizestheKondo
Hamilto-nian,doesnotworkwiththeAnderson Model. WeuseamodelHamiltonianproposedbyCoxto
represent the two-hannel Anderson Model. Using theShrieer-Wolf transformation we prove
this Hamiltonian is equivalent to the two-hannel Kondo Hamiltonian. And nally, we have
applied Numerial Renormalization Group alulations to investigate the lowest energy levels,
Ao Prof. Valter pela paiênia.
Aos olegas de grupo Vivaldo, Luís Ramos, Nilva, Marelo, Neemias, Kerson,
An-tnio,Klaus, Sandra,Cíntia eprof. LuísNunes.
AosamigosHenrique,Nazareno,AnaTereza,PauloRoberto,Viviane,Paulo
Alexan-dre, Roberto, Reginaldo,Queite,Carlos Alberto, ...
Aos funionáriosdoIFSC: Wladerez, Bruno, Luiano,Nilzeli,Cristina, Mateus, ...
À minha namorada Sueli e à minha família pelo apoio e inentivo: minha mãe
Nanuh, minhasirmãs Patríiae Joanie.
Espeialmenteaos amigos e onheidosque esquei de itar...
ÀDeus, riadordasduasmaçãs: adaonsiênia(Eva)eadoonheimento
(New-ton).
1 Apresentação 16
1.1 Introdução . . . 16
1.2 Modelo de Anderson de dois anais . . . 21
1.3 Grupo de RenormalizaçãoNumério(GRN) . . . 23
1.4 Resultado: omportamentonão-líquidode Fermi . . . 24
1.5 Organização datese . . . 27
2 Modelos de Anderson 28 2.1 Modelo de Anderson de um anal . . . 29
2.2 Modelo de Anderson de dois anais . . . 35
2.2.1 Proposta de Cox . . . 36
2.2.2 Transformação de Shrieer-Wolpara dois anais. . . 39
3 Diagonalização do Hamiltoniano de Anderson de dois anais pelo GRN 44 3.1 Grupo de RenormalizaçãoNumério: histório . . . 44
3.2 Hamiltonianode Anderson de dois anais . . . 45
3.3 Disretização logarítmia . . . 46
3.3.1 Primeira etapa dadisretização . . . 48
3.3.2 Segunda etapa dadisretização . . . 50
3.4 Simetrias. . . 53
3.5 Diagonalização iterativa . . . 55
3.5.3 Invariantes . . . 61
3.5.4 Iteração N = 1 . . . 62
3.5.5 Iteração N =0 . . . 64
3.6 Equivalênia om o Modelo de Kondo de dois anais . . . 66
3.7 GRN e pontosxos . . . 68
3.8 Cálulo dasusetibilidademagnétia e doalor espeío . . . 70
3.9 Implementaçãoomputaional . . . 72
4 Resultados 77 4.1 Pontosxos doHamiltonianode Anderson de dois anais . . . 77
4.1.1 Regime de impureza livre: V 1 =V 2 =0 e qualquer . . . 80
4.1.2 Regime anisotrópio: V 1 6=V 2 . . . 83
4.1.3 Regime isotrópio: V 1 =V 2 . . . 85
4.2 Susetibilidade magnétia . . . 87
4.2.1 Regime anisotrópio: V 1 6=V 2 . . . 88
4.2.2 Regime isotrópio: V 1 =V 2 . . . 90
4.3 Calor espeío . . . 93
4.4 Sugestões para trabalhos futuros. . . 96
A Construção dos vetores da base 98
B Construção dos elementos de matriz 102
C Construção dos Invariantes 109
1.1 Dados experimentais da susetibilidade do Th 1 x
U x
R u 2
Si 2
, retirado da
Ref. [8℄. Estesdadosmostramdivergênialogarítmiaembaixatemperatura. 17
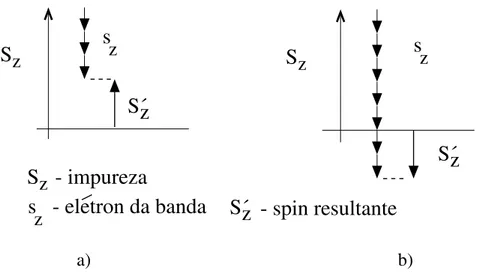
1.2 Efeito Kondo multianal. S é o spin da impureza, s é o spin dos elétrons
de ondução e S 0
é o spin resultante. Nozières e Blandin analisaramuma
impureza magnétia onsiderando sua estrutura orbital, ampo ristalino
e desdobramento spin-órbita. Isso resulta no aoplamento da impureza
om a banda de ondução através de anais (ada anal representa um
onjunto de números quântios). Quando os aoplamentos de ada anal
om a impureza forem iguais e o número de anais n for diferente de 2S,
o spin da impureza não é devidamente ompensado. No item a) temos a
situação em que n < 2S resultando num spin total S 0
diferente de zero
paralelo ao spin da impureza. No item b) n >2S,resultando emum spin
total S 0
diferentede zero antiparaleloaospin da impureza. . . 19
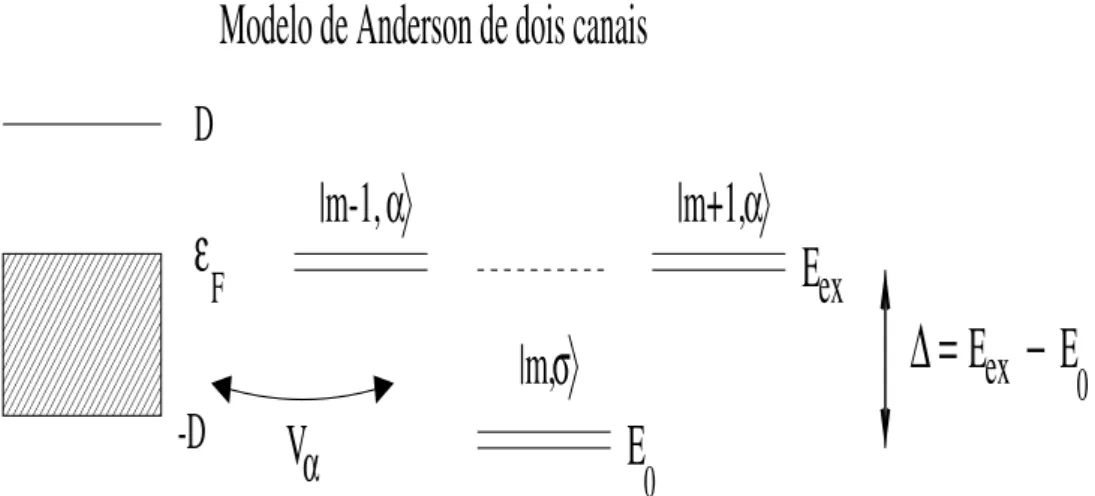
1.3 DiagramadomodelodeAndersondedoisanais. Trata-sedeumaimpureza
magnétiaemummetalhospedeironãomagnétio. Ometalérepresentado
pelasuabandade ondução,queésemi-preenhida,isotrópiaede largura
2D. A impurezaérepresentada peloseu estadofundamentalepordois dos
seus estados exitados. O estado fundamental é um dubleto que tem m
elétrons, spin total = 1=2 e energia E o
. Os estados exitados são dois
dubletos quetêm m1elétrons, spintotal nulo, energiaE ex
eanal =1
ou2. Otermode hibridizaçãoentre abanda de onduçãoea impurezaé V
T=T K
para o Modelo de dois anais. V
é o termo de hibridização entre
a impureza e os elétrons de ondução do anal ( = 1;2), D é a meia
largura dabanda de ondução dometal e =E ex
E 0
,sendo E 0
o nível
de energia do estado fundamental da impureza e E ex
a energia do estado
exitado. A linha heia é a urva universal obtida por Tsvelik et al para
o EfeitoKondo de um anal. . . 26
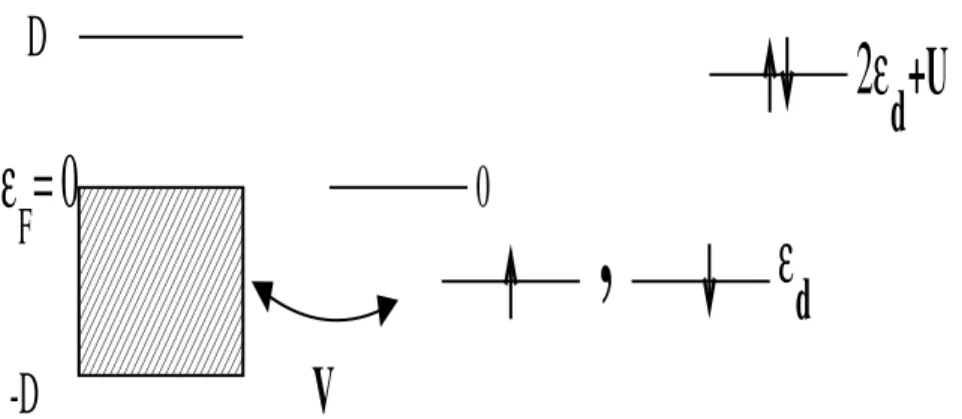
2.1 Esquema do Modelo de Anderson tradiional. A banda de ondução do
metal é semi-preenhida e isotrópia. A impureza é representada pelas
suas quatro ongurações possíveis, sendo " d
a energia do orbital quando
oupadoomapenasumelétrone2" d
+ U quandooupadopordoiselétrons.
V é a energia de hibridização. Se 2" d
+U = 0 temos o hamado Modelo
de Andersonsimétrio,que exibe simetriapartíula-burao.. . . 29
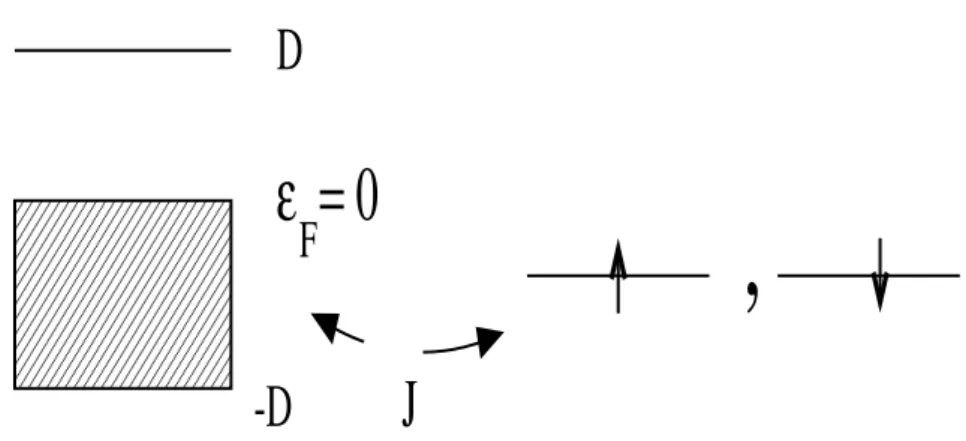
2.2 No Modelo de Kondo o spin da impureza é xo, podendo apenas mudar
sua orientação quando espalhaos elétrons de ondução. . . 31
2.3 Temperatura multipliada pela susetibilidade magnétia em função de
k B
T=D do Modelo de Anderson de um anal. A linha heia é a urva
universal do Modelo de Kondode um anal. No inset podemosperebero
omportamentolinear embaixas temperaturas. . . 33
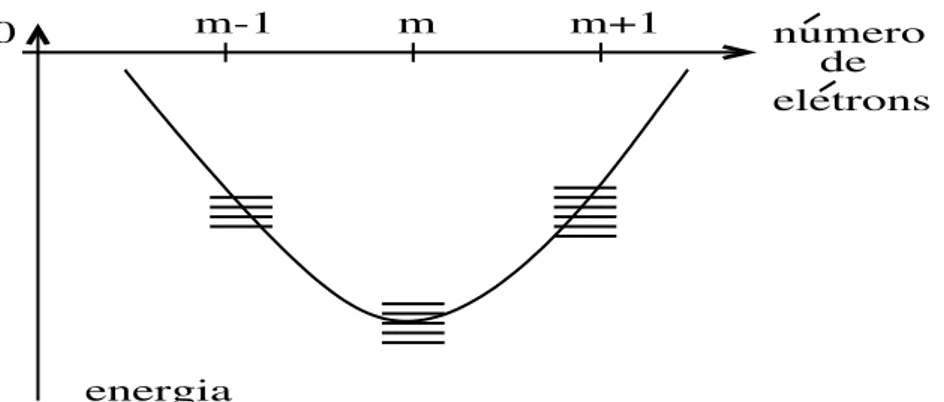
2.4 Representação hipotétia da energia de valênia de uma impureza om
orbital semi-preenhido para as ongurações de energia mais baixas. A
parábolaé dada pelaexpressão E m
=E
d
m+Um( m 1)=2, onde E d
é a
energiadoorbital(emrelaçãoaoníveldeFermi),eméonúmerodeelétrons
no orbital. Veja que fazendo m = 0, m = 1, ou m = 2 reproduzimos os
dubleto om m partíulas e spin total = 1=2 e dois dubletos omo
estadosexitados,omm1partíulas,spintotaligualazeroeomanal
.. . . 38
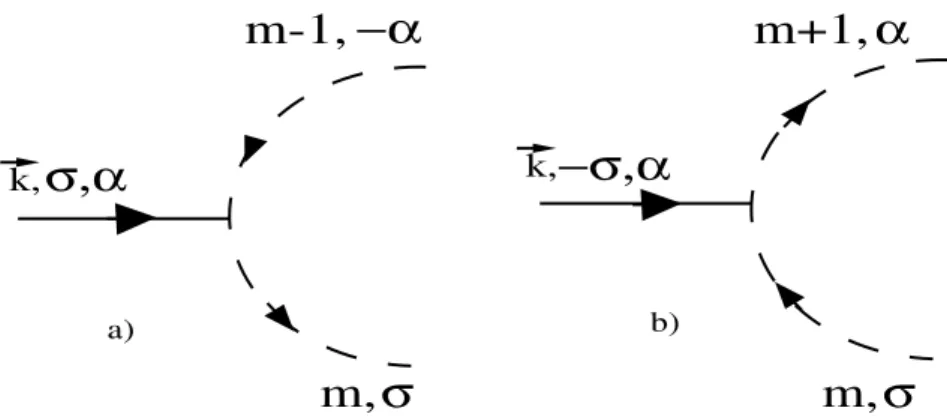
2.6 Esquema de interações entre osestados da impureza e oselétrons de
on-dução. m é o número de elétrons no orbital da impureza. = 1=2,
quando = 1, = 2 e vie-versa. Em a) um elétron de ondução
(k;; ) se hibridiza om o estado loal (m 1; ) e forma o estado de
spin . Emb)um elétronde ondução(k; ; )sehibridizaomoestado
loal (m;) em uma ombinação singleto, resultando em estado de anal
(m+1; ) (spin 0). Logiamenteproessos inversos são permitidos. . . 39
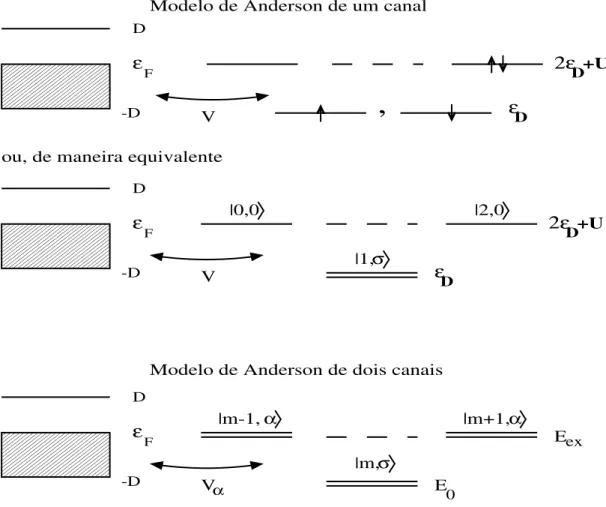
2.7 No esquema superior temos o Modelo de Andersontradiional (um anal)
na onguração de aso simétrio. Logo abaixo, temos o mesmo modelo
mas agora om notaçãojm;i onde mé onúmero de elétrons e éo spin
total doestado. Noesquema inferior temoso Modelo de Anderson de dois
anaisemqueoestado fundamentalé umdubletoom mpartíulas espin
total edois dubletos omo estadosexitados,om m1partíulas, spin
total igual a zero e om anal . . . 40
3.1 a) Banda de ondução om largura 2D, semi-preenhida e isotrópia. b)
A bandaédisretizada logaritmiamentepelos parâmetros >1, sendo
um número inteiro,ez >0onde z éum númeroreal. Oprimeirointervalo
é 1 < " k
< z
e os demais são obtidos pela divisão por (para o lado
negativo da banda o proedimento é análogo). )Multipliando por n
, n
inteiro positivo, a estrutura de níveis de mais baixa energia (próximos ao
tam asbasesdosoperadores dabandade ondução. a)Basede operadores
";;
, onde os estados têm energia bem denida mas são deloalizados
es-paialmente. A impureza está loalizadaemr =0. b)Base de operadores
{a y n;;
; b y n;;
} onde as energias dos estados estão restritas aos valores
mé-dios de ada intervalo. Veja que quanto maior é a energia assoiada aos
operadores a eb, mais emtornodaimpureza eles são (asaixasde
taman-hos diferentes mas rasuradas da mesma forma representam o mesmo par
de operadores). )Base de operadores {f y n;;
} onde osestados somentese
aoplamom estadosvizinhos de aordo oma transformaçãode Lanzos.
f 0
é o estado mais loalizadoespaialmenteem torno da impureza, mas é
o menos loalizadono espaçodas energias. Ooposto oorrepara n grande. 51
3.3 Pontos xos e trajetórias no espaço de fase. Em a) temos um ponto xo
estável. Em b) temos um ponto xo que é estável em uma direção (linha
reta), mas instável nas outras o que signia que ele tem pelo menos um
operador relevante. . . 70
3.4 Esquemadoproedimentointeraladomostrando,omoexemplo,uma
ban-dadisretizadaom =4ez =1:0(em ima),outraom =4ez =0:5
(no meio) e outra om = 2 e z = 1:0 (em baixo). Podemos ver que
interalando a banda de ima om a bandado meio teremosa banda om
=2 ez =1:0. . . 71
3.5 Duas urvas de alor espeo om os mesmos parâmetros V
1
= 0:005,
V 2
= 0:01 e = E ex
E 0
= 0:002, mas em um deles foi feito o
proedi-mento interalado. Podemos observar que as osilações são sensivelmente
N 1
já está ompletamente diagonalizado, portanto são onheidos seus
auto-estados e seus autovalores. Cada auto-estado vai gerar vários estados de
basenaiteraçãoseguinte(N),omnovosnúmerosquântiosdeaordoom
osproedimentosdelineadosnaTabela3.2. Estesnovosvetoressão
agrupa-dos de aordoomosnúmerosquântios formandosub-espaços.
Enontra-dos os elementos de matriz, os sub-espaços são diagonalizados resultando
nos autovalorese autovetores de H N
. . . 73
4.1 Diagrama do modelo de Anderson de dois anais. O estado fundamental
tem m elétrons, spin total diferente de zero e energia E o
. Os estados
exitados têm m1elétrons, spin total nulo e energiaE ex
. Esses estados
são hibridizados om a banda de ondução através do termo proporional
a V
emH N
. A diferençade energiaE ex
E 0
denominamosde . . . 79
4.2 Dois pares de gráos de banda livre V 1
= V 2
= 0. Em (a) temos = 0
enquanto que em (b) = 0:2. Como a energia mantém-se onstante em
grandepartedasiteraçõesdizemosqueosistemaestánumregimedeponto
xo, noaso, de bandalivre. A estruturados níveisde energia igualmente
espaçados arateriza omportamentode líquido de Fermi. Observe a
na-tureza dos estados fundamentais para N par ou ímpar através dos seus
dução livres (desaoplados). A banda é separada em anais 1 e 2. Cada
analtembandaparebandaímpar. Existeumadefasagemintrínseaentre
abandapar eímpardevidoàdisretizaçãologarítmia,sendoqueabanda
par temumnívelomenergiazero(oquesigniaqueelapodeestarvazia,
om um ouom doiselétrons). Como nãohánenhum tipode aoplamento
entre osanaiseaimpureza, asbandaspar eímparde adaanalmantêm
essa defasagemintrínsea. . . 82
4.4 Os gráostêm parâmetros do regimeanisotrópio V 1
6=V 2
6=0. Podemos
observar que esse ponto xo independe dos valores de V
e os níveis de
mais baixaenergia são igualmenteespaçados. Oestado fundamental para
N ímparédegeneradomostrandoqueumdosanaisoulivre(aqueleom
j0;0;1=2i) e o outro anal blindou a impureza perfazendo efeito Kondo e
resultando em spin total zero ( j0;1=2;0i para V 1
<V 2
ou j1=2;0;0i para
V 1
> V 2
). Análise semelhante pode ser feita para N par. Como expliado
no texto, não há distinçãoentre os níveisde energia para N par ouímpar
no pontoxo. . . 83
4.5 Preenhimento dos níveis de energia dosistema impureza e bandade
on-duçãoparaoregimeanisotrópioV 1
6=V 2
. Essediagramarepresentaoaso
partiular emque V 1
<V 2
, oquesignia quenopontoxoo anal1 está
livre e o anal 2 está totalmente aoplado om a impureza, blindando-a
(efeito Kondo). Podemosobservarque abandapar eímpardoanal 1não
semodiam(bandalivre),enquantoquenoanal2osníveisdeenergiada
banda par e dabanda ímpar se inverteram, efeitojá onheido naténia
1 2
xo independe dos valores de V 1
e V 2
. Os níveis de energia não são
resul-tados da ombinação de N par e N ímpar do ponto xo de banda livre,
nem são igualmenteespaçados. O estado fundamentaltem spin total 1/2,
reetindo a superompensaçãodos elétronsde ondução dos dois anais. . 86
4.7 Diagramas de pontos xos. a) Diagrama do Modelo de Anderson de um
anal: OL é o ponto xo de orbital livre, ML é o ponto xo de momento
loaleFAéopontoxofortementeaoplado. b)Diagramade pontosxos
do Modelo de Anderson de dois anais. Além dos pontosxos anteriores,
queapareemnoregimeanisotrópio,apareeumnovopontoxonoregime
isotrópio. Como veremos, esse novo ponto xo têm omportamento de
sistema não-líquidode Fermi. . . 87
4.8 Regimeanisotrópio-temperaturavezessusetibilidadeemfunçãodek B
T=D,
para vários parâmetros do modelo, todos em unidade da meia-largura da
banda D. Para >0o sistemadesenvolve momentoloaleT se
aprox-ima de 1/4 (a,b,). Para <0, não háformação de momento loale T
vaia zero rapidamente (d). . . 88
4.9 Regimeanisotrópio-temperaturavezessusetibilidadeemfunçãoda
tem-peraturaT esalada pelatemperaturaKondo T K
. A urvaheia
represen-ta o omportamento universal de T do Modelo de Kondo de um anal.
Quando T =T K
temos que T K
(T K
)=0:0705. Usamos esse ritério para
desobrir atemperaturaKondo de adaurva aima. . . 89
4.10 Regime isotrópio - susetibilidade magnétia versus temperatura. Para
> 0 (urvas b,,d,e) há formação de momento loal, enquanto para
de T=T K
para vários esalados pela temperatura de Kondo T K
. A linha
heia é a urva universal de Kondo para um anal. A urva ontínua
indiadapelasetamostraoomportamento T lnT embaixastemperaturas. 92
4.12 Nográodeimatemosaontribuiçãodaimpurezaaoalorespeíoem
função de k B
T=D para o regime anisotrópio e para o regime isotrópio.
Comoéesperado,emaltastemperaturasasurvasoinidem. Jáembaixas
temperaturas a urva azul (anisotrópia) tem omportamento de líquido
de Fermi, enquanto a outra mostra omportamento não-líquidode Fermi,
omo pode ser observado noinset. A linha ontínua sobre pio àesquerda
na urva anisotrópia é a urva universal de Kondo de uma anal om
T k
= 1:2 10 6
D. No gráo de baixo temos os graus de liberdade da
impureza obtidos através da exponenial da entropia. A temperatura T K
para a urvaisotrópiaé 1:810 7
3.1 Vetores formados pelas ombinações dos estados de ada anal. Vetores
om mesmos númerosquântios estão nomesmo grupo, difereniadospelo
índie r. Devido àdenição de arga axial3.16 e 3.17, um par de elétrons
em um anal naiteraçãoN é aompanhado pelo sinal ( 1) N
. . . 57
3.2 Tipoeombinação. NestaTabelaj 0 1
,j 0 2
e s 0
sãonúmerosquântiosdos
auto-estados da iteração N 1. . . 57
3.3 Estados que ombinam entre si. Por exemplo, oestado formadopelotipo
8 sóse ombina om osestados formados pelos tipos 2,3,5 e6. . . 60
3.4 4 ombinações possíveispara osinvariantes. . . 61
3.5 Auto-estados da iteração N = 1 e orrespondentes vetores da base de
N = 0 (lhos), riados a partir dele segundo a Tabela 3.2. Usamos a
notação jj 1
;j 2
;s;ri tipo
, onder éo índie de ontagemdos vetores que têm
o mesmo número quântio e tipo india qual o proedimento que resultou
neste vetor. . . 64
3.6 Na iteração N 1 temos um sub-espaço om tamanho 44, três om
tamanho33,dois om tamanho22e inosub-espaços om tamanho
11. . . 64
3.7 Níveis de energia de H 0
até ordemV 2
= onde F =
q V
4 1
+V 4 2
2V 2 1
V 2 2
. . 67
3.8 Oito onjuntosde parâmetrospara realizaçãodoproedimentointeralado
proedimento tipo 4 enquanto j12i N
signia vetor gerado pelo
Apresentação
Estatese temporprinipalobjetivoadiagonalizaçãode umHamiltonianoquerepresenta
oModelode Andersonparadoisanais,utilizandooGrupode RenormalizaçãoNumério.
Este apítulo apresenta a motivação para este trabalho, resume o proedimento
desen-volvido eapresenta brevemente o prinipalresultado.
1.1 Introdução
A teoria do omportamento de líquido de Fermi para sistemas em baixas temperaturas,
desenvolvida prinipalmente por Landau, pode ser onsiderada omo um dos grandes
pilares em matéria ondensada. Sua premissa básia é que elétrons de ondução
intera-gentes, mas om energiassuientementepróximosdo nível de Fermi, podem formar um
onjunto de quase-partíulas que se omportam omo livres. Por isso as propriedades
advindasdesse gásde elétronspodemsermapeadasnaquelasde elétronslivres,om
algu-masgrandezasrenormalizadas,omoporexemploamassados elétrons. Essateoriaprevê
omportamentolinearparaoalorespeíoevaloronstanteparaasusetibilidade
mag-nétia (omo funções da temperatura), em energias abaixo de uma esala araterístia
paraadaomposto. Inúmerossistemasfísiosseguemessas leissimples,partiularmente
Indubitavelmente, oModelode Kondo tradiional[1℄ está entre osmais relevantes na
obtençãode propriedadesdotipodas de umlíquidode Fermi. Essemodeloonsidera um
gás de elétrons de ondução, om spin~s, sendo espalhados por uma impureza magnétia
loalizada, om spin ~
S, segundo o termo de troa J~s ~
S. No regime de temperaturas
baixas,próximoaumvaloraraterístioonheidoomotemperaturaKondo,oselétrons
de ondução do metal hospedeiro blindam o spin da impureza, anulando o seu aráter
magnétio (fenmenoonheido omo EfeitoKondo).
A teoria de Landau e o Modelo de Kondo tiveram suesso em desrever vários
fen-menos,mas algunsmateriais,porexemplo ompostos de terras-rarasouatínideos,
apre-sentam propriedades físias que muito diferem daquelas previstas pela teoria do líquido
de Fermi [2℄. Partiularmente, medidas de alor espeío e susetibilidade magnétia
em temperaturas muito baixas mostram omportamentos não-líquido de Fermi em tais
sistemas[3℄,omo porexemplomostrado naFig. 1.1. A preisãodessasmedidaspermite
Seria por demais extenso, embora bastante interessante, desrever aqui os diversos
modelos que ontribuem para a nossa ompreensão dos sistemas não-líquido de Fermi.
Emtodos, noentanto,háaidéiabásiadeumaoumaisimpurezas aopladasaoselétrons
deonduçãoeresultandoemEfeitoKondoisoladoouoletivo. Destaamosapenasalguns
estudosrepresentativos. Na Ref. [5℄, usando um tratamentode ampomédio viafunções
de Green, o efeito de desordem em redes de Anderson (ex., UCu 5 x
Pd x
) leva a uma
distribuiçãoespaialde temperaturas Kondo sobre aamostra,induzindo omportamento
não-líquidode Fermi. Uma solução exata noaso partiular de dimensão innita para a
redede Anderson,om asimpliaçãoadiionalde orrelaçãoeletrnianula, émostrada
naRef. [6℄. Nessa abordagemoproblema éreduzidoefetivamenteaoaso de umsítioeé
tratadoporampomédiodinâmioeenontra-seumregimemetálioparaaresistividade
ompropriedadesnão-líquidode Fermi. PartiularmenteinteressanteéotrabalhodaRef.
[7℄ em que as propriedades anmalas de uma rede em uma dimensão e em temperatura
nulasão estudadas viateoria de saling de fenmenos rítios.
O nosso trabalho não foge à regra e utiliza também uma generalização do Modelo
de Kondo aima menionado. Está na ategoria dos modelos de impurezas loalizadas
e não-interagentes, oposto aos modelos de rede de impurezas. Esse limite de impurezas
isoladas tem sido tratado om muita frequênia e detalhe na literatura (uma exelente
revisão é a Ref. [8℄), onde proura-se tratá-lo de forma mais realista levando em onta
efeitos do ampo ristalino nos níveis dos multipletosde mais baixa energia (originários
do efeito spin-órbita). O modelo que utilizamos tem sua origem na análise realizada
por Nozières e Blandin [9℄ em que uma impureza omplexa ao interagir om o gás de
elétrons de ondução os divide em dois grupos, ou anais omo aram denominados.
Eles observaram, dentre outras oisas, que existiria a possibilidade da oorrênia de um
EfeitoKondosuper-ompensado,emqueaimpurezaseaoplariaomoselétronsdabanda
de ondução do metal e o resultado não seria um spin total nulo, mas sim, diferente de
S
z
z
S
z
S´z
z
z
S - impureza
z
s - eletron da banda
S´z
S´z
a)
b)
- spin resultante
Figura1.2: Efeito Kondo multianal. S é o spin da impureza, s é o spin dos elétronsde onduçãoeS
0
éospinresultante. NozièreseBlandinanalisaramumaimpurezamagnétia onsiderando sua estrutura orbital, ampo ristalino e desdobramento spin-órbita. Isso resulta no aoplamento da impureza om a banda de ondução através de anais (ada anal representa um onjunto de números quântios). Quando os aoplamentos de ada analom a impureza forem iguaise onúmerode anais n for diferente de 2S, ospin da impureza não é devidamente ompensado. No item a) temos a situação em que n <2S resultando num spin total S
0
diferente de zero paralelo aospin daimpureza. No item b) n>2S,resultandoemumspintotalS
0
diferentedezeroantiparaleloaospindaimpureza.
Omodelo maisestudado naliteraturaequeenglobaasidéias de NozièreseBlandin é
ohamado Modelo de Kondo de dois anais, ujotermo de troa(J 1
~s 1
+J 2
~s 2
) ~
S é uma
generalizaçãoimediata do Modelo de Kondo desrito iniialmente(J~s ~
S). Esse modelo
tem sido proposto por vários pesquisadores para desrever sistemas om
omportamen-to não líquido de Fermi [10℄. Sua apliação abrange até mesmo os modernos sistemas
mesosópios[11℄.
NoModelode Kondo de dois anaisquando osaoplamentosJ 1
eJ 2
(aoplamentode
ada anal om a impureza de spin S = 1=2) são iguais, as propriedades de baixa
tem-peratura fogem das araterístias de líquido de Fermi. Conjeturou-se que esse modelo
serviria para desrever o Efeito Kondo quadrupolar em íons de Urânio [12, 13℄ e outros
sistemas om propriedades anmalas de baixa temperatura. Um estudo sobre o Efeito
Kondo multianalusandoo Grupode RenormalizaçãoNumério(GRN) ombinado om
ténias de Invariânia Conforme [14℄ também indiou um omportamento não-líquido
alulassem algumas propriedades termodinâmias omo também a densidade espetral
da impureza. Para essa última, o Hamiltoniano de Kondo de dois anais não é mais
adequado, vistoque nele a valênia daimpureza é xa.
O Modelo de Kondo de um anal é o aso limite de valênia inteira do Modelo de
Andersontradiional (um anal), que ébemsuedido na ompreensãode sistemas
forte-mente orrelaionados,apesar de ser bastante simplistaseomparado àomplexidadede
materiaisreais. OHamiltoninode Andersontradiionalfoidiagonalizadonumeriamente
peloGRN [15℄ e algebriamente poransatz de Bethe [16℄. Sua generalização para o aso
de dois anais, no entanto, não é trivial, omo foi no aso Kondo. O objetivo deste
tra-balho é mostraruma possível generalização, que permite obter propriedades não triviais
em baixatemperaturae, obviamente, ter o modelotradiional omo aso partiular.
Emnosso trabalho de tese nós:
i)AnalisamosageneralizaçãodoHamiltonianodeAndersonparaoasodedoisanais.
ii)Utilizandoa Transformação de Shrieer-Wol demonstramosque oHamiltoniano
pornósutilizado(Hamiltonianode Andersonde doisanaisproposto porD.L.Cox) tem
oHamiltonianode Kondo de dois anais omo limiteem baixatemperatura.
iii) Esolhendo simetrias onvenientes do modelo, diagonalizamos numeriamente o
Hamiltonianode dois anais usando o GRN. Ao ontrário de outras métodos em que os
álulos de propriedades termodinâmias se restringem ao limite de baixas energias ou
aproximações inontroláveis, o GRN permite o álulode altas até baixas temperaturas,
e é um método não-perturbativo. Veriamos que os reentes avanços na ténia do
GRN,paraeliminaçãode osilaçõesespúriasorigináriasdoálulonumério,sãotambém
eazes emsistemas sem araterístiasde líquidode Fermi.
iv) Analisamos o omportamento do Modelo de Anderson de dois anais para dois
asos: quandoosaoplamentos(V 1
eV 2
)daimpurezaomoselétronsdeonduçãoatravés
deanaissão diferentes entre si(asoanisotrópio: V 1
6=V 2
)equandoestesaoplamentos
são iguais (aso isotrópio: V 1
=V 2
domodelo para o aso isotrópio.
v) Calulamos, pela primeiravez usando o GRN, a susetibilidade magnétia
multi-pliada pela temperatura e o alor espeío deste modelo, desde altas até baixas
tem-peraturas e para diferentes valores de aoplamentos (V 1
e V 2
). Mostramos que no aso
anisotrópio V 1
6= V 2
o Modelo de Anderson de dois anais apresenta omportamento
semelhante a um modelo de um anal (líquido de Fermi) e no aso isotrópio V 1
= V
2
apresentaomportamentonão-líquidode Fermi.
Na próximaseção vamos apresentar oModelo de Anderson de dois anais.
1.2 Modelo de Anderson de dois anais
Nestatese nós utilizamosoHamiltonianoproposto porD. L.Cox[17℄, quedenominamos
deHamiltonianodeAndersondedois anaisouHamiltonianodedoisanais. Este
Hamil-tonianoé uma generalizaçãodo Hamiltonianotradiional,onde ao invésdo aoplamento
entre a bandade ondução dometal ea impureza oorrer através de apenas um anal, o
aoplamentopodeoorreratravésde dois anaisdistintos. Osistemaaser representando
peloHamiltonianode Anderson de dois anais é uma impureza magnétia dentro de um
metalnão magnétioe está esquematizado naFig. 1.3.
Ometalérepresentadopelasuabandadeondução. Estaéisotrópia,semi-preenhida
etem umalarguratotal de 2D (2D 10eV). Aimpureza érepresentada peloseu estado
fundamental e por dois dos seus estados exitados. O estado fundamental jm;i é um
dubleto que tem m elétrons, spin total = 1=2 e energia E 0
. Os estados exitados
jm+1; i e jm 1; isão dois dubletos quetêm m1elétrons, spin total nulo, energia
E ex
eanal=1ou2. Otermode hibridizaçãoentre abandade ondução eaimpureza
éV
.
Hamil-α
V
000000
000000
000000
000000
111111
111111
111111
111111
D
-D
ε
F
|m,
σ
|m-1,
α
|m+1,
α
E
ex
E
ex
Modelo de Anderson de dois canais
∆ =
−
E
0
E
0
Figura1.3: Diagrama domodelo de Anderson de dois anais. Trata-sede uma impureza magnétia em um metal hospedeiro não magnétio. O metal é representado pela sua banda de ondução, que é semi-preenhida, isotrópia e de largura 2D. A impureza é representada peloseu estadofundamentalepordoisdos seusestadosexitados. Oestado fundamental é um dubleto que tem m elétrons, spin total = 1=2 e energia E
o . Os estadosexitadossão dois dubletosque têmm1elétrons, spintotal nulo, energiaE
ex e anal=1ou2. Otermo de hibridizaçãoentre abandade ondução eaimpureza éV
.
toniano:
H =
X
! k;;
k
y !
k;; !
k;;
+E
ex X
(jm 1; ihm 1; j+jm+1; ihm+1; j)+
+ E
0 X
jm;ihm;j+ X
! k;;
V
(f y
1;; !
k
+h::);
onde
y k;;
ria um elétron na banda de ondução om energia " k
e spin = 1=2 e
anal . Ooperador f y
1;;
hibridiza o estado fundamentalom os estadosexitados da
impureza eé denido da seguinte forma
f y
1;;
=jm;ihm 1; j+(2)jm+1; ihm; j:
Por exemplo, o termo jm;ihm 1; j!
k
representa o proesso em que a impureza
passa do estado jm 1; i para o estado jm;i ao reeber um elétron da banda de
ondução om momentum
!
k, spin e anal . No Cap. 2 vamos expliar o Modelo de
dizemosqueosistemaestánoregimeisotrópio. Comomostraremosnestatese, enquanto
oregimeanisotrópioorrespondeaoomportamentodoModelode Andersontradiional,
em que o spin da impureza é ompletamente blindado pelos elétrons de ondução, o
omportamentoisotrópioresultaemumEfeitoKondo super-ompensadoresultando em
um spin líquidoe emum omportamentonão-líquidode Fermi.
Omodeloentãopropostomisturaspin edoisanaisdeondução. Eletem uma
poten-ialapliaçãoemompostos taisomo U x
Th 1 x
Ru 2
Si 2
noregime de baixaonentração,
emque propriedadesde impurezas isoladas são esperadas [18℄.
1.3 Grupo de Renormalização Numério (GRN)
DiagonalizamosoHamiltonianodeAndersondedois anaisutilizandooGrupode
Renor-malizaçãoNumério(GRN).Esta téniafoiutilizadaporK.G.Wilsonparasoluionaro
problemaKondo[15℄. Usandoomesmoproedimento,Krishna-murthy,WilsoneWilkins
investigaramoHamiltonianodeAndersontradiional(umanal)[19℄. Importanteavanço
no GRN foi proposto no trabalho de Yoshida, Oliveira e olaboradores, que onsiste no
uso de um parâmetro adiionalde disretização da banda de ondução [20℄, ténia que
usamos nesta tese. Este novo parâmetro mostrou-se útil para o álulo de propriedades
termodinâmiasomo alor espeíoe susetibilidademagnétia [21, 22℄.
Em linhas gerais, o GRN estabelee uma transformação no Hamiltonianotal que as
esalas de energia são aresentadas ordenadamente ao problema. Assim, onstrói-se
um método iterativo em que o Hamiltoniano H é diagonalizado numeriamente a ada
iteração. O número de iterações (N) é arbitrário e está relaionado om a temperatura
que desejamos alançar. A ténia do GRN permite alançar temperaturas tão baixas
quantose queira.
Para failitaradiagonalização,utilizaram-seassimetriasexistentes nomodelo. Como
onservado (S). Assim, utilizamos esses números quântios para designar um estado
durante o proesso iterativo (jj 1
; j 2
; si). Mesmo utilizando essas simetrias, o grande
númerode grausde liberdadedoproblema torna-obastanteompliado, oqueexigiuque
desenvolvêssemos um proedimento omplexopara aimplementaçãodaténiadoGRN.
No GRN a diagonalização das matrizes é feita numeriamente. Construímos o
ódi-go omputaional utilizando o método de Programação Orientada a Objeto (POO) e a
linguagemC++. Nesse métododeprogramação,aênfase éaonstruçãode objetos:
on-juntos onstituídos por dados relaionados e suas operações. No ódigo omputaional
que desenvolvemos, um dos objetos prinipais é aquele denido pela lasse Indies, pois
guardaosvaloresimportantes para amanipulação de ada subespaçodo Hamiltonianoe
de seus elementos. Estes valores são otamanho dosub-espaço, autovalores, autovetores,
et. A lasse Indies não ontém nenhuma referênia aos números quântios j 1
, j 2
e s,
sendo esta uma araterístia que a torna fáil de ser reutilizada. O resultado é que o
ódigo omputaionaléreutilizável ompouas adaptações emnovosproblemas. Outras
araterístias da POO é a failidade da depuração do ódigo e a aloação e liberação
dinâmia,quepermite aproveitamentoeiente de memória.
Com a diagonalização dos subespaços temos os autovalores do Hamiltoniano, que já
permitemaanálise dos regimes anisotrópio(V 1
6=V 2
) eisotrópio(V 1
=V 2
) ea
identi-açãodoomportamentode líquidode Fermi ede não-líquidode Fermi respetivamente.
Com osautovalores tambémobtemos asusetibilidade magnétia eo alor espeío em
função datemperatura.
1.4 Resultado: omportamento não-líquido de Fermi
Nesta seção vamosmostrar susintamente oresultado prinipaldesta tese. Com a
diago-nalizaçãodoHamiltonianopodemosentãoveriaroomportamentodosseusautovalores
pro-aoplamentos entre aimpureza eos anais(V 1
e V 2
) , o nível de energiaE 0
do estadoda
impurezanãoionizadajm;ieonívelde energiaE ex
paraosestadosdaimpureza
ioniza-dajm+1; i e jm 1; i. Podemos analisardiferentes regimessimplesmentearbitrando
valores onvenientes para esses parâmetros.
Conforme já anteipamos e que mostraremos om mais detalhes nesta tese, o regime
anisotrópio, V 1
6= V 2
, apresenta omportamento equivalente ao Modelo de Anderson
tradiional (um anal), onde o aráter magnétio da impureza é anulado em baixa
tem-peratura[23℄.
Restringir-nos-emos nesta seção a relatar o regime isotrópio, V 1
= V
2
, no qual a
blindagem pelos elétrons de ondução, vindos de dois anais, exede o spin da impureza
(n > 2S), resultando em um spin líquido diferente de zero. Isso é responsável pelo
omportamento anmalo, ou de não-líquido de Fermi, por exemplo, da susetibilidade
magnétiaoudoalorespeío. NaFig. 1.4apresentamosTemfunção deT=T K
,onde
T K
éatemperaturaKondo,paraduasurvasnoregimeisotrópio. Podemospereberque
elasapresentamomportamentossimilaresentresi,masbemdiferentesdoomportamento
universalaraterístiodoEfeitoKondotradiional(umanal). Embaixas temperaturas
Tomporta-seproporionala Tln(T=T K
),resultadojáprevistonaliteratura[24,25,8℄
e veriado através da expressão de ajuste mostrada na Fig. 1.4. Isso ontrasta om o
omportamentolinear araterístio dos líquidos de Fermi.
Esses resultados foramapresentados noInternational Conferene onMagnetism 2000
(ICM2000) e onstarão no ICM200 Proeedings, que será publiado no Journal of
Mag-netismand Magneti Materials, em2001 [26, 27℄.
Análise semelhanterealizamos paraoalor espeío,omoestá mostrado noCap. 4.
Caberessaltarqueoálulodoalorespeíoexigeumesforçoomputaional
onsiderá-vel,esóobtivemosalgumsuessoomousodalinguagemC++,pelasuamaiorfailidade
emmanusear grandes quantidadesde memóriade proessamento. Mesmoassim, esforços
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
10
4
0
0
0.05
0.05
0.1
0.1
0.15
0.15
0.2
0.2
0.25
0.25
V1=V2=0.02 =0.002 k T =4.0 10 (b)
V1=V2=0.01 =0.002 k T =1.8 10 (c)
V1=V2=0.01 =0.006 k T =1.0 10 (d)
Curva universal do Kondo de um canal
χ
∆
0.0705
T
K
µ
B
B
k T
(g )
2
-0.103 (T/T )ln(T/T )
T
∆
∆
K K
B K
B K
-7
-11
-5
B K
b
c
d
Figura1.4: TemperaturavezessusetibilidademagnétiadaimpurezaemfunçãodeT=T K paraoModelo dedois anais. V
éotermode hibridizaçãoentreaimpurezaeoselétrons de ondução do anal ( = 1;2), D é a meia largura da banda de ondução do metal
e =E
ex E
0
, sendo E 0
1.5 Organização da tese
Finalizandoeste apítulo,apresentaremos a estrutura datese.
No Capítulo2 apresentamos o Hamiltonianode Anderson de dois anais: motivação,
omparaçãoomoHamiltonianodeAndersontradiionaledemonstração daequivalênia
omoHamiltonianodeKondodedoisanaisatravésdatransformaçãodeShrieer-Wol.
No Capítulo3apresentamos adiagonalizaçãodoHamiltonianopeloGRN:
disretiza-çãologarítmiadabandadeondução,onstrução dabase onveniente, métodoiterativo,
pontos xos, desenvolvimento do ódigo omputaional, métodos para eliminação das
osilaçõesespúrias, et.
No Capítulo 4 apresentamos os resultados: uxos dos níveis de energia dos
autova-lores do Hamiltoniano, susetibilidade magnétia e alor espeío. No nal do apítulo
Modelos de Anderson
O Modelo de Anderson tradiional é bastante onheido na literatura e desreve uma
impurezamagnétialoalizadaemum metalnão-magnétio. OModelo de Andersontem
o Modelo de Kondo omo um aso partiular, onde a impureza apresenta uma valênia
xa inteira e um momento magnétio diferente de zero. Nestes dois asos a impureza
é tratada apenas omo um orbital S representado por um nível de energia. Nozières e
Blandin[9℄analisaramaimpurezaloalizadademaneiramaisrealista,omoporexemplo,
onsiderandoseusgrausdeliberdadeorbitaleoefeitodoamporistalinodarede. Apesar
daaparenteomplexidadedessaabordagem,elesmostraramqueoefeitonaléaseparação
dabandade onduçãoemdois gruposde elétrons, denominadosgeneriamentede anais.
Omodelo om dois anais, ertamente a generalização mais simples, já é suiente para
exibiromportamento não-líquidode Fermi.
Neste apítulovamostrabalharexatamentenessadireção,mostrandoadiuldadena
generalizaçãodoModelode Andersonusualpara ummodelode doisanais.
Apresentare-mosum Hamiltonianode Andersongeneralizado esua orrespondênia om oModelode
Kondo de dois anais, atravésda transformação de Shrieer-Wol [28℄. Primeiramente,
no entanto, será bastante oportuno mostrarmos o Modelo de Anderson de um anal,
que não só motiva o trabalhoom dois anais, mas servirá para denir várias grandezas
F
ε = 0
000000
000000
000000
000000
111111
111111
111111
111111
,
-D
V
0
ε
d
2ε
d
+U
Figura2.1: EsquemadoModelode Andersontradiional. Abandade onduçãodometal ésemi-preenhidaeisotrópia. Aimpurezaérepresentadapelassuasquatroongurações possíveis, sendo"
d
aenergiadoorbitalquandooupadoomapenasum elétrone2" d
+U quando oupado por dois elétrons. V é a energia de hibridização. Se 2"
d
+U =0 temos ohamado Modelo de Andersonsimétrio,que exibe simetriapartíula-burao.
2.1 Modelo de Anderson de um anal
OModelo de Anderson tradiional foionebido para representar ligasmagnétias
diluí-das [29℄. Considera-se uma liga magnétia diluída aquela onde metais magnétios estão
dissolvidos em metais não-magnétios om uma onentração menor que um por ento,
sendoporissoonsideradosomo impurezas. Estas impurezas riammomentos
magnéti-osloalizadosquandotêmamadasdevalêniainterna(orbitaisd ouf)inompletas. Na
Figura2.1representamosoModelodeAnderson,ondeometalnãomagnétioé
simboliza-dopor uma banda de ondução de largura 2D semi-preenhida e isotrópia. Oselétrons
destabanda têm energia" k
emomento !
k. Aimpureza é representada peloseu orbitald
ouf,om energia" d
epode ganharouperder elétronsparaabanda de ondução,ando
em uma das quatro ongurações: vazia, om um elétron om spin para ima ou para
baixo, ou duplamente oupada (dois elétrons om spins ontrários). No aso da dupla
oupaçãoexiste arepulsãoCoulombianaU entre elétronsomspinopostos. Abandaestá
aoplada om a impureza através de um elementode matriz não-diagonalV e,usando a
Regra de Ouro de Fermi, a taxa de transição entre a banda de ondução e a impureza é
dada por = (" F
)V 2
, onde (" F
) é a densidade de estados de ondução por spin no
nível de Fermi. O estado fundamental depende do valorda energia " d
oloaçãode um segundo elétronom spin oposto aresentaa repulsãoCoulombiana U.
Emlinguagem de segunda quantização,o Hamiltonianopode ser esrito assim
H =
X
k; "
k
y k;
k;
+" d
X
y d;
d;
+U y d;"
d;"
y d;#
d;#
+ X
k; V
y k;
d;
+
y d;
k;
; (2.1)
onde
y k;;
ria um elétron na banda de ondução om energia " k
e om spin = 1=2,
e y d;
ria um elétron noorbital daimpureza om spin =1=2.
Noaso em que oorbitaldaimpureza tem dois elétronsom spins opostos,o nívelde
energia é 2" d
+U. Se esse valor for zero, o Hamiltonianoapresenta simetria
partíula-burao(não muda sob a transformação k;
!
y k;
e d;
!
y d;
). Nesse aso reebe o
nomedeModelode Andersonsimétrio,efoiiniialmenteexploradoporK.G.Wilsonno
desenvolvimentodaténiadoGrupode RenormalizaçãoNumério(GRN).Apesar dessa
partiularidade, o modelo ainda apresenta as araterístias mais relevantes, omo por
exemplo, o limite Kondo em baixas temperaturas. O aso generalizado para dois anais
quetrataremosmaisàfrenteorrespondeaoasosimétrio,sendoassimnosrestringiremos
amostrar apenas resultados doModelo de Anderson tradiional simétrio.
Quando " d
<0e arepulsãoCoulombiana U émuito maiorque ataxade transição ,
aonguraçãoom apenas um elétronéfavoreida. Shrieere Wol [28℄ demonstraram
queestasituaçãolimiteéequivalenteaoModelo deKondoom interaçãode troaJ igual
a
J =
8 U
(2.2)
onde =V
2
. A interaçãode troa J é, noModelo de Kondo, o termo quepermiteque
os elétrons de ondução sejam espalhados pelo spin loalizado !
S. Enquanto no Modelo
de Andersonexistetroade elétronsentre aimpureza eabandade ondução,noModelo
de Kondo a impureza tem um número xo de elétrons, om spin resultante igual a 1=2.
Por isso arma-se que o Modelo de Kondo é o limite de valênia inteira do Modelo de
000000
000000
000000
000000
111111
111111
111111
111111
-D
F
ε = 0
J
,
Figura2.2: No Modelo de Kondo o spin da impureza é xo, podendo apenas mudar sua orientação quando espalhaos elétronsde ondução.
xo, podendo apenas mudar a sua orientação. Observe a semelhança entre as Fig. 2.2e
2.1 quando no Modelo de Anderson os níveis vazio e duplamente oupado da impureza
tiverem energiamuito maiorque " d
. O Hamiltonianode Kondo de um anal édado pela
expressão
H =
X
! k;
" k
y k;
k;
1 2
X
! k;
! k
0 ;;
J
y !
k; !
;
! k
0 ;
!
S; (2.3)
onde ; são osíndies de spin. y 0;;
ria elétronsno sítioda impureza e !
é um vetor
ujas omponentes são as matrizes da Pauli. !
S = 1=2 é o spin da impureza e " k
é a
energiados elétrons de ondução medida apartir do nívelde Fermi.
O Hamiltonianode Kondo desreve um fenmenoobservado desde a déadade 1930,
bastante onheido na literatura atualmente (por exemplo ver Ref. [30℄) e que, por
is-so, relataremos aqui apenas de maneira suinta. O Efeito Kondo é um fenmeno que
se observa em várias substânias, prinipalmente ligas metálias, a baixas
temperatu-ras (em torno de 10K). À medida que a temperatura diminui, a resistividade derese
monotoniamenteaté que,emdeterminadatemperaturadiferente de zero,observa-se um
mínimo na resistividade elétria. Veriou-se experimentalmente que esse mínimo está
relaionado om a presença de impurezas magnétias no metal hospedeiro. Em geral as
impurezasquemostramesseomportamentosãoelementosdetransição3douterras-raras
4f databelaperiódia. OutraonstataçãoexperimentaléqueoEfeitoKondoéuma
expliaçãodesse fenmeno ao propor que esse efeito era resultado dainteração entre um
spinloalizado(proveniente, porexemplo de umaimpureza)om osspins doselétronsde
onduçãodometal hospedeiro. Utilizando-sede um modelobastantesimplista,omodelo
s disotrópio (que já existiae mais tardeou onheido omo Modelo de Kondo [1℄),
ele fez um álulo perturbativo e deduziu a existênia de um mínimo na resistividade.
Apesar dessesuesso, aresoluçãoperturbativade Kondosusitouoapareimentode uma
divergênia logarítmiana resistividade em uma dada temperatura, que ou onheida
omotemperaturade Kondo T K
:
k B
T K
De
1 2jJj
(2.4)
A ausa dessa divergênia é o método perturbativo que se mostra-se ineiente para
resolveroHamiltonianode Kondo paratemperaturas muito baixas. Em1975 o
Hamilto-nianode KondofoidiagonalizadosemaproximaçõespeloGRN[15℄. Emseguida,também
usandooGRN,diagonalizou-seo Modelo de Anderson[19℄,que apresenta avantagemde
permitiro álulo dadensidade espetral uma vez que não possui valênia xa.
Comoexemplo,mostraremosaseguirasusetibilidademagnétiaealorespeíodo
Modelode Anderson, obtidosatravésdoGRN.Comoessa téniaserádetalhadanoCap.
3aquinão mostraremosnenhum detalheténiodoGRN. Asusetibilidademagnétia
édenida pelarelação
k B
T (g
B )
2 =hS
2 z
i hS
z i
2
; (2.5)
onde S z
é a omponente z do spin total. A média termodinâmia é alulada usando os
autovaloresdo Hamiltonianode Andersonobtidos através doGRN [31, 22℄.
AFig. 2.3mostraaontribuiçãodaimpurezaàsusetibilidade,queéobtida
subtraindo-seovalorde T dabandalivredaquelealulado pelaEq. 2.5,emfunção da
temperatu-ra T. Podemos destaar três regiões importantes nessa gura. Em altas temperaturas,
k B
T " d
10
-8
10
-6
10
-4
10
-2
10
0
0
0
0.05
0.05
0.1
0.1
0.15
0.15
0.2
0.2
U=0.005 V=0.01
Curva universal de Kondo
4e-08
8e-08
0
0.005
0.01
0.015
0.02
k T
um canal
B
2
µ
χ
k T
D
B
B
T ~ 8.0 10 D
(g )
K
-7
1/8
Figura 2.3: Temperatura multipliada pela susetibilidade magnétia em função de k
B
T=D do Modelo de Anderson de um anal. A linha heia é a urva universal do Modelo de Kondo de um anal. No inset podemos pereber o omportamentolinear em baixas temperaturas.
o aoplamento V om a banda pode ser desonsiderado. Com isso, temos duas
ongu-rações não-magnétias (a vazia e a duplamente oupada) e duas magnétias (uma om
spin+1=2eoutraomspin 1=2)eportantoamédiadeS 2 z
vale(0+2(1=2) 2
+0)=4=1=8,
sendo o denominador 4 o valor da função de partição nesse limite de alta temperatura.
Ovalorassintótio 1/8 pode ser visto laramentenaFig. 2.3; esse limite orresponde ao
queédenominadode pontoxode impureza (banda) livre. À medidaque atemperatura
abaixa,a separação entre osníveisnão-magnétios eosmagnétios passa aser perebida
e a média de S 2 z
agora tende para o valor 2(1=2) 2
=2 = 1=4 (agora a função de partição
vale2,poistemosapenasasduas onguraçõesmagnétias). A urvade Ttendea esse
valor para k B
T=D próximo a 10 3
omo se pode ver na Fig. 2.3. Esse regime reebe o
nome de pontoxo de momento loal. O aoplamento V om a banda de ondução não
deixa T se aproximar do valor 1/4 e o apareimento da ressonânia Kondo aaba por
blindaromomentomagnétiodaimpurezaatravésdaformaçãode umanuvemeletrnia
em volta do spin loalizado, dessa forma levando T a zero. Esse regime, que aontee
para temperaturas menores que a temperatura Kondo T K
, é denominado de fortemente
(T T k
), o que arateriza omportamento líquido de Fermi. Do gráo estimamos
(T =0)=1:3210 5
. Da Eq. 5.36 da Ref. [19℄, relaionamos(0) om atemperaturade
Kondo por
(0) (g
B )
2 =
0:103 k
B T
K
: (2.6)
Assim, nossa estimativaé k B
T k
=7:810 7
Dpara a urvada Fig. 2.3.
A temperatura de Kondo é a únia esala de energia relevante no modelo embaixas
temperaturas. Assim,espera-sequetodasasgrandezasmostremomportamentouniversal
quandoexpressasemfunção deT=T K
,para T T K
. Aurvade TnaFig. 2.3podeser
justaposta,em baixas temperaturas, pelaurvaheia querepresentaa urva universalde
Kondo para T, alulada analitiamente por Bethe ansatz [16℄ ou numeriamente por
WilsonusandooGRN[15℄. Paraissoutilizamosk B
T K
=7:710 7
D,emboaonordânia
om oforneido pelovalorde (0) aima.
Enquanto a urva universal de Kondo de T sai do valor 1/4 à medida que a
tem-peraturadiminui,reetindo alei de Curie para um spin 1/2 livre,a urva do Modelo de
Andersonsaido limite1/8. Isso aontee porque enquanto oModelo de Kondotem
ape-nas duas ongurações, o Modelo de Anderson emtemperaturas muito altas (k B
T D)
tem as suas quatro ongurações (vazia, duplamente oupada e duas singelamente
ou-padas) igualmente aessíveis. Mas, à medida que a temperatura abaixa e a da ordem
de K B
T " d
+U,apenas asduas onguraçõesmagnétias (ongurações singelamente
oupadas)ontinuamaessíveis, eporissoaurvadoModelodeAndersonseaproximada
urva do Modelo de Kondo. Assim oModelo de Anderson e o Modelo de Kondo passam
adesrever efetivamentea mesmaimpureza (om spin 1/2) e aurva de Anderson tende
ase aproximar daurvauniversal de Kondo.
Tendo disutidoosaspetos físiosrelevantes doModelode Andersontradiional
Como desrito no Cap. 1, na busa de uma representação mais realista do sistema de
impurezas em um metal, Nozières e Blandin onsideraram o efeito da estrutura interna
da impureza, ampo ristalino, et [9℄. O resultado prátio disto foi a ompreensão de
quetodos estesfatores fazemom queoselétronseaimpurezainterajamatravésde mais
de um onjuntode números quântios, ada onjunto denominadode um anal.
Ooneito de anal permitea generalizaçãotrivialdo Hamiltonianode Kondo: basta
aresentar um índie a ada operador da banda de ondução: ~ k ;
!
~ k ;;
, onde =1
ou2noaso de termosdois anais. Sendoassim,o Hamiltonianoque deneoModelode
Kondo de dois anais é
H =
X
! k;;
k
y k;;
k;;
1 2
X
! k;
! k
0 ;;;
J
y !
k;; !
;
! k
0 ;;
!
S: (2.7)
Utilizando o mesmo proedimento que levou da Eq. 2.3 à Eq. 2.7, do Hamiltoniano
de Anderson tradiionalobtemos aexpressão para o modelo de dois anais:
H =
X
! k;;
" k
y !
k;; !
k;; +"
d X
y d;
d;
+
+ U
y d;"
d;"
y d;#
d;#
+ X
! k;
! k
0 ;
V
y !
k;;
d;
+
y d;
! k
0 ;;
!
: (2.8)
Assimomonomodelotradiional" d
éaenergiadoelétronnaimpurezaeU éaorrelação
eletrnia. Mas agoratem-seV
queé oparâmetrode hibridizaçãoentre aimpureza eos
elétronsde ondução do anal .
É fáil mostrar que o modelo denido pelo Hamiltonianoaima na verdade ontinua
desrevendoainteraçãodeumaimpurezamagnétiaomelétronsdometalviaapenasum
0 B B
g! k;;+ g!
k;; 1 C C A
= 0 B B
#
#
1 C C A
0 B B
! k;;1 !
k;;2 1 C C A
; om =
V 1 q
V 2 1
+V 2 2
; #= V
2 q
V 2 1
+V 2 2
; (2.9)
onde g!
k;;
são os operadores de destruição de elétrons dos novos anais = +; . A
Eq. 2.8 a, então,
H =
X
! k;;
k
g y !
k;;+ g!
k;;+ +g
y !
k;; g!
k;; !
+E
d
y d;
d;
+
+U
y d;"
d;"
y d;#
d;#
+ q
V 2 1
+V 2 2
X
! k;
g y !
k;;+
d; +h::
!
; (2.10)
que é o Hamiltoniano de Anderson tradiional om o termo de hibridização dado por q
V 2 1
+V 2 2
, junto om uma banda de ondução ompletamente desaoplada ( = ).
Portanto,aEq. 2.8nãorepresentaoModelo deAndersongeneralizado,eassim,devemos
prourarporum proedimentoalternativoque resulte num modelo não-trivial.
2.2.1 Proposta de Cox
As impurezas em nosso modelo são átomos om amadas d ou f semi-preenhidas, onde
deve-se levarem onsideraçãoa degeneresênia orbitaldestes estados de aordo om as
regrasdeHund, interaçõesspin-órbitaeefeitos doambienteloal(amporistalino). Um
proedimentoparalevarestasinteraçõesemonsideraçãoéomeçaromasongurações
de mais baixas energias do íon isolado, e então onsiderar omo elas são modiadas
quandomisturadasomoselétronsdeonduçãodohospedeiro. NaFig. 2.4representamos
uma impureza hipotétia onde seus três estados de mais baixa energia orrespondem ao
orbital de valênia semi-preenhido, um orbital om um elétron a mais e outro om um
elétrona menos.
Omodeloinio[32℄ onsideraahibridizaçãoentre oselétronsdoorbitaldaimpureza
de
eletrons
energia
Figura2.4: Representação hipotétiadaenergiade valêniade umaimpurezaomorbital semi-preenhido para as ongurações de energia mais baixas. A parábola é dada pela expressão E
m
= E
d
m +Um( m 1)=2, onde E d
é a energia do orbital (em relação ao nível de Fermi), e m é o número de elétrons noorbital. Veja que fazendo m=0, m=1, ou m = 2 reproduzimos os níveis de energia da impureza do Modelo de Anderson (Fig. 2.1).
do Modelo de Anderson. Infelizmente, este modelo é difíil de ser diagonalizado devido
aograndenúmerode parâmetros envolvidos para representar asmais diversas interações
[30℄.
Como mostrado porNozières e Blandin, usando argumentos de simetria e
universali-dadeépossívelagruparestasinteraçõesemonjuntosdenúmerosquântiosbemdenidos,
anais, reduzindo sensivelmente os números de graus de liberdadedo sistema. Esse
pro-edimentofoiseguidoporváriospesquisadores[23,18,33,34℄. Emomuniaçãopartiular
[17℄,D. L.Cox propsum HamiltonianodeAndersongeneralizadoparadois anais,onde
oestado fundamentalda impureza érepresentado porjm;i om energiaE 0
, m elétrons
espin total =1=2. Aimpurezatem aindadoisestadosexitadosjm1; i deenergia
E ex
, om m 1 elétrons, spin total zero e anal = 1 ou 2. Todos esses níveis estão
hibridizados om os elétrons de ondução do metal através dos anais = 1 ou 2. Sem
a hibridização om a banda, isto é, desaoplando banda e impureza, é fáil de se denir
esse novoHamiltoniano:
H 0
= X
! k;;
k;;
y !
k;; !
k;; +E
0 X
jm;ihm;j+
+E ex
X
α
V
000000
000000
000000
000000
111111
111111
111111
111111
D
-D
ε
F
|m,
σ
|m-1,
α
|m+1,
α
E
ex
E
ex
Modelo de Anderson de dois canais
∆ =
−
E
0
E
0
Figura2.5: ModelodeAndersondedoisanaisemqueoestadofundamentaléumdubleto ommpartíulasespintotal =1=2edoisdubletosomoestadosexitados,omm1 partíulas, spin total igual azero e om anal .
onde o primeiro termo da direita é a banda de ondução e os outros termos denem as
energiasdosníveisloalizadosjm;iejm1; i(verFig. 2.5). Comoosestadosjm+1; i
ejm 1; i têm amesma energia, omodelo apresenta simetriapartíula-burao e assim
podemos denominá-lode simétrio,aexemplo do modelotradiional de um anal.
Para denir otermo de hibridização émais ompliado. Podemos imaginardois
pro-essos: emumdelesoestadode elétrondeondução omosnúmerosquântiosf !
k;; g
é destruído e o estado loal muda de jm 1; i para jm;i; o spin iniial do elétron
neste proesso é arbitrário. O outro proesso é quando o elétron de ondução forma um
estadosingleto om jm;i o qual,por sua vez, muda para o estadonal jm+1; i.
Ess-es proessos de hibridização podem ser visualizados pelos diagramas da Fig. 2.6 e são
desritos peloHamiltoniano
H V
= X
! k;;
V
(f y
1;; !
k
+h::); (2.12)
onde V
éo aoplamentoentre a impureza eo anal (por onvenção se =1, =2
evie-versa). O operador f y
1;;
é denido assim
f y
1;;
=jm;ihm 1; j+(2)jm+1; ihm; j: (2.13)
m,
σ
σ,α
k,
m,
σ
−σ,α
k,
a)
b)
Figura2.6: Esquemadeinteraçõesentreosestadosdaimpurezaeoselétronsdeondução. m é o número de elétrons no orbital da impureza. = 1=2, quando = 1, = 2 e vie-versa. Em a) um elétron de ondução (k;; ) se hibridiza om o estado loal (m 1; ) e forma o estado de spin . Em b) um elétron de ondução (k; ; ) se hibridiza om o estado loal (m;) em uma ombinação singleto, resultando em estado de anal (m+1; ) (spin 0). Logiamente proessosinversos são permitidos.
é,então, H =H 0
+H
V :
H =
X
! k;;
k;;
y !
k;; !
k;;
+E
ex X
(jm 1; ihm 1; j+jm+1; ihm+1; j)+
+E 0
X
jm;ihm;j+ X
! k;;
V
(f y
1;; !
k
+h::): (2.14)
ÉfáilompararoModelodeAndersontradiional(umanal)simétrioomoModelo
de Anderson de dois anais proposto por Cox. Na Fig. 2.7 mostramos o Modelo de
Andersonde um analsimétrioemnotaçãosemelhanteàusada noModelo de Anderson
generalizado.
Para veriar seo Hamiltoniano dado pela Eq. 2.14 desreve o Modelo de Kondo de
dois anaisem baixas temperaturas, demonstramossua equivalêniaao Hamiltonianode
Kondo de dois anais, Eq. 2.7, através doproedimento de Shrieer-Wol.
2.2.2 Transformação de Shrieer-Wol para dois anais
ShrieereWol[28℄demonstraramqueoHamiltonianodeKondoeraumasopartiular
doHamiltonianode Anderson tradiional (um anal). Seguindo os passos de Shrieer e
000000
000000
000000
000000
111111
111111
111111
111111
D
-D
ε
F
ε
D
+U
D
2ε
V
000000
000000
000000
000000
000000
111111
111111
111111
111111
111111
D
-D
ε
F
|0,0
|2,0
|1,
σ
+U
D
2ε
ε
D
V
000000
000000
000000
000000
000000
111111
111111
111111
111111
111111
D
-D
ε
F
|m,
σ
|m-1,
α
|m+1,
α
E
ex
E
0
Modelo de Anderson de dois canais
V
α
Modelo de Anderson de um canal
ou, de maneira equivalente
,
2.14 daseguinte forma
H =H
0
+H
V
(2.15)
onde
H 0
= X
! k;
k
y !
k;; !
k;;
+E
0 X
jm;ihm;j+ (2.16)
+E ex
X
(jm 1; ihm 1; j+jm+1; ihm+1; j) (2.17)
H V
= X
! k;;
V
(f y
1;; !
k
+h::): (2.18)
A idéia é transformarH num Hamiltoniano f
H que não ontenha termos linearesem V
.
Essa transformação é feita utilizando-se um operador P , denido apropriadamente a
posteriori talque
f H=e
P He
P
=H+[P;H℄+ 1 2!
[P;[P;H℄℄+ : (2.19)
Então,
f
H =H
0
+H
V
+[P;H 0
℄+[P;H V
℄+O(V 3
): (2.20)
Ooperador P deve ser talque
[P;H 0
℄= H
V
(2.21)
eassim eliminar ostermos linearesem V
. Dessaforma teremos(desprezando ostermos
de ordem V 3
eaima),
f
H =H
0
+[P;H V
℄ : (2.22)
Enontramos o operador P usando dois auto-estados (jai e jbi) de H 0
hajH 0
P PH
0
jbi = hajH V
jbi (2.23)
eportanto
hajP jbi= H
Va;b E
a E
b ;
onde E a
e E b
são as energias dos estados jai e jbi. Multipliando à direita por jai e à
esquerdaporhbj e somando em a eb temos,
X
a;b
jaihajP jbihbj = X
a;b H
Va;b E
a E
b
jaihbj: (2.24)
Portanto,
P =
X
a;b H
Va;b E
a E
b
jaihbj: (2.25)
H Va;b
onetaestadosquesedifereniamapenasporumapartíulanaimpureza: jm;i!
jm 1; i,queorrespondeàenergia" q
E 0
+E ex
;oujm+1; i!jm;i,queorresponde
àenergia" q
+E 0
E ex
. Coleionandotodas essas possibilidadesonstruímos ooperador
P da formadaEq. (2.25 ) resultando em:
P =
X
q V
"
jm 1; ihmj
" q
E 0
+E ex
+(2)
jm; ihm+1;j "
q E
ex
+E
0 !
! q;;
h:: #
; (2.26)
onde q indiamomento,india spin e indiaanal.
Para demonstrarque o operadorP satifazà ondição [P;H 0
℄= H
V
imposta
anteri-ormentebastaonsiderarmosque,omoéusualnatransformaçãoShrieer-Wol,apenas
asenergias de exitaçãoda banda próximas àenergia de Fermi são importantes, ouseja,
" k
;" q
0(q;k k F
). Devemosobservarque
jm;ihm;j;! k;;
=0;poisjm;ihm;j
não ria ou destrói elétron, e que
jm1; ihm;j; ! k;;
= 0 pois jm1; ihm;j
[P;H V
℄= X
! k;;
2V 2 E
ex E
0
jm;ihm; j
y !
k; ; !
k;;
+
y !
k;; !
k; ; !
; (2.27)
que, usando notaçãoonveniente, pode ser esrito daseguinte forma:
[P;H V
℄= X
; J
!
S: !
s
; (2.28)
onde
! s
=
X
! k;
! q
y !
k;; !
; 2
! q ;;
; (2.29)
!
S = hmj
!
; 2
jmi; (2.30)
J
=
8V 2 E
ex E
0
; (2.31)
sendo !
;
matrizesde Pauli.
Finalmentea Eq. 2.20 a
f H
=H
0 +
X
J
!
s
!
S: (2.32)
A Eq. 2.32 é equivalente à Eq. 2.7 e representa a forma do Hamiltonianode Kondo de
dois anais. Quando E ex
> E 0
o aoplamentoJ
da impureza om a banda é
antiferro-magnétio,omo no Modelo de Kondousual.
Portanto, o Hamiltoniano dado pela Eq. 2.14 desreve o Modelo de Kondo de dois
anais.
No próximo apítulo apliaremos a ténia do Grupo de Renormalização Numério
Diagonalização do Hamiltoniano de
Anderson de dois anais pelo GRN
Nestatese utilizamosoGRNparaadiagonalizaçãodoHamiltonianodeAndersonde dois
anais. Essa ténia estabelee uma transformação no Hamiltoniano que a ada passo
aresentauma esalade energiaaoproblema. Constrói-seummétodoiterativoemqueo
HamiltonianoH é diagonalizadonumeriamente em ada iteração. Nas próximasseções
detalhamosa apliaçãodoGRN no Hamiltonianode Andersonde dois anais.
3.1 Grupo de Renormalização Numério: histório
O Grupo de Renormalização Numério (GRN) surgiu em meados de 1970, quando K.
G. Wilson, formalizando um onjunto de idéias de saling, investigou expoentes rítios
em transições de fase de segunda ordem [35, 36℄. Posteriormente Wilson apliou esta
ténianoproblema Kondo, utilizandoálulosnúmeriosnadiagonalizaçãode matrizes
[15℄. Usando o mesmo proedimento Krishna-murthy, Wilson e Wilkins investigaram o
Hamiltoniano de Anderson tradiional [19℄, sendo estes dois artigos onsiderados omo
base do GRN. Desde então uma série de trabalhos foram exeutados om esta ténia