Modelo de Heisenberg para cadeia de spins

DEPARTAMENTO DE FÍSICA

PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA

RAVENNA RODRIGUES OLIVEIRA

MODELO DE HEISENBERG PARA

CADEIAS DE SPINS

MODELO DE HEISENBERG PARA

CADEIAS DE SPINS

Dissertação de Mestrado submetida à Coor-denação do Curso de Pós-Graduação em Fí-sica, da Universidade Federal do Ceará, como requisito parcial para a obtenção do Título de Mestre em Física

Orientador: Prof. Dr. Raimundo Nogueira da Costa Filho.

MODELO DE HEISENBERG PARA

CADEIAS DE SPINS

Dissertação de Mestrado submetida à Coor-denação do Curso de Pós-Graduação em Fí-sica, da Universidade Federal do Ceará, como requisito parcial para a obtenção do Título de Mestre em Física

Aprovada em 04/08/2016

BANCA EXAMINADORA

Prof. Dr. Raimundo Nogueira da Costa Filho Universidade Federal do Ceará

Profa. Dra. Silvia Helena Roberto de Sena Universidade de Integração Internacional de Lusofonia

Afro-Brasileira

Biblioteca Setorial de Física A000p Oliveira,Ravenna Rodrigues.

Modelo de Heisenberg para cadeias de spins / Ravenna Ro-drigues OLiveira. – 2016.

58 p.;il.

Dissertação de Mestrado - Universidade Federal do Ceará, De-partamento de Física, Programa de Pós-Graduação em Física, Centro de Ciências, Fortaleza, 2016.

Área de Concentração: Física

Orientação: Prof. Dr. Raimundo Nogueira da Costa Filho.

1_{. Ferromagnetismo.} 2_{. Interação de troca.} 3_{. Modelo de}

Heisenberg.4_{. Ondas de Spin.}5_{. Efeito Zeeman. I.}

Agradeço a minha família pelo apoio financeiro e psicológico que me sempre dedicaram: Antonia Lusanira Rodrigues Oliveira e José Glairton Oliveira, meus pais, meus irmãos Romany Rodrigues Oliveira, Mairton Oliveira, Fabíola Oliveira e Fabiana Oliveira. Dedico este trabalho a Tereza Nonato do Nascimento, Gilson Aguiar Albuquerque e Maria Aila Albuquerque por todo o apoio que me foi dado.

Todo dia novas invenções tecnológicas surgem no mundo, melhorando a vida da sociedade como um todo. Para que os novos dispositivos estejam cada vez mais evoluindo, a ciência também precisa estar evoluindo. Dentro da ciência, um assunto que ganha destaque são as propriedades magnéticas dos materiais, tais quais materiais ferromagnéticos. A partir do estudo de materiais magnéticos foi possível a fabricação de dispositivos como o HD de computadores. Nos sistemas ferromagnéticos os spins vizinhos estão acoplados uns aos outros por meio da interação de troca, possuindo modos coletivos chamados de ondas de spin. Para entender as propriedades de ondas de spin utiliza-se o modelo de Heisenberg, que considera o termo de troca, juntamente com o efeito Zeeman. Nesta dissertação utilizamos o modelo de Heisenberg para ondas de spins para algumas redes. O estudo para uma rede de duas camadas onde uma é deslocada em relação à outra foi realizado, observando que o comportamento para uma rede deslocada para a esquerda e uma rede igualmente deslocada para a direita é o mesmo. Motivados pelo formato helicoidal da molécula de RNA, estudamos uma rede ao redor de um cilindro. O caso onde a rede é disposta simetricamente é encontrado degenerescência, que pode ser desfeita alterando a configuração da rede de modo que não haja mais simetria.

Everyday new technological inventions arrives in the world, improving the life of the society as one. For new devices to have improvements, science needs to be improved too. Within science, a subject that stands out is the magnetism properties of the materials, like ferromagnetic materials. Due to the studies about the magnetism properties of the materials become possible the criation of computerhard drive. In this dissertation, we use

the Heisenberg model to better understand the spin waves, which commonly appear in magnetic materials. This model considers the exchange interation of spins, together with the Zeeman effect. In this dissertation we use the Heisenberg model for spin waves applied to some networks. The study for a two layer network where one of them is displaced in relation to the other was done. The behavior for a network displaced to the left and a network equally dislocated to the right is the same. Due to the helical structure of an RNA molecule we study the Heisenberg model in a network around a cylinder. For this network, we found that case where the network is symmetrically displaced is degenerate, which can be broke by changing the network configuration, so there is no symmetry in the system.

1 Esboço do experimento Stern-Gerlach. Figura modificada de [24]. . . p. 16

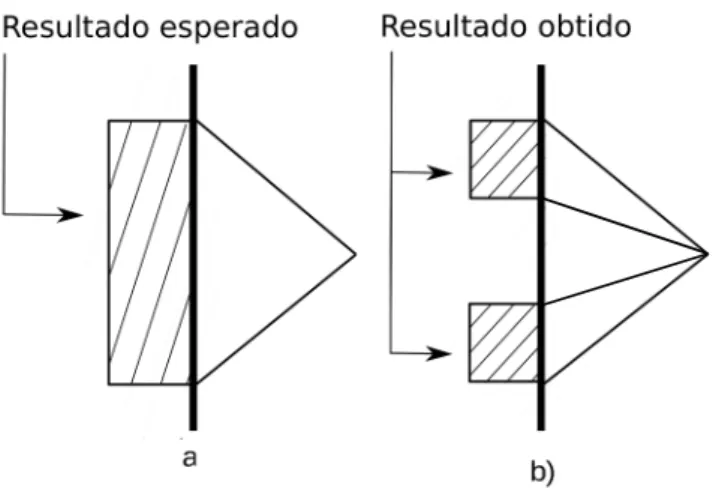
2 a) Resultado experimental que Stern e Gerlach esperavam obter. A predição clássica verificava que o feixe deveria ser espalhado verticalmente, tendo como limetes os valores do momento magnético multiplicado pelo cosseno do ân-gulo de orientação. b) Resultado obtido, sendo duas orientações do momento

magnético. Figura modificada de [7]. . . p. 17

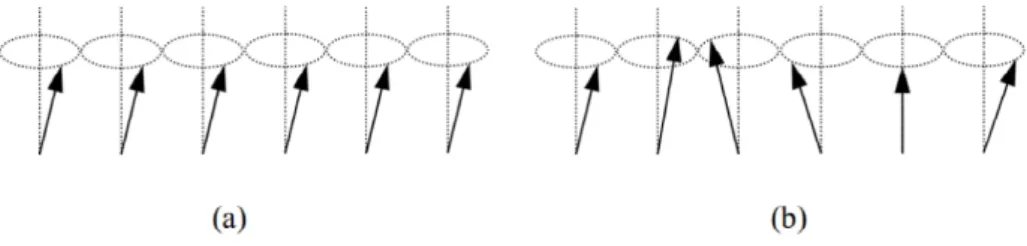
3 (a) Representa os modos uniformes, excitação de menor energia, os elé-trons possuem então a mesma fase. (b) Representa ondas de spins em

um sistema ferromagnético. Figura retirada de [10]. . . p. 21

4 Representação do alinhamento dos dipolos em uma pequena parte do material

ferromagnético após a aplicação do campo magnético. . . p. 22

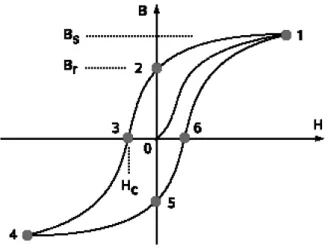
5 Curva de histeresse, onde o campo magnético é representado por B e a

corrente de magnetização por H. Figura retirada de [25]. . . p. 23

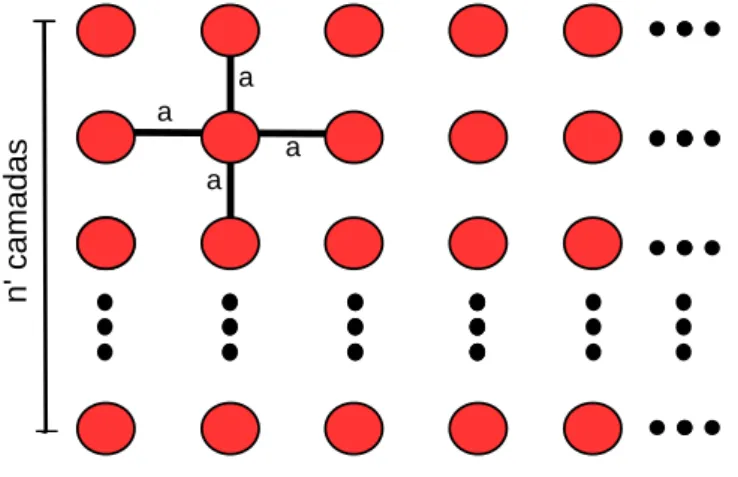
6 Exemplo de uma rede quadrada simples finita na direção Y, n′ _{representa o}

número de camadas e a o parâmetro da rede. . . p. 36

7 Exemplo de uma rede não simétrica. . . p. 39

8 Uma rede com duas camadas e deslocada na direção X. . . p. 42

9 (a) Gráfico da energia em função de k para a rede com duas camadas e des-locadas na direção X, onde J1 representa o primeiro vizinho, J2 o segundo e J3 o terceiro. Foi utilizado J1 = 1, µBH0 = 1, a = 3, b = 5 e c = 1. (b)

Configuração da rede. . . p. 44

10 (a)Gráfico da energia em função dekpara a rede com duas camadas deslocadas na direção X, onde J1 representa o primeiro vizinho, J3 o segundo e J2 o terceiro. Foi utilizado J1 = 1, µBH0 = 1, a = 3, b = 5 e c = 2. (b)

na direção X, onde J2 representa o primeiro vizinho, J1 o segundo e J3 o terceiro. Foi utilizado J1 = 1, µBH0 = 1, a = 4, b = 3 e c = 1. (b)

Configuração da rede. . . p. 45

12 (a)Gráfico da energia em função dekpara a rede com duas camadas deslocadas na direção X, onde J2 representa o primeiro vizinho, J3 o segundo e J1 o terceiro. Foi utilizado J1 = 1, µBH0 = 1, a = 4, b = 2 e c = 1. (b)

Configuração da rede. . . p. 45

13 (a)Gráfico da energia em função dekpara a rede com duas camadas deslocadas na direção X, onde J3 representa o primeiro vizinho, J1 o segundo e J2 o terceiro. Foi utilizado J1 = 1_{, µBH0} = 1_{, a} = 4_{, b} = 3 _{e c} = 3_{. (b)}

Configuração da rede. . . p. 46

14 (a)Gráfico da energia em função dekpara a rede com duas camadas deslocadas na direção X, onde J3 representa o primeiro vizinho, J2 o segundo e J1 o terceiro. Foi utilizado J1 = 1, µBH0 = 1, a = 4, b = 2 e c = 3. (b)

Configuração da rede. . . p. 46

15 Rede disposta ao longo de um cilindro. . . p. 47

16 Rede disposta ao longo de um cilindro vista de cima. . . p. 47

17 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira simétrica, onde J1 representa o primeiro vizinho,J2 o segundo eJ3 representa o terceiro vizinho. Foi utilizado J1 = 5_J0,J2 = 2_{J0, J3} = 1_{J0, µBH0} = _J0,

c= 4_{. (b) Configuração da rede.} . . . p. 49

18 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira simétrica, onde J2 representa o primeiro vizinho,J3 o segundo eJ1 representa o terceiro vizinho. Foi utilizado J1 = 5J0,J2 = 2J0, J3 = 1J0, µBH0 = J0,

c= 4_{. (b) Configuração da rede.} . . . p. 49

19 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira simétrica, onde J2 representa o primeiro vizinho,J1 o segundo eJ3 representa o terceiro vizinho. Foi utilizado J1 = 2J0,J2 = 4J0, J3 = 1J0, µBH0 = J0

c= 4_{. (b) Configuração da rede.} . . . p. 49

20 Rede disposta ao longo de um cilindro. . . p. 50

Distância entre os elementos da rede A com elementos da rede C; (c)Distância

entre os elementos da rede B com elementos da rede C. . . p. 51

23 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2, l2 = 3, l3 = 4, Ji =J0d0/di,d0 = 5, µBH0 =J0,

c= 1_,d= 2 _{e e}= 3_{. (b) Configuração da rede.} . . . p. 53

24 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2, l2 = 2, l3 = 2, Ji =J0d0/di,d0 = 5, µBH0 =J0,

c= 1_,d= 2 _{e e}= 3_{. (b) Configuração da rede.} . . . p. 54

25 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2, l2 = 3, l3 = 4, Ji =J0d0/di,d0 = 5, µBH0 =J0,

c= 3_,d= 2 _{e e}= 5_{. (b) Configuração da rede.} . . . p. 54

26 (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2_{, l2} = 3_{, l3} = 4_{, Ji} = _{J0d0/di, d0} = 5_{, J} = 1_,

1 INTRODUÇÃO p. 12

2 SPIN p. 16

2.1 Spin do elétron . . . p. 16

2.2 Princípio de exclusão de Pauli . . . p. 19

2.3 Ondas de spin . . . p. 20

3 MATERIAIS FERROMAGNÉTICOS E UMA PARTÍCULA

CAR-REGADA EM UM CAMPO MAGNÉTICO p. 22

3.1 Materiais ferromagnéticos . . . p. 22

3.2 Uma partícula carregada em um campo magnético . . . p. 24

3.3 Efeito Zeeman . . . p. 26

3.4 O modelo de Heisenberg . . . p. 27

3.4.1 Diagonalizando o Hamiltoniano de Heisenberg . . . p. 31

3.5 Rede Quadrada Simples Finita . . . p. 36

3.6 Interação entre redes não simétricas . . . p. 39

4 APLICAÇÃO DO MODELO DE HEISENBERG PARA DUAS

RE-DES NÃO SIMÉTRICAS p. 42

4.1 Rede com duas camadas deslocadas . . . p. 42

4.2 Rede ao redor de um cilindro . . . p. 46

5 CONCLUSÃO p. 55

1

INTRODUÇÃO

O desenvolvimento tecnológico está intrinsecamente ligado ao desenvolvimento cien-tífico, atuando como catalisador das mudanças na nossa sociedade. Conforme a evolução tecnológica acontece, novos dispositivos eletrônicos surgem para atender as necessidades e demandas da sociedade. Surgem a partir desse desenvolvimento novas formas de se relacionar, novas formas de trabalhar, novos hábitos para a sociedade e novos produtos surgem no mercado, de maneira que o campo de estudo científico é ampliado, surgindo novos campos de interesse científico e tecnológico.

Cada vez mais o homem procura a otimização de sua tecnologia e por consequência do estudo científico, para que dispositivos mais eficazes sejam descobertos. O estudo científico se torna imprescindível para o avanço da humanidade.

O magnetismo está relacionado a grandes invenções no passado e impulsionou a so-ciedade ao contexto atual, tendo um papel indispensável nas grandes navegações, na medicina, informática, entre outras áreas.

A bússola é um exemplo de uma invenção tecnológica que facilitou as grandes na-vegações na história da humanidade. Essa invenção se sucedeu a partir de uma outra descoberta realizada por um pastor chamado Magnes [1]. O pastor ao pastorar seu re-banho em Monte Ida, percebeu que pequenas rochas eram atraídas para seu cajado, que possuía a ponta de ferro, essas rochas chamadas magnetita, calamita ou imã de pedra foram descobertos em aproximadamente2500a.c.. Outra versão para a descoberta dessas rochas é que na região de Magnésia, na Ásia menor, foi encontrado um mineral de ferro que atraía outros metais de ferro, em homenagem ao local que foi descoberto, recebeu o nome de magnetita. A descoberta desses materiais culminou na da bússola, instrumento inventado por Flávio Gióia, em Amalfi, na Itália, em 1280[2]. A bússola funciona a

navegações. Dispositivos magnéticos ganham cada vez mais força na sociedade, sendo utilizados atualmente em portas magnéticas, sensores de posição, na produção de discos rígidos, entre outros [3, 4].

Os materiais magnéticos podem ser divididos em materiais paramagnéticos, diamag-néticos e ferromagdiamag-néticos. Materiais paramagdiamag-néticos são aqueles que ao se aplicar um campo magnético a magnetização é paralela ao campo, em materiais cujos elétrons são pares a magnetização total é nula, devido ao princípio de exclusão de Pauli, então o pa-ramagnetismo é mais comum em materiais cujos elétrons são ímpares, nesses materiais ao se retirar o campo a resposta ao mesmo é perdida. Nos materiais diamagnéticos ao se aplicar um campo magnético a magnetização é oposta ao campo, o diamagnetismo ocorre em todos os materiais, é um fenômeno mais fraco do que o paramagnetismo e o ferromagnetismo, por isso é mais facilmente visto em materiais cujos elétrons são pares. Nos ferromagnetos ao se aplicar um campo magnético a resposta ao campo é alinhar a magnetização ao campo e mesmo com a retirada do campo a magnetização continua, este é um fenômeno quântico e ocorre em materiais cujos elétrons são ímpares, esses materiais possuem uma curva característica da magnetização versus corrente, chamada de curva de histeresse [11].

Nos sistemas ferromagnéticos os spins vizinhos interagem uns com os outros de ma-neira que estão acoplados uns aos outros por meio de uma interação, chamada de interação de troca, esse acoplamento faz com que o sistema possua modos coletivos, chamados de ondas de spin [10]. A excitação de menos energia é denominada de modo uniforme, onde os spins precessionam com a mesma fase. As ondas de spins são quantizadas e seu quantum é denominado de magnon.

O estudo das ondas de spin em sistemas ferromagnéticos pode ser realizado a partir do modelo de Heisenberg, este modelo foi proposto por Heisenberg em 1926 e simulta-neamente por Dirac, o modelo propoõe que a interação de sistemas ferromagnéticos é proporcional aos spins do sistema. Outros modelos foram propostos com o mesmo in-tuito, como o modelo de Ising, proposto por Wilhelm Lenz, o caso unidimensional foi solucionado por Ernst Ising em sua tese de doutorado em 1924 [14, 15, 16]. No modelo de Ising não ocorre transições de fase e nem magnetização espontânea, necessitando de uma nova teoria para explicar esses fenômenos. Outra teoria proposta foi o modelo XY [6, 17], este modelo considera apenas as componentes X e Y dos spins.

são ondas de spins.

O capítulo 3 aborda materiais ferromagnéticos e uma partícula carregada em um campo magnético. Posteriormente o capítulo aborda uma partícula em um campo mag-nético, calculando o Hamiltoniano do sistema a partir das equações de Maxwell e do formalismo Lagrangeano. Uma partícula imersa em um campo magnético gera uma con-tribuição ao Hamiltoniano do sistema chamada de efeito Zeeman, sendo essa concon-tribuição proporcional ao campo magnético imposto e ao momento magnético. Posteriormente o capítulo 3 trata o modelo de Heisenberg, abordando duas motivações [6, 9] onde o Ha-miltoniano do sistema depende da interação entre os spins das partícula: a primeira é calculada a partir de um modelo onde se considera a interação Coulombiana para um sistema correspondente a dois elétrons e o a segunda para a interação entre dois átomos de hidrogênio. Verifica-se que o Hamiltoniano do sistema depende dos spins do mesmo. O Hamiltoniano descrito pelo modelo de Heisenberg não está naturalmente diagonalizado, surge então a necessidade de diagonalizar tal Hamiltoniano, para se obter assim a energia do sistema. Ainda neste capítulo, o modelo de Heisenberg é aplicado em uma rede qua-drada simples finita na direçãoY, para encontrar a energia do sistema em função do vetor de ondak considerando até segundos vizinhos, e utilizado para um exemplo de redes não simétricas.

2

SPIN

2.1

Spin do elétron

O spin é uma propriedade intrínseca da matéria, sendo um fenômeno quântico que pode ser observado por exemplo no experimento realizado por físicos alemães, Otto Stern e Walter Gerlach [4, 5, 7]. O experimento consiste de um forno que aquece átomos de prata (Ag). No forno existe um orifício, de fomra que alguns dos átomos passam pelo orifício encontrando um colimador. Após a passagem no colimador, os átomos passam por regiões que possuem campos magnéticos inomogêneos. A Fig.1 representa um esboço do experimento.

Figura 1: Esboço do experimento Stern-Gerlach. Figura modificada de [24].

esperado e obtido. O nome do experimento ficou conhecido como experimento de Stern-Gerlach.

Figura 2: a) Resultado experimental que Stern e Gerlach esperavam obter. A predição clássica verificava que o feixe deveria ser espalhado verticalmente, tendo como limetes os valores do momento magnético multiplicado pelo cosseno do ângulo de orientação. b) Resultado obtido, sendo duas orientações do momento magnético. Figura modificada de [7].

Os operadores de spin na mecânica quântica possuem a relação de autovalores

S2_|smsi = s(s+ 1)ℏ|smsi (2.1)

Sz|smsi = msℏ|smsi, (2.2)

onde S representa o momento angular total, _|smsi o estado no qual se encontra, Sz o

momento angular na direção Z, ℏ é a constante de Planck dividida por _2π e _s e _ms

representam os números quânticos. O experimento de Stern-Gerlach mostra que o elétron possui dois valores possíveis para a medida de seu spin, tendo seu número quântico ms

podendo variar entre+1/2e ₋1/2 [6, 8]. Os autoestados são representados por _{| ↑i} para

o estado cujo spin é +1/2, e _{| ↓i} para o estado cuja componente é ₋1/2. A partir dessa

convenção, pode ser escrito para o elétron

Sz| ↑i = +

ℏ

2| ↑i (2.3)

Sz| ↓i = −

ℏ

Os autoestados_{| ↓i}e_{| ↑i}formam uma base, obedecem as condições de ortogonalidade,

h↑ | ↑i = _{h↑ | ↑i}= 1, (2.5)

h↑ | ↓i = 0, (2.6) e um estado qualquer, _|α_i, pode ser escrito como uma combinação linear desses autoes-tados,

|α_i=c1| ↑i+c2| ↓i, (2.7) ondec1 ec2 são constantes que representam a densidade de probabilidade, isto é,|c1|2 é a probabilidade do elétron de se encontrar no estado _{| ↑i}e _|c2|2 representa a probabilidade de encontrar o elétron no estado _{| ↓i}. A soma de todas as probabilidades de um sistema é igual a 1, nesse caso_|c1|2+|c2|2 = 1.

Os autoestados do operador Sz, | ↑ie | ↓i, são escritos na forma matricial, como

| ↑i =

"

1 0

#

(2.8)

| ↓i =

"

0 1

#

. (2.9)

Os operadores Sx, Sy e Sz representam respectivamente a componente X, Y e Z do

spin. Esses operadores podem ser escritos na forma matricial,

Sx =

ℏ 2 " 0 1 1 0 #

, Sy =

ℏ

2

"

0 ₋i i 0

#

e Sz =

ℏ

2

"

1 0 0 ₋1

#

. (2.10)

As matrizes abaixo são chamadas de matrizes de Pauli [6, 7] , definidas como

σx = "

0 1 1 0

#

σy = "

0 ₋i i 0

#

e σz = "

1 0 0 ₋1

#

2.2

Princípio de exclusão de Pauli

O princípio da exclusão de Pauli afirma que duas ou mais partículas que possuem o spin semi-inteiro, chamadas de férmions, não podem ocupar o mesmo estado físico ao mesmo tempo, o que significa que as partículas não podem ter o mesmos números quânticos, como consequência a função de onda do elétron é anti-simétrica.

A função de onda do elétron deve ser composta por duas partes uma espacial e outra relacionada ao spin, sendo a função de onda total o produto das duas, como a função de onda do mesmo é antissimétrica, o elétron possui uma função de onda simétrica e outra antisimétrica, podendo ser a parte espacial simétrica e a parte relacionada ao spin antisimétrica, ou a parte espacial antisimétrica e a parte de spin simétrica.

Funções de onda simétricas são representadas porβS, e funções de onda antissimétricas

são representadas por βA. Para um sistema constituído de um próton e um elétron os

possíveis estados para o sistema são

| ↑↑i | ↑↓i | ↓↑i | ↓↓i , (2.12)

onde a primeira entrada representada está relacionada ao elétron e a segunda ao próton.

Os momentos angulares do elétron e do próton são somados para formar o momento angular do sistema [6, 7], sejaS1 o momento angular do elétron e S2 o momento angular do próton,

~

S =S~1+S~2. (2.13)

O momento angular na direção Z é a adição dos momentos angulares do elétron e do próton, Sz =S1z +S2z. Seja v1 um estado no qual apenas S1z atua e v2 um estado que apenas S2z atua, com a relação de autovalores S1zv1 =ℏm1v1 e S2zv2 =ℏm2v2,

Szv1v2 = (S1z+S2z)v1v2 (2.14) Szv1v2 = ℏ(m1+m2)v1v2, (2.15)

m = (m1 +m2) representa o número quântico do sistema composto. Como m1 e m2 variam de +1/2 à ₋1/2 para o elétron e o próton, o sistema composto tem um número

| ↑↑i onde m = 1 (2.16)

| ↑↓i onde m = 0 (2.17)

| ↓↑i onde m = 0 (2.18)

| ↓↓i onde m = ₋1. (2.19)

As representações acima mostram que existe um estado para esse sistema no qual o número quântico m = 0, onde s = 0. Basta aplicar o operador de abaixamento S− para encontrar esse estado, encontra-se

S−_{| ↑↑i}=ℏ_{(| ↑↓i +| ↓↑i )} (2.20)

Para melhor entendimento, utiliza-se a notação _|sm_i para representar o estado, os três estado no quals = 1 são

|1 1_i = _{| ↑↑i} (2.21)

|1 0_i = _√1

2[| ↑↓i+| ↓↑i] (2.22)

|1₋1_i = _{| ↓↓i}. (2.23)

Os estados onde s = 1 são denominados de tripleto, representam a função de onda

simétrica, βS. Os estados ondes = 0 e m= 0,

|0 0_i = √1

2[| ↑↓i − | ↓↑i], (2.24)

são chamados de singleto e representados por βA. A interação de duas partículas de spin

1/2 pode resultar em um sistema cujo spin é 1ou 0[8].

2.3

Ondas de spin

ao se encontrarem ocorre um espalhamento, devido à diferença nas velocidades. Freeman Dyson foi um físico inglês [12] que calculou o erro obtido por essa abordagem, sendo de

5% para a magnetização [4].

As duas principais interações que as ondas de spin sofrem são devido ao acoplamento magnético dipolo-dipolo e influências de interação de troca [4, 9]. Além desses fatores, a interação em ondas de spin também pode levar em conta a anisotropia do material, que pode ser devido a geometria do sistema, orientações do cristal e do campo magnético [4]. Ao se aplicar um campo magnético em sistemas ferromagnéticos os spins interagem a partir das interações de troca, fazendo com que as excitações do sistema sejam excitações coletivas ao redor de um ponto de equilíbrio [10], chama-se de modo uniforme a excitação que possui a menor energia, os elétrons giram com mesma fase, mantendo-se paralelos uns aos outros e giram em torno do campo magnético. A Fig.3(a) representa o modo uniforme e a Fig.3(b) representa ondas de spin em sistemas ferromagnéticos.

3

MATERIAIS

FERROMAGNÉTICOS E UMA

PARTÍCULA CARREGADA EM

UM CAMPO MAGNÉTICO

3.1

Materiais ferromagnéticos

Ao se aplicar um campo magnético em um material ele sofre induções internamente. Dizemos que o material é paramagnético se ao se aplicar o campo magnético a magne-tização é paralela ao campo. Nos materiais diamagnéticos a magnemagne-tização é oposta ao campo magnético [11, 34]. Materiais ferromagnéticos são materiais onde após a aplicação de um campo magnético a magnetização consegue ser mantida mesmo se o campo for desligado, diferentes de materiais paramagnéticos e diamagnéticos. O ferromagnetismo é um fenômenos quânticos devido aos momentos dipolos magnéticos associados aos spins, nos ferromagnéticos os dipolos são dispostos em apenas uma direção em pequenas regiões, denominadas domínios, como representado na Fig.4. Os efeitos da magnetização devido ao campo aplicado nos ferromagnéticos são maiores do que em materiais diamagnéticos e paramagnéticos, de modo que eles são relevantes para o campo total.

Figura 4: Representação do alinhamento dos dipolos em uma pequena parte do material ferro-magnético após a aplicação do campo ferro-magnético.

anulada devido as várias direções dos domínios que anulam a magnetização total do objeto. Um material feromagnético pode ser transformado em um imã permanente aplicando-se um campo magnético de modo que o torque tende a alinhar os dipolos dos domínios ao campo. Esses materiais tem a característica de em cada domínio tenderem a alinhar aos dipolos de seus vizinhos. No momento em que um campo magnético interage com esse material muitos dos dipolos no interior do objeto não irão se alinhar com o campo, no contorno do objeto ocorrerá o alinhamento de alguns domínios com o campo, o que vai gerar um alinhamento subsequente, de maneira que os domínios paralelos ao campo aumentam, enquanto os demais diminuem. Se ocorrer o alinhamento de todos os domínios, o material é considerado saturado. Após o desligamento do campo, alguns dipolos voltarão para posições aleatórias, mas outros dipolos permanecerão alinhados onde o campo estava, formando um imã permanente. A Fig.5 mostra um gráfico do campo magnético versus a corrente de magnetização, essa curva é comumente chamada de curva de histerese.

Figura 5: Curva de histeresse, onde o campo magnético é representado porB e a corrente de magnetização por H. Figura retirada de [25].

3.2

Uma partícula carregada em um campo magnético

Seja_E~ _{o campo elétrico,B}~ _{o campo magnético e ǫ0 eµ0 duas constantes, as equações} de Maxwell são representadas a por

∇ ·E~ = ρ

ǫ0

(3.1)

∇ ·B~ = 0 (3.2)

∇ ×E~ = ₋∂ ~B

∂t (3.3)

∇ ×B~ = µ0J~+µ0ǫ0 ∂ ~B

∂t. (3.4)

A Eq.3.2 torna possível escrever _B~ _{em função de outra grandeza vetorial, A}~_{, chamada} potencial vetor, onde

~

B =_{∇ ×}A.~ (3.5)

Podemos reescever a Eq.3.3 para que dependa do potencial vetor

∇ ×E~ =₋∂

∂t(∇ ×A) (3.6)

∇ × E~ +∂ ~A

∂t

!

= 0. (3.7)

Definimos uma grandeza escalar,φ, chamada potencial escalar, onde

−∇φ = E~ +∂ ~A

∂t (3.8)

~

E = _−∇φ₋ ∂ ~A

∂t. (3.9)

A força atuando sobre uma partícula de carga q sob a ação de um campo magnético é dada por

~

F = q[E~ +~v_×B~] (3.10)

md~v

dt = q

"

−∇φ₋ ∂ ~A

∂t +~v×(∇ ×A)

#

. (3.11)

Por outro lado, (~v_{× ∇ ×}A~) na direçãox é dado como segue

(~v_{× ∇ ×}A~)x = vy

∂Ay

∂x − ∂Ax

∂y

−vz

∂Ax

∂z − ∂Az

∂x

(~v_{× ∇ ×}A~)x =

∂

∂x(~v·A~)− dAx

dt + ∂Ax

∂t , (3.13)

e para as outras componentes as equações têm um formato parecido,

(~v_{× ∇ ×}A~) =_∇(~c_·A~)₋ d ~A

dt + ∂ ~A

∂t. (3.14)

A Eq.3.13 pode ser reescrita como segue

d

dt[m~v+q ~A] =∇[−qφ+q(~v·A~)]. (3.15) A equação de Euler-Lagrange é dada por

d dt

∂L ∂q˙

− ∂L_∂q = 0, (3.16)

onde a Lagrangeana é escrita, para esse caso [9], com o auxílio da Eq.3.15,

L= 1

2m~v·~v+q ~A·~v. (3.17)

O momento conjugado a coordenada x é definido

px =

∂L

∂x˙ (3.18)

px = mvx+qAx. (3.19)

Repetindo para as outras coordenadas encontra-se um momento ~p,

~p=m~v+q ~A (3.20)

~v = 1

m(~p−q ~A). (3.21)

O Hamiltoniano para o sistema pode ser escrito como

H =~v_·~p₋L (3.22)

H = 1

2m(~p−q ~A)

2_{+qφ. (3.23)}

e que a função de onda, ψ, obedece a relação Hψ=i∂ψ_∂t, onde

H = 1

2m(−iℏ∇ −q ~A)

2_{+qφ. (3.24)}

3.3

Efeito Zeeman

Ao aplicar um campo magnético em um material, observa-se uma contribuição no Hamiltoniano do sistema dado por

H =₋~µ_·B,~ (3.25)

onde~µrepresenta o momento magnético eB~ representa o campo magnético imposto. Essa contribuição foi descoberta por um físico holandês chamado Peter Zeeman em 1896 [4]. Na presença de campos magnéticos os níveis de energia atômicos são divididos em vários níveis, as linhas do espectro também são divididas [30, 32] , esse fenômeno é chamado de efeito Zeeman. A função de onda pode ser reescrita separando a variável temporal e a da posição,

ψ(~r, t) =ψ(~r)e−iǫt/ℏ

, (3.26)

a equação de autovalorHψ =ǫψ, é reescrita para o Hamiltoniano dado na Eq.3.24,

1 2m

_ℏ

i∇ −q ~A

2

ψ+qφψ = ǫψ (3.27)

−ℏ

2

2m∇ 2_ψ

−_2miℏ q[_{∇ ·}(Aψ~ ) +A~_·(_∇ψ)] +

"

q2_A~2

2m +qφ

#

ψ = ǫψ. (3.28)

A identidade vetorial a seguir é verdadeira

∇ ·(Aψ~ ) = (_{∇ ·}A~)ψ+A~_·(_∇ψ) =A~_{· ∇}ψ, (3.29) uma vez que_{∇ ·A}~ _{= 0. Temos para um campo magnético uniforme}

∇ ×(B~ _×~r) = B~_{∇ ·}~r₋~r_{∇ ·}B~ + (~r_{· ∇})B~ ₋(B~ _{· ∇})~r (3.30)

∇ ×(B~ _×~r) = (_{∇ ·}~r)B~ ₋(B~ _{· ∇})~r (3.31)

∇ ×(B~ _×~r) = 3B~ ₋B~ (3.32)

A equação

∇ ×A~ = 1

2∇ ×(B~ ×~r), (3.34)

se torna verdade e pode ser escrito para_A~_,

~ A= 1

2(B~ ×~r). (3.35)

O terceiro termo da Eq.3.28 pode ser reescrito com auxílio da Eq.3.35,

−qℏ

imA~· ∇ψ = − qℏ

2im(B~ ×~r)· ∇ψ (3.36)

= ₋ q 2mB~ ·

~r_×

_ℏ

i∇

ψ, (3.37)

uma vez que o momento linear,~p, é dado por ~p= ℏ

i∇ e o momento angular,L~, é escrito

como~r_×~p, segue

−_imqℏA~_{· ∇}ψ =₋~µ_·Bψ,~ (3.38)

onde µ= ₂q~_mL. A energia ǫz =−~µ·B~ é definida como a energia de Zeeman. O fator q2A~2

no Hamiltoniano (3.28) é constantemente ignorado, fazendo com que o Hamiltoniano do sistema seja

H = ₋ ℏ

2

2m∇ 2

− ₂q_m(~L_·B~) (3.39)

H = ₋ ℏ

2

2m∇

2_{−~µ·B.~ (3.40)}

3.4

O modelo de Heisenberg

O modelo de Heisenberg foi proposto por Werner Heisenberg e quase simultaneamente por Paul Dirac em 1926 para descrever o ordenamento ferromagnético. O modelo consiste em considerar o seguinte Hamiltoniano

H = 1 2

X

i,j

Ji,jS~i·S~j, (3.41)

comiej representando o sítio onde as partículas se encontram e Jij o termo de interação

entre os mesmos, a interação Coulombiana é dada para esse caso como segue

U(~r) = e

2

4πǫ0r12

. (3.42)

A função de onda para o sistema depende dos dois elétrons, escrevemos então uma função de onda para o sistema que tenha a combinação entre as duas soluções das duas partículas sozinhas

Ψ±=

1

√

2[ϕa(r1)ϕb(r2)±ϕa(r2)ϕb(r1)]. (3.43)

A média da energia, ǫ, é dada por R Ψ∗

±UΨ±d3r1d3r2, utilizando a função de onda acima, temos

ǫ = e

2

8πǫ0

Z

ϕ∗

a(r1)ϕ∗b(r2)

1

r12

ϕa(r1)ϕb(r2)d3r1d3r2

±

Z

ϕ∗_a(r1)ϕ∗b(r2)

1

r12

ϕa(r2)ϕb(r1)d3r1d3r2

±

Z

ϕ∗_a(r2)ϕ∗b(r1)

1

r12

ϕa(r1)ϕb(r2)d3r1d3r2

+

Z

ϕ∗

a(r2)ϕ∗b(r1)

1

r12

ϕa(r2)ϕb(r1)d3r1d3r2

. (3.44)

As partículas tratadas são partículas idênticas, podemos então permutar r1 e r2 na terceira e quarta parte da equação acima, que nos fornece

ǫ= e

2

4πǫ0

Z

ϕ∗_a(r1)ϕ∗b(r2)

1

r12

ϕa(r1)ϕb(r2)d3r1d3r2±

Z

ϕ∗_a(r1)ϕ∗b(r2)

1

r12

ϕa(r2)ϕb(r1)d3r1d3r2

. (3.45)

Seja Jtroca o termo da equação acima que representa a interação de troca e E uma

média de energia, dadas como segue

E = e

2

4πǫ0

Z

ϕ∗a(r1)ϕ∗b(r2)

1

r12

ϕa(r1)ϕb(r2)d3r1d3r2

, (3.46)

Jtroca =

e2

4πǫ0

Z

ϕ∗_a(r1)ϕ∗b(r2)

1

r12

ϕa(r2)ϕb(r1)d3r1d3r2

. (3.47)

A média da energia é então escrita como ǫ = E _±Jtroca. A média da energia depende

~

s2, então o Hamiltoniano é escrito na seguinte forma

H =₋2Jtrocas~1·s~2, (3.48)

que está no mesmo formato da Eq.3.41, representando o modelo de Heisenberg. Outra motivação para esse modelo é vista se considerarmos dois átomos de hidrogênio interagindo entre si, seja o índice 1 referente ao elétron do primeiro átomo, a referente a seu próton e 2 referente ao elétron do segundo átomo e b referente ao seu próton, para esse caso o Hamiltoniano do sistema é dado

H = p

2 1

2m + p2

2

2m − q2 cr1a −

q2 cr2b −

q2 cr1b −

q2 cr2a

+ q 2 cr12 + q 2 cRab , (3.49)

ondec= 4πǫ0,p1 ep2 o momento linear dos elétrons, m massa dos elétrons,rij a distância

entre i e j e Rab a distância entre os prótons. A distância Rab será considerada fixa

devido a massa do próton ser muito maior do que a massa do elétron. Por esse motivo também a parte cinética do próton no Hamiltoniano é desconsiderada. Devido a interação Coulombiana ser maior do que a interação magnética entre os elétrons, essa interação magnética será desconsiderada. A média da energia,ǫ, para esse caso é dada por

ǫ=

R

Ψ∗_HΨd3_r 1d3r2

R

Ψ∗_Ψd3_r 1d3r2

. (3.50)

As equações para o caso não perturbado, isto é, onde os átomos estão isolados um do outro, são dadas por

p2 1

2m − q2 ce1a

ϕa(r1) =ǫ0ϕa(r1) (3.51)

p2 2

2m − q2 ce2b

ϕb(r2) =ǫ0ϕb(r2), (3.52)

ondeǫ0representa a energia. Escrevemos funções de ondasΨ±tais que sejam combinações das soluções não perturbadas,

Ψ±(r1, r2) =

1

√

2[ϕa(r1)ϕb(r2)±ϕa(r2)ϕb(r1)]. (3.53)

Segue

Z

Ψ∗

±(r1, r2)Ψ±(r1, r2)d3r1d3r2 =

1 2

Z Z

[ϕ∗

a(r1)ϕ∗b(r2)ϕa(r1)ϕb(r2)

± ϕ∗_a(r1)ϕ∗b(r2)ϕa(r2)ϕb(r1)±ϕ∗a(r2)ϕ∗b(r1)ϕa(r1)ϕb(r2)

Fazendo

α=

Z

ϕ∗_a(r1)ϕb(r1)d3r1 =

Z

ϕ∗_a(r2)ϕb(r2)d3r2, (3.55) para simplificar a expressão acima, temos utilizando o fato de serem partículas idênticas,

Z

Ψ∗

±(r1, r2)Ψ±(r1, r2)d3r1d3r2 = 1±α2. (3.56) A segunda parte do numerador da equação da energia, ǫ, é calculada de forma análoga. SejaHi o Hamiltoniano de interação entre os dois átomos, dado por

Hi =

q2 cr12

+ q

2 cRab −

q2 cr1b −

q2 cr2a

, (3.57)

definimos V eU como segue

V =

Z

ϕ∗

a(r1)ϕ∗b(r2)Hiϕa(r1)ϕb(r2)d3r1d3r2 (3.58) e

U =

Z

ϕ∗a(r1)ϕb∗(r2)Hiϕa(r2)ϕb(r1)d3r1d3r2. (3.59)

U é denominado integral de troca porque representa a probabilidade do sistema de fazer a transição do estado ϕa(r1)ϕb(r2) para o estado ϕa(r2)ϕb(r1). Pode-se escrever

Z

Ψ∗HΨd3r1d3r2 =V ±U + 2ǫ0(1±α), (3.60) segue para a energia do estado simétrico e antissimétrico

ǫ±= 2ǫ0+

V _±U

1_±α2, (3.61)

a diferença entre as energias é então

ǫS−ǫT =−2

V α2_−U

1₋α4 . (3.62)

A função de onda das duas partículas é antissimétrica devido ao princípio de exclusão de Pauli. O objetivo agora é encontrar um operador que mostra a energia a partir das orientações dos spins, um operador que pode ser usado é S2_{. Seja ǫ}

(antissimétrico) as energias dos estados singleto e tripleto, respectivamente [9],

Hspin = ǫS+

1

2~2 [ǫT −ǫS]S

2 _(3.63)

Hspin = ǫS+

1

2~2 [ǫT −ǫS] [S 2

1 +S22+ 2S~1·S~2] (3.64) Hspin = 1

4[ǫS+ 3ǫT] + 1

~[ǫT −ǫS]S~1·S~2. (3.65)

O Hamiltoniano pode ser descrito como

H =₋2J

~2S~1·S~2, (3.66) comJ = 1₂(ǫS−ǫT) = U−V α

4

1−α4 . O Hamiltoniano descrito acima é o Hamiltoniano proposto

no modelo de Heisenberg dado pela equção (3.41).

3.4.1

Diagonalizando o Hamiltoniano de Heisenberg

O Hamiltoniano do modelo de Heisenberg é dado para um sistema com um campo magnético,H0, aplicado na direção Z como

H=₋2µBH0

X

i

S_iz₋JX

i6=j

~

Si·S~j, (3.67)

o termo ₋2µBH0PiSiz da Eq.3.67 representa o efeito Zeeman. O operador S~i depende

dos operadores Sx i, S

y

i e Siz. Por sua vez, os operadores Six e S y

i podem ser escritos em

termos dos operadores S_i+ e S−

i ,

S_ix = 1 2(S

+

i +Si−) (3.68)

S_iy = 1 2i(S

+

i −Si−). (3.69)

O produto _S~_i·S~_{j é reescrito como}

~

Si·S~j =

1 2(S

+

i Sj−+Si−Sj++ 2SizSjz). (3.70)

O comutador dos operadores S_i+ e S−

j é dado como

[S_i+, S−

j ] = 2Sizδij. (3.71)

escrito como

H =₋2µBH0

X

i

S_iz₋JX

i,j

(S_i−S_j++S_izS_jz). (3.72)

O Hamiltoniano do sistema, H, precisa ser diagonalizado para que a energia do sis-tema pode ser facilmente encontrada. Para isso utiliza-se as transformações de Holstein-Primakoff [6],

S+

i = (2S)1/2 1−

a†_iai

2S

!1/2

ai (3.73)

S−

i = (2S)1/2a

†

i 1−

a†_iai

2S

!1/2

(3.74)

S_iz = S₋a†_iai =S−ni. (3.75)

Expandindo as duas primeiras transformadas de Holstein-Primakoff, encontra-se

S_i+ = (2S)1/2

ai−

1 4Sa

†

iaiai+...

(3.76)

S_i− = (2S)1/2

a†_{i −} 1

4Sa +

i a

†

iai+...

. (3.77)

Estamos interessados no Hamiltoniano de segunda ordem, para encontrar tal Ha-miltoniano as aproximações de segunda ordem para os produtos S−

i Sj+, SizSjz e Siz são

realizadas, onde não é considerado termos de zero e primeira ordem,

S_i−S_j+ = (2S)1/2a†_i(2S)1/2aj (3.78)

S_i−S_j+ = 2Sa†_iaj. (3.79)

S_izS_jz = (S₋a†_iai)(S−a†jaj) (3.80)

O Hamiltoniano descrito em (3.72) é reescrito para termos de segunda ordem como

H(2) = 2µBH0

X

i

(a†_iai)−J X

i,j h

2Sa†_iaj+S(a†iai+a†jaj) i

(3.82)

H(2) = X

i,j h

2µBH0a†iajδij−2SJa†iaj + 2SJa†iajδij i

(3.83)

H(2) = X

i,j

[(2µBH0 + 2SJ)δij −2SJ]a†iaj, (3.84)

ondeAij = [(2µBH0+ 2SJ)δij −2SJ], segue

H(2) =X

i,j

Aija†iaj. (3.85)

O Hamiltoniano descrito na Eq.3.85 não está na forma diagonal, queremos encontrar um Hamiltoniano na forma

H(2) ₌X

k

Eka†kak, (3.86)

para isso utiliza-se as transformações de operadores de campo, ai ea†i, em operadores de

modo coletivos normais,ak e a†k, como segue

ai = X

k

ϕi_kak (3.87)

a†_i = X

k

ϕi_k∗a†_k. (3.88)

O Hamiltoniano se torna

H(2) =X

i,j X

k,k′

Aijϕik∗ϕ j k′a

†

kak′, (3.89)

para encontrarmos um Hamiltoniano na forma diagonal, utiliza-se o fato de que as auto-funções satisfazem a equação de autovalores

X

j

Aijϕjk′ =Ek′ϕ

i

segue

H(2) = X

i,k,k′

X

j

Aijϕjk′

!

ϕi_k∗a†_kak′ (3.91)

H(2) = X

i,k,k′

Ek′ϕi_k′, ϕi_k∗a †

kak′, (3.92)

utilizando as seguintes condições de ortonormalidade para as autofunções

X

i

ϕi_kϕi∗

k′ = δkk′ (3.93)

X

k

ϕi_kϕj_k∗ = δij, (3.94)

o Hamiltoniano é então descrito como

H(2) = X

k,k′ Ek′

X

i

ϕi_k′, ϕ

i∗

k !

a†_kak′, (3.95)

H(2) = X

k,k′

Ek′δ_kk′a†_ka_k′, (3.96)

H(2) = X

k

Eka†kak. (3.97)

A Eq.3.97 representa um Hamiltoniano diagonalizado, porém não se sabe o valor de Ek,

para isso utiliza-se o caso da simetria translacional, onde ϕi_k = e(i~k·r~i). Nesse caso, os operadores ai e a†i são

ai =

1

N1/2

X

k

e(i~k·r~i)_a

k, (3.98)

a†_i = 1

N1/2

X

k

e(−i~k·r~i)_a†

k, (3.99)

ondeN representa o número de partículas da rede, as Eq. (3.98) e (3.99) são as transfor-madas de Fourier de ai e a†i, as transformadas inversas são dadas como

ak = N1/2 X

k

e(−i~k·r~i)_a

i, (3.100)

a†_k = N1/2X

k

e(i~k·r~i)_a†

i, (3.101)

Fazendoϕi

respectiva-mente,

X

i

ei(~k−k~′)·r~i _{= N δ}

kk′ (3.102)

X

k

ei~k·(r~i−r~j) _{= N δ}

ij, (3.103)

onde o fator N aparece devido a normalização. O Hamiltoniano descrito na Eq.3.85 pode ser reescrito com o auxilio das Eq.3.98 e Eq.3.99,

H(2) =X

j

Aij

1

N

X

k

e(−i~k·r~i)_a†

k X

k′

e(i ~k′·r~j)_a

k′, (3.104)

com o auxílio das Eq.3.102 e Eq.3.103,

H(2) =X

j,k

Aijei~k·(r~j−r~i)a†kak, (3.105)

uma substituição do índicej porj =i+δ pode ser realizada, onde agoraδ varia, e faz-se ~

rj −r~i =~δ, onde~δ é a distância entre os pontos da rede. Temos então

H(2) =X

k

X

δ

Ai,i+δei~k· ~ δ

!

a†_kak. (3.106)

O fator em parênteses na Eq.3.106 é a transformada de Fourier de Ai,i+δ, que será

repre-sentada porAk,

H(2) =X

k

Aka†kak. (3.107)

Ao comparar esta expressão com a equação do Hamiltoniano na forma diagonalizada, Eq.3.86, identifica-se queEk =Ak, sendo a transformada de Fourier deAi,i+δ, segue

Ek = X

δ

Ai,i+δei~k·δ. (3.108)

ComoAi,i+δ = (2µBH0+ 2SJ)δi,i+δ−2SJ, a transformada de Fourier pode ser calculada

para Ek

Ek = 2µBH0+ 2S(J0−Jk), (3.109)

ondeJk =PδJei~k·

~_{δ, onde}

3.5

Rede Quadrada Simples Finita

O modelo de Heisenberg pode ser utilizado em uma rede quadrada simples finita para melhor entendimento do mesmo. Essa rede corresponde a uma rede quadrada onde em uma das direções é finita. A Fig.6 mostra um exemplo dessa rede, onde ela é limitada em uma das direções (nesse caso na direção Y), tendo n′ _camadas.

Figura 6: Exemplo de uma rede quadrada simples finita na direção Y,n′ _{representa o número} de camadas e a o parâmetro da rede.

Seja n uma quantidade que representa a camada do sítio, os operadores utilizados anteriormente a†_i e ai são modificados para essa situação da seguinte maneira,

a†_i = _√1

N

X

k,n

a†_knei~k·r~i (3.110)

ai =

1

√

N

X

k,n

akne−i~k·r~i, (3.111)

H(2) = X

i,j

Aij

1

N

X

kn

a†_knei~k·r~iX

k′_,n′

ak′_n′e−i ~k ′_·r~

j (3.112)

H(2) = X

i,j,k,n,k′_,n′ Ai,j

1

Na †

knak′_n′ei(~k−

~ k′_)·r~

i_e−i ~k′·(r~j−r~i) (3.113)

H(2) = X

j,k,n,k′_,n′ Aijei ~k

′_{·(r~j−r~i)}

a†_knak′_n′δ_kk′ (3.114)

H(2) = X

δ,k,n,n′

Ai,δ+iei~k· ~ δnn′_a†

knakn′, (3.115)

fazendoAnn′(k) =

P

δAi,i+δei~k·δnn~ ′ o Hamiltoniano se torna

H(2) = X

k,n,n′

Ann′(k)a †

knakn′. (3.116)

Foi visto anteriormente que Ai,i+δ = (2µH0+ 2SJ)δi,i+δ−2SJ, segue

Ann′(k) =

X

δ

[(2µBH0+ 2SJ)δi,i+δ−2SJ]ei~k· ~

δnn′_. (3.117)

Por outro lado Jk = P_δJei~k·a~δ e considerando apenas os primeiros e os segundos

vizinhos da rede, pode-se encontrar

Jk = J1ei~k·abi+J1e−i~k·abi+J1ei~k·abj +J1e−i~k·abj+J2ei~k·(abi+abj)

+J2ei~k·(abi−abj)+J2ei~k·(−abi+abj)+J2e−i~k·(abi+abj), (3.118) ondeJ1 representa a interação de troca dos primeiros vizinhos eJ2 representa a interação de troca dos segundos vizinhos após algumas manipulações, resulta na seguinte equação, uma vez que~k=kxbi,

Jk = 2J1cos(kxa) + 4J2cos(kxa). (3.119)

Ann′(k) = (2µ_BH₀+ 2SJ₀)δ_nn′ −4SJ₁cos(k_xa)δ_nn′

− 8SJ2cos(kxa)[δn′_,n−′ +δ_n′_,n+1] (3.120) Ann′(k) = 2 [µ_oH₀+ 4SJ₁+ 4SJ₂−2SJ₁(cosk_xa))]δ_nn′

− 8SJ2cos(kxa)(δn′_,n−1+δ_n′_,n+1). (3.121) Devido a fins práticos, fazemos as seguintes substituições

u = 2 [µoH0+ 4SJ1+ 4SJ2−2SJ1(cos(kxa))] (3.122)

v = 8SJ2cos(kxa), (3.123)

segue paraAnn′(k)

Ann′(k) = uδ_nn′ +v(δ_n′_,n−1+δ_n′_,n+1). (3.124)

O Hamiltomiano descrito na Eq.3.116 não está diagonalizado, a equação de Heisenberg é utilizada para linearizar o sistema, segue

i~dO

dt = [O, H] (3.125)

i~dakn

dt =

X

n′_,n′′_,k

An′_n′′(k′)[a_kn, a†_k′n′a_kn′′] (3.126)

i~dakn

dt =

X

n′_,n′′_,k

An′_n′′(k′)[a_k′_n′, a†_k′_n′′] +

X

n′_,n′′_,k

An′_n′′(k′)a†_k′_,n′′[akn, ak′_n′], (3.127)

uma vez que foi utilizado o operador O = aqn e a seguinte relação entre comutadores

[A, BC] = [A, B]C+B[A, C], segue

dakn

dt =− i

~

X

n′

Ann′(k)a_kn′. (3.128)

Faremos para encontrar a solução akn=akne−iE(t)/ ~

, segue

E(k)akn= X

n′

Ann′a_kn′, (3.129)

      

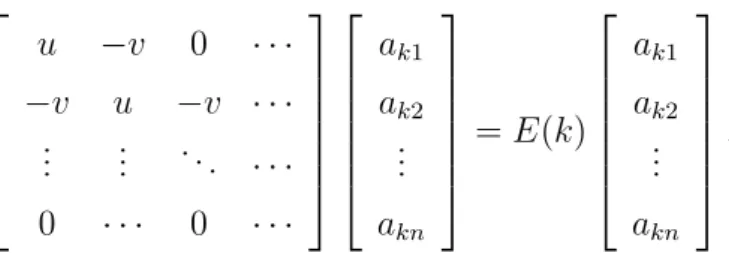
u ₋v 0 _{· · ·}

−v u ₋v _{· · ·} ... ... ... _{· · ·}

0 _{· · ·} 0 _{· · ·}

             

ak1 ak2 ... akn       

=E(k)

      

ak1 ak2 ... akn        . (3.130)

3.6

Interação entre redes não simétricas

Algumas redes não simétricas (no sentido que todos os elementos da rede não são iguais) podem ser interpretadas como a junção de duas redes simétricas. A Fig.7 repre-senta uma pequena parte de uma rede não simétrica. Existem duas redes que se juntam para formar a rede maior, essas duas redes são simétricas, os elementos da primeira rede são representados pelos elementos preenchidos (vermelho) e as da segunda rede são repre-sentadas pelos elementos hachurados (preto).

Figura 7: Exemplo de uma rede não simétrica.

O Hamiltoniano de redes como essas pode ser visto como a soma dos Hamiltonianos que representam a interação que elementos da primeira rede realizam com elementos da primeira rede, representada pora, a interação entre elementos da segunda rede, represen-tados porb, realizam com elementos da mesma rede e a interação entre elementos da rede a e da rede b.

a eH(b) _{representa o Hamiltoniano da rede b. Cada parte pode ser escrita como segue}

Ha = ₋µoH0

X

i

SZa₋ 1

2

X

i,j

J_i,jaaS~a

i ·S~ja (3.132)

Hb = ₋µoH0

X

i

SZb₋ 1

2

X

i,j

J_i,jbbS~b

i ·S~jb (3.133)

H1 = −

1 2

X

i,j

(J_i,jabS~a

i ·S~jb+Ji,jbaS~ja·S~ib). (3.134)

As aproximações de Holstein-Primakoff podem ser utilizadas para os operadores Slm i ,

ondel pode ser x, y ouz e m pode ser a ou b,

Sixa = r

S

2(a

†

i +ai) (3.135)

S_ixb =

r

S

2(b

†

i +bi) (3.136)

S_iya =

r

S

2(a

†

i −ai) (3.137)

S_iyb =

r

S

2(b

†

i −bi) (3.138)

S_iza = S₋a†_iai (3.139)

S_izb = S₋b†_ibi. (3.140)

Os produtos _S~a

i ·S~jb, S~ia·S~ja e S~ib ·S~jb podem ser reescrito em função dos operadores

a†_{, a, b}† _eb,

~ Sa

i ·S~jb = S(aib†j +a

†

ibj−a†iai−b†jbj) (3.141)

~ Sa

i ·S~ja = 2S(aia†j−a

†

iai) (3.142)

~ Sb

i ·S~jb = 2S(bib†j −b

†

ibi). (3.143)

H = X

i,j

S

1 2(J

ab

ij +Jijba+

2

SµBH0+J

aa

δij −Jaa

a†_iaj

+ X

i,j

S

1 2(J

ab

ij +Jijba+

2

SµBH0+J

bb

δij −Jbb

b†_ibj

− X

i,j

S

2 J

ab

ij +Jijba aib†j+a

†

ibj

4

APLICAÇÃO DO MODELO DE

HEISENBERG PARA DUAS

REDES NÃO SIMÉTRICAS

4.1

Rede com duas camadas deslocadas

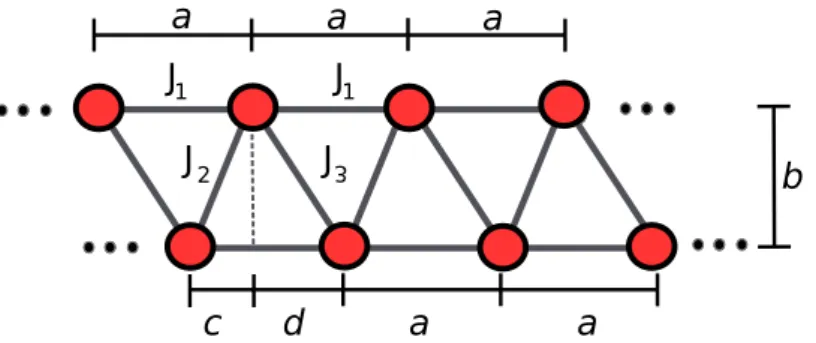
Um exemplo de uma rede que possui duas camadas na direçãoY é mostrado na Fig.8, a rede é formada como se fossem duas redes de uma camada onde uma foi transladada em relação a outra, a corresponde a distância entre um elemento e outro da rede na direção X e b a distância na direção Y das duas redes.

a a a

a a

d c

J J

J J

1 1

3

2 b

Figura 8: Uma rede com duas camadas e deslocada na direção X.

Seja J1 a interação de troca entre elementos da mesma linha, J2 a interação de troca entre um dos elementos de uma linha com outro de outra linha eJ3 a interação de troca de um elemento da linha com um de outra linha que não é representado por J2. Os Ji

correspondentes estão representados na Fig. 8. As interações Ji vão nos mostrar quem

são os, segundos vizinhos e até terceiros vizinhos, uma vez que a interação é maior para quem é primeiro vizinho. Definimos dois parâmetros reaisλ1 e λ2 tais que

J1 = λ1J2 (4.1)

J2 = λ2J3, (4.2)

representa a interação entre primeiros vizinhos, entãoJ1 > J2 eJ1 > J3, segue queλ1 >1 eλ1λ2 >1. Os parâmetros λ1 e λ2 dependem das distâncias entre os elementos,

λ1 =

√

c2_+b2

a (4.3)

λ2 =

√

d2_+b2

√

c2_+b2. (4.4)

O Hamiltoniano desse sistema é escrito como segue

H = X

k h

A(k)a†_kak+B(k)a†kbk+C(k)akb†k+D(k)b

†

kbk i

, (4.5)

com

A(k) = S

J2+J3+

2

SµBH0+J1−2J1cos(ka)

(4.6)

B(k) = ₋S[J2cos(kc) +J3cos(kd)] (4.7) C(k) = ₋S[J2cos(kc) +J3cos(kd)] (4.8) D(k) = S

J2+J3+

2

SµBH0+J1−2J1cos(ka)

. (4.9)

Devido a fins práticos, fazemos

u(k) = S

J2+J3+

2

SµBH0+J1−2J1cos(ka)

(4.10)

v(k) = ₋S[J2cos(kc) +J3cos(kd)]. (4.11) O Hamiltoniano pode ser escrito na forma matricial,

H = X

k h

a† _b† i

"

u(k) v(k)

v(k) u(k)

# "

a b

#

(4.12)

H = X

k

M†N M, (4.13)

onde

N =

"

u(k) v(k)

v(k) u(k)

#

e M =

"

a b

#

. (4.14)

A energia do sistema é encontrada calculando autovalores de N, para isso basta que a equaçãodet[N ₋E(k)I] = 0 seja resolvida, fazendo isso encontramos

ondeEλ é a energia do sistema. A solução é dada por

E(k) = S(J1+J2+J3) + 2µBH0−2SJ1cos(ka)±S(J2cos(kc) +J3cos(kd))(4.16) E(k) = 2µBH0+SJ1

1 + 1

λ1

+ 1

λ1λ2

−2SJ1cos(ka)

± SJ1

1

λ1

cos(kc) + 1

λ1λ2

cos(kd)

. (4.17)

Os gráficos da energia, E(k), contra k estão representados nas Fig. 9 à 14, onde E1 representa o sinal positivo para E(k) e E2 o sinal negativo. O resultado para J1 como primeiro vizinho é mostrado nos gráficos 9 e 10. Os gráficos 11 e 12 representamJ2 como primeiro vizinho. Os gráficos 13 e 14 representamJ3 como primeiro vizinho. O compor-tamento da rede deslocada em relação à outra para esquerda e para uma rede deslocada a mesma quantidade para a direita é igual, como pode ser notado comparando os gráficos das Fig.9 e Fig.10, Fig.11 e Fig.13 e Fig.12 e Fig.14. Esse efeito ocorre devido aos siste-mas físicos serem semelhantes. Todas as distâncias a seguir são dadas em angstrom e as energias a seguir são dadas em função deJ0.

0 0.9 1.8 2.7 3.6 4.5 5.4 6.3

k/2 0

1 2 3 4 5 6 7

Energia /J

E E

1 2

π (1/Α)

0

(a)

J

J

J

J

c d

a

b

(b)

(a)

J2 J3

c d

a

b

J1 J1

(b)

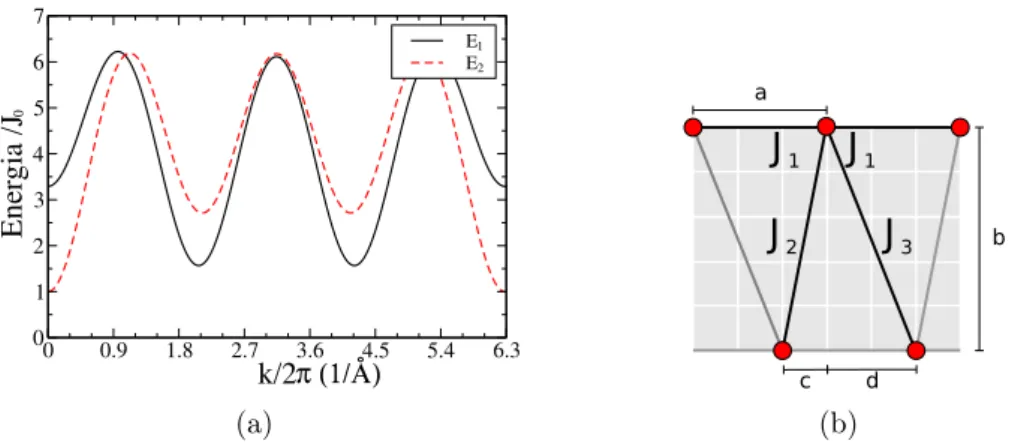
Figura 10: (a) Gráfico da energia em função de k para a rede com duas camadas deslocadas na direçãoX, onde J1 representa o primeiro vizinho, J3 o segundo e J2 o terceiro. Foi utilizado J1= 1,µBH0 = 1,a= 3,b= 5 e c= 2. (b) Configuração da rede.

0 0.9 1.8 2.7 3.6 4.5 5.4 6.3

k/2 0

2 4 6 8

Energia /J

E E

1 2

π (1/Α)

0

(a)

J1

c d

a

b

J1

J2 J3

(b)

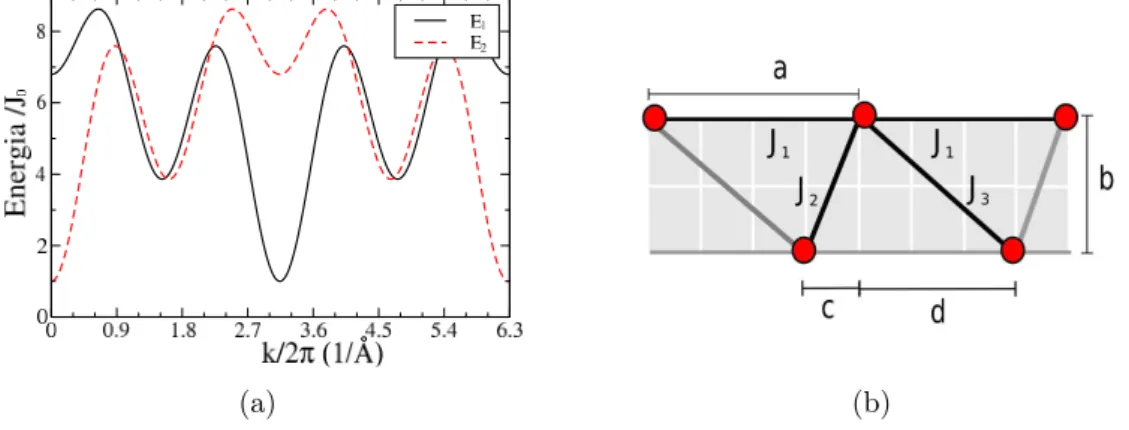
Figura 11: (a) Gráfico da energia em função de k para a rede com duas camadas deslocadas na direçãoX, onde J2 representa o primeiro vizinho, J1 o segundo e J3 o terceiro. Foi utilizado J1= 1,µBH0 = 1,a= 4,b= 3 e c= 1. (b) Configuração da rede.

(a)

c d

a

b

J1 J1

J

(b)

(a)

J1

c d

a

b J1

J2 J3

(b)

Figura 13: (a)Gráfico da energia em função de kpara a rede com duas camadas deslocadas na direção X, onde J3 representa o primeiro vizinho, J1 o segundo e J2 o terceiro. Foi utilizado J1= 1,µBH0 = 1,a= 4,b= 3 e c= 3. (b) Configuração da rede.

(a)

c _d

a

b

J1 J1

J2 J3

(b)

Figura 14: (a)Gráfico da energia em função de kpara a rede com duas camadas deslocadas na direção X, onde J3 representa o primeiro vizinho, J2 o segundo e J1 o terceiro. Foi utilizado J1= 1,µBH0 = 1,a= 4,b= 2 e c= 3. (b) Configuração da rede.

4.2

Rede ao redor de um cilindro

Motivados pela estrutura helicoidal de uma molécula de RNA, uma rede disposta em volta de um cilindro se torna interessante. Dispomos a rede de forma que no quarto elemento, o primeiro elemento volte a se repetir. A Fig.15 mostra uma parte dessa rede e a Fig.16 mostra a rede vista de cima. Pode-se dividir o problema em três redes diferentes, representadas por A, B e C na Fig.16, os elementos da rede A são representados pela cor vermelha, os da rede B pela cor azul e os da rede C pela cor preta. Seja J1 a interação entre elementos da mesma rede,J2 a interação entre elementos cuja distância é

√

l2 _+c2 eJ3 interações entre elementos cuja distância é

√

Figura 15: Rede disposta ao longo de um cilindro.

Figura 16: Rede disposta ao longo de um cilindro vista de cima.

O Hamiltoniano do sistema é a soma das interações dos elementos da rede A com elementos da rede A,Ha_{, das interações entre os elementos da rede B com elementos da}

rede B,Hb_{, das interações entre elementos da rede C com elementos da rede C,H}c_{, e das}

interações entre elementos de redes distintas (interações entre a rede A com a rede B, a interação entre elementos da rede A com a rede C e a interação entre elementos da rede B com elementos da rede C),H1,

H =Ha+Hb+Hc+H1. (4.18) O Hamiltoniano pode ser escrito em termos dos operadoresa, a†_{, b, b}† _ec,c† _{a partir das} aproximações de Holstein-Primakoff,

H = X

i,j

S

1 2(J

ab

ij +Jijba+Jijac+Jijca) +

2

SµBH0+J

aa

δij −Jaa

a†_iaj

+ X

i,j

S

1 2(J

ab

ij +Jijba+Jijbc+Jijcb) +

2

SµBH0+J

bb

δij −Jbb

b†_ibj

+ X

i,j

S

1 2(J

ac

ij +Jijca+Jijbc+Jijcb) +

2

SµBH0+J

cc

δij −Jcc

c†_icj

− X

i,j

S

2

h

J_ijab+J_ijba aib†j +a

†

ibj

+ J_ijac+J_ijca aic†j+a

†

icj

+ J_ijbc+J_ijcb bic†j +b

†

icj i

. (4.19)

H = X

k

[A(k)a†_kak+B(k)a†kbk+C(k)akb†k+F(k)b

†

kbk

+ D(k)a†_kck+G(k)a†kck+H(k)bkc†k+I(k)b

†

kck+L(k)c†kck]. (4.20)

Pode ser escrito na forma matricial,

H =X

k h

a†_k b†_k c†_k i

   

u(k) v(k) v(k)

v(k) u(k) v(k)

v(k) v(k) u(k)

        ak bk ck   

, (4.21)

onde

u(k) = 2S(J2+J3) + 2µBH0+SJ1−2SJ1cos(3kc) (4.22) v(k) = ₋S[J2cos(kc) +J3cos(2kc)]. (4.23) As energias do sistema são calculadas encontrando os autovalores da seguinte matriz,

N =

   

u(k) v(k) v(k)

v(k) u(k) v(k)

v(k) v(k) u(k)

  

. (4.24)

Para isso, basta calculardet(N ₋EλI) = 0, onde I é a matriz identidade eEλ a energia.

Fazendo isso encontramos

(u₋Eλ)3−3v2(u−Eλ) + 2v3 = 0. (4.25)

As energias para o sistema são descritas nas Eq.4.26 e 4.27,

E1(k) = u(k) + 2v(k) (4.26) E2(k) = E3(k) =u(k)−v(k). (4.27)

0 0.4 0.8 1.2 1.6 k/2 0 5 10 15 20 25 30 Energia /J E E 1 2 π (1/Α) 0 (a) (b)

Figura 17: (a) Gráfico da energia contrakpara a rede em volta do cilindro de maneira simétrica, onde J1 representa o primeiro vizinho, J2 o segundo e J3 representa o terceiro vizinho. Foi utilizadoJ1= 5_J0,J2 = 2_J0,J3= 1_J0,µBH0 =_J0,c= 4_{. (b) Configuração da rede.}

0 0.4 0.8 1.2 1.6

k/2 0 5 10 15 20 25 30 Energia /J E E 1 2 π (1/Α) 0 (a) (b)

Figura 18: (a) Gráfico da energia contrakpara a rede em volta do cilindro de maneira simétrica, onde J2 representa o primeiro vizinho, J3 o segundo e J1 representa o terceiro vizinho. Foi utilizadoJ1= 5_J0,J2 = 2_J0,J3= 1_J0,µBH0 =_J0,c= 4_{. (b) Configuração da rede.}

0 0.4 0.8 1.2 1.6

k/2 0 5 10 15 20 25 30 Energia /J E E 1 2 π (1/Α) 0 (a) (b)

O caso em que a distância vertical entre os elementos das redes e os comprimentos dos lados do triângulo são distintos, pode ser estudado. A Fig.20 representa uma parte dessa rede, onde ela continua infinitamente na direção Z e₋Z.

Figura 20: Rede disposta ao longo de um cilindro.

Figura 21: Rede disposta ao longo de um cilindro vista de cima.

A Fig.21 mostra a rede vista de cima. Existem novamente três tipos de redes distin-tas, representadas por A (vermelho), B (azul) e C (preto). Sejam os lados do triângulo representados porl1, l2 el3, ec, deeas distâncias entre um elemento e outro na vertical. O parâmetrod1 representa a distância entre elementos da mesma rede,d2 ed3 a distância entre elementos da rede a e b, d4 e d5 a distância entre elementos da rede a e c e d6 e d7 a distância entre elementos da rede b e c. A Fig.22 representa as distâncias di.

d1 = c+d+e (4.28)

d2 =

q

l2

1 +c2 (4.29)

d3 =

q

l2

1 + (d+e)2 (4.30)

d4 =

q

l2

2 +e2 (4.31)

d5 =

q

l2

2 + (c+d)2 (4.32)

d6 =

q

l2

3 +d2 (4.33)

d7 =

q

l2

(a) (b)

(c)

Figura 22: (a) Distância entre os elementos da rede A com elementos da rede B; (b) Distância entre os elementos da rede A com elementos da rede C; (c)Distância entre os elementos da rede B com elementos da rede C.

O problema pode ser solucionado dividindo o Hamiltoniano em quatro partes, uma correspondente a interação de rede de partículas do tipo A, a interação do tipo B, a interação do tipoC e o Hamiltoniano de interação entre A e B, A eC e B e C,

H = X

i,j

S

1 2(J

ab

ij +Jijba+Jijac+Jijca) +

2

SµBH0+J

aa

δij −Jaa

a†_iaj

+ X

i,j

S

1 2(J

ab

ij +Jijba+Jijbc+Jijcb) +

2

SµBH0+J

bb

δij −Jbb

b†_ibj

+ X

i,j

S

1 2(J

ac

ij +Jijca+Jijbc+Jijcb) +

2

SµBH0+J

cc

δij −Jcc

c†_icj

− X

i,j

S

2

h

J_ijab+J_ijba aib†j +a

†

ibj

+ J_ijac+J_ijca aic†j+a

†

icj

+ Jijbc+Jijcb bic†j +b

†

icj i

O Hamiltoniano pode ser escrito como

H = X

k

[A(k)a†_kak+B(k)a†kbk+C(k)akb†k+F(k)b

†

kbk

+ D(k)a†_kck+G(k)a†kck+H(k)bkc†k+I(k)b

†

kck+L(k)c†kck] (4.36)

e pode ser escrito na forma matricial

H =X

k h

a†_k b†_k c†_k i

   

A(k) B(k) C(k)

D(k) F(k) G(k)

H(k) I(k) L(k)

   

   

ak

bk

ck   

, (4.37)

onde

A(k) = S(J2+J3+J4+J5) +SJ1+ 2µBH0−2SJ1cos[k(c+d+e)] (4.38) B(k) = ₋S_{J2cos(kc) +J3cos[k(c+d)]} (4.39) C(k) = ₋S_{J4cos(ke) +J5cos[k(c+d)]} (4.40)

D(k) = B∗_{(k) (4.41)}

F(k) = S(J2+J3+J6+J7) +SJ1+ 2µBH0−2SJ1cos[k(c+d+e)] (4.42) G(k) = ₋S_{J6cos(kd) +J7cos[k(c+e)]} (4.43)

H(k) = C∗(k) (4.44)

I(k) = G∗_{(k) (4.45)}

L(k) = S(J4+J5+J6+J7) +SJ1+ 2µBH0−2SJ1cos[k(c+d+e)], (4.46)

Ji representa a interação correspondente a distânciadi . A seguinte substituição pode ser

feita para melhor visualização,

A energia do sistema é dada calculando os autovalores da seguinte matriz,

N =

   

u1(k) v1(k) v2(k) v1(k) u2(k) v3(k) v2(k) v3(k) u3(k)

  

. (4.53)

A energia em função de k para quatro casos são representadas nas Fig.23 à 26. Uma vez que a equação a ser resolvida é uma equação do terceiro grau, existem três possíveis soluções para o sistema, a curva continua (preta) representa a a primeira solução, E1, a curva pontilhada (vermelha) representa a segunda solução, E2, e a curva tracejada (azul) representa o comportamento para terceira solução,E3. Então a degenerescência do sistema é quebrada ao modificar as distâncias verticais,c,dee, ou modificar as distâncias dos lados do triângulo ao observar a rede de cima, l1, l2 e l3, isso ocorre devido a quebra de simetria. O gráfico onde as distâncias verticais são iguais e os lados do triângulo são distintos pode-se notar um comportamento onde se aproxima da degenerescência, representado na Fig.26, o pontilhado (vermelho) se aproxima da curva contínua (preta). Todas as distâncias a seguir são dadas em angstrom e assumiremos d0 = 5Å, um valor aceitável para estas interações. As energias a seguir são dadas em função de J0.

0 0.2 0.4 0.6 0.8 1

k/2

0 2 4 6 8

Energia /J

E E E 1 2

π (1/Α)

3

0

(a) (b)

0 0.2 0.4 0.6 0.8 1 k/2 0 2 4 6 8 Energia /J E E E 1 2 π (1/Α) 3 0 (a) (b)

Figura 24: (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2, l2 = 2,l3 = 2,Ji =J0d0/di, d0 = 5, µBH0 =J0, c= 1, d= 2 e e= 3. (b) Configuração da rede.

0 0.2 0.4 0.6 0.8 1

k/2 0 1 2 3 4 5 6 Energia /J E E E 1 2 π (1/Α) 3 0 (a) (b)

Figura 25: (a) Gráfico da energia contra k para a rede em volta do cilindro de maneira não simétrica, onde l1 = 2, l2 = 3,l3 = 4,Ji =J0d0/di, d0 = 5, µBH0 =J0, c= 3, d= 2 e e= 5. (b) Configuração da rede.

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

k/2 0 1 2 3 4 5 6 7 Energia/J E E E 1 2 π (1/Α) 3 0 (a) (b)