P or ta l O B M E P

P

or

ta

l

O

B

M

E

P

Material Te´

orico - M´

odulo Matrizes e Sistemas Lineares

Opera¸

c˜

oes com Matrizes

Terceiro Ano do Ensino M´

edio

P

or

ta

l

O

B

M

E

P

1

Opera¸

c˜

oes com matrizes

Neste m´odulo vamos definir algumas opera¸c˜oes b´asicas com matrizes.

1.1

Adi¸

c˜

ao de matrizes

Sejam AeBduas matrizes. Para que seja poss´ıvel som´ a-las, ´e necess´ario que ambas tenham exatamente as mesmas dimens˜oes. Suponha, ent˜ao, que A = [ai,j]m×n e B =

[bi,j]m×n sejam do mesmo tipo (ambasm×n). Chama-se

desomadeAcomBa matrizC=A+B, tamb´emmpor

n, ondeC= [ci,j]m×n ´e tal que

ci,j=ai,j+bi,j

para todos os ´ındices i ej. Assim, a soma de matrizes ´e calculada da seguinte forma:



   

a1,1 · · · a1,n

a2,1 · · · a2,n

..

. . .. ...

am,1 · · · am,n

     +     

b1,1 · · · b1,n

b2,1 · · · b2,n

..

. . .. ...

bm,1 · · · bm,n

     = =     

a1,1+b1,1 · · · a1,n+b1,n

a2,1+b2,1 · · · a2,n+b2,n

..

. . .. ...

am,1+bm,1 · · · am,n+bm,n

     .

Vejamos alguns exemplos num´ericos.

Exemplo 1. 1 2 3 4 + 5 6 7 8 =

1 + 5 2 + 6 3 + 7 4 + 8 = 6 8 10 12 . Exemplo 2.

1 2 −4

3 −1 10

+

3 −2 −7

3 3 10

=

1 + 3 2−2 −4−7 3 + 3 −1 + 3 10 + 10

=

4 0 −11

6 2 20

.

O teorema seguinte ´e consequˆencia das propriedades da adi¸c˜ao entre n´umeros reais (ou complexos). Deixamos a sua demonstra¸c˜ao como exerc´ıcio. O leitor interessado pode encontr´a-la tamb´em em [1].

Teorema 3. A soma de matrizes de n´umeros reais (ou complexos) goza das seguintes propriedades:

(a) Associatividade: (A+B) +C =A+ (B+C), para quaisquerA,B eC de mesmo tipo.

(b) Comutatividade: A+B=B+A, para quaisquerAe Bde mesmo tipo.

(c) Elemento neutro aditivo: dados m, n ∈ N_{, a matriz}

nulaNde dimens˜oesm×n´e tal queA+N=N+A=

A, para toda matrizA de dimens˜oesm×n.

(d) Inverso aditivo: Para toda matrizA, existe uma ´unica matriz A′

tal que A+A′

´e a matriz nula de mesmo tipo queA.

Observa¸c˜ao 4. O (´unico) inverso aditivo da matriz A ser´a, doravante, denotado por −A e chamado de matriz oposta de A. Ele ´e obtido invertendo-se o sinal de cada uma das entradas de A. Assim, se A= [ai,j], temos que

−A= [−ai,j].

1.2

Produto de n´

umero por matriz

O produto de um n´umero por uma matriz tamb´em ´e co-nhecido como produto por escalar. Dado um n´umerok e uma matrizA, digamosmporn, o produto dekporA´e a matrizB=k·A(ou simplesmentekA) ondeB= [bi,j]m×n

´e tal que

bi,j=k·ai,j,

para todos os ´ındices i e j. Assim, k ·A ´e uma ma-triz, tamb´em m por n, na qual cada entrada ´e obtida multiplicando-se a entrada correspondente de A por k. Ainda de outra forma, o produto por escalar ´e calculado do seguinte modo:

k·     

a1,1 · · · a1,n

a2,1 · · · a2,n

..

. . .. ...

am,1 · · · am,n

     =     

k·a1,1 · · · k·a1,n

k·a2,1 · · · k·a2,n

..

. . .. ...

k·am,1 · · · k·am,n

     .

Exemplo 5. Temos que:

2·   3 π 1 2 −1 0 8  =  

2·3 2·π

2·12 2·(−1)

2·0 2·8 

= 

 6 2π

1 −2

0 16 

.

Problema 6. Considere as matrizes: A= [ai,j]2×3 tal que

ai,j = i

2

+j2

para todos i e j, e B = [bi,j]2×3 tal que

bi,j=ij. Encontre a matrizA+ 2B.

Soluc¸˜ao 1. Seja C = A+ 2B e vamos denotar C = [ci,j]m×n. Usando as defini¸c˜oes de produto por escalar e

de soma de matrizes, temos que ci,j =ai,j+ 2·bi,j, para

todos os ´ındicesiej. Sendo assim,

ci,j = (i

2

+j2) + 2ij= (i+j)2

,

de forma que

C=

(1 + 1)2

(1 + 2)2

(1 + 3)2

(2 + 1)2

(2 + 2)2

(2 + 3)2

=

4 9 16

9 16 25

P

or

ta

l

O

B

M

E

P

podemos calcular uma a uma todas as entradas de cada uma delas:

A=

12

+ 12

12

+ 22

12

+ 32

22

+ 12

22

+ 22

22

+ 32

=

2 5 10

5 8 13

,

B=

1·1 1·2 1·3 2·1 2·2 2·3

=

1 2 3

2 4 6

,

e

2B=

2 4 6

4 8 12

.

Por fim,

A+ 2B=

2 5 10

5 8 13

+

2 4 6

4 8 12

=

4 9 16

9 16 25

.

Observa¸c˜ao 7. E evidente que a primeira solu¸c˜´ ao do Pro-blema 6 ´e bem mais elegante do que a segunda. A primeira solu¸c˜ao nos mostra uma grande vantagem de se operar com matrizes: pensamos em matrizes como uma entidade abs-trata ´unica, tratando seus termos de forma gen´erica, sem a necessidade de calcular cada um deles individualmente (exceto na hora de exibir o resultado final). Nem toda ma-triz possui uma express˜ao t˜ao simples para seu termo geral. Ainda assim, a ideia de ver a matriz como uma entidade ´

unica ´e essencial.

1.3

Produto matricial

Estudaremos aqui o produto de duas matrizes, tamb´em conhecido como produto matricial. Ao contr´ario da soma de matrizes, o produto n˜ao est´a necessariamente definido para matrizes de mesmas dimens˜oes e n˜ao ´e feito entrada a entrada. Ele ´e definido de uma maneira bastante pecu-liar que, quando vista pela primeira vez, pode n˜ao parecer natural. Por isso, vamos come¸car discutindo um exemplo pr´atico para motivar a defini¸c˜ao de tal produto.

Exemplo 8. Uma confeitaria produz trˆes tipos de bolos, vendidos em duas lojas. A matriz A abaixo possui uma linha para cada loja, uma coluna para cada tipo de bolo e indica quantos bolos de cada tipo foram vendidos por cada loja em uma dada semana.

Bolo 1 Bolo 2 Bolo 3

Loja A 5 4 3

Loja B 3 2 4 =A.

Temos tamb´em uma matriz B, onde cada linha corres-ponde a um dos bolos, cada coluna correscorres-ponde a um in-grediente do bolo e as entradas indicam as quantidades de

cada ingrediente necess´ario para fabricar cada bolo.

Farinha A¸cucar Leite Manteiga Ovos

" #

Bolo 1 500 g 200 g 500 mL 150 g 4 Bolo 2 400 g 100 g 300 mL 250 g 5 Bolo 3 300 g 150 g 600 mL 0 g 6

=B.

Qual a quantidade de ingredientes que cada loja precisou para produzir os bolos desta semana?

Soluc¸˜ao. Queremos montar uma matriz C onde cada li-nha corresponde a uma loja e cada coluna corresponde a um ingrediente, a qual indique as quantidades de cada in-grediente usado por cada loja. Para tanto, defina

Farinha A¸cucar Leite Manteiga Ovos

Loja 1 c1,1 c1,2 c1,3 c1,4 c1,5

Loja 2 c2,1 c2,2 c2,3 c2,4 c2,5

=C.

Dessa forma,c1,1 indica a quantidade de farinha usada

pela Loja 1. Essa loja produziu 5 bolos do tipo 1, gastando 500 g de farinha em cada um, ou seja, 2500 g de farinha; produziu 4 bolos do tipo 2, gastando 400 g de farinha em cada um, ou seja, 1600 g; e produziu 3 bolos do tipo 3, gas-tando 300 g de farinha em cada um, ou seja, 900 g. Ent˜ao, ao todo, a Loja 1 gastou 2500 + 1600 + 900 = 5000 gramas de farinha, de sorte que c1,1 = 5000 g. Em resumo, para

calcular c1,1 tomamos os elementos da primeira linha de

A, os multiplicamos um a um pelos elementos da primeira coluna deB e, em seguida, somamos os resultados:

c1,1 = 5·500 + 4·400 + 3·300

= 2500 + 1600 + 900 = 5000.

Vejamos outro exemplo. Como calcular c2,3, a entrada

da segunda linha e terceira coluna de C? A linha 2 cor-responde `a Loja 2 e a coluna 3 corresponde ao ingrediente leite. Vamos, ent˜ao, olhar para a linha correspondente `a Loja 2 na matriz A, que indica os n´umeros de bolos de cada tipo produzidos por ela: (3,2,4); e para a coluna do leite na matrizB, que indica a quantidade de leite em cada tipo bolo: (500,300,600). Portanto, calculamosc2,3 como

abaixo:

c2,3 = 3·500 + 2·300 + 4·600

= 1500 + 600 + 2400 = 4500,

isto ´e,c2,3= 4500 mL.

Se calcularmos cada uma das demais entradas de Cda mesma forma, obtemos a seguinte matriz:

Farinha A¸cucar Leite Manteiga Ovos

Loja 1 5000 g 1850 g 5500 mL 1750 g 58

P

or

ta

l

O

B

M

E

P

A opera¸c˜ao realizada no Exemplo 8 para obter C´e jus-tamente o que chamamos de produto matricial da matriz

Apela matrizB. Escreve-seC=A×BouA·B. De modo geral, para que seja poss´ıvel calcular o pro-duto A×B, ´e necess´ario que os tipos de A e B sejam compat´ıveis, no seguinte sentido: o n´umero de colunas de

Aprecisa ser igual ao n´umero de linhas deB(observe que esse foi o caso no exemplo anterior, quando A era uma matriz 2×3 eB uma matriz 3×5).

Suponha, pois, que A ´e do tipo m×n, com entradas

ai,j, e B´e do tipo n×p, com entradasbi,j. O resultado

do produto ser´a uma matrizC = [ci,j] do tipo m×p, de

sorte que o produto matricial assume a forma:

Cm×p=Am×n×Bn×p.

Por fim, para todos os ´ındicesiejdeC, o valor deci,j

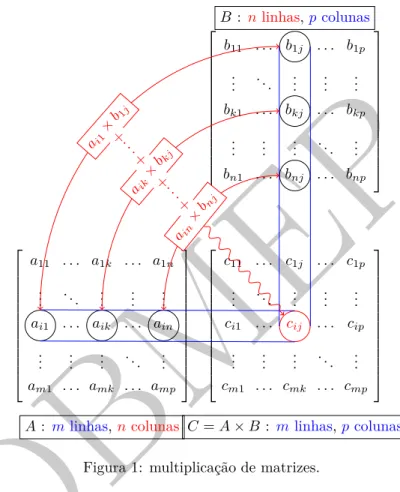
´e obtido tomando-se os elementos de linhaideAe os da colunajdeB, multiplicando-os termo a termo e somando-se os resultados. (Veja a Figura 11

.) Em s´ımbolos, para 1≤i≤me 1≤j≤p, temos que:

ci,j =ai,1b1,j+ai,2b2,j+· · ·+ai,nbn,j

=

n

X

k=1

ai,kbk,j.

O diagrama da Figura 1 ´e conhecido comoesquema de Falk. Para calcular C = A×B, escrevemos as matrizes

A,B eCnum quadro da seguinte forma:

B

A C

Escrevemos as entradas de AeB normalmente e, em se-guida, calculamos as entradas deC uma a uma.

Exemplo 9. Sejam A=

1 2 3 4

e B=

4 3 2

2 1 1

. Como

A´e2×2eB´e2×3, podemos realizar o produto matricial de A por B, obtendo a matriz C = A×B, a qual ser´a

2×3. Montamos o quadro abaixo onde cada elemento deC (em vermelho) ´e obtido multiplicando-se, termo a termo, a linha e a coluna correspondentes a ele e, depois, somando-se tais produtos:

4 3 2

2 1 1

1 2 1·4 + 2·2 1·3 + 2·1 1·2 + 2·1

3 4 3·4 + 4·2 3·3 + 4·1 3·2 + 4·1

Sendo assim,

C=

1·4 + 2·2 1·3 + 2·1 1·2 + 2·1 3·4 + 4·2 3·3 + 4·1 3·2 + 4·1

=

8 5 4

20 13 10

.

1_{Adaptada de Alain Matthes. C´odigo original dispon´ıvel em}

http://www.texample.net/tikz/examples/matrix-multiplication/.

a11 . . . a1k . . . a1n

..

. . .. ... ... ...

ai1 . . . aik . . . ain

..

. ... ... . .. ...

am1 . . . amk . . . amp

                         

A : mlinhas,ncolunas

b11 . . . b1j . . . b1p

..

. . .. ... ... ...

bk1 . . . bkj . . . bkp

..

. ... ... . .. ...

bn1 . . . bnj . . . bnp

                           

B : nlinhas,pcolunas

c11 . . . c1j . . . c1p

..

. . .. ... ... ...

ci1 . . . cij . . . cip

..

. ... ... . .. ...

cm1 . . . cmk . . . cmp

                         

C=A×B : mlinhas,pcolunas

ai1

×b 1j aik ×b kj ain ×b nj + ._{. .} + + ._{. .} +

Figura 1: multiplica¸c˜ao de matrizes.

Com certa pr´atica, podemos executar o mesmo m´etodo sem a necessidade de reescrever as matrizesAeBno qua-dro.

Exemplo 10. Sejam A =   1 −1 2 2 3 4 

 e B =

4 2 3

4 −5 1

.

Encontre o valor de A×B.

Soluc¸˜ao. Como A = A3×2 e B = B2×3, o resultado ´e

uma matriz 3×3, conforme calculado abaixo:





1·4 + (−1)·4 1·2 + (−1)(−5) 1·3 + (−1)·1 2·4 + 2·4 2·2 + 2·(−5) 2·3 + 2·1 3·4 + 4·4 3·2 + 4·(−5) 3·3 + 4·1



=

= 



0 7 2

16 −6 8

28 −14 13



.

Ao contr´ario da adi¸c˜ao, o produto entre duas matri-zes n˜ao ´e comutativo (mas satisfaz as demais propriedades an´alogas `as do Teorema 3).

Para justificar a n˜ao comutatividade, note primeira-mente que, mesmo quando A e B s˜ao compat´ıveis para realizar o produtoA×B, elas podem n˜ao ser compat´ıveis para B×A. Por exemplo, o produto Am×n×Bn×p ´e

P

or

ta

l

O

B

M

E

P

como realizar o produtoBn×p×Am×n. Al´em disso, ainda

que p = m, o produto Am×n ×Bn×m resulta em uma

matrizm×m, enquanto que o produtoBn×m×Am×n

re-sulta em uma matrizn×n. Assim, basta quem6=npara que tais produtos sejam diferentes, como ilustra o pr´oximo exemplo.

Exemplo 11. Seja A=

x y

2×1

eB=

z w

1×2. Temos

que

A×B=

x y

2×1

×

z w

1×2=

xz xw

yz yw

2×2

.

Por outro lado,

B×A=

z w

1×2×

x y

2×1

=

zx+wy

1×1.

Por fim, mesmo no caso em que m = n = p, ou seja, todas as matrizes envolvidas s˜aon×n, o exemplo a seguir mostra que ainda ´e poss´ıvel que os produtosA×BeB×A

sejam diferentes.

Exemplo 12. Seja A2×2=

1 2 0 3

e B2×2=

1 1

0 1

.

Po-demos observar que:

A×B=

1·1 + 2·0 1·1 + 2·1 0·1 + 3·0 0·1 + 3·1

=

1 3

0 3

.

Por outro lado,

B×A=

1·1 + 1·0 1·2 + 1·3 0·1 + 1·0 0·2 + 1·3

=

1 5

0 3

.

Exemplo 13. Se A ´e uma matriz quadrada de ordem n e In ´e a matriz identidade de ordem n, ent˜ao In ×A =

A×In=A.

Soluc¸˜ao. Exerc´ıcio!

Dicas para o Professor

Recomendamos que este material seja apresentado em dois encontros de 50 minutos. O material da se¸c˜ao ‘Multi-plica¸c˜ao de matrizes” ´e um t´opico fundamental e bastante sens´ıvel dentro da teoria de matrizes. ´E necess´ario fazer v´arios exemplos no quadro at´e que os alunos se acostumem com o m´etodo. Para mostrar como calcularC =A×B, recomendamos come¸car usando o quadro do esquema de Falk, fazer outros exemplos (arbitr´arios) al´em dos que est˜ao neste material, e depois seguir o mesmo m´etodo, por´em omitindo as matrizes AeBdo quadro.

Sugest˜

oes de Leitura Complementar