P
or
ta
l
d
a
O
B
M
E
P
Material Te´
orico - M´
odulo de Geometria Anal´ıtica 1
Paralelismo e Perpendicularidade
Terceiro Ano - M´
edio
P
or
ta
l
d
a
O
B
M
E
P
1
Retas paralelas
Na aula sobre a equa¸c˜ao da reta vimos que, se uma reta r n˜ao ´e paralela ao eixo das ordenadas, ent˜ao ela admite uma equa¸c˜ao reduzida da forma
y=mx+q, (1)
ondem´e o coeficiente angular eq´e o coeficente linear da reta.
Lembremos que m= tgθ, ondeθ´e o ˆangulo que a reta r faz com a parte positiva do eixo das abscissas, medido no sentido anti-hor´ario. J´a o coeficiente linearq´e a orde-nada do ponto onde a retarencontra o eixo das ordenadas (figura 1).
(0
, q
)
r
θ
Figura 1: a reta y=mx+q, comm= tgθ.
O coeficiente angular ´e uma medida da dire¸c˜ao de uma reta. Como retas paralelas tˆem a mesma dire¸c˜ao, ´e natural esperar que elas tenham o mesmo coeficiente angular. De fato, vale o seguinte:
Duas retas s˜ao paralelas se, e somente se, tˆem o mesmo coeficiente angular.
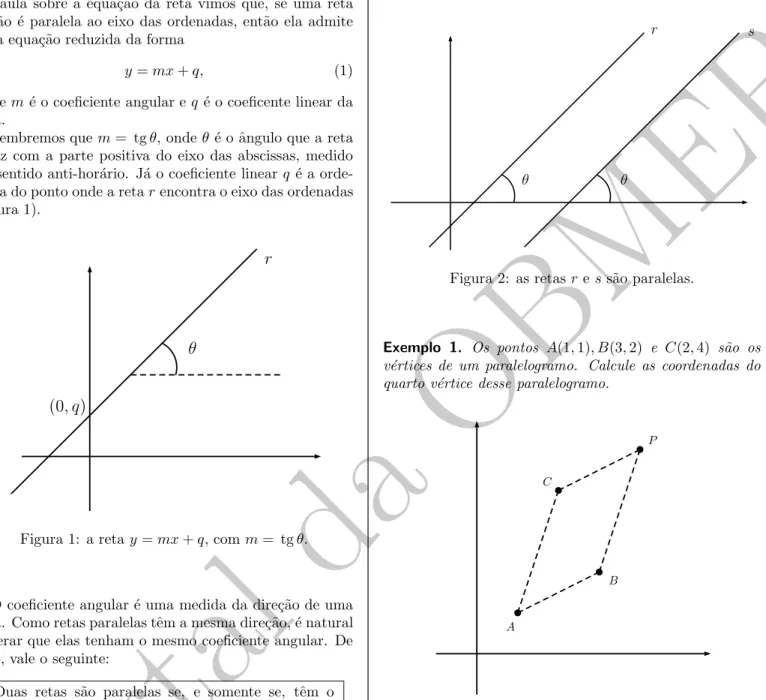
Para justificar a afirma¸c˜ao acima, devemos primeira-mente observar que retas paralelas formam um mesmo ˆangulo com uma reta transversal. Em particular, se r e s s˜ao retas paralelas, ent˜ao elas formam o mesmo ˆangulo com o eixo das abscissas (figura 2). Neste caso, se mr e
ms s˜ao os coeficientes angulares das retas r es,
respecti-vamente, ent˜ao
mr= tgθ=ms.
Reciprocamente, se as retas res tˆem o mesmo coefici-ente angular e formam ˆangulos θr e θs com a horizontal,
ent˜ao
tgθr=mr=ms= tgθs.
Por sua vez, isso implica que θr = θs, pois ambos os
ˆ
angulos est˜ao entre 0 e 180◦ .
r
θ
s
θ
Figura 2: as retasress˜ao paralelas.
Exemplo 1. Os pontos A(1,1), B(3,2) e C(2,4) s˜ao os v´ertices de um paralelogramo. Calcule as coordenadas do quarto v´ertice desse paralelogramo.
b
b
b
A
B C
b P
Figura 3: dados trˆes v´ertices A, B e C de um paralelo-gramo, encontrar o quarto v´erticeP.
Solu¸c˜ao. O v´ertice P ´e o ponto de interse¸c˜ao das retas res, que contˆem os ladosBP eCP do pararalelogramo, respectivamente.
ComoABP C´e um paralelogramo, a retar´e paralela `a reta que passa porAeC; logo, o coeficiente angularmrda
retar´e igual ao coeficiente angular da reta ←→
AC, ou seja,
mr=
P
or
ta
l
d
a
O
B
M
E
P
Da mesma forma, podemos calcular o coeficiente angularda retas, pois ela ´e paralela `a reta que passa porAeB:
ms=
2−1 3−1 =
1 2.
A retarpassa pelo pontoB, de coordenadas (3,2), e tem coeficiente angular mr = 3; logo, sua equa¸c˜ao ´e y−2 =
3(x−3). Simplificando, obtemos
r:y= 3x−7.
Analogamente, a reta spassa pelo pontoC= (2,4) e tem coeficiente angularms=1
2. Assim, sua equa¸c˜ao ´ey−4 = 1
2(x−2). Simplificando, obtemos
s: 2y=x+ 6.
Para encontrar as coordenadas do pontoP, devemos re-solver o sistema formado pelas equa¸c˜oes das retas r e s. Fazendo isso, encontramos x = 4 e y = 5 como solu¸c˜ao. Portanto, o ponto P tem coordenadasP = (4,5).
2
Retas perpendiculares
Nesta se¸c˜ao encontraremos uma condi¸c˜ao necess´aria e su-ficiente sobre os coesu-ficientes angulares de duas retas para que elas sejam perpendiculares.
Se uma das retas ´e vertical, isto ´e, paralela ao eixo das ordenadas, o problema tem solu¸c˜ao imediata: a outra reta ´e perpendicular `a reta vertical se, e s´o se, for horizontal, ou seja, for paralela ao eixo das abscissas (e, portanto, tiver coeficiente angular igual a zero). Dessa forma, podemos supor que nenhuma das retas ´e vertical.
Sejam, pois, resduas retas n˜ao verticais, e sejamy = mrx+qr ey=msx+qs as suas equa¸c˜oes reduzidas.
b
r
s α
β
Figura 4: duas retas perpendiculares.
Sejam αeβ os ˆangulos formados pelas retasres, res-pectivamente, com o eixo das abscissas (veja a figura 4), de modo quemr= tgαems= tgβ.
O ˆangulo β ´e a medida de um ˆangulo externo do triˆangulo retˆangulo formado pelas retas r e s e pelo eixo das abscissas. Pelo Teorema do ˆAngulo Externo, sua me-dida ´e igual `a soma das medidas dos ˆangulos internos n˜ao adjacentes:
β=α+ 90◦ .
Assim,
ms= tgβ= tg (α+ 90
◦
) =sen (α+ 90 ◦
) cos(α+ 90◦)
Da trigonometria, sabemos que sen (α+ 90◦) = cosα e cos(α+ 90◦) =
−senα. Logo,
ms=
cosα −senα =−
1 tgα=−
1 mr
.
Portanto, se as retas r e s s˜ao perpendiculares, ent˜ao seus coeficientes angulares satisfazem a seguinte identi-dade:
mr·ms=−1. (2)
Reciprocamente, se os coeficientes angulares as retasre ssatisfazem a condi¸c˜ao (2), ent˜ao
tgβ=ms=−
1 mr
=− 1 tgα.
Mas, de acordo com a discuss˜ao acima, temos
− 1 tgα =−
cosα senα =
sen (α+ 90◦ ) cos(α+ 90◦
) = tg (α+ 90 ◦
).
Portanto, obtemos
tgβ= tg (α+ 90◦
). (3)
Essa rela¸c˜ao, juntamente com o fato de que 90◦ < α+ 90◦
, β <180◦
, implica queβ =α+ 90◦.
Por fim, observe que, na an´alise da rec´ıproca, obvia-mente n˜ao sabemos de antem˜ao queress˜ao perpendicu-lares (de fato, ´e isso que queremos estabelecer). Contudo, exceto por esse fato, a figura 4 ainda ´e v´alida, isto ´e, β ´e um ˆangulo externo do triˆangulo formado pelas retasres e pelo eixo das abscissas. Ademais,α´e um dos ˆangulos in-ternos n˜ao adjacentes aβ. Portanto, aplicando novamente o Teorema do ˆAngulo Externo, conclu´ımos de (3) que o ou-tro ˆangulo interno n˜ao adjacente a β ´e, necessariamente, um ˆangulo reto. Ent˜ao, as retasress˜ao perpendiculares. Resumimos a discuss˜ao acima enunciando o seguinte
P
or
ta
l
d
a
O
B
M
E
P
Duas retas n˜ao verticaisres s˜ao perpendiculares se, esomente se, o produto de seus coeficientes angulares ´e igual a−1.
A seguir exibiremos uma dedu¸c˜ao do resultado acima sem o uso de trigonometria.
Na figura 5, os triˆangulosOAB eOQC s˜ao semelhantes (pelo caso AA de semelhan¸ca de triˆangulos). Realmente, ambos tais triˆangulos s˜ao retˆangulos, e os ˆangulos∠OBA e ∠OCQ, tendo lados mutuamente perpendiculares, s˜ao congruentes (analisando as somas dos ˆangulos internos dos triˆangulos BP Q e OCQ, conclu´ımos que as medidas de
∠OBAe∠OCQs˜ao ambas iguais a 90◦
−OQCb ).
Da semelhan¸ca entre os triˆangulos OAB eOQC, segue que
OQ OA =
OC
OB. (4)
Agora, sejamy=mrx+qr ey=msx+qsas equa¸c˜oes
reduzidas das retas r e s, respectivamente. Ent˜ao, nas nota¸c˜oes da figura 5, temos imediatamente que
OQ=qs e OB=−qr. (5)
Por outro lado, fazendo y = 0 em ambas tais equa¸c˜oes, obtemos como resultados as abscissas dos pontos A eC, de forma que
OA=−qr mr
e OC =−qs ms
. (6)
Substituindo (5) e (6) em (4), obtemos:
qs
−qr/mr
=−qs/ms −qr
.
Dessa igualdade segue que
−qrqs=
qrqs
mrms
.
Mas, como estamos supondo qr 6= 0 e qs 6= 0 (i.e.,
esta-mos supondo que nem rnem s´e horizontal, uma vez que nenhuma delas tamb´em ´e vertical), podemos cancelar o produtoqrqspara obter
mrms=−1. (7)
Reciprocamente, suponha que mrms = −1. Como (5)
e (6) ainda s˜ao v´alidas, levando em considera¸c˜ao (7) con-clu´ımos que a igualdade (4) tamb´em ´e v´alida.
Essa ´ultima rela¸c˜ao, juntamente com o fato de que os ˆangulos ∠AOB e ∠QOC s˜ao ambos retos, nos permite concluir (pelo caso LAL de semelhan¸ca de triˆangulos) que os triˆangulosOAB eOQC s˜ao semelhantes.
Em particular,∠OAB e∠OQC s˜ao ˆangulos congruen-tes, o que implica que os ˆangulos∠OQCe∠OBAs˜ao com-plementares. Isso mostra que o triˆanguloBP Q´e retˆangulo emP, de sorte que as retasr ess˜ao perpendiculares.
b
r
s B
O A Q
C P
Figura 5: os triˆangulosOAB eOQC s˜ao semelhantes.
Uma das aplica¸c˜oes mais interessantes do crit´erio de perpendicularidade de duas retas ´e fornecer uma demons-tra¸c˜ao bastante simples da concorrˆencia das alturas de um triˆangulo. Nesse sentido, ap´os ler o exemplo a seguir, su-gerimos ao leitor compar´a-lo com a demonstra¸c˜ao apre-sentada na Proposi¸c˜ao 3.11 do item [2] das Sugest˜oes de Leitura Complementar.
Exemplo 2. Prove que as trˆes alturas de um triˆangulo se encontram em um ´unico ponto, chamadoortocentrodo tri-angulo.
Prova. SejamA,BeCos v´ertices do triˆangulo, e escolha um sistema cartesiano de coordenadas com origem em B e tal queC esteja situado sobre o eixo das abscissas (veja a figura 6).
b
b
A
B xA C
P
P
or
ta
l
d
a
O
B
M
E
P
Ent˜ao, sendo (xA, yA), (xB, yB) e (xC, yC) ascoordena-das de A, B eC, respectivamente, temosxB =yB = 0 e
yC= 0.
Podemos supor, sem perda de generalidade, que ABC n˜ao ´e retˆangulo (porque?). Em particular, as retas AB e AC n˜ao s˜ao verticais, de forma que tˆem coeficientes angu-lares respectivamente iguais a
mAB=
yB−yA
xB−xA
= yA xA
e
mAC=
yC−yA
xC−xA
=− yA xC−xA
.
Agora, sejahABa reta suporte da altura relativa ao lado
AB. Sendo perpendicular `a retaAB, o crit´erio de perpen-dicularidade de duas retas garante quehABtem coeficiente
angular igual a
− 1 mAB
=−xA yA
.
Analogamente, sendohACa reta suporte da altura relativa
ao ladoAC, temos que seu coeficiente angular ´e
− 1 mAC
=xC−xA yA
.
Como C ∈ hAB eB ∈ hAC, conclu´ımos que tais retas
tˆem equa¸c˜oes reduzidas
hAB:y−yC=−
xA
yA
(x−xC)
hAC:y=
xC−xA
yA
x
(8)
Igualando as duas express˜oes para y obtidas a partir das equa¸c˜oes acima, encontramos a abscissa do ponto P de interse¸c˜ao das retashAB ehAC:
xC−xA
yA
·x=−xA yA
(x−xC)⇔
⇔(xC−xA)x=−xA(x−xC)⇔
⇔xCx−xAx=−xAx+xAxC⇔
⇔x=xA.
Isso significa que o ponto P de interse¸c˜ao das alturas relativas aos lados AB e AC tem a mesma abscissa do v´erticeA, isto ´e, esses dois pontospertencem `a mesma reta vertical. Por sua vez, tal reta vertical, sendo perpendicular `a reta suporte do lado BC (que ´e o eixo horizontal), ´e a reta suporte da altura relativa ao ladoBC. Ent˜ao as trˆes alturas passam pelo ponto P, ou seja, as trˆes alturas s˜ao concorrentes.
Dicas para o Professor
Dois encontros de 50 minutos cada s˜ao suficientes para cobrir o material desta aula.
A condi¸c˜ao de paralelismo entre retas pode ser explorada com a constru¸c˜ao de paralelogramos, como no exemplo 1, ou de outros pol´ıgonos que tenham lados opostos paralelos. Caso vocˆe queira evitar o uso de trigonometria na dedu¸c˜ao do crit´erio para a perpendicularidade, pode se-guir o caminho delineado no final da p´agina 2 e come¸co da p´agina 3. Este ´e apenas uma das maneiras de se chegar a esse resultado (outra ´e exibida nas v´ıdeos aulas). De qual-quer modo, ´e necess´ario utilizar semelhan¸ca de triˆangulos, ainda que de modo indireto.
Sugest˜
oes de Leitura Complementar
1. E. L. Lima et al. A Matem´atica do Ensino M´edio, vol.3. Cole¸c˜ao do Professor de Matem´atica, Editora S.B.M., Rio de Janeiro, 1998.