ii DECLARAÇÃO
Nomes: Ana Sofia Fernandes Lomar Endereço eletrónico: asflomar@gmail.com Telefone: 962897197
Número do Bilhete de Identidade: 14893054
Título do Relatório:
Exploração de diferentes representações semióticas no estudo do conceito de limite por alunos do 11º ano
Supervisor: Doutor José António Fernandes
Ano de conclusão: 2018
Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário
É AUTORIZADA A REPRODUÇÃO INTEGRAL DESTE RELATÓRIO APENAS PARA EFEITOS DE INVESTIGAÇÃO, MEDIANTE DECLARAÇÃO ESCRITA DO INTERESSADO, QUE A TAL SE COMPROMETE.
AGRADECIMENTOS
Quero agradecer ao meu supervisor, Professor José António Fernandes pelo apoio, disponibilidade e orientação durante a realização deste relatório.
Também quero agradecer ao Professor Paulo Correia, orientador cooperante do estágio, pela dedicação e amizade ao longo deste ano letivo e ao meu colega de estágio José Eduardo Faria pela amizade e partilha de ideias.
E, claro, não podia deixar de agradecer à minha família, especialmente aos meus pais e ao meu irmão, que sempre me apoiaram e incentivaram nesta longa jornada.
EXPLORAÇÃO DE DIFERENTES REPRESENTAÇÕES SEMIÓTICAS NO ESTUDO DO CONCEITO DE LIMITE POR ALUNOS DO 11.º ANO
Ana Sofia Fernandes Lomar
Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário Universidade do Minho, 2018
RESUMO
Neste estudo, que constitui o Relatório de Estágio do Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário, pretende-se explorar diferentes representações semióticas na aprendizagem do conceito de limite de uma função segundo Heine ao nível do 11.º ano de escolaridade.
Este estudo centrou-se nas três seguintes questões de investigação: (1) Quais os principais erros e dificuldades que os alunos evidenciam na aprendizagem do conceito de limite segundo Heine?; (2) Que registos de representação semiótica (gráfico, simbólico ou língua natural) são usados na exploração do conceito de limite segundo Heine? E que transformações de registos são efetuadas?; (3) Que tipo de registo de representação semiótica (gráfico, simbólico ou língua natural) facilita a aquisição, pelos alunos, do conceito de limite segundo Heine?
O estudo decorreu numa turma de Matemática A, do 11.º ano, tendo-se avaliado a aprendizagem dos alunos no conceito de limite de uma função segundo Heine através da aplicação de um teste de avaliação diagnóstica, da análise de algumas aulas da intervenção pedagógica e de uma ficha de avaliação por partes, aplicada após ter terminado a intervenção pedagógica.
Através da análise das respostas do teste diagnóstico constatou-se que os alunos apresentavam conceções erróneas acerca do conceito de limite de uma sucessão, tais como o limite é algo intransponível, o limite nunca pode ser atingido, o limite é sempre atingível, o limite é um extremo da função. Já com o desenvolvimento da intervenção pedagógica observou-se uma evolução positiva em relação aos resultados do teste de avaliação diagnóstica.
Finalmente, o desempenho dos alunos na ficha de avaliação por partes, em cada tipo de registo, vai de encontro ao que é referido na literatura, sendo que o registo mais utilizado e com mais sucesso foi o registo simbólico, em que 98% das respostas corretas continham pelo menos o registo simbólico. Relativamente aos outros dois registos de representação semiótica, 37% das respostas corretas continham pelo menos o registo em língua natural e 8% das respostas corretas continham pelo menos o registo gráfico. O fraco desempenho dos alunos no registo gráfico sugere que ele deve ser mais explorado no ensino do conceito de limite uma função segundo Heine.
EXPLORATION OF DIFFERENT SEMIOTIC REPRESENTATIONS IN THE STUDY OF THE LIMIT CONCEPT BY 11th GRADE STUDENTS
Ana Sofia Fernandes Lomar
Master in Mathematics Teaching in the 3rd Cycle of Basic Education and Secondary Education University of Minho, 2018
ABSTRACT
In this study, which constitutes the Report of the Master's Degree in Mathematics Teaching in the 3rd Cycle of Basic Education and Secondary Education, we intend to explore different semiotic representations in the learning of the Heine’s limit concept of a function at the 11th grade. This study focused on the following three research questions: (1) Which are the main mistakes and difficulties that the students show in learning the Heine’s limit concept? (2) Which semiotic representation registers (graphic, symbolic or natural language) are used in the exploration of the Heine’s limit concept? (3) What type of semiotic representation register (graphic, symbolic or natural language) facilitates the students’ acquisition of the Heine’s limit concept?
The study was carried out in a class of Mathematics A, of the 11th grade, and the students' learning was assessed in the concept of Heine’s limit of a function through the application of a diagnostic evaluation test, the analysis of some classes of the pedagogical intervention and some questions of an evaluation form, applied after the pedagogical intervention.
Through the analysis of the diagnostic test, it was found that the students presented erroneous conceptions about the limit concept of a succession, such as the limit is something insurmountable, the limit can never be reached, the limit is always attainable, the limit is one extreme of the function. With the development of the pedagogical intervention, a positive evolution was observed in relation to the results of the diagnostic evaluation test.
Finally, the performance of the students in the questions of the evaluation form, in each type of register, is in agreement with what is mentioned in the literature, and the most used and most successful register was the symbolic register, in which 98% of the answers contained at least the symbolic register. For the other two semiotic representation registers, 37% of the correct answers contained at least the natural language register and 8% of the correct answers contained at least the graphic register. The poor performance of the students in the graphic register suggests that it should be further explored in the teaching of the Heine’s limit concept of a function.
Keywords: Semiotic representation registers; High school; Heine’s definition of limit of a function; Errors and difficulties.
ÍNDICE DECLARAÇÃO ... ii AGRADECIMENTOS ... iii RESUMO ... v ABSTRACT ... vii ÍNDICE ... ix ÍNDICE DE TABELAS ... xi
ÍNDICE DE FIGURAS ... xii
CAPÍTULO I - INTRODUÇÃO ... 1
1.1. Tema, finalidade e questões de investigação ... 1
1.2. Pertinência do estudo ... 2
1.3. Estrutura do relatório ... 4
CAPÍTULO II - ENQUADRAMENTO TEÓRICO ... 7
2.1. Teoria dos registos de representação semiótica ... 7
2.2. Limites segundo Heine de funções reais de variáveis real ... 14
2.2.1. A definição de limite segundo Heine nos programas escolares ... 14
2.2.2. Obstáculos na aprendizagem do conceito de limite... 18
2.2.3. Dificuldades e erros relativos ao conceito de limite ... 21
2.2.4. Dificuldades referentes à representação verbal, simbólica e gráfica ... 23
CAPÍTULO III - ENQUADRAMENTO CONTEXTUAL ... 27
3.1. Caracterização da escola ... 27
3.2. Caracterização da turma ... 28
3.3. Estratégias de intervenção ... 30
3.4. Métodos de recolha de dados ... 34
CAPÍTULO IV - INTERVENÇÃO DE ENSINO ... 37
4.1. Avaliação diagnóstica... 37
4.1.1. Questão 1 ... 37
4.1.2. Questão 2 ... 41
4.1.3. Questão 3 ... 43
4.2. Implementação da intervenção pedagógica ... 47
4.2.1. Definição de ponto aderente e de limite de uma função num ponto segundo Heine ... 48
4.2.2. Limites laterais e existência de limite num ponto ... 55
4.2.3. Operações e propriedades de limites de funções e indeterminações ... 60
4.2.4. Levantamento de indeterminações ... 66
4.3. Ficha por partes ... 72
4.3.1. Questão 1 ... 72
x
4.3.3. Questão 3 ... 81
4.3.4. Questão 4 ... 86
4.3.5. Questão 5 ... 90
CAPÍTULO V - CONCLUSÕES, IMPLICAÇÕES E RECOMENDAÇÕES ... 93
5.1. Síntese do estudo ... 93
5.2. Conclusões ... 94
5.2.1. Quais os principais erros e dificuldades que os alunos evidenciam na aprendizagem do conceito de limite segundo Heine? ... 94
5.2.2. Que registos de representação semiótica (gráfico, simbólico ou língua natural) são usados na exploração do conceito de limite segundo Heine? E que transformações de registos são efetuadas? ... 96
5.2.3. Que tipo de registo de representação semiótica (gráfico, simbólico ou língua natural) facilita a aquisição, pelos alunos, do conceito de limite segundo Heine?... 99
5.3. Implicações e Recomendações ... 100 5.4. Limitações ... 102 BIBLIOGRAFIA ... 105 ANEXOS ... 111 ANEXO 1 ... 113 ANEXO 2 ... 115 ANEXO 3 ... 117 ANEXO 4 ... 119 ANEXO 5 ... 121 ANEXO 6 ... 123 ANEXO 7 ... 125 ANEXO 8 ... 127 ANEXO 9 ... 129 ANEXO 10 ... 131
ÍNDICE DE TABELAS
Tabela 1 ‒ Os quatro principais modelos da noção de limite adotados pelos alunos da
noção de limite ... 21
Tabela 2 – Classificações obtidas na disciplina de Matemática A ... 30
Tabela 3 – Métodos de recolha de dados segundo as questões de investigação ... 35
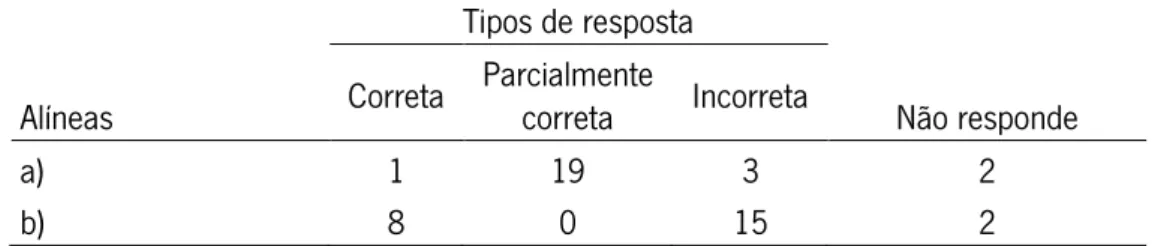
Tabela 4 — Frequências dos tipos de resposta dos alunos à questão 1 ... 37
Tabela 5 — Frequências dos tipos de resposta dos alunos à questão 2 ... 41
Tabela 6 — Frequências dos tipos de resposta dos alunos à questão 3 ... 44
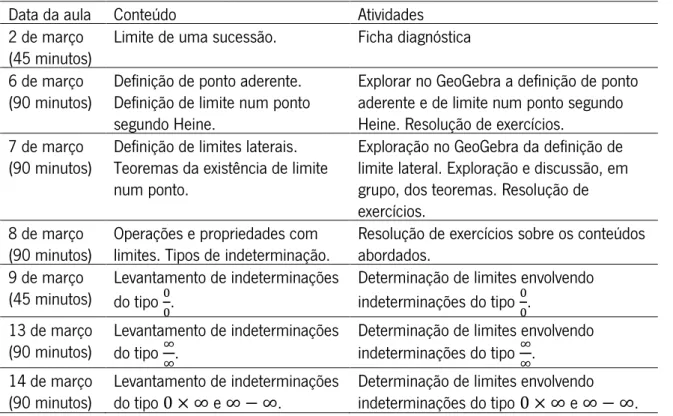
Tabela 7 – Sequência das aulas da intervenção pedagógica ... 47
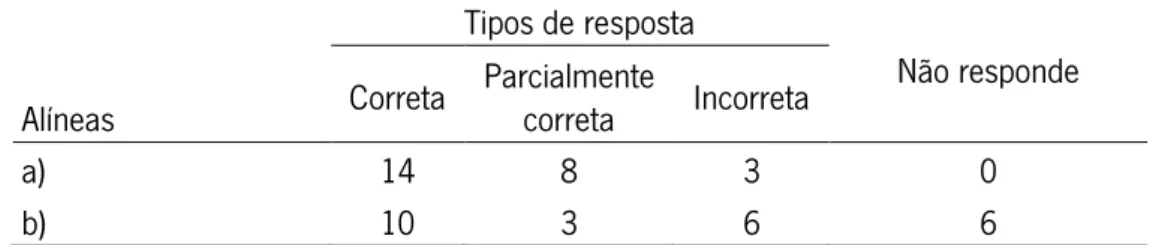
Tabela 8 — Frequências dos tipos de resposta dos alunos à questão 1 ... 72
Tabela 9 — Frequências dos tipos de registo usados pelos alunos na questão 1 ... 77
Tabela 10 — Frequências dos tipos de resposta dos alunos à questão 2 ... 78
Tabela 12 — Frequências dos tipos de resposta dos alunos à questão 2 ... 81
Tabela 13 — Frequências dos tipos de registo usados pelos alunos na questão 3 ... 86
Tabela 14 — Frequências dos tipos de resposta dos alunos à questão 2 ... 86
Tabela 15— Frequências dos tipos de registo usados pelos alunos na questão 4 ... 89
Tabela 16 — Frequências dos tipos de resposta dos alunos à questão 5 ... 90
xii
ÍNDICE DE FIGURAS
Figura 1. Representação algébrica do limite de uma função 𝑓. ... 8
Figura 2. Representação em língua natural do limite de uma função 𝑓. ... 8
Figura 3. Representação em língua natural do limite de uma função 𝑓. ... 8
Figura 4. Enunciado e resolução do exemplo 1. ... 9
Figura 5. Enunciado e resolução do exemplo 2. ... 10
Figura 6. Exemplo de uma conversão onde ocorre um fenómeno de congruência. ... 13
Figura 7. Exemplo de uma conversão de registos onde ocorre um fenómeno de não-congruência. ... 13
Figura 8. Definição de ponto de acumulação e de limite de uma função num ponto. ... 15
Figura 9. Definição de ponto aderente e de limite de uma função num ponto... 15
Figura 10. Representação gráfica de parte de uma função 𝑓. ... 16
Figura 11. Enunciado do exemplo. ... 16
Figura 12. Enunciado do exemplo. ... 17
Figura 13. Representação gráfica das funções 𝑓, 𝑔 e 𝑓 ∘ 𝑔. ... 18
Figura 14. Resposta do aluno A3 à questão 1a). ... 38
Figura 15. Resposta do aluno A10 à questão 1a). ... 38
Figura 16. Resposta do aluno A2 à questão 1a). ... 38
Figura 17. Resposta do aluno A19 à questão 1b). ... 39
Figura 18. Resposta do aluno A7 à questão 1b). ... 39
Figura 19. Resposta do aluno A13 à questão 1b). ... 39
Figura 20. Resposta do aluno A24 à questão 1b). ... 40
Figura 21. Resposta do aluno A5 à questão 1b). ... 40
Figura 22. Resposta do aluno A17 à questão 1b). ... 40
Figura 23. Resposta do aluno A6 à questão 2a). ... 41
Figura 24. Resposta do aluno A9 à questão 2a). ... 42
Figura 25. Resposta do aluno A23 à questão 2a). ... 42
Figura 26. Resposta do aluno A17 à questão 2a). ... 42
Figura 27. Resposta do aluno A12 à questão 2b). ... 43
Figura 28. Resposta do aluno A1 à questão 2b). ... 43
Figura 29. Resposta do aluno A8 à questão 3a). ... 45
Figura 30. Resposta do aluno A11 à questão 3a). ... 45
Figura 31. Resposta do aluno A12 à questão 3a). ... 45
Figura 33. Resposta do aluno A8 à questão 3b). ... 45
Figura 34. Resposta do aluno A19 à questão 3b). ... 46
Figura 35. Resposta do aluno A24 à questão 3b). ... 46
Figura 36. Resolução da alínea a) da tarefa pelo aluno A15. ... 49
Figura 37. Resolução da alínea a) da tarefa pelo aluno A15. ... 49
Figura 38. Resolução do exercício 1, da ficha de trabalho n.º 1, pelo aluno A7. ... 53
Figura 39. Resolução do exercício 1, da ficha de trabalho n.º 1, pelo aluno A15. ... 53
Figura 40. Resolução do exercício 2a), da ficha de trabalho n.º 1, pelo aluno A17. ... 54
Figura 41. Resolução do exercício 2b), da ficha de trabalho n.º 1, pelo aluno A17. ... 54
Figura 43. Resolução do exercício 2b), da ficha de trabalho n.º 1, pelo aluno A8. ... 54
Figura 45. Imagem da segunda animação no GeoGebra. ... 55
Figura 46. Resolução do exercício 3, da ficha de trabalho n.º 1, pelo aluno A8. ... 57
Figura 47. Exemplo de cada indeterminação. ... 61
Figura 48. Resumo das operações com limites em notação simbólica. ... 61
Figura 49. Resolução do exercício 1, da ficha de trabalho n.º 3, pelo aluno A11. ... 64
Figura 50. Resolução do exercício 2, da ficha de trabalho n.º 3, pelo aluno A13. ... 65
Figura 51. Resolução do exercício 2, da ficha de trabalho n.º 3, pelo aluno A5. ... 66
Figura 52. Resolução do exercício 2, da ficha de trabalho n.º 3, pelo aluno A2. ... 66
Figura 53. Resolução do exercício 1c), da ficha de trabalho n.º 4, pelo aluno A18. ... 70
Figura 54. Resolução de um exercício pelo aluno A13. ... 70
Figura 55. Desdobramento do módulo pelo aluno A16. ... 70
Figura 56. Resolução do exercício 2c), da ficha de trabalho n.º 4, pelo aluno A10. ... 71
Figura 57. Resolução do exercício 1c), da ficha de trabalho n.º 4, pelo aluno A18. ... 71
Figura 58. Resposta do aluno A13 à alínea 1a) da ficha por partes. ... 73
Figura 59. Resposta do aluno A9 à alínea 1a) da ficha por partes. ... 73
Figura 60. Resposta do aluno A5 à alínea 1a) da ficha por partes. ... 73
Figura 61. Resposta do aluno A11 à alínea 1a) da ficha por partes. ... 73
Figura 62. Resposta do aluno A3 à alínea 1a) da ficha por partes ... 74
Figura 63. Resposta do aluno A20 à alínea 1a) da ficha por partes. ... 74
Figura 64. Resposta do aluno A4 à alínea 1a) da ficha por partes. ... 74
Figura 65. Resposta do aluno A24 à alínea 1a) da ficha por partes. ... 75
Figura 66. Resposta do aluno A3 à alínea 1b) da ficha por partes. ... 75
Figura 67. Resposta do aluno A21 à alínea 1b) da ficha por partes. ... 75
Figura 68. Resposta do aluno A17 à alínea 1b) da ficha por partes. ... 76
Figura 69. Resposta do aluno A22 à alínea 1b) da ficha por partes. ... 76
Figura 70. Resposta do aluno A13 à alínea 1b) da ficha por partes. ... 76
Figura 71. Resposta do aluno A2 à alínea 1b) da ficha por partes. ... 76
Figura 72. Resposta do aluno A16 à questão 2 da ficha por partes. ... 78
Figura 73. Resposta do aluno A21 à questão 2 da ficha por partes. ... 78
Figura 74. Resposta do aluno A15 à questão 2 da ficha por partes. ... 79
Figura 75. Resposta do aluno A2 à questão 2 da ficha por partes. ... 79
Figura 76. Resposta do aluno A4 à questão 2 da ficha por partes. ... 79
Figura 77. Resposta do aluno A6 à questão 2 da ficha por partes. ... 80
Figura 78. Resposta do aluno A14 à questão 3 da ficha por partes. ... 81
Figura 79. Resposta do aluno A5 à questão 3a) da ficha por partes. ... 82
Figura 80. Resposta do aluno A24 à questão 3a) da ficha por partes. ... 82
Figura 81. Resposta do aluno A5 à questão 3a) da ficha por partes. ... 82
Figura 82. Resposta do aluno A2 à questão 3b) da ficha por partes. ... 83
Figura 83. Resposta do aluno A15 à questão 3b) da ficha por partes. ... 83
Figura 84. Resposta do aluno A8 à questão 3b) da ficha por partes. ... 84
Figura 85. Resposta do aluno A23 à questão 3c) da ficha por partes. ... 84
Figura 86. Resposta do aluno A3 à questão 3c) da ficha por partes. ... 84
xiv
Figura 89. Resposta do aluno A6 à questão 3d) da ficha por partes. ... 85
Figura 90. Resposta do aluno A16 à questão 4 da ficha por partes. ... 87
Figura 91. Resposta do aluno A4 à questão 4 da ficha por partes. ... 88
Figura 92. Resposta do aluno A21 à questão 4 da ficha por partes. ... 88
Figura 93. Resposta do aluno A19 à questão 4 da ficha por partes. ... 88
Figura 94. Resposta do aluno A19 à questão 4 da ficha por partes. ... 89
Figura 95. Resposta do aluno A15 à questão 5 da ficha por partes. ... 90
Figura 96. Resposta do aluno A24 à questão 5 da ficha por partes. ... 91
Figura 97. Resposta do aluno A5 à questão 5 da ficha por partes. ... 91
Figura 98. Resposta do aluno A10 à questão 5 da ficha por partes. ... 91
CAPÍTULO I
INTRODUÇÃO
Neste capítulo apresenta-se o tema em estudo e as suas questões de investigação, assim como a pertinência do estudo à luz do ensino e da aprendizagem da Matemática e uma breve descrição da estrutura deste relatório.
1.1. Tema, finalidade e questões de investigação
O tema escolhido para o Projeto de Intervenção Pedagógica Supervisionada foi Limites segundo Heine de funções reais de variável real, tendo por objetivo geral estudar a influência das representações semióticas do conceito de limite segundo Heine na aprendizagem dos alunos.
Segundo Blázquez e Ortega (2000), o conceito de limite, embora seja um dos conceitos mais importantes em matemática, devido às suas aplicações e ao facto de ser um conceito essencial para a aprendizagem de outros conceitos, apresenta muitas dificuldades de aprendizagem para os alunos. Estes autores defendem também que este conceito é um dos mais difíceis de ensinar. Para Silva (1994), “Questões tão importantes como a noção de função, de limite, de continuidade, de derivada, de integral, continuam a atormentar alunos e professores. Os primeiros não as entendem, os segundos não as conseguem fazer entender” (p. 1).
Segundo Tall e Vinner (1981), as conceções dos alunos relativamente ao conceito de limite podem conter fatores que geram conflitos com a definição do conceito de limite e que causam confusão na aprendizagem deste conceito. Assim, pela própria natureza do conceito de limite, existem dificuldades e obstáculos à aprendizagem deste conceito.
O uso do termo “limite” pode também estar na origem de conceções erradas dos alunos. De facto, palavras que usamos no nosso dia-a-dia relacionadas com ideia de “limite” podem assumir significados muito diferentes daqueles que são inerentes à matemática (Cornu, 1981).
Num estudo realizado por Cornu (1981) é referido que os alunos atribuem significados ao conceito de limite muito diferentes do conceito matemático de limite. Ainda relativamente a esse estudo, a expressão “tende para” não faz parte do vocabulário dos alunos em estudo, sendo que os alunos apresentavam dificuldades em escrever frases com essa expressão. Do mesmo modo, Tall (1992) refere que as expressões “tende para”, “aproxima” e “fica próximo de” também têm significados no senso comum diferentes do significado matemático.
2
Os registos de representação semiótica, como sejam o registo figural, o registo simbólico, o registo gráfico e o registo em língua natural assumem-se como um fator condicionador da aprendizagem dos conceitos matemáticos em geral (Duval, 2003), e do conceito de limite de uma função em particular.
Assim, tendo em conta o que foi referido anteriormente, formularam-se no presente estudo as seguintes questões de investigação:
1. Quais os principais erros e dificuldades que os alunos evidenciam na aprendizagem do conceito de limite segundo Heine?
2. Que registos de representação semiótica (gráfico, simbólico ou língua natural) são usados na exploração do conceito de limite segundo Heine? E que transformações de registos são efetuadas?
3. Que tipo de registo de representação semiótica (gráfico, simbólico ou língua natural) facilita a aquisição, pelos alunos, do conceito de limite segundo Heine?
1.2. Pertinência do estudo
Desde o meu tempo de aluna do ensino secundário que ouço falar nas dificuldades de aprendizagem da noção de limite de uma função. Por outro lado, encontramos na literatura muitos estudos sobre as dificuldades dos alunos na aprendizagem deste conceito, constatando-se que estas investigações se focam nas dificuldades dos alunos (e.g., Blázquez & Ortega, 2000; Cornu, 1981) e na importância do conceito de limite para a compreensão de outros conceitos (Blázquez & Ortega, 2000).
O conceito de limite é um dos conceitos matemáticos em que os alunos revelam muitas dificuldades de aprendizagem, dificuldades essas que estão ligadas ao próprio conceito de limite (Blázquez & Ortega, 2000). Para além disso, o conceito de limite é um dos mais importantes uma vez que é necessário para a aprendizagem de outros conceitos, como sejam os conceitos de continuidade, derivada e integral (Blázquez & Ortega, 2000).
Em contrapartida, o conceito de limite, para os alunos, é um conceito pouco atrativo e demasiado abstrato e que facilmente é esquecido. De facto, como já foi referido em diversos estudos (Cornu, 1991; Prezenioslo, 2004; Tall, 1992), os alunos revelam muitas dificuldades nos conteúdos implicados no conceito de limite de uma função.
Segundo Tall e Vinner (1981), as interpretações e as conceções dos alunos do conceito de limite de uma função podem conter fatores que causam conflito com a definição do conceito de
limite. Assim, as dificuldades e obstáculos na aprendizagem do conceito de limite de uma função surgem devido à natureza do próprio conceito (Prezenioslo, 2004).
Tall (1992) refere que o conceito de função é central para a matemática moderna, sendo que o conceito de limite impõe uma progressão para o plano mais elevado do pensamento matemático. O conceito de limite de uma função é o primeiro conceito matemático que não é abordado através de cálculos matemáticos simples (Cornu, 1983), estando “cercado de mistério”, onde é necessário andar por um “caminho tortuoso” (Tall, 1992).
Para além da natureza do conceito de limite ser um obstáculo na aprendizagem, os alunos podem ter conceções erradas acerca do conceito de limite de uma função devido à utilização do termo limite no dia-a-dia. No nosso quotidiano, utilizam-se muitas palavras relacionadas com a ideia de limite, mas com significados muito diferentes dos significados matemáticos.
Num estudo feito por Cornu (1981), realizado com alunos de um Liceu, concluiu-se que o significado da palavra limite não coincide com o seu significado em matemática. Do mesmo modo, os termos que se associam aos processos matemáticos de limite como, por exemplo, “tende para”, “aproxima-se de” ou “fica próximo de” também têm significados diferentes dos significados matemáticos (Tall, 1992).
Para além destes obstáculos, Thabane (1998) e Laridon (1992), citados em Jordaan (2005), referem que os alunos consideram o limite da função num ponto como a imagem da função nesse ponto e, portanto, consideram que não está definido o limite da função num ponto que não pertence ao domínio da função.
De acordo com o programa de Matemática A de 11º ano (Ministério da Educação e Ciência, 2014), o conceito de limite de uma sucessão deve ser introduzido de forma cuidada, não devendo limitar-se a uma abordagem puramente intuitiva. Posteriormente, no domínio das Funções Reais de Variável Real, recomenda-se a utilização dos conceitos introduzidos no domínio das Sucessões para se definir a noção de limite de uma função, segundo Heine, num ponto real ou em mais ou menos infinito.
Segundo Castro e Castro (1997), para se dominar um conceito matemático é necessário conhecer as suas principais representações e o seus significados, bem como converter ou traduzir representações noutras representações, reconhecendo qual a mais vantajosa para uma determinada situação. Duval (2003) refere que só existe compreensão de um objeto matemático quando o aluno consegue mobilizar os diferentes registos de representação semiótica, designadamente o registo figural, o registo em língua natural, o registo simbólico e o registo gráfico.
4
Do mesmo modo, o National Council of Teachers of Mathematics [NCTM] (2008) refere que os alunos devem conhecer e relacionar as várias representações do mesmo objeto matemático.
Deste modo, pretende-se definir limite de uma função segundo Heine, num ponto real dado ou em mais ou menos infinito, a partir dos conhecimentos adquiridos pelos alunos acerca dos limites de sucessões, representando este conceito nos diferentes registos de representação semiótica e recorrendo ao uso das novas tecnologias, concretamente à calculadora gráfica e ao software GeoGebra.
Tendo em consideração tudo o que foi antes referido, pretende-se com este relatório poder contribuir para aumentar os conhecimentos acerca das dificuldades e dos erros revelados pelos alunos no conceito de limite de uma função num ponto e como solucioná-los. Simultaneamente, espera-se que este relatório também possa fornecer contribuições sobre potencialidades do uso dos registos de representação semiótica para a aprendizagem do conceito de limite de uma função.
1.3. Estrutura do relatório
Este relatório está organizado em cinco capítulos. No Capítulo I, Introdução, apresenta-se o tema, incluindo o objetivo geral e as questões de investigação, justifica-se a pertinência do tema e apresenta-se a estrutura do relatório.
O Capítulo II, Enquadramento Teórico, encontra-se dividido em dois subcapítulos, sendo que no primeiro faz-se referência à teoria de registos de representação semiótica, enquanto o segundo está subdividido em quatro secções, que fazem referência às definições de limite de uma função segundo os programas de Matemática A, homologados em 2002 e em 2014, aos obstáculos de aprendizagem, às dificuldades e erros relativos ao conceito de limite de uma função e às dificuldades referentes à representação verbal, simbólica e gráfica.
O capítulo III, Enquadramento Contextual, está dividido em quatro subcapítulos, que são os seguintes: Caracterização da escola, Caracterização da turma, Estratégias de intervenção e Métodos de recolha de dados.
O capítulo IV, Intervenção Pedagógica, encontra-se organizado em três subcapítulos, relativos à análise das respostas dos alunos no teste diagnóstico, de alguns episódios de aulas da intervenção pedagógica, considerados importantes para o projeto, e das respostas dos alunos na ficha de avaliação por partes.
No capítulo V, Síntese, Conclusões, Implicações e Recomendações e Limitações, encontra-se dividido em quatro subcapítulos. No primeiro apreencontra-senta-encontra-se uma sínteencontra-se do estudo, no encontra-segundo apresentam-se as respostas relativas às questões de investigação propostas, no terceiro apresentam-se algumas implicações e recomendações para estudos posteriores e no quarto são referidas as limitações à execução deste projeto.
CAPÍTULO II
ENQUADRAMENTO TEÓRICO
Neste capítulo faremos uma revisão de literatura focada em dois aspetos: 1) a teoria dos registos de representação semiótica de Raymond Duval e 2) o conceito de limite de uma função segundo Heine. Dentro deste último subcapítulo abordar-se-ão as diferenças na abordagem do conceito de limite entre o programa escolar atual e o programa escolar anterior, os obstáculos na aprendizagem do conceito de limite, as dificuldades e erros na aprendizagem deste conceito e as dificuldades referentes à representação verbal, simbólica e gráfica.
2.1. Teoria dos registos de representação semiótica
O presente trabalho tem como uma das suas referências a teoria dos registos de representação semiótica, que foi introduzida pelo filósofo e pedagogo francês Raymond Duval, tendo em vista analisar a influência das diferentes representações semióticas dos objetos matemáticos no ensino e na aprendizagem da matemática.
De acordo com esta teoria, pode-se representar um objeto matemático através dos registos de representação semiótica, que são definidos por “produções constituídas pelo emprego de signos pertencentes a um sistema de representações, os quais têm suas dificuldades próprias de significado e funcionamento” (Duval, 2012, p. 39). Por outras palavras, os registos de representação, segundo Duval, são formas de representar um determinado objeto matemático. O autor, na sua teoria, refere também que o sistema onde se representa o objeto designa-se por sistema ou registo semiótico, sendo a sua importância resultado do facto de possibilitar a troca e a organização de informação acerca do objeto matemático.
Há uma grande variedade de sistemas de representações semióticas, designando-os Duval por registos de representação semiótica que classifica em quatro tipos: a língua natural, as escritas algébricas e formais, as figuras geométricas e as representações gráficas.
Nas atividades matemáticas pode-se representar o mesmo objeto matemático em diferentes registos de representação semiótica, como se pode ver nos seguintes três exemplos, que se referem ao limite da função 𝑓(𝑥) quando 𝑥 tende para 1 ser 6.
8
Figura 1. Representação algébrica do limite de uma função 𝑓.
Figura 2. Representação em língua natural do limite de uma função 𝑓.
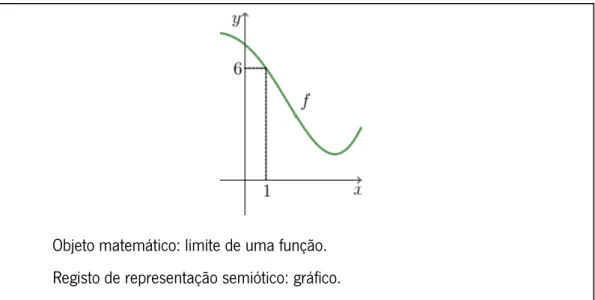
Figura 3. Representação gráfica do limite de uma função 𝑓.
Como se pode observar, através destes exemplos, a representação do objeto não é o mesmo que o objeto, pois todas as representações anteriores se referem ao mesmo objeto (limite de uma função 𝑓(𝑥) quando 𝑥 tende para 1 é 6). Embora todas as representações sejam relativas ao mesmo objeto, cada uma delas fornece informação distinta acerca das caraterísticas do objeto, revelando-se, assim, o interesse do recurso a diferentes representações para melhor compreender o objeto matemático em questão.
Para esta pesquisa consideraram-se três dos quatro registos de representação semiótica estabelecidos por Duval, especificamente: o registo em língua natural, o registo gráfico e o registo simbólico.
lim
𝑥→1𝑓(𝑥) = 6.
Objeto matemático: limite de uma função.
Registo de representação semiótico: simbólico-algébrico.
Para qualquer sucessão (𝑥𝑛) de termos pertencentes ao domínio de 𝑓, convergente para 1, as imagens da sucessão por 𝑓 tendem para 6.
Objeto matemático: limite de uma função.
Registo de representação semiótico: língua natural.
Objeto matemático: limite de uma função. Registo de representação semiótico: gráfico.
Esta teoria defende que para um indivíduo desenvolver o raciocínio é essencial que este distinga e relacione as representações semióticas de um objeto matemático. Para Duval (2006), a forma de analisar e descobrir as origens das dificuldades dos alunos está nas representações semióticas. De acordo com este autor, para que ocorra uma aprendizagem significativa é necessário que o propósito do ensino da matemática seja voltado para o desenvolvimento geral das capacidades de raciocínio, de análise e de visualização. Neste caso, a atividade matemática tem como caraterísticas a dependência das representações semióticas e a grande diversidade de representações, uma vez que os objetos matemáticos só são acessíveis através das suas representações.
Para Duval (2003) só há apreensão do objeto matemático quando o aluno consegue utilizar mais do que um registo de representação ao mesmo tempo ou alterar de registo de representação a qualquer momento. Assim, nesta perspetiva, para este autor, a compreensão em matemática é atingida quando o aluno conseguir relacionar os diversos registos de representação semiótica de um conceito.
Para que ocorra aquisição do conhecimento, o autor afirma que é essencial mobilizar dois tipos de transformações de representações semióticas, que são o tratamento e a conversão. Duval designa por tratamentos de registo as “transformações de representações dentro de um mesmo registo (Duval, 2003, p. 16) e por conversões as “transformações de representações que consistem em mudar de registo conservando os mesmos objetos denotados” (Duval, 2003, p. 16).
Para se compreender melhor cada uma destas definições, vejamos os dois exemplos a seguir apresentados.
Exemplo 1
Figura 4. Enunciado e resolução do exemplo 1.
No exemplo acima está apresentado uma transformação dentro do mesmo registo, isto é, em que o registo de partida e o registo de chegada é o registo simbólico. Assim, pode-se afirmar que a transformação da representação ocorreu através de um tratamento
Exemplo 2 Assumindo que lim
𝑥→3𝑓(𝑥) = 5, calcula lim𝑥→3 𝑓(𝑥) 3𝑥+6. Resolução: lim 𝑥→3 𝑓(𝑥) 3𝑥+6= lim 𝑥→3𝑓(𝑥) lim 𝑥→3(3𝑥+6) = 5 3×3+6= 5 15= 1 3.
10
Figura 5. Enunciado e resolução do exemplo 2.
No exemplo 2 está apresentado uma transformação que envolve a passagem do registo gráfico para os registos em língua natural e simbólico. Assim, a transformação da representação ocorreu por meio de uma conversão.
No ensino, a distinção entre tratamento e conversão raramente é feita, realizando-se tais transformações sem a existência de qualquer ato intencional do professor (Duval, 2003). Os tratamentos são uma das causas das dificuldades dos alunos, enquanto conversões entre registos raramente são faladas e aplicadas (Duval, 2003). No entanto, Duval refere que as dificuldades relacionadas com as conversões fazem com que o aluno não consiga desenvolver a capacidade de usar o conhecimento que detém para adquirir novos conhecimentos. O autor acrescenta ainda que os alunos têm dificuldade em passar de um problema de palavras para uma expressão simbólica, independentemente do conteúdo matemático. Ainda segundo Duval, uma outra dificuldade é a conversão de gráficos cartesianos em equações. Para que estas falhas sejam eliminadas, este autor refere que é preciso aumentar as investigações sobre os problemas de conversão em todas as áreas de matemática.
A conversão dos diferentes registos de representação possibilita a formação do conhecimento matemático (Duval, 2003). De facto, a mudança de um registo para outro registo é uma condição necessária para que ocorra aprendizagem. O autor refere que a originalidade da atividade matemática consiste na coordenação simultânea de pelo menos dois registos ou “na possibilidade de trocar a todo momento de registro de representação” (Duval, 2003, p. 14).
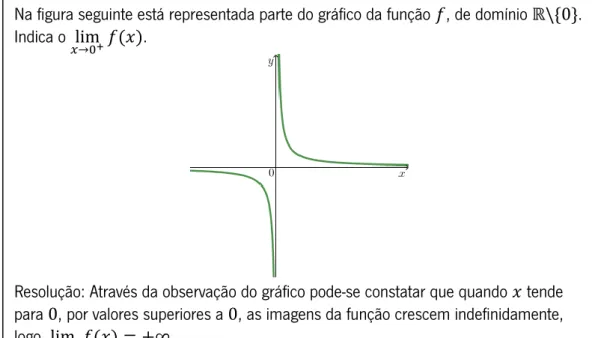
Na figura seguinte está representada parte do gráfico da função 𝑓, de domínio ℝ\{0}. Indica o lim
𝑥→0+𝑓(𝑥).
Resolução: Através da observação do gráfico pode-se constatar que quando 𝑥 tende para 0, por valores superiores a 0, as imagens da função crescem indefinidamente, logo lim
A ideia de que as representações servem apenas para exteriorizar as representações mentais é limitada pois estas têm um papel fundamental na construção do conhecimento matemático. Duval (2003) realça a importância dos registos de representação semiótica onde refere que a condição fundamental para a evolução do pensamento matemático foi o desenvolvimento das representações semióticas.
Neste sentido, a atividade matemática é caraterizada pela dependência das representações semióticas e pela diversidade das mesmas. Isto deve-se ao facto de os objetos matemáticos só serem acessíveis através das suas representações, sendo que o mesmo objeto matemático pode ter diversas representações. Duval (2003) defende que a diferença entre a matemática e as outras áreas científicas reside em três caraterísticas: a importância das representações semióticas; o paradoxo cognitivo para aceder ao saber matemático e a enorme variedade de representações semióticas usadas na matemática.
Como já foi referido acima, só se tem acesso aos objetos matemáticos a partir das representações, uma vez que, ao contrário do que acontece com as outras áreas científicas, os objetos matemáticos não são acessíveis a olho nu ou microscopicamente e, por essa razão, o acesso a esses objetos apenas é possível através das representações semióticas (Duval, 2003). De facto, o acesso aos números, por exemplo, só é possível através do uso de representações semióticas e são estas que permitem que sejam designados. Ainda assim, o mais importante não são as representações, mas sim as transformações, pois estas são o coração da atividade matemática.
Embora as representações sejam essenciais para a atividade humana, não as devemos confundir com o objeto matemático. Ora, se por um lado, é essencial que se utilize as representações semióticas para realizar qualquer atividade matemática, por outro, o objeto matemático não deve ser confundido com as suas representações (Duval, 2012). Estas duas condições levam a um paradoxo cognitivo do pensamento matemático, que pode constituir um ciclo para a aprendizagem. De facto, como é que os sujeitos não confundem os objetos matemáticos com as suas representações semióticas se os objetos matemáticos apenas são acessíveis através de representações semióticas? Esta confusão torna-se evidente quando se avalia a capacidade de os alunos realizarem a conversão de um registo para outro registo de representação distinto. Muitas vezes, o insucesso escolar advém da ausência desta capacidade.
A atividade matemática envolve diferentes sistemas de representação semiótica que, dependendo da tarefa, podem ser utilizados sem limitações. Há registos de representação
12
semiótica que permitem realizar mais facilmente uma atividade matemática que outros e há atividades que só podem ser desenvolvidas apenas com um tipo de registo de representação. Mas, segundo (Duval,2003), a maioria das vezes, o aluno não reconhece o sistema que deve usar ou não compreende que o mesmo objeto pode ter várias representações. Duval (2012) afirma que “o recurso a muitos registros parece mesmo uma condição necessária para que os objetos matemáticos não sejam confundidos com suas representações e que possam também ser reconhecidos em cada uma de suas representações” (Duval, 2012, p. 5).
Além disso, cada registo de representação de um determinado objeto matemático apresenta uma caraterística própria do objeto em estudo e à medida que o aluno vai conhecendo os diferentes registos de representação, vai-se apropriando do objeto. Portanto, pode-se afirmar que “descartar a importância da pluralidade dos registros de representação leva a crer que todas as representações de um mesmo objeto matemático têm o mesmo conteúdo ou que seus conteúdos respetivos se deixam perceber uns nos outros como por transparência” (Duval, 2003, p. 14). Mas, para que o aluno se aproprie do objeto matemático, é essencial, para além de conhecer os diferentes registos de representação do objeto, que os relacione.
Assim, pode-se afirmar que a diversidade de registos de representação é fundamental na compreensão de um conhecimento matemático. A maior parte dos alunos, ao longo do seu currículo, não atinge essa compreensão, pois esta requer a coordenação dos diversos registos de representação (Duval, 2003). Portanto, é importante que o professor utilize nas suas práticas de ensino os dois tipos de transformações de representações, tratamento e conversão, nos dois sentidos (Duval, 2003).
Normalmente, no ensino dá-se importância a conversões de um único sentido, o que pode ser uma das causas das dificuldades dos alunos. Isto vem da ideia de que quem consegue fazer as conversões num sentido, também as consegue fazer no sentido inverso. Mas segundo Pavlopoulou (1993, citado em Duval, 2003), a maioria dos alunos que realiza uma conversão de um registo de partida para um registo de chegada não consegue efetuar a transformação recíproca. Portanto, é fundamental que, no ensino, se efetue a conversão nos dois sentidos para que os alunos realizem uma aprendizagem significativa.
Após vários estudos e observações, Duval concluiu que os fracassos ou bloqueios dos estudantes aumentam cada vez que precisam de efetuar uma mudança de registo ou quando precisam de mobilizar dois registos ao mesmo tempo. Estes bloqueios ou fracassos fazem com
que o aluno não consiga reconhecer o mesmo objeto em diferentes representações ou limitam o uso da capacidade de usar conhecimentos para adquirir novos conhecimentos.
Como já foi dito anteriormente, segundo Duval, a distinção entre os tratamentos e as conversões raramente é feita, mas para se estudar as dificuldades de aprendizagem Duval afirma que é essencial estudar a conversão das representações e não os tratamentos e, para isso, deve-se analisar a repredeve-sentação no registo de partida e a repredeve-sentação no registo de chegada.
Quando se realiza uma conversão de uma forma clara, isto é, quando a mudança de um registo de partida para um registo de chegada é evidente, diz-se que ocorreu um fenómeno de congruência.
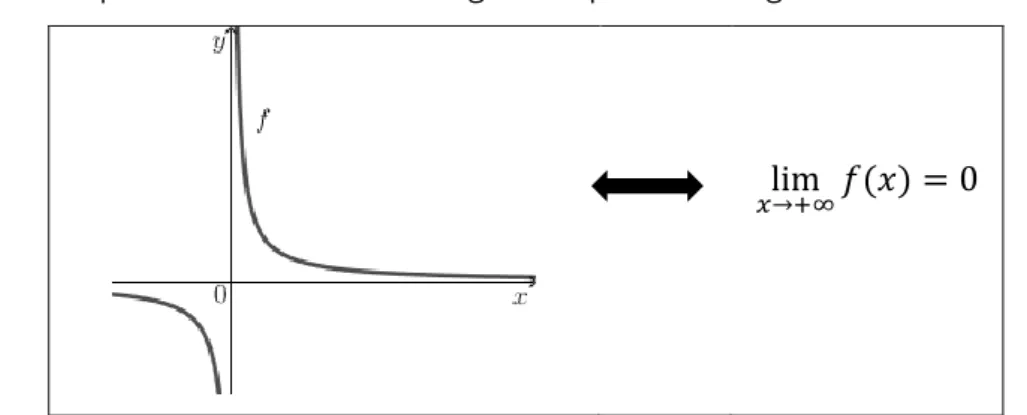
Um exemplo de um fenómeno de congruência pode ser o seguinte:
lim
𝑥→+∞𝑓(𝑥) = 0
Figura 6.Exemplo de uma conversão onde ocorre um fenómeno de congruência.
Por outro lado, se a mudança de um registo de partida para um registo de chegada exige maior raciocínio por parte dos alunos, diz-se que ocorreu um fenómeno de não-congruência.
Na figura abaixo está representado um exemplo de um fenómeno de não congruência.
lim𝑓(𝑣𝑛) = +∞
𝑣𝑛 = 1 + 1 𝑛
14
Para Duval, nas conversões entre registos, os fenómenos de não-congruência são mais comuns do que os fenómenos de congruência, sendo também mais difícil para os alunos este tipo de transformação (Duval, 2003).
2.2. Limites segundo Heine de funções reais de variáveis real
O conceito de limite segundo Heine de funções reais de variável real, segundo o atual programa, deve ser introduzido utilizando os conceitos abordados no domínio das Sucessões. Pons et al. (2011) refere que este conceito deve ser iniciado com ideias intuitivas, oralmente (Fernández-Plaza et al., 2013), seguindo-se aproximações numéricas, para depois se utilizarem expressões algébricas e, por fim, exemplificar a partir de representações gráficas. Assim, com base na combinação de diversas representações, os alunos não ficam limitados a uma única abordagem (Fallas, 2016), podendo assim desenvolver uma aprendizagem mais profunda.
2.2.1. A definição de limite segundo Heine nos programas escolares
Com a atual reforma curricular, o Programa e Metas Curriculares de Matemática A (Ministério da Educação e Ciência, 2014) apresenta algumas diferenças em relação ao programa anterior. Atualmente, o conceito de limite de uma função segundo Heine está incluído no domínio Funções Reais de variável Real, a seguir ao domínio das Sucessões, do 11º ano de escolaridade e nele estudam-se os conteúdos: limite de uma função num ponto; limites à esquerda e à direita; propriedades e operações de limites, bem como o levantamento algébrico de indeterminações.
Enquanto que no antigo programa, do 11.º ano de escolaridade, este conceito aparecia situado no Tema II: Introdução ao cálculo diferencial I e II (Ministério da Educação, 2002), onde era indicado que devia ser introduzido de forma intuitiva, para ser formalizado mais tarde. Era só no 12.º ano de escolaridade que se abordava a definição de limite segundo Heine, as propriedades operatórias sobre limites e o levantamento de indeterminações.
Para além da estrutura e organização terem sido alteradas com a recente reforma curricular, a definição de limite de uma função num ponto também foi alterada. Há, portanto, duas formas para a definição de limite, quando se considera as sucessões no domínio da função que convergem para 𝑎 mas sem nunca tomarem o valor 𝑎 e quando se considera as sucessões no domínio da função que convergem para 𝑎 podendo tomar o valor de 𝑎.
No ensino secundário em Portugal têm-se optado, nos últimos anos, antes da alteração atual, pela definição em que as sucessões não tomam o valor de 𝑎, enquanto no atual programa
se optou pela segunda opção, que apresenta diversas vantagens. Uma das justificações da atual mudança da definição de limite de uma função num ponto é que ela é mais simples de formular e também que a definição de ponto aderente é mais acessível que a noção de ponto de acumulação. Adicionalmente, esta opção permite também uma abordagem mais simples da noção de continuidade de funções. O facto de a própria noção de “limite por valores diferentes”, tal como a noção de “limite à esquerda” e “limite à direita” ser encarada como o limite da restrição inicial a um determinado conjunto é outra vantagem desta definição (Ministério da Educação e Ciência, 2014).
O que distingue as duas definições são as condições do ponto para que 𝑥 está a tender, ou seja, 𝑎. No programa de Matemática A de 2002 utiliza-se a definição de ponto de acumulação para se definir o limite de uma função num ponto, conforme se mostra na Figura 8.
Figura 8. Definição de ponto de acumulação e de limite de uma função num ponto. Já no atual programa utiliza-se a definição de ponto aderente para se definir o limite de uma função num ponto, como se pode ver na Figura 9.
Figura 9. Definição de ponto aderente e de limite de uma função num ponto.
Assim, se se considerar 𝑎 um ponto de acumulação do domínio de uma função 𝑓, as definições coincidem se o ponto 𝑎 pertencer ao domínio de 𝑓. Mas se o ponto 𝑎 não pertencer ao domínio de 𝑓, as definições podem não coincidir.
Para se compreender melhor estas diferenças, observemos a imagem seguinte, onde está representado parte do gráfico de uma função 𝑓.
Sejam 𝑋 ⊆ ℝ e 𝑎 ∈ ℝ. Diz-se que
• 𝑎 é um ponto de acumulação de 𝑋 se ∀ 𝜀 > 0, ]𝑎 − 𝜀, 𝑎 + 𝜀[ ∩ 𝑋\{𝑎} ≠ ∅. • lim
𝑥→𝑎𝑓(𝑥) = 𝑏 se e só se, para qualquer sucessão (𝑢𝑛) de termos do domínio de 𝑓 distintos de 𝑎 tal que 𝑢𝑛→ 𝑎, a sucessão (𝑓(𝑢𝑛)) é tal que 𝑓(𝑢𝑛) → 𝑏.
Sejam 𝑋 ⊆ ℝ e 𝑎 ∈ ℝ. Diz-se que
• 𝑎 é um ponto aderente a 𝑋 se ∀ 𝜀 > 0, ]𝑎 − 𝜀, 𝑎 + 𝜀[ ∩ 𝑋 ≠ ∅. • lim
𝑥→𝑎𝑓(𝑥) = 𝑏 se e só se, para qualquer sucessão (𝑢𝑛) de termos do domínio de 𝑓
16
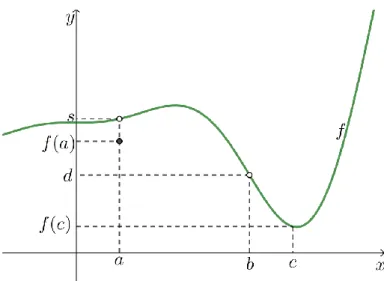
Figura 10. Representação gráfica de parte de uma função 𝑓.
Pelo programa de Matemática A do 11º ano de 2002, a definição do limite de 𝑓 quando 𝑥 tende para 𝑎, para 𝑏 e para 𝑐 existe e é 𝑠, 𝑑 e 𝑓(𝑐), respetivamente. Analisando a função 𝑓 pelo programa atual, conclui-se que o limite de 𝑓 quando 𝑥 tende para 𝑎 não existe, enquanto existe o limite de 𝑓 quando 𝑥 tende para 𝑏 e para 𝑐 e é 𝑑 e 𝑓(𝑐), respetivamente.
Uma outra razão para esta alteração da definição teve a ver com alguns cuidados complementares que a antiga definição obrigava a ter para evitar erros nos enunciados de algumas propriedades. De facto, com a definição do antigo programa, nas definições de operações sobre limites não é possível garantir com toda a generalidade que: “Se 𝑓(𝑥) e 𝑔(𝑥) tendem para limites finitos quando 𝑥 tende para um limite 𝑎 (finito ou infinito), também a soma, a diferença e o produto dessas funções tendem para limites finitos quando 𝑥 tende para 𝑎” (Martins, 2018). Pois, embora o ponto 𝑎 seja ponto de acumulação do domínio de 𝑓 e de 𝑔, pode não ser ponto de acumulação do domínio de 𝑓 + 𝑔. Vejamos o seguinte exemplo na figura 11 (Martins, 2018).
Figura 11. Enunciado do exemplo.
Quando 𝑥 tende para 2, o limite de 𝑓 e o limite de 𝑔 é 0, mas se se adicionar as funções 𝑓 e 𝑔, obtêm-se a função 𝑓 + 𝑔, cujo domínio se restringe ao ponto 2. Assim, o ponto 2 não é ponto de acumulação da função 𝑓 + 𝑔 e, então, pela definição do programa anterior, não existe limite quando 𝑥 tende para 2. Enquanto que, pela definição atual, existe lim
𝑥→2𝑓(𝑥) e é igual a 0.
Sejam 𝑓 e 𝑔 duas funções de domínio [2, +∞[ e ] − ∞, 2], respetivamente, definidas por 𝑓(𝑥) = √𝑥 − 2 e 𝑔(𝑥) = √2 − 𝑥.
É de notar que estas situações só ocorrem quando a interseção dos domínios das funções tem pontos isolados.
Com a atual definição, passa a estar disponível o teorema do limite da função composta, que é referido da seguinte forma “Sejam 𝑓 e 𝑔 duas funções reais de variável real e 𝑎 um ponto aderente a 𝐷𝑔∘𝑓. Se lim
𝑥→𝑎𝑓(𝑥) = 𝑏 ∈ ℝ e lim𝑥→𝑏𝑔(𝑥) = 𝑐 ∈ ℝ, então lim𝑥→𝑎(𝑔 ∘ 𝑓)(𝑥) = 𝑐”, que
no programa anterior não era abordado devido à definição de limite num ponto. Vejamos o seguinte exercício na Figura 12 (Martins, 2018).
Figura 12. Enunciado do exemplo.
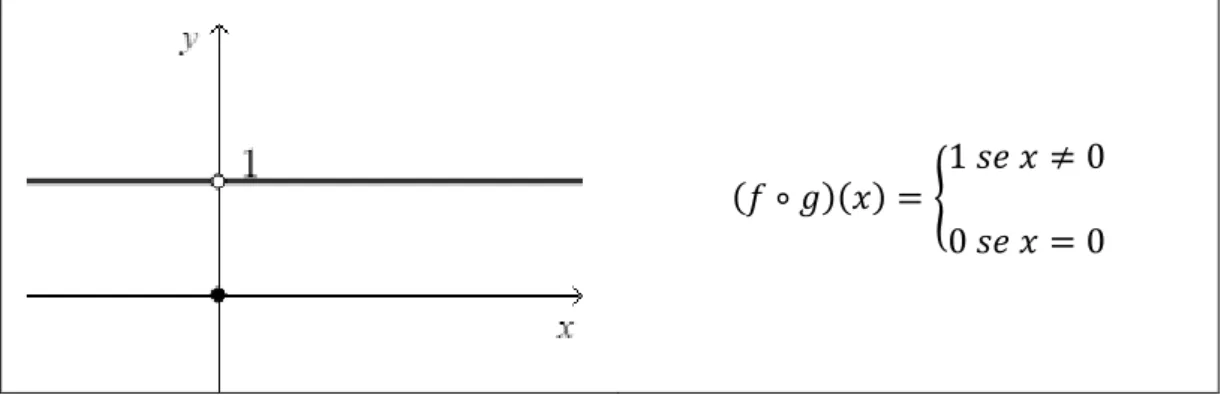
Comecemos por esboçar os gráficos das funções 𝑓 e 𝑔, para se chegar ao gráfico da função 𝑓 ∘ 𝑔. (Figura 13) 𝑓(𝑥) = { 0 𝑠𝑒 𝑥 ≠ 0 1 𝑠𝑒 𝑥 = 0 𝑔(𝑥) = { 0 𝑠𝑒 𝑥 ≠ 0 2 𝑠𝑒 𝑥 = 0 Considere as funções 𝑓 e 𝑔 definidas em ℝ por 𝑓(𝑥) = { 0 𝑠𝑒 𝑥 ≠ 0 1 𝑠𝑒 𝑥 = 0 e 𝑔(𝑥) = {0 𝑠𝑒 𝑥 ≠ 0 2 𝑠𝑒 𝑥 = 0 . Calcula lim 𝑥→0𝑓(𝑔(𝑥)) e lim𝑦→0𝑓(𝑦).
18
(𝑓 ∘ 𝑔)(𝑥) = {
1 𝑠𝑒 𝑥 ≠ 0 0 𝑠𝑒 𝑥 = 0
Figura 13. Representação gráfica das funções 𝑓, 𝑔 e 𝑓 ∘ 𝑔.
Se se considerar a definição antiga, o limite de 𝑓 ∘ 𝑔, quando 𝑥 tende para 0, é 1 e o limite de 𝑓, quando 𝑦 tende para 0, é 0. Mas se se utilizar a atual definição de limite, o limite de 𝑓 ∘ 𝑔, quando 𝑥 tende para 0, não existe, bem como o limite de 𝑓, quando y tende para 0.
Para além destas mudanças, que foram referidas anteriormente, a definição de continuidade acaba por desaparecer, uma vez que a definição de uma função contínua num ponto é igual à definição de limite nesse ponto.
2.2.2. Obstáculos na aprendizagem do conceito de limite
Para se compreender melhor os erros e dificuldades dos alunos na aprendizagem do conceito de limite, ter-se-á de investigar quais os obstáculos existentes na aprendizagem desse conceito. Assim, nesta subsecção investigar-se-á a definição de obstáculo e quais os tipos de obstáculos existentes.
Segundo Brousseau (1976), o erro não resulta só “da ignorância, da dúvida, do acaso” (p. 104), como defendem as teorias empiristas ou behavioristas. Este autor defende que o erro advém de um conhecimento anterior que no momento se revela “falso, ou simplesmente inadaptado” (Brousseau, 1976, p. 104). Mas, mesmo inadequados numa dada situação, estes erros são fundamentais para a construção de conhecimento.
Um obstáculo é um conhecimento que se obtém num determinado momento e que se revela falso e inadaptado aquando de uma nova situação (Brousseau, 1976). Quando se adquire um conhecimento que se revela satisfatório numa determinada situação, embora falso em outros casos, isso faz com que esse conhecimento se enraíze e se torne num obstáculo (Cornu, 1983). Deste modo, para que ocorra aprendizagem é fundamental que estes obstáculos sejam eliminados.
A aprendizagem não ocorre de uma forma contínua (Brousseau, 1976; Cornu, 1983), é feita através de avanços e recuos, que estão relacionados com o aparecimento e a eliminação dos
obstáculos. Daí a importância dos conflitos, pois estes são fundamentais para a deteção de um falso conhecimento e para a eliminação de um obstáculo.
Segundo Brousseau (1976), há três tipos de obstáculos, os obstáculos ontogénicos, que estão relacionados com as limitações neuropsicológicas do próprio sujeito, os obstáculos didáticos, que são o resultado de uma opção do sistema educativo e os obstáculos epistemológicos, que estão ligados com a história do próprio conceito. Também Cornu (1983), citando Gleaser (1979), apresenta uma classificação semelhante dos obstáculos, com origem:
• genética, que estão relacionados com o desenvolvimento do próprio sujeito; • didática, que estão relacionados com os processos de ensino ou do sistema
educativo;
• psicológica, que estão ligados à dimensão psicológica do sujeito; • social, que estão relacionados com a cultura e com a sociedade; • técnica, que estão ligados com tecnologias e técnicas utilizadas; • epistemológica, que fazem parte da história do próprio conceito.
No seu trabalho, Cornu (1983), referiu alguns obstáculos epistemológicos do conceito de limite e, entre eles, está o aspeto metafísico do conceito de limite. Segundo este autor, os conceitos de limite e de infinito apareciam mais relacionados com a metafísica e a filosofia, o que fazia com que os matemáticos se opusessem a utilizar tais conceitos. Para compreender o conceito de limite é fundamental que o aluno compreenda o conceito de infinito, contudo, encontram-se na literatura alguns trabalhos que referem que os alunos têm conceções muito limitadas do conceito de infinito. Cornu (1983) refere que as noções de “infinitamente pequeno” e “infinitamente grande” são obstáculos epistemológicos.
Também, segundo Jordan (2005), o conceito de limite é difícil de se compreender pois parece estar mais relacionado com a metafísica e a filosofia do que com a matemática, sendo um dos principais obstáculos à sua aprendizagem o facto de o seu cálculo não ser efetuado por métodos algébricos e aritméticos comuns.
Um outro obstáculo epistemológico referido por Cornu (1983) e Jordan (2005) reside no facto de “O limite ser ou não atingido?”. Também as ideias “uma soma infinita pode ser finita” e “o quociente de duas quantidades que tendem para zero pode ser um número finito” constituem outros obstáculos epistemológicos, segundo Cornu (1983). Ora, estas duas ideias, discutidas por diferentes matemáticos, são objeto de debate na sala de aula, o que realça a sua importância na aprendizagem da noção de limite.
20
Para além dos obstáculos na aprendizagem do conceito de limite, Cornu (1983) defende que algumas conceções dos alunos poderão constituir um obstáculo à sua aprendizagem. O autor refere que a imagem concetual (Tall & Vinner, 1981)“para descrever a estrutura cognitiva total associada ao conceito, incluindo todas as imagens mentais e propriedades e processos associados”(p. 152), já existe mesmo antes de o aluno ter contacto com o conceito.
As conceções espontâneas são definidas como “ideias a priori, que não são fruto de um ensino organizado” (Cornu, 1983, p.67) e são criadas em diversas situações do nosso quotidiano ou induzidas por outras partes da matemática. No entanto, estas conceções não desaparecem quando os alunos passam a conhecer a definição do conceito, envolvendo-se assim com as conceções “matemáticas” de que têm conhecimento (Cornu, 1983). O autor refere ainda que as conceções espontâneas podem ser identificadas através do vocabulário utilizado pelo aluno e em situações específicas, como por exemplo, na resolução de tarefas (Cornu, 1983).
As conceções próprias “contêm simultaneamente as imagens mentais, as representações, as palavras ligadas ao conceito, mas também as definições, as propriedades, os “teoremas” (por vezes falsos…), os processos, os algoritmos, os exemplos” (Cornu, 1983, p. 69). Segundo Cornu (1983), as conceções próprias podem conter contradições, mas “se os elementos contraditórios não são mobilizados simultaneamente” (Cornu, 1983, p. 69), essas contradições não aparecem. Para Cornu (1983) “o aluno, mesmo munido da definição matemática, faz apelo às suas conceções anteriores, às suas conceções espontâneas, assim que ele põe em ação a noção de limite” (Cornu, 1983, p. 111). O autor defende que estas ideias a priori combinam-se com a noção matemática que dão lugar “a conceções às quais ele fará doravante referência: as suas conceções próprias” (Cornu, 1983, p. 111).
Segundo Cornu (1981), o termo limite, para os alunos,
quase sempre significa algo estático, um limite geográfico fixo, limite a não exceder (moral ou regulamentar), fronteira que não se pode ultrapassar, “os limites da condição humana…”. Há a noção de dificuldade de atingir o limite, e portanto a noção de “se aproximar indefinidamente”. Por vezes, o limite é o que separa duas coisas: a fronteira entre um campo de trigo e um campo de milho, o número 0 é o limite entre o positivo e o negativo. Mas na maioria das vezes, o limite é o fim: não há nada do outro lado. (pp. 3-4)
No seguimento, Cornu (1981) refere os quatro principais modelos adotados pelos alunos na noção de limite, que estão apresentados na tabela seguinte.
Tabela 1 ‒ Os quatro principais modelos da noção de limite adotados pelos alunos. Modelo 𝛼 Um limite é intransponível, é uma fronteira.
Modelo 𝛽 O modelo que para alguns alunos coincide com a noção de extremo superior ou de extremo inferior.
Modelo 𝛾 O limite pode ser alcançado. Modelo 𝛿 O limite é impossível de alcançar.
Nesse artigo, Cornu (1981) destaca o modelo 𝛼, referente à intransponibilidade do limite, como o modelo com mais ênfase entre os alunos, o que pode dificultar a sua atividade matemática. Simultaneamente, a noção de limite, para muitos alunos, não se associa a ideias de variação, movimento ou de aproximação. O autor conclui também que as conceções da noção limite dos alunos não variam com a sua progressão na escolaridade, mantendo-se essencialmente semelhantes (Cornu, 1981).
2.2.3. Dificuldades e erros relativos ao conceito de limite
Como vimos na secção anterior, Cornu (1991) estudou as conceções espontâneas, as quais podem trazer consequências para a atividade matemática, criando obstáculos e dificuldades na aprendizagem do conceito de limite. Outros autores, como por exemplo Jordan (2005) e Tall e Vinner (1981), indicam que um erro muito comum entre os alunos, é considerar o limite no ponto como o valor imagem da função nesse ponto. Em consequência, é comum os alunos considerarem que não existe limite num determinado ponto quando a função não está definida nesse ponto.
Um outro fator que pode causar dificuldades na aprendizagem do conceito de limite é a utilização de expressões usadas no nosso quotidiano associadas ao conceito de limite, como por exemplo: “tende para” e “aproxima-se de”. Estas expressões que, segundo Tall (1992), são usadas para simplificar e tornar mais fácil o conceito de limite, têm significados no nosso dia-a-dia diferentes do significado matemático, o que poderá resultar em conflitos.
No entanto, Cornu (1983) não tem a mesma opinião que Tall (1992) no que concerne às expressões usadas no dia-a-dia dos alunos. Cornu (1983), através do seu estudo, concluiu que a expressão “tende para” não faz parte do vocabulário do quotidiano do aluno. Nesse estudo, Cornu pediu aos alunos para escreverem frases onde utilizassem a expressão “tende para” e reparou que as frases escritas pelos alunos eram um pouco forçadas e que os alunos substituíam a expressão “tende para” por outras expressões “ter tendência para”, “levar a” ou “parecer-se com”.
22
Existem vários significados atribuídos pelos alunos à expressão “tender para” e Cornu (1983, p. 77) distinguiu-os da seguinte forma:
• “tendência a parecer-se com”, que mostra que não há variação. Por exemplo, “este azul tende a roxo”, não quer dizer que a cor azul está a evoluir para a cor roxa. Apenas indica alguma parecença entre o roxo e o azul;
• “tendência a aproximar-se de”, mais uma vez dá a ideia de semelhança mas já denota a ideia de evolução. Por exemplo: “Este regime tende para o socialismo”; “A minha opinião política tende para a do meu pai”. Mas ainda assim, não significa que atinge o objetivo designado”;
• “aproximação inexorável a um objetivo, a um fim”, encontrando-se este tipo de significado em frases do género: “O presente tende para o futuro”; “A vida tende para a morte”;
• “tensão, esforço, em vista de algo”;
• “chegar a”, que aparece em frases do género: “a mãe chega ao filho um jogo”. Tal como o conceito de limite, também as situações de indeterminação e os seus significados são fontes de muitas dificuldades e erros dos alunos. Uma indeterminação é uma situação onde o cálculo do limite abrange transformações algébricas e não só uma simples avaliação da função (Maurice, 2005).
Maurice (2005) realizou um estudo com o objetivo de explicar as ideias e intuições erróneas dos alunos relativas ao comportamento de funções e às situações de indeterminação, atendendo às suas conceções sobre “infinito”, “zero, “divisão por zero” e “limite”. Através desse estudo, a investigadora conclui que o termo “indeterminado” para os alunos aproxima-se do significado da palavra “impossível”. A autora justifica esta conclusão pelo facto de os alunos considerarem que
𝑏
0, com 𝑏 ≠ 0, é indeterminado porque a divisão de um número diferente de zero por zero não é
possível (Maurice, 2005). Do mesmo modo, a forma 0
0 é considerada indeterminada pelos alunos
porque não existe ou é impossível.
No seguimento, Maurice (2005) refere que expressões como “não existe, “impossível”, ”indeterminado” e “não definido” fazem parte do que a autora chama underground terms porque “não sugerem nada de concreto na mente dos alunos” (p. 15). De facto, o senso comum não permite distinguir esses termos, confundindo os alunos (Maurice, 2005).
Os estudantes consideram que o significado do termo “indeterminação” é semelhante ao significado da palavra “aproximação”, pois consideram que o limite não é alcançável, como uma
aproximação, ainda que exista limite. Deste modo, pelo facto de a aproximação ser “uma ação matemática que indica um resultado impreciso e indeterminado” (Maurice, 2005, p. 15), os alunos associam a palavra “aproximação” ao termo “indeterminado” com base nos seus conhecimentos prévios. Por outro lado, quando os conceitos de "infinito" e de "indeterminação" estão presentes, os alunos tentam compensar as suas definições e, nesse caso, desenvolvem conceções compensatórias. Estas conceções compensatórias provêm de contextos matemáticos (conhecimento próximo) ou não matemáticos (senso comum) e compensam a falta das definições.
As ideias erróneas de que “0
∞ é uma indeterminação porque zero não é nada”, “ 0
0 é uma
indeterminação porque zero não é nada” e “∞ − ∞ e ∞
∞ são determinadas porque o resultado é
0 ou 1” (p. 16) não só advém das conceções de divisão por zero e de infinito mas também advêm da conceção de zero e da interpretação do operador envolvido nas indeterminações (Maurice, 2005). A investigadora explica a conceção “zero-nada” como “um retorno às conceções matemáticas transmitidas na escola primária” (p. 17) ou como “uma interferência da linguagem comum, onde o significado de nada domina o significado de zero” (p. 17).
Do mesmo modo, Maurice (2005) refere que quando 0 e ∞ estão presentes ao mesmo tempo, alguns alunos não conseguem prestar atenção simultaneamente ao significado dos símbolos e ao papel do operador. Maurice refere que os alunos hesitam entre escolher “o significado do símbolo 0 e do símbolo ∞, o qual estabelecerá a forma como determinada ou indeterminada” (p. 17).
Outros autores, como Jaffar e Dindyal (2011), referem que alguns alunos, quando confrontados com as expressões do tipo 𝑎
0 = indefinido e 𝑎
0 = ∞, consideram que o infinito e o
indefinido significam o mesmo, o que se deve ao facto de os alunos importarem conhecimentos dos números reais para o estudo do limite.
Em conclusão, Maurice (2005) refere que o professor deve conhecer estas conceções e ideias erróneas para que reconheça o seu uso e destaca a importância da criação de situações que despoletem essas tais ideias erróneas, de modo a criar situações de conflito na mente do aluno.
2.2.4. Dificuldades referentes à representação verbal, simbólica e gráfica
Para além das dificuldades referidas na secção anterior, existem também dificuldades associadas a cada tipo de representação.
24
Relativamente à representação verbal, como consequência de os alunos usarem termos pouco rigorosos e informais, surgem dificuldades relacionadas com a linguagem que o professor usa nas aulas (Cornu, 1991). Na mesma linha de pensamento, Moru (2009) considera linguagem informal como um obstáculo epistemológico do conceito de limite. De facto, como já foi referido, as palavras “tende para” ou “aproxima-se de” têm significados no quotidiano muito diferentes do significado matemático. E, ainda que seja dito aos alunos a definição formal do conceito de limite, estes mantêm a confiança nos significados que usam no quotidiano (Cornu, 1991).
Relativamente à representação simbólica, sabe-se que alguns alunos utilizam processos repetitivos no seu estudo, o que os leva a dar prioridade às técnicas utilizadas nos cálculos em detrimento da teoria abordada nas aulas ou do estabelecimento de relações através da mesma (Fallas, 2016). Como consequência desta escolha, surgem dificuldades relacionadas com a compreensão dos conceitos, uma vez que os alunos em vez de os perceberem, decoram-nos. No entanto, Gray e Tall (2007) referem que
A repetição pode fortalecer as conexões no cérebro a tal ponto que ações repetidas se tornam rotineiras e executáveis sem necessidade de um pensamento consciente. Usado corretamente, como parte de um esquema de conhecimento avançado, essa compactação é uma ferramenta valiosa e essencial. Usado sozinho, para aprender "regras sem razões", sem as subtilezas de conceitos ricos e pensáveis, é provável que leve a um conhecimento frágil que pode falhar em situações que se tornam mais complicadas. (p. 4)
Neste sentido, Gray e Tall consideram que a repetição isolada e inadequada não deve ser usada, aconselhando que a repetição deve ser usada em conjunto com outras técnicas de aprendizagem.
Ainda na representação simbólica, Moru (2009) refere que alguns alunos consideram que só se pode determinar o valor do limite de uma função quando a função está definida analiticamente.
Uma outra dificuldade relativa ao conceito de limite é o facto de que este conceito requere uma transferência das figuras geométricas para a interpretação numérica (Cornu, 1991). Ou seja, para que os alunos compreendam o conceito de limite, eles têm de interpretar numericamente uma representação geométrica, sem que seja necessário escrever a expressão algébrica da função em questão. E, de facto, segundo Moru (2009), alguns alunos não conseguem calcular o valor do limite de uma função sem ter acesso à expressão algébrica da função.
Relativamente à interpretação dos gráficos das funções, há alunos que consideram que não existe limite nos pontos onde a função não está definida (Moru, 2009) e há ainda alunos que
consideram o limite de uma função num ponto como o valor da imagem nesse ponto, confundido assim o valor do limite de uma função num ponto com o valor da imagem da função nesse ponto.