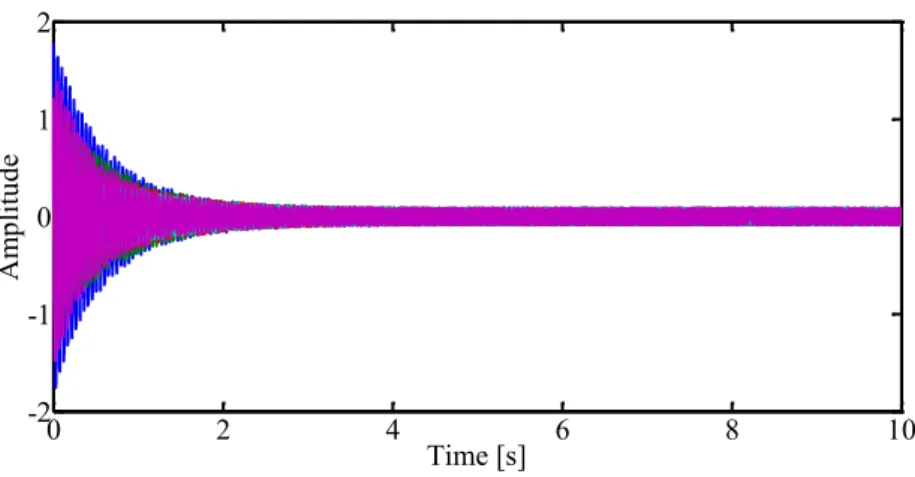
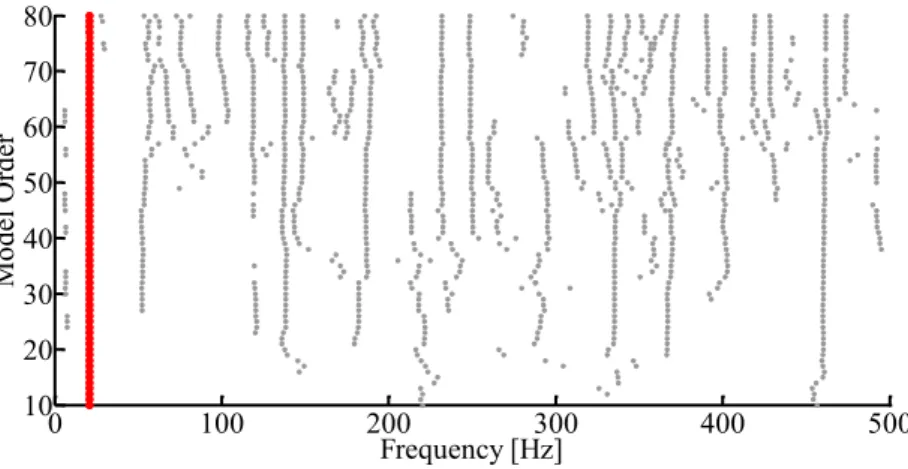
REPOSITORIO INSTITUCIONAL DA UFOP: Desenvolvimento de metodologia para identificação modal automática de estruturas.
Texto
Imagem

Documentos relacionados
4) Extensão e intensidade de violência - Imagens e sons de violên- cia repetidos à exaustão ou mostrados de forma explícitos tornam o processo de recepção mais traumático,
Para a liga 30%Fe65Nb70%Cu foi possível observar uma distribuição de partículas de Fe65Nb ao longo de toda a matriz de Cu e não foi possível notar o processo difusão entre
Esta pesquisa tem como finalidade analisar como a cultura popular esta sendo trabalhada na formação profissional de Educação Física no Brasil, a partir de uma pesquisa
Dando continuadad a los cambios políticos que ocurrierón en Venezuela a partir de 1999. El Plan de Desarrollo Económico y Social de la Nación 2007-2013 contiene
esta espécie foi encontrada em borda de mata ciliar, savana graminosa, savana parque e área de transição mata ciliar e savana.. Observações: Esta espécie ocorre
O valor da reputação dos pseudônimos é igual a 0,8 devido aos fal- sos positivos do mecanismo auxiliar, que acabam por fazer com que a reputação mesmo dos usuários que enviam
Nessa situação temos claramente a relação de tecnovívio apresentado por Dubatti (2012) operando, visto que nessa experiência ambos os atores tra- çam um diálogo que não se dá
Promovido pelo Sindifisco Nacio- nal em parceria com o Mosap (Mo- vimento Nacional de Aposentados e Pensionistas), o Encontro ocorreu no dia 20 de março, data em que também