ILIAS ESTRUTURADAS DE MODELOS COM MODELO BASE ORTOGONAL

(1)

FAM´

ILIAS ESTRUTURADAS DE MODELOS

COM MODELO BASE ORTOGONAL

Teoria e Aplica¸

c˜

oes

Disserta¸cão apresentada para obten¸cão do Grau de Doutor em Matemática com

especializa¸c˜ao em Estat´ıstica pela Universidade Nova de Lisboa, Faculdade de

Ciˆencias e Tecnologia.

Lisboa

(2)

(3)

Sendo este o espa¸co reservado para referir as pessoas que realmente me ajudaram

e apoiaram neste trabalho, come¸co pelo meu orientador, o Professor Doutor Jo˜ao

Tiago Mexia. Foi com ele que tudo isto come¸cou. Foi ele que me trouxe para o

mundo da investiga¸c˜ao, primeiro com o mestrado e agora com o doutoramento e

os projectos em que estive e continuo envolvida, dando in´ıcio a uma nova fase da

minha vida profissional onde me sinto melhor que nunca. Apesar do grande n´umero

de doutoramentos orientados pelo Prof. Mexia durante todo o per´ıodo em que se

processou o meu doutoramento, ele esteve quase sempre dispon´ıvel para responder

`as minhas d´uvidas, para me orientar no caminho a seguir e para em pouco tempo

dar um retorno sobre o material que lhe ia entregando. Mais do queO Professor, o Prof. Mexia ´e um grande amigo com a ajuda do qual sei que posso contar noutras

situa¸c˜oes.

A segunda pessoa que quero referir, ´e sem d´uvida, o meu colega do Centro de

Ma-tem´atica e Aplica¸c˜oes (CMA) e grande amigo Miguel Fonseca, sempre disposto para

discutir comigo as m´ultiplas quest˜oes que iam surgindo ao longo de todo processo.

Quero agradecer tamb´em a todos os outros meus colegas que diariamente ou

com alguma frequˆencia se encontram na sala do CMA, e que contribuem para o

bom ambiente de trabalho que a´ı se vive, o qual proporcionou a realiza¸c˜ao do meu

doutoramento.

(4)

co-orientador na ´area da hidrologia e coordenador do projecto de PTDC/AGR-AAM/

71649/2006 -“Gestão do risco em secas: Identifica¸cão, monitoriza¸cão, caracteriza¸cão,

predi¸cão e mitiga¸cão”do qual sou bolseira de investiga¸cão. Gra¸cas a ele tive

finan-ciamento durante o ´ultimo ano de doutoramento e tive tamb´em a oportunidade de

estar inserida neste projecto e de ter publicado nas melhores revistas internacionais

da ´area da hidrologia. Obrigado por acreditar em mim.

Além disso gostava também de agradecer à Professora Doutora Alexandra

Ri-beiro minha co-orientadora e coordenadora do projecto de investiga¸c˜ao POCTI/

32927/AGR/2000 - “Removal of Cu, Cr, As and creosote from impregnated wood

waste aiming its recycling”, no qual tiveram origem os dados que serviram de base

ao trabalho de aplica¸c˜ao apresentado no capitulo 9 desta disserta¸c˜ao.

Por fim dedico esta disserta¸c˜ao `a minha fam´ılia: aos meus pais, porque a eles

devo grande parte do que sou, ao meu marido Jo˜ao Paulo que sempre me incentivou

a seguir em frente e a procurar uma actividade profissional em que me sentisse

realizada e ao meu pequenino Daniel, a luz que ilumina a minha vida e que d´a

(5)

As fam´ılias estruturadas de modelos (f.e.m.) s˜ao constitu´ıdas por modelos

elementa-res que corelementa-respondem aos tratamentos do modelo base, o qual pode ser ortogonal de

efeitos fixos com cruzamento-encaixe de factores. Por sua vez, os modelos

elemen-tares podem ser regressões lineares múltiplas nas mesmas variáveis, considerando

homocedasticidade entre as regress˜oes ou ent˜ao modelos log-lineares ajustados a

tabelas de contingˆencia. No tratamento das f.e.m., numa primeira fase,

condensa-se a informa¸c˜ao contida nos vectores de obcondensa-serva¸c˜oes correspondentes aos modelos

elementares nas respectivas estat´ısticas suficientes e na segunda fase aplicam-se os

algoritmos desenvolvidos para o modelo base aos resultados obtidos na primeira fase.

Dado um modelo ortogonal λ = Pm_i=1Xiαi associado a uma álgebra de Jor-dan comutativa, diz-se que y = Lλ+ e é um modelo L-ortogonal se os vecto-res coluna de L forem linearmente independentes. No caso não equilibrado das f.e.m. com regressões múltiplas, L será uma matriz diagonal por blocos da forma L= D( ˇX1, ...,Xˇc), onde Xˇj são as matrizes das regressões individuais as quais di-ferem de tratamento para tratamento. Desta forma, ultrapassa-se a restri¸cão usual

requerendo que todas as regress˜oes tenham a mesma matriz de modelo.

Três aplica¸cões a dados reais são apresentadas. Nas duas primeiras, aplicam-se

as f.e.m. com modelos log-lineares à hidrologia, através da análise de transi¸cões

entre classes de seca. Na terceira, analisam-se dados de experiˆencias de remo¸c˜ao

(6)

(7)

Structuralized family of models (s.f.m.) are constituted by unit models

correspon-ding to the treatments of the base model, which can be orthogonal of fixed effects

with cross-nesting. On its side, the unit models can be multiple linear regressions

on the same variables, considering homoscedasticity between regressions or then,

log-linear models fitted to contingency tables. Following the treatment of s.f.m., in

a first step, information inside the observation vectors correspondent to unit models

is condensate in sufficient statistics and in second step, the algorithms developed for

the base model are applied to the results obtained in the first fase.

Given a orthogonal model λ =Pm_i=1Xiαi associated to a commutative Jordan algebra, it is said thaty=Lλ+eis aL-orthogonal model if the column vectors the matrixLare linearly independent. In the no-balanced case of the s.f.m. with multi-ple regressions,Lwill be a diagonal by blocks matrix of the formL=D( ˇX1, ...,Xˇc), whereXˇj are the model matrices of the individuais regressions which can differ from treatment to treatment. In this way, the usual restriction requiring all regressions

to have the same model matrix is overcame.

Three applications to real data are presented. In the two first applications,

s.f.m. with loglinear unit models are applied to hydrology, through the analysis of

transitions between drought classes. In the third one, data originated in experiments

of electrodialytic removal of heavy metals are analyzed using the non-balanced case

(8)

(9)

v _→ vector (letra min´uscula a negrito) 0 _→ vector nulo

1 _→ vector de 1’s

Y _→ vector aleatório (letra maiúscula a negrito) A _→ matriz (letra maiúscula a negrito)

On → matriz nula de ordem n In → matriz identidade de ordem n Jn → matriz de 1’s de ordemn AT _→ matriz transposta de A A−1

→ matriz inversa de A

A+ _→ matriz inversa generalizada de Moore-Penrose de A ⊗ → produto de Kronecker entre matrizes

Car(A) _→ caracter´ıstica da matrizA

Det(A) _→ determinante da matriz A

R(A) _→ Espa¸co imagem da matriz A

(10)

V⊥_/_{W →} _{Complemento ortogonal do sub-espa¸co} _V _{relativamente a} _W v_V _→ projec¸c˜ao ortogonal de v sobre o sub-espa¸coV

Q(V) → Matriz de projec¸c˜ao ortogonal sobre o sub-espa¸co V

⊞ _→ Soma directa ortogonal de sub-espa¸cos

E(X) → Valor esperado da variável aleatória X V(X) → Variância da variável aleatóriaX

COV(X;Y) → Covariância entre a variável aleatória X e Y

E(Y) → Vector m´edio do vector aleat´orio Y

COV(Y) → Matriz de covariˆancia do vector aleat´orioY

COV(X;Y) → Matriz de covariˆancia cruzada dos vectores aleat´oriosX e Y D(d1, ..., dn) → Matriz diagonal com elementos principais d1, ..., dn

Pr() _→ Probabilidade

UMVUE _→ Uniforme minimal variance unbiased estimator

BLUE _→ Best linear unbiased estimator

(11)

1. Introdu¸c˜ao. . . 1

2. Defini¸c˜oes e Resultados Preliminares . . . 7

2.1 Matrizes Ortogonais Estandardizadas, Diagonalizadoras Ortogonais e Matrizes Uniformizadoras . . . 7

2.2 Sub-Espa¸cos e ´Algegras . . . 9

2.3 Matrizes Inversas Generalizadas de Moore-Penrose . . . 10

2.4 Matrizes de Projec¸c˜ao Ortogonal . . . 11

2.5 Produto de Kronecker entre Matrizes . . . 12

2.6 Vector Médio, Matriz de Covariância e Matriz de Covariância Cruzada 14 2.7 Estat´ısticas Suficientes, Completas e Estimadores UMVUE . . . 16

2.8 Testes de Hip´oteses . . . 20

2.9 Vectores Normais e Testes F . . . 23

2.10 Modelos de Regress˜ao M´ultipla . . . 26

2.10.1 Introdu¸c˜ao . . . 26

2.10.2 Estima¸c˜ao dos Coeficientes da Regress˜ao . . . 29

2.10.3 Testes de Hipóteses para Modelos de Regressão Múltipla . . . 34

2.11 Modelos Log-Lineares e Tabelas de Contingˆencia . . . 38

(12)

3. ´Algebras de Jordan Comutativas . . . 43

3.1 Primeiros Resultados . . . 43

3.2 Gera¸c˜ao de ´Algebras de Jordan Comutativas . . . 48

3.3 Opera¸c˜oes Bin´arias . . . 52

4. Modelos Lineares Ortogonais . . . 55

4.1 Modelos Associados a uma ´Algebra de Jordan Comutativa . . . 55

4.2 Estimadores UMVUE . . . 60

4.3 Inferˆencia para o Modelo de Efeitos Fixos . . . 61

4.4 Vectores Estim´aveis e Testes F para os Efeitos Fixos . . . 64

4.5 Constru¸c˜ao de Modelos . . . 65

4.5.1 Modelos para Encaixe . . . 65

4.5.2 Modelos para Cruzamento-Encaixe . . . 68

5. Fam´ılias Estruturadas de Modelos: Caso Equilibrado . . . 71

5.1 Generalidades . . . 71

5.2 Modelo Base . . . 72

5.3 Modelos Elementares . . . 74

5.3.1 Regress˜oes M´ultiplas . . . 75

5.3.2 Modelos Log-Lineares . . . 79

6. Modelos L-Ortogonais para Efeitos Fixos . . . 85

6.1 Projec¸c˜oes e Estat´ısticas . . . 85

6.2 Inferˆencia . . . 87

6.3 Um Primeiro Exemplo . . . 91

(13)

6.4.1 Estrutura . . . 94

6.4.2 Inferˆencia . . . 97

7. An´alise de Transi¸c˜oes entre Classes de Seca utilizando Fam´ılias Estruturadas de Modelos Log-lineares . . . 101

7.1 Introdu¸c˜ao . . . 101

7.2 Dados . . . 102

7.3 Ajustamento de Modelos Log-lineares com Duas Dimens˜oes . . . 103

7.4 An´alise . . . 105

7.5 Resultados e Conclus˜oes . . . 111

8. An´alise de Diferen¸cas Significativas ao N´ıvel das Ocorrˆencias de Seca no Sul de Portugal . . . 115

8.1 Introdu¸c˜ao . . . 115

8.2 Dados . . . 115

8.3 An´alise da Homogeneidade . . . 117

8.4 Modelo Base “Two-Way” . . . 119

8.5 Resultados e Conclus˜oes . . . 121

9. Modela¸c˜ao Regressional da Remo¸c˜ao Electrodial´ıtica de Metais Pesados de Res´ıduos de Madeira . . . 127

9.1 Introdu¸c˜ao . . . 127

9.2 Experiˆencias e Dados . . . 127

9.3 Modela¸cão da Evolu¸cão Temporal das Concentra¸cões de Cu, Cr e As nos Electrólitos . . . 130

9.3.1 An´alise Regressional . . . 133

(14)

10. Conclus˜oes e Trabalho Futuro . . . 143

Apˆendice 153

A. Tabelas Anexas ao Capitulo 7 . . . 155

B. Tabelas Anexas ao Capitulo 8 . . . 159

(15)

2.1 Tabela de contingˆencia com 2 dimens˜oes . . . 41

7.1 Classifica¸c˜ao das classes de seca segundo o SPI . . . 102

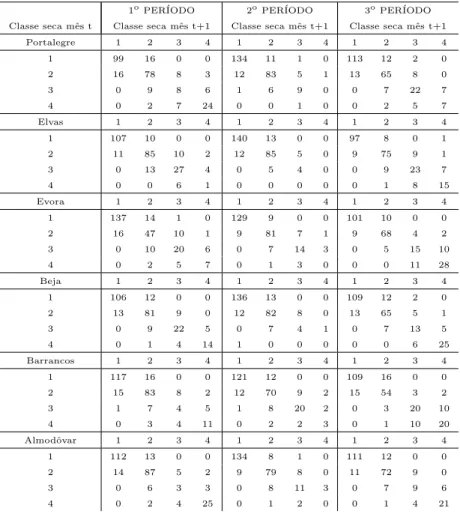
7.2 Tabelas de contingência com duas dimensões: frequências observadas para Portalegre, Elvas, Évora, Beja, Barrancos e Almodôvar . . . 103

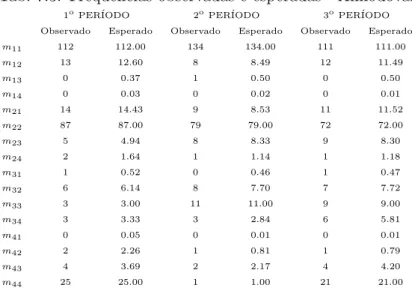
7.3 Frequˆencias observadas e esperadas - Almodˆovar . . . 106

7.4 Resultado das compara¸cões múltiplas de Scheffé para Almodôvar . . . 111

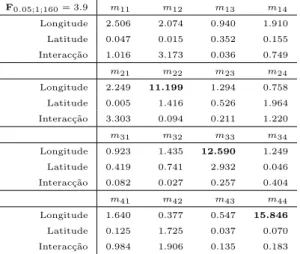
7.5 Valores da estat´ıstica_F para Portalegre, Elvas, ´Evora, Beja, Barran-cos e Almodˆovar . . . 112

8.1 Defini¸c˜ao das zonas 1, 2, 3 e 4 . . . 116

8.2 Valores das estat´ısticas_F(h) para as diferentes frequências esperadas do número de transi¸cões entre classes de seca . . . 124

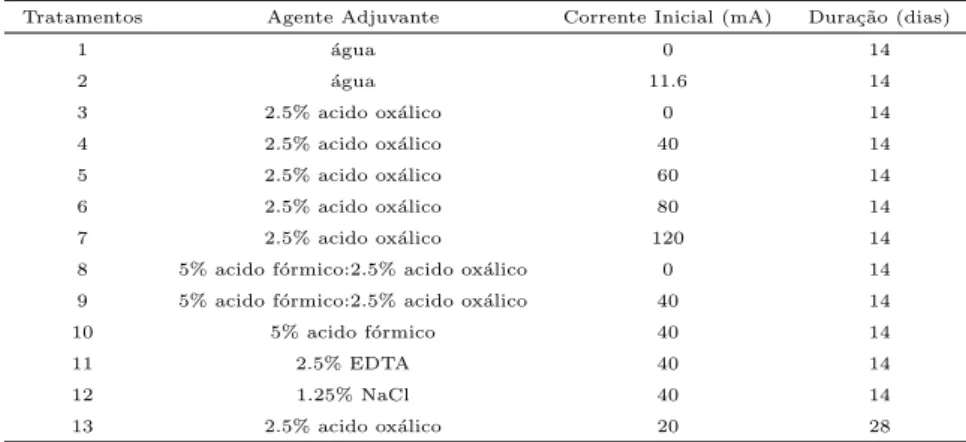
9.1 Tratamentos (condi¸c˜oes experimentais) . . . 129

9.2 Estimadores dos coeficientes das regressões para o Cobre, Crómio e Arsénio . . . 133

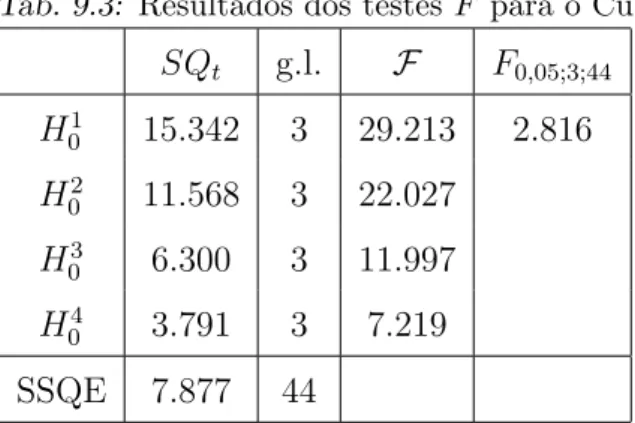
9.3 Resultados dos testes F para o Cu . . . 136

9.4 Resultados do m´etodo de Scheff´e para o Cu . . . 137

9.5 Resultados dos testes F para o Cr . . . 138

9.6 Resultados do m´etodo de Scheff´e para o Cr . . . 138

(16)

9.8 Resultados do m´etodo de Scheff´e para o As . . . 140

9.9 Resultados do m´etodo de Boferroni para o As . . . 140

A.1 Valores para os estimadores dos parˆametros dos modelos de

quasi-associa¸cão ajustados às tabelas de contingência e respectivos desvios

residuais das 6 esta¸c˜oes. . . 156

A.2 Resultado das compara¸cões múltiplas de Scheffé para Portalegre,

El-vas, ´Evora . . . 157

A.3 Resultado das compara¸cões múltiplas de Scheffé para Beja, Barrancos

e Almodˆovar . . . 158

B.1 Tabelas de contingˆencia para zona 1 e 2 . . . 160

B.2 Tabelas de contingˆencia para zona 3 e 4 . . . 161

B.3 Estimadores dos parˆametros dos modelos de quasi-associa¸c˜ao

ajusta-dos `as tabelas de contingˆencia e respectivos desvios residuais das 40

esta¸c˜oes. . . 162

(17)

As combina¸c˜oes de n´ıveis dos factores que intervˆem num modelo correspondem aos

tratamentos. Uma fam´ılia de modelos ´e estruturada quando os respectivos modelos

correspondem aos tratamentos doutro modelo. Diz-se que este ´ultimo ´e o modelo

base para o destingir dos modelos constituintes da fam´ılia estruturada, modelos esses

designados de modelos elementares.

No que diz respeito à teoria desenvolvida nesta disserta¸cão irá considerar-se o

caso em que:

1. O modelo base ´e de efeitos fixos com cruzamento-encaixe completo e

equili-brado de 2 ou mais factores e est´a associado a uma ´algebra de Jordan

comu-tativa _A, e

2. Os modelos elementares podem corresponder a regress˜oes lineares nas mesmas

vari´aveis ou a modelos log-lineares ajustados a tabelas de contingˆencia.

As fam´ılias estruturadas de modelos correspondem a uma formaliza¸c˜ao dos modelos

regressionais m´ultiplos introduzidos em Mexia (1987). Desde ent˜ao, alguns

desen-volvimentos particulares e aplica¸c˜oes tˆem sido efectuados, nomeadamente na tese de

Moreira (2004) onde foram contempladas as situa¸c˜oes de multicolinariedade e

hete-rocedasticidade dos modelos de regress˜ao m´ultipla para um modelo base de efeitos

fixos com 1 factor e correspondente aplica¸cão à remo¸cão electrodial´ıtica de metais

(18)

dos delineamentos regressionais m´ultiplos quando o delineamento base ´e de

quadra-dos latinos, blocos casualizaquadra-dos e planos completos, respectivamente. Tamb´em foi

extendida a teoria delineamentos regressionais ao caso em que o modelo base ´e um

plano factorial de base 2 em Domingues (1997) e factorial de base prima em Oliveira

(2005).

No tratamento de fam´ılias estruturadas de modelos tender´a a seguir-se uma

es-tratégia que agora irá procurar pôr-se em evidência. Assim, numa primeira fase,

come¸car-se-á por condensar a informa¸cão contida nos vectores de observa¸cões

cor-respondentes aos modelos elementares nas respectivas estat´ısticas suficientes e numa

segunda fase aplicar-se-ao os algoritmos desenvolvidos para o modelo base aos

re-sultados obtidos na primeira fase.

Em primeiro lugar, admite-se que os modelos elementares s˜ao indexados por

i = 1, ..., c, têm vectores de observa¸cão yi e vectores de parâmetros relevantes φi, com co número de tratamentos do modelo base.

Concretize-se para o caso dos modelos regressionais m´ultiplos. Neste caso, φ_i

será composto pelo vector dos coeficientes da regressãoβ_ie pela variânciaσ2

i. Muitas vezes admite-se a homocedasticidade, i.e., σ2

i = σ2, i = 1, ..., c, ou seja a variˆancia do erro n˜ao varia de modelo elementar para modelo elementar. Quando se tem

yi ∼N Xˇiβi, σ2Ini

onde Xˇi ´e a matriz do modelo regressional do tipo ni×k, as estat´ısticas suficientes ser˜ao

˜

β_i = XˇT_i Xˇi + _ˇ

XT_i yi, i= 1, ..., c e

SQEi =yTi yi −yTi Xˇiβ˜i, i= 1, ..., c

(19)

caso regular, para o qual se admite Xˇi =Xˇ, i= 1, ..., c e sup˜oe-se que Xˇ ´e do tipo

n_×(k+ 1) com vectores coluna linearmente independentes. Tem-se ent˜ao,

˜

β_i = XˇTXˇ−1XTyi ∼N βi, σ2(XˇTXˇ)−1

independente de

SQEi =yiTyi−yTi Xˇβ˜i ∼σ2χ2n−k−1. Os pares β˜_i, SQEi

, i = 1, ..., c conterão toda a informa¸cão transportada pelos vectores das observa¸cões.

Nos modelos regressionais m´ultiplos est´a-se interessado em coeficientes

individu-ais da regressão, ou nas suas combina¸cões lineares. Sendoao vector dos coeficientes duma combina¸cão linear, faz-se

ˇ

yi =aTβ˜i e

SSQE = c X

i=1

SQEi ∼σ2χ2g′

comg′ ₌_c₍_n₋_k₋_{1). Al´em disso vem}_E_(ˇ_y

i) = aTβi = ˇµi eV(ˇyi) =σ2aT(XˇTXˇ)−1a. Ordenem-se os tratamentos do modelo base mediante os ´ındices i =i(j) = 1, ..., c. Seja ˇyo vector cujas componentes são os valores ˇyi reordenados pelos ´ındicesi. Este vector será normal e irá constituir para o modelo base, o vector de observa¸cões para

o qual vem

E(ˇyi) = ˇµ

com ˇµ o vector cujas componentes s˜ao as combina¸c˜oes lineares ˇµi, com ´ındices

i= 1, ..., c, dosβ_i. Aplicando o algoritmo correspondente ao modelo base a ˇy pode-se estudar a influˆencia dos factores do modelo bapode-se nos valores das combina¸c˜oes

(20)

No que diz respeito `a estrutura da disserta¸c˜ao que segue, come¸ca-se por

apresen-tar resultados preliminares de forma a ter-se uma disserta¸c˜ao auto-suficiente. Estes

resultados ser˜ao de natureza alg´ebrica e de natureza estat´ıstica. Os resultados de

natureza algébrica referir-se-ão principalmente às álgebras de Jordan comutativas e

opera¸cões binárias sobre álgebras de Jordan. Estas álgebras são espa¸cos vectoriais

constitu´ıdos por matrizes sim´etricas que comutam e que cont´em os quadrados das

respectivas matrizes sim´etricas. As mesmas s˜ao utilizadas para estudar modelos

normais ortogonais [5], [7] e [2].

Os resultados mais importantes de natureza estat´ıstica referir-se-˜ao a estat´ısticas

suficientes e completas, estimadores UMVUE, testes de hip´oteses, vectores normais

e ao tratamento das regress˜oes lineares e modelos log-lineares.

Segue-se o tratamento de modelos ortogonais associados a ´algebras de Jordan

comutativas, come¸cando pelo caso usual

y= w X

j=1

X_jα_j+e

com os α_j, j = 1, ..., m vectores fixos, os α_j, j =m+ 1, ..., w e e vectores normais independentes com valores m´edios nulos e matrizes de covariˆancia σ2

jIcj, j = m+

1, ..., weσ2_I

nrespectivamente. Como adiante ser´a visto, admitida a normalidade do modelo, consegue-se obter estat´ısticas suficientes e completas que permitem obter

estimadores UMVUE podendo-se, em seguida, estudar-se a inferˆencia para os para

modelos de efeitos fixos. No seguimento constro˜em-se os modelos para o

cruzamento-encaixe de factores.

Com vista a conjugar a teoria dos modelos regressionais m´ultiplos com os

mo-delos ortogonais associados a ´algebras de Jordan comutativas, deparou-se com a

(21)

do caso n˜ao equilibrado, relativo aos modelos regressionais m´ultiplos, com modelo

base de efeitos fixos, caso esse em que as matrizes Xˇj poder˜ao n˜ao ser iguais para todos os tratamentos.

Para pôr em evidência a versatilidade e potência das técnicas desenvolvidas

apresentam-se aplica¸c˜oes a duas situa¸c˜oes bem distintas:

• An´alise de transi¸c˜oes entre classes de seca na hidrologia, e

• Experiências de remo¸cão electrodial´ıtica de metais pesados na remedia¸cão am-biental.

Na primeira e segunda aplica¸c˜oes os modelos elementares s˜ao log-lineares e na

(22)

(23)

2.1 Matrizes Ortogonais Estandardizadas, Diagonalizadoras

Ortogonais e Matrizes Uniformizadoras

Dado um n´umero inteiro s considerem-se as matrizes ortogonais

Ps =     

1 √

s1 sT

...

Ts     

em queTsé uma sub-matriz dePsconstitu´ıda pelas linhas dePsmenos a primeira. As linhas de Ts são vectores de contrastes mutuamente ortogonais de norma um. Vectores de contrastes são vectores cujas componentes são os coeficientes duma

combina¸cão linear sendo a soma das componentes desse vector nula. As matrizesPs assim definidas são chamadas ortogonais estandardizadas. Estas matrizes são muito utilizadas para analisar a açcão de factores com n´ıveis quantitativos [18].

Sendo A uma matriz sim´etrica de ordem k, existem matrizes ortogonais P de ordemk tais que

PAPT =D(r1, r2, ..., rk)

(24)

serão vectores próprios ortonormados de A associados aos valores próprios com o mesmo ´ındice [35].

Se A for definida positiva ter-se-´a rj >0, j = 1, ..., k, estando definida a matriz G0 =D(r−11/2, r−

1/2 2 , ..., r−

1/2 k )P que é solu¸cão da equa¸cão matricial

MAMT =Ik.

As solu¸cões desta equa¸cão serão as matrizesuniformizadoras de A, representando-se a respectiva familia por _U(A). Em particular G0 será a uniformizadora directa deA.

Mostra-se que, ver [14],

• G_{∈ U}(A)⇐⇒A−1 ₌_GT_G

• seG_{∈ U}(A) com M regular tem-se GM−1 _{∈ U}₍_MAMT_);

• seG_{∈ U}(A), G′ _{∈ U}₍_A_{) se e s´o se} _G′_G−1 _{for uma matriz ortogonal.} Assim, G_{∈ U}(A) se e s´o se G=PG0, com P ortogonal.

Tendo as matrizes sim´etricas que comutam especial interesse nesta disserta¸c˜ao,

apresenta-se o seguinte resultado

Proposi¸cão 2.1.1. SejamA1, ...,Am matrizes k×k simétricas. Então existe uma matriz ortogonal P tal que para cada i, PT_A

iP = Di é uma matriz diagonal cu-jos elementos principais são os valores próprios de Ai se e só se AiAj = AjAi para todos os pares (i, j), i, j = 1, ..., m, isto é, se e só se as matrizes A₁, ...,A_m comutarem.

(25)

2.2 Sub-Espa¸cos e ´

Algegras

Sendo_Vum sub-espa¸co vectorial próprio do espa¸co_{W ⊆}Rn_{, o conjunto dos vectores} de W ortogonais a todos os vectores de V constituem um sub-espa¸co denominado complemento ortogonal de _V relativamente a _W. Sendo _V⊥_/_W _{o complemento} ortogonal deV relativamente a W, todo o vector de W será a soma dum vector de V com um vector de _V⊥_/_W_{, sendo} _W _{a soma directa ortogonal de} _V _com _V⊥_/_W_, visto essa decomposi¸cão ser única. QuandoW =Rk_pôr-se-á_V⊥_/_W ₌_V⊥_{, tendo-se} (_V⊥₎⊥ ₌_V_.

Recorde-se que um sub-espa¸co W ⊆ Rn _{é a soma directa dos sub-espa¸cos} _V1 e _V2 se todo o vector v _{∈ W} tiver uma decomposi¸cão única v = v₁ +v₂ com vj ∈ Vj, j = 1,2. Se todo o vector de V1 for ortogonal a todo o vector de V2, então V1 e _V2 serão sub-espa¸cos ortogonais cuja soma directa ortogonal será _W. v_j será a projeçcão ortogonal dev sobre Vj, j = 1,2.

Segundo Seber(1980), dada a matrizAdo tipon_×k, o seusub-espa¸co imagem ser´a

R(A) =_{v:v=Au_} enquanto que o seusub-espa¸co nulidade ser´a

N(A) = _{u:Au=0_} tendo-se

R(AT) =N(A)⊥_.

Recorde-se agora também a defini¸cão de álgebra. Uma álgebra _A é um espa¸co linear equipado com uma opera¸cão binária_∗, usualmente chamada deproduto, para o qual as propriedades seguintes se verificam para todos osα_∈R e a,b,c_{∈ A}:

(26)

• (a+b)∗c=a_∗c+b_∗c; • α(a_∗b) = (αa)∗b=a_∗(αb).

Além do mais, uma álgebra _A éassociativase e só se, para todos os a,b,c_{∈ A}, (a_∗b)_∗c=a_∗(b_∗c)

e ´ecomutativa se e s´o se, para todos os a,b_{∈ A}, a_∗b =b_∗a.

Sublinhe-se que as propriedades associativa e comutativa não são necessárias para

que um espa¸co linear seja uma ´algebra.

2.3 Matrizes Inversas Generalizadas de Moore-Penrose

Qualquer que seja a matriz A existe uma e uma s´o matriz A+ _{tal que, ver [30],} 1)AA+A=A

2)A+AA+=A+ 3) AA+T =AA+ 4) A+AT =A+A

.

A matriz A+ _{denomina-se a} _{inversa de Moore-Penrose} _de _A_{. Se} _A _{for regular} A+₌_A−1_{. Por outro lado, sendo} _A _sim´etrica _k_×_k _com _Car₍_A_{) =} _{l < k}_{, pode-se} sempre ordenar os vectores linha de uma matrizP diagonalizadora ortogonal de A de forma a ter-se

PAPT =D(r1, r2, ..., rl,0, ...,0) com r1, r2, ..., rl os valores pr´oprios n˜ao nulos de A, tendo-se

(27)

e

A+=PTD(r−1

1 , ..., r−l 1,0, ...,0)P.

2.4 Matrizes de Projec¸c˜

ao Ortogonal

Dado_W um espa¸co vectorial soma directa ortogonal dos sub-espa¸cos_V1eV2, definiu-se atrás a projeçcão ortogonalv_V_j de v_{∈ W} sobre_Vj, j = 1,2. Ter-se-á ainda

v_V_j =Q(_Vj)v, j = 1,2

com Q(_Vj) a matriz de projec¸c˜ao ortogonal sobre _Vj, j = 1,2. Verifica-se facilmente que

Q(V⊥_{) =} _I

n−Q(V) vindo

v_V⊥ =v−v_V = (I−Q(V))v.

Recorde-se ainda que Q é matriz de projeçcão ortogonal se e só se for idempotente e simétrica.

De seguida ir˜ao ser recordados alguns resultados bem conhecidos sobre matrizes

de projec¸c˜ao ortogonal [14].

Proposi¸c˜ao 2.4.1. Dada a matriz X do tipo n×k e tomando-se Ω = R(X)

ℵ=R(XT) as matrizes de projeçcão ortogonal sobre Ω e _ℵ serão

Q(Ω) =X(XTX)+XT Q(_ℵ) = (XTX)+(XTX)

(28)

Proposi¸c˜ao 2.4.2. Para v_∈Ω tem-se   

Q(Ω)v=v Q(Ω⊥₎_v₌₀.

Proposi¸c˜ao 2.4.3. Dado um vector v, o vector u _∈ Ω que minimiza _kv₋u_k2 ´e vΩ.

Proposi¸c˜ao 2.4.4. Fazendo v = (XT_X₎+_XT_z _com _z _{um vector arbitr´ario tem-se} z_Ω =Xv, ou seja z_Ω _∈R(X).

2.5 Produto de Kronecker entre Matrizes

Dadas as matrizes A= [ai,j] do tipom×n eBdo tipop×q, o respectivoproduto de Kronecker´e dado pela matriz por blocos de ordem mp_×nq

A_⊗B =        

a11B a12B · · · a1nB

a21B a22B · · · a2nB · · · ·

am1B am2B · · · amnB        

. (2.1)

Verifica-se facilmente que, estando definidos os produtos usuais A₁A₂ e B₁B₂, se tem

(A1⊗B1)(A2⊗B2) = (A1A2)⊗(B1B2) (2.2)

(A_⊗B)T =AT _⊗BT.

(29)

tem-se

1_u_⊗1_v =1_uv I_u_⊗I_v =I_uv J_u_⊗J_v =J_uv

vendo-se ainda que o produto⊗de matrizes ortogonais, ortogonais estandardizadas, sim´etricas, idempotentes d´a respectivamente matrizes ortogonais, ortogonais

estan-dardizadas, simétricas, idempotentes. Daqui resulta que o produto ⊗ de matrizes de projeçcão ortogonal dá matrizes de projeçcão ortogonal.

SendoD(γ1) e D(γ2) matrizes diagonais cujos elementos principais s˜ao as

com-ponentes do vectores γ1 e γ2 respectivamente, tem-se

D(γ₁)⊗D(γ₂) =D(γ₁_⊗γ₂). (2.3) Dadas as matrizes sim´etricas M₁ e M₂, existem matrizes ortogonais P₁ e P₂ e matrizes diagonaisD(γ1) e D(γ2) tais que

PjMjPTj =D(γj), j = 1,2.

Os elementos principais deD(γ_j), j = 1,2 são os valores próprios deM_j correspondendo-lhes, como vectores próprios, os vectores linha dePj, j = 1,2 (seçcão 2.1). Ter-se-á então, atendendo a (2.2) e a (2.3):

(P1⊗P2) (M1⊗M2) (P1⊗P2)T = P1M1PT1

⊗ P2M2PT2

=D(γ₁_⊗γ₂) (2.4)

pelo que os valores próprios de M1 ⊗M2 serão os produtos dos valores próprios de M1 e M2 e os vectores próprios são os vectores linha de P1 ⊗ P2. Como a caracter´ıstica de uma matriz simétrica é o número dos seus valores próprios não

nulos, vˆe-se que

(30)

Sendo o determinante deMj, j = 1,2 o produto dos seus valores pr´oprios, o mesmo acontecendo para o determinante de M1⊗M2, ter-se-´a

Det(M1 ⊗M2) =Det(M1)Det(M2). (2.6) Por outro lado, ver [38], para qualquer matriz Vj tem-se

Car(Vj) =Car(VjVTj), j = 1,2 e como

(V1⊗V2) (V1⊗V2)T = V1VT1

⊗ V2VT2

ter-se-´a

Car(V1⊗V2) = 2 Y

j=1

Car VjVTj

= 2 Y

j=1

Car(Vj). (2.7) ´

E ainda f´acil de verificar que, ver [38],

m X

i=1

aiVi !

⊗ n X

j=1

bjUj !

= m X

i=1 n X

j=1

aibj(Vi ⊗Uj) (2.8)

e utilizando (2.2), tem-se

(V1⊗V2)+ =V+1 ⊗V+2. (2.9) Em particular se V1 e V2 forem regulares tem-se tamb´em

(V1⊗V2)−1 =V1−1⊗V−21. (2.10)

2.6 Vector M´

edio, Matriz de Covariˆ

ancia e Matriz de Covariˆ

ancia

Cruzada

Um vector aleatório será um vector cujas componentes são variáveis aleatórias

en-quanto que uma matriz aleatória será uma matriz cujos elementos são variáveis

(31)

Dado um vector aleat´orio X=      X1 ... Xn     

ovector médio de X terá como componentes os valores médios das componentes deX, assim

E(X) =     

E(X1) ...

E(Xn)     

quando estes valores m´edios est˜ao definidos. Analogamente os elementos da matriz

média de uma matriz aleatória serão os valores médios, supostos definidos, dos

elementos da matriz aleatória. Em particular a matriz da covariância do vector aleatório X será

COV(X) = Eh(X₋E(X)) (X₋E(X))Ti =     

V (X1) . . . COV (X1, Xn)

... . .. ...

COV(Xn, X1) · · · V (Xn)

    

supondo-se as variâncias V(Xj), j = 1, ..., n e as covariâncias COV(Xj, Xi), j, i = 1, ...n, j 6=i todas definidas. Uma matriz de covariância é sempre simétrica.

Dado o par (X;Y) de vectores aleatórios de ordem n e m respectivamente, a respectiva matriz de covariância cruzada será

COV(X;Y) = Eh(X₋E(X)) (Y₋E(Y))Ti =     

COV (X1, Y1) . . . COV (X1, Ym)

... . .. ...

COV(Xn, Y1) · · · COV (Xn, Ym)     .

(32)

Utilizando a linearidade do operador E mostra-se facilmente que

• E(AX+a) =AE(X) +a

• COV(AX+a) = ACOV(X)AT

• COV(AX+a;BX+b) =ACOV(X)BT

• COV(AX+a;BY+b) =ACOV(X;Y)BT

onde AeB s˜ao matrizes do tipor×n es×m, respectivamente eae bvectores de ordem r e s respectivamente. Al´em disso, como

X+Y = [I:I]  X

Y  

e COV(X,Y) é a matriz nula quando X e Y são independentes, pode-se mostrar então que

COV(X+Y) = COV(X) +COV(Y).

2.7 Estat´ısticas Suficientes, Completas e Estimadores UMVUE

Represente-se por_En o espa¸co amostral constitu´ıdo por todas as amostras poss´ıveis de dimensão n. Seja x uma amostra de dimensão n que será vista como uma realiza¸cão vector aleatórioX, tendo-se Pr(X _{∈ E}n) = 1. As probabilidade associadas a X podem ser determinadas pela respectiva distribui¸cão F(x_|θ) = Pr(X _≤ x_|θ), com θ um parâmetro a variar no espa¸co paramétrico Ω. A fun¸cão densidade de

(33)

Dada uma parti¸c˜ao de En em conjuntos Ci, disjuntos dois a dois, atendendo ao teorema da probabilidade total, tem-se

F(x_|θ) =X i

Pr(X_{∈ C}i|θ) Pr(X6x|X ∈ Ci,θ) = X

i

Pr(X_{∈ C}i|θ)F(x|Ci,θ) (2.11)

com

F(x_|Ci,θ) = Pr(X6x_|X_{∈ Ci}, θ).

Uma parti¸cão diz-sesuficientequando as distribui¸cões condicionais não dependem deθ, tendo-se

F(x_|θ) = X i

Pr(X_{∈ Ci|}θ)F(x_|Ci). (2.12)

Uma estat´ıstica T(x) será uma qualquer fun¸cão escalar ou vectorial definida no espa¸co amostral. As imagens inversas dadas porT(x) constituem uma parti¸cão de_En. Se a parti¸cão induzida por uma estat´ıstica for suficiente, então a estat´ıstica será suficiente. Por outras palavras, T(x) ser suficiente significa que T(x) contem toda a informa¸cão acerca de θ que está contida na amostra, podendo proporcionar

uma redu¸c˜ao de dados sem perda de informa¸c˜ao.

Um importante critério de suficiência é dado pela

Proposi¸c˜ao 2.7.1. Teorema da Factoriza¸c˜ao

A estat´ıstica T(x) é suficiente se e só se existirem fun¸cões não negativas g e h tal que

f(x_|θ) =g(T(x)_|θ)h(x) onde h(x) n˜ao depende de θ.

A seguir apresenta-se a demonstra¸c˜ao para o caso discreto, no entanto a tese

(34)

Demonstra¸cão. Admita-se que se verifica a factoriza¸cão. QuandoT(x) =t, ter-se-á Pr(T(x) = t_|θ) = X

x∈T−1₍_t₎

f(x_|θ) = X

x∈T−1₍_t₎

g(T(x)_|θ)h(x) =g(t_|θ) X

x∈T−1₍_t₎

h(x)

vindo para x_∈T−1₍_t₎

Pr(X=x_|T=t,θ) = P r[(X=x)∩(T=t)|θ] Pr(T=t_|θ) =

Pr(X=x_|θ) Pr(T=t_|θ) = g(t|θ)h(x)

g(t_|θ) P

x′_∈_T−1₍_t′₎

h(x′₎ =

h(x) P

x′_∈_T−1₍_t′₎

h(x′₎

o que mostra que as distribui¸c˜oes condicionais n˜ao dependem de θ, pelo que a

estat´ıstica ser´a suficiente.

Inversamente, por um lado igualmente se tem

Pr(X=x_|T=t,θ) = Pr(X=x|θ) Pr(T=t_|θ) =

f(x_|θ) Pr(T=t_|θ) e por outro

Pr(X=x_|T=t,θ) =h(x)

onde h(x) n˜ao depende de θ por T(x) ser suficiente. Basta pois fazer g(t_|θ) = Pr(T=t_|θ) para concluir que se tem a factoriza¸c˜ao.

Por outro lado, se para uma qualquer fun¸c˜ao g deT se tiver

E(g(T)_|θ) = 0, _∀θ _∈Ω =_⇒ Pr (g(T) = 0_|θ) = 1, _∀θ _∈Ω,

T(x) ser´a uma estat´ıstica completa. Tem-se ainda

Proposi¸cão 2.7.2. Se X tem distribui¸cão pertencente à familia exponencial de dimensão s ou seja se

f(x_|θ) = b(θ)h(x) exp s X

i=1

(35)

ondeb e li são fun¸cões do parâmetroθ e Ti são estat´ısticas e além disso se um pro-duto cartesiano de intervalos não degenerados estiver contido no espa¸co paramétrico Ω, a estat´ıstica T(x) = [T1(x)...Ts(x)] será suficiente e completa.

Demonstra¸c˜ao. Ver [13], [12] e [38].

Um estimador dum parâmetro será uma estat´ıstica cujos valores são “apro-xima¸cões” aos verdadeiros valores do parâmetro. Entre as propriedades

convenien-tes que um estimador pode ter está serUMVUE(estimador centrado de variância uniformemente m´ınima). Diz-se que ˜g(X) é UMVUEdeg(θ) se for centrado, i.e.

E(˜g(X)) =g(θ)

e se para todoθ se tem

V(˜g(X)_|θ)_≤V(ˆg(X)_|θ) onde ˆg(X) ´e qualquer outro estimador centrado deg(θ).

Como se irá ver, as estat´ısticas suficientes e completas são úteis para se obter

UMVUE’s. Com efeito tem-se o

Proposi¸c˜ao 2.7.3. Teorema de Rao-Blackwell

Seja g uma fun¸c˜ao convexa e gˆ um estimador centrado de g(θ). Dada a estat´ıstica suficiente T(x)

• g˜(t) = E(ˆg(X)_|T(x) = t) é fun¸cão da estat´ıstica suficienteT(x) =t mas não é fun¸cão de θ;

• g˜(T(x))´e um estimador centrado de g(θ); • V(˜g|θ)≤V(ˆg|θ) para todo o θ.

(36)

e o

Proposi¸c˜ao 2.7.4. Teorema de Blackwell-Lehmann-Scheff´e

Se T for uma estat´ıstica suficiente e completa e existir um estimador centrado ˆg

para g(θ), ˜g(t) =E(ˆg(X)_|T(x) = t) ser´a estimador UMVUE de g(θ).

Demonstra¸cão. Atendendo ao teorema de Rao-Blackwell, sabe-se que ˜g é estimador centrado de g e a variância deste nunca excede a variância de ˆg. Supondo agora que existia um outro estimador centrado ˇg parag, devido mais uma vez ao teorema Rao-Blackwell, sabe-se que ˇ˜g(t) = E(ˇg(X)_|T =t) é fun¸cão de t mas não de g(θ), sendo estimador centrado de g e V(ˇ˜g|θ)≤V(ˇg|θ).

Como Té estat´ıstica suficiente e completa e g(t) se ˜g(t) são fun¸cões de tcom o mesmo valor médio, qualquer que seja θ, ter-se-á Pr(˜g(T) = ˇg(T)|θ) = 1, qualquer que sejaθ, o que estabelece a tese.

2.8 Testes de Hip´

oteses

Através de um teste de hipóteses, pretende-se, de um modo geral, tomar uma decisão

ou fazer uma escolha de entre duas hip´oteses alternativas, baseada na informa¸c˜ao

conhecida. Nesta seçcão apenas serão abordados os testes de hipóteses paramétricos,

para os quais a decisão é feita relativamente a um parâmetro desconhecido θ

per-tencente a um conjunto conhecido Θ em que

θ _∈Θ0∨θ ∈Θ1, com Θ0,Θ1 ⊂Θ e Θ0∩Θ1 =∅.

Portanto, a escolha ser´a feita de entre a hip´otese

H0 :θ ∈Θ0

designada de hip´otese nula a outra hip´otese poss´ıvel

(37)

designada de hip´otese alternativa.

Considere-se uma amostraX = [X1, ..., Xn]T de vari´aveis aleat´orias independen-tes e identicamente distribu´ıdas, pertencenindependen-tes a uma classe de densidades

F=_{fθ(.) :θ∈Θ}.

Os testes de hipóteses são regras criadas para tomar uma decisão e aos quais estão

associados um risco e uma perda.

Defina-se φ(x) a regra de decis˜ao, que tomar´a o valor 0 se a H0 for aceite e o valor 1 se esta for rejeitada em favor deH1.

Em qualquer processo de decis˜ao existem associados erros. Nos testes de hip´oteses

em que existe hip´otese nula e alternativa existem 2 tipos de erro:

1. Erro tipo I: Probabilidade de rejeitar H0 quandoH0 ´e verdadeira; 2. Erro tipo II: Probabilidade de aceitar H0 quando H1 ´e verdadeira.

Associado a um teste de hipóteses existe também uma região de aceita¸cão

R0 ={x:φ(x) = 0} e umaregi˜ao cr´ıtica

R1 ={x:φ(x) = 1}. O tamanho dum teste ´e dado pelo

sup θ∈Θ

Pr(X_∈R1)

o qual representa, de facto, o valor m´aximo que o erro tipo I pode assumir. Nos

testes de hip´oteses a ser utilizados tem-se

sup θ∈Θ

(38)

ondeqrepresenta on´ıvel de significˆanciaescolhido para um teste, que usualmente pode assumir os valores 0.1, 0.05 e 0.01. Ao inverso, pode ser obtido o mais pequeno

n´ıvel de significˆancia abaixo do qual a hip´otese nula seria rejeitada. A esse valor

chama-se “p-value”.

A potˆencia dum testepara algum θ _∈Θ1 ´e dada por

P ot= Pr(X_∈R1) e a fun¸c˜ao potˆencia de um teste φ por

P otφ(θ) = Pr(X ∈R1),θ∈Θ.

A fun¸cão potência dum teste dá, em fun¸cão do parâmetro, a probabilidade de se rejeitar a hipótese nula, ou por outras palavras descreve a eficiência dum teste a

detectar o afastamento dos dados da hip´otese nula.

Nesse sentido, pretende-se pois maximizar a fun¸c˜ao potˆencia. Para tal, tomando

φ(x) =   

0, x_∈R0 1, x_∈R2 h´a que maximizar

P otφ(θ) = E(φ(x)),∀θ ∈Θ1 sujeito `a condi¸c˜ao

E(φ(x))≤q,∀θ_∈Θ0.

Quando Θ0 e Θ1 têm apenas um elemento, a solu¸cão é dada pela

Proposi¸c˜ao 2.8.1. (Lema Fundamental de Neyman-Pearson). Seja Θ0 = θ0 e Θ1 =θ1, ent˜ao existe uma constante c tal que

1. φ(x) =    

  

0, fθ1(x)

fθ0(x)

< c

1, fθ1(x)

fθ0(x)

> c

(39)

2. θ =θ₀ _⇒E(φ(X)) =q;

eφ ´e o mais potente teste paraH0 :θ =θ0 vs. H1 :θ =θ1 ao n´ıvel de significˆancia

q. Além disso, se φ_∗ for um teste mais potente então se satisfaz 1. também satisfaz 2. com probabilidade 1.

Demonstra¸c˜ao. Ver [13].

Nos testes de hipóteses é imposs´ıvel escolher a melhor regra de decisão. A solu¸cão

para este problema poder´a ser restringir a classe de regras de decis˜ao de modo que

estas retenham propriedades desej´aveis. Uma dessas propriedades ´e serem testes

n˜ao distorcidos. Um teste φ tal que

  

P otφ(θ)≤q,∀θ ∈Θ0

P otφ(θ)≥q,∀θ ∈Θ1

diz-senão distorcido, isto é, a potência do teste para θ _∈Θ1 é sempre maior que o erro tipo I. Quando P otφ(θ0) = q, a probabilidade de rejeitar H0 quando H1 é verdadeira é maior que a probabilidade de rejeitar H0 quando H0 é verdadeira.

2.9 Vectores Normais e Testes F

DadoY um vector aleatório de ordemn a respectiva fun¸cão geradora de momentos será

ϕY(u) =E

euT_Y

sendo f´acil de se verificar que

ϕAY+b(v) =eb

T_v

(40)

Sendo _  

E(Y) =µ

COV(Y) = M se a fun¸c˜ao geradora de momentos de Y for

ϕY(u) = eµ

T_u₊1

2uTMu (2.13)

o vector aleat´orioY, ver [14], ser´a normal escrevendo-se Y _∼N(µ,M).

Utilizando a expressão (2.13) é fácil de mostrar que

AY+a_∼N(Aµ+a,AMAT).

Dado agora Y _∼ N(µ, σ2_I

n), kYk2 será, ver [14], o produto por σ2 dum qui-quadrado com n graus de liberdade e parâmetro de não centralidade

δ= 1

σ2 kµk 2

escrevendo-se

kY_k2 _∼σ2χ2_n,δ.

Seja agora S ∼σ2_χ2

m independente de Y F = kYk

2

n S/m

terá, ver [14], distribui¸cão _F com n e m graus de liberdade e parâmetro de não centralidade δ, escrevendo-se

F ∼Fn,m,δ. Em particular se µ=0, δ = 0, vindo

(41)

e portantoF ter´a distribui¸c˜ao F central, escrevendo-se

F ∼Fn,m.

Mais geralmente, ver [14], seY _∼N(µ, σ2_M_{) com} _Car₍_M_{) =} _l_≤_n _tem-se (Y₋b)TM+(Y₋b)_∼σ2χ2_l,δ

com

δ = (µ−b)

T_M+₍_µ₋_b₎

σ2 eb um vector qualquer, e se SQ_∼σ2_χ2

m for independente deY, ter-se-´a que F = m

l

(Y₋b)T_M+₍_Y₋_b₎

SQ ∼Fl,m,δ.

F será a estat´ıstica de um teste de hipóteses F com l e m graus de liberdade para testar a hipótese

H0 :µ=b.

Em particular se b=µ ou seja se H0 se verificar, δ= 0, vindo (Y₋µ)TM+(Y₋µ)_∼σ2χ2_l

logo

F′ ₌ m

l

(Y₋µ)T_M+₍_Y₋_µ₎

SQ ∼Fl,m

ou seja _F′ _{tem distribui¸c˜ao} _F _{central com} _l _e _m _{graus de liberdade.} Sendo F1−q,l,m o quantil para a probabilidade 1−q deFl,m tem-se

Pr [_F′ _≤_F

1−q,l,m] = 1−q ou seja, como δ = 0 tem, neste caso, P ot = Pr [F′ _{> F}

1−q,l,m,] = q donde o teste será não distorcido. Como consequência, as desigualdades

(µ₋Y)TM+(µ₋Y)≤lF1−q,l,m

(42)

definem elipsóides de confian¸ca n´ıvel 1−q paraµ, isto é, a probabilidade deµestar coberto pelo elipsóide anterior é 1₋q, donde o teste F de n´ıvel q não rejeita a H0 se e só se b pertencer ao elipsóide de confian¸ca n´ıvel 1−q atrás definido. Diz-se, neste caso, que o teste goza de dualidade[15] e [17].

Quando Mé definida positiva, M+ ₌_M−1 _{também é definida positiva, vindo}

δ = (µ−b)

T_M−1₍_µ₋_b₎

σ2 ,

podendo reescrever-se a hip´otese nula como H0 :δ= 0, uma vez que

µ=b_⇐⇒δ = 0.

Neste caso, o teste ´e estritamente n˜ao distorcido [14].

2.10 Modelos de Regress˜

ao M´

ultipla

2.10.1 Introdu¸c˜ao

Quando se tem uma variável resposta y que depende de k variáveis independentes ou variáveis controladas x1, x2, ..., xk, a rela¸cão entre estas variáveis é caracterizada por um modelo matemático, chamado modelo regressional.

O modelo regressional pode ser linear

y=α0+α1x1+α2x2+...+αkxk+ǫ (2.14)

ou n˜ao linear, como por exemplo exponencial, logar´ıtmico, etc. A equa¸c˜ao (2.14)

representa um modelo regressional m´ultiplo linear, dado que se trata duma fun¸c˜ao

(43)

variáveis controladas xi, i 6= j são mantidas constantes e ǫ representa a variável aleatória erro do modelo, para o qual usualmente se assume ǫ_∼N(0, σ2_).

Considere-se o caso mais geral, para o qual se disp˜oe de n >(k+ 1) observa¸c˜oes

y1, y2, ..., yn para a vari´avel resposta y. A cada observa¸c˜ao yi corresponde um valor

xij, para a j-ésima variável controlada, j = 0, ..., k,i= 1, ..., n. O modelo regressio-nal multi-linear pode ser então escrito em termos de valores observados tomando-se

yi = k X

j=0

αjxij +ǫi, i= 1,2, ..., n; j = 0, ..., k (2.15)

onde os ǫ1, ..., ǫn são os erros aleatórios não correlacionados entre si. A equa¸cão (2.15) pode ser escrita na forma matricial

y=Xα+ǫ (2.16)

onde y=      y1 ... yn     

representa o vector das observa¸c˜oes,

α=      α0 ... αk     

´e o vector dos coeficientes da regress˜ao,

(44)

o vector dos erros aleat´orios e

X=        

1 x11 · · · x1k 1 x21 . . . x2k

... ... 1 xn1 · · · xnk

       

é a matriz do modelo do tipon_×(k+ 1), isto é, a matriz dos valores das variáveis controladas, havendo nesta matriz uma coluna por variável controlada.

As vari´aveis controladas poder˜ao estar relacionadas entre si como ,por exemplo,

numa regressão polinomial, onde estas são potências duma mesma variável base.

Caso exista dependência linear entre as variáveis controladas está-se perante uma

situa¸cão de multicolinariedade, em que Car(X) é inferior ao número de variáveis controladas. Considerando a situa¸cão mais geral admitir-se-á que p = Car(X) ≤

k+ 1.

Como já foi referido, é usual admitir-se que os erros aleatórios ǫi, i= 1, ..., n têm valor médio nulo e variância σ2_{, sendo também independentes entre si, donde}

COV(ǫ) = σ2In.

Contudo, dado que, na prática, existem situa¸cões de correla¸cão entre os erros, mais

uma vez considerar-se-´a o caso geral em que

COV(ǫ) =σ2C onde Cuma matriz conhecida e regular.

O modelo (2.15) representa um caso particular deste modelo.

Para o modelo em quest˜ao ter-se-´a, portanto, y normal com 

 

E(y) = Xα=µ

COV(y) =σ2C

(45)

Perante a ausˆencia de homocedasticidade no modelo, ou seja de igualdade e

independência de variâncias entre as variáveis aleatórias, há que realizar uma

trans-forma¸c˜ao em y, chamada redu¸c˜ao da heterocedasticidade, de forma a obter-se a homocedasticidade.

Com G_{∈ U}(C), tome-se

 



y′ ₌_Gy X′ ₌_GX

(2.17)

atendendo aos resultados sobre matrizes uniformizadoras, ver [14], obt´em-se 

 

E(y′_{) =}_X′_α

COV(y′_{) =} _GT_COV₍_y₎_G₌_σ2_GT_CG₌_σ2_I n passando a ter-se o modelo homoced´astico

y′ ₌_X′_α₊_ǫ′_. _(2.18)

2.10.2 Estima¸c˜ao dos Coeficientes da Regress˜ao

O método dos m´ınimos quadrados é o método mais usualmente utilizado para a

estima¸cão dos coeficientes da regressão. Este método consiste na obten¸cão de valores

para os coeficientesαj tais que a soma dos quadrados dos res´ıduos seja minimizada, ou seja, encontra-se o vectorαˆ estimador deα que minimiza

ky′₋_X′_α_k2_. _(2.19)

Para encontrar o vectorαˆ, irá ser utilizado um instrumento de álgebra matricial de grande importância na estat´ıstica, que é o de matriz de projeçcão ortogonal.

Tome-se _

 

(46)

e recorde-se que as matrizes de projeçcão ortogonal sobreℵ e Ω são, ver seçcão 2.4, 





Q(Ω) =X′₍_X′T_X′₎+_X′T Q(_ℵ) = (X′T_X′₎+₍_X′T_X′₎

(2.20)

Ora como o vector X′_α_ˆ _{que minimiza (2.19) ´e}_y′

Ω =Q(Ω)y′ (proposi¸cão 2.4.3), atendendo à primeira das expressões (2.20) vem

X′_α_ˆ ₌_X′₍_X′T_X′₎+_X′T_y′

donde

ˆ

α= (X′TX′)+X′Ty′. (2.21) Como yé normal, αˆ será também normal com

E(αˆ) = (X′TX′)+X′TE(y′) = (X′TX′)+X′TX′α=Q(ℵ)α=α_ℵ (2.22) pelo queαˆ não é necessariamente um estimador centrado deα. Contudo, os vectores estimáveis vão permitir ultrapassar a limita¸cão anterior [14].

Um vector λ = Aα diz-se estim´avel se existir um estimador linear centrado

λ∗ =By deλ.

Tem-se então Aα= E(λ∗) = E(By) = BX′_α _{para todo o} _α_{, logo} _A ₌_BX′ _e AT ₌_X′T_BT_{. Donde}_λ _{é estimável se e só se os vectores linha de}_A _{pertencerem a} ℵ.

Observe-se agora que, se c_{∈ ℵ}, tem-se E(cT_α_ˆ_{) =}_cT_α

ℵ=cTQ(ℵ)α= Q(ℵ)Tc T

α= (Q(_ℵ)c)T α=cT_α

uma vez que as matrizes de projeçcão ortogonal são simétricas e a projeçcão

(47)

Por fim, pelo conhecido Teorema de Gauss-Markov, ver [14], os estimadores da formaA ˆαsão BLUE (Estimadores Lineares Centrados Óptimos) deAαos quais têm variância m´ınima quando comparados com outros estimadores lineares centrados

deAα [15].

Atendendo `as propriedades das inversas generalizadas de Moore-Penrose tem-se

ainda

COV(αˆ) = (X′T_X′₎+_X′T_COV₍_y′₎_X′₍_X′T_X′₎+ _{= (}_X′T_X′₎+_X′T₍_σ2_I

n)X′(X′TX′)+

=σ2(X′T_X′₎+_X′T_X′₍_X′T_X′₎+₌_σ2₍_X′T_X′₎+

(2.23)

portanto, o modelo ajustado ter´a a forma

ˆ

y′ ₌_X′_α_ˆ ₌_y′

Ω. (2.24)

Uma vez ajustado o modelo ´e frequentemente necess´ario estimarσ2_{, para a qual} se tem o estimador centrado

ˆ

σ2 = SQE

n₋p (2.25)

em que

SQE =_ky′₋_y_ˆ′_k2

=_ky′₋_y′_Ωk2

representa a soma dos quadrados dos res´ıduos. Ora recorde-se que

y′₋_y′

Ω =y′Ω⊥ = (I_n−Q(Ω))y′ =Q(Ω⊥)y′

(sec¸c˜ao 2.4) pelo que

SQE =_ky′ Ω⊥k

2

=Q(Ω⊥₎_y′2 ₌_y′T_Q_(Ω⊥₎T_Q_(Ω⊥₎_y′ dadoQ(Ω⊥_{) ser idempotente e sim´etrica, logo}

SQE=y′T_Q_(Ω⊥₎_y′ ₌_y′T₍_I

(48)

vindo por fim

SQE=y′T_y′₋_y′T_X′_α_ˆ_. _(2.26) Um resultado importante é do Teorema de Fisher, ver [14], o qual estabelece que, quando yé normal,αˆ é independente de SQE e

SQE _∼σ2χ2_n₋_p.

Um outro resultado referente `as matrizes uniformizadoras de C estabelece que GT_G₌_C−1_{, ver [14], vindo}

                

X′T_X′ ₌_XT_GT_GX₌_XT_C−1_X X′T_y′ ₌_XT_GT_Gy₌_XT_C−1_y y′T_X′ ₌_yT_GT_GX₌_yT_C−1_X y′T_y′ ₌_yT_GT_Gy₌_yT_C−1_y obtendo-se para (2.21), (2.23) e (2.26) as express˜oes

ˆ

α= XTC−1_X+_XT_C−1_y _(2.27)

COV(αˆ) = σ2 XTC−1_X+ _(2.28)

SQE =yTC−1_y

−yTC−1_{X ˆ}_α _(2.29)

donde se conclui que, na realidade, estas express˜oes podem ser calculadas sem haver

necessidade de efectuar a transforma¸c˜ao (2.17), bastando para tal inverter a matriz

C.

De referir que, caso se tenha COV(y) = σ2_I

n e n˜ao haja multicolinariedade, tendo-seCar(X) = k+ 1,XT_X_{´e regular, logo (}_XT_X₎+ _{= (}_XT_X₎−1 _{vindo portanto}

ˆ

α= (XTX)−1XTy (2.30)

(49)

COV(αˆ) = σ2(XTX)−1 (2.32)

SQE =yTy₋yTX ˆα (2.33)

ˆ

σ2 = SQE

n−k−1. (2.34)

Uma medida estat´ıstica para o ajustamento do modelo regressional `as observa¸c˜oes

é dada pelo coeficiente de determina¸cão múltipla

R2 _{= 1}₋ SQE

SQT; 06R

2 ₆₁

em queSQT representa soma dos quadrados dos res´ıduos para a m´edia, dada por

SQT = n X

i=1 (y′

i −y¯′) 2

a qual ´e ainda dada por

SQT = n X

i=1

y′2

i −ny¯′2 =y′ T

y′ ₋_n_y_¯′2 _(2.35)

com

¯

y′ = n P i=1

y′2 i

n .

Este coeficiente mede a fraçcão da varia¸cão total entre observa¸cões da variável

de-pendente que é explicada pela regressão. Para atender ao número de variáveis

controladas pode substituir-seR2 _por

R2adj = 1−

SQE_/( n₋p)

SQT_/( n−1)

(2.36)

de forma a considerar-se menos bom um ajustamento conseguido aumentando muito

(50)

2.10.3 Testes de Hipóteses para Modelos de Regressão Múltipla

Testam-se hipóteses acerca dos parâmetros de modelos de regressão múltipla com o

objectivo de medir a sua significˆancia, ou seja a sua utilidade para o modelo.

Como base de partida para construir os testes admite-se que y_∼N(Xα, σ2_C_), passando a ter-se, ap´os redu¸c˜ao da heterocedasticidade, y′ _∼ _N₍_X′_α_{, σ}2_I

n) e ex-press˜oes para αˆ, COV(αˆ) e SQE independentes da uniformizadora de C.

As hip´oteses a serem testadas em geral s˜ao da forma

H0 :ψ=ψ0

onde ψ = Aα, com A uma matriz cujos vectores linha pertencem a _ℵ e ψ₀ um vector de R(A).

Dado que as componentes de ψ são estimáveis, ψˆ=A ˆα será um vector normal com

  

E(ψˆ) = E(A ˆα) =Aα=ψ

COV(ψˆ) =ACOV(αˆ)AT ₌_σ2_{A X}T_C−1_X+_AT

independente de SQE, uma vez que αˆ é independente de SQE, logo A ˆα também o é.

Com h=CarA XT_C−1_X+_AT_{, atendendo aos resultados apresentados na} sec¸c˜ao 2.9, tem-se

(ψˆ₋ψ₀)T A XTC−1_X+_AT+₍_ψ_ˆ

−ψ₀)_∼σ2χ2_h,δ (2.37)

onde

δ =

(ψ₋ψ₀)T _{A X}T_C−1_X+_AT+₍_ψ₋_ψ 0)

σ2

(51)

σ2_χ2

n−p por ser fun¸c˜ao deψˆ, tem-se

F = n−p

h

(ψˆ₋ψ₀)T _{A X}T_C−1_X+_AT+₍_ψˆ₋_ψ 0)

SQE ∼Fh,n−p,δ

o que permite utilizar_F como estat´ıstica de testeF para testar a hip´oteseH0 :ψ =

ψ₀.

Por outro lado, quandoψ =ψ₀,δ = 0, vindo

F0 = n−p

h

(ψˆ₋ψ)T_{A X}T_C−1_X+_AT+₍_ψˆ₋_ψ₎

SQE ∼Fh,n−p

ou seja _F tem distribui¸cão F central, logo estes testes são não distorcidos (seçcão 2.9). O testeF de n´ıvelqnão rejeitaH0 se e só se o vectorψ0 pertencer ao elipsóide de confian¸ca de n´ıvel 1₋q

(ψˆ₋ψ)T A XTC−1_X+_AT+₍_ψ_ˆ

−ψ)_≤hF1−q,h,n−p

SQE

(n₋p)

ondeF1−q,h,n−p é o quantil de probabilidade n´ıvel 1−q de Fh,n−p. Neste caso diz-se que o teste F goza de dualidade. Equivalentemente, a hipótese H0 é rejeitada ao n´ıvelq se e só se

F > F_{1−q,h,n−p}.

Se se tiver A XT_C−1_X_AT+ ₌ _{A X}T_C−1_X_AT−1_{, pode-se testar} directa-mente a hipótese H0 : δ = 0 e o teste será estritamente não distorcido (seçcão 2.9).

Em particular, fazendo A = Ik+1 e ψ0 = 0, facilmente se vê que está a ser testada a hipótese

H0 :α0 =α1 =...=αk = 0

(52)

H1 :αj 6= 0 pelo menos para um j

Testa-se esta hip´otese para saber se, de facto, existe uma rela¸c˜ao linear entre a

variável respostay e o conjunto de variáveis controladasx1, ..., xk . RejeitarH0 im-plica que pelo menos uma das variáveisxj, j = 1, ..., k é significativamente diferente de zero e logo contribui significativamente para o modelo, estando-se portanto na

presen¸ca de uma rela¸c˜ao linear.

Quando a matriz A é uma matriz linha cT _e _c_{∈ ℵ}_{, vem} _ψ ₌_cT_α _{e a hipótese} a testar será

H0 :ψ =ψ0

então ˆψ =cT_α_ˆ _{será uma variável aleatória normal com valor médio} _ψ _e

V( ˆψ) =σ2cT XTC−1_X+_cT

logo _F0 com as devidas substitui¸cões terá distribui¸cão F com 1 e n−p graus de liberdade, obtendo-se a partir da´ı os intervalos de confian¸ca para ψ

( ˆψ−ψ)T cT XTC−1_X+_c+_{( ˆ}_ψ₋_ψ₎_≤_F

1−q,1,n−p

SQE

(n₋p) ou, equivalentemente,

" ˆ

ψ − s

F1−q,1,n−p cT (XTC−1X)+c

SQE

n₋p; ˆψ+

s

F1−q,1,n−p cT (XTC−1X)+c

SQE

n₋p

#

ou seja tamb´em neste caso os testes F gozam de dualidade.

Como particularidade interessante tem-se que a raiz quadrada da estat´ıstica F

t0 =

ˆ

ψ₋ψ0 q

cT ₍_XT_C−1_X₎+_cSQE n−p

(2.38)

(53)

se a única componente não nula de c for a j-ésima e for igual a 1, tem-se ψ =

αj. Fazendo ψ0 = 0, os resultados anteriores corresponder˜ao agora a intervalos de confian¸ca para αj e ao teste bilateral para

H0 :αj = 0, j = 0, ..., k

contra

H1 :αj 6= 0, j = 0, ..., k reduzindo-se neste caso a estat´ısticat0 a

t0 = ˆ

αj q

wjjSQE_n₋_p

onde wjj representa o elemento da linha j e coluna j da matriz W = (XTC−1X)+. A hipóteseH0 será rejeitada ao n´ıvel de significância q se

|t0|> t1−q/2,n−p

em que t1−q/2,n−p representa o quantil de probabilidade de n´ıvel 1− q/2 de cada uma das caudas da distribui¸cão t-Student. A rejei¸cão de H0 indica pois que αj é significativamente diferente de zero e, portanto, a variável xj deve ser mantida no modelo. Se pelo contrárioH0 não for rejeitada, conclui-se que a variávelxj pode ser eliminada do modelo.

Este testet serve pois para testar hipóteses acerca dos coeficientes da regressão individualmente, sendo útil para determinar a importância de uma determinada

vari´avel controlada no modelo. Dependendo do caso, um modelo pode ser mais

eficiente se se adicionar uma ou mais vari´aveis controladas ou, pelo contr´ario, se se

eliminar alguma(s) das j´a existentes.

(54)

2.11 Modelos Log-Lineares e Tabelas de Contingˆ

encia

Os modelos log-lineares descrevem padrões de associa¸cão entre variáveis categóricas

e são utilizados para modelar as contagens por célula em tabelas de contingência

[1]. O modelo amostral de Poisson para contagens ´e usualmente usado em tabelas

de contingência e assume que as contagens são realiza¸cões de variáveis aleatórias

independentes de Poisson.

Suponha-se que se tem (n1, ..., nN) contagens emN células duma tabela de con-tingência (frequências observadas) com n =P_ini. Como já foi referido, assume-se que (n1, ..., nN) são realiza¸cões de variáveis independentes com distribui¸cão de Pois-son com parâmetros mi = E(ni), chamados de frequências esperadas, aos quais correspondem probabilidades πi, i= 1, ..., N. A fun¸cão de probabilidade para cada um dos ni, i= 1, ..., N é

exp(₋mi)mnii

ni!

(2.39)

satisfazendo V(ni) =E(ni) =mi. O modelo log-linear ´e definido por

logmi = s X

j=1

xijθj, i= 1, ..., N (2.40)

ou na forma matricial

logm=Xθ (2.41)

onde m ´e o vector cujas componentes s˜ao os mi, n o vector com componentes ni,

i = 1, ..., N, X = [xij], i = 1, ..., N, j = 1, ..., s é a matriz do modelo contendo os valores das variáveis expl´ıcitas para as N células e θ é o vector cujas componentes são os parâmetros do modelo θj, j = 1, ..., s.

Nos modelos log-lineares para amostras de Poisson independentes, a estima¸c˜ao

(55)

que neste caso a fun¸c˜ao de verosimilhan¸ca ´e dada por

L(m) = N Y

i=1

exp(₋mi)mnii

ni!

(2.42)

donde o logaritmo da fun¸c˜ao de verosimilhan¸ca que interessa maximizar ´e dado por

logL(m) = N X

i=1

nilogmi− N X

i=1

mi = N X i=1 ni s X j=1

xijθj ! − N X i=1 exp s X j=1

xijθj !

.

(2.43)

Derivando, obt´em-se

∂logL(m)

∂θj =

N X

i=1

nixij − N X

i=1

mixij (2.44)

dado que mi = exp[Psj=1xijθj]. Para obter os estimadores da máxima verosimi-lhan¸ca ˆθj de θj, j = 1, ..., s, igualam-se essas derivadas a zero. Obtém-se, deste modo, em nota¸cão matricial, as equa¸cões

XTn=XTmˆ (2.45)

ondemˆ tem componentes ˆmi = exp[Psj=1xijθˆj],i= 1, ..., N.

Na estima¸cão por máxima verosimilhan¸ca, a matriz de informa¸cão (INF) é a variância de∂logL(m)/∂θj. Ora a matriz de informa¸cão é dada pelo pela simétrica do valor esperado da matriz Hessiana. Sendo a matriz Hessiana constitu´ıda pelos

elementos

∂2_log_L₍_m₎

∂θjθk

=₋ N X i=1 xij ∂mi ∂θk =₋ N X i=1 xij ( ∂ ∂θk " exp( s X h=1

xihθh) #)

=₋ N X

i=1

xijxikmi (2.46)

os quais n˜ao dependem das frequˆencias observadas n, vem

(56)

onde D(mˆ) ´e a matriz diagonal cujos elementos principais s˜ao as componentes de ˆ

m [1].

Para um número fixo de células, o estimador da máxima verosimilhan¸ca θˆtem distribui¸cão assimptoticamente normal, com valor médio θ e matriz de covariância

igual a INF−1 [1]. Donde, para amostras de Poisson, a matriz de covariˆancia esti-mada de θˆ´e

\

COV(θˆ) = XTD(mˆ)X−1. (2.48) Para cada célulai, duma tabela de contingência, o res´ıduo estandardizado é dado por

ei =

ni−mˆi ˆ

m1/2_i . (2.49)

Quando o modelo se ajusta bem, os ei, i = 1, ..., N são assimptoticamente normais com valor médio nulo e variâncias assimptóticas inferiores a 1 [1].

Seja e = [e1, ..., eN]T, então a estat´ıstica de Pearson X2 =eTe tem distribui¸cão assimptótica qui-quadrado comN ₋s graus de liberdade. Por outras palavras, X2 tem distribui¸cão qui-quadrado aproximada, com graus de liberdade iguais ao número

de células da tabela de contingência menos o número de parâmetros linearmente

independentes estimados do modelo [1].

Nos modelos log-lineares a “bondade” do ajustamento ´e dada pelo desvio residual

G2 = 2 N X

i=1

nilog(ni/mˆi). (2.50)

Supondo queπi >0, i= 1, ..., N quando o modelo se ajusta bem en→ ∞, o desvio residual, ver [1], distribui-se assimptoticamente como um qui-quadrado com N −s

graus de liberdade, o que ´e o mesmo que dizer queG2 _{converge em distribui¸c˜ao para} um qui-quadrado com N −s graus de liberdade, ver [32], pondo-se