14
Andr
eia P
atrícia da Cunha Mour
a
O erro na regulação da aprendizagem do tema deriv
ada de uma função de alunos do 1
1
.º ano de Matemáti
ca A
Andreia Patrícia da Cunha Moura
O erro na regulação da aprendizagem
do tema derivada de uma função de
alunos do 11.º ano de Matemática A
Universidade do Minho
Instituto de Educação
Universidade do Minho
Instituto de Educação
Andreia Patrícia da Cunha Moura
O erro na regulação da aprendizagem
do tema derivada de uma função de
alunos do 11.º ano de Matemática A
Relatório de Estágio
Mestrado em Ensino de Matemática no 3.º Ciclo
do Ensino Básico e no Ensino Secundário
Trabalho efetuado sob a orientação do
Professor Doutor Floriano Augusto Veiga Viseu
Universidade do Minho
DECLARAÇÃO
Nome: Andreia Patrícia da Cunha Moura
Endereço Eletrónico: apatriciacmoura@gmail.com Telemóvel: 916954099
Número do Bilhete de Identidade: 13940575
Título do Relatório:
O erro na regulação da aprendizagem do tema derivada de uma função de alunos do 11.º ano de Matemática A
Supervisor:
Doutor Floriano Augusto Veiga Viseu
Ano de conclusão: 2014
Mestrado em Ensino de Matemática no 3.º Ciclo do Ensino Básico e no Ensino Secundário
É AUTORIZADA A REPRODUÇÃO INTEGRAL DESTE RELATÓRIO APENAS PARA EFEITOS DE INVESTIGAÇÃO, MEDIANTE DECLARAÇÃO ESCRITA DO INTERESSADO, QUE A TAL SE COMPROMETE.
Universidade do Minho ___/___/___
Agradecimentos
Dedico este espaço àqueles que de forma direta ou indireta contribuíram positivamente para a realização deste estudo. Com especial atenção:
Ao Professor Doutor Floriano Augusto Veiga Viseu, meu supervisor, pela disponibilidade, paciência, ajuda e interesse demonstrado.
Ao Mestre e Professora Carmo Cunha pela paciência demonstrada, pela troca de ideias e sugestões que me fizeram crescer como professora.
Aos alunos da turma e à direção da escola pela colaboração e disponibilidade. À Gabriela, colega de estágio, pela companhia, ajuda e todas as palavras de força.
À minha família, em especial aos meus pais Albertina e Joaquim pelo apoio em todos os momentos da minha formação.
O ERRO NA REGULAÇÃO DA APRENDIZAGEM DO TEMA DERIVADA DE UMA FUNÇÃO DE ALUNOS DO 11.º ANO DE MATEMÁTICA A
Andreia Patrícia da Cunha Moura
Mestrado em Ensino de Matemática no 3.º ciclo do Ensino Básico e no Ensino Secundário Universidade do Minho, 2014
Resumo
O presente estudo teve como principal objetivo averiguar o papel do erro na regulação da aprendizagem do tema derivada de uma função de alunos do 11.º ano de escolaridade. Para concretizar este objetivo estabeleceram-se as seguintes questões de investigação: (1) Que erros cometem os alunos na aprendizagem de tópicos de derivada de uma função? Quais as causas desses erros? (2) Que ilações retiram os alunos dos erros que cometem para a sua aprendizagem de tópicos de derivada de uma função? (3) Qual é a perceção dos alunos sobre as estratégias de ensino que valorizam o erro na sua aprendizagem? Para dar resposta a estas questões recorreu-se aos seguintes métodos de recolha de dados: questionários (um antes e outro depois da intervenção pedagógica), análise documental (planos de aula e produções dos alunos), questões no final de algumas aulas e gravação em vídeo de aulas.
A análise de dados permite concluir que na aprendizagem de tópicos de derivada de uma função os alunos cometeram vários erros, quer processuais (simplificação de expressões, substituição, interpretação e escrita matemática) quer conceituais (na definição de derivada de um ponto, na definição das regras de derivação e na noção de limite). As causas que levam os alunos a errar indiciam deverem-se a fatores de distração na realização das atividades, à falta de conhecimentos prévios e de estudo. Com a análise dos erros que cometem, a maior parte dos alunos manifesta ter a perceção onde erraram, o que os ajuda a clarificar os erros cometidos de modo a evitar que os voltem a cometer. Relativamente à perceção dos alunos sobre as estratégias que valorizam o erro na sua aprendizagem, alguns afirmam que essas estratégias lhes permitem compreender o porquê de errar e valorizam o trabalho autónomo. Mas, por outro lado, consideram que tais estratégias podem gerar desmotivação nos alunos e, por vezes, podem não ser bem conseguidas pelo facto de alguns alunos terem vergonha de expor os seus erros. Os resultados obtidos neste estudo evidenciam a necessidade de introduzir, nas aulas de Matemática, estratégias de ensino que valorizem o erro na regulação da aprendizagem de conceitos matemáticos.
MISTAKE ON THE SUBJECT’S LEARNING REGULATION DERIVED FROM A FUNCTION BY 11TH GRADE MATHEMATICS A STUDENTS
Andreia Patrícia da Cunha Moura
Master’s in Mathematics Teaching in the third cycle of Basic Education and on the Secondary Education
Minho University, 2014 Abstract
The present study have had as main goal to ascertain the role of the mistake on the subject’s learning regulation derived from a function by 11th grade students. In order to achieve this goal, the following investigation questions were established: (1) What are the mistakes that students make on the learning of subjects derived from a function? What are the causes of those mistakes? (2) Which conclusions the students draw from the mistakes that they make for their learning of subjects derived from a function? (3) What is the perception of the students about the teaching strategies that prize the mistake on their learning? To provide answers to these questions, one made use of the following data collection methods: inquiries (one before and another one after the pedagogical intervention), documentary analysis (class plans and production of students), questions in the end of some classes and video recording of classes. Data analysis allows to conclude that on the subject’s learning derived of a function, students have made several mistakes, either procedural mistakes (simplification of expressions, replacement, interpretation and mathematics writing) either conceptual (on the definition of derived from a point, on the definition of derivation rules and on the notion of limit). The causes that lead students to make the mistakes indicate being due to absentmindedness factors on the performance of the activities, to the lack of previous knowledge and study. With the analysis of the mistakes they make, the majority of the students express that have the perception about where they made mistakes, what helps them to clarify the mistakes made in order to avoid making them again. Regarding to the students’ perception about the strategies that prize the mistake on their learning, some claim those strategies allow them to understand why they made the mistake and they have prized the autonomous work. But, on the other side, they consider that such strategies can generate the lack of motivation on students and, sometimes, cannot be very successful by the fact of some students being ashamed of exposing their mistakes. The results obtained in this study showcase the need to introduce, on Mathematics classes, teaching strategies that prize the mistake on the learning regulation of mathematical concepts.
Índice Agradecimentos...iii Resumo……….v Abstract………vii Índice……….ix Índice de figuras………xi Índice de tabelas……….xiii Capítulo 1……….1
1.1. Tema, objetivos e questões de estudo………1
1.2. Pertinência do estudo………2 1.3. Estrutura do relatório……….3 Capítulo 2……….5 2.1. Enquadramento contextual………..5 2.1.1. Caraterização da Escola………5 2.1.2. Caraterização da Turma………7 2.2. Enquadramento Teórico………9
2.2.1. O ensino de derivadas no currículo de secundário………9
2.2.2. O erro na aprendizagem de conteúdos matemáticos………12
2.2.3. O erro de conceitos algébricos………15
2.2.4. Conhecimento concetual e conhecimento processual………..20
2.2.5. Atividades de regulação da aprendizagem……….22
2.3. Estratégias de intervenção………26
2.3.1. Metodologias de ensino e de aprendizagem……….27
2.3.2. Estratégias de avaliação da ação………...30
Capítulo 3……….33
3.1. Conteúdos lecionados na intervenção pedagógica……….33
3.2. Erros dos alunos na aprendizagem de tópicos de derivada de uma função………34
3.3. Análise das questões propostas no final de algumas aulas……….…..44
3.4. Perceções dos alunos antes e depois da intervenção pedagógica……….……46
Capítulo 4……….…55
4.1.1. Que erros cometem os alunos na aprendizagem de tópicos de derivada de uma função?
Quais as causas desses erros?...55
4.1.2. Que ilações retiram os alunos dos erros que cometem para a sua aprendizagem de tópicos de derivada de uma função?...56
4.1.3. Qual a perceção dos alunos sobre as estratégias de ensino que valorizam o erro na sua aprendizagem? ……….57
4.2. Limitações e Recomendações……….58
Referências Bibliográficas………..61
ANEXOS……….65
Anexo 1 – Questionário Inicial………..67
Anexo 2 – Questionário Final………69
Anexo 3 – Pedido de autorização ao Diretor da Escola………..71
Anexo 4 – Pedido de autorização aos Encarregados de Educação………73
Índice de Figuras
Figura 1. Disposição dos alunos na sala……….8
Figura 2. Distribuição dos diferentes temas estudados ao longo do ensino secundário…………..10
Figura 3. Distribuição dos diferentes temas estudados ao longo do 11.º ano de escolaridade….11 Figura 4. Distribuição dos diferentes temas estudados ao longo do 12.º ano de escolaridade….11 Figura 5. Figura do estudo de Orton (1983, p. 245)………...18
Figura 6. Vantagens do trabalho de grupo………..27
Figura 7. Tipologia de erros considerada neste relatório………..34
Figura 8. Resolução apresentada pelo grupo 1……….35
Figura 9. Resolução apresentada pelo grupo 3……….35
Figura 10. Tarefa resolvida no quadro por um aluno do grupo 4………..36
Figura 11. Gráfico apresentado por um aluno do grupo 4………36
Figura 12. Resoluções apresentadas, respetivamente, pelos grupos 2 e 3………..37
Figura 13. Resolução apresentada pelo grupo 2………..38
Figura 14. Resolução apresentada pelo grupo 1………..38
Figura 15. Resolução apresentada pelo grupo 4………..39
Figura 16. Tarefa resolvida no quadro, respetivamente, por alunos do grupo 3 e 5……….39
Figura 17. Resolução apresentada por um aluno do grupo 3……….39
Figura 18. Resolução apresentada por um aluno do grupo 5……….40
Figura 19. Resolução apresentada pelo grupo 2………..41
Figura 20. Resolução apresentada pelo grupo 5………..41
Figura 21. Resolução apresentada pelo grupo 2………..42
Figura 22. Resolução apresentada pelo grupo 3………..43
Figura 23. Resolução apresentada pelo grupo 5………..43
Figura 24. Resposta dada por um aluno relativamente à análise dos erros.……….…51
Figura 25. Resposta dada por um aluno relativamente à análise dos erros.……….51
Figura 26. Resposta dada por um aluno relativamente à análise dos erros.……….52
Índice de Tabelas
Tabela 1- Distribuição das idades dos alunos (n=21)………7
Tabela 2- Classificações dos alunos à disciplina de Matemática no 11.º ano de escolaridade (n=21).. ………8
Tabela 3- Distribuição dos alunos pelos respetivos grupos………..28
Tabela 4- Síntese dos conteúdos lecionados na intervenção pedagógica………..33
Tabela 5- Erros cometido pelos alunos, segundo a sua perspetiva, durante as aulas………..44
Tabela 6- Causas que levaram os alunos a cometer erros durante as aulas………45
Tabela 7- Sugestões enunciadas pelos alunos para não voltarem a cometerem os mesmos erros………45
Tabela 8- Vantagens do trabalho de grupo para a aprendizagem de conceitos matemáticos……46
Tabela 9- Desvantagens do trabalho de grupo para a aprendizagem de conceitos matemáticos……….…..47
Tabela 10- Erros que os alunos cometem nas aulas de Matemática………47
Tabela 11- Percentagem de alunos segundo as opções de resposta relativamente ao trabalho de grupo nas aulas de derivada de uma função……….48
Tabela 12- Percentagem de alunos segundo as opções de resposta relativamente às causas dos erros nas aulas de derivada de uma função………..48
Tabela 13- Percentagem de alunos segundo as opções de resposta relativamente à análise/discussão dos erros nas aulas de derivada de uma função………49
Tabela 14- Percentagem de alunos segundo as opções de resposta relativamente à apresentação dos erros nas aulas de derivada de uma função………..49
Tabela 15- Aspetos positivos das estratégias de ensino que valorizam o erro nas atividades de aprendizagem………..50
Tabela 16- Aspetos negativos das estratégias de ensino que valorizam o erro nas atividades de aprendizagem………..50
CAPÍTULO 1 INTRODUÇÃO
Este capítulo, dividido em 3 secções, apresenta o tema, o objetivo e as questões de investigação que orientaram a minha prática pedagógica. De seguida, apresenta a pertinência deste estudo e, por fim, uma breve descrição da estrutura deste relatório.
1.1. Tema, objetivo e questões de estudo
O tema deste estudo incide sobre o erro na regulação da aprendizagem do tema derivada de uma função de alunos do 11.º ano de Matemática A. A minha experiência enquanto aluna e a observação de aulas foram fatores decisivos para a escolha deste tema. Enquanto aluna, fui penalizada várias vezes por ter errado. Poucos foram os professores que optavam por uma estratégia de ensino que valorizasse o erro, fazendo dele um fator de aprendizagem importante. Na observação de aulas, na escola onde realizei a minha prática pedagógica, pude constatar que alguns alunos manifestavam receio de exprimir o que não compreendiam e o que faziam nas aulas de Matemática. Essa falta de compreensão resulta, em certas ocasiões, da divergência entre os seus processos e os que são explanados no quadro, como também da divergência entre os seus resultados e os que são referidos oralmente na turma ou registados no quadro. Por detrás destas divergências há uma intenção e uma forma de pensar que nem sempre são considerados, ficando ao critério do aluno o modo como regula as suas atividades. Quantas vezes o resultado final incorreto não teve um bom raciocínio e se deve a um pequeno erro? A valorização do resultado final, em detrimento do processo, faz com que muitos alunos desanimem e percam o seu interesse em trabalhar na disciplina de Matemática. O professor por mais que incentive os alunos a apresentarem as suas dúvidas e as suas dificuldades nem sempre obtém da parte destes qualquer intervenção. Os alunos tendem a manifestar receio de apresentar as suas ideias e os seus processos para não caírem no ‘ridículo’ perante os seus colegas e o professor.
Tacitamente institui-se a norma de que o que está certo será validado pelo professor ou pelos melhores alunos, mesmo sem se compreender o que se fez ou o que se diz. O problema surge nos momentos de avaliação das aprendizagens, em que a falta de compreensão dos conceitos matemáticos resulta na ausência de resposta ou em respostas erradas. Em tais
momentos o erro adquire um carácter penalizador em detrimento do formativo (NCTM, 1999). Uma forma de valorizar o erro na aprendizagem passa por, no desenvolvimento das atividades da sala de aula, atender ao que o aluno diz e faz (Nicol, 1999). Ao ter oportunidade de argumentar as suas ideias e processos e de os confrontar com os produzidos pelos restantes colegas ou pelo professor, o aluno apercebe-se das razões que o levaram a errar. A perceção dos alunos sobre os erros que cometem favorece a aprendizagem dos conceitos matemáticos, principalmente no que diz respeito na forma como estabelecem conexões entre as diferentes representações de conceitos (NCTM, 2007). Esta é uma das principais razões que me levou à escolha do tema deste estudo, pretendendo averiguar o papel do erro na regulação da aprendizagem do tema derivada de uma função de alunos do 11.º ano de escolaridade. Com a finalidade de concretizar este objetivo, pretendo responder às seguintes questões de investigação:
– Que erros cometem os alunos na aprendizagem de tópicos de derivada de uma função? Quais as causas desses erros?
– Que ilações retiram os alunos dos erros que cometem para a sua aprendizagem de tópicos de derivada de uma função?
– Qual é a perceção dos alunos sobre as estratégias de ensino que valorizam o erro na sua aprendizagem?
Como a aprendizagem resulta, em grande parte, da atividade que os alunos fazem por si mesmos, os alunos podem melhorar as suas capacidades de aprender através da regulação dessa atividade. Trata-se de um processo de questionamento sobre o que o aluno faz e diz no desenvolvimento das atividades da sala de aula: o que fiz bem? O que fiz mal? Porque errei? Que diferenças há entre o que fiz e o que os meus colegas fizeram? O que retiro para a minha aprendizagem? Com este tipo de questões o aluno tira partido das atividades que realiza na aula, debatendo, analisando e clarificando os seus processos e resultados.
1.2. Pertinência do Estudo
Na organização curricular, a disciplina de Matemática tem no ensino básico o mesmo programa para todos os alunos que frequentam cada um dos nove anos de escolaridade, o que já não acontece nos três anos do ensino secundário, cujo programa depende do curso que os alunos escolhem. Aqui chegados, os que seguem os cursos de Ciências e Tecnologias e Ciências Socioeconómico têm Matemática A, os que seguem o curso de Artes Visuais têm Matemática B
e os que seguem o curso de Línguas e Humanidades têm Matemática Aplicada às Ciências Sociais (MACS). Para além destes cursos, os alunos podem frequentar diferentes cursos profissionais, cujo programa de Matemática também depende de curso para curso. Na transição do ensino básico para o ensino secundário, na escolha do curso, para além da vocação intrínseca, muitos alunos ponderam a relação que tiveram com a disciplina de Matemática no seu percurso escolar. Nem todos eles tiveram um desempenho regular nesta disciplina devido, por exemplo, às suas capacidades cognitivas, aos ritmos de aprendizagem, como também a estratégias de ensino que nem sempre atenderam às dúvidas e dificuldades dos alunos.
São frequentes os erros e as dificuldades dos alunos em conceitos matemáticos, no entanto “cometer erros ou dizer as coisas de modo imperfeito ou incompleto não é um mal a evitar, é algo inerente ao próprio processo de aprendizagem” (Abrantes, Serrazina & Oliveira, 1999, p. 27).
Em suma, o desenvolvimento deste projeto incidiu no ensino e na aprendizagem de conceitos relacionados com a derivada de uma função tendo por base a valorização do erro, dando, sempre que possível, a oportunidade ao aluno que errou de rever o seu raciocínio/resolução para ser ele próprio a identificar e a corrigir o erro. Com esta estratégia procurei dar importância a problemas de situação de vida real para que os alunos conferissem a utilidade dos conceitos de Cálculo Diferencial desenvolvidos ao longo da minha intervenção pedagógica.
1.3. Estrutura do relatório
Este relatório está organizado em quatro capítulos, pelo que se apresenta uma breve descrição de cada um. No primeiro capítulo – Introdução – apresenta-se o tema, o objetivo e as questões que orientaram a prática pedagógica. Além disso, a pertinência deste estudo é também mencionada neste capítulo onde são referidas as razões que estiveram na base desta escolha e, por fim, a estrutura do relatório.
O segundo capítulo – Enquadramento Contextual e Teórico – está dividido em três secções. Na primeira, caraterizam-se a escola e a turma onde este projeto se desenvolveu. Na segunda secção, o enquadramento teórico, apresenta-se a fundamentação teórica deste trabalho. Na última secção delineiam-se as metodologias de ensino e de aprendizagem e as estratégias de avaliação da ação.
No terceiro capítulo – Intervenção Pedagógica – apresenta-se e analisa-se o processo de intervenção pedagógica através dos seguintes tópicos: conteúdos desenvolvidos, erros cometidos pelos alunos da turma durante a intervenção, análise das questões propostas no final de algumas aulas e perceções dos alunos antes e depois da intervenção pedagógica. No primeiro tópico são expostos os conteúdos lecionados e um pequeno resumo de como funcionaram as aulas. O segundo ilustra o ensino e a aprendizagem do conceito derivada de uma função dando ênfase aos erros cometidos pelos alunos. No terceiro tópico é feita a análise à apreciação dos alunos sobre a estratégia delineada. O último tópico apresenta as perceções dos alunos, em dois momentos distintos da intervenção pedagógica, sobre a estratégia desenvolvida através de um questionário inicial e de um questionário final.
No quarto capítulo – Conclusões, Limitações e Recomendações – apresentam-se e problematizam-se os resultados obtidos através das questões de investigação delineadas. Por fim, apontam-se algumas limitações e recomendações para projetos futuros.
CAPÍTULO 2
ENQUADRAMENTO CONTEXTUAL E TEÓRICO
Este capítulo tem por finalidade descrever o contexto onde realizei a minha intervenção pedagógica, fazendo referência à Escola e à Turma em causa, e explicitar, à luz da literatura, o tema que lecionei, o erro, o processo de regulação e as metodologias de ensino e de avaliação das estratégias delineadas na concretização deste projeto.
2.1. Enquadramento contextual
Antes de descrever a minha prática pedagógica e discutir os pressupostos teóricos que a sustentam, importa caraterizar a Escola e a Turma onde realizei essa prática pedagógica.
2.1.1. Caraterização da Escola
A escola secundária onde implementei o meu projeto é uma escola, com 3.º ciclo do ensino básico, que pertence a um agrupamento de escolas localizada na cidade de Braga. Trata-se de uma escola que foi sujeita a obras de requalificação (2009 a 2010), no âmbito da intervenção do Parque Escolar, reunindo nas suas instalações as condições essenciais ao desenvolvimento da ação educativa. O Parque Escolar tem por objetivo o planeamento, gestão, desenvolvimento e execução do programa de modernização da rede pública de escolas secundárias e outras afetas ao Ministério de Educação.
Em termos de oferta educativa, a escola capta uma população estudantil diversificada e segundo o seu projeto educativo integra alunos provenientes de todas as freguesias da cidade. Do ponto de vista sociológico, esta escola integra alunos oriundos de famílias de nível social médio-alto e alto, como também uma parcela significativa de alunos oriundos de famílias de nível social médio-baixo e baixo. A heterogeneidade do perfil global desta instituição, com a integração de alunos provenientes dos mais diversos meios sociais, económicos, culturais e com diversas experiências de vida tem sido encarado como um desafio pedagógico permanente.
A escola desenvolve um projeto educativo com grande envolvimento dos alunos em atividades extra curriculares, que potenciam a integração e o desenvolvimento de competências sociais. Dessas atividades, destacam-se as que são realizadas nos seguintes clubes e oficinas na escola: Atelier de Artes; Clube de Arqueologia; Clube do Ambiente; Desporto Escolar; Oficina de Latim e Língua Portuguesa; Oficina de Robótica; Oficina de Teatro; Rádio, Televisão e uma
Revista. Uma aluna da turma onde realizei a minha prática pedagógica fez parte da Oficina de Robótica. Uma das vantagens por fazer parte deste clube é beneficiar de mais um valor, no final do ano letivo, numa disciplina à escolha. A aluna em causa beneficiou de mais um valor na disciplina de Matemática pois esta era a disciplina com a classificação mais baixa.
A escola, para além de oferecer atividades extra curriculares, como as que foram referidas e que funcionam durante quase todo o ano letivo, dá a oportunidade aos alunos de participar em atividades organizadas por diferentes departamentos. Das atividades organizadas ao longo do ano, destaco aquelas que envolveram o núcleo de matemática na sua realização, o canguru matemático e o torneio de xadrez. O canguru matemático é um concurso anual internacional de matemática. É dirigido aos alunos dos 2.º, 3.º e 4.º anos de escolaridade, dos 2.º e 3.º ciclos do ensino básico e do ensino secundário. A sua promoção é de iniciativa da Associação Canguru sem Fronteiras, uma associação de âmbito internacional que congrega personalidades ligadas à disciplina de matemática em diversos países. Aberto a todos os estudantes, sem seleção prévia, o concurso tem lugar no mesmo dia em todos os países participantes. A prova consiste num questionário de escolha múltipla de cerca de trinta questões de dificuldade crescente. A promoção desta atividade foi feita através de cartazes afixados pela escola e de um aviso que percorreu todas as salas de aula. Apesar de bem promovida, a adesão a esta prova foi fraca, visto que só se inscreveram 40 alunos e no dia da prova só apareceram 18 alunos. O torneio de xadrez foi realizado pelo segundo ano consecutivo na escola e teve como principal apoio o clube de xadrez de Braga. O apoio deste clube foi fundamental, pois foi ele que forneceu todo o material necessário para o decorrer do torneio, à escola coube o papel de fornecer o espaço, de promover esta atividade aos alunos e de arranjar prémios para entregar aos vencedores da prova. A prova foi divulgada através de cartazes afixados pela escola e de um aviso que percorreu todas as salas de aula. A participação neste torneiro foi expandida às escolas de todo o agrupamento onde está inserida esta escola. A adesão desta atividade, em geral, foi elevada, participando apenas da escola onde desenvolvi a minha prática pedagógica 2 alunos.
Por fazer parte do núcleo de Matemática, mesmo sendo estagiária, participei na concretização destas duas atividades. Participei na promoção das duas atividades e no dia da realização do canguru matemático fiquei responsável por vigiar uma das salas onde foi feita a prova. No dia do torneio de xadrez fiquei responsável por verificar se tudo estava a correr bem e por distribuir o lanche aos alunos. Foi importante para mim a participação nestas atividades,
porque, para além de ter contato com outros alunos, que não os da minha turma de intervenção, deu para ter a noção que a escola não se resume só a aulas e que as atividades extra-aulas são importantes para o desenvolvimento dos alunos.
2.1.2. Caraterização da Turma
A turma onde realizei a prática pedagógica é da área Científico - Humanístico de Ciências Socioeconómico, que no ano letivo de 2013/2014, se encontrava no 11.º ano de escolaridade. Ao longo do 1.º e 2.º períodos houve dois alunos que trocaram de turma e um aluno que mudou de escola. Em contrapartida, houve uma aluna que integrou a turma. Esta nova aluna veio do curso Científico - Humanístico de Ciências e Tecnologias. Deste modo, a turma ficou constituída por 21 alunos, 6 raparigas (29%) e 15 rapazes (71%), com idades compreendidas entre os 15 e os 18 anos. A idade média dos alunos da turma é de 16 anos, o que traduz a idade dos alunos que, geralmente têm um percurso escolar sem retenções.
Tabela 1- Distribuição das idades dos alunos (n=21).
Idades Número de alunos Percentagem de alunos
15 3 14%
16 16 76%
17 1 5%
18 1 5%
Da análise das respostas dos alunos a um questionário, entregue no início do ano letivo, que teve como objetivo a caracterização da turma, quatro alunos (19%) referem ter dificuldades na disciplina de Matemática e oito alunos (38%) referem-na como a disciplina preferida. Pela observação das aulas, no período que antecedeu a minha prática pedagógica, apercebi-me que os alunos eram trabalhadores mas um pouco perturbadores, o que fazia com que, muitas vezes, se gastasse muito tempo das aulas para os disciplinar. Relativamente à organização das suas atividades no contexto de sala de aula, os alunos revelaram que não estavam habituados a trabalhar em grupo, mas quando trabalhavam em pares mostravam, em geral, motivação e empenho. Em termos sociais, a turma manifestava ser unida e com um sentido de se protegerem uns aos outros, o que se traduzia num bom ambiente entre os alunos.
Em relação à disciplina de Matemática, o nível de desempenho dos alunos no final do 10.º ano de escolaridade foi um pouco melhor que o obtido no final do 1.º período deste ano
letivo. No 10.º ano de escolaridade, a classificação destes alunos traduziu-se numa média final de 11,5 valores, sendo a nota mínima de 8 valores e a nota máxima de 17 valores. No final do 1.º período do 11.º ano de escolaridade, as classificações desceram um pouco, havendo 13 negativas e 8 positivas e uma média de, aproximadamente, 9 valores. No final do 2.º período as notas permaneceram quase iguais, existindo o mesmo número de positivas e negativas, e a média neste período foi de 9 valores. Só no final do ano letivo é que as classificações destes alunos melhoraram um pouco, obtendo uma média final de ano de 10,4 valores, ficando assim com a média final de 11.º ano inferior à média do 10.º ano de escolaridade (Tabela 2).
Tabela 2- Classificações dos alunos à disciplina de Matemática no 11.º ano de escolaridade (n=21).
Períodos 1.º 2.º 3.º
Nota Mínima 5 2 2
Nota Máxima 18 19 20
Média 9.1 9 10.4
Em todas as aulas da minha intervenção pedagógica os alunos foram organizados em grupos, ficando distribuídos na sala da forma como se apresenta na Figura 1.
Legenda: P – Porta Q – Quadro C – Computador S.P – Secretária Professora A – Aluno
Figura 1. Disposição dos alunos na sala de aula.
Esta organização da sala de aula facilitou a dinamização de momentos de discussão entre os elementos do grupo. O facto de a sala estar organizada em três filas permitiu-me, nas minhas atividades de ensino, percorrer os diferentes grupos de modo a acompanhar o desenvolvimento das suas atividades.
2.2. Enquadramento teórico
Este subcapítulo destina-se à fundamentação teórica deste trabalho, atendendo ao objetivo e às questões de investigação delineadas, tratando do ensino de derivadas no secundário, dos erros cometidos pelos alunos na aprendizagem de conceitos matemáticos, em geral, e de conceitos algébricos, em particular e da diferença entre conhecimento concetual e conhecimento processual. Por fim, trata de diferentes processos de regulação: a avaliação, o feedback e o erro.
2.2.1. O ensino de derivadas no currículo do secundário
Na minha intervenção pedagógica lecionei vários tópicos, entre eles estão a taxa média de variação e taxa de variação instantânea/derivada recorrendo à noção de limite. Estes tópicos estão integrados no tema das funções do 11.º ano de escolaridade, que é um tema de grande importância no currículo e que tem como um dos seus objetivos introduzir o Cálculo Diferencial.
Numa perspetiva histórica, é difícil perceber quem foi o matemático que esteve na origem do Cálculo Diferencial. Apesar do aparecimento do deste tema estar associado, segundo vários autores, a Newton e Leibniz, muitos outros trabalharam para esta descoberta. São exemplo disso, os métodos da determinação das tangentes de Fermat e o método proposto por Descartes (Boyer, 2010). Com o intuito de determinar áreas delimitadas por curvas, determinar curvas e as suas propriedades, determinar tangentes e resolver problemas de máximos e mínimos, Newton e Leibniz, de forma quase simultânea e independente, descobriram um método geral para a resolução de problemas associados, por um lado, ao problema da tangente a uma dada curva (cálculo diferencial) e, por outro lado, aos problemas de áreas delimitadas por curvas e volumes de sólidos gerados por revolução (cálculo integral) (Boyer, 2010).
As primeiras ideias de Newton acerca do Cálculo vieram diretamente da maneira pela qual Fermat traçava tangentes a curvas (Simmons, 2010). Simmons (2010) refere que os cálculos feitos por Fermat já tinham a ideia do infinitamente pequeno. Stewart (2006) afirma que o primeiro matemático a desenvolver as ideias de limite como base do Cálculo Diferencial foi Newton. Leibniz percebeu que a determinação da reta tangente a uma curva dependia da razão das diferenças das ordenadas e das abcissas, quando se tornam infinitamente pequenas (Boyer, 2010).
A noção de limite que Newton e Leibniz tinham não era bem clara, a precisão da definição sobre limites, que hoje conhecemos, foi dada por d’Alembert. Esta precisão surgiu após d’Alembert perceber a importância central do limite no Cálculo Diferencial (Boyer, 2010).
A perspetiva analítica e gráfica ainda hoje são estudadas no ensino secundário, dando-se mais ênfase ao estudo analítico. Analiticamente, a derivada de uma função é lecionada como sendo a taxa de variação instantânea de uma função.
Taxa de variação de uma função f real de variável real, em xx0, caso exista, é um número real, para que tende o quociente f x( 0 h) f x( 0)
h
, quando h
tende para zero, e pode ser representada por f x'( )0 ou
0 d d x x f x . 0 '( )
f x também é designada por derivada da função f no ponto de abcissa x0
0 0 0 0 ( ) ( ) '( ) lim h f x h f x f x h ou 0 0 0 0 ( ) ( ) '( ) lim x x f x f x f x x x
Nota: Considerando x x 0 h, obtém-se a expressão anterior. (Costa & Rodrigues, 2013, p. 63).
Com a intenção de perceber se o ensino da derivada de uma função sempre se debruçou entre as duas perspetivas (analítica e gráfica), optei por fazer uma comparação entre o programa atual de Matemática A (Ministério da Educação, 2002) e o programa anterior de Matemática (Ministério da Educação, 1995). No programa de Matemática de 1995, o Cálculo Diferencial era o tema estudado com mais ‘peso’ durante o ensino secundário (Figura 2).
Figura 2. Distribuição dos diferentes temas estudados ao longo do ensino secundário. A sua distribuição nos 11.º e 12.º anos era feita da seguinte forma:
Figura 3. Distribuição dos diferentes temas estudados ao longo do 11.º ano de escolaridade. No 11.º ano de escolaridade, o Cálculo Diferencial e a Geometria apareciam com a mesma percentagem (39%) e as Sucessões com menor percentagem (22%). No 12.º ano de escolaridade, o Cálculo Diferencial era o maior tema estudado preenchendo quase metade do programa desse ano letivo (46%), seguindo-se as Probabilidades (39%) e por último os Números Complexos (15%).
Figura 4. Distribuição dos diferentes temas estudados ao longo do 12.º ano de escolaridade. Ainda de acordo com o Programa de Matemática de 1995, no 11.º ano de escolaridade o tema de ‘derivada de uma função’ era iniciado com o estudo da noção de taxa média de variação e a sua interpretação geométrica passando depois para a noção de taxa de variação (valor para que tende a taxa média de variação quando a amplitude do intervalo tende para zero) e a sua interpretação geométrica. Seguia-se o estudo da relação entre o sinal da função derivada, o sentido de variação e os possíveis extremos relativos de uma função e, por fim, o estudo da determinação da derivada em casos simples (função afim, funções polinomiais de 2.º e 3.º grau, função racional de 1.º grau e função módulo), recorrendo a problemas envolvendo derivadas num contexto de aplicações. Relativamente ao 12.º ano de escolaridade, o Cálculo
Diferencial iniciava-se com o estudo de funções racionais e das regras de derivação (demonstração da regra da soma e do produto; informação das restantes regras) seguindo-se o estudo das derivadas de funções elementares e o teorema da derivada da função composta. Por último, fazia-se o estudo das segundas derivadas e da sua relação com o sentido e os pontos de inflexão da concavidade dos gráficos da função (informação baseada em intuição geométrica).
Segundo o atual Programa de Matemática A (Ministério da Educação, 2002), os tópicos lecionados no 11.º ano de escolaridade, no que diz respeito ao cálculo diferencial, são os mesmos que os mencionados no Programa de Matemática de 1995. Apenas é feita uma alteração na ordem, passando o estudo da relação entre o sinal da função derivada, o sentido de variação e extremos relativos de uma função a ser feito após o estudo da determinação da derivada em casos simples. Relativamente ao 12.º ano de escolaridade não houve qualquer alteração na passagem de um programa para o outro.
Em suma, o estudo do Cálculo Diferencial faz parte do 11.º e 12.º anos de escolaridade nos dois programas. Os conhecimentos sobre este tema são essenciais para qualquer aluno como pré-requisito em todas as disciplinas científicas que usem a matemática como “ferramenta”. Segundo o programa de Matemática A (2002), este conceito é importante para as disciplinas de Economia, Física e Química. No caso da turma onde realizei a minha intervenção pedagógica a disciplina de Economia é fundamental.
A assimilação acrítica de conceitos de derivada, a partir de procedimentos mecânicos de manipulação de expressões algébricas, não favorece a compreensão desses conceitos, pode estar na origem dos erros que os alunos cometem nas atividades que realizam neste tema (Azcárate, Casadevall, Casellas & Bosh, 1996).
2.2.2. O erro na aprendizagem de conteúdos matemáticos
Na realização das atividades de aprendizagem, nem sempre os alunos respondem corretamente às tarefas que lhes são propostas, o que se deve a conflitos entre os significados institucionais e os significados pessoais (Godino, Batanero & Font, 2008). Como exemplo desses conflitos cognitivos surgem as diferentes formas dos alunos apresentarem as respostas para além do esperado pelo professor. A forma como as questões são colocadas poderá induzir os alunos a um tipo específico de resposta. Tais conflitos tendem a traduzir-se em respostas com erros, o que, por várias razões, fazem parte do quotidiano da sala de aula e podem surgir em produções orais e escritas dos alunos em situações de ensino - aprendizagem de conceitos
matemáticos. As implicações que o erro tem na aprendizagem dos alunos têm despertado a atenção de professores, educadores e da investigação no âmbito da educação.
Ao longo dos tempos, a forma como se analisa a problemática do erro nas atividades de aprendizagem dos alunos tem-se modificado. O erro não deve ser visto como sendo algo negativo na sala de aula, antes pelo contrário deve ser aproveitado no processo cognitivo da aprendizagem de matemática (Correia, 2005). Porém, nem sempre esta ideia foi considerada, como se constata na análise que Correia (2005) faz dos trabalhos de Macedo e de Piaget sobre a temática do erro. Para Macedo, o erro era associado à ideia de ‘pecado’, assumindo uma conotação religiosa: fazer algo errado deve ser punido só porque errou. Nas memórias dos nossos pais e avós este caráter punitivo está bem presente sob o signo da régua na sala de aula do ensino primário, que ao mínimo erro, por exemplo da tabuada ou de ortografia, este instrumento de ‘purificação’ entrava em ação. Esta visão foi mudando ao longo do tempo. Aos poucos, a perspetiva do erro enquanto fracasso foi dando lugar a uma ideia que admite o erro como elemento que pode ajudar na construção do conhecimento. Esta ideia é apoiada por Piaget, para quem o ‘erro necessário’ faz com que o aluno aprenda errando. Não se pode considerar que o aluno seja incapaz só por ter errado, deve-se aproveitar esse erro para orientar e direcionar os processos de ensino e de aprendizagem. Este trabalho deve ser feito desde os primeiros anos de escolaridade onde se pode transformar o erro em recurso pedagógico. Numa perspetiva similar, Bachelard (citado por Santos, 1991) considera que o erro é “um elemento motor do conhecimento” (p. 130), não resulta apenas como uma consequência do nosso limite, ele faz parte do nosso progresso. Nesta perspetiva, o erro é um elemento positivo, com ele aprendemos sempre qualquer coisa. Para este autor, não existem verdades iniciais, pelo contrário, a verdade resulta de uma rejeição sucessiva de erros, considerando que o tratamento do erro deve ser feito logo que os alunos começam a frequentar a escola. Só assim se pode transformar o erro em recurso pedagógico. Segundo Brousseau (1983), o erro é considerado necessário para: (i) desencadear o processo da aprendizagem do aluno; e (ii) o professor perceber as conceções dos alunos e assim adaptar a sua situação didática.
A abordagem do erro na disciplina de Matemática faz emergir a importância de se saber de que forma se pode classificar. São vários os autores que ao abordar a temática do erro o classificam segundo diferentes perspetivas. Exemplos disso são as seguintes classificações: uma que associa o erro à ideia de pecado e uma outra que, sendo mais recente, associa o erro ao processo de aprendizagem. Segundo Norrisch (citado por Santos, 2010), o erro pode ser
considerado como ausência de conhecimento, um engano, um lapso ou uma distração. Para Norrisch, o erro é considerado como ausência de conhecimento quando o aluno se desvia substancialmente da resposta. Os professores tendem a associar esta ausência aos alunos com mais dificuldades. Se a imagem que o professor tem de um aluno é que ele sabe, que é um bom aluno, raramente o erro por ele cometido é considerado como ausência de conhecimento. O erro é considerado um engano quando o aluno é inconstante na sua realização, umas vezes acerta e outras vezes erra. O erro é visto como um lapso quando o aluno acerta normalmente e erra pontualmente. Segundo Norrisch, estes dois últimos pontos tendem a ser um pouco confundidos. Por fim, o erro é considerado como uma distração quando, embora o aluno responda corretamente, a resposta não está exatamente conforme o que é perguntado.
Um outro autor, Brousseau (2001), classifica os erros da seguinte forma: (i) erro a um nível prático, quando o professor considera que são erros de cálculo; (ii) erro na tarefa, neste ponto são considerados os erros que o professor atribui como descuido; (iii) erro de técnica, quando o professor critica a execução de um procedimento conhecido; (iv) erros de tecnologia, neste ponto são considerados os erros em que o professor critica a escolha do método de resolução; e (v) erros de nível teórico, quando o professor ‘culpabiliza’ os conhecimentos teóricos do aluno.
Analisando estas diferentes perspetivas podemos constatar que a cultura do erro enquanto fracasso tem dado lugar a uma cultura que admite o erro como elemento que pode ajudar na construção do conhecimento. Tão importante como classificar um erro, quando este é detetado, importa conhecer a sua causa. Ao conhecer as causas que levam os alunos a errar, os professores têm a vida facilitada para os corrigir. Os professores para conseguirem ajudar os seus alunos a superar os erros que cometem é importante conhecer a origem desses erros.
São várias as causas que levam os alunos a errar. Vinner (1991) considera que uma das causas que leva os alunos a errar em conceitos matemáticos é a distinção entre conceito imagem e conceito definição. Segundo este autor, o conceito imagem é usado para descrever a estrutura cognitiva que é associada a um determinado conceito. O conceito imagem inclui todas as imagens mentais, propriedades que lhes estão associadas e processos. O conceito definição é a definição verbal que explica o conceito de modo exato. A imagem que os alunos possuem de imensos objetos nem sempre corresponde à sua definição exata, como, por exemplo, o conceito subtração. Numa primeira fase, este é utilizado só em números inteiros positivos e a imagem que as crianças retiram deste conceito é que o resultado da subtração é sempre um “número”
menor que aquele que está a ser subtraído. Embora isto seja uma afirmação verdadeira, irá causar imensas dificuldades ou até mesmo erros quando os alunos passarem a trabalhar com números negativos (Tall & Vinner, 1981). Para combater estas dificuldades, Vinner (1991) refere que para introduzir um novo conceito matemático nunca se deve começar pela definição mas sim com exemplos e contraexemplos.
O erro surge conciliado aos obstáculos que os alunos se deparam nas suas atividades de aprendizagem (Socas, 1997). Para este autor, os erros têm origens diferentes, mas em qualquer uma delas é visto como a presença de um processo cognitivo inadequado e não apenas como consequência de uma distração ou de uma falta de conhecimentos. Este autor agrupou as causas dos erros em cinco categorias: (i) complexidade dos objetos matemáticos; (ii) processos do pensamento matemático; (iii) processos de ensino desenvolvidos para a aprendizagem da matemática; (iv) processos de desenvolvimento cognitivo dos alunos; e (v) atitudes afetivas e emocionais face à matemática. Este autor afasta a ideia de que os erros em Matemática se devem exclusivamente aos alunos.
Em jeito de síntese, o erro nas atividades de aprendizagem de conteúdos matemáticos tem despertado a atenção de vários intervenientes no processo educativo e com a valorização dos processos cognitivos na aprendizagem a sua perspetiva penalizadora deu lugar a uma perspetiva que considera o erro um fator de aprendizagem. Atualmente, o erro na sala de aula está associado não só aos alunos mas também a outros indicadores, como, por exemplo, as estratégias de ensino concretizadas pelo professor. Compete ao professor perceber a origem dos erros que os alunos cometem e adaptar as suas estratégias de modo a envolvê-los na identificação das razões desses erros e na sua clarificação.
2.2.3. O erro de conceitos algébricos
Esta parte do trabalho destina-se aos erros que os alunos cometem em Álgebra, de um modo geral, e no estudo da derivada de uma função, em particular. A Álgebra quando surgiu apenas estava associada ao estudo dos métodos de resolver equações (NCTM, 2007). Atualmente, a Álgebra é muito mais que a manipulação de símbolos, as ideias algébricas estão presentes em muitas áreas do conhecimento. Segundo o NCTM (2007), a competência algébrica é tão importante na vida adulta, no trabalho e na preparação para o ensino superior que todos os alunos deveriam aprender Álgebra.
Embora a Álgebra não seja referida de forma explícita nos currículos antes do 3.º ciclo do ensino básico, ela está contida na matemática desde os primeiros anos de escolaridade, por isso compete aos professores “ajudar os alunos a construir uma base sólida baseada na compreensão e nas suas experiências como preparação para um trabalho algébrico mais aprofundado no 3.º ciclo e no secundário” (NCTM, 2007, p. 39). Sem esta preparação, o estudo da Álgebra tende a ser um fracasso. Kaput (1996) considera que o fracasso neste campo deve-se à formalização precoce da linguagem algébrica, pois existem muitas atividades matemáticas que têm como características intrínsecas a generalização e a formalização. Esta falha, na aprendizagem da Álgebra, deve-se à falta de experiências de aprendizagem promotoras de construção de significados de regras. Quando se aprende algum conceito, se este não tem sentido, esse sentimento mantém-se ao longo do tempo (Kaput, 1996). Numa perspetiva mais ampla, Mason (1996) pondera que o mundo dos problemas da matemática se situa entre a Aritmética e a Álgebra. Esses problemas na Álgebra aparecem quando é necessário encontrar valores desconhecidos mediante: (i) a manipulação de símbolos; (ii) a manipulação de expressões simbólicas, por exemplo, os polinómios; (iii) a utilização das fórmulas; e (iv) o estudo da estrutura matemática abstrata.
Ao analisar possíveis causas do erro em Álgebra, Ruano, Socas e Palarca (2003) defendem que alguns desses erros surgem na introdução de conceitos. Para que o aluno aprenda um novo conceito este deve ter significado para ele próprio, deve-se, para isso, acrescentar um novo conhecimento utilizando os conhecimentos prévios. Já para MacGregor (1996), uma das possíveis causas para os alunos errarem no campo da Álgebra é o deficiente conhecimento da Aritmética. Para este autor, os alunos não aprendem as propriedades operatórias dos números, nem reconhecem relações e procedimentos gerais. Para Hall (citado por Vale, 2010) a terminologia é uma das causas para ao alunos errarem neste campo. Existem erros que mostram, por exemplo, que os alunos não fazem distinção entre os significados de expressão e de equação. Estas diferentes causas podem originar em: (i) erros por eliminação, por exemplo, simplificar 40x3 como 37x ou 2xy2x como y; (ii) erros por troca de
membros, por exemplo, considerar a equivalência x38150 x 38 150 verdadeira; (iii)
erros por redistribuição, os alunos ao considerar, por exemplo, a equação x1025 subtraem 10 ao primeiro membro e adicionam 10 ao segundo, obtendo x10 10 25 10 ; (iv) erros por
transposição, um exemplo deste erro é apresentado na equivalência 3 2 3 4 2
erro ocorre porque os alunos tendem a generalizar a regra eficaz em equações simples, tal como
2 4
2
x
x
; (v) erros de exaustão, são erros que ocorrem com mais frequência próximo do fim de uma resolução. Como exemplo, Hall apresenta a seguinte resolução
2 2 6 ( 2)( 3) 2 2 1 ( 4)( 3) 4 4 2 12 x x x x x x x x x x
. Nesta resolução, o aluno poderia ter cometido o erro
logo no início da expressão, ter feito logo o ‘corte’ na expressão inicial (cortando o 2
x ) em vez de
efetuar o ‘corte’ do x no final; e, por último, (vi) a ausência de uma estrutura, é quando ocorre uma confusão estrutural (por exemplo, no uso de um sinal de igual ou na aplicação de algoritmos).
No que diz respeito ao tema de derivada de uma função, os erros que os alunos cometem nesta temática despertaram a atenção de investigadores em estudar as suas razões, como são exemplo os estudos realizados por Cardoso (1995), com alunos do 11.º ano, por Orton (1983), com 110 alunos com, pelo menos um ano de Cálculo, por Vinner (1992), com 119 alunos universitários e por Viseu (2000), com futuros professores de matemática.
Cardoso (1995) realizou um estudo, em que parte envolveu o ensino-aprendizagem do tópico derivada de uma função, com uma turma do 11.º ano de escolaridade que revelava dificuldades não só em Matemática mas em todas as disciplinas. A turma era da área vocacional de desporto e era composta, no início da experiência, por 14 alunos, com idades compreendidas entre os 16 e os 21 anos. O objetivo deste estudo consistiu em estudar formas de ensino de conceitos de Análise Matemática que valorizem aspetos de visualização gráfica, raciocínio intuitivo, experimentação, indução e formulação de leis, num ambiente de trabalho de cooperação e com a utilização de calculadoras gráficas. A autora conclui que as dificuldades de aprendizagem de derivadas estão relacionadas com: (i) a compreensão do papel das variáveis, os alunos ao fazerem o gráfico de uma função à mão não sabiam distinguir a variável independente e a variável dependente; (ii) hesitações na escolha da unidade na representação gráfica, os alunos demonstravam demasiado tempo a decidir as unidades a colocar nos eixos ordenados; (iii) tentativa e erro não organizada, isto verificava-se com maior frequência quando os alunos não sabiam que janela de visualização utilizar na calculadora, eles experimentavam valores até lhes aparecer um gráfico aceitável; (iv) a influência de estruturas concetuais muito arreigadas, os alunos ficam ligados a certos conceitos e que quando se aprende um novo é difícil ‘desligar-se’ do antigo; (v) raciocínios incompletos, notou-se muitas vezes que os alunos não concluíam as resoluções; e (vi) o código linguístico restrito, os alunos apresentavam uma
competência linguística muito pobre, a falta desta competência provoca dificuldades de comunicação dos alunos. Relativamente ao tema da derivada, Cardoso (1995) refere que a complexidade dos conceitos matemáticos neste tema exige um empenhamento pessoal fora da aula por parte dos alunos. No entanto, no seu estudo, houve vários alunos que não o faziam regularmente, não produzindo a fase de assimilação nesses alunos.
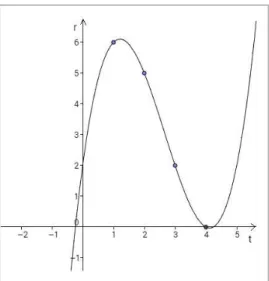
Um outro estudo sobre derivadas foi realizado por Orton (1983) com 110 alunos ingleses, entre os 16 e os 22 anos, com pelo menos um ano de Cálculo. Com este estudo, o autor constatou que os alunos apresentavam um bom domínio nos algoritmos de cálculo de derivadas, pelo menos para funções simples, mas apresentavam dificuldades sobre a conceptualização geométrica de limite, que está na base da noção de derivada. Por exemplo, quando questionados sobre o que acontece às secantes PQn, quando o ponto Qn se move
sobre a curva aproximando-se do ponto fixo P (Figura 5), cerca de 40% dos alunos não foram capazes, mesmo quando fortemente induzidos, de concluir que o processo conduzia à reta tangente à curva no ponto P.
Figura 5. Figura do estudo de Orton (1983, p. 245).
Outra dificuldade observada foi no uso de representações gráficas. Os alunos participantes no estudo mostraram-se capazes de responder corretamente a perguntas do tipo “calcule o declive da reta tangente a uma dada curva num dado ponto” mas, cerca de 90% revelaram dificuldades quando confrontados com a obtenção da mesma velocidade de crescimento através do gráfico. O autor notou também dificuldades na atribuição de significado correto dos símbolos usados. Por exemplo, quando se lhes pedia para explicar o significado de
dy
dx, cerca de 65% dão respostas incorretas do tipo
var
" "
var
velocidade de iação de y
velocidade de iação de x ,
A valorização que o conceito imagem tem na formação dos conceitos matemáticos despertou a atenção de Vinner (1992). Com a preocupação de averiguar o que permanece nas “mentes” dos alunos depois de terem terminado o ensino secundário, o autor efetuou um estudo com 119 alunos universitários no início de um curso de Cálculo, esperando que os mesmos se relembrassem de conceitos básicos, escolhendo como exemplo o conceito de função. Considerando que o conceito de função possui várias configurações, Vinner optou por fazer perguntas sobre tópicos de derivada de uma função, como é exemplo a seguinte questão: “o que é uma derivada”? As respostas a esta questão foram classificadas pelo autor nas seguintes categorias:
I. “uma conceção correta de derivada como um limite (6%). Nesta categoria foram incluídas respostas do tipo:
0 ( ) ( ) lim h f x h f x h ;
II. uma conceção correta de derivada segundo uma interpretação visual (25%). Nesta categoria foram incluídas respostas do tipo: a derivada é uma função que indica o declive da função original em cada ponto; a derivada é o declive da parte crescente ou decrescente de uma função num certo momento; III. uma conceção instrumental de derivada, que relaciona com os métodos de a
obter ou com as suas aplicações, mas que ignora o seu significado (23%). Exemplos: a derivada é uma função obtida de uma dada função através de regras matemáticas fixas; a derivada é uma subfunção de uma função original, por exemplo: 3 2
2 3 , ' 6 3
y x x y x ; uma derivada é um meio de investigar os domínios de crescimento ou de decrescimento de uma dada função; é uma fórmula matemática;
IV. uma referência vaga e inaceitável ao conceito de limite (8%). Exemplos: é uma função que tende para infinito; é o lim ( ) /f x dx , quando dx ; 0 V. uma referência vaga e inaceitável ao aspeto visual de derivada (26%).
Exemplos: é uma função que é tangente a outra função; é a equação da tangente a uma determinada função; a derivada é uma função cuja representação gráfica é uma tangente; o ângulo que a função forma com o eixo dos x;
VI. respostas totalmente irrelevantes ou não respondidas (12%)”. (pp. 210-211)
As respostas incluídas nas categorias 4, 5 e 6 (46%) foram as que mais preocuparam Vinner por serem formuladas de uma forma vaga, imprecisa e sem sentido. Os alunos recordavam palavras, símbolos e gráficos relacionados com derivadas, mas não possuíam uma ideia com significado.
Relativamente às categorias 1 e 2, o autor afirma que os alunos se lembravam melhor dos aspetos visuais do conceito de derivada do que dos seus aspetos analíticos. No entanto, os aspetos analíticos são importantes para a aplicação das derivadas nos diferentes ramos da ciência.
Referindo-se à categoria 3, Vinner acredita que as respostas dadas realçam uma tendência comum na aprendizagem da Matemática. Quando um conceito é usado como uma ferramenta, o seu significado original é esquecido. Assim, os aspetos instrumentais do conceito ocupam o lugar do próprio conceito. Vinner acrescenta que há uma tendência para a compreensão instrumental predominar mas que os conceitos são melhor recordados no modo relacional. Isto é suportado pelo facto de as categorias 1 e 2, juntas, terem uma percentagem superior à da categoria 3, a categoria instrumental.
Num outro estudo, realizado por Viseu (2000) com 19 professores estagiários, procurou-se identificar as conceções sobre repreprocurou-sentações gráficas da derivada de uma função. A maior parte dos futuros professores manifestou dificuldades em aplicar os conhecimentos analíticos que adquiriram na sua formação, desde os seus estudos no ensino secundário, em situações gráficas que não lhes fornecia dados que lhes permitisse recorrer a processos analíticos. O autor conclui que as principais dificuldades que esses futuros professores revelaram foram: (i) identificar e justificar se uma dada reta é tangente a uma curva num ponto; (ii) fazer a transposição da informação do gráfico de uma dada função para um possível esboço da sua derivada e vice-versa; e (iii) relacionar o sinal da segunda derivada de uma dada função com a variação da primeira derivada dessa função e, consequentemente, fazer a ligação entre os zeros da segunda derivada e os extremos da primeira derivada. Para o autor, estas dificuldades devem-se a estratégias de ensino e de aprendizagem que não potenciam a conexão entre as diferentes representações dos conceitos estudados no tema de derivada de uma função.
Em suma, a análise do erro pode contribuir para a aprendizagem dos alunos, para isso o professor deve incentivar a análise das suas próprias resoluções. Com isto, os alunos terão oportunidade de identificar e compreender os seus erros, podendo assim desenvolver processos de verificação e autocorreção que os ajudem a refazer o ‘caminho’ (Hadji, 1994).
2.2.4. Conhecimento concetual e conhecimento processual
No desenvolvimento das atividades de ensino, as estratégias delineadas pelo professor visam aproximar o conhecimento institucional e o conhecimento pessoal (Godino et al., 2008).
Quando isto não acontece, o aluno depara-se com obstáculos que não lhe permitem assimilar e acomodar esse conhecimento. Os problemas de aprendizagem têm despertado a atenção de investigadores, como é exemplo o estudo de Tall e Vinner (1981) sobre problemas de aprendizagem de limites de sucessões, de limites de funções e de continuidade. Para estes autores, tais problemas devem-se, na aprendizagem destas noções matemáticas, à diferença que existe entre os conceitos matemáticos definidos formalmente e os processos cognitivos utilizados para os conceber. Por definição do conceito, estes autores entendem ser uma sequência de palavras ou uma definição verbal que explica o conceito com precisão. Poder-se-á distinguir entre as definições formais, aceites pela comunidade científica matemática, e as definições pessoais, que são utilizadas pelos alunos na construção de uma definição formal.
Na aprendizagem de tópicos matemáticos, Schneider e Stern (2005) caracterizam dois tipos de conhecimento: conhecimento concetual e conhecimento processual. Para estes autores, o conhecimento concetual traduz o conhecimento de conceitos e princípios fundamentais e das suas inter-relações num determinado domínio. Pela sua natureza abstrata, este tipo de conhecimento pode ser verbalizado e transformado através de processos de inferência e de reflexão. Para Arends (1995), o conhecimento concetual consiste na capacidade para aprender a definir um conceito com base noutros conceitos aprendidos anteriormente e reconhecer a relação do novo conceito com outros conceitos.
Já o conhecimento processual é, segundo Schneider e Stern (2005), visto como o conhecimento instrumental relativo aos operadores e às condições em que estes podem ser utilizados para atingir determinados fins. Este tipo de conhecimento permite que os alunos possam resolver problemas e outras tarefas matemáticas, por vezes de forma autómata. Este processo de automação é realizado através da prática e permite uma rápida ativação e execução deste tipo de conhecimento. A aplicação deste conhecimento envolve pouca atenção e poucos recursos cognitivos. Arends (1995) considera que o conhecimento processual se refere à capacidade do aluno utilizar o conceito de uma forma discriminativa.
Schneider e Stern (2005) referem que a distinção entre os dois tipos de conhecimento é similar à distinção entre o conhecimento declarativo e o processual, considerando o conhecimento declarativo como o conhecimento de exemplos e de definições específicas. Numa tentativa de tentar perceber qual é o primeiro tipo de conhecimento que é adquirido pelos alunos, estes autores constataram que não há unanimidade. Há quem defenda que o conhecimento concetual é adquirido em primeiro lugar. Por exemplo, os alunos começam por
ouvir explicações verbais e com a prática é que adquirem o conhecimento processual. Porém, também há quem considere que o conhecimento processual é adquirido em primeiro lugar. Por exemplo, os alunos através de tentativa e erro adquirem o conhecimento concetual. E também há quem defenda que os dois tipos de conhecimento são adquiridos em simultâneo, sendo o aumento de um o aumento do outro.
Os desenvolvimentos teóricos atuais e os resultados da investigação em educação abrem perspetivas para o desenvolvimento de intervenções inovadoras, que valorizem um ‘sujeito interpretativo’, que interpreta e compreende o conhecimento de acordo com as suas ideias, crenças e sistemas de valores, e não um ‘sujeito recetor’ de conhecimentos instituídos. O conhecimento adquire-se, não pela interiorização de algo externo que é dado, senão construindo-o desde construindo-o intericonstruindo-or.
2.2.5. Atividades de regulação da aprendizagem
Para conseguir ultrapassar um erro é necessário que exista um momento de reflexão. Vale (2010) considera que “o erro, por si só, não conduz a nada se não for seguido de uma reflexão sobre a sua ocorrência, tendo em vista o modo de o ultrapassar” (p.35). Na sua prática escolar o aluno deve ser autónomo e criar as suas próprias estratégias de pensamento, devendo regular o seu processo de aprendizagem. Segundo Silva, Duarte, Sá e Simão (2004), “a aprendizagem regulada pelo próprio estudante resulta da interação de conhecimentos, competências, e motivações, que são necessários ao planeamento, à organização, ao controlo e à avaliação dos processos adotados e dos resultados atingidos” (p. 13). Entenda-se por regulação a autonomia dos alunos. Para Perrenoud (1999, p. 2), “regular as aprendizagens significa contribuir com o desafio cognitivo em todos os processos suscetíveis de fortalecimento dos esquemas de aprendizagem ou dos saberes”. Segundo este autor, toda a regulação pode ser considerada autorregulação. Cambra-Fierro e Cambra-Berdún (2007) veem a autorregulação como sendo uma capacidade inerente ao aluno que lhe permite “estabelecer objetivos; planear a sua atuação; observar de forma crítica; e avaliar à luz de critérios pré-determinados. Cabe ao professor criar contextos potenciadores do desenvolvimento, por parte dos alunos, da sua capacidade de reflexão, de diálogo e de negociação” (p. 2). Segundo Morin (2001), para colocar atividades de regulação em prática é necessário ensinar estratégias que permitem que os alunos enfrentem os imprevistos, o inesperado e a incerteza, modificando assim o seu normal desenvolvimento.