Dissipação no Modelo FermiUlam

(1)

Dissipac¸˜ao no Modelo Fermi-Ulam

Fortaleza

(2)

Dissipac¸˜ao no Modelo Fermi-Ulam

Tese apresentada ao Curso de Pós-graduação em F´ısica da Universidade Federal do Ceará como parte dos requisitos para a obtenção do T´ıtulo de Doutora em F´ısica.

Orientador:

Prof. Dr. Raimundo Nogueira da Costa Filho

Co-orientador:

Prof. Dr. Edson Denis Leonel

UNIVERSIDADEFEDERAL DOCEARA´ CENTRO DE CIENCIASˆ

DEPARTAMENTO DEFÍSICA CURSO DE P ÓS-GRADUAÇ ÃO EM FÍSICA

Fortaleza

(3)

! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! !

"#$%&!'()*+(#,-%(#-&!$*!.#)#/%0#12%!(#!345/-,#12%! 6(-7*+&-$#$*!8*$*+#/!$%!.*#+9!

:-5/-%)*,#!$%!.4+&%!$*!8;&-,#! !

!

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<! !

=>>?$!!!!!Sousa , "#(-/#!8*+(#($*& Tavares de!

!!!!!!!!!!!!!!!!!!!!!!!!"-&&-A#12%!(%!B%$*/%!8*+C-D6/#C!E!"#(-/#!8*+(#($*&!=#7#+*& de SousaF!8%+)#/*G#@!>HI>F!

!!!!!!!!!!!!!!!!!!!!!!!!IJ1!LFM!-/F!,%/%+F@!*(,FN!JH!,CF! !

!!!!!!!!!!!!!!!!!!!!!!!!=*&*!O"%4)%+#$%P!6(-7*+&-$#$*!8*$*+#/!$%!.*#+9@!.*()+%!$*!.-Q(,-#&@!"*A#+)#C*()%! !!!!!!!!!!!!!!!!!!$*!8;&-,#@!8%+)#/*G#@!>HI>F!

!!!!!!!!!!!!!!!!!!!!!!!!R+*#!$*!.%(,*()+#12%M!8;&-,#!S*+#/M!8;&-,#!./9&&-,#F! !!!!!!!!!!!!!!!!!!!!!!!!T+-*()#$%+M!3+%LF!"+F!U#-C4($%!V%04*-+#!$#!.%&)#!8-/W%F! !

!!!!!!!!!!!!!!!!!!!!!!!IF!8;&-,#!X&)#);&)-,#F! >F!Y-&)*C#&!"-(ZC-,%&F! 'F!=;)4/%F! !

(4)

Dissipação no Modelo Fermi-Ulam

Tese submetida à Coordenação do Curso de Pós-Graduação em Física, da Universidade Federal do Ceará, como requisito parcial para a obtenção do grau de Doutor em Física.

Aprovada em 17 / 02 / 2012

BANCA EXAMINADORA

____________________________________________________

Dr. Raimundo Nogueira da Costa Filho – Orientador

UFC

____________________________________________________

Dr. Edson Denis Leonel – Co-Orientador

UNESP

____________________________________________________

Dr. Wandemberg Paiva Ferreira

UFC

____________________________________________________

Dr. Ascânio Dias Araújo

UFC

_____________________________________________________

Dr. Juliano Antônio de Oliveira

UNESP

(5)

(6)

Ao meu orientador e amigo, Prof. Raimundo Nogueira da Costa Filho, meus sinceros agrade-cimentos não só pela orientação, mas pela confiança, incentivo e amizade que fez a diferença ao longo do trabalho.

Ao meu Co-orientador, Prof. Edson Denis Leonel, pela confianc¸a e pelas valiosas discuss˜oes.

Ao Prof. Murilo, por me permitir usufruir das instalações do Laboratório de Simulação Numérica e Rede de Óleos Pesados.

Aos membros da banca examinadora, pelas contribuic¸˜oes.

Aos amigos que conquistei ao longo desses quatro anos.

`

A minha fam´ılia pelo encorajamento e por me ajudar a suportar a saudade e a distˆancia.

`

A Deus, sem o qual n˜ao teria conseguido.

(7)

(8)

In this work, we revisit the Fermi accelerator model, also known as Fermi-Ulam model. This model consists of a classical particle of unitary mass wich is confined to bounce between two rigid walls. One of them is fixed and the other one is assumed to move periodically in time. The particle collisions with the walls are assumed to be elastic. The description of the dynamic is made everytime the particle collides with the moving wall, so that we know the particle’s time and velocity at each collision needed to describe the dynamic of the system. Two versions for this model are studied: the complete and the simplified versions. In the simplified version, two walls of the model are assumed to be fixed. The Fermi-Ulam model is a conservative model because it preserves area of the phase space. Our analytical and numerical results for this conservative model are presented and discussed. Some dynamical properties for a particle suffering the action of a drag force are obtained for a dissipative Fermi-Ulam model. The dissipation is introduced via a viscous drag force, like a gas, wich is assumed to be proportional to any power of the velocity, F =₋ηVγ. The dynamics of the models are described by two dimensional nonlinear mappings obtained via the solution of the second Newtons’ law of motion. We prove analytically that the decay of high energy is given by a continued fraction wich recovers the following expressions: (i) linear for γ =1, (ii) exponential for γ=2 and (iii) second degree polynomial type forγ =1.5. For any value ofγ, the numerical results shows a polynomial behavior for the velocity decay. Our results are discussed for both the complete and simplified versions. The phase spaces and the basin of attraction for some values of γ are obtained. Complementing our studies on this dissipative version of the Fermi-Ulam model, a mixed model was proposed. In this model, one particle travels through two different media. It started in a medium with no dissipation lets say vacuum and at some point it enters a region with a dissipative medium. The dissipation is also introduced by a viscous drag force, such that F =₋ηVγ_{. In particular, for the study of the mixed model we use}

(9)

ξ posic¸ ˜ao da parede imaginaria dos modelos mistos´

η coef iciente de viscosidade

ǫ amplitude de oscilac¸ ˜ao do movimento da parede movel´

ω f requˆencia angular da parede movel´ w wall(denota parede movel´ )

l distância entre a parede f ixa e a posiç ão de equil´ıbrio da parede movel´

ε grandeza adimensional(amplitude de oscilac¸ ˜ao da parede movel´ )

φ grandeza adimensional(f ase da parede movel´ ) λ expoente de Lyapunov

ǫ0 distância inf initesimal de uma condiç ão inicial

γ expoente da velocidade da part´ıcula(_∈ ℜ∗₊)

(10)

1 Introduc¸˜ao p. 11

2 Modelo Fermi-Ulam Conservativo p. 17

2.1 Introduc¸˜ao . . . p. 17

2.2 Modelo Completo . . . p. 18

2.2.1 Mapeamento . . . p. 18

2.2.2 Matriz Jacobiana . . . p. 25

2.3 Modelo Simplificado . . . p. 28

2.3.1 Mapeamento . . . p. 28

2.4 Resultados Num´ericos . . . p. 30

2.4.1 Espac¸os de Fases . . . p. 30

2.4.2 Precis˜ao Num´erica . . . p. 34

2.4.3 Expoentes de Lyapunov . . . p. 35

3 Modelos Fermi-Ulam Dissipativos p. 41

3.1 Introduc¸˜ao . . . p. 41

3.2 Forc¸a Dissipativa Proporcional `a Velocidade da Part´ıcula: F =₋V . . . p. 42 3.2.1 Modelo Completo . . . p. 42

3.2.3 Resultados Num´ericos para o Modelo Completo . . . p. 48

3.2.4 Modelo Simplificado . . . p. 52

(11)

3.3.1 Modelo Completo . . . p. 55

3.3.3 Resultados Num´ericos para o Modelo Completo . . . p. 64

3.3.6 Resultados Num´ericos para o Modelo Simplificado . . . p. 67

4 Modelo Fermi-Ulam: Descrição Genérica para um Caso Dissipativo p. 75

4.1 Introduc¸˜ao . . . p. 75

4.2 Modelo Completo . . . p. 76

4.2.1 Mapeamento . . . p. 76

4.2.3 Comportamento da Velocidade . . . p. 85

4.3 Modelo Simplificado . . . p. 87

4.3.1 Mapeamento . . . p. 87

4.3.3 Resultados Num´ericos para o Modelo Simplificado . . . p. 89

5 Modelos Fermi-Ulam Mistos p. 100

5.1 Introduc¸˜ao . . . p. 100

5.2 Modelo Misto 1: Regi˜ao Conservativa versus Regi˜ao Dissipativa comγ=1 . . p. 100

5.2.1 Modelo Completo . . . p. 101

5.2.3 Resultados Num´ericos . . . p. 110

5.3 Modelo Misto 2: Regi˜ao Conservativa_×Regi˜ao Dissipativa comγ =2 . . . . p. 113 5.3.1 Modelo Completo . . . p. 113

(12)

6 Conclus˜oes e Perspectivas p. 126

(13)

1 Introduc¸˜ao

Em todos os ramos da ciência um dos conceitos centrais no entendimento dos fenômenos natu-rais é o de evolução no tempo. A descrição dinâmica, na qual o tempo exerce o papel essencial de parâmetro de referência, é utilizada nas mais variadas áreas da f´ısica, da astronomia, da matemática

aplicada e da engenharia.

Com o sucesso da mecânica newtoniana onde a evolução temporal dos sistemas é representada matematicamente pelas chamadas leis de Newton, estabeleceu-se um modelo básico constituindo o ponto de partida para o que se chama hoje de “teoria dos sistemas dinâmicos”. Um sistema dinâmico é descrito por qualquer conjunto de grandezas (chamadas variáveis dependentes) que

variam no tempo (variável independente). O estado do sistema é representado pelos valores, num dado instante de tempo, do conjunto completo de variáveis dependentes. O espaço de estados poss´ıveis para o sistema é denominado espaço de fases. A evolução de um tal sistema é descrita por um conjunto de equações discretas ou cont´ınuas (diferenciais) que constituem a regra que permite

prever o seu comportamento futuro, global ou parcialmente, uma vez conhecido seu estado inicial. Se as variáveis dependentes e o tempo forem cont´ınuos essas regras serão equações diferenciais ordinárias; caso existam outras variáveis independentes, também cont´ınuas - como as coordenadas espaciais, no caso da f´ısica dos meios cont´ınuos ou nas teorias de campo - teremos as equações

diferenciais parciais. A existência de alguma variável discreta leva à regra com diferenças finitas, genericamente denominadas de mapeamentos.

A concepção determin´ıstica da mecânica clássica, exposta por Laplace, em 1814 [1], pretendia a previsibilidade quantitativa absoluta para um sistema clássico, se o seu estado inicial fosse conhe-cido com exatidão. Maxwell, já em 1873 [1], com aguda sensibilidade e intuição f´ısica, alertava

para as limitações da visão determinista laplaciana e mostrava a existência de sistemas que, mesmo com poucas part´ıculas, exigiam uma descrição probabil´ıstica em função de apresentarem grande sensibilidade à variação das condições iniciais. Ou seja, uma variação extremamente pequena nas condições iniciais induziria variações grandes no comportamento futuro desses sistemas, tornando

(14)

Mas essas idéias não empolgaram seus contemporâneos e só com advento dos computadores e com a geração recente de novos conceitos, provenientes de diversas áreas do conhecimento, o

estudo de sistemas com comportamento ca´otico viriam se ampliar enormemente.

A classe de problemas dos bilhares constitui um dos tipos mais simples de sistemas dinâmicos [2]. Eles consistem de uma part´ıcula confinada numa região do espaço delimitada por uma fron-teira. As colisões da part´ıcula com a fronteira podem ser elásticas ou inelásticas. A fronteira atua como uma força externa e sua posição no espaço pode ser estática ou dependente do tempo.

Dependendo da geometria das fronteiras, os bilhares podem apresentar dinâmica integrável, não integrável ou caótica, mesmo para os casos em que a fronteira é estática. Quando a posição da fronteira do bilhar é dependente do tempo [2], a energia cinética da part´ıcula pode apresentar crescimento ilimitado, fenômeno conhecido como Aceleração de Fermi ou permanecer limitada.

Embora os bilhares possam ser descritos através da formulação Hamiltoniana, é mais fácil des-crevê-los por meio de mapas discretos. Como o movimento da part´ıcula entre uma colisão e outra é trivial, estes mapas descrevem a dinâmica dos bilhares no instante de cada colisão. Apesar de simples, estes sistemas apresentam dinâmica bastante rica, o que motiva a investigação numérica

e anal´ıtica de suas propriedades.

Neste trabalho, revisitamos o Modelo do Acelerador de Fermi, que ´e um tipo de bilhar

unidi-mensional, descrito por um mapeamento bidiunidi-mensional, buscando entender e descrever algumas de suas propriedades dinâmicas. Os estudos sobre o modelo unidimensional do Acelerador de Fermi iniciaram-se em 1949 [3], quando Enrico Fermi tentou descrever um mecanismo de aceleração dos raios cósmicos no meio interestelar. Este mecanismo simula as interações desses raios com

campos magnéticos oscilantes. Um sistema dinâmico que corresponde ao modelo original pro-posto por Fermi, foi depois propro-posto por Ulam [4]. Este modelo consiste de uma part´ıcula clássica confinada e colidindo elasticamente entre duas paredes r´ıgidas. Uma das paredes é assumida como sendo fixa enquanto que a outra move-se periodicamente no tempo. Tal modelo ficou conhecido

como Modelo Fermi-Ulam [5–8] e, desde então, vem sendo estudado em muitas outras diferentes versões. Dentre algumas das modificações sofridas e estudadas no modelo, podemos citar a in-clusão de campos externos, colisões inelásticas, coeficientes de amortecimento e também efeitos quânticos [9–16]. Uma versão alternativa do modelo, na presença de campo gravitacional, também

chamada de bouncer [17], consiste de uma part´ıcula colidindo em uma plataforma vertical móvel, sob um campo gravitacional constante. A propriedade mais importante do modelo bouncer e que se opõe ao modelo Fermi-Ulam é que ele mostra, para uma combinação espec´ıfica de parâmetros de controle e condições iniciais, o fenômeno da aceleração de Fermi. Uma versão h´ıbrida dos

(15)

resultados do modelo Fermi-Ulam no limite de campo externo zero e mostra propriedades do mo-delo bouncer para campo gravitacional intenso. Al´em disso, para um certo conjunto de parˆametros

de controle, propriedades que s˜ao caracter´ısticas individuais do modelo Fermi-Ulam e do modelo

bouncer, podem coexistir na vers˜ao h´ıbrida do modelo.

Considerando a introdução de dissipação, uma consequência imediata é que a dinâmica do modelo é drasticamente afetada. Sabemos que existem muitas diferentes maneiras de se introduzir forças de amortecimento no sistema. Uma delas é considerar colisões inelásticas da part´ıcula com

uma das paredes ou com as duas. Assim, a part´ıcula sofre uma perda fracional de energia a cada colisão. Como consequência, o sistema não preserva área do espaço de fases, cuja estrutura mista é destru´ıda. Em especial, é poss´ıvel observar diferentes comportamentos assintóticos à medida que o coeficiente de amortecimento é variado. Dentre eles, efeitos de transiente [19], pontos fixos

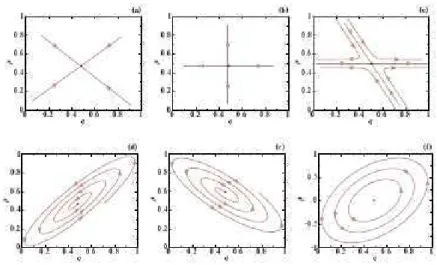
atrativos [20] e atratores caóticos [21, 22]. A figura 1.1 mostra a classificação dos pontos fixos quanto a sua estabilidade.

Figura 1.1: Em (a) temos um ponto fixo est´avel. Em (b) temos um ponto fixo inst´avel. A figura (c)

ilustra um ponto de sela. Os pontos fixo espirais (d) e (e) correspondem, respectivamente, a um ponto estável e um instável. A figura (f) ilustra trajetórias em torno de um ponto fixo el´ıptico.

O atrator é definido como sendo um ponto ou um conjunto de pontos para o(s) qual(is) a evolução temporal de uma condição inicial converge(m) no espaço de fases para tempos suficien-temente longos. Em sistemas que contraem medida no espaço de fases, os pontos fixos das figuras

1.1(a) e (d) correspondem a atratores. O tempo que a part´ıcula gasta vagando até convergir para um ou mais destes pontos é chamado de transiente. Em sistemas com muitos atratores, o interesse está centrado na determinação das bacias de atração de cada atrator, cujas fronteiras podem ser cont´ınuas ou fractais. A bacia de atração é uma região no espaço de fases cuja evolução temporal

(16)

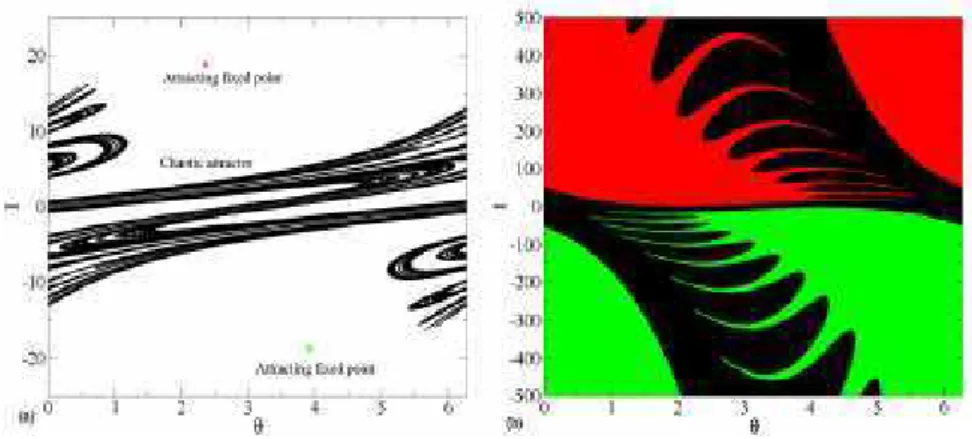
Figura 1.2: Em (a) pontos fixos atrativos e um atrator caótico. Em (b) as bacias de atração

correspondentes aos pontos fixos atrativos e ao atrator ca´otico.

importante propriedade que pode ser extra´ıda da presença de dissipação na dinâmica do modelo é a ocorrência de crises de fronteira [22]. A figura 1.3 mostra a caracterização de um evento de crise de fronteira.

Figura 1.3: Caracterização de uma crise de fronteira. As variedades instaáveis dos pontos

fi-xos de sela são mostradas nas cores vermelha e verde, ao passo que as variedades estáveis são mostradas nas cores azul e cinza. Em (a), comportamento do sistema antes das crises e, em (b), comportamento do sistema após as crises.

Um evento de crise de fronteira acontece quando dois ramos de variedades estáveis de um ponto fixo do tipo sela, que estabelecem os limites das fronteiras das bacias de atração, colidem com as bordas do seu atrator caótico. É sabido que num ponto fixo do tipo sela, que é um ponto de

(17)

estáveis estabelecem as fronteiras entre o ponto fixo atrativo e o atrator caótico. Em outras palavras, os dois ramos das variedades instáveis evoluem de modo que um deles converge para o ponto

fixo atrativo enquanto que o outro converge para o atrator caótico. Os dois ramos da variedade estável geram as fronteiras da bacia de atração, tanto para o atrator caótico quanto para o ponto fixo atrativo. Reduzindo-se a força de dissipação do sistema, os dois ramos da variedade estável colidem com as bordas do seu atrator caótico. Essa colisão implica na súbita destruição do atrator

caótico e também de sua bacia de atração. Após a crise, o atrator caótico é substitu´ıdo por um transiente caótico que é descrito por uma lei de potência [15, 23]. Outra opção diferente de se introduzir força de amortecimento no sistema é considerar que a part´ıcula move-se na presença de uma força de arrasto. Este tipo de dissipação age ao longo de toda a trajetória da part´ıcula, ao

contrário das colisões inelásticas, onde ela atua somente no instante de cada impacto. Este tipo de froça de dissipação será tratado nesta tese.

O principal objetivo deste trabalho é caracterizar os efeitos de uma força dissipativa no Modelo Fermi-Ulam. Esta força dissipativa é introduzida no sistema via um movimento relativo de uma part´ıcula dentro de um fluido, como um gás. Uma consequência deste tipo de força de

amorte-cimento introduzida no sistema é ter o determinante da matriz Jacobiana apresentando somente a propriedade de contração de área do espaço de fases. Adicionalmente, para uma dada combinação de parâmetros de controle o sistema exibe um número arbitrariamente grande de pontos fixos atra-tivos e órbitas periódicas. Órbita é a sequência de posições de um sistema em seu espaço de fases,

para uma dada condição inicial, por onde a solução passa à medida que o tempo evolui. Este grande número de órbitas periódicas produz uma complexa estrutura de bacia de atração, cujos limites percorrem quase todo o espaço de fases. Em particular, são observados muitos atratores de baixo per´ıodo. ´E importante salientar que estudos de sistemas dinâmicos considerando um single

rotor [24], tem mostrado que, no caso de sistemas Hamiltonianos, o sistema exibe um vasto n´umero

de órbitas periódicas estáveis e cada uma delas converge para um ponto fixo atrativo quando uma pequena dissipação é aplicada. Além disso, é esperado que a complexidade de tal modelo possa ser extendida para sistemas de alta dimensão, como por exemplo, o double rotor [25], onde para

parâmetros de controle espec´ıficos são encontrados mais de 1000 atratores periódicos de baixo per´ıodo. Os modelos Fermi-Ulam dissipativos estudados aqui também são modelos que exibem grande número de atratores periódicos coexistentes. Neste trabalho, vamos estudar as principais propriedades quantitativas e qualitativas observadas nestes sistemas.

O trabalho est´a organizado da seguinte forma: no Cap´ıtulo 2 apresentamos o modelo Fermi-Ulam conservativo e discutimos as principais caracter´ısticas do sistema. No Cap´ıtulo 3,

(18)

discu-tido no Cap´ıtulo 3 é apresentado. No Cap´ıtulo 5, estudamos dois modelos Fermi-Ulam mistos. Os modelos são divididos em duas regiões distintas separadas por um parâmetroξ. No primeiro modelo, a região 1 é assumida como sendo conservativa e a região 2 é dissipativa com força de arrasto do tipoF =₋ηV; no segundo modelo, a região 1 continua sendo conservativa e a região 2 agora passa a sofrer a ação de uma força do tipo F =₋ηV2_{. Finalmente, nossas conclusões e}

(19)

2 Modelo Fermi-Ulam Conservativo

2.1 Introduc¸˜ao

O acelerador de Fermi é um sistema dinâmico proposto por Enrico Fermi [3] com o objetivo de compreender o processo pelo qual os raios cósmicos adquirem altas energias. Este modelo consiste basicamente de uma part´ıcula carregada que interage com campos magnéticos dependentes do

tempo. Posteriormente, vários autores propuseram versões do modelo original adaptadas para diferentes aplicações.

Quando Enrico Fermi propôs seu estudo, ele não utilizou equações matemáticas para descrever a dinâmica do modelo. Seu estudo se concentrou na análise do comportamento dinâmico do sis-tema apenas de forma qualitativa. Foi então que Stanislaw Ulam [4], propôs um sissis-tema dinâmico que corresponde à essência do modelo original proposto por Fermi. Deste modo, ele pôde

equaci-onar a dinâmica do sistema e estudar numericamente o modelo. O modelo, então, ficou conhecido como modelo Fermi-Ulam [5–8], também chamado de modelo bouncing ball, que consiste de uma part´ıcula clássica de massamconfinada entre duas paredes r´ıgidas e colidindo elasticamente com elas. Uma das paredes é assumida como sendo fixa ao passo que a outra move-se periodicamente

no tempo. Por ser um modelo relativamente simples, unidimensional e que produz resultados ex-tremamente interessantes, serviu de instrumento de estudo de muitos f´ısicos e matemáticos, que acrescentaram uma variedade de modificações no modelo e estudaran suas propriedades. Ainda nos dias de hoje o modelo Fermi-Ulam tem despertado muito interesse uma vez que muitas de suas

propriedades dinˆamicas podem ser descritas por leis de potˆencia [3, 15].

O Modelo Fermi-Ulam é um modelo conservativo, pois preserva medida do espaço de fa-ses. Neste tipo de modelo, a estrutura caracter´ıstica de sistemas Hamiltonianos é observada, com espaço de fases misto, contendo ilhas Kolmogorov-Arnold-Moser (KAM), curvas invariantes

spanning separando diferentes porções do espaço de fases e mares de caos. As ilhas KAM são

(20)

As curvas invariantes spanning percorrem o espac¸o de fases totalmente ao longo do eixo hori-zontal, a fase, e s˜ao invariantes por iterada. Assim, uma part´ıcula na curva jamais sai dela. Como

consequência de sua disposição no espaço de fases, limitam o ganho de energia da part´ıcula per-correndo o mar de caos. Tal região do espaço de fases é muito sens´ıvel às variações nas condições iniciais. Um bom indicador de caos é o conhecido expoente de Lyapunov, que mede a taxa de afastamento da evolução de duas condições iniciais muito próximas e consequentemente levando

à perda de previsibilidade de condições iniciais muito próximas.

Neste Cap´ıtulo, fazemos uma breve revisão do modelo de Fermi Conservativo e discutimos uma simplificação no modelo, a qual é chamada de versão simplificada [8]. Na versão completa do modelo assumimos que uma das paredes está fixa ao passo que a outra move-se periodicamente no tempo. Na versão simplificada assumimos que as duas paredes do modelo estão fixas. Constru´ımos

os espaços de fases para as duas versões, onde observamos a existência de ilhas KAM, mares de caos e curvas invariantes spanning. Na última seção do cap´ıtulo, caracterizamos e avaliamos numericamente os expoentes de Lyapunov para a região no mar de caos localizada abaixo da primeira curva invariante spanning do espaço de fases dos modelos completo e simplificado.

2.2 Modelo Completo

2.2.1 Mapeamento

Nesta seção, vamos descrever os passos necessários para a construção do mapa não-linear bidimensional que descreve o modelo Fermi-Ulam conservativo.

O modelo do acelerador de Fermi, como tamb´em ´e conhecido, consiste de uma part´ıcula

clássica de massa unitária, confinada ao interior de duas paredes r´ıgidas, sendo uma delas fixa e a outra com posição dependente do tempo, sofrendo colisões elásticas com as paredes. A parede fixa está localizada emx=le a parede móvel tem a equação da posição dada porxw=εcos(ωt),

onde ε é a amplitude de oscilação do movimento, ω é a frequência angular et é o tempo. Neste modelo, a part´ıcula não experimenta a influência de nenhum campo externo. A figura (2.1) ilustra o modelo.

A região compreendida no intervalo dex_∈[₋ǫ, ǫ] é chamada de zona de colisão. Na figura,l é a distância entre a parede fixa e a posição de equil´ıbrio da parede móvel. A velocidade da parede móvelvw é dada pela derivada da sua posição em relação ao tempo, ou seja,vw= (dxw/dt), que

fornecevw=−εωsin(ωt). Considera-se que a velocidade da parede m´ovel n˜ao seja afetada pelas

(21)

Figura 2.1: Esquema ilustrativo do modelo Fermi-Ulam.

A dinâmica do modelo pode ser descrita pelo uso de um mapeamento discreto, bidimensional, não-linear, escrito nas variáveis (v, t), ondev etcorrespondem, respectivamente, à velocidade da part´ıcula e o tempo imediatamente após a colisão com a parede móvel. Dependendo da combinação de condições iniciais e parâmetros de controle, duas situações devem ser consideradas:

(1) A part´ıcula sofre mais de uma colisão com a parede móvel antes de sair da zona de colisão, emx_∈[₋ǫ, ǫ]. A este tipo de colisão daremos o nome de Colisão Múltipla.

(2) A part´ıcula sofre uma única colisão com a parede móvel e abandona a zona de colisão. A

este tipo de colis˜ao daremos o nome de Colis˜ao Simples.

Caso (1): O mapeamento para colis˜oes m´ultiplas, caso em que a part´ıcula colide sucessivas

vezes com a parede móvel antes de deixar a zona de colisão, é definido como uma aplicação T(vn, tn) = (vn+1, tn+1), que nos permite determinar os valores dessas variáveis no instantetn+1

(próxima colisão), uma vez conhecidos os valores dessas variáveis no instantetn(colisão anterior).

Supomos, como condição inicial, a situação em que a part´ıcula, no instantet=tn, tem posição

dada porxp(tn) =xw(tn) =εcos(ωtn). A part´ıcula est´a com velocidade inicialvn>0, uma vez

que est´a viajando no sentido positivo do eixox.

A velocidade da part´ıcula é obtida considerando a conservação de energia e momento no

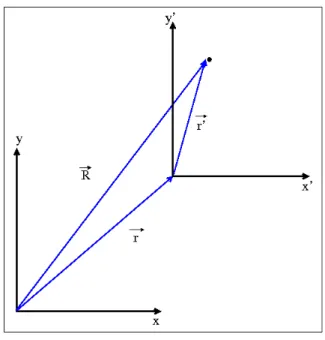
re-ferencial da parede móvel. A seguir, vamos descrever o processo de obtenção desta velocidade através deste princ´ıpio. A figura (2.2) mostra, de forma esquemática, como é feita a mudança de referenciais.

(22)

Figura 2.2: Esquema ilustrativo da mudança de referenciais. O planoxyrepresenta o referencial inercial, ou seja, a parede fixa. O plano x′y′ representa o referencial não inercial, ou seja, a parede móvel.

dinâmica é unidimensional, a partir daqui não consideraremos mais a notação vetorial) medida no

referencial inercial, dada por

vp=vp′+vw, (2.1)

onde v′_p é a velocidade da part´ıcula vista do referencial não inercial e vw é a velocidade da

pa-rede medida no referencial inercial. Identificando o instante imediatamente anterior ao choque pelo ´ındicej e o instante imediatamente posterior ao choque pelo ´ındicek, podemos reescrever a equac¸˜ao (2.1) nestes dois instantes,

v_p,j′ =vp,j−vw,j, (2.2)

v′_p,k=vp,k−vw,k. (2.3)

No sistema não inercial, a velocidade da part´ıcula depois da colisão é a mesma de antes da colisão (condição de colisões elásticas), porém com o sentido contrário, ou seja

v_p,k′ =₋v′_p,j. (2.4)

Substituindo a equação (2.2) na equação (2.4), encontramos que,v_p,k′ =₋(vp,j−vw,j), ou ainda

(23)

Tendo encontrado no sistema não inercial a velocidade da part´ıcula depois da colisão, voltamos novamente ao referencial inercial da parede fixa, combinando a equação (2.3) com a equação (2.5)

e obtemos

vp,k=−vp,j+vw,j+vw,k. (2.6)

Podemos reescrever esta equação com novos ´ındices, substituindo, do lado esquerdo, o ´ındice (k)que caracteriza o instante posterior ao impacto pelo ´ındice(n+1), que caracteriza o próximo impacto (n+1), uma vez que o mapeamento sempre considera as velocidades após os impactos com a parede móvel. O lado direito da expressão será modificado levando-se em conta que a velocidade com que a part´ıcula alcança a parede móvel no momento anterior ao impacto (´ındice j), é igual à velocidade da part´ıcula logo após o impacto anterior (´ındicen) e que a velocidade da parede imediatamente anterior ao impacto é igual à sua velocidade imediatamente após ao impacto, calculada no instante(n+1). Assim,

v_p,₍_n₊1)=−vp,(n)+2vw,(n+1). (2.7)

Uma vez que a velocidade da parede m´ovel ´e vw = −εωsin(ωt), temos que a velocidade da

part´ıcula para o caso das colisões múltiplas é dada por:

vn+1=−vn−2εωsin(ωtn+1). (2.8)

O próximo passo é obter o instante da colisão da part´ıcula com a parede móvel (tc). Este

instante é obtido da condição de que xw(t) =xp(t), ou seja, no instante do choque, a posição

da parede móvel é igual à posição da part´ıcula. Sabemos que a velocidade da part´ıcula do nosso

modelo é sempre constante, consequentemente sua aceleração é nula. Assim podemos, de forma mais genérica, utilizar a equação da posição da cinemática,x₋x0=v0(t−t0) + (1/2)a(t−t0)2,

para encontrarmos a posição da part´ıcula no instante de colisão com a parede móvel. Considerando a aceleração nula, o segundo termo depois da igualdade da equação acima se torna zero, reduzindo

nossa equac¸˜ao a x₋x0=v0(t−t0). Isolandox, encontramosx=x0+v0(t−to). Combinando

esta equac¸˜ao com os dados do nosso problema, obtemos que

xw(tn+1) =xp(tn+1) =xp(tn) +vntc, (2.9)

ondexw(tn+1) é a posição da parede móvel no instante da colisão(n+1)com a part´ıcula,xp(tn)

é a posição da part´ıcula no instante da colisão n evn é a velocidade da part´ıcula no intervalo tc

entre as colisões. Combinando as equações anteriores, encontramos

(24)

que fornece,

g(tc) =εcos(ω[tn+tc])−εcos(ωtn)−vntc. (2.10)

O instante de tempo tc é obtido numericamente resolvendo-se g(tc) =0. Se a função g(tc) não

admitir soluc¸˜ao no intervalo tc ∈ (0,2π/ω], podemos concluir que a part´ıcula deixa a zona de

colisão sem experimentar colisões múltiplas com a parede móvel. Entretanto, considerando que a part´ıcula está na zona de colisão, o tempo na próxima colisão(tn+1) é, então, dado por

tn+1=tn+tc, (2.11)

ondetnrepresenta o tempo inicial da evolução etco instante da colisão da part´ıcula com a parede

m´ovel.

Assim, podemos escrever o mapeamento que descreve a dinâmica do modelo para colisões múltiplas da part´ıcula com a parede móvel, dado pelas Eqs.(2.8) e (2.11), na forma

TM : (

vn+1=−vn−2εωsin(ωtn+1)

tn+1=tn+tc

. (2.12)

onde o ´ındice “M” denota colis˜oes m´ultiplas.

Considerando, agora, o caso (2), em que a part´ıcula sofre uma única colisão com a parede móvel antes de abandonar a zona de colisão, vamos contruir o seu mapeamento.

Num instante inicialtn, supomos novamente que a posic¸˜ao da part´ıcula seja a mesma que a

posição da parede móvel,xp(tn) =xw(tn), e que sua velocidade inicial seja positiva,vn>0, uma

vez que a part´ıcula está se deslocando no sentido positivo ao longo do eixo x. A part´ıcula viaja em direção à parede fixa, colide elasticamente e é refletida em direção à parede móvel. Para obter a fase da parede móvel na próxima colisão, precisamos determinar o tempo que a part´ıcula gasta para percorrer este caminho, saindo de xp(tn) =xw(tn) e viajar atéx=l, ser refletida e viajar

novamente até a próxima colisão. A figura (2.3) mostra o trajeto percorrido pela part´ıcula.

Considerando a velocidade constante vn com que a part´ıcula viaja para a direita, temos que

vn = (l−εcos(ωtn))/td, onde td ´e o intervalo de tempo que a part´ıcula gasta viajando para a

direita. Isolandotd, encontramos

td=

l₋εcos(ωtn)

vn

.

Considerando, agora, a velocidade constante ve com que a part´ıcula viaja para a esquerda, com

(25)

Figura 2.3: Trajeto percorrido pela part´ıcula saindo da zona de colis˜ao, colidindo elasticamente

com a parede fixa, sendo refletida e entrando novamente na zona de colis˜ao.

gasta viajando para a esquerda, até alcançar a zona de colisão. Isolandote, encontramos

te=

l₋ǫ vn

.

De volta à zona de colisão, a part´ıcula colide com a parede móvel no instante em quexw(t) =xp(t)

e, para que esta condição seja satisfeita, vamos utilizar a equação da posição dada pela equação (2.9). Considerando (i) o tempo de viagem da part´ıcula para a direita (td), do instante do choque

com a parede móvel até o choque com a parede fixa, incluindo o tempo para abandonar a zona de colisão; (ii) o tempo de viagem da part´ıcula para a esquerda(te), da parede fixa até a entrada na

zona de colisão; (iii) e o intervalo de tempo (tc) entre a entrada na zona de colisão e a próxima

colisão, podemos substituir estes valores na equação (2.9) e obtermos,

εcos[ω(tn+td+te+tc)] =ε−vntc,

que é a equação que fornece o tempo de colisão da part´ıcula com a parede móvel tc. O sinal da

velocidade é negativo devido a part´ıcula estar viajando para a esquerda, no sentido negativo do eixoxantes de colidir com a parede móvel. Chamando esta equação def(tc)e fazendof(tc) =0,

obtemos

f(tc) =εcos[ω(tn+td+te+tc)]−ε+vntc. (2.13)

O tempotn+1no instante do choque(n+1), ser´a dado pela somas dos tempos do argumento

da função cosseno da equação (2.13), ou seja

tn+1=tn+td+te+tc. (2.14)

(26)

anteriormente. Assim, da equac¸˜ao (2.7), temos quevn+1=−ve+2vw. Considerando como

ante-riormente queve =−vndevido ao choque elástico, obtemos a equação,

vn+1=vn+2vw. (2.15)

Sabemos que vw(tn) =−εωsin(ωtn)no instantetn. Analogamente, no instantetn+1, a equac¸˜ao

da velocidade da parede fica vw =−εωsin(tn+td+te+tc). Note que a soma dos tempos no

argumento da função seno desta equação é o próprio tn+1. Considerando que a velocidade da

part´ıcula para a esquerda é negativa e substituindo na equação (2.15) estas expressões encontradas, a velocidade da part´ıcula na próxima colisão é então dada por

vn+1=vn−2εωsin(ωtn+1), (2.16)

ou seja, a velocidade da part´ıcula ap´os o choque com a parede m´ovel.

Assim, as Eqs.(2.14) e (2.16) formam o mapeamento geral para o caso das colis˜oes simples, dado por

TS : (

vn+1=vn−2εωsin(ωtn+1)

tn+1=tn+td+te+tc

, (2.17)

onde o ´ındice “S” denota colis˜oes simples.

Para obtermos tc, precisamos encontrar uma raiz para a equação (2.13), que é uma equação

transcendental. Desse modo,tcn˜ao pode ser obtido analiticamente de forma expl´ıcita, mas apenas

numericamente.

A funçãof(tc)pode admitir mais de uma raiz no intervalotc∈[0,2π/ω], mas a colisão entre

a parede m´ovel e a part´ıcula ´e representada pela raiz de menor valor dentro deste intervalo.

Como podemos ver, existe um número excessivo de parâmetros de controle nos mapas(2.12) e (2.17), como ω, ε e l e nem todos são relevantes para a descrever a dinâmica, portanto, para descrever a dinâmica do sistema não precisamos de todas elas. Então, torna-se conveniente definir variáveis adimensionais mais apropriadas. Assim, definimos ǫ =ε/l, Vn =vn/(ωl) e o tempo

é medido em termos do número de oscilações da parede móvel, consequentemente, φn =ωtn.

Incorporando estas novas vari´aveis no modelo, o mapaT, tal queT(Vn, φn) = (Vn+1, φn+1), pode

ser escrito como

T :

(

Vn+1=Vn∗−2ǫsin(φn+1)

φn+1=φn+∆Tn mod(2π)

, (2.18)

onde o termoV_n∗=₋Vne o termo∆Tn=φc, comφc obtido da equac¸˜ao

(27)

comφc∈(0,2π], para o caso das Colis˜oes M´ultiplas.

No caso das Colis˜oes Simples, o termo V_n∗ =Vn e o termo ∆Tn = ([(1−ǫcos(φn))/Vn] +

[(1₋ǫ)/Vn] +φc), comφcobtido da equac¸˜ao

F(φc) =ǫcos(φn+φd+φe+φc)−ǫ+Vnφc, (2.20)

comφc∈[0,2π].

A func¸˜aomod(2π)foi introduzida para manter a fase dentro do intervalo[0,2π].

2.2.2 Matriz Jacobiana

O cálculo da matriz Jacobiana será usado para a obtenção dos expoentes de Lyapunov nas

sec¸˜oes seguintes.

A matriz Jacobiana J do mapa T é a matriz cujos coeficientes são dados pelas derivadas parciais em relação às equações do mapa dado por(2.18), definido em termos da velocidadeVn+1

e da faseφn+1. Esta matriz ´e escrita como

J=



  

∂Vn+1

∂Vn

∂Vn+1

∂φn

∂φn+1

∂Vn

∂φn+1

∂φn     .

Considerando o caso (1), para as colisões múltiplas, os elementos da matriz Jacobiana são

dados por

∂Vn+1

∂Vn = −

1₋2ǫcos(φn+1)

∂φn+1

∂Vn ,

∂Vn+1

∂φn

= ₋2ǫcos(φn+1)

∂φn+1

∂φn

,

∂φn+1

∂Vn =

∂φc

∂Vn,

∂φn+1

∂φn

= 1+∂φc ∂φn

,

onde os termos ∂φc

∂Vn e

∂φc

∂φn são obtidos derivando-se implicitamente G(φc) =0 em relação àVn e

φn, respectivamente. Assim,

−ǫsin(φn+1)

∂φc

∂Vn

φc−Vn

∂φc

∂Vn

(28)

∂φc

∂Vn =

φc

−Vn−ǫsin(φn+1)

, (2.21)

−ǫsin(φn+1)

1+∂φc ∂φn

+ǫsin(φn)−Vn

∂φc

∂φn

=0,

∂φc

∂φn

= ǫsin(φn+1)−ǫsin(φn)

−Vn−ǫsin(φn+1)

. (2.22)

O determinante da matriz Jacobiana é dado pela seguinte multiplicação

det(J) =

∂Vn+1

∂Vn

·

∂φn+1

∂φn

−

∂Vn+1

∂φn

·

∂φn+1

∂Vn

.

Assim, depois de alguma ´algebra, encontramos que o determinante da matriz Jacobiana para o

caso das colisões múltiplasdet(JM) é dado por,

det(JM) =

Vn+ǫsin(φn)

Vn+1+ǫsin(φn+1)

. (2.23)

O ´ındice “M” denota colis˜oes M´ultiplas.

De posse do determinante da matriz Jacobianadet(JM), podemos verificar por que o modelo

Fermi-Ulam é chamado de conservativo. Para isso, vamos analisar a evolução de uma medida

infinitesimal do espac¸o de fases bidimensional deste modelo, como mostra a figura (2.4).

Figura 2.4: Exemplo de evolução de uma medida infinitesimal do espaço de fases do modelo

Fermi-Ulam. Na figura,dA=dV dφ.

(29)

a seguir,

d(An+1) =det(J) d(An).

A equação acima nos diz que a medida no instante(n+1)é igual ao determinante da matriz Jacobi-ana multiplicado pela medida num dado instante inicial(n). Substituindo o valor do determinante det(JM)para colisões múltiplas na equação acima, obtemos

d(An+1) =

Vn+ǫsin(φn)

Vn+1+ǫsin(φn+1)

d(An).

A evolução das medidas, por definição, é dada pela evolução da velocidade da part´ıcula e da fase da parede móvel no instante da colisão. Reorganizando os termos, ficamos com

d(Vn+1) d(φn+1) (Vn+1+ǫsin(φn+1)) = (Vn+ǫsin(φn)) d(Vn) d(φn).

Chamando o termo do lado esquerdo do sinal da igualdade de (dµn+1)e o termo do lado direito

do sinal de igualdade de(dµn), obtemos,

dµn+1=dµn.

Podemos observar que todos os termos com ´ındice (n+1)ficaram do lado esquerdo da equação enquanto que os termos com ´ındice(n)ficaram do lado direito. Este resultado nos mostra que a evolução das medidas no instante(n+1)é igual à evolução das medidas no instante(n). É impor-tante enfatizar que o formato da medida no insimpor-tante inicial da evolução não tem necessariamente o mesmo formato geométrico da medida no instante final da evolução.

Considerando o caso (2), colis˜oes simples, os elementos da matriz Jacobiana s˜ao dados por

∂Vn+1

∂Vn

= 1₋2ǫcos(φn+1)

∂φn+1

∂Vn

, ∂Vn+1

∂φn

= ₋2ǫcos(φn+1)

∂φn+1

∂φn

,

∂φn+1

∂Vn

= ǫcos(φn)−l Vn2

+ǫ−l Vn2

+∂φc ∂Vn

,

∂φn+1

∂φn

= 1+ǫsin(φn) Vn

+∂φc ∂φn

.

Os termos ∂φc

∂Vn e

∂φc

∂φn são obtidos derivando-se implicitamenteF(φc) =0 em relação à Vn e φn,

respectivamente. Assim,

−ǫsin(φn+1)

−1−ǫ_Vcos2(φn)

n −

1₋ǫ V2

n

+∂φc ∂Vn

+φc+Vn

∂φc

(30)

∂φc

∂Vn

= ǫ

sin(φn+1)

h

ǫcos(φn)−l

Vn2 +

ǫ−l Vn2

i

−φc

Vn−ǫsin(φn+1)

. (2.24)

−ǫsin(φn+1)

1+ǫsinφn Vn

+∂φc ∂φn

+Vn

∂φc

∂φn

=0,

∂φc

∂φn

=

ǫsin(φn+1)

h

1+ǫsin(φn)

Vn

i

Vn−ǫsin(φn+1)

. (2.25)

Encontrados os elementos, agora podemos obter o determinante da matriz Jacobiana (JS) que,

depois de algum algebrismo, nos d´a que

det(JS) =

Vn+ǫsin(φn)

Vn+1+ǫsin(φn+1)

, (2.26)

onde o ´ındice “S” denota colis˜oes Simples.

Pela mesma análise da evolução de uma medida infinitesimal do espaço de fases discutida anteriormente, podemos concluir que o determinante da matriz Jacobiana para o caso das colisões simples também conserva medida do espaço de fases do modelo completo de Fermi-Ulam. Por

esta razão, este modelo é chamado de Modelo Conservativo. O fato dedet(J)não ser igual a 1 se deve ao fato das variáveis usadas na descrição do mapeamento não serem pares canônicos.

A matriz Jacobiana também constitui um dos requisitos para se obter os expoentes de Lyapu-nov de um determinado sistema, como veremos na seção 2.4.2.

2.3 Modelo Simplificado

2.3.1 Mapeamento

No modelo Fermi-Ulam completo, o tempo entre colisões da part´ıcula com a parede móvel é obtido resolvendo numericamente uma equação transcendental. Entretanto, existe uma simplificação do modelo em que o deslocamento da parede móvel é desprezado, considerando o tempo entre dois choques com a parede móvel dado por∆t=2/V, em queV é a velocidade da part´ıcula [11]. A transferência de momento entre a parede móvel e a part´ıcula, no entanto, continua a ocorrer como descrito na versão completa. Esta aproximação permite que as simulações sejam realizadas mais rapidamente, uma vez que o tempo entre colisões,∆t, não é obtido de uma equação transcenden-tal. Nesta simplificação, as colisões sucessivas não existem e, em decorrência disto, a dinâmica da

(31)

versão simplificada do modelo Fermi-Ulam, além de acelerar as simulações numéricas, mantém a não-linearidade do problema e muitas de suas propriedades dinâmicas.

No modelo simplificado do acelerador de Fermi considera-se que as duas paredes est˜ao fixas,

uma emx=0 e a outra emx=1, já considerando variáveis adimensionais. Ao colidir com uma das paredes (com a parede emx=0, por exemplo), a part´ıcula sofre uma troca de energia e momentum como se a parede estivesse se movendo. As equações transcendentais no modelo completo são obtidas no momento em que a part´ıcula colide com a parede móvel. Uma vez que a parede emx=0 no modelo simplificado é assumida como sendo fixa, as equações produzidas no ato da colisão não são mais transcendentais, reduzindo-se significantemente o tempo das simulações numéricas.

Para a construção do mapeamento, supomos que a part´ıcula parte da posiçãox=0 e viaja em direção à parede emx=1. A velocidade inicial da part´ıcula éV0>0, pois está se deslocando na

direção positiva do eixox. O tempo gasto pela part´ıcula neste trajeto é, então,(1/V0). A part´ıcula

colide elasticamente com a parede em x= 1 e tem sua velocidade invertida. Para percorrer o trajeto de volta, a part´ıcula gasta um tempo correspondente a (1/V0). Portanto, para completar

uma viagem partindo dex=0, colidir emx=1 e retornar emx=0, a part´ıcula gasta um tempo total de (2/V0). Logo, a fase na próxima colisão será dada pela soma da fase inicial φ0 com o

tempo total gasto para completar o trajeto, ou seja,φ1= [φ0+ (2/V0)]mod(2π).

A velocidade inicial da parede emx=0, dada a transferência de energia e momento no instante da colisão com a part´ıcula, é dada porV =₋ǫsin(φ), em analogia ao modelo completo. Portanto, da equação (2.7), encontramos a expressão da velocidade da part´ıcula na próxima colisão, que é dada porV1=V0−2ǫsin(φ1). Para evitar queV1assuma valores negativos, o que corresponderia

à part´ıcula viajar em uma região externa às paredes, impomos que a velocidade da part´ıcula seja

sempre positiva, introduzindo arbitrariamente na expressão da velocidadeV1uma função módulo.

Eliminadas as divergˆencias e definindo vari´aveis adimensionais tais comoǫ=ε/l,Vn=vn/(ωl)e

φn=ωtn, o mapeamento para o modelo Fermi-Ulam simplificado pode ser escrito como

T :







Vn+1=|Vn−2ǫsin(φn+1)|

φn+1=

h

φn+_V2_n i

(32)

2.3.2 Matriz Jacobiana

A matriz Jacobiana(J)para este modelo simplificado tem elementos dados por

∂Vn+1

∂Vn

= sign[Vn−2ǫsin(φn+1)][1−2ǫcos(φn+1)]

∂φn+1

∂Vn

,

∂Vn+1

∂φn =

sign[Vn−2ǫsin(φn+1)][−2ǫcos(φn+1)]

∂φn+1

∂φn ,

∂φn+1

∂Vn

= 2

Vn2

,

∂φn+1

∂φn

= 1.

e o determinante desta matriz ´e

det(J) = sign[Vn−2ǫsin(φn+1)].

Este determinante nos dá exatamente a idéia do conceito de módulo. Se a expressão deVn+1 for

maior que zero, então o sinal da expressão dentro do módulo é(+1), ao passo que, se for negativa, a expressão dentro do módulo é(₋1). Assim, fica assegurado que a part´ıcula ficará confinada na região entre as paredes e o determinante(J)pode ser escrito como,

det(Jn) =±1. (2.28)

Pelo teorema de Liouville [27], que diz que se o determinante da matriz Jacobiana de um sistema é igual a_±1, então o sistema é conservativo. Logo, o modelo Fermi-Ulam simplificado conserva medida do espaço de fases.

2.4 Resultados Num´ericos

2.4.1 Espac¸os de Fases

A Fig.(2.5) mostra o espac¸o de fases para o modelo Fermi-Ulam completo.

Na construção da figura (2.5) foram usadas 400 condições iniciais iteradas a partir das equações do mapa (2.18), de modo que a fase e a velocidade iniciais foram divididas em 20 incrementos

igualmente espac¸ados nos intervalos deφ0∈[0,2π]eV0∈[0.01,0.25]. O procedimento para

sa-ber se houve ou não colisão sucessiva da part´ıcula com a parede móvel consiste em encontrar, numericamente, ra´ızes (ou zeros) para as funçõesG(φc)eF(φc), dadas pelas Eqs.(2.19) e (2.20),

respectivamente. Se a funçãoG(φc)admitir solução no intervalo deφc∈(0,2π], então houve

(33)

Figura 2.5: Espac¸o de fases para o modelo Fermi-Ulam. O parˆametro de controle usado na

construc¸˜ao da figura foiǫ=5_×10−3.

contrário, uma raiz para a função F(φc) é encontrada e as equações do mapa (2.18) são iteradas

para o caso (2). Em seguida, uma nova raiz paraG(φc)´e procurada e todo o processo se repete at´e

que o número de iterações (colisões) estabelecido no in´ıcio da simulação seja atingido.

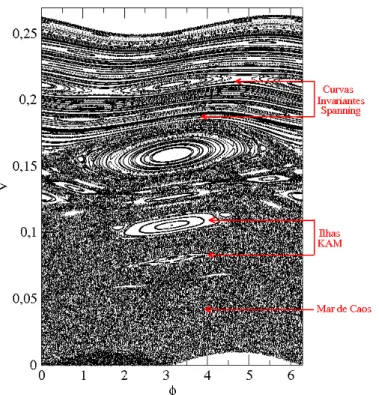
No espaço de fases mostrado na figura (2.5) podemos observar que a região de mais baixa energia é limitada por uma curva invariante do tipo spanning. Nesta região existem ilhas KAM que por sua vez estão envoltas por um mar de caos. As ilhas KAM têm a caracter´ıstica de não permitirem o trânsito livre de uma órbita entre seu interior e o mar de caos. Assim, a evolução de

uma condição inicial que esteja em seu interior jamais sai de lá, da mesma forma que uma órbita pertencente ao mar de caos jamais penetra na ilha KAM. A região que está acima da primeira curva invariante spanning é a região convencionada como de alta energia e apresenta basicamente pequenas ilhas KAM separadas por outras curvas invariantes spanning e podem, eventualmente,

possibilitar o surgimento de pequenos mares de caos entre as curvas, mas este fato n˜ao ´e sempre observado.

O espaço de fases para o modelo Fermi-Ulam simplificado é bastante similar ao do modelo completo, apresentando a mesma hierarquia de comportamentos com ilhas KAM, mar de caos e curvas invariantes spanning. Existe apenas uma pequena diferença na região perto das velocidades

(34)

Na construção do espaço de fases do modelo simplificado, iteramos as equações do mapa (2.27) utilizando 400 condições iniciais divididas em 20 incrementos igualmente espaçados nos

intervalos deφ0= [0,2π]eV0= [0.01,0.25](os mesmos utilizados no modelo completo). Cada

condição inicial foi iterada 500 vezes. A figura (2.6) mostra o espaço de fases para o modelo Fermi-Ulam simplicado.

Figura 2.6: Espac¸o de fases para o modelo Fermi-Ulam simplificado. O parˆametro de controle

usado na construc¸˜ao da figura foiǫ=5_×10−3.

Podemos observar que o espac¸o de fase para o modelo simplificado ´e muito semelhante ao do

modelo completo, apresentando ilhas KAM circundadas por um mar de caos na região de mais baixa energia, limitada pela primeira curva invariante spanning e ilhas KAM separadas por outras curvas invariantes spanning na região de alta energia (acima da primeira curva). A diferença notada se limita à região com velocidades próximas de zero que se deve à introdução do módulo

na equac¸˜ao da velocidade do mapeamento.

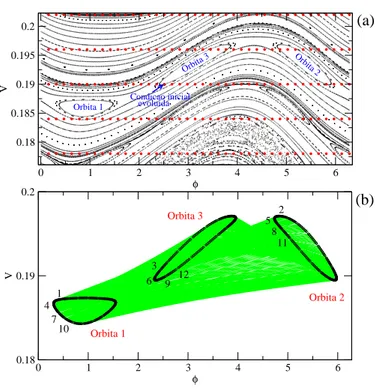
Uma curiosidade que surgiu em relação ao espaço de fases do modelo Fermi-Ulam conser-vativo, foi sobre a convergência das trajetória para cada arranjo de comportamentos mostrado no espaço de fases do tipo misto, especialmente naquelas regiões onde nenhuma condição inicial era evolu´ıda. As regiões “em branco” observadas neste espaço de fases são visitadas em algum

(35)

converge, n˜ao para uma ´unica ilha KAM, mas para um conjunto delas ao mesmo tempo. Veja a figura.

0 1 2 3 4 5 6

φ

0.18 0.185 0.19 0.195 0.2

V

0 1 2 3 4 5 6

φ

0.18 0.19 0.2

V

1

2

3

4

5

6

7

8

9

10

11

12

Orbita 1

Orbita 3

Orbita 2

(a)

(b)

Orbita 1

Orbita 3

Orbita 2

Condicao inicial evoluida

Figura 2.7: Convergência de uma condição inicial para três ilhas KAM dos espaço de fases do

modelo Fermi-Ulam conservativo simplificado. Em (a) vemos o detalhe da região estudada e, em (b), é mostrada em que órbita a trajetória se inicia e a sequência em que ela evolui.

Na figura (2.7)(a) é mostrado o espaço de fases simplificado do Modelo Fermi-Ulam Conser-vativo, na cor preta, em escala ampliada, de modo a destacar a região onde fizemos a análise da evolução de uma condição inicial. Os pontos, na cor vermelha, mostram as coordenadas de todas

as condições iniciais evolu´ıdas. Podemos observar que, a condição inicial escolhida está contida na órbita 3. A figura (2.7)(b), mostra, em detalhes, que a condição inicial evolu´ıda converge para três órbitas. Neste modelo, a trajetória percorrida por esta condição inicial soma um total de 500 pontos, mostrados na cor preta. É mostrada também, a sequência em que a part´ıcula transita pelo

espaço dando origem às órbitas (traços na cor verde). Podemos ver que a trajetória se inicia na órbita 1, passa pela órbita 2, segue para a órbita 3 e retorna para a órbita 1. Esta sequência é matida até o final da convergência e um detalhe importante a se observar é que ela cresce sempre no sentido anti-horário das órbitas. Enfatizamos, ainda, que o grupo das três ilhas, escolhidas para

(36)

Observe que, tanto a órbita 2 quanto a órbita 3 possuem condições iniciais em suas órbitas. Assim, é razoável de esperar que a evolução dessas condições iniciais percorram todos os pontos da

órbita em que está inserida. Já com a órbita 1, o mesmo não acontece. Veja que nenhuma condição inicial está em sua órbita mas, mesmo assim, ela é visitada. Da´ı nossa curiosidade em descobrir, qual condição inicial percorre a órbita 1. A figura (2.7)(a) mostra que a coordenada [0.19,2.51], para a velocidade da part´ıcula e a fase, respectivamente, é a condição inicial que converge para a

órbita 1, além das órbitas 2 e 3 e que a órbita 1 é a primeira delas a ser visitada.

Este comportamento ocorre, também, em outras regiões do espaço de fases, formando, assim, a rica e complexa hierarquia de estruturas que compõem o espaço de fases do Modelo Fermi-Ulam conservativo, tanto completo quanto simplificado.

2.4.2 Precis˜ao Num´erica

O estudo das propriedades de sistemas caóticos é frequentemente realizado de forma numérica. Portanto, é importante conhecer as vantagens e limitações dos métodos numéricos dispon´ıveis. Normalmente, ao estudar sistemas não-lineares devemos escolher qual a melhor maneira de

resol-ver o problema. Contudo, mesmo utilizando a técnica mais apropriada, a solução numérica obtida não é um resultado exato. Os computadores trabalham com um número finito de algarismos sig-nificativos. Devido a esta limitação, o procedimento numérico gera erros de tal forma que, após um determinado tempo, a solução não corresponde ao estado inicial do sistema, mas corresponde,

por exemplo, ao estado de uma configuração inicial vizinha à que foi utilizada. Assim, devemos interpretar os resultados e julgar até que ponto o resultado é confiável.

Nesta seção vamos descrever o método numérico utilizado na solução das equações transcen-dentais G(φc) e F(φc) responsáveis pelo tempo da colisão da part´ıcula com a parede móvel do

nosso problema.

O método que adotamos para resolver estas equações foi o método da bisseção [28], que é um método numérico de refinamento de ra´ızes, feito via processo iterativo. Um método iterativo

consiste em uma sequência de instruções que são executadas passo a passo, algumas delas são repetidas em ciclos. A execução de um ciclo recebe o nome de iteração. A principal caracter´ıstica do método da bisseção é reduzir a amplitude do intervalo [a, b], onde contém a solução, sempre pela metade, até atingir uma precisão tal que b₋a < tol, onde tol é a tolerância previamente estabelecida. A seguir, vamos descrever os cálculos para obtenção de zeros de funções utilizando o método da bisseção.

Seja uma funçãof(x). O método da bisseção exige quef(x)seja cont´ınua emx_∈[a, b] =I0

(37)

sinal diferente def(b). Se isto ocorrer, esta condição garante que a funçãof(x)intercepta o eixo xemx_∈[a, b]pelo menos uma vez. Se a derivada def(x)não muda de sinal emx_∈(a, b), então esta interseção é única. O segundo passo é encontrar umx0=a+₂b e avaliarf(x0). Sef(x0)tem o

mesmo sinal def(a), ent˜ao o novo intervalo parax´ex_∈_a₊_b

2 , b

=I1, mas sef(x0)tem o mesmo

sinal def(b), ent˜aox_∈

a,a+₂b

=I1. No pr´oximo passo,x1 assume o valor m´edio do intervalo

I1 e o mesmo procedimento é repetido várias vezes até se encontrar umx∗ tal que|f(x∗)|< tol,

ondetol é uma tolerância pré estabelecida.

Incorporando este método ao nosso modelo, temos que o intervalo onde as equações g(t) e f(t). O procedimento para obter as soluções de t são: após a colisão com a parede móvel, procuramos uma solução para g(t). Seg(t) não admitir solução emt_∈(0,2π], então não houve colisão múltipla, de modo que a part´ıcula colide com a parede fixa emx=0 e retorna. Neste caso, a função f(t) é resolvida e g(t) é testada novamente. Se g(t) admitir uma solução no intervalo (0,2π], então ocorreu uma colisão múltipla eg(t) é resolvida. Esse processo é realizado todas as vezes que a part´ıcula colide com a parede móvel. Salientamos que tanto a funçãog(t)quanto af(t) podem ter mais de uma solução no intervalo t_∈[0,2π]. Neste caso, a solução que tem interesse f´ısico é somente a primeira delas, que representa o instante da primeira colisão. As outras soluções devem ser desconsideradas.

Para garantir que encontramos a solução desejada, que retrata o instante em que ocorreu a colisão, dividimos o intervalo original em n intervalos menores, dados por I0 =

0,2_nπ

, I1 =

₂_π n,

4π n

, I2=

₄_π n ,

6π n

; ..., In =

h₍_n₋₁₎₂_π

n ,2π

i

. Para cada sub-intervalo, na ordem crescente, as condições de sinais distintos nos extremos são verificadas parag(t)ef(t). Se a primeira condição é satisfeita emI0, então a segunda condição do sinal da derivada é verificado. Se existir mudança

no sinal da derivada, então o intervalo é refinado novamente e assim por diante até que o método da bisseção possa ser usado. Se a solução não estiver contida em I0, o intervalo I1 é verificado

e isto acontece até o último intervalo In. A solução é admitida se existir umt∗ tal que |g(t∗)|<

tol ou _|f(t∗)_|< tol. Aqui, tol é a tolerância e, quando utilizamos precisão dupla na simulação computacional, como geralmente acontece,tol=1_×10−16.

O método da bisseção tem convergência lenta quando comparado com outros métodos, como o método de Raphson, por exemplo, mas a solução obtida é confiável. O método de Newton-Raphson pode fornecer uma solução da equação que não tem interesse f´ısico, ou seja, uma solução

fora do intervalot_∈[0,2π]no nosso caso, o que n˜ao representa um resultado de interesse.

2.4.3 Expoentes de Lyapunov

Vimos, na seção anterior, que os espaços de fases do modelo Fermi-Ulam, tanto completo

(38)

na região de mais baixa energia. Sabemos que o que determina um comportamento caótico é a perda de previsibilidade de condições iniciais muito próximas e que uma única condição inicial

iterada naquela região caótica do espaço de fases do modelo Fermi-Ulam é suficiente para pre-encher toda a região acess´ıvel. Os expoentes de Lyapunov são bons indicadores de caos e muito utilizados na caracterização de tais sistemas. Eles indicam se uma órbita é sens´ıvel ou não às condições iniciais, ou seja, se elas se separam uma da outra com o passar do tempo. Nosso

obje-tivo, nesta seção, é utilizar o cálculo do expoente de Lyapunov para caracterizar o comportamento caótico encontrado no espaço de fases do modelo Fermi-Ulam conservativo.

Para obter os expoentes de Lyapunov, precisamos verificar se duas órbitas, partindo de condições iniciais vizinhas, divergem exponencialmente uma da outra com o passar do tempo. Se tal di-vergência ocorre, então as órbitas são classificadas como caóticas. Se duas órbitas permanecerem

próximas ou divergem apenas linearmente, então não são sens´ıveis às condições iniciais e, conse-quentemente, não são caóticas.

Vamos agora efetuar os cálculos para obtenção dos expoentes de Lyapunov. Iniciaremos com um mapeamento unidimensional e generalizaremos para mapas bidimensionais.

Seja o mapa unidimensional,

Xn+1=F(Xn). (2.29)

Considerando o mapeamento discreto unidimensional representado porF(X)eX0uma condic¸˜ao

inicial, podemos definir a distância relativa entre duas trajetórias, na n-ésima iteração, pela razão,

d ǫ0 ≡

|F(n)(X0+ǫ0)−F(n)(X0)|

ǫ0

, (2.30)

ondeǫ0 ´e arbitrariamente pequeno. Considerando o limite em queǫ0→0, podemos definir,

lim

ǫ0→0

F(n)(X0+ǫ0)−F(n)(X0)

ǫ0

=_|F′(n)(X0)| ≡e(λn). (2.31)

Tomando logar´ıtmo de ambos os lados da equação (2.31) e reorganizando os termos, obtemos que o expoente de Lyapunov, para mapeamentos unidimensionais, é dado por,

λ= 1 n ln|F

′(n)

(X0)|. (2.32)

Considerando o caso em que n_→∞, a expressão para o cálculo do expoente de Lyapunov é dada por,

λ= lim

n→∞

1 n

n

∑

i=1

ln_|F′(Xi)|. (2.33)

(39)

s˜ao dados por

λj= lim n→∞

n

∑

i=1

1 nln|Λ

i

j|, com j=1,2. (2.34)

O termoΛi_j representa os autovalores da matrizM =∏n_i₌₁Ji(Vi, φi)eJi ´e a matriz Jacobiana do

mapeamento avaliada na órbita(Vi, φi). É importante salientar que a implementação direta de um

algoritmo computacional para avaliar a equação (2.34), implica em profundas limitações para se obter a matrizM. Mesmo no limite de pequenos(n), as componentes deM podem assumir muitas ordens de grandeza diferentes para órbitas caóticas e atratores periódicos, tornando impraticável

a implementação do algoritmo. Em outras palavras, o cálculo da matrizM pode gerar problemas numéricos. Para evitar tais problemas, vamos utilizar um algoritmo chamado de Algoritmo de

Triangularizac¸˜ao, proposto por Eckman em 1985 [29].

O algoritmo consiste em escrever a matrizJa partir do produto de uma matriz Triangular(T) por uma matriz Ortogonal(Θ), tal como,

J =ΘT,

onde(J)´e a matriz Jacobiana.

Uma matriz é dita ser ortogonal quando sua transposta é igual à sua inversa, ou seja,

Θ−1₌_ΘT_.

Usando estas definic¸˜oes, podemos reescrever a matrizM como

M=Jn Jn−1Jn−2, ..., J2J1=JnJn−1, ..., J2Θ1Θ1−1J1,

ondeT1=Θ1−1J1. Um produto deJ2Θ1define uma novaJ2′. Em um pr´oximo passo, ´e poss´ıvel

mostrar que

M =JnJn−1, ..., J3Θ2Θ2−1J2′T1.

O mesmo procedimento pode ser usado para obterT2=Θ2−1J2′e assim por diante. Usando este

procedimento, o problema se resume a avaliar os elementos da diagonal principal da matriz(T): T11eT22. Para tanto, devemos encontrar as express˜oes deΘ1−1J1=T1, dadas por

cos(θ) sin(θ)

−sin(θ) cos(θ)

!

. j11 j12 j21 j22

!

= T11 T12 0 T22

!

.

(40)

j11cos(θ) +j21sin(θ) j12cos(θ) +j22sin(θ)

−j11sin(θ) +j21cos(θ) −j12sin(θ) +j22cos(θ)

!

= T11 T12 0 T22

!

.

Como ´e uma igualdade de matrizes, podemos escrever

−j11sin(θ) +j21cos(θ) =0,

−j11sin(θ) =−j21cos(θ),

sin(θ) cos(θ) =

j21

j11

.

Para melhor visualizar quem são o cateto oposto e o cateto adjacente das razões trigonométricas acima, vamos utilizar a ilustração contida na figura (2.8).

Figura 2.8: No triângulo retângulo da figura, encontramos quem são o cateto oposto (CO) e

o cateto adjacente (CA) usados na obtenção do sin(θ) e do cos(θ) e aplicamos o Teorema de Pitágoras para encontrarmos a hipotenusa (HI).

Da figura (2.8), podemos concluir que

sin(θ) = q j21

j2 11+j212

,

cos(θ) = q j11

j2 11+j212

.

Dessas express˜oes, podemos agora reescrever os autovalores da matriz(T), ou seja

T11=j11cos(θ) +j21sin(θ) =

j2 11+j212

q

(j2

11+j212 )

(41)

T22=j22cos(θ) +j12sin(θ) =

j11j22−j12j21

q

(j2

11+j212 )

. (2.36)

Encontrados os autovaloresT11eT22da matriz Triangular, podemos encontrar numericamente

os expoentes de Lyapunov para uma órbita caótica do espaço de fases do modelo Fermi-Ulam.

Em sistemas Hamiltonianos, os expoentes de Lyapunov aparecem aos pares, com sinais contrários (Robert C. Hilborn) [26]. O expoente que determina se uma órbita é caótica é o expoente de Lya-punov positivo, pois, pela equação (2.31), vemos que com λ positivo, o valor da distância dvai aumentando exponencialmente, caracterizando uma separação entre as órbitas vizinhas cada vez

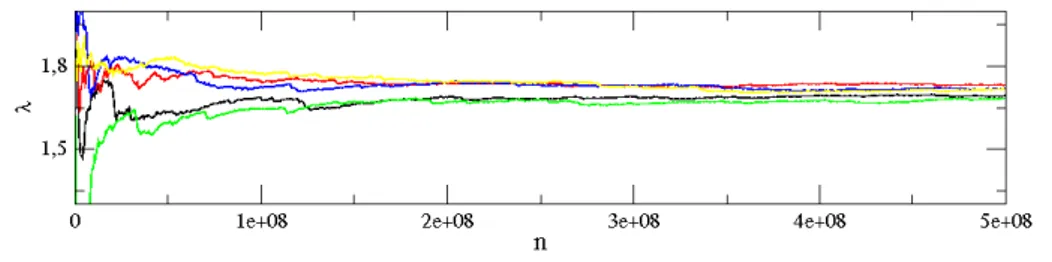
mais rápida. Esta perda de previsibilidade das condições iniciais é o que define uma órbita caótica. A figura (2.9) mostra a convergência dos expoentes de Lyapunov, para o modelo Fermi-Ulam completo, em função do número de iterações.

Figura 2.9: Convergˆencia dos expoentes de Lyapunov para o modelo Fermi-Ulam completo.

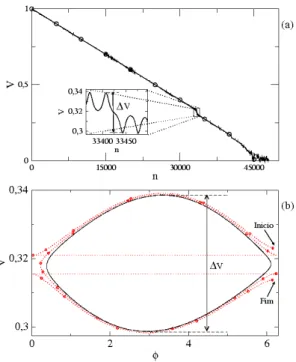
Foram usadas cinco condições iniciais diferentes, iteradas 5_×107 vezes na região de mais baixa energia do espaço de fases, correspondente à região do mar de caos. Este valor do número de iterações foi escolhido por possibilitar a visualização de uma boa convergência das curvas. As condições iniciais utilizadas na construção da figura foramV0=1×10−4, ǫ=1×10−4 e cinco

valores deφ, no intervaloφ_∈[0,2π). Para estes parâmetros de controle, o expoente de Lyapunov positivo encontrado foiλ=0.78_±0.02. O erro_±0.02 representa o desvio padrão das cinco séries temporais.

Também calculamos os expoentes de Lyapunov para o modelo Fermi-Ulam simplificado. Como mostra a figura (2.10), uma boa convergência dos resultados foi obtida, como função do

n´umero de colis˜oes.

Os parˆametros de controle usados foramǫ=1_×10−4,V0=1×10−4e cinco valores deφ, no

(42)

Figura 2.10: Convergˆencia dos expoentes de Lyapunov para o modelo Fermi-Ulam simplificado.

Nossos resultados mostram que os pares de expoentes de Lyapunov encontrados possuem mesmo módulo e sinais contrário, cuja soma é nula. Este fato era esperado uma vez que o mo-delo Fermi-Ulam, tanto completo quanto simplificado, é descrito por um sistema Hamiltoniano e tem medida do espaço de fases preservada. Em sistemas conservativos, a soma dos expoentes de

(43)

3 Modelos Fermi-Ulam Dissipativos

3.1 Introduc¸˜ao

Neste cap´ıtulo revisitamos o Modelo Fermi-Ulam dissipativo. Nosso objetivo ´e entender e

descrever algumas de suas propriedades dinâmicas, quando uma força dissipativa do tipo arrasto gasoso é introduzida no sistema.

Uma consequência da introdução de dissipação no sistema é que sua dinâmica é drasticamente afetada. Sabemos que existem muitas diferentes maneiras de se introduzir forças de amortecimento em um sistema. Uma delas é considerar colisões inelásticas da part´ıcula com uma das paredes ou

com as duas. Assim, a part´ıcula sofre uma perda fracional de energia a cada colisão. Como consequência, o sistema não preserva medida do espaço de fases. Com isso, a estrutura mista é destru´ıda. Em especial, é poss´ıvel observar diferentes comportamentos assintóticos à medida que o coeficiente de amortecimento é variado. Dentre eles, efeitos de transiente [19], pontos fixos

atrativos [20] e atratores ca´oticos [21].

Nosso objetivo neste Cap´ıtulo ´e, ent˜ao, estudar as principais propriedades quantitativas e

qua-litativas observadas no modelo Fermi-Ulam, sob a influência de uma força dissipativa introduzida via um arrasto viscoso, como um gás. Vamos estudar o modelo considerando, primeiramente, a força de arrasto viscoso diretamente proporcional à velocidade da part´ıcula,F =₋V, onde o ex-poente da velocidade é (γ=1). Leonel and McClintock [30] mostraram que, para uma força de amortecimento proporcional à velocidade da part´ıcula, o sistema produz determinantes das matri-zes Jacobianas que ora contraem a medida do espaço de fases e ora preservam medida do espaço de fases. Em seguida, vamos considerar a força de arrasto diretamente proporcional ao quadrado da

velocidade da part´ıcula,F =₋V2_{, onde o expoente da velocidade ´e}₍_γ₌₂₎_{. Uma consequˆencia}