Espaços Fuzzy e aspectos quânticos dos buracos negros

(1)

Espa¸cos fuzzy e aspectos quˆ

anticos dos

buracos negros

Fortaleza

(2)

Espa¸cos fuzzy e aspectos quˆ

anticos dos

buracos negros

Tese submetida à Coordena¸cão do Curso de Pós-Gradua¸cão em F´ısica, da Universidade Federal do Ceará, como requisito parcial para a obten¸cão do grau de Doutor em F´ısica

Orientador:

Ricardo Renan Landim de Carvalho

universidade federal do ceara - Departamento de F´ısica

Fortaleza

(3)

Espa¸cos fuzzy e aspectos quˆ

anticos dos

buracos negros

Tese submetida à Coordena¸cão do Curso de Pós-Gradua¸cão em F´ısica, da Universidade Federal do Ceará, como requisito parcial para a obten¸cão do grau de Doutor em F´ısica

Aprovada em 30 de setembro de 2011

BANCA EXAMINADORA

Prof. Dr. Ricardo Renan Landim de Carvalho (Orientador)

UFC

Prof. Dr. Luis Paulo Collato Cefet - RJ - UnED Petr´opolis

Prof. Dr. Amilcar Rabelo Queiroz UNB

Prof. Dr. Carlos Alberto Santos de Almeida UFC

(4)

(5)

(6)

(7)

(8)

INTRODUC¸ ˜AO p. 9

1 BURACOS NEGROS p. 12

1.1 Introdu¸cão . . . p. 12 1.2 As leis da mecânica dos buracos negros . . . p. 16 1.2.1 Prova da lei zero . . . p. 17 1.2.2 Prova da primeira lei . . . p. 18 1.2.3 Prova da segunda lei . . . p. 23 1.3 Segunda lei generalizada . . . p. 26 1.4 O efeito Hawking . . . p. 28 1.4.1 Produ¸cão de part´ıculas em espa¸cos-tempo não estacionários . . p. 31 1.4.2 Produ¸cão de part´ıculas por buracos negros . . . p. 32 1.5 Dois desafios: entropia e informa¸cão . . . p. 40

2 ESPAC¸ OS FUZZY p. 41

2.1 Introdu¸cão . . . p. 41 2.2 A esfera fuzzy . . . p. 44 2.3 Mudan¸ca de topologia para espa¸cos fuzzy . . . p. 45 2.3.1 Um prelúdio às álgebras de Hopf . . . p. 45 2.3.2 O grupo das álgebras de convolu¸cão . . . p. 49 2.3.3 O _∗-morfismo G∗ _→ _S2

F . . . p. 51

(9)

3 MUDANC¸ A DE TOPOLOGIA DE ESPAC¸ OS FUZZY E A

TER-MODIN ÂMICA DOS BURACOS NEGROS p. 59 3.1 Introdu¸cão . . . p. 59 3.2 Mudan¸ca de topologia de espa¸cos fuzzy e a origem da termodinâmica dos

buracos negros . . . p. 61 3.3 O ensemble de estados . . . p. 62 3.4 Evapora¸c˜ao dos buracos negros . . . p. 67 3.4.1 Entropia emitida por um buraco negro durante sua evapora¸c˜ao . p. 70

CONCLUS ˜AO p. 73

Apêndice A -- Estrutura causal e diagramas de Penrose p. 75 A.1 Propriedades assintóticas do espa¸co-tempo de Minkowski . . . p. 76 A.2 Diagrama de Penrose para a solu¸cão de Kruskal . . . p. 78

(10)

INTRODUC

¸ ˜

AO

Não seria um exagero dizermos que uma das predi¸cões mais excitantes da teoria da relatividade geral é a de que buracos negros devam existir. Buracos negros são, por defini¸cão, objetos dos quais nenhum corpo ou sinal f´ısico pode escapar, devido ao campo gravitacional fort´ıssimo produzido pelos mesmos. A prova de que tais objetos, de fato existem, e a análise de suas propriedades possuem uma significância que vai além da astrof´ısica. De fato, o que está envolvido nesta situa¸cão não é simplesmente a descoberta de mais um objeto astrof´ısico, mais sim, uma forma de sabermos se o nosso conhecimento a respeito de regimes onde os campos gravitacionais são extremamente fortes está correto. As pesquisas em f´ısica dos buracos negros ganharam um grande vigor a partir dos anos setenta quando um novo e inesperado resultado, obtido por Hawking, chamou a aten¸cão dos f´ısicos para os buracos negros. Hawking chegou ao resultado de que, como resultado da instabilidade do vácuo na presen¸ca do campo gravitacional produzido por um buraco negro, estes objetos são fontes de radia¸cão quântica. Hawking mostrou, então, que buracos negros possuem propriedades termodinâmicas como temperatura e entropia. A descoberta de Hawking estimulou um grande número de artigos analisando carac-ter´ısticas espec´ıficas de efeitos quânticos em buracos negros. Os resultados de Hawking, de fato, conseguiram estabelecer uma profunda conexão entre a f´ısica de buracos negros e outras área da f´ısica, a princ´ıpio, bastante distantes da primeira, como termodinâmica, teoria da informa¸cão e teoria quântica de campos.

(11)

natureza dos poss´ıveis estados do buraco negro é obscura. Portanto, a origem da entro-pia dos buracos negros não é clara. Além disso, para justificar a designa¸cão “entroentro-pia”, deveria-se explicar o porquê de a soma da entropia do buraco negro com a a entropia de sua vizinhan¸ca ser uma fun¸cão não-decrescente do tempo, ou seja, o porquê dos buracos negros obedecem a uma segunda lei generalizada da termodinâmica.

A situa¸cão se torna ainda mais complicada se nós considerarmos a natureza da ra-dia¸cão emitida por um buraco negro em seu processo de evapora¸cão. Desde que o único produto resultante da evapora¸cão de um buraco negro é a sua radia¸cão, poder´ıamos espe-rar que alguma informa¸cão a respeito do estado da matéria que colapsou em um buraco negro pudesse estar presente nela. Entretanto, Hawking mostrou, usando argumentos semiclássicos que a radia¸cão emitida por um buraco negro é térmica, ou seja não carrega nenhuma informa¸cão à respeito de sua fonte. Este resultado obtido por Hawking nos leva à uma situa¸cão problemática, desde que o mesmo implica que a matéria que formou o buraco negro evoluiu de um estado puro para um estado misto. Isto entra em contradi¸cão com um dos conceitos fundamentais da mecânica quântica que é o conceito de unitarie-dade, o qual afirma que um estado puro só pode evoluir para outro estado puro, nunca para um estado misto [1–5]. Este impasse entre a f´ısica de buracos negros e a mecânica quântica é conhecido na literatura como paradoxo da perda de informa¸cão por buracos negros.

Diversas propostas surgiram no sentido de resolver o problema da perda de informa¸cão. Entre as mesmas, está a proposta de mudan¸ca de topologia, que será usada por nós nesta tese. A ideia dessa proposta é que, devido a flutua¸cões quânticas do espa¸co-tempo, uma nova região, topologicamente desconectada do nosso universo, poderia surgir no interior do buraco negro e que a informa¸cão a respeito do estado quântico inicial do buraco negro poderia ser preservada nessa região. Este cenário seria produzido durante o colapso gravitacional, ocasião em que uma região com uma grande densidade de energia, onde efeitos de gravidade quântica se tornariam importantes, seria produzida.

(12)

even-tos, com as regras de sele¸cão para essas transi¸cões sendo fornecidas a partir das regras de sele¸cão para o decaimento da esfera fuzzy. A partir da´ı, obteremos o espectro de área, assim como a entropia relacionada ao horizonte de eventos do buraco negro. Finalmente, mostraremos que o processo de evapora¸cão de um buraco negro obedece a segunda lei generalizada da termodinâmica. O problema da perda de informa¸cão por buracos negros também será discutido.

Os resultados obtidos nesta tese est˜ao presentes em dois artigos publicados ao longo da prepara¸c˜ao da mesma:

• C.A.S. Silva, Fuzzy spaces topology change as a possible solution to the black hole information loss paradox, Phys.Lett.B 677 (2009), 318-321.

(13)

1 BURACOS NEGROS

1.1 Introdu¸c˜

ao

O termo buraco negro foi cunhado por Wheeler em 1967 embora o estudo teórico destes objetos possua uma história mais antiga. De fato, a possibilidade de existência de tais objetos foi primeiramente discutida por Michell e Laplace no contexto da teoria Newtoniana no final do século XVIII [6–8]. No contexto de relatividade geral, o problema surgiu apenas um ano após a teoria ter sido desenvolvida, ou seja, após Schwarzschild ter obtido a primeira solu¸cão exata (esfericamente simétrica) das equa¸cões de Einstein no vácuo. Algo que tem de ser citado é que foi necessário mais que um ter¸co de século para que se chegasse, de fato, a uma compreensão da situa¸cão introduzida por Schwarzschild. Foram participantes deste esfor¸co Flamm (1916) [9], Weyl (1917) [10], Eddington (1924) [11], Lemaˆıtre (1933) [12], Einstein e Rosen (1935) [13], Synge(1950) [14], Finkelstein (1958) [15], Fronsdal (1959) [16], Szekeres (1960) [17] e Novikov (1963, 1964) [18,19]. Todo esse intervalo de tempo pode ter sido influenciado pela cren¸ca geral de que a natureza não poderia admitir a existência de um corpo cujo tamanho fosse comparável ao seu raio gravitacional. Este ponto de vista foi compartilhado até mesmo por Einstein [7]. Isto apesar dos estudos de algumas propriedades de sistemas gravitacionais extremamente compactos terem sido estimulados, nos anos trinta, após o trabalho de Chandrasekhar (1931) [20], e de Oppenheimer e Volkoff (1939) [21], os quais mostraram que é poss´ıvel a existência de estrelas de nêutrons com um raio apenas algumas vezes maior do que o seu raio gravitacional. O colapso gravitacional de estrelas massivas que produzem buracos negros foi descrito, pela primeira vez, por Oppenheimer e Snyder (1939) [22].

(14)

rota¸cão. Antes deste per´ıodo, os especialistas consideravam buracos negros como “objetos mortos”, o estágio final da evolu¸cão de estrelas massivas. As designa¸cões “estrelas conge-ladas”, ou “estrelas colapsadas“, usadas pelos especialistas até o final dos anos sessenta, refletiam esta atitude.

Por volta da metade dos anos sessenta, uma nova perspectiva ganhou ascendência no meio dos teóricos de relatividade geral. Este ponto de vista come¸cou a ser desenvol-vido, historicamente, a partir do trabalho de Oppenheimer e Snyder (1939) [22], onde foi mostrado que um observador localizado sobre a superf´ıcie de uma estrela colapsante não perceberia nenhum tipo de “congelamento”, mas poderia registrar eventos que ocorrem tanto dentro como fora da região delimitada pelo raio gravitacional. Este ponto de vista trouxe à tona o fato de que um objeto formado depois do colapso gravitacional poderia ser considerado, em certo sentido, como um “buraco” no espa¸co tempo. Foi justamente neste per´ıodo que Wheeler (1968) [25] cunhou o nome “buraco negro”. Logo em seguida, este nome foi adotado com entusiasmo por toda comunidade cient´ıfica.

Os teoremas, que hoje chamamos de clássicos, os quais estabelecem que buracos ne-gros não possuem outros atributos externos, exceto sua massa, momento angular e carga elétrica (Teorema No Hair), que buracos negros possuem uma singularidade em seu in-terior, e de que a sua área não pode diminuir, foram provados durante o per´ıodo citado acima. Estes e outros resultados tornaram poss´ıveis construir um entendimento qualita-tivo da forma¸cão de um buraco negro, sua posterior evolu¸cão, e sua intera¸cão com matéria e campos f´ısicos clássicos. Muitos destes resultados foram sumarizados na conhecidas mo-nografias de Zel’dovich e Novikov [26–28], Misner, Thorne, e Wheeler (1973) [29], Hawking e Ellis (1973) [30], Thorne, Price e Macdonald (1986) [31], como, também, nas de Novikov e Frolov (1989) [32].

(15)

A descoberta de Hawking estimulou um grande número de artigos analisando carac-ter´ısticas espec´ıficas de efeitos quânticos em buracos negros. Os resultados de Hawking, de fato, conseguiram estabelecer uma profunda conexão entre a f´ısica de buracos negros e outras área da f´ısica, a princ´ıpio, bastante distantes da primeira, como termodinâmica, teoria da informa¸cão e teoria quântica de campos. Entretanto o caráter térmico da ra-dia¸cão Hawking possui uma consequência f´ısica que chama a aten¸cão. No processo f´ısico que leva à forma¸cão de um buraco negro, a informa¸cão relacionada ao estado dos campos quânticos presentes no interior do buraco negro é perdida para observadores externos. Mesmo se no in´ıcio do processo ( antes do colapso gravitacional) o sistema que deu ori-gem ao buraco negro estivesse em um estado quântico puro, depois da forma¸cão do buraco negro, fora do horizonte de eventos, o seu estado será misto, sendo, dessa forma, descrito por uma matriz densidade, o que é proibido pela mecânica quântica. Os fundamentos de mecânica estat´ıstica relacionados à f´ısica de buracos negros ainda permanecem um dos mais intrigantes problemas em f´ısica teórica.

´

E, por outro lado, interessante citar que por volta de trinta a trinta e cinco anos atrás, os buracos negros eram considerados como objetos exóticos, sendo a atitude geral da comunidade cient´ıfica (de fato daqueles que não trabalhavam no assunto), em rela¸cão a estes objetos, bastante cautelosa. A situa¸cão passa a mudar à medida que mais e mais dados astrof´ısicos relacionados a buracos negros passam a surgir e à medida que um maior desenvolvimento da teoria relacionada aos mesmos acontece, destacando-se os desenvolvimentos alcan¸cados por Hawking.

Em rela¸cão à comprova¸cão observacional de buracos negros, muito embora não te-nhamos, até hoje, realizado uma deteçcão que garanta em cem por cento a existência de buracos negros, vários objetos tem sido considerados pelos astrof´ısicos como fortes candi-datos a serem um deles. Após a descoberta de pulsares (estrelas de nêutrons), astrof´ısicos come¸caram a levar a sério a perspectiva da deteçcão observacional de buracos negros. A análise da acre¸cão de matéria ao redor de buracos negros isolados mostrou-se como um poderosa fonte de raios X [33–35]. O progresso da astronomia de raios X e os estudos usando satélites, que come¸caram na década de setenta, levaram à descoberta de um bom número de fontes de raios X. Foi, então, proposta a hipótese de que algumas destas fontes poderiam ser buracos negros em sistemas de estrelas binários.

(16)

Existem, também, boas razões para se acreditar que o núcleo de possivelmente todas as galáxias, como também quasares, possuam buracos negros massivos ou supermassi-vos [38–40]. Também, foram feitas descobertas nos anos noventa por astrônomos usando o telescópio Hubble [41,42], e outra por radioastrônomos [43], as quais forneceram evidências claras da presen¸ca de enormes buracos negros nos centros das galáxias. Em ambos os ca-sos, as observa¸cões revelaram discos de gás orbitando objetos centrais, sendo poss´ıvel se apresentar argumentos robustos de que estes objetos não possam ser outra coisa senão buracos negros supermassivos.

Muitos outros aspectos da f´ısica de buracos negros também se tornaram importan-tes para aplica¸cões em astrof´ısica. A colisão de um buraco negro com uma estrela de nêutrons, ou a coalescência de dois buracos negros em sistemas binários é uma potente fonte de radia¸cão gravitacional, a qual pode ser potente o bastante para chegar até o nosso planeta e ser detectada pelo LIGO, LISA, entre outros. A deteçcão de ondas gravi-tacionais dessas fontes requer uma descri¸cão detalhada do campo gravitacional do buraco negro durante a colisão. Em princ´ıpio, isto abre notáveis possibilidades de testarmos as teorias gravitacionais que temos hoje no limite de campos gravitacionais fortes. Para que consigamos este objetivo, entretanto, além da constru¸cão de antenas gravitacionais, precisamos obter as solu¸cões das equa¸cões de relatividade geral que descrevem este tipo de situa¸cão. Até agora, não possu´ımos ferramentas anal´ıticas para cumprir esta tarefa. Sob estas condi¸cões, torna-se importante o estudo numérico do problema da colisão de buracos negros.

Há um bom número de artigos de revisão que sumarizam os principais resultados em f´ısica de buracos negros desenvolvidos durante as décadas de setenta e oitenta. Podemos citar como referência os trabalhos de Penrose [44], Carter [45, 46], Sexl [47], Israel [48], Markov [52, 53], De Witt [54], Bekenstein [55], Flolov e Novikov [56], Townsend [57], Jacobson [58, 59]. É, também, interessante a leitura do artigo de revisão por Israel [7], o qual descreve a evolu¸cão histórica do conceito de buraco negro.

(17)

1.2 As leis da mecˆ

anica dos buracos negros

Como vimos no resumo histórico apresentado na introdu¸cão deste cap´ıtulo, a pes-quisa cient´ıfica em buracos negros ganhou um vigor especial a partir dos anos setenta. Isto se deu, principalmente, devido aos progressos obtidos por Hawking, entre outros, os quais conseguiram estabelecer uma profunda conexão entre a f´ısica de buracos negros e outras áreas da f´ısica, a princ´ıpio, bastante distantes da primeira, como termodinâmica por exemplo. O estabelecimento dessa conexão foi motivado pela observa¸cão da analogia existente entre as leis clássicas da mecânica dos buracos negros, as quais são resultados de geometria diferencial e as leis da termodinâmica. A mecânica clássica dos buracos negros pode ser sumarizada nos três teoremas básicos a seguir:

Lei zero: Se o tensor momentum-energia Tµν obedece `a condi¸c˜ao dominante de energia,

ent˜ao a gravidade superficialκ´e constante sobre o horizonte de eventos futuro H+_.1

Primeira lei: Seja um buraco negro estacion´ario de massaM, cargaQ, momento angular

J, e com gravidade superficial κ, potencial eletrost´atico φH e velocidade angular ΩH

definidos sobre o horizonte de eventos futuro H+_{. Se este buraco negro ´e perturbado de}

forma que ele se transforme em um buraco negro com massa M +dM, carga Q+dQ e momento angular J+dJ, ent˜ao,

dM = κ

8πdA+ ΩHdJ+φHdQ . (1.1)

Segunda lei: estabelece que a área do horizonte de eventos de um buraco negro é uma fun¸cão não-decrescente do tempo,

δA_≥0 (1.2)

Além disso, a segunda lei estabelece que, quando dois buracos negros colidem e se fundem, a área do horizonte do buraco negro resultante será sempre maior, ou igual, à soma das áreas dos dois horizontes originais.

(18)

1.2.1 Prova da lei zero

Para a prova do primeiro teorema, o qual leva o nome de lei zero da mecˆanica dos buracos negros, temos que o horizonte de eventos futuro H+ _{´e um horizonte de Killing. Das}

propriedades dos horizontes de Killing [57], isto significa que podemos tomar um campo vetorial de Killingξµ _{que seja normal a} _H+_{, de forma que, sobre o horizonte de eventos,}

n´os tenhamos

Rµνξµξν = 0 (1.3)

e

ξ2 = 0 , (1.4)

onde Rµν ´e o tensor de Ricci.

As equa¸c˜oes de Einstein implicam que

0 = Tµνξµξν |H+

= Jµξµ|H+ (1.5)

onde J = (₋Tµνξν)∂µ ´e tangente a H+.

Segue-se, ent˜ao, que J pode ser expandido em termos de uma base de vetores tangentes aH+_.

J =aξ+b1η(1)+b2η(2) , sobre H+. (1.6)

Entretanto, desde que ξ_·η(i) _{= 0,} _J _{´e tipo-espa¸co ou nulo (para} _b

1 = b2 = 0). Por

outro lado,J deveria ser tipo-tempo ou nulo pela condi¸c˜ao dominante de energia. Assim, a condi¸c˜ao dominante de energia implica que J _∝ξ e, portanto

0 = ξ[σJσ]|H+=ξ_[_σTλ σ]ξλ |H+

(19)

= ξ[σ∂σ]κ|H+ (1.7)

Isto implica que

∂σκ ∝ ξσ (1.8)

⇒t_·∂κ = 0 (1.9)

para todot pertencente ao espa¸co tangente a H+ _{e, portanto,}_κ _{´e constante sobre} _H+_.

1.2.2 Prova da primeira lei

Para a prova do segundo teorema, o qual é designado como a primeira lei da mecânica dos buracos negros, considere uma hipersuperf´ıcie tipo-espa¸co Σ, no espa¸co-tempo esta-cionário exterior ao buraco negro, com um de seus limites,H sobre o horizonte de eventos futuro e um outro limite emi0_{, como mostra a figura (1). A superf´ıcie}_H _{é uma 2-esfera,}

a qual pode ser considerada como a fronteira do buraco negro.

Figura 1:

Temos que as trˆes grandezas que caracterizam um buraco negro, ou seja, sua massa, seu momento angular e a sua carga s˜ao definidas pelas seguintes integrais [57]

M =₋ 1 8π

I

∞

dSµν∇µkν ; J =

1 16π

I

∞

(20)

Q= 1 16π

I

∂V

dSµν∇µξν ; (1.11)

ondedSµν é o elemento de área de∂Σ (a fronteira de Σ),kν,mν eξν são campos vetoriais

de Killing associados `a energia, ao momento angular e `a carga do sistema.

Usando a lei de Gauss e as equa¸c˜oes de Einstein, podemos escrever a integral para a massa M do buraco negro como

M = 1

8π

Z

Σ

dSµ∇ν∇µkν +

1 16π

I

H

dSµν∇µkν

= ₋ 1

4π

Z

Σ

dSµRµνkν−

1 8π

I

H

dSµν∇µkν

=₋ Z

Σ

dSµ(2Tνµkν−T kµ)−

1 8π

I

H

dSµν∇µkν

(1.12)

De forma semelhante, o momento angular e a carga podem ser escritos, respectiva-mente, como

J =

Z

Σ

dSµ(Tνµmν −

1 2T m

µ_{) +} 1

16π

I

H

dSµν∇µmν

Q =

Z

Σ

dSµ(Tνµξν−

1 2T ξ

µ_{) +} 1

16π

I

H

dSµν∇µξν (1.13)

Ainda, considerando o caso do espa¸co-tempo de um buraco negro estacionário e axi-simétrico, temos que é satisfeita a propriedade de ortogonalidade “t₋φ”, o que garante que o horizonte de eventos é um horizonte de Killing. Neste caso, a normaliza¸cão do campo vetorial de Killingξµ_{é fixada por requerermos que}

ξµ=kµ+ ΩHmµ (1.14)

Dessa forma, considerando que o ´unico campo f´ısico existente seja o campo eletro-magn´etico, de forma que gµν_T

(21)

M = ₋2 Z

Σ

dSµTνµ(F)ξν −

1 8π

I

H

dSµν∇µξν (1.15)

+ 2ΩH

Z

Σ

dSµTνµ(F)mν +

1 16π

I

H

dSµν∇µmν

= ₋2

Z

Σ

dSµTνµ(F)ξν −

1 8π

I

H

dSµν∇µξν+ 2ΩHJ . (1.16)

Al´em disso, temos que

dSµν = (ξµnν −ξνnµ)dA (1.17)

onde nµ ´e tal que n·ξ =−1

Com isso, a segunda integral acima pode ser escrita como

− 1

8π

I

H

dSµν∇µξν = −

1 4π

I

H

dA(ξµnν −ξνnµ)∇µξν

= ₋ 1

4π

I

H

dA(ξ_{· ∇}ξ)νnν +

1 4π

I

H

dA(ξνnµ∇µξν). (1.18)

Temos, ainda, que

ξνnµ∇µξν = nµ

0

z }| {

∇µ(ξνξν)−ξνnµ∇µξν

= ₋ξνnµ∇µξν → ξνnµ∇µξν = 0,

e, portanto, a segunda integral em (1.18) se anula e n´os ficamos com

−₈1_π

I

H

dSµν∇µξν = −

1 4π

I

H

dA(ξ_{· ∇}ξ)ν | {z }

(22)

= ₋ κ 4π

I

H

dA(ξ_·n

|{z}

−1

)

= κ

4πA (1.19)

onde A´e a ´area do horizonte H. Temos, ainda, que

−2 Z

Σ

dSµTνµ(F)ξν =φHQ (1.20)

onde Q é a carga elétrica l´ıquida do buraco negro e φH é o potencial eletrostático

co-rotacional.

Assim, chegamos, finalmente `a seguinte express˜ao:

M = κA

4π + 2ΩHJ +φHQ , (1.21)

a qual ´e conhecida como f´ormula de Smarr.

Temos, agora queAeJ possuem dimensão de massa ao quadrado, enquanto Q possui dimensão de massa. Dessa forma, pelo teorema de Euler para fun¸cões homogêneas,

1

2M = A

∂M ∂A +J

∂M ∂J +

1 2Q

∂M ∂Q

= κ

8πA+ ΩHJ+

1

2φHQ , (1.22)

(23)

A∂M ∂A −

κ

8π

+J∂M ∂J −ΩH

+ 1

2Q

_∂M

∂Q −φH

= 0. (1.23)

Sendo A, J, e Qindependentes, teremos

∂M ∂A =

κ

8π ; ∂M

∂J = ΩH ; ∂M

∂Q =φH . (1.24)

O que nos d´a

dM = ∂M

∂AdA+ ∂M

∂J dJ + ∂M

∂QdQ

= κ

8πdA+ ΩHdJ+φHdQ (1.25)

(24)

1.2.3 Prova da segunda lei

Para a prova do terceiro teorema, o qual leva o nome de segunda lei da mecˆanica dos buracos negros, consideremos a uni˜ao de todos os horizontes de eventos futuros ˙J−₍_ℑ+_),

em um espa¸co-tempo assintoticamente plano. Vamos dividir os geradores de geod´esicas nulas sobre ˙J−₍

ℑ+_{) em um grande n´}_{umero de feixes infinitesimais, sendo cada um}

iden-tificado por um n´umerok, como mostra a figura:

Figura 2:

(25)

1) Teorema de Penrose A uni˜ao de todos os horizontes futuros ˙J−₍

ℑ+_{) ´e gerada}

por geod´esicas nulas que n˜ao possuem pontos finais no futuro. De forma mais precisa:

• Os geradores de ˙J−₍_ℑ+_{) s˜ao geod´esicas nulas, as quais ( pelo menos para um}

lapso finito do parˆametro afim) permanecem em ˙J−₍_ℑ+_).

• (Teorema) Quando percorrido na dire¸cão do passado, um gerador poderá, mas não necessariamente, deixar ˙J−₍_ℑ+_{). Cada evento em que isso ocorre}

´e chamado de “c´austica” de ˙J−₍_ℑ+_{). Quando geradores deixam ˙}_J−₍_ℑ+_{) os}

mesmos entram em J−₍

ℑ+_{) (o passado causal de} _ℑ+_).

• Uma vez que um gerador, sendo percorrido na dire¸c˜ao do futuro, entra em ˙

J−₍_ℑ+_{), a partir de}_J−₍_ℑ+_{), o mesmo nunca mais poder´a deixar ˙}_J−₍_ℑ+_{), nem}

poder´a intersectar outro gerador. Geradores podem intersectar-se somente em c´austicas, ao entrarem em ˙J−₍

ℑ+_).

• Por cada evento que n˜ao seja uma c´austica em ˙J−₍

ℑ+_{) passa um e somente}

um gerador ( a menos da normaliza¸c˜ao do parˆametro afim).

2) Teorema “focussing”A ´areaaK da se¸c˜ao transversal de um feixe de geradores,

a qual independe da velocidade do observador, muda de evento a evento ao longo do feixe de forma que:

d2_a1/2

K

dλ2

k

≤0 (1.26)

se a condi¸cão fraca de energia é válida. Aqui λk é o parâmetro afim ao longo do

(26)

A partir desses dois resultados, vamos agora supor que a grandeza da

1/2

K

dλk seja negativa

em algum evento p ao longo do feixe de geradores. Ent˜ao, de acordo com o teorema “focussing”, da

1/2

K

dλk sempre se manter´a negativa para todos os outros eventos sobre o feixe,

desde que a sua varia¸cão é negativa. Assim, após um lapso do parâmetro afim dado por

∆λk ≤

_a1/2

k −da1_k/2/dλk

, em p (1.27)

a1_k/2 ir´a a zero.

No ponto em que a1_k/2 zera, geod´esicas adjacentes no feixe cruzam-se dando origem a eventos em ˙J−₍

ℑ+_{) atrav´es dos quais passam mais de um gerador, o que viola o teorema}

de Penrose. Dessa forma, ou a suposi¸c˜ao de que da

1/2

K

dλk é negativa está errada, ou então esta

grandeza permanece negativa, mas antes que os geradores tenham a chance de cruzarem-se, os mesmos encontram uma singularidade e deixam de existir.

Para provar a segunda lei da mecânica dos buracos negros, é necessário assumir que nenhuma singularidade pode ser encontrada pelos geradores de ˙J−₍_ℑ+_{), de forma que} da1K/2

dλk

não possa ser negativa. Isto corresponde à hipótese do censor cósmico [60], que diz que não existem singularidades nuas, admitindo assim que o nosso universo é previs´ıvel, o que não seria poss´ıvel com a presen¸ca desse tipo de singularidade, desde que não conhecemos as leis que as governam. Assumindo, assim, a hipótese do censor cósmico, temos que da

1/2

K

dλk

´e n˜ao-negativa ao longo de todo o feixe k.

Este resultado nos diz que a área da se¸cão transversal de cada feixe de geradores nunca decresce, ao percorrermos o mesmo na dire¸cão do futuro. Desde que novos feixes podem ser criados, mas os antigos nunca podem ser destru´ıdos à medida que se move na dire¸cão do futuro, a área total da se¸cão transversal de ˙J−₍_ℑ+_{) não pode decrescer quando}

(27)

1.3 Segunda lei generalizada

Efeitos quânticos, que discutiremos na próxima se¸cão, podem violar as condi¸cões de aplicabilidade do teorema de área de Hawking. Dessa forma, a evapora¸cão quântica reduz a área de um buraco negro, e a desigualdade (1.2) é violada. Por outro lado, a radia¸cão de um buraco negro possui caráter térmico, de forma que a evapora¸cão do mesmo é acompanhada de um aumento da entropia no espa¸co ao redor do buraco negro. Assim, alguém ainda poderia esperar que uma entropia generalizada, definida pela soma da entropiaSBH do buraco negro com a entropia SM da radia¸cão e da matéria na parte

externa ao buraco negroS =SBH+SM, nunca decrescesse.

De fato, nós notamos que a taxa de aumento da massa e da entropia da matéria na região exterior ao buraco negro, medida pelo relógio de um observador distante, devido a irradia¸cão de uma part´ıcula sem massa de spin s, pode ser escrita na forma

dMM

dt =

dMH

dt =

1

4σshsΣsθ

4 _, _(1.28)

dSM

dt =

1

3σsBshsΣsθ

3 _, _(1.29)

onde hs é o número de polariza¸cões do campo; σs = π2/30 para bosons e 7π2/240 para

férmions; Σs é a se¸cão transversal efetiva do buraco negro; θ é a temperatura sobre o

horizonte de eventos, eBs ´e um coeficiente adimensional da ordem da unidade.

Por outro lado, a mudan¸ca na entropia SH de um buraco negro sem rota¸c˜ao ´e

relaci-onada com a sua massaM pela express˜ao:

dSH =θ−1dMH (1.30)

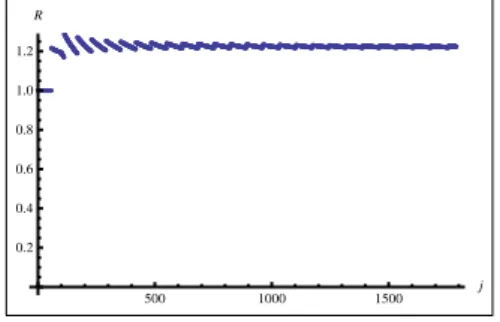
Comparando as express˜oes acima, n´os podemos encontrar [61]

R=₋dS

M

dSH =

4

(28)

Resultados num´ericos demonstraram que o coeficienteBs ´e sempre maior que 3/4 [61, 62]

e, portanto, a soma da entropia de um buraco negro com a entropia de sua vizinhan¸ca cresce quando o mesmo emite radia¸c˜ao.

Pode-se mostrar [61] que se há radia¸cão de corpo negro a uma temperatura ˜θna região exterior ao buraco negro, a entropia generalizada, mais uma vez, cresce exceto no caso em que ˜θ =θ. Neste caso especial, o aumento na entropia no espa¸co ao redor do buraco negro devido ao processo de evapora¸cão é compensada, exatamente, pelo decréscimo na entropia deste espa¸co devido à acres¸cão de radia¸cão térmica para o interior do buraco negro.

Estes argumentos nos fornecem suficiente embasamento para assumir que a seguinte lei ´e v´alida:

Segunda lei generalizada: Em qualquer processo f´ısico envolvendo buracos negros, a entropia generalizada S =SBH+SM nunca decresce.

A segunda lei generalizada coloca, sob o mesmo patamar as diferentes quantidades

SM relacionada à desordem em um sistema f´ısico composto por matéria e radia¸cão usuais

e SH, a qual é uma caracter´ıstica geométrica do buraco negro. Esta rela¸cão possui o

mesmo esp´ırito das equa¸cões de Einsten, as quais relacionam caracter´ısticas da matéria com as caracter´ısticas geométricas do espa¸co-tempo.

Vemos, então, que os teoremas descrevendo as intera¸cões de buracos negros, os quais são resultados de geometria diferencial, são formalmente idênticos às leis da termodinâmica, se identificamos a gravidade superficial de um buraco negro κ a um múltiplo da tempe-ratura T e a área do horizonte com a entropia S.

Somos incondicionalmente tentados, então, a perguntar se esta identifica¸cão é mais que formal. Tal conjectura, obviamente, requereria uma mudan¸ca drástica no significado das caracter´ısticas geométricas de um buraco negro. Temos que temperatura é uma medida da energia média de um sistema com uma grande quantidade de graus de liberdade, da ordem de 1023_{. Por outro lado, entropia mede o n´}_{umero de configura¸cões microscópicas dos}

(29)

temperatura e entropia, então o mesmo deve emitir radia¸cão. Esta ideia encontra um grande problema com a própria defini¸cão de um buraco negro, que, como citamos acima, é um objeto de onde nada pode sair.

Não obstante, em 1973, Bekenstein [63] sugeriu que, de fato, deveria-se estabelecer uma conexão f´ısica entre as leis da mecânica dos buracos negros e as leis da termodinâmica. Em 1975, Hawking publicou um cálculo que mostra que buracos negros podem, de fato, irradiar. Na próxima se¸cão, mostraremos o cálculo feito por Hawking. Em seguida, discutiremos os problemas que ainda estão em aberto no estabelecimento da conexão entre a f´ısica de buracos negros e outras áreas da f´ısica como a termodinâmica e a mecânica quântica.

1.4 O efeito Hawking

Os cálculos feitos por Hawking se baseiam em um tratamento semiclássico da gra-vita¸cão. A ideia básica desse tipo de tratamento é que, em regimes de energias bem mais baixas que as encontradas na escala de Planck, podemos, com boa aproxima¸cão tratar os campos de matéria quanticamente, conservando o espa¸co-tempo clássico.

Para considerarmos uma teoria quântica de campos em um espa¸co curvo clássico, vamos concentrar nossa aten¸cão na descri¸cão de um campo escalar que, classicamente, satisfaz a equa¸cão de onda:

gµν_∇µ∇νφ= 0. (1.32)

Uma forma padrão de implementar a quantiza¸cão canônica desse campo é escolher uma base completa fω de solu¸cões da equa¸cão de campo (1.32), no espa¸co-tempo com

métricagµν. Como consequência da equa¸cão de onda a base formada pelas fun¸cões fω é

ortonormal, (fω, fω′) = δ(ω−ω′), em rela¸c˜ao ao produto interno 2

(f, h) = ₋i

Z

Σ

d3x√₋g(fh˙∗

−f h˙ ∗₎_, _(1.33)

onde a integral ´e tomada sobre uma superf´ıcie de Cauchy Σ, e o ponto denota a derivada temporal.

O campo quˆantico φ pode ser expandido, nessa base, como :

2_{No espa¸co de Minkowiski. A escolha padr˜}_{ao, feita nesse caso, ´e a base de fun¸c˜}_oes _{_f

ω, fω∗}, onde fω= (2ω)−1e−i(ωt−k·x) eω= +

√

(30)

φ = Z

dω(aωfω+a†ωf

∗

ω), (1.34)

onde os coeficientes na expans˜ao, aω e a†ω, s˜ao operadores3.

As rela¸cões de comuta¸cão canônicas para o campo escalar, então, implicam as seguin-tes rela¸cões de comuta¸cão para os operadoresaω e a†ω:

[aω′, a†_ω] = δ(ω′−ω) (1.35)

[aω′, a_ω] = [a

†

ω′, a

†

ω] = 0

O vácuo, ou estado de mais baixa energia, o qual denotamos por _|0_i, é o estado que é aniquilado por todos os operadores aω,

aω |0i= 0, ∀ ω >0. (1.36)

O espa¸co de Hilbert é o espa¸co de Fock constru´ıdo a partir da aplica¸cão arbitrária dos operadores de cria¸cão a†

ω a |0i e, portanto, tem como base o conjunto

{|0_i, a†

ω |0i, a†ωa

†

ω′ |0i, ...} (1.37)

O operador n´umero ´e definido como

Nω =a†ωaω (1.38)

de forma que

h0_|(aω)†nNω(aω)n|0i=n (1.39)

Um detalhe importante para as nossas discussões é que a base (1.37) para o espa¸co de Hilbert é determinada pela escolha do vácuo e a escolha do vácuo, por sua vez, depende da escolha da base de fun¸cões_{fω}.

Poder´ıamos, então, definir uma segunda base _{pω, pω′} de solu¸cões para a equa¸cão

3_{Por simplicidade, estamos escrevendo, somente os autovalores de energia e suprimindo os outros}

(31)

(1.32). O campo escalarφ ter´a, nessa nova base, a seguinte expans˜ao:

φ = Z

dω (bωpω+b†ωp

∗

ω). (1.40)

Com novos operadores de cria¸cão e aniquila¸cão satisfazendo às rela¸cões de comuta¸cão usuais. A partir desses novos operadores, é definindo um novo estado de vácuo e, a partir dele, um novo espa¸co de Fock.

A rela¸cão entre as duas bases _{fω} e{pω}é fornecida pelas chamadas transforma¸cões

de Bogoliubov

pω =

Z

dω′₍_α

ωω′f_ω′ +β_ωω′f_ω∗′) (1.41)

fω =

Z

dω′(α∗_ω′_ωpω′ −β_ω′_ωp∗_ω′) (1.42)

Temos que os coeficientes nessa expans˜ao, αωω′ e β_ωω′, chamados de coeficientes de

Bogoliubov, s˜ao fornecidos pelos produtos internos:

αωω′ = (p_ω, f_ω′) (1.43)

βωω′ = −(p_ω, f_ω∗′)

Os coeficientes de Bogoliubov satisfazem à seguinte rela¸cão, como uma consequência da ortonormalidade das fun¸cões de base,

Z

dω′(_|αωω′ |2 − |β_ωω′ |2) = δ(ω−ω′) (1.44)

Al´em disso, temos a rela¸c˜ao entre os operadores aω e bω:

bω =

Z

dω′₍_α∗

(32)

1.4.1 Produ¸c˜

ao de part´ıculas em espa¸cos-tempo n˜

ao estacion´

arios

Algumas consequˆencias interessantes podem ser extra´ıdas da teoria desenvolvida na se¸c˜ao anterior. Considere, por exemplo, o espa¸co-tempo M = M−∪M0∪M+, descrito

na figura (3), o qual possui uma fase estacion´aria em instantes de tempo anteriores at1 e

posteriores a t2, passando por uma per´ıodo n˜ao-estacion´ario entre estes dois instantes.

t

2

t ₁

M₊: espaço-tempo estacionário ( t > t ₂)

M_-: espaço-tempo estacionário ( t < t ₁) M

0 : métrica dependente do tempo

t

Figura 3:

Podemos expandir, emM−, um campo escalar, o qual é solu¸cão da equa¸cão de

Klein-Gordon (1.32), como na equa¸c˜ao (1.34)

φ = Z

dω(aωfω+aω†fω∗) em M−. (1.46)

As fun¸cões fω são solu¸cões da equa¸cão de Klein-Gordon em M−, mas não em M, de

forma que a sua continua¸cão através deM0irá conduzir a novas fun¸cõespω emM+. Assim

φ = Z

dω (bωpω+b†ωp∗ω), (1.47)

onde, do que vimos na se¸cão anterior, temos que a rela¸cão entre as bases para o campo escalar em M− e M+ é obtida através das transforma¸cões de Bogoliubov (1.41) e (1.42).

Os operadores número para o modo de frequência ω são definidos em M− e M+,

respectivamente, como

N(M−)

(33)

N_ω(M+) =b†_ωbω. (1.49)

O estado sem part´ıculas emM−, o qual denotaremos por|0iM−, ´e tal queaω |0iM− =

0, _∀ ω. O número de part´ıculas esperado para o modo de frequência ω em M+ é então,

usando (1.45)

h0_|(N_ω(M+))_|0_iM− = h0|(bω)

†n₍_b

ω)n|0iM− (1.50)

= Z

dω′ _|βωω′ |2

Portanto, vemos que embora o estado de v´acuo em M− seja vazio, em geral ele ir´a

conter part´ıculas emM+.

1.4.2 Produ¸c˜

ao de part´ıculas por buracos negros

Sabemos, da teoria da relatividade geral, que um colapso gravitacional irá produzir um buraco negro. Este, rapidamente, irá assumir um estado de equil´ıbrio estacionário e axi-simétrico, caracterizado completamente por sua massa, carga elétrica e momento angular. Durante a forma¸cão do buraco negro, entretanto, o espa¸co-tempo associado a um corpo colapsante não é estacionário. Este é o ponto chave para que se espere a forma¸cão de part´ıculas, por buracos negros: o fato de que durante o colapso gravitacional, o espa¸co-tempo ser caracterizado por uma métrica dependente do espa¸co-tempo.

Este fluxo de part´ıculas pode continuar em instantes posteriores ao colapso, desde que, devido `a dilata¸c˜ao temporal infinita no horizonte de um buraco negro, as part´ıculas criadas durante o colapso, podem demorar um tempo arbitrariamente longo para ser emitidas.

Em um instante de tempo no passado distante do in´ıcio colapso gravitacional, o espa¸co-tempo é do tipo Minkowski, exceto nas proximidades da estrela que dará origem ao buraco negro. Dessa forma, podemos assumir que os campos se encontram em um estado quântico, que chamaremos de _|0_iℑ−, em que ele não possui part´ıculas nas proximidades

de _ℑ−_{. A estrela, ent˜ao, colapsa para formar o buraco negro. Mostraremos, agora que}

próximo a _ℑ+_{, haverá um fluxo térmico de part´ıculas, as quais chamaremos de radia¸cão}

Hawking.

(34)

Schwarzschild, o qual obedece à equa¸cão de campo (1.32). Vamos escrever uma base de fun¸cões que defina estados de part´ıculas, em um instante de tempo no passado dis-tante do in´ıcio colapso gravitacional. Para isso, vamos escolher uma base ortonormal completa (fω, fω′) da equa¸cão de onda (1.32) emℑ−, de forma que o campo escalar φseja

escrito, sobre_ℑ−_{, como:}

φ = Z

dω(aωfω+a†ωf

∗

ω) (1.51)

e o estado de v´acuo_|0_iℑ− ´e tal que

aω |0iℑ− = 0 (1.52)

para todo ω >0. Notemos que este estado ´e aniquilado por aω em qualquer instante de

tempo.

No sentido de definir um conjunto completo de estados de part´ıculas em instantes posteriores ao colapso, precisamos definir modos tanto sobre _ℑ+_{, como sobre o horizonte}

de eventos H+_{, desde que} _ℑ+ _{não é em si uma superf´ıcie de Cauchy, mas} _H+S_ℑ+ _{o é.}

Dessa forma, o campo escalar passa a ser escrito como:

φ= Z

dω_{pωbω+p∗ωb†ω+qωcω+qω∗c†ω} (1.53)

onde _{p_ω} definem estados de part´ıculas sobre _ℑ+_{, enquanto} _{_q_ω} _{definem estados de}

part´ıculas sobre H+_.

Vamos examinar as solu¸c˜oes para a equa¸c˜ao de onda (1.32) em uma geometria do tipo Schwarzchild. Podemos escrever φ como o produto

φωlm(t.r∗, ω) =ψ(r∗)Ylm(Ω)e−iωt , (1.54)

onde r∗ ₌ _r₊_r

gln

r rg −1

é a coordenada Tortoise, enquanto Ylm são os harmônicos

esf´ericos.

Dessa forma, a equa¸cão (1.32) se reduz à equa¸cão radial

[∂_t2₋∂_r2∗ +W(r)]ψ = 0, (1.55)

(35)

W(r) = (1₋rg

r)( rg

r3 +

l(l+ 1)

r2 ). (1.56)

Podemos notar que

W(r)_→  



l(l+1)

r2 se r→ ∞, r∗ → ∞

er

∗

rg _se _r _→_r

g, r∗ → −∞,

de forma que, tanto no infinito, como nas proximidades do horizonte, as solu¸c˜oesφωlms˜ao

ondas planas emt_±r∗_{, ou ondas planas em}_u₌_t

−r∗ _e_v ₌_t₊_r∗_{. Estas solu¸c˜oes ser˜ao}

usadas para definir as bases para o espa¸co de Hilbert.

Dessa forma, vamos considerar os estados sobre _ℑ+ _{como as solu¸c˜oes da equa¸c˜ao de}

onda com condi¸c˜oes de contorno tais que

pω(u, v)→e−iωu sobre ℑ+ (1.57)

onde ué o parâmetro afim para geodésicas nulas em _ℑ+_.

Estaremos, aqui interessados em encontrar uma forma para as fun¸c˜oes _{fω}, as quais

formam uma base para o campo escalar em _ℑ−_{. Para isso, vamos considerar uma}

apro-xima¸cão de ótica geométrica na qual a linha mundo de uma part´ıcula pode ser interpre-tada como um raio de luzγ. Vamos então, considerar a continua¸cão desse mesmo raio na dire¸cão do passado a partir de _ℑ+_.

O modo (1.57) propaga-se atrav´es do raio γ, o qual sai de _ℑ+ _{ao longo de uma}

geod´esica u = u1, passando pr´oximo ao horizonte do buraco negro H+. O raio passa

através da estrela colapsante e propaga-se na dire¸cão de _ℑ−_{, ao longo de uma geodésica}

v =v1, pr´oxima a v = 0 . 4

O raioγ est´a conectado aH+_{e a} _v _{= 0 atrav´es do vetor}_ǫna_com_ǫ_{pequeno e positivo.}

Na parte do caminho em que o raio passa junto aH+_, _na_{é tangente às geodésicas nulas,}

as quais, sobreH+ _{são do tipo “ingoing”. A normaliza¸cão é fixa pela condi¸cão}_na_l

a =−1,

onde la ´e um gerador de geod´esicas nulas emH+.

Notemos que u assume um valor infinito nas proximidades do horizonte de eventos e, portanto, o mesmo não corresponde a uma boa coordenada a ser utilizada na situa¸cão 4_{Consideraremos o instante de tempo} _v _{= 0 como o ´}_{ultimo em que uma geodésica nula pode deixar}

ℑ−_{, passar pelo interior da estrela e encontrar}_ℑ+_{. Raios que porventura saiam do interior da estrela em}

(36)

\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/ \/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/

I+

i

0

I -H+

U

0

U = - ε, u = - (1/κ) ln ε

Continuação, na direção do passado, da geodésica nula geradora de H+

v = 0

v = - ε v

raio de

luz

Figura 4:

que estamos analisando. Por outro lado,U =₋e−κu_{´e finito sobre o horizonte de eventos,}

de forma que vamos usar esta coordenada como parˆametro afim. Ao longo de γ,U =₋ǫ

de forma que, a express˜ao (1.57) fica escrita como

pω →e

iω

κln(ǫ) emℑ+ (1.58)

Vamos tra¸car, agora, o raio γ através da estrela colapsante, com o mesmo sendo refletido, em seguida, na origem do sistema de coordenadas, seguindo, a partir dai, uma geodésica nula de fase constantev <0 na dire¸cão de_ℑ−_{. Sendo}_γ

H o gerador de geod´esicas

nulas de H+_{, temos que os vetores}_n _e _l _{sofrem, simplesmente um trasporte paralelo, ao}

longo da continua¸cão deγH na dire¸cão deℑ−. Considerando que esta mesma continua¸cão

encontra _ℑ− _em _v _{= 0, obteremos que as duas geod´esicas,} _{v <} _{0 e} _v _{= 0, s˜ao, ainda,}

conectadas pelo vetor ǫna _{e, desde que o espa¸co-tempo ´e aproximadamente plano nessa}

regi˜ao, que

v =₋ǫ=e−κu. (1.59)

(37)

desde que s˜ao aprisionados pelo buraco negro.

Dessa forma, como solu¸cão da equa¸cão (1.32) que tem, como condi¸cão de contorno,

pω ∼e−iω em ℑ+, temos, sobre ℑ−,

fω(v)∼

 



0 se v >0

expiω_κln(₋v) se v <0. (1.60)

Antes de calcularmos o n´umero de part´ıculas produzidas pelo buraco negro e chegando a _ℑ+_{, precisamos ter em mente que o potencial gravitacional em torno do buraco negro}

pode provocar o espalhamento dessas mesmas part´ıculas. Um pacote de onda com pico em torno de uma frequˆencia ω que se propaga de _ℑ− _{na dire¸c˜ao do horizonte de um}

buraco negro eterno, pode ter uma fra¸c˜ao sua, 1₋Γω, sendo espalhada pela curvatura

do espa¸co-tempo propagando-se, logo em seguida, para _ℑ+_{, sem ter a sua frequˆencia}

alterada. Uma outra parte, Γω, pode propagar-se paralelamente a H+, sendo absorvida

pelo buraco negro. É essa segunda fra¸cão que está relacionada à produ¸cão de part´ıculas. Podemos, portanto, escrever fω =fω(1)+fω(2), onde os ´ındices (1) e (2) denotam as duas

partes do pacote de onda (espalhada e absorvida) descritas acima. Podemos definir, da mesma forma, as fun¸c˜oesqω epω. 5

Os coeficientes de Bogoliubov podem, ent˜ao, ser escritos como

αωω′ =α(1)_ωω_′+α_ωω(2)_′ , β_ωω′ =β_ωω(2)_′ (1.61)

Al´em disso, o coeficiente de espalhamento Γω ´e definido como

Γω =

Z

dω′₍

|α(2)_ωω′ |

2 _{− |}_β(2)

ωω′ |

2₎ _(1.62)

No c´alculo do n´umero de part´ıculas produzidas por um buraco negro, deve-se ignorar a primeira componente da onda. Por simplicidade, no que se segue, vamos omitir os ´ındices (1) e (2).

Os coeficientes de Bogoliubov s˜ao dados por 5_{O coeficiente Γ}

ω, obtido por calculo direto, ´e dado por:

Γω→

1 se ωM ≫1,

A

4πω

2 _se _ωM _≪₁_.

(38)

αωω′ = (p_ω, f_ω′)_ℑ− =

1 2π√ωω′

Z 0

−∞

ω′₋ ω κv

eiω′veiωκln(−v) (1.63)

= 1

iπ√ωω′(iω ′

)−iωκΓ

1 +iω

κ

βωω′ =−iα_ω,₋_ω′ (1.64)

Tomemos, agora, a transformada de Fourier da fun¸c˜ao fω(v), definida pela equa¸c˜ao

(3.4.1)

˜

fω(−ω′) =

Z ∞ −∞

eiω′vfω(v)dv (1.65)

= Z 0

−∞

expniω′_v₊ iω

κ ln(−v)

o

dv

Consideremos a ramifica¸cão da fun¸cão logaritmo que aparece na expressão (1.65) como estando no eixo real de um plano complexo relacionado à variávelv. Para ω′ _>_{0, vamos}

percorrer o contorno, mostrado na figura, em dire¸cão à parte negativa do eixo imaginário e, então, tomarv =₋ix(rota¸cão de Wick). Com isso, nós obtemos:

˜

fω(ω′) = −i

Z ∞

0

expn₋ω′_x₊ iω

κ ln(xe

−iπ/2₎o_dx _(1.66)

= ₋expπω

2κ

Z ∞

0

expn₋ω′_x₊ iω

κ ln(x)

o

dx

Para ω′ _< _{0, iremos percorrer o contorno, mostrado na figura, em dire¸c˜ao `a parte}

positiva do eixo imaginário, tomando, então,v =ix. Com isso, nós obtemos:

˜

fω(ω′) = i

Z ∞

0

expnω′x+ iω

κ ln(xe

iπ/2₎o_dx _(1.67)

= exp−πω

2κ

Z ∞

0

expnω′x+ iω

κ ln(x)

o

dx

(39)

\/\/\/\/\/\/\/\/\/|

Branch cut

∞

∞ Contorno de integração Para ω' < 0.

Contorno de integração Para ω' > 0.

X

Figura 5:

˜

fω(−ω′) =−e

−πω

κ f˜_ω(ω′). (1.68)

O resultado obtido acima nos diz que um modo de frequˆencia positiva ω em _ℑ+

corres-ponde a um misto de modos positivos e negativos em_ℑ−_.

Obtemos, ainda

βωω′ =−iα_ω₍₋_ω′₎ =−exp

−πω_κ αωω′ para ω′ >0 (1.69)

E da rela¸cão (1.44) e (1.51), obtemos, então, o número de part´ıculas emitidas pelo buraco negro

hN_ω(ℑ+)_i = Z

dω′ _|βωω′ |2 =

Γω

e2πω/κ₋₁ (1.70)

onde Γω ´e o coeficiente de espalhamento.

A equa¸c˜ao (1.70) descreve o espectro de um corpo negro com temperatura

T =ℏ κ

(40)

onde κ= 1/4M para um buraco negro de Schwarzschild.

Nós conclu´ımos, portanto, que um buraco negro pode irradiar sua energia a uma temperatura dada por (1.71). Este resultado faz com que os teoremas da mecânica dos buracos negros e as leis da termodinâmica passem a ter entre si muito mais que uma mera analogia.

Dos resultados acima, podemos, ainda, atribuir uma entropia ao buraco negro, a qual ´e dada por:

SBH =

A

4l2

P

(1.72)

Outro resultado interessante que queremos acrescentar aos nossos coment´arios, decorre da lei de Stephan. Para um buraco negro podemos escrever:

dE

dt ⋍−σAT

4

H,

σ= π

2_k4

B

60ℏ3_c2

, (1.73)

onde A ´e a ´area do horizonte de eventos. Usando o fato de que

E =M c2, kBTH ∼

ℏ_c3

GM. (1.74)

E, para um buraco negro de Schwarzchild

A= 4πM G c2

2

, (1.75)

n´os obtemos

dE dt ∼

ℏ_c4

G2_M2 (1.76)

o que nos implica em um tempo de vida finito para o buraco negro:

τ _∼G

2

ℏ_c4

(41)

1.5 Dois desafios: entropia e informa¸c˜

ao

Os resultados obtidos acima nos levam a algumas questões interessantes. A pri-meira delas está relacionada à entropia dos buracos negros. Temos que, em f´ısica es-tat´ıstica, entropia conta o número de micro-estados acess´ıveis que podem ser ocupados por um sistema, onde todos os estados são tomados como tendo a mesma probabilidade de ocorrência. Por outro lado, temos que buracos negros podem ser caracterizados completa-mente, por um observador externo, a partir de apenas três parâmetros: sua massa, carga elétrica e momento angular (teorema no hair). Qualquer informa¸cão adicional desaparece, por trás do horizonte de eventos, aos olhos de um observador externo e, dessa forma, a natureza dos micro-estados do buraco negro torna-se obscura. Então, qual é a origem da entropia de um buraco negro? Além disso, no sentido de justificarmos o nome entropia, precisamos, ainda responder o porquê da entropia do sistema formado pelo buraco negro e sua vizinhan¸ca ser uma fun¸cão não-decrescente do tempo, ou seja, o porquê de os bu-racos negros obedecerem a uma segunda lei generalizada da termodinâmica. Apesar de já terem surgido muitas possibilidades para a origem da entropia dos buracos negros (ver por exemplo [64, 65]), ainda não existe um consenso a respeito dessa questão.

(42)

2 ESPAC

¸ OS FUZZY

2.1 Introdu¸c˜

ao

Foi o próprio desenvolvimento da mecânica quântica que levou, seus fundadores, mais notavelmente na figura de Heisenberg, a sugerir a associa¸cão de uma estrutura não-comutativa às coordenadas do espa¸co-tempo, em escalas de comprimentos muito pequenos. Foi Snyder [66,67] quem primeiro formalizou esta ideia em um artigo totalmente devotado ao assunto. Ele foi motivado pela necessidade de controlar as divergências que empesta-vam certas teorias como a eletrodinâmica, por exemplo. Esta ideia se mostrou superior às sugestões anteriores de regulariza¸cão na rede, desde que mantinha a invariância de Lorentz. Entretanto, esta sugestão acabou sendo posteriormente ignorada, tendo sido o motivo principal disto o surgimento do procedimento de renormaliza¸cão, o qual obteve grande sucesso por fazer predi¸cões numéricas acuradas dos valores dos observáveis f´ısicos em eletrodinâmica quântica.

A ideia por trás da não-comutatividade do espa¸co-tempo está arraigada no próprio esp´ırito da mecânica quântica. Um espa¸co de fase quântico é definido pelo procedimento de trocarmos as variáveis canônicas de momentum e posi¸cão pµ _e _xµ _{por operadores}

hermitianos ˆpµ_{e ˆ}_xµ_{, os quais satisfazem às rela¸cões de comuta¸cão de Heisemberg [ˆ}_xµ_,_p_ˆν_{] =}

iℏ_δµν_{. Sob este procedimento, a no¸c˜ao de ponto no espa¸co de fase ´e perdida, de forma}

que temos de substitu´ı-la pela ideia de “c´elulas de Planck”. Recuperamos o espa¸co de fase ordin´ario, quando fazemosℏ_→_0.

Foi von Neumann o primeiro a descrever tal “espa¸co quântico”, introduzindo o ape-lido de “pointless geometry”, referindo-se ao fato de que a no¸cão de ponto não possui significado no espa¸co de fase devido ao princ´ıpio da incerteza de Heisemberg. Isto levou ao desenvolvimento das álgebras de von Neumann e foi, essencialmente, o nascimento da “geometria não-comutativa”, referindo-se ao estudo de espa¸cos topológicos cuja álgebra comutativa de fun¸cões C∗ _{é trocada por álgebras não-comutativas [68–71]. Neste}

(43)

(abandonando a no¸c˜ao de “ponto”), permitindo, portanto, ricas generaliza¸c˜oes.

Da mesma forma que acontece com a quantiza¸cão do espa¸co de fase clássico, um espa¸co-tempo não-comutativo é obtido ao trocarmos as coordenadas do espa¸co-tempo xµ

por operadores hermitianos ˆxµ _{de uma álgebra não-comutativa} _C∗ _{de fun¸cões sobre o}

espa¸co-tempo [68–71], os quais obedecem à rela¸cão de comuta¸cão

[ˆxµ,xˆν] =iθµν (2.1)

O caso mais simples da equa¸cão (2.1) é aquele em que θµν _{é uma matriz real}

anti-simétrica constante D_×D (D sendo a dimensão do espa¸co-tempo), com dimensão de comprimento ao quadrado. Desde que as coordenadas não comutam, elas não podem ser diagonalizadas simultaneamente e, portanto, o espa¸co-tempo clássico é substitu´ıdo por um espa¸co de Hilbert de estados.

Devido da existˆencia da rela¸c˜ao de incerteza

∆xµ∆xν _≥ 1

2|θ

µν

| (2.2)

pontos no espa¸co-tempo são substitu´ıdos por células de Planck de dimensão dada pela área de Planck. Dessa forma, podemos interpretar as coordenadasxµ _{de uma variedade como}

parâmetros macroscópicos obtidos por um “coarse-graining” sobre escalas menores que uma escala fundamental Λ_∼√θ. Para descrever fenômenos em escalas da ordem deθ, as coordenadas xµ _{perdem o seu significado e devem ser trocadas por elementos de alguma}

álgebra não-comutativa. A ideia de Snyder foi a de que se fosse encontrada uma descri¸cão coerente para a estrutura do espa¸co-tempo em escalas de comprimento muito pequenas, onde a no¸cão de ponto é perdida, então as divergências ultravioletas presentes na teoria quântica de campos poderiam ser eliminadas. Isto seria equivalente a aplicar um cutoff ultravioleta Λ nas integra¸cões sobre o espa¸co dos momenta para calcular os diagramas de Feymann, levando implicitamente a uma escala de comprimento fundamental Λ−1_{, abaixo}

da qual todos os fenômenos seriam ignorados. O que se acreditava, portanto, era que a forma mais simples, elegante e que respeitaria a invariância de Lorentz de introduzir Λ, seria através do uso de um espa¸co não-comutativo.

(44)

álgebras C∗ _{arbitrárias, e também para grupos quânticos e pseudo-grupos de matrizes.}

Juntamente com a defini¸cão de uma integra¸cão generalizada [75], estes esfor¸cos levaram a descri¸cão, em termos de álgebras de operadores, de espa¸cos-tempo não-comutativos base-ada totalmente em álgebras de fun¸cões e possibilitou a defini¸cão de teorias de Yang-Mills sobre uma larga classe de espa¸cos não-comutativos. Um exemplo concreto de f´ısica em um espa¸co-tempo não-comutativo é a teoria de Yang-Mills sobre um toro não-comutativo [75]. Por algum tempo, as aplica¸cões f´ısicas foram baseadas em interpreta¸cões geométricas do modelo padrão, seus vários campos e constantes de acoplamento ( o conhecido modelo de Connes-Lott) [76–78]. Nessa mesma linha, outras teorias de campos quânticos também foram estudadas, como o modelo de Schwinger e teorias de calibre unificadas [79,80]). Gra-vidade foi, também, eventualmente introduzida neste contexto, no sentido da unifica¸cão da mesma com as outras intera¸cões [81–85]. A ideia central por trás disso foi o uso de uma forma modificada do mecanismo de Kaluza-Klein na qual dimensões extras ocultas são substitu´ıdas por estruturas não-comutativas [86]. Por exemplo, nesta interpreta¸cão do modelo padrão [76–78], o campo de Higgs é um campo de calibre discreto Z2 sobre

um espa¸co não-comutativo, considerado como uma excita¸cão do tipo Kaluza-Klein. Isto conduz a uma demostra¸cão automática do mecanismo de Higgs, independentemente de detalhes relacionados ao potencial de Higgs. Os parâmetros de entrada são as massas de todos os quarks e léptons, enquanto a massa de Higgs é uma predi¸cão do modelo. Entre-tanto, esta abordagem encontrou muitas deficiências e sucumbiu. Entre estas deficiências, podemos destacar que as corre¸cões radioativas quânticas não puderam ser incorporadas de forma a fornecer predi¸cões satisfatórias. Apesar de tudo isso, o modelo levou a um reavivamento das ideias de Snyder de que a relatividade geral clássica não funcionaria em escalas de comprimento muito pequenas, desde que, nessas escalas, o espa¸co-tempo não seria mais descrito por uma variedade diferenciável [87–89]. Nesta escala de compri-mento, flutua¸cões de gravidade quântica (flutua¸cões na métrica) se tornariam grandes e não poderiam ser ignoradas [90, 91]. Este tipo de regime poderia ocorrer, por exemplo, nas proximidades da singularidade de um buraco negro.

(45)

determinada. Estes espa¸cos são então rotulados por um parâmetro de não-comutatividade 1/N, de forma que o espa¸co clássico é recuperado quando tomamos o limite de N muito grande. Na próxima se¸cão, estudaremos um dos tipos mais simples de espa¸cos fuzzy que está sendo amplamente estudado na literatura, a qual é chamada de esfera fuzzy [92–98].

2.2 A esfera fuzzy

Esferas fuzzy são variedades compactas que são obtidas quando trocamos uma álgebra comutativa de fun¸cões definida sobre uma esfera usualS2_{por uma álgebra não-comutativa}

de matrizes.

Temos que qualquer fun¸cão que seja definida sobre uma esfera usual pode ser expressa em termos de harmônicos esféricos Ylm como

f(x)_|S2=

∞

X

l=0

l

X

m=−l

clmYlm(x), (2.3)

onde clm são coeficientes complexos. O produto dessas fun¸cões é comutativo.

A introdu¸cão da geometria não-comutativa é feita promovendo as coordenadas xµ

definidas sobre S2 _{a um caráter de operador através da transforma¸cão}

xµ_→xˆµ ₌_k_Jˆµ _, _(2.4)

com

ˆ

xµ_x_ˆ

µ =r21, (2.5)

onde ˆJµ _{formam a representa¸c˜ao N-dimensional irredut´ıvel do grupo} _SU_{(2), enquanto} _r

´e o raio da esfera fuzzy, e

κ= _√ r

N2₋₁ (2.6)

Dessa forma, n´os temos

(46)

ondeλ/, o qual exerce um papel análogo ao da constante de Planck em mecânica quântica, é dado por

λ/= 2 r

2

√

N2 ₋₁ (2.8)

Esse procedimento introduz um cuttof N, sobre a expans˜ao (2.3), de forma que a mesma passa a ser escrita como:

f(x)_|S2

F=

N

X

l=0

l

X

m=−l

clmYˆlm(x), (2.9)

onde ˆYlm(x) s˜ao, agora, matrizes.

Dessa forma, a fun¸cão f(x) se torna uma matriz (N + 1)_×(N + 1), de forma que o produto das mesmas se torna não-comutativo. O limite comutativo é obtido tomando -se

N _{→ ∞}.

Uma das caracter´ısticas mais interessantes da abordagem fuzzy reside no fato desse procedimento de quantiza¸cão preservar as simetrias e as caracter´ısticas topológicas da variedade. Isto é fundamental para uma outra caracter´ıstica interessante desses espa¸cos que é a sua rela¸cão ´ıntima com álgebras de Hopf, as quais serão introduzidas na próxima se¸cão. As álgebras de Hopf nos servirão para compor um processo de mudan¸ca de topologia para espa¸cos fuzzy, de onde partem as ideias básicas desta tese.

2.3 Mudan¸ca de topologia para espa¸cos fuzzy

2.3.1 Um prel´

udio `

as ´

algebras de Hopf

Nessa se¸cão vamos introduzir os conceitos básicos para a defini¸cão de uma álgebra de Hopf.

Def ( Álgebra) : Uma álgebra A é definida como sendo o trio A = (A, M, u), onde A é um espa¸co vetorial,M :A_⊗A_→Aeu:C_→A são morfismos de espa¸cos vetoriais, onde

M é chamado de produto eude unidade, satisfazendo a condi¸cão dos seguintes diagramas serem comutativos, ondeCé o corpo dos números complexos. 1_,

(47)

A_{⊗ ⊗}A A A_⊗A

A_⊗A A

Id ⊗ M

M ⊗ Id

M

Figura 6:

A_⊗A

C_⊗A A_⊗C

A u ⊗ Id

~ _~

Id u

⊗

M

Figura 7:

Def (Co-álgebra) : Uma co-álgebra é definida pelo trio C = (C,∆, ε), onde C é um espa¸co vetorial, ∆ : C _→C_⊗C eε : C _→Csão morfismos entre espa¸cos vetoriais tais que os seguintes diagramas sejam comutativos:

C C_⊗C

C_⊗C C⊗ ⊗C C Δ

Δ

Δ ⊗ Id

Id ⊗Δ

Figura 8:

M

~

Id ⊗ u ~

C_⊗C

C⊗C C⊗C

C

ε Id

⊗

Figura 9:

Observemos que o sentido das setas foi, simplesmente, invertido. Nesta defini¸c˜ao ∆ ´e chamado de coproduto e ε de co-unidade.

Como exemplo, vamos considerar o espa¸co vetorial formado pelas matrizes de ordem

N, M at(N). Neste caso, o coproduto e a co-unidade s˜ao definidos como

(48)

∆(eij) = X

i≤p≤n

eip_⊗epj (2.10)

ε(eij) =δij (2.11)

(eij)αβ =δαiδ j

β (2.12)

sendoeij_{, 1}_≤_{i, j} _≤_n_{, a base de} _{M at}

(n).

Def (Bi-álgebra): Uma bi-álgebra é um espa¸co vetorialH equipado com uma estrutura de álgebra e de co-álgebra, de forma que os diagramas abaixo sejam comutativos, com

τ :H_⊗H _→H_⊗H´e chamado de mapeamento “twist” definido porτ(h1⊗h2) =h2⊗h1,

∀h1,2 ∈H.

H⊗H H

H⊗ ⊗ ⊗H H H

M

Δ ⊗Δ

H⊗ ⊗ ⊗H H H H⊗H

M ⊗M

Id ⊗ττ⊗Id

Δ

Figura 10:

H H⊗ H

C⊗C

M

ε ⊗ε

C C

Id φ

ε

Figura 11:

(49)

C _H

C⊗C

u

φ-1 Δ

H⊗H

u u ⊗

Figura 12:

C _H

C

u

Id ε

Figura 13:

H H

H⊗H

u

Δ ε

H⊗H

Id S, S Id⊗ ⊗ C ε

Figura 14:

Def ( Álgebra de Hopf ) Uma álgebra de Hopf é uma bi-álgebra com um antipodo.

O exemplo mais simples de uma álgebra de Hopf é a álgebra de um grupo. Para a álgebra de um grupo, define-se o coproduto ∆, a co-unidadeεe o antipodo S como segue:

∆(g) =g_⊗g ; ε(g) = 1 _∈C (2.13)

S(g) = g−1 _(2.14)

(50)

Pode-se verificar facilmente que ∆, ε e S, definidos acima, satisfazem às condi¸cões de consistência derivadas da comutatividade dos diagramas que definem a estrutura da álgebra de Hopf.

2.3.2 O grupo das ´

algebras de convolu¸c˜

ao

A ´algebra de grupo consiste das combina¸c˜oes lineares:

Z

SU(2)

dµ(g)α(g)g , (2.15)

de elementos g do grupo, sendo α uma fun¸c˜ao suave sobre o mesmo, enquanto dµ(g) ´e a medida de Haar sobre o grupo.

O produto da ´algebra ´e induzido pelo produto do grupo:

Z

SU(2)

dµ(g)α(g)g

Z

SU(2)

dµ(g′₎_β₍_g′₎_g′ ₌

Z

SU(2)

dµ(g) Z

SU(2)

dµ(g′₎_α₍_g₎_β₍_g′₎_gg′ _(2.16)

o segundo membro de (2.16) pode ser escrito como:

Z

SU(2)

dµ(s)(α_∗c β)(S)S (2.17)

onde _∗c ´e o produto de convolu¸c˜ao definido por:

(α_∗cβ)(S) =

Z

SU(2)

dµ(g′₎_α₍_g₎_β₍_g−1_S₎ _(2.18)

A álgebra de convolu¸cão consiste em fun¸cões suavesαdefinidas sobre G, com _∗c como

seu produto.

Usando, agora, o mapeamento

Z

SU(2)

dµ(g)α(g)g _→α (2.19)

Temos que a equa¸cão (2.16) torna-seα_∗cβ, de forma que a álgebra do grupo e a álgebra