Modelagem Matemática Rodney

Modelagem Matemática

Rodney C. Bassanezi

S

UMÁRIO

I. Uma Introdução à Biomatemática

4

0.1. Introdução . . . 5

0.2. Primeiros modelos de dinâmica populacional . . . 6

0.2.1. Modelo Malthusiano . . . 8

0.3. Modelos Subjetivos de Crescimento Populacional . . . 26

0.3.1. Modelo Estocástico de Pielou . . . 26

0.4. Modelos Variacionais Fuzzy (veja[1]) . . . 30

0.4.1. Modelo fuzzy do tipo Malthusiano (variação fuzzy) . . . 33

0.4.2. Sistemas Dinâmicos p-Fuzzy: Fuzziness demográfica . . . . 34

0.4.3. Sistemas dinâmicos fuzzy . . . 40

0.5. Modelos de Interação entre espécies . . . 43

0.5.1. Modelo de Lotka - Volterra . . . 43

0.5.2. Modelo Geral de Kolmogorov . . . 49

0.5.3. Modelo de Holling-Tanner . . . 51

0.5.4.

Modelo do tipo Lotka-Volterra: vespa

broca

0.5.5.

Modelo de Nicholson - Bailey

Parte I.

0.1. Introdução

A Biomatemática é uma interface entre a Biologia e a Matemática, caracterizada por uma grande extensão de contato que experimenta atualmente um processo de aprofundamento acelerado. Deste processo de mão dupla, tanto questões básicas de Biologia tem sido resolvidas, como novas linhas de pesquisa em Matemática emergiram e adquirem vida própria. Além disso, é importante notar a emergên-cia de novas áreas em Matemática Aplicada tais como algoritmos genéticos, redes neurais, algoritmos sociobiológicos, lógica fuzzy etc, que poderíamos designar de Matemática Biológica, já que, em muitos casos, devem os seus conceitos básicos à Biologia Teórica.

A Biomatemática contemporânea pode ser classificada em três ramos distintos quanto aos métodos e abordagem: a tradicional interface oferecida por problemas biofísicos e biomecânicos, a mais recente dedicada à análisegenômicae uma terceira que denominaremos deDinâmica de Populações. A maior ênfase do programa deste minicurso será dirigida à Dinâmica de Populações que, no seu sentido mais amplo engloba o estudo de populações de moléculas, células, microorganismos, organis-mos superiores, enfermidades e sociedades humanas. A síntese e o fundamento desta vasta linha de pesquisa procedem de uma variedade de modelos matemáti-cos descritos por equações variacionais: equações diferenciais ordinárias e parciais, contínuas e discretas e equações variacionais que contemplam a subjetividade de parâmetros e variáveis de estado (equações fuzzy).

O emprego de matemática na formulação de leis biológicas está ainda em sua fase inicial se comparado com o desenvolvimento e uso nas ciências Físicas, porém nos últimos anos, juntamente com a evolução do setor computacional, tem se mostrado uma ferramenta indispensável nas pesquisas de ponta de várias áreas.

grau de pertinência de seus elementos e portanto, a subjetividade vem embutida no próprio conceito de variável de estado ou dos parâmetros. De qualquer forma, os modelos determinísticos, embora não descrevam corretamente a realidade, podem ser abalizadores de muitos modelos estocásticos ou fuzzy – Quando se trabalha com uma amostra grande de indivíduos, pode-se dizer que o processo segue uma tra-jetória determinística que representa a solução média dos caso isolados. Nos mod-elos fuzzy, a solução é um conjunto fuzzy de soluções determinísticas que, quando defuzzificado, representa a média das soluções. Ainda, das soluções determinísticas que compõem a solução fuzzy, a que tem maior grau de pertinência ou confiabili-dade é a solução da média inicial denominada "preferida” [1].

0.2. Primeiros modelos de dinâmica populacional

itbpF2.2917in2.8202in0inmultidao₋243x300.bmp

Uma pista para o entendimento da dinâmica populacional é considerar queas pop-ulações interagem para persistirem, e para tal necessitam aumentar.

A proposta de utilização da matemática para descrever o crescimento de uma pop-ulação humana começou com o economista inglês T. R. Malthus (An Essay on the Principle of Population - 1798). Seu modelo assume que ocrescimento de uma popu-lação é proporcional à popupopu-lação em cada instante, e desta forma a população humana deveria crescer sem nenhuma inibição.

O modelo de Malthus propõe um crescimento de vida otimisada, sem fome, guerra, epidemia ou qualquer catástrofe, onde todos os indivíduos são idênticos, com o mesmo comportamento. O objetivo principal da introdução deste modelo foi o de chocar a opinião pública da época uma vez que estabelecia um crescimento em progressão geométrica para a população enquanto que a alimentação crescia em progressão aritmétrica. O modelo de Malthus se baseia numa equação diferencial muito simples mesmo para época em que foi formulado. A previsão da população mundial, segundo o modelo malthusiano, atingia numeros astronômicos em pouco tempo o que tornaria a Terra um planeta superlotado e inabitável . Também as pre-visões drásticas em relação à alimentação estavam erradas pois não se supunha o grande salto que ocorreu na produção mundial de alimentos entre os anos de 1950 a 1998, quando passou de 247 quilos per capita para 312 quilos (Veja no_{39, set/99,}

A modelagem matemática para descrever o crescimento populacional evoluiu, pas-sando por várias modificações após Malthus - Um dos modelos mais importante e conhecido é do sociólogo belga P. F. Verhulst (1838) que supõe que toda população é predisposta a sofrer inibições naturais em seu crescimento, devendo tender a um valor limite constante quando o tempo cresce. É um modelo de crescimento mais significativo, do ponto de vista biológico.

Os modelo de Malthus e Verhurst foram formulados para tempo contínuo, onde se supõe que os indivíduos se reproduzem a todo instante, o que na realidade pou-cas populações biológipou-cas satisfazem. Os modelos discretos podem ser consider-ado mais realísticos, neste caso, uma vez que contemplam a reprodução dos indi-víduos sazonalmente - tais modelos, em Ecologia, foram introduzidos somente a partir de 1975 pelo ecólogo austríaco Robert M. May [13] que observou a complexa dinâmica do modelo logístico discreto sob a luz da teoria do caos, mostrando que uma equação de aparente ingenuidade pode ter solução sem comportamento pre-visível [13] [?] [?].

As formulações estocásticas dos modelos determinísticos de Malthus e Verhurst só apareceram a partir de 1924 (Yule), sendo usados posteriormente por Bailey (1964) e Pielou (1977).

Na década de 40, Leslie (1945-48), modelou o crescimento populacional comparti-mentalizando a população por idade e estudando o fluxo entre os compartimentos através da álgebra matricial.

0.2.1. Modelo Malthusiano

SejaP o número de indivíduos em uma população animal ou vegetal. Este número

é dependente do tempo e assim podemos escrever

P =P(t) (0.2.1)

Na realidade,P(t)assume somente valores inteiros sendo pois uma função discreta

det. Entretanto, quando o número de indivíduos é suficientemente grande, P(t)

pode ser aproximado por uma função contínua, variando continuamente no tempo. Admitimos, neste modelo, que a proporção de indivíduos reprodutores permanece constante durante o crescimento da população. Admitimos também que as taxas de fertilidaden e de mortalidade m sejam constantes. Estas hipóteses são realísticas

em uma população grande que varia em condições ideais, isto é, quando todos os fatores inibidores do crescimento estão ausentes (a espécie tem recursos ilimitados e não interage com competidores ou predadores).

Temos queα =n₋m(coeficiente de natalidade menos o de mortalidade) é ataxa

de crescimento específicoda populaçãoP(t), aqui considerada constante. Assim,

P(t+ 1)₋P(t)

P(t) =n−m =α. (0.2.2)

Esta formulação matemática indica que avariação relativada população é constante ou, em outras palavras, que avariação da população é proporcional à própria população em cada período de tempo.

O modelo discreto(tempo discreto)de Malthusé dado por

P(t+ 1)₋P(t) = αP(t). (0.2.1)

Considerando dada a população inicialP(0) = P0, a solução de (0.4.5) é obtida por

recor-rência da expressão:

(

Pt+1 = (1 +α)Pt

P(0) =P0

(0.2.2)

ou seja,

Pt= (α+ 1)tP0 (cf. parágrafo 2.4) (0.2.3)

(0.2.3), fazendo

(α+ 1)t=Pt/P0 ⇒ α=

t

r

Pt

P0−

1 (0.2.4)

Por exemplo, se a população do Brasil de 1940 eraP0 = 41.236.351e, dez anos depois,

P10 = 51.944.397, então a taxa de crescimento populacional média (relativa), entre 1940 e

1950 foi de:

α = 10

r

51944397

41236351 −1 = 1,0233539−1 = 0,0233539

ou, aproximadamente, 2,3% ao ano.

Se consideramos as populações entre os censos de 1940 e 1991 quando a população era de 146.825.475 habitantes,αé dada por

α= 51

r

146825475

41236351 −1 = 0,0252131, o que nos permite afirmar que a população brasileira

cresceu a uma taxa média de, aproximadamente, 2,5% ao ano nestes 51 anos. Lembrando quePt = (1 +α)tP0 pode ser escrito na forma exponencial

Pt=P0eln(1+α)t (0.2.5)

Podemos comparar a solução do Modelo de Malthus discreto (0.2.2) com a solução do o modelo contínuo correspondente, considerando que

dP

dt = lim∆t→0

P(t+ ∆t)₋P(t) ∆t

e queP(t+ ∆t)₋P(t) =βP(t)∆t(modelo discreto).

Assim, podemos escrever o modelo contínuo por: 

 

dP

dt =βP(t) P(0) =P0

(0.2.6)

cuja solução é dada por

P(t) =P0eβt

Portanto, os modelos discreto (com taxa α) e contínuo (com taxa β) fornecem a

mesma soluçãoquandoβ = ln(1 +α).

Se considerarmos o modelo Malthusiano para projetar a população brasileira, ter-emos

α= 0,0252131para o modelo discreto eβ = 0,0249para o contínuo.

A equação

P(t) = 41,236e0,0249t (0.2.7)

fornece a população (em milhões de habitantes) em cada anot.

O modelo malthusiano discreto, por ser bem simples, é frequentemente utilizado para se fazer previsões a curto prazo, sendo corrigido depois de cada censo.

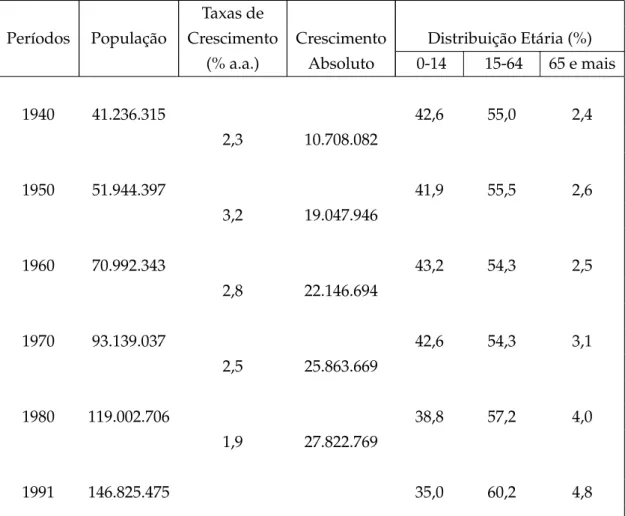
Exercício A tabela 1 fornece os censos demográficos do Brasil de 1940 a 1991:

Taxas de

Períodos População Crescimento Crescimento Distribuição Etária (%)

(% a.a.) Absoluto 0-14 15-64 65 e mais

1940 41.236.315 42,6 55,0 2,4

2,3 10.708.082

1950 51.944.397 41,9 55,5 2,6

3,2 19.047.946

1960 70.992.343 43,2 54,3 2,5

2,8 22.146.694

1970 93.139.037 42,6 54,3 3,1

2,5 25.863.669

1980 119.002.706 38,8 57,2 4,0

1,9 27.822.769

1991 146.825.475 35,0 60,2 4,8

Tabela 1 (Fonte: FIBGE.): Censos Demográficos do Brasil de 1940 a 1991. NEPO/UNICAMP

Modelo Logístico contínuo (Verhurst)

Se observamos os valores entre censos consecutivos de uma determinada população verificamos que as taxas de crescimento relativo tendem a diminuir com o tempo. O primeiro modelo que atende à variação da taxa de crescimento (ou razão intrínseca do crescimento populacional) foi formulado pelo matemático belga Pierre F. Ver-hurst em 1837. O Modelo de VerVer-hurst supõe que uma população, vivendo num determinado meio, deverá crescer até umlimite máximo sustentável, isto é, ela tende a se estabilizar. Desta forma, a equação incorpora a queda de crescimento da popu-lação que deve estar sujeita a um fator inibidor de proporcionalidade. Este modelo teve um impacto maior quando, no início do século XX, os pesquisadores ameri-canos R. Pearl e L. Reed utilizaram-no para projetar a demografia americana (veja [21], pp.86-87 ).

O modelo de Verhurst é, essencialmente, o modelo de Malthus modificado, con-siderando a taxa de crescimento relativaβ(P)decrescente em relação à população

P, em cada instante. Assim

dP

dt =β(P)P (0.2.8)

comβ(P) = r

P∞−P

P∞

, r >0eP∞ sendo o valor limite da população ou capaci-dade suporte. Desta formaβ(P)tende a zero quandoP _→P∞.

Explicitandoβ(P)na equação (0.2.8), e supondo queP(0) = P0 seja dado, temos o modelo clássico de Verhurst ou modelo logístico:

  

dP dt =rP

1₋ P

P∞

P(0) =P0, r >0

(0.2.9)

Observamos que P(t) _≡ 0eP(t) _≡ P∞ são soluções da equação diferencial dada

em (0.2.9). A solução analítica de (0.2.9) é obtida por integração após a separação das variáveis, isto é,

Z _dP

P(1₋P/P∞)

=

Z

rdt;

Usando a técnica das frações parciais para resolver a integral do 1o¯ membro, obte-mos

Z _dP

P(1₋P/P∞)

=

Z ₁

P +

1/P∞

1₋P/P∞

dp= ln_|P_{| −}ln

1−

P P∞

Logo, ln

P(t) 1₋P(t)/P∞

=rt+c

Usando a condição inicialP(0) = P0, podemos determinar o valor da constante de

integraçãoc:

c= ln

P0

1₋ P0

P∞ = ln

P0P∞

P∞−P0 Portanto ln

P(t)P∞

P∞−P(t)

=rt+ ln

P0P∞

P∞−P0 ou seja, ln

P(P∞−P0)

P0(P∞−P)

=rt ⇒

P P∞−P

= P0

P∞−P0

ert

ExplicitandoP(t), temos

P(t) = P∞ (P∞

P0 −1)e

−rt_{+ 1} =

P∞P0

(P∞−P0)e−rt+P0

(0.2.10)

A curvaP(t)é denominadalogística(fig. 6.3) e, de sua expressão (0.2.10), podemos

observar que

a) SeP0 < P∞ entãoP0 < P(t) < P∞ e P(t) tende a P∞, crescendo. Neste caso a

equação (0.2.9) mostra claramente que dP

dt >0;

b) SeP0 > P∞entãoP(t)tende aP∞, decrescendo (verifique que, neste caso,

dP dt <

0);

c) Da equação (0.2.9) temos que

dP

dt =rP −r P2

P∞

ou seja,dP

dt , como função deP, é uma parábola com concavidade voltada para baixo

(veja fig. 6.2) e cujas raízesP = 0eP =P∞são os pontos de equilíbrio ou soluções de equilíbrioda equação diferencial (0.2.9), pois dP

dt = 0nestes pontos.

d) Como r > 0, temos que dP

dt é crescente se 0 < P(t) < P∞

P∞

2 < P(t) < P∞. O valor máximo de

dP

dt , relativamente a P, é atingido quando P = P∞

2 , isto é, quando a população for igual à metade da população limite.

e) Se considerarmos em (0.2.10),P(t) = P∞

2 , podemos determinar o instantetmem

que a população atinge a máxima variação:

P∞

2 =

P0P∞

(P∞−P0)e−rt+P0 ⇒

ert= P∞−P0

P0 e portanto

tm =

1

rln

P∞−P0

P0

, (0.2.11)

considerando queP0 <

P∞

2 .

Assim, parat=tm temos:

i) P(tm) = P∞/2 (0.2.12)

ii) dP

dt |t=tm =r

P∞

2

1₋P∞/2

P∞

= r

4P∞>0 (0.2.13)

iii) d

2_P

dt2 |t=tm =r

dP dt −

2r P∞

PdP dt =r

dP dt

1₋2 P

P∞

_P=P∞

2

= 0

Logot=tmé umponto de inflexãodeP(t). Desta forma,

.SeP0 =

P∞

2 ⇒ tm = 0

.Se P∞

2 < P0 < P∞ ⇒a curva não tem ponto de inflexão

itbpF5.1335in2.4639in0inf ig2.jpg

F ig2₋(a)Variação de P(t) (b)Curva logística

Exercício Use os dados da tabela1 e determine um modelo logístico de projeção da população brasileira.

Sugestões:

1) Para estimar o valor deP∞use o método de Ford-Walford, ou seja, considere um

ajuste da funçãoPn+1 =f(Pn)e resolva o sistema

(

Pn+1 =f(Pn)

2) A expressão da curva logística é

P(t) = P∞ (P∞

P0 −1)e

−rt_{+ 1} =

P∞

be−rt_{+ 1}

e uma estimação dos parâmetrosr ebpode ser feita, por meio de um ajuste linear z(t), com a seguinte mudança de variáveis

z = ln

P P∞

1_{− P}P

∞

!

ou seja,

z= ln

1

be−rt₊₁

1₋ 1

be−rt₊₁

!

= ln

1

be

rt

Logo,

z =rt₋lnb

:

Projeto 1 – Modelo Logístico discreto

O Modelo de Verhurst pode ser formulado também através de uma equação de diferenças [?].

SejaPna população no instanten. Então, o crescimento absoluto dePné dado por

Pn+∆n−Pn = (α−βPn)Pn∆n (0.2.14)

ConsiderandoP0 dado, podemos obterPn em função de P0 através da fórmula de

recorrência _

 

Pn+∆n = (α∆n+ 1)Pn

1₋ β

α∆n+ 1

Pn

P0 dado

(0.2.15)

A equação (0.2.15) pode ser dada na forma normalizada por 

 

Nn+1 =rNn(1−Nn)

N0 =

P0

P∞

(0.2.16)

ondeNn=

β α∆n+ 1

Pn e (α∆n+ 1) =r.

P∞é obtido de (0.2.14), considerando que, quandoné muito grande,Pn+∆n ≃Pn=

P∞(valor de estabilidade ou valor máximo sustentável), e portantoP∞ =

α∆n

Quando os valores de ∆n são diferentes para cada n (como os da tabela 6.1), o

cálculo dos parâmetros e deP∞podem ser efetuados ajustando a expressão

Pn+∆n−Pn

∆n

por uma parábola

f(Pn) =aPn−bPn2

– Faça um ajuste def(Pn) = aPn−bPn2 com os dados dos censos demográficos de

população brasileira (Tabela 6.1).

– Estime os valores dos parâmetros dos modelos (0.2.15) e (0.2.16) e compare as projeções dadas por estes modelos com o modelo contínuo (??).

-DetermineP∞ considerando a intersecção da parábolaf(Pn)com a retaPn+∆n =

Pne estime o valor da população brasileira no ano 2000.

——————–

Uma das limitações do modelo de Verhurst consiste no fato que o ponto de inflexão (ou de crescimento máximo) da curva está sempre localizado no pontoPm =

P∞

2 , o

que nem sempre acontece na maioria das variáveis relacionadas a fenômenos com tendência assintótica.

Montroll em 1971 propôs um modelo geral para traduzir o crescimento assintótico de uma variável, levando em conta que o posicionamento da variação máxima pode ser qualquer valor entreP0 eP∞.

Modelo de Richard (1959)

Seja P∞ o valor limite finito de uma população P = P(t)e λ a sua taxa de

cresci-mento relativa quandoP é “pequeno” – O modelo de Montroll é dado pela equação

diferencial não linear

dP

dt =λP

1₋

P P∞

α

, λ >0 e α >0 (0.2.17)

O valor do parâmetro α é o indicador da posição do ponto de inflexão da curva.

Quandoα= 1, a equação (0.2.17) é simplesmente o modelo de Verhurst (0.2.9).

Para determinar a posição do ponto de inflexão da curvaPm,onde o crescimento

é máximo, é suficiente considerar a equação d2P

dt2 = 0, uma vez que

dP

0< P < P∞.

d2_P

dt2 = λ

dP dt

1₋ P

P∞

α

−αλ P P∞

P P∞

α−1

dP dt

= λdP dt 1₋ P P∞ α −α P P∞ α Logo,

d2_P

dt2 = 0 ⇔

P P∞

α

= 1

α+ 1 ⇔

P P∞

=

1

α+ 1

1

α

e portanto,

Pm =P∞

1 1 +α

1/α

(0.2.18)

Assim, dadoP∞, o valor dePmdepende somente do parâmetroα:

α = 3 _→ Pm = 0,6299P∞

α = 2 _→ Pm = 0,5773P∞

α = 1 _→ Pm = 0,5P∞ (modelo de Verhurst)

α= 0,5 _→ Pm = 0,4444P∞

α= 0,25 _→ Pm = 0,4096P∞

O objetivo principal deste modelo geral é propor diferentes formas possíveis de decrescimento das taxas de variação. Podemos considerar estas taxas como sendo dadas pela expressão

r =f(P, α) =λ

1₋ P P∞ α (0.2.19)

itbpF2.3419in2.2174in0inf ig3.jpg

f ig.3₋Taxa de crescimento do modelo de Richard

Observamos de (0.2.18) que quandoα > 0decresce, o ponto de inflexãoPm

tam-bém decresce e tende a um valor positivo igual aP∞

e ∼= 0,3678P∞. De fato, tomando α_→0,por valores positivos(α_→0+_{), temos}

lim

α→0+Pm =P∞_αlim_→0+

1 1 +α

Do Cálculo Diferencial, sabemos que seF(x)é uma função contínua no intervalo (a, b)então

F( lim

x→a+g(x)) = lim_x→a+F(g(x)),

Usando este fato, podemos escrever

ln

"

lim

α→0+

1 1 +α

1/α#

= lim

α→0+

"

ln

1 1 +α

1/α#

=₋ lim

α→0+

ln(1 +α)

α

Aplicando a regra de L’ Hopital, vem

− lim

α→0+

ln(1 +α)

α =−αlim→0+

1

1 +α =−1

Logo,

lim

α→0+

1 1 +α

1

α

=e−1 ₌ 1

e ∼= 0,3678

Veremos no próximo parágrafo quePm =

1

eP∞corresponde ao famoso modelo de

Gompertz de 1825.

Por outro lado, quando α cresce, o ponto Pm tende ao próprio valor P∞ – Isto

decorre do fato que

lim

α→+∞

1 1 +α

1/α

= 1 (verifique!)

Os pontos de estabilidade do modelo geral de Montroll são obtidos considerando

dP

dt = 0na equação 0.2.17, isto é,

λP 1₋ P P∞ α

= 0 _⇔ P = 0 ou P =P∞

Um esboço das soluções da equação (0.2.17) é dado na figura 6.6

itbpF4.8248in3.2742in0inf ig4.jpg

F ig.4₋Soluções do modelo de Richard com distintosα

mod-elador, na busca de um melhor “grau de aproximação”, não pode perder de vista o significado intrínsico das variáveis e parâmetros utilizados no modelo e que de-vem sempre traduzir ou explicar o fenômeno analisado. Em outras palavras, muitas vezes um ajuste ótimo de dados experimentais pode causar erros de projeções fu-turas – Uma curva ajustada aos dados reais não é necessariamente um modelo da situação estudada, ela simplesmente fornece informações que podem ser usadas na elaboração do modelo!

Um modelo clássico frequentemente utilizado na área das ciências biológicas é o modelo de Gompertz, onde o fator de desaceleração do crescimento deP não é dado

na forma de uma potência deP, como em (0.2.19).

Modelo de Gompertz (1825)

O modelo de Gompertz utiliza uma taxa de inibição da variável de estado propor-cional ao logarítimo desta variável – Isto significa que a taxa de crescimento é grande no início do processo, mudando rapidadamente para um crescimento mais lento. É um modelo bastante adequado para traduzir crescimentos celulares (plantas, bac-térias, tumores etc), sendo que, no início, todas as células são meristemáticas, per-dendo esta propriedade num intervalo de tempo relativamente pequeno.

O modelo de Gompertz é dado pelo problema de Cauchy (equação diferencial com condição inicial): _

 

dx

dt =ax−bxlnx=x(a−blnx) x(0) =x0 com a >0 e b >0

(0.2.20)

A taxa de crescimentor(x) = a₋blnx >0decresce comxe o valor de estabilidade

dexé obtido considerando-ser(x) = 0, isto é,

dx

dt = 0 ⇔(a−blnx) = 0 ⇔ x∞ =e

a/b _{,com x >0}

Observamos que quandoxé muito pequeno,r(x)é muito grande pois

lim

x→0+r(x) = +∞

Agora, como 0 = a₋ blnx∞, podemos tomar a = blnx∞ na equação (0.2.20) e

0(∗)_{Este fenômeno é característico das reações enzimáticas (veja [11] - pg 109) onde os valores de}

reescrevê-la como

dx

dt =bxlnx∞−blnx=bxln

_x∞

x

=xlnx∞

x

b

(0.2.21)

e neste caso,r(x) = lnx∞

x

b

.

A solução de (0.2.20) é obtida considerando-se a mudança de variávelz = lnx:

dz dt =

1

x dx

dt =a−bz

Integrando, _Z

dz a₋bz =

Z

dt _{⇔ −}1

b ln|a−bz|=t+c

Parat= 0, obtemosc=₋1

b ln|a−blnx0|.

Portanto,ln_|a₋bz_|=₋bt+ ln_|a₋blnx0|,

a₋bz = (a₋blnx0)e−bt ⇔z(t) =

1

b[a−(a−blnx0)e

−bt_]

Voltando à variávelx=ez, obtemos

x(t) = eab.exp

h

−a_b −lnx0

e−bti_{, ou (0.2.22)}

x(t) = x∞

x0

x∞

e−bt

(0.2.23)

A curvax(t)tem um ponto de inflexão quando

t =tm =

1

b ln

_a

b −lnx0

(0.2.24)

e

x(tm) =

1

ex∞ =

1

ee

a b =e

a−b

b (0.2.25)

Os modelos de Gompertz são bastante usados também no estudo da evolução de tumores sólidos. Neste caso, é assumido que a taxa de crescimento diminui quando a massa tumoral aumenta pois as células centrais não recebem nutrientes e oxigênio suficientes para sua multiplicação ([22]).

equivalentes do modelo de Gompertz

a)dx

dt =λxe

−αt _(0.2.26)

b)

    

dx dt =γx dγ

dt =−αγ

(0.2.27)

Projeto 2

– Considere os dados da Tabela 1 (população brasileira). (i) Faça o ajuste linear dos valores das taxas de variação

ri =

xi+1−xi

(ti+1−ti)xi

relacionados com lnxi;

(ii) Determinex∞=ea/bondeaebsão os coeficientes da reta ajustada em (i);

(iii) Determine o valor detm, sabendo-se quex(tm) =

x∞

e ;

(iv) Calcule o valor de x0, usando (i) e (ii), e escreva o modelo de Gompertz da dinâmica populacional na forma

x(t) =x∞

x0

x∞

e−bt

(v) Construa o gráfico da curvax(t).

Levando em conta que o crescimento deyé inibido e assintótico (e portanto, a taxa

de variação deyé decrescente e tende a zero quandoy _→ y∞), podemos construir

modelos particulares que tenham as características de crescimento assintótico. Existe um grande número destes modelos, onde a diferença essencial está na posição do ponto de inflexão. Citaremos alguns exemplos e o leitor interessado em seus de-talhes pode consultar [23]:

Modelo de Smith(1963)

dP

dt =λln P∞

P , λ >0 (0.2.28) Modelo de Blumberg(1968)

dP dt =rP

α

1₋ P

P∞

Para este modelo o ponto de inflexão é dado por

Pm =

α α+γP∞

A solução dste modelo é denominadahiperlogística.

Modelo de Turner - Blumenstein - Sebaugh (1969)

dP dt =rP

1+β(1−γ) "

1₋

P P∞

β#γ

com γ <1 + 1

β

Neste caso, o ponto de inflexão é dado por

Pm =

1₋ βγ 1 +β

1

β

P∞

Modelo de Ayala - Ehrenfeld - Gilpin(1973)

dP

dt =P(λ−aP +be

−P_{); a >0, b >0 e λ >0 (0.2.29)}

Projeto 3

– Analise o modelo alternativo de Smith (0.2.28), comparando-o com os modelos de Verhurst e Gompertz.

- Estude o modelo de Turner.

Modelo geral

– Em termos de dinâmica populacional, os modelos apresentados através das E.D.O. (modelos contínuos), representam o desenvolvimento de populações isoladas e sem migrações.

A forma geral destes modelos é uma equação autônoma do tipo

dP

dt =r(P)P (0.2.30)

onder(P)é denominadataxa de crescimento densidade-dependente. Nos modelos que supõem estabilidade das populações tem-se que

r(P)_→0 quando P _→P∞.

Em relação aos modelos da forma (0.2.30) ainda é suposto que dP

dt

P=0

= 0,

isto é, não se admite geração expontânea, e portanto, “todo organismo deve ter pais” (Axioma de Parenthood).

Quando (0.2.30) é escrita na forma

dP

dt =rP −g(r)P

2_{, (0.2.31)}

g(r)é o termo decompetição inter-específica – e indica que a inibição é proporcional

à taxa deencontros entre pares de indivíduos da população. Os indivíduos podem competir por alimentos, espaço, ou outros recursos limitados.

Quandor(P)em (0.2.30) é da forma

r(P) =a1+a2P +a3P2, coma2 >0 ea3 <0

obtemos o chamadoefeito Alleee neste caso, temos que a taxa de reprodução é máx-ima em densidades intermediárias (veja [10], pag. 215).

Os modelos de crescimento populacional da forma (0.2.30) são, na melhor das hipóteses, aproximações grosseiras da realidade e frequentemente são usados como instrumentos para verificação das tendências dos dados observados. Os modelos mais realistas exigem um alto grau de sofisticação matemática, como asequações diferenciais parciais, quando se quer considerar a dinâmica dependente da idade, fecundidade, taxas de mortalidade variáveis, habitat etc. ou asequações diferen-ciais não homogêneas, quando se considera os parâmetros variando com o tempo (modelos mesoscópicos). – Entretanto, os modelos mais sofisticados são, invariavel-mente, aperfeiçoamentos dos modelos simples e cujas limitações não devem ser ig-noradas. A evolução de modelos é, de fato, a característica mais importante do pro-cesso de modelagem, em qualquer nível de pesquisa ou de ensino-aprendizagem.

Modelos Mesoscópicos

Se examinarmos mais atentamente o crescimento de certas populações ou mesmo de um indivíduo, verificamos que pode existir comportamentos diferentes em relação ao tamanho limiteP∞, pré estimado.

à sua idade – Existe uma desaceleração no crescimento, seguido de um estirão na puberdade (entre 10 e 12 anos para mulheres e 11 e 13 anos para homens).

Também, o crescimento populacional na Terra é um caso típico deste processo, onde os valores pré-estimados deP∞estão ligados a acontecimentos históricos.

As-sim,

P∞ ≃ 107 -antes do advento das ferramentas (até aproximadamente 10.000 anos

atrás);

P∞≃108-com a Revolução Agrícola (entre 10.000 e 1.000 anos atrás)

P∞≃5.109-com a Revolução Industrial.

Modelos que traduzem estes fenômenos devem levar em consideração, outros pon-tos de equilíbrio além deP = 0eP =P∞(fixo).

itbpF3.6729in2.6351in0inf ig5.jpg F ig5₋Crescimento populacional da Terra

Outro exemplo de mudança de tendência de estabilidade é dado pelos valores da população americana onde o valor estimado para a população limite era 197,273 milhões de habitantes. Com o advento da 2a _{Guerra Mundial e a forte migração}

para os Estados Unidos houve um aumento da taxa de crescimento populacional e foi necessário reavaliar uma nova tendência de crescimento e de estabilidade.

Uma primeira tentativa para modelar a dinâmica da população, quando a capaci-dade suporte é alterada, é considerar um modelo logístico em cada período.

Se quizermos um modelo dado por uma única expressão podemos levar em con-sideração que a taxar(P)deve ter a forma de um polinômio de 3o _{grau e portanto}

dP

dt = r(P)P será um polinômio do 4

o _{grau. Uma maneira mais simples para}

esta nova modelagem pode ser realisada, considerando uma forma generalizada do modelo logístico

P(t) = P∞P0

(P∞−P0)ef(t)+P0

(0.2.32)

ondef(t)representartdo modelo clássico.

A expressão paraf(t), obtida da equação anterior, é dada por:

f(t) =₋ln

P0(P∞−P)

P(P∞−P0)

Aplicação: Dinâmica Populacional de molusco

– O estudo populacional do Donax gemmula (um pequeno molusco, comum nas praias do sul do Brasil), formulado através de modelos determinísticos mesoscópi-cos, deve considerar o efeito das tempestades, na forma de parâmetros variáveis sazonalmente, como um dos fatores abióticos responsáveis pela inibição da espécie (veja em [5]).

Considerando P = P(t) a densidade populacional do molusco, um modelo do

tipo logístico poderia dar globalmente a tendência demográfica da espécie. Entre-tanto, se levarmos em consideração os fatores abióticos que influenciam na tendên-cia macroscópica da dinâmica populacional, o modelo pode ser formulado pela equação (0.2.34)

        

dP

dt =R(t)

1₋ P

k

P ₋[d(t) +βf(t)]P

P(t0) = P0, t em meses

(0.2.34)

onde,R(t), f(t)ed(t)são funções periódicas, de mesmo períodow >0;

R(t): taxa de recrutamento;

f(t): medida da intensidade de tempestades;

d(t): taxa de mortalidade fisiológica;

k: capacidade suporte do meio;

β: constante de proporcionalidade da mortalidade abiótica

Os parâmetros do modelo (0.2.34) foram obtidos através de simulações numéricas ([6]), usando dados experimentais colhidos por Paes no litoral do Rio Grande do Sul em 1989.

R(t) =r1+

r2

2

1₋cosπt 6

, r1 = 0,3 e r2 = 0,2;

d(t) = 0,2

0,3025 + 0,1225 sen

π(t₋3) 6

;

f(t) = 1,3083 + 3,5279 cos

πt

6 +

π

12

β = 0,003, obtido empiricamente;

k= 650, obtido do ajuste de dados;

Um agrupamento dos parâmetros em (0.2.34) fornece a equação simplificada 

     

dP

dt =α(t)P −γ(t)P

2

P(t0) = P0 >0

(0.2.35)

A solução de (0.2.35) converge assintoticamente para uma solução de equilíbrio

P∞(t)periódica ([6]).

Exercício

– Analise o crescimento de uma variávelP(t)através da figura dada pela equação

autônoma dP

dt =P f(P)

itbpF3.096in1.8498in0inf ig6.jpg F ig6₋Crescimento de uma população P

– Quantos pontos de equilíbrio temos neste caso? – Dê uma expressão analítica paraf(P).

– Mostre que uma composição de 2 modelos assintóticos simples pode fornecer um modelo para esta situação.

Projeto 4

-Estude o crescimento populacional mundial ( Tabela 2).

Ano População

1804 1

1927 2

1960 3

1974 4

1987 5

1999 6

.

Tabela 2- População mundial (em bilhões de

pessoas)

A previsão da Fnuap é que em 2050 a população mundial será de 8,9 bilhões

⊲Determine qual o modelo que foi utilizado para prever o nascimento do bebê de

número 6 bilhões.

⊲ J. Cohen, diretor do Laboratório de Populações da Universidade Rochefeller,

acredita que se não houver grandes mudanças no comportamento de consumo, a Terra pode suportar uma população de 10 bilhões de pessoas. Utilize este dado para melhorar seu modelo.

⊲Com uma mudança nos hábitos de consumo, os demógrafos acreditam que nosso

planeta pode comportar até 20 bilhões. Formule um modelo bilogístico com este novoP∞.

⊲Dê umaexplicação para a afirmação: ”Em 1960 a população européia era o dobro da

africana. Em 2050 haverá três vezes mais africanos que europeus” (Veja,39, set/99).

⊲ Os países mais populosos do mundo são (% do total): China 21,2%, Índia

-16,7%, EUA - 4,6%, Indonésia - 3,5%. O Brasil tem 2,8% da população mundial. Faça uma previsão da população destes países para o ano 2050, usando o modelo logístico formulado anteriormente para a população mundial.

0.3. Modelos Subjetivos de Crescimento

Populacional

O processo de crescimento populacional é geralmente estocástico e, num dado in-stante, este crescimento não é necessariamente proporcional à população presente (conforme foi observado experimentalmente com leveduras). Apresentaremos, como ilustração deste fato, o modelo clássico de Pielou que mostra a importância da solução determinística como uma aproximação da solução média estocástica e o modelo malthusiano fuzzy onde se considera a variável de estado como um con-junto subjetivo.

0.3.1. Modelo Estocástico de Pielou

O modelo de Pielou estocástico determina o processo evolutivo de uma população através das distribuições de probabilidades relacionadas por equações diferenciais. Para a formulação do modelo devemos fazer algumas considerações ([16]):

(a) A probabilidade de que, num pequeno intervalo de tempo ∆t, um indivíduo

reproduza exatamente uma vez é igual a

p(P + 1,∆t) =αP∆t+h1(∆t) (0.3.1)

onde h1(∆t) é um infinitésimo de ordem menor que ∆t, isto é, lim

h1(∆t)

Denotaremos esta propriedade porh1(σ∆t).

(b) A probabilidade de que um indivíduo reproduza mais de uma vez num inter-valo de tempo∆té ”muito pequena”h2(σ∆t).

(c) A reprodução em intervalos de tempo disjuntos é um evento independente, isto é, se I1 ∩I2 = φ então a reprodução no intervalo de tempo I2 independe de já ter reproduzido ou não no intervaloI1.

Seja p(P; ∆t) a probabilidade de uma população do tamanho P reproduzir apenas

um indivíduo no intervalo de tempo(t, t+ ∆t). Observamos que, para que este evento

ocorra é necessário que apenas um indivíduo da população reproduza e(P₋1)

indi-víduos não reproduzam. Desta forma, existemP possibilidades para o nascimento

de um único indíviduo e (P ₋ 1) possibilidades para o nascimento de qualquer

quantidade.

Logo, podemos escrever

p(P; ∆t) = P[α∆t+h1(σ∆t)].[1−(α∆t+h1(σ∆t)]P−1 (0.3.2) Considerando a expansão binomial do 2o¯ termo (binômio de Newton) e agrupando os elementos de ordem inferior a∆t, obtemos

p(P; ∆t) =αP∆t+H(σ∆t)

Por outro lado, temos que

p(P;t+∆t)é a probabilidade de se ter menos que(P₋1)elementos num instantet,

acrescida da probabilidade de se ter dois ou mais elementos no intervalo(t, t+ ∆t),

isto é,

p(P;t+ ∆t) =p(P;t)(1₋αP∆t) +p(P ₋1;t)α(P ₋1)∆t+H1(σ∆t) ou

p(P;t+ ∆t)₋p(P;t)

∆t =α(P −1)p(P −1;t)−αP p(P;t) +

H1(σ∆t)

∆t

Passando ao limite quando∆t_→0, obtemos a equação diferencial

dp(P;t)

dt =α[(P −1)p(P −1;t)−P p(P;t)] (0.3.3)

nascimento no intervalo de tempo(t, t+ ∆t). Logo,

p(P0;t+ ∆t) =p(P0;t)(1−αP0∆t) +H2(σ∆t) ou

p(P0;t+ ∆t)−p(P0;t)

∆t =−αP0p(P0;t) +

H2(σ∆t

∆t

Agora, considerando o limite com∆t_→0, obtemos

dp(P0;t)

dt =−αP0p(P0;t) (0.3.4)

As equações diferenciais (0.3.3) e (0.3.4) determinam as distribuições de probabili-dades_{p(P;t)_}P≥P0, P = P0 + 1, P0+ 2, ..., P0+n, e portanto, o processo evolutivo

de uma população, dada inicialmente porp(P0; 0)).

Se a população inicialP0for conhecida precisamente, isto é sep(P0,0) = 1, então a avaliação dep(P0;t)é obtida da equação (0.3.4), através da solução do problema de

valor inicial _

   

dp(P0;t)

dt = −αP0p(P0;t)

p(P0,0) = 1

(0.3.5)

ou seja,p(P0;t) = e−αP0t.

A evolução da população a partir de P0, isto é, a obtenção de p(P0 +n;t)é feita passo a passo, considerando-se a equação (0.3.3)

dp(P0+ 1;t)

dt =α[P0p(P0;t)−(P0+ 1)p(P0+ 1;t)]

Substituindo a expressão dep(P0;t), obtida anteriormente de (0.3.5), vem

dp(P0+ 1;t)

dt =αP0e

−αP0t_−α(P

0+ 1)p(P0+ 1;t)] (0.3.6) que é uma equação linear não-homogênia - Sua solução geral é dada pela soma de uma solução particular com a solução da equação homogênea correspondente:

Temos que:

p(P0 + 1;t) = P0e−αP0t é uma solução particular de (0.3.6).

Então,

p(P0+ 1;t) = [ke−αt+P0]e−αP0t é a solução geral de (0.3.6).

Agora, comop(P0+ 1;t) = 1entãop(P0+ 1; 0) = 0e portanto,k =−P0. Logo,

p(P0+ 1;t) = P0e−αP0t

1₋e−αt

Continuando o processo, obtemos de maneira análoga que

p(P0+ 2;t) =

P0(P0−1)

2 e

−αP0t₍₁

−e−αt₎2

Donde, podemos conjecturar1 _{que a probabilidade de se ter P}

0 +n elementos no instanteté dada por

p(P0+n;t) =

P0(P0+ 1)...(P0+n−1)

n! e

−αP0t₍₁

−e−αt₎n

Considerando uma população geralP = P0 +n, obtemos a expressão do modelo de Pielou estocástico:

p(P;t) = (P −1)! (P ₋P0)!(P0−1)!

e−αP0t_(1−e−αt₎(P−P0) (0.3.7)

Como afunção densidade de probabilidadeé dada por (0.3.7), podemos determinar seu

valor esperadoE(P)(média populacional), isto é,

P(t) = E(P) =

∞

X

P=0

P p(P;t) = P0eαt (0.3.8)

Portanto, neste caso, o modelo determinístico (modelo de Malthus) expressa o es-tado médio obtido no processo estocástico.

Observamos que este resultado, válido para o crescimento malthusiano, pode ser ou não verdadeiro em casos mais gerais – A razão entre o desvio padrão D(P) e

E(P) :

CV(P) = D(P)

E(P),

dá ocoeficiente de variaçãodeP.

Temos que

D(P) =pP0e2αt−P0eαt = p

P0eαt(1−e−αt)1/2 Logo

CV(P) =

1₋e−αt

P0

1/2

e portanto, CV(P)_{→ √}1

P0

quandot_{→ ∞}.

Isto mostra que o erro de aproximação entre os modelos determinístico e estocástico varia inversamente com√P0,à medida que o tempo passa.

Portanto, quanto maior a população inicialP0, melhor será a aproximação entre a

solução determinística e a solução estocástica.

0.4. Modelos Variacionais Fuzzy (veja[1])

“Conforme a complexidade de um sistema aumenta, nossa habilidade

de fazer afirmações precisas e significativas sobre seu comportamento diminui, até um limiar em que a precisão e relevância tornam-se praticamente características mutuamente exclusivas”.

Princípio da Incompatibilidade - Zadeh

Os modelos estocásticos, como o de Pielou, são frequentemente utilizados para analisar variações sujeitas às distribuições de dados estatísticos. Entretanto, se pre-tendemos modelar alguma população onde seus elementos são heterogêneos relati-vamente a alguma característica, devemos considerar o comportamento desta carac-terística no processo evolutivo. Por exemplo, se temos uma população de “fumantes” num instantet0, sujeita a alguma taxa de mortalidade, podemos querer saber como

dos fumantes desta população, podemos usar um modelo estocástico para estudar a evolução desta distribuição inicial. Agora, se a característica de ser fumante de-pender da quantidade de cigarros que se fuma diariamente, qualidade dos cigarros, intermitência do ato de fumar etc., devemos caracterizar também ograude ser fu-mante. Neste caso, cada indivíduo pertence à população de fumantes com umgrau específico de pertinência : Se não fumar, seu grau de pertinência é zero- se fumar 3 carteiras diárias podemos dizer que é uma fumante de grau 1.

No caso de se estudar a dinâmica de uma população, muitas vezes as informações que temos sobre os parâmetros e variáveis são parciais ou não temos certeza, nem mesmo, das condições iniciais.

A população de predadores de uma determinada espécie pode ser considerada como um subconjunto fuzzy, se associarmos a cada predador seu grau de predação.

Uma população de presas é composta de elementos cada qual com um grau distinto de ser presa, um jovem por exemplo é menos predado que um velho e doente.

Os modelos variacionais fuzzy podem comportar vários tipos de subjetividades (fuzziness), dependendo da escolha da variável de estado e dos parâmetros dos modelos. Temos umafuzziness demográficaquando a variável de estado é um subcon-junto fuzzy, efuzziness ambientalquando somente os parâmetros são considerados subconjuntos fuzzy. Em geral ambos os tipos de fuzziness estão presentes nos fenô-menos biológicos. Os modelos formulados através de equações variacionais com fuzziness demográfica geralmente têm um tratamento matemático muito complexo a não ser que nos restrinjamos aos modelos lineares.

As equações variacionais fuzzy têm sido estudadas por meio de distintos méto-dos. Os primeiros trabalhos na direção de contemplar subjetividades não aleatórias em sistemas dinâmicos [[?],[?]] utilizavam a derivada de Hukuhara. Este método

não teve muito sucesso por conta da instabilidade das soluções pois proporciona o aumento do diâmetro das soluções.

Um segundo método, bastante simples, é dado pelos sistemas dinâmicos p-fuzzy (puramente fuzzy) que são alimentados por um sistema de regras intuitivas ou fornecidas por especialistas. Um especialista pode fornecer informações que pro-porcionam associações de entrada e saída linguísticas e os sistemas fuzzy podem produzir estimativas de sistemas complexos sem a ajuda de modelos matemáticos.

como solução uma família de curvas determinísticas sendo que, para cada possível valor do parâmetro e/ou condição inicial, a curva tem um grau de pertinência ao subconjunto fuzzy das soluções. Estes graus de pertinência são os mesmos de suas condições iniciais, ou seja, cada solução mantem o mesmo grau de pertinência do início[[?]].

Salientamos que os processos fuzzy adotados nos casos citados, para se estudar sistemas variacionais, são quase sempre provenientes ou derivados de sistemas de-terminísticos.

Considerando-se que a habilidade das atividades humanas está sempre ligada à velocidade de operações, isto exige uma aproximação de dados e informações sen-soriais, codificados por meio de termos imprecisos ou vagos. A manipulação de incertezas é uma atividade característica do ser humano, desenvolvida através de gerações. A etnomatemática não é muito mais que uma base de regras usada para entender ou resolver certas situações e não necessita de fundamentação matemática para mostrar que funciona. A troca da precisão pela velocidade é muitas vezes um fator decisivo na luta pela sobrevivência e, nos sistemas complexos, a precisão matemática perde sua força conforme oprincípio de incompatibilidadede Zadeh. En-tretanto, não queremos fazer uma apologia da imprecisão em detrimento da exati-tude fornecida pela matemática clássica, simplesmente queremos mostrar ferramen-tas alternativas para modelar o raciocínio natural dos homens quando relacionado com o processo de mudanças de variáveis de estado.

Em resumo podemos dizer que existem pelo menos três maneiras distintas de in-corporar graus de subjetividade em sistemas dinâmicos fuzzy:

1. Usando a variação como sendo dada pela derivada de Hokuhara; 2. Usando uma base de regras e obtendo-se um sistema p-fuzzy; 3. Usando o Princípio de Extensão de Zadeh.

Todos estes métodos são provenientes de estruturas que tem características baseadas na teoria fuzzy na qual o conceito de conjunto fuzzy é fundamental.

Um subconjunto fuzzyA de um conjunto U é caracterizado por uma função µA : U →

[0,1],chamada grau de pertinência, ondeµA(x)atribui o grau com que o elementoxpertence

ao subconjunto fuzzyA.

µA(x)indica o grau com que o elementoxdeU está em “concordância” com o conceito que

caracteriza os “elementos” deA.

Observamos que seAfor um subconjunto clássico deU, então os únicos valores deµA(x)

0.4.1. Modelo fuzzy do tipo Malthusiano (variação fuzzy)

Um modelo fuzzy do tipo malthusiano consiste de uma equação gerada pela hipótese de crescimento populacional proporcional à população em cada instante, considerando a variável de estadoP como sendo um conjunto fuzzy em cada instante (cada indi-víduo pode mudar seu grau de pertinência ao conjunto considerado com o tempo -Por exemplo, no conjunto dos predadores, a predação de cada indivíduo depende de sua idade).

SejaPA(t)a função grau de pertinência do subconjunto fuzzyApara cada valor de

t. Podemos subentender o subconjunto fuzzyA como sendo a própria função PA.

Por simplicidade, denotamos o subconjunto fuzzyPAporP.

Definimos oα-nível de um subconjunto fuzzyP,como sendo o subconjuntodos números

reais,dado por:

[P]α =_{x_∈IR:P(x)_≥α_} se 0< α_≤1

Quando osα-níveis deP forem intervalos fechados, colocaremos

[P(t)]α = [P₁α(t), P₂α(t)] para cada t_≥0.

O modelo fuzzy do tipo malthusiano é dado pela equação 

   

P′_{(t) =aP(t)}

P0 =PA(0) onde, P0é um conjunto fuzzy ea ≥0

(0.4.1)

A solução desta equação (veja [8]) é obtida da solução do sistema de equações determinísticas de seusα-níveis:

        

dPα

1

dt =aP

α

1 (t) , P1α(0) =P01α

dPα

2

dt =aP

α

2 (t) , P2α(0) =P02α

(0.4.2)

Para cadaα, a solução existe e é dada por

(

Pα

1(t) =P01αeat

Pα

2(t) =P02αeat

(0.4.3)

onde[Pα

01, P02α] = [P(0)]α.

itbpF3.3901in2.1845in0inf ig8.jpgitbpF3.563in2.1897in0inf ig7.jpg

F ig7₋Solução de um modelo fuzzy-malthusiano com variaçãoadecrescente

Se[P(0)]1 _{tiver somente um ponto, isto é,P}

01 =P02=P0 então[P(t)]1 se comporta como a solução do modelo determinístico de Malthus:[P(t)]1 _=P

0eat.

A solução do modelo (0.4.1) quandoa < 0, é obtida do sistema de α₋níveis dado

por:

dPα

1

dt =aP α

2 (t) , P1α(0) =P01α

dPα

2

dt =aP1α(t) , P2α(0) =P02α

(0.4.4)

0.4.2. Sistemas Dinâmicos p-Fuzzy: Fuzziness demográfica

Neste parágrafo vamos desenvolver exemplos de sistemas dinâmicos baseados em relacionamento e controle de regras cujo objetivo principal é considerar a incerteza nas próprias variáveis de estado, o que caracteriza a fuzziness demográfica.

As “soluções” obtidas dos sistemas p-fuzzy são aparentemente mais grosseiras e menos exatas que as determinísticas mas muito mais realísticas pois englobam toda a subjetividade descrita por um especialista do fenômeno estudado. Evidentemente, quanto mais informações se tem, mais próximas da realidade serão as soluções.

Os exemplos estudados aqui são específicos de dinâmica de populações. Claro que as técnicas da lógica fuzzy que são utilizadas aqui podem ser aplicadas a outras situações, como por exemplo, em epidemiologia ou mesmo em sistemas dinâmicos mais gerais.

Controlador fuzzy e os sistemas dinâmicos

infor-mações contidas em uma regra foi testada ou pode ser induzida sem muitas difi-culdades; O controlador agrega as informações contidas no conjunto de regras e fornece uma saída “média” usando expressões simples; O processamento das in-formações (cada regra é processada individualmente) é computacionalmente muito rápido, com resultados que podem ser testados manualmente e, se uma informação não for muito correta isto não influi substancialmente no resultado devido à ro-bustez destes controladores([[?]]).

Para nossas aplicações vamos usar o controlador de Mamdani que consiste basica-mente de três estágios: Uma entrada (fuzzificador), um processador (composto de uma base de regras e um método de inferência) e uma saída (defuzzificador). Como defuzzificador usamos o centro de massa embora qualquer outro não cause grandes alterações.

itbpF3.442in2.6143in0inmini11.jpg F ig8₋Controlador de Mamdani

Sistemas p-fuzzy

Um controlador fuzzy proporciona ao usuário uma tomada de decisão cada vez que é acionado. Se realimentarmos o controlador, compondo cada saída com a próxima entrada obtemos um sistema iterativo equivalente a um sistema dinâmico discreto tradicional.

Um sistema p-fuzzy emRné um sistema dinâmico discreto, (

xk+1 =xk+△xk

x0 ∈Rn

(0.4.5)

onde, a variação_△xk é obtida por meio de um controlador fuzzy. Dependendo da

situação estudada as variações podem depender também do tempo ou da posição de interaçãok.

A arquitetura de um sistema p-fuzzy pode ser visualizada na Figura 9:

itbpF4.7617in2.1949in0inmini12.jpg

Fig 9 -Arquitetura de um sistema p-fuzzy

Exemplo:Modelo p-fuzzy de Malthus O modelo p-fuzzy é construído a partir de um sistema baseado em regras fuzzy, onde a entrada é a população (P) e a saída a variação da população∆P ou dP_dt.

. A base de regras fuzzy utilizada é: 2_{Se população é muito baixa então} dP

dt é muito baixa.

2_{Se população é baixa então} dP

dt é baixa.

2_{Se população é média então} dP

dt é média.

2_{Se população é alta então} dP

dt é alta.

itbpF5.2658in1.5022in0inmini1.bmp

F ig10.(a)Funções de pertinência da população (b) Funções de pertinência variação

E utilizando o sistema baseado em regras fuzzy determinamos o valor de dP

dt no

es-tágio seguinte. Assim, calculamos o próximo valor deP, com integração numérica,

especicamente o método é o da regra do trapézio. Repetimos o mesmo raciocínio em 100 iterações obtendo a trajetória da população no tempo como mostra a Figura 11,

itbpF2.6351in2.1223in0inmini2.jpg F ig11₋Solução (população) via Mamdani

. O método de inferência utilizado é o Método de Mamdani e o de defuzzicação é o Centro de Gravidade.

Aplicação: Espalhamento daPodridãoda Maçã

itbpF3.8761in3.0727in0inma??1.jpg

A cultura da macieira (Malus domestica) é uma atividade econômica muito impor-tantes em alguns estados do Brasil, sobretudo em Santa Catarina e Paraná. Perdas substanciais da produção de maçãs resultam de doenças que afetam os frutos após a colheita. As principais doenças são do tipo podridão, causadas pelos patógenos

Botryosphaeria dothidea (podridão branca), Glomerella cingulata (podridão amarga),

Penicillium expansum(mofo azul) ePezicula malicorticis(olho-de-boi).Tais patógenos

armazenados[[26]].

A armazenagem das maçãs é feita em câmaras frigoríficas onde são depositadas em caixas de madeira (bins) sobrepostas que comportam, aproximadamente 3000 frutas. Quando alguma maçã está contaminada compodridão,a doença se propaga rapidamente contaminando as outras frutas ao seu redor - estima-se que em 12 dias, 80% das maçãs da caixa são contaminadas, comprometendo posteriormente todo o estoque.

Nosso objetivo é analisar a dinâmica da doença utilizando modelagem matemática. Neste caso específico em que a dinâmica é essencialmente discreta e a contaminação de maçãs depende de uma geometria, relativamente complexa, de contato entre as frutas (veja[[27]]), vamos usar um modelo p-fuzzy.

A escolha do modelo matemático é determinante para se ter uma previsão de al-gum fato. Modelos determinísticos de um mesmo fenômeno podem prever resulta-dos diferentes. Isto acontece invariavelmente porque nem sempre é possível dispor de todas as variáveis que atuam no fenômeno. Neste sentido, por mais exataque seja a matemática, por mais determinísticos que sejam os modelos, sempre tere-mos soluçõesaproximadasde alguma realidade. Assim, o uso de uma matemática menos determinística e mais grosseira pode ser muitas vezes tão eficaz para pre-visões quanto às obtidas pelos processos clássicos. De qualquer modo, o modelo fuzzy dá uma idéia da dinâmica da doença, podendo ser útil para a formulação de modelos determinísticos e estimação de seus parâmetros.

Definição das variáveis lingüísticas Definir funções de pertinência na forma tri-angular é muito comum nas aplicações da teoria fuzzy. Entretanto, uma outra es-colha coerente não acarreta grandes modificações num resultado final

Conjuntos fuzzy para níveis de maçãs contaminadas _◦População de Contam-inadas,muito baixa: Pbi, comϕPbi =

600−x

600 se 0≤x <600eϕPbi = 0caso contrário;

◦ População de Contaminadas, baixa: Pb, com ϕPb =

x−300

450 se 300 ≤ x < 750 ;

ϕPb =

1200−x

450 se750 ≤x <1200eϕPb = 0caso contrário;

◦População de Contaminadas,média: Pm, comϕPm =

x−900

450 se900 ≤x <1350; ϕPm =

1800−x

450 se1350≤x <1800eϕPm = 0caso contrário;

◦População de Contaminadas,média alta: Pma,comϕPma =

x−1500

500 se1500 ≤x <

2000;ϕPma =

2400−x

400 se2000≤x <2400eϕPma = 0caso contrário;

◦ População de Contaminadas, alta: Pa, com ϕPa =

x−2200

300 se 2200 ≤ x < 2500;

ϕPa =

2800−x

◦População de Contaminadas, muito alta: Pat,com ϕPat =

x−2600

200 se 2600 ≤ x <

3000;Pat = 1sex≥3000ePat = 0sex <2600.

As funções de pertinência dos subconjuntos fuzzy, usadas para modelar a popu-lação contaminada e aqui estabelecidas como funções triangulares, podem ser visu-alizadas na Figura 12:

itbpF6.263in1.8827in0inmini18.jpg

Fig.12 - Funções de pertinência de populações de frutas contaminadas

Observamos que para cada valor dex , a função de pertinência da densidade de

infestação ϕP(x) pode pode ser dada por até dois valores. Senão vejamos, seja x

um valor dado no intervalo[900,1200)por exemplo, sex= 1000, entãoϕPb(1000) =

200

450 = 0,444,isto é,1000maçãs podres tem grau de pertinência0,444no subconjunto fuzzy contaminação baixaPb. Também, ϕP m(1000) = 100₄₅₀ = 0,222 é o grau de

pert-inência de1000 ao subconjunto fuzzy contaminação médiaPm. De maneira análoga

obtemosϕP(x)para outros valores dex.

Variação da população contaminada ou incidência da doença Para o cresci-mento da população de contaminadas definimos as variáveis lingüísticasIncidência da Doença:

V0 :incidência baixíssima;

Vbi:incidência muito baixa;

Vb :incidência baixa;

Vm :incidência média;

Va:incidência alta;

Vat :incidência muito alta.

As funções graus de pertinência dasincidências de doenças∆P são dadas por (veja

Figura 10.3):

Se0_≤∆p < 100entãoϕ∆P(∆p) =

100−∆p

100 /V0 + ∆p

100/Vbi; Se100_≤∆p <200entãoϕ∆P(∆p) =

200−∆p

100 /Vbi+

∆p−100 100 /Vb; Se200_≤∆p <300entãoϕ∆P(∆p) =

300−∆p

100 /Vb+

∆p−200 100 /Vm; Se300_≤∆p <400entãoϕ∆P(∆p) =

400−∆p

100 /Vm+

∆p−300 100 /Va; Se400_≤∆p <500entãoϕ∆P(∆p) =

500−∆p

100 /Va+

∆p−400 100 /Vat; Se500_≤∆p entãoϕ∆P(∆p) = 1/Vat.

podem ser visualizados na Figura 13:

itbpF3.0441in1.5567in0inmini19.jpg

Fig.13-Funções grau de pertinência da variação de P

Base de regras A base de regras fornece o entendimento do fenômeno e é da forma "SE....ENTÃO... "

Para o fenômeno analisado parece coerente a seguinte base de regras

1. 2. 3. 4. 5. 6.

SE população contaminada ENTÃO incidência

Pbi Vbi

Pb Vm

Pm Va

Pma Vat

Pa Va

Pat Vbi

Tabela 4- Base de regras para a contaminação de maçã

Controlador Fuzzy O método de inferência que vamos adotar aqui é o de Man-dani que, como já vimos, dá como saída um conjunto fuzzy da forma

M(x, u) = _

1≤j≤n

{Aj(x)∧Bj(u)}

No nosso caso específico este conjunto é bem simples de ser obtido.

No exemplo anterior tomamos x = 1000 maçãs podres que corresponde ao con-junto fuzzy ϕP(1000) = 0,444/Pb⊕0,222/Pm. Pela inferência da Tabela 4, teremos

como saída o conjunto fuzzy∆P cuja função de pertinência éϕ∆P(u) = 0,444/Vm⊕

0,222/Va. O que devemos fazer agora é defuzzificar este conjunto de incidência de

doença, isto é, tomar alguma medida deste conjunto. Isto pode ser feito, por exem-plo, considerando como defuzzificador o centro de máximo:

∆P(u) =

[ϕPb(x)×maxϕVm] + [ϕP m(x)×maxϕV a]

ϕPb(x) +ϕP m(x)

= 0,444×300 + 0,222×400

0,444 + 0,222 = 222

podres. O modelo dinâmico proposto para previsão da doença é dado por: (

Pn+1 =Pn+ ∆Pn

P0 = 1

(0.4.6)

O processo iterativo pode ser feito à mão, como mostramos, ou usando o Toolbox do Matlab e o resultado final de previsão ou solução pode ser visualizado na Figura 14.

itbpF4.4157in2.3739in0inf ig12.jpg

Fig.14-Solução do modelo p-fuzzy

Muitas vezes, principalmente em fenômenos biológicos, as equações são parcial-mente conhecidas, isto é, o campo de direções é conhecido apenas qualitativaparcial-mente. Nesse caso, uma ferramenta que temos utilizados é a teoria dos conjuntos fuzzy, mais especicamente os controladores fuzzy que, com o auxílio da lógica fuzzy e de um especialista, são capazes de captar informações fundamentais de um determi-nado fenômeno. O leitor interessado nesse assunto pode consultar[[25],[29, ?][30],[28]].

0.4.3. Sistemas dinâmicos fuzzy

Vamos supor uma situação em que temos uma população inicial "em torno de"P0 , isto é, não conhecemosP0com exatidão e queremos estudar sua dinâmica supondo que sua variação seja dada por uma funçãof(P).Um problema como este,

aparente-mente mal posto do ponto de vista da matemática clássica, pode ser resolvido com a subjetividade proveniente da lógica fuzzy. Formalmente, podemos denotar este problema com a formulação variacional, denominada sistema fuzzy:

( _dP

dt(t) = f(t, P(t))

P(0) =Pb0 ∈(slR)

(0.4.7)

onde,Pb0 ∈(slR)significa que a condição inicial é um número fuzzy.

Consideramos agora o sistema determinístico associado ao sistema fuzzy 0.4.7 ( _dP

dt(t) =f(t, P(t))

P(0) =P0 ∈slR

(0.4.8)

derivada contínua em [a, b] - Isto garante a existência e unicidade da solução de

0.4.8 que é determinada pela condição inicialP0.

A solução de 0.4.8, denotada por ϕt(P0), é um fluxo gerado pelo campo vetorial f satisfazendo: ϕ0(P0) = P0 e ϕ,t(P0) = dϕt_dt(P0) =f(ϕt(P0)).

A solução ϕ_bt(P0) para o sistema fuzzy 0.4.7 é definida como sendo a extensão de

Zadeh do fluxo2 _ϕ

t(P0). Em outras palavras, a solução do sistema fuzzy é um con-junto fuzzyϕ_bt(P0)⊆ R+×Ronde, cada elemento é uma soluçãoϕt(P0)do sistema determinístico associado 0.4.7 tal que o grau de pertinência deϕt(P0)emϕbt(P0)é o mesmo grau de pertinência deP0 emPb0.

Observamos que no caso do fluxo fuzzyϕ_bt(P0),temosχϕbt(P0)(ϕt(P0)) = χ_Pb₀(P0)Exemplos

1. Modelo de Malthus fuzzy

Consideremos uma população que tem uma condição inicial dada por um número fuzzyPb0 ∈(slR)e um decrescimento exponencial

( _dP

dt(t) =αP(t)

P(0) =Pb0 ∈(slR)eα <0

Então, o fluxo fuzzy é dado por

b

P(t) = ϕ_bt(Pb0) =Pb0eαt

cujo gráfico é dado na Figura 15:

itbpF4.158in2.9395in0inmini4.jpg

F ig.15₋Solução do modelo malthusiano fuzzy comαnegativo

2. Modelo Logístico fuzzy

2_{A Extensão de Zadeh de uma funçãof : R → Ré a funçãofb: ̥(R) → ̥(R)onde, o grau de}

pertinência é dado por

χf(A)(x) =

sup_y∈f−1(x)χA(y) sef−1(x)6=φ

0 se f−1(x) =φ

O modelo logístico fuzzy (condição inicial fuzzy) 

   

dP

dt =αP(1−P)

P(0) =Pb0 ∈(slR)

denota a evolução de uma população que tem uma condição inicial imprecisa e uma capacidade suporte bem definida. Sua solução

b

P(t) =ϕ_bt(Pb0) =

P∞Pb0

(P∞−Pb0)e−αt+Pb0

é a extensão de Zadeh da solução do modelo clássico que na Figura 16 se apresenta com uma coloração mais escura

itbpF3.8969in2.6169in0inmini3.jpg

F ig.16₋Solução fuzzy do modelo logístico com condição inicial imprecisa

Podemos ter ainda subjetividade no parâmetro α. Neste caso, recaímos no caso

anterior, acrescentando outra equação, isto é, olhando o parâmetro como sendo var-iável e adotando, no modelo determinístico original (??), o par (α, P0)como condição

inicial. _

             

dP

dt =αP(1−P) dα

dt = 0

P(0) =Pb0 ∈(slR)

α(0) =α_b0 ∈(slR)

(0.4.9)

A solução do sistema 0.4.9 é a extensão de Zadeh da solução do modelo determinís-tico associado a 0.4.9 que tem como condição inicial o par(P0, α0),ou seja,

b

P(t) =ϕ_bt(Pb0,αb0) =

P∞Pb0

(P∞−Pb0)e−αb0t+Pb0

itbpF4.4892in3.0649in0inmini17.jpg

F ig.17₋Solução do modelo fuzzy com parâmetroα_b0 impreciso

0.5. Modelos de Interação entre espécies

Os modelos matemáticos de competição e predação tiveram sua origem com os trabalhos de Lotka (1925), Volterra (1926), Kostitzin e outros poucos (veja [7]) formulados em termos de sistemas não-lineares de equações diferenciais ordinárias. Muito tem sido escrito e pesquisado sobre estes modelos, originando uma enorme quantidade de modelos alternativos. Entretanto, com excessão de experimentos em laboratórios efetuados por Gause (1934), os ecólogos colocam fortes resistências so-bre sua validade na Natureza. Por outro lado, amedida de competiçãocarece de novas ferramentas matemáticas que estão sendo desenvolvidas a partir da Teoria Fuzzy ([4] e [15]).

0.5.1. Modelo de Lotka - Volterra

Dentre os modelos de interação entre espécies vamos destacar o clássico modelo presa-predadorque, por sua simplicidade e beleza, cativou grande número de pesquisadores que passaram a utilizá-lo como paradigma de seus modelos modificados. A analo-gia pode ser facilmente observada nos modelos epidemiológicos, biodigestores, cresci-mento de tumores, aplicações quimioterápicas, uso de herbicidas etc. O modelo presa-predador também conhecido por modelo Lotka-Volterra tem sido também ponto de partida para o desenvolvimento de novas técnicas e teorias matemáticas.

O modelo presa-predador trata da interação entre duas espécies, onde uma delas (presa) dispõe de alimentos em abundância e a segunda espécie (predador) tem como suprimento alimentar exclusivamente a população de presas. Vamos admitir tam-bém que durante o processo, num intervalo de tempo∆t, o meio não deve mudar

favorecendo alguma das espécies e que qualquer adaptação genética é suficiente-mente lenta.

As variações são dadas pelas seguintes equações:

              

variações do número de presas

!

= aumento

natural !

− destruição

pelos predadores !

variações do número de predadores

!

=₋ morte na

ausência de presas !

+ aumento causado pela

alimentação disponível !

x=x(t)a densidade populacional das presas, e

y=y(t)a densidade da população dos predadores destas presas, em cada instante

t.

Simplificadamente, o modelo de Lotka-Volterra supõe que as presas crescem ex-ponencialmente na ausência dos predadores (modelo de Malthus) e que a taxa de mortalidade dos predadores, na ausência das presas, é proporcional a sua população

y(t)em cada instante (morte por falta de alimento).

Admitindo que o encontro das duas espécies seja ao acaso, então quanto maior o número de presas, mais fácil será encontrá-las e quanto mais predadores, mais alimento será necessário. É razoável supor que a taxa de destruição das presas deve ser proporcional ao número de encontros possíveis entre as duas espécies!

A taxa de nascimento dos predadores depende exclusivamente, neste modelo, da quantidade de presas devoradas em cada encontro.

Se modelarmos osencontros possíveispelo termo bilinearxy, então o sistema

presa-predador, simplificado pelas imposições à cima, é dado por 

       

dx

dt =ax−bxy dy

dt =−αy+βxy

(0.5.1)

ondea, b, α, β são constantes positivas.

O sistema (0.5.1) apesar de ser não-linear, pode ser analisado qualitativamente no plano de fase, eliminando a variável independentet, através da regra da cadeia:

dx dt dy dt

= dx

dy.

A equação autônoma, correspondente a (0.5.1) é dada por

dx dy =

x(a₋by)

y(₋α+βx) (0.5.2)

que pode ser resolvida analiticamente por integração das formas diferenciais com variáveis separadas

Z

−α+βx x dx=

Z _a −by