Introdução aos métodos de determinação de estruturas cristalinas por difração de...

U N I V E R S I D A D E D E S A O P A U L O

I N S T I T U T O D E F f S I C A E Q u f M I C A D E S A O C A R L O S

I N T R O D U C ; A o A O S M E T O D O S D E D E T E R M I N A C ; A o D E E S T R U T U R A S C R I S T A L I N A S P O R D I F R A C ; A o D E R A I O S - X : C O M P L E X O S D E R U T E N I O .

D i s s e r t a ~ a o a p r e s e n t a d a a o I n s t i t u t o d e F f s i c a e Q u i m i c a d e S a o ~ a r l o s , U S P , p a r a a o b t e n ~ a o d o t i t u l o d e MESTRE EM FisICA APLICADA

~ISS~

U N IV ~ R S ID A D E

. DE SAO PAULO

Instituto de F fsica e Q uim lca de SioC arlos

t J 5 ~

---~~~---Fane (0162) 72-6222 Fax (0162) 72-2218

Av. Dr. Carlos Botelho. 1465 Caixa Postal 369

CNPQ

Aos meus pais. Marisa Mattos Fontes e Antonio Carlos Fontes e a minha esposa Sonia

Ao meu orientador. Prof.Glaucius Oliva. peta orien~ao. apoio. ensinamentos e sobretudo a valiosa amizade.

Aos Profs. Eduardo E. Castellano. Yvonne P. M:ascarenbas. pdos valiosos ensina:mentos

e pela constante disposi~ em colaborar.

Aos Profs. Richard C. Garratt, Julio Zukerman-Schpector. Oscar Pico, Carlos de Oliveira

P. Santos e Ignez Caracelli pelos valiosos ensinarnentos e pela constante disposi~ao em colaborar.

Aos colegas de grupo Fernando, Dulce. Valma. Walter, PauUo, Tereza. Geraldo pelos

ensinamentos. ajuda. compreensao e amizade.

Ao Prof. Alzir A. Batista pelo fornecimento das amostras e uteis disCllSSOeS.

A Salete L. Queiroz pela coopera~ao e ensinamentos.

Aos ~cnicos Wanda. Valdir, Geraldo. Augusto e Sr. Trombella.

A secretciria do grupo Maria Helena e a Vladerez.

E a todas as pessoas que de algoma forma me ajudaram em todos estes anos de estudo

ABRE\'lAC;OES

D P P B l.4-bis(difenilfostmo )butano

D P P B O I.4-bis( difenilfosf'moil)butano DPPA .Difenilfosfinamida

P y Piridina

Ph Fenil

P P h_{J • • • • • • • . •}Trifenil-fosfma 1m Imidazol

,

SUMARIO

N

INTRODUc;:AO ...•... 1

PARTE 1: INTRODU<;Ao TE6RICA

1.2.1 - EspalhaInento por UI1leletron 6

\

1.3.2 - Lei de Bragg, retfculo recfproco e a constru~io de Ewald ll

CAPITULO III

INTRODu<;Ao AOS MErODOS DE DETE&\.1lNA<;Ao DE ESTRtrfURAS CRIST ALINAS

S E R V IC O D E B IB L IO T E C A E IN F O R M A C A O - IF o s e

ID3.2 - Fatores de estrutura quase-normalizado. normalizado e unitirio 35

IDJ.J - R.d.3\~Je de~.l1~ __~ ~_._.__.. .. ._._.. ..__ .38

ID.3.4 - Rda.;Oes de probabilidade 43

lll3.4.1 - Estruturas centro-sirnetricas- .. _ 43

lll3.4.2 - Estru~ nao centro-simetriticas.._ _.._ _ 45

ID.3.5 - Invariantes e Semi-invariantes de estrutura 47

ID.3.6 - Defini\'ao da origem e enantiom6rfos 47

ID.3.7 - Metodo da Multi-solu\'ao 48

ill.3.7.1 - Introdu\'ao 48

ill.3.7.2 - Escolha e ger~ao de novas fases, programa SHELX86 ..49

ill3.7.3 - Mapas de E(h) 51

illA - Sfntese de Fourier e Fourier-diferen\'a 51

ill.5 - Refmamento por mfnimos quadrados 54

CO~SID ERA

CO

ES ~ICIAIS

60

CAPITl1.0 IV

E..~1RUTURA CRISTALINA DO 1,4-BIS(DIFENILFOSFINOIL)BUTANO

ClS"lS02P2

IV.l - Introdu~ao 64

IV.2 - Parte experinlental 64

IV.2.t - Escolhae montagem do cristal 64

IV.2.2 - Obten~ao da cela unitma e coleta de dados 65

IV.2.3 - An41ise preliminar dos dados e determin~ao do gropo espacial 65

IV.2.4 - Solu~ao e refinamento da estrutura 66

IV.3 - Descri~ao da estrutura e conclusOes 69

CAPITULO V

ESTRUTURA CRIST ALINA 00

trans-(CARBONILPIRIDINA)TETRACLORORUTENATO(III) DE PIRIDINIO

PyH[RuCI₄(CO)Py]

V.l - Introdu~ao 74

V .2.1- Sfntese. escolha emontagerndo cristal 74 V .2l- ~-lo da cea:mithia e ~ dr dadcs-.---.---. 75

V.23 - Analise prdiminar dos dados edetermin~ao do grupo espar..-iaL ..75

V.2.4 - ~ e refinaI:nento da estrutura- 76

V.3 - ~ da estrutura ecooclusOes.. __ _ _ _._ 80

CAPITULO VI

ESTRUTURA CRIST ALINA 00

trans-BIS(PIRIDL~A)TETRACLORORUTENATO(lD) DE PIRIDINIO

PyH[RuCI4( P y ) 2 ]

VI.I - Introdu~ao 86

VI.2 -Parte experimental 86

VI.21 -Sfntese, escolha e montagem do cristal 86

VI.22 -Obten~io da cela unitma e coleta de dados 87

VI.2.3 - Analise prelirninar dos dados e detennina~ao do grupo espacial 88

VI.24 -Solu~ao e refinamento da estrutura 90

CAPITULO

vn

ESTRlillltA CRlST.•J.l~'-" 00

DICLOROCARBO~lL~1ETA~OL-Bis(I.~fETILBfIDAZOL)Rl TI:\lOtIl)

[ R u OZ(~feIm)Z(CH30 HnCOJJ

vn.l - Introdu~ao 100

vn.2 - Parte experimental 100

vn.2.1 - Sfntese, escolha e montagem do cristal lOO

vn.2.2 - Obten~ao da cela unitma e coleta de dados IOI

vn.2.3 • AnMise prelirninar dos dados e determina~ao do gropo espacial

... 10 I

vn.2.4 - Solu~ao e refinamento da estrutura. I04

vn.3 • Descri~ao da estrutura e conclusOes 106

CONSID ERA<;O ES FIN AIS 112

APE ND ICE A 114

APEND ICE 8 124

APEND ICE C 140

APEND I CE D 154

Tabeta I: Resumo cristalogrffico 07

Tabela II: Coordenadas atomicas e fatmes de temperatura isotr6picos equivalentes e

isotr6picos (atOlllOS de H)

(A

2) _ 68

Tabela m :Fatores de temperatura anisotr6picos. 68

Tabeta IV: Distancias interatomicas (A) 70

Ta beta V: Angulos interatomicos (0) 70

Tabela VI: Coordenadas ortogonalizadas dos grupos fenil com suas respeetivas distancias

(A) aos respectivos pIanos mMios e seus desvios padrao (Esd) 71

Ta bela VII: Resunx> cristalogrcifico 78

Tabela

vm:

Coordenadas atomic as e fatores de temperatura isotr6picos equivalentes e

isotr6picos (~omos do anet piridina 2)

(A

2) 79

Tabela IX: Fatores de temperatura anisotr6picos 79

Ta bela X: Distancias interatOn1icas (A) 81

Ta beta XI: Angulos interatomicos (0) 81

Tabela XII: Coordenadas ortogonalizadas dos ~omos dos pIanos 1 e 2 com suas

distancias (A.) aos respcctivos pIanos medios e seus desvios padrao (Esd) 82

Ta beta XIII: Resunx> cristalogrcifico 89

Tabela XIV: Mapa de Patterson (contendo dcz maiores picos) 90

Tabela XV: Coordenadas atomic as e fatores de temperatura isotr6picos equivalentes

(A.2) 92

Tabela XVI: Fatores de temperatura anisott6picos 92

Tabela XVII: Dist3ncias interatOmicas (A.) 94

Tabela XV III: Angulos interatomicos

e )

94

Tabela XIX: Coordenadas onogonalizadas dos Atomos dos pIanos (Py2)' (Rua~ e do

PyH com suas distincias (A.) aos respectivos pIanos m~dios e seus desvios paddo

( E s d ) 9S

Tabela XXI: Mapa

&:

Patterson (contendo dez maiores picos)

.l04

Tabe1a XXII: Coordenadas atomicas e fatores de temperatura isotr6picos equivaIentes e

isotr6picos (atoITlOsde H)

(A~

105

Tabe1a XXIII: Fatores detemperatura anisotr6picos .l<Xi

Ta be1a XXIV: DistIDcias interatomicas (A) 1f17

Ta beta XX

v:

Angulos interatOmicos

(0)

1(J7

Tabela XXVI:

Coordenadas oftogonalizadas dos

grupos

-(CO).-(CH₃

0H) e

dos aneis

MeIm. suas distancias(A)aos respectivos pIanos medios e seus desvios padrao estimados

(Esd) 108

Tabela XXVU: Compara~ao entre liga~Oes medias(··) de varios complexos (A). A s

Figura I: Espalhamento de wn ponto P relativo a origem 0 8

Figura 2:Esfera de Ewald. 12

FIgura J:E..~ema do GoniOmelro Kappa do difratOrnetro CAD-4 17

Figura 4: Perfil da intensidade de urna reflexao 19

Figura 5: Espalhamento de raios-X poe urn el~tron 21

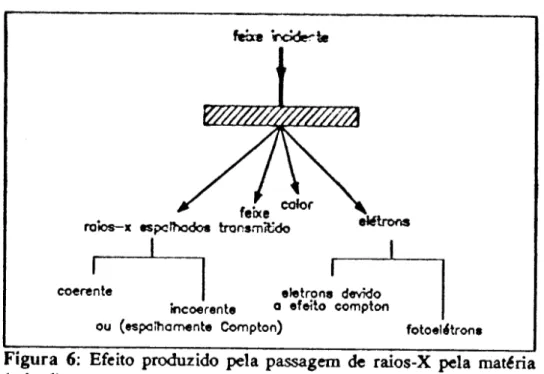
Figura 6: Efeito produzido pela passagem de eaios-X pela mat~ria (cristal) 24

Figura 7: Feixe de raios-X atravessando urn cristal de forma arbitdria. 2 5

Figura 8: F~ao distribui~ao Q(x) 32

Figura 9: Valoees mMios de F(h) e £(h) em fun~ao de sen9jA. 37

Figura 10:Varia~ao do determinante de 3' oedem de Kasper-Hauptman 41

Figura 11: 0 fatoe de estrutura F(h) de fase ~b) e suas componentes devido a !tomos

leves e pesados (F L(h)+F P(h) ) 5 2

Figura 12: Represent~ao esquern!tica dos angulos esfericos polares ~p,

p,. ~•.

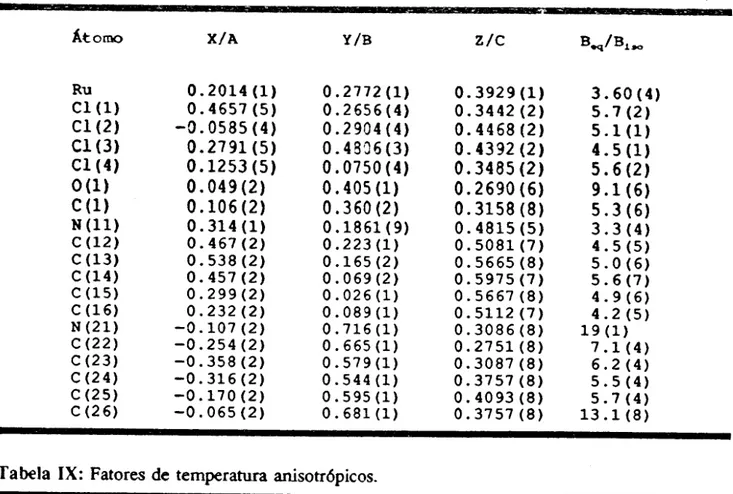
p. 58

Figura 13: Visao ern perspeetiva (corn os !tornos identificados. exceto hidrogenios) da

moMcula de 1,4-bis( difenilfosfinoil)butano 69

Figura 14: Ernpacotamento da rnol~cula de DPPBO 72

Figura 15: Visao ern perspeetiva (corn os !tomos identificados. exceto hidrogenios) da

mol~ula de Py H [R uCI,i CO) Py ) 80

Figura 16: Empacotarnento da rnolecula de PyH[RuCI .•(CO)Py) 84

Figura 17: Visao em perspectiva (corn os !tomos identificados. exceto hidrogenios) da

mol~ula de P yH[ R uCI.py 2) 93

Figura 18: Empacotarnento da mol~cula de PyH[RuCI .•PY2)' Plano b-c 97

Figura 19: Empacotarnento da molecula de PyH[RuCI)JY2)' Plano a-c 97

Figura 20: Visao em perspeetiva (com os !tomos identificados. exceto hidrogenios) da

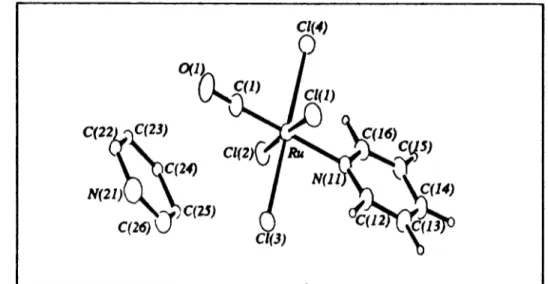
molecula de [RuCI2(Me ImMCH,JO H)(CO) J .•••••..•••••.••..••.•••.•••••••.•.•.•••.••..••.••••••..•..••••....••. 107

Esta dissertaliao consiste de duas partes:

Parte I: Descri~ao te6rica suscinta des fundamentos da cristalografia de raios-X.

Parte ll: Reso~ao de quatro estroturas cristalinas, tres complexos de ruteruo (capftulos

V. VI. Vll) e urn ligante commnente encontrado em complexos de ruteruo, 0 c;.~0~2.

A s estruturas resolvidas, foram:

I) c;.H2S0~2' Mr--458.48, triclfnico,

Pi

8=5.826(1), b=8.862(1), c=12.517(2)".

a=100.29(1), p=102.67(1), 1=104.22(1)°, V=592.5(3)A\ Z=1, 0ll=1.285 g.em"),

A(MoKa)=O.71073". p=2.00 em"', F(OOO)=242,T=296K, R.-=O.OI, R=O.031, Rw=O.030 para

1390 reflexOes independemes observadas [1>30(1)]. Os Momos P estao a 0.126(I)A do plano

fonnado pelo grupo -(CHJ4-' Os an~is fenil sao planares dentro da rnargem de erro experimental.

Os Momos P tern uma confi~ao tetr~drica distorcida.

2) PyH[RuOiCO)Py], Mr--430.11, monoclfnico, P2Jn, 8=7.821(1), b=10.337(3),

c=19.763(3)A, 8=93.07(1)°, V=1595.5(5)A\ Z=4, 0ll=1.791 g.em"), A(MoKa)=O.710703,

p=14.86 em·', F(OOO)=843.9, T=296K, ~=O.03, R=O.062, Rw=O.063 para 1478 reflexOes

independentes observadas [1>30(1)]. A estrutura ~ cornposta essencialmente por dois pIanos

perpendicu1ares entr~ si; urn formado pelos quatro Momos de cloro (com angulo de

aproximadamente 90° entre si), 0 outro pelos grupos Py e carbonila, e 0 'tomo de Ru na

intersec~ao destes. 0 complexo tern carga Hquida negativa, sendo necessmo a presen~a do grupo

PyH (com carga Ifquida positiva), para a estabi1iza~ao do cristal.

3) PyH(RUo.Py2)' Mr=481.20, monoclfnico, P2in, 8=8.080(7), b=22.503(7),

c=10.125(6)A, 8=93.19(6)°, V=1838(2)A\ Z=4, 0ll=1.739 g.em"), A(MoKa)=O.710703,

p=13.06 em"I, F(OOO)=959.9, T=296K, ~=O.03, R=O.038, Rw=O.039 para 1553 reflexOes

independentes observadas [1>30(1)].Esta estrutura ~ bastante similar com a 2) descrita acima, ou

seja, ~ compost a essencialmente por dois pIanos perpendiculares entre si; urn formado pelos

quatro ~ornos de cloro (com ingulo de aprox.imadamente 90° entre si),0 outro pelos dois grupos

Py, e 0 'tomo de Ru na intersec\ao destes. Pelo mesmo argurnento usado acima. h' urn grupo

4) [Ru~(MeIm)2(CH30H)(CO)], Mr=396.24, triclfnico, Pi, a=8.OO9(3), b=8.060(3),

c=10.581(4)A, (1;:77.78(3), f3=88.43(3), y=66.88(3)O, V=740.4(5)A3, Z=2, D1=1.777 g.cm-3,

A(MoKa)=O.71073A, p=12.80 em-I, F(OOO)=386,T=296K, Ru.=O.OO4,R=O.025, Rw=O.027para

2489 reflexOes independentes observadas [1>30(1)].

As distincias e ingulos medios das liga~Oes dos quatro complexos aqui descritos sio

This work consists of two parts:

Part I: A brief theoretical description of the basic principIes of X-ray crystallography.

Part fi: Resolution of the four crystal struetures; three ruthenium compounds (chapter V,

VI, Vll) and a ligand commonly found in ruthenium complexes, ~~OJ» 2.

The struetuIes resolved, were:

1) ~~OJ»2' Mr=458.48, triclinic, pi, 8=5.826(1), b=8.862(1), c=12.517(2)Â,

a.=100.29(1), ~102.67(1), ')"=104.22(1)°, V=592.5(3)Â3, Z=1, 011=1.285 g.em-3,

Â(MoKa)=O.71073Â, J1=2.00 em-I, F(OOO)=242,T=296K, final R=O.031 for 1390 independent

observed retlections. The P atoms 0.126(I)Â away from plane fonned by -(C~)~-. Both phenyl

rings are planar to within experimental accuracy. The P atom has a distorted tetrahedral

configuration.

2) PyH[Rua~(CO)Py], Mr=430.11 , monoclinic, P2₁/n, 8=7.821(1), b=10.337(3),

c=19.763(3)Á, 8=93.07(1)°, V=1595.5(5)Á3, Z=4, 0₁₁=1.791 g.em-3, Â(MoKa)=O.710703,

J1=14.86 em-I, F(OOO)=843.9, T=296K, Ru-=O.03, fmal R=O.062 and Rw=O.063 for 1478

independent observed retlections [1>30(1)]. The strueture is essentially composed of two

perpendicular planes; one consisting offour chlorine atoms (in a square-planar arrangement), and

a second plane composed of Py and carbonyl groups, with the ruthenium atom at intersection of

them. The molecules have a net negative charge and the presence of the PyH group (with net

positive charge), is necessary for crystal stabilization.

3) PyH(Rua~Py2)' Mr=481.20, monoclinic, P21/n, 8=8.080(7), b=22.503(7),

c=10.125(6)Á, 8=93.19(6)°, V=1838(2)Á3, Z=4, 0₁₁=1.739 g.em-3, Â(MoKa)=0.710703,

J1=13.06 em-I, F(OOO)=959.9, T=296K, Ru-=O.03, final R=O.038 and Rw=O.039 for 1553

independent observed retleetions [l>3a(1)]. This strueture is very similar to that described in 2)

above, being essentially composed of two perpendicular planes; one composed of four chlorine

atoms (in a square-planar arrangement), and the other composed of two Py groups, with the

ruthenium atom at the interseetion of them. For the reason given above, there is one PyH group

4) [Rua1~feImh(CH)OH)(CO)]. M.r=396.24. tridinic. pi a=8.609(3). b=8.060(3).

c=lO.581(4)Â. a=n.78(3). ~8.43(3). y=66.88(3)o. V=740.4(S)Âl. 'b=2. Da=I.m g.em-'.

A(MoKa):=O.71073Â, p=12.80 roil. F(OOO)=386. T=296K. Rw=O.OO4.final R=O.02S and

Rw=O.027 for 2489 independent observed reflectioos [I>3<r(I)]. In chapter

vn.

the average

interatomic di.stances and angles for lhe four compoands are compate ooe with anotbec mel widl

A determinação de estruturas tri-dimensionais de mol6:ulas ~. hoje em dia. vital para o

desenvolvimento da ciência em geral. nos mais diferentes ramos.. tal como na Flsica. Química.

Biologia. Geologia etc.

O seu desenvolvimento foi iniciado no começo do atual s&u1o mas seu advento só foi

possfvel com o aperfeiçoamento dos computadores (devido l grande quantidade de cálculos a

serem realizados); hoje. já ~ possível a resolução de grandes estruturas macromoleculares. com

milhares de átomos, na sua maioria de molkulas biol6gicas que muitas vezes. requer o uso de

radiação de luz síncroton (radiação de raios-X de alta intensidade). devido principalmente ao

caráter degradativo das mol~as biológicas quando expostas a radiação ionizante dos raios-X.

É neste contexto que este trabalho se insere, ou seja, tem como principal objetivo a

introdução de mais um crístalógrafo, neste ramo do conhecimento humano, este que ~

extremamente vasto, complexo e com muito ainda a produzir, como por exemplo na área

biol6gica ou no desenvolvimento de novos materiais.

Assim, esta dissertação tem os seguintes objetivos principais: aprendizado da teoria da

cristalografia de raios-X. utilização dos equipamentos do Laboratório de Cristalografia do

DFCM-IFQSC/USP, tal como: difratômetro automãtico CA0-4, câmaras de precessão e

Weissenberg e demais equipamentos; al~m do domínio das t~cnicas de resolução de pequenas

estruturas cristalinas, que requerem o uso extensivo de t~cnicas implementadas

computacionalmente.

Desta maneira. esta dissertação foi dividida em duas partes:

não de modo original, mas sim uma coletânia que o autor fez nos diversos livros, artigos, teses

e dissertações que há nesta área. É lógico que para quem está iniciando no estudo de

cristalografia será necessário o estudo em outras fontes que são dadas de modo selecionado na

seção referências bibliográficas. Esta parte divide-se em três capítulos: I - Fundamentós da

teoria de difração de raios-X por monocristais, 11 - Coleta, redução e análise preliminar dos

feitas as experiencias de coleta de dados, lratamento destes, dete~ao do grupo espaciaL

sot~ao e refinamento da estrutura, e finalrnente, descreve-se e discute-se a estrutura

tri-dimensional deste. comparando-ocomOUtros complexos com estruturas similares. de modo a verificar 08dados obtidos.

N a U l t i m a parte, Coosidera~ Finais, hi algumascondusOes e pIanos para futuros

PAR TE 1

CAPITULO I

Foi descoberto pelo Físico alemão W. Roentgen em 1895.Éuma radiação eletromagnétka

que ocupa uma região no espectro entre os raios gama e violeta (com ~.I-lOOÃ).

Este tipo de radiação pode -atravessar"" materiais -opacos-" devido ~ seu pequeno

comprimento de onda e coosequentemente pouca absorção, produzindo difração pelos átomos de

um cristal que têm distância de ligação da ordem de 1Ã . São produzidos quando qualquer

partícula carregada eletricamente de energia suficiente ~ rapidamente desacelerada.

Quando um feixe de raios-X atinge algum material, as partículas carregadas livres são

forçadas a oscilar devido ao campo eletromagnético da radiação tornando-se uma nova fonte

espalhadora em todas as direções.

Porém", as partículas carregadas da matéria, pr6tons e elétrons têm a mesma carga e, mas

a massa do pr6ton é 1840 vezes a massa do el~tron, então pode-se considerar que somente o

sistema eletrônico ~ afetado.

Este espalhamento pode ter mesmo comprimento de onda da radiação incidente, o

chamado "espalhamento coerente" ou "espalhamento Thomsonlt

(causando a difração de raios-X

propriamente dita) ou pode ter comprimento de onda diferente, o chamado "espalhamento

incoerente" ou "espalhamento Compton". O espalhamento Compton ocorre porque os f6tons da

radiação incidente, quando colidem com os elétrons são espalhados com certa energia, ou seja,

apenas uma fração da energia total do f6ton ~ transferida para os el~trons e estes vibrarão com

um comprimento de onda menor do que a da radiação incidente. Podm, sob as condições de

difração de raios-X, um número muito grande de átomos espalham cooperativamente, então as

amplitudes do espalhamento coerente de diferentes átomos são adicionadas. enquanto para o

espalhamento incoerente as intensidades é que são adicionadas, assim as contribuições coerentes

nas experiências de difração de raíos-X por mooocrista.is. sendo notadas. muitas vezes. pela

radiação de fundo nas medidas expetimentais.

Embora o raio-X seja espalhado em todas as direções pelo elfuon. a intensidade depende

do mguIo de espaIhamento. Thomson(I) mostrou que a intensidade espalhada I. a um ângolQ 29

do feixe de raios-X não polarizado. ~ dada por:

onde: p = (l + cos229)!2 ~ chamadofator de polarização, r ~ a distância do elétron espalhador ao ponto de observação, e a carga do elétron, m a massa deste, e c a velocidade da luz.

Pode-se considerar que todos os fatores da equação (lI) são constantes (para um dado

valor r) exceto o p ; assim, quanto mais o feixe incidente for paralelo ao espalhador, maior a sua

intensidade (veja {tem n.1.2).

Seja uma distnbuição eletrônica não unifonne Q(r) dependente da distância r referente

a uma dada origem O.

Considere um elétron na posição P, seja a direção da radiação incidente dada pelo vetor

50 e a espalhada pelo vetor s. Considerando que 150I

=

15I

=

IA.

Da figura I, a diferença de caminho entre os feixes 1 e 2 ~ p-q, onde p=Â.r.50e q=Â.r.s. Então, tem-se que a diferença de fase = 27t1Àx diferença de caminho.

Deste modo a diferença de fase = 27t r.(5₀·s) = 27t r.S, onde S = 5₀.5.

O vetor S ~ usado para descrever uma posição no chamadoespaço recfproco, assim como

o vetor r ~ usado para descrever uma posição no espaço real. A onda espalhada por um volume

dv em uma posição r terá amplitude proporcional a Q(r)dv e fase 21tr.S, então a onda espalhada

por um elétron na posição r em relação a um elétron em O ~ dada por: Q(r)exp(2mr.S)dV.

A onda espalhada para um átomo ~ então, a soma das ondas espalhadas pelos elétrons do

[ ( S ) : : ! o { r ) e x p ( 2 ' X i r . S ) d v

r

oode f{S) ~ chamado deJ a t a r t k t s p a l h i I m m t o a r o m l c o e ~ a transfonnada de Fourier da

dm9dade cletrOoica Q (r).

Id se calcular agora, a expressao para 0 espalhamento de urn conjunto de N atomos

localizados em posi~Oes espedficas, formando urna molecula.

Seja urn Momo 1 que est! a urna distancia rI da origem. Tern-se entao urna mudan~a na

origem do centro do atomo, significando que a distancia r na equa~ao (1.2) toma-se-a r + r_l,

A onda total espalhada por todos os atomos e a soma das contribui~Oesde cada atomo

da molecula considerada. Bntao:

N

G ( S ) =

E

fjexp ( 2 1 t i r_j, S )

j=l

1.3 - DIFRACAO DE RAIOS-X POR CRIST AIS:

Para 0c81culo do fator de estrutura de urn cristal, que nada mais e que a soma das ondas

espalhadas pelas celas unit8.riasdeste cristal, considera-se inicialmente urn cristal com urn arranjo unidimensional de celas de comprimento a.

Da equa~ao (1.3) tem-se 0 espalhamento para uma cela; a cela seguinte, relativamente a

mesma origem, tem espalhamento igual a G(S)exp(21tia 'S) e assim sucessivamente ate a n-esima cela unit8.ria que tera espalhamento igual a G(S)exp(21ti(n-l)a·S). A onda espalhada por todas as celas sera:

N

F ( S )

=:E

G ( S ) exp (21ti ( n -1 ) a, S ) n = l

onde N e 0 nUmero total de celas unit8.rias.

o

espalhamettto sera observado somente se a diferen~a de fase entre sucessivas ondas for urn nUmero inteiro multiplo de 21t: 2xa.S=27th, ou seja: a.S=h onde h e nUmero urn inteiro.

As equ3\Oes acima

sao

conhecidas como e q u a ~ o e s d e L a u e .

Pode-se, desta forma, escrever a expressao para a onda total espalhada pelo cristal:

N

F ( S }

=

E

fjexp (2Ttir j' S )

j=l

onde: rFa~+bYj+c2j

Porem, rj.S

=

xp.S+yjb.S+zjc.S

=

hxj+kyj+~ usando as equa~Oes de Laue. A equa~ao (1.6) toma-se:

N

F (rJd ) =

E

f j e x p [2Tti( h xj + k Y j + l z j ) ]

j - l

F(S) ou F(hkl) das equa~oes (1.6) ou (1.7) chamam-se F a t o r d e E s t r u t u r a . Esta representa

a transformada de Fourier da densidade eletronica do cristal no retfculo redproco de indices hId.

o

fator de estrutura, deste modo,

e

urn mlmero complexo que pode ser dividido em

amplitude e fase. Por difra~io de raios-X pode-se medir apenas a amplitude; para 0 caIculo da

fase existem metodos de aproxima~ao que serao vistos no capftulo m .

Na realidade 0 que se mede

e

a intensidade dos feues difratados; esta

e

relacionada com

o fator de estrutura pela seguinte expressao ideal:

1 } 'L _ ,." .••",. _ _~ ." .•.• _.._ ,,~ , _ "_ '''.''.~ ",~ ~ ~ Sl:R Vic,:O D E BIJLiO lEC ,A, !:: ii'tG i~ I"\A i.;A O - IF Q S a

1.3.2 • Lei de Bragg, Reticul0 redproco e a Coostru~Q de Ewald

o

espa1hamento de raios-X pot urn crlst3l em termos dos planos de reflexao foi analisado

iniciaImente por Bragg (1913). Interferencias coostrutiv3S entre feixes somente serlo espalhadas

se a difer~ de cmllnho er..tre estes for equivalente a urn

nWne.ro

inkiro de

cOClprimentos

de

onda, isto ~:

Esta equa~ao ~ conhecida como: l e i d e B r a g g

Desde que

Is I

=

Iso I

= If)..., enta.o:

s

=

2s e n e

=-!

J.. d

Pois, A tern dimensao de comprimento assim como d, deste modo S define a posi~ao no esp~ redproco que ~ inversamente proporcional ~ distancia no esp~o direto. Pode-se, entao defmir: S=ha*+kb*+Ic*,onde os vetores a*,b*,c*sao os comprimentos da cela unitMia no espa~o redproco.

Ewald (1921) propOs urna simples constru~ao geom~trica que permite urna f~cil visualiza~ao do espa~o recfproco. Esta consiste de urna esfera desenhada do centro do cristal (C) com raio I(A.. A origem do espa~o recfproco ~ 0, 0 feixe incidente est! na dire\ao do vetor s•.

A condi~ao para que urn particular feixe, eE , difrate na dire~ao do vetor s, ~ que E represente

urn ponto do retfculo redproco (h,k,l), isto ~,que 0vetor OE seja urn vetor do retfculo redproco

S=ha*+kb*+lc*. (figura 2).

Para a devida orienta~ao de pIanos de urn retIculo sao defInidos os charnados f n d i c e s d ~

M i l l e r , que sao 0 recfproco do intercepto fracionArio que os pIanos fazem com os eixos

cristalogrMicos, indicado como plano (hkl).

E

interessante notar que pIanos cristalinos com £ndices (hkl) baixos tern gran~s

reflexOes com baixos indices de Miller e baixos angulos tern grande intensidade devido ~ difra~ao de raios-X (equa~ao 1.9).

A lei de Friedel refere-se ~ rela\ao entre F(hkl) e F(hkl). Usando a equa\ao 1.7, pode-se deduzir que:

fA . _{VfBRA<;<)ES TER\IIC.-\S}

Ate este momento, foi considerado no caIculo de fatores de estrutura, que os atomos estivessem em repouso, porem

e

sabido que estes estao em constante vibra\ao. Debye (1914) mostrou que este movimento termico causa uma mudan\a no fator de estrutura, considerando 0

caso em que estas vibra\Oes sac harmonicas e isotr6picas, e utilizando-se a distribui\ao de Boltzmann, obtem-se a seguinre rela\ao (usando-se h para representar 0 vetor (hkl» para 0 fator

onde a segunda exponencial

e

coobecida comofa to r d e t e m p e r ~ '1 U a 0 1 1t U D t b ) '~ ~P lJ I lu e B

e

dado por: 8~{u~, em que (1l~6 a amplitude quadratica mediA de vibl"a\ao.

Considerando agora,0caso mais geral, isto ~,0 que 0~omo pode vibrar igualmente em

quaIquer dire~ao, ou seja an.isotropicamente, 0 fator de Debye-Waller pode ser representado por:

onde bT ~ 0 transposto do vetor h e U ~ dada por:

(U₁2) (U₁U

2) (U1U3) U = ( U . U t ) = ( U₂ U 1) ( U₂2) (U_aU 3)

( U

3 U1) ( U3 U2) ( U ) 2)

chamada de matriz dos deslocamentos m e m o s . Euti! notar que esta

e

uma matriz simetrica e que s6 h ! seis parametros a serem determinados.

Considerando agora.,a seguinte equa~ao quaddtica:

Se a matriz U for diagonaIizada. resolvendo a equa~ao acima, obtem-se a e q u a ~ a o d o

e l i p s 6 i d e d e v i b r a , a o t / r m i c a , que

e

dada por:

cujos semi-eixos maiores estao ao longo dos eixos cartesianos e os comprimentos sao as ralzes quadradas dos deslocamentos quaddticos mMios ao longo dessas dire~Oes.

onde C2

e

wna co nst ante .

A fun\ao densidade de probabilidade na superficie deste.s elips6ides

e

defmida pof';

A integral de P(u) sobre 0volume do elips6ide

e

mna coostante independente de {JI. Para c = 1.5382. esta integral ~ igual a 0.5 e este elips6ide

e

chamado de elips6ide de vibra\ao tc~nnica

com 50% de probabilidade. Nos desenhos moleculares desta dissert<l\ao ~ usado 0 programa

CAPITULO II

o

primeiro passo antes de iniciar a coleta de dados (em qualquer sistema de coleta) ~ a

escolha de urn b o r n cristal que deve apresentar propriedades 6ticas regulares (tal como, boa

transparencia). ter fonnas hem definidas de suas faces e ter dimens5es parecidas de suas arestas,

alem de ter wn tamanho razo1vel (tipicamente de O.lnun a O.5mm, para nao see muito maior nem

menor que 0 feixe e nem absorver excessivamente raios-X devido ao tamanho exagerado). Deve-se testar a sua monocristalinidade usando wn microsc6pio polarizador; em seguida, este deve ser montado em urna fibra de vidro ou dentro de urn capilar de vidro, se necessmo ficar em contato com 0 Hquido mae do cristal (que ocoere normalmente com cristais protefcos), este deve ser acoplado entao, a urna cabe~a goniometrica.

Foi utilizado para a coleta de dados urn difratometro automc1ticoCAD-4 da Enraf-Nonius no Laborat6rio de Cristalografia do Departamento de Ffsica e Ciencia dos Materiais do IFQSQ-USP.

Com 0 cristal montado sobre a cabe~a goniometrica6 necessArio alIDha-Io no centro plano

de reflexao (plano H), figura 3.

Para facilitar0entendimento do difratometro e uti! imaginar a esfera de reflexao pas sando

pelo cristal. No momento em que 0 vetor recfproco S coincidir com a esfera de reflexao (neste

caso urn drculo pois se esta em urn plano) ter-se-a wna reflexao de Bragg e podera se medic as5im a sua intensidade.

o

difratometro CAD-4 consta de urn Goniometro (charnado de Goniometro Kappa) que possui tres graus de liberdade e mais urn quarto grau para a posi~ao do detetor.

A cabe~a goniometrica (onde esta 0 cristal) esta no eixo f que esta apoiada sobre 0 bloco

K ; este pode girar em tome do eixo le, e este bloco, por sua vez, esta apoiado no bloco ro,

podendo girar em tome do eixo ro, suportado pela base do difratometro.

o

detetor esta associado a urn eixo 29 independente, coincidente com 0 eixo ro.

termos de wn sistema de coordenadas cartesianas XYZ de origem no centro do goniometro. 0 eixo X est! na dire~ao cia foote de raios-X. 0 eixo Z est1 na dir~ao do eixo Cl)e 0 eixo Y

cornpleta 0 sistema ortogonal (figura 3).

Com 0 cristal centralizado 0 pr6ximo passo

e

obter a orienta\ao absoluta no sistema

cristalino recfproco (al)c·) com rela\ao ao sistema X Y Z flXO Acabe\a goniometrica. Para tanto

e necessmo medir urn cecto ofuneeo de posi\Oes angulares de reflexOes (~5) e annazenA-Ias. Para tal medida, pode-se fazer uma procura automAtica de reflexOes com uma simples varredura em uma certa regiao do esp3fSo,atraves de rota~Oes em intervalos fixos ou por uma procura feita manualmeme pelo operador.

De posse destas reflexOes constr6i-se urn conjunto de vetores (V ) em coordenadas X Y Z

obtidos dos veto res recfprocos S\ de cada reflexao e os vetores soma e diferen\a de cada urn de1esSI% j tornados dois a dois.

Oeste conjunto (V). seleciona-se tres vetores de acoedo com os seguintes criterios: S, : menor vetor de (V).

~ : menor vetor de (V). que ~ " m a i s perpendicular" ao plano fonnado por

S

Ie ~.

PO<.Y-se caIcular entao, os fndices aproximados destes vetore~ construiOOo-se uma matriz

de orient4\ao

Su,

oode carla coluna representa urn destes:

hi Xi

X

_j

: : S ) . ) Y i

(II. I)

1

j Zj

Esses fudices sao normalmente fracionmos, pois ~,.l ~ urna matriz apmxirnada, para

deix!-los 0 mais pr6ximo possfvel de mlmeros inteiros ~ calculado urn fator comum de

multiplic~ao. E feito enrao, urn refinamento por mfnimos quadrados para indexar outros vetores 81e pode-se, deste modo, incluir outros vetores na base e obter uma nova orienta~ao. Obtem-se

assim, uma cela unitma tentativa.

A analise do Tensor Metrico Associado, definido como:

[

a .a a .b a .c ]

2'

=

b . a b . b b . c c . a c . b c . e

permite obter a tmsforma~ao a qualquer outra cela unitciria, eventualmente aquela que possua a simetria maxima do sistema.

Obtem-se, fmalmente os parametros a,b,c,a,~;y, assim como os seus respectivos desvios

Todas estas etapas sao realizadas com a ajuda de urn conjunto de programas associados ao difratometro CAD-4.

Obtida a cela unitma, pode-se posicionar os vetores recfprocos Sr~a·+~b·+~c·, com~, ~ e ~ inteiros e medic as intensidades de c ada uma destas reflex5es.

Para minimizar 0 movimento do goniometro e consequentemente 0 tempo de coleta,

o

tipo de varredura angular (CJ)-29. Cl)ou outro tipo) deve tamMm. see fomecido pelo

operador. levando em conta se as eeflexOes sao completamente varridas. se a radi~ao de !undo

~ corretamente estimada e se esta n30 ~ afetada por reflex5es vizinhas.

Com uma varredura angular obtem-se 0 seguinte perfil para 0 febee difratado (figura 4). do qual pode-se medir a intensidadc integrada.

Na figura 4, A~

e

0 angulo de varredura, A e C 530 regi5es que se considera 56 haver

radia~ao de fundo A

=

C

=

~/6 e NA' N_B, Nc

e

0 mlmero de contagens feitas em cada regiao

A, B, C e sejaco a velocidade no qual

e

feita a varredura e Olmu a velocidade maxima para esta~

I L 2 - REDr~AO DOS DADOS

As intensidades me&das para cada reflexao h k l e os seus respectivos desvios padrao 0'(1),

s30 todas as infonna~ experimenuis nece.ssmas para a

~ao

da estrutura cristalina.

Porem.,esus ~ esUo afetadas par uma

sene

de fatores que predsam see corrigidos

para

0

cAlculo do m6dulo dos fatores de estrutura que sao proporcionais b intensidades medidas

(ver equa~ao1.8); esta proporcionalidade ~dada pela seguinte rel~ao:

I

_F

I - ~

K Ih l c 1 h k 1

-Lp

ondep 6 conhecido como fator de polariza~ao, L como fator de Lorentz e K 6 uma constante

devida a vArios fatores, tais como: tamanho e absor~ao do cristal, intensidade do feixe etc.

o

que irA se fazer nos pr6ximos tres {tens 6 determinar expressOes para 0 cAlculo destes fatores para obter 0 m6dulo do fator de estrutura e seus respectivos desvios padrao o(F ) que

serio utilizados para 0 cAkulo dos mapas de densidades eletronicas (ver {tern m.4) etas quais pode-se derivar as posi~Oes atomicas e a estrutura cristalina.

No item 1.2.1 foi introduzido 0 rator de polariza~ao pea equa~ao (11), que serA agora

deduzida.

Thomson(l) demonstrou a seguinte rela~ao entre a intensidade I de urn feixe espalhado por urn e16tron de carga e e massa m , a uma distAnciar do e16tron:

onde10 ~ a intensidade da radia\ao incidente e a 0 Angulo entre a dire\ao do espalhamento e a

d.ir~ao da acelera~ao do el~tron.

Supondo que a onda inddente viaja no eixo O x (figura 5) e 6 nao polarizada, entao, 0 seu vetor campo el~trico E estA no plano y z e a intensidade espalhada em urn ponto P que est' no

SER VIC O D E BIBLIO TEC A E IN FO R M AC ,l.O _ IFose

plano n rode OP

e

inclinado de 29 em rel~io ao feixe iocidente.

o

,,-etorE pode 'ie1' ~t'rn:J"C'S:onas cOO"I.ponentes E, e E.~

A componente y acelera0 eletron na dire~ao O y , entao a intensidade espalhada pot esta

componente no ponto P

e:

desde que ex = .6..yOP = Tt/2.

Similarmente, para a componente z: •

I_{p z}= I_{o z} a cos228

desde que a

=

AzOP

=

x/2 -29.

De5:e modo a radi~io t.QU1~.all-.ada 00 ponto P

e

obt..i(h scmaodo as intensidades das

duas compooentes y e z:

que

e

a eq.I.l que se queria demonstrar.

o

fator de polariza\ao p , que

e

0 termo entre parenteses da 6.ltima equa\ao, sed usado

para corrigir as intensidades medidas antes de iniciar a resolu\ao da estrutura cristalogrMica. No caso do difratometro autom!tico CAD-4, a radia~ao

e

monocromatizada por urn cristal de grafite que causa urna polariza~ao adicional da radia\ao.

o

fator de polariza~ao neste casd5_{,6) toma-se:}

cos2₂₆

m + co s

2

26

1 + co s2₆

m

onde 9_m 6 0 Angulo de reflexao de Bragg usado para monocromatiza~ao (pelo cristal

monocromador), c

e

uma constante que leva em considera~ao 0 grau de mosaicidade do cristal

monocromador (a mosaicidade est! presente em todos os cristais e ocorre porque estes nao sao perfeitos, mas siro formados de diminutos blocos chamados de m o s a i c o s ) . H! dois casos lirnites:

c~ 1 quando 0 cristal 6 idealmente perfeito e c~O quando 0 cristal 6 idealmente imperfeito. 0

valor de c pode ser obtido experimentalmente(6),porem foi utilizado nesta disserta\ao 0 valor O.~

Este ~ urn fatoe ge.ornetrico que leva em considefa\OO 0 tmlpO relativo que carla reflexao

gasta na posi~ao de

refletio. j!

que nao ~

instantaneo

(pois os n6s de difr~10 nao sao

infm.itesimais) e este tempo

nao ~

constante,

devido

a

vmos

fa!ores, tais como imperfei\Oes

cristalinas que ocorrem pelo carater de mosaiddade dos cristais; sendo assim 0 cristal difratar!

em uma filia centrada no angulo de Bragg

e

(figura 4).

No caso de sistemas que possuem 0 eixo de r~ao nonnal ao plano de espalhamento que

6 0 caso do difratometro CAD-4, tem-se:

L

=

1

sen28

Naturalrnente, em sistemas com outras geometrias de difra~ao, 0fa to r d e L o re n tz see'

diferente da rela~ao II.B, porem ter' depedencia apenas de 9.

E urn fenomeno fisico que ocorre quando uma onda eletromagn6tica atravessa algum

material.

A absor~ao de raios-X por urn s6lido (como em muitos outros fenomenos de absor~ao)

6 dada pela seguinte rela~ao emp(rica:

Onde p 6 0 coeficiente de absor~ao linear e 't 0 caminho percorrido dentro do s6lido.

Tem-se, do {tern1.2.1 que pode ser feita a aproxirna~ao que os feixes de raios-X s6 afetam

f.elXe eofor

roios-x espclhodos tronsm rooo

....

",n ...

t,~""

dMlo

incoerente a efeJto com pton

ou (espolhom ente C om pton)

Figura 6: Efeito produzido pela passagem de raios-X pela mat~ria (cristal).

1) Espalhamento ineoerente ou Compton (ver ftern 1.2.1).

2) Verdadeira abso~ao: eausada basicarnente por gasto de energia e~tiea pelo eletrons.

em forma de el~trons. fotoeletrons ou calor.

A absor~io e urna das rnaiores fontes de erros sistem~iCos na resolu~io de estrutuIas

cristalinas, prineipalmente quando se est! interessado em medidas preeisas de padmetros t~rmieos

ou quando usa-se metodos que utilizam diferen~as de intensidades (como por exemplo 0 m~todo

da substitui~ao isomorfa).

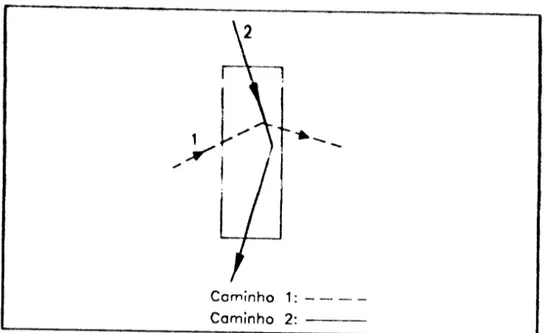
Este erro decorre principalmente peto fato de que feixes de raios-X atravessam eaminhos

6tieos diferentes dentro de urn cristal de forma arbitrma. Da figura 7, pode-se nota! que quando

o feixe atravessa 0 cristal peto caminho 1 sofre meIlQS absor~io do que quando pereorre 0

caminho 2, afetando deste modo as medidas experimentais. Este efeito pede set minimizado

usando-se cristais com formas esferieas ou mesmo cillndrieas.

A corr~io da absor~ao nem sempre e uma tarefa f!ell e 0 que se eonsegue. na maio ria

dos easos, nada mais e que uma corr~ao aproximada Para tanto foram desenvolvidos vUios

metodos aproximados nos Ultimos cinqtienta anos, os quais podem set divididos em m lto d o s

a n a /ttic o s. se m i-e m p lric o s e n n p lric o s.

C orninho 1: - - --C am inho 2:

---Figura 7:Feixe de raios-X atravessando urn cristal de forma arbitrma.

A '"1.

f

e-Il(P + 9 ) d V

P.s V v

onde J.l (coeficiente de absor~ao linear) deve ser obtido preliminarmente, p e s sac os caminhos

6ticos dos feixes incidente e difratado do cristal, respectivamente.

Este metodo tem as seguintes desvantagens principais: sac necessmas medidas precisas

das dimens5es do cristal e nao se leva em considera~ao absorvedores extemos ao cristal (tais

como: cola na motagem do cristal ou capitar e Hquido mae quando montados em capilares).

Os metodos semi-emp£ricos(S.9.10.1I)se baseiam na utiliza~ao de informa~oes obtidas quando

se mede uma mesma reflexao em diferentes posi~Oes do cristal, obtidas por rota~ao deste ao redor

do vetor difra~ao.

o

metodo emp£rico de Walker e Stuart (1983)(12)foi 0 utilizado nesta disserta~ao. Este

usa 0 fato que pequenos erros sistematicos de posicionamento inacurado dos atomos do mapa

Fourier diferen~a (veja ftem IDA) no esp~o direto podem ser distribufdos uniforrnemente atraves

do espa~o recfproco; para tanto

e

utilizado urna serle de Fourier para modelar a discrepancia entre

os fatores de estrutura observados (Fo) e os fatores de estrutura calculados (Fe). Oeste modo, esta

corr~ao tera que ser feita depois da estrutura ter side detenninada, e tendo se obtido urn modele

o

d.ifratOrrrtro ruliz.a algumas medidas de reflexOes equivalentes.

seja

por

simetria

cristalina

OU

pela lei de Friedel. Como esses valores deveriam

see

iguais, uma compar~ao entre

eles, fornece urna medida da qualidade dos dados que podem

see

obtidos calculando

0 (ndice de

L

[N E W « (r eq}-.r) 2 ]1 /2

II •

E

eN-I)

E

'N F l

tl •

onde os Indices u e e nas somat6rias da equa~ao acima representam a soma sobre todas as

reflexOes Unicas e reflexOes equivalentes, respectivamente; N representa 0 nUmero de retlexOes

equivalentes, (F~ 6 0 valor memo dos fatores de estrutura observados das reflexOeS

equivalentes e W 6 0peso aplicado a cada reflexao.

o ~ possibilita uma razo~vel estimativa do fator R (itern m.5).

Quando se examina os dados de difra~ao de raios-X pode-se frequentemente detenninar

o grupo espacial do cristal sem ambigiiidade ou pelo menos se aproximar da re5pQsta ficando

entre a escolha de dois ou tres grupos.

Para tanto, sao essenciais as extin~Oessistem~ticas que sao reflexOes que tern intensidade

sisternaticamente ze ro , devido ao arranjo particular dos ~tomos da unidade assimetrica (rnenor

por~ao da cela unitma que nao pode ser gerada por urna oper~ao de simetria).

Estas ocorrern sempre quando h~ urn elemento de simetria que envolve uma transla~ao

(eixos helicoidais, pIanos de reflexao com deslizamento ou "glide" e no caso de retfculos nao

prirnitivos).

devido

aos elementos de

simetria este deve

aparecer

em

-x.-y.-z;~ln.-y.ln.+z

e

-x.tn.+y.ln.-L

o

(ator de estrutun pode set escri10 como (·•.eja ~1o

16\ onde ~

f 0 fator de

espalhamento atOmico

me

0j-6imo homo:

Assirn F(hOl)=O se 1=2n+l, onde n ~ urn mlmero inteiro, ou seja, se 1 ~ fm p a r tem-se

extin~Oes sistem!ticas para reflexOesdo tipo hOl.

Para reflexOes do tipo OkO,tem-se:

Assirn F(OkO)=O se k

e

fm p a r tem-se extin~Oes para reflexOes do tipo OkO.

As extin~Oes sistemMicas encontram-se tabeladas para todos os grupos espaciais(\3).

E

interessante notar que normalmente nao

e

necessmo coletar dados em toda a esfera de

reflexOes, mas normalrnente em apenas uma parte desta, prirneiramente devido a lei de Friedel

({tern 1.3.3) e tam~m porque muitas reflexOes estlo relacionadas com outras devido aos

elementos de simetria dos grupos espaciais.

Antes de iniciar a resolu\io de uma estrutura cristalina

e

util fazer uma compara~ilo

compara\ao, pennite colocar os fatores de estrotura observados em uma escala aproximadamente

abs<lluta e ~r uma estimativa dos efeitos dos mo~.mentos ttnnkos dos !tomos; este ~

coohecido como metodo grMico de Wi1son~l3j.

Definindo a intensidade espalhada media, corrigida pelos efeitos de Lorentz e polariza~ao

(l/lp).

romo:

- f' '2 \

I.

•..__A_!

="

I' _I

(ll17)

onde 0 segundo tenno da equ~ao acima representa a media do m6dulo ao quadrado do fator de

estrutura.

E seja, a intensidade media te6rica para uma cela unitaria contendo N Momos, dada por:

onde utilizou-se a equ~ao 111.

A razao entre aiabs e ~el pode dar 0 fator de escala requerido entre eles para colocar os

~el individuais em uma escala comum. Entao, chamando esta constante de proporcionalidade de

C, tem-se:

Se for considerado que B

i tern 0 mesmo valor para todos os atomos, pode-se colocar 0

Construindo-se urn grMico do primeiro termo da equa~ao acima em ~ao de sen2_Sf).}

com roeflCic1te angular -28 e coeflCinte linear InC, pode-se estimar B e C. A re1ataao entre

IF•• ' e iFal ~dada por:

se:

k

= ~

CAPITULO

III

INTRODU<;AO AOS ~IETODOS DE DETER~nNA<;AO DE

No Item 1.2 foram deduzidas as equa\Oes para 0c~culo do fator de estrutura

se

conhedda

a densidade eletronica Q(r),

porem

0 objetivo principal ~ ohter a densidade eletronica, islo ~,

tm: •..se aqui 0 proNema Irwerso. que pode set resoh·ido cakulando a transformada de Foorier

inversa do fator de estrutura.

Reescrevendo a eq. 16 em termos de urna soma connnua sobre 0 volume da cela unitMia

e utilizando a eq. 1.2, tem-se:

F (S }

=

f

p (r) e2_{'tlr ,s d v}

v

Multiplicando ambos os lados por e-2K ir3

e integrando sobre 0 volume do espa\o

rec(proco. obtem-se:

p (r)

=

f

I'(S } e-27Clr,sdu

u

on4e

u

e 0 volume no espa\o redproco.

Pode-se substituir a integral por uma soma, desde que F(S) e nao contfnuo. ou seja, e

dis<;reto nos pontos do retkulo redproco, assim:

.- +- •.•

p (r)

=

~ L

E

L " (h k l)e -2 7 C .1 (h x ~ k y + lZ )

h ,. -. k ~ -. 1 ~ -.

Se 0 fator de estrutura F(hkl) e conhecido para todas as reflexOes, a densidade eletronica

~,e ser obtida para cada ponto da cela unitMia. Porem, como foi visto no {tem1.3.1 0 fator de

est1lltura e urn D6mero complexo composto de amplitude IF(hkl)

I

e fase ~hkl) mas por difra\ao

de faios-X 56 se pode medic a amplitude e toda a informa~ao sobre a fase e perdida.

Oeste modo, 0 problema central na detennina~ao de estruturas cristalinas e 0 cMculo da

fase,. Com este prop6sito e.ustem vmos metodos, tais como: Metodo de Patterson, Metodos

dir~tos, Metodo da substitui\ao isomorfa, Metodo do espalhamento anomalo.

Nos pr6ximos {tens secao descritos os dois primeiros metodos, que sao os mais utilizados

m.2·

~IETODO

DE PATIERSON

Estruturas molerulares que possuem urn ou alguns .1tomos distinguivelmente mais pe~ados

que os demais.

sao

mais facilmentes resolvidas do que as estruturas que nao os possuem. Ern tais

estrntuns.

e

possfvel localizar atoroos pe-sados sem 0 conhecimento das fases e posteriormcnte

criar urn modelo para estas, das quais as posi\Oes dos outros atamos podem see detenninadas.

Uma tecruca para a Iocaliz~ao dos Momos pesados

e

0

metodo de Patterson(I~, que sed

descrito a seguir.

Consideremos inicialmente 0 problema em uma dimensao, por simplkidade. Seja uma

distribui~ao de densidade eletronica normal ao plano cristalogrMico cujo • espa~amento

e

d . Esta densidade pode ser expressa na forma:

••

p (x ) = 1.

L

r ( h ) e - 2 x lh .x

dh --.

Seja a cueva da figura 8 representando uma fun~ao distribui~ao e considerando urn

elemento dx a distancia x da origem. A distribui~ao ao redor deste elemento pode ser expressa

Supondo-se pesar esta distnOui\ao por Q(x)dx. que representa a quantidade de materia

espaIhada no elemento dx e

complltar

a distribui\ao mbfia pesada

sobre

qual~r elemento dx

quando x ~ pennitido assumir

todes

os valores dentro do

perlodo,

obtem-se asslln, uma

fun\ao

distribui\ao mMia P(t), dada

par.

•

P (t) =

f

p

(x )

p

(x+ t)

dx

•

&sa integral 6 coohedda da teona da sene de Fourier como a convolu~ao de Q(x) e

Q(x+'t) e a fun~ao P(t) 6 chamada de fun~ao de Patterson.

Substituindo (llI.4) em (llI.5), obtem-se:

E

util notar que a fun~ao de Patterson 6 a transformada de Fourier de IF(h)12, em vez

de F(h), que pode sempre scr calculado das intensidades de di.fra\ao.

Pode-se ver que as principais contribui~Oes para P(t) serao quando Q(x) e Q(x+t) tern

grandes valores, entao urn pica na curva P(t) para urn dado valor de 't='tl' significa que pode-se

ter dois !tomos separados pela distancia 'tl' Oeste modo, a ~ao de Patterson representa urn

mapa de vetores interatomicos.

Outro rato a ser noudo 6 que sempre haver! urn pica na origem, isto 6, para 't=O.

Para tres dimensOes, a equa~ao (llI.6), toma-se:

.- .-

+-P (u v w ) =

~ L

E

L

I,(h k l) 12e -2 •i(h .u + k.vd .•••)

h --- Jc---

1---ou de uma forma simplificada, usando h e u que representam os vetores (hId) e (uvw),

respectivamente:

A ~ao de Patterson contem urn centro de sirnetria na origem, embora a estrutura em

o grupo espacial ~ diferente daquele da estrutura real, este pode see derivado da estrutura real

pela adi~aode urn centro de simetria e penla de elementos de simetria transladonais (ver

International Tables Vol1)(l3) forrnando 0 chamado grupo de simetria de Laue.

Algumas estruturas sao resolvidas usando sornente 0 m etodo de Pane~ mas 0 que ~

feito normalrnente

e

identLficar

urn ou rnais pkos referen!es

30S

homos pe:s.ados que

sa<> u..~

para modeIar a fase do restante da estrutura que pode ser compleuda usando sfntese de Fourier

e Fourier-diferen~a ({tern m.4).

E

irnportante notar que depois de localizar os picos referentes aos veto res interatomicos

~ necess.mo localizar os Momos na cela. Isto ~ feito usando os elementos de simetria do grupo

espacial do cristal a ser estudado que embora nao apare\am explicitamente nom a p a d e P a tte rso n ,

deixam urn tra\o caracterfstico em forma de urna distribui\ao caraeterlstica de vetores, conhecidos

como /in h a s e p Ia n o s d e H a rk e

r

.l1 ).

Para entender como esta localiza\ao ~ feita se mostrar! alguns exemplos a seguir:

No caso do gropo espacial

Pi

que possue as posi\Oes equivalentes x,y,z e -x,-y,-z. 0 pico

referente ao Atomopesado aparecer! na posi\ao geralU ,V,w que corresponde a posi\ao 2x.2y,2z,

ou seja, de posse dos valores de u,v,w dado pelo mapa de Patterson, pode-se obter as

coordenadas do Momo na cela apenas dividindo-as por dois. neste caso particular.

Para 0 gropo espacial P2₁que possue as posi~Oesequivalentes x,y.z e -x,y+ In..-z 0 pico

referente ao Atomo pesado aparecerA no plano de Halker u,ln..w que corresponde a posi\ao

2x.ln..2z.

Oeste modo pode-se obter as coordenadas dos Atomospara qualquer grupo espacial. urna

tabela completa pode ser obtida na International Tables Vol.r13

~es ~~ de re~ao deestr'.ltu...ras ITlt:l~.lareshiseiarn-se 00 c~culo direto da$

fases

l

partir

das

amplitudes medidas.

A prindpio, sabe-se que amplitudes e fases de uma onda

sao

duas quantidades

independentes, porem pode-se obter informa~Oesdas fases atraves das amplitudes usando metodos

matemAticos. Deve-se notar porem, que estes procedimentos matematicos estao baseados em

ideias fisicas que estao implkitamente contidas nas medidas experimentais.

As duas ideias principais sao as seguintes:

- A densidade eletrOnicaQ(r) e sempre positiva ou nula.

aproxima~ao, sao discretos, esfericamente simetricos e, em muitos casos, iguais.

Oeste modo, tem-se duas restri~Oes para a densidade eletronica que se expressam em

rela~Oes matematicas e sac poderosasfe rra m e n ta s na resolu~ao de estruturas cristalinas.

No desenvolvimento da teoria dos metodos diretos

e

interessante defmir previamente os

fatores de estrutura quase-normalizados, normalizados e unitarios.

A necessidade do fator de estrutura quase-normalizado vem do fato que no infcio da

resolu~ao de estruturas se est! interessado somente nas posi~Oes atomicas e nao no detalhe da

forma de distribui~ao de Q(r), desta maneira os efeitos de forma podem ser desprezados se for

considerado cada Atomo como urn ponto geometrico de peso igual ao seu numero atomico.

"

"

e ( b }

=

<E

f ; >

-:/2E

fje271iborJ

J-: ]-:

rode N

e

0 n~TO de atomos.

Considerando que 0 fJtOl' de espaTh..lI::1erlto arOmico tenha a mesma fur:rr.a para to&Js os

§l0ffi0S da cela unitma, ter-se·a: ~

= = ~ .

onde ~

e

0 n6mero atOmko para 0 j--esinxJ.itomo de

cela unitMia ego fator de espalhamento unitario.

Assim, (Ill.9) fica da seguinte forma:

N N

e { b )

=

( E

g 2 Z J ) - 1 / 2 E g Z j e 2 7 d l J . r j

j-l j-l

onde r r r_k sao os vetores interatomicos da estrutura.

o

valor m~dio de I E(b)12

e:

Pode-se desprezar 0 segundo termo, pois sup3e-se que a estrutura tenha urn grande

nfunero de atomos distribuidos aleatoriamente pela cela unitaria, deste modo a equa~ao adena

toma-se:

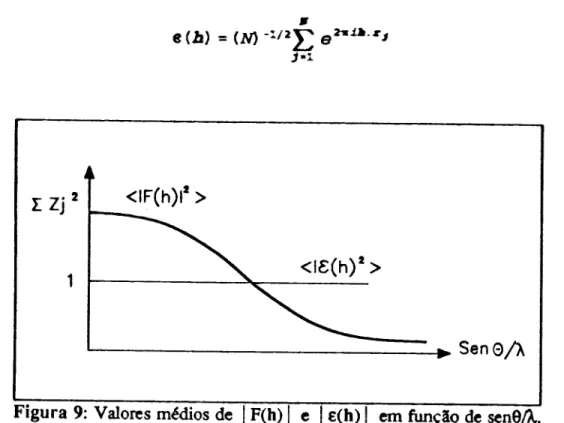
Na figura 9 est! representado graficamente < IF(b) I> e < !£(b) I> em ~o de senSA No caw de ~OIDQS com ru1merosatomicos aprox1m.ad.3rne:rJ.e l& '.a ls . tem-se:

•

e ( 1 1 )

=

( N ) -:/2E e h i . J l . a " J Jal

< IF ( h ) 12>

Figura 9: Valores medios de IP(h) I e I£(h) I em fun~io de senSA.

E(b}

=

F(lI)

~et

f j

j - l

onde £ ~ urn mlmero inteiro que leva em conta 0 efeito da simetria do grupo espadal. Por~m,

£(h) = E(h) se ocorrem reflexOes gerais do tipo hId, quando £=1.

o

fator de estrutura unitdrio 6 deftnido como:

N

Desde que E ,

,..

_~ 6 0 maior valor poss{vel para P(h), pode-se facilmente notar que

!C

Pode ser

e.."Crito

fir:. ~

= IIp que ~ chamado de (ator de espalliamento

atomico

urutmo,

..• ~

pois

tn.

=

1.

pol --.

Para

estruturas com ~omos de Dfuneros

atomic

os aproximadamente iguais, escreve-se que:

•

U (b ) = (h1-:E e ~ ·rJ

jt:'

U (b )

=

e (b )

IN

q U (b ) 12) • l/N

Uma lista completa de fatores Epara diferentes elementos de simetria ~ dada por Rogers

(1965><19) obtida por metodos computacionais. Uma checagem util dos fatores de estrutura

normalizados obtidos por estes m~todos computacionais ~ feita atraves da distribui~ao de Wilson

(1949><20).

densidade eletronica para a determina~ao de fases fazendo uso da desigualdade de Cauchy dada

abaixo:

Pode-se aplicar esta desigualdade para estabelecer rela~Oes dos fatores de estrutura

unitmos para cada grupo espadal.

•

U (b } ::

E

D J C O S (2 ~ b . rJ)

;-:

N 2

II:

apjl

=

IU {b ) 12

j-l

N N

E

Ibjl2 =

E

njCOS

2_21tlJ.

r j = ; (1 + U (2 ,b »

j-l j-l

IU (b ) 12 _~ 1._{(1 + U (2 b »}

2

A desigualdade acima somente pode see satisfeita se 0 sinal de U(2h) for positivo e se

as reflex5es sejam suficientemente intensas.

Posteriormente Karle & Hauptman (1950)('22)desenvolveram outra desigualdade que

expeessa a condi~ao que a soma das series de Fourier devem sempre ser positivas.

Esta desigualdade pode ser expressa, em termos do fator de estrutura unitcirio, da seguinte

mane ira('22):

U (O ) U (~ ) U (Iia ) U (J i n )

U (~ ) U (O ) U (~ -~ ) U (~ _{-b n)}

U (~ ) U (~ -~ ) U (O ) U (~ -,b n ) ~ 0 (m.22)

Este detenninante pode ser de qualquer ordein, porem para ilustrar seu use, sed derivado

urn

C4..'O

especial do determinante de onkm 3:

u {e )

Utli} u(2li)

U (b )

U(O)

u(li)

~ 0

U (2 b )

U(b)

u(O)

ou seja: IU (b ) 12 _~ -.!. _{(1 + U (2 b » que}

e

_{identica a equa~ao (lII.21).}

2

Karle e Hauptman (1950) mostraram que pode-se obter urn extenso e fundamental sistema

de desigualdades entre coeficientes [U(h)] de uma serle de Fourier que representa uma fun~ao

positiva (o(r» utilizando-se a equa~ao (llI.22); para determinantes de segunda e terceira ordem

derlva-se as seguintes desigualdades:

U (O ) U (J i)

U (b ) U (O )

U (k ) U (J c -b )

u(1C)

U (b -k )

U(O)

-Novamente supondo uma estrutura centro-simetrica, U(h)=U(h), tem-se:

Se os m6dulos de tooos os U(h) sao fuados, a desigualdade depende somente do sinal

do produto U(h )U(k)U(h-k) e se as reflexOesforem fortes os Atomos devem ocupar posi~Oesque

Para m6dulos dos fatores de estruturas suficientemente grandes e para pequenas estruturas,

em que U(O)3 seja pequeno, a desigualdade acima estabelece uma restri~ao aos valores permitidos

de 'Ii+~k~h-k' como mostrado na figura 10.

As desigualdades dcscritas at~ aqui neste ftem, requerem grandes valores de U(h) para

prover a informa~ao da fase e desde que 0 valor m~dio de U(h) ~ N"1/2 (onde N ~0 mlmero de

atomos), conclui-se que esw condi~Oesfavocaveis nao sao comumente encontradas em estruturas

mais complex as (maior mlmeco de atomos). Oeste modo, estas desigualdades tern uso limitado,

por isso foi necessario 0 desenvolvimento de outras equa~Oes tal como a E q u a fo o d e S a y re que

sera descrita a seguir.

espacia1mente hem resolvidas. os fatores de estrutura sac inter-relacionados por equa\Oes exatas,

tais como:

oode

f ~0

fat(J{de espalhamento atOmiro comum

1todcs

os itomos, g ~

0

fator de espalhaI!lenlo

C(){OO{i'} )OS

innos

at) quaCrado.

A equa;ao acima representa urn conjunto de equ34;Oesnao lineares simultaneas tendo as

fases como inc6gnitas. Estas equa\Oes sao resolvidas por metodos interativos, desde que haja urna

solu~ao aproximada no inIcio da determin~ao das fases.

Da e{{Ua~aode Sayre pode-se obter a re la ~ d o d e S a y re . que ~ semelhante a re la ~ d o d e

sin a is (obtida na p~gina anterior), porem utilizando 0 sinal "=" que significa: a p ro x im a d a m e n re ig u a l.

Normalmente a equa~ao de Sayre nao ~ utilizada em sua forma original, mas sim urn

ponto de partida para outros trabalhos, tais como 0 de Cochran (1952)(2'), e 0 de Zachariasen

(1952)(25); Zachariasen observou que a rela~ao de Sayre ~ provalvelmente correta, mas nao

necessariarnente e que a maioria dos procedimentos analfticos para a detennina\ao de estruturas

envolvem urn processo de cadeia, em que urn sinal incorreto pode acarretar em urn grande

nfunero de sinais incorretos. Ele propos a seguinte expressao:

onde 0 • •significa a media sobre todos os valores de k.

Hughes (l9 5 3 l2

6 ) propOs que a equa\ao de Sayre fosse expressa em termos de V 's ou de

1

E (b )

=

N 2 (E (k )E (b -k ))

Hauptman e Karle (1953

p1)

derivaram, entre outras, duas rela\Oes comumente utilizadas

srE '~ b ) ~:I

s[E

E (k ) E (b -.t)]

k

A reI~ao

!:l ~

uma

ge--ueraliz3llao

da equa.;ao

(IlI.n),

relll\ao

de Harker e Kasper, e a

rel~ao ~

e

uma gener~ao da rela\ao de Sayre, equa~ao (TII.26). Como a rela~ao de Sayre

e

apenas provalvelmente verdadeira,

e

importante saber como estimar 0 grau de confiabilidade

das fases atraves de tt~cnicasprobabillsticas «(tern ID.3.4).

F6nnulas com medidas quantitativas da probabilidade da rela~ao de Sa)'Te(equa\ao m.27)

ser verdadeira foram publicadas por vmos autores; destas a mais prAtica, e a de Cochran e

W oolfson (1955PS) para 0 caso de estruturas centro-simetricas. Tomando como base este

trabalho, uma reprodu~ao resumida serAapresentada aqui.

Para valores fIxos de h e k, Cochran e Woolfson acharam que 0 fator de estrutura

nonnalizado E.-k' possue 0 seguinte valor medio: (E)=N-II2EIl~' com a varian~a unitiria (0 2 = 1 ).

A probabilidade que F..-k possa tomar qualquer valor particular, E, e dado pela seguinte fun~ao:

ou usando a defini~ao acima: P (E )

=

1 exJ - (E - (E ))

2]

21t

1 /

2

'" 2

+

I ~!

ou

-I ~ I

que sao dados por P+ e p. respectivamente:

Desde que se tern a condi~ao de normaliz3.\ao: P++ p.

=

1.

Fazendo 0 quociente entre PJP., simplificando a expressao e expressando-a em termos

de tangente hiperb61ica tem-se, finalmente:

Esta e a probabilidade do produto dos tres sinais s(h), s(k) e s(h-k) serem positivos.

Claramente, como ja havia sido estimado no item ill.3.3, quanto maior 0 produto dos tres

mudulos maior a probabilidade da rela~ao (m.2?) ser positiva.

E util notar tambem, que devido ao fator N·l/2 no argumento da ta n h , quanto maior 0

ntimero de atomos da estrutura menor sera a probabilidade do sinal ser positivo na rela~ao

(ID.2?). Esta e a principal razao da limita~ao dos metodos diretos na resolu~ao de grandes

A equa~ao (ill.35) foi obtida assumindo atomos iguais na estrutura, porem se os Momos

nao sac iguais, uma analise mais exata mostra que 0 fatorN·l/2 devera ser substitufdo por 0l02·lll,

onde:

e ~

e

0 numero atornico do j-esimo Momo.

• serem estimados (para b constante), este pode ser combinado para formar uma Il()va média e

variança. e não ~ diffcil mostrar que a probabilidade do sinal de h ~ dada por.

As fórmulas de probabilidade para estruturas não centro-simétricas foram apresentadas

pela primeira vez por Cochran (1955><29)e posterionnente desenvolvidas por Karle e Karle

(1966)(30),outro trabalho foi publicado mais recentemente por Heinerman el. ai. (l977pt)

fazendo uma unificação para uma estrutura qualquer.

Seja x = E(h)E(k)E(b-k), onde {x}

=

N-I/l e cT(x)

=

I, com a condição de serem as

posições atômicas igualmente prováveis, tem-se(29):

K(lJ, k)

=

2N-i_IE(li) E(k) E(lJ-k) I

e I.,(K) é a função de Bessel modificada de segunda espécie(32).

A distribuição acima (equação III.38) é aproximadamente gaussiana, com valor máximo

para ~"k=O' que fornece as seguinte relação entre fases:

Nota-se, também, que há maior aglomeração, isto é, a função gaussiana toma-se mais

acentuada, para maiores valores de K(h,k) (consequentemante, maiores valores de E's), deste

modo, a indicação de fase toma-se mais confiável para maiores valores de E's.

A equação (m.38) dá uma distribuição de probabilidades da fase ~h), dadas as fases

pode-se combin!-los na seguinte distribui~ao de probabilidades:

rode C

e

uma COlblante de normaliza\ao.

Desen\'olvendo

a

equ~ao

acimaC2'),

pode-se

~~'e-la

da

~guinte fQfID3:

~~~

=

C .

exp{«

(11) C O S [~ (11)

-p

(11) ]}

E

K (b , k ) s e n [~ (b ) +~ (b -k )]

= _ k _

E

K (b , k ) cas [~ (b ) +4> (b -k ) ]

.t

o

mhimo da curva de probabilidade ocorrer~ quando ~ (h )

=

~ (h ), com ~ (h ) dado pela

equa\ao acima que ~ conhecida comofo rm u la d a ta n g e n te .

Karle e Karle (1966i3O), calcularam a varian\a (isto ~, a confiabilidade da estimativa de

~ (h ) como fun\ao de cx(h», que

e

dada por:

onde C1(h)~ dado pela equa\3.o (TII.44) e I..ssao fun\Oes modificadas de Bessel de 11especie(32).

Pode-se notar da equa\3.o (TII.43), que a confiabilidade de ~ (h )

e

maior quanto maior 0

valor de cx(h), 0 qual

e

maior quanto maior os valores dos E(h)'s e 0 numero de tennos na

somat6ria da f6nnula da tangente (equa\3.om .4 S ).

SERVICO DE B!BLlO TEC A 'tiT~fOR~v'lAC;:AO _ IFO se

E

Knportante as de~ de in,,·ari.m!ese semi-invariantesestrutuIais no estudo dos

mftOCos diret~ pois pennite especificara origem dos eixos cristalogrfficos que sao uteis na

de$(:~ preliminar das f3scs.

Urn

lm 'a ria n u th tstrutura

e

urn fatot de estrutura

Unico

OU

urn!

combina\ao

de fatores

de estrutura cuja fase

e

independente

eta

posi~ao

eta

origem em qualquer grupo espadal. Pode-se

verificar que U(h )U(h-k)U(k)

e

urn invariante de estrutura usando a seguinte propriedade: Q

de~locamento da origem por urn vetor ro mudar<i a fase do fator de estrutura de 27th.ro' deste

modo a mudan~a na fase de U(b)U(h-k)U(k) ser~ ~

=

-27th.r 0 + 27t(h-k).r_o + 27tk.f_o

=

O.

De urn modo mais geral, 0produto dos fatores de estrutura

IT

F(h_i) sofrer<iurna mudan\a

I

de fase de E27th_i.f_o com uma mudan~a na origem de r_o' e ser<iurn invariante de estrutura se

I

LI\

=

O.

I

Urn S e m i-in v a ria n te d e e stru tu ra

e

urn fator de estrutura Unico ou urna combina~ao de

fatores de estrutura cuja fase

e

invariante com uma mudan~a de origem, desde que esta se

restrinja a pontos na cela unitaria com identica simetria de grupo pontual. Urn exemplo de

semi-invariante para estruturas centro-simetricas, em que a origem est! num centro de simetria

restrito as posi~Oes ~=O ou 1(2,Yo=O ou 1(2,zo=O ou 1(2

e

U(2h). Isto

e

facilmente demonstrado

da mesma maneira que para 0 caso invariante, ou seja, com urna mudan~a na origem de f_o, a

mudan~a de fase serA: ~~21t1h.r 0 e, fazendo ro=(Xo,yo,zo) com os valores acima, tem-se:

.1 ~ 2 1 m (n inteiro), mantendo deste modo, U(2h) invariante.

De modo geral, 0 produto de fatores de estrutura

IT

F (!\)

e

urn invariante se:

E

I\.f_o

=

n.

I I

Como as amplitudes dos fatores de estruturas observados sao independentes da posi~ao

da origem e escolha dos enantiom6tfos, eles podem somente dermic 0 valor absoluto das fases

dos fatores de estrutura invariantes e semi-invariantes, ou seja, tem-se apenas as rela~Oes entre

as fases, porem necessita-se dos valores expHcitos das fases individuais para a deterrnina\ao da