Um método de pontos interiores primal-dual viável para minimização com restrições...

primal-dual viável para minimização

com restrições lineares de grande porte

John Lenon Cardoso Gardenghi

Dissertação apresentada

ao

Instituto de Matemática e Estatística

da

Universidade de São Paulo

para

obtenção do título

de

Mestre em Ciências

Programa: Ciência da Computação

Orientador: Prof. Dr. Ernesto G. Birgin

Durante o desenvolvimento deste trabalho, o autor recebeu auxílio financeiro da Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), processo no _{2012/05725-0.}

Um método de pontos interiores

primal-dual viável para minimização

com restrições lineares de grande porte

Esta versão da dissertação contém as correções e alterações sugeridas pela Comissão Julgadora durante a defesa da versão original do trabalho, realizada em 16/04/2014. Uma cópia da versão original está disponível no Instituto de Matemática e Estatística da Universidade de São Paulo.

Banca Examinadora

Agradecimentos

Ao Prof. Ernesto, pela orientação, disponibilidade e companheirismo durante o desenvolvi-mento deste trabalho, bem como pela motivador interesse com que conduziu nossos trabalhos.

Ao Prof. Mario, pelas inestimáveis sugestões dadas ao desenvolvimento deste trabalho, desde sua concepção até o final.

À Profa. Sandra, pela ativa contribuição neste trabalho e durante todo o meu desenvolvi-mento acadêmico até aqui, desde a minha iniciação científica.

Aos meus amigos, que me proporcionaram momentos de descontração, bem como de reflexão e motivação. Em especial, aos meus amigos do grupo de otimização contínua, pelas sugestões que colaboraram ao desenvolvimento deste trabalho.

Ao meu pai, que sempre me acompanhou, investiu e acreditou em mim.

Resumo

Neste trabalho, propomos um método de pontos interiores para minimização com restrições lineares de grande porte. Este método explora a linearidade das restrições, partindo de um ponto viável e preservando a viabilidade dos iterandos. Apresentamos os principais resultados de conver-gência global, além de uma descrição rica em detalhes de uma implementação prática de todos os passos do método. Para atestar a implementação do método, exibimos uma ampla experimentação numérica, e uma análise comparativa com métodos bem difundidos na comunidade de otimização contínua.

Palavras-chave: programação não linear, restrições lineares, problemas de grande porte, pontos

interiores viáveis, busca linear.

Abstract

In this work, we propose an interior-point method for large-scale linearly constrained opti-mization. This method explores the linearity of the constraints, starting from a feasible point and preserving the feasibility of the iterates. We present the main global convergence results, together with a rich description of the implementation details of all the steps of the method. To validate the implementation of the method, we present a wide set of numerical experiments and a comparative analysis with well known softwares of the continuous optimization community.

Keywords: nonlinear programming, linear constraints, large-scale problems, feasible interior-point,

line search.

Sumário

1 Introdução 1

1.1 Notação e organização deste texto . . . 1

2 Algoritmo de pontos interiores com busca linear 3 2.1 O método . . . 3

2.2 Resolução do subproblema . . . 5

2.3 Resolução do sistema primal-dual . . . 7

2.4 Modelo algorítmico para a resolução do subproblema . . . 9

2.4.1 Boa definição . . . 10

2.4.2 Análise da convergência global . . . 12

2.5 Modelo algorítmico para a resolução do problema . . . 16

2.5.1 Boa definição . . . 16

2.5.2 Análise da convergência global . . . 17

3 Detalhes de implementação 19 3.1 Critérios de parada . . . 19

3.2 Escalamento do problema original . . . 20

3.3 Computação do ponto inicial . . . 21

3.3.1 Computação do ponto inicial usando programação linear . . . 22

3.3.2 Computação do ponto inicial resolvendo problemas de viabilidade . . . 22

3.4 Estimativa inicial para os multiplicadores de Lagrange . . . 23

3.5 Lidando com direções de busca pequenas . . . 23

3.6 Correção de inércia . . . 24

4 Experimentos numéricos 27 4.1 Parte I - Resultados gerais . . . 27

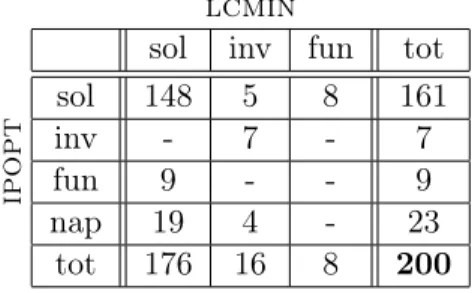
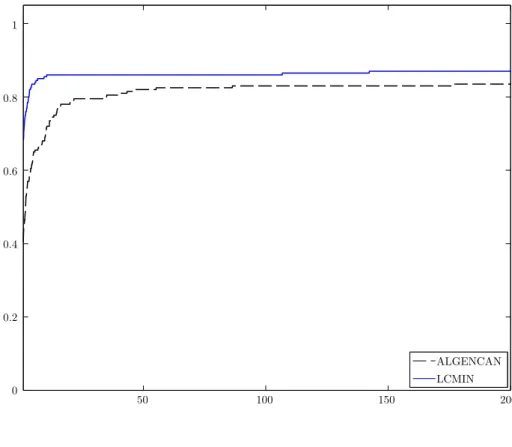
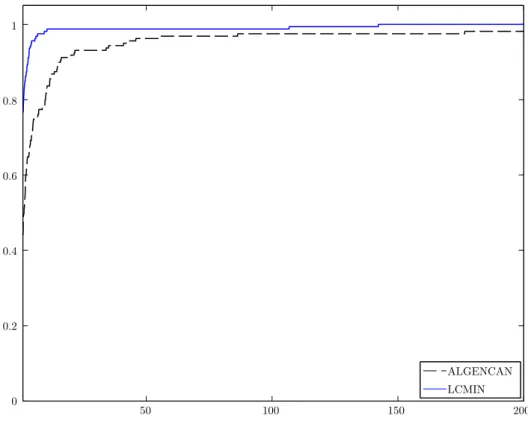
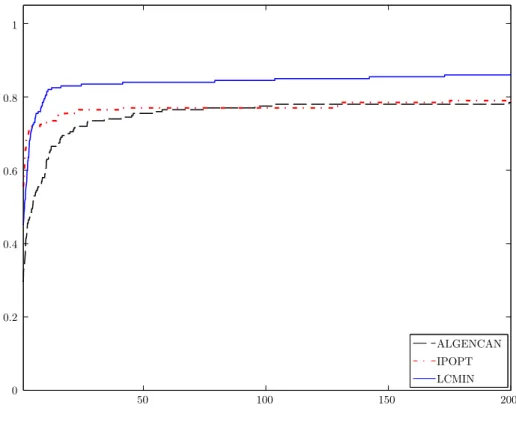
4.2 Parte II - Análise comparativa . . . 31

5 Considerações finais e trabalhos futuros 37

Apêndices

A Condições de qualificação do problema 41

Capítulo 1

Introdução

Métodos para minimização restrita compõem uma teoria muito ampla e que permanece em constante desenvolvimento. Em particular, problemas de minimização sujeitos a restrições lineares possuem uma série de propriedades teóricas e computacionais que problemas de minimização com restrições gerais – lineares e não lineares – não possuem. Neste contexto, métodos para resolução de problemas não lineares linearmente restritos são amplamente estudados. Muitos dos métodos clássicos para minimização com restrições lineares baseiam-se na consolidada estratégia de restrições ativas, como é o caso do método Simplex para programação linear. Em contrapartida, métodos de pontos interiores surgiram em programação linear e se mostraram competitivos com as estratégias clássicas até então desenvolvidas, inclusive para problemas com função objetivo não linear [15], e começaram a ser empregados na teoria e prática em otimização contínua [4, 10, 11, 25].

Métodos de pontos interiores para programação não linear podem ser divididos em dois grupos [21]. No primeiro grupo, estão os métodos que possuem sólido embasamento nas ideias propostas para programação linear. Estes métodos são baseados em busca linear, em que as dire-ções de busca são determinadas resolvendo-se um sistema de equadire-ções lineares através de métodos tradicionais, como o de Newton para sistemas não lineares. Nestes casos, a aceitação e definição do passo são estabelecidos por procedimentos unidimensionais. Por outro lado, temos o segundo grupo, nos quais as direções são obtidas pela minimização de um modelo quadrático, em torno de um ponto, restrito a uma região que garante convergência e globalização, os chamados métodos de regiões de confiança.

Neste trabalho, objetivamos propor um método de pontos interiores para minimização com restrições lineares. A principal característica deste método é que o processo iterativo de otimiza-ção deve ser iniciado em um ponto viável e, ao longo do processo, esta viabilidade é preservada. Neste contexto, queremos verificar se uma tal abordagem é válida e competitiva com os métodos correntemente usados na comunidade de otimização.

1.1

Notação e organização deste texto

Seja v ∈ Rn um vetor. Sua i-ésima componente é denotada pelo subíndice _vi, enquanto

supraíndices denotam iterandos: vk _{denota o k-ésimo iterando de uma sequência qualquer. Se}

o vetor possuir um subíndice como parte de seu nome (e.g., vℓ), então denotamos sua i-ésima

componente por[vℓ]i. Por outro lado, seaé um escalar, entãoak denota ok-ésimo iterando. Neste

contexto, idenota sempre componentes de vetores, enquanto j e k denotam iterações. Ademais,e representa um vetor, de dimensão apropriada ao contexto, cujas componentes são 1. Os operadores k · k1,k · k∞ e k · k2 representam a norma1, infinito e Euclidiana, respectivamente.

Capítulo 2

Algoritmo de pontos interiores com

busca linear

Neste capítulo descreveremos um método de pontos interiores aplicado ao problema

min

x f(x)

s. a Ax=b

ℓ≤x≤u,

(2.1)

com x _∈ Rn, _{A ∈} Rm×n, _{ℓ, u ∈ (}R_{∪ {−∞,+∞})}n e m < n. O método que apresentaremos é

inspirado noIpopt[25]. A principal contribuição deste é a preservação da viabilidade das restrições lineares. Deste modo, este algoritmo se torna competitivo por usar uma abordagem específica para resolução do problema (2.1). Denotaremos por_Fo conjunto de pontos viáveis para o problema (2.1), isto é,

F={x∈Rn_|Ax=be _{ℓ≤x≤u}.}

Começaremos com a seguinte definição.

Definição 1. O interior relativo do conjunto viável do problema (2.1), denotado por

F0 ={x∈Rn|Ax=b e ℓ < x < u},

é formado pelos pontos que satisfazem as restrições de igualdade e ao mesmo tempo, estritamente, as restrições de caixa do problema (2.1).

Para o presente método assumiremos que

Hipótese 1. O conjunto _F0 é não vazio.

Hipótese 2. A função objetivo f :Rn_→R _{é contínua e pelo menos duas vezes diferenciável.}

Além disso, sem perda de generalidade, suporemos que A possui posto linha completo. De fato, caso isto não ocorra, a Hipótese 1 nos garante que o sistema Ax=b é compatível e, portanto, é possível eliminar suas equações redundantes e redefiní-lo.

2.1

O método

Consideremos _Iℓ e Iu conjuntos de índices tais que

Iℓ={i:ℓi6=−∞}e Iu={i:ui6=∞}. (2.2)

As condições KKT do problema (2.1) são

∇f(x) +ATλ₋νℓ+νu = 0 (2.3a)

Ax₋b = 0 (2.3b)

xi−ℓi ≥ 0, ∀i∈ Iℓ (2.3c)

ui−xi ≥ 0, ∀i∈ Iu (2.3d)

[νℓ]i ≥ 0, ∀i∈ Iℓ (2.3e)

[νu]i ≥ 0, ∀i∈ Iu (2.3f)

[νℓ]i(xi−ℓi) = 0, ∀i∈ Iℓ (2.3g)

[νu]i(ui−xi) = 0, ∀i∈ Iu (2.3h)

ondeλ∈Rmé o vetor de multiplicadores de Lagrange associados às restrições de igualdade e_{νℓ, νu ∈} Rnsão os vetores de multiplicadores de Lagrange associados às restrições de caixa. Consideraremos

que [νℓ]i = 0, para cada i 6∈ Iℓ e [νu]i = 0, para cada i 6∈ Iu. Como o conjunto viável do

problema (2.1) é descrito por restrições lineares, sem qualquer hipótese extra este conjunto já é qualificado, no sentido que todo minimizador local cumpre as condições de Karush-Kuhn-Tucker (KKT). Além disso, a Hipótese 1 implica que todo ponto viável do problema satisfaz a condição de qualificação de Mangasarian-Fromovitz (MFCQ), o que implica que, para todo ponto x que satisfaz as condições KKT, o conjunto de multiplicadores de Lagrange associado é limitado (veja Apêndice A).

O método consiste em resolver aproximadamente uma sequência de subproblemas da forma

min

x f(x)−µk

X

i∈Iℓ

log(xi−ℓi)−µk

X

i∈Iu

log(ui−xi) s. a Ax=b, (2.4)

comµk o parâmetro barreira, positivo para todo k, de tal maneira que

lim

k→∞µk= 0.

Às iterações que definem a sequência de subproblemas chamaremositerações externas, enquanto às iterações despendidas para resolver o k-ésimo subproblema chamaremos iterações internas. Neste contexto, utilizaremos como ponto inicial para o k-ésimo subproblema a solução aproximada do subproblema k−1, de modo que a estimativa inicial para o primeiro subproblema será o ponto inicial calculado durante o pré-processamento (ver Seção 3.3 adiante). As condições de Lagrange do subproblema (2.4) são:

∇f(x) +AT_λ−µ

kL†e+µkU†e = 0

Ax−b = 0. (2.5)

onde Le U são matrizes diagonais de ordemntais que

Li,i=

xi−ℓi, sei∈ Iℓ

0, em caso contrário e Ui,i=

ui−xi, sei∈ Iu

0, em caso contrário (2.6)

e L† eU† são suas pseudoinversas, de forma que

L†_i,i =

  

1

xi−ℓi

, sei_{∈ I}ℓ

0, em caso contrário e U

† i,i=    1

ui−xi

, sei_{∈ I}u

0, em caso contrário.

Se considerarmos variáveis auxiliares

[zℓ]i =

( µ_k

xi−ℓi

, sei_{∈ I}ℓ

0, em caso contrário e [zu]i =

( µ_k

ui−xi

, sei_{∈ I}u

2.2. RESOLUÇÃO DO SUBPROBLEMA 5

ou, matricialmente,LZℓ_e−µ

ke= 0eU Zue−µke= 0, comZℓ =diag(zℓ)eZu =diag(zu), podemos

reescrever (2.5) como

∇f(x) +ATλ−zℓ+zu = 0 (2.8a)

Ax₋b = 0 (2.8b)

Lzℓ−µke = 0 (2.8c)

U zu−µke = 0 (2.8d)

Encontrar umxk _{que resolva aproximadamente (2.4) equivale a encontrar (x}k_{, λ}k_{, z}k

ℓ, zku) que

satis-faça aproximadamente (2.8). Na prática, as equações (2.7) não são usadas; o método consiste em encontrar soluções aproximadas para o sistema (2.8) fazendo µk tender a zero. O fato da função

objetivo de (2.4) não estar definida para x_6∈(ℓ, u) e ir para o infinito quando alguma componente de x se aproxima de ℓ ou de u implica que ℓ < xk _{< u. Este fato, as equações (2.8c) e (2.8d)}

e a positividade de µk implicam que [z_ℓk]i ≥ 0, para todo i ∈ Iℓ e [zuk]i ≥ 0 para todo i ∈ Iu.

Notemos que a resolução de uma sequência de equações do tipo (2.8) com µk tendendo para zero

pode ser vista como um método homotópico para resolver as condições KKT (2.3) perturbadas. Neste contexto, zk

ℓ e zuk assim definidos são aproximações dos multiplicadores de Lagrange νℓ e νu

do problema original (2.1), mais exatas quanto menor for o valor de µk.

Na seção a seguir, apresentaremos a estratégia para a resolução dos subproblemas.

2.2

Resolução do subproblema

Na k-ésima iteração externa, definimos

ϕµk(x)

def

=f(x)−µk

X

i∈Iℓ

log(xi−ℓi)−µk

X

i∈Iu

log(ui−xi) (2.9)

e consideramos o problema

min

x ϕµk(x)

s. a Ax=b. (2.10)

Pressupomos que temos (xk,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u )naj-ésima iteração interna, comj≥0, comxk,j ∈ F0, z_ℓk,j e zk,ju positivos e descreveremos uma iteração de um método de busca linear para calcular

(xk,j+1_{, λ}k,j+1_{, z}k,j+1

ℓ , z k,j+1

u ) tal quexk,j+1 ∈ F0,[zℓk,j+1]i >0 para cadai∈ Iℓ e[zuk,j+1]i>0para

cadai_{∈ I}u. Para tanto, a cada iteração deverá ser calculada uma direção (dxk,j, dk,j_λ , dk,jzℓ , d k,j zu), com

dk,jx de descida paraϕµk(·) a partir dex

k,j_{, e um passoα}

k,j tal que a condição de Armijo dada por

ϕµk(x k,j_+α

k,jdk,jx )≤ϕµk(x

k,j_{) +γα}

k,j∇ϕµk(x

k,j₎T_dk,j

x (2.11)

seja satisfeita, para algumγ _∈(0,1).

As condições de otimalidade do problema (2.10) são dadas por (2.8). A direção de Newton para o sistema (2.8) em(xk,j_{, λ}k,j_{, z}k,j

ℓ , z k,j

u )é a solução do sistema linear de dimensão3n+m dado

por

   

∇2f(xk,j_{) A}T _{−I I}

A 0 0 0

Zℓ

k,j 0 Lk,j 0

−Zu

k,j 0 0 Uk,j

        

dk,jx

dk,j_λ dk,jzℓ

dk,jzu

     =−     

∇f(xk,j_{) +A}T_λk,j_−zk,j ℓ +z

k,j u

0

Lk,jz_ℓk,j−µke

Uk,jzuk,j−µke

O sistema linear (2.12) é chamadoprimal-dual [21]. Seus dois últimos blocos de equações implicam que

Zℓ k,jd

k,j

x +Lk,jdk,jzℓ = −Lk,jz k,j ℓ +µke

−Z_k,ju dk,jx +Uk,jdk,jzu = −Uk,jz k,j u +µke.

Colocando em evidenciadk,jzℓ e d k,j

zu, temos que

dk,j_zℓ =L†_k,j(₋Lk,jZk,jℓ e+µke−Zk,jℓ dk,jx ) = −z k,j ℓ +µkL

† k,je−L

† k,jZ

ℓ

k,jdk,jx (2.13a)

dk,j_zu =U_k,j† (₋Uk,jZk,ju e+µke+Zk,ju dk,jx ) = −zuk,j+µkU_k,j† e+U_k,j† Zk,ju dk,jx . (2.13b)

Substituindo dk,jzℓ e d k,j

zu no primeiro bloco de equações do sistema (2.12) obtemos o sistema de

dimensão n+m dado por

Hk,j AT

A 0

dk,jx

dk,j_λ

!

=− ∇f(xk,j) +ATλk,j−µkL

†

k,je+µkU † k,je 0 ! , (2.14) onde

Hk,j=∇2f(xk,j) +L†_k,jZk,jℓ +U † k,jZ

u

k,j. (2.15)

A resolução do sistema (2.14) requer alguns cuidados, que discutiremos na Seção 2.3. Uma vez calculadosdk,jx edk,j_λ , encontramosdk,jzℓ ed

k,j

zu usando (2.13). Tendo calculado as direções, definimos

xk,j+1 = xk,j+αk,jdk,jx (2.16a)

λk,j+1 = λk,j+dk,j_λ (2.16b)

¯

z_ℓk,j+1 = zk,j_ℓ +αzℓ k,jd

k,j

zℓ (2.16c)

¯

zu,j+1 = zk,j_u +αzu k,jd

k,j

zu, (2.16d)

de forma queαk,j, αz_k,jℓ , αz_k,ju ∈(0,1]determinam os tamanhos de cada passo a serem dados em (2.16).

Dado que ℓ < xk,j _{< u, [z}k,j

ℓ ]i >0 para cada i∈ Iℓ e [zk,ju ]i >0 para cada i∈ Iu, cuidamos para

que o passo tomado conserve tais propriedades no novo ponto. Para isto, definimos uma fração à fronteira

τ = max_{τmin,1−µ_k}, (2.17)

onde τmin ∈(0,1)é o menor valor para esta fração, e calculamos

αℓ

k,j = max{α∈(0,1] : (x k,j

i +α[dk,jx ]i)−ℓi≥(1−τ)(xk,ji −ℓi)},parai∈ Iℓ∩ Dk,j− (2.18a)

αuk,j = max{α∈(0,1] :ui−(x k,j i +α[d

k,j

x ]i)≥(1−τ)(ui−xk,ji )},parai∈ Iu∩ D+k,j (2.18b) αzℓ

k,j = max{α∈(0,1] : [z k,j

ℓ ]i+α[dk,jzℓ ]i≥(1−τ)[z k,j

ℓ ]i},parai∈ Iℓ∩ D+k,j (2.18c) αzu

k,j = max{α∈(0,1] : [z k,j

u ]i+α[dk,jzu]i≥(1−τ)[z k,j

u ]i},parai∈ Iu∩ D−k,j, (2.18d)

onde _Dk,j

− ={i: [d k,j

x ]i <0} eDk,j₊ ={i: [dk,jx ]i >0}, obtendo, por fim,

αmax_k,j = min{αℓ_k,j, αu_k,j}. (2.19)

Depois, fazemosbacktracking para obterαk,j ∈(0, αmaxk,j ]de forma quexk,j+αk,jdk,jx satisfaça (2.11).

Por fim, o último cuidado é atentar para que z_ℓk,j+1 e zuk,j+1 conservem, aproximadamente,

2.3. RESOLUÇÃO DO SISTEMA PRIMAL-DUAL 7

garantem que a matriz do noroeste do sistema (2.14) é uma aproximação para a matriz Hessiana da função barreira (2.9). Assim sendo, tomamos

[z_ℓk,j+1]i=

       max ( min (

[¯zk,j+1_ℓ ]i, κz µk xk,j+1_{i −}ℓi

!)

, 1 κz

µk xk,j+1_{i −}ℓi

!)

, sei_{∈ I}ℓ

0, caso contrário

(2.20)

e

[z_uk,j+1]i=

       max ( min ( ¯

z_iu,j+1, κz µk ui₋xk,j+1_i

!)

, 1 κz

µk ui₋xk,j+1_i

!)

sei_{∈ I}u

0, caso contrário.

(2.21)

com i= 1, . . . , n e κz ≥1 uma constante definida. Com isso, teremos que

[z_ℓk,j+1]i ∈

"

1

κz

µk

xk,j_i +1₋ℓi

!

, κz

µk

xk,j_i +1₋ℓi

!#

, parai_{∈ I}ℓ e (2.22a)

[zuk,j+1]i ∈

"

1

κz

µk

ui−xk,j_i +1

!

, κz

µk

ui−xk,j_i +1

!#

, parai∈ Iu, (2.22b)

ou seja, que z_ℓk,j+1 e zuk,j+1 satisfarão a relação (2.7) de acordo com uma tolerância κz. Neste

contexto, é interessante tomar valores altos para κz, de tal maneira que a correção não influa na

convergência do algoritmo. Diante disso, consideraremos κz= 1010.

Para cada subproblema (2.10) consideraremos que um ponto (xk,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u ) é uma

solução aproximada quando

Eµk(x

k,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u )≤κεµk, (2.23)

sendo

Eµ(x, λ, zℓ, zu) =

 

∇f(x) +ATλ−zℓ+zu

Lzℓ−µe

U zu−µe

  ∞ (2.24)

e κε >0. Desse modo, (2.23) implica que as equações (2.8a), (2.8c) e (2.8d) são aproximadamente

satisfeitas e, pela definição do método, Axk,j _{=b, o que satisfaz (2.8b), logo(x}k,j_{, λ}k,j_{, z}k,j ℓ , z

k,j u )

sa-tisfaz aproximadamente as condições de otimalidade de primeira ordem (2.8) do subproblema (2.10). Tendo resolvido um subproblema, obtemos um novo parâmetro de barreira

µk+1= min

n

κµµk, µθ_kµ

o

(2.25)

onde κµ∈(0,1)e θµ ∈(1,2). Deste modo, o parâmetro de barreira pode eventualmente convergir

a zero superlinearmente.

2.3

Resolução do sistema primal-dual

Nesta seção, discutiremos alguns detalhes sobre a resolução do sistema primal-dual reduzido, apresentado na equação (2.14). Em primeiro lugar, é necessário garantir que (2.14) possua solução. A priori, nada garante que (2.14) possui solução, dado que a matriz do sistema pode ser singular. Queremos também cuidar para que a direçãodk,jx calculada seja uma direção de descida paraϕµk(·),

Definição 2. Seja K uma matriz simétrica qualquer. Sua inércia, denotada por In(K), é a tripla

(a+, a−, a0) onde a+, a− e a0 denotam o número de autovalores positivos, negativos e nulos da matriz K, respectivamente.

Para o desenvolvimento das ideias desta seção, consideraremos uma forma geral do sis-tema (2.14) dada por

_ˆ

H AT

A 0 dx dλ =₋

∇f(x) +AT_λ−µ

kL†e+µkU†e

0

, (2.26)

onde A_∈Rm×n _{é uma matriz com posto linha completo e H}ˆ _∈Rn×n_.

A seguinte proposição, adaptada de [21, Teorema 16.3] e cuja demonstração pode ser encon-trada com detalhes em [16, Lema 3.4], nos dá um resultado interessante para obter o que queremos.

Proposição 3. Consideremos a forma geral do sistema primal-dual reduzido (2.14) dada em (2.26), e suponhamos que A possui posto completo. Então,

In

_ˆ

H AT

A 0

=In(WTHWˆ ) + (m, m,0),

onde W ∈Rn×(n−m) _{é uma matriz cujas colunas formam uma base para o núcleo da matriz A.}

A Proposição 3 nos permite concluir que a matriz do sistema (2.14) será não singular desde que a matriz do noroeste do sistema projetada no núcleo daA não possua autovalores nulos. Con-sideremos ainda o seguinte resultado.

Lema 4. Consideremos a forma geral do sistema primal-dual reduzido (2.14) dada em (2.26). Se

ˆ

H for definida positiva no núcleo da matriz Ae dx, obtida como solução do sistema (2.26), for não

nula, então dx será uma direção de descida para ϕµk(·) a partir de x.

Demonstração. Pela primeira equação do sistema (2.26), temos que

ˆ

Hdx+ATdλ =−∇f(x)−ATλ+µkL†e−µkU†e. (2.27)

Como∇ϕµk(x) =∇f(x)−µkL †_e+µ

kU†e, de (2.27) segue que

ˆ

Hdx+ATdλ=−∇ϕµk(x)−A

T_{λ. (2.28)}

A segunda equação do sistema (2.26), por sua vez, implica que dx pertence ao núcleo da matrizA.

Em vista disto, pré-multiplicando (2.28) por ₋(dx)T, vem que

∇ϕµk(x) T_d

x =−(dx)THdˆ x. (2.29)

Logo, se _Hˆ _{for definida positiva no núcleo da A, então (dx)}T_Hdˆ

x >0 sempre que dx 6= 0, o que,

junto com (2.29), implica que dx é um direção de descida para ϕµk(·) a partir dex.

A Proposição 3 e o Lema 4, juntos, implicam que se _Hˆ _{for definida positiva no núcleo da}

matriz A, então qualquer sistema da forma (2.26) admite solução única dx, edx é uma direção de

descida para ϕµk(·) a partir de x sempre que for não nula. Mais ainda, a Proposição 3 implica

que a inércia da matriz do sistema (2.26) será(n, m,0)se, e somente se, _Hˆ _{for positiva definida no}

núcleo da A. Assim sendo, caso a matriz do sistema (2.14) não possua inércia (n, m,0), repetimos a fatoração da matriz

Mk,j =

Hk,j+ξk,jI AT

A 0

2.4. MODELO ALGORÍTMICO PARA A RESOLUÇÃO DO SUBPROBLEMA 9

até encontrarξk,j>0tal que Mk,j possua a inércia desejada. Com isso, resolvemos o sistema (2.14)

perturbado

Mk,j

dk,jx

dk,j_λ

!

=₋

∇ϕµk(x

k,j_{) +A}T_λ k,j

0

. (2.31)

2.4

Modelo algorítmico para a resolução do subproblema

Nesta seção, apresentaremos o modelo algorítmico que descreve o método para a resolução do subproblema (2.10). A fim de facilitar a leitura, apresentamos um glossário da notação usada no algoritmo.

Notação

n: quantidade de variáveis κµ: fator para cálculo deµ m: quantidade de restriçõesAx=b θµ: fator para cálculo deµ

k: contador de iterações externas ξk,j: termo de correção da inércia do sistema (2.31)

j: contador de iterações internas κz: termo de ajuste das variáveiszℓ ezu f: função objetivo γ: constante de Armijo

ϕµ: função barreira (2.9) dk,j

x : direção de busca emxk,j Eµ: erro de otimalidade (2.24) dk,j_λ : direção de busca emλk,j xk,j_{: iterando primal d}k,j

zℓ : direção de busca emz k,j ℓ λk,j_{: iterando dual d}k,j

zu: direção de busca emz k,j u z_ℓk,j: iterando dual αℓ

k,j: passo máximo dexk,j inferiormente zk,j

u : iterando dual αuk,j: passo máximo dexk,j superiormente εtol: tolerância de otimalidade αmax_k,j : passo máximo dexk,j

κε: fator de tol. de otimalidade do subproblema αzℓ

k,j: passo máximo dez k,j ℓ µk: parâmetro barreira αzu

k,j: passo máximo dezk,ju Lk,j: matriz diagonal (2.6) comx=xk,j _I

ℓ: {i:ℓi>−∞} Uk,j: matriz diagonal (2.6) comx=xk,j _I

u: {i:ui <∞} Zℓ

k,j: diag(z k,j

ℓ ) D

k,j

+ : {i: [dk,jx ]i>0} Zu

k,j: diag(zk,ju ) D k,j

− : {i: [dk,jx ]i<0}

Algoritmo 1. Método de pontos interiores - Algoritmo interno.

Entrada: xk,0 _{∈ F0, λ}k,0 _∈Rm_{, z}k,0

ℓ ∈Rn e z k,0

u ∈Rn tais que [z_ℓk,0]i >0 parai∈ Iℓ e [zk,ℓ 0]i = 0

caso contrário, e[zk,u0]i >0 parai∈ Iu e [zuk,0]i= 0 caso contrário,A∈Rm×n com posto

linha completo e µk > 0; constantes κε > 0, γ ∈ (0,1), τmin > 0, κz ≥ 1; ξ0,−1 ← 0 e j_←0.

Passo 1. SeEµk(x

k,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u )≤κεµk, entãopareeretorne(xk,j, λk,j, zℓk,j, z k,j

u )como ponto

aproximadamente estacionário.

Passo 2. Utilizando ξk,j−1, calculeξk,j ≥0tal que In(Mk,j) = (n, m,0), onde

Mk,j= ∇

2_f(xk,j_{) +L}† k,jZ

L k,j+U

† k,jZ

U

k,j+ξk,jI AT

A 0

!

.

Passo 3. Encontredk,jx e dk,j_λ solução do sistema

Mk,j d

k,j x

dk,j_λ

!

=−

∇ϕµk(x

k,j_{) +A}T_λk,j

0

Passo 4. Calcule

dk,jzℓ = −z k,j ℓ +µL

† k,je−L

† k,jZ L k,jd k,j x e

dk,jzu = −z k,j

u +µU_k,j† e+U_k,j† Z_k,jU dk,jx . Passo 5. Calcule τ = max_{τmin,1−µk} e

αℓ

k,j = max{α∈(0,1] : ([xk,j]i+α[dk,jx ]i)−ℓ≥(1−τ)([xk,j]i−ℓi)},parai∈ Iℓ∩ Dk,j− ,

αu

k,j = max{α∈(0,1] :ui−([xk,j]i+α[d k,j

x ]i)≥(1−τ)(ui−[xk,j]i)},parai∈ Iu∩ D+k,j, αzℓ

k,j = max{α∈(0,1] : [z k,j

ℓ ]i+α[d k,j

zℓ ]i≥(1−τ)[z k,j

ℓ ]i},parai∈ Iℓ∩ D k,j

+ , αzu

k,j = max{α∈(0,1] : [z k,j

u ]i+α[dk,jzu]i≥(1−τ)[z k,j

u ]i},parai∈ Iu∩ Dk,j−

e

αmax_k,j = min_{αℓ_k,j, αu_k,j}.

Passo 6. Faça αk,j ←αmax_k,j . Se

max

1≤i≤n

(

|(dk,jx )i|

(1 +_|xk,j_{i |})

)

6≤10εmach,

então, enquanto ϕµk(x k,j_+α

k,jdk,jx )> ϕµk(x

k,j_{) +γα}

k,j∇ϕµk(x

k,j₎T_dk,j

x , faça αk,j ← 1₂αk,j.

Passo 7. Faça xk,j+1_=xk,j_+α

k,jdk,jx e λk,j+1=λk,j+dk,j_λ . Passo 8. Faça z¯k,j_ℓ +1=z_ℓk,j+αzℓ

k,jd k,j zℓ ,z¯

k,j+1

u =zk,ju +αz_k,judk,jzu,

[z_ℓk,j+1]i=

     max min

[¯z_ℓk,j+1]i, κz

_µk

[xk,j+1_] i−ℓi

, 1 κz

_µk

[xk,j+1_] i−ℓi

, sei_{∈ I}ℓ,

0, caso contrário e

[zk,j+1 u ]i=

     max min

[¯z_uk,j+1]i, κz

_µk

ui₋[xk,j+1_] i

, 1 κz

_µk

ui₋[xk,j+1_] i

, sei_{∈ I}u,

0, caso contrário.

Passo 9. Faça j←j+ 1e vá para o Passo 1.

2.4.1 Boa definição

Queremos, nesta seção, mostrar que o Algoritmo 1 está bem definido. Em primeiro lugar, pela Hipótese 1, existe um ponto xk,0 _{∈ F}

0. O resultado a seguir diz respeito ao cálculo de ξk,j no

Passo 2, que será computado usando o Algoritmo 3.

Lema 5. Suponha que estamos no Passo 2 do Algoritmo 1. Então, existe ξk,j ≥0 suficientemente

grande tal que In(Mk,j) = (n, m,0).

Demonstração. Seja _H˜_ξ

k,j = ∇

2_f(xk,j_{) +L}†

k,jZk,jL +U †

k,jZk,jU +ξk,jI e W ∈ Rn×n−m uma matriz

cujas colunas formam uma base para o núcleo da A. Notemos que, se _H˜_ξ

k,j for definida positiva,

então WT_H˜

ξk,jW também é. De fato, para todoω ∈R

n−m _{não nulo, temos que}

ωTWH˜ξk,jW ω=y T_H˜

2.4. MODELO ALGORÍTMICO PARA A RESOLUÇÃO DO SUBPROBLEMA 11

haja visto que y=W ω6= 0 poisω6= 0 e as colunas deW são linearmente independentes.

Logo, se, por um lado, H0˜ for positiva definida, então WTH0W˜ também é e, pela Proposi-ção 3 aplicada ao sistema (2.31), vem que In(Mk,j) = (n, m,0) paraξk,j = 0. Se, por outro lado,

˜

H0 não for positiva definida, consideremos λ1 ≤λ2 ≤. . . ≤λn os autovalores deH˜0, com λ1 ≤0. Então a matriz H˜|λ1|+ǫ, paraǫ >0, possuirá autovalores

ǫ_≤λ2+|λ1|+ǫ≤. . .≤λn+|λ1|+ǫ,

donde segue que_H˜

|λ1|+ǫ é uma matriz positiva definida e, portanto,W T_H˜

|λ1|+ǫW também é. Deste

modo, pela Proposição 3 aplicada ao sistema (2.31), In(Mk,j) = (n, m,0)paraξk,j ≥ |λ1|+ǫ.

O resultado a seguir diz respeito ao cálculo das direções de busca.

Lema 6. Suponha que estamos no Passo 3 do Algoritmo 1. Então, é possível calcular as direções de busca dk,jx e dk,j_λ como solução do sistema (2.31) e, se dk,jx 6= 0, então dk,jx será uma direção de

descida para ϕµk(·) a partir de x k,j_.

Demonstração. Pelo Lema 5, é possível encontrarξk,jtal que In(Mk,j) = (n, m,0). Portanto,Mk,j é

uma matriz não singular, e o sistema (2.31) possui solução única. Mais ainda, pelo Lema 4 aplicado ao sistema (2.31), como In(Mk,j) = (n, m,0), temos que se dk,jx 6= 0, então dk,jx será uma direção de

descida paraϕµk(·) a partir dex k,j_.

Por fim, mostramos no Lema 7 que o procedimento de busca linear do Passo 6 do Algoritmo 1 está bem definido.

Lema 7. Suponha que estamos no Passo 6 do Algoritmo 1. Então, existe α¯ _∈R _{tal que para todo}

αk,j∈(0,α¯] a condição de Armijo (2.11) se cumpre.

Demonstração. Se dk,jx = 0, então naturalmente a condição de Armijo (2.11) valerá para todo

αk,j ∈ (0, αmaxk,j ]. Suponhamos então que d k,j

x 6= 0. Pelo Lema 6, vem que ∇ϕµk(x

k,j₎T_dk,j x <0.

Comoϕµk(·) é uma função diferenciável, temos que sua derivada direcional ao longo ded k,j

x é dada

por

lim

α→0+

ϕµk(x

k,j_+αdk,j

x )−ϕµk(x k,j₎

α =∇ϕµk(x

k,j₎T_dk,j x <0.

Assim sendo,

lim

α→0+

ϕµk(x

k,j_+αdk,j

x )−ϕµk(x k,j₎

α_∇ϕµk(xk,j)Td k,j x

= 1.

Tomando γ _∈(0,1), existe α¯ suficientemente pequeno tal que, para todo α_∈(0,α¯),

ϕµk(x

k,j_+αdk,j

x )−ϕµk(x k,j₎

α_∇ϕµk(x

k,j₎T_dk,j x

≥γ.

Por conseguinte, como ∇ϕµk(x

k,j₎T_dk,j

x <0, vem que

ϕµk(x

k,j_+αdk,j

x )≤ϕµk(x

k,j_{) +γα}

∇ϕµk(x

k,j₎T_dk,j x ,

para todo α_∈(0,α¯).

Por conseguinte, o Algoritmo 1 para apenas no Passo 1, em que o ponto corrente satisfaz, aproximadamente, as condições de otimalidade do problema (2.10). Estabelecemos então a boa definição do Algoritmo 1 na seguinte proposição.

2.4.2 Análise da convergência global

A análise da convergência global possui forte embasamento no trabalho de Chen e Gold-farb [12]. Para mostrar as propriedades de convergência global do Algoritmo 1, faremos as seguintes hipóteses adicionais.

Hipótese 3. A sequência _{xk,j_{} gerada pelo Algoritmo 1 é limitada, para todo k.}

Hipótese 4. As matrizes H¯k,j=Hk,j+ξk,jI satisfazem

dTH¯k,jd≥σkdk2,

para todo d₆= 0 tal que Ad= 0, para algum σ >0 e para todok e todoj.

Embora a Hipótese 3 seja uma conjectura feita sobre a sequência gerada pelo método, ela será satisfeita sempre que existirem restrições de caixas para todas as variáveis, isto é, quando −∞ < ℓi ≤ui <+∞, para todoi= 1, . . . , n, ou sempre que o conjunto {x ∈ F | f(x) ≤f(x0)}

for limitado, onde x0 _{∈ F}

0 é um ponto inicial estritamente viável. A Hipótese 4, por sua vez, estabelece que as matrizes{H¯k,j}devem ser uniformemente positivas definidas no núcleo da matriz

A. Em comparação com a exigência semelhante no trabalho de Chen e Goldfarb [12, Condição C-5], esta hipótese é mais fraca, visto que o Lema 5 garante que é possível encontrarξk,j no Passo 2 do

Algoritmo 1 tal que H¯k,j é definida positiva. Deste modo, a Hipótese 4 deve ser assegurada pela

natureza numérica do método de correção de inércia usado no Algoritmo 3.

A boa definição estabelecida na Proposição 8 implica que o Algoritmo 1 para apenas no Passo 1 quando o ponto corrente satisfizer, aproximadamente, as condições de otimalidade de pri-meira ordem do subproblema (2.10). Nos resultados que seguem, analisamos o comportamento do Algoritmo 1 quando não para, isto é, quando gera sequências infinitas.

Lema 9. Suponhamos que as Hipóteses 1, 2 e 3 valem e seja_{xk,j+1_{, λ}k,j+1_{, z}k,j+1

ℓ , z k,j+1

u }a

sequên-cia gerada pelo Algoritmo 1. Então, existe δ >0 tal que

I. para todoj vale

(a) ℓi+δ≤xk,ji +1, para todo i∈ Iℓ e

(b) xk,j_i +1≤ui−δ, para todo i∈ Iu;

II. para todo j vale

(a) [z_ℓk,j+1]i∈

µk

δ

1

κz

, κz

, para todo i∈ Iℓ e

(b) [z_uk,j+1]i∈

µk

δ

1

κz

, κz

, para todo i_{∈ I}u.

Demonstração. Para demonstrar a parte (I), suponhamos, por contradição, que existe um conjunto infinito_{J ⊂}

∞

N e um índiceˆ_{i∈ Iℓ} tais que

lim

j∈Jx k,j+1

ˆ_i =ℓˆi. (2.32)

Pelo Passo 1, temos que Eµk(x

k,j+1_{, λ}k,j+1_{, z}k,j+1

ℓ , z k,j+1

u )> κεµk e, pela busca linear do Passo 6,

ϕµk(x

k,j+1_)≤ϕ

µk(x

k,j_{) +γα}

k,j−1∇ϕµk(x

k,j₎T_dk,j

2.4. MODELO ALGORÍTMICO PARA A RESOLUÇÃO DO SUBPROBLEMA 13

Não obstante, pelas Hipóteses 2 e 3, as sequências {f(xk,j+1_{)}, {x}k,j+1

i −ℓi}, para todo i ∈ Iℓ e

{ui−xk,ji +1}, para todo i∈ Iu, são limitadas. Deste modo, por (2.32) e pela definição da função

ϕµ(·) em (2.9),

lim

j∈Jϕµk(x

k,j+1_{) = +∞,}

o que contradiz (2.33). Analogamente, vale o mesmo se existir um conjunto infinito _{J ⊂}

∞

N e um

índiceˆ_{i∈ Iu tais que{x}k,j+1

ˆi }j∈J →uˆi.

Quanto à parte (II), basta notarmos que o Passo 8 implica que z_ℓk,j+1 e zk,ju +1 satisfazem

as relações (2.22) para todoj. Este fato e a parte (I) deste lema juntos implicam o que queríamos demonstrar.

Lema 10. A sequência _{H¯k,j} gerada pelo Algoritmo 1 é limitada.

Demonstração. Pelas Hipóteses 2 e 3, temos que a sequência{∇2_f(xk,j_{)}gerada pelo Algoritmo 1 é}

limitada. Mais ainda, a Hipótese 3 e o Lema 9(I) implicam que a sequência {L†_k,j, U_k,j† _}gerada pelo Algoritmo 1 é limitada. Não obstante, o Lema 9(II) implica que a sequência{ZL

k,j, Zk,jU }gerada pelo

Algoritmo 1 é limitada. Finalmente, o Algoritmo 3 implica que ξk,j = 0 ou 06=ξk,j ∈[ξmin, ξmax]. Por conseguinte, segue o resultado.

Lema 11. Suponhamos que as Hipóteses 1, 2 e 3 valem. Então, a sequência_{dk,jx , λk,j+1, z_ℓk,j+1, zuk,j+1}

gerada pelo Algoritmo 1 é limitada.

Demonstração. Pelo Lema 9(II), temos que a sequência {z_ℓk,j+1, zuk,j+1}é limitada. Então, a fim de

construir uma contradição, suponhamos que existe J ⊂

∞

Ntal que

lim

j∈Jk(d k,j

x , λk,j+d k,j

λ )k= +∞, (2.34)

haja visto que, por (2.16b), λk,j+1 _{= λ}k,j _+dk,j

λ . Primeiro, notemos que as Hipóteses 2 e 3 e o

Lema 9(I) implicam que a sequência

{∇ϕµk(x k,j₎

}j∈J ={∇f(xk,j)−µkL†k,je+µkUk,j† e}j∈J

é limitada. Isto, junto com os Lemas 9(II) e 10 acarreta a existência de _{J ⊂}ˆ

∞J tal que

lim

j∈Jˆ∇

ϕµk(x

k,j_{) =∇ϕ} µk(x

k,∗_{), (2.35)}

lim

j∈Jˆ

(z_ℓk,j, zuk,j) = (zk,∗ℓ , z k,∗ u ),

lim

j∈Jˆ

¯

Hk,j= ¯Hk,∗. (2.36)

Podemos reescrever o sistema (2.31) e obter

Mk,j d

k,j x

λk,j_+dk,j λ

!

=₋

∇ϕµk(x k,j₎

0

, (2.37)

sendo que (2.36) implica que

lim

j∈Jˆ

Por (2.35) temos que o lado direito do sistema (2.37) possui limite para j ∈ Jˆ. Além disso, o Passo 2 do Algoritmo 1 garante queMk,j será não singular para todoj. Por conseguinte, de (2.37)

segue que

lim

j∈Jˆ

dk,j

λk,j+dk,j_λ

= lim

j∈Jˆ−

M_k,j−1

∇ϕµk(x k,j₎

0

=₋M_k,∗−1

∇ϕµk(x k,∗₎

0

,

contradizendo (2.34).

Lema 12. Suponhamos que as Hipóteses 1, 2, 3 e 4 valem. Então, a sequência{dk,jx } gerada pelo

Algoritmo 1 tende a zero quando j tende a infinito.

Demonstração. Pelo Lema 11, a sequência_{dk,jx } é limitada, portanto possui alguma subsequência

convergente. Consideremos, por contradição, que existe um conjunto infinito J ⊂

∞Ntal que

lim

j∈Jd k,j

x =dk,∗x 6= 0, (2.38)

Pelo Lema 10, pela Hipótese 3 e pelo Lema 11, existe _{J ⊂}ˆ

∞J tal que

lim

j∈Jˆ

¯

Hk,j= ¯Hk,∗ e lim j∈Jˆ

(xk,j, λk,j, z_ℓk,j, zuk,j) = (xk,∗, λk,∗, zℓk,∗, z k,∗ u ).

Pré-multiplicando o primeiro bloco de equações do sistema (2.31) por dk,jx , que, pelo segundo bloco

de equações do sistema (2.31), pertence ao núcleo da matrizA, vem que

(dk,jx )TH¯k,jdk,jx = −(dk,jx )T∇ϕµk(x k,j₎

≥ σkdk,jx k2, pela Hipótese 4.

Logo, temos que

∇ϕµk(x

k,j₎T_dk,j

x ≤ −σkdk,jx k2. (2.39)

Passando ao limite em (2.39) paraj _∈Jˆ, vem que

∇ϕµk(x

k,∗₎T_dk,∗

x ≤ −σkdk,∗x k2. (2.40)

Pelo Lema 9(I), temos que ℓi +δ ≤xk,ji , para todo i∈ Iℓ e xk,ji ≤ui−δ, para todo i∈ Iu, com

δ >0. Tomando o limite para j_∈Jˆ, temos que ℓi < xik,∗, para todoi∈ Iℓ e xk,∗i < ui, para todo

i∈ Iu. Portanto, existeαˆ ∈(0,1]tal que, para todo α∈(0,αˆ],

ℓi < xk,∗i +α[dk,∗x ]i, para todo i∈ Iℓ exk,∗i +α[dk,∗x ]i < ui, para todo i∈ Iu. (2.41)

Comodk,∗x 6= 0 e (2.40) implica que∇ϕµk(x

k,∗₎T_dk,∗

x <0, então existeα˜ ∈(0,αˆ]tal que para todo

α_∈(0,α˜]vale (2.41) e

ϕµk(x

k,∗_+αdk,∗

x )≤ϕµk(x

k,∗_{) + ¯γα∇ϕ} µk(x

k,∗₎T_dk,∗ x ,

com ¯γ ∈ (γ,1). Notemos que esta é uma condição de decréscimo suficiente, o que assegura a existência deα˜(veja Lema 7), entretanto é uma condição mais rigorosa que a exigida no Passo 6 do Algoritmo 1, já queγ > γ. Como¯ ϕµ(·)é uma função continuamente diferenciável, da interioridade

estrita (2.41) e do fato dedk,∗x ser uma direção de descida a partir dexk,∗, conforme (2.40), definimos

2.4. MODELO ALGORÍTMICO PARA A RESOLUÇÃO DO SUBPROBLEMA 15

tal que

αk,∗

def

= ˜α

1 2

ρ∗

≤αk,j

e

ϕµk(x k,j_+α

k,∗dk,jx )≤ϕµk(x

k,j_{) +γα}

k,∗∇ϕµk(x

k,j₎T_dk,j

x (2.42)

para todo j∈Jˆ,j suficientemente grande. Logo

ϕµk(x

k,j+1_{) ≤ ϕ}

µk(x

k,j_{) +γα}

k,j∇ϕµk(x

k,j₎T_dk,j x

≤ ϕµk(x

k,j_)−γα

k,jσkdk,jx k2, por (2.39)

≤ ϕµk(x

k,j₎₋1

2γαk,jσkdk,∗x k2, por (2.38)

≤ ϕµk(x

k,j₎₋1

2γαk,∗σkd

k,∗

x k2, paraj suficientemente grande,

o que implica que

lim

j∈Jˆ

ϕµk(x

k,j_{) =−∞,}

contradizendo as Hipóteses 2 e 3.

O teorema a seguir estabelece o resultado de convergência global do Algoritmo 1.

Teorema 13. Suponhamos que as Hipóteses 1, 2, 3 e 4 valem. Então, qualquer ponto limite da sequência_{xk,j_+α

k,jdk,jx , λk,j+dk,j_λ , z_ℓk,j+αz_k,jℓ dk,jzℓ , z k,j

u +αz_k,judk,jzu} gerada pelo Algoritmo 1 satisfaz

as condições de otimalidade de primeira ordem (2.8) do subproblema (2.10).

Demonstração. Seja (xk,∗, λk,∗, zk,∗_ℓ , zuk,∗) um ponto limite qualquer da sequência

{xk,j+αk,jdk,jx , λk,j+d k,j λ , z

k,j ℓ +α

zℓ k,jd

k,j zℓ , z

k,j

u +αzk,jud k,j zu},

digamos para a subsequência cujos índices pertencem ao conjunto J ⊂

∞N. Passando ao limite

em (2.31) para j_{∈ J}, pelo Lema 12 vem que

ATλk,∗=_−∇ϕµk(x

k,∗_{) =−∇f(x}k,∗_{) +µ}

kL†_k,∗e−µkU_k,∗† e,

ou seja,

∇f(xk,∗) +ATλk,∗−µkL†_k,∗e+µkU_k,∗† e= 0. (2.43)

O Lema 12 implica que, para j ∈ J suficientemente grande, dk,jx será suficientemente pequena, e,

por isso, as condições (3.17) serão satisfeitas. Por conseguinte,αzℓ k,j =α

zu

k,j = 1e, passando ao limite

em (2.13) para j_{∈ J}, por (2.16) temos que

z_ℓk,∗ =µkL†_k,∗ee zuk,∗=µkU_k,∗† e. (2.44)

Deste modo, (2.43) e (2.44) juntos implicam que

∇f(xk,∗) +ATλk,∗−z_ℓk,∗+zuk,∗ = 0

Lk,∗zℓk,∗−µke = 0

Uk,∗zuk,∗−µke = 0.

(2.45)

2.5

Modelo algorítmico para a resolução do problema

Nesta seção, apresentamos o método para a resolução do problema (2.1).

Algoritmo 2. Método de pontos interiores - Algoritmo externo.

Entrada: x0 _{∈ F}0,λ0 ∈Rm,zℓ0∈Rnezu0∈Rntais que[zℓ0]i>0parai∈ Iℓ e[zu0]i>0parai∈ Iu

eµ0 >0; constantesεtol>0,κε>0,κµ∈(0,1),θµ∈(1,2);k←0.

Passo 1. Encontre uma solução aproximada xk+1 _de

min

x ϕµk(x)

s.a Ax=b

e λk+1_{, z}k+1

ℓ e zuk+1 tais queEµk(x

k+1_{, λ}k+1_{, z}k+1

ℓ , zku+1)≤κεµk. Passo 2. Computeµk+1 = min{κµµk, µ

θµ k }. Passo 3. Faça k←k+ 1e volte ao Passo 1.

2.5.1 Boa definição

Em primeiro lugar, a Hipótese 1 garante que é possível encontrar x0 _{∈ F}0. Deste modo, a boa definição do Algoritmo 2 é condicionada pela execução, bem definida e em tempo finito, do método a ser usado no Passo 1, que é o Algoritmo 1. Como a Proposição 8 estabelece a boa definição do Algoritmo 1, nos resta apresentar o seguinte lema.

Lema 14. Sejam válidas as Hipóteses 1, 2, 3 e 4. Então, para todo k, é possível encontrar

(xk+1_{, λ}k+1_{, z}k+1

ℓ , zuk+1), tal que

Eµk(x

k+1_{, λ}k+1_{, z}k+1

ℓ , z k+1

u )≤κεµk,

em uma quantidade finita de passos do Algoritmo 1.

Demonstração. Primeiro, notemos queµ0 >0e, pelo Passo 2,µk>0para todok. Portanto, temos

queκεµk>0para todok. Não obstante, para cadak, o Teorema 13 implica que, comjtendendo ao

infinito, o Algoritmo 1 é capaz de encontrar(xk,∗, λk,∗, z_ℓk,∗, zuk,∗)tal queEµk(x

k,∗_{, λ}k,∗_{, z}k,∗ ℓ , z

k,∗ u ) = 0

(de acordo com (2.45)). Por conseguinte, para j suficientemente grande, o Algoritmo 1 é capaz de encontrar um ponto (xk,j_{, λ}k,j_{, z}k,j

ℓ , z k,j

u ) tal que Eµk(x

k,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u ) ≤ κεµk. Deste modo, é

possível obter (xk+1_{, λ}k+1_{, z}k+1

ℓ , zku+1) = (xk,j, λk,j, z k,j ℓ , z

k,j

u ) em uma quantidade finita de passos

do Algoritmo 1.

Assim sendo, o Lema 14 implica a boa definição do Algoritmo 2, que é estabelecida a seguir.

2.5. MODELO ALGORÍTMICO PARA A RESOLUÇÃO DO PROBLEMA 17

2.5.2 Análise da convergência global

O seguinte resultado nos dá a convergência global do Algoritmo 2.

Teorema 16. Suponhamos que o Algoritmo 2 gera uma sequência infinita de iterandos e que as Hipóteses 1, 2, 3 e 4 valem para todo µk com as mesmas constantes para os limitantes. Se a

sequência gerada pelo Algoritmo 2 admitir algum ponto limite (x∗_{, λ}∗_{, z}∗

ℓ, zu∗), então

E0(x∗, λ∗, z∗ℓ, zu∗) = 0, (2.46)

com Eµ(x, λ, zℓ, zu) como definido em (2.24).

Demonstração. Seja _{K ⊂}

∞

Num conjunto infinito tal que

lim

k∈K(x

k+1_{, λ}k+1_{, z}k+1

ℓ , z k+1

u ) = (x∗, λ∗, z∗ℓ, zu∗). (2.47)

Suponhamos que (2.46) não vale. Deste modo

k∇f(x∗) +ATλ∗₋z∗_ℓ +z_u∗_k∞ > 0 ou (2.48a)

kL∗Z∗ℓek∞ > 0 ou (2.48b)

kU∗Z∗uek∞ > 0. (2.48c)

Pelo Passo 1 do Algoritmo 2, temos que

Eµk(x

k+1_{, λ}k+1_{, z}k+1

ℓ , z k+1

u )≤κεµk,

para todo k, isto é,

k∇f(xk+1) +ATλk+1−z_ℓk+1+z_uk+1k∞ ≤ κεµk e (2.49a)

kLk+1Zkℓ+1e−µkek∞ ≤ κεµk e (2.49b)

kUk+1Zku+1e−µkek∞ ≤ κεµk, (2.49c)

para todo k. Como K ⊂

∞N, temos, pelo Passo 2 do Algoritmo 2, que

lim

k∈Kµk= 0. (2.50)

De (2.47), (2.48b) e (2.49b), para todo ksuficientemente grande temos que

0<_kLk+1Zkℓ+1ek∞−µk≤κεµk,

ou seja,

0< µk(κε+ 1),

Deste modo, chegamos a um absurdo, já que (2.50) vale. De maneira análoga, de (2.47), (2.48c) e (2.49c) chegamos à mesma contradição. Não obstante, de (2.47), (2.48a) e (2.49a), para todo k suficientemente grande

0<_k∇f(xk+1) +ATλk+1₋z_ℓk+1+zk_u+1_k∞≤κεµk,

isto é,

0< κεµk,

Notemos que o resultado obtido no Teorema 16 implica que, dada qualquer sequência gerada pelo Algoritmo 2, se essa sequência admitir ponto limite, então este ponto limite satisfaz (2.8) para µk = 0. Deste modo, temos que este ponto limite satisfaz (2.3), já que z∗ℓ e zu∗ são não negativos,

pela definição do método, e satisfazem as relações de complementaridade por (2.8c) e (2.8d) com µk= 0. Por conseguinte, temos o seguinte corolário.

Corolário 17. Suponhamos que o Algoritmo 2 gera uma sequência infinita de iterandos e que as Hipóteses 1, 2, 3 e 4 valem para todo µk com as mesmas constantes para os limitantes. Se a

sequência gerada pelo Algoritmo 2 admitir algum ponto limite(x∗_{, λ}∗_{, z}∗

ℓ, z∗u), então este ponto é um

Capítulo 3

Detalhes de implementação

O algoritmo apresentado neste trabalho foi implementado usando Fortran 90 [14, 20], e a esta implementação demos o nome delcmin_{. Neste capítulo, apresentaremos alguns detalhes desta} implementação.

3.1

Critérios de parada

No método apresentado no Algoritmo 2, o objetivo é parar quando um ponto aproxima-damente estacionário para o problema (2.1) for encontrado, isto é, quando um ponto satisfizer aproximadamente as condições KKT (2.3) do problema (2.1). Por outro lado, para cada subpro-blema, paramos quando o resíduo do sistema (2.8) for suficientemente pequeno (veja Passo 1 do Algoritmo 2). A fim de facilitar esta parada e possibilitar aquela, definimos

E_µs(x, λ, zℓ, zu) = max

k∇f(x) +ATλ−zℓ+zuk∞

sd

,kLZ

ℓ_e−µek ∞

sℓ

,kU Z

u_e−µek ∞

su

(3.1)

como sendo o erro escalado do sistema (2.8) (sem considerar a viabilidade (2.8b), já que todo xk satisfaz Axk_{=b), onde}

sd= max

smax,k

λk1+kzℓk1+kzuk1

m+ 2n

/smax

e

sℓ = max

smax,k zℓk1

n

/smax e su = max

smax,k zuk1

n

/smax, (3.2)

de forma que smax ≥1 é uma constante definida (utilizaremos smax = 100), e consideraremos que um ponto(xk, λk, z_ℓk, zuk) é aproximadamente estacionário para o problema (2.1) quando

E₀s(xk, λk, z_ℓk, zk_u)_≤εtol, (3.3)

com εtol >0 (na prática, consideramosεtol = 10−8). Tal critério de parada implica que as equa-ções (2.3a, 2.3g, 2.3h) são aproximadamente satisfeitas (com νℓ = zℓ e νu = zu), enquanto as

equações (2.3b, 2.3c, 2.3d, 2.3e, 2.3f) são satisfeitas pelo ponto inicial e pelos pontos gerados pelo método, já que, para todo k,xk _{satisfaz Ax}k _{=b e [z}k

ℓ]i ≥0, para i∈ Iℓ e [zku]i ≥0, para i∈ Iu.

Logo, as condições de otimalidade (2.3) do problema (2.1) são aproximadamente satisfeitas em

(xk_{, λ}k_{, z}k

ℓ, zuk). Os fatores sd, sℓ e su calculados fazem com que o erro de otimalidade (3.1) seja

controlado quando os multiplicadores λ,zℓ ezu tomarem valores arbitrariamente grandes.

De maneira análoga, para cada subproblema (2.4), consideraremos que (xk,j_{, λ}k,j_{, z}k,j ℓ , z

k,j u )

é um ponto aproximadamente estacionário quando

Eµsk(x

k,j_{, λ}k,j_{, z}k,j ℓ , z

k,j

u )≤κεµk, (3.4)

com κε >0 (na prática, consideramos κε = 10). Assim sendo, este será o critério considerado no

Passo 1 do Algoritmo 2. Notemos que

Es_µ(x, λ, zℓ, zu)≤Eµ(x, λ, zℓ, zu),

com Eµ definido em (2.24). Portanto, ao considerar o critério de parada (3.4) ao invés de (2.23),

estamos potencialmente adiantando a parada no Passo 1 do Algoritmo 2.

A fim de evitar problemas numéricos, a cada subproblema o novo parâmetro barreira é obtido como

µk+1= max

nε_tol

10,min{κµµk, µ

θµ k }

o

, (3.5)

onde κµ ∈(0,1)e θµ ∈ (1,2) como em (2.25) (na prática, κµ= 0.2 e θµ = 1.5). Esta atualização

faz com queµk não assuma valores demasiadamente pequenos, desnecessários para satisfazer (3.3),

evitando problemas numéricos em subproblemas no final do processo de otimização.

Além dos critérios referentes à otimalidade, usamos alguns critérios de salvaguarda. Pri-meiro, declaramos parada quando, no Algoritmo 1,

kxk,j_k∞≥κx,

onde κx é um valor muito grande (na prática, consideramosκx = 1020). A satisfação deste critério

significa que os iterandos estão divergindo, o que indica que a função objetivo do problema pode ser ilimitada.

Por outro lado, paramos sempre que uma quantidade máxima de iterações for excedida. Neste contexto, o processo de otimização é encerrado se

k_≥kmax,

para algumkmax>0 (na prática, consideramos kmax = 50), isto é, caso o Algoritmo 2 exceder um limite de iterações, ou se

j≥jmax e µk=

εtol

10 ,

para algum jmax >0 (na prática, tomamos jmax= 200), ou seja, caso o Algoritmo 1 exceder uma quantidade máxima de iterações e o parâmetro barreira for o menor possível, de acordo com a regra de atualização do mesmo (3.5). Caso a quantidade máxima de iterações do Algoritmo 1 for excedida e o parâmetro barreira não for o menor possível, ele é atualizado de acordo com (3.5) e a resolução de um novo subproblema se inicia.

3.2

Escalamento do problema original

Como a direção de Newton computada em (2.14) é invariante ao escalamento da função objetivo e das restrições, substituiremos f,Aebno problema (2.1) porsff(x),SAAeSAb,

respec-tivamente, com sf >0e SA=diag(sA₁, . . . , sAm).

A estratégia de escalamento que adotamos aqui pressupõe que o problema já possui um bom escalamento e não exigirá modificações, a não ser em casos extremos. Assim sendo, partindo do limiargmax>0 (utilizaremosgmax= 100), definimos

sf = min

1, gmax k∇f(x0_)k

∞

3.3. COMPUTAÇÃO DO PONTO INICIAL 21

onde x0 é o ponto inicial computado usando o método da Seção 3.3, e

sA_i = min

1, gmax kaT

i k∞

, parai= 1, . . . , m,

onde aT

i é ai-ésima linha da matriz A.

Suponhamos que lcmin encontre um ponto aproximadamente estacionário _(x∗_{, λ}∗_{, z}∗

ℓ, zu∗)

para o problema (2.1) escalado. Naturalmente, devemos obter (¯x∗_,λ¯∗_,z¯∗

ℓ,z¯u∗) de (x∗, λ∗, zℓ∗, zu∗) que

seja uma solução para o problema (2.1) original, não escalado. Temos que

E₀s(x∗, λ∗, z∗_ℓ, z_u∗)_≤εtol

com os respectivos valores escalados em (3.1). Assim sendo, temos que

ksf∇f(x∗) +SAATλ∗−zℓ∗+zu∗k∞≤εtol,

ou seja, sf ∇

f(x∗) +AT

1

sf

SAλ∗

−

1

sf

z∗_ℓ

+

1

sf

z∗_u

≤

εtol.

Por conseguinte, se tomarmos

¯

x∗=x∗, λ¯∗ = 1

sf

SAλ∗, z¯ℓ∗=

1

sf

z∗_ℓ e z¯u∗ =

1

sf

zu∗, (3.7)

vem que

k∇f(¯x∗) +ATλ¯∗₋z¯ℓ∗+ ¯zu∗k∞=

1

sfk

sf∇f(x∗) +SAATλ∗−z∗ℓ +zu∗k∞≤

1

sf

εtol.

Assim sendo, definindo (¯x∗,λ¯∗,z¯∗_ℓ,z¯_u∗)de acordo com (3.7), temos que

E₀s(¯x∗,λ¯∗,z¯∗_ℓ,z¯_u∗)_≤ 1

sf

εtol,

isto é, o ponto satisfaz uma tolerância de otimalidade, não escalada, para o problema original. Logo, é importante notar que, ao optar por resolver um problema escalado, com uma cons-tante sf para escalamento da função objetivo, a solução encontrada satisfará a precisão de

oti-malidade em εtol/sf, ou seja, será menos precisa quando sf < 1. Na prática, observa-se que um

algoritmo de otimização, suas estratégias de inicialização e de parada costumam comportar-se de maneira distinta frente a diferentes fatores de escala do problema original, de maneira especial se tais fatores forem extremos, isto é, muito pequenos ou muito grandes. Deste modo, pelo escalamento da função objetivo e das restrições, queremos que o erro de otimalidade que determina quando um determinado ponto é solução do problema, bem como o valor escolhido para a tolerânciaεtol, façam mais sentido numericamente.

3.3

Computação do ponto inicial

É comum que métodos computacionais de otimização iniciem sua execução com uma estima-tiva inicial da soluçãox¯0fornecida pelo usuário. Todavia, métodos de pontos interiores pressupõem iterandos estritamente viáveis, em nosso caso, iterandos que pertençam ao conjunto_F0 6=∅. Neste contexto, não é natural pedir que o próprio usuário forneça um ponto inicial estritamente viável, mas o mais razoável seria calcular um ponto inicial que leve em conta, de alguma forma, a estimativa

¯

3.3.1 Computação do ponto inicial usando programação linear

Esta estratégia consiste em encontrar x0 como solução do seguinte problema:

min

x0 kx

0_−x¯0_k 1 s. a Ax0=b

ℓi+ [δℓ]i ≤x0i ≤ui−[δu]i, parai= 1, . . . , n,

(3.8)

comδℓ, δu ∈Rn+ perturbações para as restrições de caixa. A solução deste problema é um pontox0 tal queAx0 =b, ℓ < x0 < ue que está o mais próximo possível (na norma 1) do ponto x¯0 dado pelo usuário. Se considerarmosr=x0₋x¯0, podemos reescrever (3.8) como

min

r krk1

s. a Ar=b−Ax¯0

ℓi+ [δℓ]i−x¯0i ≤ri≤ui−[δu]i−x¯0i, parai= 1, . . . , n.

(3.9)

Fazendo a mudança de variáveis r =v₋w, com vi ≥0 e wi ≥0 para todo i= 1, . . . , n, é possível

reformular (3.9) como um problema de programação linear

min

v,w

Pn

i=1vi+Pn_i=1wi

s. a A(v₋w) = b₋Ax¯0

ℓi+ [δℓ]i−x¯0i ≤ vi−wi ≤ ui−[δu]i−x¯0i, parai= 1, . . . , n

vi ≥ 0, parai= 1, . . . , n

wi ≥ 0, parai= 1, . . . , n.

(3.10)

Para eliminar do problema restrições do tipoxi ≥ −∞ exi ≤ ∞, consideraremos os conjuntosIℓ e

Iu definidos em (2.2) e reescrevemos (3.10) como

min

v,w

Pn

i=1vi+Pn_i=1wi

s. a A(v₋w) = b₋Ax¯0

vi−wi ≥ ℓi+ [δℓ]i−x¯0i, parai∈ Iℓ

−vi+wi ≥ −ui+ [δu]i+ ¯x0i, parai∈ Iu

vi ≥ 0, parai= 1, . . . , n

wi ≥ 0, parai= 1, . . . , n.

(3.11)

Encontrar uma solução(v∗_{, w}∗_{)para (3.11) equivale encontrar uma solução para (3.8). Desta forma,}

o ponto inicial desejado define-se como x0 = ¯x0+ (v∗−w∗). Assim formulado, o problema (3.8) aproveita, de certa forma, o ponto inicial fornecido pelo usuário. As perturbações δℓ e δu garantem

que x0 _{satisfaça estritamente as restrições de caixa. Para calcular essas perturbações, seguiremos} as sugestões em [25, p. 44], definindo

[δℓ]_i = min{κ1max{1,|ℓi|}, κ2(ui−ℓi)} (3.12a)

[δu]i = min{κ1max{1,|ui|}, κ2(ui−ℓi)}, (3.12b)

parai= 1, . . . , n, comκ1>0eκ2∈(0,1₂). Na implementação, tomaremosκ1 =κ2= 10−2. Assim calculada, temos a garantia que a perturbação aplicada à restrição de caixa inferior não fará com que esta se aproxime demais da superior, e vice-versa.

3.3.2 Computação do ponto inicial resolvendo problemas de viabilidade

Neste caso, computamos o ponto inicialx0 como solução do problema de

min

x kAx−bk

2 2

s. a ℓi+ [δℓ]i ≤xi≤ui−[δu]i, parai= 1, . . . , n,

3.4. ESTIMATIVA INICIAL PARA OS MULTIPLICADORES DE LAGRANGE 23

comδℓ eδu como definidos em (3.12). Para resolver o problema (3.13), usamos o Algencan[1, 2]

com a opção Ignore-objective-function, que faz uso da rotina Gencan [3, 8, 9]. Neste caso, fornecemos como ponto inicial o mesmo dado pelo usuário. Desta forma, o ponto inicial do usuário é aproveitado de certa forma na computação do ponto inicial para o nosso método.

3.4

Estimativa inicial para os multiplicadores de Lagrange

Tendo calculado o ponto inicial conforme a Seção 3.3 e atribuído valores iniciais para zℓ e

zu, é possível estimar os multiplicadores de Lagrange λ das restrições de igualdade

resolvendo-se o sistema linear indeterminado (2.8a) usando quadrados mínimos. Para isto, consideremos c=_∇f(x0_)−z

ℓ+zu, queremos resolver o problema

min

λ∈Rmq(λ) =

1 2kA

T_λ+c

k2, (3.14)

cuja soluçãoλ∗ _{será nossa estimativa inicial para os multiplicadores de Lagrange. O problema (3.14)}

é convexo e sua solução é dada por λ∗ tal que ∇q(λ∗) = 0. Assim sendo, podemos encontrar λ∗ resolvendo-se o seguinte sistema de equações lineares:

A(ATλ+c) = 0. (3.15)

Tomando β =AT_{λ+c, podemos reescrever o sistema (3.15), obtendo}

ATλ−β = −c

Aβ = 0,

ou, matricialmente,

−I AT

A 0

β λ

=₋

c

0

. (3.16)

Notemos que a matriz dos coeficientes do sistema (3.16) é simétrica e esparsa, o que torna o sistema mais barato de ser resolvido e nos permite usar uma rotina apropriada. Após obtida a solução

(β∗, λ∗), β∗ é descartado e caso λ∗ seja muito grande, isto é, se kλ∗k∞ > λmax (utilizaremos λmax = 103 em nossa implementação), descartamos a solução encontrada e tomamos λ= 0 como nossa estimativa inicial. A solução pode assumir valores muito altos se algumas linhas de A forem quase linearmente dependentes. Em [25, p. 44], Wächter e Biegler propõem a inicialização dos multiplicadores associados às restrições de caixa como1. Embora pareça mais natural inicializá-los com os valores definidos em (2.7), os valores propostos podem fazer com que o sistema (3.16) seja numericamente mais estável, e as correções eventualmente aplicadas usando (2.20) e (2.21) fazem com que os valores obtidos durante a otimização permaneçam dentro de um intervalo aceitável.

3.5

Lidando com direções de busca pequenas

Em algumas situações, pode acontecer que a direçãodk,jx encontrada seja muito pequena com

relação ao tamanho dexk,j_{. Isso pode ocorrer quandox}k,j _{está próximo da solução, masλ}k,j_{, z}k,j ℓ e

zuk,j não estão. Nesse caso, em primeiro lugar pode ser que o procedimento debacktracking não seja

bem sucedido. Diante disso, a primeira medida consiste em permitir que αk,j=αmax_k,j sempre que

max

1≤i≤n

(

|(dk,jx )i|

(1 +_|xk,j_{i |})

)

com εmach sendo uma aproximação da precisão da máquina (em nossa implementação, εmach é um valor da ordem de 10−16). No caso disso ocorrer duas vezes consecutivas, o algoritmo considera que o subproblema de barreira foi resolvido e atualiza o parâmetro de barreira como será mostrado adiante. Caso o valor do parâmetro de barreira seja muito pequeno (εtol/10), o algoritmo decreta falha de convergência.

Além disso, pode ser necessário dar passo unitário nas variáveis zℓ e zu quando dk,jx for

suficientemente pequeno (veja a análise de convergência global do método na Seção 2.4.2 adiante). Para que αzℓ

k,j = 1 satisfaça (2.18c), é necessário que

[z_ℓk,j]i+ [dzk,jℓ ]i ≥(1−τ)[z k,j

ℓ ]i, parai∈ Iℓ∩ D k,j

+ .

De (2.13a) vem que

[z_ℓk,j]i−[z_ℓk,j]i+ [µkL†k,je]i−[L † k,jZ

ℓ

k,jdk,jx ]i ≥(1−τ)[z_ℓk,j]i, parai∈ Iℓ∩ D+k,j.

Por conseguinte,

µk−[z_ℓk,j]i[dk,jx ]i ≥(1−τ)[Lk,jz_ℓk,j]i, parai∈ Iℓ∩ D+k,j.

Comoxi ≥ℓi, temos que (1−τ)[Lk,jzk,j_ℓ ]i ≥0, o que implica que quando

[dk,jx ]i≤

µk

[z_ℓk,j]i

, parai∈ Iℓ∩ Dk,j+ ,

a condição de (2.18c) é satisfeita. De maneira semelhante, para que αzu

k,j = 1 satisfaça (2.18d), é

necessário que

[z_uk,j]i+ [dzk,ju]i ≥(1−τ)[z k,j

u ]i, parai∈ Iu∩ Dk,j− .

De (2.13b) vem que

[zuk,j]i−[zuk,j]i+ [µkU_k,j† e]i+ [U_k,j† Zk,ju dk,jx ]i≥(1−τ)[zuk,j]i, parai∈ Iu∩ D−k,j.

Por conseguinte,

µk+ [zk,ju ]i[dk,jx ]i≥(1−τ)[Uk,jzuk,j]i, parai∈ Iu∩ Dk,j₋ .

Comoxi ≤ui, temos que(1−τ)[Uk,jzuk,j]i≥0, o que implica que quando

[dk,jx ]i ≥ −

µk

[zk,ju ]i

, parai∈ Iu∩ D−k,j,

a condição de (2.18d) é satisfeita. Assim sendo, αzℓ _{= α}zu _{= 1} satisfazem as condições de (2.18c)

e (2.18d) sempre que

h

dk,j_x i

i ≤

µk

[z_ℓk,j]i

, para todo i∈ Iℓ∩ Dk,j+ e (3.17a)

h

dk,j_x i

i ≥ −

µk

[zuk,j]i

, para todoi_{∈ I}u∩ Dk,j₋ . (3.17b)

3.6

Correção de inércia

O valor de ξk,j deve ser suficientemente grande para que Mk,j possua a inércia desejada.

3.6. CORREÇÃO DE INÉRCIA 25

que seja o menor possível, para que o erro da solução encontrada de (2.31) com relação à solução de (2.14) não interfira na convergência do algoritmo. Não obstante, há problemas em que a matriz do sistema (2.14) pode ser estruturalmente singular, o que implica correção de inércia em todas as iterações. Deste modo, haverá uma fatoração desnecessária em todas iterações, o que é indesejável. Para evitar este tipo de situação, se em três iterações seguidas tivermos uma perturbação com ξk,j >0, a matriz do sistema (2.14) não será mais fatorada, mas somente a matriz do sistema (2.31)

para algum ξk,j >0. Segue, no Algoritmo 3, o método para encontrar um valor para ξk,j.

Algoritmo 3. Cálculo deξk,j – correção de inércia.

Entrada: Constantes 0< ξmin< ξmax; 0< κ−_ξ <1< κ_ξ+<¯κ+_ξ;ξini >0,ξk,j−1 a correção anterior, paraj >1, ouξ0,−1 = 0, paraj= 0.

Passo 1. ξk,j ←0.

Passo 2. Se a inércia da matriz do sistema (2.14) for(n, m,0), faça ξk+1,−1=ξk,j e pare.

Passo 3. Se ξk,j−1 = 0, então ξk,j ←ξini, senãoξk,j ←max{ξmin, κ−_ξξ_k,j−1}.

Passo 4. Se a inércia da matriz do sistema (2.31) for(n, m,0), faça ξk+1,−1=ξk,j e pare.

Passo 5. Se ξk,j−1 = 0, então ξk,j ←¯κξ+ξk,j, senãoξk,j ←κ+ξξk,j.

Passo 6. Seξk,j> ξmax, entãopare, não foi possível computar um valor paraξk,j. Senão, vá para

o Passo 4.