Fotodissociação no oscilador de Morse forçado

UNIVERSIDADE DE SAO PAULO INSTITUTO DE FisICA DE SAO CARLOS

F O T O D I S S O C I A Q A O N O O S C I L A D O R D E M O R S E F O R Q A D O

USPIIFSC/SBI

1 1 1 1 1 1 1 1 I II

III

I

II1 II1 I

8 -2

- 0 0 1 2 1 5

Fotodissocia<;:ao no Oscilador de Morse for<;:ado jGabriel Amorim Costa.-Sao Carlos, 1997.

<65> p.

~

n = c ; ~

U N IV E R S ID A D E .1 1

Il~

llr~_J--..~

D E S A O P A U L O

l""llllllllllll" I n s t i t u t o d e F i s i c a d e S a o C a r l o s A v. D r. C arlos botelho. 1465

C E P 13560-250 - S ao C arlos - S P B rasil

Fone (016) 274-3444 Fax (016) 272-2218 M E M B R O S D A C O M iS sA o JU LG A D O R A D A D IS S E R T A C A o D E M E S TR A D O D E G A B R I E L A M O R I M C O S T A A P R E S E N TA D A A O IN S TITU TO D E FislC A D E sA o C A R LO S , D A U N IV E R S ID A D E D E sA o P A U LO , E M 29 D E A G O S TO D E 1997.

M J 1 ~ M D l

A os m eus pais,

E s te tr a b a lh o te v e 0 a p o io

A g r a d e c i m e n t o s

Gostaria de agradecer a todos que contribufram para a realizac;;aodeste trabalho. Em especial:

• ao Prof. Hornos, orientador e educador, pela paciencia e confianc;;a no exito do projeto.

• a P. Hammill, R. Fripp, C. Cutler e todos os outros pela ms-pirac;;ao.

• a todos os colegas de nosso grupo de pesquisa e do departamento por toda a ajuda, principalmente a Mauro e Ghandi com a incrlvel rede de computadores.

• aos velhos e bons amigos: Tadeu, Marcelo (Mosca), Leozinho, Ricardo (Nalha) e etc.

R E S U M O

A B S T R A C T

,

C a p i t u l o

1

I N T R O D U Q A O

U rn fe n o m e n o q u e v e m ja d e lo n g a d a ta a tra in d o a a te n < ;a o d e p e sq u isa d o re s d o m u n d o

in te iro e a in te ra < .;a o d a m a te ria c o m u rn c a m p o d e ra d ia < .;a o . E m b o ra fre q iie n te , p o

-d e n -d o in c lu siv e le v a r it fra g m e n ta < .;a o d a m a te ria , e ste fe n o m e n o e sta a in d a lo n g e d e

se r c o m p le ta m e n te c o m p re e n d id o . 0 p re se n te tra b a lh o te rn c o m o a lv o d e e stu d o a

e v o lu < .;a ote m p o ra l d o siste m a q u a n tic o fo rm a d o p o r u rn a m o le c u la d ia to m ic a su je ita a

u rn c a m p o e le tric o e x te rn o e o sc ila t6 rio .

It

sa b id o (e o b se rv a d o e x p e rim e n ta lm e n te ) q u e

a m o le c u la p o d e v ir a se d isso c ia r, d e p e n d e n d o d o s p a ra m e tro s d o c a m p o c o m o a m p

li-tu d e e fre q u € m c ia : e o fe n o m e n o d a f o t o d is s o c ia « ; a o , q u e v e m se n d o e x a u stiv a m e n te

e stu d a d o e m b u sc a d e m a io r c o m p re e n sa o d a s lig a < .;6 e sm o le c u la re s.

In fe liz m e n te , e ste e u rn p ro b le m a d iflc il d e se r tra ta d o p o r d u a s ra z 6 e s p rin c ip a is: 0

e le v a d o n lim e ro d e g ra u s d e lib e rd a d e q u e c a ra c te riz a m e sm o o s m a is sim p le s siste m a s

m o le c u la re s o b stru i u rn a so lu < .;a oa b in itio , e m q u e te ria m q u e se r le v a d a s e m c o n

si-d e ra < .;a o to si-d a s a s p a rtfc u la s e n v o lv id a s (e le tro n s e n u c le o s). A le m d isso , p o r se r u rn

p ro b le m a d e p e n d e n te d o te m p o , su a so lu < .;a oa p re se n ta se v e r a s d ific u ld a d e s. A p e sa r d a

im p o rta n c ia d e ta is p ro b le m a s a in d a sa n ra rfssim o s o s m o d e lo s so lu v e is d e p e n d e n te s d o

te m p o , e n tre o s q u a is p o d e m o s c ita r 0p ro b le m a d a p a rtfc u la liv re su je ita a u rn c a m p o

o sc ila n te . O s p ro b le m a s (c la ssic o s) d e p e n d e n te s d o te m p o te rn sid o m u ito e stu d a d o s,

a ssim c o m o 0 c o m p o rta m e n to c a 6 tic o q u e g e ra lm e n te su rg e n e sse s siste m a s a o v a ria

r-se o s p a ra m e tro s. M e sm o u rn siste m a sim p le s c o m o u rn p e n d u lo c la ssic o a m o rte c id o

su b m e tid o a u rn to rq u e e x te rn o q u e v a ria se n o id a lm e n te n o te m p o a p re se n ta c o m p o

ta m b e m d a n a o -lin e a rid a d e d a e q u a c ;a o d e m o v im e n to . A q u e s ta o d o c a o s e m s is te m a s

q u a n tic o s p e rm a n e c e a in d a s o b in v e s tig a c ;a o .

C o m o a lte rn a tiv a p a ra a s o lu c ;a oa b i n i t i o , e c o m u m 0 e m p re g o d e m o d e lo s q u e d e s

-c re v a m ra z o a v e lm e n te b e m a m o le c u la . E s te tra b a lh o u tiliz a u rn d o s m a is c o n h e c id o s :

o p o te n c ia l d e M o rs e2

, u rn p o te n c ia l u n id im e n s io n a l q u e d e s c re v e s a tis fa to ria m e n te

b e rn , e m te rm o s q u a lita tiv o s , 0 e s p e c tro v ib ra c io n a l d e m o le c u la s d ia to m ic a s . 8 0 lu c ;o e s

p a ra 0 p o te n c ia l n a o -p e rtu rb a d o s a o e x a ta s , a n a litic a s e c o n h e c id a s . P a ra re s o lv e rm o s

o p o te n c ia l p e rtu rb a d o p e lo c a m p o d e p e n d e n te d o te m p o la n c ;a re m o s m a o d e re c m s o s

n u m e ric o s d e re s o lu c ;a o d e e q u a c ;o e s d ife re n c ia is e d e m e to d o s p e rtu rb a tiv o s . O o b je tiv o

e a o b te n c ;a o d a fu n c ;a o d e o n d a d a m o Ie c u la e m v a rio s m o m e n to s , d e m o d o a s e p o d e r

a c o m p a n h a r 0 p ro c e s s o d e d is s o c ia c ;a o .

N o C a p itu lo 2 a p re s e n ta m o s 0 p o te n c ia l d e M o rs e , s u a s c a ra c te ris tic a s e s u a re s o

-lu c ;a o , o b te n d o a s a u to -fu n c ;o e s e a s a u to -e n e rg ia s , a le m d a s o lu c ;a o p a ra 0 o s c ila d o r d e

M o rs e c la s s ic o .

o

C a p itu lo 3 e 0 m a is im p o rta n te d a d is s e rta c ;a o , c o n c e n tra n d o 0 e s tu d o fe ito a

re s p e ito d o o s c ila d o r d e M o rs e fo rc ;a d o . N e le s a o a p re s e n ta d o s a s o lu c ;a o p ro p o s ta p o r

W a lk e r e P re s to n3 (e m te rm o s d a e x p a n s a o s o b re o s e s ta d o s lig a d o s d o p o te n c ia l),

b e m c o m o u rn m e to d o p e rtu rb a tiv o e o s d o is m e to d o s p o r n o s d e s e n v o lv id o s , s e n d o 0

p rim e iro u m a e x p a n s a o s o b re a u to -fu n c ;o e s d o o s c ila d o r h a rm o n ic o e 0 s e g u n d o u m a

e x p a n s a o s e m e lh a n te p o re m e fe tu a d a n a o s o b re 0 p o te n c ia l d e M o rs e fo rc ;a d o , m a s s im

s o b re u rn n o v o p o te n c ia l d e d e p e n d e n c ia te m p o ra l im p lic it a , o b tid o a p a rtir d a s o lu c ;a o

p a ra 0 p ro b le m a d a in te ra c ;a o d e u m a p a rtic u la liv re c o m 0 c a m p o p e rtu rb a tiv o .

o

C a p itu lo 4 e re s e rv a d o a o s re s u lta d o s e d is c u s s a o , s e n d o a p re s e n ta d o s g ra fic o s d e

fu n c ;o e s d e o n d a d is s o c ia n te s o b tid o s p e lo s n o s s o s m e to d o s .

F in a lm e n te , a s c o n d u s o e s s e e n c o n tra m n o C a p itu lo 5 , a p 6 s 0 q u e a d ic io n a m o s u rn

C a p i t u l o

2

o

P O T E N C I A L

D E

M O R S E

o

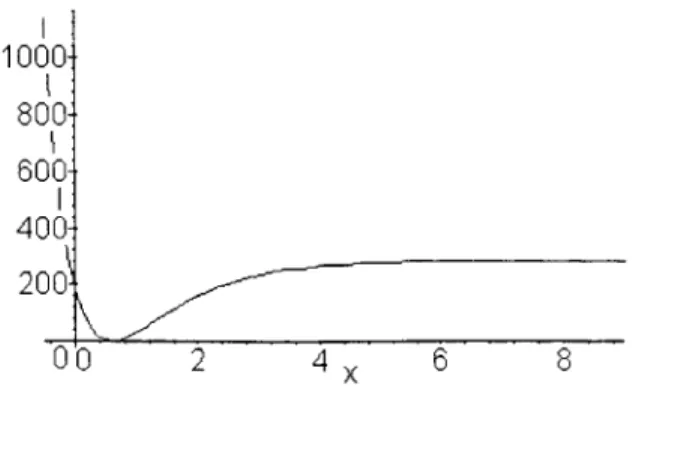
potencial de Morse foi proposto em 1929 pOI Philip MOIse2 _{como urn modelo para} o modo vibracional de moleculas diatomicas. 0 potencial tern a forma

como referencial urn dos atomos que a constitui. Assim sendo, 0 problema passa a ser o de urn corpo (de massa igual a jJ, a mass a reduzida) cuja distancia J ; ao outro varia em torno de x o , a posi<,:aode equilibrio representada pelo ponto de minimo no poten-cial. D = I7 2 /2 e a san os parametros, que devem ser ajustados para cada molecula, sendo que D e a profundidade do po<;o do potencial, ou seja, a energia de dissocia<;ao classic a no modelo. Por causa de seu carater unidimensional, a descri<,:aoque 0

poten-I 1000

\ 800

\

600

I

400

200

cial fornece nao e quantitativa, e sim qualitativa. Nao obstante, ele tern sido empregado por causa de sua praticidade e alto grau de analiticidade: SaDextremamente raros os potenciais quanticos para os quais existem solugaes analiticas e fechadas, como veremos adiante. 0 potencial esta graficado na figura 2.1, ja no sistema de unidades atomicas ( n

=

m

=

a

=

1)que sera empregado no decorrer de todo 0 trabalho (vide Apendice

A). Os parametros us ados na figura 2.1 saD 7]= V568.8, X Q = 0.6 e a = 1.

culares; nem poderia ser, uma vez que estas curvas precisam todas das mesmas ca-racterfsticas, a saber: a tendencia assint6tica para uma constante em grandes \'alores de x , justamente para permitir a dissociagao; a existencia de urn ponto de minimo, a sepa- ragao internuclear de equilibrio; e a existencia de uma acentuada barreira para

x

<

0, caracterizando a repulsao entre os nucleos.

A fim de encontrarmos 0 espectro deste potencial e suas auto-funQaes, de\'emos

resolver a equaQao de Schrodinger independente do tempo,

onde k~=7]2-2En' Aqui x Q foi tornado igual a zero por conveniEmcia,0 que no sistema flsico da molecula diatomica significaria que 0 ponto de repouso da oscilaQao de urn

atomo e exatamente sobre 0outro. Porem em se tratando da resohlQao do problema isso

[

8

2

₈

z 2 ]

Z 2 _

+

z - - -

+

7 1 Z - k2 W = 0

8 z 2 8 z 4 '/ n n ,

onde 0 termo z elevado a kn provem da equagao indicial da serie de Frobenius e a

exponencial e a solugao assint6tica da equagao, quando z tende ao infinito. l\Iediante esta transformagao a equagao se torna

Esta equagao tern a forma da equagao para os polinomios de Laguerre, sendo que para existir uma solugao finita em z ---t 00 devemos impor

E n

=

T J ( n

+

1/2) - 1 / 2 ( n

+

1/2)2, n

=

0, 1 ,2 . . . in t ( T J - 1/2) (2.9)

Note-se que este potencial possui urn numero finito de estados ligados, ao contnirio do que ocorre com os potenciais harmonico e Coulombico. A figura 2.2 mostra 0

I

\

... ... ... /

/

"

/

I

/

!

\ I

\ / \ !

A func;ao de onda para 0 potencial de Morse, ja normalizada

a

unidade, e entao

dada (em unidades atomicas) par

Algumas dessas func;6es (na verdade seus modulos ao quadrado, tambem para 0 HF) estao plotadas nas figuras 2.3 a 2.6.

Vma interessante resoluC;ao do oscilador de Morse quantico, usando um metodo algebrico, foi feita por Berrondo e Palmall

.

Agora mostramos que a soluc;ao classica para uma particula no oscilador de Morse

e

0 logaritmo natural da soluC;aopara a particula no oscilador harmonico.

1.8

1.6

1A 1 .2

\ 1

0.8

0.6

OA

0.2

Figura 2.6: (Jltimo estado ligado ( W 2 3 ) para 0 H F .

x (t)

=

In f(t) ::::;.e -x

=

ftt)'

. ( ) f(t) x t = f(t)

.. ·2

.. .2 ry2

f f - f

=

-(1 -

f).

m

2

[A

+

B C O S (w t

+

c p )] [-B w2

C O S (w t

+

c p )]_ B2

w2

sin2

(w t+ c p ) =

'!L

(1 -

A - B c o s(w t

+

c p ))

m

(2 .2 0 )

c o s(w t

+

c p ) [-A B W2

+

ry :B ] _ w2

B2

- : (1 - A ) =0 , (2 .2 2 )

A

_-

ry2 (2 .2 3 )

mw2

B

2 ry2

(A -

1)

-w2

C a p i t u l o

3

o

O S C I L A D O R

D E

M O R S E

F O R Q A D O

Agora queremos resolver 0 problema dependente do tempo. ou seja. a interaQao da

molecula com urn campo de radiaQao, necessitando para tanto resolver a equaQao de Schrodinger dependente do tempo,

t i2 _{[)2 'T l2} H ( x , t) = --;:) 2

+

_ ( e -2 x

- 2 e -x

+

1)

+

A o x cos(wt),

2 f- L u x 2

onde 0 Ultimo termo representa a contribuiQao do campo de amplitude Ao e frequencia W , e f - L representa a massa reduzida dos dois atomos que constituem a moh?cula. Aqui, portanto, 0 campo e descrito classicamente e 0 momento de dipolo molecular

e

suposto linear.

o

que ocorre com urn auto-est ado de Morse quando perturbado pelo campo? Antes de tentar responder a esta pergunta, analisemos 0 caso (mais simples) do oscilador

(onde foi usada a coordenada adimensional q = ~ w x ), pode ser encontrada em termos dos est ados coerentes de Glauber 8,9. A expressao para a densidade de

probabilidade 1 'lJ ( q , t)12 para qualquer tempo t, sendo w ( q , 0) 0 est ado fundamental do

( )

__

VOl

[sin(2:t) sin(.6.t) sin(2:t) Sin(.6.t)]

q o t -

y2

2:

+

.6.

'

1

2(w+0)

1

- ( w - 0).

2

q o (t) descreve a trajetoria cl<issica do oscilador harmonico for~ado no espaGo de configurac;6es e a densidade de probabilidade na equaGao 3.3 nada mais e do que uma distribuic;;ao Gaussiana em torno deste valor. Temos uma oscila<;;aor<ipida de freqw?ncia L: superimposta a outra de frequencia.6.. Assim, 0 pacote permanece coerente, com in-certeza minima. Nada disso pode, porem, ser garantido para urn osciladar anarmonico como 0 de Morse.

N

'lJ (X , t) =

L ;J n (

t )'lJ

n (

X )

n=O

a:;

= -i;J m E m - iA o c o s(w t)

t

;In (t) ('lJ m lx l'lJ n )

n = O

Este metodo foi pOI nos reproduzido, com os elementos de matriz ('lJ m lx l'lJ n ) cal-culados numericamente pelo metodo de integra<;ao de Gauss, e a propaga<;ao dos co-eficientes feita atraves do metodo Rlmge--Kutta de quart a OIdem7

, implement ado em Fortran. Porem, nao importando os parametros do campo, nao observaremos disso-cia<;ao. De fato, estamos proibidos de observa-la pela propria constru<;ao do metodo, que expande 'lJ na base dos estados ligados do potencial. Dessa forma, a probabilidade de dissocia<;ao e

N

P

=

1 -

L

I( 'lJn I

'lJ)

12

=

0 .

n = O

Logo e esperado que a descri<;ao fornecida pelo metodo W P seja acurada (e 0 e) na regiao de baixas energias, enquanto que no regime de altas energias, proximo ao topo do potencial (justamente a regiao de nosso maiOI interesse), essa descri<;ao deve ser falha.

3 . 2

0

m e t o d a

d a e x p a n s a o h a r m o n i c a ( E H )

Com 0 intuito de resolver 0Oscilador de Morse for<;ado,vamos prop or urn Hamiltoniano

Este Hamiltoniano possui dois panimetros a mais : p e 0 parametro que" liga" ou

"desliga" 0 campo externo; ja )., por sua vez, transforma esse Hamiltoniano em urn de

oscilador harmonico (quando feito igual a zero) ou de oscilador de Morse (quando igual a 1). 0 oscilador harmonico foi aqui introduzido nao apenas por urn carater didatico, mas tambem para servir de teste para 0 program a que efetuara a propagagao temporaL

uma vez que 0 comportamento deste oscilador quando submetido a urn campo externo

oscilat6rio e bem conhecido. Observe-se que foi tornado 0 cuidado de, ao mesclarmos

os dois potenciais, ajustarmos 0 harmonico de forma a que ele se encaixe 0 melhor

possivel no "fosso" do potencial de Morse; isso foi £eito, evidentemente, fazendo 0

"kj2" do primeiro igual ao coeficiente de segunda ordem na expansao em Taylor do segundo.

Para resolvermos portanto a equagao de Schrodinger dependente do tempo (em unidades atomicas) para 0 Hamiltoniano acima, efetuaremos uma expansao da £un<,;ao

de onda na base das auto-fungoes do oscilador harmonico : 00

\lJ (x , t)

=

e -iE o t

2:

a n (t) < Pn (x ) , (3.10)

n = O

onde

~

< P_n (x ) =

e -2 H_n (jiix )

(3.11)

J ~ 2 n n !

e

7] 1

(3.12) E o

= -

--2

8

Aqui Hn sao os polinomios de Hermite e Eo e a energia do est ado fundamental do

oscilador de Morse, de forma que a exponencial na expansao e simplesmente a fase caracterlstica da evolugao temporal desse estado, que e0 estado que iremos pertnrbar

com 0 campo. Poderfamos ter expandido \lJ na base das auto-fungoes de I\Iorse, como ja fizeram Walker e Preston3 , mas essa ideia foi descartada pelos seguintes motivos :

1 - Embora de fato a base das auto-fungoes harmonicas nao seja uma boa base para descrever as fungoes do Oscilador de Morse (e boa, isso sim, para descrever 0 oscilador

2 -

0

fato de propagarmos, atraves da equac;ao de Schrodinger, uma func;ao finita e localizada (que vai a zero no infinito) significa que sempre iremos obter uma func;ao que va a zero no infinito, sendo que uma func;ao dissociante se alastra para x muito grande. Porem tal func;ao sera muito melhor representada por urn conjunto infinito de fun~6es ligadas do que par urn conjunto finito; tambem de nada adiantaria a inclusao de est ados livres do oscilador de Marse pois estes est!ldos oscilam em x infinito e portanto nao sao soluc;6es da equac;ao de Schrodinger: partindo de uma func;ao localizada, normalizada

a

unidade, nunca poderemos, atraves de propagac;ao pela equac;ao de Schrodinger, obter uma func;ao de norma infinita.

3 - Os elementos de matriz a serem calculados possuem forma analitica na base harmonica, ao contrario da de Morse, cujas auto-func;6es sao bem mais complicadas; 0

calculo desses elementos nesta base exige pesadas integrac;6es numericas.

Substituindo a expressao 3.10 para W na equac;ao de Schrodinger , multiplicando

a

esquerda por 1>m( x ) e integrando, teremos (ja lanc;ando mao das condic;6es de ortonar-malidade das func;6es1»

i

[:t

a m - iE o a m ] T /(m

+

1 /2 )a m +

iE o a m - iT /(m

+

1 /2 )a m

+

(3.14)

), { -/~ ~ [ E 2m n - 2 E lm nJ a n

+

ir ~ ~ X 2m n a n - i ~a m }

- iA o c o s (w t)

L

X lm nanP n=O

inc1uir na expansao 3.10, e sua solu<,;ao

e

urn conjunto de coeficientes a , com os qnais se pode construir a func,;aode onda por meio da citada expansao.

00

E 2 m n

=

(< p m le-2 x l< pnJ

=

J

e -r y x2H n (y'iix)H m (yfijx)e-2 X [ 71 I ,] 1/2 d x (3 .1 5 ) 1 r 2n+mn .m .

00

[

71 ] 1/2 e1/ry

J (

1)2

2 n+_m " hi e - z + VTi H n (z )H m (z )

1r . n .m . y71 -00

A liltima integral possui solu<,;aoanalftica exata4

, sendo que a expressao final para E 2m n

e

n-m 1 m-n~! 2

E 2 m n = 2 -2 -e 1 ) 71-2- --I (_ 1 )n -m L r :n -m (_ -).

~ 1 [ 1 ]1 /2 C 2 " '28 X 2 m n _- ~

+

_

----

---

y7r .m .n .

2 "1 4 "1 7 r 2n

₊

m_{n ! m ! (8 - 2 )!(8 - m ) ! ( 8 - n ) ! '}

m + n + 2

8=----2

8

_{m n}

X 2m n ₌

2"1·

A n a lo g a m e n te (e u sa n d o H1(z )= 2 z ) e sc re v e m o s

[

1

]

1 /2 .[ i1 ! m ! n ! 28

X1

m n

=

(1)ml

x

l1>n)

=

---

(

)

7 r 2n

₊

m_{n ! m ! (8 - 1 )!(8 - m ) ! 8 - n !}

m + n +

1

8=----2

T e n d o e n ta o to d o s o s e le m e n to s d e m a triz e m m a o s, p o d e m o s e sc re v e r u rn p ro g ra m a

p a ra a re so lu ~ a o d o siste m a d e e q u a ~ 6 e s 3 .1 4 . E ste p ro g ra m a re so lv e 0 H a m ilto n ia n o

3 .9 , a ju sta v e l p a ra o s o sc ila d o re s h a rm o n ic o e d e M o rse . In ic ia lm e n te ro d a m o s 0 p ro

e sta d o fu n d a m e n ta l p e rm a n e c e u rn p a c o te G a u ssia n o q u a n d o p e rtu rb a d o p e lo c a m p o ,

a p e n a s c o m 0 se u c e n tro c o rre n d o a o lo n g o d a d ire c ;a ox n u m m o v im e n to o sc ila to rio d e

fre q u e n c ia

w).

E m se g u id a ro d a m o s 0p ro g ra m a p a ra A = l, p = O , to m a n d o 0 c u i d a d o d e

u sa r c o m o c o n d ic ;a o in ic ia l o s a lfa s q u e e x p a n d e m 0 e sta d o fu n d a m e n ta l d e M o rse n a

b a se h a rm o n ic a , c o m o se ra e x p lic a d o a d ia n te . P ro p a g a m o s 0 e sta d o e sta c io m irio (se m

o c a m p o e x te rn o ) a te u rn te m p o t, e c h ~ a m o s se 0 p a c o te

(1\l11

2

) p e rm a n e c e im o v e l

e p o r q u a n to te m p o , p a ra sa b e rm o s a p re c isa o d a c o m p u ta c ;a o . F in a lm e n te e n ta o ,

e n tra n d o c o m A e p ig u a is a u rn , p ro p a g a m o s 0 o sc ila d o r d e M o rse fo rc ;a d o .

T e n d o to d o s e sse s te ste s sid o re a liz a d o s, c o n stru im o s u rn p ro g ra m a p a ra re so lv e r

d ire ta m e n te 0 H a m ilto n ia n o 3 .1 , re la tiv o a o o sc ila d o r d e M o rse (le m b ra n d o q u e a in

-c lu sa o d o o sc ila d o r h a rm o n ic o fo i fe ita a p e n a s p a ra te sta r 0 p ro g ra m a ). F a z e n d o a

m e sm a e x p a n sa o n a b a se h a rm o n ic a e su b stitu in d o n a e q u a c ;a o d e S c h ro d in g e r p a ra 0

H a m ilto n ia n o 3 .1 , te re m o s a g o ra 0 se g u in te c o n ju n to d e e q u a c ;6 e s d ife re n c ia is a c o p la d a s

d

d t a m - iE o a m

-2 0 0 0 0 2

-i ~

L

[ E 2 m n - 2 E 1 m nJ a n -

i

L

D 2 m n a n -

i~a m

-n = O n = O

-iA

o s in (w t)

L

X1

m nan

P

n = O

3 .2 .1

O s P r o g r a m a s p a r a

0

_{M e t o d o d a e x p a n s a o h a r m o n i c a}

o

p ro g ra m a M a trix , e sc rito n a lin g u a g e m M a p le , c a lc u la e e sc re v e n u rn a rq u iv o

to d o s o s e le m e n to s d e m a triz a c im a c ita d o s. A d im e n sa o d a m a triz (q u e re p re se n t a

o n u m e ro d e te rm o s n a e x p a n sa o 3 .1 0 e 0 n u m e ro d e e q u a c ;6 e s d ife re n c ia is a se re m

d e v e m o s fo rn e c e r a o p ro g ra m a a in fo rm a c ;a o d e q u e a fu n g a o in ic ia l a s e r p ro p a g a d a

(c o n d ic ;a o in ic ia l) e u rn d o s a u to -e s t a d o s d o p o te n c ia l h a rm o n ic o . Is to e fe ito fa z e n d o

a p e n a s u rn d o s c o e fic ie n te s a lfa in ic ia is , a q u e le c o rre s p o n d e n te a o e s ta d o q u e s e q u e r

p ro p a g a r ig u a l a u n id a d e , e to d o s o s o u tro s ig u a l a z e ro . S e , to d a v ia , d e s e ja rm o s e s tu d a r

o c o m p o rta m e n to d o e s ta d o fu n d a m e n ta l d o o s c ila d o r d e M o rs e

W

o , d e v e m o s fo rn e c e r

a o p ro g ra m a , c o m o c o n d c ;a o in ic ia l, a e x p a n s a o d e s s e e s t a d o n a b a s e h a rm o n ic a , 011

s e ja , o s c o e fic ie n te s in ic ia is a lfa ta l q u e

Is to e fe ito p e lo p ro g ra m a E x p m o r, ta m b e m p a ra M a p le , q u e d ia g o n a liz a a m a triz

s o m a d o s e le m e n to s a c im a c ita d o s (e x c e to X1m n, re la tiv o a o c a m p o e x te rn o ), d e fo rm a

q u e 0 _{a u to -v e t o r a s s o c ia d o a o m e n o r a u to -v a lo r e a e x p a n s a o d o e s ta d o fu n d a m e n ta l}

d e M o rs e n a b a s e h a rm o n ic a . 0 p ro g ra m a e n ta o e s c re v e e s ta e x p a n s a o n o a rq u iv o

E x p m o r.d a t. E s te a rq u iv o , c o m a s c o n d ig o e s in ic ia is p a ra a p ro p a g a g a o , s e ra lid o p e lo

p ro g ra m a M o rs e 1 a , e m F o rtra n , q u e Ie ta m b e m d a d o s c o m o a m p litu d e e fre q u e n c ia

d o c a m p o e x te rn o , 0 te m p o e m q u e s e q u e r a fu n c ;a o d e o n d a fin a l e o s p a n im e tro s

>.

e p d e s c rito s a n te rio rm e n te (q u e d e te rm in a m , re s p e c tiv a m e n te , 0 p o te n c ia l a q u e

e s ta ra s u je ita a fu n c ;a o in ic ia l e a p re s e n c ;a o u n a o d e c a m p o e x te rn o ). N o c a s o d o

p ro g ra m a M o rs e 1 b , 0_{H a m ilto n ia n o re s o lv id o e} 0_{3 .1 , n a o s e n d o n e c e s s a rio} 0_{p a ra m e tro}

>..

0

_{p ro g ra m a M o rs e la (o u M o rs e 1 b ) e n ta o p ro p a g a o s c o e fic ie n te s a lfa n o te m p o d e}

a c o rd o c o m 0 s is te m a 3 .1 4 (o u 3 .2 8 ), s e rv in d o -s e p a ra ta n to d o m e to d o R u n g e -K u tta7

d e q u a rt a o rd e m , n o q u a l fo i fe ito u m a v e to riz a c ;a o p a ra p e rm itir a re s o lu c :a o d e u rn

s is te m a d e q u a n ta s e q u a c ;o e s d ife re n c ia is a c o p la d a s s e q u e ira . F e ito is s o , c a lc u la a

fu n c ;a o d e o n d a a tra v e s d a e x p a n s a o 3 .1 0 e e s c re v e s e u m o d u lo a o q u a d ra d o n o a rq u iv o

P s i.d a t.

E fe tu a n d o a p ro p a g a c ;a o d o e s t a d o fu n d a m e n ta l d e M o rs e n a s m e s m a s c o n d ig o e s

(m e s m o o s c ila d o r d e 1 0 e s ta d o s (7 ]= 9 .6 ) e m e s m o c a m p o ) u tiliz a n d o o s m e to d o s

\i\TP

e

o d a e x p a n s a o h a rm o n ic a o b tiv e m o s o s g ra fic o s m o s tra d o s n a s fig u ra s 3 .1 a 3 .1 0 , q u e

m o s tra m a c o n c o rd a n c ia e n tre o s m e to d o s (e x c e to a s fig u ra s 3 .9 e 3 .1 0 , q u e ja m o s tra m

u m a lig e ira d ife re n g a , p ro v a v e lm e n te d e v id a a s lim ita g o e s d o m e to d o

\i\TP).

P a ra m e tro s

2 1.8 1.6 1.4 1.2

1 \lJ ( x ) 12 1 0.8 0.6 0.4

0.2 0

-3 -2 -1 0 1

x 2 1.8 1.6 1.4 1.2

1 \lJ ( x ) [2 1 0.8

0.6 0.4

0.2 0

-3 -2 -1 0 1

1.8

1.6

1.4

1.2

1

1 \l1 ( x ) 12

0.8

0.6 0.4

0.2

0

-3 -2 -1 0 1

x 1.8 1.6 1.4 1.2 1

1 \l1 ( x ) 12

0.8

0.6 0.4

0.2

0

-3 -2 -1 0 1

1.4

1.2

1

0.8

1 \lJ ( x ) 12 0.6

0.4

0.2

0

-3 -2 -1 0 1

x

0.8

1\lJ(x)1

2

o

1.2

1

0.8

['lJ ( x ) 12 0.6

0.4

0.2

0

-3 -2 -1 0 1

x

1.2

1

0.8

['lJ ( x ) 1

2 _0.6

0.4

0.2

0

-3 -2 -1 0 1

o

-3

o

3 .3

0

m e t o d o p e r t u r b a t i v o

E ste e u rn m e to d o ite ra tiv o m u ito sim p le s p a ra a re so lu < ;a o d o H a m ilto n ia n o 3 .1 , q u e

c o n siste e m su c e ssiv a s a p ro x im a < ;6 e s d a fu n < ;a o d e o n d a .

3 .3 .1

F o r m a l i s m o d e S c h r o d i n g e r

i~ W =_H

w

a t

s

t

w (t) - w (O ) =

_-i

J

_{H s (t')W (t')d t'}

o

B e e sta e x p re ssa o e v a lid a p a ra t, e n ta o ta m b e m 0 e p a ra t ' e a ssim p o r d ia n te , d e

t t t ·

'1 J (t) = _{'1 J (0 ) -}

i

J

_{H s(t')w (O )d t'}

+

_{(_i)2}

J

_{d t'}

J

_{H s(t')H s(tl)w (t" )d t"}

000

t t t·

U s(t) =

1

_-

_i

J

_{H s(t')d t'}

+

_{(_ i)2}

J

_{d t'}

J

_{H s(t')H s(tl)d t"}

₊

o 0 0

t t· t"

(_ i)3

J

d t'

J

d t"

J

H s (t')H s (t")H s(t"')d t'"

+ ...

o 0 0

P o re m , c o m o H s= H o + Hp, o n d e Hp e a p e rtu rb a < ;a o , n o ta m o s q u e p a ra c a lc u la r

to d o s o s te rm o s e m , d ig a m o s, p rim e ira o rd e m e m H_{p ,} te m o s q u e so m a r a se rie in te ira

Para que urn form alism o seja aceitavel ele deve preservar 0espectro dos auto-valores e os

produtos escalares. Essas condic;6es saG autom aticam ente satisfeitas por urn form alism o

cujos estados saG obtidos atraves de um a transform ac;ao unitaria e cujos operadores saG

obtidos atraves de um a transform ac;ao de sim ilaridade. Em particular, 0 form alism o

de Interac;ao sera de grande utilidade :

Com 0 _{intuito de descobrir a equac;ao para W I vam os substituir W}s na equac;ao de

Schrodinger :

m ultiplicando

a

esquerda por eiH o t terem os (lem brando que Ho com uta com esse operador exponencial) :

·2 '3

e iH o tx e -iH o t =x

+

i[ H o t, x ]

+ ;

[ H o t, [ H o t, x ] ]

+ ;

[ H o t, [ H o t, [ H o t, x ] ] ]

+ ...

(3.39)

2. 3.

[ H o t, x ]

[ H o t, - t

:x]

A gora que sabem os calclllar H I podem os im plem entar 0 m etodo pertm bativo no

form alism o de intera<::ao :

t t t ·

1 - _i

J

_{H I ( t') d t'}

+

_{( _ i) 2}

J

_{d t'}

J

_{H I ( t') H I ( t" ) d t"}

₊

o 0 0

t t · t "

( _ i) :l

J

d t'

J

d t"

J

H I ( t') H I ( t" ) H I ( t" ') d t'"

+ ....

o 0 0

A qui

w

1 ( 0 ) = W o . estado fundam ental de ?vIorse. A sorie de figm as 3.11 a 3.13

m ostra a evolu<;ao tem poral de 1 .IJI(t) . Pon?m devem os calcular 1 .IJs(t) (que obcdece it

equagao de Schrodinger) :

Im plem entando este m etodo no program a l\Iaple conseguim os um a fU ll<;aode x ('

t que obedece

a

equa<:ao de Schrodinger pon§m n a o e norm alizada, um a vez que 0

operador unitario de propaga<,;ao foi trnncado. 0 processo de reversao ao form alism o

de Schrodinger 3.43 , no entanto, e bastante pesado para a m aquina, tendo sido ate

agora conseguido apenas 0 que

e

m ostrado na figm a 3.14. Este portanto nao C lU ll

m etodo quantitativo:

e,

isso sim , urn born m etodo qualitativo pelo qual se pode tel'

um a ideia do com portam ento do sistem a.

E

tam bem urn m etodo de fadl m anuseio no

sentido em que ele nos fornece um a fun<,;aoanalitica de x e t, de form a que pode-se

Figura 3.13: A norm a continua aum entando, em vista das truncagens efetuadas no

3 . 3 . 3 0 p r o g r a m a p a r a 0 m e t o d o p e r t u r b a t i v o

o

program a Perturb foi escrito em M aple elida com fun~oes analiticam ente. 0 pro-gram a calcula a transform a~ao de sim ilaridade 3.39 ate terceira ordem , bem com o \{!I

tam bem em terceira ordem de perturba~ao.

3 . 4 0 p o t e n c i a l a l t e r n a t i v o

Prim eiram ente, enfoquem os 0 problem a de um a particula livre sob a a~ao apenas do

cam po externo de radia~ao, problem a este para 0 _{qual vam os procurar um a solll~ao}

analftica.

1

f) 2

H ( x , t) =_--.') 2

+

A o x cos(w t)

2 u x

A equac;ao de Schrodinger dependente do tem po pode ser resolvida encontrando-se

1

_a

2

a

- - a 2 U o ( t, to )

+

A o x c o s ( w t) U o ( t, to ) =i- a U o ( t, to )

2

x t

[

1

a2 b ( t) 2 . a ] a . a

- 2

a x 2

+

-2-

+

z b ( t) a x UO l( t, to ) + A o x c o s ( w t) UO l ( t, to ) =x a t b ( t)

U

Ol( t, to ) + z a t UO l( t, to ) .

(3.48)

a

a t b ( t)

b (t)

A o c o s (w t)

A

o sin(w t) .

w

(3.49)

(3.50)

Fazem os um a segunda transform ac;ao, agora com 0 objetivo de elim inar 0 term o

proporcional a

:x:

U

Ol( t, to )

=

e - i c ( t ) P U 0 2 (t, to )

=

e - c ( t )

tx

U 0 2 (t, to )

Esta transform ac;ao, quando substituida na equac;ao de Schrodinger, result a em

a

a t

c(

t)

c(t)

- b ( t ) =- A

o sin(w t)

w

A o

- 2 ( c o s ( w t) -

1) .

b (t) 2

- 2 - UO :3( t,to )

U m ( t. to )

t '2

a

- i J ~ d t

ia t U_{0 3 ( t, to )} ===? U_{0 3 ( t, to )} =e 0 '2

A2

e ~ iB ( t) , onde B ( t) = -JL,. [ w t - c o s ( w t) sin(w t)]

4 w ')

D essa form a nosso propagador tem poral para 0problem a da part{cula livre sujeita

apenas a u m cam po de radiaQ ao

e

dado por

onde P eo operador m om ento (P=-i

a /a x )

e as funQ oes b(t), B(t) e c(t) saG com o

listadas acim a.

V oltando agora ao O scilador de M orse fon;ado, em preguem os um a nova estrategia

com 0 intuito de resolver a equaQ ao de ondas para 0 H am iltoniano descrito em 3.1.

Essa transform a~ao incorpora na solu<~aodo oscilador de f\Iorse for~ado inform aQ oes

sobre a intera<;ao com 0 cam po de radiaQ ao, e a equaQ ao de Schrodinger, apos a

subs-titui<;ao de 'lJ ( x , t) com o acim a, assum e a form a:

b (

)2

- ic ( t) P

2

_ t_ e - iC ( t) P 'lJ

+

ib ( t) e - ic ( t) P ~'lJ _ e a 'lJ

+

+

1 3

( t) e - iC ( t) P \lJ

+

ie - ic ( t) P ~ \lJ

1

a t

1

C o m o o s e le m e n to s B ( t) , b ( t) e c ( t) fo r a m c o n s tru id o s d e fo rm a q u e 1 3 = b2

/2 ,

c=

- b

e b =Ao / w s in (w t) , o c o rre m c a n c e la m e n to s e 0 _{q u e re s ta e}

1

_{[)2 [)}

--;:) 2\lJ 1 ( x , t)

+

U ( x

+

c ( t) ) \lJ1( x , t) =i~ \lJ l( X ' t) ,

2 u x u t

A q u i fo i u s a d a a a tu a < ,;a o d o o p e ra d o r e - ic ( t) P : e - ic ( t) P F ( x ) =_{F ( x - c ( t) ) (0 o p e ra}

-d o r m o m e n to lin e a r p ro m o v e tra n s la < ,;6 e s n o e s p a < ,;o ,a s s im c o m o 0 m o m e n to a n g u la r

p ro m o v e ro ta < ,;6 e s e o H a m ilto n ia n o p ro m o v e tra n s la < ,;6 e s n o te m p o ).

o

q u e a c a b a m o s d e o b te r e u m a e q u a < ,;a od e S c h ro d in g e r p a ra u rn p o te n c ia l m u ito

s im ila r a o d e M o rs e , p o re m tra n s la d a d o d a q u a n tid a d e c (t).

E

p o rta n to u rn p o te n c ia l q u e " a b s o rv e u " a p e rtu rb a < ,;a o d e v id a a o c a m p o , to rn a n d o -a u m a d e p e n d € m c ia te m p o ra l

im p lfc ita .

A s s im , re s o lv e n d o a e q u a < ,;a o d e S c h ro d in g e r p a ra e s s e p o te n c ia l a lte rn a tiv o (p o r

m e io d a e x p a n s a o e m a u to -fu n < ,;6 e s h a rm o n ic a s ), o b te m o s u rn fu n < ,;a od e o n d a

(\lJ

1

(x,

t))

q u e d e v e s e r tra n s la d a d a : u m a v e z fe ito is s o , 0 s e u m o d u lo a o q u a d ra d o c o rre s p o n d e n i

a o d a fu n < ,;a oq u e e s o lu < ,;a op a ra 0p o te n c ia l a b in itio , c o n fo rm e 3 .6 0 .

3.4.1

0

_{programa para}

0

potencial alternativo

o

p ro g ra m a M o rs e 2 e id e n tic o a o M o rs e l, a s u n ic a s d ife re n < ,;a sc o n s is tin d o n a tro c a d o

te rm o A o x c o s ( w t) p e la s e x p o n e n c ia is d o tip o e -C

e n a tra n s la < ,;a o q u e

e

fe ita n a v a ria v e l

C a p i t u l o

4

R E S U L T A D O S

E

D I S C U S S A O

o

_{m etodo perturbativo aqui apresentado e de facil m anuseio e tern com o vantagem} it

apresentac;ao de um a fun<;,aoanalitica de x e t . Entretanto, com o e apenas m Il m Etodo

qualitativo, nao se pode com pani-lo diretam ente aos dem ais.

Foi observado que nos prim eiros instantes da a<;,aodo cam po, 0estado fundam ental

de M orse se m ove sem m uita perda de coen?ncia, de m aneira sim ilar ao que ocorre no

oscilador harm onico. D ecorrido urn pouco m ais de tem po, porem , a coerEm cia se perde

e 0 pacote com e<;,aa se espalhar, aum entando sua incerteza. Este com portam ento esta

de acordo com 0 observado por W alker-Preston3 e M arquardt-Q uack10.

o

m etodo \V P e sim ples (sua m aior dificulade consiste na obten<.:aodos elem entos de m atriz por integra<.:8.onum erica), relativam ente rapido e fornece excclentes resultados

quando no regim e em que a energia fornecida pelo cam po nao e m uito grande. Porem ,

com o vim os, esse m etodo nao e capaz de descrever 0 fenom eno da fotodissocia<;ao.

o

m etodo num erico da expansao harm onica

e

pesado com putacionalm ente, a llnica

vantagem nesse sentido consist indo na analiticidade dos elem entos de m atriz necessarios

a

propagac;ao. Para verificar seu funcionam ento, este m etodo foi com parado com 0_{\V P,}

tendo sido obtidas func;oes de onda idEm ticas com am bos os m etodos. Este m etodo

diverge m ais rapidam ente do que 0 W P (que, em ultim a am ilise, m m ca diverge), de

form a que propagando urn oscilador de 24 est ados (com o

e

0 _{caso do H F) obtem}

-se func;oes identicas ate 0 ponto em que a norm a das fun<;,oesobtidas por este m etodo

incapaz de descrever a evolu~ao do sistem a corretam ente: tudo 0 _{que dele se obtem}

saG fun~oes "bem com portadas ", enquanto que este m etodo, utilizando 31 fun~oes

harm onicas para expandir a fun~ao de onda, e m elhor sucedido, no sentido em que

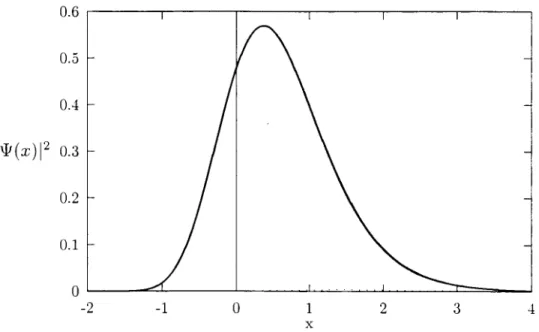
m ostra fun~oes dissociantes _{(figuras 4.1 a 4.5 - A o=21.864,} w = 2 .5 2 2 5 - energia m aior

do que a do po~o de potencial, para garantir a dissocia~ao).

Com a inten~ao de observar m elhor a evolu~ao do processo, foi feita um a m aior

investiga~ao sobre os prim eiros instantes da propagac;ao, com 0 m esm o A o e w = 0.2

, ou seja, energia m enor do que a do poc;o de potencial, constituindo portanto m n

result ado m ais interessante .. A probabilidade de dissociac;ao P foi calculada

(P=l-Po-PI) e pode-se observar que ela cresce com 0tem po, ate atingir a unidade. A s figuras 4.6

a 4.25 saG gnificos do m odulo ao quadrado da fun~ao de onda, bem com o do quadrado

das partes real e im aginaria. A s legendas dessas figuras trazem os valores de Po =

[('11

0

1'11)1

2 e PI =

1('11

1

1'11)1

2, respectivam ente as projec;oes nos estados fundam ental e

excitado.

E

im portante observar que, para tate 0.2 aproxim adam ente, 0 _{m odulo ao}

quadrado da fun~ao de onda perm anece praticam ente im ovel, enquanto que suas partes

real e im aginaria com e~am a adquirir carater oscilante. Essa oscilac;ao e que acarreta

dim inuic;ao no o v e r l a p da func;ao de onda com os auto-est ados do oscilador, significando

que a probabilidade de dissociaC;3,oesta aum entando. N ao obstante, a densidade de

probabilidade de se encontrar a particula perm anece inalterada, ate que a dissocia<:ao

seja com pleta.

D ecorrido urn certo tem po, porem , a oscilac;ao das partes real e im agim iria dim inui,

e a probabilidade de dissocia~ao volta a cair, com o m ostra a figura 4.26, onde estao

graficadas as proje<:oes Po e Pi contra 0 tem po. l'vlais ainda, a figura m ostra um a

oscilac;ao nas projec;oes: 0 pacote volta a se concentrar no estado fundam ental e depois

"liberta-se" novam ente, num a oscilac;ao de proje<:oes cuja frequencia com e~a proxim a

de 1, para em seguida ir aum entando, ate que, por volta de t=7, as proje~oes com e~am a

se m isturar. Este fenom eno ocorre porque 0 cam po, variando com urn co-seno, tern em

t=O am plitude m axim a, ou seja, assim que 0 cam po e ligado ele surge com am plitude

m axim a. A frequencia do cam po usada foi de 0.2, 0 que significa urn per{odo de

211"/0.2 ~ 31.4 : isso quer dizer que, na figura 4.26, 0_{cam po esta sem pre apontando na}

m esm a direc;ao, com a intensidade dim inuindo - a figura nao chega nem a m ostrar m eia

35

0.6

0.5

0.4

['lJ (x )12 _0.3

0.2

0.1

0

-3 -2 -1 0 1 2 3 ;)

x

e urn cam po quase que constante, que foi ligado repentinam ente e retirou 0sistem a do

estado fundam ental ern que se encontrava - sim ilar ao efeito Stark. A ssim , a expressao

para a probabilidade de dissociagao P=1-PO-P1 nao

e

correta, pois nese caso 0 sistem a

nao esta nos est ados 0 e 1, m as tam bem nao esta dissociado: ele esta em algum a especie

prim eiros instantes de tem po, e pode-se observar que este potencial e parecido com um

pogo infinito - 0 pacote oscila com o se estivesse num a caixa infinita. A frequencia da

caixa infinita (estado fundam ental) e W = 1 f 2 f i2 j2 m l2. N as nossas unidades fi = m = 1

e l, a largura da caixa,

e

de cerca de 2 (vide fig. 4.27), 0 que nos da um a frequencia de

oscilagao da ordem de 1 -

e

esta a frequencia de oscilagao das projegoes na fig. 4.26.

E esta frequencia com ega a aum entar com 0 tem po, pois 0 cam po com ee,:a a ter sua

intensidade dim inuida e a barreira em x

>

0 no potencial efetivo com ega a descer (fig.

4.28), perm itindo um a m aior am plitude de oscilagao por parte do pacote.

A penas quando a barreira do potencial efetivo abaixa (a partir de t=7, aproxim

ada-m ente) e que e possivel observar a fungao de onda se libertando e se estendendo para

urn x m aior (figs. 4.29 - 4.33), enquanto que pela prim eira vez a projee,:ao no estado excitado torna-se m aior do que a no fundam ental (fig. 4.26): e 0 inicio do processo de

0.9

0.8

0.7

0.6

1 'lJ (x ) 12 0.5

0.4

0.3

0.2

0.1

0

-3 -2 -1 0 1

x

2.5

2

1.5

1'lJ(x)1

2

1

0.5

0

-3 _-2 -1 0 1 2

0.8

0.7

0.6

0.5

1 \lJ (x ) 12 0.4

0.3

0.2

0.1

0

-3 -2 -1 0 1

x

0.8

0.7

0.6

0.5

1\lJ(x)1

2 0.4 0.3

0.2

0.1

0

0.6

0.5

0.4

1 \lJ (X ) 1

2 _0.3

0.2

0.1

0

-2 -1 0 1 2 3 4

x

Figura 4.6: Este grafico e os seguintes m ostram 0 _{m odulo ao quadrado da fun~ao de}

onda (linha m ais escura), bem com o os quadrados das partes real (linha m ais fraea)

0.6

0.5

0.4

1 \lJ (x ) 12 0.3

0.2

0.1

0

-2 -1 0 1 2 3 4

o

-2

0.6

0.5

0.4

1 \lJ (x )12 _0.3

0.2

0.1

0

-2 - 1 0 1 2 3 4

o

-2

o

o

-2

o

o

-2

o

0.6

0.5

0.4

1 \lJ (x ) 1

2 _0.3

0.2

0.1

0

-2 -1 0 1 2 3

x

o

o

-2

0.6

0.5

0.4

1 1 J !(x )[2 0.3

0.2

0.1

0

-2 -1 0 1 2 3 4

o

-2

0.9

0.8

0.7

0.6

0.5

1 '1 J (x ) 12 0.4

0.3

0.2

0.1

0

-2 -1 0 1 2 3 4

x 0.9 0.8 0.7 0.6 0.5

['1 J (X ) /2

0.4

0.3

0.2

0.1

0

-2 -1 0 1 2 3 4

0.8

0.7

0.6

0.5

1 \lJ (x ) 12 0.4

0.3

0.2

0.1

0

-2 -1 0 1 2

x

0.7

0.6

0.5

0.4

1 \lJ (x ) 12

0.3

0.2

0.1

0

-2 -1 0 1 2 3 ₄

1

P O

-0.9

P1

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

U \,,

-'\

0

"

0

1

2

3

4

5

6

7

8

t

//

/

//

140

120

100

80

60

40

20

1.2

1

0.8

0.6

0.4

0.2

0

-2 -1 0 1 2 3 4 5 6

x

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0

-2 -1 0 2 3 4 5 6

0.5

0.45

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0

-2 -1 0 2 3 4 5 6

x

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0

-2 -1 0 2 3 4 5 6

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

-2

-1

0 1 2 3 4 5 6

x

o

_{m e to d o d a e x p a n s a o h a rm o n ic a p a ra} 0 p o te n c ia l a lte rn a tiv o fo i ta m b e m b e m

-s u c e d id o a o re p ro d u z ir 0 _{c o m p o rta m e n to n o rm a l W P , e ta m b e m a p re s e n to u d is s o}

-c ia -c ,;a o . O b s e rv a n d o o s g n ific o s d o s d o is p o te n c ia is (fig u ra s 4 .3 4 e 4 .3 5 ), e fa c il e n te n d e r

o

C a p i t u l o

5

C O N C L U S O E S

E ste tra b a lh o a p re se n ta m e to d o s d e p ro p a g a < ;a o d e fu n < ;6 e s d e o n d a q u e sa c b e m

-su c e d id o s a o d e sc re v e r a e v o lu < ;a o d o o sc ila d o r d e M o rse fo r< ;a d o , te n d o p o rta n to

c u m p rid o se u o b je tiv o .

M e to d o s p e rtu rb a tiv o s v e m se n d o e x a u stiv a m e n te e m p re g a d o s n o a p rim o ra m e n to

d o c a .lc u lo d e u rn se m n m n e ro d e g ra n d e z a s n a C ie n c ia . N a o o b sta n te , e ste m e to d o n a o

fo i v a n ta jo so n a re so lu < ;a o d e ste p ro b le m a p o is fo i n e c e ssa rio 0 u so d o fo rm a lism o d e

in te ra < ;a o , q u e e m b o ra p e rm it a a p rin d p io 0 c a Ic u lo d a fu n < ;a o d e o n d a tra z ta m b e m

se v e r a s d ific u ld a d e s te c n ic a s.

O s v a rio s m e to d o s q u a n tita tiv o s (W P ,

EH

e

EH

c o m p o te n c ia l a lte rn a tiv o ) fo ra m

c o m p a ra d o s c o m su c e sso n o re g im e d e b a ix a e n e rg ia e m q u e 0 m e to d o

WP

d e sc re v ia

c o rre ta m e n te a e v o lu < ;a o d a fu n < ;a o . F o ra m o b tid a s c o m su c e sso fu n < ;6 e s d e o n d a a tra v e s

d e sse s m e to d o s, a p re c isa o d o c a lc u lo te n d o sid o m o n ito ra d a a tra v e s d a n o rm a d a

fu n < ;a o (u n ita rie d a d e d a p ro p a g a < ;a o ). D e p o sse d a s fu n < ;6 e s d e o n d a fo ra m c a lc u la d a s

a s p ro je < ;6 e s n o s e st a d o s n a o -p e rtu rb a d o s d o o sc ila d o r e e ssa s p ro je < ;6 e s a c o m p a n h a d a s

n o d e c o rre r d o te m p o .

E

c u rio so , n o d e c o rre r d a e v o lu < ;a o ,0 p e rfo d o d e te m p o e m q u e 0 p a c o te d e o n d a

p e rm a n e c e im o v e l e n q u a n to su a s p ro je < ;6 e s n o s e sta d o s lig a d o s d im in u e m . N o e n ta n to ,

e in d isc u tfv e l q u e 0 p a c o te re a lm e n te e sta g a n h a n d o e n e rg ia c in e tic a d o c a m p o n e sse

p e rfo d o , c o isa q u e se n o ta fa c ilm e n te o b se rv a n d o a c re sc e n te o sc ila < ;a o d a s p a rte s re a l

Foi constatado 0 que parece ser urn efeito Stark nos prim eiros instantes ap6s 0

cam po ser ligado: 0 potencial efetivo passa a ser sim ilar a urn poc;o infinito, 0 que

explica as prim eiras oscilac;6es da func;ao de onda (e das projec;6es nos estados

nao-perturbados), com frequEm cia sim ilar

a

do poc;o quadrado infinito. 0 fato deste poc;o

tel' seu m inim o num a regiao

a

esquerda (no eixo x ) do pO Q Odo potencial de M orse

nao-perturbado explica 0_{porque do pacote de onda, em dado m om ento, ser arrastado}

nessa direQ ao.

o

fato de terem sido observados os fenom enos acim a e um a prova definitiva de que os program as propagadores funcionam e represent am corretam ente a f{sica do sistem a.

o

_{que foi observado neste trabalho e 0 in{cio do processo dissociativo. Po rem tudo}

indica que a dissociac;ao com pleta podeni ser observada, bastando prosseguir com a

propagaQ ao para tem pos m aiores.

Com o continuaQ ao deste trabalho pretendem os nao apenas observar a dissociac;ao

com pleta, com o tam bem :

- com parar com algum experim ento: em bora os resultados aqui obtidos sejam

para osciladores de dois estados, nada im pede que caJculos sejam feitos para osciladores

cujos panlm etros "fitam " m oleculas verdadeiras.

- tentar um a soluQ ao exata via potencial alternativo, aproveitando 0 fato de

A p e n d i c e

A

U n i d a d e s

A t o m i c a s

M o stra m o s a q u i a s u n id a d e s a t6 rn ic a s p a ra 0 o sc ila d o r d e M o rse q u e "fita " a m o le c u la

d e

HF,

d a n d o u rn e x e m p lo c o m u rn c a m p o h ip o te tic o .

P a ra m e tro s d e M o rse p a ra 0

HF :

D

T /2 /2 =_{6 .1 2 5 e V}

a - 1 .1 7 4 1 a

o

1

X o - 1 .7 3 3 ao

J-L - M H M F /(M H

+

M F ) = 1 .5 8 9 6 1 0 -2 7K g

Ao 0 .3 e V /a o

fiw - 0 .4 8 6 3 e V

Q u e re m o s u rn siste m a d e u n id a d e s ta l q u e , n e le e x p re sso s,

fi

=J-L = a = 1 .

A ssim , n o ssa u n id a d e d e m a ssa se ra

a = lO ~ 7 ~ 1A n g stro n s-1 . L o g o n o ssa u n id a d e d e c o m p rim e n to se ra

n

=

6.63 1O-34_/27f

₌

_{[E] [T]}

₌

[AWf

J2 _{,que sera feito igual a 1. Entao}

N essas unidades, os param etros do cam po e a profundidade do po<.;ode potencial

no m odelo serao :

0 .3 e V / a =_0.31.60210-19_0.45056 =_11.864

o 3.4510-21 0.529 1.60210-19

6 .1 2 5 [E ] =284.4

1.60210-19

[1] - Kautz, R L - Am erican Journal of Physics 61 (5) , M ay 1993

[2] - M orse, P M - Physical Review 34, 57 (1929)

[3] - W alker and Preston - Journal of Chem ical Physics vol 67, No.5, Sep 1977

[4] - Gradschtein, Handbook of M ath. Functions - p. 837, eq. 7.374-7

[5] - Gradschtein, Handbook of M ath. Functions - p. 838, eq. 7.375-2

[6] - Fetter and W alecka, Quantum Theory of M any-particle System s, p. 116 ex.32

[7] - Abram owitz, M ./Stegun 1. - Handbook of M athem atical Functions, eq. 25.5.10

[9] - Carruthers and Nieto, Am . J. Phys. 33,537 (1965); Carruthers and Dy, Phys.

Rev. 1 4 7 , 214 (1966)

[10]-M arquardt and Quack - Journal of Chem ical Physics vol 90, p 6320 (1989)