Classificação dos RA Loops

(1)

DEPARTAMENTO DE MATEM ´ATICA

CLASSIFICAC

¸ ˜

AO DOS RA LOOPS

Mariana Garabini Cornelissen Hoyos

Orientador: Prof. Dr. Francisco C´esar Polcino Milies

Tese apresentada ao Instituto de Ciˆencias Exatas, da Universidade de Federal de Minas Gerais, como parte dos requisitos para obten¸c˜ao do t´ıtulo de “Doutor em

Matemática - Área de Concentra¸cão: Álgebra”.

(2)

`

(3)

Não poderia deixar de registrar aqui, meus sinceros agradecimentos a todos que contribu´ıram, direta ou indiretamente, para a realiza¸cão dessa tese de doutorado. Como foram cinco anos de trabalho, infelizmente, não vou conseguir me lembrar e nem tão pouco citar nesse peda¸co de papel o nome de todos os envolvidos...

Primeiramente, gostaria de agradecer ao meu marido Miguel, pela paciência, apoio e incentivos constantes durante toda essa jornada. Não posso deixar de agrade-cer também aos meus amados pais, responsáveis por tudo isso, e aos meus irmãos queridos, incluindo o Andrey.

A todos os professores, funcion´arios e colegas do Departamento de Matem´atica da UFMG, com carinho especial ao Prof. Michel Spira.

`

A Pontif´ıcia Universidade Católica de Minas Gerais, pelo apoio financeiro na reta final desse trabalho. Aos professores e funcionários do Departamento de Matemática da Universidade Federal de Vi¸cosa, institui¸cão da qual fui docente durante o segundo ano de realiza¸cão dessa tese, pelo apoio. E também ao CNPq - Conselho Nacional de Pesquisa - pela bolsa recebida no in´ıcio de meu doutoramento.

(4)

Resumo

Nesse trabalho, fizemos uma classifica¸cão completa dos grupos indecompon´ıveis fini-tamente gerados, cujo quociente pelo seu centro é isomorfo ao produto direto de dois grupos c´ıclicos de ordem prima p. Como aplica¸cão desse resultado, no caso p = 2, classificamos os RA loops indecompon´ıveis finitamente gerados, generalizando as-sim, a classifica¸cão feita em 1995, por César Polcino Milies, Eric Jespers e Guilherme Leal, para o caso finito. Ainda nessa tese, provamos uma extensão do Teorema de Perlis Walker: seGé um grupo abeliano finitamente gerado eH é outro grupo qual-quer com lQG≃ lQH então G≃ H. Como consequência desse resultado, estudamos também o problema do isomorfismo para álgebras de RA loops sobre os racionais. Mostramos que se L1 e L2 são RA loops finitamente gerados então lQL1 ≃ lQL2 se, e somente se, L1 / L′1 ≃ L2 / L′2 e ∆(L1, L′1) ≃ ∆(L2, L′2), onde L′i é o subloop de

Li gerado pelo conjunto de todos comutadores e associadores, e ∆(Li, L′i) ´e o n´ucleo

da aplica¸c˜aolQLi →lQ(L_Li′

(5)

In this work, we provide a complete classification of finitely generated indecom-posable groups whose quotient by its center is isomorphic to the direct product of two cyclic groups of prime order p. Applying this result to the case p = 2, we classify all the finitely generated indecomposable RA loops, further generalizing the classification done in 1995, by Eric Jespers, Guilherme Leal and C´esar Polcino Milies for the finite case. Still in this thesis, we prove an extension of the Perlis-Walker Theorem: if G is a finitely generated abelian group and H is another group such that lQG ≃ lQH, then G ≃ H. As a consequence of this result, we also study the isomorphism problem for rational RA loop algebras. We show that, if L1 and L2 are finitely generatedRA loops then lQL1 ≃lQL2, if, and only if, L1 / L′

1 ≃ L2 / L′2 and ∆(L1, L′

1)≃∆(L2, L′2) where L′i is the subloop of Li generated by the set of all

commutators and associators and ∆(Li, L′i) is the kernel of the maplQLi →lQ(L_Li′

(6)

Sum´

ario

Introdu¸c˜ao 2

1 Preliminares 4

1.1 An´eis Alternativos . . . 4

1.2 Loops . . . 8

1.3 Loops de Moufang . . . 10

1.4 Exemplos de Loops de Moufang . . . 11

1.5 An´eis de Loop . . . 13

1.6 RA Loops . . . 15

1.7 Caso Finito . . . 17

2 Classificando Grupos 19 2.1 Teorema da Decomposi¸c˜ao . . . 19

2.2 Teoremas de Classifica¸c˜ao . . . 25

2.3 Classifica¸c˜ao dos Grupos . . . 42

3 Classificando Loops 43 3.1 RA Loops Indecompon´ıveis . . . 43

3.2 Constru¸c˜ao de RA Loops Finitamente Gerados . . . 46

3.3 Teorema de Classifica¸c˜ao . . . 50

3.4 Fam´ılias de Loops N˜ao Isomorfos . . . 54

3.5 Fam´ılias de Loops Indecompon´ıveis . . . 58

4 Sobre Isomorfismos 67 4.1 Caso Finito . . . 67

4.2 Uma extens˜ao do Teorema de Perlis-Walker . . . 69

4.3 Um resultado sobre Isomorfismo . . . 72

Referˆencias Bibliogr´aficas 73

(7)

Se usarmos os elementos de um grupo G como base para um módulo livre sobre um anel R comutativo, associativo e com unidade, e estendermos a opera¸cão de multiplica¸cão deGpara o módulo através das leis distributivas, obteremos um anel associativo, chamado anel de grupo de G sobre R e denotado por RG. Podemos repetir a mesma constru¸cão, come¸cando com um loop L ao invés de um grupo G. A idéia da não exigência da associatividade e da constru¸cão de anéis de loop ou álgebras de loop, foi devida à R. H. Bruck. Em 1944, ele publicou um trabalho mostrando que existe uma versão do Teorema de Maschke num contexto não as-sociativo. Ele mostrou que sobre um corpo de caracter´ıstica 0, ou caracter´ıstica positiva relativamente prima à ordem do grupo multiplicativo de um loop finito 1_, a álgebra de loop é uma soma direta de álgebras simples.

Um pouco antes disso, na década de 30, surgiram dos trabalhos de Ruth Moufang, os anéis alternativos. São anéis não associativos que satisfazem duas identidades im-portantes: a identidade alternativa à direita, (yx)x=yx2_{, e a identidade alternativa} à esquerda,x2_y₌_{x(xy). Os estudos de Moufang estavam voltados para a estrutura} multiplicativa de um anel de divisão alternativo. Assim como os elementos não nulos de um corpo formam um grupo multiplicativo, os elementos não nulos de um anel de divisão alternativo formam um loop de Moufang com a multiplica¸cão.

Nessa tese, estaremos interessados em RA loops, que foram definidos em 1980, por Edgar G. Goodaire, como sendo aqueles loops cuja álgebra de loop sobre qual-quer anel comutativo, associativo, com unidade e caracter´ıstica diferente de 2 é alternativo. A descoberta de que determinada classe de álgebras de loops satisfazia

1_{Mult(L) = grupo multiplicativo de um loop} _L _{= subgrupo do grupo sim´etrico em} _L _gerado

pelas transla¸cões à direita e à esquerda.

(8)

3

importantes identidades, como as identidades alternativas à direita e à esquerda, tornou o estudo dessas álgebras bastante significativo.

Em 1986, Orin Chein e Edgar G. Goodaire deram uma descri¸cão completa dos RA loops. Eles mostraram que todos os RA loops podem ser descritos através de um caso particular de uma constru¸cão conhecida de loops de Moufang. Mostraram também que os RA loops são “quase” grupos (eles possuem um subgrupo normal de ´ındice 2) e são “quase” comutativos (o subloop comutador é de ordem 2).

Todo RA loop é o produto direto de um RA loop indecompon´ıvel por um grupo abeliano. Em 1995, Eric Jespers, Guilherme Leal e C. Polcino Milies, classificaram os RA loops indecompon´ıveis finitos descrevendo assim completamente a classe dos RA loops finitos. Eles mostraram que qualquer RA loop dessa forma pertence a uma de 7 fam´ılias distintas de loops. Nesse trabalho, generalizaremos as idéias desses autores e daremos uma descri¸cão completa dos RA loops indecompon´ıveis finitamente gerados. Mostraremos que existem 16 fam´ılias não isomorfas de tais RA loops.

(9)

Preliminares

O objetivo desse cap´ıtulo é apresentar algumas defini¸cões básicas e também alguns resultados já conhecidos sobre loops, que serão necessários para o entendimento desse trabalho. Todas as demonstra¸cões não apresentadas nesse cap´ıtulo podem ser encontradas em [7].

1.1 An´

eis Alternativos

Um anel (não necessariamente associativo) é uma tripla (R,+,·) onde (R,+) é um grupo abeliano,·é uma opera¸cão binária fechada emRe valem as leis distributivas: a(b+c) = ab+ac e (a+b)c=ac+bc.

Se além disso, (R,+) é um módulo sobre um anelAcomutativo e associativo tal queα(ab) = (αa)b =a(αb),α∈A,a, b∈R, então (R,+,·) diz-se uma álgebra (não necessariamente associativa) sobre A.

Duas importantes fun¸cões na teoria de anéis não associativos são ocomutador e oassociador que são definidas, respectivamente, por:

[a, b] =ab−ba e

[a, b, c] = (ab)c−a(bc).

(10)

CAP´ITULO 1. PRELIMINARES 5

SeX, Y, Z s˜ao subconjuntos de R, denotaremos por XY ={xy|x∈X, y ∈Y}, [X, Y] ={[x, y]|x∈X, y ∈Y} e [X, Y, Z] ={[x, y, z]|x∈X, y ∈Y, z ∈Z}.

Defini¸c˜ao 1.1 Um anel R ´e alternativo se

[x, x, y] = 0, identidade alternativa `a esquerda e

[y, x, x] = 0, identidade alternativa `a direita para todos x, y ∈R.

Qualquer anel associativo é alternativo, mas a rec´ıproca não é verdadeira. O primeiro exemplo de um anel alternativo que não é associativo foi descoberto por J.T.Graves em 1843 e é o anel dos números de Cayley.

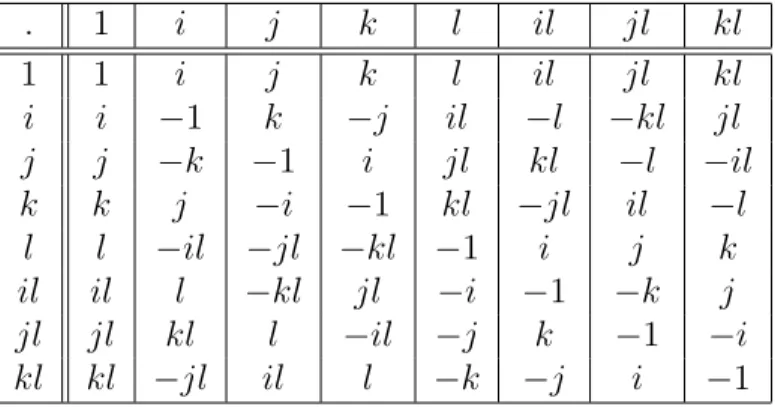
Seja H(IR) = {a+bi+cj+dk | a, b, c, d∈ IR, i, j, k indeterminadas} a álgebra dos quatérnios hamiltonianos, com a soma de dois elementos feita coordenada a coordenada e a multiplica¸cão feita através da distributividade e da tabela abaixo:

· 1 i j k

1 1 i j k

i i −1 k −j j j −k −1 i k k j −i −1

Tabela 1.1: Tabela de multiplica¸c˜ao para 1, i, j, k nos quat´ernios.

O anel dos n´umeros de Cayley ´e o seguinte conjunto:

(11)

onde a soma ´e dada por

(a+bl) + (c+dl) = (a+c) + (c+d)l e a multiplica¸c˜ao ´e da seguinte forma

(a+bl)(c+dl) = (ac−db) + (da¯ +b¯c)l,

onde a, b, c, d s˜ao quat´ernios e se q = a1 + a2i +a3j + a4k ∈ H(IR) definimos ¯

q=a1−a2i−a3j −a4k.

Em particular, temos que

bl·dl =−db¯ a·dl= (da)l bl·c= (b¯c)l.

Esse conjuntoCdos números de Cayley é uma álgebra de divisão não comutativa, alternativa e não associativa, de dimensão 8 sobre IR. Na verdade, IR, lC, H(IR) e C

são as únicas álgebras de divisão alternativas de dimensão finita sobre os números reais ([7], Corolário I.4.13).

Proposi¸c˜ao 1.2 Qualquer anel alternativo tamb´em satisfaz a identidade flex´ıvel [x, y, x] = 0.

Demonstra¸cão: Se trocarmosxporx+zna identidade alternativa à esquerda, e usarmos o fato de que o associador é uma fun¸cão linear de cada um dos seus argumentos, obtemos:

0 = [x+z, x+z, y] = [x, x, y] + [z, x, y] + [x, z, y] + [z, z, y].

Como por hipótese, o anel é alternativo, segue que [x, x, y] = [z, z, y] = 0, o que implica que [x, z, y] =−[z, x, y]. Analogamente, trocando ypor y+z na identidade alternativa à direita, segue que [x, y, z] = −[x, z, y]. Logo, [x, y, z] = [z, x, y]. Em

(12)

O nome alternativo vem do fato de que em um anel alternativo, o associador é uma fun¸cão alternativa, isto é, para qualquer permuta¸cãoσ de 1,2,3, temos que

[aσ(1), aσ(2), aσ(3)] =sgn(σ)[a1, a2, a3],

ondesgn(σ) =

½

1, seσ ´e par;

−1, caso contr´ario.

Teorema 1.3 Em qualquer anel alternativo, as seguintes identidades s˜ao verdadeiras:

1. [x2_{, y, z] =}_{x[x, y, z] + [x, y, z]x} 2. [xy, x, z] = [y, x, z]x

3. [yx, x, , z] =x[y, x, z]

4. ((xy)x)z =x(y(xz)), identidade de Moufang `a esquerda 5. ((xy)z)y=x(y(zy)), identidade de Moufang `a direita 6. (xy)(zx) = (x(yz))x, identidade de Moufang mediana.

O próximo teorema nos dá uma outra caracteriza¸cão para os anéis alternativos.

Teorema 1.4 (Teorema de Artin Generalizado) Se a, b e c são elementos de um anel alternativo que se associam em alguma ordem, então o subanel gerado por a, b, cé associativo.

Como em um anel alternativox2_y ₌_{x(xy) e}_yx2 ₌_{x(xy) são identidades válidas,} segue o resultado abaixo, que é uma consequência direta do teorema anterior e também uma propriedade fundamental dos anéis alternativos:

(13)

1.2 Loops

Defini¸cão 1.6 Um loop é um par (L, .) onde L é um conjunto não vazio, (a, b)7→a·b é uma opera¸cão binária fechada em L que possui um elemento identi-dade bilateral 1 e com a propriedade que dados a, c ∈ L existe um único b ∈ L tal quea·b=ce dados b, c∈L existe um único a∈L tal que a·b=c.

Portanto, um loop é um conjunto com uma opera¸cão não necessariamente asso-ciativa, onde todo elemento tem um inverso à direita e um inverso à esquerda não necessariamente iguais. Claramente, todos os grupos são exemplos de loops. Podemos citar como exemplo de um loop que não é um grupo, o loop de Cayley, denotado porM16(Q8), que é um subconjunto do anel dos números de Cayley,C, definido na se¸cão anterior.

Seja{1, i, j, k, l, il, jl, kl}a base usual dos n´umeros de Cayley. Usando as rela¸c˜oes al·bl=−¯ba

a·bl= (ba)l al·b = (a¯b)l.

para a, b∈ {±1,±i,±j,±k}, obtemos a Tabela 1.2 abaixo:

. 1 i j k l il jl kl

1 1 i j k l il jl kl

i i −1 k −j il −l −kl jl j j −k −1 i jl kl −l −il k k j −i −1 kl −jl il −l

l l −il −jl −kl −1 i j k il il l −kl jl −i −1 −k j jl jl kl l −il −j k −1 −i kl kl −jl il l −k −j i −1

Tabela 1.2: Tabela de Multiplica¸c˜ao para a base dos n´umeros de Cayley

(14)

de um elemento são iguais e a multiplica¸cão é não associativa pois (ik)l=−jl

i(kl) =jl.

Daqui em diante, omitiremos a nota¸cão da opera¸cão binária do loopLe escreve-remos apenas “o loop L” ao invés de “o loop (L,·)”. Também, a partir de agora, escreveremosab ao invés de a.b para denotar o produto dos elementos a e b de um loop. E para expressarmos o produto não necessariamente associativo de mais de dois elementos de um loop, usaremos parênteses e pontos para indicar a ordem da multiplica¸cão; por exemplo, (a.xy)b indicará o produto (a(xy))b.

Defini¸c˜ao 1.7 Sejam a, b e c elementos de um loop L. O comutador de a e b ´e o ´

unico elemento (a, b) de L tal que

ab= (ba)(a, b)

e o associador de a, b e c´e o ´unico elemento (a, b, c) de L tal que (ab)c= (a.bc)(a, b, c).

SeX, Y eZ s˜ao subconjuntos de um loopL, denotaremos por (X, Y) e (X, Y, Z), respectivamente, o conjunto de todos os comutadores da forma (x, y) e todos os associadores da forma (x, y, z) onde x∈X, y ∈Y ez ∈Z.

Um subloopHde um loop Lé um subconjunto deLque com a opera¸cão binária de L é também um loop. Como, para h ∈ H, a equa¸cão hx = h tem uma única solu¸cão emL, segue que os elementos identidade de H e L são iguais.

Defini¸c˜ao 1.8 O subloop comutador-associador de um loop L ´e o subloop

L′ =<(L, L, L),(L, L)>

(15)

1.3 Loops de Moufang

As próximas defini¸cões estão relacionadas com a classe de loops que discutiremos nesse trabalho.

Defini¸c˜ao 1.9 Um loop L tem a propriedade do inverso se todo x ∈ L tem um ´

unico inverso bilateral, que denotaremos por x−1_{, e se, todos} _{x, y} _∈_L _satisfazem

x−1(xy) = y, propriedade do inverso `a esquerda e

(yx)x−1 =y, propriedade do inverso `a direita.

Observe que o loop de Cayley, citado no in´ıcio da se¸c˜ao anterior, ´e um exemplo de um loop que possui a propriedade do inverso.

O resultado abaixo é essencial para a próxima defini¸cão e sua demonstra¸cão pode ser encontrada em [7].

Teorema 1.10 Em qualquer loop as seguintes identidades s˜ao equivalentes:

1. ((xy)x)z =x(y(xz)), identidade de Moufang `a esquerda 2. ((xy)z)y=x(y(zy)), identidade de Moufang `a direita 3. (xy)(zx) = (x(yz))x, identidade de Moufang mediana.

Se L é um loop satisfazendo qualquer uma dessas identidades acima, então L tem a propriedade do inverso e também satisfaz:

(yx)x = yx2, identidade alternativa `a direita x(xy) = x2y, identidade alternativa `a esquerda (xy)x = x(yx), identidade flex´ıvel.

(16)

O nome Moufang ´e em homenagem `a Ruth Moufang, que foi quem introduziu esses loops em um artigo sobre geometria em 1935 ([13]).

Portanto, em um loop de Moufang, todo elemento possui um ´unico inverso bi-lateral e as seguintes identidades s˜ao verdadeiras:

• x−1_{(xy) =} _y

• (yx)x−1 ₌_y

• ((xy)x)z =x(y(xz))

• ((xy)z)y=x(y(zy))

• (xy)(zx) = (x(yz))x

• (yx)x=yx2

• x(xy) = x2_y

• (xy)x=x(yx).

1.4 Exemplos de Loops de Moufang

Como o anel dos números de Cayley,C, definido na primeira se¸cão desse cap´ıtulo, é um anel alternativo, segue pelo Teorema 1.3 que esse anel satisfaz as identidades de Moufang. O loop de Cayley,M16(Q8), é um subconjunto deC e, portanto, M16(Q8) é um loop de Moufang.

Veremos agora outros importantes exemplos de loops de Moufang, que n˜ao s˜ao grupos, com os quais iremos trabalhar.

Sejam G um grupo n˜ao abeliano, go ∈ G um elemento central, g 7→ g∗ uma

involu¸c˜ao (antiautomorfismo de ordem 2) de G tal que go∗ = go e gg∗ pertence ao

(17)

opera¸c˜ao bin´aria deG para L da seguinte forma: g(hu) = (hg)u

(gu)h = (gh∗)u (gu)(hu) = goh∗g

para todog, h∈G. Denotaremos Lpor M(G,∗, go).

Proposi¸cão 1.12 M(G,∗, go) com a opera¸cão definida acima é um loop de

Moufang.

Demonstra¸cão:Claramente a opera¸cão binária definida acima é fechada em L e possui 1G como elemento identidade bilateral.

Dados gu, hu ∈L existe um ´unico elemento x ∈ L tal que gu.x =hu. De fato, basta tomarx= (g−1_h)∗_{. Agora, dados}_{gu, h}_∈_{L, o elemento}_x_{= (hg}

o−1g−1)∗u´e tal

quegu.x=h. Se g, hu∈L então tomando x= (hg−1_)u _{segue que} _g.x₌_{hu. Logo,} mostramos que dadosa, c∈Lexiste um únicob∈Ltal quea.b=c. Analogamente, conseguimos mostrar que dados b, c ∈ L existe um único a ∈ L tal que a.b = c. Portanto L = M(G,∗, go) é um loop. Observe que L não é um grupo, pois, caso

contr´ario, para quaisquer g, h ∈ G ter´ıamos (gh)u = g(hu) = (hg)u, o que implica em gh = hg. Portanto, G seria um grupo abeliano, o que contradiz nossa escolha deG.

Vamos mostrar agora que a identidade 1 do Teorema 1.10 é verdadeira em L. Para tal, calcularemos ambos os lados da referida igualdade e mostraremos que esses lados são iguais. Temos duas possibilidades para cada elemento: x =g ou x=gu, y = h ou y = hu e z = m ou z = mu, o que nos dá um total de 8 possibilidades de identidades que ter´ıamos que mostrar que são verdadeiras. Mostraremos para 3 casos, pois todas as outras são análogas.

Suponhamos primeiramente que x=gu, y =hu e z =mu. Assim,

((gu . hu)gu)mu= (goh∗g . gu)mu= (ggoh∗g)u . mu=gom∗ggoh∗g =go2m∗gh∗g

(18)

Agora, suponhamos x=gu, y =h e z =mu. Ent˜ao,

((gu . h)gu)mu= ((gh∗)u . gu)mu = (gog∗gh∗)u . mu= (mgog∗gh∗)u

gu(h(gu . mu)) =gu(hgom∗g) = g(hgom∗g)∗u= (gg∗mgo∗h∗)u

Como gg∗ _{´e central e} _g

o∗ = go, segue que g comuta com g∗ e, portanto, as duas

equa¸c˜oes acima s˜ao iguais.

Sex=gu, y =h e z =m, temos que:

((gu . h)gu)m = ((gh∗)u . gu)m=gog∗gh∗m

gu(h(gu . m)) =gu(h .(gm∗)u) = gu .(gm∗h)u=go(gm∗h)∗g =goh∗mg∗g.

Lembrando novamente quegg∗ _{´e central em} _{G, obtemos a igualdade.} _¥

Loops de Moufang desse tipo foram descobertos por Orin Chein ([3]). O menor loop de Moufang que não é um grupo é o M(S3,∗,1), onde S3 é o grupo simétrico de ordem 6 e a involu¸cão emS3 dada por g∗ =g−1 para todo g ∈S3 ([2]). Podemos notar que seQ8é o grupo dos quatérnios de ordem 8, então M(Q8,−1,−1) é o loop dos números de Cayley.

1.5 An´

eis de Loop

Defini¸cão 1.13 O anel de loop de L com coeficientes em um anel R, denotado por RL, é o R-módulo livre de base L com multiplica¸cão dada pela extensão da multiplica¸cão de L através das leis distributivas.

Assumiremos que o anel dos coeficientes R tem unidade e identificaremos o elemento 1l deRL com o elementol do loopL. Dessa forma, podemos pensar em L como subconjunto de RL e o elemento identidade de L ´e o elemento identidade desse anel de loop RL.

Os elementos deRL s˜ao da forma RL ={X

l∈L

(19)

com as opera¸c˜oes de soma e multiplica¸c˜ao dadas por

X

l∈L

αll+

X

l∈L

βll =

X

l∈L

(αl+βl)l

(X

l∈L

αll)(

X

l∈L

βll) =

X

l∈L

(X

hk=l

αhβk)l.

O resultado abaixo fornece condi¸c˜oes equivalentes para que o anel de loop de L = M(G,∗, go), o loop de Moufang que constru´ımos na se¸c˜ao anterior, seja um

anel alternativo.

Teorema 1.14 Seja R um anel comutativo, associativo e com unidade e seja L=M(G,∗, go) um loop de Moufang constru´ıdo a partir de um grupo n˜ao abeliano

G, conforme a se¸c˜ao anterior. S˜ao equivalentes:

1. RL satisfaz a identidade alternativa `a esquerda, [x, x, y] = 0. 2. RL satisfaz a identidade alternativa `a direita, [y, x, x] = 0. 3. g+g∗ _{pertence ao} _{Z(RG), o centro de} _{RG, para cada} _g _∈_G.

4. Se car(R) 6= 2, ent˜ao para cada g ∈ G, h−₁

gh ∈ {g, g∗_} _{para todo} _h _∈ _{G; se}

car(R) = 2, ent˜ao, para cada g ∈G, ou g =g∗ _ou _h−1_gh_{∈ {}_{g, g}∗_} _{para todo}

h∈G.

Nessa tese, trabalharemos somente com anéis de loopRL, onde o anel dos coefi-cientesR tem caracter´ıstica diferente de 2. Assim, de acordo com o teorema acima, fixaremos nossa aten¸cão nos grupos G não abelianos que possuem uma involu¸cão g 7→g∗ _{tal que} _h−1_gh_{∈ {}_{g, g}∗_}_{, para todo} _{g, h}_∈_{G. Assim, estaremos encontrando}

condi¸c˜oes suficientes para queRL com L=M(G,∗, go), seja um anel alternativo.

(20)

Observe que essa defini¸cão implica que quadrados são sempre centrais em um loop de Moufang que satisfaz a propriedadeLC. Portanto, os comutadores também são centrais nesses loops, pois (x, y) =x−2_(xy−1₎2_y2_.

Caracterizaremos agora os gruposG, n˜ao abelianos, que possuem uma involu¸c˜ao satisfazendo a alternativa (4) do Teorema 1.14, no caso de caracter´ıstica diferente de 2.

Teorema 1.16 Seja G um grupo não abeliano. As seguintes afirma¸cões são equivalentes:

1. G tem uma involu¸c˜ao g 7→ g∗ _{com a propriedade que} _h−1_gh _{∈ {}_{g, g}∗_} _para

todos g, h∈G.

2. G tem a propriedade LC e um ´unico comutador n˜ao identidade.

3. G/Z(G)≃C2×C2, ondeZ(G) ´e o centro do grupoG eC2 ´e um grupo c´ıclico de ordem 2.

Para tais grupos G, a involu¸c˜ao ´e dada por g∗ ₌

½

g, se g ´e central;

sg, caso contrário. onde s é o único comutador não identidade de G.

Vimos na se¸cão anterior que se G é não abeliano então o loop de Moufang L=M(G,∗, go) é não associativo e portanto,RLé também não associativo. Usando

os Teoremas 1.14 e 1.16 o Corol´ario abaixo ´e imediato.

Corolário 1.17 Seja R um anel comutativo, associativo, com unidade e carac-ter´ıstica diferente de 2. SejaL o loop M(G,∗, go)onde Gé um grupo não abeliano,

g 7→g∗ _{´e uma involu¸c˜ao em}_{G, e} _g

o ´e algum elemento central de G. Ent˜ao o anel de

loopRLé um anel alternativo e não associativo se, e somente se,G/Z(G)≃C2×C2. Nesse caso, a involu¸cão em Gé dada como no Teorema 1.16.

1.6 RA Loops

(21)

Defini¸cão 1.18 Um RA loop é um loop L cujo anel de loop RL sobre um anel R comutativo, associativo, com unidade e caracter´ıstica diferente de 2, é alternativo, mas não associativo.

O nome RA loop deriva das iniciais das palavras em inglˆes Ring Alternative loop.

Como um anel alternativo satisfaz as identidades de Moufang e o anel de loop RL contem o loop L, segue que todo RA loop é um loop de Moufang. Além disso, temos o seguinte resultado que será muito usado posteriormente.

Proposi¸cão 1.19 Se L é um RA loop então

• L′ _=<_{(L, L),}_{(L, L, L)} _{>, o subloop comutador-associador de} _{L, ´e um grupo}

central de ordem 2.

• L tem a propriedade LC.

O ´ultimo resultado dessa se¸c˜ao nos mostra que os loops da forma M(G,∗, go)

introduzidos na Se¸c˜ao 1.4 como exemplos de loops de Moufang, descrevem, na ver-dade, toda a classe de RA loops.

Teorema 1.20 (Descri¸cão de um RA loop) Se L é um RA loop com subloop comutador-associador L′ ₌_{_{1, s}_}_{, então} _L₌_M_(G,_∗_{, g}

o), onde G ´e qualquer grupo

contendo o centro de L e dois elementos n˜ao comutativos de L, go ´e um elemento

central de G e a involu¸c˜ao g 7→g∗ _{´e definida por}

g∗ =

½

g, se g ∈Z(G); sg, se g /∈Z(G).

Reciprocamente, para qualquer grupo n˜ao abeliano G com a propriedade LC, um ´

unico comutador não identidade s, uma involu¸cão ∗, o loop M(G,∗, go) é um RA

loop para qualquer go∈Z(G), onde ∗ ´e dada como acima.

(22)

1.7 Caso Finito

Em 1995, Eric Jespers, Guilherme Leal e C. Polcino Milies classificaram os grupos finitosG tais que G/Z(G)≃C2×C2, onde Z(G) denota o centro do grupoG e C2 ´e um grupo c´ıclico de ordem 2.

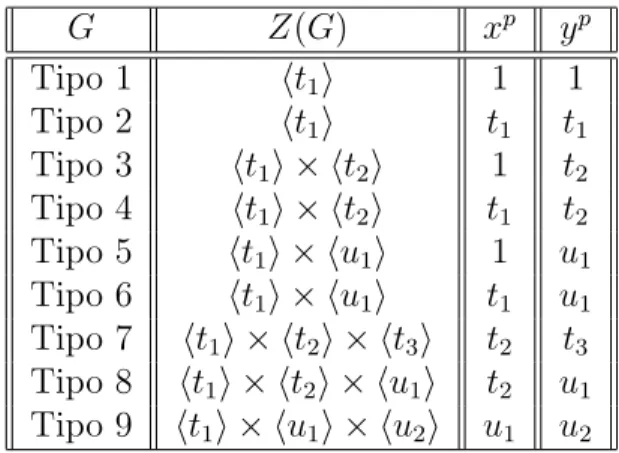
Teorema 1.21 Existem apenas 5 tipos de grupos G finitos e indecompon´ıveis tais queG/Z(G)≃C2×C2, a saber:

1. G1 =< x, y, t1 |x2 =y2 =t12

m₁

= 1> 2. G2 =< x, y, t1 |x2 =y2 =t1, t12

m₁

= 1 > 3. G3 =< x, y, t1, t2 |x2 =t12m1

=t22m2

= 1, y2 =t2 > 4. G4 =< x, y, t1, t2 |x2 =t1, y2 =t2, t12m1

=t22m2

= 1> 5. G5 =< x, y, t1, t2, t3 |x2 ₌_{t2, y}2 ₌_{t3, t1}2m₁

=t22m₂

=t32m₃

= 1> onde s= [x, y] =t12m₁−1

, t1, t2, t3 s˜ao centrais, m1, m2, m3 ≥1.

Como consequˆencia do resultado acima, os autores obtiveram a classifica¸c˜ao dos RA loops indecompon´ıveis finitos.

Teorema 1.22 Qualquer RA loop finito indecompon´ıvel pertence a uma das sete classes listadas abaixo que s˜ao n˜ao isomorfas duas a duas.

1. L1 =< x, y, t1, u|x2 =y2 =u2 =t12

m₁

= 1> 2. L2 =< x, y, t1, u|x2 =y2 =u2 =t1, t12

m₁

= 1 > 3. L3 =< x, y, t1, t2, u|x2 =u2 = 1, y2 =t2, t12

m₁

=t22m₂

= 1 > 4. L4 =< x, y, t1, t2, u|x2 =u2 =t1, y2 =t2, t12

m₁

=t22m₂

= 1> 5. L5 =< x, y, t1, t2, t3, u|x2 =t2, y2 =t3, u2 = 1, t12

m₁

=t22m₂

=t32m₃

= 1> 6. L6 =< x, y, t1, t2, t3, u|x2 =t2, y2 =t3, u2 =t1, t12

m₁

=t22m₂

=t32m₃

(23)

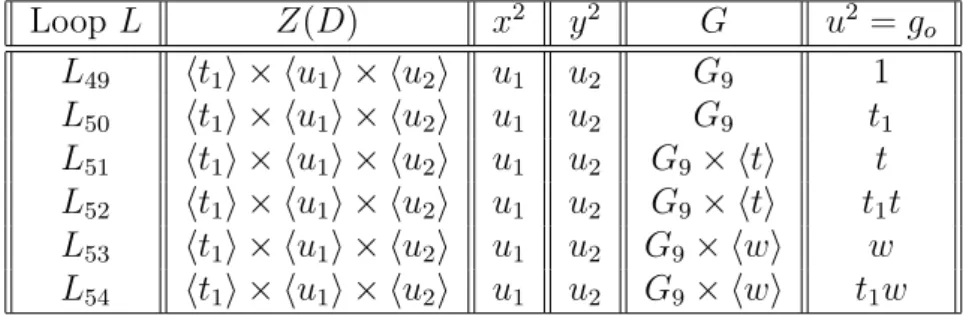
7. L7 =< x, y, t1, t2, t3, u, w | x2 = t2, y2 = t3, u2 = w, w2

r

= 1, t12m₁

= t22m₂

= t32m₃

= 1>

ondet1, t2, t3, w s˜ao centrais e m1, m2, m3, r ≥1.

(24)

Cap´ıtulo 2

Classificando Grupos

Vimos no cap´ıtulo anterior, que para atingirmos nosso objetivo de classificar os RA loops indecompon´ıveis finitamente gerados, é necessário classificar os grupos finitamente gerados cujo quociente pelo seu centro é isomorfo ao produto direto de dois grupos c´ıclicos finitos de ordem dois. Nesse cap´ıtulo faremos uma classifica¸cão um pouco mais geral: vamos descrever todos os grupos finitamente gerados cujo quociente pelo seu centro é isomorfo ao produto direto de dois grupos c´ıclicos de ordemp, onde pé um inteiro primo qualquer.

2.1 Teorema da Decomposi¸c˜

ao

Seja G um grupo finitamente gerado com centro denotado por Z(G). Nessa se¸c˜ao mostraremos que seG/Z(G)≃Cp×Cp, onde Cp denota um grupo c´ıclico de ordem

primap, ent˜aoGse decomp˜oe de uma maneira bem particular. Antes, precisaremos de dois lemas.

Lema 2.1 ([11], Lema 1.1) Seja G um grupo tal que G/Z(G)≃Cp×Cp. Ent˜ao

o subgrupo comutador G′ ₌_h_{[x, y]}_|_{x, y} _∈_G_i _{´e c´ıclico de ordem} _p.

Demonstra¸c˜ao: Considere x, y, z ∈ G. Denotando o comutador de x e y por [x, y] =x−1_y−1_xy _{e a conjuga¸c˜ao por [x, y]}z

=z−1_x−1_y−1_{xyz, ´e f´acil ver que:}

[x, y] = [y, x]−1 (2.1)

(25)

[xy, z] = [x, z]y[y, z] e [x, yz] = [x, z][x, y]z. (2.2) Como, por hip´otese,G/Z(G) ´e abeliano, segue que G′ _⊂_{Z(G) e, nesse caso:}

[xy, z] = [x, z][y, z] e [x, yz] = [x, z][x, y]. (2.3)

Se G/Z(G) ≃ Cp ×Cp ent˜ao existem x, y ∈ G tais que G = hx, y, Z(G)i com

xp_{, y}p _∈ _{Z(G). Portanto,} _G′ ₌ _h_[xn_ym_ai_{, x}r_ys_bj_] _| _{a, b} _∈ _{Z(G), n, m, r, s, i, j} _∈ _IN_i_.

Mas, pela equa¸c˜ao (2.3) acima, segue que [xn_ym_ai_{, z] = [x}n_ym_{, z][a}i_{, z] = [x}n_ym_{, z],}

poisai _∈_Z_{(G). Logo, podemos escrever:}

G′ =h[xn_ym_{, x}r_ys_]_|₀_≤_{n, m, r, s < p}_i

Usando as equa¸c˜oes (2.1) e (2.3) novamente, obtemos:

[xnym, xrys] = [xn, xrys][ym, xrys] = [xn, ys][xn, xr][ym, ys][ym, xr] = [x, y]ns[xn_{, x}r_][ym_{, y}s_{][y, x]}mr

= [x, y]ns[xn, xr][ym, ys][x, y]−mr Agora, [xn_{, x}r_{] = [x, x]}nr

= 1 e [ym_{, y}s_{] = [y, y]}ms

= 1. Ent˜ao, [xn_ym_{, x}s_yr_{] = [x, y]}ns

[x, y]−mr = [x, y]ns−mr o que implica queG′ _{´e c´ıclico, gerado por [x, y].}

E, comoyp _∈_{Z(G), segue que [x, y}p_{] = [x, y]}p

= 1. Assim, |G′ _|₌_p. _¥

Lema 2.2 Seja U um grupo abeliano livre de posto n. Então todo subgrupo V 6= 0 de U também é livre de posto k ≤n. Além disso, existem bases {u1, u2, . . . , un} de

U e {v1, v2, . . . , vk} de V, tais que vi =uǫii para algum inteiro positivo ǫi.

(26)

CAP´ITULO 2. CLASSIFICANDO GRUPOS 21

Teorema 2.3 Um grupo finitamente gerado G ´e tal que G/Z(G) ≃ Cp ×Cp se,

e somente se, G pode ser escrito na forma G = H × K onde K é um grupo abeliano finitamente gerado e H é um grupo não abeliano indecompon´ıvel tal que H = hx, y, Z(H)i, onde Z(H), o centro de H, pode ser escrito como Z(H) = ht1i × hz2i × hz3i, com o(t1) = pm1_, _m1 _≥ ₁ _e _o(z

i) = pmi, mi ≥ 0

ou o(zi) = ∞, i = 2,3, s = [x, y] = x−1y−1xy = tp

m₁−1

1 , xp ∈ ht1i × hz2i, yp _{∈ h}_t1_{i × h}_z2_{i × h}_z3_i_.

Demonstra¸c˜ao: Suponhamos primeiramente que G/Z(G) ≃ Cp×Cp. Logo,

existem elementos x, y ∈ G tais que G = hx, y, Z(G)i, com xp_{, y}p _∈ _{Z(G). Como}

Z(G) é um grupo abeliano finitamente gerado, podemos escreverZ(G) = A×B×F ondeA é um p-grupo, p não divide |B| eF é o produto direto de um número finito de grupos c´ıclicos de ordem infinita.

Podemos assumir que xp_{, y}p _∈ _A _× _F_{. De fato, suponha que} _xp ₌ _hb _com

h ∈ A×F e b ∈ B, bn _{= 1. Como a aplica¸c˜ao} _g _7→ _gp _{´e um automorfismo de} _B,

podemos encontrar um elementoγ ∈B tal que γp ₌_bn−1_{. Fazendo} _x′ ₌_γx _vemos

que x′p

= (γx)p ₌ _γp_xp ₌_bn−1_hb₌ _h _∈_A_×_F_{. Analogamente podemos encontrar} y′ _{tal que} _G₌_h_x′_{, y}′_{, Z(G)}_i _e _x′p

, y′p _∈_A_×_F_.

Assim, supondo G = hx, y, A×Fi ×B, com xp_{, y}p _∈ _A_×_F_{, temos pelo Lema}

2.1 que G′ ₌ _h_s_{i ⊂} _{Z(G) ´e um} _{p-grupo, donde} _s _∈ _{A. Encontraremos agora uma}

decomposi¸c˜ao de A na qual s= [x, y] perten¸ca ao primeiro fator.

Seja A = ht1i × ht2i ×. . .× htki, com o(ti) = pmi, uma decomposi¸c˜ao de A na

quals se escreve como um produto com um n´umero m´ınimo de fatores, digamos s=ta1

1 t

a2

2 . . . t

al

l

com l≤k. Como

1 = sp =tpa1

1 . . . t

pal

l =t pm₁

1 . . . t

pml

l

segue pela escolha da decomposi¸c˜ao queai =pmi−1 e

s =tp₁m1−1. . . tp_lml−1. Suponhal >1 e m1 ≥m2. Ent˜ao,

A=ht1i × ht2i ×. . .× htki=ht1i × ht pm₁−m₂

(27)

com s ∈ htp₁m1−m2t2i × . . .× htki j´a que s = (tp

m₁−m₂

1 t2)p

m₂−1

. . . tp_lml−1. Mas isso contradiz nossa escolha da decomposi¸c˜ao deA. Portanto, l = 1 e s=t₁pm1−1 ∈ ht1i.

Sejaxp ₌_ta1

1 ta22. . . t

ak

k f ondef ∈F. Sepdivide ai entãotaii não é um gerador de

htiidondeti−ai também não é gerador. Logo, podemos substituirxporx′ =xt

−ai p

i de

tal forma quex′p

n˜ao tenha componente emhtii. Repetindo esse processo, podemos

assumir que xp ₌_ta1

1 t

a2

2 . . . tammf onde ht ai

i i=htiie o(t2)≥o(t3)≥. . .≥o(tm).

Sef = 1, ent˜aoxp ₌_ta1

1 ta22. . . tamm e

ht2i × ht3i ×. . .× htmi=hta22i × ht

a3

3 i ×. . .× ht

am

m i=

=hta2

2 t

a3

3 . . . tammi × ht a3

3 i ×. . .× htammi.

Trocando t2 por ta2

2 . . . tamm, obtemos xp ∈ ht1i × ht2i.

Se f 6= 1, xp ₌ _ta1

1 t

a2

2 . . . tammf, denote t a2

2 . . . t

ak

k f por f′. Assim, xp ∈

ht1i × hf′_i_, _h_f′_{i ⊆} _F_{. Pelo Lema 2.2, existe uma base} _{_{u1, u2, . . . , u}

l} para F e

outra base{v1} para hf′_i_{tal que} _v1 ₌_uα

1 para algum α∈IN. Lembre-se que

Z(G) = ht1i × ht2i ×. . .× htki × hu1i × hu2i ×. . .× huli

e reordenando, se necess´ario, podemos escrever

Z(G) = ht1i × hu1i × ht2i ×. . .× htki × hu2i ×. . .× huli

ondexp _{∈ h}_t1_{i × h}_u1_i_, _{o(u1) =}_∞_.

Em ambos os casosxp _{pertence no m´aximo aos primeiros dois fatores}_h_t1_{i × h}_z2_i

deZ(G).

Suponha agora que xp _{∈ h}_t1_{i × h}_t2_i_, _o(t

i) = pmi, i = 1,2. An´alogo ao que

fizemos comxp_{, podemos assumir que} _yp ₌_tb1

1 t

b2

2 t

b3

3 . . . tbnnfy onde todos os tibi’s s˜ao

geradores do subgrupo htii. Reordenando, se necess´ario, podemos tamb´em supor

queo(t3)≥o(t4)≥. . .≥o(tn).

Sefy = 1 ent˜ao yp =tb11t2b2tb33. . . tbnn e

ht3i × ht4i ×. . .× htni=htb33i × ht

b4

(28)

=htb3

3 t

b4

4 . . . tbnni × ht b4

4 i ×. . .× htbnni.

Trocando t3 por tb33t

b4

4 . . . tbnn conclu´ımos queyp ∈ ht1i × ht2i × ht3i.

Mas, se fy 6= 1, denotamos tb33t4b4. . . tbnnfy por fy′; assim, yp ∈

ht1i × ht2i × hf′

yi. Novamente, por 2.2, existe uma base{u1, u2, . . . , ul}paraF e uma

base {v} para hf′

yi tal que v =u β

1 para algumβ ∈IN. Logo, yp ∈ ht1i × ht2i × hu1i e reordenandoZ(G) temos yp _{pertencendo no m´aximo aos trˆes primeiros fatores de}

Z(G).

Agora suponha xp _{∈ h}_t1_{i × h}_u1_i_{, com} _{o(u1) =} _∞_,

Z(G) =ht1i × hu1i × ht2i ×. . .× htki × hu2i ×. . .× huli.

Escrevemos ent˜aoyp ₌_tb1

1 u

β1

1 t

b2

2 . . . tbnnfy ondefy ∈ hu2i × hu3i ×. . .× hulie

reorde-nando, se necess´ario, podemos supor queo(t2)≥o(t3)≥. . .≥o(tn).

Sefy = 1 trocamos o gerador t2 deZ(G) portb₂2. . . tbnn. Como

ht2i ×. . .× htni=ht2b2i ×. . .× htbnni=

=htb2

2 . . . tbnni × ht b3

3 i ×. . .× htbnni

segue queyp _{∈ h}_t1_{i × h}_u1_{i × h}_t2_i_.

Sefy 6= 1, denotamos tb22. . . tbnnly por fy′ onde fy′ ∈F. Escrevemos

f_y′ =uα

1.fy′′

com hf′′

yi ⊆ hu2i × hu3i ×. . .× huli. Logo existe uma base {v2, v3, . . . , vl} para o

grupo livre hu2i ×. . .× huli e uma base {w} para hfy′′i tal que w =v γ

2 para algum γ ∈IN. Portanto, yp _{∈ h}_t1_{i × h}_u1_{i × h}_v2_i_.

Mostramos que em qualquer caso, yp _{∈ h}_t1_{i × h}_z2_{i × h}_z3_i_{. Consequentemente,}

podemos escrever

G=hx, y,ht1i × hz2i × hz3ii ×K

onde K ´e um grupo abeliano finitamente gerado, o(t1) = pm1_, _o(z

i) = pmi ou ∞,

i= 2,3,s = [x, y] =t₁pm1−1, xp _{∈ h}_t

1i × hz2i e yp ∈ ht1i × hz2i × hz3i.

(29)

De acordo com o teorema acima, se G´e um grupo indecompon´ıvel, finitamente gerado comG/Z(G)≃Cp×Cp, ent˜ao G=hx, y, Z(G)i onde

• Z(G) = ht1i × hz2i × hz3i,

• o(t1) = pm1_,_m1 _≥_1,_o(z

i) =pmi,mi ≥0, ou o(zi) = ∞,i= 2,3,

• s = [x, y] =tp₁m1−1,

• xp ₌_tα1

1 z

α2

2 ,αi ≥0,i= 1,2

• yp ₌_tβ1

1 z

β2

2 z

β3

3 , βj ≥0, j = 1,2,3.

Lema 2.4 Usando a nota¸c˜ao acima, podemos supor que os expoentes αi, i= 1,2 e

βj, j = 1,2,3 pertencem a {0,1,2, . . . , p−1}.

Demonstra¸c˜ao: Suponha que wα _{´e um fator de} _xp_,_w_{∈ {}_t

1, z2}.

Seo(w) =pmi ent˜ao troquexporx′ =

(

xwpmip−α, se α´e m´ultiplo de p ;

xwpmi−q_, _se _α₌_pq₊_{r, r} _{∈ {}_1,_{2, . . . , p}₋₁_}_.

Seo(w) = ∞, troque x porx′ ₌

½

xw−pα, se α´e m´ultiplo de p ;

xw−q_, _se _α₌_pq₊_{r, r} _{∈ {}_1,_{2, . . . , p}₋₁_}_.

Note que, em ambos os casos, seα é múltiplo dep então x′p _{não contem}_wα _{e se}

α não é múltiplo de p então x′p _{contem um fator}_wr_{, onde} _α₌_pq₊_r.

Repetindo esse processo tamb´em para os fatores de yp_{, podemos escolher}

ele-mentos x′_{, y}′ _∈_G _{tais que} _α

i, βj ∈ {0,1, . . . , p−1}. ¥

Na próxima se¸cão, faremos uso indiscriminado desse lema inúmeras vezes e também do seguinte lema, cuja demonstra¸cão é imediata por indu¸cão.

Lema 2.5 Sejam x, y dois elementos n˜ao comutativos de um grupo G tais que [x, y]∈Z(G). Ent˜ao

(xa_yb₎m ₌_xma_ymb_sm(m−₂1)ab

(30)

Como caso particular do lema acima, temos que (xy)p ₌_xp_yp_sp(p₂−1)_{. Portanto,}

sep= 2, (xy)2 ₌_x2_y2_s₌_x2_y2_t2m₁−1

1 e se p6= 2 ent˜ao (xy)p =xpyp, pois pelo Lema 2.1, sp _{= 1.}

2.2 Teoremas de Classifica¸c˜

ao

Veremos nesta se¸c˜ao que qualquer grupo indecompon´ıvel finitamente gerado satis-fazendo a propriedade de que G/Z(G) ≃ Cp × Cp, pertence a um de nove tipos

distintos de grupos.

Na se¸cão anterior, mostramos que o posto do centro de tais grupos é no máximo três. Portanto, para descrever tais tipos de grupos, consideraremos separadamente essas três possibilidades para o centro.

Teorema 2.6 Seja G um grupo indecompon´ıvel finitamente gerado e tal que G/Z(G) ≃ Cp ×Cp. Se posto (Z(G)) = 1, ent˜ao G pertence a um dos dois tipos

abaixo:

Tipo 1=hx, y, t1 |xp ₌_yp ₌_tpm₁

1 = 1i Tipo 2=hx, y, t1 |t₁pm1 = 1, xp =yp =t1i

onde, em cada caso, t1 ´e central, m1 ≥1 e s = [x, y] =tp₁m1−1.

Denotaremos por Gi a fam´ılia de todos os grupos do Tipo i, i= 1,2.

Demonstra¸c˜ao: Suponha que G = hx, y, Z(G)i com Z(G) = ht1i e xp_{, y}p _∈

Z(G). Pelo Teorema 2.3 segue que o(t1) = pm1_{. Nesse caso,} _G _{´e finito e podemos}

supor quexp ₌ _t

1a, yp =t1b com a, b ∈ {0,1, . . . , p−1}. Se p = 2, já foi mostrado em [[9], Proposi¸cão 3.2] que G ∈ G1 ou G ∈ G2. Podemos supor, portanto, p 6= 2. Se a = b = 0 então G ∈ G1 e se a = b = 1 segue que G ∈ G2. Se a = 0 e b 6= 0, troque x por x′ ₌ _{xy; assim, (x}′₎p _{= (xy)}p ₌ _xp_yp ₌ _t1b_{. Se} _b _{= 1, temos que}

G ∈ G2 e se b ∈ {2,3, . . . , p−1}, temos um caso particular de xp = t1a, yp = t1b com a, b ∈ {2,3, . . . , p−1}. Nesse ´ultimo caso trocamos x por x′ ₌ _xyn _onde _n _´e

tal que a+nb≡1 (mod p). Dessa forma, podemos supor que (x′₎p ₌_t1 _e _yp ₌_t1b_.

Agora, trocamosy pory′ _{= (x}′₎m_y _onde _m_{´e tal que} _b₊_m_≡_{1 (mod} _{p). Segue que}

G=hx′_{, y}′_{, Z}_(G)_i _{com (x}′₎p _{= (y}′₎p ₌_{t1, o que implica que} _G_{∈ G}

(31)

Observe que a troca de geradores feita acima ´e poss´ıvel pois,

G=hx, y, Z(G)i=hxy, y, Z(G)i=hxy2, y, Z(G)i=. . .=hxyn, y, Z(G)i

=hx′, y, Z(G)i=hx′, x′y, Z(G)i=hx′, x′2y, Z(G)i=. . .=hx, x′my, Z(G)i

ondex′ ₌_xyn_.

Proposi¸cão 2.7 As fam´ılias G1 e G2 do Teorema 2.6 são fam´ılias de grupos in-decompon´ıveis. Além disso, grupos em fam´ılias diferentes não são isomorfos entre si.

Demonstra¸cão: Seja G ∈ G1 ou G2 e suponhamos G decompon´ıvel. Pelo Teorema 2.3 segue queG=H×K, comHum grupo não abeliano, indecompon´ıvel, de centro não trivial eK um grupo abeliano. Logo,Z(G) = Z(H)×K o que implica queK ={1} pois posto (Z(G)) = 1. Portanto, G=H é indecompon´ıvel.

Suponhamos agora G1 = hx, y, t1 | xp ₌ _yp ₌ _t1pm₁

= 1i ∈ G1 e G2 = hx, y, t1 | xp ₌ _yp ₌ _{t1, t1}pm′1

= 1i ∈ G2 com G1 ≃ G2. Como os elemen-tos de G1 ou G2 s˜ao da forma xa_yb_t1c _com _xi _e _yj _{∈ h}_t1_i _para _{i, j} _≥ _{p, segue que}

| G1 |= pm1+2 _e _| _G2 _|₌ _pm′1+2. Mas, como estamos supondo G1 ≃ G2, segue que

m1 =m′1. Agora, note que exp(Z(G1)) =pm1 e exp(Z(G2)) = pm1+1, um absurdo.

Portanto, G1 6≃G2. ¥

Antes de estudarmos as outras duas possibilidades para o posto do centro de G, mostraremos o seguinte lema:

Lema 2.8 Seja G =hx, y, Z(G)i = H×K, onde xp_{, y}p _∈ _Z(G) _e _{H, K} _{s˜ao como}

no Teorema 2.3. Ent˜ao existem y1, y2 ∈ H tais que y1 = yz e y2 = xz′ _onde

z, z′ _∈_Z_(G).

Demonstra¸c˜ao: ComoG/Z(G)≃Cp×Cp e|Cp×Cp |=p2, podemos escrever

Gcomo a uni˜ao disjunta de classes laterais da forma xi_yj_Z_{(G), com 0}_≤_{i, j} _≤_p₋_1.

(32)

Considere ent˜aoxa_yb_z1 _e _xn_ym_z2 _{pertencentes a} _H _onde _{z1, z2} _∈_Z(G).

(xaybz1).(xnymz2) = xa+nyb+mz1z2sbn (xnymz1).(xaybz2) = xn+aym+bz1z2sam.

Como esses dois elementos n˜ao comutam, segue que am−bn 6≡ 0 (mod p). Portanto, o sistema linear abaixo tem solu¸c˜ao:

½

aα+nβ ≡0 (mod p) bα+mβ ≡1 (mod p). Logo existem α, β ∈IN tais que

y1 = (xaybz1)α.(xnymz2)β =yz ondez ∈Z(G). (Lembre-se de que s, xp _e_yp _{s˜ao centrais!)}

Analogamente, existem α′, β′ ∈IN tais que

y2 = (xa_yb_z1)α′

.(xn_ym_z2)β′ =xz′

ondez′ _∈_Z(G). _¥

Agora sim, veremos primeiro o que acontece quando o posto do centro de G ´e igual a 2.

Teorema 2.9 Seja G um grupo indecompon´ıvel, finitamente gerado e tal que G/Z(G) ≃ Cp ×Cp. Se posto (Z(G)) = 2, ent˜ao G pertence a um dos quatro

tipos abaixo:

Tipo 3=hx, y, t1, t2 |tp₁m1 =tp₂m2 = 1, xp _{= 1, y}p ₌_t2_i

Tipo 4=hx, y, t1, t2 |tp₁m1 =t₂pm2 = 1, xp =t1, yp =t2i

Tipo 5=hx, y, t1, u1 |t₁pm1 = 1, xp = 1, yp =u1i

Tipo 6=hx, y, t1, u1 |t₁pm1 = 1, xp =t1, yp =u1i

(33)

Demonstra¸c˜ao: Suponhamos que G =hx, y, Z(G)i com Z(G) =ht1i × hz2i e xp_{, y}p _∈_{Z(G). Pelo Teorema 2.3, segue que}_{o(t1) =}_pm1 _e_{o(z2) =}_pm2 _ou_{o(z2) =} _∞_.

Seja ¯G=G /hz2i=hx,¯ y,¯ t¯1i onde ¯xp,y¯p ∈ ht¯1i=Z( ¯G). Como ¯G ´e indecompon´ıvel (pois seu centro o ´e), usando o Teorema 2.6 temos

(1) ¯xp = ¯yp = ¯1 ou (2) ¯xp = ¯yp = ¯t1.

Se ¯xp _{= ¯}_yp _{= ¯1 temos quatro possibilidades para} _xp _e_yp_:

(1.1) xp ₌_yp _{= 1}

(1.2) xp _{= 1, y}p ₌_z2a

(1.3) xp ₌_z2a_{, y}p _{= 1}

(1.4) xp ₌_z

2a, yp =z2b

onde, pelo Lema 2.4, podemos supor a, b ∈ {1,2, . . . , p −1}. Daqui em diante, faremos uso in´umeras vezes desse lema, sem fazer referˆencia ao mesmo.

No primeiro caso,Gé o produto diretohx, y, t1i×hz2i, que não é indecompon´ıvel. Se z2 = t2, com o(t2) = pm2, podemos supor p 6= 2, já que no caso p = 2, foi demonstrado em [[9], Proposi¸cão 3.3] queG∈ G3ouG∈ G4. No caso (1.2), podemos trocart2 por t′

2 =t2a poisht2i=ht2ai; assimG∈ G3. O terceiro caso é simétrico ao anterior, trocando x por y. Já no último caso, troque x por x′ ₌_xn_y _onde _n _{é tal}

que an+b ≡ 0 (mod p). Podemos assumir portanto que x′p _{= 1 e} _yp ₌ _t2b_{. Mas}

Z(G) =ht1i × ht2i =ht1i × ht2b_i_{, pois} _b _{∈ {}_1,_{2, . . . , p}₋₁_}_{. Trocando ent˜ao} _t2 _por

t2b _{obtemos que} _G_{∈ G}

3.

Suponhamos agoraz2 =u1 com o(u1) =∞. No caso (1.2), se p= 2 ent˜ao a= 1 donde G ∈ G5 e se p 6= 2, podemos supor que a ∈ {2,3, . . . , p−1}, pois, quando a = 1 temos G ∈ G5. Trocando y por y′ ₌ _yb _onde _b _{´e tal que} _ab _≡ _{1 (mod} _p)

podemos assumir que xp _{= 1 e}_y′p ₌_{u1, o que implica que} _G_{∈ G}_{5. O terceiro caso}

é simétrico ao (1.2) e no último caso, se p= 2 então x2 ₌_y2 ₌_{u1. Trocando} _y _por y′ ₌_{xy, podemos supor} _y′2 ₌_x2_y2_s ₌_t2m₁−1

(34)

x′ ₌_xyn _onde _n _{´e tal que} _a₊_nb _≡_{0 (mod} _{p). Dessa forma, existe} _x′′ _∈_G _{tal que}

G=hx′′_{, y, Z(G)}_i_{com (x}′′₎p _{= 1 e} _yp ₌_u1b_{, que pelo caso (1.2) implica que}_G_{∈ G}_5.

Se ¯xp _{= ¯}_yp _{= ¯}_{t1, ent˜ao temos tamb´em quatro possibilidades para} _xp _and _yp_:

(2.1) xp ₌_yp ₌_t1

(2.2) xp ₌_t

1, yp =t1z2a (2.3) xp ₌_t1z2a_{, y}p ₌_t1

(2.4) xp ₌_t1z2a_{, y}p ₌_t1z2b

ondea, b∈ {1,2, . . . p−1}.

O caso (2.1) não pode ocorrer, senão G = hx, y, t1i × hz2i, o que contradiz nossa hipótese da indecomponibilidade de G. Vamos analisar novamente as duas possibilidades paraz2: z2 =t2,o(t2) =pm2 _ou_z2 ₌_u1,_{o(u1) =}_∞_{, em cada um dos}

casos acima.

Suponhamos primeiramente que z2 = t2 com o(t2) =pm2_{. Nesse caso podemos}

suporp6= 2, pois o casop= 2 já foi estudado em [[9], Proposi¸cão 3.3]. No caso (2.2) trocandoy por y′ ₌_xn_y _onde _n _{é tal que} _n_{+ 1} _≡_{0 (mod}_{p), podemos assumir que}

xp ₌ _t1 _e _y′p ₌ _t2a_{. Fazendo} _t′

2 = t2a temos que G ∈ G4. O caso (2.3) ´e sim´etrico ao (2.2), bastando trocar x por y e no caso (2.4) trocando x por x′ ₌ _xn_y _onde

n ´e tal que n + 1 ≡ 0 (mod p), podemos supor que x′p ₌ _t2a+nb_{, y}p ₌ _t1t2b_{. Se}

a+nb ≡ a′ _(mod _{p) e} _a′ _6≡ _{0 (mod} _{p) ent˜ao trocamos} _y _por _y′ ₌ _x′m

y onde m ´e tal que b+m(a′₎ _≡ _{0 (mod} _{p). Assim podemos obter} _x′p ₌ _t

2a ′

, y′p ₌ _t

1; fazendo t′

2 =t2a ′

, obtemos queG∈ G4.

Mas se a′ _≡ _{0 (mod} _{p), ent˜ao podemos supor} _xp _{= 1, y}p ₌ _t1t2b_{. Se} _m2 _≥ _m1

ent˜ao Z(G) =ht1i × ht2i =ht1i × ht2b_i ₌_h_t1_{i × h}_t1t2b_i_{. Trocando} _t2 _por_t′

2 =t1t2b, obtemosG∈ G3. Sem2 < m1, tomamost′1 =t1t2b. Assimht1i × ht2i=ht1t2bi × ht2i, onde s = (t1t2b₎pm₁−1

e, portanto, G = hx, y, t′

1i × ht2i ´e decompon´ıvel, o que ´e absurdo.

(35)

Fazendou′

1 =t1bu1 segue que Z(G) =ht1i × hu1i=ht1i × ht1bu1i dondeG∈ G6. O caso (2.3) é simétrico ao anterior. No último caso, se p= 2 então temos x2 ₌_y2 ₌ t1u1. Trocando x por x′ =xy podemos assumir que x′2 =t12

m₁−1₊₂

e y2 ₌_t 1u1; se m1 >1 ent˜ao, usando novamente o Lema 2.4, podemos supor x′2 _{= 1 e} _y2 ₌_t1u1 _o que implica que G ∈ G5 bastando trocar u1 por u′1 = t1u1; se m1 = 1 ent˜ao segue quex′2 ₌_{t1, y}2 ₌_{t1u1, donde} _G_{∈ G}

6 se trocarmos u1 por u′1 =t1u1. Agora, se p6= 2 e xp ₌_t

1u1a, yp =t1u1b, trocamos x por x′ =xyn, onde n ´e tal quen+1≡0 (modp). Assim, existex′′ _∈_G_{tal que}_x′′p ₌_u1a+nb_{. Se}_a′ ₌_a_+nb_6≡₀

(mod p), trocamos y por y′ _{= (x}′′₎m_y _onde _m _{´e tal que} _b₊_ma′ _≡ _{0 (mod} _{p). Isso}

implica que existey′′ _∈_G_{tal que}_y′′p ₌_t

1 ex′′p =u1a ′

. Trocamos ent˜aox′′_{por (x}′′₎c

ondec´e tal que a′_c_≡_{1 (mod} _{p). Finalmente, podemos obter geradores} _x′′′_{, y}′′ _∈_G

tais que x′′′p ₌ _{u1, y}′′p ₌_{t1, donde} _G_{∈ G}_{6. Mas, se} _a′ _≡ _{0 (mod}_{p), existe} _x′′′ _∈_G

onde x′′′p _{= 1. Assim, trocando} _y _por _y′ ₌ _yd_{, onde} _d _{´e tal que} _db _≡ _{1 (mod} _p)

obtemosy′′_∈_G_{tal que} _G₌_h_x′′′_{, y}′′_{, Z(G)}_i_{, com}_x′′′p _{= 1, y}′′p ₌_t1d_u1 _{o que implica}

queG∈G5 bastando para isso trocar t1d_u1 _por _u′

1. ¥

Proposi¸cão 2.10 As fam´ılias G3,G4,G5 eG6 do Teorema 2.9 são fam´ılias de grupos indecompon´ıveis. Além disso, grupos em fam´ılias diferentes não são isomorfos entre si.

Demonstra¸cão: Primeiro mostraremos que os grupos das quatro fam´ılias apresentadas não são dois a dois isomorfos. Pela cardinalidade, temos que provar somente queG3 6≃G4 eG5 6≃G6, com Gi ∈ Gi, para 3≤i≤6.

Para mostrar que G3 6≃ G4, note que x é um elemento não central de ordem p em G3. Mostraremos que não existe tal elemento emG4. De fato, suponhamos que w = xa_yb_t1c_t2d _∈ _G4, _{w /}_∈ _Z_{(G4) e} _wp _{= 1. Se} _p _{= 2 então já foi mostrado em}

[[9], Proposi¸c˜ao 3.3] queG3 6≃G4. Assumimos, portanto, p6= 2. EmG4, temos que xp ₌ _t1 _e _yp ₌ _{t2. Logo,} _wp ₌ _t1a+cp_t2b+dp _{= 1 e como} _h_t1_{i ∩ h}_t2_i ₌ _{₁_}_{, obtemos}

pm1 _| _(a₊_{cp) e} _pm2 _| _(b₊_{dp) o que implica que} _p _| _a _e _p _| _{b. Usando novamente}

o fato que em G4, xp ₌ _t1 _e _yp ₌ _t2 _{segue que} _w ₌ _t1a′ t2b′

t1c_t2d _∈ _Z_{(G4), uma}

contradi¸c˜ao.

(36)

que emG5,xé um elemento não central de ordemp. Mostraremos que todo elemento de ordem p em G6 é central. Suponhamos que w =xa_yb_t1c_u1d _∈ _G6, _{w /}_∈ _{Z(G6) e}

wp _{= 1. Se} _p₆_{= 2 ent˜ao} _wp ₌_t

1a+cpu1b+cp = 1. Masht1i ∩ hu1i={1} e o(u1) = ∞, o que implica queb=−dp e p|a. Portanto, w=t1a′₊_c

∈Z(G6), uma contradi¸c˜ao. Se p = 2, w2 ₌ _t1a+2c+2m₁−1_ab

u1b+2d _{= 1, o que implica que} _b ₌ ₋_2d _{e 2} _| _a _donde

w∈Z(G6), outra contradi¸c˜ao.

Agora mostraremos que os grupos dessas quatro fam´ılias são indecompon´ıveis. SejaG=hx, y, Z(G)i um tal grupo com Z(G) =ht1i × hz2i. Se Gé decompon´ıvel, então pelo Teorema 2.3 podemos escrever

G=H×K

onde K é um grupo abeliano não trivial e H é um grupo indecompon´ıvel não abeliano de centro Z(H) não trivial, já que s = [x, y] ∈ Z(H). Como o posto Z(G) = 2, Z(G) = Z(H)×K, com s ∈ Z(H) e sp _{= 1, segue que} _Z_{(H) é c´ıclico}

finito de ordem potˆencia de p, ou seja, Z(H) = ht1az2bi, (t1az2b)p

r

= 1. Portanto, s=t1apr−1_j

z2bpr−1_j

onde pn˜ao divide j. Assim temos s =t1apr−1_j

z2bpr−1_j

=tp₁m1−1. (2.4)

Se G pertence a G3 ou G4, então z2 = t2 com o(t2) = pm2. Pela equa¸cão acima segue que pm2 _| _bpr−1_{j, o que implica que} _r₋₁ _≥ _m2 _{ou que} _b _{é m´}_{ultiplo de} _p.

Pelo Lema 2.8 sabemos que existe y1 ∈ H tal que y1 = yz com z ∈ Z(G). Logo, y1p ₌ _yp_zp ₌ _t2(t1α_t2β₎p _∈ _H_∩_Z(G) _⊆ _Z_{(H) e podemos escrever} _y1p _{= (t1}a_t2b₎n_.

Assim

t1ant2bn=t1αpt21+βp. (2.5) Pela equa¸cão (2.5), vemos que p não divide n e p não divide b, donde r−1≥ m2. ComoZ(H) é um fator direto deZ(G) de ordempr_{, e os fatores de}_{Z(G) tem ordem}

pm1 _e _pm2_{, segue que} _r ₌_m1.

Afirmamos quea também não é múltiplo dep. Caso contrário, (t1a_t2b₎pm₁−1

= 1, o que ´e absurdo, pois o(t1a_t2b_{) =} _pr ₌ _pm1_{. Mas, pela equa¸c˜ao (2.5), segue que}

pm1 _| _(αp₋_{an) o que implica que} _p _divide _{an. Como} _p _{n˜ao divide} _{n, temos uma}

(37)

Portanto, se Gpertence a G3 ou G4,G ´e indecompon´ıvel.

Agora suponhamos que G perten¸ca a G5 ou G6. Nesse caso, z2 = u1 com o(u1) = ∞. Assim segue pela equa¸c˜ao (2.4) que u1bpr−1_j

= 1, donde b = 0. Logo Z(H) = ht1ai e a equa¸cão (2.5) se torna t1an = t1αpu11+βp. Logo 1 +βp = 0 o que é absurdo pois β é um inteiro. Portanto, os grupos em G5 e G6 também são

indecompon´ıveis. ¥

Finalmente, veremos no próximo teorema o que acontece quando o posto do centro de G é igual a três. Nesse caso, o grupo G poderá pertencer a uma de três fam´ılias.

Teorema 2.11 Seja G um grupo indecompon´ıvel finitamente gerado e tal que G/Z(G) ≃ Cp ×Cp. Se posto (Z(G)) = 3 ent˜ao G pertence a um dos trˆes tipos

abaixo:

Tipo 7=hx, y, t1, t2, t3 |tp₁m1 =t₂pm2 =t₃pm3 = 1, xp ₌_{t2, y}p ₌_t3_i

Tipo 8=hx, y, t1, t2, u1 |tp1m1 =t

pm₂

2 = 1, xp =t2, yp =u1i Tipo 9=hx, y, t1, u1, u2 |t₁pm1 = 1, xp =u1, yp =u2i

onde, em cada caso, t1, t2, t3, u1, u2 s˜ao centrais, m1, m2, m3 ≥ 1 e s= [x, y] =t1pm₁−1

.

Denotaremos por Gi a fam´ılia de todos os grupos de Tipo i, i= 7,8,9.

Demonstra¸c˜ao: Suponhamos que G = hx, y, Z(G)i com Z(G) =

ht1i × hz2i × hz3i e xp_{, y}p _∈ _{Z(G). Pelo Teorema 2.3 segue que} _{o(t1) =} _pm1_,

m1 ≥ 1 e o(zi) = pmi ou o(zi) = ∞. Seja ¯G = G /hz3i = hx,¯ y,¯ t1,¯ z2¯i, onde

¯

xp_,_y_¯p _{∈ h}_t1_¯_{i × h}_z2_¯_i₌_{Z( ¯}_{G). Se ¯}_G_{´e indecompon´ıvel ent˜ao, pelo Teorema 2.9, segue}

que

(1) ¯xp _{= ¯1,}_y_¯p _{= ¯}_z2 _{ou (2) ¯}_xp _{= ¯}_t1,_y_¯p _{= ¯}_z2_.

Se ¯xp _{= ¯1 e ¯}_yp _{= ¯}_z2_{, ent˜ao temos quatro possibilidades para}_xp_{, y}p_:

(38)

(1.2) xp _{= 1, y}p ₌_z2z3a

(1.3) xp ₌_z3a_{, y}p ₌_z2

(1.4) xp ₌_z3a_{, y}p ₌_z2z3b

ondea, b∈ {1,2, . . . , p−1}.

No primeiro caso, G=hx, y, t1, z2i × hz3i, o que ´e absurdo.

Suponhamos que zi = ti, com o(ti) = pmi, para i = 2,3. No caso (1.2), se

m2 ≥ m3, ent˜ao Z(G) = ht1i × ht2t3a_{i × h}_t3_i _{e fazendo} _t′

2 = t2t3a temos que G é decompon´ıvel, uma contradi¸cão. Se m2 < m3, então trocamos t3 por t′

3 = t2t3a; assim G = hx, y, t1, t′3i × ht2i, o que também é uma contradi¸cão. Logo, nessas condi¸cões, o caso (1.2) também não pode ocorrer.

J´a no caso (1.3), fazendo t3a ₌ _t′

3 temos que G ∈ G7. No último caso, se p = 2 já foi mostrado em [[9], Proposi¸cão 3.4] queG∈ G7. Podemos assumir então p6= 2. Trocando y por y′ = xn_{y, onde} _n _{é tal que} _b₊_na_≡ _{0 (mod} _{p), existe} _y′′ _∈ _G _tal

que (y′′₎p ₌_{t2. Fazendo} _t3a₌_t′

3 segue que G∈ G7.

Suponhamos agora z2 = t2, com o(t2) = pm2 _e _z3 ₌ _u1 _com _{o(u1) =} _∞_{. Em}

(1.2), se p= 2 temos que x2 _{= 1 e} _y2 ₌_t2_{u1; trocando} _u1 _por _u′

1 =t2u1 segue que G=hx, y, t1, u′

1i × ht2i, absurdo. Se p6= 2, trocamos y pory′ =yb, ondeb´e tal que ab≡ 1 (mod p). Assim, existe y′′ _∈_G _{tal que (y}′′₎p ₌_t2b_{u1, o que tamb´em implica}

que G´e decompon´ıvel, se trocarmos u1 por u′

1 = t2bu1. J´a no caso (1.3), trocando xpor x′ ₌_xb_{, com} _ab_≡_{1 (mod} _{p), segue que} _G_{∈ G}_8.

No ´ultimo caso, se p = 2 temos x2 ₌ _u1 _e _y2 ₌ _{t2u1; trocando} _y _por _x′ ₌ _xy

podemos supor y′2 ₌_t12m₁−1

t2. Se m1 = 1 então x2 ₌_u1 _e _y′2 ₌_t1t2 _{o que implica} que G ∈ G8 trocando t2 por t′2 = t1t2. Se m1 > 1, então podemos supor y′2 = t2, donde tambémG∈ G8. Agora, se p6= 2, trocamosy por y′ ₌_xn_{y, onde}_n _{é tal que}

an+b ≡o ((mod p)) e trocamos tamb´emx porx′ ₌_xc _onde_ac_≡_{1 (mod}_{p). Dessa}

forma, podemos assumir quey′p ₌_t2 _e _x′p ₌_u1 _{o que implica que}_G_{∈ G}_8.

Finalmente suponhamos zi = ui−1, com o(ui−1) = ∞, i= 2,3. No caso (1.2) se

trocarmos u1 por u′

(39)

(mod p), segue que G∈ G9.

No ´ultimo caso, tamb´em trocando x por x′ ₌ _xb_{, como em (1.3), e chamando}

u′

1 =u1u2a, temos G =hx′, y,ht1i × hu1u2ai × hu2ii, com x′p =u2 e yp =u′1, o que implica que G∈ G9.

Agora, se (2) acontece, ent˜ao ¯xp _{= ¯}_t1 _{e ¯}_yp _{= ¯}_z2 _{e temos tamb´em outras quatro}

possibilidades para xp_{, y}p_:

(2.1) xp ₌_{t1, y}p ₌_z2

(2.2) xp ₌_{t1, y}p ₌_z2_z3a

(2.3) xp ₌_t

1z3a, yp =z2 (2.4) xp ₌_t1z3a_{, y}p ₌_z2z3b

ondea, b∈ {1,2, . . . , p−1}.

No primeiro caso, tamb´em temos G = hx, y, t1, z2i × hz3i decompon´ıvel, con-tradizendo nossa hip´otese.

Sezi =ti,o(ti) = pmi comi= 2,3, ent˜ao no caso (2.2) trocamost2 port′2 =t2t3a sem2 ≥m3 e, caso contr´ario, trocamos t3 port′

3 =t2t3a. Em ambos os casos, temos Gdecompon´ıvel, absurdo.

No caso (2.3), se m3 ≥m1, podemos trocar t3 por t3′ =t1t3a e obtemos G∈ G7. Se m3 < m1 ent˜ao fazemos t′

1 = t1t3a. Observe que essa troca ´e poss´ıvel j´a que s=t1pm₁−1

= (t1t3a₎pm₁−1

. Assim,G=hx, y, t′

1, t2i × ht3i, uma contradi¸c˜ao.

No último caso, podemos suporp6= 2, pois no caso p= 2 já foi demonstrado em [[9], Proposi¸cão 3.3] queG∈ G7.

Se m1 ≥ m2 ≥ m3 ent˜ao trocamos x por x′ ₌ _xyn_{, onde} _n _{´e tal que}

a+nb≡0 (mod p). Assim,x′p ₌_t1_t2n_{. Se} _n_≡_{0 (mod} _{p) ent˜ao podemos supor que}

x′p ₌ _{t1. Nesse caso,} _G _{´e decompon´ıvel, pois podemos trocar} _t2 _por _t′

2 = t2t3b obtendo G = hx, y, t1, t′2i × ht3i. Suponhamos ent˜ao x′p = t1t2a, yp = t2t3b onde a, b ∈ {1,2, . . . , p −1}. Podemos escrever Z(G) = ht1t2a_{i × h}_t2t3b_{i × h}_t3_i _{o que}

implica que G´e decompon´ıvel se trocarmos t1 por t′