Universidade Federal do Rio Grande do Norte
Centro de Ciˆencias Exatas e da Terra
Programa de P´os-Gradua¸c˜ao em Matem´atica Aplicada e Estat´ıstica
Alex Wagner Pereira
CONSEQUˆ
ENCIAS DA AN ´
ALISE
INADEQUADA DE UM EXPERIMENTO
FATORIAL
2
kEM PARCELAS SUBDIVIDIDAS E
SEM REPLICA ¸
C ˜
AO
CONSEQUˆ
ENCIAS DA AN ´
ALISE
INADEQUADA DE UM EXPERIMENTO
FATORIAL
2
kEM PARCELAS SUBDIVIDIDAS E
SEM REPLICA ¸
C ˜
AO
Disserta¸c˜ao apresentada ao Programa de P´os-Gradua¸c˜ao em Matem´atica Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento `as exigˆencias legais para obten¸c˜ao do t´ıtulo de Mestre.
´
Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica
Orientadora:
Prof
a. Dr
a. Carla Almeida Vivacqua
.
CONSEQUˆ
ENCIAS DA AN ´
ALISE
INADEQUADA DE UM EXPERIMENTO
FATORIAL
2
kEM PARCELAS SUBDIVIDIDAS E
SEM REPLICA ¸
C ˜
AO
Disserta¸c˜ao apresentada ao Programa de P´os-Gradua¸c˜ao em Matem´atica Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento `as exigˆencias legais para obten¸c˜ao do t´ıtulo de Mestre.
´
Area de Concentra¸c˜ao: Probabilidade e Estat´ıstica
Aprovado em: / /
Banca Examinadora:
Profa. Dra. Carla Almeida Vivacqua
Departamento de Estat´ıstica - UFRN Orientadora
Prof. Dr. Andr´e Luis Santos de Pinho Departamento de Estat´ıstica - UFRN
Examinador Interno
Dra. Aline de Holanda Nunes Maia
Dedicat´
oria
Dedico esse trabalho `a minha av´o Mercedes
Agrade¸co, em primeiro lugar a Deus, por iluminar meu caminho ao longo dessa jornada. Agrade¸co tamb´em ao meu pai, que foi o exemplo maior de toda minha vida, `a minha m˜ae pelo papel fundamental na minha forma¸c˜ao e `a minha irm˜a, melhor amiga e maior incentivadora do meu crescimento, bem como a todos da minha fam´ılia que me deram coragem para continuar; `a minha esposa que de forma carinhosa me ajudou a traduzir todos os textos pertinentes ao meu mestrado; aos meus filhos Tiago e Pedro que me levam a querer progredir mais e mais; `a professora Carla pela paciˆencia na orienta¸c˜ao e brilhantismo inspirador que me ajudaram na conclus˜ao deste trabalho; aos professores, de um modo geral, pelo incentivo, pela compreens˜ao e amizade; ao amigo Fl´avio pela contribui¸c˜ao inestim´avel no desenvolvimento do programa que permitiu realizar todas as simula¸c˜oes da pesquisa; e a colegas de curso pelo conv´ıvio e apoio constantes.
Resumo
Em experimentos com v´arios fatores em que alguns s˜ao mais dif´ıceis de mudar que outros, pode ser inconveniente executar as provas do experimento em uma forma completamente aleat´oria, levando o pesquisador a criar naturalmente uma restri¸c˜ao na ordem de execu¸c˜ao para poupar tempo ou reduzir os custos. Este tipo de restri¸c˜ao pode resultar em uma generaliza¸c˜ao do planejamento fatorial, conhecida como experimentos em parcelas subdivididas. Na pr´atica, ´e comum executar um experimento em parcelas subdivididas e analis´a-lo como se fosse completamente aleatorizado.
O objetivo principal do trabalho ´e avaliar o impacto de analisar um experimento com restri¸c˜ao na aleatoriza¸c˜ao como completamente aleatorizado. Com esse intuito, utiliza-se uma simula¸c˜ao de dados, executada segundo um experimento em parcelas subdivididas. A simula¸c˜ao pode ser vista como um experimento fatorial em parcelas subdivididas do tipo 42 ×2 considerando que a raz˜ao entre as variˆancias do efeito na
parcela/subparcela (1; 4,75; 16 e 49) e a quantidade de repeti¸c˜oes (10, 100, 1000 e 10000) s˜ao fatores associados `as parcelas e o modo como o experimento foi analisado, utilizando o m´etodo de Lenth, (completamente aleatorizado e parcelas subdivididas) o fator associado `as subparcelas. Assim, observa-se que o modo como o experimento foi analisado e a raz˜ao entre a variˆancia do efeito da parcela e da subparcela afetam a habilidade de identificar efeitos ativos.
Palavras-chave:Aleatoriza¸c˜ao; Experimenta¸c˜ao; M´etodo de Lenth; Parcelas Sub-Divididas; Split-Plot.
In experiments with several factors, in which some are harder to change than others, it may be inconvenient to execute the tests of the experiment in a completely random way, taking the researcher to naturally create a restriction in execution order to save time or reduce costs. This type of restriction may result in a generalization of the fac-torial planning, known as experiments in split-plot designs. In practice, it is commom to execute an experiment as a split-plot design and analyze this experiment it as if it were a completely randomized design.
The main objective of the work is to evaluate the impact of analyzing an experiment with restriction in the randomization as completely randomized. With this intention, we use a simulation, executed according to a split-plot experiment. The simulation can be seen as an factorial experiment of type a 42×2 split-plot factorial design
conside-ring that the ratio beteween the plot and subplot variances (1; 4.75; 16 and 49) and the amount of repetitions (10, 100, 1000 and 10000) are factors associated with plots and the way the experiment was analyzed (completelly randomized and split plot) the factor associated with subplots. Thus, we observe that the way the experiment was analyzed and the ratio between the effect variance of the plot and the subplot affect the ability to identify active effects.
Keywords: Randomization; Experimentation; Lenth’s Method, Split-Plot.
Sum´
ario
1 Introdu¸c˜ao 1
1.1 Motiva¸c˜ao . . . 3
1.2 Objetivos . . . 7
1.2.1 Objetivo Geral . . . 7
1.2.2 Objetivos Espec´ıficos . . . 7
2 Conceitos B´asicos em Experimenta¸c˜ao 8 2.1 Fases da Experimenta¸c˜ao . . . 9
2.2 Princ´ıpios B´asicos Para o Planejamento Experimental . . . 10
2.2.1 Replica¸c˜ao . . . 10
2.2.2 Blocagem . . . 10
2.2.3 Aleatoriza¸c˜ao . . . 10
2.3 Tipos de Aleatoriza¸c˜ao . . . 11
2.3.1 Experimentos Completamente Aleatorizados . . . 11
2.3.2 Experimentos Aleatorizados em Parcelas Subdivididas . . . 12
2.4 M´etodos de An´alise de Experimentos Fatoriais N˜ao Replicados . . . 13
2.4.1 Gr´aficos de Probabilidade Normal . . . 13
2.4.2 O M´etodo de Lenth . . . 14
3 Estudo do Impacto do Plano Experimental na An´alise do Experi-mento 16 3.1 Cen´arios da Simula¸c˜ao do Experimento . . . 19
3.2 Resultados . . . 24
3.3 Crit´erios de Avalia¸c˜ao . . . 42
4 Conclus˜ao 61
5 Referˆencias Bibliogr´aficas 64
A.2 Programa 2 - Gr´aficos . . . 72 A.2.1 Gr´afico de Probabilidade Normal e do M´etodo de Lenth . . . . 72 A.2.2 Histogramas . . . 73 A.2.3 Estat´ıstica . . . 73
B Histogramas das distribui¸c˜oes dos efeitos 74
B.1 10 Repeti¸c˜oes . . . 74 B.1.1 σ2
1 = 1 e σ02 = 1 . . . 74
B.1.2 σ2
1 = 4 e σ02 = 1 . . . 76
B.1.3 σ2
1 = 16 e σ20 = 1 . . . 78
B.1.4 σ2
1 = 49 e σ20 = 1 . . . 80
B.2 100 Repeti¸c˜oes . . . 83 B.2.1 σ2
1 = 1 e σ02 = 1 . . . 83
B.2.2 σ2
1 = 4 e σ02 = 1 . . . 85
B.2.3 σ2
1 = 16 e σ20 = 1 . . . 87
B.2.4 σ2
1 = 49 e σ20 = 1 . . . 89
B.3 1000 Repeti¸c˜oes . . . 91 B.3.1 σ2
1 = 1 e σ02 = 1 . . . 91
B.3.2 σ2
1 = 4 e σ02 = 1 . . . 93
B.3.3 σ2
1 = 16 e σ20 = 1 . . . 95
B.3.4 σ2
1 = 49 e σ20 = 1 . . . 97
B.4 10000 Repeti¸c˜oes . . . 99 B.4.1 σ2
1 = 1 e σ02 = 1 . . . 99
B.4.2 σ2
1 = 4 e σ02 = 1 . . . 101
B.4.3 σ2
1 = 16 e σ20 = 1 . . . 103
B.4.4 σ2
1 = 49 e σ20 = 1 . . . 105
C Tabelas 107
C.1 Valores Cr´ıticos . . . 108 C.2 1000 Repeti¸c˜oes . . . 109
C.2.1 σ2
1 = 1 e σ02 = 1 . . . 109
C.2.2 σ2
1 = 4,75 e σ02 = 1 . . . 110
C.2.3 σ2
1 = 16 e σ20 = 1 . . . 111
C.2.4 σ2
1 = 49 e σ20 = 1 . . . 112
C.3 10000 Repeti¸c˜oes . . . 113
C.3.1 σ2
1 = 1 e σ02 = 1 . . . 113
C.3.2 σ2
1 = 4,75 e σ02 = 1 . . . 114
C.3.3 σ2
1 = 16 e σ20 = 1 . . . 115
C.3.4 σ2
1 = 49 e σ20 = 1 . . . 116 D A simula¸c˜ao como um experimento fatorial 4×4×2 117
D.1 O FATOR C - Considerado, na simula¸c˜ao, como Inativo . . . 117 D.1.1 Os dados . . . 117 D.1.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 118 D.1.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 118 D.2 O FATOR D - Considerado, na simula¸c˜ao, como Ativo . . . 119 D.2.1 Os dados . . . 119 D.2.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 119 D.2.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 120 D.3 A INTERA ¸C ˜AO AD - Considerado, na simula¸c˜ao, como Ativo . . . 120 D.3.1 Os dados . . . 120 D.3.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 120 D.3.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 121 D.4 A INTERA ¸C ˜AO AE - Considerado, na simula¸c˜ao, como Ativo . . . 122 D.4.1 Os dados . . . 122 D.4.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 123 D.4.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 123 D.5 A INTERA ¸C ˜AO AB - Considerado, na simula¸c˜ao, como Inativo . . . . 124 D.5.1 Os dados . . . 124 D.5.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 124 D.5.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 125 D.6 A INTERA ¸C ˜AO AC - Considerado, na simula¸c˜ao, como Inativo . . . . 125 D.6.1 Os dados . . . 125 D.6.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 125 D.6.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 126 D.7 A INTERA ¸C ˜AO BC - Considerado, na simula¸c˜ao, como Inativo . . . . 127 D.7.1 Os dados . . . 127 D.7.2 Gr´afico de Probabilidade Normal com os efeitos da parcela . . . 128 D.7.3 Gr´afico de Probabilidade Normal com os efeitos da subparcela . 128
Introdu¸
c˜
ao
O mercado atual est´a a cada dia que passa mais competitivo e exigente, por isso, ´e indispens´avel que as empresas lancem no mercado produtos com pre¸cos acess´ıveis que atendam e excedam as expectativas dos consumidores. Para satisfazer aos seus clientes, sem abrir m˜ao do lucro, as organiza¸c˜oes investem, cada vez mais, em projetos de melhoria, buscando sistemas de produ¸c˜ao de alta qualidade e de baixos custos. Neste contexto, experimentos s˜ao ´uteis.
Experimentos s˜ao empregados para resolver problemas de fabrica¸c˜ao, decidir entre diferentes processos de manufatura, diferentes conceitos de produto, etc... Muito do que se sabe hoje se deve ao aprendizado com experimentos.
Quando um experimento ´e executado, procura-se adquirir conhecimento sobre os produtos e/ou processos envolvidos, em que o maior desafio ´e planejar e executar esses experimentos de forma eficiente, considerando as restri¸c˜oes f´ısicas e econˆomicas de cada processo de produ¸c˜ao. ´E a´ı, exercendo um papel fundamental na procura desses novos produtos e na melhoria de processos e de produtos existentes, que entram os experi-mentos planejados. Desta forma, podemos entender o planejamento de experiexperi-mentos como uma parte da Estat´ıstica que busca permitir ao experimentador a obten¸c˜ao de dados que lhe sejam ´uteis, no sentido de fornecer informa¸c˜oes de acordo com o objetivo, de uma forma t˜ao econˆomica quanto poss´ıvel.
´
E importante destacar que o planejamento ´e um dos grandes desafios na realiza¸c˜ao dos experimentos. Por exemplo, nos experimentos industriais a existˆencia de muitos fatores a serem avaliados pode gerar um gasto grande de tempo e um alto custo na execu¸c˜ao das provas.
Na ind´ustria, devido `a sua simplicidade e eficiˆencia, os experimentos fatoriais s˜ao os mais utilizados (Ye, Hamada & Wu, 2001) e, em particular, os experimentos fatoriais 2k (caso em que todos os k fatores possuem dois n´ıveis) destacam-se entre os planos
2
fatoriais (Montgomery, 2001).
Situa¸c˜oes em que muitos fatores s˜ao de interesse e deseja-se saber quais deles podem ser desconsiderados s˜ao cen´arios indicados para a utiliza¸c˜ao de experimentos fatoriais 2k. A principal vantagem desse plano, ´e que com um n´umero reduzido de provas, o
experimentador tem condi¸c˜oes de testar muitos fatores simultaneamente.
Quando um experimento tem um alto custo ou a sua execu¸c˜ao exige muito tempo, ´e interessante para o pesquisador a diminui¸c˜ao do n´umero de provas e, por isso, ´e fre-quente a realiza¸c˜ao de experimentos sem a presen¸ca de r´eplicas. Em um experimento sem r´eplicas, a an´alise precisa ser cuidadosa pois fica-se sem graus de liberdade sufici-entes para estimar diretamente a variˆancia do erro experimental, por isso, dificultando a utiliza¸c˜ao de testes para determinar a significˆancia dos efeitos.
Nesse caso, uma boa alternativa para a an´alise dos efeitos ´e a constru¸c˜ao de gr´aficos de probabilidade normal (Daniel, 1959). A grande desvantagem desse m´etodo ´e a subjetividade para obter as conclus˜oes.
Em 1989, Lenth desenvolveu um m´etodo objetivo de an´alise. O m´etodo de Lenth, mesmo na ausˆencia de r´eplicas, utiliza uma f´ormula simples para obter uma estimativa do erro padr˜ao dos contrastes estimados. Este m´etodo foi depois reformulado por Ye, Hamada, & Wu (2001).
Em experimentos com v´arios fatores em que alguns s˜ao mais dif´ıceis de mudar que outros, pode ser imposs´ıvel aleatorizar a ordem de todas as observa¸c˜oes, obrigando o pesquisador a criar uma restri¸c˜ao na aleatoriza¸c˜ao para poupar tempo ou reduzir os custos. Este tipo de restri¸c˜ao pode resultar em uma generaliza¸c˜ao do planejamento fatorial, conhecida como experimentos aleatorizados em parcelas subdivididas.
Os experimentos fatoriais em parcelas subdivididas sem r´eplicas s˜ao candidatos a planos experimentais que atendem `as caracter´ısticas pr´aticas de experimentos indus-triais, sendo, portanto, ´uteis e representam o foco do nosso trabalho. Na pr´atica, ´e muito comum executar um experimento em parcelas subdivididas (com restri¸c˜ao na aleatoriza¸c˜ao) e analisar esse experimento sem considerar essa restri¸c˜ao.
O QUE ACONTECE QUANDO QUANDO SE IGNORA A RESTRI-¸
C ˜AO NA ALEATORIZA ¸C ˜AO?
1.1
Motiva¸
c˜
ao
A motiva¸c˜ao para este trabalho foi um experimento executado segundo um deli-neamento em parcelas subdivididas descrito em Bisgaard, Fuller e Barrios (1995). O objetivo do experimento era utilizar plasma para alterar as caracter´ısticas da superf´ıcie do papel, para assim torn´a-lo mais suscet´ıvel `a tinta. Neste experimento foram utiliza-dos cinco fatores com dois n´ıveis cada. Segundo Bisgaard, Fuller e Barrios (1995), um plasma ´e uma mistura de pr´otons e el´etrons. Os plasmas s˜ao geralmente criados em uma cˆamara de baixo v´acuo e, cada vez que o reator ´e aberto para inserir uma nova amostra, demora cerca de 40 minutos para atingir novamente o v´acuo.
Os cinco fatores utilizados e seus respectivos n´ıveis s˜ao apresentados no Quadro 1.1.
Quadro 1.1 - Fatores utilizados e seus respectivos n´ıveis
Fator N´ıvel (+) N´ıvel (−) A: Press˜ao alta baixa B: Energia alta baixa C: Fluxo de G´as alto baixo D: Tipo de G´as Oxigˆenio Si Cl4
E: Tipo de papel I II
Para economizar trabalho e tempo, duas amostras, uma de cada tipo de papel, foram inseridas no reator ao mesmo tempo (com isso a dura¸c˜ao da experiˆencia foi reduzida `a metade).
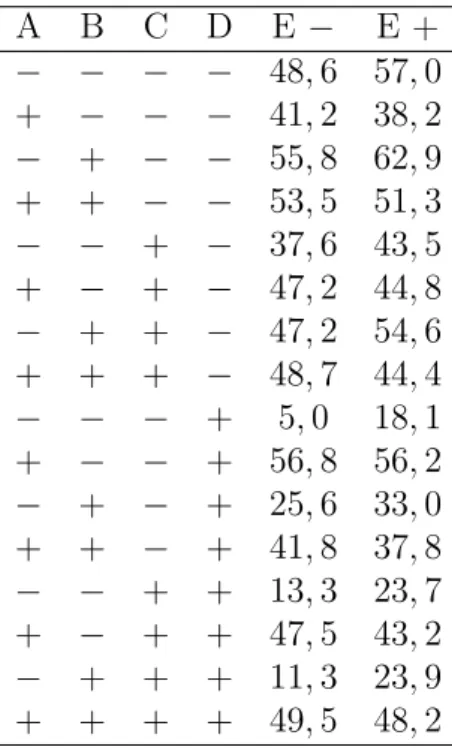
A matriz de projeto est´a apresentada na Tabela 1.1. Observe que a primeira linha, por exemplo, indica que os dois tipos de papel (fator E) foram colocados numa confi-gura¸c˜ao do reator em que press˜ao (fator A), energia (fator B), propor¸c˜ao do fluxo de g´as (fator C) e tipo de g´as (fator D) est˜ao nos seus n´ıveis (−) e foram encontradas as respostas 57,0 para o tipo I e 48,6 para o tipo II.
Para analisar este caso experimental, foram divididos, nas Tabelas 1.2 e 1.3, os 31 efeitos em dois grupos, aqueles com variˆancia de erro associados `a parcela (whole plot)relacionados com o reator (fatores dif´ıceis de mudar: A, B, C e D) e aqueles com variˆancia de erro associados `a subparcela (sub plot) relacionados com as amostras de papel (fator f´acil de mudar: E)
Em experimentos fatoriais 2k com restri¸c˜oes na aleatoriza¸c˜ao ´e prefer´ıvel usar
1.1 Motiva¸c˜ao 4
Tabela 1.1: Matriz de projeto e resposta para experimento em parcelas subdivididas na produ¸c˜ao de plasma
A B C D E − E +
− − − − 48,6 57,0 + − − − 41,2 38,2
− + − − 55,8 62,9 + + − − 53,5 51,3
− − + − 37,6 43,5 + − + − 47,2 44,8
− + + − 47,2 54,6 + + + − 48,7 44,4
− − − + 5,0 18,1 + − − + 56,8 56,2
− + − + 25,6 33,0 + + − + 41,8 37,8
− − + + 13,3 23,7 + − + + 47,5 43,2
− + + + 11,3 23,9 + + + + 49,5 48,2
Tabela 1.2: Efeitos estimados agrupados por tipo de variˆancia de erro
Tabela 1.3: Efeitos estimados agrupados por tipo de variˆancia de erro Contraste Efeito IE 3,1 AE -5,9 BE -0,3 CE -0,1 DE 1,0 ABE 0,1 ACE -0,1 ADE -0,8 BCE 0,9 BDE -0,2 CDE 0,3 ABCE -0,4 ABDE 0,3 ACDE -0,2 BCDE 0,9 ABCDE 0,2
No caso em que os dados dos gr´aficos de probabilidade normal aparecem como uma linha reta (figuras 2 e 3), o coeficiente angular dessa reta ´e o valor aproximado do desvio padr˜ao dos efeitos associados. ´E importante observar que o valor do desvio padr˜ao dos efeitos associados `a subparcela (sub plot) ´e consideravelmente menor (≈1) que o des-vio (≈7) dos efeitos associados `a parcela(whole plot) ilustrando que a variˆancia entre diferentes utiliza¸c˜oes do reator ´e maior que a variˆancia entre as amostras colocadas em cada reator.
1.2
Objetivos
1.2.1
Objetivo Geral
Avaliar o impacto de analisar um experimento em parcelas subdivididas como com-pletamente aleatorizado.
1.2.2
Objetivos Espec´ıficos
1.2 Objetivos 8
como se fosse completamente aleatorizado.
Conceitos B´
asicos em
Experimenta¸
c˜
ao
Neste trabalho, s˜ao abordados conceitos fundamentais para o planejamento, execu-¸c˜ao e an´alise de experimentos. Um desses conceitos ´e a aleatorizaexecu-¸c˜ao que torna poss´ıvel a gera¸c˜ao de uma distribui¸c˜ao de referˆencia, base para an´alise estat´ıstica, sem a necessi-dade de suposi¸c˜oes sobre a distribui¸c˜ao dos dados. Quando o ensaio cient´ıfico deixa de ser adequadamente aleatorizado, ele pode fornecer estimativas tendenciosas dos efeitos dos fatores bem como da variˆancia do erro experimental, o que pode levar a conclus˜oes equivocadas.
Muitas vezes, a presen¸ca de fatores que s˜ao mais caros, que consomem mais tempo ou que s˜ao mais dif´ıceis de mudar que outros, pode tornar invi´avel a realiza¸c˜ao do experimento em uma ordem completamente aleatorizada, obrigando o pesquisador a criar uma restri¸c˜ao na aleatoriza¸c˜ao para reduzir custos e poupar tempo. Uma op¸c˜ao pr´atica de planejamento, nesses casos, s˜ao os delineamentos em parcelas subdivididas. Na pr´atica por´em, ´e muito comum executar o experimento como parcela subdividida e analisar como completamente aleatorizado. Por isso, vamos dar ˆenfase `a importˆancia de realizar o que foi planejado e de examinar o que foi executado. Para exemplificar essa situa¸c˜ao ´e abordado um experimento fatorial 2k em que alguns fatores s˜ao dif´ıceis
de mudar e, por isso, o experimento ´e executado com restri¸c˜ao na aleatoriza¸c˜ao. Para haver uma melhor compreens˜ao do conte´udo abordado, apresenta-se a termo-logia b´asica e os principais conceitos de Planejamento de Experimentos.
• Resposta - ´e a caracter´ıstica de interesse que ser´a medida no estudo.
• Fator - ´e a caracter´ıstica que ser´a controlada no experimento.
2.1 Fases da Experimenta¸c˜ao 10
• Efeito - ´e a mudan¸ca na resposta produzida por uma modifica¸c˜ao no n´ıvel do fator.
• Tratamento - ´e uma combina¸c˜ao dos n´ıveis dos fatores.
• Unidade Observacional - ´e a unidade onde as medi¸c˜oes s˜ao feitas, ´e ela que fornece a resposta.
• Unidade Experimental - ´e a unidade a qual um tratamento ´e aplicado.
2.1
Fases da Experimenta¸
c˜
ao
O planejamento experimental ´e um conjunto de t´ecnicas estat´ısticas que auxiliam na coleta de dados e na obten¸c˜ao de conclus˜oes consistentes sobre uma pesquisa. Uma experiˆencia bem planejada permite a obten¸c˜ao de dados ´uteis, a um m´ınimo de custos, tempo e riscos; como tamb´em garante a validade das conclus˜oes (Vivacqua; Pinho, 2008). Vamos dividir as estrat´egias de experimenta¸c˜ao em trˆes etapas: elabora¸c˜ao (planejamento), execu¸c˜ao e avalia¸c˜ao (an´alise).
Planejamento
• Reconhecer e definir o problema.
• Separar fatores, n´ıveis e definir faixas de varia¸c˜ao para os fatores.
• Selecionar a vari´avel resposta.
• Escolher o tipo de delineamento experimental.
Execu¸
c˜
ao
• Realizar o experimento.
An´
alise
• Analisar estatisticamente os dados.
2.2
Princ´ıpios B´
asicos Para o Planejamento
Expe-rimental
Segundo Montgomery (2001) s˜ao trˆes os princ´ıpios b´asicos de um planejamento de experimentos: replica¸c˜ao, aleatoriza¸c˜ao e blocagem.
2.2.1
Replica¸
c˜
ao
Replica¸c˜ao ´e o ato de aplicar o mesmo tratamento a diferentes unidades experi-mentais. Existem duas propriedades importantes desse princ´ıpio. Primeiro, permite ao pesquisador obter estimativas do erro experimental e esse c´alculo ´e importante para determinar a existˆencia de diferen¸cas estatisticamente significativas entre os tratamen-tos. Segundo, d´a liberdade ao executante para adquirir um cˆomputo mais preciso dos efeitos (Montgomery, 2001).
´
E importante diferenciar replica¸c˜ao de repeti¸c˜ao. Na replica¸c˜ao, um mesmo trata-mento ´e aplicado a unidades experimentais diferentes e na repeti¸c˜ao, diferentes obser-va¸c˜oes s˜ao feitas de uma mesma unidade experimental. Por exemplo, duas medidas de uma mesma unidade experimental s˜ao repeti¸c˜oes e as medi¸c˜oes de duas unidades experimentais diferentes que receberam o mesmo tratamento s˜ao replica¸c˜oes.
2.2.2
Blocagem
Blocagem ´e uma t´ecnica extremamente importante, utilizada com o objetivo de aumentar a precis˜ao de um experimento. Em certos processos, podemos controlar e avaliar, sistematicamente, a variabilidade resultante da presen¸ca de fatores conhecidos que perturbam o sistema, mas que n˜ao temos interesse em estud´a-los. A blocagem ´e usada, por exemplo, quando uma determinada medida experimental ´e feita por duas pessoas diferentes, levando a uma poss´ıvel n˜ao homogeneidade nos dados. Essa t´ecnica permite criar uma experiˆencia mais homogˆenea e aumentar a precis˜ao das respostas que s˜ao analisadas (Gald´amez, 2002).
2.2.3
Aleatoriza¸
c˜
ao
2.3 Tipos de Aleatoriza¸c˜ao 12
sem a necessidade das suposi¸c˜oes de normalidade e independˆencia do erro experimen-tal e, consequentemente, das observa¸c˜oes. Por´em, situa¸c˜oes pr´aticas enfrentadas por pesquisadores limitam, em muitos casos, a aleatoriza¸c˜ao do experimento.
2.3
Tipos de Aleatoriza¸
c˜
ao
2.3.1
Experimentos Completamente Aleatorizados
Inicialmente, mostramos um exemplo fict´ıcio de um experimento fatorial 2k sem
replicas para entendermos melhor um arranjo em Parcelas Subdividias. No experimento fatorial 2k todos os fatores (quantitativos ou qualitativos) possuem dois n´ıveis. A
nota¸c˜ao 2k significa que o expoente (k) indica o n´umero de fatores, a base da potˆencia
(2) indica o n´umero de n´ıveis (alto (+) e baixo (−)) e o resultado da potˆencia (2k) indica o total de tratamentos.
O nosso exemplo ´e de um experimento que possui dois fatores A e B e dois n´ıveis alto (+) e baixo (−). Esta ´e uma estrutura fatorial 22 cujos quatro tratamentos seriam
definidos pelas combina¸c˜oes dos n´ıveis dos fatores A e B como mostra a tabela a seguir. Tratamento Fator A Fator B Intera¸c˜ao AB Resposta
(1) − − + y1
a + − − y2
b − + − y3
ab + + + y4
A presen¸ca das letras a e b indica que os fatores A e B est˜ao no n´ıvel alto para aquele determinado tratamento e o s´ımbolo (1) representa o tratamento no qual todos os fatores est˜ao no seu n´ıvel baixo. A coluna correspondente `a intera¸c˜ao ´e obtida atrav´es da multiplica¸c˜ao das colunas associadas aos fatores envolvidos, e as respostas em cada linha correspondem `as observa¸c˜oes para o tratamento presente na respectiva linha.
O objetivo principal de um experimento fatorial ´e avaliar a poss´ıvel influˆencia dos fatores e suas intera¸c˜oes nas vari´aveis respostas, que ´e medida atrav´es dos efeitos. O efeito de um fator (ou da intera¸c˜ao) ´e calculado pela diferen¸ca entre a m´edia das res-postas dos tratamentos que foram executados com o n´ıvel alto e a m´edia das resres-postas obtidas naqueles tratamentos em que este mesmo fator (ou da intera¸c˜ao) foi aplicado no n´ıvel baixo.
Assim, por exemplo, para estimarmos o efeito do fator A, devemos fazer:
Ef eito A= y2+y4
2 − y1+y3
Seguindo esta ideia ´e poss´ıvel estimar quaisquer efeitos (ou intera¸c˜oes) em um fa-torial 2k atrav´es das respostas observadas.
Do ponto de vista te´orico, ´e recomendada a realiza¸c˜ao de r´eplicas para que se possa ter uma ideia n˜ao apenas de um valor m´edio que a resposta pode assumir, mas tamb´em da varia¸c˜ao que existe entre uma aplica¸c˜ao e outra do mesmo tratamento e com isso, obter uma estimativa da variˆancia do erro experimental. Por´em, na pr´atica, quando o n´umero de fatores ou o custo da execu¸c˜ao ´e alto, a replica¸c˜ao pode tornar-se impratic´avel e, com a ausˆencia de r´eplicas, n˜ao ´e poss´ıvel ter ideia da variabilidade, e ´e preciso algum outro crit´erio para julgar se as estimativas dos efeitos devem realmente ser consideradas razo´aveis.
Diante disso, Daniel (1959) propˆos a utiliza¸c˜ao de gr´aficos de probabilidade nor-mal para identificar, de forma subjetiva, a presen¸ca de efeitos ativos em um estudo envolvendo estrutura fatorial de tratamentos. Nestes gr´aficos, os efeitos ativos s˜ao identificados pelos pontos mais claramente afastados de uma reta imagin´aria formada pelos pontos restantes. A grande desvantagem deste m´etodo ´e a subjetividade presente na an´alise, o que levou Lenth a sugerir um m´etodo objetivo de an´alise que ´e discutido mais adiante.
2.3.2
Experimentos Aleatorizados em Parcelas Subdivididas
Como foi visto anteriormente, algumas vezes ´e invi´avel executar um experimento fatorial seguindo um delineamento completamente aleatorizado e isso, normalmente resulta em uma generaliza¸c˜ao do experimento fatorial chamado de arranjo em parcelas subdivididas (split - plot).
Segundo Montgomery (2001) os arranjos em parcelas subdivididas devem ser ana-lisados como experimentos fatoriais 2k combinados (ou superpostos). Ou seja, um
2.4 M´etodos de An´alise de Experimentos Fatoriais N˜ao Replicados 14
2.4
M´
etodos de An´
alise de Experimentos Fatoriais
N˜
ao Replicados
Alguns importantes m´etodos s˜ao propostos para an´alise de um experimento fatorial n˜ao replicado. Por exemplo, os gr´aficos de probabilidade normal e seminormal, o M´etodo de Daniel (1959) - guard rails, o M´etodo de Box e Meyer (1986), o M´etodo de Lenth (1989), o M´etodo de Dong (1993), o M´etodo de Lawson, Grimshaw e Burt (1998) e o M´etodo de Lenth Descendente (2001). Escolhemos analisar os dados usando o gr´afico de probabilidade normal, o M´etodo de Lenth e uma adapta¸c˜ao ao M´etodo de Lenth proposta em Hamada e Wu (2009).
2.4.1
Gr´
aficos de Probabilidade Normal
A utiliza¸c˜ao dos gr´aficos de probabilidade normal para identificar efeitos possivel-mente ativos em experimentos fatoriais n˜ao replicados foi proposta por Daniel (1959). A ideia de Daniel ´e bastante utilizada at´e os dias de hoje por se tratar de um m´e-todo simples e por conseguir apontar a dire¸c˜ao correta dos efeitos em grande parte dos experimentos.
A constru¸c˜ao desses gr´aficos tamb´em ´e bastante simples. Inicialmente, os valores
yn dos efeitos observados s˜ao colocados em ordem crescente: y(1) ≤ y(2) ≤ ... ≤y(n) e
depois, o gr´afico de probabilidade normal ´e obtido a partir dos pontos cujas coordenadas s˜ao (y(i), φ−1[(i−0,5)/n]) onde, φ−1 ´e a fun¸c˜ao acumulada da normal padr˜ao ey(i) ´e o
i-´esimo dos n efeitos ordenados. Se o conjunto desses pontos segue um padr˜ao linear, h´a fortes ind´ıcios que a distribui¸c˜ao normal serve como modelo para a popula¸c˜ao que produziu a amostra e, nesse caso, a inclina¸c˜ao da reta vai indicar o desvio padr˜ao da popula¸c˜ao da qual a amostra foi obtida. Mais adiante, ser´a mostrado um exemplo em que o gr´afico de probabilidade normal foi usado para analisar o experimento.
Apesar do gr´afico de probabilidade normal ser muito utilizado e importante para an´alise de um experimento fatorial, sua interpreta¸c˜ao ´e subjetiva, pois cabe a quem est´a analisando identificar que efeitos s˜ao significativos e que valores s˜ao discrepantes nos dados. Existem casos em que estes gr´aficos podem levar pesquisadores distintos a conclus˜oes diferentes e por isso s˜ao considerados como m´etodos subjetivos de an´alise.
2.4.2
O M´
etodo de Lenth
Procurando m´etodos menos subjetivos e mais formais para a an´alise de experimen-tos fatoriais n˜ao replicados, Lenth (1989) apresentou uma metodologia relativamente simples de ensaio que permite expressar os resultados graficamente. A base desse m´e-todo ´e o princ´ıpio da esparsidade dos efeitos, que sugere que geralmente apenas um pequeno n´umero dos contrastes deve ser diferente de zero no processo observado. Num experimento fatorial, com efeitos principais e intera¸c˜oes de ordem cada vez maior, tem-se obtem-servado empiricamente que os efeitos principais e intera¸c˜oes de baixa ordem s˜ao significativos com uma maior frequˆencia, por´em estes representam apenas uma parte do grupo composto por todos os efeitos, ou seja, intera¸c˜oes de alta ordem envolvendo trˆes ou mais fatores s˜ao mais raras e, sendo assim, a quantidade de efeitos estatisti-camente significativos em um experimento fatorial n˜ao deve ser grande. Para verificar a ocorrˆencia desta condi¸c˜ao, o m´etodo utiliza-se de uma f´ormula simples para o erro padr˜ao das estimativas dos contrastes.
Lenth definiu um pseudo erro padr˜ao (PSE) dos contrastes como sendo
P SE = 1,5.mediana(|cj|<2,5So)|cj|
2.4 M´etodos de An´alise de Experimentos Fatoriais N˜ao Replicados 16
Definiu tamb´em uma margem de erro (ME) com aproximadamente 95% de confian¸ca como sendo M E = t(0,975;d).P SE e uma margem de erro simultˆanea (SME) como
SM E=t(γ;d).P SE em qued=n/3,γ = (1+0,951/n)/2 e n ´e o n´umero de observa¸c˜oes.
Depois de calculados as margens de erro para as estimativas dos contrastes, os efeitos s˜ao colocados em um gr´afico com a estrutura semelhante `a de um gr´afico de barras e os limites ±M E e ±SM E s˜ao adicionados a esse gr´afico. A an´alise ser´a feita do seguinte modo: um efeito ser´a considerado ativo se o seu valor ultrapassar SME, n˜ao ser´a considerado ativo se n˜ao ultrapassar ME e o efeito ser´a classificado como marginalmente ativo, isto ´e, ele pode ou n˜ao ser significativo se o seu valor estiver entre ME e SME.
Observe agora o exemplo (Figura 5) onde o limite SME est´a representado pela linha horizontal tracejada e o limite ME pela linha horizontal cheia. Nesse exemplo, os fatores A e D e as intera¸c˜oes AD, AE e ABCD (1o, 4o, 8o, 9o e 26o contrastes,
respectivamente) s˜ao classificados como ativos, os 2o, 3o, 5o, 6o, 7o, 11o e 17o contrastes
Estudo do Impacto do Plano
Experimental na An´
alise do
Experimento
“Em grande parte dos casos, os objetivos propostos pelos trabalhos cient´ıficos per-mite classific´a-los quanto `a abordagem utilizada para resolu¸c˜ao dos problemas levan-tados” (Saldanha - 2008). A partir desse ponto de vista, h´a trˆes grupos de estudo que podem classificar uma pesquisa: estudo explorat´orio, descritivo e explicativo.
Faz-se uso dos estudos explicativos para identificar os fatores que contribuem ou influenciam a ocorrˆencia de um fenˆomeno, ou tamb´em para determinar atrav´es da raz˜ao o fundamento das coisas. J´a um estudo descritivo tem como objetivo a descri¸c˜ao das caracter´ısticas de um determinado fenˆomeno, assim como o estabelecimento de rela¸c˜oes entre as vari´aveis e os fatos.
Segundo Vergara (1997) uma pesquisa explorat´oria ´e aquela realizada em ´area na qual h´a pouco conhecimento acumulado ou sistematizado e, muitas vezes, ´e a primeira etapa de uma investiga¸c˜ao que ser´a mais aprofundada. Sendo assim, vamos classificar o nosso trabalho como descritivo e explicativo.
Inicialmente foi feito um estudo do artigo de Bisgaard Fuller e Barrios (1996). O ob-jetivo era entender melhor erros associados aos fatores que ocorrem quando analisamos um experimento com restri¸c˜ao na aleatoriza¸c˜ao como se fosse completamente aleatori-zado. Nesse artigo, a an´alise do experimento ´e feita utilizando gr´aficos de probabilidade normal para detectar os efeitos ativos dos fatores escolhidos.
Para ilustrar melhor, observamos um exemplo mais simples: Consideremos um ex-perimento com trˆes fatores (A, B e C) com dois n´ıveis (+ e −), sendo que os fatores A e B s˜ao dif´ıceis de mudar e o fator C n˜ao. Esse ´e um experimento em parcelas
18
subdivididas (split - plot) 22 x 21, representado pelo modelo:
yi(j) =f(xij) +ǫ1j +ǫ0i(j), i= 1,2; j = 1, . . . ,4
Esse ´e um modelo de efeitos fixos e xij s˜ao as linhas da matriz do delineamento,
f ´e uma fun¸c˜ao linear, ǫ1j s˜ao erros associados `a parcela principal com variˆancia σ12,
e ǫ0i(j) s˜ao erros associados `as subparcelas com variˆancia σ02. Primeiro, constru´ımos
uma tabela, onde os fatores A e B s˜ao fatores alocados as parcelas principais e C ´e fator alocadoa `a subparcela para podermos identificar quais s˜ao os efeitos que tem erro relacionado `as parcelas principais e quais tem erro relacionado `a subparcela.
Tabela 3.1: Representa¸c˜ao esquem´atica dos fatores em delineamento aleatorizado em parce-las subdivididas: (A e B s˜ao fatores principais e C fator secund´ario)
A B C− C+
− − y1(1) y2(1)
+ − y1(2) y2(2)
− + y1(3) y2(3)
+ + y1(4) y2(4)
´
E importante observar que estamos usando um modelo de ´ındices escritos na forma i(j) para indicar que a subparcela i est´a aninhada dentro da parcela j. Sendo assim, quando verificamos a respostay1(3), estamos observando sub-parcela 1 (C(−)) que est´a
dentro da parcela 3 (A(−)eB(+)).
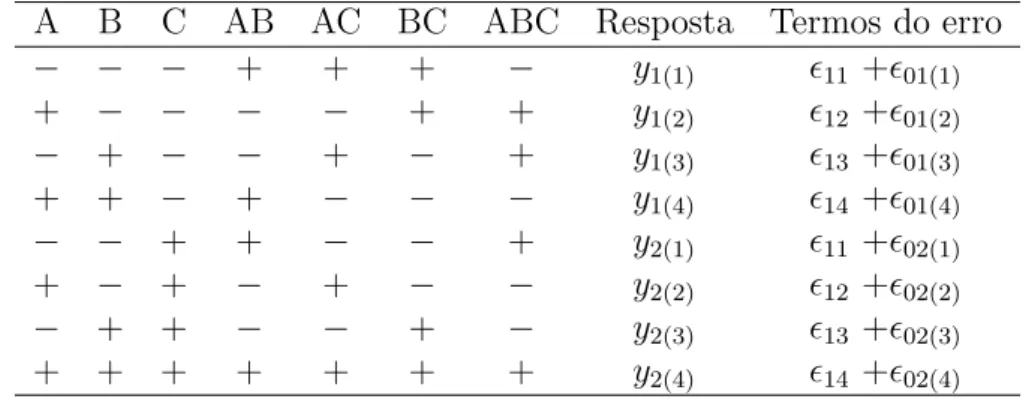
Na tabela 3.2, apresentamos os termos do modelo ignorando a fun¸c˜ao linear f(xij)
para identificar os efeitos que tem erro padr˜ao relacionado `a sub-parcela ou relacionados `a parcela.
Tabela 3.2: Representa¸c˜ao esquem´atica dos fatores em delineamento aleatorizado em parce-las subdivididas: com os sete efeitos e a indica¸c˜ao dos termos de erro
A B C AB AC BC ABC Resposta Termos do erro
− − − + + + − y1(1) ǫ11 +ǫ01(1)
+ − − − − + + y1(2) ǫ12 +ǫ01(2)
− + − − + − + y1(3) ǫ13 +ǫ01(3)
+ + − + − − − y1(4) ǫ14 +ǫ01(4)
− − + + − − + y2(1) ǫ11 +ǫ02(1)
+ − + − + − − y2(2) ǫ12 +ǫ02(2)
− + + − − + − y2(3) ǫ13 +ǫ02(3)
+ + + + + + + y2(4) ǫ14 +ǫ02(4)
ˆ
A= 1
4(y1(2)+ǫ12+ǫ01(2)+y1(4)+ǫ14+ǫ01(4)+y2(2)+ǫ12+ǫ02(2)+y2(4)+ǫ14+ǫ02(4)−
y1(1)−ǫ11−ǫ01(1)−y1(3)−ǫ13−ǫ01(3)−y2(1)−ǫ11−ǫ02(1)−y2(3)−ǫ13−ǫ02(3))
Como o modelo ´e de efeitos fixos, apenas focamos nos termos dos erros para deter-minar o erro padr˜ao. Sendo assim, podemos escrever:
ˆ
A= 1
4(2ǫ12+ 2ǫ14−2ǫ11−2ǫ13+
2
X
j=1
ǫ0j(2)+ 2
X
j=1
ǫ0j(4)+ 2
X
j=1
ǫ0j(1)+ 2
X
j=1
ǫ0j(3))
Observando que os erros n˜ao s˜ao correlacionados, determinamos a variˆancia, e te-mos a estimativa do erro do efeito principal A, associado `as parcelas principais.
V ar{Aˆ}= 1 16(4σ
2
1 + 4σ12+ 4σ12+ 4σ12+ 2σ02+ 2σ02+ 2σ20+ 2σ20) = σ12+
σ2 0
2
Determinamos agora, a estimativa do efeito C associado `as subparcelas conside-rando apenas os termos dos erros para determinar o erro padr˜ao. Ent˜ao, podemos escrever:
ˆ
C= 1 4(
2
X
j=1
ǫ0j(1)+ 2
X
j=1
ǫ0j(2)+ 2
X
j=1
ǫ0j(3)+ 2
X
j=1
ǫ0j(4))
Assim, a estimativa da variˆancia de ˆC ´e:
V ar{Cˆ}= 1 16(2σ
2
0 + 2σ02+ 2σ02+ 2σ02) =
σ2 0
2
Esses c´alculos, segundo Bisgaard (2000), podem ser estendidos para o caso geral de um projeto de parcelas subdivididasN = 2k−p x 2q−r. Ser´a representado por P o efeito
associado `a parcela inteira e por SP o efeito associado `a subparcela. Ent˜ao, temos:
V ar{P}=V ar{ 2
N(2
q−r 2k−p
X
j=1
±ǫ1j + N
X
j=1
∓ǫ0j)}=
=4
N(2
k−r x 22(q−r)σ2
1 + Nσ20) =
=4
N(2
3.1 Cen´arios da Simula¸c˜ao do Experimento 20
V ar{SP}=V ar{2
N
N
X
j=1
ǫ0j}=
4
N2N σ 2 0 = =4 Nσ 2 0
Segundo Bisgaard (2000), em geral, para um projeto de parcelas subdivididas 2k−p
x 2q−r existem um total de 2k−p x 2q−r −1 efeitos poss´ıveis. Se o experimento for
executado com restri¸c˜ao na aleatoriza¸c˜ao, todos os 2q−r−1 efeitos principais (e suas
intera¸c˜oes) gerados da parcela principal ter˜ao a variˆancia da parcela e todos os 2k−p x
2q−r−1 efeitos ter˜ao a variˆancia do erro da subparcela.
No caso do artigo de Bisgaard (1996), temos um projeto de parcelas subdivididas 24 x 21 com 31 (24 x 21−1) efeitos poss´ıveis, sendo 15 (24−1) efeitos da parcela e 16
(24 x(21−1)) efeitos da subparcela.
Em um primeiro momento, foi feita a separa¸c˜ao dos 31 efeitos obtidos do experi-mento: em um grupo com os fatores dif´ıceis de mudar (parcela principal) e em outro, com fatores f´aceis de mudar (subparcela). Na an´alise desse experimento foram feitos gr´aficos separados de probabilidade normal. O motivo para esta separa¸c˜ao ´e que na an´alise de variˆancia de experimentos em parcelas subdivididas recai em duas partes se-paradas onde h´a dois erros n˜ao correlacionados, o erro ǫ1j associado ao reator (parcela
principal), com variˆancia σ2
1, e o erro ǫ0i(j) entre as amostras de papel (subparcela),
dentro do reator, e com uma variˆancia menorσ2 0.
O modelo matem´atico de ANOVA do experimento em parcelas subdivididas ´e
yi(j) =f(xij) +ǫ1j+ǫ0i(j), i= 1,2; j = 1,2, ...,16
onde xij s˜ao as linhas da matriz do projeto, f ´e uma fun¸c˜ao linear, ǫ1j s˜ao erros
associados `a parcela principal com variˆanciaσ2
1, eǫ0i(j)s˜ao erros associados `a subparcela
com variˆanciaσ2 0.
Em um segundo momento foi feito apenas um gr´afico de probabilidade normal com todos os 31 efeitos.
Ap´os a separa¸c˜ao dos efeitos e da plotagem dos gr´aficos de probabilidade normal para os efeitos associados `as parcelas principais e `a subparcela, foi poss´ıvel observar quais efeitos considerados influentes seriam ignorados, o que mostra como seria errada a an´alise se fosse utilizado um gr´afico de probabilidade normal para todos os efeitos.
3.1
Cen´
arios da Simula¸
c˜
ao do Experimento
pr´oximo passo do trabalho: a simula¸c˜ao de cen´arios experimentais para avaliar o modelo experimental adotado na an´alise, sobre um experimento com restri¸c˜ao na aleatoriza¸c˜ao como completamente aleatorizado.
Foram realizadas simula¸c˜oes para os seguintes cen´arios:
• Quantidade de repeti¸c˜oes: 10, 100, 1000 e 10000
Observamos que as simula¸c˜oes com 10 e 100 repeti¸c˜oes n˜ao acrescentaram muitas informa¸c˜oes aos nossos estudos por n˜ao estarem est´aveis.
• Variˆancia do efeito na parcela: 1; 4,75; 16 e 49
Vimos que a variˆancia tinha grande influˆencia nos resultados encontrados, pois quanto maior a variˆancia dos efeitos, maior era o erro do tipo I (classificar ativo um efeito nulo). Por isso, nas simula¸c˜oes, optamos em alterar apenas a variˆancia dos efeitos da parcela, mantendo constante a variˆancia do efeito da subparcela.
• Variˆancia do efeito na subparcela: 1
Utilizando as rela¸c˜oes apresentadas anteriormente para N = 2k−px2q−r
V ar{P}= 4
N(2
q−rσ2 1+σ02)
V ar{SP}= 4
Nσ
2 0
Para N = 32 (24x21), constru´ımos a seguinte tabela:
Var efeito Parcela Var efeito Subparcela Var erro Parcela Var erro Subparcela Var{P} Var{SP} σ2
1 σ02
1 1 - 8
4,75 1 15 8
16 1 60 8
49 1 192 8
• Quantidade total de efeitos ativos: 5
3.1 Cen´arios da Simula¸c˜ao do Experimento 22
• A magnitude dos efeitos do modelo ´e: A = 11,825; D = - 15,1; E = 3,1375; AD = 16,5625; AE = - 5,9 a m´edia = 40,98125 e todos os outros efeitos s˜ao iguais a zero.
• A distribui¸c˜ao do erro no modelo foi a Normal.
Para que a an´alise do experimento n˜ao seja baseado em apenas crit´erios subjetivos como na fase inicial do estudo, foi usado como crit´erio para exame dos efeitos, o m´etodo de Lenth. Com isso, encontramos resultados anal´ıticos com um procedimento formal. Nessa segunda fase, consideramos as seguintes hip´oteses:
H0 :Ef eito= 0
H1 :Ef eito6= 0
Como j´a foi mostrado, o m´etodo de Lenth define uma margem de erro (ME) como
M E=t(0,975;d).1,5.mediana|cj|<2,5.1,5mediana|cj|e uma margem de erro simultˆanea (SME)
como SM E = t(γ,d).1,5.mediana|cj|<2,5.1,5mediana|cj| sendo que c1, c2, . . . , cj, . . . , cm s˜ao
as estimativas dos efeitos, d = m
3 e γ = (1 + 0,95
1
m)/2, onde esses valores servir˜ao
como referˆencia na classifica¸c˜ao da existˆencia de um efeito ativo. Ap´os calcularmos esses valores, o m´etodo de Lenth e ilustrado em um gr´afico de barras dos efeitos, tendo como referˆencia, linhas relativas ao±M E e±SM E. Um efeito ser´a considerado ativo quando a sua barra ultrapassar a linha referente a SME e ser´a considerado inativo quando a barra n˜ao ultrapassar uma das linhas referentes a ME. Quando a barra de um efeito ficar entre ME e SME, n´os vamos classificar esse efeito como marginalmente ativo.
A seguir, s˜ao constru´ıdos separadamente, os gr´aficos das estimativas dos contrastes para os efeitos cujos erros est˜ao relacionados `as parcelas principais ou relacionados `a subparcela.
3.1 Cen´arios da Simula¸c˜ao do Experimento 24
Ap´os a an´alise dos dados verificamos a necessidade de controlar melhor o erro do tipo I (classificar como ativo um efeito nulo) por isso, seguimos a sugest˜ao de Ha-mada e Yo (2000) de usar a tabela de valores cr´ıticos elaborada a partir de estudo feito baseado em 10000 simula¸c˜oes. Assim, deixamos de usar os valores calculados pelo m´etodo de Lenth para a margem de erro (ME) e para margem de erro simultˆa-nea (SME) e passamos a considerar, ainda com confian¸ca de aproximadamente 95%,
M E = 2,06.P SE e SM E = 3,92.P SE quando o experimento ´e analisado como com-pletamente aleatorizado e M E = 2,06.P SE e SM E = 3,92.P SE para a an´alise da parcela e M E = 2,133.P SE e SM E = 4,226.P SE para a an´alise da subparcela quando o experimento ´e analisado como Parcelas Subdivididas (Split Plot).
3.2
Resultados
3.2 Resultados 26
artigo de Bisgaard et al (1995) e, quanto aos efeitos da parcela (whole plot), al´em do desvio padr˜ao igual a 7 (como sugerido no artigo) foram usados os desvios 1, 2 e 4.
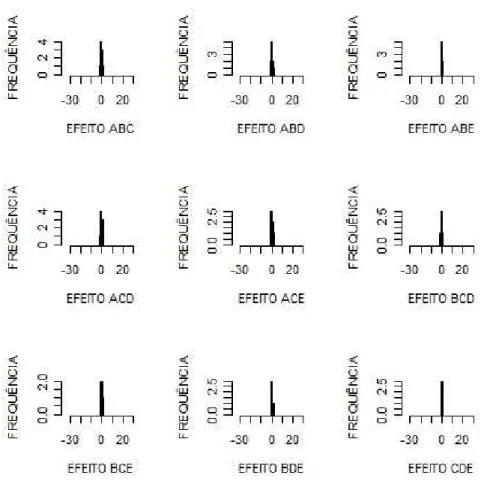
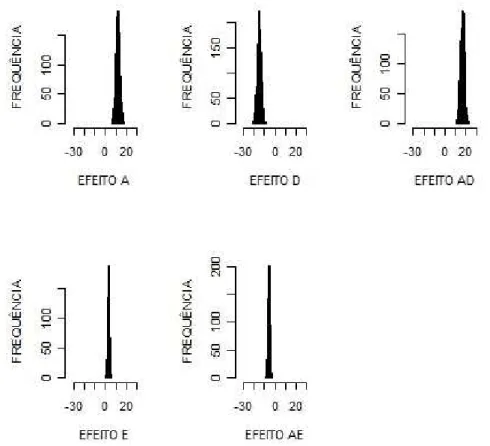
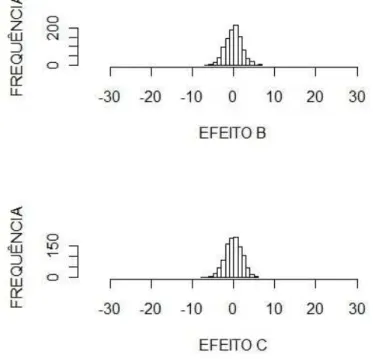
Verificamos que com uma quantidade pequena de repeti¸c˜oes (10 e at´e mesmo 100) n˜ao foi poss´ıvel tirar conclus˜oes importantes sobre o estudo, j´a que os dados, como mostram alguns histogramas da distribui¸c˜ao dos efeitos a seguir, n˜ao estavam est´aveis. Todos os histogramas analisados encontram-se dispon´ıveis no apˆendice B.
10 Repeti¸c˜
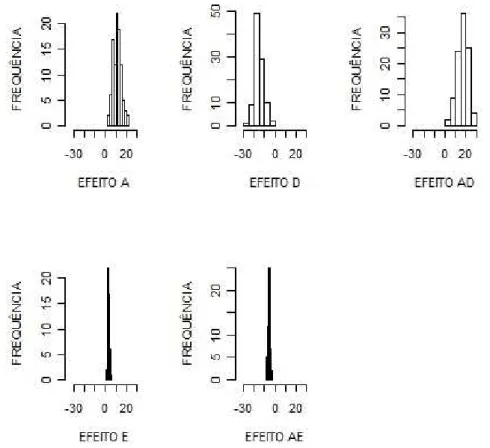
oes - Efeitos Ativos.
Variˆ
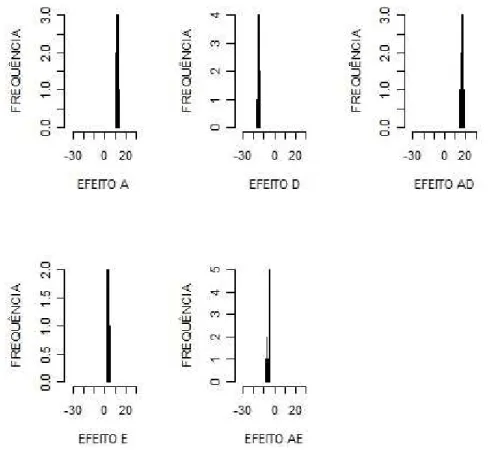
ancia do efeito da parcela = 1 e da subparcela = 1
Figura 9: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 28
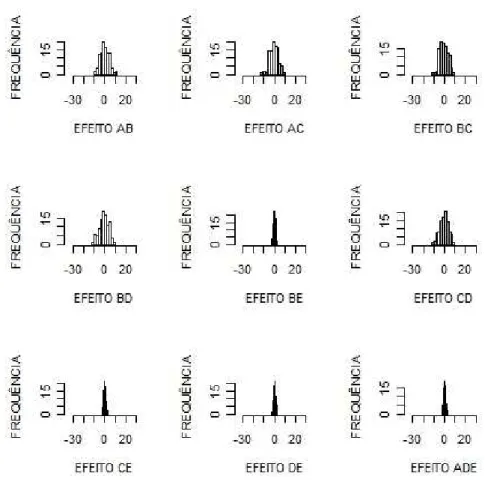
10 Repeti¸c˜
oes - Efeitos Inativos.
Variˆ
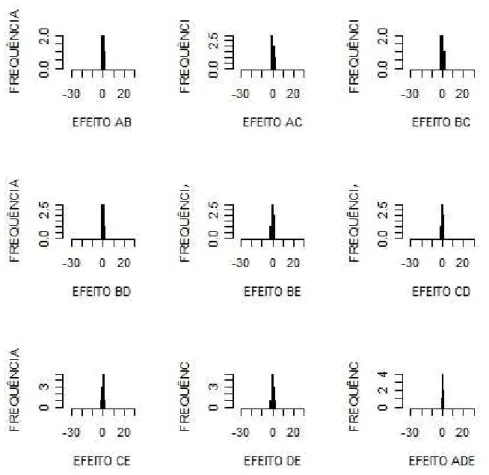
ancia do efeito da parcela = 1 e da subparcela = 1
Figura 10: Histogramas de frequˆencia dos efeitos do experimento
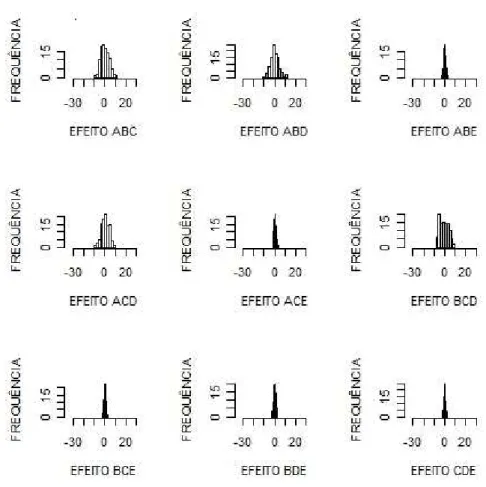
Figura 11: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 30
Figura 12: Histogramas de frequˆencia dos efeitos do experimento
Magnitude dos efeitos inativos = 0
100 Repeti¸c˜
oes - Efeitos Ativos
Variˆ
ancia do efeito da parcela = 16 e da subparcela = 1
Figura 13: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 32
100 Repeti¸c˜
oes - Efeitos Inativos
Variˆ
ancia do efeito da parcela = 16 e da subparcela = 1
Figura 14: Histogramas de frequˆencia dos efeitos do experimento
Figura 15: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 34
Figura 16: Histogramas de frequˆencia dos efeitos do experimento
Magnitude dos efeitos inativos = 0
O desvio padr˜ao dos efeitos da parcela ´e igual a 4 (variˆancia do efeito
igual 16 e variˆancia do erro da parcela igual a 60) e desvio padr˜ao dos
efeitos da subparcela igual a 1 (Variˆancia do efeito igual 1 e variˆancia
do erro da subparcela igual a 8), mesmo com cem repeti¸c˜oes, os dados
ainda n˜ao est˜ao est´aveis.
1000 Repeti¸c˜
oes - Efeitos Ativos.
Variˆ
ancia do efeito da parcela = 4 e da subparcela = 1
Figura 17: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 36
1000 Repeti¸c˜
oes - Efeitos Inativos.
Variˆ
ancia do efeito da parcela = 4 e da subparcela = 1
Figura 18: Histogramas de frequˆencia dos efeitos do experimento
Figura 19: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 38
Figura 20: Histogramas de frequˆencia dos efeitos do experimento
Magnitude dos efeitos inativos = 0
10000 Repeti¸c˜
oes - Efeitos Ativos
Variˆ
ancia do efeito da parcela = 49 e da subparcela = 1
Figura 21: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 40
10000 Repeti¸c˜
oes - Efeitos Inativos
Variˆ
ancia do efeito da parcela = 49 e da subparcela = 1
Figura 22: Histogramas de frequˆencia dos efeitos do experimento
Figura 23: Histogramas de frequˆencia dos efeitos do experimento
3.2 Resultados 42
Figura 24: Histogramas de frequˆencia dos efeitos do experimento
Magnitude dos efeitos inativos = 0
3.3
Crit´
erios de Avalia¸
c˜
ao
Utilizamos o programa R para, al´em de simular os efeitos, calcular as
margens de erro ME e SME e definir os efeitos ativos. Todos os dados
foram armazenados em tabelas do seguinte modo:
•
O t´ıtulo da tabela indica o n´
umero de r´eplicas, a variˆancia do efeito
da parcela e da subparcela.
•
A primeira coluna indica o fator que foi analisado.
•
A segunda, terceira e quarta colunas, mostram que se o experimento
tivesse sido executado como completamente aleatorizado,
apresen-taria resultados que indicariam, respectivamente, frequˆencia
rela-tiva de experimentos em que o fator analisado foi classificado ativo,
marginalmente ativo e inativo (neste caso, o experimento n˜ao foi
analisado como foi executado).
•
A quinta, sexta e s´etima colunas, apresentam resultados que
indi-cam, respectivamente, frequˆencia relativa de experimentos em que
o fator que foi analisado corretamente, de acordo com o
delinea-mento em parcelas subdivididas (Split Plot) foi classificado ativo,
marginalmente ativo e inativo.
A seguir, ser˜ao mostradas quatro tabelas com esses resultados. Para
facilitar a an´alise, a tabela foi dividida, por uma linha dupla, em duas
partes: a parte superior da tabela est˜ao os efeitos ativos (A de magnitude
11,8; D de magnitude
−
15,1; E de magnitude 3,1; AD de magnitude
16,6 e AE de magnitude
−
5,0) e na parte inferior os efeitos inativos
(todos com magnitude zero).
3.3 Crit´erios de Avalia¸c˜ao 44
Tabela 3.3: Frequˆencia relativa de experimentos em que cada fator foi classificado como “ativo”, “marginalmente ativo ” ou “inativo” considerando a an´alise correta (delineamento aleatorizado com parcelas subdivididas) ou a an´alise incorreta (delineamento completamente aleatorizado);N = 1000;σP2 = 1;σ2SP = 1
Completamente Aleatorizado Parcelas Subdivididas
Fator ativo marg ativo inativo ativo marg ativo inativo A 100.0 0.0 0.0 100.0 0.0 0.0 D 100.0 0.0 0.0 100.0 0.0 0.0 AD 100.0 0.0 0.0 100.0 0.0 0.0 E 27.2 53.3 19.5 26.4 47.0 26.6 AE 90.5 9.5 0.0 78.5 20.7 0.8
Tabela 3.4: Frequˆencia relativa de experimentos em que cada fator foi classificado como “ativo”, “marginalmente ativo ” ou “inativo” considerando a an´alise correta (delineamento aleatorizado com parcelas subdivididas) ou a an´alise incorreta (delineamento completamente aleatorizado);N = 1000;σP2 = 16;σ2SP = 1
Completamente Aleatorizado Parcelas Subdivididas
Fator ativo marg ativo inativo ativo marg ativo inativo A 87.61 9.80 2.59 22.42 41.56 36.02 D 97.00 2.73 0.27 37.01 45.65 17.34 AD 98.72 1.18 0.10 43.46 44.97 11.57 E 4.47 36.86 58.67 23.44 50.97 25.59 AE 39.91 54.52 5.57 79.27 20.50 0.23
3.3 Crit´erios de Avalia¸c˜ao 46
Tabela 3.5: Frequˆencia relativa de experimentos em que cada fator foi classificado como “ativo”, “marginalmente ativo ” ou “inativo” considerando a an´alise correta (delineamento aleatorizado com parcelas subdivididas) ou a an´alise incorreta (delineamento completamente aleatorizado);N = 10000;σ2P = 4,75;σSP2 = 1
Completamente Aleatorizado Parcelas Subdivididas
Fator ativo marg ativo inativo ativo marg ativo inativo A 99.52 0.48 0.00 86.98 12.78 0.24 D 99.98 0.02 0.00 97.82 2.18 0.00 AD 100.00 0.00 0.00 99.14 0.86 0.00 E 8.72 48.76 42.52 23.40 50.09 26.51 AE 61.54 37.47 0.99 79.47 20.18 0.35
Tabela 3.6: Frequˆencia relativa de experimentos em que cada fator foi classificado como “ativo”, “marginalmente ativo ” ou “inativo” considerando a an´alise correta (delineamento aleatorizado com parcelas subdivididas) ou a an´alise incorreta (delineamento completamente aleatorizado);N = 10000;σ2P = 49;σ2SP = 1
Completamente Aleatorizado Parcelas Subdivididas
Fator ativo marg ativo inativo ativo marg ativo inativo A 73.55 14.05 12.40 4.60 18.92 76.48 D 86.06 8.49 5.45 8.16 28.40 63.44 AD 89.57 6.54 3.89 10.28 33.28 56.44 E 3.54 32.01 64.45 23.58 50.45 25.97 AE 33.63 56.80 9.57 79.17 20.44 0.39
B 32.62 25.86 41.52 0.37 2.73 96.90 C 32.58 25.81 41.61 0.34 2.85 96.81 AB 31.97 25.53 42.50 0.39 2.63 96.98 AC 31.97 26.11 41.92 0.25 2.78 96.97 BC 31.88 25.41 42.71 0.33 2.78 96.89 BD 32.31 25.42 42.27 0.29 2.69 97.02 BE 0.00 0.31 99.69 0.30 3.87 95.83 CD 32.53 25.81 41.66 0.28 2.80 96.92 CE 0.01 0.28 99.71 0.37 3.80 95.83 DE 0.00 0.44 99.56 0.47 3.84 95.69 ABC 32.99 25.42 41.59 0.40 2.81 96.79 ABD 31.86 25.70 42.44 0.31 2.52 97.17 ABE 0.02 0.36 99.62 0.34 3.99 95.67 ACD 31.76 24.89 43.35 0.32 2.74 96.94 ACE 0.00 0.35 99.65 0.29 3.54 96.17 ADE 0.00 0.41 99.59 0.44 3.78 95.78 BCD 32.11 25.21 42.68 0.37 2.60 97.03 BCE 0.00 0.28 99.72 0.34 4.09 95.57 BDE 0.01 0.36 99.63 0.37 3.74 95.89 CDE 0.01 0.25 99.74 0.39 4.02 95.59 ABCD 32.22 25.91 41.87 0.26 2.45 97.29 ABCE 0.00 0.30 99.70 0.32 3.79 95.89 ABDE 0.02 0.34 99.64 0.36 3.78 95.86 ACDE 0.00 0.29 99.71 0.45 4.26 95.29 BCDE 0.00 0.41 99.59 0.39 3.83 95.78 ABCDE 0.01 0.27 99.72 0.29 3.97 95.74
3.3 Crit´erios de Avalia¸c˜ao 48
Outra observa¸c˜ao importante, ´e a ordem proporcional ao valor
abso-luto da magnitude dos efeitos ativos (AD que tem a maior magnitude
(16
,
6) tem a porcenagem maior e E que tem a menor magnitude (3
,
1)
tem a porcentagem menor).
Para analisarmos os dados das tabelas, inicialmente constru´ımos
gr´a-ficos de intera¸c˜oes em que, no eixo horizontal, aparecem as raz˜oes entre
o desvio padr˜ao do efeito na parcela pelo desvio padr˜ao do efeito na
subparcela. No eixo vertical, aparecem as porcentagens que o efeito,
indicado nesse eixo, foi classificado como inativo.
3.3 Crit´erios de Avalia¸c˜ao 50
O efeito E ´e, na simula¸c˜ao, considerado ativo e tem magnitude 3,1.
Ap´os a an´alise dos gr´aficos de intera¸c˜ao, foi observado que a maneira
como o experimento foi analisado (como completamente aleatorisado ou
como parcelas subdivididas) e a raz˜ao entre a variˆancia do efeito da
parcela e a variˆancia do efeito da subparcela tinham grande significado
para determinar se um fator era classificado como ativo ou n˜ao. Al´em
disso, era preciso verificar, dependendo do modo que o experimento foi
analisado, se um fator ativo foi classificado como inativo ou se um fator
inativo foi classificado como ativo.
3.3 Crit´erios de Avalia¸c˜ao 52
porcentagem que determinado fator foi classificado como inativo ´e a
res-posta procurada. Tivemos assim o seguinte cen´ario:
•
Fator A - Raz˜ao entre a variˆancia do efeito da parcela e a variˆancia
do efeito da subparcela.
N´ıveis: 1; 4
,
75; 16 e 49.
A raz˜ao 1 corresponde a
A
1(
−
)
A
2(
−
), a raz˜ao 4 corresponde a
A
1(+)
A
2(
−
), a raz˜ao 16 corresponde a
A
1(
−
)
A
2(+) e a raz˜ao 49
corresponde a
A
1(+)
A
2(+).
•
Fator B - Repeti¸c˜oes.
N´ıveis: 10, 100, 1000 e 10000
B
1(
−
)
B
2(
−
) representa 10 repeti¸c˜oes,
B
1(+)
B
2(
−
), representa 100
repeti¸c˜oes,
B
1(
−
)
B
2(+), representa 1000 repeti¸c˜oes e
B
1(+)
B
2(+)
representa 10000 repeti¸c˜oes.
•
Fator C - Tipo de an´alise.
N´ıveis: Completamente Aleatorizado e Parcelas Subdivididas
C
(
−
) indica que o experimento foi analisado como se tivesse sido
executado como Completamente Aleatorisado e
C
(+) indica que o
experimento foi analisado como Parcelas Subdivididas.
FATOR A (press˜ao) - Considerado, na simula¸c˜ao, como Ativo.
Tabela 3.7: Porcentagem em que o fator A foi classificado como inativo
A1 A2 B1 B2 C − C +
− − − − 0 0 + − − − 0 0
− + − − 0 30 + + − − 20 60
− − + − 0 0 + − + − 0 0
− + + − 1 45 + + + − 11 70
− − − + 0 0 + − − + 0 0,1
− + − + 2,59 36,02 + + − + 11,5 74,5
− − + + 0 0 + − + + 0 0,24
3.3 Crit´erios de Avalia¸c˜ao 54
3.3 Crit´erios de Avalia¸c˜ao 56
FATOR B (energia) - Considerado, na simula¸c˜ao, como Inativo.
Tabela 3.8: Porcentagem em que o fator B foi classificado como inativo
A1 A2 B1 B2 C - C +
− − − − 100 100 + − − − 70 100
− + − − 50 100 + + − − 60 100
− − + − 96 97 + − + − 85 97
− + + − 66 99 + + + − 42 99
− − − + 96,2 95,6 + − − + 85,5 95,5
− + − + 63 96,24 + + − + 43,5 96,9
− − + + 95,91 94,9 + − + + 83,52 94,54
3.3 Crit´erios de Avalia¸c˜ao 58
FATOR E (tipo de papel) - Considerado, na simula¸c˜ao, como Ativo.
Tabela 3.9: Porcentagem em que o fator E foi classificado como inativo
A1 A2 B1 B2 C - C +
− − − − 40 20 + − − − 50 40
− + − − 70 30 + + − − 60 0
− − + − 19 26 + − + − 42 23
− + + − 58 32 + + + − 66 24
− − − + 19,5 26,6 + − − + 41,4 24,6
− + − + 58,67 25,59 + + − + 60,2 26,7
− − + + 19,43 25,76 + − + + 42,52 26,51
3.3 Crit´erios de Avalia¸c˜ao 60
A figura 33 indica os efeitos da subparcela (C e suas intera¸c˜oes) e ´e
observado que a maneira que o experimento ´e analisado ´e significativa.
Cap´ıtulo 4
Conclus˜
ao
Experimentos de parcelas subdivididas, sem r´eplicas, al´em de reduzir
o trabalho e o custo, s˜ao sempre melhores para detectar os efeitos ativos
das subparcelas.
Uma das desvantagens desse delineamento ´e n˜ao existir uma
estima-tiva independente das varia¸c˜oes dos erros e, por isso, a necessidade de
supor modelos com apenas poucos efeitos significativos, assumindo que
intera¸c˜oes de ordem mais altas s˜ao insignificantes, e podem ser
combi-nadas para produzir estimativas das variˆancias de erros.
Devido `a incapacidade ou ao custo de aleatorizar completamente o
experimento, frequentemente, mais restri¸c˜oes s˜ao inseridas no ensaio
ci-ent´ıfco.
A regra da separa¸c˜ao (como sugerido nas tabelas 1.2 e 1.3) possibilita
identificar quais fatores considerados influentes seriam ignorados se um
experimento de parcelas subdivididas
(split plot)
fossem analisados como
sendo um experimento completamente aleatorizado. Isso ocorre porque
ao analisar um experimento como completamente aleatorizado, quando
n˜ao ´e o caso, a distribui¸c˜ao do erro da parcela
(whole plot)
se mistura
com a distribui¸c˜ao do erro da subparcela
(sub plot)
e essa distribui¸c˜ao
se sobrep˜oe a alguns efeitos verdadeiramente significativos.
Quando o experimento ´e analisado de forma incorreta (considerando o
delineamento como completamente aleatorizado), ao ser avaliado o erro
do tipo I (classificar como ativo um efeito inativo) observa-se que para
os fatores associados `a parcela, quanto maior a raz˜ao entre a variˆancia
do efeito da parcela e da subparcela ´e, em m´edia, maior a frequˆencia dos
efeitos inativos que s˜ao classificados como ativos e, em rela¸c˜ao ao fator
associado `a subparcela, a frequˆencia relativa do erro tipo I foi, em m´edia,
menor que 6% como pode ser visto no quadro 4.1.
Quadro 4.1 - Frequˆencia do erro tipo I quando o experimento ´e analisado de forma incorreta
Raz˜ao entre variˆancias Efeitos associados `a parcela Efeitos associados `a subparcela
1 < 10% < 6%
4,75 ≈20% < 6%
16 ≈40% < 6%
49 ≈60% < 6%
Quando o experimento ´e analisado de forma correta (considerando o
delineamento como parcelas subdivididas), ao ser avaliado o erro do tipo
I observa-se que para os fatores associados `a parcela e `a subparcela, a
frequˆencia relativa do erro tipo I ´e, em m´edia, menor que 10%.
64
Quadro 4.2 - Frequˆencia do erro tipo II quando o experimento ´e analisado de forma incorreta
Raz˜ao entre variˆancias Efeitos associados `a parcela Efeitos associados `a subparcela
1 0% ≈22%
4,75 0% ≈44%
16 ≈1% ≈61%
49 ≈9% ≈63%
Quadro 4.3 - Frequˆencia do erro tipo II quando o experimento ´e analisado de forma correta
Raz˜ao entre variˆancias Efeitos associados `a parcela Efeitos associados `a subparcela
1 0% ≈24%
4,75 0% ≈28%
16 ≈26% ≈29%
49 ≈63% ≈20%
Referˆ
encias Bibliogr´
aficas
[1] Bisgaard, S; Fuller, H. T. and Barrios, E. (1995) -“Quality Quandaries * Two-Level Factorials Run as Split Plot Experiments”,Quality Engineering 1996, v.8, no
4, p.705 - 708.
[2] Bisgaard, S. (2000)“The Design and Analysis of 2k−p x 2q−r Split Plot Ex-periments”, Journal of Quality Engineering 2000, v. 32, p.39 - 56.
[3] Bisgaard, S. and Box, G.E.P.(1987)“The scientific context of qualitynimpro-vements”, Journal Mechamical Engineering 1988, p.32 - 40.
[4] Bisgaard, S. and Vivacqua, C. A. (2004) -“Strip Block and Eperiments for Process Improvement and Robustness”,Quality Engineering, v 16, p. 495 - 500.
[5] Bisgaard, S. and Vivacqua, C. A. (2009) -“Post - Fractionated Strip Block Designs”,Technometrics 2009, v 51, no
1, p. 47 - 55.
[6] Box, G. (1996) - “Quality Quandaries: Split-Plot Experiments”, Quality Engineering, v.8, No
3
[7] Box, G.E.P and Jones, S. (1990) -“Split - Plot Designs for Robust Product Experimentation”, Journal of Applied Stat´ıstics, 1992, v. 19, no
1, 3 - 26.
[8] Daniel, C. (1959) -“Use of Half - Normal Plots in Interpreting Factorial“,
Technometrics, Vol.1, No
4. Pp. 311-341.
[9] Hamada, M. & Balakrishnan, N. (1998) -“Analyzing unreplicated factorial experiments: A review with some new proposals”,Journal Statistica sinica, 1998, v.8, p. 1-41.
66
[10] Montgomery, D.C.“Design and Analysis of Experiments”, 5ed. New York: John Willy Sons, Inc., 2001.
[11] Nobrega M.P. (2010) -´´Estudo Comparativo de Gr´afico de Probabilidade Normal para An´alise de Experimentos Fatoriais N˜ao replicados.”. 194f. Dis-serta¸c˜ao (Mestrado Matem´atica Aplicada e Estat´ıstica)- Universidade Federal do Rio Grande do Norte. UFRN
[12] Saldanha I.C.C. (2008) -“Aleatoriza¸c˜ao em Planejamento de Experimentos: Um estudo de Caso”, 99f. Disserta¸c˜ao (Mestrado em Engenharia de Produ¸c˜ao) -Pontif´ıcia Universidade Cat´olica do Rio de Janeiro. PUC - Rio.
[13] Ye, K.Q, Hamada, M. & Wu, C.F.J. (2001),“A step-down Lenth method for analyzing unreplicated factorial designs”, Journal of Quality Technology 33, 140 - 152.
Comandos no R
A.1
Programa 1 - Gerando os dados
# In´ıcio do programa de gerar dados efA<- 11.825 efB<- 0 efC<- 0 efD<- -15.1 efE<- 3.1375 efAB<- 0 efAC<- 0 efAD<- 16.5625 efAE<- -5.9 efBC<- 0 efBD<- 0 efBE<- 0 efCD<- 0 efCE<- 0 efDE<- 0 efABC=efABD=efABE=efACD=efACE=efADE=efBCD=efBCE=efBDE =efCDE=efABCD=efABCE=efABDE=efACDE=efBCDE=efABCDE=0 media<-40.98125
#(MODELO): Z = media + [(efA+efD+efE+efAD+efAE)/2]+erro whole + errosubp Efeito<-matrix(c(efA,efB,efC,efD,efE,efAB,efAC,efAD,efAE,efBC,efBD,efBE,efCD, efCE,efDE,efABC,efABD,efABE,efACD,efACE,efADE,efBCD,efBCE,efBDE,efCDE, efABCD,efABCE,efABDE,efACDE,efBCDE,efABCDE)) ALL<-matrix(c(A<-matrix(rep(c(-1,1),16)),B<-matrix(c(rep(-1,2),(rep(1,2))),32), C<-matrix(c(rep(-1,4),(rep(1,4))),32),D<-matrix(c(rep(-1,8),(rep(1,8))),32), E<-matrix(c(rep(-1,16),(rep(1,16))),32),A*B,A*C,A*D,A*E,B*C,B*D,B*E,C*D,C*E, D*E,A*B*C,A*B*D,A*B*E,A*C*D,A*C*E,A*D*E,B*C*D,B*C*E,B*D*E,C*D*E, A*B*C*D,A*B*C*E,A*B*D*E,A*C*D*E,B*C*D*E,A*B*C*D*E),ncol=31) Z<-media+(ALL%*%(Efeito/2)) WContador<-1 # in´ıcio do loop
A.1 Programa 1 - Gerando os dados 68
while (WContador<10001)
w<-0
w<-rnorm(16,0,sqrt(0)) #desvio whole = 1 s<-rnorm(32,0,sqrt(8)) # desvio subp = 1 iz<-1
iw<-1 is<-1 YY<- 1:32 dim(YY)<-(32)
while (iz<33){
Y<-matrix(c(Z[iz]+w[iw]+s[is])) YY[iz]<-(Y)
iz<- iz + 1 is<- is + 1 iw<- iw + 1 if (iw==17) iw<-1
}
Efeito<- 1:31 dim(Efeito)<-(31)
somaN<- 0 somaP<- 0 iz<-1 WW<-1
m<- 1:5 dim(m)<-(5) m[1]<-1 m[2]<-1 m[3]<-1 m[4]<-1 m[5]<-1
while (WW<32){
somaN<- 0 somaP<- 0 iz<-1
while (iz<33){
if (WW==1) m[1]<-A[iz] if (WW==2) m[2]<-B[iz] if (WW==3) m[3]<-C[iz] if (WW==4) m[4]<-D[iz] if (WW==5) m[5]<-E[iz]
if (WW==6){m[1]<-A[iz] m[2]<-B[iz]
if (WW==7){m[1]<-A[iz] m[3]<-C[iz]
}
if (WW==8){m[1]<-A[iz] m[4]<-D[iz]
}
if (WW==9){m[1]<-A[iz] m[5]<-E[iz]
}
if (WW==10){m[2]<-B[iz] m[3]<-C[iz]
}
if (WW==11){m[2]<-B[iz] m[4]<-D[iz]
}
if (WW==12){m[2]<-B[iz] m[5]<-E[iz]
}
if (WW==13){m[3]<-C[iz] m[4]<-D[iz]
}
if (WW==14){m[3]<-C[iz] m[5]<-E[iz]
}
if (WW==15){m[4]<-D[iz] m[5]<-E[iz]
}
if (WW==16){m[1]<-A[iz] m[2]<-B[iz]
m[3]<-C[iz]
}
if (WW==17){m[1]<-A[iz] m[2]<-B[iz]
m[4]<-D[iz]
}
if (WW==18){m[1]<-A[iz] m[2]<-B[iz]
m[5]<-E[iz]
}
if (WW==19){m[1]<-A[iz] m[3]<-C[iz]
m[4]<-D[iz]
}
if (WW==20){m[1]<-A[iz] m[3]<-C[iz]
m[5]<-E[iz]
}
if (WW==21){m[1]<-A[iz] m[4]<-D[iz]
m[5]<-E[iz]
}
if (WW==22){m[2]<-B[iz] m[3]<-C[iz]
m[4]<-D[iz]