Modelos de risco de mercado com fat tail: análise empírica de value at risk and expected shortfall para ativos financeiros brasileiros

MARCELO FERREIRA SANTOS

MODELOS DE RISCO COM FAT TAIL

ANÁLISE EMPÍRICA DE VALUE AT RISK E EXPECTED SHORTFALL PARA ATIVOS FINANCEIROS BRASILEIROS

MODELOS DE RISCO COM FAT TAIL

ANÁLISE EMPÍRICA DE VALUE AT RISK E EXPECTED SHORTFALL PARA ATIVOS FINANCEIROS BRASILEIROS

Dissertação apresentada à Escola de Economia de São Paulo da Fundação Getúlio Vargas como requisito para obtenção do título de Mestre em Finanças e Economia Empresarial

Campo de conhecimento:

Finanças de Mercado Financeiro Orientador:

Prof. Dr. José Evaristo dos Santos

Santos, Marcelo Ferreira.

Modelo de risco com Fat Tail: análise empírica de Value at Risk e Expected Shortfall para ativos financeiros brasileiros / Marcelo Ferreira Santos. – 2008. 59 f.

Orientador: José Evaristo dos Santos

Dissertação (mestrado) – Escola de Economia de São Paulo

1. Value at Risk. 2. Expected Shortfall. 3. Risk Management. 4. Distribuição Estável. 5. Mercado Financeiro – I. Santos, José Evaristo. II. Dissertação (mestrado) – Escola de Economia de São Paulo. III. Título.

MODELOS DE RISCO COM FAT TAIL

ANÁLISE EMPÍRICA DE VALUE AT RISK E EXPECTED SHORTFALL PARA ATIVOS FINANCEIROS BRASILEIROS

Dissertação apresentada à Escola de Economia de São Paulo da Fundação Getúlio Vargas, como requisito para obtenção do título de Mestre em Finanças e Economia Empresarial

Campo de conhecimento:

Finanças de Mercado Financeiro Data de aprovação:

__ / __ / __

Banca examinadora:

Prof. Dr. José Evaristo dos Santos (Orientador)

FGV-EAESP

Prof. Dr. Afonso de Campos Pinto FGV-EAESP

Prof. Dr. Marcos Eugênio da Silva USP

Primeiramente a Deus, origem e fim de tudo que somos. Nunca nos esquecendo de que se os homens criam oportunidades, Deus cria os homens.

Ao mestre e guru Evaristo pelo carinho e atenção desde os tempos da graduação e agora, por ter nos exemplificado, a cada conversa, o verdadeiro sentido de que ao dividir seus conhecimentos o homem torna-se mais nobre.

Ao senhor Nelson Sussumu Niskioka, ex-chefe e agora precioso amigo, que não somente incentivou esse curso, mas tem auxiliado no desenvolvimento profissional e pessoal do autor.

Ao senhor Fábio de Aguiar Faria, por confiar no trabalho desse profissional, mesmo em momentos apertados do curso e, sobretudo, nos contratempos de vida.

Ao senhor Afonso de Campos Pinto, por seu grande profissionalismo e sua valiosa amizade.

Ao senhor Marcos Eugênio da Silva, por suas fundamentais colocações que ajudaram a enriquecer o presente trabalho.

Ao senhor Márcio Larini Polleti, professor do IBMEC-SP, que nos deu provas de grande desprendimento e atenção nas discussões sobre a modelagem econométrica desse trabalho.

Aos senhores Milena Gordon, Sueli Bresciani, Rodrigo Grigolin, Éber Luciano da Silva, Nicolau Assali, Marcelo Cano, Leonardo Curi, Octávio de Barros, Gilberto César e Arthur Lima, os quais não foram somente colegas de curso, mas amigos para mais de uma vida.

À querida Mirian Kanashiro, a qual foi peça fundamental para que pudesse realizar esse curso e me compreender melhor como profissional.

Aos professores e seus respectivos monitores pelo desprendimento em compartilhar experiências.

Aos funcionários da escola (inspetores, faxineiros, seguranças, porteiros, bibliotecários e quaisquer que tenha esquecido), sem os quais nada poderia transcorrer normalmente sem a presença de tais.

Aos meus amigos, sejam eles de Ribeirão Preto, São Paulo ou desse “mundo afora”, os quais souberam me ouvir, uma vez mais, quando a paciência parecia se esgotar.

O objetivo deste trabalho foi mostrar modelagens alternativas à tradicional maneira de se apurar o risco de mercado para ativos financeiros brasileiros. Procurou-se cobrir o máximo possível de fatores de risco existentes no Brasil; para tanto utilizamos as principais proxies para instrumentos de Renda Fixa.

Em momentos de volatilidade, o gerenciamento de risco de mercado é bastante criticado por trabalhar dentro de modelagens fundamentadas na distribuição normal. Aqui reside a maior contribuição do VaR e também a maior crítica a ele. Adicionado a isso, temos um mercado caracterizado pela extrema iliquidez no mercado secundário até mesmo em certos tipos de títulos públicos federais. O primeiro passo foi fazer um levantamento da produção acadêmica sobre o tema, seja no Brasil ou no mundo. Para a nossa surpresa, pouco, no nosso país, tem se falado em distribuições estáveis aplicadas ao mercado financeiro, seja em gerenciamento de risco, precificação de opções ou administração de carteiras. Após essa etapa, passamos a seleção das variáveis a serem utilizadas buscando cobrir uma grande parte dos ativos financeiros brasileiros. Assim, deveríamos identificar a presença ou não da condição de normalidade para, aí sim, realizarmos as modelagens das medidas de risco, VaR e ES, para os ativos escolhidos,

As condições teóricas e práticas estavam criadas: demanda de mercado (crítica ao método gausiano bastante difundido), ampla cobertura de ativos (apesar do eventual questionamento da liquidez), experiência acadêmica e conhecimento internacional (por meio de detalhado e criterioso estudo da produção sobre o tema nos principais meios). Analisou-se, desta forma, quatro principais abordagens para o cálculo de medidas de risco sendo elas coerentes (ES) ou não (VaR).

É importante mencionar que se trata de um trabalho que poderá servir de insumo inicial para trabalhos mais grandiosos, por exemplo, aqueles que incorporarem vários ativos dentro de uma carteira de riscos lineares ou, até mesmo, para ativos que apresentem risco não-direcionais.

The goal of this work was to show alternatives models to the traditional way of measuring market risk for Brazilian financial assets. In order to cover the maximum possible risk factors in Brazil, we have used the main proxies for Fixed Income products. In times of volatility, market risk management is highly criticized for working in models based on normal distribution. Here it is the best contribution of the VaR and also the greatest criticism of it. In addition, our financial market is characterized by extreme illiquidity in the secondary market in spite of certain governmental bonds. The first stage was to research academic production about the theme in Brazil or worldwide. To our surprise, little has been said in country about stable distribution applied to financial market, whether in risk management, options pricing, or portfolio management. After this step, we selected a set of variables to be used aiming to cover a large part of Brazilian financial assets. Thus, we were able to identify or not a presence of normality condition so that we could model risk measure, VaR and ES, for chosen assets.

The theoretical and practical conditions were created: market demand (heavy criticisms of Gausian approach), ample selection of assets (in spite of eventual doubts about liquidity), academic experience, and international knowledge (by means of detailed and meticulous study of the production about the theme in the main circles). In this way, four principal approaches have been analyzed in order to calculate risk measures whether they be coherent or not.

It is important to mention that this work might be useful for large initiatives, for example, those which incorporate several assets within linear risk portfolios or, even, for non-linear portfolios.

TABELA 1–INDICADORESDAFAMÍLIAIMAEPERÍODODEESTUDO ...24

TABELA 2–VALORESADMISSÍVEISDETOLERÂNCIAPARAVAR ...49

TABELA 3–LIMITESDETOLERÂNCIAPARAVAR...49

TABELA 4–EXCEÇÕESNOSMODELOSESTUDADOSDEVARPARANÍVELDE

SIGNIFICÂNCIADE95% ...50

TABELA 5–EXCEÇÕESNOSMODELOSESTUDADOSDEVARPARANÍVELDE

GRÁFICO2–HISTOGRAMADOSRETORNOSDIÁRIOSDOIBOVESPA...29

GRÁFICO3–EVOLUÇÃODOSRETORNOSDIÁRIOSDOIMA-S...30

GRÁFICO4–HISTOGRAMADOSRETORNOSDIÁRIOSDOIMA-S...30

GRÁFICO5–EVOLUÇÃODOSRETORNOSDIÁRIOSDOIMA-B...31

GRÁFICO6–HISTOGRAMADOSRETORNOSDIÁRIOSDOIMA-B...31

GRÁFICO7–EVOLUÇÃODOSRETORNOSDIÁRIOSDOIMA-C ...32

GRÁFICO8–HISTOGRAMADOSRETORNOSDIÁRIOSDOIMA-C...32

GRÁFICO9–EVOLUÇÃODOSRETORNOSDIÁRIOSDOIRF-M ...33

GRÁFICO10–HISTOGRAMADOSRETORNOSDIÁRIOSDOIRF-M...33

GRÁFICO11–EVOLUÇÃODOSRETORNOSDIÁRIOSDAPTAX-V...34

GRÁFICO12–HISTOGRAMADOSRETORNOSDIÁRIOSDAPTAX-V ...34

GRÁFICO13–DISTRIBUIÇÃOTEÓRICANORMALDOIBOVESPA ...35

GRÁFICO14–DISTRIBUIÇÃOTEÓRICANORMALDA PTAX-V ...35

GRÁFICO15–DISTRIBUIÇÃOTEÓRICANORMALDOIRF-M...36

GRÁFICO16–DISTRIBUIÇÃOTEÓRICANORMAL DO IMA-B ...36

GRÁFICO17–DISTRIBUIÇÃOTEÓRICANORMAL DO IMA-C...36

GRÁFICO18–DISTRIBUIÇÃOTEÓRICANORMAL DO IMA-S ...36

GRÁFICO19–DISTRIBUIÇÃODERETORNOSNEGATIVOS DO IBOVESPA ...45

GRÁFICO20–DISTRIBUIÇÃODERETORNOSNEGATIVOS DA PTAX-V...45

GRÁFICO21–DISTRIBUIÇÃODERETORNOSNEGATIVOS DO IRF-M ...45

GRÁFICO22–DISTRIBUIÇÃODERETORNOSNEGATIVOS DO IMA-B ...45

GRÁFICO23–DISTRIBUIÇÃODERETORNOSNEGATIVOS DO IMA-C ...45

1. INTRODUÇÃO ...13

2.REVISÃOBIBLIOGRÁFICA ...17

3. ASPECTOS CONCEITUAIS...21

3.1SÉRIES ...21

3.1.1 PTAX-V ...22

3.1.2 IBOVESPA ...22

3.1.3IMA-ÍNDICESDEMERCADOANDIMA ...22

3.2 RETORNOS LOGARÍTMICOS ...25

3.3HOLDINGPERIOD...25

3.4 JANELA MÓVEL...25

3.5 NÍVEL DE SIGNIFICÂNCIA ...25

3.6THRESHOLDUDOPOT...26

3.7 BACKTESTING ...26

4. ANÁLISE ESTATÍSTICA TRADICIONAL...28

4.1IBOVESPA ...28

4.2 IMA-S...29

4.3IMA-B...30

4.4 IMA-C ...31

4.5 IRF-M...32

4.6PTAX-V...33

4.7 IDENTIFICAÇÃO DE HEAVY FAT TAIL ...34

5.DEFINIÇÕESEMODELOS...37

5.1 DEFINIÇÕES...36

5.1.2 EXPECTED SHORTFALL ...38

5.2MODELOS...39

5.2.1 ABORDAGEM EMPÍRICA OU HISTÓRICA...39

5.2.2 ABORDAGEM GAUSIANA ...40

5.2.3ABORDAGEMDEVALORESEXTREMOS ...40

5.2.4 ABORDAGEM PARETIANA ESTÁVEL ...42

5.3JUSTIFICATIVA ...44

6. RESULTADOS EMPÍRICOS ...47

6.1 TESTE DE HIPÓTESE ...47

6.2ANÁLISEDOSRESULTADOS...49

6.2.1 ANÁLISE DO VAR ...49

6.2.1.1IBOVESPA ...50

6.2.1.2 IMA-S...50

6.2.1.3 IMA-B...51

6.2.1.4IMA-C ...51

6.2.1.5 IRF-M...51

6.2.1.6 PTAX-V...51

6.2.2ANÁLISEDOES...52

7.CONCLUSÕES ...54

REFERÊNCIASBIBLIOGRÁFICAS ...56

“…...the biggest problem we now have with the whole evolution of the risk is the fat-tailed problem, which is really creating very large conceptual difficulties. Because as we all know, the assumption of normality enables us to drop off the huge amount of complexity in our equations. Because once you start putting in non-normality assumptions, which is unfortunately what characterizes the real world, then these issues become extremely difficult."

Alan Greenspan

1) Introdução

Uma das principais atribuições das instituições financeiras é avaliar sua

exposição ao risco - a tarefa é chamada de Risk Management, isto é, controlar as

diversas modalidades de risco em que elas incorrem: risco de crédito, risco operacional, risco de mercado, risco de jurídico e risco de modelagem, e seus inter-relacionamentos. Este trabalho concentra-se em risco de mercado - o risco decorrente da mudança no valor de posições em função de mudanças nos preços e taxas dos ativos e passivos dos quais as posições dependem (preços de ações,

commodities e bônus, taxas de câmbio, taxas de juros e indicadores inflacionários,

por exemplo).

Embora Steinherr (1998) tenha descrito o Risk Management como “one of the

most important innovations of the 20th century” e que as técnicas a ele associadas se

tenham propagado a partir do início da década de 90 do século passado, suas origens são anteriores a tal. Markowitz (1952) produziu o trabalho original que resultou na teoria do portfólio, estabelecendo o binômio risco/retorno e rompendo o viés até então existente de dedicar atenção somente ao retorno.

relaciona o retorno esperado de um ativo ao retorno esperado de um ativo livre de risco, ao retorno esperado do mercado e à covariância entre os retornos do ativo e do mercado. Nesse modelo os retornos do mercado são a única fonte de aleatoriedade. Buscando assegurar maior robustez econométrica, Ross (1976) desenvolveu sua APT – Arbitrage Pricing theory, a qual contempla mais fontes de incerteza; estava criado assim um modelo multifatorial de apreçamento de ativos. Os

instrumentos de hedge e alavancagem já circulavam em mesas de operações de

derivativos – sem muito controle e sem que a real dimensão de eventuais impactos negativos fosse bem avaliada. Teorias acadêmicas bem fundamentadas e alertas da iniciativa privada apontavam para potenciais problemas, dando margem à publicação, em julho de 1993, do relatório “Derivatives: Practices and Principles”

pelo Group of Thirty, organização não-governamental composta por banqueiros, financistas e acadêmicos, que buscava mais bem compreender o ambiente econômico financeiro da época.

O pano de fundo para o surgimento do efetivo gerenciamento de risco estava pronto. A iniciativa privada tomou a frente: em outubro de 1994, l JP Morgan

apresentou ao mundo um sistema de gerenciamento de risco a que denominou Risk

Metrics, que contemplava a matriz de covariâncias para uma vasta gama de fatores

de risco. O VaR, termo cunhado inicialmente por Till Guldimann, na época chefe

mundial da área de Research do mesmo JP Morgan na década de 80, deveria

integrar tal matriz às posições inerentes a cada portfólio ou instituição. Em seqüência, mais especificamente em abril de 1995, o Basle Committee da Basiléia do BIS – Bank for International Settlements divulgou que os bancos estavam autorizados a mensurar seu risco de mercado por meio de modelos proprietários. Em janeiro de 1996, o mesmo comitê estabeleceu critérios quantitativos e qualitativos que os modelos internos das instituições financeiras deveriam adotar. Também estabeleceu a utilização do VaR para medir o risco de mercado, autorizando os bancos a utilizar modelos internos para estimá-lo.

Inglaterra, Metallgesellschaft na Alemanha, Orange County e LTCM nos E.U.A,

Daiwa no Japão, Banco Marka e Fonte Cindam no Brasil e, mais recentemente, o

hedge fundAmaranth.

O VaR é uma realidade e muito se desenvolveu desde 1995; sobre essa pequena sigla desenvolveu-se uma vastíssima produção acadêmica. Modelos de otimização de carteiras migraram da abordagem tradicional de Markowitz para a abordagem do VaR, novos matizes e adeptos eram e são conquistados, levando, por exemplo, empresas não-financeiras a adotarem modelos de risco de mercado nele calcados.

O VaR é uma poderosa e excelente maneira de controlar o risco, mas não é

“ciência pura” e muito menos um “conceito fechado”. O Risk Manager não se deve

iludir com o número obtido – deve analisá-lo antes de divulgá-lo, à luz das limitações a ele inerentes. Tais limitações se associam principalmente ao risco de modelagem – a saber, a escolha do sistema, parâmetros e fatores de risco. Este trabalho tem foco justamente nessas limitações. Assim, o objetivo do trabalho será mostrar se modelagens alternativas aos modelos histórico e gaussiano para a apuração do VaR e do Expected Shortfall são aplicadas aos ativos financeiros brasileiros.

A dissertação encontra-se assim estruturada. No primeiro capítulo fazemos uma breve revisão da bibliografia que explora as diferenças entre o VaR – que não é

coerente no sentido de Artzner et al (1997) - e o Expected Shortfall, - que o é. Na

parte final desse capítulo destacamos a produção bibliográfica brasileira e internacional sobre o tema.

No segundo capítulo registramos a metodologia adotada. Definimos formalmente as medidas de risco discutidas e os modelos empregados, e justificamos as proxies, o chamado threshold u e o método de backtesting. No

No quarto capítulo apresentamos os resultados das modelagens desenvolvidas, salientando os principais aspectos quantitativos verificados, sem negligenciar os aspectos qualitativos. Registramos o grau de precisão de cada

modelo e o modelo mais indicado para cada benchmark, chegando à determinação

da adequada relação entre ambos. Especial atenção é dedicada a conceitualização de distribuição paretianas estáveis, matéria não tão difundida no universo brasileiro de gerenciamento de risco de mercado.

2) Revisão Bibliográfica

“As coisas mais importantes nunca devem

ficar à mercê das coisas menos

importantes.”

Goethe

Realizando um exercício de abstração, é difícil imaginarmos as instituições financeiras não mensurando seus riscos, sobretudo o financeiro. O VaR provocou uma verdadeira revolução na maneira de como o negócio bancário e, mais recentemente, empresas não-financeiras, devem construir suas estratégias. Como usual em todo “fato novo”, a conseqüência natural é o debate, tanto acadêmico quanto prático, sobre as principais características do VaR e sua eficiência.

Artzner et al (1997) deram origem a essa discussão, formalizando-a matematicamente em Artzner et al (1998), com a apresentação de axiomas a que medidas de risco devem obedecer1_{. A partir daí tanto a comunidade acadêmica}

quanto à de risk managers começou a dar maior atenção ao chamado Expected

Shortfall – doravante, ES.

Yamai e Yoshiba (2002a, 2002b e 2002c) exploram as diferenças entre o VaR e o ES. O primeiro aborda os aspectos de coerência2_{, erro de estimação}

(estimation error), possibilidade de decomposição e aplicabilidade de métodos de

otimização, e demonstra que: a) o ES é coerente, enquanto o VaR não é; b) para um mesmo nível de precisão, o ES exige maior número de observações que o VAR; c) o ES é facilmente decomponível e otimizável, diferentemente do VaR. No segundo, os autores mostram que o ES é consistente com o paradigma de maximização da utilidade esperada. No último, mostram que ambas as medidas podem subestimar o risco de ativos que apresentem fat-tails e altos potenciais de perda, mas que,

quando o VaR é utilizado para o gerenciamento de risco, existe o perigo de

1

Mais adiante veremos quais são tais axiomas. Os artigos em questão provavelmente são os trabalhos mais freqüentemente citados na área de gerenciamento de risco nos últimos dez anos.

2

investimento em posições sujeitas a perdas extremas, pois o VaR fornece uma informação que não considera o risco caudal – contrariamente ao ES.

O aspecto de não-coerência do VaR e coerência do ES também é explorado em Acerbi and Tasche (2001 e 2002) e Tasche (2002), que mostram os problemas que possíveis descontinuidades na distribuição de perdas podem causar na estimação de medidas de risco; em tais circunstâncias, o ES pode ser estimado de maneira eficiente, enquanto o VaR pode falhar. Por sua vez, Acerbi et al (2006) retomam a idéia de que VaR não é uma medida coerente de risco e adicionam pontos interessantes à análise - por exemplo, a dificuldade de estimá-lo quando há vários fatores de risco e a demora em capturar eventuais “estragos financeiros”. Concluem, então, que o ES é um sucessor natural do VaR. Em linha semelhante, Rau-Bredow (2002) analisa as implicações que a suposição de normalidade dos retornos e a não obediência do VaR à propriedade de sub-aditividade (não-coerência) trazem para os cálculos de exigência de capital. Estendidas ao ES, as mesmas análises mostram a adaptabilidade dessa medida a tais situações. O aspecto de não-normalidade dos retornos também é abordado em Bormetti et al (2006), que propõem uma abordagem, em termos de uma distribuição de t-student, o cálculo do VaR e do ES e os exemplificam com uma carteira de ações italianas.

A sensibilidade do VaR e do ES de portfolios sujeitos a netting de posições é

investigada em Fermanian e Scaillet (2004), que derivam distribuições assintóticas das primeiras derivadas do VaR e do ES, enquanto Rosenberg e Schuermann (2005) estudam a correlação entre os diferentes tipos de risco (de crédito, de mercado etc.) a que uma instituição financeira está exposta. Em ambas as dimensões, os resultados também são favoráveis ao ES.

A preocupação em evitar que uma empresa possa quebrar é merecedora de atenção de todos os agentes econômicos. Anderson et al (2005) mostram as diferenças entre o VaR e o ES de empresas ditas too-big-to-fail. Na mesma linha,

porém sob a ótica de regulação, Leippold et al (2003) comparam a eficiência de parâmetros regulamentares utilizando VaR e ES, e concluem: “If regulators were to replace VaR by a coherent risk measure such as expected shortfall, the unattractive effects of VaR-based regulation would disappear.”

Na vertente de trabalhos puramente empíricos, dois trabalhos se destacam. O primeiro, Kerkhof et al (2003) focaliza a utilização de derivativos como instrumentos de hedge, lançando mão de árvores binomiais. Somente foi possível a construção de

árvore para o cálculo do VaR, contudo, pois o do ES exigiria informações sobre a distribuição na cauda inferior. A lição importante é que, independentemente da medida de risco, a volatilidade implícita do contrato é fundamental para a boa compreensão do risco de um derivativo a ser hedgeado, seja no mercado acionário ou no mercado de moedas. O segundo, Glavan (2004), mostra o cálculo do VaR e do ES de portfolios, detalhando ao máximo a distribuição de Profit and Losses

(P&L), à luz da qual pôde concluir que, diferentemente do VaR, o ES é medida adequada de sensibilidade do portfólio a variações nos fatores de risco.

Da Silva (2004) nos fornece um aprofundado estudo sobre a coerência de medidas de risco no contexto brasileiro, com base nos retornos de dez ações de alta liquidez na Bolsa de Valores de São Paulo. Ratificando estudos empíricos internacionais, seus resultados mostram a superioridade do ES.

Como se sabe, a validação do sistema de risco adotado – via backtesting - é

tão importante quanto o próprio sistema. Angelidis e Degiannakis (2004) descrevem

e analisam a potência (power) dos principais testes dessa natureza, enquanto Novak

(2004) verifica o comportamento e a magnitude do VaR e do ES no episódio do

crash de 1987.

Cada dia mais, em diferentes esferas do conhecimento humano, existe grande preocupação com eventos raros e suas conseqüências. A Teoria de Valores

rupturas de mercado; todavia, é recente o reconhecimento de sua aplicabilidade em

Finanças. McNeil (1999) apresentou o trabalho seminal que emprega a TVE ao Risk

Management, dedicando especial atenção ao método do Peaks Over Threshold e

mostrando de que forma ele pode ser incorporado à estrutura de cálculo de volatilidade estocástica na determinação das medidas de risco e suas particularidades. Rachev et al (2006) abordam modelos univariados para cálculo do VaR e do ES, ancorados em stable laws3 e na TVE. Igualmente, muitos outros

estudos sobre o tema permeiam a academia e as áreas de Risk Management das

instituições.

Como se pode observar na breve revisão acima apresentada, uma das

maiores falhas do VaR é não capturar o comportamento de fat-tail dos retornos dos

ativos financeiros. Assim, o foco do presente dirige-se a essa questão. Veremos o

comportamento do VaR e do ES para proxies de ativos financeiros brasileiros para o

modelo histórico (ou empírico), gaussiano (ou normal), Pareto Generalizado (utilizando POT – Peaks over Threshold) e distribuição paretiana estável (Stable

Paretian Distribution). A contribuição do trabalho reside na utilização dessa última

alternativa – até agora não adotada em nenhum estudo brasileiro, até onde saibamos. Nossa principal referência metodológica é Harmantzis et al (2005).

3) Aspectos Conceituais

“The role of science is nothing more than a refinement of everyday thinking”

Albert Einstein

Nesta seção iremos mostrar o comportamento das variáveis analisadas frente às medidas tradicionais de Estatística, realizando tratamentos individuais e mostrando, por fim, o rompimento da condição de normalidade através de do teste Jarque Bera. De posse das informações contidas nesse capítulo e no próximo começaremos a questionar os modelos tradicionais de mensuração de risco de mercado.

3.1) Séries

Buscando cobrir a maior parte possível dos ativos financeiros brasileiros,

optamos pela escolha de proxies dos principais fatores de risco existentes, a saber:

Ibovespa fechamento, PTAX-V(800) divulgada pelo Bacen (Banco Central do Brasil), IRF-M (Índice de Renda Fixa de Mercado), IMA-S (Índice de Mercado da Andima série S), IMA-B (Índice de Mercado da Andima série B) e IMA-C (Índice de Mercado da Andima série C). Os três últimos são calculados e divulgados diariamente pela Andima (Associação Nacional das Instituições do Mercado Financeiro) e se referem aos mercados de ativos com os seguintes fatores de risco: juros prefixados, cupom

IPC-A e cupom de IGP-M.4

Escolhidas as proxies, determinou-se coletar as informações entre 1º de

março de 1999, após a flutuação da taxa de câmbio no Brasil, e 28 de setembro de

2007.5 O período compreendido é bastante rico para análises, pois cobre períodos

de estresse (de raízes internas ou externas) e de euforia. Por exemplo, o ano de 2001 foi marcado por momentos agudos de estresse no mercado financeiro brasileiro em função do atentado a Nova Iorque, da ruptura da bolha do Nasdaq e do

4 _{O autor sente-se confortável com tais índices, pois participou de grupos de trabalho que estudaram} sua elaboração e divulgação.

5_{O ativo utilizado como parâmetro de data foi a Ptax-V. Em feriados municipais em São Paulo não há}

apagão elétrico no Brasil. No ano seguinte, nosso mercado continuou sensível, em decorrência das incertezas políticas acerca de um novo governo. Os anos de 2005 e 2006 caracterizaram-se por relativa euforia - redução de taxas de juros, alta nas bolsas de valores, valorização do câmbio e descolamento entre economia e política. Todavia, o início de 2007 mostrou que o ambiente de volatilidade baixa e controlada não perduraria por muito mais tempo, culminando com a crise imobiliária norte-americana dos sub-primes a partir de agosto de 2007 e não finalizada até a

conclusão desse trabalho. Assim, mostrou-se importante compreender o comportamento dos ativos financeiros e administrar adequadamente o risco das instituições.

Na próxima sub-seção iremos detalhar um pouco mais sobre as proxies de

ativos utilizadas no presente trabalho para auxiliar o leitor na posterior compreensão do texto.

3.1.1) Ptax-V

Representa a taxa de câmbio entre a moeda local (Real) e a moeda norte-americana (Dólar), calculada ao final de cada dia. É a taxa média de todos os negócios em dólares realizados no dia, no mercado interbancário de câmbio, com liquidação em D+ 2. A base de dados para essa variável perfaz 2144 observações.

3.1.2) Ibovespa

De maneira semelhante à série da Ptax-V, a base de dados do Ibovespa inicia-se em 1º de março de 1999 e se encerra em 28 de setembro de 2007, perfazendo 2144 observações.

3.1.3) IMA – Índices de Mercado Andima

está em curso, motivada, principalmente, pela queda nas taxas de juros e pela estabilidade macroeconômica, que levam a maior previsibilidade das variáveis.

Tais indicadores apresentam algumas vantagens que mostram por que optamos por eles em nosso trabalho, a saber:

Transparente: os ativos constituintes e os pesos são claramente definidos; Replicável: existe a possibilidade de comprar ativos de forma a replicar o(s)

índice(s) desejado(s);

Mensurável: seu retorno é facilmente apurado;

Segmentável: como existem vários índices, podem ser consistente com o estilo do gestor ou da política de investimentos estipulada;

Abrangente: contemplam a grande maioria os títulos públicos federais existentes no mercado;

Consistente: títulos novos ou antigos são inseridos ou retirados através de critérios claros e objetivos; e

Confiáveis: calculados por entidades isentas e de reconhecido mérito no mercado financeiro.

Criados em 2005 numa parceria entre a Andima e a Secretaria do Tesouro Nacional, os índices representam uma carteira teórica de títulos públicos em mercado, segregados por tipo de remuneração conforme tabela abaixo.

Os ativos componentes das carteiras dos IMAs sofrem o processo diário de

Marking to Market. Dessa forma, oscilações nas curvas de juros afetam diretamente,

em maior ou menor grau, a variação dos índices - mesmo aqueles com rentabilidade

definida na emissão. Assim, acreditamos que são excelentes proxies para refletir o

Índice Composição Fatores de Risco

Data de início da amostra

Data final da amostra

Quantidade de observações

IRF-M LTN e NTN-F Expectativa

de inflação + prêmio + maturidade (prazo)

02/02/2000 28/09/2007 1910

IMA-S LFT Prêmio

sobre a taxa Selic

04/12/2001 28/09/2007 1452

IMA-B NTN-B Expectativa

de juros

reais e maturidade (prazo)

17/09/2003 28/09/2007 1009

IMA-C NTN-C Expectativa

de juros

reais e maturidade (prazo)

04/12/2001 28/09/2007 1452

Tabela 1 – Indicadores da família IMA e período de estudo Fonte: Andima - dados trabalhados pelo autor.

3.2) Retornos Logarítmicos

Como assinalado por Morettin e Toloi (2006), é desejável a utilização de retornos logarítmicos, pois são livres de escala e podem ser agregados temporalmente – o retorno logarítmico de um mês é a soma dos retornos logarítmicos dos dias que o compõem. Em um mês típico da Bovespa, por exemplo, há 21 dias úteis de pregões, de modo que o log-retorno desse mês é dado por

20

1 ...

) 21

( = t + t₋ + + t₋

t r r r

r para todo t.

Como nosso interesse é modelar as perdas e ganhos diários dos ativos supramencionados, iremos nos valer dos log retornos e, em seguida, multiplicá-los, por menos 1:

) P ln -P

(ln _{t t-1}

− = t

r , onde P_t e P_t-1 são os preços dos ativos em dois dias úteis

consecutivos.

3.3) Holding Period

De acordo com as melhores práticas de gerenciamento de risco para ativos financeiros, iremos adotar 1 dia útil para o holding period no cálculo do VaR e do Expected Shortfall. A título de ilustração, as câmaras de compensação de

derivativos também estipulam esse mesmo prazo para o cálculo das margens de garantia que exigem de suas “contrapartes”.

3.4) Janela Móvel

Utilizamos a sistemática mais difundida nas áreas de Risk Management do

mercado brasileiro: janela móvel (em oposição à janela ancorada) com extensão de 252 dias úteis (1 ano).

3.5) Nível de Significância

valores intermediários; todavia, a quantidade de informação prejudicaria a análise dos resultados.

3.6) Threshold u do POT

Ao trabalharmos com valores extremos é fundamental determinar qual o nível adequado de “corte” para afirmarmos com segurança qual o nível tido como valor extremo. Em termos estatísticos formais, é o chamado índice de cauda e poderíamos estimá-lo através do processo de Hill, porém não há clara definição de critérios objetivos para qual o nível adequado para o corte (tail index) a ser realizado

no método POT conforme Embrechts et (1997). Ao realizar esse trabalho, ratificamos a idéia de Souza (1999) na sua dissertação:“métodos automatizados” de escolha ótima deveriam ser buscados, mas que não substituem por completo o bom senso e as outras informações descritivas que um bom modelador pode extrair da amostra e que o ajudam a encontrar ou corroborar um valor ótimo para o número de estatísticas de ordem utilizadas na estimação.”

No nosso trabalho nos valemos do método utilizado e proposto por Harmantzis et al. (2006): índice de cauda = 10%* k, ou seja, utilizaremos o 10% maior valor das perdas históricas para a janela de volatilidade utilizada.

3.7) Backtesting

Nós realizaremos Backtesting para os quatro6 modelos apresentados adiante

no capítulo 5. Assim, a exceção ao VaR acontecerá quando a perda for superior ao

VaR calculado. Conforme mencionado na seção 2.2, as violações sempre serão

positivas. Também faremos uma breve análise sobre a magnitude dos eventuais “estouros” na modelagem.

Existem várias formas de backtesting, mas nos valeremos do método de

Kupiec para determinar o grau de acurácia de cada modelo. Os detalhes mais

técnicos serão discutidos adiante. O Risk Manager deverá ter bastante cuidado com

6

4) Análise Estatística Tradicional

“No futuro, o pensamento estatístico será tão necessário para a cidadania eficiente como saber escrever e ler.”

Herbert George Wells

Nesta seção iremos mostrar o comportamento das variáveis analisadas frente às medidas tradicionais de Estatística, realizando tratamentos individuais e mostrando, por fim, o não atendimento à condição de normalidade, através do teste Jarque-Bera, cuja hipótese nula afirma que os retornos encontram-se estatisticamente distribuídos normalmente. De posse das informações contidas nesse capítulo e no próximo, começaremos a questionar os modelos tradicionais de

mensuração de risco de mercado.7

4.1) Ibovespa

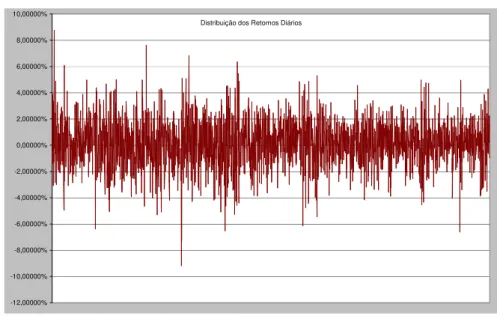
Distribuição dos Retornos Diários

-12,00000% -10,00000% -8,00000% -6,00000% -4,00000% -2,00000% 0,00000% 2,00000% 4,00000% 6,00000% 8,00000% 10,00000%

Gráfico 1 – Evolução dos retornos diários do Ibovespa Fonte: Bovespa; dados trabalhados pelo autor.

Análise visual da série não nos permite identificar nenhum comportamento destoante da condição de normalidade. Assim, aplicamos o teste de Jarque-Bera para nos certificarmos de tal. O resultado nos mostra que a hipótese nula de normalidade deve ser rejeitada, para um nível de significância bastante superior a 99%, dado o p-valor praticamente nulo.

0 40 80 120 160 200 240 280

-0.05 0.00 0.05

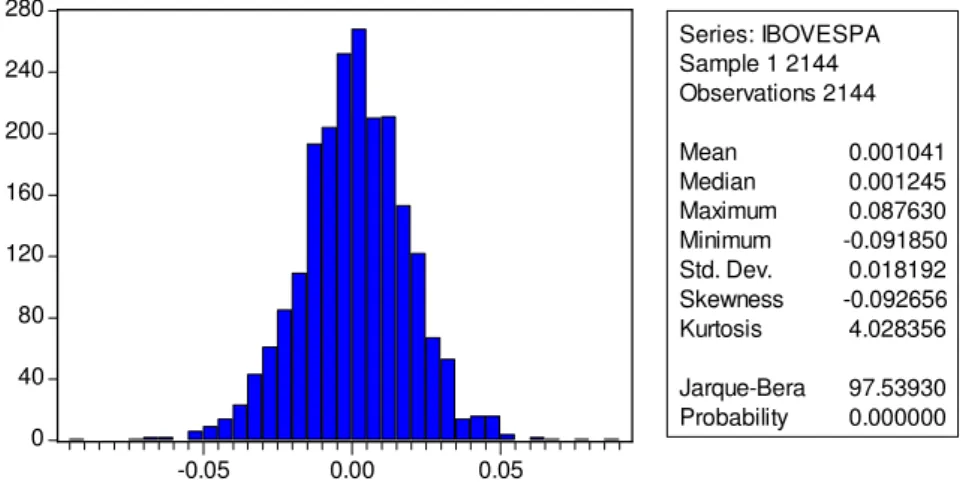
Series: IBOVESPA Sample 1 2144 Observations 2144 Mean 0.001041 Median 0.001245 Maximum 0.087630 Minimum -0.091850 Std. Dev. 0.018192 Skewness -0.092656 Kurtosis 4.028356 Jarque-Bera 97.53930 Probability 0.000000

Gráfico 2 – Histograma dos retornos diários do Ibovespa

4.2) IMA-S

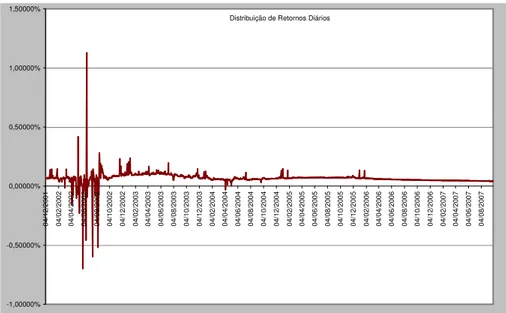
No gráfico 3, observamos concentração de picos e vales no início da série. Como mencionado, razões de liquidez não serão consideradas nesse trabalho; todavia, a explicação para tal efeito está baseada nisso. Em adição, tal efeito inicial

leva a série a apresentar um comportamento indesejável de fat tail, por se tratar de

uma proxy dos ativos constituintes de fundo referenciados existentes no mercado

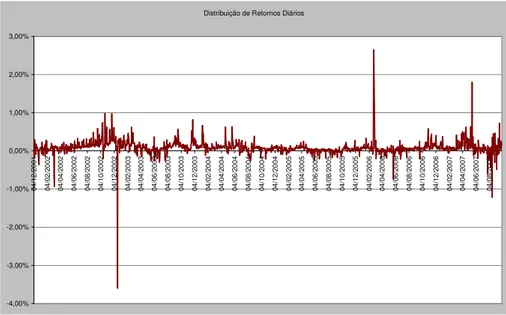
Distribuição de Retornos Diários -1,00000% -0,50000% 0,00000% 0,50000% 1,00000% 1,50000% 04 /1 2/ 20 01 04 /0 2/ 20 02 04 /0 4/ 20 02 04 /0 6/ 20 02 04 /0 8/ 20 02 04 /1 0/ 20 02 04 /1 2/ 20 02 04 /0 2/ 20 03 04 /0 4/ 20 03 04 /0 6/ 20 03 04 /0 8/ 20 03 04 /1 0/ 20 03 04 /1 2/ 20 03 04 /0 2/ 20 04 04 /0 4/ 20 04 04 /0 6/ 20 04 04 /0 8/ 20 04 04 /1 0/ 20 04 04 /1 2/ 20 04 04 /0 2/ 20 05 04 /0 4/ 20 05 04 /0 6/ 20 05 04 /0 8/ 20 05 04 /1 0/ 20 05 04 /1 2/ 20 05 04 /0 2/ 20 06 04 /0 4/ 20 06 04 /0 6/ 20 06 04 /0 8/ 20 06 04 /1 0/ 20 06 04 /1 2/ 20 06 04 /0 2/ 20 07 04 /0 4/ 20 07 04 /0 6/ 20 07 04 /0 8/ 20 07

Gráfico 3 – Evolução dos retornos diários do IMA-S Fonte: Andima, dados trabalhados pelo autor.

Ao realizarmos o teste de normalidade dos retornos de tal ativo (Gráfico 4), confirmamos o efeito mencionado no parágrafo anterior.

0 200 400 600 800 1000 1200

-0.005 0.000 0.005 0.010

Series: IMAS Sample 1 1452 Observations 1452 Mean 0.000664 Median 0.000660 Maximum 0.011270 Minimum -0.006960 Std. Dev. 0.000554 Skewness 0.201701 Kurtosis 150.4588 Jarque-Bera 1315528. Probability 0.000000

Gráfico 4 – Histograma dos retornos diários do IMA-S

4.3) IMA-B

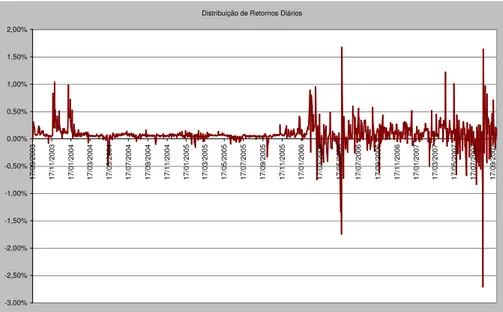
Distribuição de Retornos Diários -3,00% -2,50% -2,00% -1,50% -1,00% -0,50% 0,00% 0,50% 1,00% 1,50% 2,00% 17 /0 9/ 20 03 17 /1 1/ 20 03 17 /0 1/ 20 04 17 /0 3/ 20 04 17 /0 5/ 20 04 17 /0 7/ 20 04 17 /0 9/ 20 04 17 /1 1/ 20 04 17 /0 1/ 20 05 17 /0 3/ 20 05 17 /0 5/ 20 05 17 /0 7/ 20 05 17 /0 9/ 20 05 17 /1 1/ 20 05 17 /0 1/ 20 06 17 /0 3/ 20 06 17 /0 5/ 20 06 17 /0 7/ 20 06 17 /0 9/ 20 06 17 /1 1/ 20 06 17 /0 1/ 20 07 17 /0 3/ 20 07 17 /0 5/ 20 07 17 /0 7/ 20 07 17 /0 9/ 20 07

Gráfico 5 – Evolução dos retornos diários do IMA-B Fonte: Andima

Nota: Dados trabalhados pelo autor

0 100 200 300 400 500 600 700 800

-0.02 -0.01 -0.00 0.01

Series: IMAB Sample 1 1009 Observations 1009

Mean 0.000753

Median 0.000600

Maximum 0.016700

Minimum -0.027100

Std. Dev. 0.002271

Skewness -1.655441

Kurtosis 37.79743

Jarque-Bera 51367.49

Probability 0.000000

Gráfico 6 – Histograma dos retornos diários do IMA-B

4.4) IMA-C

Tal como as demais variáveis analisadas, o IMA-C apresenta fortes evidências de fat tail, seja pela análise visual das estatísticas descritivas e,

Distribuição de Retornos Diários -4,00% -3,00% -2,00% -1,00% 0,00% 1,00% 2,00% 3,00% 04 /1 2/ 20 01 04 /0 2/ 20 02 04 /0 4/ 20 02 04 /0 6/ 20 02 04 /0 8/ 20 02 04 /1 0/ 20 02 04 /1 2/ 20 02 04 /0 2/ 20 03 04 /0 4/ 20 03 04 /0 6/ 20 03 04 /0 8/ 20 03 04 /1 0/ 20 03 04 /1 2/ 20 03 04 /0 2/ 20 04 04 /0 4/ 20 04 04 /0 6/ 20 04 04 /0 8/ 20 04 04 /1 0/ 20 04 04 /1 2/ 20 04 04 /0 2/ 20 05 04 /0 4/ 20 05 04 /0 6/ 20 05 04 /0 8/ 20 05 04 /1 0/ 20 05 04 /1 2/ 20 05 04 /0 2/ 20 06 04 /0 4/ 20 06 04 /0 6/ 20 06 04 /0 8/ 20 06 04 /1 0/ 20 06 04 /1 2/ 20 06 04 /0 2/ 20 07 04 /0 4/ 20 07 04 /0 6/ 20 07 04 /0 8/ 20 07

Gráfico 7 – Evolução dos retornos diários do IMA-C Fonte: Andima; dados trabalhados pelo autor.

0 200 400 600 800 1000 1200

-0.025 0.000 0.025

Series: IMAC Sample 1 1452 Observations 1452

Mean 0.000869

Median 0.000700

Maximum 0.026400

Minimum -0.035900

Std. Dev. 0.001937

Skewness -2.427285

Kurtosis 121.0027

Jarque-Bera 843866.0

Probability 0.000000

Gráfico 8 – Histograma dos retornos diários do IMA-C

4.5) IRF-M

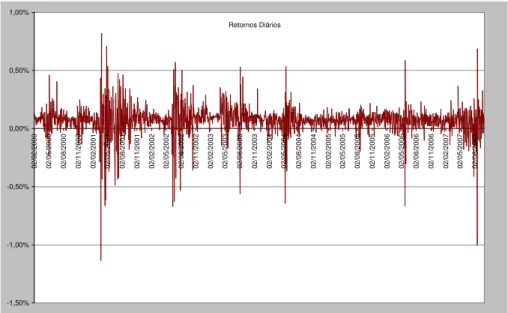
Retornos Diários -1,50% -1,00% -0,50% 0,00% 0,50% 1,00% 02 /0 2/ 20 00 02 /0 5/ 20 00 02 /0 8/ 20 00 02 /1 1/ 20 00 02 /0 2/ 20 01 02 /0 5/ 20 01 02 /0 8/ 20 01 02 /1 1/ 20 01 02 /0 2/ 20 02 02 /0 5/ 20 02 02 /0 8/ 20 02 02 /1 1/ 20 02 02 /0 2/ 20 03 02 /0 5/ 20 03 02 /0 8/ 20 03 02 /1 1/ 20 03 02 /0 2/ 20 04 02 /0 5/ 20 04 02 /0 8/ 20 04 02 /1 1/ 20 04 02 /0 2/ 20 05 02 /0 5/ 20 05 02 /0 8/ 20 05 02 /1 1/ 20 05 02 /0 2/ 20 06 02 /0 5/ 20 06 02 /0 8/ 20 06 02 /1 1/ 20 06 02 /0 2/ 20 07 02 /0 5/ 20 07 02 /0 8/ 20 07

Gráfico 9 – Evolução dos retornos diários do IRF-M Fonte: Andima; dados trabalhados pelo autor.

0 100 200 300 400 500 600 700

-0.010 -0.005 0.000 0.005

Series: IRFM Sample 1 1910 Observations 1910 Mean 0.000704 Median 0.000700 Maximum 0.008200 Minimum -0.011300 Std. Dev. 0.001158 Skewness -1.662072 Kurtosis 21.65724 Jarque-Bera 28581.76 Probability 0.000000

Gráfico 10 – Histograma dos retornos diários do IRF-M

4.6) Ptax-V

Distribuição de Retornos Diários -10.00000% -8.00000% -6.00000% -4.00000% -2.00000% 0.00000% 2.00000% 4.00000% 6.00000% 8.00000% 1/ 3/ 19 99 1/ 6/ 19 99 1/ 9/ 19 99 1/ 12 /1 99 9 1/ 3/ 20 00 1/ 6/ 20 00 1/ 9/ 20 00 1/ 12 /2 00 0 1/ 3/ 20 01 1/ 6/ 20 01 1/ 9/ 20 01 1/ 12 /2 00 1 1/ 3/ 20 02 1/ 6/ 20 02 1/ 9/ 20 02 1/ 12 /2 00 2 1/ 3/ 20 03 1/ 6/ 20 03 1/ 9/ 20 03 1/ 12 /2 00 3 1/ 3/ 20 04 1/ 6/ 20 04 1/ 9/ 20 04 1/ 12 /2 00 4 1/ 3/ 20 05 1/ 6/ 20 05 1/ 9/ 20 05 1/ 12 /2 00 5 1/ 3/ 20 06 1/ 6/ 20 06 1/ 9/ 20 06 1/ 12 /2 00 6 1/ 3/ 20 07 1/ 6/ 20 07 1/ 9/ 20 07

Gráfico 11 – Evolução dos retornos diários da Ptax-V Fonte: Bacen; dados trabalhados pelo autor

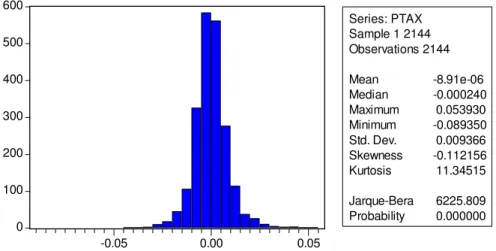
0 100 200 300 400 500 600

-0.05 0.00 0.05

Series: PTAX Sample 1 2144 Observations 2144

Mean -8.91e-06

Median -0.000240

Maximum 0.053930

Minimum -0.089350

Std. Dev. 0.009366

Skewness -0.112156

Kurtosis 11.34515

Jarque-Bera 6225.809

Probability 0.000000

Gráfico 12 – Histograma dos retornos diários da Ptax-V

4.7) Identificação de Heavy Fat Tail

Existem técnicas econométricas para identificação da presença de fat tails,

como pode ser visto em detalhes em Rachev (2003), mas a análise gráfica de quão distante da distribuição teórica a distribuição real se situa é de grande valia, como acentua Da Silva (2006). Quanto mais próximo a uma reta de 45º a distribuição dos retornos estiver, menor será o efeito de fat tails.

-6 -4 -2 0 2 4 6

-.10 -.05 .00 .05 .10

IBOVESPA

N

or

m

al

Q

ua

nt

ile

Theoretical Quantile-Quantile

-12

-8 -4 0 4 8

-.12 -.08 -.04 .00 .04 .08

PTAX

N

or

m

al

Q

ua

nt

ile

Theoretical Quantile-Quantile

Gráficos 13 e 14 – Distribuições Teóricas Normais do Ibovespa e da Ptax-V

Apesar de ambas as séries apresentarem o mesmo número de observações e não apresentarem problemas de liquidez, a distribuição de retornos do Ibovespa tem caudas mais leves, em comparação com a distribuição de retornos da Ptax-V.

De um modo geral, nas proxies de renda fixa, o comportamento de fat-tails é

-8 -6 -4 -2 0 2 4 6

-.015 -.010 -.005 .000 .005 .010 IRFM N or m al Q ua nt ile Theoretical Quantile-Quantile -12 -8 -4 0 4 8

-.03 -.02 -.01 .00 .01 .02 IMAB N or m al Q ua nt ile Theoretical Quantile-Quantile

Gráficos 15 e 16 – Distribuições Teóricas Normais do IRF-M e do IMA-B

-15 -10 -5 0 5 10 15

-.04 -.03 -.02 -.01 .00 .01 .02 .03 IMAC N or m al Q ua nt ile Theoretical Quantile-Quantile -15 -10 -5 0 5 10 15 20

-.008 -.004 .000 .004 .008 .012 IMAS N or m al Q ua nt ile Theoretical Quantile-Quantile

5) Definições e Modelos

“É inútil dizer ao rio que ele pare de correr; a melhor coisa a fazer é aprender a nadar na direção da correnteza.”

Berthold Brecht

Neste capítulo apresentamos as principais definições e modelos testados. A literatura é extensa e difundida, tanto no âmbito local quanto no internacional, razão pela qual não tivemos preocupação entrar em detalhes de cada modelo, com

exceção do chamado stable model, em razão da inexistência de pesquisas

brasileiras sobre ele.

5.1) Definições 5.1.1) Value at Risk

Segundo Rachev e Mittinik (2000), o VaR é a máxima perda possível num certo período de tempo, dado um certo intervalo de confiança. Formalmente, o VaR é definido com o limite superior de um intervalo de confiança mono caudal

[

]

P∆ _{( )} < =

Onde: α é o intervalo de confiança e ∆P(τ)=∆P_t(τ) é a mudança relativa

(retorno) no valor do portfólio num dado horizonte de tempo τ .

P(t) -) P(t ) (

P τ = +τ

∆ t

Onde:

) (t S log )

P(t+τ = +τ é o logarítmo do valor à vista S em t+τ , P(t) = log S(t),

S(t) é o valor do portfólio em t, o período de tempo é dado por

[ ]

τ

t é o tempo presente.

O horizonte de tempo ou holding period deve ser determinado pela liquidez do

empresas não-financeiras. O maior mérito de tal medida é conseguir resumir, em um único número, a perda a que determinado agente está exposto.

Existem várias críticas à utilização do VaR. Uma das mais severas refere-se à ausência de coerência como medida de risco - embora em alguns casos isso se verifique (em distribuições elípticas, por exemplo). Acerbi et al (2001) e Artzner et Al.(1997) caracterizam quais as condições necessárias para que uma medida seja coerente. Sejam X, Y, ρ(X) ρ(Y), respectivamente, as perdas e medidas de risco de dois ativos X e Y. Para ser considerada coerente, uma medida de risco deve atender a quatro propriedades, a saber:

1) Sub-aditividade : ρ(X +Y)≤ρ(X)+ρ(Y)

A medida de risco da carteira deve ser igual ou inferior à soma das medidas individuais. Percebe-se que a sub-aditividade reflete a idéia de diversificação: na formação de carteiras, não há criação de risco adicional.

2) Monotonicidade : se X ≤Y para cada cenário, então ρ(X)≤ρ(Y).

3) Homogeneidade positiva : para todoλ≥0tem-se que ρ(λX)=λρ(X).

4) Invariância de translação : para toda constante c, tem-se que

c (X) )

( + = ρ +

ρ c X _.

Muitos trabalhos demonstram que o VaR viola o princípio da sub-aditividade - penalizando a diversificação, ao invés de premiar. Outra crítica ao VaR se relaciona com o fato de ele nada informar sobre o nível das perdas que podem acontecer

quando o intervalo de confiança estabelecido é excedido. O ES - Expected Shortfall

surgiu para tentar sanar tais deficiências, como veremos na seção seguinte.

Expected Shortfall é definido em termos de esperança condicional, isto é,

dado que o VaR foi excedido, pergunta-se qual a perda possível.8 _{Arcebi et al (2001)}

demonstram formalmente que o ES atende às propriedades de coerência de risco acima relacionadas, no que é seguido por Fabozzi et al (2005), que adicionalmente mostra que ele representa uma forma conveniente de apresentação de estudos de otimização de carteiras.9

Recorremos a Föellmer et al (2002) para uma definição formal:

} P(A) : {E[X/A] f

in -(X)

ES_α = >α

Seja X uma distribuição contínua. Então, especificamente para esse caso, temos que o ES no α −quartil de X é:

] (X) Q X | E[X -(X)

ES_α = ≤ _α

5.2) Modelos

Foram quatro os modelos que estudamos: 1) abordagem empírica ou histórica. 2) abordagem gaussiana; 3) abordagem de valores extremos; e 4) abordagem paretiana estável (stable Paretian).

5.2.1) Abordagem Empírica ou Histórica

Seja Fnum processo empírico de perdas observadas X1, X2,...,Xn, dado por:

) (

n 1 ) (

1

t X I t

F

n

i i

n =

∑

=

,

onde: I() é a função indicativa e X_ié uma variável independente e

identicamente distribuída (i.i.d) com distribuição não conhecida F.

Por procedimentos estatísticos usuais, segundo Van Der Vaart (1998), o

quartil

−

α F−1(α)pode ser estimado por:

8_{O ES também é conhecido como}

ETL – Expected Tail Loss e CvaR – Conditional Value-at-Risk. Ver Fabozzi et al (2005).

     ∈ = − n i , n 1 -i , ) ( ₍₎

1 α α

i n

n X

F ,

onde Xn₍₁₎ ≤ Xn₍₂₎ ≤Xn₍₃₎...≤ Xn₍n₎ sãoestatísticasdeordem.

Assim, o VaR para o método histórico ou empírico obedece à equação acima.

O ES histórico ou empírico pode ser estimado como:

(

)

∑

5.2.2) Abordagem Gaussiana

Seja uma amostra X_i, i = 1,2,..., n, i.i.d, regida por

(

)

µ

N com µ e σ2 não

conhecidos. Geralmente se supõe que µ é igual a zero.

Então temos que o VaR com certo nível de confiança igual α é dado por z_ασ ,

onde z_αé tal que P(Z > z_α)=α, com Z≈N(0,1). Então o problema se reduz a

estimar σ :

2 1 2 ) ( 1 -n 1 M X n i i

n =

∑

=

σ com

∑

= = n i i X n M 1 1 .

Já o ES gaussiano é dado por:

) | / ( ) / ( ) /

(X X VaR E X X z_ασ σ E X σ Xσ Z_α

E

ES = > = > = _{t t t} > ,

onde Z_α é igual a uma função φ−1

( )

distribuição normal padrão e φ é a distribuição acumulada da função normal

padronizada.

Define-se também um threshold u dado por:

)) ( 1 /( ) ( ) |

(Z Z u u u

E > =ϕ −φ ,

em que ϕ é a distribuição normal padronizada.

5.2.3) Abordagem de Valores Extremos

a) Método dos máximo de blocos (BM - Block Maxima)

b) Picos acima do threshold (POT- Peaks over Threshold)

Neste trabalho pressupomos que as variáveis em estudo seguem a distribuição paretiana generalizada (DPG), a qual depende de dois parâmetros, a saber:

        + −

= −ε

σ

ε ε σ

1 , (x) 1 (1 x/ )

H para ε ≠0

{

}

) (

,σ σ

ε x x

H = − − para ε =0

O parâmetro εé conhecido como o parâmetro de forma ou índice de cauda da

DPG e H_ε,σdefine o tipo de distribuição, principalmente a família de distribuições

possíveis de acordo com os parâmetros de localização e de escala. A distribuição de valores extremos acima é generalizada no sentido de que a forma da função assume três tipos possíveis em função do parâmetro ξ .

O VaR e o ES para a distribuição paretiana generalizada são assim apresentados:         −       + = − 1 ξ ξ σ p N n u VaR u p

(

)

ES_{p p}

Onde:

p é o intervalo de confiança;

σ é o parâmetro de escala;

ué o threshold; e

ξé o parâmetro de forma ou índice de cauda.10

5.2.4) Abordagem Paretiana Estável

O conceito de distribuição estável remonta a Pierre Lévy na década de 20 do século passado. Utilizaremos a conceitualização apresentada em Fabozzi (2005); Rachev e Mittnik (2000) também se constituem em excelente fonte. Adler et al (1998) apresentam aspectos introdutórios porém fundamentais para a compreensão de distribuições estáveis. John Nolan – em Nolan (2004) e em outros trabalhos - tem contribuído sensivelmente para a difusão do conhecimento sobre essa área e aplicações ao mundo financeiro. Idéias sobre simulações podem ser encontradas em Janicki and Weron (1994).

Fabozzi et al (2005) mencionam que existem inúmeras distribuições não-normais que podem ser utilizadas para modelar valores extremos, mas que somente as distribuições estáveis apresentam propriedades matemáticas adequadas - seja sob a óptica de trading, de otimização ou de gerenciamento de risco de mercado.

Temos uma distribuição bastante adequada para a modelagem financeira e que não segue uma distribuição normal. Além disso, em meados do século passado, Benoit Mandlebrot (1963) já havia estudado que as propriedades de estabilidade são altamente desejáveis para os retornos dos ativos.

Como assinalam Khindanova and Rachev (2000), a preocupação inicial para estimar os parâmetros de estabilidade e, por conseguinte, sua aplicabilidade para as medidas de risco, VaR e ES, reside na dificuldade de existirem poucas observações para estimar o índice de cauda (tail index). Assim, também supusemos que os

retornos das séries dos ativos financeiros seguem a lei da estabilidade. Da mesma forma que os autores anteriores, derivamos medidas estáveis e analisamos suas

propriedades tendo como benchmark as medidas gaussianas de risco.

A estimação dos parâmetros foi realizada através método de máxima

verossimilhança, seguindo Embrechts et al (2003).11 Tendo em vista as dificuldades

inerentes ao fato de as distribuições paretianas não apresentarem “formas

fechadas”, esses autores demonstram que, mesmo utilizando simulação de Monte Carlo, esse método de estimação se mostra robusto.

Seguindo a lei de estabilidade, cujas definições e formalizações encontram-se em Rachev e Mittnik (2000) já citados anteriormente, o somatório de distribuições

idênticas e independentes segue uma distribuição conjunta com diferentes

parâmetros. Tal distribuição é caracterizada por quatro parâmetros: Índice de estabilidade ou expoente característico: (α∈

(

]

Parâmetro de escala (ou de dispersão): (σ ≥0)

Parâmetro de assimetria: (β ∈

[ ]

Parâmetro de localização: (µ∈ℜ)

Visto que tanto a função densidade quanto a função distribuição não possuem formas fechadas conhecidas, as distribuições estáveis são especificadas pelas suas funções características.

A variável aleatória X segue a uma distribuição estável com função

distribuição F se, e somente se, sua função característica apresentam as seguintes expressões:           = + ∏ + −    ≠ + ∏ − − = 1 se , ] | | ln ) ( sin 2 1 [ | | exp 1 se , ] 2 tan ) ( sin 1 [ | | exp ) ( α µ β σ α µ α β

σα α

t i t t al i t t i t al i t x F

A distribuição normal é denotada por X~N ( 2

,σ

µ ); já a distribuição estável pode

ser escrita da seguinte forma: X ~S_α(σ,β,µ). Quando o β da distribuição estável é

zero, a distribuição será simétrica ao redor de µ. Verificamos a presença de

skewness quando o valor do parâmetro βfor diferente de zero. Tal parâmetro oscila

entre -1 e +1. Quando é positivo, temos assimetria à direita; quando negativo, à

esquerda. Uma outra forma de analisarmos é verificarmos que o parâmetro µ indica

expansão ou contração ao redor de µ. Quando o parâmetro αé menor que 2, os

eventos extremos acontecem de maneira mais freqüente que na distribuição normal, para a qual tal parâmetro é igual a 2.

Podemos assim assumir que a distribuição estável padrão é: X ~S_α(1,β,0).

A partir da distribuição de retornos diários das variáveis, o VaR estável e o ES estável são apurados a partir de diferentes intervalos de confiança utilizando o método histórico descrito no tópico 2 dessa seção. Não há fórmulas analíticas para tais cálculos.

5.3) Justificativa

De posse dos resultados encontrados no capítulo 3 e o início do mesmo, é importante ressaltar que existem inúmeras críticas às modelagens tradicionais de VaR ou ES. Nossa preocupação, contudo, está focada naquilo que observaram Rachev e Mittinik (2000): “empirical observations on returns of financial instruments

do not exhibit the normal distribution and, thus, the tradicional VaR technique does

not fit well data with heavy tails”. Nos gráficos abaixo, podemos observar o efeito do

heavy ou fat tail nas proxies utilizadas.

Em todas as variáveis analisadas, o comportamento de não normalidade é verificado. Algumas apresentam o comportamento de peso de cauda mais pronunciado, justificado pelo elevado valor de curtose (o IMA-C e o IMA-S, por exemplo). Por outro lado, alguns apresentam o coeficiente de assimetria elevado e negativo (o IRF-M e IMA-B). A combinação desses dois efeitos deve ser uma preocupação de qualquer profissional responsável por administração de risco.

Nos gráficos que se seguem podemos observar o comportamento de fat tail

para as principais proxies de fatores de risco para os ativos financeiros brasileiros.12

-0.04 -0.02 0.0 0.02 0.04 0. 01 0. 02 0. 03 0. 04 0. 05 Threshold M ea n E xc es s

-0.04 -0.02 0.0 0.02 0.04

0. 01 0. 02 0. 03 0. 04 0. 05 Threshold M ea n E xc es s

Gráficos 19 e 20 – distribuição de retornos negativos do Ibovespa e Ptax-V

-0.5 0.0 0.5

0. 2 0. 4 0. 6 Threshold M ea n E xc es s

-1.5 -1.0 -0.5 0.0 0.5 1.0

0. 5 1. 0 1. 5 Threshold M ea n E xc es s

Gráficos 21 e 22 – distribuição de retornos negativos do IRF-M e do IMA-B

-2 -1 0

0. 0 0. 5 1. 0 1. 5 2. 0 2. 5 Threshold M ea n E xc es s

-1.0 -0.5 0.0 0.5

0. 0 0. 2 0. 4 0. 6 0. 8 1. 0 Threshold M ea n E xc es s

Gráficos 23 e 24 – distribuição de retornos negativos do IMA-C e do IMA-S

Segundo Zivot e Wang (2006), um boa forma de identificarmos o

comportamento de Fat-Tail é plotar os retornos negativos das séries e aquelas que

apresentam inclinação positiva, confirmam o comportamento bastante acentuado de

cauda. Poderíamos ainda tentar estimar qual o threshold adequado para cada

Neil, Frey e Embrechts (2005); todavia, como já citado anteriormente, foge ao escopo do nosso trabalho.

6) Resultados Empíricos

“Só se pode confiar num palpite que possa ser explicado.”

7º grande axioma de Zurique, Max Gunther

Como sabemos, após a elaboração de modelos de risco faz-se mister a realização de backtesting para se saber a eficácia do modelo construído. Existem

inúmeros métodos quantitativos e qualitativos para realizar o backtesting, dos quais

o mais amplamente utilizado é o e sugerido por Kupiec (1995) que tem como premissa o teste da freqüência binomial que exceda o valor estipulado pela

modelagem. Assim, ao estimarmos o VaR para certo intervalo de confiança α ,

espera-se que o número de violações ao modelo seja 1-α .

6.1) Teste de Hipótese

O teste de hipótese utilizado baseou-se no número de exceções comparado com a precisão dos modelos construídos anteriormente.

Sendo α o intervalo de confiança para o cálculo do VaR. Iremos testar a

hipótese nula da equação abaixo para um holding period igual a 1 dia:

α − = −

<

∆ ] 1

[ P_t VaR_t P

Onde:

t

P

∆ é a mudança relativa do valor do portfólio, isto é, a rentabilidade diária nas nossas variáveis analisadas;

t

VaR é a medida calculada para um holding period t igual a 1;

] , 1 [ T

t∈ donde T é o intervalo de tempo a ser analisado para cada modelo

O modelo será considerado eficaz quando o número de violações estiver

próximo de relação 1-α .

Seja b_ta função indicativa 1{R_t <−VaR_t},1≤t≤T , a qual assume os valores

1 } {

1 _t <− _t =

t R VaR

b , se probabilidade = 1-α

0 } {

1 t <− t =

t R VaR

b , se probabilidade = α .

Seja E (Rt <−VaRt) o número de exceções ou violações nos modelos

apresentados nos respectivos períodos de análise para as diferentes séries

apresentadas. Segue-se então que a variável E, igual a

∑

= T t t b 1

, segue a distribuição

binomial.

Assim, a regra do teste será a rejeição da hipótese nula dado um nível de significância α :

2 ) 1 ( 0 α α α ≤ −       ₋ =

∑

E t t t T ou 2 1 ) 1 ( 0 α α

α ≥ −

−       ₋ =

∑

E t t t T

Como menciona Rachev (2000), para elevados valores de T e níveis de confiança suficientemente altos, a distribuição binomial pode ser aproximada por uma distribuição normal. Fizemos essa pressuposição, pois todas as amostras apresentam T superior a 1000 observações, e, portanto, a hipótese nula será rejeitada para certo nível de confiança α se:

α α

α) α (1 )

1 ( 2 1 − − − < − T Z T

E ou (1 α) _α (1 α)α

2 1 − + − > − T Z T

E ,

onde Zpé percentil da distribuição normal padronizada.

Apresentamos na primeira tabela abaixo os limites de valores admissíveis de tolerância para o cálculo do VaR para as diferentes variáveis.

Tabela 2 – Valores admissíveis de tolerância para VaR.

Já na próxima tabela, a título de curiosidade, mostramos qual o nível de tolerância dado cada intervalo de confiança.

Tabela 3 – Limites de tolerância para o VaR.

De maneira similar ao realizado para o VaR, o ES também deverá sofrer o processo de validação. Todavia, o teste de validação do ES lida com a discrepância existente entre a perda realizada e o ES estimado, dado que o VaR estourou. Como pontuam bem Embrechts et al (2005), tais discrepâncias poderão ser positivas, negativas ou zero, mas geralmente se supõe que elas sejam independentes e identicamente distribuídas, com valor esperado igual a zero – o que fizemos.

De posse de tal arcabouço conceitual, passaremos aos resultados encontrados para os diferentes modelos e variáveis estudadas.

6.2) Análise dos Resultados

6.2.1) Análise do VaR

Tabela 4 – Exceções esperadas versus exceções observadas para nível de confiança igual a 95%.

Tabela 5 – Exceções esperadas versus exceções observadas para nível de confiança igual a 99%.

6.2.1.1) Ibovespa

Para os modelos apresentados, independente do nível de significância, podemos verificar que os números de exceções observadas encontram-se entre os limites inferior e superior do nível tolerável.

6.2.1.2) IMA-S

observadas mostrou-se superior ao limite superior de aceitação. Já para o nível de 99%, o único modelo descartado é o de valores extremos.

6.2.1.3) IMA-B

Para tal ativo observamos que as abordagens histórica e estável apresentaram-se bastante adequadas, independentes do nível de confiança utilizado. Já o modelo gaussiano, para o nível de 95%, o número de exceções observadas foi inferior ao número de exceções esperadas, levando assim uma superestimativa do VaR; para um nível de 99%, o modelo apresentou-se dentro da faixa de aceitação. Interessante observar que o modelo de valores extremos não é adequado para o nível de significância mais elevado, uma vez que o número de exceções observadas é superior ao seu limite superior, conferindo assim um VaR subestimado.

6.2.1.4) IMA-C

Para nível de significância de 99%, qualquer modelo analisado o número de exceções observadas situa-se dentro dos limites aceitáveis. Em contrapartida, para nível de 95%, somente para o modelo histórico podemos afirmar o mesmo. Já os demais modelos superestimam o VaR.

6.2.1.5) IRF-M

Fenômeno semelhante ao ocorrido para o ativo anterior, para um intervalo de confiança de 95%, os modelos gaussiano, valores extremos (POT) e estável superestimam o VaR. Exceção somente o modelo histórico. Já os modelos de valores extremos e estável enquadram-se nos limites toleráveis para intervalo de confiança igual a 99%, já os modelos histórico e gaussiano subestimaram o VaR.

6.2.1.6) Ptax-V

Pelo ativo ser uma excelente proxy, na realidade, ser um ativo financeiro com