Propriedade de Bernoulli para bilhares hiperbólicos com fronteiras focalizadoras...

Propriedade de Bernoulli para bilhares

hiperbólicos com fronteiras focalizadoras

quase planas.

Rodrigo Manoel Dias Andrade

Tese apresentada

ao

Instituto de Matemática e Estatística

da

Universidade de São Paulo

para

obtenção do título

de

Doutor em Ciências

Programa: Matemática Aplicada

Orientador: Prof. Dr. Rodrigo Bissacot

Co-orientador: Prof. Dr. Roberto Markarian

Durante o desenvolvimento deste trabalho o autor recebeu auxílio financeiro da CAPES

Propriedade de Bernoulli para bilhares hiperbólicos

com fronteiras focalizadoras quase planas.

Propriedade de Bernoulli para bilhares hiperbólicos

com fronteiras focalizadoras quase planas.

Esta versão da tese contém as correções e alterações sugeridas pela Comissão Julgadora durante a defesa da versão original do trabalho, realizada em 09/10/2015. Uma cópia da versão original está disponível no Instituto de Matemática e Estatística da Universidade de São Paulo.

Comissão Julgadora:

• Prof. Dr. Roberto Markarian (co-orientador) - Universidad de la República • Prof. Dr. Fábio Tal - IME-USP

• Prof. Dr. Ricardo dos Santos Freire Jr - IME-USP • Prof. Dr. Rodrigo Bissacot Proença - IME-USP • Profa

. Dra

Dedicatória

Agradecimentos

Primeiramente, agradeço a Deus por me conduzir às pessoas certas para a realização deste tra-balho. Em particular, ao Rodrigo Bissacot pela sua orientação, dedicação e disponibilidade desde o início do meu doutorado. Ao Roberto Markarian, pelo convite ao Uruguai, onde quase toda parte do trabalho foi desenvolvida lá sob sua supervisão, paciência e hospitalidade.

Aos meus pais Manoel e Inês, por estarem sempre presente pessoalmente ou via skype nos mo-mentos que eu mais precisei. Sem o carinho e incentivo de vocês, esse trabalho nada seria. Família é tudo!

Ao meu irmão e amigo de quarto Plinio, pela convivência e conselhos ao longo desses anos.

À minha irmã pelo amor e apoio incondicional.

À minha namorada Juliana por saber entender o que é a vida de um doutorando.

Ao meu amigo de instituto Edgardo, muito obrigado pelo apoio e amizade.

Um agradecimento especial é devido também aos membros da banca examinadora pelas suges-tões e correções do texto.

Ao grupo de Investigação CSIC-Universidad de la República “Sistemas Dinâmicos” pelo apoio financeiro em Montevideo.

À CAPES pelo apoio financeiro no Brasil e Uruguai.

Resumo

Dias Andrade, R. M.Propriedade de Bernoulli para bilhares hiperbólicos com fronteiras focalizadoras quase planas. 2015. 120 f. Tese (Doutorado) - Instituto de Matemática e Estatís-tica, Universidade de São Paulo, São Paulo, 2015.

Neste trabalho, mostramos que os bilhares hiperbólicos construídos originalmente por Bussolari-Lenci têm a propriedade de Bernoulli. Tais bilhares não satisfazem as técnicas standard de Wojtkowski-Markarian-Donnay-Bunimovich para bilhares focalizadores hiperbólicos, a qual requer que o diâme-tro da mesa do bilhar seja de mesma ordem que o maior raio de curvatura ao longo da componente focalizadora. Nossa prova, utiliza um teorema ergódico local que nos diz que sob certas condições, existe um conjunto de medida total do espaço de fase do bilhar tal que cada ponto desse conjunto possui uma vizinhança contida (mod 0)em uma componente Bernoulli da aplicação do bilhar.

Palavras-chave: Bilhares hiperbólicos, Ergodicidade, Propriedade de Bernoulli.

Abstract

Dias Andrade, R. M.Bernoulli property for hyperbolic billiards with nearly flat focusing boundaries. 2015. 120 f. Tese (Doutorado) - Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, 2015.

In this work, we show that hyperbolic billiards constructed originally by Bussolari-Lenci has the Bernoulli property. These billiards do not satisfy the standard Wojtkowski-Markarian-Donnay-Bunimovich technique for the hyperbolicity of focusing or mixed billiards in the plane, which requires the diameter of a billiard table to be of the same order as the largest ray of curvature along the focusing boundary. Our proof employs a locally ergodic theorem which says that under a few con-ditions, there exists a full measure set of the billiard phase space such that each of its points has a neighborhood contained, up to a zero measure set, in one Bernoulli component of the billiard map.

Keywords:Hyperbolic Billiards, Ergodicity, Bernoulli property.

Sumário

Lista de Símbolos xi

Lista de Figuras xiii

1 Introdução 1

2 Preliminares 5

2.1 Domínio do bilhar. . . 5

2.2 Espaço de fase. . . 5

2.3 Aplicação do bilhar. . . 6

2.4 Conjunto de singularidades. . . 6

2.5 Campos de cone e tempos de focalização . . . 7

2.6 Formas quadráticas . . . 9

2.7 Diferencial de _F . . . 10

3 Hiperbolicidade. 13 4 Ergodicidade Local. 17 4.1 Método de Hopf. . . 17

4.2 Principais resultados . . . 18

4.3 Ergodicidade local . . . 19

4.3.1 Condição L1 - Regularidade . . . 20

4.3.2 Condição L2 - Alinhamento . . . 23

4.3.3 Condição L3 - Sinai-Chernov ansatz . . . 24

4.3.4 Condição L4 - Contração . . . 33

4.3.5 Campos de Jacobi e semi-normas.. . . 33

4.3.6 Blocos de decomposição. . . 36

4.3.7 Provando a propriedade de não contração. . . 37

4.3.8 Conclusão da prova de L4. . . 42

A Teorema da Decomposição Espectral 45

Referências Bibliográficas 47

Lista de Símbolos

Ω Domínio do bilhar

∂Ω Fronteira deΩ

Γi i-ésima componente de∂Ω

K Curvatura da componente

M Espaço de fase

F Mapa do bilhar

R±k Conjuntos singulares de F±k

{C(x)_}x∈U Campo de cone

F± Pontos focais

f± Distâncias focais relativos aos pontos F± DxF Diferencial deF no ponto x

σ(DxFk) Taxa de expansão gerada pela ação da derivada DFk

Dβ Disco fechado de raio1/|βK|

Vs _{Variedade estável local}

Vu Variedade instável local

J(t) Campo de Jacobi

Lista de Figuras

2.1 A reta tangente t(s) e alguns discos Dβ(s). A parte amarela da trajetória é o lugar

geométrico dos pontos focaisF+ _{correspondendo a um certo cone. . . . 11}

2.2 Uma representação geométrica da Proposição 1. A figura da esquerda representa as duas primeiras equivalências (componente focalizadora). Os conjuntos amarelo/azul de pontos focaisF− _{são mapeados em conjuntos amarelo/azul de pontos focaisF}+_{.. 12}

3.1 A mesa de bilhar estudada em [BL08]. . . 14

3.2 Condição 3 para duas escolhas de s′_{. . . . 14}

4.1 Uma cadeia de Hopf conectando x e y. . . 17

4.2 A principal mesa de bilhar. . . 18

4.3 Prova da Proposição 2. . . 19

4.4 Γ1 eΓ2 no sistema de coordenadas cartesianas(X, Y). . . 21

Capítulo 1

Introdução

Um bilhar planar é o sistema mecânico consistindo de um ponto material movendo livremente no interior de um domínio conexo Ω _⊂R2 _{com fronteira diferencial por partes, e refletindo sobre}

∂Ωde modo que o ângulo de incidência é igual ao ângulo de reflexão.

O estudo das dinâmicas desordenadas no bilhar está diretamente relacionado com a conhecida Hipótese Ergódica de Boltzmann formulada há mais de cem anos pelo físico alemão Ludwing Boltz-mann. Tal Hipótese é parte de um modelo mecânico para explicar as propriedades dos gases.

As características específicas dos bilhares aparecem quando o papel da fronteira (curvatura, posição relativa, etc.) é muito mais importante que o da variedade subjacente. Algumas questões interessantes surgem ao estudar os bilhares, como por exemplo: a partícula visita as vizinhanças de todos os pontos da fronteira? Para qualquer ponto inicial, a trajetória de uma partícula é densa no espaço de fase da transformação? O que podemos dizer sobre a ergodicidade desses sistemas? Propriedades como mistura, Kolmogorov (propriedade K) ou Bernoulli implicam em ergodicidade e, portanto, são propriedades fortemente estudadas na teoria de bilhares.

Nesse trabalho, iremos nos concentrar nos bilhares hiperbólicos construídos por Bussolari-Lenci [BL08], isto é, um tipo particular de bilhar cujo mapa possui expoentes de Lyapunov não nulos.

A teoria matemática de bilhares hiperbólicos foi iniciada por Sinai. Em [Sin70], Sinai mostrou que a aplicação do bilhar de um sistema em um toro bidimensional com uma quantidade finita de obstáculos convexos (curvatura positiva) é hiperbólico e K-automorfismo e, portanto, misturador com respeito a sua medida natural finita. Neste, é utilizado o chamado método de Hopf, que consiste na prova de ergodicidade de um sistema a partir da existência de variedades estáveis e instáveis absolutamente contínuas. Gallavotti e Ornstein [GO74] provaram que o bilhar de Sinai também é Bernoulli. Pouco depois, Bunimovich provou que bilhares em alguns domínios com fronteira formada por arcos convexos focalizadores e segmentos de retas, são também hiperbólicos [Bun74,Bun79]. O mais importante exemplo de um bilhar de Bunimovich é o estádio, a região limitada por dois semi-círculos conectados por segmentos paralelos. As únicas componentes focalizadoras admissíveis em bilhares de Bunimovich são os arcos de círculo. Essa limitação foi resolvida por Wojtkowski, Marka-rian, Donnay e Bunimovich. Usando novas técnicas para estabelecer a positividade de expoentes de Lyapunov [Woj86,Mar88], eles provaram independentemente, que vários outros arcos focalizadores podem ser usados para construir bilhares hiperbólicos [Woj86,Mar88,Bun90b,Don91].

As hipóteses da teoria standard de bilhares hiperbólicos de Wojtkowski, Markarian, Donnay e Bunimovich ([CM06], Teo. 9.19) requer que os círculos de semi-curvatura em qualquer ponto de uma componente focalizadora não deve intersectar outras componentes, ou o círculo de semi-curvatura relativo à outras componentes focalizadoras (em [Mar88] tem uma condição similar). Tal condição é requerida para aplicar o chamado mecanismo de desfocagem, que pode ser descrito da seguinte

2 INTRODUÇÃO 1.0

forma: deseja-se um feixe divergente de trajetórias para manter-se divergente após cada colisão com a fronteira. Mas em uma porção focalizadora da fronteira, um feixe divergente pode ser rebatido como um feixe convergente. Uma maneira de contornar esse problema, é deixar viajar intacto um feixe convergente por um tempo suficientemente longo até as trajetórias concentrar-se em si e, em seguida, começarem a divergir novamente.

O mecanismo de desfocagem provém da óptica geométrica, porém há formulações analíticas se-melhantes na literatura, veja [Mar88,Mar93]. Tal mecanismo, é a extensão mais próxima da original idéia de Sinai de extrair hiperbolicidade das características de fronteiras dispersoras [Sin70].

Entre bilhares de Sinai e Bunimovich, somente casos especiais dos bilhares hiperbólicos restan-tes foram provados ser ergódicos [LW86, MM13a, Bun90a, CT98, Mag01, Mar93, Szá92]. Nosso principal objetivo é mostrar que os bilhares iniciados por Bussolari-Lenci [BL08], os quais não se aplica a teoria standard de bilhares hiperbólicos de Wojtkowski, Markarian, Donnay e Bunimovich, tem a propriedade de Bernoulli (ou equivalentemente, dizemos ‘Bernoulli’ ), isto é, isomorfo a um shift de Bernoulli. A propriedade de Bernoulli está no topo da hierarquia ergódica: ela implica K-propriedade, mixing e ergodicidade. Foi mostrado que vários bilhares, incluindo os bilhares de Sinai e Bunimovich, tem a propriedade de Bernoulli [LW86,Bun90a,CT98,Mag01,Mar93,Szá92,MM03]. Recentemente, Del Magno-Markarian [MM14] provaram que para uma grande classe de bilhares hi-perbólicos satisfazendo certas condições, têm a propriedade de Bernoulli. Notavelmente, essa classe inclui os bilhares hiperbólicos construídos por Donnay [Don91]. Para o nosso conhecimento, to-dos os bilhares hiperbólicos 2-dimensional cumprem tais condições com a exceção de dois casos [BL08,BM99]. Nosso principal objetivo é provar que, os bilhares em [BL08] são localmente ergódi-cos e têm a propriedade de Bernoulli.

Um passo central na prova da ergodicidade de um bilhar hiperbólico é mostrar que é localmente ergódico, isto é, todas as suas componentes ergódicas de medida positiva são abertas (mod 0). Resultados desse tipo são chamados de Teoremas Ergódicos Local (LETs). Em [MM13a], foi pro-vado que sob certas condições, simplectomorfismos hiperbólicos com singularidades são localmente ergódicos. Esse resultado generaliza um teorema ergódico local de Liverani e Wojtkowski para si-tuações quando o sistema admite um campo de cone invariante contínuo por partes ao invés de contínuo em toda parte [LW86]. Ambos teoremas, são baseados nas idéias e métodos de Sinai. Ele obteve o primeiro teorema ergódico local para bilhares [Sin70], usando uma versão probabilística do argumento devido a E. Hopf para demonstrar a ergodicidade de fluxos geodésicos em superfícies compactas de curvatura negativa [Hop39]. Outros refinamentos do teorema de Sinai foram obtidos em [LW86,CH96,KSS90,SC87].

O teorema ergódico local que iremos aplicar nesse trabalho é o mesmo em [MM13a] que também pode ser encontrado em [MM14] com as devidas modificações, ou seja, iremos verficar todas as suas condições (chamadas de L1-L4). Esse é o principal foco do trabalho. Todas as hipóteses se refere às propriedades da dinâmica próximas ou sobre o conjunto de singularidades R+k (resp. R−k) com

k _∈ N do espaço de fase consistindo de elementos cujo _k-ésimo (resp. _−k-ésimo) iterado atinge

um vértice do domínio do bilhar ou possui uma colisão tangencial com a fronteira do domínio. A condição L1 requer que os conjuntos R±k seja uniões finitas de subvariedades C2 do espaço de

fase do bilhar. Já a condição L2 requer que os espaços tangentes à _R+

k (resp. R−k) estejam

1.0 3

Capítulo 2

Preliminares

Um sistema de bilhar pode ser descrito ou por um fluxo ou por uma transformação. Nesse trabalho, iremos nos concentrar na transformação do bilhar. Para a relação entre a transformação do bilhar e o fluxo do bilhar, recomendamos ao leitor a referência [CM06]. Nessa seção, iremos definir a transformação do bilhar para um domínio 2-dimensional, veja [CM06]. Observe que há diferenças entre as parametrizações de ângulo e a orientação das distâncias focais nos trabalhos [BL08] e [CM06].

2.1

Domínio do bilhar.

Um subconjunto Γ_⊂R2 é chamado _{um arco} de classe _Ck com _{k ≥0} se _Γ é a imagem de um

homeomorfismo (sobre sua imagem)γ : [0,1]_→R2 _{de classe C}k_{. A fronteira de um arco Γ é dada}

por ∂Γ =γ(0)∪γ(1). Um subconjuntoΓ⊂R2 é chamado uma_{curva fechada de classe C}k se_Γ é

difeomorfo ao círculo unitárioS1. Vemos que ∂Γ =_∅seΓ é uma curva fechada.

Seja Ω _⊂ R2 _{um aberto conexo e limitado, a qual chamamos de mesa do bilhar. Assumimos}

que ∂Ω é uma união finita de curvas fechadas de classe C0 disjuntas. Também assumiremos que

Γ := ∂Ω = Sn

i=1Γi com n > 0 e Γi sendo ou um arco de classe C3 ou uma curva fechada de

classe C3_{. Denotemos por L}

i o comprimento da componente Γi. Consideremos a parametrização

γi: [0, Li]→R2deΓipelo comprimento de arco com a propriedade de que o interior deΩpermaneça

do lado esquerdo do vetor tangente γ_i′(s)paras_∈[0, Li]. Assumiremos também que:

• a curvatura de Γi, calculada com respeito a parametrização γi, poderá ser somente

estrita-mente negativa, estritaestrita-mente positiva ou identicaestrita-mente igual a zero,

• Γi∩Γj ⊂∂Γi∩∂Γj parai6=j,

• o conjunto de pontos onde∂Ωnão é C3 _{é exatamente} Sn

i=1∂Γi.

Os conjuntosΓ1, . . . ,Γnsão chamados decomponentes de∂Ω. A união de todas as componentes

com curvatura positiva (componentes focalizadoras), curvatura negativa (componentes dispersoras) e curvatura zero (componentes flat) são denotadas por Γ+,Γ− e Γ0, respectivamente. Vemos que uma componente flat é um segmento de reta. Um ponto de Sn

i=1∂Γi := Γ∗ é chamado de vértice de ∂Ω e um ponto de∂Ω\Γ∗ := ˜Γé chamado de ponto regular de fronteira.

2.2

Espaço de fase.

Para cada i= 1, . . . , n defina Mi := [0, Li]×[−π/2, π/2] com elementos (0, α) e (Li, α)

iden-tificados quando Γi é uma curva fechada. Segue que Mi é um retângulo ou um cilindro. Assim,

M=_∪iMi é identificado com o retângulo[0, L]×[−π/2, π/2], ondeL=Pni=1Li é o comprimento

total de ∂Ω. Um elemento x ∈ M é, portanto, um par ordenado (i,(s, α)), o qual é chamado de um estado ou uma colisão. Definimos i(x) = i, s(x) = s e α(x) = α para x = (i,(s, α)) _{∈ M}.

6 PRELIMINARES 2.4

Para simplificar a notação, identificamos cada x ∈ M com o correspondente par (s, α) omitindo (salvo exceções) o índice i da representação (i,(s, α)). Quando necessitarmos especificar i escre-vemos ‘x _{∈ M}i’. Dado x = (s, α) ∈ Mi, defina q(x) = γi(s) ∈ Γi e u(x) o vetor unitário de

R2 apontando para dentro da mesa do bilhar. O conjunto _M é uma variedade diferenciável com

fronteira ∂M = Sn

i=1∂Mi. Também, identificaremos o espaço tangente TxM com R2 tal que se

v _∈TxM, então v = (ds, dα). Denotemos porM+,M− e M0 a união de todos os conjuntos Mi

comΓi sendo focalizadora, dispersora ou flat, respectivamente.

Equipamos M com a métrica Riemanniana g = {gx}x∈M e a forma simplética ω = {ωx}x∈M dada porgx =ds2+dα2 eωx = cosα(x)ds∧dαparax∈ M. A norma gerada porgé denotada por

k · k. A métrica Riemannianaginduz uma distância usual dem cadaMi, a qual pode ser estendida

em todo M colocando d(x, y) = 1 sempre que x ∈ Mi e y ∈ Mj com i 6= j. Denotemos por m

a medida volume gerada por g. Assim, µ= (2L)−1cosα(x)m é a medida de probabilidade gerada porω. Dados A ⊂ Meǫ >0, sejaA(ǫ) =_{y_{∈ M}:d(y,_A)< ǫ_} aǫ-vizinhança deA.

Observamos que existe uma involução naturalI :M → Mdada porI(s, α) = (s,−α)para cada

(s, α)_{∈ M}i. Para efeito de notação, iremos escrever−x ao invés deI(x). Se B é um subconjunto

de M, então −B será denotado por{−x:x_∈B_}.

2.3

Aplicação do bilhar.

Sejax= (s, α)_{∈ M}ie definaρ(x) ={t >0 : (q(x), q(x)+tu(x))⊂Ω}, onde(q(x), q(x)+tu(x))

é um segmento aberto de R2 com extremidades _q(x) e _{q(x) +tu(x)}. Defina também, _{τ(x) = 0} se

ρ(x) = 0, eτ(x) = supρ(x)caso contrário, e q1(x) =q(x) +τ(x)u(x). Seja

M′ ={x∈ M:q1(x) não pertence a um vertice de∂Ω}.

Se x ∈ M′_{, então existe um único i}

1(x) tal que q1(x) pertence ao interior de Γi1(x). Portanto, podemos definir s1(x) =γ_i−1_1(x)(q1(x)). Considere,

u1(x) =u(x)−2hγi′′1(x)(s1(x)), u(x)iγi′′1(x)(s1(x)),

onde h·,·idenota o produto escalar emR2. Denotemos por_{α1(x)∈[−π/2, π/2]}o ângulo orientado

(no sentido horário) entreu1(x) e o vetor normalγ′′_i1(x)(s1(x))apontando para dentro da mesa. A aplicação do bilhar para o domínioΩé a transformação F :M′_{→ Mdada por}

Fx= (i1(x),(s1(x), α1(x))) parax∈ M′.

Notamos que tal transformação não é diferenciável: existem pontos de _M′_{, chamados de pontos} singulares para os quaisF não é contínua ou duas vezes difrenciável. Daremos agora uma descrição detalhada desses pontos.

2.4

Conjunto de singularidades.

A1 = {x∈ M:sestá em um vértice de ∂Ω},

A2 = {x∈ M:α∈ {−π/2, π/2}},

A3 = {x∈ M \∂M:s1 está em um vértice de ∂Ω},

A4 = {x∈ M \(∂M ∪A3) :Fx∈A2}.

Vemos que∂_M=A_1∪A2. Defina também,S1+=A3∪A4eS1− =−S1+, e para cadak≥1, defina iterativamente _S+

2.5 CAMPOS DE CONE E TEMPOS DE FOCALIZAÇÃO 7

O conjunto R+k contém os pontos de M onde Fk ou não está definido ou não é duas vezes

diferenciável. Analogamente, o conjuntoR−k contém on pontos deMonde ouF−knão está definido

ou não é duas vezes diferenciável. Os conjuntos_R+

k eR−k são chamados deconjuntos singulares de

Fk _eF−k _{respectivamente.}

Sob as hipóteses acima F : M \ R+1 → M \ R−1 é uma aplicação com singularidades, do tipo estudada por Katok e Strelcyn em [KS86]. Nesse mesmo trabalho, é mostrado que _F é um

C2 _{difeomorfismo que preserva a forma simplética ω e a medida de probabilidade µ (veja [KS86],} Corolários 4.1 e 4.4, Part V). Para os bilhares considerados nesse trabalho, mostraremos (veja Subseção4.3.1) que os conjuntos_R+

k eR−k são uniões finitas de arcos de classeC2que se intersectam

somente nas extremidades. Assim, com essa propriedade e da invariância de µ segue queµ(_R+_k) = µ(R−k) = 0para cadak≥1. Finalmente, observamos queFé tempo-reversível, isto é,I◦F =F−1◦I

em_{M \ R}+ 1.

Seguindo [MM14], definimos os seguintes conjuntos:

• R±∞:= S

k≥1R±k,

• R:=_R−

∞∩ R+∞, • N±_{:={x∈ M \ R}±

∞:∃k >0 tal que F(±)nx∈ M0 ∀n≥k}, • N :=N−_{∩ N}+_,

• N′ _{:= (R}−

∞∩ N+)∪(R+∞∩ N−).

Observação 1. O significado geométrico dos conjuntos anteriores é: R+

∞ (resp. R−∞) é o conjunto de colisões com semi-órbita finita positiva (resp. negativa); _R é o conjunto de colisões com órbita finita; _N+ _{(resp. N}−_{) é o conjunto de colisões com semi-órbita positiva (resp. negativa) visitando} certamente somente componentes flat de ∂Ω; N é o conjunto de colisões com ambas semi-órbitas visitando certamente somente componentes flat de ∂Ω; _N′ é o conjunto de colisões com uma semi-órbita sendo finita e a outra semi-semi-órbita visitando certamente somente componentes flat de ∂Ω.

Ainda entre os resultados de Katok e Strelcyn em [KS86] encontra-se uma versão do Teorema de Oseledec que garante para quase todo (s, α) :=x_{∈ M}:

1. Uma decomposição do espaço tangenteTxMemEx+⊕Ex−. Esses espaços uni-dimensionais são

dinamicamente invariantes no sentido de (D_F)xEx±=EF±x, onde(DF)x denota a diferencial

de F em x.

2. A existência de expoentes de Lyapunov λ±(x), definidos como

λ±(x) := lim

n→+∞

1

nlogk(DF

n₎ xv±k,

comv±∈Ex±. Comoµé absolutamente contínua com respeito a medida de Lebesgue em M,

então λ+(x) =−λ−(x). Adotaremos a convenção queλ+(x)≥0.

O sistema dinâmico, por definição, é hiperbólico se λ+(x)>0para quase todox∈ M. Se além disso, o sistema é ergódico, então λ+(x) =const:=λ+.

2.5

Campos de cone e tempos de focalização

Seguindo [Woj86,LW86], recordaremos as técnicas básicas de campos de cone invariante para a hiperbolicidade de bilhares planares. A invariância do campo de cone é também uma ferramenta muito útil nas provas da ergodicidade dos bilhares estudadas nesse trabalho. Restringiremos as presentes definições e propriedades dos campos de cone ao setting bidimensional.

Seja V um espaço vetorial bidimensional. Dados dois vetores linearmente independentes X1 e

8 PRELIMINARES 2.5

X1 e X2. Também definimos intC={a1X1+a2X2 :a1a2>0} ∪ {0}e C′(X1, X2) =C(X1,−X2), chamados interior deC(X1, X2) e cone complementar de C(X1, X2), respectivamente.

Agora, seja U um conjunto aberto de _M, e suponhamos que X1 e X2 são dois campos de vetores mensuráveis emU tais queX1(x) eX2(x)são linearmente independentes para todox∈U. Um campo de cone C em U, denotado por (U, C), é uma família de cones {C(x)}x∈U dado por

C(x) =C(X1(x), X2(x))⊂TxM para cadax∈U. Um campo de cone (U, C)é chamado contínuo

se o campo de vetores X1 eX2 são contínuos em U. Um campo de cone (U, C) é dito:

• invariante(resp.estritamente invariante) seDxFC(x)⊂C(Fkx)(resp.DxFC(x)⊂intC(Fkx)),

parax_∈U e_Fk_{x∈U com k >0.}

• certamente estritamente invariante se é invariante, e para quase todox∈U, existe k(x)>0

tal que _Fk(x)_{x∈U e D}

xFk(x)C(x)⊂intC(Fk(x)).

O próximo teorema foi provado em [Woj85].

Teorema 1. Dada uma aplicação do bilhar F como descrita acima, se existe um campo de cone mensurável, definido para µ-quase todo ponto x ∈ M, que é certamente estritamente invariante, então o expoente de Lyapunov λ+(x) é positivo para µ-quase todox∈ M.

Notamos que para verificar a invariância dos cones no sentido acima, não precisamos conhecer

DxF em si, mas somente como a derivada age sobre as retas em TxM passando pela origem, isto

é, no espaço projetivo real 1-dimensional.

Aqui daremos algumas ideias de como Wojtkowski em [Woj86] mostrou que o expoente de Lyapunovλ+ pode ser de fato estimado inferiormente em termos projetivos.

Assuma que para (µ-q.t.p.) cada x ∈ M escolhamos uma coordenada projetiva t, −∞ ≤t ≤

+_∞, no espaço projetivo 1-dimensional de retas em TxM (isto é, para coordenadas euclidianas

apropriadas(u1, u2)emTxMt, −∞< t <+∞corresponde à retau2 =tu1 et=±∞corresponde à retau1 = 0, ou seja, té a tangente de ângulo de u2 = 0 com a reta emTxM). As retas no cone

C(x) formam um intervalo fechado I(x) no espaço projetivo, I(x) = {t |l(x) ≤ t ≤ r(x)}, onde

l(x)< r(x). Se o campo de coneC(x),x_{∈ M}, é invariante por_F, então as retas no coneDxFC(x)

formam um sub-intervalo I1(x)de I(F(x)). SeI1(x) ={t |l1(x)≤t≤r1(x)}, l1(x)< r1(x), então temos µ-q.t.p. l(F(x))≤l1(x)< r1(x)≤r(F(x)). Seja N ={x∈ M | l(F(x))< l1(x) e r1(x) <

r(_F(x))_}, e para x _∈ N seja ζ(x) o cross ratio [l1(x), r1(x), l(F(x)), r(F(x))] dos quatro pontos, isto é,

ζ(x) = r(F(x))−l1(x) r(F(x))−r1(x) ·

r1(x)−l(F(x))

l1(x)−l(F(x))

. (2.1)

Vemos que ζ(x) > 1 para x _∈ N. ζ(x) não depende da escolha da coordenada projetiva t

mas somente dos cones C(F(x)) e DxFC(x). Heuristicamente, ζ(x) representa o quociente das

diferenças entre os limitantes (superior e inferior) dos campos de coneC(_Fx) e DxFC(x).

Teorema 2. (Wojtkowski, [Woj86]) Se um campo de cone mensurável C(x), x∈ M, é invariante sobre _F, então

Z

M

λ+dµ≥ Z

N

ln

√

ζ+ 1

√

ζ₋1dµ,

onde N e ζ são definidos acima.

2.6 FORMAS QUADRÁTICAS 9

Para fins de notação, dada uma subvariedade B de M e um ponto x ∈ B, denotamos T_x∗B para

TxB\ {0}.

Seja x _{∈ M}. Para um vetor tangente v _∈ T∗

xM no espaço de fase é naturalmente associado

uma curva diferenciável ϕ: (−ǫ, ǫ)−→ Mtal queϕ(0) =xe ϕ′(0) =v. Por construção,σ 7→ϕ(σ)

é unicamente determinado na aproximação linear em torno de 0. Usando a representação de M como um subconjunto de Ω_×S1_{, e a notaçãoϕ(σ) = (q(σ), u(σ))∈Ω×S}1_{, construimos a família} de retas, l+_{(σ) := {q(σ) +ru(σ)|r ∈ R}. Também denotando por u}−_{(σ) o vetor pré-colisional de}

u(σ) apontando para fora em q(σ) ∈ Γ, definimos l−(σ) := {q(σ) +ru−(σ)|r ∈ R_}. Na primeira

aproximação, isto é, quando ǫ _→ 0+_{, o feixe infinitesimal de retas focaliza em um ponto, isso} significa que todas as retas, até os ajustes de ordemǫem(q(σ), u(σ))tem uma interseção comum. Consideramos também o caso onde a interseção comum é no infinito. Esse ponto focal é claramente uma função de v somente: tal ponto é denotado por F+(v) para a família _{l+(σ)_} e F−(v) para a família {l−_{(σ)}. Denotamos porf}±_{(v) as distâncias com sinal, ao longo de l}±_{(0), entreF}±_{(v) e}

q0 =q(0)(l±(σ) possui orientação induzida pelo parâmetro r∈R, isto é, fora paral−(σ) e dentro paral+(σ), relativo a Ω). Daqui para frente, omitiremos a dependência de v de todas as notações sempre que não houver ambiguidade. Indicando por (ds, dα)as componentes de0₆=v_∈T_M(s0,α0)

na base natural {∂/∂s, ∂/∂α}, temos

f±=

 



cosα0 ±K(s0)−dα_ds

, ds6= 0

0, ds= 0

(2.2)

Aqui _K(s) denota a curvatura deΓ no ponto de coordenada s, em que é positiva em pontos de componente focalizadora e negativa em pontos de componente dispersora. A fórmula em (2.2) pode ser encontrada em [Woj86].

Observação 2. Um cone bidimensional C pode ser naturalmente identificado com um intervalo fechado I do espaço projetivo P_{(V). Da mesma forma, intC e C}′ _{são então identificados com o}

interior deI e o intervalo fechadoP_{(V)\intI, respectivamente. Seja(U, C)um campo de cone com}

U ⊂ M\A2. Parax∈U\A2, como os tempos de focalizaçãof+ ef−são transformações projetivas de TxM, existem dois intervalos fechadosI+(x) e I−(x) deR∪ {∞} tais que o cone C(x)∈TxM

pode ser convenientemente descrito de duas maneiras diferentes:

C(x) =_{v_∈T_x∗_M:f+(v)_∈I+(x)} ∪ {0}, ou

C(x) =_{v_∈T_x∗_M:f−(v)_∈I−(x)} ∪ {0}.

O próxima lema é conhecido na óptica como a equação do espelho [CM06,Woj86].

Lema 1. Para um feixe infinitesimal de trajetórias colidindo em torno do pontos_∈Γ com ângulos de reflexão em torno de α, tem-se

− 1

f− +

1 f+ =

2K(s) cosα.

2.6

Formas quadráticas

Considere um campo de cone(U, C)gerado pelos campos de vetoresX1eX2. A forma quadrática

Q={Qx}x∈U associada à(U, C) é definida por

Qx(v) =ωx(v1, v2) para x∈U,

onde v1 e v2 são vetores dos subespaços gerados por X1(x) e X2(x), respectivamente, tal que

v=v1+v2.

10 PRELIMINARES 2.7

• monótona (resp. estritamente monótona) se Q_Fk_x(D_xFkv) ≥Q_x(v) (resp. Q_Fk_x(D_xFkv) > Qx(v)) para todov∈Tx∗Msempre quex∈U e Fkx∈U comk >0.

• certamente estritamente monótona se é monótona, e para quase todox∈U, existe um inteiro

k(x)>0tal que Q_Fk(x)_x(DxFk(x)v)> Qx(v) para todo v∈Tx∗M.

Seguindo [LW86], definiremos agora a taxa de expansão gerada pela ação de DFk _{com k > 0}

nos vetores em(U, C) com respeito a formaQ.

Definição 1. Seja C um campo de cone invariante definido em U, e seja Q a forma quadrática associada. Para cada x_∈U e k >0 tal que _Fk_{x∈U, seja}

σC(DxFk) = inf v∈intC(x)

s

Q_Fk_x(D_xFkv) Qx(v)

e

σ_C∗(DxFk) = inf v∈intC(x)

p

Q_Fk_x(D_xFkv) kv_k .

Parak <0, definimos σC e σC∗ substituindo o campo de cone na definição acima com o seu campo

de cone complementar C′(x) e −Q, respectivamente.

• O campo de cone (U, C) é invariante (resp. estrit. invariante) ⇐⇒ a forma quadrática Q é monótona (resp. estrit. monótona),

• (U, C)é certamente estritamente monótona _⇐⇒ Qé certamente estritamente monótona.

Além disso,DxFkC(x)⊂C(Fkx)(resp.DxFkC(x)⊂intC(Fkx)) parax∈U tal queFkx∈U

com k > 0 é equivalente à σC(DxF) ≥ 1 (resp. σC(DxF) > 1). Veja [LW86] para uma prova

detalhada dessas propriedades.

Das definições de invariância estrita de um campo de cone, σC e σ∗C, pode-se deduzir que se

k1, k2, n∈Zcomk1k2 ≥0, então

σC(DxFn)>1 =⇒σC∗(DxFn)>0, (2.3)

e

σ∗_C(DxFk1+k2)≥σC∗(DxFk1)·σC(DFk_1xFk2). (2.4) Definição 2. Sejan(x) = sup_{j_≥0 :x_{∈ M \ R}+_j e x,_Fx, . . . ,_Fj_{x∈ M}

i(x)} para x∈ M \A2, onde _R+₀ :=_∅. Se x_{∈ M}−, observamos que n(x) = 0.

O número n(x) é sempre finito, e representa o número de colisões consecutivas da trajetória de

x com a componenteΓ_i(x)⊂Γ+ _{antes de deixá-la.}

Definição 3. Dada Γi ⊂Γ+, defina Ei ={x∈ Mi\A2 :n(−x) = 0}. Também, sejaE+ a união de todos os E′

is.

Vemos que, se x _∈ Ei então {x,Fx, . . . ,Fn(x)x} é a maior sequência de colisões consecutivas

comΓi; qualquer outra colisão que antecedex deverá pertencer àMj comj6=i.

2.7

Diferencial de

_F

Identificaremos a diferencial de DxF com a diferencial da transformação(s, α)7→(s1, α1). Para cadax∈ M \ R+1 a matriz da diferencial DxF é dada por (veja [CM06]):

DxF =−

1 cosα1

−τK+ cosα τ

τ_{KK1− K}cosα1− K1cosα −τK1+ cosα1

2.7 DIFERENCIAL DEF 11

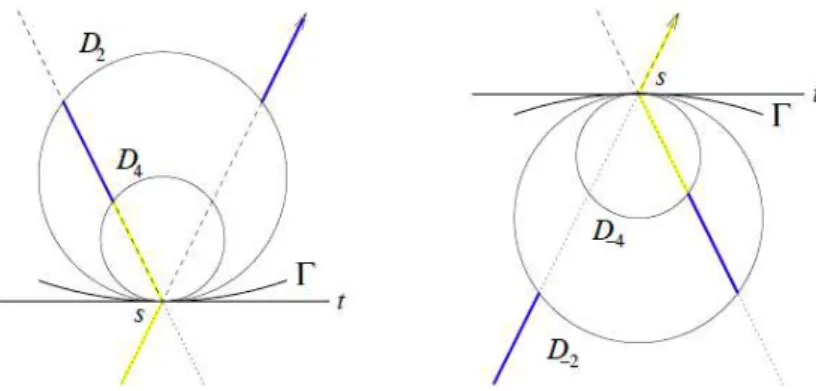
Apresentaremos agora, uma descrição visual do cone C(x) =C(s, α) no plano de configuração contendoΩque foi construído em [BL08]. Para s∈∂Ωe β >0, denotamos porDβ o disco fechado

de raio1/|βK(s)|tangente à∂Ωemssobre o lado externo deΩ. Considere também, dois semiplanos fechados delimitados port(s), a reta tangente à∂Ωems: sejaD0+(s)o semiplano interno, relativo à Ω, e D0−(s)o externo. Veja Figura 2.1. O interior de Dβ é indicado comD◦_β(s).

Figura 2.1: A reta tangentet(s)e alguns discosDβ(s). A parte amarela da trajetória é o lugar geométrico dos pontos focaisF+ _{correspondendo a um certo cone.}

Os próximos resultados bem como suas respectivas provas podem ser encontrados em [BL08]. Lema 2. Dado um campo de cone C(s, α) como na Subseção 2.5, v ∈ C(s, α) corresponde à

F+(v)∈l+(0)∩D, ondeD⊂R2 _{é um dos seguintes conjuntos:}

(a) D=Dβ1(s), para algumβ1 ∈R; (b) D=Dβ1(s)\D

◦

β2(s), para alguns β1, β2 ∈R com |β1|<|β2|; (c) D=Dβ1(s)∪Dβ2(s), para alguns β1, β2 com β1 ≥0 e β2 ≤0; (d) D=R2_\(D◦

β1(s)∪D ◦

β2(s)∪ {s}), para alguns β1, β2 com β1 ≥0 e β2≤0. Além disso, F+(v)∈∂Dβ(s)\ {s} ⇐⇒f+(v) =

2 cosα β|K(s)|.

Veremos que descrevendo os cones em termos dos discos Dβ(s) será eliminada a dependência

sobre α na equação do espelho no Lema1.

Lema 3. Para um feixe infinitesimal de trajetórias colidindo em torno des_∈∂Ω,F−_∈∂D

β(s)se,

e somente, seF+∈∂Dβ′(s), ondeβ′= 4 sgn(K(s))−β(em queF±∈∂D_0±significaF±∈ {s,∞}).

Com as ferramentas da Subseção 2.5, o problema da invariância do campo de cone ao longo de uma dada trajetória pode ser reduzida ao estudo de pontos focais de perturbações a um parâmetro dessa trajetória.

A proposição a seguir será útil em nossa prova.

Proposição 1. Para um feixe infinitesimal de trajetórias colidindo em torno de s, temos: Se s_∈

M+_{, então:} • F∓_∈D

4(s)⇐⇒F±∈D0−(s);

• F∓∈D2(s)\D4◦(s)⇐⇒F±∈D0+(s)\D◦2(s). Ses_{∈ M}−_i para algum i, então:

• F∓∈D−4(s)⇐⇒F±∈D0+(s);

• F∓_∈D

−2(s)\D−4◦ (s)⇐⇒F±∈D0−(s)\D−2◦ (s).

Para o interior de tais cones, segue com equivalências análogas. A situação é ilustrada na Figura

12 PRELIMINARES 2.7

Capítulo 3

Hiperbolicidade.

Nesse capítulo, iremos descrever os bilhares estudados em [BL08].

Tome um quadrado unitário e substitua três de seus lados por arcos circulares de curvatura Kd∈(−

√

2,0)tendo suas extremidades nos vértices do quadrado. A condição_|Kd|<

√

2 assegura que cada par de arcos adjacentes intersecta somente na extremidade comum. Agora, substitua o quarto lado em um arco circular focalizador de curvatura Kf ≪ 1e cole duas faixas formadas por

regiões poligonais com ângulos interiores racionais como mostra numa versão simplificada a Figura

3.1. Denotamos a altura e comprimento dessas faixas porh e l, respectivamente.

Para a prova da hiperbolicidade desse sistema de bilhar, Bussolari-Lenci em [BL08], não usam exatamente a seção de Poincaré que foi introduzida na Seção 2.1, mas uma seção similar que ne-gligencia colisões nas componentes flat’s. Esse é um procedimento padrão na teoria de bilhares hiperbólicos em que as colisões contra uma componente flat não alteram as características hiper-bólicas de um feixe de trajetórias. Um maneira de ver isso é fazer o desdobramento do bilhar ao longo de uma dada trajetória: após o ponto material colidir com uma componente flat, deixamos sua trajetória mover em linha reta, onde é feita a reflexão da mesa em torno desse lado flat; além desse movimento rígido da mesa do bilhar, nada se altera para a trajetória ou qualquer de suas perturbações infinitesimais.

Dessa forma, denotamos _{Γ := Γ}˜ +_∪Γ−_{. Com o usual abuso de notação, um ponto q ∈Γ será} identificado com o seu comprimento de arcose definimosM= ˜Γ×[−π/2, π/2]cujos elementos cha-mamos de(s, α)oux. Vemos que _Mé uma seção transversal global para o fluxo do bilhar, ou seja, para quase todas as trajetórias do bilhar tem colisões com _Γ˜_{. Isso se deve ao fato de um resultado}

conhecido da teoria de bilhares poligonais (veja [BKM78], Seção 5, pág. 539): sejaP a união fechada das duas faixas comR, ondeRé o quadrilátero unindo as duas extremidades abertas das faixas.P

é um polígono racional, o que significa, que todos os seus ângulos são múltiplos racional de π. Em um bilhar poligonal racional, quase toda trajetória do fluxo não singular no espaço de configuração (isto é, o conjunto {q(t)}t∈R desde que não contenha vértice de P) com vetor velocidade inicial

u, é denso em P [BKM78]. Isso implica que para quase toda condição incial (q, u), com q _∈ P, a trajetória do bilhar em P, colide com a fronteira de R, que significa que a verdadeira trajetó-ria do bilhar, relativo a mesaΩ, colide com_Γ˜_{. Esse resultado implica imediatamente queµ(N}±_{) = 0.}

Assim, como M é uma seção transversal global para o fluxo, consideramos F definida para quase todox∈ M sua aplicação de primeiro retorno.

Em [BL08], foi mostrada a hiperbolicidade de um sistema de bilhar tendo como Ω a região explicada acima, definindo um campo de cone que explora o fato que a componente focalizadora é quase plana, e assim quase sempre age como uma fronteira semidispersora.

As constantes geométricas l,_Kf eKd são escolhidas via o seguinte procedimento. Inicialmente,

fixe valores arbitrários deheKd. EntãoKf é determinado por uma condição geométrica que depende

14 HIPERBOLICIDADE. 3.0

Figura 3.1: A mesa de bilhar estudada em [BL08].

Figura 3.2: Condição 3 para duas escolhas des′_.

de _Kd e h que descrevemos aqui com ajuda da Figura3.2. Para s′ ∈ M− e s′′ ∈ M+, considere a

reta passando pors′ es′′, e sejaI(s′, s′′) sua interseção com o discoD−2(s′). A curvaturaKf deve

ser pequena de modo que

∀s′ ∈ M−,∀s′′∈ M+, I(s′, s′′)⊂D4(s′′). (3.1) Finalmente, lé escolhido tal que

l_≥1/_Kf.

Observação 3. Evidentemente, as hipóteses da teoria standard de Wojtkowski, Markarian, Donnay e Bunimovich (veja [CM06], Teorema 9.19) são violadas na condição (3.1), uma vez que D4(s′′) contém grandes porções de _M− para todo s_{∈ M}+.

Para qualquer x = (s, α) _{∈ M} e n _∈ Z, denotemos _{xn := (sn, αn) := F}n_x e seja _τn o

com-primento (equivalentemente ao tempo) entre as colisões em sn e sn+1 (vemos que pode haver um número arbitrário de colisões comΓ0 entresn esn+1). Também, sejaKn=K(sn) a curvatura deΓ

emsn. Analogamente, dadov∈TxM, denotemos porvn:= (DFn)xv. O feixe infinitesimal de

tra-jetórias determinado porvn(e assim porv) em torno de (sn, αn) irão ter focos pré- e pós-colisional

denotados, respectivamente, por F_n− := F−(vn) e Fn+ := F+(vn). As correspondentes distâncias

com sinal ao longo das retas pré- e pós-colisional são indicadas com f−

n e fn+.

Vemos que:

F_n−=F_n+₋₁, (3.2)

f_n− =₋(τn−1−fn+−1). (3.3) Ainda seguindo [BL08], definimos os três seguintes cones em TxMpara cadax∈ M:

• C0(x) é o conjunto de todos os vetores tangentes cuja correspondente família de retas focaliza na aproximação linear dentro deD−2(s). Usando a distância focal f+,

C0(x) :=

v_∈TxM:−

cosα

|K| ≤f

+_(v)≤0

. (3.4)

• C1(x) é o conjunto de todos os vetores tangentes cuja correspondente família de retas focaliza na aproximação linear dentro de D0−(s), isto é, todas as famílias divergentes de retas. Em termos projetivos,

3.0 15

• C2(x) é o conjunto de todos os vetores tangentes cuja correspondente família de retas focaliza na aproximação linear dentro deD2(s)\D4◦(s), isto é,

C2(x) :=

v_∈TxM:

cosα 2_|K| ≤f

+_(v)

≤ cosα |K|

. (3.6)

Os cones acima são usados para definir por partes um campo de cone invariante C:=_{C(x)_}x.

Para cada x = (s, α), a escolha C(x) := Ci(x) irá depender sobre s , s−1, e o que ocorre com a

trajetória entre as colisões em s−1 es.

(A) Ses∈Γ−, definaC(x) :=C0(x). (B) Ses_∈Γ+, então existem dois subcasos:

(B.1) Ses−1 ∈Γ+, defina C(x) :=C2(x).

(B.2) Se s−1∈Γ−, há ainda dois subcasos, dependendo se o pedaço da trajetória entre s−1 es possui colisões comΓ0:

(B.2.1) Nenhuma colisão com Γ0 _entres

−1 e s: defina C(x) :=C1(x).

(B.2.2) Pelo menos uma colisão com Γ0 entres−1 e s: defina C(x) :=C2(x).

Observamos que C(x) é uma função mensurável dex.

Teorema 3. (Bussolari-Lenci, [BL08]) O campo de cone C definido acima é certamente estrita-mente invariante relativo à aplicação _F.

Dessa forma concluímos que _F é hiperbólica.

Capítulo 4

Ergodicidade Local.

Quase todas as provas de ergodicidade para sistemas hiperbólicos estão baseadas no método de Hopf [Hop39] que serão introduzidas aqui informalmente, deixando as formalidades para a referência [CM06].

4.1

Método de Hopf

Suponhamos que F :M _→ M é uma transformação suave, hiperbólica que preserva a medida de probabilidade µ. Suponhamos ainda que para cadax∈M, exista uma variedade estávelWs(x)

e uma variedade instável Wu(x). A prova da afirmação que fazemos abaixo pode ser encontrada nos detalhes em [CM06].

Afirmação 1. Quase toda variedade estável e instável pertence(mod0)a uma componente ergódica da transformaçãoF.

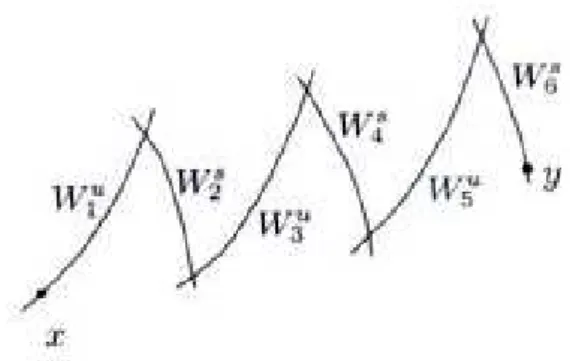
ConsidereW1, W2, . . . , Wnuma sequência de variedades estáveis e instáveis tais queWi∩Wi+16= ∅ para todo i = 1, . . . , n₋1. Isso é possível se as variedades estáveis e instáveis se alternam. Se essas variedades são típicas e se elas intersectam em pontos típicos, então pela afirmação acima, a união_∪Wi pertence (mod0)a uma componente ergódica de F.

A sequência de variedades estáveis e instáveis é chamada de cadeia de Hopf ou um zig zag. Tal sequência é um instrumento na construção de componentes ergódicas para transformações hiperbólicas.

Figura 4.1:Uma cadeia de Hopf conectandoxey.

Seja A _⊂ M tal que quaisquer dois pontos típicos x, y _∈ A podem ser conectados por uma cadeia de Hopf como na figura anterior. EntãoA pertence(mod0)a uma componente ergódica de

F. SeA=M, então a transformação F é ergódica.

Dessa forma, o método de Hopf se concentra no seguinte fato: para provar a ergodicidade de uma transformação hiperbólicaF, é suficiente mostrar que quaisquer dois pontos típicosx, y∈M podem ser conectados por uma cadeia de Hopf de variedades estáveis e instáveis típicas intersectando-se em

18 ERGODICIDADE LOCAL. 4.2

pontos típicos. Para transformações não ergódicas, o método de Hopf pode ser usado para identificar suas componentes ergódicas.

O setting que permite a construção de uma cadeia de Hopf, chamadas de condições de Katok-Strelcyn, são listadas em [CM06] como (H1)-(H6) na Seção 6.3. A saber, todas essas hipóteses são satisfeitas em nosso bilhar.

Para provarmos a ergodicidade da transformação F, pode-se empregar a seguinte estratégia:

• Encontrar um conjunto M1 ⊂ M tal que para cada ponto x ∈ M1, existe uma vizinhança

U(x)que pertence (mod0)a uma componente ergódica deF.

• Mostrar queM1 tem medida total e é conexo por caminhos.

O primeiro passo é conhecido como ergodicidade ‘local’, enquanto que o segundo como ergodi-cidade ‘global’.

4.2

Principais resultados

Primeiramente, notamos que as técnicas utilizadas nas provas da ergodicidade, estão baseadas nos trabalhos de Del Magno-Markarian [MM14]. Dessa forma, necessitamos trabalhar em todo o bilhar.

Denotamos por M = M+ _{∪ M}− _{∪ M}0 _{e M = M}+_{∪ M}− _{e consideramos F : M −→ M} a aplicação do bilhar definido em todo espaço de fase M com a propriedade que Fx = Fk(x)x,

x _{∈ M}, onde Fnx_{∈ M}0_{, para 0< n < k(x), com k(x) 6= 1. Aqui F denota a aplicação do bilhar} de Bussolari-Lenci.

Figura 4.2: A principal mesa de bilhar.

A Figura 4.2 mostra a mesa de bilhar que estamos interessados para o resto do trabalho. Por [BL08], sabemos que F é hiperbólica, o que implica pelo teorema espectral (veja Teorema 5 no Apêndice A) que _F tem no máximo um número enumerável de componentes ergódicas de medida positiva (para a medida natural µ) com cada componente ergódica decomposta em um número finito de componentes Bernoulli ciclicamente permutadas por F. Nós provamos que, existe um conjunto _{H ⊂ M} de medida total tal que, para todo x _{∈ H}, existe uma vizinhança U _{⊂ M}

contida (mod 0)em uma componente Bernoulli de F (veja Teorema A). Por essa razão, esse tipo de resultado é as vezes chamado de Teorema Ergódico Local. Por um argumento de conexidade, finalmente, mostramos que_F é Bernoulli.

Definimos H := _{M \ R}. Vemos que µ(_H) = 1, pois pela regularidade do conjunto R+k (veja

Subseção 4.3.1), concluimos que µ(R+k) = 0.

O principal resultado desse trabalho é o seguinte teorema e será provado na próxima seção:

Teorema A. Cada ponto x ∈ H possui uma vizinhança contida (mod 0) em uma componente Bernoulli de_F.

Corolário 1. Cada componente Bernoulli de F é aberta (mod 0).

Demonstração. Seja B uma componente Bernoulli. Como µ(B) > 0, então µ(B _{∩ H}) > 0. Seja

x∈B∩ H, e seja U a vizinhança dex como no Teorema A. O conjuntoV :=S

4.3 ERGODICIDADE LOCAL 19

Corolário 2. A aplicaçãoF :H −→ H é Bernoulli.

Antes de mostrarmos o corolário, precisamos da proposição a seguir. Lembre que _Hconsiste de componentes conexasMi.

Proposição 2. Cada componente conexa _Mi do espaço H pertence (mod 0) a uma componente

Bernoulli deF.

Demonstração. Como R é enumerável (veja [MM13b]), então o complementar Mi \ R é conexo

por caminhos. Suponhamos que x, y ∈ Mi\ R são conectados por uma curva contínua compacta

C ⊂ Mi \ R. Cada ponto z ∈ C satisfaz o Teorema A, assim existe vizinhança Uz pertencente

(mod 0) a uma componente Bernoulli de F. Devido a compacidade de C, pode-se cobrir por um número finito de tais vizinhanças abertas, veja figura abaixo.

Figura 4.3: Prova da Proposição2.

Nessas condições, demonstramos o Corolário 2.

Demonstração. Pelo Teorema A, cada ponto de _H possui uma vizinhança contida, a menos de um conjunto de medida nula, em uma componente Bernoulli de _F. Pela Proposição 2, o mesmo é verdade para cada componente conexa deH; e então para cada Mi∩ Htal que Mi ⊂ M−∪ M+.

Comoµ(_H) = 1, podemos concluir que cada_Mi⊂ M−∪ M+ está contido(mod0)em uma única

componente Bernoulli de_F. ComoΩé conexo, segue que todos_Mipertencem a mesma componente

Bernoulli, ou seja,F é Bernoulli.

4.3

Ergodicidade local

Nessa seção, enunciaremos os principais resultados para a prova do Teorema A. Isso será feito aplicando o Teorema4à aplicação_F. Inicialmente, enunciaremos o Teorema4e em seguida daremos as noções requeridas para a sua formulação. Esse teorema é a versão para bilhares planares de um Teorema Ergódico Local para simplectomorfismos com singularidades em qualquer dimensão provado em [MM13a]. O Teorema4 possui quatro hipóteses chamadas de Condições L1-L4.

Demonstração do Teorema A. A conclusão do Teorema segue aplicando o Teorema 4aos pontos de H. Para isso, precisamos mostrar que cada ponto de _H é suficiente (veja Definição 7), e que para cada um desses pontos, as Condições L1-L4 do Teorema4são satisfeitas. O primeiro fato é provado no Corolário3, enquanto que o segundo fato está provado nas Proposições 3,4,6 e13.

20 ERGODICIDADE LOCAL. 4.3

4.3.1 Condição L1 - Regularidade

Definição 4. Um conjunto X _{⊂ M}é dito regular se X é uma união finita de arcos de classe C2 que intersectam somente nas extremidades. A coleção de tais arcos é chamada uma decomposição de X.

Definição 5. Dizemos que a Condição L1 é satisfeita se os conjuntos_R+_k e _R−_k são regulares para cadak >0.

Antes de garantirmos a regularidade dos conjuntos R+k e R−k, definimos o conceito de arco

singular e daremos um novo sistema de coordenadas locais para _M que foram introduzidos em [MM13b].

Arcos singulares

A grosso modo, um arco singular é um arco de classe C2 contido emR+

m para algum m >0.

Definição 6. Um arco Σ de classe C2 é chamado negativamente singular se ou Σ ⊂ ∂M ou se existem j >0 e arcos Σ0, . . . ,Σj−1 tais que após definirΣj = Σ tem-se:

• Σ0⊂∂M;

• Σi∩ S1+⊂∂Σi para 0≤i < j;

• intΣi+1=F(intΣi) para 0≤i < j;

• Σi∩∂M ⊂∂Σi para 0≤i≤j.

Um arco positivamente singular é definido similarmente substituindo _F com _F−1_.

Coordenadas locais para _M

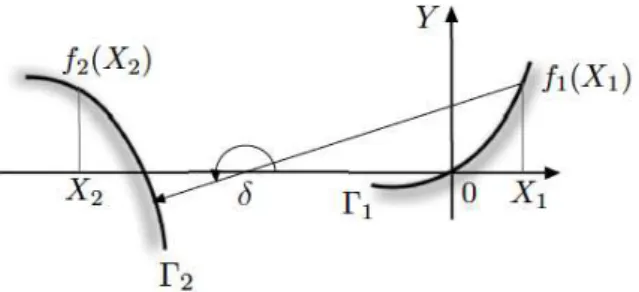
Suponhamos que Σ1 é um arco negativamente singular tal que Σ1∩ S1+ ⊂ ∂Σ1. Nesse caso, cada conjuntoq(Σ1) e q1(intΣ1) está contido em uma única componente de ∂Ω. Sejam Γ1 e Γ2 as componentes de fronteira contendo q(Σ1) eq1(intΣ1), respectivamente.

Dado z1 ∈Σ1, sejam p1 = q(z1) e p2 o ponto de interseção entre Γ2 e o raio emergindo de z1 tendo a distância mínima dep1. Estudamos agora, a imagem deΣ1sob a aplicação do bilharF para todas as possíveis escolhas de Γ1 e Γ2. Para efeito de cálculo, é conveniente obter uma descrição analítica da configuração formada por Γ1 e Γ2 em um sistema de coordenadas cartesianas (X, Y) paraR2. Ao fazer isso, obtemos um novo sistema de coordenadas locais para_M. Podemos escolher

o sistema de coordenadas cartesianas(X, Y) (veja Fig.4.4) tal que • p1 = (0,0)e p2= ( ¯X,0)comX¯ ≤0 em coordenadas (X, Y);

• existem dois intervalos fechados U1 e U2 de R com U1 contendo 0 e U2 contendo X¯ e duas funções C3 _f

1 : U1 → R e f2 : U2 → R com f1(0) = f2( ¯X) = 0 tal que Γ1 = graf(f1) e

Γ2 = graf(f2); além disso, temos ou f1′′ ≡ 0 (Γ1 flat) ou f1′′ > 0 em U1 (Γ1 curva), e/ou

f₂′′_≡0 (Γ2 flat) ou |f2′′|>0 emU2 (Γ2 curva).

Dadox_{∈ M1∪ M2}, seja X aX-coordenada deq(x), e sejaδ _∈[0,2π) o ângulo entre o eixoX

e o vetoru(x). Recorde queM1∪ M2 está equipado com as coordenadas locais (s, α). O par(X, δ)

forma outro sistema de coordenadas locais emM1∪ M2. Em coordenadas(X, δ)temosz1 = (0, π). A relação entre(s, α) e(X, δ) em_M1 segue como na equação (17) de [MM13b], difere apenas com relação a parametrização do ângulo:

s =

Z X 0

q

1 +f′2

1 ( ˜X)dX˜

α =

δ−tan−1f₁′(X)−π/2, se f₁′(X)≥0,

4.3 ERGODICIDADE LOCAL 21

Figura 4.4:Γ1 eΓ2 no sistema de coordenadas cartesianas(X, Y).

A transformação é uma C2 mudança de coordenadas.

Como o arco Σ1 é um intervalo fechado mergulhado, existe um intervalo fechado I1 = [a1, b1] com a1 < b1 e duas funções C2 X1 : I1 → R e δ1 : I1 → R com (X1′(a), δ′1(a)) 6= (0,0) para todo a _∈I1 tal que γ1 := (X1, δ1) :I1 → Σ1 é um C2 difeomorfismo. Escolha ¯a∈ [a1, b1] tal que

γ1(¯a) =z1. Pela escolha do sistema de coordenadas(X, Y), segue queX1(¯a) = 0 e δ1(¯a) =π. No próximo lema, é dado a expressão do tempo de focalização de γ₁′(a) em coordenadas (X, δ), veja Lema 6.3 de [MM13b].

Lema 4. Temos

f+(γ1(a), γ1′(a)) =  



[tanδ1(a)−f1′(X1(a))] cosδ1(a)

X′ 1(a)

δ₁′(a), se δ

′

1(a)6= 0

∞, se δ′

1(a) = 0

(4.1)

A relação entre duas colisões consecutivas, a primeira ocorrendo em Γ1e a segunda emΓ2, pode ser expressa como zeros simultâneos das funçõesF :_{M1× M2 →}Re_{G:M1× M2 →}Rdefinidas

por

F(X1, δ1, X2, δ2) = f1(X1)−f2(X2)−tanδ1·(X1−X2),

G(X1, δ1, X2, δ2) = δ1+δ2−2α2(X2) +π,

para cada(X1, δ1, X2, δ2)∈ M1×M2. A funçãoα2 denota o ângulo formado pelo eixoXcom a nor-mal àΓ2em(X2, f2(X2))apontando para dentro do domínio do bilharΩ. A relaçãoF(X1, X2, δ1, δ2) =

0 é a equação da reta tendo inclinação igual à tanδ1 e passando pelos pontos (X1, f1(X1)) e

(X2, f2(X2)), enquanto que a relação G(X1, X2, δ1, δ2) = 0 descreve a igualdade dos ângulos de incidência e reflexão em (X2, f2(X2)).

Recorde que I1 ∋ a 7→ (X1(a), δ1(a)) é uma parametrização do arco singular Σ1. Sejam F1 : M2×I1 →ReG1 :M2×I1 →Rfunções C2 diferenciáveis dadas por:

F1(X1, δ1, X2, δ2) = F1(X1(a), δ1(a), X2, δ2),

G1(X1, δ1, X2, δ2) = G1(X1(a), δ1(a), X2, δ2),

para cada(X2, δ2, a)∈ M2×I1. Defina também:

D1(X2, δ2, a) = det

∂δ2F1 ∂aF1

∂δ2G1 ∂aG1

= [tanδ1(a)−f1′(X1(a))]X1′(a) +

δ′₁(a) cos2_δ

1(a)

,

para cada(X2, δ2, a)∈ M2×I1. Vemos queD1está bem definida, pois de acordo com nosso setting, sempre temoscosδ1 6= 0 paraasuficientemente próximo dea.

asso-22 ERGODICIDADE LOCAL. 4.3

ciadas à colisãoγ1(a). Para a sua prova, veja Lema 6.6 de [MM13b]. Recorde que τ(γ1(a))denota o comprimento do segmento conectandoq(γ1(a))e q1(γ1(a)).

Lema 5. Temos

D1(X2, δ2, a) =  



[f+(γ1(a), γ1′(a))−τ(γ1(a))]

δ′ 1(a)

cosδ1(a)

, se δ′

1(a)6= 0

[tanδ1(a)−f1′(X1(a))]X1′(a), se δ1′(a) = 0

(4.2)

Proposição 3. A Condição L1 é satisfeita.

Demonstração. Dado um arco Σ1 ⊂ R±k para algum k >0, a proposição será provada no sistema

de coordenadas cartesianas (X, Y) estudado acima. Para garantir que o arco Σ1 é de classe C2, usaremos o Teorema da Função Implícita. Assim, devemos garantir que o determinante da derivada (Lema5) é diferente de zero nos pontos da imagem deΣ1. Primeiramente vamos analisar o caso em queδ′

1(a)6= 0, isso se reduz a estudarmos a diferençafj+−τj−1 para algum1≤j≤k. É suficiente provar a proposição somente para os conjuntos _R+

k. De fato, o resultado se estende para R

−

k pelo

tempo de reversibilidade de_F.

Assim, dadoΣ1 ⊂ R+_k para algumk >0, considerez∈ −Eipara algumi. SejaUz vizinhança de

ze tomex= (s, α)_{∈ −}Ei∩Uz∩Σ1\A2, assim existe1≤j≤ktal que Fjx=xj = (sj, αj)∈Ej.

Estudemos os casos possíveis:

1. xj−1 ∈ M− e xj ∈ M−: Nesse caso, C(xj−1) = C0(xj−1) e C(xj) = C0(xj). Ou seja,

F_j+∈D◦₋₂(sj) e, portanto, fj+<0. Como τj−1 ≫0, temosτj−1≫fj+.

2. xj−1 ∈ M− exj ∈ M+: AquiC(xj) =C0(xj), porém o coneC(xj) pode ter duas formas. Se

não houver colisão comΓ0_entres

j−1esj, entãoC(xj) =C1(xj)daíF_j+∈D0−(sj)i.éf_j+≤0.

Novamente, como τj−1 ≫ 0 segue o resultado. Se há pelo menos uma colisão com Γ0 entre

sj−1 esj então C(xj) =C2(xj), assimFj+∈D◦2(sj)\D4(sj), isto é, fj+<cosα/Kf ≤1/Kf,

porémτ >2l_≥2/_Kf, que implicaτj−1 ≫fj+.

3. x _{∈ M}+ e _Fj_{x ∈ M}−_{: Por definição, C(x}

j) = C0(xj) (se houver ou não colisão com Γ0).

Assim,f_j+_≤0 logoτ _≫f_j+.

4. xj−1 ∈ M+ e xj ∈ M+: Aqui C(xj) =C2(xj) por definição, assim f_j+ ≤cosα/Kf. E temos

dois subcasos: se não houver colisão comΓ0entresj−1esj então o pedaço da trajetória é uma

corda de comprimento τj−1 = 2(cosα)/Kf > cosα/Kf. Notamos que nesse caso cosα ≫ 0,

uma vez que as colisões sucessivas contra a componente focalizadora produzem ângulos iguais aos de entrada. Se a entrada na focalizadora é proveniente da componente flat, o ângulo αj

poderá estar próximo de π/2, porém a trajetória deverá ir novamente para a parte flat, mas isso somente ocorre em um número finito de vezes, dessa forma, basta tomar o ângulo αj em

que a trajetória vai para a parte dispersora. Se a entrada na focalizadora é proveniente da dispersora é trivial. Portanto, τj−1 ≫ fj+. Se houver pelo menos uma colisão com Γ0 entre

sj−1 esj então τj−1>2l≥2/Kf, ou seja,τj−1 ≫cosα/Kf que implicaτj−1 ≫fj+.

Suponhamos agora queδ′

1(a) = 0. SeX1′(a) = 0então γ1′(a) = (X1′(a), δ1′(a)) = (0,0)o que não ocorre pela parametrização do arco singular Σ1. Agora, por construção do sistema de coordenadas segue quef₁′(X1(a))6= tanδ1(a). Portanto, o determinante da derivada dado no Lema5é diferente de zero.

4.3 ERGODICIDADE LOCAL 23

4.3.2 Condição L2 - Alinhamento

Definição 7. Um ponto x_{∈ M \}∂_M é chamado suficiente se existeml _∈Z, N _∈N, O aberto e um campo de cone invariante (O∪ F−N_{O, K) tais que:}

1. x /∈ R+_|l|∩ R−_|l|,

2. O é uma vizinhança deFl+N_{x e O∩ R}−

N =∅,

3. σK(DyFN)>3 para todo y∈ F−NO.

Dizemos que x é um ponto suficiente com quádrupla (l, N, O, K).

No Corolário 3 iremos provar que todo x _{∈ H}é suficiente, assim supomos aqui a existência de uma quádrupla(l, N, O, K) associada.

Definição 8. Dizemos quex satisfaz a Condição L2 se o subespaço tangenteTyΣ está contido em

K(y)(resp. K′_{(y)) para cada k >0, cadaC}2_-arcoΣdeR−

k (resp.R+k) e caday∈Σ∩ F−NO (resp.

Σ∩O).

Proposição 4. Cada pontox∈ H satisfaz a Condição L2.

Demonstração. Seja Σ_{⊂ R}−_k um arco C2 _{com k > 0. Podemos supor sem perda de generalidade} queΣ6⊂∂M, pois caso contrário teríamos Σ∩ F−N_{O =∅pela condição (2) da Definição 7.}

A idéia da prova é estudar a evolução de um feixe de trajetórias emergindo de um vértice (ou tangência). Denotemos tal vértice por z. Ou seja, basta analisarmos a imagem do vetor v = (ds, dα) = (0,1) ∈ TzM (ou v = (1,0) ∈ TzM de modo análogo) em diferentes componentes.

Assim, seja y ∈Σ∩ F−N_{O tal que y=Fz= (ds}

1, dα1). Utilizando a fórmula (2.5) da diferencial de _F, obtemos

DzFv= (ds1, dα1) =

−τ cosα1

, τK cosα1 −

1

⇒ dα_ds1 1

=_−K+cosα1 τ .

Logo, pela fórmula (2.2), tem-se

f₁+(v) = τcosα1 2_Kτ ₋cosα1

. (4.3)

(I) Se z= (0, α) ∈ M−1 ∩ M−2 e y ∈ M−3, temos por definição que K(y) :=C0(y). Logo devemos provar que DzFv ∈ C0(y). De fato, como Kd < 0 temos 2Kdτ −cosα1 < 0 e assim f1+(v) ≤ 0. Agora, suponhamos que

f₁+(v) = τcosα1 2Kdτ −cosα1

< cosα1

Kd

isso implicaria (cosα1)/Kd> τ >0 comKd<0, o que é um absurdo. Logo,f1+(v)≥(cosα1)/Kd.

(II) Sez= (0, α)∈ M−1 ∩ M2− e y∈ M+, entãoK(y) pode ter duas formas:

(II.I) se não houver colisão com Γ0 entre s= 0 e s1 então K(y) :=C1(y). Nesse caso, Kf >0

porém pela propriedade (3.1) segue que z _∈ D4(y), isso significa que o comprimento do segmento determinado porye∂D4(y)ao qualzpertence, é maior queτ. Em outras palavras,(2 cosα1)/4Kf >

τ, ou seja,2_Kfτ −cosα1 <0, e portanto,f1+(v)≤0.

(II.II) se houver pelo menos uma colisão com Γ0 _{entre s= 0 e s1, então K(y) :=C}

2(y). Aqui

τ >2l≥2/Kf, pois l≥1/Kf. Assim,

2τ_Kf −cosα1 >4−cosα1 > τKf ⇒

1 2τKf−cosα1

< 1 τKf

daí,

f₁+(v) = τcosα1 2τKf −cosα1 ≤

cosα1 Kf

24 ERGODICIDADE LOCAL. 4.3

Agora,

2

Kf

< τ ⇒ 1

4 2

Kf

< 1 4τ ⇒

cosα1

2_Kf

< τcosα1

4 ≤

τcosα1

2τ_Kf −cosα1

=f₁+(v),

uma vez que2τ_K1−cosα1 ≤4.

(III) Se z= (0, α)∈ M0_{∩ M}+ _{ey ∈ M}−_{, entãoK(y) :=C}

0(y) e segue de modo análogo ao caso (I) (com ou sem colisão com Γ0).

(IV) Se z= (0, α)_{∈ M}0_{∩ M}+ _{e y∈ M}+_{, então K(y) :=C}

2(y) e temos duas possibilidades: (IV.I) Ou há pelo menos uma colisão com Γ0 entre s= 0 e s1, daí K(y) := C2(y) e segue de modo análogo ao caso (II.II).

(IV.II) Ou não há colisão comΓ0 _{entres= 0es1, assim o pedaço da trajetória é uma corda de} comprimentoτ = (2 cosα1)/Kf, substituindo em (4.3) temos

f₁+(v) = 2 cosα1 3_Kf

,

ou seja,

cosα1

2_Kf ≤

f₁+(v)_≤ cosα1

Kf

.

4.3.3 Condição L3 - Sinai-Chernov ansatz

Definição 9. Um ponto x_{∈ M \}∂_Mé chamado u-essencial se para cada α >0, existe nx,α ∈N,

uma vizinhança Ox,α dex e um campo de cone invariante (Ox,α∪ Fnx,αOx,α, Kx,α) tal que Ox,α∩

R+

n =∅eσ∗Kx,α(DyF

nx,α_{)> αpara caday∈O}

x,α. Analogamente, um pontox∈ M\∂Mé chamado

s-essencial se na definição anterior, _F e _R+_n são substituídos por _F−1 e _R−_n, respectivamente. O campo de cone (O, K) na Definição7é certamente estritamente invariante. Por um resultado em [Woj85, Mar88] segue que os expoentes de Lyapunov de _F são não nulos quase sempre em S

k∈ZFkO. Esse fato juntamente com a teoria de Katok-Strelcyn [KS86] nos dá a Proposição abaixo (Parte (3) é provada em [MM13a] Proposição 5.3). Para a definição de continuidade absoluta de uma foleação, nos referimos a [CM06,KS86].

Proposição 5. Seja x ∈ M \∂M um ponto suficiente com quádrupla (l, N, K, O). Então existe um conjunto invariante Λx ⊂ Sk∈ZFkO com µ((

S

k∈ZFkO) \Λx) = 0 e duas famílias de C2 subvariedades invariantes Vs ={V_ys}y∈Λx e V

u _={Vu

y}y∈Λx tais que para cada y∈Λx, tem-se 1. Vs

y ∩Vyu ={y},

2. V_ys e V_yu são difeomorfos a intervalos abertos,

3. TyVys⊂K′(y) e TyVyu ⊂K(y) dado quey∈O∪ F−NO,

4. _FVs

y ⊂VFsy e F−1Vyu⊂VFu−1_y,

5. d(Fn_y,Fn_{z)→0exponencialmente quando n→+∞para cadaz∈V}s

y, e o mesmo é verdade

quando n_{→ −∞} para cada z_∈V_yu,

6. V_ys e V_yu variam mensuravelmente com y∈Λx,

7. Vs e Vu tem a propriedade de continuidade absoluta.

Definição 10. As subvariedades formando as famílias Vs _{e V}u _{são chamadas variedades estável}