Desenho de grafos: uma abordagem utilizando programação linear inteira

(1)

Universidade Federal de Minas Gerais

Escola de Engenharia

Programa de P´

os-Gradua¸c˜

ao em Engenharia El´etrica

Disserta¸c˜ao de Mestrado

Desenho de Grafos: Uma Abordagem

utilizando Programa¸c˜

ao Linear Inteira

Felipe Marques Terra

Disserta¸cão de mestrado submetida à Banca Examinadora designada pelo Colegiado do Programa de Pós-Gradua¸cão em Engenharia Elétrica da Universidade Federal de Minas Gerais, como requisito parcial para obten¸cão do t´ıtulo de Mestre em Engenharia Elétrica.

Orientador: Prof. Renato Cardoso Mesquita

(2)

(3)

Resumo

Um problema importante em visualiza¸cão de dados é como organizar a informa¸cão a ser mostrada em estruturas que mostram entidades e as rela¸cões entre elas. Quando se tem um número extenso de entidades e de rela¸cões este problema pode ser muito complexo. Para um número grande de dados ou quando vários requisitos estéticos tem que ser obedecidos, o desenho automático de grafos se torna um problema relevante.

Este trabalho tem como objetivo o estudo de metodologias e o desenvolvimento de uma ferramenta computacional capaz de gerar desenhos de grafos de maneira automática, otimi-zando fatores como complexidade visual da informa¸cão representada no grafo, legibilidade, e diversos critérios estéticos. Para isso foram aplicadas técnicas de Programa¸cão Linear Inteira (PLI) em etapas de algoritmos de desenho de grafos, para que restri¸cões espec´ıficas de desenhos de circuitos alimentadores de energia elétrica fossem contempladas de maneira mais eficiente.

Duas abordagens são apresentadas. A topologia-forma-métrica, que consiste em tratar o desenho em três etapas: planariza¸cão, responsável por definir um embutimento planar para o grafo; ortogonaliza¸cão, responsável por definir ângulos de vértices e arestas; e com-pacta¸cão, responsável por obter coordenadas de um desenho o mais compacto poss´ıvel. Outra abordagem, a hierárquica, visa dispor vértices em camadas, ou n´ıveis, e possui resul-tados interessantes quando aplicada a determinados problemas de desenho de grafos, tais como esquemas que precisam real¸car informa¸cões de dire¸cão de fluxos, como é o caso de alguns diagramas de sistemas de energia elétrica.

Desenhos de grafos gerados pelas diferentes abordagens são discutidos e comparados. Os resultados obtidos indicam que a abordagem PLI permite a inclusão de restri¸cões de forma mais simples, possibilitando a inser¸cão de mais requisitos estéticos nos desenhos automáticos.

(4)

(5)

Abstract

An important problem in data visualization is the information organization into struc-tures that show entities and their relationships. This problem can be more complex as the number of entities increases. The way a graph is drawn can directly impact on the information quality and reliability. For large amount of data, or, when large number of aesthetic requirements had to be defined, the automatic graph drawing problem becomes a very relevant problem. The methodology study and the development of a computational tool designed to build automatic graph drawing are the objectives of this work, optimizing the graph data visual complexity, readability and many kinds of aesthetic requirements. To achieve these goals, the Integer Linear Programming (ILP) approach was used in al-gorithm steps, just for treating electric circuits drawing requirements in an efficient way. Two approaches are presented: the topology-metric-shape deals the drawing in three steps: planarization, responsible for the definition of a planar embedding; orthogonalization, re-sponsible for vertices and edges angles definition; and the compaction, which defines the compact drawing coordinates. Another approach, the hierarchical one, targets a draw-ing in levels, and achieves better results in some kinds of graph drawdraw-ing problems, like flow schemas in electric power systems diagrams. Graph drawings built with the different approaches are largely discussed and compared. The obtained results show that the ILP approach allows the insertion of requirements in the system in a simple way. This enables the insertion of many aesthetic requirements.

(6)

(7)

Agradecimentos

Primeiramente a Deus por simplesmente permitir que tudo isto esteja acontecendo e que eu tivesse sa´ude para conseguir trabalhar neste projeto.

`

A toda minha fam´ılia por sempre me apoiar.

Ao meu orientador Renato Cardoso Mesquita e pela oportunidade que me foi dada e pelo aux´ılio valioso.

Aos amigos do GOPAC (Grupo de Otimiza¸cão e Projeto Assistido por Computador) pela grande amizade e pelas ajudas freqüentes. Em especial: Adriano Lisboa, Alexandre Ramos, Dalmy Júnior, Diogo Batista, Douglas Vieira, Leonardo Mozelli, Luciano Pimenta, Marcelo Guedes, Marcos Flávio, Miguel Lima e Ricardo Adriano.

Aos alunos de inicia¸c˜ao cient´ıfica Christiano Gouveia, Raphael Duarte, Thiago Campos e Vitor Baracho pela preciosa ajuda e dedica¸c˜ao.

Ao Vin´ıcius Magalh˜aes (Light/RJ), Daniel, Esdras, Arthur e Gisele (Concert Technolo-gies) pela coopera¸c˜ao no projeto P&D.

`

A Ana Fl´avia pela compreens˜ao, carinho e amor.

Aos meus amigos por entenderem meus longos per´ıodos de ausˆencia.

A todos que direta ou indiretamente contribu´ıram para a realiza¸c˜ao desse trabalho. A todos vocˆes, muito obrigado.

(8)

Sum´ario viii

Lista de Figuras x

Lista de Tabelas xii

Lista de S´ımbolos xiii

1 Introdu¸c˜ao 1

1.1 Motiva¸c˜ao . . . 1

1.2 Trabalhos relacionados . . . 2

1.3 Objetivos . . . 3

1.4 Organiza¸c˜ao do texto . . . 3

2 Desenho de Grafos 5 2.1 Grafos . . . 5

2.2 Paradigmas em Desenho de Grafos . . . 7

2.2.1 Conven¸c˜oes de Desenho . . . 8

2.2.2 Crit´erios Est´eticos . . . 10

2.2.3 Restri¸c˜oes . . . 13

2.2.4 Eficiˆencia dos algoritmos . . . 14

2.2.5 Precedência entre Critérios Estéticos . . . 14

2.3 Topologia-Forma-M´etrica . . . 15

2.3.1 Planariza¸c˜ao . . . 16

2.3.2 Ortogonaliza¸c˜ao . . . 17

2.3.3 Compacta¸c˜ao . . . 20

2.4 Metodologia Hier´arquica . . . 23

3 Desenhos de Grafos baseados em PLI 25 3.1 Modelagem por Programa¸c˜ao Linear Inteira . . . 25

3.2 Ortogonaliza¸c˜ao em Programa¸c˜ao Linear Inteira . . . 26

(9)

SUM ´ARIO ix

3.2.2 Restri¸c˜oes Especiais em Ortogonaliza¸c˜ao . . . 29

3.3 Compacta¸cão com Vértices de Tamanho Pré-Determinado . . . 36

3.3.1 Compacta¸c˜ao ´Otima . . . 37

3.3.2 Compacta¸c˜ao R´apida . . . 40

3.3.3 Sistema PLI da Compacta¸c˜ao . . . 42

4 Desenho Hierárquico 45 4.1 Defini¸cões Básicas . . . 45

4.2 Algoritmo Sugiyama . . . 46

4.2.1 Normaliza¸c˜ao e Atribui¸c˜ao de N´ıveis . . . 48

4.2.2 Redu¸c˜ao de Cruzamentos . . . 48

4.2.3 Atribui¸c˜ao de Coordenadas Horizontais . . . 50

4.2.4 Desempenho do Algoritmo de Sugiyama . . . 51

5 Biblioteca de Gera¸cão de Esquemáticos Ortogonais 53 5.1 Sistema de Gera¸cão de Diagramas Ortogonais . . . 53

5.1.1 Requisitos Para o Desenho de Circuitos de Redes de Transmiss˜ao 54 5.1.2 Componentes da Solu¸c˜ao Computacional . . . 56

6 Resultados 63 6.1 Testes Simples Pontuais . . . 63

6.2 Testes Preliminares com Circuitos Alimentadores da Light . . . 64

6.2.1 Desempenho dos Testes Preliminares . . . 64

6.2.2 Resultados dos Testes Preliminares . . . 64

6.3 Resultados Para Compara¸c˜ao entre Abordagens . . . 71

6.4 Resultados dos Testes Definitivos . . . 76

7 Conclus˜oes 79

(10)

2.1 Um grafo com 13 v´ertices e 13 arestas. . . 6

2.2 Exemplo de um d´ıgrafo. . . 6

2.3 Dois desenhos de um mesmo grafo . . . 7

2.4 Grafo desenhado utilizando a conven¸c˜ao linhas-retas. . . 9

2.5 Grafo desenhado utilizando as conven¸c˜oes ortogonal, planar e grid. . . 9

2.6 Grafo utilizando a conven¸c˜ao de desenho direcionado (downward). . . 9

2.7 Minimiza¸c˜ao de ´area . . . 11

2.8 Minimiza¸c˜ao de dobras . . . 12

2.9 Raz˜ao de Aspecto . . . 12

2.10 Exemplo de uso de restri¸c˜oes de forma no desenho. . . 13

2.11 Dois desenhos ortogonais do mesmo grafo . . . 14

2.12 Ângulos-vértice e ângulos-aresta . . . 18

2.13 Ângulos-vértice e ângulos-aresta . . . 20

2.14 Desenho: exemplo de ˆangulos de arestas . . . 21

2.15 Montagem da rede de fluxo na ortogonaliza¸c˜ao . . . 22

2.16 Redes ηver eηhor . . . 23

3.1 Defini¸c˜ao de faces . . . 26

3.2 Defini¸c˜ao der(u,v) e l(u,v) . . . 27

3.3 Um exemplo para um desenho com base em Kandinsky. . . 29

3.4 Trecho de desenho upward mostrando o eixo de balanceamento. . . 30

3.5 Caracteriza¸c˜ao dos elementos especiais . . . 33

3.6 Exemplo de controle de tamanho m´ınimo de v´ertice . . . 34

3.7 Resultados de 4 m´etodos diferentes de Compacta¸c˜ao . . . 37

3.8 Grafo Simples. . . 38

3.9 Caracteriza¸c˜ao dos segmentos em um desenho de grafo. . . 39

3.10 Decomposi¸c˜ao de uma face. . . 40

3.11 Exemplo de caracteriza¸cão do explosão de vértices. . . 42

3.12 Exemplo de uma chave seccionadora de 3 posi¸c˜oes. . . 42

(11)

LISTA DE FIGURAS xi

4.1 Exemplo de diagrama hier´arquico. . . 46

5.1 Diagrama ortogonal da LSA - Cavado da Light. . . 55

5.2 Diagrama ortogonal da LSA-Cavado da Light, gerado por desenhista. . . . 56

5.3 Arquitetura da Plataforma. . . 57

5.4 Chaves de 3 posi¸c˜oes. . . 59

5.5 Chaves `a g´as. . . 59

5.6 Diagrama de Classes da biblioteca OGDF. . . 62

6.1 Resultados dos testes programados . . . 66

6.2 Teste para v´ertice com controle de sa´ıda de aresta. . . 67

6.3 Teste para v´ertice com controle de sa´ıda de aresta, v´arias arestas. . . 67

6.4 Teste com alimentador 1. . . 68

6.7 Sin´otico gerado pelo antigo sistema da Light. . . 70

6.8 Compara¸c˜ao de grau de compacta¸c˜ao. . . 70

6.9 Teste para alimentador 4. . . 71

6.12 Teste para alimentador 6 definitivo. . . 74

6.13 Teste para alimentador 4 definitivo. . . 74

6.14 Compara¸c˜ao de grau de compacta¸c˜ao. alimentador 4. . . 74

6.15 Teste alimentador 7 definitivo. . . 75

6.16 Teste definitivo. . . 76

(12)

6.1 M´edia de tempos de execu¸c˜ao . . . 65

(13)

Lista de S´ımbolos

α(u, v) Parâmetro utilizado na designa¸cão do ângulo entre duas arestas de H.

β(u, v) Parˆametro que indica o n´umero de dobras de uma aresta em H.

η Rede de fluxos de um grafo ortogonal planar.

ηhor Rede de fluxo horizontal para compacta¸c˜ao

ηver Rede de fluxo vertical para compacta¸c˜ao

Γ O desenho de um grafo.

λ, µ, χ Limite inferior, a capacidade e o custo de um arco (u, v) emη.

σ(x) Fluxo de uma entidade x (face, v´ertice).

θ Custo de fluxo em uma rede.

ε Ordem c´ıclica que define um embutimento planar.

Ah Conjunto de arcos horizontais para um grafo restrito.

Av Conjunto de arcos verticais para um grafo restrito.

c(v,w) Angulo entre a extremidade esquerda do eixo de balan¸co horizontal deˆ v e a extremidade w da aresta (v, w) incidente a v.

D(v) O conjunto de arestas com origem em um v´ertice V.

Dh Grafo restrito com arcos horizontais.

Dh Grafo restrito com arcos verticais.

E Conjunto de arestas de um grafo.

E Uma aresta qualquer de um grafo.

Eh Conjunto de arestas horizontais do grafo.

Ev Conjunto de arestas verticais do grafo.

(14)

G Um grafo.

H Representa¸c˜ao ortogonal de um grafo.

m(v,w) c(v,w) mod 4.

Sd(v) O conjunto de arestas a serem anexadas a um lado d do v´ertice v.

Sh Conjunto de segmentos horizontais do grafo.

Sv Conjunto de segmentos verticais do grafo.

V Conjunto de v´ertices de um grafo.

f Face de um grafo

p Total de ângulos-vértice em um vértice

(15)

Cap´ıtulo 1

Introdu¸c˜

ao

1.1 Motiva¸c˜

ao

Desenho de grafos endere¸ca o problema de construir representa¸cões gráficas de grafos, redes e estruturas combinatoriais relacionadas. As representa¸cões geométricas dos grafos vêm sendo investigadas pela matemática há séculos, tanto para a visualiza¸cão das estruturas quanto para desenvolver a intui¸cão sobre as estruturas tratadas. A organiza¸cão e visualiza-¸cão de informavisualiza-¸cão através de estruturas que demonstram entidades e rela¸cões de adjacência é uma problema importante quando tais informa¸cões forem complexas ou numerosas. A forma como um grafo é visualizado pode ser extremamente importante (Battista et al., 1999), se analisarmos que a qualidade do entendimento, confiabilidade e eficiência em termos de quantidade de informa¸cão são dependentes do resultado da visualiza¸cão.

A gera¸cão automática de desenhos de grafos tem várias aplica¸cões. Exemplos incluem a Engenharia de Software (diagramas de fluxos de dados, grafos de chamadas de sub-rotinas, hierarquias de classes e diagramas de objetos em programas orientados a objeto), Bancos de Dados (diagramas entidade/relacionamento), Sistemas de Informa¸cão (diagramas orga-nizacionais), Sistemas de Tempo Real (redes de Paterson (1977), diagramas de transi¸cão de estado), Sistemas de Suporte à Decisão (redes PERT, árvores de atividade), Projeto de circuitos integrados (diagramas de circuitos), Sistemas de Energia (diagramas das redes de transmissão e distribui¸cão), Inteligência Artificial (diagramas de representa¸cão do conheci-mento), etc. Devido à natureza combinatorial e geométrica dos problemas investigados e à ampla faixa de dom´ınios de aplica¸cão, a pesquisa em Desenho de Grafos tem sido condu-zida em diversas áreas, incluindo a Matemática Discreta (teoria topológica de grafos, teoria geométrica de grafos), Algoritmos (algoritmos em grafos, estruturas de dados, geometria computacional, VLSI), Computa¸cão Gráfica (linguagens visuais, interfaces gráficas, visuali-za¸cão de software) e Engenharia (nas diversas aplica¸cões do desenho de grafos, como, por exemplo, em sistemas de energia e no projeto de circuitos). Por este motivo, um grande número de publica¸cões na área está dispon´ıvel. Um tutorial de Battista et al. (1994) indica mais de 300 artigos sobre o assunto e, certamente, este número é atualmente muitas vezes

(16)

maior.

Especificamente, o problema proposto a ser resolvido por este trabalho se refere aos circuitos alimentadores da Light/RJ. Tais circuitos representam as informa¸cões de conec-tividade entre os elementos elétricos que compõem a transmissão de energia, desde o ali-mentador, até o receptor. Além disso, foi visto que para gerar os esquemáticos de circuitos alimentadores, uma série de regras, ou critérios de desenho deveriam ser seguidos.

Este trabalho procura focar em uma metodologia que trata de maneira mais intuitiva os fatores que definem o problema da visualiza¸cão de grafos. Um estudo foi feito para se implementar um sistema que pudesse ser moldado conforme o problema a ser resolvido (tratando critérios espec´ıficos do problema). A capacidade de especializa¸cão da solu¸cão, amparada por uma metodologia genérica que oferece esta especializa¸cão de maneira mais intuitiva foi o objetivo principal deste trabalho.

1.2 Trabalhos relacionados

Um desenho de um grafo pode ser gerado por diferentes abordagens, as quais estabele-cem rela¸cões de precedência variadas entre critérios estéticos. Cada contexto de aplica¸cão dita quais são as caracter´ısticas desejadas para o desenho. Diagramas ortogonais, por exem-plo, são utilizados em uma ampla gama de aplica¸cões. Usualmente, desenhos de grafos que correspondem a este tipo de diagrama também adotam a conven¸cão grid, na qual as coor-denadas de vértices e dobras de arestas são números inteiros. Muitos algoritmos de desenho que seguem esse modelo são conhecidos (Battista et al., 1994).

O Giotto é um algoritmo para desenho de grafos em grid mais eficiente em termos de vários critérios estéticos (Battista et al., 1994). Este algoritmo segue a metodologia

topologia-forma-métrica(Tamassia, 1987) composta pelas etapas de planariza¸cão, respon-sável por definir um embutimento planar para o grafo; ortogonaliza¸cão, responrespon-sável por definir ângulos de vértices e arestas; e compacta¸cão, responsável por obter coordenadas de um desenho o mais compacto poss´ıvel. A vertente do algoritmo Giotto, utilizada em grafos com vértices que possuem n arestas de entrada e/ou sa´ıda (com n podendo ser maior que 4) é chamada Kandinsky (Fößmeier and Kaufmann, 1996, 1997). O algoritmo

Column(T.Biedl and Kant, 1998) trabalha sob premissas de ser independente do processo de planariza¸cão, que pode gerar vários vértices fict´ıcios ao grafo, os quais contribuem para o aumento de complexidade e dificuldade de implementa¸cão do desenho. A primeira fase do algoritmo é responsável por ordenar os vértices de um grafo biconectado a partir de uma fonte e um sumidouro. Em seguida, os vértices do grafo são adicionados em linhas conse-cutivas do grid e colunas são alocadas para suas arestas, em uma combina¸cão ótima. O algoritmoPair (Papakostas and Tollis, 1994) segue as mesmas premissas do Column com modifica¸cões de implementa¸cão que o torna mais simples embora menos eficiente. Melo (2007) desenvolveu uma biblioteca genérica para manipula¸cão de grafos, contendo rotinas para desenho de grafos baseadas nestas abordagens.

(17)

1.3. OBJETIVOS 3

compacta¸cão é poder ter simplicidade em se modelar as restri¸cões de desenho. Como dito antes, isso é vital quando o contexto da aplica¸cão dita quais critérios estéticos devem ser obedecidos em desenhos de grafos.

Desenhos de circuitos elétricos possuem caracter´ısticas bem determinadas, como por exemplo, a idéia de fluxo de potência transferida entre os elementos do circuito. Algumas abordagens foram criadas para se evidenciar desenho de diagramas unifilares.

Rao and Deekshit (2003) apresentam, em seu trabalho, uma maneira de gerar diagramas unifilares com um método iterativo. Tal trabalho foi desenvolvido sob métricas de sistemas de circuitos alimentadores elétricos. Este trabalho concentra-se em estudar métodos de desenhos unifilares que privilegiam os critérios estéticos de agradabilidade e legibilidade. Entretanto, a preocupa¸cão com compacta¸cão do desenho (que poderia ser adquirida com um roteamento, resultado da ortogonaliza¸cão no Giotto) é minimizada. Ong et al. (2000) mostram uma vertente do algoritmo de recoloca¸cão para gerar diagramas elétricos unifilares automaticamente em modo grid, não ortogonais. Neste trabalho, os autores mostram ganhos em eficiência ao utilizar estruturas especiais na abordagem de recoloca¸cão. Mas por se tratar de um algoritmo para desenho de diagramas unifilares, possui uma carência evidente, em termos de critérios estéticos mais abrangentes. Estes trabalhos mostram resultados para o problema de desenhos de circuitos elétricos, sob forma de diagramas unifilares. Além da necessidade da legibilidade, e da compacta¸cão do desenho, outros critérios estéticos fazem parte da gama necessária para se gerar bons esquemáticos de circuitos elétricos.

Sugiyama et al. (1981) mostram em seu trabalho uma abordagem eficiente, para dese-nho de hierarquias. Tal abordagem incorpora critérios importantes para desedese-nho de circuitos elétricos e se mostra vantajosa, por simplicidade e eficiência, em compara¸cão com outras similares.

1.3 Objetivos

Este trabalho tem como objetivo o desenvolvimento de uma ferramenta computacio-nal capaz de gerar desenhos de grafos de maneira automática, otimizando fatores como complexidade visual da informa¸cão representada no grafo, legibilidade, e diversos critérios estéticos. Para isso foi proposto que seriam aplicadas técnicas de Programa¸cão Linear In-teira (PLI) em etapas de desenho dos grafos, para que restri¸cões espec´ıficas em desenhos de grafos de circuitos alimentadores de energia elétrica fossem contempladas de maneira mais eficiente.

(18)

1.4 Organiza¸c˜

ao do texto

O cap´ıtulo 2 apresenta diversos conceitos relacionados ao desenho de grafos, frisando as metodologias para desenho.

O cap´ıtulo 3 apresenta a metodologia de desenhos de grafos baseada em Programa¸cão Linear Inteira. Na etapa de ortogonaliza¸cão, são definidos os ângulos entre arestas e dobras de arestas. Dada uma topologia, o passo de ortogonaliza¸cão determina a forma de um de-senho. Em uma representa¸cão ortogonal, vértices não possuem coordenadas e cada aresta (u,v) é equipada com uma lista de ângulos. Tal lista descreve as dobras que a representa-¸cão ortogonal da aresta (u,v) terá no desenho final. Esta etapa faz parte da metodologia

Topologia-Forma-Métricadetalhada na se¸cão 2.3. Em se¸cão espec´ıfica, a ortogonaliza¸cão será descrita em sua abordagem baseada em PLI. O cap´ıtulo ainda apresenta a etapa onde são geradas as coordenadas dos desenhos de grafos, definindo uma métrica para o esquemá-tico. Esta etapa, a compacta¸cão, tem como entrada a sa´ıda da etapa de ortogonaliza¸cão. Uma se¸cão detalha a compacta¸cão em uma abordagem PLI onde são definidos tamanhos pré-determinados para os vértices, através de restri¸cões inseridas no sistema.

O cap´ıtulo 4 apresenta a metodologia hierárquica para desenho de grafos. Tal metodo-logia dispõe os vértices e arestas em n´ıveis e possui outros critérios estéticos e restri¸cões para constru¸cão do esquemático. Nesta metodologia é destacado o processo de otimiza¸cão do posicionamento de vértices que busca a minimiza¸cão do número de cruzamentos de arestas num desenho.

O cap´ıtulo 5 mostra as implementa¸cões desenvolvidas para a solu¸cão de Gera¸cão Au-tomática de Esquemáticos Ortogonais da empresa Light. Nesse cap´ıtulo são detalhados os componentes que configuram o sistema, sob o ponto de vista da obten¸cão dos dados atra-vés de informa¸cões dos circuitos alimentadores e da gera¸cão dos desenhos de tais circuitos. Os resultados das implementa¸cões são mostrados no cap´ıtulo 6.

(19)

Cap´ıtulo 2

Desenho de Grafos

Nas diversas áreas onde se empregam rotinas de gera¸cão de desenho de grafos, existem requisitos que devem ser observados para que seja poss´ıvel gerar bons desenhos, e, em cada área, tais requisitos podem ser bastante diferentes. Um desenho pode ser considerado ótimo em determinado contexto, mas pode não atender aos requisitos de alguma outra aplica¸cão. O elemento essencial para uma metodologia de desenho de grafos é o ambi-ente particular no qual o desenho será utilizado. Na realidade, palavras como dom´ınio de aplica¸cão ou ambiente onde será utilizado são muito abstratas para serem utilizadas em algoritmos computacionais. Existem conceitos mais espec´ıficos para se descrever os requisi-tos de um desenho, a saber, as conven¸cões de desenho, os critérios estéticos e as restri¸cões (Battista et al., 1999). As próximas se¸cões abordam, separadamente, cada um deles. Para entender os conceitos discutidos na seqüência, é importante estabelecer uma terminologia básica (Gross and Yellen, 1999; Harary, 2009; Bondy and Murty, 1976; Biggs et al., 1976; West, 2006; Wilson, 1996).

2.1 Grafos

Grafos são estruturas combinatoriais formadas por elementos simples que consistem em um conjunto de vértices e um conjunto de arestas. Vértices representam objetos concretos ou não, que possuem entendimento próprio e podem possuir propriedades adicionais como peso, cor, ou qualquer outro atributo que seja útil dentro do contexto da aplica¸cão. As arestas representam as rela¸cões entre os vértices. Grafos podem representar modelos f´ısicos como um circuito elétrico ou uma rede de computadores (Gross and Yellen, 1999; Harary, 2009; Bondy and Murty, 1976).

Defini¸cão 1 Um grafo G= (V;E) consiste na composi¸cão dos conjuntos finitos V con-tendo nv vértices e E, contendo ne arestas. O conjunto E é formado por pares

n˜ao-ordenados de v´ertices (u;w), onde u, w ∈ V.

(20)

Figura 2.1: Um grafo com 13 v´ertices e 13 arestas.

Uma aresta (u;w) com u=wé chamada de auto-ciclo (self-loop). Se a aresta ocorre mais de uma vez em E, ela é uma aresta paralela. Um grafo simples é um grafo que não possui auto-ciclos ou arestas múltiplas. O grafo da figura 2.1 é simples. Os vértices finais ou extremidades de uma arestae= (u;w)são os vérticesuew. O vértice ué chamado de adjacente ao vérticewe a aresta eé chamada de incidente aos vérticesuew. No grafo da figura 2.1, os vértices 1 e 3 são adjacentes, porém os vértices 1 e 5 não são. O(s) vizinho(s) de um vértice w são os vértices adjacentes a w. No grafo da figura 2.1, os vizinhos de 1 são os vértices 2, 3, 4 e 7. O grau de um vértice wé o número de vizinhos que ele possui. No grafo da figura 2.1, o grau do vértice 1 é igual a 4.

Um grafo direcionado ou d´ıgrafo é aquele onde as arestas são direcionadas, criando-se uma ordem para os vértices. No desenho de grafos direcionados, geralmente as arestas são representadas por setas, como na figura 2.2.

Figura 2.2: Exemplo de um d´ıgrafo.

Um caminho (direcionado) em um grafo (direcionado) G = (V;E) é uma seqüência (v1;v2;...;vh) de vértices distintos de G, tal que (vi; vi+1) ∈ E para 1 ≤ i ≤ h−1.

(21)

2.1. GRAFOS 7

a seqüência (1, 7, 6, 5) é um caminho direcionado. Um caminho (direcionado) é um ciclo (direcionado) se (vh; v1) ∈ E. Um grafo (direcionado) é ac´ıclico se não possui

ciclos (direcionados). No grafo da figura 2.1 o caminho (1, 4, 6, 7, 1) é um ciclo. O grafo direcionado da figura 2.2 não possui ciclos direcionados. Um desenho Γde um grafo (d´ıgrafo)Gé uma fun¸cão que mapeia cada vérticev a um ponto distintoΓ(v)e cada aresta (u, v)a uma curva simples aberta Γ(u, v), com pontos finais emΓ(u)eΓ(v). Um desenho de Gé planar, se não houver interse¸cão de arestas distintas. O grafo G é dito planar, se ele admite pelo menos um desenho planar. O grafo da figura 2.2 é planar.

Um desenho planar particiona o plano em regiões conectadas chamadas de faces. Uma face f é um la¸co de arestas, ou, uma seqüencia fechada de arestas. A face ilimitada é chamada de face externa, enquanto que as outras são chamadas de faces internas. Um embutimento planar de um grafo, é uma classe de equivalência de desenhos que se diferem pela ordem circular no sentido horário dos vizinhos de cada vértice. A figura 2.3 mostra um mesmo grafo apresentado com embutimentos planares diferentes.

Figura 2.3: Dois desenhos de um mesmo grafo. Ambos embutimentos representam um mesmo grafo.

(22)

2.2 Paradigmas em Desenho de Grafos

Para desenhar um grafo G é importante levar em considera¸cão as suas propriedades combinatoriais. O conhecimento sobre algumas propriedades predominantes de G (se é ac´ıclico, direcionado, planar) pode direcionar qual tipo de algoritmo para desenho deve ser aplicado. Geralmente conhecemos a classe de grafos a qual Gpertence. Essa classifica¸cão permite que determinados algoritmos próprios a determinadas classes de grafos destaquem melhor as propriedades combinatoriais do mesmo. Por exemplo, seGé um d´ıgrafo ac´ıclico, então pode ser importante desenhar todas as arestas seguindo a mesma dire¸cão, para enfatizar a inexistência de ciclos.

Assim, define-se que a classe do grafo em questão é um parâmetro de entrada para uma metodologia de desenho. Outros pontos de decisão também devem ser levados em considera¸cão no desenho. Ítens como a percep¸cão humana sobre as informa¸cões do dese-nho, ou mesmo, o ambiente em que será apresentado o desenho do grafo exercem grande dependência sobre os requisitos envolvidos na gera¸cão do desenho.

Nas se¸cões que seguem, serão mostrados conceitos sobre conven¸cão de desenhos, cri-térios estéticos e restri¸cões, entre outros. Tais conceitos modelam a lista de requisitos necessários para que uma determinada classe de grafo (em conjunto com determinadas decisões de visualiza¸cão) seja mais adequadamente descrita num desenho.

2.2.1 Conven¸c˜

oes de Desenho

Uma conven¸cão de desenho corresponde a uma regra básica que deve ser satisfeita pelo desenho. Por exemplo, para um desenho de diagrama de fluxo de dados relativo a uma aplica¸cão de engenharia de software, podemos adotar a conven¸cão de representar todos os vértices como caixas e todas as arestas como cadeias poligonais consistindo de segmentos horizontais e verticais. Uma conven¸cão de desenho de um aplicativo real pode ser extremamente complexa e envolver vários detalhes do desenho. Algumas conven¸cões bastante utilizadas estão descritas em seguida (Battista et al., 1999).

• Poligonal - Cada aresta do grafo ´e desenhada como uma cadeia poligonal. • Linhas-retas - Cada aresta do grafo ´e desenhada com segmentos retos.

• Ortogonal - Cada aresta do grafo é desenhada como uma cadeia poligonal de seg-mentos horizontais e verticais. Curvas (de ângulo reto) entre segseg-mentos de arestas são chamadas dobras.

• Grid - V´ertices, cruzamentos de arestas e dobras de arestas possuem coordenadas inteiras.

• Planar - Conven¸cão onde não há cruzamento de arestas no desenho.

• Desenhos direcionados - Um desenho de um grafo direcionado ´e chamado de

(23)

2.2. PARADIGMAS EM DESENHO DE GRAFOS 9

para cima e nenhum voltado para baixo. Para o contr´ario (arestas direcionadas para baixo) ´e chamado de downward.

Figura 2.4: Grafo desenhado utilizando a conven¸c˜ao linhas-retas.

Figura 2.5: Grafo desenhado utilizando as conven¸c˜oes ortogonal, planar e grid.

Figura 2.6: Grafo utilizando a conven¸c˜ao de desenho direcionado (downward).

(24)

orto-gonais são amplamente utilizados em circuitos esquemáticos e diagramas da engenharia de software. Desenhos planares são esteticamente atraentes, embora nem todos os grafos admitam tal desenho. D´ıgrafos ac´ıclicos representando estruturas hierárquicas (ex.: diagra-mas de PERT, diagradiagra-mas de heran¸ca de classes) são exemplos de desenhos direcionados ascendentes. Também é poss´ıvel que um desenho adote mais de uma conven¸cão. Desenhos de circuitos elétricos são normalmente executados utilizando as conven¸cões Ortogonal, Grid e Planar.

2.2.2 Crit´

erios Est´

eticos

Os Critérios estéticos especificam propriedades do desenho que devem ser aplicadas ao máximo poss´ıvel, de maneira a se alcan¸car a facilidade de compreensão do desenho como um todo. Os seguintes critérios são comumente utilizados (Batine et al., 1985; Purchase and Cohen, 1995; Sugiyama et al., 1981):

• Cruzamentos - Minimiza¸cão do número de cruzamentos entre arestas do grafo. O cenário ideal seria desenhos sempre planares, entretanto, nem todo grafo admite uma representa¸cão planar.

• Area´ - Minimiza¸cão da área. Talvez um dos critérios mais importantes, pela neces-sidade de todo desenho caber em um local limitado. Este critério é especialmente importante na conven¸cão grid, onde o tamanho das arestas é no m´ınimo uma unidade do grid (o desenho não pode ser reduzido ilimitadamente). Há duas formas de definir a área de um desenho: pelo fecho convexo (menor pol´ıgono convexo que engloba o desenho) ou pelo menor retângulo com lados horizontais e verticais cobrindo o desenho.

• Comprimento total das arestas - Minimiza¸cão da soma do comprimento total das arestas. É um critério complementar à busca da minimiza¸cão da área, assim como os outros critérios sobre comprimento de aresta.

• Máximo comprimento das arestas - Minimiza¸cão do comprimento máximo de qualquer aresta.

• Comprimento uniforme das arestas - Minimiza¸c˜ao da variˆancia no comprimento das arestas.

• Número de dobras- Minimiza¸cão do número total de dobras nas arestas. Especi-almente importante quando a conven¸cão Ortogonal é utilizada. Por outro lado, não faz sentido se a conven¸cão Linhas Retas é utilizada.

• Máximo de dobras por aresta - Minimiza¸cão do número máximo de dobras em uma aresta.

(25)

• Resolu¸cão Angular- Maximiza¸cão do menor ângulo entre duas arestas incidente no mesmo vértice. Especialmente importante quando a conven¸cão linhas-retas é usada. Critério que atua diretamente na legibilidade das informa¸cões do desenho.

• Razão de Aspecto - Aproxima¸cão da razão de aspecto ótima do desenho. A ra-zão de aspecto é definida como uma rela¸cão do comprimento da maior aresta e o comprimento da menor aresta do menor retângulo com cobertura (fecho convexo) horizontal e vertical. Importante em sistemas em que o desenho deve se adequar o mais perfeitamente poss´ıvel às dimensões de um visualizador (ex.: sistemas sinóticos com visores de grande largura).

• Simetria - Enfatizar as simetrias do grafo. Existem modelos matem´aticos que definem precisamente tais simetrias e seus respectivos desenhos (Melo, 2007; Battista et al., 1999; Lipton et al., 1985).

(a)

(b) (c)

(26)

(a) (b)

Figura 2.8: Exemplo de desenhos com número de dobras de arestas diferentes. A minimiza¸cão de número de dobras de arestas busca oferecer um desenho mais leg´ıvel (menos complexo).

Figura 2.9: Controlar a razão de aspecto ou, a rela¸cão entre largura e altura de um desenho, permite adequar o grafo a uma tela sem que se tenha perdas de informa¸cão do desenho, por eventual mal posicionamento.

(27)

Entretanto, é comum a existência de conflitos entre critérios indicando que um sistema de otimiza¸cão que tente contemplar todos simultaneamente pode não ser fact´ıvel. Con-seqüentemente, as metodologias de desenho de grafos estabelecem rela¸cões de precedência e adotam uma abordagem de divisão do processo em subetapas, nas quais cada algoritmo resolve um problema espec´ıfico de forma independente, conforme veremos na subse¸cão 2.2.5.

2.2.3 Restri¸c˜

oes

Enquanto conven¸cões de desenho e estética são regras e critérios gerais que se referem ao desenho do grafo como um todo, restri¸cões se referem a subgrafos espec´ıficos e subdesenhos. As restri¸cões mais utilizadas estão listadas abaixo (Kosak et al., 1994; Tamassia et al., 1988):

• Centraliza¸c˜ao - Posicionar um dado v´ertice no centro do desenho.

• Externaliza¸cão - Posicionar um dado vértice no limite exterior do desenho. • Agrupamento - Posicionar um conjunto de vértices próximos uns dos outros. • Seqüência (esquerda/direita e cima/baixo) - Desenhar um dado caminho

hori-zontalmente alinhado da esquerda para direita (verticalmente alinhado de cima para baixo).

• Forma - Desenhar determinado subgrafo em uma forma predefinida.

2.2.4 Eficiˆ

encia dos algoritmos

Este critério é extremamente importante quando tem-se que obter respostas em tempo real, por exemplo, em certos sistemas. Nesse caso, é comum a utiliza¸cão de heur´ısticas que podem diminuir ordens de grandezas em determinados algoritmos (levando-se em con-sidera¸cão a separa¸cão de metodologias em sub-partes, que resolvem problemas distintos e independentes em desenho de grafos).

As conven¸cões, critérios estéticos, o contexto da aplica¸cão, a eficiência dos algoritmos e as restri¸cões formam os parâmetros fundamentais associados às metodologias de desenho de grafos (Battista et al., 1999).

2.2.5 Precedˆ

encia entre Crit´

erios Est´

eticos

A maior parte das metodologias de desenho estão baseadas nas seguintes observa¸cões: • Os critérios estéticos freqüentemente entram em conflito uns com os outros. Desse

(28)

(a) Centraliza¸c˜ao

(b) Seq¨uencia (c) Externaliza¸c˜ao (d) Agrupamento

Figura 2.10: Exemplo de uso de restri¸cões de forma no desenho. O posicionamento de um elemento ou um grupo de elementos pode mudar a forma do desenho, centralizando um dado grupo de elementos, externalizando, ou até mesmo colocando elementos em seqüencia.

• Ainda que os critérios estéticos não entrem em conflito, é geralmente dif´ıcil levar em conta todos eles ao mesmo tempo.

Por exemplo, na figura 2.11 há dois desenhos em conven¸cão grid ortogonal, um mini-mizando o número de dobras e outro minimini-mizando o número de cruzamentos. Para este grafo, não existe um desenho em grid ortogonal que minimize ambos critérios estéticos simultaneamente.

´

E notado que a precedência de um critério sobre outro é diretamente ligado à adequa¸cão da aplica¸cão. As estratégias apresentadas na literatura geralmente dividem o processo de desenho de grafos em uma seqüência de passos algor´ıtmicos, cada um adequado para satisfazer uma certa subclasse de critérios estéticos. As metodologias mais populares são:

• Topologia-Forma-Métrica: (Tamassia, 1987; Tamassia et al., 1988; Batini et al., 1986). Esta estratégia foi projetada para construir desenhos ortogonais em grid, com tratamento homogêneo de uma grande variedade de critérios estéticos e restri¸cões. Será melhor detalhada em se¸cão próxima (2.3).

(29)

2.3. TOPOLOGIA-FORMA-M ´ETRICA 15

(a) Minimiza¸c˜ao de Dobras (b) Minimiza¸c˜ao de Cruzamentos

Figura 2.11: Dois desenhos ortogonais do mesmo grafo

• Visibilidade: (Battista and Tamassia, 1988; Battista et al., 1992), é uma metodo-logia de propósito geral para o desenho de grafos que utilizam a conven¸cão poligonal. • Aumento: É outra metodologia de propósito geral, para o desenho de grafos na conven¸cão poligonal. Porém é menos apropriada que as anteriores para a adi¸cão de restri¸cões (Battista et al., 1999).

• Direcionada por For¸ca: (Battista et al., 1999). Simula um sistema de for¸cas defi-nido no grafo de entrada e gera um desenho de “m´ınima energia“. Interessante para grafos n˜ao direcionados na conven¸c˜ao linhas-retas.

• Dividir para Conquistar: Bastante aplicada no desenho de grafos que possam ser, recursivamente, divididos em subgrafos. As principais aplica¸cões são o dese-nho de árvores (Reingold and Tilford, 1981; Walker, 1990) e d´ıgrafos série-paralelos (Bertolazzi et al., 1994).

2.3 Topologia-Forma-M´

etrica

Uma caracter´ıstica marcante desta metodologia é que ela tem como resultado desenho adequado nas conven¸cões planar, ortogonal e grid. Battista et al. (1994) apresenta alguns de muitos algoritmos que implementam esta metodologia. Um exemplo clássico de aplica-¸cão prática é a confecaplica-¸cão de circuitos integrados, nos quais o diagrama elétrico deve ser desenhado sob restri¸cões de uma área espec´ıfica (Soukup, 1972).

(30)

• Topologia: está relacionada à natureza do grafo, ou, o esquema (mapa) das liga¸cões vértices/arestas. Dois desenhos ortogonais possuem a mesma topologia se um pode ser obtido a partir do outro apenas através de deforma¸cões cont´ınuas, que não alteram as seqüências das arestas contornando as faces do desenho. Isso significa que a defini¸cão da topologia de um grafo é a defini¸cão de um dos seus embutimentos planares.

• Forma: trata-se da obten¸cão de ângulos e dire¸cões de dobras entre arestas de um grafo (complementando a topologia). Desenhos ortogonais possuem a mesma forma se eles têm a mesma topologia e um pode ser obtido a partir do outro modificando apenas o comprimento dos segmentos que representam as arestas do grafo, sem alterar os ângulos formados por elas.

• Métrica: caracterizada pela obten¸cão de coordenadas (tamanhos, posicionamento) do desenho. Ambos dois grafos possuem mesma métrica, se o que diferem entre si é somente opera¸cões de rota¸cão e transla¸cão.

´

E poss´ıvel perceber uma rela¸cão incremental, entre as propriedades descritas anterior-mente. Isso significa que existe uma forte tendência de divisão em etapas, para algoritmos que implementam a metodologia (Batini et al., 1986). A saber, as etapas são:

1. Planariza¸c˜ao: obt´em um embutimento planar;

2. Ortogonaliza¸cão: obtém informa¸cões de ângulos entre arestas e entre segmentos de arestas (dobras);

3. Compacta¸c˜ao: obt´em as coordenadas do desenho;

Cada uma destas etapas implementam os resultados esperados para cada uma das pro-priedades da metodologiaTopologia-Forma-Métrica. Outros critérios estéticos e restri¸cões podem ser introduzidos. Por exemplo, na etapa de planariza¸cão podemos for¸car que certos vértices fiquem na área externa do desenho (objetivando um aumento de foco na visua-liza¸cão deste vértice, ou, determinando associa¸cões f´ısicas, por exemplo, para o caso de vértices que representam entrada e sa´ıda de circuitos). Na etapa de ortogonaliza¸cão po-demos for¸car que certas arestas não possuam dobras, ou impor seqüências espec´ıficas de dobras em algumas arestas. Na etapa de compacta¸cão, podemos for¸car que certos vértices tenham coordenadas maiores ou menores que outros vértices.

(31)

2.3.1 Planariza¸c˜

ao

Uma das técnicas de planariza¸cão de grafos é constru´ıda a partir de sucessivas aplica¸cões de uma opera¸cão de planariza¸cão, a qual possui como princ´ıpio básico a substitui¸cão de cruzamentos de arestas por vértices falsos. Um teste averiguando o critério de parada deste algoritmo é necessário: determina se um desenho já é planar. A fórmula de Euler (Bondy and Murty, 1976) garante que em um grafo simples planar, com V vértices, o número de arestas, E, máximo, é dado por E ≤3V −6. No entanto, isso não garante que grafos simples planares com número de arestas menor que 3V −6 sejam planares. Além disso, a planariza¸cão não apenas testa a planaridade do grafo, mas constrói um embutimento planar para o mesmo.

De forma sucinta, o objetivo principal da planariza¸cão é reduzir ao máximo o número de cruzamento de arestas. Este problema é equivalente ao problema do máximo subgrafo planar, bastante estudado por Jünger and Mutzel (1997), Jayakumar et al. (1986), Kant (1992) e Nardelli and Talamo (1984). Ambos são problemas NP-hard, o que leva grande parte dos algoritmos de planariza¸cão a utilizarem heur´ısticas.

Uma heur´ıstica bastante comum para computa¸cão de um máximo subgrafo planar é apresentada por Battista et al. (1999) e é definida por inser¸cão de arestas, uma a uma do grafo original, verificando-se se cada inser¸cão torna o grafo planar ou não. Nesse processo, para cada aresta (u, v), é preciso encontrar um caminho de custo m´ınimo no grafo dual do embutimento atual (que está sendo montado incrementalmente), e assim, inserir a aresta ao embutimento.

Dado um grafo planar, G, seu dual (geométrico), G∗, pode ser constru´ıdo de acordo com os passos apresentado por Wilson (1996). Existem vários algoritmos para cálculo do caminho de menor custo. Quando todas arestas do grafo possu´ırem o mesmo peso, uma busca em largura (BFS) pode ser utilizada. Para os outros casos, os algoritmos de Dijkstra (Dijkstra, 1959) e Bellman-Ford (Bellman, 1958) e (Ford and Fulkerson, 1962) são boas op¸cões. O importante é que exista alguma forma de navegabilidade entre o grafo dual e o primal, já que o caminho m´ınimo é encontrado no primeiro, e a adi¸cão de arestas é feita no segundo.

O resultado das itera¸cões de inser¸cões das arestas é um embutimento planar (quando isto for poss´ıvel).

2.3.2 Ortogonaliza¸c˜

ao

A etapa de ortogonaliza¸cão é responsável por criar uma representa¸cão ortogonal H, a partir de um embutimento planar resultante da planariza¸cão. O resultado desta etapa é a obten¸cão dos ângulos entre arestas que partem ou chegam em cada vértice, e os ângulos das dobras das arestas, que determinam sua dire¸cão.

(32)

ˆangulo de π/2.

A seguir é descrito o método original de ortogonaliza¸cão de embutimento planar baseado em fluxo de redes que minimiza o número de dobras de arestas. Este algoritmo possui custo quadrático e foi primeiramente apresentado por Tamassia (1987) com varia¸cões, refinamentos e extensões dadas em Fößmeier and Kaufmann (1996), Tamassia (1985) e Tamassia et al. (1988).

Sendo Γ um desenho ortogonal de um embutimento planar G′_{, existem dois tipos de} ˆangulos em Γ:

• Angulo gerado por duas arestas incidentes em um vértice comum, chamado deˆ ângulo-vértice.

• Angulos formados por dobras de arestas (entre segmentos de aresta consecutivos),ˆ chamados ˆangulos-aresta.

(a) Ângulos-vértice (b) Ângulos-arestas

Figura 2.12: ˆAngulos em torno de um v´ertice e dentro de uma face em um desenho ortogonal planar

Isto nos leva `as seguintes conclus˜oes:

Lema 1 Em um desenho planar ortogonal, a soma dos ângulos-vértice de cada vértice deve ser igual a2π.

Lema 2 Para cada face interna f de Γ, a soma dos ângulos-vértice e de dobras é igual a

π(p−2), onde pé o total de ângulos. Para a face externa, a soma é igual a π(p+ 2).

A prova destes lemas ´e apresentada em Tamassia (1987).

Considere um embutimento planar de um grafo bidirecional G, com vértices de grau máximo quatro. O número total de ângulos-vértice dentro de uma face f é designado comona(f). ComoGé bidirecionado, para cada aresta e= (u, v), também existe a aresta

e = (v, u). A aresta que percorre determinada face f no sentido anti-horário é chamada de aresta anti-horário. O conjunto de arestas com origem em um vérticeV é denotado por

(33)

Dado um desenho planar ortogonal deG, s˜ao definidos os seguintes valores para cada uma de suas arestas:

• α(u, v)·π/2é o ângulo em um vérticeuformado pelos primeiros segmentos da aresta (u, v) e a próxima aresta anti-horário ao redor de u.

• β(u, v)é o número de dobras ao longo da aresta (u, v)com o ângulo deπ/2em seu lado esquerdo.

Os parâmetros α e β são definidos como os parâmetros que caracterizam uma repre-senta¸cão ortogonal (desenhos com os mesmos valores destes parâmetros são considerados equivalentes). Portanto, uma representa¸cão ortogonal H é definida através da atribui¸cão de valores inteiros α e β para todas arestas de G, de forma que as seguintes propriedades sejam satisfeitas:

1. 1≤ α(u, v)≤ 4 2. β(u, v)≥ 0

3. Para cada v´erticeu, a soma deα(u, v)para todas as arestas orientadas a partir de u

´e 4, ou:

X

(u,v)∈ D(f)

α(u, v) = 4 (2.1)

4. Para cada face internaf, a soma deα(u, v) +β(v, u) +β(u, v)para todas as arestas anti-hor´ario de f ´e igual a 2na(f)−4.

X

(u,v)∈ D(f)

α(u, v) +β(v, u) +β(u, v) = 2na(f)−4 (2.2)

5. Para a face externa, esta mesma soma ´e igual a 2na(f) + 4, ou:

X

(u,v)∈ D(f)

α(u, v) +β(v, u) +β(u, v) = 2na(f) + 4 (2.3)

Tais ´ıtens definem o sistema que dever´a ser obedecido na minimiza¸c˜ao das dobras de arestas.

Transforma¸c˜ao do problema em fluxo de redes

(34)

A premissa desta metodologia (em associar os ângulos ao fluxo) é de determinar um fluxo de custo m´ınimo, o que corresponde um desenho com menor número de dobras. A descri¸cão abaixo explica como essa rede deve ser constru´ıda. Os valores deλ(u, v),µ(u, v) e χ(u, v) indicam, respectivamente, o limite inferior, a capacidade e o custo de um arco (u, v), veja a figura 2.13:

(a) arcos de η de nodos-v´ertice

para nodos-face.

(b) arcos deη entre nodos-face.

Figura 2.13: Rede η associada a um embutimento planar do grafo G (mostrado em linhas pontilhadas). Cada nodo-face f de η ´e mostrado com a quantidade de fluxo

σ(f) consumida: (a) arcos deη de nodos-v´ertice para nodos-face; (b) arcos de η entre nodos-face.

Os nós da redeηsão os vértices e faces deG. Um nó derivado de um vértice é chamado nó-vértice. Um nó derivado de uma face é chamado nó-face. Um nó-vérticeV deηproduz fluxoσ(v) = 4, e, um nó-facef deη consome um fluxo σ(v) = 2na(f)−4, sef é interna,

ouσ(v) = 2na(f) + 4 para faces externas. Para cada aresta(u, v)de G, com facesf e G

a sua esquerda e direita, respectivamente,η possui dois arcos:

• Arco (u, f): Este arco possuiλ(u;f) = 1,µ(u;f) = 4eχ(u;f) = 0. O arco(u;f) representa a quantidadeα(u, v). O limite inferior e a capacidade são colocados dessa forma em decorrência da defini¸cão de produ¸cão de fluxo por um vértice V. O custo associado a esse arco é zero, pois o ângulo se trata de um ângulo de vértice (note que o arco é do vértice upara face f) e a solu¸cão buscada é a de m´ınimo número de dobras (ângulos nas arestas).

• Arco (f, g): Este arco possui λ(f, g) = 0, µ(f, g) = ∞ e χ(f, g) = 1. O arco (f;g)representa a quantidade β(u, v). O limite inferior e a capacidade indicam que a aresta pode ou não conter dobras. A unidade do custo equivale à unidade de fluxo definida (π/2). Como ele ocorre em uma aresta (note que o arco é da face f para a face G), deve ser contabilizado.

(35)

X

v

σ(v)−X

f

σ(f) =X

v

4−X

f

(2na(f)−4)−8 (2.4)

O custo de um fluxoθ em uma rede constru´ıda conforme a descri¸cão acima equivale ao número total de dobras de uma representa¸cão ortogonal H de G. Além disso, o fluxo de um arco entre nodos-vértices e nodos-faces, θ(u;f), corresponde ao valorα(u, v)da aresta associada em H, enquanto que o fluxo de um arco entre nodos-faces, θ(f;g), corresponde ao valor β(u, v)dessa mesma aresta.

As figuras 2.14 e 2.15 mostram exemplos de montagem de uma rede de fluxo para um exemplo de desenho compactado.

Figura 2.14: Exemplo de ortogonaliza¸c˜ao.

2.3.3 Compacta¸c˜

ao

A compacta¸cão é a etapa onde as coordenadas são atribu´ıdas a uma representa¸cão ortogonal. Na compacta¸cão, os comprimentos das arestas são determinados seguindo um objetivo de construir um desenho de pequena área, utilizando apenas coordenadas inteiras para os pontos, já que a conven¸cão grid é adotada.

A estratégia mostrada neste texto exige que as faces do grafo sejam retangulares. Todas as arestas (u, v) ∈ D(f) devem possuir α(u, v) ≤ 2 e β(v, u) = 0. Na face externa, todas as arestas (u, v) ∈ D(h)devem possuir α(u, v)≥2 e β(u, v) = 0. Casos onde as faces não são retangulares, devem ser tratados refinando-se representa¸cões ortogonais com tais faces não retangulares afim de se obter faces sempre retangulares. Isso é conseguido inserindo-se vértices, ou arestas falsas.

O problema da compacta¸cão também pode ser resolvido através de abordagem de fluxo de redes. Neste caso, duas redes são criadas (ηhor e ηver) , unindo-se pontos interiores

(36)

(37)

2.4. METODOLOGIA HIER ´ARQUICA 23

tamanhos: horizontal e vertical. A figura 2.16 mostra a distribui¸c˜ao dos pontos para as redes de fluxo citadas.

Figura 2.16: Redesηver eηhorpara configura¸c˜ao do sistema de compacta¸c˜ao das arestas.

Estes sistemas de fluxos de rede horizontal e vertical são responsáveis por definir os tamanhos das arestas dispostas nas duas dire¸cões, e possuem como restri¸cão básica a dimensão unitária para uma aresta sem dobras ligando dois vértices. Portanto, o problema é encontrar o fluxo de menor custo, em uma rede com limites inferiores nos arcos.

Complexidade da Compacta¸c˜ao e Ortogonaliza¸c˜ao por Fluxo de Redes

A complexidade de tempo das etapas de ortogonaliza¸cão e compacta¸cão da aborda-gem apresentada aqui é determinada pelos algoritmos de fluxo em redes. Os algoritmos de fluxo máximo por incremento de caminhos e fluxo máximo por forma¸cão de pré-fluxo pos-suem complexidade de tempo diferentes e fortemente dependentes da densidade do grafo (Sedgewick, 2002). De qualquer forma, nenhum deles garante complexidade de tempo inferior a O(V2_{). Segundo Foulds (1992) é poss´ıvel obter um algoritmo mais elaborado} chegando em uma complexidade de O(V7/4_logV_).

2.4 Metodologia Hier´

arquica

(38)

onde se deve enfatizar a informa¸cão das camadas hierárquicas do desenho. A metodologia hierárquica também é tratada em passos:

1. Distribui¸cão em Camada: nesta etapa, primeiramente, são distribu´ıdas as camadas (através de critérios espec´ıficos de requisitos, ou, automaticamente, via busca por largura). Cada aresta liga uma camada à sua posterior. Para o caso em que uma aresta liga dois vértices de camadas distantes, falsos vértices são criados em n´ıveis das camadas intermediárias.

2. Redu¸cão de Cruzamentos: nesta etapa, o resultado da etapa de Distribui¸cão em camadas é recebido como entrada. Para reduzir os cruzamentos, a ordem dos vértices em cada n´ıvel é otimizada, mirando-se um resultado de minimiza¸cão de cruzamentos global. Neste caso, um sistema linear pode ser usado para tal minimiza¸cão.

3. Atribui¸cão de Coordenadas x: nesta metodologia, cada n´ıvel definido na hierarquia possui elementos com mesma coordenada y. Nesta etapa de atribui¸cão de coorde-nadas x são produzidas coordenadas finais para os vértices preservando a ordena¸cão e a redu¸cão de cruzamentos obtidos no passo anterior. No final dos passos, o dese-nho final é obtido pela primeira representa¸cão de cada aresta com um segmento de linha reta e então ocorre a remo¸cão dos vértices ”fict´ıcios”. (Desta maneira, arestas compridas podem ser representadas por linhas poligonais).

(39)

Cap´ıtulo 3

Desenhos de Grafos baseados em PLI

A estratégia mais efetiva para tratar desenhos ortogonais é a que usa os conceitos apresentados anteriormente, de topologia, forma e métrica. A implementa¸cão mais efi-ciente de tal estratégia, segundo Eiglsperger et al. (2000) é o GIOTTO (Tamassia, 1987; Tamassia et al., 1988; Battista et al., 1995). Nesta estratégia, como visto antes, são efetu-adas três etapas para forma¸cão do desenho, a Planariza¸cão, a Ortogonaliza¸cão e a Compac-ta¸cão. Tidas como cr´ıticas para a abordagem, as etapas de Ortogonaliza¸cão e Compacta¸cão são problemas resolvidos através de sistemas de fluxo de redes, como problemas de mini-miza¸cão iterativos.

A versão original do algoritmo GIOTTO atendia apenas a desenho de grafos de grau máximo igual a 4. Na abordagem Kandinsky (Fößmeier and Kaufmann, 1996, 1997) o conceito GIOTTO foi estendido de maneira que grafos com grau maior que 4 pudessem ser desenhados sem perda do controle do número final de vértices.

Neste cap´ıtulo é apresentado um método para ortogonaliza¸cão considerando uma larga variedade de restri¸cões, onde se tem uma maior flexibilidade no desenho de grafos de acordo com os requisitos dos usuários (Eiglsperger et al., 2000). A abordagem aqui mostrada é baseada nos algoritmos GIOTTO e Kandinsky.

3.1 Modelagem por Programa¸c˜

ao Linear Inteira

Em um modelo de programa¸c˜ao linear inteira (Papadimitriou and Steiglitz, 1982; Chvatal, 1983), existe a necessidade de se otimizar (maximizar ou minimizar) uma fun-¸c˜ao objetivo da forma:

f(x1, x2, ..., x3) = a1x1 + a2x2 + ... +anxn (3.1)

sujeita a restri¸cões modeladas por equa¸cões e inequa¸cões lineares, tais como:

A[x] ≤ b

x ≥ 0 (3.2)

(40)

Nas equa¸cões 3.1 e 3.2, x é o vetor das variáveis, a matriz A é chamada matriz de coeficientes e o vetor b vetor de restri¸cões. Se as variáveis do sistema são inteiras, diz-se que a programa¸cão linear é inteira. O objetivo de um problema de PLI como o mostrado acima é minimizar ou maximizar a fun¸cão objetivo, determinando o valor de cada variável. A grande vantagem deste tipo de modelagem no desenho de grafos está no fato de que qualquer novo critério estético a ser aplicado ao desenho exige apenas a inclusão de novas inequa¸cões ( que modelam uma restri¸cão) na matriz de coeficientes, sem necessidade de altera¸cões no algoritmo em si. Esta caracter´ıstica torna as metodologias baseadas em PLI bastante atraentes tendo em vista a flexibilidade oferecida por estas para a inclusão de novas restri¸cões.

3.2 Ortogonaliza¸c˜

ao em Programa¸c˜

ao Linear Inteira

A etapa de ortogonaliza¸cão PLI (Eiglsperger et al., 2000; Eiglsperger and Kaufmann, 2001), da mesma forma que a baseada em fluxo, recebe como entrada do sistema um embutimento planar, resultante da etapa de Planariza¸cão, de um grafo G = (V, E), com vértices V e arestas E, dados pela ordem c´ıclica em sentido horário das arestas incidentes de cada vértice v. ε(v) é a seqüencia c´ıclica de arestas atrelada a cada vértice v. Cada aresta e = (v, w) pertencente a E aparece duas vezes em ε: uma vez como (v, w) em

ε(v) e outra como (w, v) em ε(w). Complementando o conjunto de dados apresentado, define-se como F o conjunto de faces do grafo. Seja Fin o conjunto de faces internas, e

Fout o conjunto de faces externas, cada face f ´e armazenada como uma lista de arestas

ordenadas. Cada aresta e em uma facef ´e direcionada tal que a face prescrita f esteja `a direita de e (figura 3.1).

Para modelar um sistema PLI equivalente ao problema de fluxo de redes da ortogona-liza¸cão, a defini¸cão de dobras de arestas deve ser implementada, pois, é exatamente este o ponto de minimiza¸cão de todo o sistema de ortogonaliza¸cão. Para cada aresta (u, v) pertencente a ε, há uma variável r(u,v), que conta o número de dobras de ângulo de π/2

(dobras `a direita, seguindo o sentido definido para ε) e uma vari´avel l(u,v), que conta o

número de dobras de3π/2(dobras à esquerda), ambas ao longo da aresta na dire¸cãou−v. As variáveis r(u,v) e l(u,v) contam o número de dobras da dire¸cão contrária (v−u) (uma dobra de3π/2em uma dire¸cão é uma dobra deπ/2na dire¸cão contrária) (figura 3.2). Para se obter um desenho com número m´ınimo de dobras, minimiza-se a soma das variáveis de dobras:

X

(u,v)∈ E

(r(u,v) + l(u,v)) (3.3)

Nesta modelagem é necessário, ainda, que seja modelado um outro tipo de variável, que definirá as dire¸cões de sa´ıda de arestas em cada vértice. A variável a(u,v) define um valor de ângulo entre e = (u, v) e seu predecessor c´ıclico em ε(v), no vértice v. O valor

(41)

3.2. ORTOGONALIZA ¸C ˜AO EM PROGRAMA ¸C ˜AO LINEAR INTEIRA 27

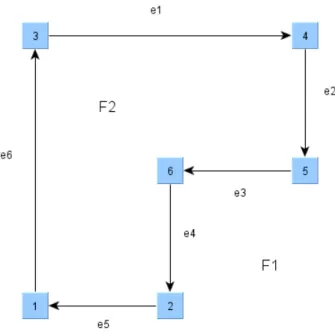
Figura 3.1: Defini¸c˜ao de faces utilizada em Eiglsperger et al. (2000). Nesta figura h´a duas faces: F1 :{e1, e6, e5, e4, e3, e2} eF2 :{e1, e2, e3, e4, e5, e6}.

Figura 3.2: Percorrendo-se e(1,2), tem-se duas dobras à direita (r(1,2) = 2 ) e uma à esquerda (l(1,2) = 1). Na dire¸cão contrária,e(2,1), tem-se r(2,1) = 1 e l(2,1) = 2.

Todos os ângulos incidentes têm que ser múltiplos de π/2, de forma que se deve demandar, explicitamente, que as variáveis possuam valores inteiros.

Isto leva ao seguinte sistema de minimiza¸c˜ao inteira (Eiglsperger et al., 2000):

min P

(v,w)∈ E(r(v,w) + l(v,w)) sujeito a

(T1) P

(v,w)∈ ε(v)a(v,w) = 4 ∀v ∈ V (T2) P

(v,w)∈ f(a(v,w)+l(v,w)−r(v,w)) =

2k−4 f ∈ Fin, |f|=k

2k+ 4 f ∈ Fout, |f|=k

∀ f ∈ F

(T3) l(v,w) = r(w,v) ∀ (v, w) ∈ ε

l(v,w), r(v,w) ∈ N ∀ (v, w) ∈ ε

a(v,w) ∈ 1, ...,4 ∀ (v, w) ∈ ε

(42)

Em Tamassia (1987), mostra-se que as condi¸c˜oes acima s˜ao suficientes para gerar de-senhos ortogonais.

3.2.1 Kandinsky

O algoritmo Kandinsky pode tratar vértices com grau superior a quatro, permitindo ângulo zero entre arestas incidentes a um dos quatro lados de um vértice. Neste modelo, tem-se um grid de linhas mais espessas, pois atribui-se a cada uma delas um conjunto de linhas mais finas onde as arestas são roteadas. Isto significa que os vértices, neste modelo, têm largura e altura.

Para assegurar um desenho correto, a propriedadebend-or-end deve ser mantida, o que implica no controle do tamanho dos vértices. Existe também uma preocupa¸cão com os casos em que arestas sairão num mesmo lado de um vértice: nesse caso, há uma grande possibilidade destas arestas se cruzarem, caso um controle de sa´ıda não seja efetuado. Tal controle pode ser efetuado via dobras de vértice, um conceito aderido à modelagem Kandinsky e garante por meio de ângulos de sa´ıda de arestas que a interse¸cão para estes casos seja evitada.

Cada aresta pode ter duas dobras de vértice, uma para cada vértice que nela incide. Para este propósito, introduz-se para cada aresta (v, w) pertencente a ε quatro variáveis:

lbv

(v,w),rbv(v,w) ,lbw(v,w)erbw(v,w), que representam as dobras de vértice nos vérticesv ew. As variáveislb(v,w) erb(v,w) que denotam as dobras de face (como as definidas na modelagem anterior) na aresta (v, w). Para simplificar, escreve-se l(v,w) = lbv(v,w)+lb(v,w)+lbw(v,w) e

r(v,w) =rbv(v,w)+rb(v,w)+rbw(v,w). Comparando a nota¸cão entre as formula¸cões GIOTTO e Kandinsky, observa-se que l(v,w) é sempre o número total de dobras à esquerda de (v, w). A formula¸cão Kandinsky completa é dada pelo conjunto de equa¸cões 3.5:

min P

(v,w)∈ E(r(v,w) + l(v,w)) sujeito a

(K1) P

(v,w)∈ ε(v)a(v,w)= 4 ∀ v ∈ V (K2) P

(v,w)∈ f(a(v,w)+l(v,w)−r(v,w)) =

2k−4 f ∈ Fin, |f|=k

2k+ 4 f ∈ Fout, |f|=k

∀f ∈ F

(K3) lbv

(v,w)+rbv(v,w) ≤ 1 ∀ (v, w) ∈ ε

(K4) a(u,v)+lbv(v,w)+rbv(v,w) ≥ 1 ∀ (v, w),(v, u)subseq¨uente em ε(v) (K5)

     lbv

(v,w) = rbv(w,v)

lb(v,w) = rb(w,v)

lbw

(v,w) = rbw(w,v)

∀ (v, w) ∈ ε

lbv

(v,w), rbv(v,w), lbw(v,w), rbw(v,w) ∈ N ∀(v, w) ∈ ε

lb(v,w), rb(v,w) ∈ N ∀ (v, w) ∈ ε

a(v,w) ∈ 0, ...,4 ∀(v, w) ∈ ε

(43)

Figura 3.3: Um exemplo para um desenho com base em Kandinsky.

redes de fluxo é bastante complicada. A configura¸cão da PLI pode ser formulada de uma maneira muito mais elegante e emprega maior facilidade na inser¸cão de restri¸cões variadas de desenho. A se¸cão a seguir detalha a modelagem de algumas restri¸cões para desenhos ortogonais, bastante importantes no âmbito de desenho de circuitos elétricos/eletrônicos.

3.2.2 Restri¸c˜

oes Especiais em Ortogonaliza¸c˜

ao

Existem alguns tipos de requisitos de desenho de grafos, que permitem o importante ob-jetivo de se ler grandes quantidades de informa¸cões em grandes grafos, numa área pequena. Requisitos básicos como os que compõem a formula¸cão descrita anteriormente objetivam minimiza¸cão de área, de número de cruzamentos, entre outros. Outros tipos de requisitos poderiam ser:

• Defini¸c˜ao das dire¸c˜oes das arestas (upward, rightward).

(44)

• Defini¸c˜ao de tamanho de v´ertices.

Como este trabalho objetiva a implementa¸cão de um sistema de quadros sinóticos au-tomático para os circuitos alimentadores da empresa Light/RJ, alguns critérios espec´ıficos deste sistema (listados com detalhes no cap´ıtulo referente ao Sistema Light) tiveram que ser modelados. Tais critérios puderam descrever bem alguns elementos especiais dos cir-cuitos alimentadores (tais como algumas chaves seccionadoras utilizadas na representa¸cão da Light).

Como dito anteriormente, a modelagem de critérios estéticos em desenho de grafos dentro da abordagem de programa¸cão linear inteira se dá através da inser¸cão de equa¸cões e inequa¸cões ao modelo previamente estabelecido.

Mostra-se, nesta se¸cão, um conjunto de restri¸cões encontradas na literatura (Eiglsperger et al., 2000) para a modelagem de critérios estéticos (restri¸cões). Algumas destas modelagens foram utilizadas no sistema de gera¸cão de sinóticos implementado neste trabalho de mestrado.

Direcionamento de arestas

Eiglsperger et al. (2000) apresenta um modelo de restri¸cões capaz de direcionar grafos em um desenho. A referência chama tais restri¸cões como restri¸cões de aresta. Como definido anteriormente, um desenho upward é um desenho onde todas as arestas ver-ticais sempre apontam para cima. Como requisito para um desenho upward, é preciso que o embutimento planar seja um embutimento upward (Fößmeier and Kaufmann, 1994; Garg and Tamassia, 1994). Este é um embutimento onde as arestas incidentes de um vér-tice v qualquer são somente ordenadas em sentido horário, e também possuem a primeira aresta de chegada (se não possuir arestas de chegada, a primeira aresta de sa´ıda) marcada como uma aresta ancora(v) (Eiglsperger et al., 2000). Uma aresta ancora é uma aresta definida como inicial na seqüencia c´ıclicaε.

A idéia básica para este algoritmo é introduzir um eixo de balanceamento para cada vértice. Tal eixo de balanceamento divide o vértice em dois retângulos. Para um desenho

upward, por exemplo, o eixo se define horizontalmente, e, todas as arestas de sa´ıda dos vértices devem estar conectadas no retângulo de cima, e as arestas que chegam nos vértices, devem estar conectadas no retângulo de baixo. A figura 3.4 mostra a disposi¸cão dos eixos de balanceamento num trecho de desenho upward.

Para complementar esta idéia, e definindo as regras para este grupo de restri¸cões, é preciso ressaltar que todos os eixos de balanceamento dos vértices que compõem o grafo devem ser orientados na mesma dire¸cão. Além disso, as dobras das arestas não podem criar segmentos de arestas que ferem o direcionamento do desenho (por exemplo, nos desenhos

upward n˜ao s˜ao permitidos segmentos de arestas apontando para baixo).

Para gerar as restri¸cões que caracterizam as condi¸cões escritas, é preciso definir, para cada arestae = (v, w) ∈ ε(v); ce, denotando o ângulo entre a extremidade esquerda do

(45)

e 2, para arestas de sa´ıda. Dessa forma, fica intuitivo perceber que as arestas de sa´ıda se posicionam por cima do eixo. Também é poss´ıvel perceber que, para uma aresta e′ seguindo e em ε(v), ce′ =c_e+a_e′. Desta equa¸cão, tem-se que c_e pode ser expresso como

ce = Pe′ _∈ _A₍_e₎ae′ + cv, onde A(e) ⊆ ε(v) ´e o conjunto de arestas entre ancora(v)

e e = (v, w) em ε(v), incluindo e, e, a vari´avel cv denota o ˆangulo entre ancora(v) e a

extremidade esquerda do eixo de balan¸co. Para assegurar que todas as arestas incidam no lado correto do vértice, as condi¸cões seguintes têm que ser inseridas na formula¸cão PLI:

−2 ≤ c(v,w) ≤ 0 ∀ v ∈ V,∀ (v, w) ∈ εi(v)

0 ≤ c(v,w) ≤ 2 ∀v ∈ V,∀ (v, w) ∈ εo(v)

Para estas restri¸c˜oes, εi(v)´e o subconjunto de ε(v) composto das arestas de entrada.

εo(v)´e o subconjunto an´alogo, para arestas de sa´ıda.

Entretanto, ainda são necessárias algumas condi¸cões adicionais, que garantirão que os eixos de balanceamento dos vértices do grafo estejam em dire¸cões sempre paralelas. Para isso, a restri¸cão seguinte é suficiente (Eiglsperger et al., 2000):

c(v,w) − l(v,w) + r(v,w) − c(w,v) = 2 ∀ (v, w) ∈ εo(v) (3.6)

Este critério é fundamental para constru¸cão de desenhos que devem mostrar sentido de fluxo (como é o caso dos desenhos dos circuitos elétricos alimentadores da Light). Vere-mos, mais adiante, que a inser¸cão deste tipo de restri¸cão ao sistema impactaria bastante negativamente o número de solu¸cões fact´ıveis para os desenhos. Após vários testes con-frontando o resultado visual e legibilidade, foi decidido que uma abordagem hierárquica, ortogonal, seria mais eficiente e simples de se implementar, sob ponto de vista de controle das poss´ıveis solu¸cões não fact´ıveis que poderiam surgir ao se inserir outras restri¸cões junto desta.