Mestrado Profissional em Matemática em Rede Nacional
PROPMAT
DISSERTAÇÃO DE MESTRADO
Noções de Matemática Básica
aplicada à Matemática Pinanceira
Aldo Agustinho Alves
UNIVERSIDADE FEDERAL DE ALAGOAS
INSTITUTO DE MATEMÁTICA
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL
ALDO AGUSTINHO ALVES
NOÇÕES DE MATEMÁTICA BÁSICA
APLICADA À MATEMÁTICA
FINANCEIRA
NOÇÕES DE MATEMÁTICA BÁSICA APLICADA À
MATEMÁTICA FINANCEIRA
Dissertação de Mestrado apresentada ao Mes-trado Profissional em Matemática em Rede Na-cional do Instituto de Matemática da Universi-dade Federal de Alagoas como requisito parcial para obtenção do grau de Mestre em Matemá-tica.
Orientador: Prof. Dr. Fernando Pereira Micena
Catalogação na fonte
Universidade Federal de Alagoas
Biblioteca Central
Divisão de Tratamento Técnico
Bibliotecária Responsável: Helena Cristina Pimentel do Vale
A474n Alves, Aldo Agustinho .
Noções de matemática básica aplicada à matemática financeira / Aldo Agustinho Alves. – 2016.
76 f. : il.
Orientador: Fernando Pereira Micena.
Dissertação (Mestrado Profissional em Matemática) – Universidade Federal de Alagoas. Instituto de Matemática. Programa de Pós-Graduação de Mestrado Profissional em Matemática em Rede Nacional. Maceió, 2016.
Bibliografia: f. 91-92. Anexos: f. 93-95.
1. Matemática – Estudo e ensino. 2. Matemática financeira – Estudo e ensino.
I. Título.
Agradeço primeiramente a Deus pela oportunidade e pela saúde que me concedeu para hoje está terminando este curso. Os meus sinceros agradecimentos a minha esposa Maria do Socorro que sempre me incentivou bastante durante todo o mestrado e as minhas filhas Cinthya Vanessa e Harla e minha neta Maria Eduarda “Madu” que me trouxeram sempre bastante força de vontade nos momentos difíceis do curso.
Agradeço ao Prof. Dr. Fernando Pereira Micena pela orientação neste trabalho. Os meus sinceros agradeço aos professores Prof. Dr. Vanio Fragoso de Melo e Prof. Dr. Carlos Ar-golo Pereira Alves membros da banca examinadora deste trabalho, e a todos os professores do PROFMAT.
“Embora ninguém possa voltar atrás e fazer um novo começo, qualquer um pode começar agora e fazer um novo fim”
O objetivo deste trabalho é subsidiar uma abordagem da matemática básica aplicada a mate-mática financeira com situações vivenciada pelos alunos, provocando neles seu lado crítico e assim contribuindo na sua educação financeira. Neste, encontra-se um breve relato da história e teorias de assuntos pertinente a matemática financeira como: razão, proporção, porcentagem, progressões, logaritmo e exponencial. As aplicações nele contida são situações financeiras do cotidiano de qualquer cidadão, como juros, desconto, plano de pagamento, empréstimos, inflação e investimento.
A
BSTRACT
The goal of this work is to support a basic mathematical approach applied financial mathematics with situations experienced by the students, tauting them their critical side and thus contributing to their financial education. This is a brief account of the history and theories of relevant issues to financial mathematics as: reason, proportion, percentage, progressions, logarithm and exponential. The applications contained therein are financial situations of everyday life for all citizens, as interest, discount, payment plan, loans, inflation, investment.
1 INTRODUÇÃO 11
2 FUNDAMENTOS DE RAZÃO, PROPORÇÃO E PORCENTAGEM 13
2.1 Contexto Histórico . . . 13
2.2 Razão . . . 13
2.3 Proporção . . . 14
2.4 Porcentagem . . . 15
2.4.1 Variação percentual ou taxa de crescimento . . . 17
3 FUNDAMENTOS DE PROGRESSÕES ARITMÉTICAS E GEOMÉTRICAS 18 3.1 Contexto Histórico . . . 18
3.2 Progressão Aritmética (P.A) . . . 18
3.3 Progressão Geométrica (P.G) . . . 21
4 FUNDAMENTOS DE LOGARITMOS E EXPONENCIAIS 26 4.1 Contexto Histórico . . . 26
4.2 Logaritmos . . . 26
4.3 Exponenciais . . . 31
5 NOÇÕES BÁSICAS DE MATEMÁTICA FINANCEIRA 34 5.1 Contexto Histórico . . . 34
5.2 Fundamentos de Razão, Proporções e Porcentagens aplicados à Matemática Fi-nanceira . . . 35
5.3 Fundamentos de PA’S e PG’S Aplicadas à Matemática Financeira . . . 39
5.3.1 Sistema ou Regime de Capitalização . . . 39
5.3.1.1 Capitalização Simples (Juros Simples) . . . 39
5.3.1.2 Capitalização Composta (Juros Compostos) . . . 41
5.3.2 Sistemas de Amortização . . . 45
5.3.2.1 Sistema Price . . . 45
5.3.2.2 Empréstimo . . . 48
5.3.2.3 Sistema SAC . . . 49
5.3.3 Investimentos . . . 56
5.4 Fundamentos de Logaritmos e Exponenciais Aplicados à Matemática Financeira . 58 5.4.1 Planos de Pagamentos . . . 59
5.4.2 Inflação . . . 60
5.4.3 Desconto . . . 61
5.4.4 O Número
e
e a Matemática Financeira . . . 616 ATIVIDADES SUGERIDAS 64
6.1 Oficina 1: Fundamentos de Razão, Proporções e Porcentagens aplicados à
Mate-mática Financeira . . . 65
6.2 Oficina 2: Fundamentos de PA’S e PG’S aplicados à Matemática Financeira . . . . 71
6.3 Oficina 3: Fundamentos de Logaritmos e Exponenciais aplicados à Matemática
Financeira . . . 72
Como educador sabemos que é difícil, em um trabalho escolar, desenvolver a matemática de forma rica para todos os educandos. O educador precisa estar sempre se apropriando de novos conhecimentos, logo é com esse olhar que pensamos nesse trabalho, como uma proposta de trabalhar em sala a importância da Matemática Financeira no ensino básico. A escolha do tema foi devido à importância da Educação Financeira na formação dos alunos como cidadão crítico e consciente. Pensar o ensino e a aprendizagem da educação do tema, pressupõe antes de tudo compreender a importância de lidar com o dinheiro na aplicabilidade da Matemática.
O presente trabalho tem por objetivo apresentar uma metodologia para o desenvolvimento de uma ação pedagógica com aplicabilidade em questões com as quais a população tem lidado, esta é uma das questões centrais do Ensino de Matemática Financeira. É um assunto que, emi-nentemente, remete à contextualização. Decidir entre comprar à vista ou a prazo faz parte da vida do brasileiro. Identificar se as taxas de juros anunciadas coincidem com as realmente utili-zadas no cálculo de um financiamento, se as prestações estão corretas, entender como funciona a incidência de juros sobre o saldo devedor, são situações reais, importantes e necessárias para a construção de um pleno exercício da cidadania. É preciso, urgentemente, que essas decisões sejam orientadas e façam parte da formação matemática do cidadão brasileiro.
A preocupação com a Matemática Financeira não é nova, apesar de seu estudo ter-se inten-sificado recentemente, principalmente, desde a recomendação de sua inclusão nos Parâmetros Curriculares Nacionais (PCN’S). Sua inclusão no currículo da Educação Básica e dos Cursos de Licenciatura contribui para a formação de um cidadão que, em muitos casos, não conse-gue identificar as armadilhas embutidas nas ofertas duvidosas. Isso justifica a necessidade da exploração de situações do cotidiano nas aulas de Matemática Financeira.
O cidadão comum atualmente vem se defrontando, constantemente, com ofertas das mais diversas formas, como por exemplo, a venda de produtos a taxa zero de juros. Algumas des-sas ofertas escondem armadilhas que levam o desatento cidadão a prejuízos financeiros, tais como pagamento a longo prazo igual ao pagamento à vista, sem juros. Estaríamos preparando o futuro cidadão adequadamente para enfrentar os desafios financeiros que ocorrem no seu co-tidiano? Como ensinar nossos alunos a decidir qual a melhor maneira de efetuar o pagamento: à vista ou a prazo?
Podemos dizer que as respostas a essas perguntas estão condicionadas a vários fatores con-tido neste trabalho que está organizado do seguinte modo:
No primeiro capítulo, que está fundamentado na referência [IHD06], abordamos fundamen-tos de razão, proporção e porcentagem com alguns exemplos.
No segundo capítulo, fundamentado nas referências [LCW99b] e [MWZ01], tratamos de progressões aritméticas e geométricas
No terceiro capítulo, fundamentado nas referências [LCW99a] e [Lim10], apresentamos logaritmos e exponenciais contruíndos a partir de suas propriedades.
No quarto capítulo, fundamentado nas referências [HP07], [MWZ01], [Mao08] e [RSA15], são introduzidos os conceitos de matemática financeira de modo natural, como aplicações de progressões aritméticas e geométricas, logaritmos e exponencias.
12
No quinto capítulo, fundamentado nos capítulos anteriores e na referência [Bra99], propo-mos algumas atividades e roteiros para algumas delas.
ÇÃO E PORCENTAGEM
2.1.
Contexto Histórico
Relatos históricos datam que o surgimento dos cálculos percentuais aconteceu por volta do século I a.E.C., na cidade de Roma. Nesse período, o imperador romano decretou inúmeros impostos a serem cobrados de acordo com a mercadoria negociada. Um dos impostos criados pelos chefes romanos era denominado centésimo rerum venalium, e obrigava o comerciante a pagar um centésimo pela venda das mercadorias no mercado. Naquela época, o comércio de escravos era intenso e sobre as vendas era cobrado um imposto de 1/25 (um vinte e cinco avos). Os cálculos eram feitos sem a utilização do símbolo de porcentagem, eram realizados de forma simples, com a utilização de frações centésimais. Por exemplo, na cobrança de um imposto no valor de 6/100 da comercialização, eles cobravam seis centésimos do preço do produto, isto é, dividiam o produto em cem partes iguais e pegavam seis partes, basicamente, o que é feito hoje sem a utilização de calculadoras.
Disponível em http://www.brasilescola.com/matematica/historia-das-porcentagens.htm. Acesso em 10 de Nov. de 2015.
Para não delongarmos demais, apenas observarmos, que a técnica de “falsa posição”, conhe-cida em várias culturas antigas, é uma aplicação da proporcionalidade. Voltaremos, no entanto, a nossa atenção para dois aspectos da matemática grega em relação à teoria de razões e propor-ções. O primeiro aspecto da matemática grega que queremos comentar é o de que não se acha nela o conceito de “função”, que foi desenvolvido somente a partir do século XVIII. Na au-sência do referido conceito, usava-se, primordialmente, a proporcionalidade para a elaboração de equações. Isto é um aspecto da matemática - especialmente da matemática aplicada - que perduraria na Idade Média e no Renascimento. O segundo aspecto da matemática grega que queremos comentar é o fato de que a noção de razão está presente no próprio conceito grego de número (arithmós), pois isso é concebido como uma coleção de unidades. Isso tem várias consequências. Visto, por exemplo, que a unidade não tem partes, ela não pode ser partida e, assim, o conceito de fração não faz sentido. Dessa maneira, na matemática teórica, as razões fizeram o papel de frações e, na matemática prática, o conceito de razão foi concretizado pelos sistemas de mensuração, pois nesse contexto não há, aparentemente, problema com a existência de submúltiplos, nem a escolha de unidades menores.
Fonte: Edição Especial da Revista Brasileira de História da Matemática. Vol. 11, nº23 - páginas 1-6.
2.2.
Razão
Definição 2.2.1. Razão- Sejamaebgrandezas, comb6=0, tal que o quociente a
b representa uma relação deaporbque chamamos razão.
14
Exemplo 2.2.1. A velocidade média em geral é uma grandeza obtida pela razão entre uma distância percorrida e um tempo gasto neste percurso.
Velocidade média = distância percorrida / tempo gasto no percurso
Suponhamos que um carro percorreu150km em2horas. A velocidade média do carro nesse percurso será calculada a partir da razão:
Vm=
150
2 =75km/h
O que significa que, em 1 hora o carro percorreu75km.
Exemplo 2.2.2. Escala é a comparação entre o comprimento observado no desenho (mapa, por exemplo) e o comprimento real correspondente, ambos na mesma unidade de medida.
Escala = comprimento do desenho / comprimento real
Em um mapa, um comprimento de5mestá representado por2,5cm. Qual a escala usada para fazer esse mapa?
5m=500cm
Escala = 2,5
500 =
1
200 ou ainda escala1 : 200,como é mais comum nos desenhos e mapas. Isto significa que cada1cmmedido no desenho é igual a200cmno tamanho real.
2.3.
Proporção
Definição 2.3.1. - Dadas as sequências (x1,x2, . . . ,xn) e (y1,y2, . . . ,yn), dizer que os
núme-rosy1,y2, . . . ,ynsão proporcionais aos números x1,x2, . . . ,xn equivale a afirmar que existe um númerok(o fator de proporcionalidade) tal quey1 =kx1,y2 =kx2,y3 =kx3,···,yn =kxn.
Propriedade 2.3.1. sejax7→yuma proporcionalidade. Sex17→y1,x27→y2, . . . ,xn7→ynentão x1+ x2+ x3+ ···+ xn7→y1+ y2+ y3+ ···+ yn.
Com efeito, tendo-sey1 =kx1,y2 =kx2,y3 =kx3,···,yn =kxn, segue-se quey1+ y2+
y3+ ···+ yn=k(x1+ x2+ x3+ ···+ xn). Noutras palavras, se
y1
x1 =
y2
x2 =
y3
x3 =···=
yn xn então
y1+ y2+ y3+ ···+ yn x1+ x2+ x3+ ···+ xn
= y1
x1 =
y2
x2 =
y3
x3 = ···=
yn xn
.
Exemplo 2.3.1. Um turista brasileiro sente-se mal durante uma viagem à Nova Iorque. Ao ser examinado em um hospital local a enfermeira lhe diz que sua temperatura no momento era101, mas que ele deveria ficar tranquilo, pois já havia baixado5. Após o susto, o turista percebeu que sua temperatura havia sido medida em uma escala Fahrenheit. Sabendo que 0C=32F e
100C=212F qual era a sua temperatura anteriormente e qual sua temperatura atual em graus centrígados?
Anterior:101+5=106F
x−0
100−0 =
106−32
212−32⇒
x
100 =
74
Atual:101F
x−0
100−0 =
101−32
212−32 ⇒
x
100 =
69
180 =38,3C.
Exemplo 2.3.2. Quando se trata de transporte ferroviário de passageiros, a Ásia e a Europa detêm as malhas ferroviárias mais avançadas e com os veículos mais velozes, sendo o Japão o pioneiro na implementação do trem-bala com o Shinkansen Série Zero, ativado em1964. Con-siderado um símbolo do renascimento do Japão no Pós-Guerra, o modelo permaneceu operando por40 anos sem ter registrado nenhum acidente, e desde então essa tecnologia vem conquis-tando seu espaço e hoje é um dos meios de transportes mais sofisticados e orgulho para diversos países mundo a fora.
Disponível em http://www.transportabrasil.com.br.Acesso em:31out.2015.
China - O trem CRH380, em suas diferentes versões, é capaz de atingir velocidades de até 450km/h em suas quatro rotas que passam por cidades como Pequim, Xangai, Nanjing e Guangzhou.
Alemanha - A linha InterCity Express (ICE3) corre entre Franfkurt e Colônia, no Vale do Reno, e entre Munique e Nuremberg, na Bavária, com nove linhas que atingem velocidades de até320km/h. O trem CRH380, deslocando-se a uma velocidade média de410km/h, faz um determinado percurso em 3 horas. Em quanto tempo faria esse mesmo percurso, o trem ICE3, deslocado-se a uma velocidade média de300km/h?
Solução. SendoVm= ∆ S ∆T
• para o trem CRH380, temos410= ∆S1
3 ,
• para o trem ICE3, temos300= ∆S2 ∆T , • sendo∆S1=∆S2,
• então300·∆T =410·3→∆T = 1230
300 .
• Isto é,∆T =4,1hou∆T =4h6min.
2.4.
Porcentagem
Observe nas lojas os encartes e nos meios de comunicação (jornal, rádio, internet, e.t.c) a quantidade de vezes que a representação % (por cento) está presente. Trata-se de uma lingua-gem amplamente difundida.
16
Historicamente, a expressão por cento aparece nas principais obras de aritmética de autores italianos do século XV. O símbolo % surgiu como uma abreviatura da palavra cento utilizada nas operações mercantis.
Exemplo 2.4.1. Para indicar um índice de 10 por cento, escrevemos10% e isto significa que em cada100unidades de algo, tomaremos10unidades. O cálculo de10%de90, por exemplo, pode ser obtido como o produto de 10% por 90, isto é: 10%.90= 10
100·90=900/100=9. Situações mais elementares, como a citada anteriormente, podem ser resolvidas “de cabeça” (cálculo mental). Imagine que os 90citados são na verdade o valor da conta de um jantar em família; sobre esse valor vamos acrescentar a taxa de serviço de garçom que é de10%sobre o consumo total. Sendo assim, basta dividir por10o valor da conta, resultando em9, ou melhor, em9,00reais e somar este resultado ao total consumido:R$9,00+R$90,00=R$99,00.
Em geral, para indicar um índice de Mpor cento, escrevemos M% e para calcularM% de
um númeroN, realizamos o produto: Produto=M%.N= ( M
100)·N.
Exemplo 2.4.2. Um Smartphone é vendido em, no máximo, três prestações mensais e iguais, totalizando o valor de R$ 1050,00. Caso seja adquirido à vista, a loja o vende por R$ 924,00. Como calcular o desconto em percentual sobre o Smartphone na compra à vista?
Solução. Quando dividimos 924,00
1050,00 encontramos o valor0,88ou 88
100 =88%, isto é, o preço à vista tem12%de desconto.
Exemplo 2.4.3. O preço de um produto sofreu um reajuste de12%, aumentando paraR$ 94,08.
Qual era o preço desse produto antes do reajuste?
Solução. Sendo po preço antes do reajuste, temos:
• p+ 12%·p=94,08
• p+ 12
100·p=94,08 • p+ 0,12·p=94,08
• 1,12·p=94,08 • p= 94,08
1,12 =84
2.4.1 Variação percentual ou taxa de crescimento
Definição 2.4.2. Consideremos uma grandeza que assuma um valorV0na data 0e o valorVt numa data futura t. Chamamos de variação percentual dessa gradeza entre as datas 0 e t, e indicamos por jo número dado por:
j=Vt−V0
V0 ,
(2.1)
isto é, variação percentual ou taxa de crescimento é a razão entre o aumento da grandeza e seu valor inicial.
Exemplo 2.4.4. O preço de um produto sofreu um reajuste de12%, aumentando paraR$ 94,08.
Qual era o preço desse produto antes do reajuste?
Solução. SendoV0o preço antes eVt o preço depois do reajuste, temos: • j=12%= 12
100 =0,12eVt=94,08
• 0,12=94,08−V0 V0
• 0,12·V0=94,08−V0
• 0,12·V0+V0=94,08
• 1,12·V0=94,08 • V0=94,08
1,12 =84
3. FUNDAMENTOS DE PROGRESSÕES
ARIT-MÉTICAS E GEOMÉTRICAS
3.1.
Contexto Histórico
As progressões foram estudadas desde povos muito antigos como os babilônios. Inicial-mente, procurou-se estabelecer padrões como o da enchente do Rio Nilo, onde os egípcios de 5000 anos atrás tiveram que observar os períodos em que ocorria a enchente do rio, pois para poderem plantar na época certa e assim garantir seus alimentos, os egípcios precisavam saber quando haveria inundação. Havia, portanto, necessidade de se conhecer o padrão desse acontecimento.
Eles observaram que o rio subia logo depois que estrela Sirius se levantava a leste, um pouco antes do sol. Notando que isso acontecia a cada 365 dias, os egípcios criaram um calendário solar composto de doze meses, de 30 dias cada mês. Os egípcios dividiram os doze meses em três estações de quatro meses: período de semear, período de crescimento e período da colheta.
3.2.
Progressão Aritmética (P.A)
Definição 3.2.1. Progressão Aritmética-PA - Uma progressão aritmética é uma sequência de números(a1,a2,a3, ...,an, ...)na qual é constante a diferença entre cada termo an e o seu an-tecessoran−1. Essa diferença constante é chamada de razão da progressão e será representada
por r. Assim, uma progressão aritmética de razãoré uma sequência(an)na qualan−an−1=r,
para todoninteiro e positivo.
Exemplo 3.2.1. O preço de um certo carro novo éR$ 39.000,00. No final do primeiro ano de
uso ele valeR$ 36.600,00e no final do segundo ano de uso ele valeR$ 34.200,00.Como saber o preço desse carro com 8 anos de uso? São comuns, na vida real, gradezas que sofrem variações iguais em intervalos de tempos iguais. Note que o valor do carro, decresce de R$ 2.400,00
em R$ 2.400,00 para cada ano de uso. Este valor é chamado de razão desta sequência e tal sequência é chamada de Progressão Aritmética (PA).
Classificação 3.2.1. As progressões aritméticas (PA) podem ser classificadas em:
I. Crescentes - são as PA‘S em que cada termo é maior que o anterior. É imediato que isso ocorre somente ser>0, pois:
an>an−1⇔an−an−1>0⇔r>0.
Por exemplo: (11,18,25,···)(PA crescente,r=7)(cada termo é igual ao anterior mais 7).
II. Constantes - são as PA‘S em que cada termo é igual ao anterior. Isso só ocorre quando r=0, pois:
an=an−1⇔an−an−1=0⇔r=0.
Por exemplo:(−1,−1,−1,···)(PA constante,r=0)(todos os termos iguais).
III. Decrescente - são as PA‘S em que cada termo é menor que o anterior. Isso ocorre somente ser<0, pois:
an<an−1⇔an−an−1<0⇔r<0.
Por exemplo: (12,3,−6,···) (PA decrescente, r =−9)(cada termo é igual ao anterir menos9).
Teorema 3.2.1. Sean é uma progressão aritmética de razão r, entãoan=a1+ (n−1)r, para todo n inteiro e positivo.
Demonstração. Pela definição de progressão aritmética, temos
a2−a1=r a3−a2=r
a4−a3=r
. . .
an−an−1=r
Somando essas n−1 igualdades, obtemosan−a1= (n−1)r, isto é, an=a1+ (n−1)r. Esta expressão representa o termo geral da progressão aritmética.
Exemplo 3.2.2. Em cada região especificada pela Agência Nacional de Telecomunicação (Ana-tel), as frequêcias das emissoras de rádio FM devem variar de 87,9MHz a 107,9MHz, e a diferença entre duas frequências consecutivas deve ser 0,2MHz. Qual o número máximo de emissorasFM que podem funcionar em uma mesma região determinada pela Anatel?
Solução. Como a diferença entre as frequências de duas emissoras consecutivas deve ser 0,2MHz, temos que todas as frequências de determinada região formam uma P.A de razão r=0,2, coma1=87,9ean107,9. Para saber o número máximo de emissoras, basta determinar o número de elementos dessa P.A, ou seja, determinar n tal que an =107,9. Sendo an = a1+ (n−1)r, temos107,9= 87,9+ (n−1)·0,2→20= (n−1)·0,2→100− n−1. isto é,
n=101. Portanto,101emissoras de rádioFM.
Quando o grande matemático Carl F. Gauss (1777-1855) tinha sete anos de idade, seu pro-fessor lhe pediu que calculasse a soma dos inteiros de 1 até 100. O propro-fessor, esperando que o trabalho durasse pelo menos uma hora, ficou supreso quando, em poucos minutos, o pequeno Gauss anunciou que o valor da soma era 5050. A resposta estava correta e, curioso, o profes-sor lhe perguntou como conseguira fazer o cálculo tão rapidamente. Gauss explicou-lhe que
20
resposta era 50×101=5050
Baseado nessa mesma idéia, podemos calcular a soma dos termos de uma progressão arit-mética (PA) qualquer.
Teorema 3.2.2. A soma dosnprimeiros termos da progressão aritmética(an) = (a1,a2,···,an,···) é igual a
Sn=
(a1+an)n
2 .
Demonstração.
Sn=a1+a2+a3+··· +an−2+an−1+an e
Sn=an+an−1+an−2+···+a3+a2+a1.
Daí,
2Sn= (a1+an) + (a2+an−1) + (a3+an−2) +···+ (an+a1).
Obeserve que, ao passar de um parênteses para o seguinte, a primeira parcela aumenta dere a
segunda parcela diminui der, o que não altera a soma. Portanto, todos os parênteses são iguais
ao primeiro,(a1+an).
Logo, 2Sn= (a1+an)n ou
Sn=
(a1+an)n
2 .
(3.1)
Exemplo 3.2.3. A razão de uma P.A. é igual a12%do primeiro termo. Sabendo que o11termo vale33, determine o valor da soma dos20primeiros termos dessa P.A.
Solução.
• Temosr=12%a1=0,12a1,
• a11=33⇒a1 + (11−1)·0,12a1=33⇒a1=15.
• Portanto,r=0,12·15=1,8ea20 =15 + (20−1)·1,8=49,2.
• Assim,S20= (15+492,2)·20 ⇒S20=642.
Exemplo 3.2.4. Senhor Paulo resolveu dar a seu filho Chiquinho uma mesada de R$ 300,00
por mês. Chiquinho, que é muito esperto, disse a seu pai que, em vez da mesada deR$ 300,00, gostaria de receber um pouquinho a cada dia: R$ 1,00no primeiro dia de cada mês e, a cada
ao final do primeiro mês, logo percebeu que havia saído no prejuízo. Calcule quanto, em um mês com30dias, Chiquinho receberá a mais do que receberia com a mesada deR$ 300,00.
Solução. Como Chiquinho recebe R$ 1,00 no primeiro dia e um R$ 1,00 a mais que no dia anterior, é fácil ver que os valores diários formam uma P.A. crescente de razão igual1. O montante em30dias é a soma dessa P.A. Portanto,
• a1=1
• a30=1+29·1=30
• S30= (a1+2a30)n = (1+302)·30
• S30= 31·30
2 =31·15=465.
Logo, Chiquinho receberá a maisR$ 165,00.
3.3.
Progressão Geométrica (P.G)
Definição 3.3.1. Progressão Geométrica PG - Uma progressão geométrica é uma sequência de números(a1,a2,a3, . . . ,an, . . .)na qual é constante o quociente da divisão de cada termo a partir do segundo pelo seu antecessor. Esse quociente constante é representado porqchamado de razão da progressão. Logo, para avançar do primeiro termo para o segundo, multiplicamos porqeste termo, ou seja,a2=a1qe do segundo termo para o terceiro de novo multiplicamos
por q este termo e temos a3 =a2q. Assim, uma progressão geométrica de razão q é uma
sequência(an)na qualan=an−1q, para todo n inteiro positivo.
Exemplo 3.3.1. São progressões geométricas:
• (1,2,4,8,16, . . .)em quea1=1eq=2
• (−1,−3,−9,−27, . . .)em quea1=−1eq=3
• (21,21,21, . . .)em quea1=21eq=1.
Classificação 3.3.1. As progressões geométricas (PG) podem ser classificadas em:
I. Crescente - São as PG‘S em que cada termo é maior que o anterior. Notemos que isso ocorre de duas maneiras:
(a) PG com termos positivos
an>an−1⇔ an
an−1 >1⇔q>1
22
(b) PG com termos negativos
an>an−1⇔0< an
an−1 <1⇔0<q<1
por exemplo:(−28,−14,−7,−7
2 , . . .)em quea1=−28eq= 1 2.
II. Constante - São PG‘S em que cada termo é igual ao anterior. Observemos que isso ocorre em duas situações:
(a) PG com termos todos nulosa1=0eqqualquer.
(b) PG com termos iguais e não nulos
an=an−1⇔ an
an−1 =1⇔q=1
por exemplo:(5,5,5,5, . . .)em quea1=5eq=1.
III. Decrescente - São as PG‘S em que cada termo é menor que o anterior. Notemos que isso ocorre de duas maneiras:
(a) PG com termos positivos
an<an−1⇔0< an
an−1 <1⇔0<q<1
por exemplo:(5,1,1 5,
1
25, . . .)em quea1=5eq= 1 5 (b) PG com termos negativos
an<an−1⇔ an
an−1 >1⇔q>1
por exemplo:(−3,−12,−48,−192, . . .)em quea1=−3eq=4.
IV. Altenantes - São as PG‘S em que cada termo tem sinal contrário ao do termo anterior. Isso ocorre quandoq<0. Por exemplo:(3,−6,12,−24, . . .)em quea1=3eq=−2.
V. Estacionária - São as PG‘S em quea16=0e a2=a3=a4=. . .=0. Isso ocorre quando
q=0. Por exemplo:(√3,0,0,0, . . .)em quea1=√3eq=0.
Teorema 3.3.1. Em toda progressão geométrica(an)de razão q, tem-se,an=an−1q, para todo
n inteiro e positivo.
a2=a1q
a3=a2q
a4=a3q
...
an=an−1q
multiplicando essas n−1 igualdades, obtemos an=a1qn−1. Esta expressão representa o termo geral da progressão geométrica.
Exemplo 3.3.2. Determinar o9termo da PG(3,12,48, . . .)
Solução.Devemos determinaran=a1qn−1dessa PG tal que: a1=3
q= a2
a1 =
12
3 =4
n=9
Logo,a9=3·48=3·65.536=196.608
Exemplo 3.3.3. Uma estimativa prevê um crescimento anual de0,15%na população de uma cidade. Supondo que essa estimativa esteja correta, calcular a população dessa cidade daqui a 12anos, sabendo que a população atual é de63.500habitantes.
Solução. A sequência crescente das populações, ano a ano, dessa cidade, a partir do mo-mento atual, é a PG de razão 1,0015 e primeiro termo 63.500. O termo a12 dessa PG é a
população da cidade daqui a12anos. Pela expressão do termo geral, temos que a12=63.500·(1,0015)11
com o auxílio de uma calculadora, obtemos(1,0015)≈1,017e, portanto, a12≈63.500·1,017=64.579,5
Logo, daqui a12anos a população da cidade será de64.579habitantes, aproximadamente.
Teorema 3.3.2. A soma dos nprimeiros termos de uma progressão geométrica(an)de razão q6=1é igual a
Sn=a1·1−q
n 1−q.
(3.2)
Demonstração. (Primeiro método)
24
Subtraindo essas iguldades, obtemos
Sn−qSn=a1−anq=a1−a1qn,
ou seja,Sn(1−q) =a1(1−qn).
Daí, já queq6=1, temosSn=a1·1−q
n 1−q .
Demonstração. (Segundo método: utilizando Indução Matemática)
ConsidereSn=a1·1−q
n 1−q .
Note queP(1): S(1) =a1·1−q 1
1−q =a1é verdadeiro.
Agora, suponhamos que para algumn∈N, tenhamos P(n)verdadeiro, isto é, a fórmula(2.2) é válida para tal valor n. Queremos provar que P(n+1) é verdadeiro, isto é, Sn+1 =a1·
[1−qn+1]
1−q .Desenvolvendo, temos que
Sn+1=Sn+an+1.Sn+1=a1·1−q
n
1−q +a1·q n
Sn+1=a1·[1−q
n+ (1−q)·qn]
1−q
Sn+1=a1·[1−q
n+qn−qn+1]
1−q
Sn+1=a1·[1−q
n+1]
1−q .
Exemplo 3.3.4. Calcule a soma das10parcelas iniciais da série(1 +3 +9 +27 +. . . .)
Solução.
• Seq=3,a1=1en=10
• aplicando a fórmula(2.2), então,
• S10=1·(1−3 10)
1−3 =29.524.
Exemplo 3.3.5. Haroldo fez um regime alimentar durante nove meses. No primeiro mês, ema-greceu4Kge, em cada um dos demais meses, emagreceu metade do que emagrecera no mês anterior. Quantos quilogramas Haroldo perdeu nesses nove meses?
Solução. É fácil ver que os valores mensais formam uma P.G decrescente de razão igual 1
• (4, 2,1, 1 2,
1 4,
1 8,
1 16,
1 32,
1 64)
• indiquemos porS9a soma de seus nove termos
• S9=a1·1−q
9
1−q =4·
1−(1 2)9
1−1
2
=4·1− 1 29
1 2
• S9=8·(1−5121 ) =8−5128 =8−641 = 51264−1= 51164
• S9=7,984
4. FUNDAMENTOS DE LOGARITMOS E
EX-PONENCIAIS
4.1.
Contexto Histórico
Com o desenvolvimento da astronomia e da navegação no fim do séculoXV I, a matemática
dos cálculos aritméticos utilizados, se tornaram mais longos e laboriosos. Então, achar um método que permitisse efetuar com rapidez multiplicações, divisões, potenciações e extrações de raízes era na época um problema fundamental.
A invenção dos logaritmos veio a ter um tremendo impacto sobre a estrutura da matemática nos cálculos aritméticos. Diversos matemáticos contribuíram para o desenvolvimento dos lo-garitmos que conhecemos hoje, mas o escocês John Napier (1550-1617) foi de fato o primeiro a publicar uma obra em 1614 sobre logaritmo, sendo que idéias muito semelhantes foram de-senvolvidas independentemente pelo suíço Jost Bürgi (1552-1632), mais ou menos ao mesmo tempo. Porém, Bürgi só públicou seus resultados em 1620.
4.2.
Logaritmos
Definição 4.2.1. Para todo número real positivo a6=1, uma função real loga:R+ →R, cujo
domínio é o conjunto R+ dos números reais positivos, chama-se uma função logarítmica de
baseaou um sistema de logaritmos quando tem as seguintes propriedades:
A) Sea>1,logaé uma função crescente, isto é,x<y⇒logax<logay; B) loga(xy) =logax+logaypara quaisquerx,y∈R+.
Para todox∈R+, o númerologaxchama-se o logaritmo dex.
A lista de propriedades das funções logarítmicas que seguem abaixo, são consequências de
AeBacima enunciadas.
Propriedade 4.2.1. Uma função logarítmicaloga:R+→Ré sempre injetiva, isto é, números
diferentes têm logaritmos diferentes.
Demonstração. Com efeito, sex,y∈R+ são diferentes, então oux<youy<x. No primeiro
caso, resulta da propriedadeAque logax<logay. No segundo caso tem-se logay<logax. Em qualquer hipótese, dex6=yconclui-se quelogax6=logay.
Propriedade 4.2.2. loga1=0.
Demonstração. Com efeito, pela propriedadeBtemos
loga1=loga(1·1) =loga1+loga1, logologa1=0.
Propriedade 4.2.3. Uma função logarítmica não está definida parax=0.
Demonstração. Com efeito, se existisse loga0, para x 6=0, teríamos loga0 =loga(x·0) =
logax+loga0, então logax=0. Assim a função seria identicamente nula, o que contraria a
propriedadeA.
Propriedade 4.2.4. Os números maiores do que1têm logaritmos positivos e os números po-sitivos menores do que1têm logaritmos negativos.
Demonstração. Com efeito, sendo a >1, temos loga crescente, de 0 <x <1 < y resulta
logax<loga1<logay, isto é logax<0<logay.
Propriedade 4.2.5. Para todox>0, tem-seloga(1x) =−logx
Demonstração. Com efeito, de x·(1x) = 1 resulta que logax+loga(1x) =loga1=0, donde
loga(1x) =−logax
Propriedade 4.2.6. Para quaisquerx,y∈R+, vale
loga(x
y) =logax−logay
Demonstração. Com efeito,
loga(x
y) =loga(x(
1
y)) =logax−logay.
Propriedade 4.2.7. Para todox∈R+e todo número racionalr= qp tem-selogaxr =rlogax.
Demonstração. Em primeiro lugar, observa-se que logaxy=logax+logayse estende para o
produto de um número qualquer de fatores. Por exemplo,
loga(xyz) =loga(xy)z=logaxy+logaz=logax+logay+logaz.
E assim por diante:
loga(x1x2x3···xn) =logax1+logax2+logax3+···+logaxn.
Em particular, sen∈Nentão
loga(xn) =loga(x·x·x···x) =logax+logax+logax+···+logax=nlogax.
Portanto, vale quandor=né um natural. Para todo númerox∈R+, tem-se quex0=1, logo
28
Consideremos agora o caso em que r =−n,n∈N, isto é, onde r é um inteiro negativo.
Então, para todox>0 temosxn·x−n=1.Logo
loga(xn) +loga(x−n) =loga1=0, e daí
loga(x−n) =−loga(xn) =−nlogax.
Finalmente, o caso geral, em quer= pq, ondep∈Zeq∈N.Para todox∈R+temos
(xr)q= (x
p
q)q=xp.
Logo q·loga(xr) =loga[(xr)q] =log
a(xp) = p·logax, em virtude do que já foi provado. Da igualdade q·loga(xr) = p·logax resulta que loga(xr) = (qp)·logax, ou seja, que loga(xr) = r·logax.
Propriedade 4.2.8. Uma função logarítmica log:R+ −→R é ilimitada superior e
inferior-mente.
Demonstração. Primeiro iremos provar que ela é ilimitada superiormente. Sejaa>1.
Supo-nhamos que nos seja dado um número real β e que sejamos desafiados a achar um número
x∈R+ tal que logax>β. Procederemos da seguinte maneira: tomamos um número natural
n tão grande que n> β
log2. Como log2 é positivo (Propriedade 3.2.4), temos n·loga2>β.
Usando a Propriedade 5, vemos que n·log2=loga(2n). Portanto, log
a(2n)>β. Agora é só escolherx=2n.Temos log
ax>β.Isto mostra que log é ilimitada superiormente.
Para provar que log também é ilimitada inferiormente, basta lembrar que loga1x =−logax.
Dado qualquer número realα, como vimos acima, podemos acharx∈R+tal quelogx>−α.
Então, pondoy= 1x, teremos logay=−logax<α.
Teorema 4.2.1. Dadas as funções logarítmicasL,M:R+ →R, existe uma constantec>0tal
queM(x) =c·L(x)para todox>0.
Demonstração. Suponhamos inicialmente que exista um númeroa>1 tal que L(a) =M(a).
Mostraremos, neste caso, que L(x) =M(x)para todo x>0. SendoL(a) =M(a)concluímos que L(ar) =M(ar) para todo r racional, pois L(ar) =r·L(a) =r·M(a) =M(ar). Suponha-mos, por absurdo, que existisse algumb>0 tal queL(b)6=M(b).Sem perda de generalidade, consideramosL(b)<M(b).Escolhamos um númeronsuficientemente grande tal que
n·[M(b)−L(b)]>L(a). Então
M(b)−L(b)>L(a)
n =L(a
1
n).
Por simplicidade, escrevamosc−L(a1n). Os números c, 2c, 3c, . . . dividem a reta real (R+)
números, digamosm·c, pertence ao interior do intervalo(L(b),M(b)), ou seja,L(b)<m·c<
M(b). Daí tem-se que,
m·c=m·L(a1n) =L(a m
n) =M(a m
n).
Então
L(b)<L(amn) =M(a m
n)<M(b).
ComoL(x)é crescente, segue da primeira desigualdadeb<amn.Por outro lado, comoM
tam-bém é crescente, a segunda desigualdade implica amn <b.Esta contradição mostra que bnão
existe: devemos terM(x) =L(x)para todox>0.
O caso geral reduz-se ao caso particular acima. DadasLeM, funções logarítmicas
arbitrá-rias, consideremos os númerosL(x0)>0 eM(x0>0)para algumx0>1.Sejac= M(x0)
L(x0) >0.
Consideremos a função logarítmicaN:R+→R, definida porN(x) =c·L(x). ComoN(x0) =
c·L(x0) = M(x0)
L(x0) ·L(x0) =M(x0), segue-se do que se provou acima queN(x) =M(x)para todo
x>0, ou seja, queM(x) =c·L(x)para todox>0, como queríamos demonstrar.
Teorema 4.2.2. Toda função logarítmica é sobrejetiva, isto é , dado qualquer número realc, existe sempre um (único) número real positivoxtal queL(x) =c.
Para verificar a validade do teorema acima, faremos uso do seguinte lema
Lema 4.2.1. SejaL:R+ →R uma função logarítmica. Dados arbitrariamente dois números
reaisu<v, existex>0tal queu<L(x)<v.
Demonstração do Lema. Fixemos um número naturalnmaior do que L(2)
v−u. Logo, é válido n> L(2)
v−u ⇒
L(2)
n <v−u.
Considerandoc= L(2)
n , temos que os múltiplos inteiros
m·c=m
n ·L(2) =L(2
m
n),m∈Z,
decompõem a reta real(R+) em intervalos justapostos, cujo comprimentoc= L(2)
n é menor
do que o comprimentov−udo intervaloI= (u,v).Portanto, pelo menos um desses múltiplos
m·c=L(2mn)cai no interior do intervaloI(u,v). Denotandox=2 m
n, temosu<L(x)<v.
Antes de demonstrar o Teorema, lembremos que todo número real admite representação decimal
α =α0,α1α2. . .αn. . .=α0+
α1
10+
α2
102+. . .+
30
onde a parte inteira α0 é um número inteiro qualquer e os algarismos decimais αn, n≥1,
podem assumir os valores 0, 1, . . . ,9.Para todon≥0, escrevemos
α =α0,α1α2. . .αn=α0+
α1
10+
α2
102+. . .+
αn 10n.
Tem-seαn≤α eα−αn< 1
10n para todon≥0.
Se um número realx é menor do queα, então deve existir umn≥0 talque x<αn.Com
efeito,x<α significa queα−xé número real positivo. Tomemosntão grande que
1
10n <α−x. Então
α−αn< 1 10nα−x logoα−αn<α−x. Daí resultax<αn.
Demonstração do Teorema 3.2.2. Dado arbitrariamente um número realb, devemos obter um
número real positivoα tal queL(α) =b.Vamos obterα determinando cada um dos seus
alga-rismos que compõe a sua representação decimal. Para determinar a parte inteiraα0, lembramos
queL é uma função crescente ilimitada, logo devem existir inteiros ktais que L(k)>b.Seja α0+ 1 o menor inteiro tal queL(α0+1)>b. Então temosL(α0)≤b<L(α0+1).
Em seguida, consideremos os números
α0, α0+ 1
10, α0+ 2
10, . . . , α0+ 9
10, α0+ 1.
ComoL(α0)≤b<L(α0+1) devem existir dois elementos consecutivosα eα1+ 1
10 nessa
sequência tais queL(α1)≤b<L(α1+ 1
10), isto é, deve existirα1inteiro, 0≤a1≤9, tal que, pondo
α1=α0, α1=α0+α101.
Tem-se
L(α1)≤b<L(α1+ 1
10).
Analogamente, considere os números
α1, α1+ 1
102,α1+
2
102, . . . , α1+
9
102, α1+
1 10, vemos que existeα2, 0≤α2≤9, tal que, pondo
α2=α0,α1 α2=α0+α1
10+
α2
tem-se
L(α2)≤b<α2+ 1
102.
Prosseguindo analogamente, encontramos a representação decimal de um número real
α =α0,α1α2. . .αn=α0+
α1
10+
α2
102+. . .+
αn 10n+. . . tal que , pondoαn=α0α1α2. . .α−n, tem-se:
L(αn)≤b<L(αn+ 1 10n)
para todon≥0.
Afirmamos queL(α) =b.De fato, se fosseL(α)<b, usaríamos o Lema para obterx>0 tal que L(α)<L(x)<b Como L é crescente, isto implicaria α <x. Então, tomando n tão
grande quex−α> 1
10n teríamosα+
1
10n <x, logo
αn+ 1
10n ≤α+
1 10n <x.
ComoLé crescente, dex>αn+ 1 10n
resultaria
L(x)>L(αn+ 1
10n)>b, um absurdo, pois o númeroxfoi obtido de modo queL(x)<b.
Analogamente, não se pode terL(α)>b. Com efeito, usando novamente o Lema,
obtería-mosx>0 tal que
b<L(x)<L(α).
ComoLé crescente, deL(x)<L(α)concluiríamos quex<α.Isto implicaria, entretanto, que
x<αnpara algumn. EntãoL(x)<L(αn)≤b, contrariando o fato de quexfoi obtido de modo a satisfazerb<L(x).
Corolário 4.2.1. Toda função logarítmicaL:R+ →Ré uma correspondência biunívica
(bije-ção) entreR+eR.
4.3.
Exponenciais
Definição 4.3.1. Exponencial - Uma bijeçãoE :R→R+ chama-se uma função exponencial,
indicada pela notaçãoE(x) =ax, quando sua inversaL:R+→Ré uma função logarítmica, ou
seja,
L(x) =y=logax⇔ay=x.
Sejaaum número real positivo diferente de 1.A bijeçãoE :R→R+, comE(x) =ax, é dita função exponencial de basea.
32
Propriedade 4.3.1. E(x+y) =E(x)·E(y).
Com efeito,
E(x+y) =ax+y=ax·ay=E(x)·E(y).
Propriedade 4.3.2. SeE(x0) =0para algumx0∈R, entãoE é identicamente nula.
Com efeito, se existir algumx0∈Rtal queE(x0) =0então, para todox∈Rteremos
E(x) =E(x0+ (x−x0)) =E(x0)·E(x−x0)) =0·E(x−x0) =0,
logoE será indenticamente nula.
Mais ainda, a função é sempre positiva,E(x)>0, para todox∈R, pois,
E(x) =E(x
2+
x
2) =E(
x
2)·E(
x
2) = [E(
x
2)]
2>0.
Propriedade 4.3.3. E(1) =a.
Com efeito, comoE(1) =x⇔logax=1⇔x=a.Então,E(1) =a.
Propriedade 4.3.4. x<y⇔ax<ay, quandoa>1ex<y⇔ax>ay, quando0<a<1.
A propriedade diz que a função exponencial é crescente paraa>1 e decrescente quando 0<a<1.
Daí resultará que existe uma única maneira de definir o valor de E(x) = ax quando x é irracional. Supondo quea>1, entãoax tem a seguinte propriedade
r<x<s, comr,s∈Q⇒ar<ax<as.
Não podem existir dois números reais diferentes, digamos α <β, com a propriedade acima.
Se existissem taisα eβ teríamos
r<x<s, r,s∈Q⇒ar<α <β <as
e então o intervalo[α,β]não conteria nenhuma potência deacom expoente racional, o que é um absurdo.
Portanto, quandoxé irracional,ax é o único número real cujas aproximações por falta são as potênciasar, r<xe cujas aproximações por excesso são as potênciasas, x<s
Propriedade 4.3.5. A funçãoE:R→R∗+,E(x) =ax,a6=1, é ilimitada superiormente. Sea>1, entãoaxcresce, indefinidamente quandox>0, ou seja,
lim x→∞a
x= +
∞.
E se0<a<1,ax torna-se arbitrariamente grande quandox<0, ou seja,
lim x→−∞a
x= +
Propriedade 4.3.6. A função exponencial é contínua.
Isto significa que, dadox0∈Ré possível tornar a diferença|ax−ax0 |tão pequeno quanto
se deseja, desde quexseja tomado suficientemente próximo dex0, ou seja
lim x→x0a
x=
ax0.
Suponhamosa>1e h=x−x0>0.Dado arbitrariamenteε>0, mostraremos que, tomandoh
pequeno, teremosah<1+ε.Sejan∈Ntal quen>a−1
ε , temos quenε>a−1logo,a<1+nε.
Desigualdade de Bernoulli1. Sen∈Nex≥ −1,vale(1+x)n
≥1+nx.Pela desigualdade,
temos(1+ε)n>1+nε, entãoa<(1+ε)ne a1n <1+ε.
Agora fixadox0∈Re h=x−x0, temos
ax−ax0 =ax0+h−ax0 =ax0(ah−1).
Sexse aproxima dex0, h tende a zero,ahtendea0,ah−1tende a zero, logo
lim x→x0(a
x
−ax0) =0,
ou seja,
lim x→x0a
x=ax0.
Propriedade 4.3.7. A funçãoE:R→R∗+,E(x) =ax,a6=1, é sobrejetiva.
Esta afirmação quer dizer que para todo número realb>0existe algumx∈Rtal queax=b.
Supomosa>1,n∈N, escolhemos uma potênciaarn, comr
n, no intervalo(b−1n,b+1n)de modo que|b−arn|< 1
n. Portanto,
lim x→x0a
rn =b.
Assim, escolhemos as potênciasrnsucessimente, tais que ar1 <ar2 <···<arn <···<b.
Assim, (rn)é uma sequência crescente, limitada superiormente pors.Logo, osrn são valores aproximados por falta de um número realx, tal que
lim
x→x0rn=x. A função exponencial sendo contínua, temos então
ax= lim
x→x0a rn =b,
como queríamos demonstrar.
Vemos, pois, que para todo número real positivo a, diferente de 1, a função exponencial E:R→R+, dada porE(x) =ax, é uma correspondência biunívoca entreReR+, crescente se
a>1, decrescente se 0<a<1, com propriedade de transformar somas em produtos, isto é, E(x+y) =E(x)·E(y).
5. NOÇÕES BÁSICAS DE MATEMÁTICA
FI-NANCEIRA
A Matemática Financeira tem importância significativa na tomada de decisões corretas tais como: empréstimos, nas compras, no orçamento familiar, bem como economizar, investir e poupar.
Uma boa compreensão dos conteúdos referentes à Matemática Financeira poderá facilitar o controle financeiro em transações comerciais, bancárias, orçamento familiar entre outros, que são essenciais para um bom desempenho do indivíduo na sociedade. A falta de conhecimento sobre o assunto resultará em dificuldades que levarão a um controle financeiro inadequado. Portanto, como utilizar os conceitos Matemáticos Financeiros no cotidiano do aluno para uma boa Educação Financeira? Para responder esta questão busca-se proporcionar os conhecimen-tos básicos da Matemática Financeira no ensino médio e a reflexão sobre a importância no orçamento familiar no cotidiano do aluno.
A proposta aqui sugerida é a de se trabalhar a Matemática Financeira no Ensino Médio por meio de situações mais próximas da realidade e que possam suscitar nos alunos algum interesse acerca dessas relações financeiras.
O contorno em que serão apresentadas as atividades busca promover a Educação Finan-ceira, através da informação e experimentação acerca de temas que um dia esses alunos terão contato, seja na compra de um bem móvel ou imóvel, na hora de programarem uma poupança para viagem ou mesmo, quando já estiverem no mercado de trabalho como assalariados ou empregadores.
5.1.
Contexto Histórico
No passado, os homens viviam em comunidades distantes uma das outras, plantando e criando animais para assim suprir as suas necessidades. Com o desenvolvimento do artesanato e da cultura, passou a ser necessário realizar trocas, que foram aumentando gradativamente entre as comunidades.
Surge assim o escambo1, como primeira troca comercial. Devido ao crescimento das trocas,
em pouco tempo, o Homem percebeu a necessidade de um elemento de valor que intermediasse a operação. Assim surgiu a moeda, o dinheiro, o sistema monetário mais organizado com alguns princípios e padrões.
Pode-se citar alguns exemplos de mercadorias que eram utilizadas na intermediação das trocas. Como é o caso nas ilhas do Pacífico, as mercadorias foram estimadas em colares de pérolas ou de conchas. Após certo período, começou-se por trocar faixas de tecido por animais ou objetos. O tecido era a moeda; a unidade era o palmo da fita de duas vezes oitenta fios de largura.
Na medida em que o comércio se desenvolvia, os metais de valor desempenharam um papel
1Troca de mercadoria ou serviços sem fazer uso de moeda
importante nas transações comerciais, o que acabou se tornando a moeda de troca preferida dos vendedores e compradores. As mercadorias passaram a ser feitas através do peso, com um padrão que era relacionado a um metal ou a outro.
Utilizando esses metais e seus padrões se realizavam pagamento e multas, no caso das multas se tem uma noção dos primeiros cálculos de juros.
Disponível em http://www.somatematica.com.br/historia/matfinanceira.php/tempo. Acesso em: 12 out. de 2015.
5.2.
Fundamentos de Razão, Proporções e Porcentagens
apli-cados à Matemática Financeira
Exemplo 5.2.1. Com a proximidade do evento e com muitos ingressos disponíveis, Carlos que é cambista passou a ofererecer um desconto de50% sobre o preço de venda de certo tipo de ingresso. Mesmo dando o desconto, o Carlos ainda obteve um lucro de40%sobre o preço de custo (preço de bilheteria) desse ingresso. Se não tivesse dado o desconto, mas tivesse, mesmo assim, vendido o ingresso, o lucro de Carlos seria de quanto?
Solução. Uma estratégia para resolver questões que envolvem apenas porcentagem (questões
que não são apresentados valores fixos) é atribuir um valor para um dos termos.
Considere que o preço do ingresso na bilheteria (custo) sejaR$ 100,00. Teremos então:
• Lucro de Carlos quando oferece 50% de desconto éR$ 40,00.
• Valor do ingresso vendido por Carlos (com desconto) → R$ 100,00+ R$ 40,00 =
R$ 140,00.
• Valor do ingresso vendido por Carlos (sem desconto) → R$ 140,00+ R$ 140,00=
R$ 280,00.
Portanto, o lucro de Carlos ao vender o ingresso sem desconto é deR$ 180,00 ou 180%
do valor da bilheteria.
Exemplo 5.2.2. Nas figuras abaixo temos duas faturas uma de energia elétrica e outra de água. Analizando essas faturas, responda:
Solução. a) Sabendo que o valor do salário mínimo em vigência no Brasil é de R$ 788,00 e que
o dono destas faturas recebe dois salários mínimos e meio, contribuindo 9% para previdência social (INSS). Qual a porcentagem ele gasta do seu salário líquido com essas faturas?
• dINSS=788×9%=788×
9
• p= Ptotal Sl
=187,41 717,08
• p≈0,2613 ou p≈26,13%
b) Qual o percentual cobrado na fatura de energia pela contribuição da iluminação pública? Solução.
• p= 19,23
146,20=0,1315 ou p=13,15%
c) Qual o percentual cobrado na fatura de água pela contribuição do PIS e COFINS (Lei 12.741 de 2012)?
Solução.
• p= 3,81
41,21 ≈0,0924 ou p≈9,24%
Exemplo 5.2.3. (A matemática financeira no contracheque)- O Sr Azulão é funcionário das lojas VT Eletro. Trabalhando como vendedor recebe um salário mínimo mais uma comissão de 1,3%sobre as vendas. Tendo vendido, no mês de agosto, um total deR$143.000,00e levando
em consideração todos os descontos, vamos preencher contracheque e descobrir seu salário líquido.
Solução. • salário base
SB=R$788,00
• comissão sobre vendas
COMISSÃO=R$143.000,00×1,3%=R$143.000,00×0,013=R$1.859,00 • vale transporte
V T =R$9,00×24=R$216,00
DESCONTO VT=R$788,00×6%=R$788,00×0,06=R$47,28
• vale alimentação
VA=R$15,00×24=R$360,00
DESCONTO VA=R$788,00×20%=R$788,00×0,2=R$157,60
• salário bruto
SBr = SB + COMISSÃO
SBr=R$788,00+R$1.859,00=R$2.647,00
• previdência
INSS = SBr×alíquota
38
• imposto de renda
IRRF = (SBr - INSS)×alíquota - dedução
IRRF= (R$2.647,00−R$291,17)×7,5%−R$142,80
IRRF= (R$2.355,83)×0,075−R$142,80=R$33,89 • fundo de garantia
FGTS = SBr×alíquota
FGT S=R$2.647,00×8%=R$2.647,00×0,08=R$211,76
• preenchendo o contracheque2
Disponível em http://www.lugardasdicas.com.br/modelos-de-holerite
2Fontes das alíquotas:
5.3.
Fundamentos de PA’S e PG’S Aplicadas à Matemática
Financeira
5.3.1 Sistema ou Regime de Capitalização
A capitalização é a forma de apuração e incorporação dos juros quanto à incidência de taxa sobre o capital e é dividida em: Simples e Composta
5.3.1.1 Capitalização Simples (Juros Simples)
- É a forma de capitalização em que a taxa ide juro íncide sempre sobre o capital inicial
C0para a formação dos jurosJ=i·C0e estes não são incoporados ou integralizados ao capital
inicial ao longo do prazo em que perdure o empréstimo ou aplicação. A integralização dar-se-á ao final do prazo e sua progressão é aritmética (PA), ou seja, se um capital inicial for aplicado
a juros simples, à taxaipor período, durantenperíodos de tempo temos que
• Juros após 1 período:J1=i·C0
• Juros após 2 período:J2=i·C0+i·C0=2i·C0
• Juros após 3 período:J3=i·C0+i·C0+i·C0=3i·C0
...
• Juros apósnperíodo:Jn=i·C0+i·C0+i·C0+. . .+i·C0=n i·C0
O montante éCn=C0+Jn=C0+n i·C0ouCn=C0·(1+n·i)resultando em um crescimento de juros linear. Esse regime de capitalização normalmente é utilizado para curtíssimo período de tempo ou para cálculo de juro de mora.
Exemplo 5.3.1. Parcelar ou não?
Muitas vezes o comprador possui o dinheiro para pagar à vista, mas escolhe a prazo. Nesses casos, é comum que sejam cobrados juros que encarecem o produto.
Acompanhe a situação:
Juventino é um chefe de família que decide comprar um Velocípede para seu filho Robertinho. A loja oferece dois planos de pagamento:
I. À vista porR$ 480,00.
II. Em duas parcelas iguais deR$ 270,00, sendo a primeira no ato da compra e a segunda um mês após a compra.
40
Solução. • A 1ł prestação (na compra parcelada) é paga no ato da compra e, dessa forma,
não incidem juros sobre ela
• Preço à vista:R$ 480,00 (esse é o valor da mercadoria sem juros)
• Preço a prazo:R$ 540,00=R$ 270,00+ R$ 270,00
• Após pagar a 1ł parcela, à vista, o valor que ele estará devendo éR$ 480,00−R$ 270,00= R$ 210,00
• Se optar por efetuar o pagamento da 2ł parcela após 1 mês, terá de pagarR$ 270,00 (e
nãoR$ 210,00)
• Logo, os juros cobrado serão J =i·C em que J =270−210 =60, C=210, isto é,
i= 60
210≈0,286=28,6% ao mês.
Exemplo 5.3.2. Carlito financia um carro 0km em60meses. O boleto abaixo corresponde a uma dessas parcelas, com as informações contida nele, responda:
Figura 5.1 Boleto bancário
Fonte:Banco GMAC S.A
a) Qual a taxa de juros de multa cobrada após o vencimento? Solução.
• p= 10,88
543,83≈0,02oup≈2%
• p= 2,36
543,83≈0,0043oup≈0,43%
c) Carlito pagará o boleto no dia07/10/2015. Qual o valor cobrado no boleto?
Solução.
• Temos3dias de atraso, logo,C3=543,83+ 3·0,0043·543,83≈543,83+ 7,01
• C3≈550,84
Portanto Carlito pagará aproximadamenteR$ 550,84.
Exemplo 5.3.3. Theobaldo aplicouR$ 800,00em certo banco, com a taxa de juros simples de 1,5%ao mês. Qual o montante acumulado após 5 meses?
Solução. O montante acumulado após 5 meses será no 6° mês, logo:
• n=6 an=a6
• a1=R$ 800,00capital inicial
• r→valor do lucro obtido por mês • r=800·1,5
100 =8·1,5=12
• a6=a1+ (6−1)r=800+5·12=860
O montante acumulada após 5 meses foi deR$ 860,00.
5.3.1.2 Capitalização Composta (Juros Compostos)
- É o regime de capitalização em que há a incorporação dos juros ao capital em cada período. O crescimento dos juros é de progressão geométrica (PG). É a forma utilizada largamente no mercado para cálculo das prestações a pagar, resgate de empréstimo, cheque especial ou aplicações financeiras.
Para entender melhor a ideia como funciona os juros compostos, que não “adiciona”, antes, “compõe”, vejamos o exemplo a seguir:
Exemplo 5.3.4. (Poupança Simples) Suponha que uma pessoa deposite numa poupançaR$ 1.000,00
em um banco que pague5%de taxa de juros anualmente. No final de um ano, o principal de R$ 1.000,00valerá
R$ 1.000,00+ (5%de R$ 1.000,00) = (R$ 1.000,00+ 5
100·R$ 1.000,00) = = (R$ 1.000,00+R$ 50) =R$ 1.050,00.
42
primeiro ano. Logo, depois de dois anos, o principal é
R$ 1.050,00+ (5%de R$ 1.050,00) = (R$ 1.050,00+ 5
100·R$ 1.050,00) = = (R$ 1.050,00+R$ 52,50) =R$ 1.102,50.
Continuando o cálculo para cada um dos aniversário, obtemos
3º aniversário: R$ 1.157,63,
4º aniversário: R$ 1.215,51,
e assim por diante. (Desse modo, não apenas a soma original recebe juros anuais, mas também juros sobre o principal - daí a expressão “juros compostos”.) Percebemos que o saldo cresce numa progressão geométrica, com a taxa comum de1,05(razão dessa progressão).
A partir do exemplo acima, podemos formalizar o conceito. Seja pt o principal depois
t-ésimo aniversário e seja p0o principal inicial. Sejara taxa de juros, onder= 1005 no exemplo
acima. O principal pt ao t-ésimo aniversário pode ser calculado usando o principal pt−1 do
aniversário anterior. De fato, é dado pela relação
pt= pt−1+r·pt−1=pt−1(1+r), t≥1.
Expandindo recursivamente a fórmula, vemos que
pt = pt−1(1+r)
= (pt−2(1+r))(1+r) =pt−2(1+r)2
= ···
= p0(1+r)t, t≥1 (5.1)
Esta é a fórmula do montante de um capital p0sujeito a uma taxa de jurosrnum períodot.
Teorema 5.3.1. No regime de juros compostos de taxar, um principal p0 transforma-se, emt
períodos de tempo, em um montante igual a pt =p0(1+r)t.
Demonstração. Para cadak, seja pka dívida apóskperíodos de tempo. Temos
pk+1=pk+r pk= (1+r)pk.
Daí,(pk)é uma progressão geométrica de razão 1+rePt= p0(1+r)t.
Exemplo 5.3.5. (Poupança Contínua) A senhora Mariana pretende comprar um terreno, à vista, no prazo de doze meses. Para tanto depositando regulamente em uma poupança com juros anuais de 7,97% (digamos, no início de cada mês) uma quantia de R$ 900,00, quanto é que terá no décimo segundo mês?
• P=900depósito mensal na conta poupança,
• i= 7,97
12 =0,664%a.mou i=
0,664
100 =0,00664taxa de juro constante durante os 12
meses,
• n=12meses duração da poupança,
• Mno montante da conta após12meses,
• depositandoR$ 900,00no primeiro dia, depois de um mês, o juro é calculado e deposi-tado na conta, e ela também deposita um adicional deR$ 900,00. Ao final do primeiro
mês, o balanço é de
• M1=900+0,00664·900+900=900·(1+0,00664) +900.
• Ao final do segundo mês, o balanço é deM2=M1·(1+0,00664) +900.
• ···
• Ao final de12meses, o montante é de
• M12=900·(1+0,00664)12+900·[1+(1+0,00664)+(1+0,00664)2. . .+(1+0,00664)11]
• M12 =900·(1,00664)12+900·[1+ (1,00664) + (1,00664)2. . .+ (1,00664)11]
• M12 =900·[1+ (1,00664) + (1,00664)2. . .+ (1,00664)11+ (1,00664)12]
• [1+ (1,00664) + (1,00664)2. . .+ (1,00664)11+ (1,00664)12]é a soma de uma PG de 13termos ondea1=1e razão1,00664.Logo,
• a13=1·1−(1,00664) 13
1−1,00664 ≈13,53
• M12 ≈900·13,53=12.177
Logo, o saldo será aproximadamenteR$ 12.177,00.
Teorema 5.3.2. (Desigualdade de Bernoulli) Sen∈ Nex >−1, vale
(1+x)n≥1+n·x
(5.2)
Demonstração. Considere(1+x)n≥1+n·x.
Note queP(1): (1+x)1≥1+1·x é verdadeiro.
Agora, suponhamos que para algum n∈N, tenhamosP(n)verdadeiro, isto é, a desigualdade
(4.2)é válida para tal valor den. Queremos mostrar que
(1+x)n+1≥1+ (n+1)·x.
44
• (1+x)n(1+x)≥(1+n·x)(1+x) • (1+x)n+1≥1+nx+x+nx2
• (1+x)n+1≥1+ (n+1)x+nx2≥1+ (n+1)x
• (1+x)n+1≥1+ (n+1)x
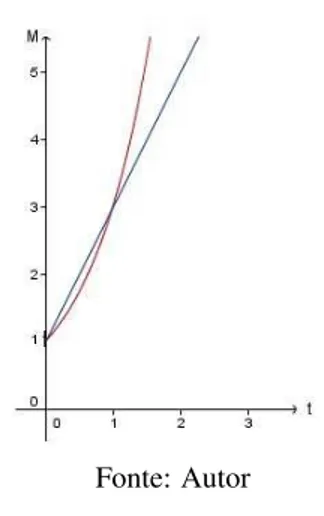
Exemplo 5.3.6. Juros Simples×Juros Compostos
Maria Eduarda tem R$ 1000,00 para investir em um banco durante 11 meses. O gerente de investimentos ofereceu duas altenativas:
i -Aplicação a juros simples de2,7%ao mês.
ii -Aplicação a juros compostos de2,7%ao mês.
Qual a melhor altenativa para Maria Eduarda?
Solução. Sabemos que a juros simples, os montantes constituem uma progressão aritmética (de razãoiC0) ondeC0é o capital investido e, a juros compostos, os montantes constituem uma
progressão geométrica (de razão1+i).
Sendo M11 =C0+11iC0=C0(1+11i) o montante do juros simples e M11 =C0(1+i)11 o
montante do juros compostos, temos que(1+i)11 ≥(1+11i) por(4.2). Portanto, a segunda
altenativa é a melhor para Maria Eduarda, pois,C0(1+i)11≥C0(1+11i).
Observe que: a juros compostos, os montantes constituem uma P.G. e, a juros simples, uma P.A.
Figura 5.2 juros simples×juros compostos
Fonte: Autor
Observação 5.3.1. Na vida real, juros simples são raramente uasados. É de interesse dos detentores do capital que os juros sejam composto. A exceção ocorre se o prazo for menor que a unidade de tempo; neste caso, juros simples darão maior montante. Esta é a única situação da vida real - que ocorre tipicamente em juros de mora, isto é, nos juros que são cobrados por pequenos atrasos em pagamentos - em que juros simples são usados.
5.3.2 Sistemas de Amortização
Ao tomarmos um capital emprestado ou ao fazermos um financiamento, poderemos devol-ver esse capital ou o valor do financiamento em parcelas ou em um pagamento único. Nos dois casos, amortizar significa devolver o capital que se tomou emprestado.
No Brasil, temos mais de uma forma de realizar essa amortização. Temos, assim, os cha-mados Sistema de amortização. Vamos, a seguir, estudar os dois principais desses sistemas.
5.3.2.1 Sistema Price
1. Sistema Price - Parcelas Iguais
O Sistema Francês de Amortização, muito utilizado no setor financeiro e de capitais, é
tam-bém conhecido comoSistema Price. Nesse sistema, é adotado o critério de rendas imediatas,
ou seja, a amortizações crescentes, juros decrescentes e prestações ocorrem em parcelas perió-dicas, iguais e sucessivas, com o primeiro pagamento ao fim do primeiro período contratado. Trata-se do sistema mais adotado pelas instituições financeiras.
Exemplo 5.3.7. Uma instituição financeira concedeu a um indivíduo um crédito no valor de R$ 5.800,00, para ser pago em 12 parcelas iguais, com vencimento da1łparcela em 30 dias e periodicidade mensal de amortização e juros de3,40%a.m.. Então:
a) Determine o valor da parcela a ser paga mensalmente;
b) Determine o valor de cada parcela de juros paga e o valor a ser amortizado mensalmente; Prestações Iguais - Sistema Price
Solução. A questão principal envolvida nesse problema é a do pagamento de um crédito concedido pelo Banco no valor deR$ 5.800,00. A taxa cobrada pela instituição era de3,40%
a.m. e o prazo para liquidação total do débito era de 12 meses. A priori, podemos afirmar que nesse período o Banco deveria receber a quantia deR$ 7.160,16(R$ 5.800,00pelo principal e R$ 1.360,19pelos juros). Uma das formas existentes de efetuar tal pagamento é utilizar uma
modalidade de financiamento denominada Sistema Price .
O financiamento nesse sistema é pago em prestações iguais, cada uma sendo subdividida em duas parcelas:
46
b) amortização do principal (correspondente ao pagamento parcial ou integral do principal e obtida a partir da diferença do valor da prestação e o valor dos juros no período).
Resumindo: no sistema “Price”, para qualquer prestação é válida a relação
PRESTAÇÃO = JUROS + AMORTIZAÇÃO.
Dessa maneira ao longo do tempo, os jurosJ1,J2,J3, . . . ,Jnformam uma sequência decrescente (pois o saldo devedor vai diminuindo) ao passo que as amortizaçõesA1,A2,A3, . . . ,Anformam uma sequência crescente (pois em qualquer instante tem-se Pn=Jn+An), de tal modo que a soma dessas duas parcelas se mantenha sempre igual ao valor constante da prestação. Assim o gráfico das prestações em função do tempo tem o aspecto da figura abaixo:
Figura 5.3 Gráfico prestação x tempo