UNIVERSIDADE DO ESTADO DE SANTA CATARINA - UDESC CENTRO DE CIˆ ENCIAS TECNOL ´ OGICAS - FEJ DEPARTAMENTO DE ENGENHARIA EL´ ETRICA - DEE MESTRADO EM AUTOMAC ¸ ˜ AO INDUSTRIAL DISSERTAC ¸ ˜ AO DE MESTRADO Mestrando: Marcos Ferg¨

(1)

DEPARTAMENTO DE ENGENHARIA EL´ETRICA - DEE

MESTRADO EM AUTOMAC¸ ˜AO INDUSTRIAL

CONTROLE EM MODOS DESLIZANTES DO SERVOMOTOR C.A.

MARCOS FERG ¨UTZ

(2)

DEPARTAMENTO DE ENGENHARIA EL´ETRICA - DEE

MESTRADO EM AUTOMAC¸ ˜AO INDUSTRIAL

DISSERTAC¸ ˜AO DE MESTRADO

Mestrando: Marcos Ferg¨utz

Graduado em Engenharia El´etrica - FEJ/CCT/UDESC

CONTROLE EM MODOS DESLIZANTES DO SERVOMOTOR C.A.

DISSERTAC¸ ˜AO APRESENTADA PARA

OBTENÇ ÃO DO TÍTULO DE MESTRE

EM AUTOMAC¸ ˜AO INDUSTRIAL PELA

UNIVERSIDADE DO ESTADO DE SANTA

CATARINA/CENTRO DE CIˆENCIAS

TEC-NOL ´OGICAS/FEJ, ORIENTADA PELO PROF. DR. ALCINDO DO PRADO JR. E CO-ORIENTADA PELO PROF. MSc. LUIZ CARLOS DE SOUZA MARQUES.

(3)

MARCOS FERG ¨UTZ

Esta disserta¸cão foi julgada adequada para a obten¸cão do t´ıtulo de MESTRE EM AUTOMAÇ ÃO INDUSTRIAL

ênfase em Controle de Sistemas Dinâmicos e aprovada em sua forma final pelo Programa de Pós-Gradua¸cão da Universidade do Estado de Santa Catarina.

Prof. Alcindo do Prado JR., Dr. Orientador

Prof. Marcelo da Silva Hounsell, Dr. Coordenador dos Cursos de P´os-Gradua¸c˜ao

BANCA EXAMINADORA:

Prof. Alcindo do Prado JR., Dr. Prof. Luiz Carlos de Souza Marques, Msc.

Presidente Co-Orientador

(4)

pela mulher e companheira que ´es.

(5)

Agrade¸co ao Prof. Dr. Alcindo do Prado Jr., pelo apoio e coopera¸c˜ao na orienta¸c˜ao deste trabalho.

Sou profundamente grato ao Prof. Msc. Luiz Carlos de Souza Marques, que na quali-dade de co-orientador deste trabalho empenhou dedica¸cão e competência na condu¸cão desta pesquisa. Agrade¸co, sobretudo, sua amizade e confian¸ca.

Agrade¸co, de maneira especial, ao Prof. Bertoldo Ignácio Fergütz, meu pai, pela con-tribui¸cão ´ımpar na revisão do texto.

Agrade¸co ao Prof. Oscar Fergütz, meu irmão, pela sua valiosa coopera¸cão na revisão do artigo e do abstract.

Sou muit´ıssimo grato a todos os companheiros do Departamento de Engenharia Elétrica da UDESC que acreditaram nas minhas potencialidades e apoiaram o meu aperfei¸coamento profissional. A conclusão deste trabalho é, certamente, uma vitória deste grupo.

Agrade¸co a todos os demais familiares e amigos que pacientemente torceram e acreditaram no ˆexito deste trabalho.

(6)

Este trabalho apresenta um estudo sobre o controle descont´ınuo por modos deslizantes aplicado ao motor s´ıncrono de ´ımã permanente, também denominado de servo motor C.A.. Os objetivos maiores do trabalho são dois: o primeiro é analisar a robustez da técnica frente `

a perturba¸cões de carga e nas resistências estatóricas; o segundo objetivo, é o estudo de alternativas para a redu¸cão do “chattering”. A primeira parte do trabalho inclui um estudo sobre a modelagem do motor s´ıncrono convencional e do motor à ´ımã permanente, ambos de pólos salientes. Os objetivos buscados são o estudo de modelos utilizados para o controle do movimento das referidas máquinas no referencial s´ıncrono ortogonal. Na segunda parte desenvolvemos um estudo sobre o controle por modos deslizantes de primeira ordem, incluindo o método de minimiza¸cão do chaveamento em alta freqüência (“chattering”). Apresentamos resultados de simula¸cão que comprovam a eficiência das técnicas aplicadas. Na terceira parte estudamos o controle por modos deslizantes de ordem superior, objetivando minimiza¸cão do “ chattering”. São desenvolvidos os conceitos para um controlador de 2a. ordem. Apresentamos resultados de simula¸cão que comprovam a eficiência do controlador.

(7)

This work presents a study about non-continuous sliding modes control applied to Per-manent Magnetic AC motor (PMAC), also called AC Servomotor. The two main objectives of this work are: to analise the robustness of the technique related to load disturbance and variations in the windings resistance; and to study alternative ways to reduce chattering. The first part includes a study about the modeling of conventional synchronous motors and PMAC motors, both with salient poles. The aim is to study the models used in the movement control of the referred motors in the synchronous reference frame. The second part presents a study about first order sliding modes control, including a method of high frequency switching (chattering)minimization. Simulation results are presented that confirm the efficiency of the techniques applied. Finally, in the third part we study higher order sliding modes control, aiming at chattering minimization. The concepts developed are those for a 2nd order control. Again, simulation results are presented that confirm the efficiency of the techniques applied.

(8)

Introdu¸c˜ao Geral 11

1 Modelamento do Motor S´ıncrono 15

1.1 Introdu¸c˜ao . . . 15

1.2 Motor S´ıncrono de P´olos Salientes Convencional . . . 15

1.3 Motor com Rotor a ´Im˜a Permanente . . . 27

1.4 Conclus˜ao . . . 30

2 Modos Deslizantes de 1a. Ordem 32 2.1 Introdu¸c˜ao . . . 32

2.2 O Controle por Modos Deslizantes Convencional . . . 32

2.2.1 Formula¸c˜ao do Problema de Controle . . . 32

2.3 Redu¸c˜ao do Chattering . . . 37

2.3.1 Altera¸c˜oes da Lei de Controle . . . 37

2.4 Aplica¸c˜ao ao Motor S´ıncrono . . . 40

2.5 Estudo de Simula¸c˜ao . . . 43

2.5.1 Condi¸c˜oes de Simula¸c˜ao . . . 44

2.5.2 Parˆametros do motor . . . 45

2.5.3 Controle com Realimenta¸cão para Simplifica¸cão . . . 46

2.5.4 Controle sem Realimenta¸cão para Simplifica¸cão . . . 59

2.6 Conclus˜ao . . . 64

3 Modos Deslizantes de 2a. Ordem 65 3.1 Introdu¸c˜ao . . . 65

(9)

3.4 Resultados da Simula¸c˜ao . . . 72 3.5 Conclus˜ao . . . 76

Conclus˜ao Final 78

(10)

1.1 Modelo do motor s´ıncrono de p´olos salientes convencional . . . 16

1.2 Varia¸cão das indutâncias próprias . . . 18

1.3 Sistemas de coordenadas . . . 22

2.1 Fenˆomeno do chattering . . . 36

2.2 Camada Limite . . . 37

2.3 Fun¸c˜ao sat1(S, x, t)) . . . 39

2.4 Fun¸c˜ao sat2(S, x, t)) . . . 39

2.5 Referˆencia de velocidade . . . 44

2.6 Perturba¸c˜ao de carga . . . 45

2.7 Velocidade do motor e referˆencia . . . 47

2.8 Velocidade do motor e referˆencia (amplia¸c˜ao) . . . 47

2.9 Corrente de eixo direto . . . 48

2.10 Corrente de eixo direto (amplia¸c˜ao) . . . 49

2.11 Corrente de eixo em quadratura . . . 50

2.12 Tensão estatórica trifásica . . . 50

2.13 Corrente estat´orica trif´asica . . . 51

(11)

3.5 Tensão trifásica de estator (amplia¸cão) . . . 75

3.6 Corrente trif´asica de estator (amplia¸c˜ao) . . . 75

(12)

A aplica¸cão das máquinas elétricas girantes trouxe um grande avan¸co para os meios pro-dutivos. Por serem altamente eficientes na conversão eletromecânica de energia, sua utiliza¸cão em larga escala foi fundamental para o desenvolvimento da industrializa¸cão no mundo con-temporâneo.

Durante muitos anos a maioria das aplica¸cões dos motores elétricos era elementar dentro do processo produtivo, ou seja, não havia qualquer exigência de controle, seja em posi¸cão, velocidade ou torque. Sendo assim, era apenas requerido o funcionamento da máquina a uma dada velocidade praticamente constante e, portanto, sem exigências de quaisquer a¸cões de controle no acionamento. Contudo, com o desenvolvimento tecnológico e o advento da automa¸cão industrial, muitas aplica¸cões têm requerido acionamentos controlados, com maior precisão na resposta e com altos desempenhos dinâmicos, na busca de uma maior eficiência e economia.

Até o in´ıcio dos anos oitenta, os motores de corrente cont´ınua (C.C.) foram largamente empregados nas aplica¸cões que exigiam rapidez e precisão no controle de posi¸cão e velocidade. Isto devido à simplicidade do controle do movimento desta máquina em fun¸cão do desacopla-mento natural entre a corrente de campo, responsável pelo fluxo, e a corrente de armadura, que estabelece o torque da máquina. Este desacoplamento se dá em virtude da ortogonalidade entre os campos magnéticos de estator e rotor, o que é uma caracter´ıstica intr´ınseca da forma construtiva da máquina C.C. . Porém, o motor C.C. apresenta certas limita¸cões, tais como a pequena capacidade de sobrecarga, a estreita faixa de opera¸cão da velocidade e o alto custo de fabrica¸cão e manuten¸cão, devido à existência de escovas e do comutador, o que restringe a utiliza¸cão em áreas inflamáveis, onde o faiscamento do comutador é inviável.

(13)

de alternativas à utiliza¸cão do motor C.C.. Recentemente, com o advento dos microproces-sadores, com o desenvolvimento de materiais magnéticos e com a tecnologia dos semicondu-tores reuniram-se condi¸cões técnicas para o uso de mosemicondu-tores de corrente alternada (C.A.) em sistemas que necessitam de alto desempenho do controle.

Dentre os tipos de motores C.A., os motores s´ıncronos, em especial os de ´ımãs permanentes (servos C.A.), têm sido objeto de estudos e aplica¸cões. Atualmente os servomotores C.A. têm encontrado emprego crescente em aplica¸cões sofisticadas do ponto de vista do controle do movimento, onde o desempenho dinâmico, as altas taxas de acelera¸cão, a reduzida rela¸cão massa/potência e a alta eficiência são requisitos importantes. Os servos C.A., muito embora sejam mais dif´ıceis de controlar, pois, seus modelos matemáticos são não lineares, fortemente acoplados e multi-variáveis, apresentam vantagens significantes relativamente aos motores C.C.[20], [13], tais como: (i) a razão entre potência/massa (kW/kg) é cerca de 30% superior; (ii) a ausência de escovas e de comutador no rotor reduz os custos de manuten¸cão e não sofre restri¸cão a aplica¸cões em áreas restritas (inflamáveis), pois não há faiscamentos; (iii) a obten¸cão de maiores faixas de opera¸cão em velocidade; (iv) o baix´ıssimo momento de inércia do rotor em fun¸cão da ausência de enrolamentos e de comutador; (v) as possibilidades de constru¸cão de motores com carca¸cas hermeticamente vedadas, o que torna este tipo de motor próprio para aplica¸cões aeroespaciais e robótica; (vi) a ausência de perdas rotóricas, aumentando a eficiência.

A forma construtiva, a grande robustez eletromecânica, o baixo custo de fabrica¸cão e de manuten¸cão são fatores que os tornam atrativos para o setor industrial.

(14)

Nas últimas duas décadas, a técnica de controle baseada em sistemas de estruturas variáveis (SEV) ou controlador de estrutura variável (CEV) em modos deslizantes, tem rece-bido especial aten¸cão dos pesquisadores. Matematicamente, a base desta técnica remonta ao final da década de cinqüenta [10]. Porém, somente na década de setenta é que esta técnica come¸ca a ter maior divulga¸cão no ocidente, através dos trabalhos de Utkin [38] e Itkis [19].

O controlador de estrutura variável baseia-se [38] na imposi¸cão de restri¸cões ao sistema, delimitando uma região no espa¸co de estados, designada de superf´ıcie. Através da aplica¸cão de uma lei de controle descont´ınua (estrutura variável), a trajetória do sistema é levada para sobre a superf´ıcie projetada. Uma vez mantendo-se sobre a superf´ıcie, temos a garantia de que o sistema está cumprindo o desempenho desejado.

Tecnicamente, o controle por modos deslizantes se mostra bastante interessante, com algumas caracter´ısticas importantes tais como robustez às perturba¸cões internas e externas, desacoplamento, facilidade de implementa¸cão e redu¸cão de ordem [40], [39], [34], [12] e [17].

Porém, para manter o sistema sobre a superf´ıcie projetada, o controlador necessita de um chaveamento excessivo da estrutura, sendo este chaveamento conhecido como fenômeno do ”chattering”. Na prática esse fenômeno é indesejável, pois pode excitar dinâmicas não mode-ladas, as quais podem levar o sistema à instabilidade. Também pode acarretar o chaveamento excessivo dos atuadores f´ısicos, levando-os à fadiga.

Na década de oitenta e in´ıcio dos anos noventa, as pesquisas se concentraram em buscar alternativas para a lei de controle, visando minimizar o efeito do “chattering”[34], [17], [21], [29] e [12]. Porém, as alternativas desenvolvidas, embora minimizem o “chattering”, intro-duzem uma perda de precisão no sistema, o que requer nos projetos a adequada observa¸cão da rela¸cão “chattering”/precisão.

Mais recentemente, ao final da década de noventa, uma nova abordagem do controle por modos deslizantes com redu¸cão de “chattering”e sem perda de precisão tem sido desenvolvida. A técnica é denominada de controle por modos deslizantes de ordem superior [11], [5], [25], [24].

(15)

Outras abordagens com diferentes técnicas para o controle de motores s´ıncronos podem ser encontradas, como é o caso da técnica de controle vetorial [37], do controle adaptativo [2] e de lineariza¸cão por realimenta¸cão de estados (“feedback linearization”) [27] . Também os conceitos de redes neurais [30] e lógica Fuzzy [26] têm sido empregados para o estudo do controle dos motores s´ıncronos.

Este trabalho trata do controle por modos deslizantes aplicado ao motor s´ıncrono de ´ımã permanente. Apresenta um estudo completo do controle em modos deslizantes de primeira ordem focando a robustez às perturba¸cões internas e externas e a redu¸cão do “chattering”. Com o mesmo objetivo é desenvolvido um estudo com um controlador em modos deslizantes de segunda ordem, a fim de comprovar e comparar com as técnicas de redu¸cão do “chattering”do controlador de primeira ordem.

O Cap´ıtulo 1 trata da modelagem do motor s´ıncrono convencional, com enrolamento no rotor e da modelagem do motor s´ıncrono de ´ımã permanente, visando os objetivos de controle. A aplica¸cão de transforma¸cões de coordenadas permite obter os modelos bifásicos no sistema de coordenadas s´ıncrono dq.

O Cap´ıtulo 2 apresenta um estudo da aplica¸cão do controle por modos deslizantes ao motor de ´ımã permanente. Inicialmente é empregado um controle padrão de 1a. ordem com de-scontinuidade introduzida através da fun¸cão sinal. São estudados alguns métodos de redu¸cão do fenômeno do “chattering”, baseados no conceito de camada limite numa vizinhan¸ca da superf´ıcie de deslizamento. São apresentados resultados de simula¸cão para o controle da velocidade, sob severas condi¸cões de varia¸cões da resistência estatórica e do torque de carga. O Cap´ıtulo 3 trata da abordagem do controle por modos deslizantes de ordem superior ao servomotor C.A. . O objetivo é estudar as possibilidades desta abordagem relativamente à redu¸cão do “chattering”sem perda na precisão. O controlador implementado é de segunda ordem e os resultados de simula¸cão apresentados são para o controle de velocidade, sendo aplicadas as mesmas condi¸cões de desempenhos exigidas para o controlador de primeira or-dem.

(16)

Modelamento do Motor S´ıncrono

1.1 Introdu¸

c˜

ao

Este cap´ıtulo apresenta um estudo sobre a modelagem dinâmica do motor s´ıncrono trifásico e simétrico. A relevância deste estudo está no estabelecimento das rela¸cões en-tre os parâmetros trifásicos e os parâmetros bifásicos da máquina, utilizados nos algoritmos de controle .

Serão apresentados dois estudos de modelo para o motor s´ıncrono trifásico de pólos salientes: um para o motor convencional com enrolamento no rotor e outro, para o motor com rotor a ´ımã permanente.

Em fun¸cão dos objetivos de controle que serão especificados nos cap´ıtulos posteriores, deste trabalho, o modelo do motor será explicitado em termos das dinâmicas das seguintes variáveis: posi¸cão(θm) e velocidade(ω)do eixo do motor; corrente de eixo direto(isd) e corrente

de eixo em quadratura(isq) do estator.

1.2 Motor S´ıncrono de P´

olos Salientes Convencional

Nesta se¸cão apresentamos o desenvolvimento do modelo bifásico no referencial s´ıncrono (dq) a partir do modelo trifásico do motor s´ıncrono de pólos salientes convencional.

(17)

Figura 1.1: Modelo do motor s´ıncrono de p´olos salientes convencional

Inicialmente vamos considerar a representa¸cão do motor s´ıncrono, conforme a Figura (1.1). Podemos observar que o motor é composto de um estator sobre o qual estão distribu´ıdas uni-formemente as bobinas de cada uma das três fases e, de um rotor de pólos salientes com um enrolamento concentrado, no caso da máquina convencional, e com ´ımãs permanentes, no caso do servomotor C.A.. As seguintes hipóteses são assumidas:

- os enrolamentos estatóricos são idênticos e igualmente defasados entre si de 120◦_;

- o material ferro-magnético não sofre satura¸cão;

- a densidade de fluxo magnético no entreferro só apresenta componente radial e sua dis-tribui¸cão é co-senoidal;

- não são consideradas perdas magnéticas.

A partir das leis f´ısicas, podemos obter a equa¸c˜ao circuital matricial para os enrolamentos do estator:       Vsa Vsb Vsc       =      

Rs 0 0

0 Rs 0

0 0 Rs

(18)

ondeVsa, Vsb, Vsc representam as tens˜oes aplicadas aos enrolamentos do estator, eIsa, Isb, Isc

s˜ao as correntes que circulam pelas respectivas bobinas do estator e ˙φa,φ˙b,φ˙c representam

as derivadas temporais dos fluxos magn´eticos concatenados com as respectivas bobinas do estator. De uma forma mais compacta, podemos representar a equa¸c˜ao (1.1) por:

[Vs3] = [Rs3] [Is3] +

˙ φs3

(1.2)

sendo

[Vs3] =

      Vsa Vsb Vsc      

[Rs3] =

     

Rs 0 0

0 Rs 0

0 0 Rs

     

[Is3] =

      Isa Isb Isc       ˙ φs3

=       ˙ φa ˙ φb ˙ φc      

Considerando que Mab, Mac e Mbc são os valores das indutâncias mútuas entre as

re-spectivas fases do estator, podemos escrever a equa¸c˜ao matricial do fluxo do estator como sendo:       φa φb φc       =      

La Mab Mac

Mab Lb Mbc

Mac Mbc Lc

            Isa Isb Isc       +       Mar Mbr Mcr      

Ir (1.3)

onde La, Lb e Lc são as indutâncias próprias por fase do estator, Mar, Mbr e Mcr são as

indutâncias mútuas entre as fases do estator e o enrolamento do rotor eIr é a corrente do

enrolamento do rotor.

Em uma forma mais compacta temos:

[φs3] = [Ls3] [Is3] + [Msr]Ir (1.4)

onde

[φs3] =

      φa φb φc      

[Ls3] =

     

La Mab Mac

Mab Lb Mbc

Mac Mbc Lc

     

[Is3] =

      Isa Isb Isc      

[Msr] =

(19)

Em fun¸cão da forma construtiva do rotor com pólos salientes, as indutâncias próprias e mútuas podem ser modeladas em fun¸cão do ângulo de deslocamento do rotor (θ) e da distribui¸cão senoidal do fluxo no entreferro [23] como sendo:

La = Ls−Lmcos2(θ+π₂)

Lb = Ls−Lmcos2(θ−π₆)

Lc = Ls−Lmcos2(θ+π₆)

Mab = −1₂Ls−Lmcos2(θ+π₆)

Mac = −1₂Ls−Lmcos2(θ−π₆)

Mbc = −1₂Ls−Lmcos2(θ−π₂)

Mar = Lsrcos(θ)

Mbr = Lsrcos(θ−2₃π)

Mbr = Lsrcos(θ+2₃π)

(1.5)

onde Ls é o valor médio de indutância própria da bobina, Lm é a máxima varia¸cão da

indutância e Lsr é a máxima varia¸cão das indutâncias mútuas entre as fases do estator e o

enrolamento do rotor. A Figura (1.2) esbo¸ca o comportamento das indutˆancias pr´oprias tal como descrito.

(20)

A equa¸cão elétrica para o rotor é dada por:

Vr=RrIr+

˙ φr

(1.6)

onde o fluxo no rotor ´e dado por:

φr=LrIr+MarIsa+MbrIsb+McrIsc

sendo Lr a indutˆancia pr´opria do enrolamento do rotor e φr o fluxo concatenado com o

enrolamento do rotor.

Uma vez que temos definidas as equa¸cões eletromagnéticas que representam o compor-tamento do motor s´ıncrono de pólos salientes convencional, podemos fazer a aplica¸cão da transforma¸cão trifásica-bifásica (K) [4] às equa¸cões estatóricas. Com isto, temos o estator trifásico transformado num equivalente bifásico, no referencial estacionário αβ0. A trans-forma¸cão utilizada é definida pela seguinte matriz K:

K = 2 3      

1 −1₂ −1₂

0 √₂3 − √ 3 2 1 √ 2 1 √ 2 1 √ 2       (1.7)

que ´e invariante em potˆencia. Deste fato resulta que [K]−1 _{= [K]}T_.

Aplicando a transforma¸c˜ao K na equa¸c˜ao(1.2) temos:

K[Vs3] =K[Rs3] [Is3] +K

˙ φs3

(1.8)

A rela¸cão de transforma¸cão K nos permite escrever a seguinte rela¸cão:

[Is3] =K−1[Is20] (1.9)

sendo Is20= [Iα, Iβ, I0]T, comI0 sendo a componente de seq¨uˆencia zero.

(21)

Is2, como Is2 = [Iα, Iβ]T.

Aplicando a equa¸c˜ao (1.9) em (1.8), temos:

K[Vs3] =K[Rs3]K−1[Is2] +K

˙ φs3

Contudo, como [Rs3] ´e proporcional `a matriz identidade, temos queK[Rs3]K−1 = [Rs3].

Com isso podemos escrever:

[Vs2] = [Rs2] [Is2] +

˙ φs2

(1.10)

sendo Vs2 = [Vα, Vβ]T,φs2 = [φα, φβ]T e

Rs2 =



 

Rs 0

0 Rs



 

Observamos que Vs2 e φs2 j´a est˜ao definidos desprezando as respectivas componentes de

seqüência zero. Podemos verificar que a matrizRs2 está definida como a sub-matriz (2x2) da

matriz Rs3, onde desprezamos a terceira linha e terceira coluna.

Do mesmo modo, se aplicarmos a transforma¸c˜ao K na equa¸c˜ao(1.4) teremos:

K[φs3] =K[Ls3] [Is3] +K[Msr]Ir

Utilizando a rela¸c˜ao dada por (1.9) podemos escrever:

K[φs3] =K[Ls3]K−1[Is2] +K[Msr]Ir

Finalmente obtemos a seguinte equa¸c˜ao para o fluxo do estator no referencial bif´asico:

[φs2] = [Ls2] [Is2] +

3

2φr2[Mθ] (1.11)

sendo φr2 =LsrIr,Mθ= [cos(θ), sen(θ)]T e:

Ls2=



 

1.5Ls−1.5Lm+ 3Lmcos2(θ) 3Lmsen(θ)cos(θ)

3Lmsen(θ)cos(θ) 1.5Ls+ 1.5Lm−3Lmcos2(θ)





(22)

Se substituirmos a equa¸c˜ao(1.11) em (1.10), obtemos:

[Vs2] = [Rs2] [Is2] +Ls2

˙ Is2

+Ls2lθ[I˙ s2] + [Mθl] ˙θKm (1.13)

ondeKm =

3

2φr2,Mθl = [−sen(θ), cos(θ)]T e

Ls2l=



 

−6Lmsen(θ)cos(θ) 3Lm(cos2(θ)−sen2(θ))

3Lm(cos2(θ)−sen2(θ)) 6Lmsen(θ)cos(θ)





 (1.14)

Da equa¸cão(1.13) podemos escrever a equa¸cão da dinâmica das correntes como:

˙ Is2

=−[Ls2]−1[Rs2] [Is2]−[Ls2]−1Ls2lθ[I˙ s2]−[Ls2]−1[Mθl] ˙θKm+ [Ls2]−1[Vs2] (1.15)

Até este ponto, o que temos é o modelo de uma máquina equivalente bifásica, onde as grandezas trifásicas f´ısicas do estator foram transformadas segundo um referencial bifásico ortogonal estacionário e as grandezas do rotor estão segundo o seu referencial girante. O passo seguinte é a transforma¸cão de todas as grandezas da máquina para um único sistema de coordenadas fixado no rotor, conhecido na literatura como sistema de coordenadas s´ıncrono dq. Para tanto lan¸caremos mão da transforma¸cão de rota¸cão (T) [28] e que, matematicamente,

est´a definida como:

T = 

 

cos(θ) sen(θ)

−sen(θ) cos(θ)





 (1.16)

a qual transforma as grandezas do referencialαβem grandezas no referencialdq. Em s´ıntese, o referencial dq é um sistema de eixos ortogonais onde o eixo direto deste é alinhado com o eixo direto do rotor e, portanto, gira com velocidade igual à do rotor. A Figura 1.3 mostra a rela¸cão entre os sistemas de eixos estacionário αβ e s´ıncronodq.

Aplicando a transforma¸cão de rota¸cão na equa¸cão (1.13) temos:

T[Vs2] =T[Rs2] [Is2] +T Ls2

˙ Is2

+T Ls2lθ[I˙ s2] +T[Mθl] ˙θKm (1.17)

(23)

β

elétrica do rotor Velocidade

==>

.

θ = ω

θ

q d

α

Figura 1.3: Sistemas de coordenadas

estacion´arioαβ e no referencialdq:

[Is2] =T−1[Isdq] (1.18)

sendo Isdq = [isd, isq]T.

Derivando os dois lados da igualdade da equa¸c˜ao (1.18) obtemos:

˙

Is2 = ˙T−1θI˙ sdq+T−1[ ˙Isdq] (1.19)

Aplicando (1.18) e (1.19) na equa¸c˜ao (1.17) temos:

T[Vs₂] =T[Rs₂]T−1[Isdq] +T Ls₂T−1θ˙[Isdq] +T Ls₂T−1[ ˙Isdq] +T Ls₂lT−1θ˙[Isdq] +T[Mθl] ˙θKm

(1.20)

Como um dos objetivos deste estudo é obter as rela¸cões entre os parâmetros do modelo bifásico e os parâmetros f´ısicos da máquina, desenvolvendo o coeficiente do segundo termo da equa¸cão (1.20), podemos escrever:

[Lsdq] =T[Ls2]T−1=



 

1.5(Ls+Lm) 0

0 1.5(Ls−Lm)





 (1.21)

(24)

a indutˆancia de eixo direto (Ld) e a indutˆancia de eixo em quadratura (Lq), segundo os

parâmetros f´ısicos do motor (Ls eLm), através das seguintes rela¸cões:

Ld = 1.5(Ls+Lm)

Lq = 1.5(Ls−Lm)

(1.22)

ent˜ao podemos reescrever a equa¸c˜ao (1.21) como:

Lsdq=



 

Ld 0

0 Lq



 

Resolvendo os demais coeficientes da equa¸cão (1.20), obtemos a seguinte expressão de tensões para o referencial dq:

Vsdq = [Rs2][Isdq] + [Lsdq] ˙θ[Isdq] + [Lsdq][ ˙Isdq] + [Lsldq] ˙θ[Isdq] + [Mθdq] ˙θKm (1.23)

ondeVsdq= [vsd, vsq]T e

Lsldq=



 

0 3Lm

3Lm 0



 

Mθdq =

   0 1    (1.24)

A partir da equa¸cão (1.23) obtemos a equa¸cão da dinâmica das correntes de estator no referencial dq como sendo:

[ ˙Isdq] = [LRdq][Isdq] + [LLdq][Isdq] ˙θ+ [LMdq]Kmθ˙+ ˙θ[Isqd] + [Lsdq]−1[Vsdq] (1.25)

onde

LRdq =



 

−RLds 0 0 −R_Ls_q



 

LLdq =



 

0 −3_LL_dm

−3LLqm 0 

(25)

LMdq=



 

0

−_L1_q





 (1.26)

Temos então determinadas todas as equa¸cões de tensões e correntes para o estator segundo o referencial s´ıncrono dq.

Para o rotor podemos escrever a equa¸c˜ao do fluxo como sendo:

φr=LrIr+ [Msr]T[Is3] (1.27)

Verificamos que a equa¸cão (1.27) é fun¸cão das correntes e das indutâncias mútuas referidas ao referencial trifásico. Aplicando a transforma¸cão K às correntes trifásicas podemos escrever:

φr=LrIr+ [Msr]TK−1[Is2]

para a qual, resolvendo o coeficiente do segundo termo, obtemos a equa¸cão do fluxo rotórico segundo o referencial estacionárioαβ:

φr=LrIr+ [Msr2][Is2] (1.28)

sendo

[Msr2] = [Msr]TK−1 =

3

2[Lsrcosθ Lsrsenθ]

Da mesma forma, se aplicarmos a transforma¸cão de rota¸cão à matriz [Is2] na equa¸cão

(1.28), podemos escrever:

φr=LrIr+ [Msr2]T−1[Isdq]

da qual, após resolvermos o coeficiente do segundo termo, podemos escrever a equa¸cão do fluxo rotórico segundo o referencialdq:

φr =LrIr+ [Msrdq][Isdq] (1.29)

com [Msrdq] =

3

2[Lsr 0].

(26)

direto com o eixo direto do rotor, eliminando a componente em quadratura do fluxo. Então a equa¸cão (1.6) que descreve a tensão do rotor pode ser reescrita, no referencial s´ıncrono, como:

vr =Rrir+Lri˙r+Msrd˙isd (1.30)

sendo Msrd =

3 2Lsr.

Finalmente temos determinadas todas as equa¸cões elétricas do estator e do rotor nos três referenciais, ou seja, referencial trifásico, referencial estacionário e referencial s´ıncrono.

Com rela¸cão à equa¸cão mecânica, vamos iniciar analisando a equa¸cão da potência elétrica (P) absorvida pelo motor:

P = vsdisd+vsqisq+vrir

= Ldisdi˙sd+Lqisqi˙sq+Lrir˙ir+Msrdir˙isd

+Rs(i2sd+i2sq) +Rrir2+ [(Ld−Lq)isd+Km]isqθ˙

(1.31)

Na equa¸cão (1.31) podemos observar que a potência elétrica é composta por três termos distintos: o primeiro pela potência(Pmag) referente à energia armazenada no campo magnético

dos enrolamentos de eixo direto e de eixo em quadratura do estator e do enrolamento do rotor; um segundo termo referente às perdas (PJ) por efeito Joule nas resistências estatóricas

e rotóricas; e um termo relativo à potência mecânica (Pm), desenvolvida no eixo do motor.

De uma forma quantitativa, cada termo ´e dado por:

Pmag = Ldisdi˙sd+Lqisqi˙sq+Lrir˙ir+Msrdir˙isd

PJ = Rs(i2sd+i2sq) +Rri2r

Pm = [(Ld−Lq)isd+Km]isqθ˙

(1.32)

Devemos observar que a velocidade angular mecˆanica ωm se relaciona com a velocidade

angular el´etricaω, pela seguinte equa¸c˜ao:

ω = θ˙ = pωm (1.33)

ondepé o número de pares de pólos do rotor.

(27)

mecˆanica (Pmec) como sendo:

Pm = p[(Ld−Lq)isd+Km]isqωm (1.34)

Da rela¸cão mecânica torque-potência [36] temos:

Tm = P_ωm_m

= p[(Ld−Lq)isd+Km]isq

(1.35)

A equa¸cão dinâmica do torque para o motor é dada por:

Tm−Tb−Tl = Jω˙m (1.36)

onde Tl é o torque de carga, J é o momento de inércia do motor e Tb é o torque de perdas

por atritos, modelado como proporcional `a velocidade:

Tb = bωm (1.37)

Se substituirmos as equa¸cões (1.35) e (1.37) em (1.36), podemos escrever a seguinte equa¸cão para a dinâmica da velocidade mecânica:

˙

ωm = p_J[(Ld−Lq)isd + Km]isq − fJvωm − TJl (1.38)

e sendo a rela¸c˜ao entre posi¸c˜ao e velocidade do eixo do motor dado por:

˙

θm =ωm (1.39)

(28)

pelo seguinte conjunto de equa¸c˜oes diferenciais:

˙

θm = ωm

˙

ωm = _Jp[(Ld−Lq)isd+Km]isq− fv

Jωm−TJl

˙

isd = −R_L_dsisd+pL_L_dqωmisq+_L1_dvsd

˙

isq = −R_L_qsisq−pL_L_qdωmisq−pK_L_qmωm+ _L1_qvsq

vr = Rrir+Lr˙ir+Msrdi˙sd

(1.40)

Na próxima se¸cão determinaremos o conjunto de equa¸cões para o modelo do motor com rotor a ´ımã permanente.

1.3 Motor com Rotor a ´

Im˜

a Permanente

Nesta se¸cão será apresentado o desenvolvimento para a obten¸cão do modelo no referencial s´ıncronodqpara o motor com rotor a ´ımã permanente. Basicamente a mudan¸ca construtiva se dá somente no rotor, onde o enrolamento bobinado sobre o maci¸co ferro-magnético com pólos salientes é substitu´ıdo por um maci¸co ferro-magnético recoberto por um material magnético (´ımã), o qual conforma os pólos salientes de modo a fornecer um fluxo magnético co-senoidal no entreferro.

Contudo, uma vez que a dedu¸c˜ao completa foi desenvolvida para o motor convencional, aqui apresentaremos apenas as diferen¸cas que decorrem da modifica¸c˜ao na forma constru-tiva do rotor.

Inicialmente, a primeira equa¸cão a ser afetada pela ausência de enrolamento do rotor e pela presen¸ca do ´ımã permanente é a equa¸cão (1.3), a qual passamos a escrever como:

      φa φb φc       =      

La Mab Mac

Mab Lb Mbc

Mac Mbc Lc

(29)

onde φar, φbr e φcr s˜ao o fluxo concatenado do rotor com as respectivas fases do estator e,

devido `a forma construtiva do rotor, temos:

φar = φsrmcos(θ)

φbr = φsrmcos(θ− 2₃π)

φbr = φsrmcos(θ+ 2₃π)

(1.42)

sendo φsrm o m´aximo fluxo concatenado do rotor com as fases do estator.

Ent˜ao a equa¸c˜ao (1.4), na forma mais compacta, fica:

[φs3] = [Ls3] [Is3] + [φsr] (1.43)

sendo [φsr] = [φar φbr φcr]T.

Outra diferen¸ca entre os motores se dá na equa¸cão(1.5), onde, em fun¸cão da diferen¸ca de permeabilidade entre o núcleo do rotor bobinado e o núcleo do rotor a ´ımã permanente, as indutâncias próprias e mútuas sofrem uma modifica¸cão no seu modelamento. Com isso o conjunto de equa¸cões dado por (1.5) passa a ser:

La = Ls+Lmcos2(θ+π₂)

Lb = Ls+Lmcos2(θ−π₆)

Lc = Ls+Lmcos2(θ+π₆)

Mab = −1₂Ls+Lmcos2(θ+ π₆)

Mac = −1₂Ls+Lmcos2(θ− π₆)

Mbc = −1₂Ls+Lmcos2(θ− π₂)

(1.44)

Em fun¸cão das altera¸cões no fluxo concatenado do rotor com o estator e das altera¸cões nas indutâncias próprias e mútuas, redefinimos a constante φr2, que aparece na equa¸cão (1.11),

como sendoφr2 =φsrm, e a matrizLs2, dada pela equa¸c˜ao(1.12) passamos a escrever como:

Ls2=



 

1.5Ls+ 1.5Lm−3Lmcos2(θ) −3Lmsen(θ)cos(θ)

−3Lmsen(θ)cos(θ) 1.5Ls−1.5Lm+ 3Lmcos2(θ)





(30)

reescrevemos a equa¸c˜ao (1.14) como:

Ls2l=



 

6Lmsen(θ)cos(θ) 3Lm(sen2(θ)−cos2(θ))

3Lm(sen2(θ)−cos2(θ)) −6Lmsen(θ)cos(θ)





 (1.46)

Também a equa¸cão (1.21) sofre altera¸cões passando a ser escrita como:

[Lsdq] =T[Ls2]T−1=



 

1.5(Ls−Lm) 0

0 1.5(Ls+Lm)





 (1.47)

Com isso pode ser determinada a diferen¸ca fundamental entre os dois tipos de motores s´ıncronos, que é a forma diferente para o cálculo da indutância de eixo direto e da indutância de eixo em quadratura para cada um dos motores. Reescrevemos a equa¸cão (1.22) como sendo:

Ld = 1.5(Ls−Lm)

Lq = 1.5(Ls+Lm)

(1.48)

Ainda podemos verificar que a matriz LLdq, dada pela equa¸c˜ao (1.49), passa a ser:

LLdq =



 

0 3Lm

Ld

3Lm

Lq 0





 (1.49)

com o que determinamos as equa¸cões elétricas para o motor com rotor a ´ımã permanente. A presen¸ca do ´ımã permanente no rotor deixa sem par todas as equa¸cões escritas para a tensão e o fluxo rotórico do motor com rotor bobinado. Com isso reescrevemos a equa¸cão (1.31), que rege a potência elétrica absorvida pelo motor, como sendo:

P = vsdisd+vsqisq

= Ldisdi˙sd+Lqisqi˙sq+Rs(i2_sd+i2sq) + [(Ld−Lq)isd+Km]isqθ˙

(1.50)

ent˜ao a equa¸c˜ao (1.32) fica:

Pmag = Ldisdi˙sd+Lqisqi˙sq

PJ = Rs(i2sd+i2sq)

Pm = [(Ld−Lq)isd+Km]isqθ˙

(31)

Para as equa¸cões mecânicas não há nenhuma altera¸cão na equa¸cões (1.38) e (1.39), ficando o modelo completo do motor a ´ımã permanente definido como:

˙

θm = ωm

˙

ωm = _Jp[(Ld−Lq)isd+Km]isq− fv

Jωm−TJl

˙

isd = −RLdsisd+

pLq

Ldωmisq+

1

Ldvsd

˙

isq = −R_L_qsisq−pL_L_qdωmisq−pK_L_qmωm+ _L1_qvsq

(1.52)

sendo que os valores das indutˆancias de eixo direto e de eixo em quadratura s˜ao calculadas de formas diferentes para os dois tipos de motor s´ıncrono analisados.

1.4 Conclus˜

ao

Neste Cap´ıtulo desenvolvemos as equa¸cões elétricas no referencial s´ıncronodqe as equa¸cões mecânicas tanto para o motor s´ıncrono convencional, quanto para o motor com rotor a ´ımã permanente. Com isso atingimos os objetivos propostos, que eram os de escrever formal-mente os passos empregados no modelamento, visando obter um perfeito entendimento das transforma¸cões empregadas e, ainda, explicitar de forma clara as rela¸cões entre os parâmetros elétricos (resistência e indutâncias ) no referencialdq com os parâmetros f´ısicos da máquina. Podemos concluir afirmando que as equa¸cões que modelam os dois tipos de motores são as mesmas, porém, as indutâncias de eixo direto e de eixo em quadratura têm valores diferentes para cada caso, uma vez que as relutâncias de eixo direto e de eixo em quadratura se alteram conforme o tipo de rotor utilizado. Enquanto o motor convencional tem a indutância de eixo direto maior que a do eixo em quadratura, o motor com ´ımã permanente apresenta situa¸cão contrária, ou seja, a indutância de eixo em quadratura é maior que a de eixo direto.

(32)

rotor.

(33)

Modos Deslizantes de 1a. Ordem

2.1 Introdu¸

c˜

ao

Este cap´ıtulo apresenta uma abordagem de controle baseada nos modos deslizantes de 1a. ordem e sua aplica¸cão ao motor s´ıncrono de ´ımã permanente e pólos salientes (servo motor C.A.). A técnica considerada é bem estabelecida na literatura e tem sido aplicada ao controle do movimento dos motores C.A. [13] e [1].

Primeiramente apresentamos os conceitos básicos da abordagem para o controle de uma classe de sistemas não lineares multi-variáveis. Na segunda parte tratamos da aplica¸cão ao controle da velocidade do motor s´ıncrono. Por fim, com um estudo de simula¸cão, comprova-mos a eficácia da técnica ao problema considerado e são realizadas compara¸cões entre alguns métodos de redu¸cão do “chattering”.

2.2 O Controle por Modos Deslizantes Convencional

2.2.1 Formula¸c˜ao do Problema de Controle

Seja a seguinte classe de sistemas n˜ao lineares representada por:

˙

x=f(x, t) +g(x, t)u(t) +ξ(t) y=h(x, t)

(2.1)

(34)

onde x(t) ∈ ℜn _{é o vetor de estados,} _y₍_t₎ _{∈ ℜ}m _{é o vetor de sa´ıda,} _u₍_t₎ _{∈ ℜ}m _{é o}

ve-tor de entrada e f(x, t), g(x, t) e h(x, t) são fun¸cões conhecidas, limitadas e continuamente diferenciáveis em rela¸cão a todos os argumentos. O vetor ξ(t) representa uma perturba¸cão desconhecida, porém limitada em norma.

A metodologia considerada baseia-se nos dois pontos seguintes: 1. obten¸c˜ao de uma superf´ıcie de deslizamentoS(x, ξ, t)∈ ℜm_{, que garanta a convergˆencia do erro de seguimento}

de sa´ıday∈ ℜm_{para zero, e 2. obten¸c˜ao de uma lei de controle}_u

n, que garanta a atratividade

da origem da superf´ıcie considerada em um tempo ﬁnito.

O projeto da superf´ıcie considera o problema do seguimento de sa´ıda. Sendo assim, cada componente da superf´ıcie S(x, ξ, t), para cada uma das sa´ıdas a ser controlada, ´e escrita na forma:

Sj = rj−₁

i=0

lji(yjref −yj)

i ₍_j _{= 1}_{, ..., m}₎ _(2.2)

onderj ´e o grau relativo da sa´ıdayj(t) [18]. Podemos notar que o projeto da superf´ıcie, para

sa´ıdas com grau relativo superior a 1, constitui-se numa dinˆamica linear de erro de seguimento (yref −y)1. Assim, uma vez estando o sistema sobre a superf´ıcie de deslizamento, o erro de

seguimento converge exponencialmente para a origem, com a constante de tempo regulada pelo valor dos ganhoslji.

No caso de o grau relativo da sa´ıda ser igual a 1, a fun¸cão (2.2) não apresenta dinâmica, o que leva a convergência do erro de seguimento para a origem ser não assintótica.

Uma vez que a superf´ıcie S tenha sido deﬁnida, passamos ao projeto de uma lei de controle que garanta a atratividade da superf´ıcie considerada.

Supondo queS =w(x, ξ, t), podemos escrever ˙S(x, u, t) como:

˙

S = ∂w_∂ξξ˙+∂w_∂t +∂w_∂xx˙

= ∂w

∂ξξ˙+

∂w

∂t +

∂w

∂x[f(x, t) +g(x, t)u(t) +ξ(t)]

= a(x, t) +η(ξ) +b(x, t)u(t)

(2.3)

1

Para a sa´ıdayj com grau relativo 2 (rj = 2), a equa¸c˜ao (2.2), no deslizamento (S = 0), ser´a ˙e=−kje,

(35)

onde

a(x, t) = ∂w_∂t +∂w_∂xf(x, t)

η(ξ) = ∂w_∂ξξ˙+∂w_∂xξ

b(x, t) = ∂w_∂xg(x, t)

A simplifica¸cão e o desacoplamento de (2.3) com rela¸cão ao controle podem ser feitos com a seguinte lei de controle:

u=−[b(x, t)]−1

a(x, t) + [b(x, t)]−1

un (2.4)

onde consideramos que a matriz [b(x, t)] é não-singular para todo e qualquer tempo. A aplica¸cão de (2.4) em (2.3) leva a:

˙

S(x, u, ξ, t) =un+η(ξ) (2.5)

A garantia da estabilidade do sistema (2.5) para a origem é obtida com um controle un projetado com base no critério de estabilidade de Lyapunov. Seja a seguinte fun¸cão de

Lyapunov:

V(S) = 1 2S

T_S _(2.6)

Essa fun¸cão é sempre positiva para valores de S = 0 e nula em S = 0. Sua derivada temporal fica:

˙

V(S) = ST_S_˙ ₌ _ST₍_u

n+η) (2.7)

A negatividade de ˙V(S) ´e garantida com o uso da seguinte lei de controle descont´ınua:

un=−Ksign(S) (2.8)

Assim podemos reescrever (2.7) como:

˙

(36)

Sendoη uma perturba¸cão limitada em norma, por suposi¸cão de projeto, é poss´ıvel obtermos um valor de K que satisfa¸ca a condi¸cão K > |η|, tornando ˙V(S) negativa. Com isso temos garantida a estabilidade de ˙S para a origem deS. A lei de controle resultante é:

u= [b(x, t)]−1

(−a(x, t)−Ksign(S)) (2.10)

Com esse controle a trajet´oria do sistema converge para S(x, t) = 0 e, estando sobre esta, haver´a o deslizamento para a origem do erro de seguimento.

Visando otimizar os tempos computacionais da implementa¸cão do controlador, apresen-tamos uma alternativa de implementa¸cão para a lei de controle dada pela equa¸cão (2.4). O objetivo é implementar a lei de controle desprezando o termo de simplifica¸cãoa(x, t), tal como proposto inicialmente. Portanto, prevendo apenas o desacoplamento, a nova lei de controle fica:

u= [b(x, t)]−1

un (2.11)

Se aplicarmos essa lei `as dinˆamicas de cada superf´ıcie, teremos:

˙

S(x, u, ξ, t) =un+a(x, t) +η(ξ) (2.12)

Novamente temos que garantir a estabilidade do sistema (2.12) para a origem. Para tanto, projetamos o controleun baseado no crit´erio de estabilidade de Lyapunov. A fun¸c˜ao

de Lyapunov adotada ´e:

V(S) = 1 2S

T_S _(2.13)

Essa fun¸cão é sempre positiva para valores de S = 0 e nula em S = 0. Sua derivada temporal fica:

˙

V(S) = ST_S_˙ ₌ _ST₍_u

n+a(x, t) +η) (2.14)

Para satisfazermos o crit´erio de estabilidade de Lyapunov precisamos garantir a negativi-dade de ˙V(S). Para tanto consideramos a seguinte lei de controle descont´ınua:

(37)

Assim podemos reescrever (2.14) como:

˙

V(S) = ST₍₋_Ksign₍_S_{) +}_a₍_{x, t}_{) +}_η₎ _(2.16)

sendo a(x, t) e η fun¸cões limitadas em norma, por suposi¸cão de projeto, é poss´ıvel obtermos um valor de K, que satisfa¸ca a condi¸cão K > |a(x, t) +η|, o que, portanto, torna ˙V(S) negativa. Com isso temos garantida a estabilidade de ˙Spara a origem deS. A lei de controle resultante é:

u= 1

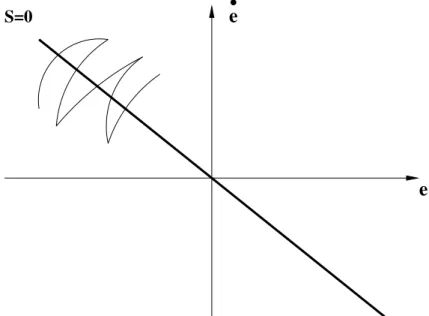
b(x, t)(−Ksign(S)) (2.17) Assim fica garantido que a dinâmica do sistema tem convergência para S(x, t) = 0 e que, estando sobre esta, haverá o deslizamento com a dinâmica de erro convergente para a origem. Contudo, devemos ressaltar que esse deslizamento sobre S = 0, somente ocorre para o caso ideal, pois, na prática, os atrasos relacionados ao tempo de chaveamento e de processa-mento fazem com que o sistema não permane¸ca exatamente sobre a superf´ıcieS= 0, mas sim, numa vizinhan¸ca em torno desta. Esse fato pode levar o controle a sucessivos chaveamen-tos, mostrados na Figura 2.1(para grau relativo 2), conhecidos por “chattering”, que pode restringir a aplica¸cão do controle de modos deslizantes a sistemas f´ısicos.

S=0

.

e

(38)

2.3 Redu¸

c˜

ao do Chattering

Como foi exposto na se¸cão anterior, o “chattering”, ou seja, o excessivo chaveamento do controle é um fenômeno inerente ao controle descont´ınuo por modos deslizantes clássico e pode excitar dinâmicas não modeladas, as quais podem levar o sistema à instabilidade. Nesta se¸cão iremos desenvolver um estudo sobre as técnicas de redu¸cão do “chattering”aplicadas ao controlador de 1a. ordem.

2.3.1 Altera¸c˜oes da Lei de Controle

Para o controle em modos deslizantes de 1a. ordem, a idéia que tem sido utilizada para minimizar os efeitos negativos do “chattering”introduz a no¸cão de camada limite [34] na vizinhan¸ca da superf´ıcie de deslizamento. O conceito de camada limite é ilustrado na Figura 2.2.

e

CAMADA LIMITE

ε

.

S=0

e

Figura 2.2: Camada Limite

(39)

ainda, são utilizadas as duas considera¸cões, propiciando trechos com controle linear e trechos com banda morta, tal qual utilizada por Glumineau [13]. A utiliza¸cão da camada limite implica uma perda da precisão, uma vez que não se exigirá que o sistema permane¸ca sobre a superf´ıcie e, sim, em sua vizinhan¸ca. Com isso o parâmetroǫserá usado para a determina¸cão de desempenho do sistema, uma vez que o seu ajuste implica em um compromisso entre a precisão e a redu¸cão do “chattering”.

No controle por modos deslizantes clássico, o controle descont´ınuo é implementado com o uso da fun¸cão sinal (sign). A utiliza¸cão da camada limite implica altera¸cão da estrutura de controle e, portanto, há a necessidade de definirmos as novas fun¸cões matemáticas que nos permitirão usar a no¸cão de camada limite. Para o nosso estudo iremos definir duas novas fun¸cões, conforme segue:

a) Camada limite com controle linear (sat1)

A fun¸cão é definida matematicamente como:

sat1(S, x, t) =

     

    

−1 ,−ǫ < S(x, t);

S

ǫ ,−ǫ≤S(x, t)≥ǫ;

1 , S(x, t)> ǫ.

(2.18)

O gráfico relativo à fun¸cão é mostrado na Figura 2.3.

b) Camada limite com zona morta (sat2)

A fun¸cão que introduz uma zona morta no interior da camada limite é definida pela seguinte fun¸cão matemática:

sat2(S, x, t) =

     

    

−1 ,−ǫ < S(x, t); 0 ,−ǫ < S(x, t)< ǫ; 1 , S(x, t)> ǫ.

(2.19)

(40)

+ε

−ε

f(S)

S

Figura 2.3: Fun¸c˜aosat1(S, x, t))

+ε

S

f(S)

+1

−1

−ε

(41)

2.4 Aplica¸

c˜

ao ao Motor S´ıncrono

Nesta se¸cão aplicamos a técnica apresentada na se¸cão 2.2.1 ao controle do movimento do motor s´ıncrono de ´ımãs permanentes e pólos salientes. Para tanto, consideramos o modelo em coordenadas ortogonais no referencial s´ıncrono fixo no rotor [23]. Consideramos como perturba¸cão a carga mecânica (Tl) e as varia¸cões na resistência estatórica (∆Rs) devidas à

varia¸cão na temperatura interna do motor. Ambas as perturba¸cões são consideradas limitadas

em norma. Ent˜ao, a equa¸c˜ao (2.1) pode ser escrita para o motor como:

x= [Θ, ωm, isd, isq]T , u= [vsd, vsq]T, h= [ωm, isd] (2.20)

f(x) =

         ωm

(p/J) (Ldqisd+Km)isq−(fv/J)ωm

−(Rs/Ld)isd+ (pLq/Ld)isqωm

(Rs/Lq)isq−(pLd/Lq)isdωm−(pKm/Lqωm)

         (2.21) g=   

0 0 1/Ld 0

0 0 0 1/Lq



 

T

, ξ=

0 −Tl/J −∆R_L s

d isd −

∆Rs

Lq isq

T

(2.22)

ondeLdeLqs˜ao, respectivamente, as auto-indutˆancias de eixo direto e de eixo em quadratura

do estator e Km é o fluxo do rotor, o qual consideramos constante. J é a inércia do sistema

(motor e carga),pé o número de pares de pólos,fvé o coeficiente de viscosidade. O parâmetro

Ldq ´e deﬁnido por:

Ldq = (Ld−Lq)

Conforme apresentado em (2.20), os estados do sistema s˜ao a posi¸c˜ao e a velocidade

mecânica e as componentes ortogonais da corrente de estator. As entradas são as tensões de

estator e as sa´ıdas do sistema s˜ao a velocidade e a corrente de eixo direto.

Para a escolha das vari´aveis de sa´ıda levamos em considera¸c˜ao os seguintes aspectos: a

velocidade foi escolhida porque o objetivo básico de controle de um motor elétrico é o seu

(42)

testarmos a t´ecnica considerada; a escolha da corrente de eixo direto tem o objetivo de anular

o torque de relutância devido à forma construtiva dos pólos salientes.

Inicialmente determinamos o projeto das duas superf´ıcies a serem utilizadas para realizar

o controle da velocidade e da corrente. Para tanto, das equa¸c˜oes de estado do motor (equa¸c˜ao

(2.1), particularizada por (2.20), (2.21) e (2.22)), devemos observar que a velocidade tem grau

relativo 2, enquanto que a corrente tem grau relativo 1. Ent˜ao, utilizando a equa¸c˜ao (2.2)

aplicada a cada vari´avel de sa´ıda, obtemos:

   S1 S2   =   

( ˙y1ref −y˙1) +l1(y1ref −y1)

l2(y2ref −y2)

  =    ˙

ωmref −ω˙m+l1(ωmref −ωm)

l2(−isd)





 (2.23)

Devemos atentar para o fato de que o controle da corrente de eixo direto tem o intuito de

anular o torque de relutância e, por isso, a referência é considerada zero (isdref = 0).

Para a obten¸c˜ao da lei de controle utilizamos a derivada da superf´ıcie. Portanto, derivando

(2.23) temos:    ˙ S1 ˙ S2   =   

(¨ωmref −ω¨m) +l1( ˙ωmref −ω˙m)

l2( ˙−isd)





 (2.24)

Devemos identiﬁcar, para cada superf´ıcie, os termos que n˜ao dependem das entradas de

controle e os termos que est˜ao relacionados com elas, conforme a equa¸c˜ao (2.3). Assim

podemos escrever:

˙

S1(x, u, t) =a1(x, t) +η1(ξ) +b11(x, t)vsd(t) +b12(x, t)vsq (2.25)

e:

˙

S2(x, u, t) =a2(x, t) +η2(ξ) +b21(x, t)vsd(t) +b22(x, t)vsq (2.26)

Para determinarmos os termos a(x, t), b(x, t) e η(ξ), para cada uma das superf´ıcies,

uti-lizaremos as rela¸cões matemáticas definidas em (2.3). O termo a1(x, t) da superf´ıcie de

velocidade, ´e dado por:

(43)

onde

aω1 = ¨ωmref +l1ω˙mref

aω2 = (Jp(Ldqisd+Km))(

pLdωmisd

Lq +

Rsisq

Lq +

pKmωm

Ld )

aω3 = (_Jp(Ldqisq))(pLq_Lωm_disq −R_Lsi_dsq)

aω4 = (Jb −l1)(

p(Ldqisd+Km)isq

J )

(2.28)

O termo de perturba¸c˜ao η1 ﬁca:

η1 =

˙

Tl

J −( b J −l1)(

Tl

J) +

pisq∆R(LdqisdKm)

JLq

+ pLdqisdisq∆R

JLd

Os termos que dependem do controle, relacionados `a dinˆamica da superf´ıcie de velocidade,

b11(x, t) e b12(x, t), s˜ao:

b11(x, t) =−

pLdqisq

JLd

(2.29)

b12(x, t) =−

p(Ldqisd+Km)

JLq

(2.30)

Para a superf´ıcie de corrente, o termo independente das entradas a2(x, t) ´e dado por:

a2(x, t) =−l2(−Rsisd

Ld

+pLqωmisq

Ld

) (2.31)

O termo de perturba¸c˜ao η2(ξ) vale:

η2(ξ) = l2isd∆R

Ld

Com rela¸c˜ao aos termos dependentes das entradas de controle obtemos:

b21(x, t) =−

l2

Ld

(2.32)

b22(x, t) = 0 (2.33)

(44)

deslizantes para o motor como: v=    vsd vsq   =−   

b11 b12

b21 b22



 

−₁_

 

a1+Kωsign(S1)

a2+Kisign(S2)





 (2.34)

sendo que Kω>0 eKi>0 s˜ao os ganhos que determinam a velocidade de convergˆencia das

dinâmicas em dire¸cão às superf´ıcies de deslizamento.

Finalmente, devemos garantir que a matriz b(x, t) da equa¸c˜ao (2.34) tenha sempre a sua

inversa, evitando que o sistema seja levado a alguma singularidade. A condi¸c˜ao a ser satisfeita

´e detb= 0. O determinante da matriz ´e dado por:

detb=

−pLdqisq

J Ld −

p(Ldqisd+Km)

J Lq

−l2

Ld 0

(2.35)

de onde conclu´ımos que, se:

isd =−

Km

Ldq

(2.36)

for satisfeita, a matriz b n˜ao apresentar´a singularidades. Portanto, o controle deve ser

proje-tado de forma a evitar que a corrente de eixo direto alcance o valor dado por (2.36).

Na próxima se¸cão estaremos validando a técnica apresentada, através de simula¸cões para

um dado desempenho desejado.

2.5 Estudo de Simula¸

c˜

ao

Esta se¸cão mostra resultados de simula¸cão obtidos com a aplica¸cão da técnica de controle

ao motor s´ıncrono de ´ım˜a permanente, apresentada na se¸c˜ao 2.2.

S˜ao objetivos do estudo: 1. analisar o desempenho do controlador apresentado, no que

se refere à resposta dinâmica e à robustez relativamente a perturba¸cões de carga e varia¸cões

nas resistências estatóricas; 2. analisar os desempenhos dos controladores com (equa¸cão 2.4)

e sem a realimenta¸cão para simplifica¸cão (equa¸cão 2.11); 3. analisar os resultados para as

diferentes fun¸c˜oes de chaveamento, visando a redu¸c˜ao do “chattering”(Figura 2.3 e 2.4).

A se¸cão está organizada da seguinte forma: primeiramente apresentamos uma subse¸cão

(45)

item, são analisados três casos: (i) controle descont´ınuo com a fun¸cão sinal (sign); (ii) controle

com camada limite e fun¸cão linear no interior da camada, através da aplica¸cão da fun¸cãosat1

(Figura 2.3); e (iii) controle com camada limite e zona morta no interior da camada, atrav´es

da utiliza¸cão da fun¸cão sat2 (Figura 2.3). Por fim, apresentamos uma subse¸cão com os

resultados obtidos utilizando o controle sem realimenta¸cão para simplifica¸cão, com o objetivo

de reduzir os tempos computacionais e, aplicando a fun¸c˜aosat1, visando obter a caracter´ıstica

de redu¸c˜ao de “chattering”, dada por esta fun¸c˜ao.

2.5.1 Condi¸c˜oes de Simula¸c˜ao

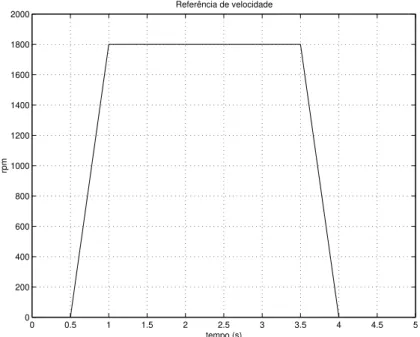
Para a valida¸c˜ao dos objetivos de controle, iremos analisar o desempenho do sistema

através da aplica¸cão de uma referência de velocidade e de uma perturba¸cão de carga, as quais

est˜ao mostradas na Figura 2.5 e Figura 2.6, respectivamente.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0 200 400 600 800 1000 1200 1400 1600 1800 2000

Referência de velocidade

tempo (s)

rpm

Figura 2.5: Referˆencia de velocidade

As especiﬁca¸c˜oes de desempenho visam reproduzir caracter´ısticas de sistemas

industri-ais, tais como, pontes rolantes, guindastes e esteiras transportadoras, os quais apresentam

restri¸cões de acelera¸cões e varia¸cões de torque.

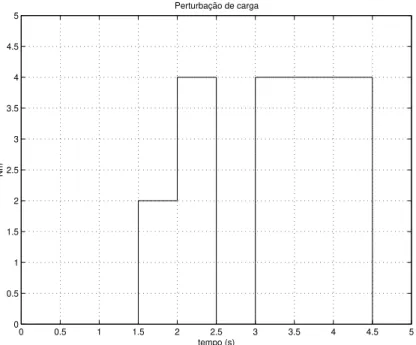
Em uma an´alise das Figuras 2.5 e 2.6 podemos observar que o motor sofre uma acelera¸c˜ao

(46)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

Perturbação de carga

tempo (s)

Nm

Figura 2.6: Perturba¸c˜ao de carga

de uma desacelera¸c˜ao e a parada total da m´aquina.

Relativamente à resistência estatórica, consideramos um erro de +50% do valor nominal,

para todos os casos estudados.

2.5.2 Parˆametros do motor

O motor s´ıncrono de ´ım˜a permanente utilizado apresenta os seguintes valores nominais:

Potˆencia Nominal: 736 W

N´umero de pares de p´olos: 2

Velocidade nominal: 1800 rpm

Tens˜ao nominal: 208 V

Corrente nominal: 3,5 A

Resistˆencia estat´orica: Rs= 1,5 Ohm

Indutˆancia de eixo direto: Ld= 0,0424 H

Indutˆancia de eixo em quadratura: Lq = 0,0795 H

In´ercia (motor e carga): J = 0,003N m/rad/s2

Coeﬁciente de atrito viscoso: fv = 0,8x10−3 Nm/rad/s

(47)

2.5.3 Controle com Realimenta¸c˜ao para Simplifica¸c˜ao

Nesta se¸c˜ao vamos analisar os resultados de simula¸c˜oes obtidos para a lei de controle dada

pela equa¸c˜ao 2.4.

Controle Descont´ınuo - fun¸c˜aosign

Para a realiza¸cão da simula¸cão deve haver o ajuste dos ganhosl1 el2, os quais definem a

dinâmica de convergência do erro, quando o sistema está em deslizamento sobre a superf´ıcie. A

sintonia desses parâmetros é feita de modo a obter-se a não satura¸cão do controle equivalente

[9], permitindo, assim, a aplica¸c˜ao do controle descont´ınuoun.

Além da escolha dos parâmetros das superf´ıcies temos, ainda, o ajuste dos parâmetros

Kω e Ki, os quais s˜ao os ganhos do controle descont´ınuo, e que deﬁnem a velocidade de

con-vergência das dinâmicas em dire¸cão à superf´ıcie de deslizamento. Portanto, estão diretamente

ligados ao chaveamento do controle ou “chattering”, sendo a sintonia desses parˆametros o

re-sultado do compromisso entre a minimiza¸c˜ao do chaveamento e a precis˜ao da resposta do

sistema.

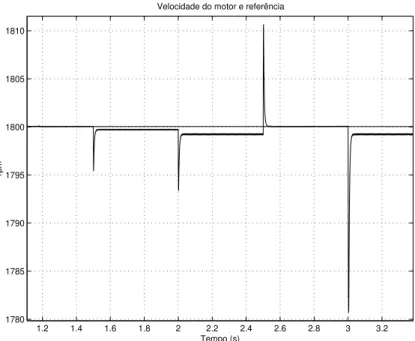
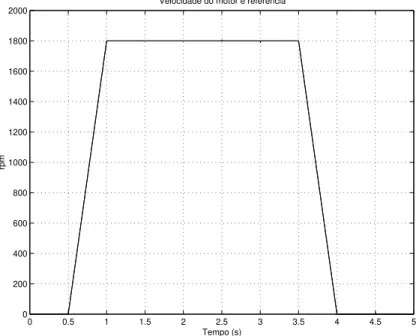
A Figura 2.7 mostra o comportamento da velocidade do motor2_{. Uma excelente dinˆamica}

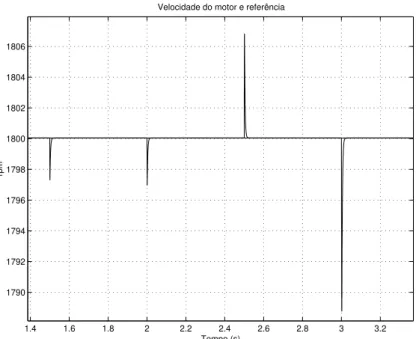
é obtida para o seguimento de uma referência de velocidade. Para uma melhor percep¸cão da

resposta de velocidade, a Figura 2.8 mostra, em escala ampliada, o per´ıodo em que a m´aquina

encontra-se `a velocidade nominal (1800rpm).

Podemos observar que, durante esse intervalo de tempo, o torque mecˆanico varia,

con-forme Figura 2.6, onde vemos que, ora a carga ´e adicionada em parte ou totalmente, ora ´e

retirada totalmente. Para essa varia¸c˜ao da carga, o sistema tem como resposta um transit´orio

reduzido, cujo pior valor de pico (t=3s) resulta em um erro m´aximo de−1% do valor nominal

da velocidade. Já para a situa¸cão de regime o erro máximo de velocidade fica da ordem de

−0,05% da nominal. Isto mostra um bom desempenho do controlador quanto ao seguimento

de referência da velocidade, apresentando robustez às perturba¸cões de carga e às varia¸cões

de resistˆencia estat´orica.

Ao projetarmos o controlador foi utilizada uma segunda premissa para determinar a

su-2

Os valores dos ganhos das superf´ıcies (l1 el2) e do controle descont´ınuo (Kw eKi), para esta simula¸c˜ao,

(48)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 0

200 400 600 800 1000 1200 1400 1600 1800 2000

Velocidade do motor e referência

Tempo (s)

rpm

Figura 2.7: Velocidade do motor e referˆencia

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 3.2

1780 1785 1790 1795 1800 1805 1810

Tempo (s)

rpm

(49)

perf´ıcie de corrente, qual seja, de que a referˆencia da corrente de eixo direto isd seria

con-siderada nula para minimizar os efeitos do torque de relutˆancia e garantir que a matriz de

desacoplamento do controle, [b], tivesse sempre inversa. A Figura 2.9 mostra o

comporta-mento da corrente de eixo direto.

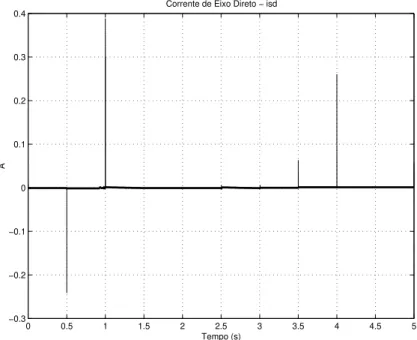
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4

Corrente de Eixo Direto − isd

Tempo (s)

A

Figura 2.9: Corrente de eixo direto

Fica clara a capacidade do controlador de levar e manter a sa´ıda de controle para muito

próximo de zero e que os transitórios de corrente são de curt´ıssima dura¸cão, apresentando,

no pior caso (t=1s), um valor de pico de 400mA. Para uma melhor an´alise, a Figura 2.10

apresenta, em uma escala ampliada, o comportamento da corrente de eixo direto.

Podemos veriﬁcar que, em regime, o valor da corrente ﬁca compreendido,

aproximada-mente, entre±3mA. Portanto, tanto o valor de pico no transit´orio, quanto o valor de regime,

são ´ınfimos se comparados ao valor nominal da corrente do motor, que é da ordem de 3,8

A. Conseqüentemente, podemos afirmar que o controlador tem pleno êxito no controle dessa

vari´avel.

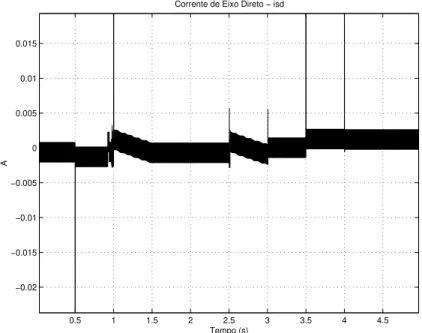
Por´em, havemos de notar que, na Figura 2.10, o valor da corrente n˜ao se estabiliza em

um determinado valor, mas sim, ﬁca oscilando em torno da origem, fato esse que denota um

chaveamento de alta freqüência, ou seja, a ocorrência do fenômeno designado por

(50)

0.5 1 1.5 2 2.5 3 3.5 4 4.5 −0.02

−0.015 −0.01 −0.005 0 0.005 0.01 0.015

Tempo (s)

A

Figura 2.10: Corrente de eixo direto (amplia¸c˜ao)

atrasos impostos pelos tempos computacionais e dos atrasos nos circuitos eletrˆonicos, fazendo

com que, ao controlador perceber que a superf´ıcieS = 0 foi atingida e, portanto, que a a¸c˜ao

do controle descont´ınuo deve ser retirada, na verdade isso ´e feito quando a superf´ıcie j´a foi

ultrapassada. Então, no próximo ciclo computacional já haverá novamente a informa¸cão para

que o controle descont´ınuo volte a atuar, procurando levar a dinˆamica novamente para a

superf´ıcie de deslizamento. Esse efeito se dar´a continuamente gerando o fenˆomeno do

“chat-tering”, o qual ´e altamente indesej´avel, pois diminui o rendimento do sistema, aumentando

as perdas e ru´ıdos, sendo ainda que o mesmo pode excitar dinˆamicas de ordem superior, as

quais não foram modeladas e, conseqüentemente, podendo levar à instabilidade do sistema.

Para melhor evidenciar a ocorrência do “chattering”, na seqüência são mostradas as

Figuras 2.11, 2.12 e 2.13, as quais representam a resposta da corrente de eixo em quadratura,

a tensão estatórica trifásica e a corrente estatórica trifásica, respectivamente.

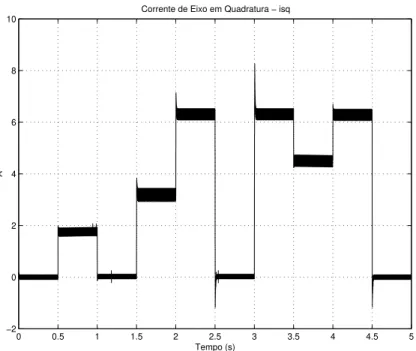
Podemos observar claramente o efeito do chaveamento na corrente isq. Uma vez que a

correnteisdé mantida próxima de zero, o torque mecânico será fun¸cão única deisqe, portanto,

teremos uma resposta de torque com oscila¸cões, o que é um outro fato indesejável.

Destacamos, com maior ˆenfase para a curva da tens˜ao (Figura 2.12), que o “chattering”,

(51)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 −2

0 2 4 6 8 10

Corrente de Eixo em Quadratura − isq

Tempo (s)

A

Figura 2.11: Corrente de eixo em quadratura

2.095 2.1 2.105 2.11 2.115 2.12 2.125 2.13

−250 −200 −150 −100 −50 0 50 100 150 200 250

Tensões Estatóricas

Tempo (s)

V

(52)

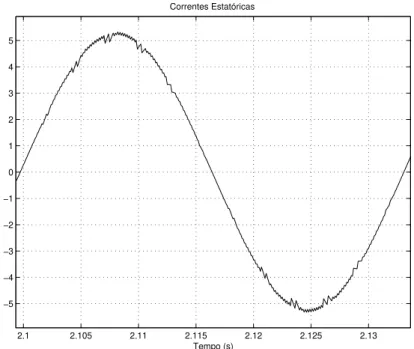
2.1 2.105 2.11 2.115 2.12 2.125 2.13 −5

−4 −3 −2 −1 0 1 2 3 4 5

Correntes Estatóricas

Tempo (s)

A

Figura 2.13: Corrente estat´orica trif´asica

módulo de potência um chaveamento cont´ınuo, o que implica maior gera¸cão de ru´ıdos, gera¸cão

de harmˆonicos, conseq¨uentemente reduzindo o rendimento do sistema e aumentando as perdas

no motor.

Controle com Camada Limite - fun¸c˜aosat1

Nesta subse¸cão apresentamos o resultado das simula¸cões para as fun¸cões sat1 e sat2,

conforme definidas na se¸cão 2.3. Os valores de ǫ, para cada uma das fun¸cões, são ajustados

de forma a obter uma boa rela¸cão custo/benef´ıcio entre a redu¸cão do “chattering”e a obten¸cão

de uma precisão que não degrade o desempenho do sistema. É importante observar que, para

todas as simula¸c˜oes realizadas, consideramos uma varia¸c˜ao de +50% do valor nominal para

as resistˆencias estat´oricas.

A aplica¸cão da fun¸cão sat1 se dará tanto para o controle da velocidade, quanto para a

corrente de eixo direto. Os valores de ǫs˜ao diferentes para cada uma das fun¸c˜oes sat1, em

razão do ajuste da rela¸cão “chattering”/precisão, de cada variável de controle. O ajuste foi

feito na base da tentativa/erro, sendo que, ap´os algumas simula¸c˜oes, obtivemos os seguintes

valores:

(53)

ondeǫω deﬁne a camada limite para o controle da velocidade eǫi deﬁne a camada limite para

o controle da corrente de eixo direto.

O gráfico da Figura 2.14 representa a resposta da velocidade3 _{à referência imposta.}

Podemos observar que h´a uma excelente resposta do sistema, por´em, para melhor

veriﬁ-0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0 200 400 600 800 1000 1200 1400 1600 1800 2000

Tempo (s)

rpm

Figura 2.14: Velocidade do motor e referˆencia

carmos os resultados, a Figura 2.15 mostra, em escala ampliada, o per´ıodo em que o motor

está à velocidade nominal e sofre varia¸cões de carga.

Verificamos, pela compara¸cão entre as Figuras 2.15 e 2.8, que a dinâmica da resposta

de velocidade ´e superior `aquela obtida com o controle por modos deslizantes sem o uso da

camada limite. Podemos observar que a resposta transit´oria tem uma sens´ıvel redu¸c˜ao em

seu valor de pico, sendo que no pior caso (t = 3s) o valor ﬁca em torno de −0,6% do valor

nominal e, em regime, n˜ao h´a um valor percept´ıvel de erro, enquanto que no caso anterior,

os valores eram, respectivamente, de −1% e −0,05%.

A Figura 2.16, mostra a resposta completa da corrente de eixo direto. Na Figura 2.17,

temos, em escala ampliada, o comportamento da correnteisd.

Podemos veriﬁcar que esta, em compara¸c˜ao com a Figura 2.9, ambas apresentam

tran-3

Os valores dos ganhos das superf´ıcies (l1 el2) e do controle descont´ınuo (Kw eKi), para esta simula¸c˜ao,

(54)

1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3 3.2 1790

1792 1794 1796 1798 1800 1802 1804 1806

Tempo (s)

rpm

Figura 2.15: Velocidade do motor e referˆencia (amplia¸c˜ao)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−0.5 0 0.5 1

Tempo (s)

A

(55)

0.5 1 1.5 2 2.5 3 3.5 4 4.5 −8

−6 −4 −2 0 2 4 6

8x 10

−4 _{Corrente de Eixo Direto − isd}

Tempo (s)

A

Figura 2.17: Corrente de eixo direto (amplia¸c˜ao)

sitórios de curt´ıssima dura¸cão, porém, enquanto aquele mostra oscila¸cões em torno do valor

zero (±2,5mA), neste não registramos qualquer oscila¸cão em regime, mas sim, a variável bem

deﬁnida sobre o valor zero, o que denota ausˆencia de “chattering”. Devemos ressaltar que o

gr´aﬁco da Figura 2.17 tem a amplitude da corrente registrada na ordem de 10−4

A, o que nos

assegura uma excelente resposta do sistema.

Para completar o estudo das respostas obtidas com a fun¸c˜ao sat1, est˜ao mostradas as

Figuras 2.18, 2.19 e 2.20, que representam, respectivamente, a correnteisq, a tens˜ao trif´asica

aplicada ao motor e a corrente trif´asica de estator.

Na análise das três figuras supracitadas, podemos observar que o fenômeno do

“chatter-ing”foi minimizado significativamente. Também, ao termos aplicada ao motor uma tensão

puramente senoidal, reduzimos a gera¸c˜ao de ru´ıdos e harmˆonicos, minimizando, com isto, as

perdas.

Controle com Camada Limite - fun¸c˜aosat2

Com o prop´osito de compararmos o desempenho, analisamos o comportamento do sistema

com a utiliza¸cão da fun¸cãosat2 na implementa¸cão do controlador. É importante ressaltarmos

(56)

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 −2

0 2 4 6 8 10

Corrente de Eixo em Quadratura − isq

Tempo (s)

A

Figura 2.18: Corrente de eixo em quadratura

2.095 2.1 2.105 2.11 2.115 2.12 2.125 2.13

−200 −150 −100 −50 0 50 100 150 200

Tensões Estatóricas

Tempo (s)

V