Open Solução tipo monopolo: com violação e sem violação da simetria de Lorentz

UNIVERSIDADE FEDERAL DA PARA´IBA

PROGRAMA DE P ´OS-GRADUAC¸ ˜AO EM F´ISICA

SOLUC

¸ ˜

AO TIPO MONOPOLO: COM

VIOLAC

¸ ˜

AO E SEM VIOLAC

¸ ˜

AO DA SIMETRIA

DE LORENTZ

A

driano

R

ocha

S

oares

O

rientador

: P

rof

. D

r

. J

os

e

´

R

oberto

S

oares do

N

ascimento

PROGRAMA DE P ´OS-GRADUAC¸ ˜AO EM F´ISICA

SOLUC

¸ ˜

AO TIPO MONOPOLO: COM

VIOLAC

¸ ˜

AO E SEM VIOLAC

¸ ˜

AO DA SIMETRIA

DE LORENTZ

A

driano

R

ocha

S

oares

Dissertac¸˜ao apresentada ao Programa de P ´os-Graduac¸˜ao em F´ısica da Universidade Federal da Para´ıba, como parte dos requisitos para a obtenc¸˜ao do t´ıtulo de Mestre em F´ısica, ´area de concentrac¸˜ao: F´ısica das part´ıculas elementares e campos

Orientador: Prof. Dr. Jos´e Roberto Soares do Nascimento

S676s Soares, Adriano Rocha.

Solução tipo monopolo: com violação e sem violação da simetria de Lorentz / Adriano Rocha Soares.- João Pessoa, 2016.

71f. : il.

Orientador: José Roberto Soares do Nascimento Dissertação (Mestrado) - UFPB/CCEN

1. Física. 2. Defeitos topológicos. 3. Monopolo. 4. Violação da simetria de Lorentz.

`

Primeiramente agradec¸o a Deus, autor e consumador da minha f´e. Agradec¸o

tamb´em `a minha fam´ılia, principalmente aos meus irm˜aos Dirceu R. Soares e Diego R. Soares, pelo apoio incondicional.

Ao meu orientador, Prof. Dr. Jos´e Roberto Soares do Nascimento, pela compre-ens˜ao, paciˆencia e orientac¸˜ao. Aos competentes professores do departamento de f´ısica da UFPB, sempre dispostos a contribuir.

`

A minha namorada, Hidayane G. da Silva e sua fam´ılia, sempre atenciosos. Aos meus amigos: Ruydeiglan G. Lima, Danilo C. Moreira, Ricardo L. Lima Vitoria, Ricardo

Andres M. Von Dossow e Anderson A. Meireles, pelas discuss ˜oes esclarecedoras e amizade.

”Eu amo a noite solit ´aria e muda, quando no vasto c ´eu fitando os olhos, al ´em do escuro, que lhe tinge a face, alcanc¸o deslumbrado milh ˜oes de s ´ois a divagar no espac¸o, como em salas de espl ˆendido banquete mil tochas arom ´aticas ardendo entre nuvens dlncenso!... ”

Neste trabalho, apresenta-se uma abordagem bibliogr´afica sobre defeitos topol ´ogicos com destaque para os monopolos com ausˆencia de campos de gauge. Inicia-se in-troduzindo uma recapitulac¸˜ao gradual sobre os principais tipos de defeitos e, como suas abordagens variam `a medida que a lagrangiana assume maiores grupos de si-metria. Em seguida, mant´em-se atenc¸˜ao apenas em modelos que suportam soluc¸ ˜oes tipo monopolo. Primeiramente, estuda-se o monopolo globalSO(3), apresentando por meio de uma abordagem anal´ıtica suas principais caracter´ısticas, tais como espac¸o assint ´otico com d´eficit angular e interac¸˜ao gravitacional nula. Posterior-mente, mostra-se que soluc¸ ˜oes tipo monopolo podem surgir, tamb´em, em teorias de campo com violac¸˜ao da simetria de Lorentz.

A

bstract

In this work, it present a bibliographical approach about topological defects especi-ally the monopoles with absence of gauge fields. It begins by introducing a gradual recap on the major types of defects, and how their approaches change as the Lagran-gian assumes greater symmetry groups. Next, remains attention only to models that support monopoles. Firstly , it’s studied the global monopole SO(3), presen-ting through an analytical approach, its main features such as asymptotic space with angular deficit and null gravitational interaction. Posteriorly, it’s shown that monopole solutions can arise also in field theory with Lorentz symmetry violation.

2.1 Mapeamento (2.1) . . . 14

2.2 Mapeamento (2.2) . . . 14

2.3 Mapeamento (2.3) . . . 15

2.4 Gr´afico do potencialV(φ) . . . 16

2.5 Potencial da Part´ıcula . . . 17

2.6 kink (vermelho) e antikink (Azul) . . . 19

2.7 Densidade de energia . . . 19

2.8 PotencialV(φ) . . . 23

2.9 A regi˜ao cinza delimita a ´area do fluxoΦ(r, θ) . . . 29

S

um

ario

´

CAP´ITULO 1 – INTRODUC¸ ˜AO 10

CAP´ITULO 2 – DEFEITOS TOPOL ´OGICOS 13

2.1 Algumas Considerac¸ ˜oes sobre Homotopia . . . 14

2.2 Kinks . . . 15

2.3 V ´ortices Abelianos . . . 20

2.3.1 V ´ortices no modelo abeliano de Higgs . . . 22

2.4 Monopolos . . . 27

2.4.1 O Monopolo de Dirac . . . 28

2.4.2 Monopolo de ’t Hooft - Polyakov . . . 30

CAP´ITULO 3 – MONOPOLO GLOBAL 35 3.1 Lagrangiana do Monopolo Global: Topologia e Equac¸ ˜oes de Campo . . 35

3.2 Ansatz para Soluc¸˜ao da Equac¸˜ao de Campo . . . 37

3.3 An´alise Assint ´otica do Espac¸o-tempo do Monopolo Global . . . 43

3.4 Considerac¸ ˜oes Sobre a evoluc¸˜ao de Monopolos Globais . . . 44

CAP´ITULO 4 – SOLUC¸ ˜AO TIPO MONOPOLO EM TEORIA DE CAMPO COM VIOLAC¸ ˜AO DA SIMETRIA DE LORENTZ 46 4.1 Acoplamento do Tensor Energia-Momento com a M´etrica . . . 50

AP ˆENDICE A – TENSOR ENERGIA-MOMENTO DO MONOPOLO GLOBAL 59

AP ˆENDICE B – SOBRE O MONOPOLO COM VIOLAC¸ ˜AO DA SIMETRIA DE

LORENTZ 63

B.1 Tensor Energia-Momento . . . 63

B.2 Equac¸˜ao de campo do espac¸o curvo . . . 66

Cap´ıtulo 1

I

ntroduc

¸ ˜

ao

Em geral, um determinado sistema f´ısico pode apresentar-se em diversas fases, que na ´otica da mat´eria condensada, tem propriedades macrosc ´opicas bem definidas. Por

exemplo, os supercondutores apresentam resistˆencia el´etrica nula e s ´olidos cristalinos tˆem estruturas at ˆomicas regulares. Contudo, dependendo das condic¸ ˜oes f´ısicas, tais como temperatura e press˜ao, o sistema pode transicionar entre uma fase e outra; que podem apresentar maior ou menor simetria. A transic¸˜ao de fase pode ser descrita por

um mecanismo que os f´ısicos chamam de quebra espontˆanea de simetria (Q.E.S) e, ´e fundamental para compreender tais processos.

O conceito de simetria est´a relacionado com a propriedade que alguns sistemas tˆem de manterem-se invariantes mediante algum tipo de transformac¸˜ao. Do ponto de vista das teorias de campo, elas podem ser distinguidas em dois tipos: global, quando

a transformac¸˜ao ´e a mesma ao longo do espac¸o-tempo, e local, quando a transformac¸˜ao pode variar de um ponto a outro ao longo do espac¸o-tempo. Al´em disso, a simetria pode ser discreta ou cont´ınua.

A formulac¸˜ao lagrangiana das teorias de campo s˜ao descritas por uma densidade lagrangiana, que apresenta simetria de alguma natureza. Obtendo-se a func¸˜ao den-sidade de hamiltoniano, pode-se em princ´ıpio, obter as configurac¸ ˜oes de campo que

minimizam a energia do sistema, tamb´em chamada de variedade do v´acuo. Como ser´a explicitamente demonstrado ao longo deste trabalho, as configurac¸ ˜oes de m´ınima energia n˜ao preservam a simetria da densidade lagrangiana, no entanto, apresentam um n´ıvel de simetria menor1. Desde que a variedade do v´acuo seja degenerada, isto ´e, tenha v´arios estados fisicamente equivalentes de m´ınima energia, a transic¸˜ao do

1_{O grupo de simetria da variedade do v´acuo ´e um subgrupo do grupo de simetria da densidade}

espontˆanea de simetria.

As soluc¸ ˜oes conectando os estados de m´ınima energia s˜ao denominadas defeitos topol ´ogicos. Como o pr ´oprio nome sugere, eles apresentam propriedades assint ´oticas

que permitem classific´a-los em setores topol ´ogicos e, isto ´e realizado utilizando-se um ramo da matem´atica chamado Homotopia2, que ´e muito ´util no estudo das soluc¸ ˜oes de campo.

Dentre os v´arios tipos de defeitos, neste trabalho ser˜ao abordados trˆes: kinks, advindos da quebra de simetria discreta Z_{2; v ´ortice, advindo da quebra de simetria}

U(1); e monopolo, advindo da quebra de simetriaSO(3). Os diferentes tipos de quebra

de simetria d˜ao origem a distintos tipos de defeitos com propriedades, em princ´ıpio, bem diferentes.

Os defeitos topol ´ogicos est˜ao presentes em todos os ramos da f´ısica, das cl´assicas at´e as modernas teorias quˆanticas de campo. No entanto, o tema central desta dissertac¸˜ao s˜ao os monopolos, cuja simetria subjacente `a lagrangiana ´e cont´ınua e n˜ao

apresen-tam campos de gauge. Eles n˜ao se assemelham a part´ıculas, tais como monopolos magn´eticos. Eles ser˜ao estudados em dois contextos: com violac¸˜ao e, sem violac¸˜ao da simetria de Lorentz.

Monopolos s˜ao teoricamente previstos como resultado das transic¸ ˜oes de fases so-fridas pelo universo imediatamente ap ´os o Big Bang e sua existˆencia ´e uma exigˆencia

das teorias de grande unificac¸˜ao [3, 4]. Devido serem isoladamente est´aveis, acredita-se que eles possam ainda estar presentes no universo. Tais objetos, at´e o momento ainda n˜ao foram observados. Apesar de apresentarem grande densidade ap ´os a transic¸˜ao de fase, poss´ıveis mecanismos reduziram significativamente o n ´umero deles.

No cen´ario sem violac¸˜ao da simetria de Lorentz, o estudo ´e feito com base no trabalho de Barriola e Vilenkin [5] entre outros. Nesse trabalho, os autores prop ˜oem

um modelo com auto acoplamento de um tripleto de campos escalares, cujo grupo de simetria da lagrangiana ´e o SO(3) e, o estado de v´acuo quebra espontaneamente essa simetria em U(1). Esse defeito, chama-se monopolo global, devido a simetria da lagrangiana ser global. Al´em disso, ela pertence a um grupo n˜ao abeliano. No

caso seguinte, considera-se a quebra de uma fundamental simetria do espac¸o tempo, a simetria de Lorentz.

2_{Area da topologia que lida com deformac¸ ˜oes cont´ınuas entre espac¸os topol ´ogico.´ Para uma}

1 Introduc¸˜ao 12

Sabe-se que a teoria da relatividade de Einstein, especial e geral, s˜ao muito bem sucedidas e, baseadas no grupo de simetria de Lorentz. No entanto, motivados por encontrar uma teoria de campo unificada3, muito cientistas tˆem considerado a possibi-lidade de violac¸˜ao da simetria de Lorentz [7, 8]. Neste trabalho, a violac¸˜ao ´e obtida por um campo tensorial antissim´etrico de rank 2, cujo valor esperado no v´acuo ´e diferente de zero. Sendo assim, o v´acuo da teoria apresentar´a uma estrutura geom´etrica ao longo do espac¸o tempo, o que obviamente viola a simetria de Lorentz. A forma como esse

tipo de quebra de simetria ´e implementada est´a demonstrada detalhadamente ao longo do cap´ıtulo 3.

Esta dissertac¸˜ao, constitui-se basicamente em um estudo bibliogr´afico sobre um tipo de defeito topol ´ogico denominado monopolo e est´a dividida em trˆes cap´ıtulos, al´em da introduc¸˜ao e conclus˜ao. No cap´ıtulo 2, faz-se um estudo sobre defeitos topol ´ogicos

com ˆenfase em kinks, v ´ortices e monopolos. O cap´ıtulo 3 dedica-se exclusivamente ao estudo do monopolo global. A lagrangiana do modelo ´e escrita em termos de um tripleto de campos escalares. Analisa-se suas propriedades topol ´ogicas e apresenta-se uma soluc¸˜ao assint ´otica para as equac¸ ˜oes de Einstein. No cap´ıtulo 4, mostra-apresenta-se

que defeitos tipo monopolo podem surgir em uma teoria com violac¸˜ao da simetria de Lorentz. Analisa-se as equac¸ ˜oes de Einstein assintoticamente, tomando-se o limite BPS, que fornece uma simplificac¸˜ao muito ´util. E por ´ultimo, tem-se a conclus˜ao, com uma breve an´alise geral do trabalho e suas perspectivas.

O sistema de unidades naturais, onde ¯h=c =1, ´e adotado ao longo de todo o trabalho. Todas as dimens ˜oes s˜ao expressas em termos de energia, cuja unidade b´asica adotada ser´a o el´etron-volt (eV):

[Energia]=[Massa]=[Comprimento]−1=[Tempo]−1

3_{Segundo [6], candidatos promissores s˜ao: teorias de cordas, D-branas e teorias de gravidade}

D

efeitos

T

opol

ogicos

´

Defeitos topol ´ogicos s˜ao soluc¸ ˜oes de equac¸ ˜oes diferenciais n˜ao lineares que, em teoria de campo, ocorrem naturalmente em modelos dinˆamicos com quebra espontˆanea

de simetria. Em geral, a simetria da lagrangiana que descreve um dado modelo n˜ao ´e compartilhada pelo estado de v´acuo da mesma, ou seja, o estado de m´ınima energia. Ent˜ao, quando o sistema tende a esses m´ınimos, h´a uma quebra da simetria e, em func¸˜ao do tipo de simetria que ´e quebrada classifica-se os diferentes tipos de defeitos.

Para esta finalidade, usa-se resultados da teoria da homotopia, um ramo da matem´atica que tem fornecido importantes ferramentas para a compreens˜ao de diversas ´areas da f´ısica, tais como f´ısica da mat´eria condensada, f´ısica de part´ıculas, cosmologia e etc.

Defeitos topol ´ogicos desempenham um papel important´ıssimo em f´ısica, em es-pecial, nas ´areas de mat´eria condensada e cosmologia. Neste ´ultimo, por meio do

mecanismo de Kibble [3], que descreve a formac¸˜ao de defeitos topol ´ogicos atrav´es de transic¸ ˜oes de fase no universo primordial.

Neste cap´ıtulo, faz-se um estudo sistem´atico, no ˆambito cl´assico1, sobre os tipos de defeitos topol ´ogicos mais abordados na literatura. Nas sec¸ ˜oes seguintes s˜ao apresen-tados dois conceitos imprescind´ıveis para compreens˜ao do tema, s˜ao eles: uma breve introduc¸˜ao a teoria homot ´opica, sem ater-se a demonstrac¸ ˜oes dos resultados e a quebra

espontˆanea de simetria, que ser´a discutida conforme apresenta-se os tipos de defeitos.

2.1 Algumas Considerac¸˜oes sobre Homotopia 14

2.1

Algumas Considerac¸ ˜oes sobre Homotopia

A teoria de homotopia ´e um ramo da matem´atica amplo e muito rico, entretanto, neste trabalho, faz-se uma abordagem introdut ´oria, simples e intuitiva, mas suficiente para introduzir os resultado que ser˜ao usados posteriormente.

Define-se o grupo fundamental π1(X,x0) como um conjunto de lac¸os contidos no

espac¸oXdefinidos a partir de um pontox_0∈X. Dados dois lac¸os quaisquer pertencentes aX, eles correspondem ao mesmo elemento do grupo fundamental se, um puder ser continuamente deformado no outro, caso contr´ario, eles correspondem a dois elementos distintos do grupo [9]. Para ilustrar estes conceitos, considera-se o mapeamento de um

circuloS′₁(caracterizado por uma func¸˜ao deθ) em outro circuloS₁(caracterizado pelo ˆangulo 0≤θ≤2π), que pode ser pensado como o espac¸oX[10] .As equac¸ ˜oes (2.1) e (2.2) abaixo, representam dois mapeamentos (lac¸os) sobre S1, que est´a esquematicamente

representado pelo c´ırculo preto nas figuras (2.1) e (2.2).

f₀(θ)=0 para todo θ (2.1)

e

f₀′(θ)=

      

tθ, para 0≤θ < π

t(2π−θ), para π≤θ <2π. (2.2)

Onde o parˆametro realtpode assumir qualquer valor no intervalo [0,1].

Figura 2.1: Mapeamento (2.1) Figura 2.2: Mapeamento (2.2)

A express˜ao (2.1) ilustrada na figura (2.1), mostra que o mapeamento f0(θ) reduz-se a

um ´unico ponto sobreS1. J´a a express˜ao (2.2), ilustrada na figura (2.2), mostra que o

mapeamento f₀′(θ) vai de 0 aπno sentido anti-hor´ario e retorna a 0 no sentido hor´ario.

Pode-se observar que conforme t tende continuamente a zero, o segundo ma-peamento tende suavemente ao primeiro; do ponto de vista topol ´ogico ambos s˜ao equivalentes. De forma geral, sempre que um mapeamento poder ser suavemente

Figura 2.3: Mapeamento (2.3)

Seja um terceiro mapeamento sobreS1, dado por:

f1(θ)=θ, (2.3)

que est´a ilustrado na figura (2.3). Como pode-se observar, n˜ao h´a como deformar

suavemente o mapeamento descrito por (2.3) em (2.1) ou (2.2), a raz˜ao ´e simples e intuitiva, o mapeamento (2.3) d´a uma volta completa em torno de S1, enquanto os

outros dois, n˜ao. A grosso modo, para que os mapeamentos fossem topologicamente equivalentes, seria necess´ario que o mapeamento (2.3) fosse interrompido em algum

ponto, n˜ao permitindo-o completar uma volta sobreS₁.

Matematicamente todos esses mapeamentos s˜ao escritos comoπ1(S1)=Z, ondeZ

pertence ao conjunto dos n ´umeros inteiros e, corresponde ao n ´umero de vezes que (S′₁) ”enrola-se” em S1. Ent˜ao fica claro que Z identifica diferentes classes topol ´ogica do

grupo. Por exemplo, o mapeamento (2.1) e (2.2) pertencem aπ1(S1)=0, enquanto que

(2.3) pertence aπ1(S1)=1.

Estas noc¸ ˜oes de homotopia, estudadas em um circulo, podem ser generalizadas

para grupos de ordem mais alta, tais comoπ2(S2)=Z, que representa o mapeamento

entre duas superf´ıcies esf´ericas. Por ´ultimo, um grupo no qual todos os seus elementos s˜ao equivalentes chama-se grupo trivial e ´e denotado porπ1(S1)=I.

2.2

Kinks

Dentre os tipos de defeitos topol ´ogicos, o mais simples ´e denominado kink, mas n˜ao menos importante, ele apresenta as caracter´ısticas fundamentais presentes nos demais

tipos de defeitos, por´em, de forma mais simples, j´a que trata-se de uma teoria cl´assica de campos em (1+1) dimens ˜oes (uma dimens˜ao espacial mais uma dimens˜ao temporal) com um ´unico campo escalar real [11]. O modelo mais simples que suporta soluc¸ ˜oes

sim-2.2 Kinks 16

plesmente por lagrangiana)

L=1

2(∂µφ)(∂

µ_{φ)−V(φ). (2.4)}

Com o potencial

V(φ)=₋1

2φ

2_m2₊1

4λφ

4₊1

4v

4₌ λ

4(φ

2_−v2₎2_{, (2.5)}

ondev2= m2

λ , comm2eλambos positivos.

De (2.5) tem-se que os m´ınimos desse potencial s˜aoφ0=±v, tamb´em chamados de

variedade do v´acuo (M) desta teoria. A figura (2.4) mostra o gr´afico desse potencial.

−v +v

V(φ)

φ

Figura 2.4: Gr´afico do potencialV(φ)

A dupla degenerescˆencia nos valores de m´ınima energia ´e consequˆencia da invariˆancia da lagrangiana (2.4) sob o grupo de simetria discreta Z_{2, ou seja, ela ´e invariante} mediante a transformac¸˜ao globalφ→ −φ. Entretanto, os estados de m´ınima energia n˜ao o s˜ao. Sendo assim, quando o sistema tende a um desses m´ınimos, que s˜ao fisicamente equivalentes, ocorre uma quebra espontˆanea da simetria discretaZ_2.

A equac¸˜ao de movimento2e a express˜ao para a energia3s˜ao dadas respectivamente por:

d2φ

dt2 − d2φ

dx2 =−λ(φ

2_−v2_{)φ (2.6)}

e

E=

∞ Z

−∞       1 2

dφ

dt

!2

+1

2

dφ

dx

!2

+λ

4(φ

2_−v2₎2

    

dx. (2.7)

2_{Obtida da equac¸˜ao de Euler-Lagrange:} ∂L

∂φ−∂µ

∂L

∂µφ

=0.

3_{Obtida deE=} R∞

−∞

T00dx, ondeT00 ´e a densidade de energia do tensor energia- momento can ˆonico

Para um campo estacion´arioφ(x), as equac¸ ˜oes (2.6) e (2.7) reduzem-se a:

d2φ

dx2 =λ(φ

2_−v2_{)φ (2.8)}

e

E=

∞ Z

−∞       1 2

dφ

dx

!2

+λ

4(φ

2_−v2₎2

    

dx. (2.9)

Soluc¸ ˜oes fisicamente aceit´aveis da equac¸˜ao de movimento(2.8) devem ter energia finita. Assim, da equac¸˜ao (2.9) conclui-se que o campo φ(x) deve ser constante em

x_{→ ±∞}e, a energia potencial deve ser nula. Dessa maneira, conclui-se que a soluc¸˜ao

deve tender aos valoresφ(x)=_±v(os m´ınimos do potencial) quandox_{→ ±∞}.

Neste ponto, ´e preciso esclarecer que as soluc¸ ˜oes devem conectar os dois m´ınimos

distintos do potencial. Fazendo-se a seguinte identificac¸˜ao: x→teφ(x)→x, a equac¸˜ao (2.8) torna-se exatamente igual a equac¸˜ao de movimento newtoniana para uma part´ıcula de massa unit´aria, submetida a um potencialU=₋V(φ), com V(φ) dado por (2.5). A energia dessa part´ıcula seria ent˜ao dada por:

W= dφ

dx

!2

−V(φ). (2.10)

Mas de acordo com a discuss˜ao anterior, emx→ ±∞o campo tende aos m´ınimos do potencial, que s˜ao valores constantes, de modo que a energia total da part´ıcula seria

nula. Em seguida, a figura(2.5) mostra o gr´afico do potencial supondo que ele tenha um m´ınimo em 2.5(a) e, dois em 2.5(b), que ´e o caso real. Esta suposic¸˜ao ´e ´util para compreender porque a soluc¸˜ao deve conectar os dois m´ınimos distinto do potencial

V(φ).

U=₋V(φ)

φ

v0

(a) Um m´ınimo

U=₋V(φ) φ

−v0 v0

(b) Dois m´ınimos

2.2 Kinks 18

A partir da figura 2.5(a), observa-se que, uma vez que a part´ıcula esteja fora da posic¸˜aov0, ela n˜ao pode mais voltar ao estado de m´ınima energia, porque sua energia

potencial sempre ser´a negativa, de modo que sua energia cin´etica nunca ser´a nula e,

portanto, n˜ao poder´a estabelecer repouso e retornar a v0. Agora, se h´a pelo menos

dois m´ınimos como em 2.5(b), ´e poss´ıvel que a part´ıcula saia deφ=₋v0com aumento

da energia cin´etica at´eφ=0, em seguida a energia potencial tende a zero, portanto, a energia cin´etica tamb´em, de modo que a part´ıcula entra em repouso emφ=v₀. Em termos da teoria de campos, isto significa que uma soluc¸˜ao n˜ao trivial e n˜ao singular deve necessariamente conectar os dois m´ınimos distintos do potencial quandox→ ±∞.

Do Ponto de vista topol ´ogico, isto significa que o mapeamento dos contornos espaciais(x_{→ ±∞}) na variedade do v´acuo (_M) n˜ao podem ser reduzidos a um ´unico ponto, em outras palavras, o grupo de homotopia da variedade do v´acuo n˜ao pode ser

trivial. Isto ´e descrito de maneira compacta comoπ0(M),I.

Passando para as soluc¸ ˜oes, uma das formas de se obter a soluc¸˜ao da equac¸˜ao (2.8)

´e multiplicando ambos os lados por d_dxφ e resolvˆe-la por quadratura.

dφ

dx

!

d2φ

dx2 = dφ

dx

!

λ(φ2−v2)φ

d dx

      1 2

dφ

dx

!2     

= d

dx

_λ

4(φ

2_−v2₎2

dφ

dx

!2

= λ

2(φ

2_−v2₎2_{. (2.11)}

A partir da equac¸˜ao (2.11) e admitindo que o campo ´e nulo em x=x0, ou seja,

φ(x₀)=0, obt´em-se:

Z x

x0

dx′ = _±√2

λ Z φ(x)

0

dφ′

(φ′2_−v2₎. (2.12)

O ´ındice linha (’) serve pra distinguir entre a vari´avel de integrac¸˜ao e os limites de integrac¸˜ao. Executando a operac¸˜ao de integrac¸˜ao, obt´em-se a soluc¸˜ao:

φ(x)=_±√m

λtanh

"

m

√

2(x−x0) #

. (2.13)

x

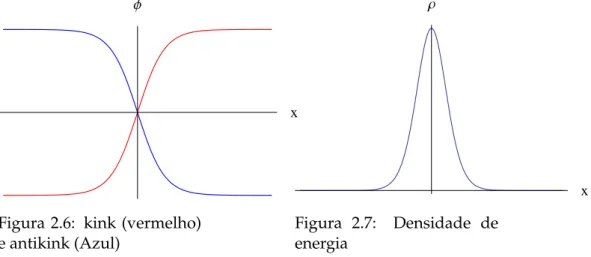
Figura 2.6: kink (vermelho) e antikink (Azul)

x

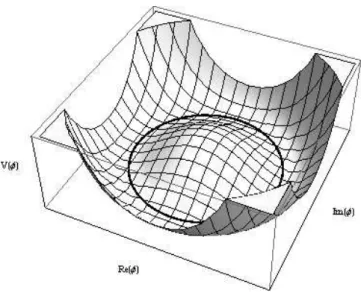
Figura 2.7: Densidade de energia

Substituindo a equac¸˜ao (2.11) na express˜ao (2.9), obt´em-se a energia:

E=

Z ∞

−∞

ρdx=

Z ∞

−∞ λ 2(φ

2_−v2₎2_{dx. (2.14)}

Onde a express˜aoρ= λ

2(φ2−v2)2 ´e a densidade de energia do Kink. Substituindo (2.13)

emρ, tem-se:

ρ= m

4

2λtanh

4

"

m

√

2(x−x0) #

−m

4

λ tanh

2

"

m

√

2(x−x0) #

+m

4

2λ, (2.15)

e com aux´ılio da express˜ao hiperb ´olica: sech2x=1₋tanh2x, mostra-se que:

ρ= λ

2(φ

2_−v2₎2₌m4

2λsech

4

"

m(x₋x₀) √

2 #

. (2.16)

Substituindo a express˜ao (2.16) em (2.14), obt´em-se a energia total do kink-antikink:

E=2

√ 2 3

m3

λ . (2.17)

O gr´afico da densidade de energiaρesta ilustrado na figura (2.16).

Mostrou-se anteriormente, atrav´es da analogia mecˆanica com uma part´ıcula, que as soluc¸ ˜oes de campo, n˜ao singulares e n˜ao triviais, devem conectar m´ınimos distintos do potencial. Entretanto, o campo pode ser um dos m´ınimos do potencial em todo o espac¸o, neste caso, tem-se a soluc¸˜ao trivial. Diante disto, existem quatro soluc¸ ˜oes

fisicamente poss´ıveis para a equac¸˜ao de campo, cada uma determinada a partir das pro-priedades assint ´oticas dos campo. A primeira e segunda s˜ao triviais, respectivamente caracterizadas por: φ(x)=₋veφ(x)= +vao longo de todo o espac¸o. A terceira ´e tal que

lim

x→−∞φ(x)=−v e limx→+_∞φ(x)= +v. A quarta ´e tal que: limx→−∞φ(x)=v e limx→+_∞φ(x)=−v.

2.3 V´ortices Abelianos 20

dado setor n˜ao podem ser continuamente deformadas em soluc¸ ˜oes pertencentes a um setor distinto, caso contr´ario, a condic¸˜ao de energia finita seria violada. Isto pode ser explicitamente colocado por meio de leis de conservac¸˜ao topol ´ogica.

Define-se carga topol ´ogica como:

Q=

Z +∞

−∞

K0dx onde Kµ=ǫµν∂νφ. (2.18) Aqui,ǫµν´e o tensor antissim´etrico de Levi-Civita em duas dimens ˜oes e,Kµ ´e a corrente conservada, uma vez que∂µKµ=0. De maneira explicita:

Q=_φ(x=_∞)−φ(x=_−∞). (2.19) As soluc¸ ˜oes comQ,0 s˜ao ditas soluc¸ ˜oes topol ´ogicas e, desde que a energia do sistema

seja finita, s˜ao est´aveis. O mesmo n˜ao se pode dizer de soluc¸ ˜oes n˜ao topol ´ogicas, onde

Q=0, desde que compartilhem o mesmo m´ınimo do potencial, podem ser suavemente deformadas uma na outra sem violar o requerimento da energia finita.

Em suma, denomina-se Kink-Antikink como um tipo de defeito topol ´ogico decor-rente da quebra espontˆanea da simetria Z_{2, cujo grupo topol ´ogico da variedade do} v´acuo ´e tal queπ0(M),I. Nas pr ´oximas sec¸ ˜oes ficar´a claro que os tipos de defeitos

mais conhecidos s˜ao classificados por meio da quebra espontˆanea de simetria e do grupo de homotopia da variedade do v´acuo.

2.3

V ´ortices Abelianos

Na ´ultima sec¸˜ao, mostrou-se que uma soluc¸˜ao tipo kink ´e um defeito topol ´ogico definido em (1+1) dimens˜ao, cujo grupo de homotopia da variedade ´e π0(M),I.

O pr ´oximo passo em direc¸ ˜oes com dimens ˜oes mais altas, seria estender o modelo do kink (2.4) para pelo menos (1+2) dimens ˜oes, com grupo de homotopia dado por π1(M),I. Entretanto, desde que as soluc¸ ˜oes procuradas sejam n˜ao triviais, est´aticas

e tenham energia finita, esta extens˜ao n˜ao pode ser realizada em uma teoria contendo

apenas campos escalares. Essa limitac¸˜ao ´e expressa por meio do teorema de Derrick4 [13]. Considere, no entanto, a tentativa de generalizar o modelo do kink para duas dimens ˜oes.

4_{Este teorema aplica-se a lagrangianas da forma: L=∂}

µφa∂µφa−V(φa), onde existe uma soma de

se v ´ortice, e decorre de uma teoria com somente um campo escalar complexo [14], cuja lagrangiana ´e:

L=_|∂µφ|2−V(φ) com V(φ)=λ(|φ|2−v2)2, (2.20) como em (2.5),λ ´e positivo.

Os valores que minimizam o potencial e que s˜ao representados porφ0, s˜ao tais que V(φ0)=0. A fim de que a topologia da variedade do v´acuo n˜ao seja trivial (π0(M),I) ´e

necess´ario que os m´ınimos do potencial tenham valores distintos em direc¸ ˜oes distintas do plano. Portanto, em coordenadas polares (r, θ):

φ0=v einθ quando r→ ∞. (2.21)

Ondeθ ´e a coordenada angular enpertence ao conjunto do n ´umeros inteiro.

Para uma configurac¸˜ao est´atica, a lagrangiana e o hamiltoniano do sistema s˜ao dados respectivamente por:

L=_−|∇φ|2₋V(φ) e H=_|∇φ|2+V(φ). (2.22) No limiter_{→ ∞}, tˆem-se φ→φ0 , de modo que, lim

r→∞V(φ)=0. Nestas condic¸ ˜oes, de acordo com (2.22), o hamiltoniano do sistema reduz-se a_H=_|∇φ|2. De forma que,

H =

∂φ0

∂r eˆr+

1

r

∂φ0

∂θ eˆθ !

2

=

−1

rinve

−inθ 1

rinve

inθ₌ n2v2

r2 . (2.23)

A energia, emr→ ∞, ´e ent˜ao dada por:

E =

Z ∞

n2v2

r2 rdrdθ=2πn 2_v2

Z ∞ 1

rdr. (2.24)

Esta divergˆencia logar´ıtmica no valor da energia mostra que o modelo (2.20) n˜ao admite soluc¸ ˜oes est´aticas com energia finita.

O problema da divergˆencia na energia pode ser resolvido adicionando-se um campo de gauge (Aµ) que acopla-se ao campo carregado escalar complexo (φ) via derivada covariante de gauge:

2.3 V´ortices Abelianos 22

ondee ´e a constante de acoplamento m´ınimo. Ent˜ao, escolhendo-se um gauge onde

A0=0 e A= 1

e∇(nθ), em r→ ∞, (2.26)

tˆem-se

Ar=0 e Aθ=

n

re. (2.27)

A energia desta configurac¸˜ao est´atica, agora obtida da parte espacial de (2.25), ´e dada por:

E=

∞ Z

|(∇ −ieA)φ|2dr. (2.28)

Mas a partir das componentes (2.27),

(∇ −ieA)φ = 1

r

∂φ ∂θ !

−ie

_n

re

einθ. (2.29)

Ao substituir a (2.21) em (2.29) mostra-se que:

(_{∇ −}ieA)φ= in

r e

inθ₋in

r e

inθ_{=0. (2.30)}

Portanto, o lim

r→∞E=0, de forma que recupera-se a condic¸˜ao de energia finita, que juntamente com o grupo de homotopia n˜ao trivial do v´acuo desta teoria, constitui o tipo de soluc¸˜ao desejada.

2.3.1

V ´ortices no modelo abeliano de Higgs

Como discutido e verificado anteriormente, existe uma impossibilidade na extens˜ao

do modelo tipo kink para duas dimens ˜oes espaciais usando modelos com somente campos escalares. Tamb´em verificou-se que, ao inserir um campo de gauge no modelo essa dificuldade pode ser contornada sem comprometer a energia e a estabilidade da soluc¸˜ao. Um modelo com tais caracter´ısticas, e que ser´a aqui estudado,

L=₋1

4F µν_F

µν+(Dµφ)∗(Dµφ)−V(φ), (2.31) onde

V(φ)=λ(|φ|2−v2)2. (2.32) As constantesλevs˜ao positivas. Fµν ´e o tensor eletromagn´etico da eletrodinˆamica de Maxwell, e (Dµφ)∗ ´e o conjugado de (Dµφ).

A lagrangiana (2.31) ´e invariante mediante a transformac¸˜ao local de gauge:

φ→φ′=eiβ(x)φ, (2.33)

ou seja, a lagrangiana ´e invariante sob transformac¸ ˜oes locais pertencentes a U(1), que ´e um grupo de simetria abeliano.

Figura 2.8: PotencialV(φ)

A partir da express˜ao (2.32), conclui-se que os m´ınimos (φ0) do potencial s˜ao tais

que

|φ0|2=v2. (2.34)

Esta condic¸˜ao determina, sobre o plano complexo das componentes do campo, um c´ırculo de raio v, que posteriormente ser´a reconhecido como a variedade do v´acuo. O c´ırculo preto no gr´afico do potencial (figura 2.8) representa o conjunto de m´ınimos fisicamente equivalentes, matematicamente expressos por (2.34).

Da express˜ao (2.34), obt´em-se de forma mais simples [14] que, os m´ınimos do potencial s˜ao da forma :

2.3 V´ortices Abelianos 24

sendo θ a coordenada polar do plano espacial (r, θ). O passo seguinte, consiste em calcular o tensor energia-momento e em seguida obter a densidade de energia, a fim de mostrar que a configurac¸˜ao (2.35) corresponde a m´ınima energia do sistema. Com

aux´ılio do tensor energia-momento m´etrico,

Tλσ=2 ∂L

∂gλσ−gλσL, (2.36)

ondegλσ ´e o tensor m´etrico, e da lagrangiana (2.31) na forma

L=gµα(Dµφ)∗(Dαφ)−1 4g

µα_gνβ_F

µνFαβ−V(φ), (2.37)

torna-se simples calcular o tensor energia-momento, que ´e feito como segue.

∂L

∂gλσ = (Dµφ)∗(Dαφ)

∂gµα

∂gλσ

! −1

4FµνFαβ "

∂gµα

∂gλσ

!

gνβ+ ∂g

νβ

∂gλσ

! gµα # =      

δµ_λδα_σ+δµ_σδα_λ 2      (Dµφ)

∗_(D

αφ)−1

4FµνFαβ            

δµ_λδα_σ+δµ_σδα_λ 2      g νβ +        

δν_λδβ_σ+δν_σδβ_λ 2         gµα        

= (Dλφ)

∗_(D

σφ)+(Dσφ)∗(Dλφ) 2

! −1

4 " _F

λνFσβ+FσνFλβ 2

!

gνβ

+ FµλFασ+FµσFαλ

2

!

gµα

#

∂L

∂gλσ =

(D_λφ)∗(Dσφ)+(Dσφ)∗(Dλφ) 2

!

+1

4(FλβF β

σ+FσβFβλ). (2.38) Ao inserir a equac¸˜ao (2.38) na (2.36) obt´em-se a express˜ao para o tensor energia-momento:

Tλσ= 1 2(FλβF

β

σ+FσβFβλ)+(Dλφ)∗(Dσφ)+(Dσφ)∗(Dλφ)−gλσL. (2.39) Deseja-se aqui, da mesma forma como no caso do kink, estudar configurac¸ ˜oes de

campos est´aticos, entretanto, segundo [17] n˜ao existem soluc¸ ˜oes carregadas com energia finita no modelo Maxwell-Higgs, de modo que, ser´a adotado o gaugeA0=0. Partindo

ρ=T00= B 2

2 +|Diφ|

2_+λ(|φ|2_−v2₎2_{, (2.40)}

E=

Z "

B2

2 +|Diφ|

2_+λ(|φ|2_−v2₎2

#

d2x. (2.41)

Da express˜ao para a energia total, conclui-se que para uma soluc¸˜ao com energia finita ´e necess´ario que:

lim

r→∞φ=φ0, onde φ0=ve

nθ_{. (2.42)}

Isto implica que a (2.42) corresponde a variedade do v´acuo, dito de outra forma, o

campo deve tender aos m´ınimos do potencial quando as dimens ˜oes espaciais do plano tendem ao infinito. Quanto ao valor de n, ele determina o n ´umero de vezes que o mapeamento (2.42) ”enrola-se” no espac¸o assint ´otico bidimensional. Para n,_{0 o}

grupo de homotopia da variedade do v´acuo n˜ao ´e trivial, ou seja, π1(M),I. Os

valores de n tamb´em caracterizam diferentes classes de homotopia. S ´o reiterando, soluc¸ ˜oes pertencentes a uma dada classe n˜ao podem ser deformadas em soluc¸ ˜oes de outra classe, desde que o requerimento de energia finita n˜ao seja violado.

Pode-se observar facilmente que os m´ınimos do potencial n˜ao compartilham da simetria U(1) da lagrangiana, de modo que, quando o sistema escolhe um dos m´ınimos, ocorre uma quebra espontˆanea de simetria.

Como observado, a condic¸˜ao (2.42) ´e necess´aria, mas n˜ao ´e suficiente para que as

configurac¸ ˜oes de campo tenham energia finita. De (2.41), esse requerimento ´e expresso matematicamente por:

lim

r→∞B=0 , rlim→∞φ=φ0 e rlim→∞Diφ=0. (2.43) Em particular, a terceira express˜ao revela que

(_{∇ −}ieA)φ = 0 emr_{→ ∞}

∇φ = ieAφ

A = 1

ie

∇φ

φ =

1

ie∇(lnφ)=

1

e∇(nθ). (2.44)

A equac¸˜ao (2.44) implica na quantizac¸˜ao do fluxo magn´etico (Φ) da configurac¸˜ao de campo:

Φ =

Z

Bd2x=

Z

(∇ ×A)d2x=

I

2.3 V´ortices Abelianos 26

Na passagem da segunda express˜ao para a terceira, usou-se o teorema de Stokes. Com aux´ılio da express˜ao (2.27),

I

A.dl =

I

n rerdθ

Φ = n2π

e . (2.46)

´E importante ressaltar que o fluxo magn´etico ´e uma quantidade topol´ogica conservada, que por depender den, consequentemente depende da classe topol ´ogica da soluc¸˜ao.

At´e aqui, discutiu-se sobre v´arias propriedades dos v ´ortices, tais como energia e estabilidade sem, no entanto, se preocupar com o formato das soluc¸ ˜oes. Este ser´a o

objetivo do restante desta sec¸˜ao. As equac¸ ˜oes de campo ser˜ao obtidas por meio do limite BPS [18], m´etodo muito conhecido, que d´a origem a soluc¸ ˜oes de m´ınima energia advinda de equac¸ ˜oes de primeira ordem. A abordagem que ser´a utilizada aqui faz uso da seguinte relac¸˜ao, chamada de auto dualidade [19]

|D_iφ|2=_|(D_1±iD₂)φ|2±eB_|φ|2±ǫij∂iJj, (2.47)

ondeJj ´e a densidade de corrente. Ao substituir a (2.47) na(2.41) obtˆem-se:

E =

Z "

B2

2 +|(D1±iD2)φ|

2_±eB|φ|2_±ǫij_∂

iJj+λ(|φ|2−v2)2 #

d2x

=

Z 1 2(B

2_±2eB|φ|2_)+|D

±φ|2±ǫij∂iJj+λ(|φ|2−v2)2

d2x. (2.48)

Onde D_±φ=D1±iD2. De acordo com o teorema de Stokes,

R

(ǫij∂iJj)d2x= H

J.dl=0. Agora, ao somar os seguintes termos

±eBv2_∓eBv2 e +e

2

2(|φ|

2_−v2₎2₋e2

2(|φ|

2_−v2₎2 _(2.49)

em (2.48), tˆem-se que:

E =

Z 1 2[B

2_±2eB(|φ|2_−v2₎2_+e2_(|φ|2_−v2₎2_]+|D

±φ|2±ǫij∂iJj+λ(|φ|2−v2)2

− e

2

2(|φ|

2_−v2₎2_∓eBv2

#

d2x

E =

Z " 1

2[B±e(|φ|

2_−v2_)]2_+|D

±φ|2+ λ−e

2

2 !

(_|φ|2−v2)2_∓eBv2

#

d2x. (2.50)

I e II, porque em geral, a massa dos campos de Higgs e de gauge s˜ao distintas para diferentes valores deλ. Por meio do mecanismo de Higgs ´e poss´ıvel demonstrar que as

massas dos campos de higgs e de gauge s˜ao respectivamentemφ=

√

2evemA=2 √

λv. Quandomφ>mAtˆem-se um supercondutor tipo I, quandomφ<mAtˆem-se um

super-condutor tipo II, o limite de separac¸˜ao entre eles acorre quandomφ=mA, que ´e o caso

tratado aqui, ou seja,λ= e2

2.

A energia ´e limitada inferiormente por um m ´ultiplo do fluxo magn´etico, para um

fluxo positivo escolhe-se o sinal inferior, para um fluxo negativo escolhe-se o sinal superior, de modo que:

E_≥v2_|Φ_|. (2.51)

Tomando-se o caso em que o fluxo ´e positivo, tem-se que ao saturar o limite BPS, encontra-se as seguintes equac¸ ˜oes:

B+e(|φ|2−v2)=0 (2.52)

e

(D1+iD2)φ=0. (2.53)

Embora n˜ao tenham sido obtidas pelo m´etodo usual da equac¸˜ao de Euler-lagrange, qualquer soluc¸˜ao destas equac¸ ˜oes acopladas tamb´em resolve as equac¸ ˜oes de Euler-Lagrange. As soluc¸ ˜oes destas equac¸ ˜oes (2.52 e 2.53), al´em de descreverem v ´ortices n˜ao interagentes na teoria de supercondutores, por serem bem conhecidas, tˆem aplicac¸ ˜oes

em muitos ramos da f´ısica, da cosmologia ao modelo padr˜ao da f´ısica de part´ıculas.

2.4

Monopolos

O objeto de estudo desta sec¸˜ao, os monopolos, s˜ao classificados em dois tipos. O primeiro chama-se monopolo global, devido a transformac¸˜ao de gauge, pela qual a lagrangiana permanece invariante, ser global. O segundo tipo apresenta transformac¸˜ao de gauge local. O monopolo global ser´a estudado detalhadamente no cap´ıtulo 3.

A primeira formulac¸˜ao te ´orica significativa acerca dos monopolos, a saber,

2.4 Monopolos 28

Em 1974, ’t Hooft [22] e Polyakov [23] mostraram que monopolos magn´eticos podem surgir naturalmente a partir de uma teoria de gauge n˜ao abeliana com o seguinte padr˜ao da quebra espontˆanea de simetria: SU(2)_→U(1). Em seguida, estas ideias s˜ao

apresentadas de forma mais detalhada.

2.4.1

O Monopolo de Dirac

Seguindo o racioc´ınio original de Dirac, observa-se que as equac¸ ˜oes de Maxwell no v´acuo,

∇E=0, ∇ ×E=₋1

c

∂B

∂t,

∇B=0, ∇ ×B=1

c

∂E

∂t.

s˜ao sim´etricas mediante a transformac¸˜aoE→Be−B→E. Para que tal simetria fosse estabelecida no caso geral, na presenc¸a de cargas e correntes, ele prop ˆos uma construc¸˜ao te ´orica na qual existe uma carga magn´etica g, tal que, o campo magn´eticoBseja dado

por:

B=g r

r3. (2.54)

Portanto, o fluxo magn´etico (Φ_m) atrav´es de uma superf´ıcie fechada contendog´e ent˜ao:

Φ_m =

Z

S

(B.n)dS=

Z

S|

B|dS=4πr2B

Φ_m = 4πg. (2.55)

Onder ´e o raio da superf´ıcie limitando o volume contendo a carga magn´etica, en ´e o versor de orientac¸˜ao do elemento de ´area.

A func¸˜ao de onda Ψ(r)_≡Ψpara uma part´ıcula com carga el´etricae no campo de um monopolo, ´e expressa por:

Ψ =ψexp

−ie ¯

hcA.r

, (2.56)

ondeA ´e o potencial vetor, eψ ´e func¸˜ao de onda para o el´etron livre5. A (2.56) pode ser expressa como:

Ψ =_ψeiα (ondeα ´e uma fase, dada por α=₋ e

¯

hcA.r). (2.57)

A mudanc¸a total sofrida pela fase (∆_α) ao percorrer-se um ciclo fechado, com r e θ 5_{A equac¸˜ao de onda para o el´etron livre ´e:ψ=|ψ|exp}h_i

¯

h(p.x−Et) i

, a forma da (2.56) deve-se a mudanc¸a

p→p−eA

∆_α = e

¯

hc

I

A.dl= e

¯

hc

Z

S

(_{∇ ×}A).dS= e

¯

hc

Z

S

B.dS (2.58)

∆α = e

¯

hcΦ(r, θ). (2.59)

A figura (2.9) esquematiza a ´area onde se calcula o fluxoΦ(r, θ).

Figura 2.9: A regi˜ao cinza delimita a ´area do fluxoΦ(r, θ)

Ent˜ao, em θ=0 tem-se Φ(r, θ)=0, conforme o ciclo desce sobre a esfera,θ→πe

Φ(r, θ)_→4πg. Acontece que emθ→π, o ciclo reduz-se novamente a um ponto. Mas desde que o fluxo seja finito, A apresenta uma singularidade em θ=π. Como isto n˜ao depende der, qualquer esfera ter´a a mesma caracter´ıstica, por issoA ´e singular ao longo de toda parte negativa do eixoz6, nessa regi˜aoΨ ´e indeterminada.

A condic¸˜ao de quantizac¸˜ao de Dirac poder ser obtida exigindo-se que Ψ seja un´ıvoca, dos argumentos acima, tem-se que:

∆_α=2πn = e

¯

hc4πg eg = n

2hc¯ (comninteiro).

Retomando o sistema de unidades naturais (¯h=c=1), obt´em-se:

eg= n

2. (2.60)

Logo, a existˆencia de monopolos magn´eticos leva a quantizac¸˜ao da carga el´etrica, no entanto, o inverso n˜ao ´e necessariamente verdade. Por isso, isto n˜ao significa que de

6_{Isto chama-se corda (string) de Dirac, uma abordagem sobre monopolo magn´etico sem corda ´e dada}

2.4 Monopolos 30

fato monopolos magn´eticos existam. Em seguida, apresenta-se o monopolo de ’t Hooft e Polyakov, uma teoria cujo grupo de simetria da lagrangiana ´e mais amplo que o grupo da eletrodinˆamica de Maxwell.

2.4.2

Monopolo de ’t Hooft - Polyakov

Deseja-se aqui, estudar defeitos topol ´ogicos em (1+3) dimens ˜oes, uma temporal e 3 espaciais. O modelo capaz de fornecer soluc¸ ˜oes est´aticas n˜ao triviais e com energia finita, chama-se monopolo de ’t Hooft-Polyakov, proposto em 1974 [22, 23]. Este modelo

´e uma teoria n˜ao abeliana de gauge, e o grupo de simetria da lagrangiana ´e oSU(2). Por estas raz ˜oes, este modelo ´e mais complicado que os demais, no entanto, os m´etodos usados nesta sec¸˜ao s˜ao similares aos demais anteriores.

A lagrangiana ´e dada por:

L=₋1

4G

a

µνGaµν+ 1 2

DµφaDµφa

−1₄λ(φaφa−η2)2. (2.61)

Ondea´e um ´ındice interno e, varia de 1 a 3. Ent˜ao, express ˜oes da formaφaφaapresentam

uma soma de Einstein sobre o ´ındicea. Al´em disto, tˆem-se:

Ga_µν = ∂µAaν−∂νAaµ+gǫabcAbµAcν. (2.62) e a derivada covariante de gauge:

Dµφa=∂µφa+gǫabcAbµφc. (2.63) As constantesλ e gs˜ao positivas e ǫabc ´e o s´ımbolo de Levi-Civita. Observa-se que a

lagrangiana (2.61) ´e similar ao modelo abeliano de Higgs ( equac¸˜ao 2.31) mediante a comparac¸˜aoGa_µν→Fµν eAaµ →Aµ. Neste caso,Aaµ corresponde a um vetor no espac¸o interno. Embora esta lagrangiana (2.61) parec¸a complexa, ela ´e constru´ıda pra ser invariante mediante uma transformac¸˜ao de gauge local7.

As equac¸ ˜oes de campo s˜ao obtidas da equac¸˜ao de Euler-Lagrange de maneira usual.

Aplicando-a aos camposφa eAa_µ, obtˆem-se, respectivamente:

DµDµφa=−λ(φbφb−η2)φa (2.64)

7_{Ou seja, a o atuac¸˜ao do grupo SU(2) sob o campo φ}a_=(φ1_{, φ}2_{, φ}3_{) n˜ao altera a lagrangiana (2.61),}

DµGaµν=gǫabc

Dνφbφc. (2.65)

Restringindo-se a soluc¸ ˜oes est´aticas e comAa₀=0 para todoa, tˆem-se:

D_iDiφa=_−λ(φbφb−η2)φa (2.66)

DiGaij=gǫabc

Djφbφc. (2.67)

O ´ındices i e j s˜ao ´ındices puramente espaciais, n˜ao devendo ser confundido com o

´ındiceado espac¸o interno.

A Energia (E) pode ser calculada a partir do hamiltoniano8, fornecendo:

E=

Z 1 4G

a ijGaij+

1 2Diφ

a_Di_φa₊1

4λ(φ

a_φa_−η2₎2_d3_{x. (2.68)}

A energia torna-se m´ınima se as seguintes condic¸ ˜oes forem satisfeitas:

φaφa=_η2 Aa_i =0 Diφa=0. (2.69)

Portanto, conforme o campo tende ao infinito, estas condic¸ ˜oes devem ser obedecidas, a fim de que se tenha soluc¸ ˜oes fisicamente aceit´aveis. A condic¸˜aoφaφa=_η2, determina uma superf´ıcie esf´erica de raioηno espac¸o interno e, constitui a variedade do v´acuo (M) deste modelo. O mapeamento da variedade bidimensional assint ´otica do espac¸o f´ısico9( denota-se por _S) em _M pode pertencer a diversas classes topol ´ogicas, que na representac¸˜ao matem´atica ´e descrito comoπ2(M)=Z, onde Z ´e um n ´umero real,

que caracteriza o n ´umero de vezes queS”enrola-se” emM, conforme percorre-seM. Para tornar isto mais claro, pode-se considerar o caso em queZ_{=1, isto implica que} para cada direc¸˜ao no espac¸o f´ısico, tem-se uma direc¸˜ao bem determinada na superf´ıcie esf´erica do espac¸o interno φaφa= _η2. Sendo assim, assintoticamente o campo tem diferentes valores para diferentes orientac¸ ˜oes.

´E importante ressaltar, que mesmo que o gradiente deφa, comr_{→ ∞}, n˜ao seja nulo, isto n˜ao constituir´a um problema, desde que lim

r→∞Diφ

a_{=0. A sec¸˜ao 2.3 apresenta, com}

mais detalhes, uma abordagem similar para o caso do v ´ortice.

8_{O hamiltoniano pode ser calculado de maneira direta por: H=}P s

∂L

∂q˙sqs˙ − L, osq’s s˜ao os campos e

˙

q’s s˜ao as derivadas temporais.

9_{Esta variedade pode ser pensada como uma superf´ıcie esf´erica de raior→ ∞do espac¸o}

2.4 Monopolos 32

Pode-se definir uma corrente topol ´ogica10[25] dada por:

Kµ= 1

8πǫµνρσǫabc∂

ν_φˆa_∂ρ_φˆb_∂σ_φˆc_{. Onde, φˆ}a₌ φa

|φ|. (2.70)

Comoǫµνρσ ´e antissim´etrico, por definic¸˜ao:

∂µKµ=0. (2.71)

Isto significa que a corrente topol ´ogica ´e conservada. A carga topol ´ogica associada a

(2.70 ) ´e dada por:

Q =

Z

K0d3x (2.72)

Q = 1

8π Z

h

ǫijkǫabc∂iφˆa∂jφˆb∂kφˆc i

d3x

Q = 1

8π Z

h

ǫijkǫabc∂i( ˆφa∂jφˆb∂kφˆc) i

d3x

Q = 1

8π Z

S h

ǫijkǫabc( ˆφa∂jφˆb∂kφˆc) i

d2Si. (2.73)

Esta ´ultima integral ´e sobre S, o espac¸o f´ısico assint ´otico. S pode ser descrito pelos parˆametrosα1 eα2, que podem ser os ˆangulos azimutal e polar, por exemplo. Assim,

pode-se escrever [10, 26]:

∂iφˆa= ∂φˆa

∂αp

∂αp

∂xi

(2.74)

e

d2Si=

1

2ǫimnǫpq

∂xm

∂αp

∂xm

∂xqd

2_{α p,q=1,2. (2.75)}

Esta ´ultima express˜ao, relaciona o elemento de ´area em termos dexm eαq. Ao inserir a

(2.75) e (2.74) em (2.73), mostra-se que:

Q= 1

8π Z      ǫ abc_ǫ pqφˆa

∂φˆb

∂αp

∂φˆc

∂αq      d

2_{α. (2.76)}

Observe que o termo

ǫabcǫpqφˆa ∂φˆb

∂αp

∂φˆc

∂αqd

2_{α (2.77)}

corresponde a 2d2Sint_a , por comparac¸˜ao com (2.75). O sub´ındice ”int” indica que o elemento de ´area na (2.76) ´e com respeito ao espac¸o interno, ao contr´ario da (2.75).

10_{Esta corrente topol ´ogica n˜ao deve ser confundida com as cargas e correntes associadas ao teorema}

Q= 1

4π Z

ˆ

φad2Sint_a = 1

4π Z

d2Sint. (2.78)

Portanto, Q representa o n ´umero de vezes que a variedade do v´acuo M ´e enrolada conforme o espac¸o f´ısico assint ´otico ´e percorrido. De modo que pode-se fazer a seguinte identificac¸˜aoQ=_π2(_M).

Uma quest˜ao pertinente ´e: por que este modelo chama-se monopolo magn´etico? Como ele relaciona-se a eletrodinˆamica de Maxwell? Em primeiro lugar, deve-se

ter em mente que o grupo de simetria da eletrodinˆamica de Maxwell, o U(1), ´e um subgrupo deSU(2), o grupo de simetria do modelo (2.61). Portanto, espera-se que o eletromagnetismo j´a esteja incorporado no modelo (2.61). De fato isto acontece, ’t Hooft

apresentou [10] uma definic¸˜ao generalizada para o tensor eletromagn´eticoFµν, que ´e um invariante de gauge.

Fµν≡φˆaGaµν− 1

gφˆ

a_D

µφˆbDνφˆc. (2.79)

Recupera-se a eletrodinˆamica de Maxwell ao tomar-se um gauge particular em queφa aponta sempre para a mesma direc¸˜ao no espac¸o interno. Paraφa_=(0,0,1),F

µνtorna-se

Fµν=∂µA3ν−∂νA3µ .

Sabe-se, da eletrodinˆamica de Maxwell, que∂µF∗_µν=0. Onde

F∗_µν= 1

2ǫµνρσF

ρσ _(2.80)

´e o dual do tensor eletromagn´etico Fµν =∂µAν−∂νAµ. Ao contr´ario da teoria de Maxwell, o divergente do dual de (2.79) n˜ao ´e nulo. Pode-se mostrar que paraFµνdado por (2.79), tem-se:

∂νF∗_µν= 1

2ǫµνρσ∂

ν_Fρσ₌ 1

2gǫµνρσǫabc∂

ν_φˆa_∂ρ_φˆb_∂σ_φˆc_{. (2.81)}

Com aux´ılio da (2.70 ), obt´em-se:

1

2ǫµνρσ∂

ν_Fρσ₌ 4π

g Kµ. (2.82)

De modo que, tomando-seµ=0, tem-se: 1

2ǫ0νρσ∂

ν_Fρσ₌ 4π

g K0→

1 2ǫijk∂

i_Fjk₌ 4π

g K0, (2.83)

2.4 Monopolos 34

forma usual,Bi= 1₂ǫijkFjk, a (2.83 ) implica em: ∇.B= 4πK0

g . (2.84)

Onde K0

g ´e a densidade de carga magn´etica. A carga magn´etica total ´e ent˜ao dada por:

m=

Z

K0 g d

3_x= Q

g. (2.85)

OndeQ ´e a carga topol ´ogica, equac¸˜ao (2.78).

Conclui-se, portanto, que o modelo n˜ao abeliano do monopolo estudado nesta sec¸˜ao, ao contr´ario da teoria de Maxwell, j´a apresenta naturalmente monopolos magn´eticos. Como discutido brevemente no in´ıcio, isto j´a era esperado, j´a que o grupo de simetria

M

onopolo

G

lobal

O monopolo global encaixa-se em uma classe de defeitos topol ´ogicos conhecida como defeitos globais, cuja simetria da lagrangiana ´e global; em contraste `a aqueles

que acoplam-se a campos de gauge, cuja simetria da lagrangiana ´e local. Por n˜ao apre-sentarem campos de gauge, o principal m´etodo para detectar os efeitos do monopolo global ser´a gravitacional, via soluc¸˜ao das equac¸ ˜oes de Einstein para a m´etrica externa ao n ´ucleo do monopolo. Isto ser´a feito com base, sobre tudo, nos trabalhos de

Ma-noel Barriola e Alexander Vilenkin [5]. A assinatura da m´etrica adotada nos pr ´oximos cap´ıtulos ´e tipica da literatura no contexto da Relatividade Geral, (−,+,+,+).

3.1

Lagrangiana do Monopolo Global: Topologia e Equac¸ ˜oes

de Campo

A lagrangiana do monopolo global ´e dada por:

L=₋1

2(∂µφ

a_)(∂µ_φa₎₋1

4λ(φ

a_φa_−η2₎2_{, com λ >0 e η >0. (3.1)}

Onde o ´ındice a vai de 1 a 3 e, n˜ao deve ser confundido com os ´ındices de Lorentz,

das dimens ˜oes do espac¸o-tempo. O tripleto de campos escalaresφacomporta-se como um vetor no espac¸o interno1, de modo que,φa_φa_=(φ1₎2_+(φ2₎2_+(φ3₎2_{. Claramente, a}

lagrangiana (3.1) ´e invariante sob o grupo de simetria cont´ınuaSO(3) do espac¸o interno. Isto pode ser observado, notando-se que para um dadoφa, tal queφaφa=constante>0, uma rotac¸˜ao deφano espac¸o interno deixa a lagrangiana invariante. Em seguida, com aux´ılio da equac¸˜ao de campo, mostra-se que esta simetriaSO(3) ´e quebrada em U(1)

1_{Espac¸o ondeφ}a_=(φ1_{, φ}2_{, φ}3_{) comporta-se como um vetor no espac¸o tridimensional Euclidiano, no}

3.1 Lagrangiana do Monopolo Global: Topologia e Equac¸˜oes de Campo 36

pela variedade do v´acuo.

De maneira geral, as equac¸ ˜oes de campo paraφa_{podem ser obtidas da equac¸˜ao de}

Euler-Lagrange:

∂ν

"

∂L

∂(∂νφ)

#

−∂_∂φL =0. (3.2)

Os termos da (3.2) est˜ao explicitamente calculados abaixo,

∂L

∂φb =−

2 4λ(φ

a_φa_−η2₎₂∂φa

∂φbφ

a_=−λ(φa_φa_−η2_)φb_{, (3.3)}

∂L

∂(∂νφ)

!

= ₋1

2 "_∂(∂

µφa)

∂(∂νφb)

(∂µφa)+∂(∂

µ_φa₎

∂(∂νφb)

(∂µφa)

#

= ₋1

2[2δ ν

µδa_b(∂µφa)]=−∂νφb. (3.4) Sendo assim, ao substituir as equac¸ ˜oes (3.3) e (3.4) em (3.2), obt´em-se a equac¸˜ao de movimento:

∂ν∂νφb−λ(φaφa−η2)φb=0. (3.5) Qualquer tripleto de campos escalares constantes, satisfazendoφaφa=η2, al´em de satis-fazer a equac¸˜ao (3.5), corresponde a soluc¸˜ao de m´ınima energia. Sendo assim, o v´ınculo φaφa =_η2 define a variedade do v´acuo (_M). Escolhendo-se, por exemplo, o tripleto (0,0, η) e submetendo-o a uma rotac¸˜ao arbitr´aria no espac¸o interno, ele n˜ao permanece

invariante, muito embora conduza a um outro vetor da variedade do v´acuo. Agora, se ele rotacionar em torno de si mesmo (no caso, o eixoφ3) por um ˆangulo arbitr´ario, permanece invariante. Em outras palavras, quando o campo tende a variedade do v´acuo, a simetriaSO(3) ´e espontaneamente quebrada emU(1).

Sabe-se que para uma teoria suportar defeitos, ´e necess´ario que a topologia da

variedade do v´acuo seja correta. No caso do monopolo, entende-se que a variedade do v´acuo deve ser uma superf´ıcieS2n˜ao contra´ıvel. De fato, isto ´e claramente observ´avel na relac¸˜ao φaφa =_η2, ent˜ao, ao mapear-se a variedade do v´acuo na variedade bidi-mensional do espac¸o f´ısico assint ´otico, garante-se que o mapeamento n˜ao seja trivial,

matematicamente π2(M),I. Em suma, mostra-se que a lagrangiana (3.1) apresenta

3.2

Ansatz para Soluc¸˜ao da Equac¸˜ao de Campo

Havendo soluc¸˜ao, espera-se que a mais simples seja est´atica e esfericamente sim´etrica. O ansatz proposto em [5], para uma tal configurac¸˜ao de campo, ´e dado por:

φa=ηf(r)x

a

r , onde x

a_xa_=r2_{. (3.6)}

Deve-se enfatizar que esta simetria est´a relacionada ao espac¸o tempo e, n˜ao ao espac¸o interno.

O elemento de linha mais geral para a m´etrica est´atica com simetria esf´erica pode ser escrito como

ds2=₋M2(r)dt2+N2(r)dr2+r2(dθ2+sin2θdϕ2). (3.7) OndeM2(r) eN2(r) s˜ao func¸ ˜oes da coordenada radialr.

As componentes da conex˜ao m´etrica associadas a (3.7) s˜ao obtidas da express˜ao:

Γµ

αβ= 1 2g

µλ_(∂

αgλβ+∂βgλα−∂λgαβ), (3.8) de modo que, as componentes n˜ao nulas s˜ao:

Γ0

01 = M′

M, Γ 1 00=

MM′

N2 , Γ 1 11=

N′

N, (3.9)

Γ1

22=− r

N2, Γ 1 33=−

rsin2θ

N2 , Γ 2 12 =

1

r, (3.10)

Γ2₃₃=₋sinθcosθ, Γ3₁₃= 1

r, Γ 3

23=cotθ. (3.11)

Com aux´ılio da conex˜ao e da m´etrica, pode-se encontrar a equac¸˜ao para f(r). Para isto, ´e necess´ario substituir o ansatz (3.6) na equac¸˜ao de campo (3.5)2:

∇ν(∂νφb)−λ(φaφa−η2)φb=0.

Ao realizar-se a soma sobre o ´ındiceν, no primeiro termo, encontra-se:

∇ν(∂νφb)=g00∇0(∂0φb)+g11∇1(∂1φb)+g22∇2(∂2φb)+g33∇3(∂3φb). (3.12)

2_{A derivada∂}

ν→ ∇νdevido ao princ´ıpio de acoplamento m´ınimo [28], por estar-se no sistema de

3.2 Ansatz para Soluc¸˜ao da Equac¸˜ao de Campo 38

A express˜ao para φb _{em coordenadas esf´ericas, com b=1 , por meio da (3.6) d´a}

origem a:

φ1=_ηfsinθcosϕ, (3.13)

de forma que os elementos da (3.12) podem ser explicitamente calculados, resultando

em:

g00∇0(∂0φb) = g00[∂0(∂0φ1)−Γν₀₀(∂νφ1)]= M

′

MN2f′ηsinθcosϕ, (3.14) g11_∇1(∂1φb) = ηsinθcosϕ

f′′ N2−

N′f′ N3

!

, (3.15)

g22∇2(∂2φb) = −ηsinθcosϕ f r2−

f′ rN2

!

, (3.16)

g33_∇3(∂3φb) = ηsinθcosϕ f′ rN2−

f r2

!

. (3.17)

Onde, f′(r) corresponde a derivada de f(r) em relac¸˜ao ar. Ao substituir as express ˜oes (3.14 - 3.17) na (3.12) obtˆem-se que

∇µ(∂µ)=ηsinθcosϕ

"

f′′ N2+

2

rN2− N′ N3+

M′ MN3

!

f′₋2f r2

#

∇µ(∂µ)=ηsinθcosϕ

"

f′′ N2+

2

rN2+

1 2M2

M2 N2

!′!

f′−2f

r2

#

. (3.18)

O segundo termo da (3.5) ´e obtido lembrando-se que,

φaφa=_η2f2(x

a₎2 r2 =η

2_f2_.

Portanto,

λ(φaφa−η2)φ1=ληfsinθcosϕ(η2f2−η2). (3.19) Ao substituir a (3.19) e a (3.18) na (3.5), finalmente encontra-se a equac¸˜ao para f(r),

que ´e dada por:

f′′ N2+

" 2

rN2+

1 2M2

M2 N2

!′#

f′₋2f r2 −λη

2_f(f2_{−1)=0. (3.20)}

No espac¸o plano, as func¸ ˜oesM2(r) eN2(r) s˜ao iguais a 1, e ent˜ao a equac¸˜ao (3.20) pode ser escrita como:

d dr f

′₊₂f

r

!