Geometria Basica Aula7 Volume1

Aula 7 – C´

ırculos

Objetivos

• Apresentar as posi¸c˜oes relativas entre retas e c´ırculos.

• Apresentar as posi¸c˜oes relativas entre dois c´ırculos.

• Determinar a medida de um ˆangulo inscrito.

Introdu¸

c˜

ao

O c´ırculo ´e considerado por muitos como a forma geom´etrica plana mais perfeita poss´ıvel. Relacionados aos c´ırculos est˜ao grandes problemas da Geometria, como o da quadratura do c´ırculo e o da determina¸c˜ao do valor do n´umeroπ_.

Daremos, agora, a defini¸c˜ao formal de c´ırculo.

Defini¸c˜ao 18

C´ırculo ´e uma figura geom´etrica formada por todos os pontos do plano que est˜ao a uma mesma distˆancia de um ponto fixado no plano. O ponto fixado ´e chamado centro do c´ırculo, e a distˆancia de qualquer ponto do c´ırculo ao centro ´e chamada raio do c´ırculo. Tamb´em chamamos de raio a qualquer segmento que liga o centro a um ponto do c´ırculo. Veja a figura 112.

O c

Fig. 112: C´ırculo de centro O e raio c

Qualquer segmento ligando dois pontos de um c´ırculo ´e chamado de

corda. Uma corda que passa pelo centro ´e chamada de diˆametro.

A medida de um diˆametro ´e tamb´em chamada de diˆametro. Veja a figura 113. O A B C D

Fig. 113: Cordas de um c´ırculo.

Um c´ırculo divide o plano em duas regi˜oes: interior do c´ırculo e exterior do c´ırculo. Um ponto est´a no interior (ou dentro) de um c´ırculo de raio r

se a distˆancia desse ponto ao centro do c´ırculo for menor do que r_{. Se essa}

distˆancia for maior do quer_{, o ponto est´a noexterior (ou fora) do c´ırculo.}

Arcos e medida de arcos

O n´umeroπe a quadratura do c´ırculo

Oπ´e um n´umero com caracter´ısticas muito especiais. Uma delas ´e ser transcendente, ou seja, n˜ao ´e um n´umero alg´ebrico, pois n˜ao ´e raiz de nenhum polinˆomio com coeficientes racionais. A possibilidade de constru¸c˜ao com r´egua e compasso de um quadrado de ´area igual a de um c´ırculo dado ´e chamado de problema da quadratura do c´ırculo. A solu¸c˜ao desse problema dependia inteiramente de oπ_{ser ou} n˜ao alg´ebrico. O teorema de Lindemann provou ent˜ao a transcendˆencia doπ_{e que o} problema da quadratura do c´ırculo ´e imposs´ıvel pelas regras da Geometria grega. Portanto, a transcendˆencia doπimplica que n˜ao existe uma constru¸c˜ao com r´egua e compasso para construir um quadrado com ´area igual `a de um c´ırculo dado.

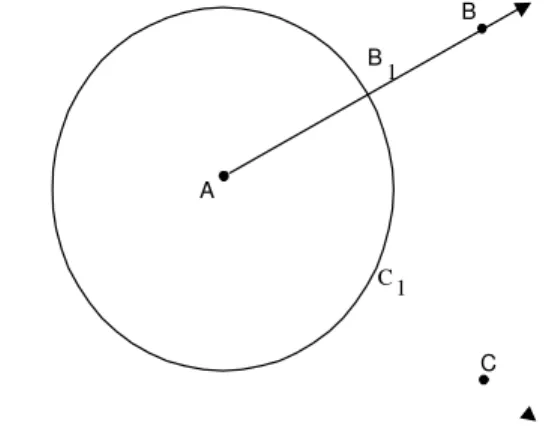
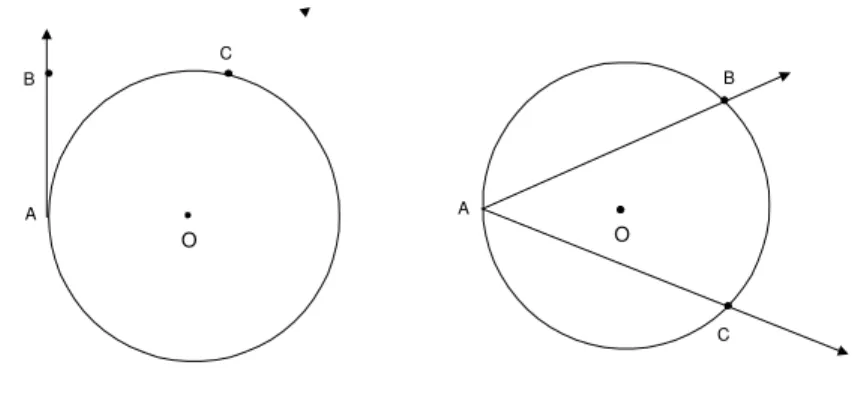
Considere um ˆangulo BACˆ _{e, com centro em} A_{, trace um c´ırculo de}

raio qualquer, como na figura 114.

A B C B 1 C 1

Fig. 114: O ˆanguloBACˆ _{divide o c´ırculo em dois arcos.}

Esse c´ırculo intersecta os lados de BACˆ _{em pontos} B_{1 e} C_{1. O ˆangulo}

ˆ

BAC _{divide o c´ırculo em dois arcos. Como denotar cada um desses arcos?}

Note que os dois tˆem como extremidade os mesmos pontosB_{1 e}C_{1. Quando}

houver d´uvida, consideraremos dois outros pontos,X _eY_{, um em cada arco,}

e usaremos a nota¸c˜ao B

⌢

⌢

para designar o arco que cont´emY _{(veja a figura 115).}

A

B

C B

1

C₁

X Y

Fig. 115: Arcos determinados pelo ˆangulo ˆA_.

Vocˆe sabia que...

Carl Louis Ferdinand von Lindemann

1852-1939 d.C. Alemanha.

Lindemann foi o primeiro a provar queπ_´e

transcendental. Naquela ´

epoca j´a havia sido provado que o n´umeroe_´e

transcendental. Usando m´etodos similares aos usados para o n´umeroe, Lindemann provou queπ´e

transcendental. Consulte:

http://www-groups.dcs. st-nd.ac.uk/~history/ Mathematicians/Lindemann. html

QuandoBACˆ _{mede 180}o

, dizemos que o arcoB

⌢

⌢

assim determinado ´e umsemic´ırculo. Melhor dizendo, cada um dos arcos de-terminados por uma reta que corta o c´ırculo passando pelo centro ´e um semic´ırculo. A medida de um semic´ırculo, por defini¸c˜ao, ´e 180o

e de um c´ırculo inteiro (de raio qualquer) ´e 360o

. ´E claro que essa maneira de medir n˜ao d´a o “comprimento”do c´ırculo (que certamente depende do tamanho do raio, e que est´a relacionado com o n´umeroπ _{que mencionamos anteriormente}

- para entender melhor, veja a figura 116).

A

C

B _B

1 C 1

Y X

180o

Fig. 116: Medida em graus de um c´ırculo: 360o .

Definiremos, a seguir, a medida de um arco qualquer.

Defini¸c˜ao 19

Dado um ˆangulo agudo BACˆ _{e um c´ırculo centrado em} A_{, a medida do}

menor arco determinado por BACˆ _{´e a mesma medida de} BACˆ _{e a medida}

do maior arco determinado por BACˆ _{´e 360}o₋BACˆ _.

Usaremos a mesma nota¸c˜ao para designar o arco e a sua medida. Por

exemplo, chamaremos a medida do arco B

⌢

⌢

Posi¸

c˜

oes relativas entre retas e c´ırculos

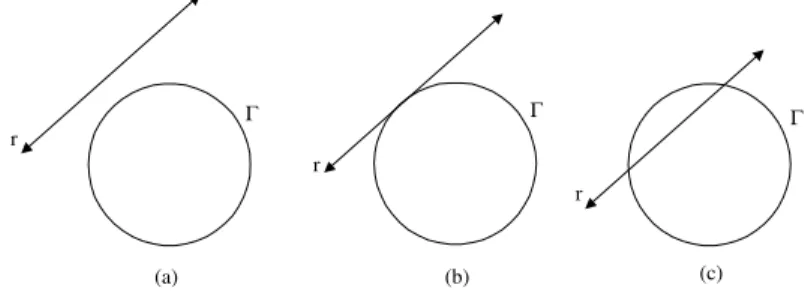
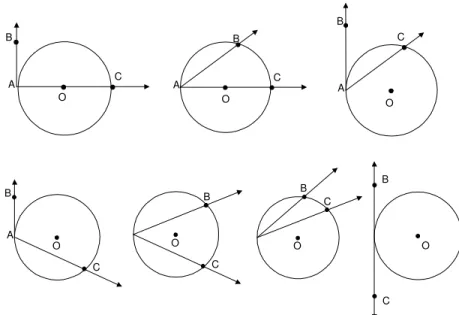
Dados uma retar _{e um c´ırculo Γ no plano, existem trˆes possibilidades:} r _{n˜ao intersecta Γ (} r _{´e exterior a Γ),} r _{intersecta Γ em dois pontos (}r _´e secante a Γ) our _{intersecta Γ em apenas um ponto (}r _{´etangentea Γ). Veja}

essas possibilidades na figura 117.

r (a) r (b) r (c)

Γ Γ _Γ

Fig. 117: a) Reta exterior. b) Reta tangente. c)Reta secante.

Vocˆe sabia que...

Hipparkhus (ou Hiparco) nasceu em Nic´eia, na Bit´ınia, viveu em Alexandria, mas trabalhou sobretudo em Rodes, entre 161 e 126 a.C. Destacou-se pelo m´etodo e rigor de suas observa¸c˜oes. Hipparkhus foi um dos cientistas mais representativos da ´epoca alexandrina. Como os babilˆonios, ele tamb´em acreditava que a melhor base para realizar contagens era a base 60. Os babilˆonios n˜ao haviam escolhido a base 60 por acaso. O n´umero 60 tem muitos divisores e pode ser facilmente decomposto num produto de fatores, o que facilita muito os c´alculos, principalmente as divis˜oes. Consulte:

http://www-groups.dcs. st-and.ac.uk/~history/ Mathematicians/ Hipparchus.html

Considere agora um c´ırculo Γ de centro no ponto O_{, um ponto} A_{∈ Γ}

e o segmento OA _{que liga o centro do c´ırculo ao ponto} A_{. Seja} r _{a reta}

que passa porA_{e ´e perpendicular ao segmento}OA_{(veja figura 118). Vamos}

mostrar a seguir quer_{´e tangente ao c´ırculo Γ. De fato, se tomarmos qualquer}

outro pontoB _emr_{e considerarmos o triˆangulo}OAB_{, veremos que o ˆangulo} BAOˆ _{, que mede 90}o

, ´e o seu maior ˆangulo. Como o lado oposto a ele ´eOB_,

esse segmento ´e maior que OA_{. Como a medida de} OA _{´e o raio do c´ırculo,}

o ponto B _{est´a fora de Γ. Mostramos ent˜ao que um ponto de}r _{que n˜ao seja} A _{est´a fora de Γ, ou seja, que} A _{´e o ´unico ponto na interse¸c˜ao de} r _{e Γ.}

Portantor _{´e tangente a Γ.}

B A

O r

Fig. 118: Reta que passa porA_{e ´e perpendicular a}OA_.

Qualquer reta que passe por A _{diferente de} r _{intersecta Γ em dois}

pontos. Embora esse fato seja bastante intuitivo, ele necessita de uma prova. No Apˆendice apresentamos uma prova deste fato. Podemos ent˜ao afirmar que uma reta passando porA _{´e tangente a Γ se, e somente se, ´e perpendicular a} OA_{. Destacamos este resultado logo a seguir.}

• Toda reta tangente a um c´ırculo ´e perpendicular ao raio no ponto de tangˆencia.

• Toda reta perpendicular a um raio em sua extremidade ´e tan-gente ao c´ırculo.

Trataremos, agora, das posi¸c˜oes relativas entre c´ırculos.

Posi¸

c˜

oes relativas entre c´ırculos

Dados dois c´ırculos, temos as seguintes possibilidades: os dois c´ırculos n˜ao se intersectam, os dois c´ırculos se intersectam em um ponto ou os dois c´ırculos se intersectam em dois pontos. Por´em, cada um desses casos pode ser subdividido, como veremos a seguir.

C´ırculos que n˜ao se intersectam

Para o caso em que os c´ırculos n˜ao se intersectam, h´a duas possibilida-des: cada c´ırculo est´a contido no exterior do outro (veja figura 119) ou um dos c´ırculos est´a contido no interior do outro (veja figura 120).

O O'

Γ

Γ 1

2

Fig. 119: C´ırculo exterior a outro c´ırculo.

O O'

Γ

Γ

1

2

Fig. 120: C´ırculo interior a outro c´ırculo.

C´ırculos secantes

Dizemos que dois c´ırculos s˜ao secantes quando eles se intersectam em dois pontos (veja figura 121).

O O' Γ

Γ

1

2 A

B

Fig. 121: C´ırculos secantes.

Nesse caso, prova-se que a reta que liga os dois centros O _e O′ _{´e a}

mediatriz do segmento determinado pelos pontos de interse¸c˜ao dos c´ırculos.

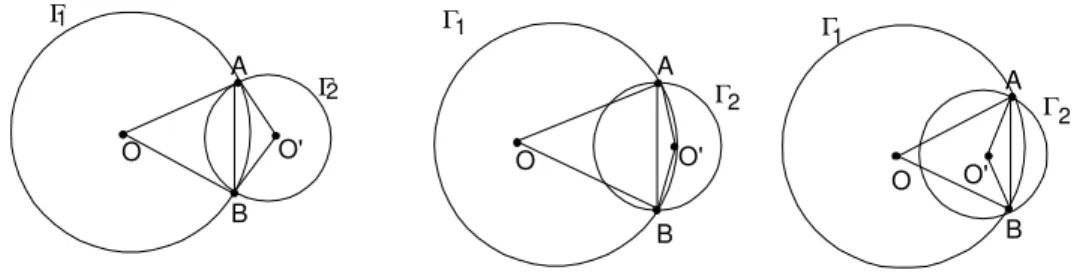
Com efeito, tra¸cando-se os segmentos OA_, OB_, O′A_, O′B _e AB_,

for-mamos os triˆangulos is´oscelesOAB _eO′AB_{, ambos de base} AB_{(veja figura}

122). Mas sabemos do exerc´ıcio 15 da aula 6 que num triˆangulo is´osceles a mediatriz da base passa pelo v´ertice oposto. Assim, a mediatriz deAB_passa

porO _{e por} O′_{, ou seja, a reta}←OO−→′ _{´e mediatriz de}AB_.

O O'

Γ

Γ

1

2 A

B

O O'

Γ

Γ

1

2 A

B

O O'

Γ

Γ

1

2 A

B

Fig. 122: A reta contendoO_eO′_{´e mediatriz de}AB_.

C´ırculos tangentes

Dizemos que dois c´ırculos s˜ao tangentes quando eles se intersectam em um ponto.

Para c´ırculos tangentes temos dois casos a considerar: c´ırculos tangen-tes exteriormente e c´ırculos tangentangen-tes interiormente.

No primeiro caso, os dois c´ırculos intersectam-se em um ponto e todos os outros pontos de cada um deles est´a no exterior do outro (veja figura 123).

O O'

Γ

Γ

1

2

Fig. 123: C´ırculos tangentes exteriormente.

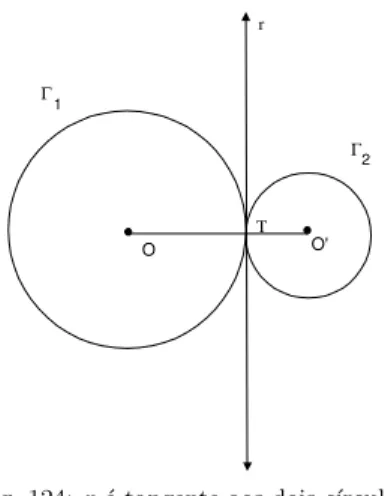
Nesse caso, o ponto de encontro pertence ao segmento OO′ _{e a reta}

perpendicular `a reta ←OO−→′ _{no ponto de encontro ´e tangente aos dois c´ırculos}

(veja o exerc´ıcio 7). O ponto de encontro ´e chamado de ponto de tangˆencia. Veja a figura 124.

O O'

Γ

Γ

1

2

r

T

Fig. 124: r_{´e tangente aos dois c´ırculos.}

No caso de c´ırculos tangentes interiormente, os dois c´ırculos intersectam-se em um ponto e todos os outros pontos de um deles est´a no interior do outro (veja a figura 125).

O Γ

Γ

1

2

O'

Fig. 125: C´ırculos tangentes interiormente.

Nesse caso,O_,O′ _{e o ponto de encontro s˜ao colineares e a reta tangente}

a um dos c´ırculos no ponto de encontro ´e tamb´em tangente ao outro (veja o exerc´ıcio 8). O ponto de encontro ´e chamado ponto de tangˆencia (veja a figura 126).

O Γ

Γ

1

2

O'

r

T

Fig. 126: r_{´e tangente aos dois c´ırculos.}

ˆ

Angulos centrais e ˆ

angulos inscritos

Vamos agora ver algumas defini¸c˜oes de ˆangulos relacionadas a c´ırculos.

Defini¸c˜ao 20 (ˆAngulo central)

Um ˆangulo central de um c´ırculo ´e um ˆangulo com v´ertice no centro do c´ırculo.

Defini¸c˜ao 21 (ˆAngulo inscrito)

Um ˆangulo inscrito ´e um ˆangulo com v´ertice sobre o c´ırculo e cujos lados s˜ao semi-retas tangentes ou secantes ao c´ırculo (veja a figura 127).

O A B C O A B C

Fig. 127: ˆAngulos inscritos.

Dado um ˆangulo inscritoBACˆ _{de um c´ırculo Γ, o arco de c´ırculo contido}

na uni˜ao do interior com os lados deBACˆ _{´e chamado arcosubentendido por} BACˆ _{. Diz-se tamb´em que} BACˆ _{subentende tal arco (veja figura 128).}

O

A

B

C D

Fig. 128:

⌢

Vocˆe sabia que...

Erat´ostenes

276-194 a.C. Cirene, Gr´ecia.

Medida do ˆ

angulo inscrito

Podemos agora determinar a medida de um ˆangulo inscrito atrav´es da seguinte proposi¸c˜ao:

Proposi¸c˜ao 15

A medida de um ˆangulo inscrito ´e a metade da medida do arco que ele subentende.

Prova:

Seja BACˆ _{um ˆangulo inscrito em um c´ırculo Γ centrado em} O_.

Divi-diremos a prova em v´arios casos, dados pela figura 129. Faremos a prova de alguns casos e deixaremos os demais como exerc´ıcio.

A B

C

A

B

C

O O

A B

C

O

A B

C O

C O

B _C

O B

C O B

Fig. 129: Diversas configura¸c˜oes de ˆangulos inscritos.

Caso 1: Um dos lados do ˆangulo BACˆ _{´e tangente ao c´ırculo e} o outro passa pelo centro.

Suponha que −→AB _{seja o lado tangente e} −→AC _{o lado que passa por} O_.

Nesse caso j´a vimos que BACˆ _{mede 90}o

. Como o arco subentendido por

BACˆ _{´e um semic´ırculo (mede 180}o

), n˜ao h´a o que provar.

Caso 2: Os dois lados de BACˆ _{s˜ao secantes ao c´ırculo e um} deles passa pelo centro.

Suponha que −→AC _{seja o lado que passa por} O _{e trace o segmento} BO_,

como na figura 130.

O

A

B

C

Fig. 130: Caso 2.

Sabemos que BAOˆ ₊ABOˆ ₊AOBˆ _{= 180}o

. Assim,

BAOˆ ₊ABOˆ _{= 180}o₋AOBˆ ₌BOCˆ

Como BOCˆ _{´e um ˆangulo central, sua medida ´e a mesma do arco que}

ele subentende. Como o triˆanguloOAB _{´e is´osceles com base}AB _(poisAO_e BO _{s˜ao raios), temos que} BAOˆ ₌ABOˆ _{, e, portanto,} BACˆ _{mede a metade}

do arco que ele subentende.

Caso 3: Um dos lados de BACˆ _{´e tangente ao c´ırculo e o ponto} O _{est´a fora de} BACˆ _.

Suponha que −→AB _{seja o lado tangente e trace a semi-reta} −→AO_{. Seja} D

o ponto em que essa semi-reta intersecta Γ e escolha um pontoX _{em Γ que}

esteja no interior de DACˆ _{(figura 131).}

O

A

C

D

X

B

Fig. 131: Caso 3.

Pelo caso 1, BADˆ _{= 90}o

. Pelo caso 2, CADˆ ₌ m(

⌢

2 . Da´ı, como

ˆ

BAC ₌BADˆ ₋CADˆ _{, temos}

ˆ

BAC _{= 90}o₋ m(

⌢

2 =

m₍ACD

⌢

⌢

2 .

Da´ı conclu´ımos que a medida de BACˆ _{´e a metade da medida do arco}

que ele subentende.

Caso 4: Um dos lados de BACˆ _{´e tangente ao c´ırculo e o ponto} O _{pertence ao interior de} BACˆ _.

Suponha que −→AB _{seja o lado tangente e trace a semi-reta} −→AO_{. Chame}

deD _{ao outro ponto onde} −→AO _{intersecta Γ (figura 132).}

O

A

C D

X

B

Y

Fig. 132: Caso 4.

Segue dos casos 1 e 2 desta demonstra¸c˜ao que BADˆ _{= 90}o

e DACˆ ₌

m₍DX C

⌢

2 , onde X ´e um ponto de Γ no interior do ˆanguloDACˆ .

Logo,

BACˆ ₌ BADˆ ₊DACˆ

= 90o+m(DX C

⌢

2

= m(AY D

⌢

2 +

m₍DX C

⌢

2

= m(ADC

⌢

2 .

Os dois pr´oximos casos tˆem demonstra¸c˜ao muito parecida com a deste caso: em ambos deve ser tra¸cada a semi-reta −→AO_{. Vamos deixar as}

de-monstra¸c˜oes como exerc´ıcio. Procure usar os casos anteriores para prov´a-los. Abaixo seguem os enunciados.

Caso 5: Os dois lados de BACˆ _{s˜ao secantes e o ponto} O _est´a no interior de BACˆ _{(figura 129).}

Caso 6: Os dois lados de BACˆ _{s˜ao secantes e o ponto} O _est´a no exterior de BACˆ _{(figura 129).}

Caso 7: Os dois lados de BACˆ _{s˜ao tangentes a Γ.}

Nesse caso, BACˆ _{´e um ˆangulo raso (180}o

) e o arco subentendido por

BACˆ _{´e a circunferˆencia inteira (360}0_{). Veja a figura 129.}

Resumo

Nesta aula vocˆe aprendeu...

• Quais as posi¸c˜oes relativas entre retas e c´ırculos.

• Quais as posi¸c˜oes relativas entre dois c´ırculos.

• Que uma reta ´e tangente a um c´ırculo em um ponto se, e somente se, ela ´e perpendicular ao raio que passa por esse ponto.

• Qual a medida de um ˆangulo inscrito.

Exerc´ıcios

1. Fa¸ca as provas dos casos 5 e 6 da proposi¸c˜ao 15.

2. Na figura 156, o arco AX D

⌢

e o arco BY C

⌢

. De-termine a medida do ˆangulo ˆE_.

X

C B

A

D Y

E

Fig. 133: Exerc´ıcio 2.

3. Na figura 157, o arco BX D

⌢

e o arco AY C

⌢

. Deter-mine a medida do ˆangulo BEDˆ _.

X B C

A

D Y

E

Fig. 134: Exerc´ıcio 3.

4. Determine o valor do ˆangulo ˆA _{na figura 135, sabendo que} AB _´e

tan-gente ao c´ırculo.

B

A

C

D

90 130o

o

Fig. 135: Exerc´ıcio 4.

5. Determine os valores dos ˆangulos ˆA _{e ˆ}B _{da figura 136.}

B A

C D 60

o

70o

Fig. 136: Exerc´ıcio 5.

6. Na figura 158, O_{´e o centro do c´ırculo,} AB_,AC _eP R_{s˜ao tangentes ao}

c´ırculo e ˆA_{= 28}o_{. Determine} P ORˆ _.

B

C O

P

Q

R

A

Fig. 137: Exerc´ıcio 6.

7. Sejam Γ1 e Γ2 c´ırculos tangentes exteriormente em um ponto T. Sejam

O_{o centro de Γ1 e}O′_{o centro de Γ}

2. Prove queT pertence ao segmento

OO′ _{e que a reta perpendicular a}OO′_emT _{´e tangente aos dois c´ırculos.}

8. Sejam Γ1 e Γ2 c´ırculos tangentes interiormente em um ponto T. Sejam

O_{o centro de Γ1 e}O′ _{o centro de Γ}

2. Prove queO,O′ eT s˜ao colineares

e que a reta tangente a Γ1 em T ´e tamb´em tangente a Γ2.

9. SejaAB _{uma corda (que n˜ao ´e um diˆametro) de um c´ırculo. Prove que}

a mediatriz de AB _{passa pelo centro do c´ırculo.}

10. Sejam AB _{uma corda de um c´ırculo centrado em} O _e A′_B′ _{uma corda}

de um c´ırculo centrado emO′_{. Se os dois c´ırculos tˆem o mesmo raio e}

AB_≡ A′_B′_{, prove que os ˆangulos centrais AOB}ˆ _{e A}′_Oˆ′B′ _s˜ao

congru-entes.

11. Sejam Γ um c´ırculo er_{uma reta. Seja Γ}′ _{a figura formada pelos reflexos}

de todos os pontos de Γ em rela¸c˜ao ar_{. Prove que Γ}′ _{´e um c´ırculo.}

12. (Desafio) SejaAB _{um segmento e}r_{uma reta paralela `a reta} ←AB→_{, como}

na figura 138.

B C

A

Fig. 138: Exerc´ıcio 12.

Determine o pontoC _∈r_{para que o ˆangulo}ACBˆ _{seja o maior poss´ıvel.}

Apˆ

endice: Para saber mais...

Nos argumentos abaixo, vocˆe encontra uma prova do seguinte fato: “Se uma reta r _{corta um c´ırculo de centro} O _{no ponto} A_{, e} r _{n˜ao ´e}

perpendi-cular ao segmentoOA_ent˜aor_{corta o c´ırculo tamb´em em um outro ponto}C_”.

Seja OA _{um segmento e seja}−→AB _{uma semi-reta tal que} OABˆ _{seja um}

ˆangulo agudo (figura 139). Mostre que existe um ponto C ₆₌ A _em −→AB _tal

queOA_≡OC_.

O A

B

Fig. 139:

Como conseq¨uˆencia, se A _{´e um ponto de um c´ırculo Γ centrado em} O

er _{for qualquer reta que passe por} A _{e n˜ao seja perpendicular a} ←OA→_{, ent˜ao} r _{corta o c´ırculo em dois pontos (figura 140).}

A C

O

r

A

C O

r

Fig. 140: