2.17 – EXERCÍCIO – pg. 53 - CalA_2_17.pdf

2.17 – EXERCÍCIO – pg. 53

1. Construir os gráficos das funções lineares. Dar o domínio e o conjunto imagem. a) y =kx, se k =0,1,2,12,−2.

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x

k=0

( )

( ) { }

0

Im =

=

f IR f D

k=1

( )

( )

f IR

IR f D

= =

Im

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=2x

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=1/2x

k=2

( )

( )

f IR

IR f D

= =

Im

k=1/2

( )

( )

f IR

IR f D

= =

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=-x

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=-2x

k=-1

( )

( )

f IR

IR f D

= =

Im

k=-2

( )

( )

f IR

IR f D

= =

Im

b) y=x+b, se b=0,1,−1.

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x+1

b=0

( )

( )

f IR

IR f D

= =

Im

b=1

( )

( )

f IR

IR f D

= =

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x

y=x-1

b=-1

( )

( )

f IR

IR f D

= =

Im

c) y=1,5x+2

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=1,5x+2

( )

( )

f IR

IR f D

= =

Im

2. Construir o gráfico das funções quadráticas. Dar o domínio e o conjunto

imagem.

a) 2

ax

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x2

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=1/2x2

a=1

( )

( )

=

[

+∞

)

=

, 0

Im f

IR f D

a=1/2

( )

( )

=

[

+∞

)

=

, 0

Im f

IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=-2x2

a=-2

( )

( ) (

,0

]

Im = −∞

=

f IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x

y=x2

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x

y=x2₊₁

c=0

( )

( )

=

[

+∞

)

=

, 0

Im f

IR f D

c=1

( )

( )

=

[

+∞

)

=

, 1

Im f

IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x2_+1/2

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=x2_-3

c=1/2

( )

( )

=

[

+∞

)

=

, 2 1

Im f

IR f D

c=-3

( )

( )

=

[

− +∞

)

=

, 3

Im f

IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=(x-1)2

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=1+(x-1)2

0

=

o

y

( )

( )

=

[

+∞

)

=

, 0

Im f

IR f D

1

=

o

y

( )

( )

=

[

+∞

)

=

, 1

Im f

IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3

x y

y=-1+(x-1)2

1

− =

o

y

( )

( )

=

[

− +∞

)

=

, 1

Im f

IR f D

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3 4 5 6 7 8 9

x

y=x2_-2x+5

5 2 2

+ −

= x x

y

( )

( )

=

[

+∞

)

=

, 4

Im f

IR f D

3. Construir os gráficos das funções polinomiais. Dar o domínio e o conjunto imagem.

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3 4 5 6 7

x y

y=2+(x-1)3

-3 -2 -1 1 2 3

-3 -2 -1 1 2 3 4 5 6 7

x y

y=x4

a) y =2+

(

x−1

)

3

( )

( ) { }

f IR IR f D

= =

Im

b) y =x4

( )

( )

=

[

+∞

)

=

, 0

Im f

-3 -2 -1 1 2 3

-5 -4 -3 -2 -1 1 2 3 4 5

x y

y=2x2_-4

c) 2 2 4

− = x y

( )

( )

=

[

− +∞

)

=

, 4

Im f

IR f D

4. Construir os gráficos das funções racionais. Dar o domínio e o conjunto imagem.

-3 -2 -1 1 2 3

-7 -6 -5 -4 -3 -2 -1 1 2 3

x y

( ₁)2 2

− − =

x y

-3 -2 -1 1 2 3

-4 -3 -2 -1 1 2 3 4

x y

x y=1

a)

(

)

2

1 2

− − =

x y

( )

{ }

( ) (

,0

)

Im

1

∞ − =

− =

f IR f D

b)

x y =1

( )

{ }

( )

{ }

0

Im

0

− =

− =

IR f

-8 -7 -6 -5 -4 -3 -2 -1 1 2 3

-4 -3 -2 -1 1 2 3 4

x

4 1

+ − =

x x y

c)

4 1

+ − =

x x y

( )

{ }

( )

{ }

1

Im

4

− =

− − =

IR f

IR f D

5. A função f

( )

x é do 1° grau. Escreva a função se f

( )

−1 =2 e f

( )

2 =3.

( )

( )

( )

( )

2 2 3

2 1

1

= + =

= + − = −

+ =

b a f

b a

f

b ax x f

= +

= + −

3 2

2

b a

b a

ou

3 7 7

3 3 2

4 2 2

= ∴ =

= +

= + −

b b

b a

b a

3 1 3

6 7 2 3 7

2

= − = − =

− =

a b a

6. Determinar quais das seguintes funções são pares ou ímpares.

a) Par

( )

(

)

(

)

(

)

( )

x f x x x x x f x x x f = + − = + − − − = − + − = 1 2 3 1 2 3 1 2 3 2 4 2 4 2 4

b) Ímpar

( )

( )

(

)

(

)

(

x x

)

f

( )

x x x x x x f x x x f − = + − = + − = − − − = − = 2 5 2 5 2 5 2 5 3 3 3 3

c) Não é par nem ímpar

( )

(

) (

)

(

)

2 2 2 2 2 2 2 2 2 + − = + − + − = − + + = s s s s s f s s s f d) Par

( )

( ) ( )

( )

t f t t t f t t f = − = − − = − − = 4 4 4 6 6 6 e) Par

( )

(

)

( )

x f x x x f x x f = = − = − =

f) Ímpar

( )

(

)

(

)

(

)

(

)

(

)

_{( )}

x f y y y y y y y y y y f y y y y f − = + − − = + + − = + − − − − = − + − = 1 1 1 1 2 3 2 3 2 3 2 3

( )

(

)

(

)

1 1 1 1 1 1 1 1 − + = + − + − = + − − − = − + − = x x x x x x x f x x x f h) Par

( )

(

)

(

)

(

( )

)

(

)

_{( )}

x f a a a a x f a a x f x x x x x x = + = + = − + = − − − − − 2 1 2 1 2 1

i) Ímpar

( )

(

)

(

)

(

)

(

)

(

)

(

)

[

]

( )

x f x x x x x x x x x x x f x x x f − = − + − = − − + − = + − − = + − = − − − = − − + = 1 1 ln 1 ln 1 ln 1 ln 1 ln 1 1 ln 1 1 ln 1 1 ln

j) Ímpar

( )

(

)

(

)

(

)

(

)

(

)

(

2

)

2 2 2 2 2 1 lg 1 lg 1 lg 1 1 lg 1 lg 1 lg 1 lg x x x x x x x x x x x f x x x f + + − = + + − = + + = + + − = − + + − = − + + =

7. Demonstre que se f e g são funções ímpares, então

(

f +g

)

e

(

f −g

)

são também funções ímpares.

f é ímpar

( )

( )

x f

(

x

)

f

def

− − =

⇔ (1)

g é ímpar

( )

( )

x g

(

x

)

g

def

− − =

⇔ (2)

(

) ( )

( )

( )

(

)

(

)

(

)

(

)

[

]

(

) (

)

[

f g x

]

x g x f x g x f x g x f x g f − + − = − − − − = − − − − = + = +

Portanto,

(

f + é g

)

ímpar.

(

) ( )

( )

( )

(

)

[

(

)

]

(

)

(

)

(

)

(

)

[

]

(

) (

)

[

f g x

]

x g x f x g x f x g x f x g x f x g f − − − = − − − − = − + − − = − − − − − = − = −

Portanto,

(

f − é g

)

ímpar.

8. Demonstre que se f e g são funções ímpares, então f ⋅g e f g são funções

pares.

f é ímpar ( )

( )

x f

(

x

)

f

def

− − =

⇔ (1)

g é ímpar ( )

( )

x g

(

x

)

g

def

− − =

⇔ (2)

De (1) e (2) escrevemos

(

) ( )

( ) ( )

(

)

[

(

)

]

(

) (

)

(

x

)

g f x g x f x g x f x g x f x g f − ⋅ = − ⋅ − = − − ⋅ − − = ⋅ = ⋅

Portanto, f ⋅g é par.

(

) ( )

( )

( )

(

)

(

)

(

)

(

)

(

f g

) (

x

)

x g x f x g x f x g x f x g f − = − − = − − − − = =

9. Mostre que a função

[

f

( )

x + f

(

−x

)

]

2 1

é par e que a função

[

f

( )

x − f

(

−x

)

]

2 1

é

ímpar.

Seja g x =

[

f

( )

x + f

(

−x

)

]

2 1 )

( . Temos,

( )

[

( )

(

)

]

(

)

( )

[

]

(

x

)

g

x f x f

x f x f x

g

− =

+ − =

− + =

2 1 2 1

Portanto, g(x)é par.

Seja h

( )

x =

[

f

( )

x − f

(

−x

)

]

2

1

. Temos,

(

)

[

(

)

( )

]

( )

(

)

[

]

( )

x h

x f x f

x f x f x

h

− =

− − −

=

− − =

−

2 1 2 1

Portanto, h(x)é ímpar.

10.Demonstre que qualquer função f :IR→IR pode ser expressa como a soma de uma função par com uma função ímpar.

Queremos mostrar que se h

( )

x é uma função qualquer podemos escrever:

( )

x f

( )

x g

( )

x

h = + , sendo que f

( )

x é par e g é

( )

x ímpar. Usando o exercício anterior podemos fazer

( )

x

[

h

( )

x h

(

x

)

]

f = + −

2 1

e g

( )

x =

[

h

( )

x −h

(

−x

)

]

2

1 De fato

( )

x g

( )

x h

( )

x h

(

x

)

h

( )

x h

(

x

)

h

( )

x

f + = + − + − − =

2 1 2

1 2

1 2

11.Expresse as funções seguintes como a soma de uma função par e uma função ímpar.

a)

( )

2 2

+ = x x f

Basta fazer f(x)= f1(x)+ f2(x) com:

( )

[

(

)

]

[

]

2 4 2 2 1 2 2 2 1 2 2 2 2 1 + = + = + − + + = x x x x x f

Temos f₁(x) par.

( )

[

(

)

]

[

]

0 2 2 2 1 2 2 2 1 2 2 2 2 2 = − − + = − − − + = x x x x x f

Temos f₂(x)ímpar.

b) f

( )

x =x3 −1

Basta fazer f(x)= f₁(x)+ f₂(x) com:

( )

[

(

)

]

[

]

(

2

)

1

2 1 1 1 2 1 1 1 2 1 3 3 3 3 1 − = − = − − − = − − + − = x x x x x f

Temos f₁(x) par.

( )

[

(

)

]

[

]

3 3 3 3 3 3 2 2 2 1 1 1 2 1 1 1 2 1 x x x x x x x f = = + + − = + − − − =

Temos f₂(x)ímpar

c)

( )

1 1 + − = x x x f

( )

(

) (

) (

) (

)

(

) (

)

(

) (

)

(

)

(

)

1

1 1 2 2 2 1 1 1 2 1 2 2 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 2 2 2 2 2 2 2 1 − + = − − − − = − − + + − + − − = − + + − − + − − = + − − − + + − = x x x x x x x x x x x x x x x x x x x x f

Temos f₁(x) par.

( )

(

)

(

)

1 2 1 4 2 1 1 1 2 1 2 2 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 2 2 2 2 2 2 2 2 2 − − = − − = − − − − + − = − + − − = − + − + − = + − − − − + − = x x x x x x x x x x x x x x x x x x x x x f

Temos f₂(x)ímpar.

d) f

( )

x = x + x−1

( )

[

]

[

]

[

2 1 1

]

2 1 1 1 2 1 1 1 2 1 + + − + = − − + + − + = − − + − + − + = x x x x x x x x x x x x f

( )

[

]

[

]

[

1 1

]

2 1

1 1

2 1

1 1

2 1

2

+ − − =

+ − − − + =

− − − − − − + =

x x

x x x

x

x x x

x x

f

Temos f₂(x)ímpar.

12.Seja f

( )

x uma função cujo gráfico para x≥0, tem o aspecto indicado na figura. Completar esse gráfico no domínio x<0 se:

(a) f é par (b) f é ímpar

(a) f é par (b) f é ímpar

x y

x y

13. Em cada um dos exercícios determine a fórmula da função inversa. Fazer os

gráficos da função dada e de sua inversa.

a) y=3x+4

3 4

4 3

− =

− =

y x

y x

Assim, a função f(x)=3x+4 tem com função inversa a função

( )

3

4 − = x x

g . O gráfico

-3 -2 -1 1 2 3 4

-3 -2 -1 1 2 3 4

x f(x)=3x+4

g(x)=(x-4)/3

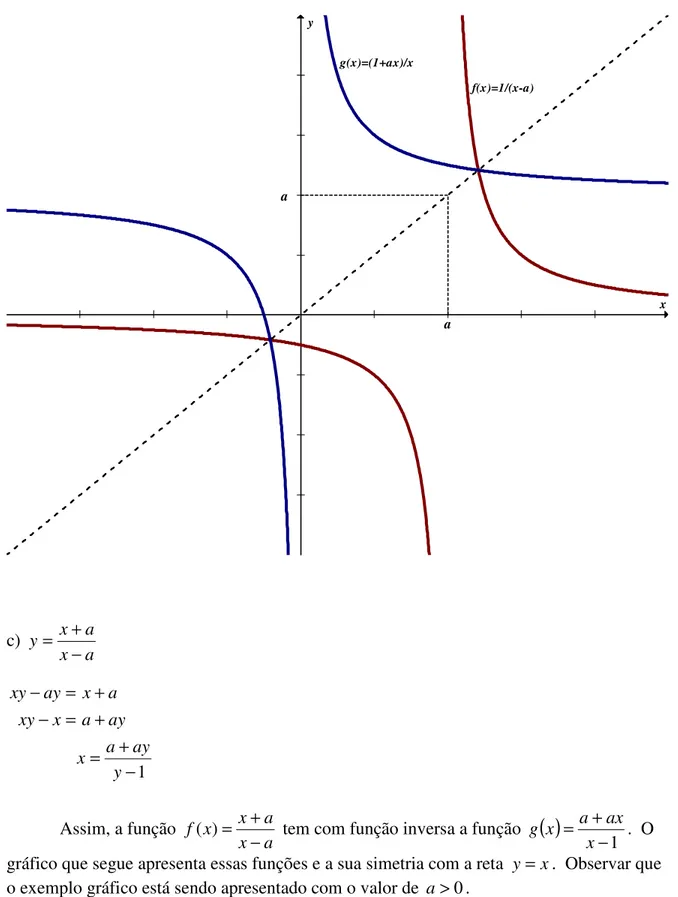
b)

a x y

−

= 1

(

)

y ay x

ay xy

a x y

+ = = −

= −

1 1 1

Assim, a função

a x x f

−

= 1

)

( tem com função inversa a função

x ax x

g( )= 1+ . O

gráfico que segue apresenta essas funções e a sua simetria com a reta y= x. Observar que

x y

f(x)=1/(x-a) g(x)=(1+ax)/x

a

a

c)

a x

a x y

− + =

1

− + =

+ = −

+ = −

y ay a x

ay a x xy

a x ay xy

Assim, a função

a x

a x x f

− + =

)

( tem com função inversa a função

( )

1

− + =

x ax a x

g . O

gráfico que segue apresenta essas funções e a sua simetria com a reta y= x. Observar que

x f(x)=(x+a)/(x-a)

g(x)=(a+ax)/(x-1)

a

a

d) = 1, x>0

x y

0 ,

1 1

> =

=

y y x xy

Assim, a função =1, x>0

x

y tem com função inversa a função

( )

x x

g = 1. O

gráfico que segue apresenta essas funções e a sua simetria com a reta y= x. Observar que

as funções coincidem.

1 2 3 4 5

1 2 3 4 5 6

x y

e) y= x−1, x≥1

0 ,

1 1

2 2

≥ +

= − =

y y

x x y

Assim, a função y= x−1, x≥1 tem com função inversa a função

( )

2 1, 0

≥ +

=x x

x

g . O gráfico que segue apresenta essas funções e a sua simetria com a

reta y= x.

1 2 3 4

1 2 3 4

x y

1 , 1 ) (x= x− x≥

f

0 , 1 ) (_x=x2_{+ x≥}

g

f) y=− a−x, x≤a 0 ,

2 2

≤ − =

− =

y y a x

x a y

Assim, a função f(x)=− a−x,x≤a tem com função inversa a função

( )

2, 0

≤ −

=a x x

x

g . O gráfico que segue apresenta essas funções e a sua simetria com a

x

a

a

a x x a

y=− −, ≤

( )_x=a−x2,_x≤0

g

g) 0

1 2

2

≥ +

= x

x x y

(

)

1 0

, 1 1 1 1

2 2

2 2

2 2

< ≤ − = − − =

− − =

− = −

− = −

= +

y y y y

y x

y y x

y y

x

y x yx

x y yx

Assim, a função 0

1 )

( ₂

2

≥ +

= x

x x x

f tem como inversa a função

1 0

, 1 )

( ≤ <

−

= x

x x x

g . O gráfico que segue apresenta essas funções e a sua simetria com

x y

0 1 ) ( 2

2

≥ +

= x

x x x f

1 0 , 1 )

( ≤< −

= x

x x x g

h) 2 4, 0

≤ −

=x x

y

4 4 2

+ − =

+ =

y x

y x

( )

x =− x+4, x≥−4

g

Assim, a função f(x)=x2−4, x≤0 tem como inversa a função

( )

x =− x+4, x≥−4

g . O gráfico que segue apresenta essas funções e a sua simetria

x

0 , 4

2_{− ≤}

=x x

y

( )x=−x+4, x≥−4

g

i) 2 4, 0

≥ −

= x x

y

4 4 2

+ =

+ =

y x

y x

4 ,

4 )

(x = x+ x≥−

g

Assim, a função 2 4, 0

≥ −

=x x

y tem como inversa a função

4 ,

4 )

(x = x+ x≥−

g . O gráfico que segue apresenta essas funções e a sua simetria com

x y

0 , 4

2_{− ≥}

=x x y

4 , 4 ) (x=x+ x≥−

g

14.Mostre que a função

( )

1 2 2 − + = = x x x f

y coincide com a sua inversa, isto é, x= f

( )

y

ou f

[

f

( )

x

]

=x.

(

2 1

)

2

2 2 2 2 2 1 , 1 2 2 + = − + = − + = − ≠ − + = y y x y x xy x y yx x x x y

( )

y f y y x = − + = 1 2 2 com 2 1 ≠ y ou

( )

[

]

x x

x x x x x x x x x x x x x x f x f

f ⋅ − =

15.Dada a função

( )

₂

1 x x x

f y

+ =

= definida para todo x real, demonstrar que sua

inversa é a função

( )

2

1 y

y y

g x

− =

= definida para y <1

(

2

)

2

2

2 2 2 2

2 2 2 2

2 2 2

2

1 1

1

y y x

y x y x

x y x y

x x y

x x y

= −

= + −

= +

+ =

+ =

2 2 2 2

1 1

y y x

y y x

− =

− =

considerando-se que

(

) (

)

1 1

0 1

1

0

1 2

< < −

≥ + −

≥ −

y y y y

ou y <1

16.Dada

( )

> ≤ ≤ < =

9 ,

27

9 1

, 1 ,

2

x x

x x

x x x

f

verifique que f tem uma função inversa e encontre f −1

( )

x .

Para x<1, temos y= x.

Para 1≤x≤9, temos y= x2 ∴ x= y

2 2

2 2 2

27 27

27 27

= =

⋅ = =

y y

x

x y

x y

Assim,

( )

> ≤ ≤ < =

81 ,

27

81 1

, 1 ,

2

y y

y y

y y y

g ou

( )

> ≤ ≤ < =

−

81 ,

27

81 1

, 1 ,

2 1

x x

x x

x x x f

17. Se f(x) e g(x) são periódicas de período T, prove que: (a) h(x)= f(x)+g(x) tem período T.

(b) h(x)= f(x)⋅g(x) é periódica de período T.

(c) , ( ) 0

) (

) ( )

( = g x ≠

x g

x f x

h para todo x é periódica de período T.

Se f(x) é periódica de período T temos que existe um número real T ≠0

tal que f(x+T)= f(x) para todo x∈D(f).

Se g(x) é periódica de período T temos que existe um número real T ≠0 tal que g(x+T)= g(x) para todo x∈D(g).

Assim:

(a) h(x)= f(x)+g(x)= f(x+T)+g(x+T)=h(x+T) para o número real T ≠0 com )

(f g

D

x∈ + . Portanto h(x)= f(x)+g(x) é periódica de período T.

(b) h(x)= f(x)⋅g(x)= f(x+T)⋅g(x+T)=h(x+T) para o número real T ≠0 com )

(fg D

x∈ . Portanto h(x)= f(x)⋅g(x) é periódica de período T.

(c) ( ), ( ) 0

) (

) ( ) (

) ( )

( = + + ≠

+ + =

= h x T g x T

T x g

T x f x g

x f x

h para o número real T ≠0 com

) /

(f g

D

x∈ . Portanto h(x)= f(x)/g(x) é periódica de período T.

18. Se f(x) é periódica de período T, prove que 3T também é período de f.

Se f(x) é periódica de período T temos que existe um número real T ≠0

Aplicando novamente a definição, temos ) ( ) ( ) ) (( ) 2

(x T f x T T f x T f x

f + = + + = + = . Dessa forma, x+2T∈D(f). Repetindo

o raciocínio, vem:

) ( ) 2 ( ) ) 2 (( ) 3

(x T f x T T f x T f x

f + = + + = + = , para todo x∈D(f).

Podemos concluir, então, que 3T é período da função f(x).

19. Sabendo que f(x) é uma função par e periódica de período T=4, complete o seu

gráfico.

Segue o gráfico da solução.

-6 -5 -4 -3 -2 -1 1 2 3 4 5 6

-2 -1 1 2 3 4 5 6

x y

20. Se

( )

x

x

f =2 , mostre que f

(

x

)

f

(

x

)

f

( )

x

2 15 1

3 − − =

+

(

)

( )

2 15 2 2 15 2

1 16 2 2 1 8 2 2 2 2

2 2 15 2

2

1 3

1 3

x f

x x

x x

x x

x

= =

− =

− =

− = −

− − +

21. Seja

( )

x =

(

ax +a−x

)

2 1

ϕ e

( )

x =

(

ax −a−x

)

2 1

ψ . Demonstrar que:

(

x y

)

ϕ

( ) ( )

x

ϕ

y

ψ

( )

x

ψ

( )

y

Temos,

( ) ( )

( )

( )

(

) (

)

(

) (

)

(

)

(

)

(

)

(

)

(

)

(

x y

)

a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a y x y x y x y x y x y x y x x y y x y x y x x y y x y x y x y x y x y x y x y x y x y x y y x x y y x x + = + = + = + − − + + + + = − − − + + + + = − − + + + = = + − − + − − + − − − − + − − − − + − − − − − − − − − − − −

ϕ

ψ

ψ

ϕ

ϕ

2 1 2 2 4 1 4 1 . . . . 4 1 . . . . 4 1 2 1 . 2 1 2 1 . 2 1 . .

(

x y

)

ϕ

( )

x

ψ

( )

y

ϕ

( )

y

ψ

( )

x

ψ

+ = . + .

Temos,

( )

( )

( )

( )

(

) (

)

(

) (

)

(

)

(

)

( )

(

)

(

x y

)

a a a a a a a a a a a a a a a a a a a a x y y x y x y x y x y x y x x y x y y x y x y x y x y x x x y y y y x x + = − = − = − + − + − + − = − + + − + = = + + − + − − + − − + − − + − − + − − + − − − − ψ ψ ϕ ψ ϕ 2 1 2 2 4 1 4 1 2 1 . 2 1 2 1 . 2 1 . .

22. Construir o gráfico das seguintes funções exponenciais.

a) x

a

y = , se ,

(

2,718

)

2 1 ,

2 =

= e e

-4 -3 -2 -1 1 2 3 4 5

-2 -1 1 2 3 4 5 6

x

x

y

=

2

-4 -3 -2 -1 1 2 3 4 5

-2 -1 1 2 3 4 5 6

x y

x y =

-4 -3 -2 -1 1 2 3 4 5

-2 -1 1 2 3 4 5 6

x y

x

e

y =

b) x

y=101

-4 -3 -2 -1 1 2 3 4 5

-2 -1 1 2 3 4 5 6

x y

x

y ₁₀1

c) y=e

-2 -1 1 2

-1 1

x y

2

x

e

y₌ −

d) x

y=−2

-2 -1 1 2

-2 -1 1

x y

x

y=−2

23. Dada

( )

x x x

+ − =

1 1 lg

ϕ

. Verifique a igualdade

( )

( )

+ + =

+

ab b a b

a

1

( )

( )

(

) (

)

(

) (

)

( )

a

( )

b b a ab b a ab b a ab ab ab b a ab b a ab ab ab b a ab b a ab b a ab b a ab b a ab a b b a b a b b a a b b a a b a

ϕ

ϕ

ϕ

ϕ

ϕ

+ = + + + − − + = + + + + ⋅ + − − + = + + + + ⋅ + + − = + + + + + − = + + + + + + − − = + + − − = + − + − = + − + + − = + 1 1 lg 1 1 1 1 lg 1 1 1 1 lg 1 1 1 1 lg 1 1 1 lg 1 1 1 1 lg 1 1 . 1 1 lg 1 1 lg 1 1 lg

24. Dado f

( )

x =logx e

( )

3

x x

g = . Forme as expressões.

a) f

[

g

( )

2

]

( )

[

2

]

[ ]

23

( )

8 log8

= =

= f f

g f

b) f

[

g

( )

a

]

, a>0

( )

[

g a

]

f

[ ]

a a a

f 3 log 3 3log

= =

=

c) g

[

f

( )

a

]

, a>0

( )

[

]

[

]

(

)

3 log

loga a

g a f

g = =

25. Construir o gráfico das seguintes funções logarítmicas.

-3 -2 -1 1 2

-4 -3 -2 -1 1 2 3

x f(x)=ln(-x)

b) y =lnx

-3 -2 -1 1 2

-4 -3 -2 -1 1 2 3

x y

c) y =ln

(

x+1

)

-2 -1 1 2

-3 -2 -1 1 2 3

x y

f(x)=ln (x+1)

d) y=log_a x se a=10, 2 e 12

-1 1 2 3 4

-2 -1 1 2

x y

-1 1 2 3 4

-2 -1 1 2

x

f(x)=log

2

x

-1 1 2 3 4

-2 -1 1 2

x y

f(x)=log

1/2

x

-1 1 2 3 4

-2 -1 1 2

x y

f(x)=x lnx

26. Se f

( )

x =arctg x prove que

( )

( )

− + =

+

xy y x f y f x f

1 Temos que:

( )

( )

− + =

− +

= =

xy y x tg arc xy

y x f

y tg arc y f

x tg arc x f

1 1

Portanto,

( )

( )

− + =

− +

= =

xy y x f tg xy

y x

y f tg y

x f tg x

Usando a fórmula trigonométrica b tg a tg b tg a tg b a tg . 1 ) ( − + =

+ , vem

(

)

( )

( )

( )

( )

xy

y x y f tg x f tg y f tg x f tg y f x f tg − + = − + = + 1 . 1 ) ( ) ( . Portanto, − + = − + = + xy y x f xy y x tg arc y f x f 1 1 ) ( ) ( .

27. Prove que arctg a−arccotg b=arctg b−arccotg a.

Por definição temos que:

a tg arc a

g

arc = −

2

cot

π

(1)

b tg arc gb

arc = −

2

cot

π

(2)

Fazendo a subtração (1) –(2) temos:

a tg arc b tg arc b tg arc a tg arc b g arc a g

arc − = − − − = −

2 2

cot

cot

π

π

.

Portanto, a g arc b tg arc b g arc a tg

arc − cot = − cot .

28. Dado f

( )

θ

=tg

θ

. Verifique a igualdade.

( )

( )

( )

[

]

2 1 2 2

θ

θ

θ

f f f − =

Temos que mostrar que:

(

)

(

)

(

)

b tg a tg b tg a tg b b sen a a sen b b sen a a sen b sen a sen b a b sen a b a sen b a b a sen b a tg . 1 cos . cos 1 cos cos . cos . cos . cos cos . cos − + = − + = − + = + + = +

Fazendo a=b=θ vem:

[

]

2 1 2 2

θ

θ

θ

tg tg tg − = .

29. Seja f

( )

x =arccos

(

log₁₀ x

)

. Calcular.

(

)

(

)

( )

π

= − = = 1 cos 10 1 log cos 10 1 ₁₀ arc arc f

ou n

π

para n inteiro impar.

( )

(

)

π

π

k arc arc f + = = = 2 0 cos 1 log cos 1 ₁₀

com k inteiro.

( )

(

)

1 cos 10 log cos 10 ₁₀ arc arc f = =

=n

π

, n inteiro par ou 2nπ, n∈Ζ.

30. Determinar o domínio das seguintes funções.

a) x x arc y + = 1 2 cos Temos que: 1 1 2 1 ≤ + ≤ − x x

b) y=arc sen

(

log₁₀ x₁₀

)

Temos que:

0 0 10

> >

x x

e

100 1

10 10 10

1 10 log 1

1 1

10

≤ ≤

≤ ≤

≤ ≤

−

− −

x x

x

c)

0 2

2 ≥ =

x sen

x sen y

Assim,

[

] [

] [

]

( )

[

, 2

]

2 3 , 2 , 0 2 ,

π

π

π

π

π

π

π

π

+ ∪

=

∪ ∪

− − ∈

Ζ

∈ n n

f D x

n

31. Construir o gráfico das seguintes funções trigonométricas. Verificar se são

periódicas e, em caso afirmativo, determinar o período.

a) y=senkx,k 2,3,12 e 13

-3π/2 -π -π/2 π/2 π 3π/2

-2 -1 1 2

x y

y=sen 2x

-3π/2 -π -π/2 π/2 π 3π/2

-2 -1 1 2

x y

y=sen 3x

Periódica de período igual a 3 2

π

.

-3π/2 -π -π/2 π/2 π 3π/2

-2 -1 1 2

x y

y=sen [(1/2)x]

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-2 -1 1 2

x

y=sen [(1/3)x]

Periódica de período igual a 6 . π

b) y =k cos x k =2,3,12,13 e 1−

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-2 -1 1 2

x y

y=2 cos x

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-5 -4 -3 -2 -1 1 2 3 4 5

x y

y=3 cos x

Periódica de período igual a 2 π

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y=1/2 cos x

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2

x

y=1/3 cos x

Periódica de período igual a 2 . π

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y= - cos x

Periódica de período igual a 2 . π

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y= 2 cos 2x

Periódica de período igual a

π

.

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y= - cos 2x

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y= (1/2) cos 2x

Periódica de período igual a

π

. Periódica de período igual a

π

.

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2

x

y = sen (x - ππππ/2))))

Periódica de período igual a 2 . π

e) y =cos

(

x+

π

2

)

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y = cos (x + ππππ/2))))

Periódica de período igual a 2 . π

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y = tg (x - 3ππππ/2))))

Periódica de período igual a

π

.

g) y=cotg

(

x+

π

4

)

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y = cotg (x + ππππ/4))))

Periódica de período igual a

π

.

h) y tg x

2 1

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2

x

y = tg (1/2) x

Periódica de período igual a 2 . π

i) y=1+ senx

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2

-3 -2 -1 1 2 3

x y

y = 1 + sen x

Periódica de período igual a 2 . π

-5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2 -3 -2 -1 1 2 3 x y

y = 1 + |sen 2x|

Periódica de período igual a π/2.

32. Dada a função f

( )

x =2senhx−3tg hx, calcule f

( ) ( )

2, f −1 e f

( )

0

( )

0 0 0 . 3 2 2 0 3 0 2 0 0 0 0 0 0 0 = − = + − − − = − = e e e e e e h tg h sen f

33. Prove as identidades.

(a)

(

)

(

)

(

) (

)

(

)

(

)

(

_{e e}

)

e e h u

e e e e e e e e e e e e e e e e e e e e e u h u h tg u u u u u u u u u u u u u u u u u u u u u u u u 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 sec 2 4 2 2 1 1 sec 1 = + = + = + − + − + + = + − − + = + − − = + − − = − − − − − − − − − − − − − (b)

(

)

(

)

(

)

(

_{e e}

)

e e h u

e e e e e e e e e e u h u h g u u u u u u u u u u u u u u 2 2 2 2 2 2 2 2 2 2 2 2 sec cos 2 4 2 2 1 sec cos cot 1 − = − − = − − = − − − + + − = − + − − = − − − − − − − −

34. Defina uma função inversa para y =coshx, para x≤0. Esboce o gráfico.

Temos f :(−∞,0)→[1,+∞), y= f(x)=coshx. A sua inversa será uma função ] 0 , ( ) , 1 [ : 1 −∞ → +∞ − f . Usando 2 cosh y y e e y x − + =

= , podemos escrever ey−2x+e−y =0 ou

0 1 2 2 = + − y y xe e .

1 2

4 4

2 2

2

− ± = − ±

= x x x x

ey .

Como y∈(−∞,0), temos 0<ey <1. Portanto, usamos o sinal negativo, ou seja,

1

2

− − =x x

ey . Tomando o logaritmo natural, vem y=ln(x− x2 −1). A figura que

segue mostra o gráfico da função e da sua inversa no intervalo considerado.

-4 -3 -2 -1 1 2 3 4

-4 -3 -2 -1 1 2 3 4

x y

35. Mostre a validade das expressões:

(

1

)

, 1

ln cos

arg

) hx= x+ x2 − x≥

a ,

Seja y=argcosh x, x≥1 . Por definição temos que x=cosh y, y≥0 e

0 ,

2 ≥

+ =

−

y e

e x

y y

Podemos reescrever a última expressão como:

0 1 2

1 2

2

2

2

= + −

+ =

+

= −

y y

y y

y y

xe e

e e x

e e x

Aplicando a fórmula de Bhaskara vem:

0 ,

1 2

4 4

2 2

2

≥ −

± = − ±

= x x x x y

Sabemos que y≥0 e x≥1, logo, e ≥1 Quando 1 1 1 1 1 1 2 2 < − − > = − + = x x x x x x

Portanto podemos desprezar o sinal

( )

− em (1) e arccosh x=ln

(

x+ x2 −1

)

, x≥1

b) − + = x x x h tg 1 1 ln 2 1

arg −1< x<1

Pela definição

x h tg

y=arg ⇔ x=tg h y. Temos,

(

y y

)

y y

y y y y e e e e x e e e e x − − − − − = + + − =

(

)

(

)

− + = − + = − + = + = − + = − − = + − = + − − x x y x x y x x e x x e x xe e e x xe e e e e x y y y y y y y y y y 1 1 ln 2 1 1 1 ln 2 1 1 1 1 1 1 2 2 2 2 2 2

com −1< x<1.

c) = + −

x x x h 2 1 1 ln sec

arg , 0<x≤1.

x x x x x x e x e xe e x xe xe xe e e x y h x y y y y y y y y y 2 2 2 2 2 1 1 2 1 2 2 2 4 4 2 0 2 2 2 2 sec − ± = − ± = − ± = = + − = + = + + = = − −

Como no exercício anterior consideramos só o sinal +. Tomando o logaritmo, vem

− + = x x y 2 1 1

ln , 0<x≤1.

36. Sendo f

( )

x =cosh x, mostrar que f

[

ln

(

x+ x2 −1

)

]

=x.

(

)

x x x x x x x x x x x = × − + − = × − + − + = 2 1 1 1 2 2 1 1 1 2 2 2 2 2 2 2

37. Mostre que as funções senh x, tgh x, cotgh x e cosech x são ímpares.

(i) 2 ) ( x x e e senhx x f − − = = e ) ( 2 2 ) ( )

( x senh x e e e e f x

f x x x x − = − − = − = − = − − − .

(ii) _{x x}

x x e e e e tghx x f ₋ − + − = = ) ( e ) ( ) ( )

( f x

e e e e e e e e x tgh x

f _{x x}

x x x x x x − = + − − = + − = − = − ₋ − − − .

(iii) _{x x}

x x e e e e ghx x f ₋ − − + = =cot ) ( e ) ( ) ( cot )

( f x

e e e e e e e e x gh x

f _{x x}

x x x x x x − = − + − = − + = − = − ₋ − − − .

(iv) _{x x}

e e echx x f ₋ − =

=cos 2

) ( e ) ( 2 2 ) ( cos )

( f x

e e e e x ech x

f _{x x x x} =−

− − = − = − = − _{− −} .

38. Mostre que as funções cosh x e sech x são pares

(i) 2 cosh ) ( x x e e x x f − + = = e ) ( 2 2 ) cosh( )

( x x e e e e f x

(ii) _{x x}

e e hx x

f ₋

+ =

=sec 2

) (

e

) ( 2

2 )

( sec )

( f x

e e e e x h x

f _{x x x x} =

+ = + = − =

− _{− −} .

39. Analisar a função

( )

_{24 3} 2

x x x

f = − e verificar a possibilidade de representar uma

função receita total. Em caso afirmativo identifique a função demanda e responda: (a) Qual a quantidade demandada quando o preço unitário é R$ 5,00?

(b) Qual é o preço do produto quando a receita é máxima?

A função receita é dada por R= p⋅q sendo p = preço eq = demanda. Supondo

que x = preço, a função demanda é dada por q=24−3x sendo f

( )

x =24x−3x2 a função receita total.

a)

9 15 24

5 3 24 5

= − =

⋅ − = =

q q q p

b)

A função receita total é uma função do segundo grau e, portanto, o seu valor

máximo está no seu vértice em x=4, ou seja, o preço de R$ 4,00.

40. As funções de demanda e oferta de um determinado produto no mercado são dadas por

p

qd =15−4 e qo =6p−1, respectivamente.

(a) Determine o preço de equilíbrio.

(b) Represente graficamente as funções demanda e oferta, mostrando o ponto de equilíbrio. Esboce os dois gráficos juntos.

a) O preço de equilíbrio é dado por:

0

q q_d =

6 , 1 16 10

15 1 6

4

1 6 4 15

= =

− − = −

− = −

p p p p

p p

ou seja 61 unidades monetárias. ,

-1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

-1 1 2 3 4

p

41. Uma imobiliária cobra uma comissão de 12% do valor da venda de um imóvel mais 00

, 25 $

R fixo para as despesas de correio e divulgação. Denote por x o valor do imóvel (em reais) e por f(x) o valor cobrado pela imobiliária.

(a) Descreva a função f(x).

(b) Qual o valor recebido pela imobiliária na venda de um imóvel por 00

, 000 . 185 $

R ?

(a) Considerando:

x = valor do imóvel

( )

x

f = valor cobrado pela imobiliária

temos:

( )

25

25 3

+

= x

x

f .

(b) 185.000 25 22.225

25 3 ) 000 . 185

( = ⋅ + =

f ou seja R$ 22.225,00.

42. O preço de venda de um produto é de R$27,00. A venda de 100 unidades dá um lucro

de R$260,00. Sabendo-se que o custo fixo de produção é de R$540,00 e que o custo variável é proporcional ao número de unidades produzidas, determine:

(a) A função receita total.

(a) A função receita é dada por R

( )

q =27.q

(b) Temos que a função lucro é dada por

( )

q C

( )

q R

L= − _t

sendo que C_t

( )

q =540+C_vq. Assim,

(

)

540 27

540 27

− − =

+ − =

q C q

q C q

L

v v

Considerando-se que L(100)=260 vem:

19

260 540 2700 100

540 100 100

. 27 260

=

− − =

− ⋅ − =

v v

v

C C

C

Assim o custo variável de uma unidade é dado por R$ 19,00 e a função custo variável é dada por C_v

( )

q =19.q. Temos, C_v

(

2000

)

=19.2000=38000, ou seja, R$38.000,00.

(c)

( )

000 3

8 000 24

540 23460 8

540 8

23460

540 8

= =

+ =

− =

− =

q q q

q q q L

(43) Uma indústria comercializa um certo produto e tem uma função custo total, dada por 700

20 )

( 2

+ +

= x x

x

C , sendo x o número de unidades produzidas. A função receita total é

dada por R(x)=200x. Determine:

(a) O lucro para a venda de 100 unidades.

(b) Em que valor de x acontecerá o lucro máximo?

(a)

( )

( )

( )

700 180

700 20

200

2 2

− +

− =

− − − =

− =

x x

x x

x x C x R x L

(

)

7300

700 000 18 000 10 100

=

− +

− =

ou seja RS/ 7.300,00.

(b) A função lucro é uma função do segundo grau, assim o seu valor máximo encontra-se no encontra-seu vértice, ou encontra-seja, em x=90.

(44) Determinar graficamente a algebricamente o equilíbrio do mercado considerando as seguintes funções de demanda e oferta:

(a)

− =

− =

1 6

4 10

P Q

P Q

s d

(b)

− =

− =

1 4

4 2

P Q

P Q

s d

(a) Temos:

1 , 1 10 11

1 6 4 10

= =

− = −

P P P P

O gráfico que segue apresenta a solução gráfica. Observe que é indiferente para a solução gráfica a posição das variáveis no sistema de eixos.

-1 1 2 3 4

-1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

p q

b)

1

2 6 4 2

20 16 4 0 5 4

1 4 4

2

2

=

± − = + ± − = = − +

− = −

p p p p

-1 1 2 3 4

-1 1 2 3 4

p q

(45) Uma caixa sem tampa na forma de um paralelepípedo tem um volume de ₁₀ 3

cm . O

comprimento da base é o dobro da largura. O material da base custa R$ 2,00 por 2

m ao

passo que o material das laterais custa R$ 0,02 por 2

m . Expressar o custo total do material

em função da largura da base.

Seja x a largura da base e h a altura da caixa. Temos,

2 2

3

5 10 2

10 2

x h h x

cm h

x x V

= = = × × =

(

)

. 10

6 4

5 12 , 0 4

6 02 , 0 4

2 2 2 02 , 0 2 2

2

2 2

2

x x

C

x x x

xh x

h x xh

x x C

t t

+ =

⋅ +

=

⋅ + =

⋅ ⋅ + +

× × =

(46) Traçar o gráfico das funções trigonométricas. Comparar cada conjunto

identificando a transformação ocorrida. Identificar domínio, conjunto imagem, máximos e mínimos, crescimento e decrescimento.

(a) f

( )

x =sen x g

( )

x =2sen x h

( )

x sen x

2 1

=

-3π/2 -π -π/2 π/2 π 3π/2

-2 -1 1 2

x g(x)

h(x)

f(x)

( )

f D

( )

g D

( )

h

D = = .

( )

[

1,1

]

Im f = − Im

( )

g =

[

−2,2

]

( )

= −

2 1 , 2 1

Im h .

As funções assumem valores máximos e mínimos em pontos com x coincidentes.

Os intervalos de crescimento e decrescimento coincidem.

De f para g houve uma expansão vertical e de f para h uma contração

vertical.

(b) f

( )

x =sen x g

( )

x = sen2x h

( )

x =sen x

2 1

-3π/2 -π -π/2 π/2 π 3π/2

-2 -1 1 2

x y

g(x)

h(x)

f(x)

( )

f D

( )

g D

( )

h

D = =

( )

f Im

( )

g Im

( )

h

Im = =

( )

( )

( )

= + ∈Ζ

Ζ ∈ +

=

Ζ ∈ +

=

k k x

h

k k x

g

k k x

f

, 4

, 4

, 2 2

π

π

π

π

π

π

Pontos de mínimo:

( )

( )

( )

=− + ∈Ζ

Ζ ∈ +

=

Ζ ∈ +

− =

k k x

h

k k x

g

k k x

f

, 4

, 4 3

, 2 2

π

π

π

π

π

π

Intervalos de crescimento e decrescimento

:

f Crescimento em −

π

+ k

π

π

+2k

π

k∈Ζ

2 , 2

2 e decrescimento em

Ζ ∈ +

+ k

π

π

k

π

k

π

2 2 3 , 2

2 .

:

g Crescimento em −

π

+k

π

π

+k

π

k∈Ζ

4 ,

4 e decrescimento em

Ζ ∈ +

+k

π

π

k

π

k

π

4 3 ,

4 .

:

h Crescimento em

[

−

π

+4k

π

,

π

+4k

π

]

k∈Ζ decrescimento em

[

π

+4k

π

,3

π

+4k

π

]

k∈Ζ.

-3π/2 -π -π/2 π/2 π 3π/2

-4 -3 -2 -1 1 2 3 4

x

g(x)

h(x)

f(x)

( )

f D

( )

g D

( )

h

D = = .

( )

[

1,1

]

Im f = − Im

( )

g =

[

2,4

]

Im

( )

g =

[

−4,−2

]

.

De f para g houve um deslocamento vertical para cima e de f para h houve

um deslocamento vertical para baixo.

Os pontos de máximo e mínimo coincidem para f , g e h, bem como os

intervalos de crescimento e de decrescimento.

(d) f

( )

x =cosx g

( )

x = cos

(

x+2

)

h

( )

x =cos

(

x−2

)

-3π/2 -π -π/2 π/2 π 3π/2

-1 1

x y

g(x)

h(x)